| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | ||
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
| 1 | Trovare la Derivata — d/dx | натуральный логарифм x | |
| 2 | Вычислим интеграл | интеграл натурального логарифма x по x | |
| 3 | Trovare la Derivata — d/dx | e^x | |
| 4 | Вычислим интеграл | интеграл e^(2x) по x | |
| 5 | Trovare la Derivata — d/dx | 1/x | |
| 6 | Trovare la Derivata — d/dx | x^2 | |
| 7 | Trovare la Derivata — d/dx | 1/(x^2) | |
| 8 | Trovare la Derivata — d/dx | sin(x)^2 | |
| 9 | Trovare la Derivata — d/dx | sec(x) | |
| 10 | Вычислим интеграл | интеграл e^x по x | |
| 11 | Вычислим интеграл | интеграл x^2 по x | |
| 12 | Вычислим интеграл | интеграл квадратного корня из x по x | |
| 13 | Trovare la Derivata — d/dx | cos(x)^2 | |
| 14 | Вычислим интеграл | интеграл 1/x по x | |
| 15 | Вычислим интеграл | интеграл sin(x)^2 по x | |
| 16 | Trovare la Derivata — d/dx | x^3 | |
| 17 | Trovare la Derivata — d/dx | sec(x)^2 | |
| 18 | Вычислим интеграл | интеграл cos(x)^2 по x | |
| 19 | Вычислим интеграл | интеграл sec(x)^2 по x | |
| 20 | Trovare la Derivata — d/dx | e^(x^2) | |
| 21 | Вычислим интеграл | интеграл в пределах от 0 до 1 кубический корень из 1+7x по x | |
| 22 | Trovare la Derivata — d/dx | sin(2x) | |
| 23 | Trovare la Derivata — d/dx | tan(x)^2 | |
| 24 | Вычислим интеграл | интеграл 1/(x^2) по x | |
| 25 | Trovare la Derivata — d/dx | 2^x | |
| 26 | График | натуральный логарифм a | |
| 27 | Trovare la Derivata — d/dx | cos(2x) | |
| 28 | Trovare la Derivata — d/dx | xe^x | |
| 29 | Вычислим интеграл | интеграл 2x по x | |
| 30 | Trovare la Derivata — d/dx | ( натуральный логарифм от x)^2 | |
| 31 | Trovare la Derivata — d/dx | натуральный логарифм (x)^2 | |
| 32 | Trovare la Derivata — d/dx | 3x^2 | |
| 33 | Вычислим интеграл | интеграл xe^(2x) по x | |
| 34 | Trovare la Derivata — d/dx | 2e^x | |
| 35 | Trovare la Derivata — d/dx | натуральный логарифм 2x | |
| 36 | Trovare la Derivata — d/dx | -sin(x) | |
| 37 | Trovare la Derivata — d/dx | 4x^2-x+5 | |
| 38 | Trovare la Derivata — d/dx | y=16 корень четвертой степени из 4x^4+4 | |
| 39 | Trovare la Derivata — d/dx | 2x^2 | |
| 40 | Вычислим интеграл | интеграл e^(3x) по x | |
| 41 | Вычислим интеграл | интеграл cos(2x) по x | |
| 42 | Trovare la Derivata — d/dx | 1/( квадратный корень из x) | |
| 43 | Вычислим интеграл | интеграл e^(x^2) по x | |
| 44 | Вычислить | e^infinity | |
| 45 | Trovare la Derivata — d/dx | x/2 | |
| 46 | Trovare la Derivata — d/dx | -cos(x) | |
| 47 | Trovare la Derivata — d/dx | sin(3x) | |
| 48 | Trovare la Derivata — d/dx | 1/(x^3) | |
| 49 | Вычислим интеграл | интеграл tan(x)^2 по x | |
| 50 | Вычислим интеграл | интеграл 1 по x | |
| 51 | Trovare la Derivata — d/dx | x^x | |
| 52 | Trovare la Derivata — d/dx | x натуральный логарифм от x | |
| 53 | Trovare la Derivata — d/dx | x^4 | |
| 54 | Оценить предел | предел (3x-5)/(x-3), если x стремится к 3 | |
| 55 | Вычислим интеграл | интеграл x^2 натуральный логарифм x по x | |
| 56 | Trovare la Derivata — d/dx | f(x) = square root of x | |
| 57 | Trovare la Derivata — d/dx | x^2sin(x) | |
| 58 | Вычислим интеграл | интеграл sin(2x) по x | |
| 59 | Trovare la Derivata — d/dx | 3e^x | |
| 60 | Вычислим интеграл | интеграл xe^x по x | |
| 61 | Trovare la Derivata — d/dx | y=x^2 | |
| 62 | Trovare la Derivata — d/dx | квадратный корень из x^2+1 | |
| 63 | Trovare la Derivata — d/dx | sin(x^2) | |
| 64 | Вычислим интеграл | интеграл e^(-2x) по x | |
| 65 | Вычислим интеграл | интеграл натурального логарифма квадратного корня из x по x | |
| 66 | Trovare la Derivata — d/dx | e^2 | |
| 67 | Trovare la Derivata — d/dx | x^2+1 | |
| 68 | Вычислим интеграл | интеграл sin(x) по x | |
| 69 | Trovare la Derivata — d/dx | arcsin(x) | |
| 70 | Оценить предел | предел (sin(x))/x, если x стремится к 0 | |
| 71 | Вычислим интеграл | интеграл e^(-x) по x | |
| 72 | Trovare la Derivata — d/dx | x^5 | |
| 73 | Trovare la Derivata — d/dx | 2/x | |
| 74 | Trovare la Derivata — d/dx | натуральный логарифм 3x | |
| 75 | Trovare la Derivata — d/dx | x^(1/2) | |
| 76 | Trovare la Derivata — d/d@VAR | f(x) = square root of x | |
| 77 | Trovare la Derivata — d/dx | cos(x^2) | |
| 78 | Trovare la Derivata — d/dx | 1/(x^5) | |
| 79 | Trovare la Derivata — d/dx | кубический корень из x^2 | |
| 80 | Вычислим интеграл | интеграл cos(x) по x | |
| 81 | Вычислим интеграл | интеграл e^(-x^2) по x | |
| 82 | Trovare la Derivata — d/d@VAR | f(x)=x^3 | |
| 83 | Вычислим интеграл | интеграл 4x^2+7 в пределах от 0 до 10 по x | |
| 84 | Вычислим интеграл | интеграл ( натуральный логарифм x)^2 по x | |
| 85 | Trovare la Derivata — d/dx | логарифм x | |
| 86 | Trovare la Derivata — d/dx | arctan(x) | |
| 87 | Trovare la Derivata — d/dx | натуральный логарифм 5x | |
| 88 | Trovare la Derivata — d/dx | 5e^x | |
| 89 | Trovare la Derivata — d/dx | cos(3x) | |
| 90 | Вычислим интеграл | интеграл x^3 по x | |
| 91 | Вычислим интеграл | интеграл x^2e^x по x | |
| 92 | Trovare la Derivata — d/dx | 16 корень четвертой степени из 4x^4+4 | |
| 93 | Trovare la Derivata — d/dx | x/(e^x) | |
| 94 | Оценить предел | предел arctan(e^x), если x стремится к 3 | |
| 95 | Вычислим интеграл | интеграл (e^x-e^(-x))/(e^x+e^(-x)) по x | |
| 96 | Trovare la Derivata — d/dx | 3^x | |
| 97 | Вычислим интеграл | интеграл xe^(x^2) по x | |
| 98 | Trovare la Derivata — d/dx | 2sin(x) | |
| 99 | Вычислить | sec(0)^2 | |
| 100 | Trovare la Derivata — d/dx | натуральный логарифм x^2 |
| ГОСТы, СНиПы Карта сайта TehTab.ru Поиск по сайту TehTab.ru | Навигация по справочнику TehTab.ru: главная страница / / Техническая информация/ / Математический справочник/ / Таблицы численных значений. (Таблица квадратов, кубов, синусов ….) + Таблицы Брадиса / / Таблица синусов углов от 0° — 360°. Углы с шагом в 1°. Таблица значений синусов.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Нашли ошибку? Есть дополнения? Напишите нам об этом, указав ссылку на страницу. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
TehTab.ru Реклама, сотрудничество: [email protected] | Обращаем ваше внимание на то, что данный интернет-сайт носит исключительно информационный характер. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Все риски за использование информаци с сайта посетители берут на себя. Проект TehTab.ru является некоммерческим, не поддерживается никакими политическими партиями и иностранными организациями. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Вот почему вам стоит использовать оператор Walrus в Python / Хабр
Выражение присваивания (также известное как оператор walrus) — это функциональность, которая появилась в Python недавно, в версии 3. 8. Однако применение walrus является предметом дискуссий и множество людей испытывают безосновательную неприязнь к нему.
8. Однако применение walrus является предметом дискуссий и множество людей испытывают безосновательную неприязнь к нему.
Под катом эксперт компании IBM Мартин Хайнц*, разработчик и DevOps-инженер, постарается убедить вас в том, что оператор walrus — действительно хорошее дополнение языка. И его правильное использование поможет вам сделать код более лаконичным и читаемым.
*Обращаем ваше внимание, что позиция автора может не всегда совпадать с мнением МойОфис.
Рассмотрим основы
Если вы вдруг не знакомы с оператором := (walrus), давайте для начала рассмотрим некоторые основные случаи использования этого оператора.
В первом примере я покажу вам, как можно использовать оператор walrus, чтобы сократить количество вызовов функции.
Давайте представим функцию func(), которая производит какие-то очень ресурсоемкие расчеты. Она требует много времени для вычисления результатов, поэтому мы не хотим вызывать ее многократно:
# "func" вызывает трижды result = [func(x), func(x)**2, func(x)**3] # Переиспользуем результат функции без разделения кода на несколько строк result = [y := func(x), y**2, y**3]
В первой форме объявления списка, func(x) вызывается трижды, каждый раз возвращая один и тот же результат, который каждый раз тратил ресурсы вычислительной машины. Когда мы перепишем выражение с использованием оператора walrus,
Когда мы перепишем выражение с использованием оператора walrus, func() будет вызвана только один раз, присваивая результат вычисления y и повторно используя значение для оставшихся двух элементов списка. Вы можете сказать «Просто добавь y = func(x) перед объявлением списка и тебе не понадобится оператор walrus!». Можно так сделать, но для этого потребуется еще одна дополнительная строка кода и, на первый взгляд, без знания о том, что func(x) очень медленная, может быть неясно, зачем эта переменная нужна.
Если первый пример не убедил вас, вот еще один. Рассмотрим следующие способы объявления списка тоже с ресурсоемкой func():
result = [func(x) for x in data if func(x)] result = [y for x in data if (y := func(x))]
В первой строке func(x) вызывается дважды в каждой итерации. Альтернатива — использовать оператор walrus. Значение рассчитывается однократно — в условном выражении, и используется повторно. .*(not present).*»
m = re.match(pattern1, test)
if m:
print(f»Matched the 1st pattern: {m.group(1)}»)
else:
m = re.match(pattern2, test)
if m:
print(f»Matched the 2nd pattern: {m.group(1)}»)
# ———————
# Или иначе
if m := (re.match(pattern1, test)):
print(f»Matched 1st pattern: ‘{m.group(1)}'»)
elif m := (re.match(pattern2, test)):
print(f»Matched 2nd pattern: ‘{m.group(1)}'»)
.*(not present).*»
m = re.match(pattern1, test)
if m:
print(f»Matched the 1st pattern: {m.group(1)}»)
else:
m = re.match(pattern2, test)
if m:
print(f»Matched the 2nd pattern: {m.group(1)}»)
# ———————
# Или иначе
if m := (re.match(pattern1, test)):
print(f»Matched 1st pattern: ‘{m.group(1)}'»)
elif m := (re.match(pattern2, test)):
print(f»Matched 2nd pattern: ‘{m.group(1)}'»)
Используя walrus мы сократили один и тот же код с 7 до 4 строк, сделав его более читаемым через удаление ненужных if.
Следующий пример — это так называемая идиома «loop-and-half»:
while True: # Loop
command = input("> ")
if command == 'exit': # And a half
break
print("Your command was:", command)
# ---------------------
# Или иначе
while (command := input("> ")) != "exit":
print("Your command was:", command)Обычное решение заключается в использовании бесконечного цикла, в котором управление циклом осуществляется через объявление break. Вместо этого мы можем задействовать оператор walrus, чтобы заново присвоить значение исполненной команды и затем использовать его в условии остановки цикла на той же строке, делая код более явным и коротким.
Вместо этого мы можем задействовать оператор walrus, чтобы заново присвоить значение исполненной команды и затем использовать его в условии остановки цикла на той же строке, делая код более явным и коротким.
Простое упрощение может быть применено также к другому циклу, while — например, в случае чтения файлов построчно или получения данных из сокета.
Суммирование данных прямо на месте
Обратимся к более продвинутым примерам использования оператора walrus. В этот раз рассмотрим возможность суммирования данных прямо по месту применения:
data = [5, 4, 3, 2] c = 0; print([(c := c + x) for x in data]) # c = 14 # [5, 9, 12, 14] from itertools import accumulate print(list(accumulate(data))) # --------------------- data = [5, 4, 3, 2] print(list(accumulate(data, lambda a, b: a*b))) # [5, 20, 60, 120] a = 1; print([(a := a*b) for b in data]) # [5, 20, 60, 120]
В первых двух строках показано, как можно использовать walrus для расчета суммы значений. В этом простом случае функция
В этом простом случае функция accumulate лучше подходит для этой цели (как видно из следующих двух строк). Однако применение itertools с увеличением сложности и объема кода делает его менее читаемым и, по моему мнению, версия с := намного приятнее, чем с lambda.
Если вы все еще не убеждены, посмотрите сводные примеры в документации (например, сложный процент или логистическую карту): они не выглядят читаемыми. Попробуйте переписать их на использование выражения присваивания :=, и они будут смотреться намного лучше.
Именованные значения в f-string
Этот пример показывает возможные случаи и ограничения использования := в сравнении с лучшими практиками.
Если хотите, то можете использовать оператор walrus в f-string:
from datetime import datetime
print(f"Today is: {(today:=datetime.today()):%Y-%m-%d}, which is {today:%A}")
# Today is: 2022-07-01, which is Friday
from math import radians, sin, cos
angle = 60
print(f'{angle=}\N{degree sign} {(theta := radians(angle)) =: . 2f}, {sin(theta) =: .2f}, {cos(theta) =: .2f}')
# angle=60° (theta := radians(angle)) = 1.05, sin(theta) = 0.87, cos(theta) = 0.50
2f}, {sin(theta) =: .2f}, {cos(theta) =: .2f}')
# angle=60° (theta := radians(angle)) = 1.05, sin(theta) = 0.87, cos(theta) = 0.50В первом выражении print используется := для определения переменной today, которая затем повторно используется на той же строке, предотвращая повторный вызов функции datetime.today().
Похожим образом во втором примере объявлена theta переменная, которая затем используется снова для расчета sin(theta) и cos(theta). В данном случае в выражении также встречается сочетание символов, которое выглядит как «обратный» walrus. Символ = отвечает за вывод выражения на экран, а в связке с : используется для форматированного вывода значения выражения.
Заметим также, что выражение с оператором walrus требует обрамления в скобки, чтобы внутри f-string оно интерпретировалось корректно.
Any и ALL
Можно использовать функции any() и all() для проверки удовлетворения условию любых или всех значений в итерируемом объекте. А что, если вы захотите также значение, которое оставляет
А что, если вы захотите также значение, которое оставляет any() для возвращаемого значения True (так называемый «свидетель») или же значение, которое не удовлетворило проверке all() (так называемый «контрпример»)?
numbers = [1, 4, 6, 2, 12, 4, 15] # Возвращает только результат логического выражения, не значение print(any(number > 10 for number in numbers)) # True print(all(number < 10 for number in numbers)) # False # --------------------- any((value := number) > 10 for number in numbers) # True print(value) # 12 all((counter_example := number) < 10 for number in numbers) # False print(counter_example) # 12
Обе функции any() и all() используют короткую схему вычисления результата. Это означает, что они остановят вычисление, как только найдут первого «свидетеля» или «контрпример». Поэтому переменная, созданная с помощью оператора walrus, всегда будет давать нам первого «свидетеля»/»контрпример».
Подводные камни и ограничения
Ранее в тексте я пытался мотивировать вас использовать оператор walrus. Полагаю, важно также предупредить о некоторых недостатках и ограничениях в отношении этого оператора.
В предыдущем примере было показано, что короткая схема может быть полезна для захвата значений в any()/all(), но в некоторых случаях это может привести к неожиданным результатам:
for i in range(1, 100):
if (two := i % 2 == 0) and (three := i % 3 == 0):
print(f"{i} is divisible by 6.")
elif two:
print(f"{i} is divisible by 2.")
elif three:
print(f"{i} is divisible by 3.")
# NameError: name 'three' is not definedВо фрагменте выше приведено условное выражение с 2 объединенными присваиваниями, проверяющими, на сколько делится число — на 2, 3 или 6 в порядке очередности (если условие 1 верно, то 2 и 3 тоже верно). На первый взгляд это может казаться интересным трюком, но благодаря короткой схеме вычисления, если выражение (two := i % 2 == 0) будет неверным, то следующее условие будет пропущено, а переменные останутся не определены или будут иметь неактуальные значения от предыдущей итерации. .*(present).*»
for test in tests:
m = re.match(pattern1, test)
if m:
print(f»Matched the 1st pattern: {m.group(1)}»)
else:
m = re.match(pattern2, test)
if m:
print(f»Matched the 2nd pattern: {m.group(1)}»)
# Соответствие первому шаблону: thing
# Соответствие второму шаблону: present
for test in tests:
if m := (re.match(pattern1, test) or re.match(pattern2, test)):
print(f»Matched: ‘{m.group(1)}'»)
# Соответствие: ‘thing’
# Соответствие: ‘present’
.*(present).*»
for test in tests:
m = re.match(pattern1, test)
if m:
print(f»Matched the 1st pattern: {m.group(1)}»)
else:
m = re.match(pattern2, test)
if m:
print(f»Matched the 2nd pattern: {m.group(1)}»)
# Соответствие первому шаблону: thing
# Соответствие второму шаблону: present
for test in tests:
if m := (re.match(pattern1, test) or re.match(pattern2, test)):
print(f»Matched: ‘{m.group(1)}'»)
# Соответствие: ‘thing’
# Соответствие: ‘present’
Мы уже рассматривали версию этого фрагмента в разделе «Рассмотрим основы», где использовали if/elif вместе с оператором walrus. Здесь же представлено упрощение через схлопывание условия в один if.
Если вы только познакомились с оператором walrus, то можете заметить, что он заставляет область видимости переменных вести себя иначе в list comprehensions.
values = [3, 5, 2, 6, 12, 7, 15] tmp = "unmodified" dummy = [tmp for tmp in values] print(tmp) # Как ожидалось, переменная "tmp" не была переопределена.# Она по-прежнему имеет привязку к значению "unmodified" total = 0 partial_sums = [total := total + v for v in values] print(total) # 50
С использованием обычных list/dict/set comprehensions, область видимости переменной цикла остается внутри конструкции и, следовательно, любая существующая переменная с тем же именем останется неизменной. Однако с использованием оператора walrus, переменная из comprehension total остается доступной после вычисления значения конструкции, получая присвоенное значение внутри comprehension.
Когда использование walrus в коде становится более удобным для вас, вы можете попробовать использовать его в других случаях. Но есть один случай, в котором вам не удастся его использовать — выражения с with (менеджером контекста):
class ContextManager:
def __enter__(self):
print("Entering the context...")
def __exit__(self, exc_type, exc_val, exc_tb):
print("Leaving the context. ..")
with ContextManager() as context:
print(context) # None
with (context := ContextManager()):
print(context) # <__main__.ContextManager object at 0x7fb551cdb9d0>
..")
with ContextManager() as context:
print(context) # None
with (context := ContextManager()):
print(context) # <__main__.ContextManager object at 0x7fb551cdb9d0>Когда мы используем обычный синтаксис with ContextManager() as context: ..., контекст привязывается к возвращаемому значению context.enter(), тогда же как при использовании версии с := происходит связь с результатом самого ContextManager(). Зачастую это не важно, потому что context.enter() обычно возвращает self, но в случае, если это не так, будет крайне сложно отладить проблему.
Для более практического примера рассмотрим ниже, что происходит при использовании оператора walrus с контекстным менеджером closing:
from contextlib import closing
from urllib.request import urlopen
with closing(urlopen('https://www.python.org')) as page:
for line in page:
print(line) # Выводится вебсайт в формате HTML
with (page := closing(urlopen('https://www. .*(thing).*", text)) and flag:
print(match.groups()) # ('thing',)
.*(thing).*", text)) and flag:
print(match.groups()) # ('thing',)Здесь нам нужно обрамлять выражение присваивания в скобки для обеспечения гарантии, что результат re.match(...) будет записан в переменную. Если мы этого не сделаем, выражение and будет рассчитано в первую очередь и переменной будет присвоен логический результат выражения.
И наконец, есть некоторая ловушка или скорее легкое ограничение. В данный момент нельзя использовать аннотации типов на той же строке с оператором walrus. Следовательно, если вы хотите определить тип переменной, то выражение следует разделить на 2 строки:
from typing import Optional
value: Optional[int] = None
while value := some_func():
... # Описание действияЗаключительные мысли
Как в случае с любой особенностью синтаксиса языка, злоупотребление оператором walrus может привести к ухудшению ясности и читаемости кода. Не следует внедрять его в коде при каждом удобном случае. Воспринимайте этот оператор как инструмент — будьте осведомлены о его преимуществах и недостатках и используйте его там, где это уместно.
Если хотите ознакомиться с большим количеством практических использований оператора walrus, сверьтесь с его представлением в стандартной библиотеке CPython — все изменения могут быть найдены в этом PR.
Кроме того, я также рекомендую прочитать PEP 572: в нем содержится еще больше примеров, а также обоснование внедрения оператора в стандартную библиотеку.
{-1} (\csc 6)$$$$=(\pi-2)-2+(4-\pi)-(2\pi-4)+(2\pi-6)-(2 \pi-6)$$ $$=-2\pi+4$$
Но данный ответ равен $5\pi-16$. Я перепроверил все основные ветки, и все они кажутся правильными. Где использовал неправильное значение?
- тригонометрия
- проверка решения
- обратная функция
$\endgroup$
8
$\begingroup$
9{-1}$ равно $[-\frac {\pi}{2} , \frac{\pi}{2}]$ , а $6$ принадлежит четвертому квадранту, то есть уже находится в заданной области, пока когда мы вычитаем $2\pi$, получаем $6 — 2\pi$ (а поскольку косекансы обоих этих углов отрицательны, это имеет смысл).
Теперь оценка дает правильный ответ.
$\endgroup$
2
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Обязательно, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
. Исчисление
Исчисление— Предел $\lim_{x \to 0} \dfrac{\sin(1-\cos x)}{x} $
спросил
Изменено 6 лет, 7 месяцев назад
Просмотрено 1к раз
$\begingroup$
$$\lim_{x \to 0} \dfrac{\sin(1-\cos x)}{ x} $$
Что неверно в этом аргументе: когда $x$ стремится к нулю, оба $x$ и $(1-\cos x)$ приближается к $0$. Таким образом, ограничение составляет $1$.
- Как мы можем доказать, что они стремятся к нулю с одинаковой скоростью?
Речь идет не о решении предела, потому что я уже решил его, а о стремлении обеих функций к нулю.
м относительно $$\lim_{x \to 0} \dfrac{\sin x}{x} =1 $$
- исчисление
- реальный анализ
- пределы
- неопределенные формы
$\endgroup$
7
$\begingroup$
Согласно вашему аргументу, $$\lim_{x\to 0}\frac{x}{x}$$ также равно $0$, потому что, когда $x$ приближается к нулю, и $x$, и $x$ приближаются к $0$, таким образом, предел составляет $ 0 $.
$\endgroup$
$\begingroup$
Что не так с этим аргументом ; когда $x$ приближается к нулю, и $x$, и $(1-\cos x)$ приближаются к $0$.
Неправильно то, что и числитель, и знаменатель вашего выражения одновременно достигают $0$, и тогда ваш предел принимает форму $\frac{0}{0}$, что является неопределенным и неубедительным.
СКОРОСТЬ ОБЕИХ ФУНКЦИЙ, ОБРАЩАЮЩИХСЯ К НУЛЮ
В основном вам нужно вычислить производную функции $2$, чтобы увидеть, какая из них достигает $0$ раньше.
Теперь $$\frac{d}{dx}\left(\sin x\right)=\cos x$$ и $$\frac{d}{dx}\left( x \right)= 1$$
И мы знаем, что $\cos x \le 1$ Итак, вы знаете, кто первым дойдет до $0$.
АЛЬТЕРНАТИВНОЕ РЕШЕНИЕ
Однако лучше использовать правильную формулу для пределов и решать ее следующим образом: $$\lim_{x \to 0} \dfrac{\sin(1-\cos x)}{x} $$ $$=\left[\lim_{(1-\cos x) \to 0} \frac{\sin(1-\cos x)}{(1-\cos x)}\right] \cdot \lim_{ x \to 0} \frac{(1-\cos x)}{ x} $$ $$= 1\cdot \lim_{x \to 0} \frac{(1-\cos x)}{ x}$$
А предел имеет более простую форму и имеет вид $\frac{0}{0}$.
Так что лучше применить правило Лопиталя.
$$ \lim_{x \to 0} \frac{(1-\cos x)}{ x}$$ $$= \lim_{x \to 0} \frac{\sin x)}{ 1 }$$ $$= 0$$
Следовательно, можно сказать, что предел равен $0$ по математической строгости.
$\endgroup$
$\begingroup$
Аргумент ошибочен в том смысле, что если и числитель, и знаменатель стремятся к 0, о пределе мало что можно сказать. Помните, что $\frac{0}{0}$ не определено. Важно то, как быстро каждый из них достигает 0,9.2)$. Это становится $ O (x) $ при делении на знаменатель $ x $, так что предел равен $ 0 $.
$\endgroup$
2
$\begingroup$
Что не так с этим аргументом ; когда $x$ приближается к нулю, и $x$, и $(1-\cos x)$ приближаются к $0$.
Таким образом, предел равен 1.2$ стремятся к нулю, но предел равен $+\infty$. 92$ и $x$ стремятся к нулю, но предел равен $0$.
А для $\lim_{x\to 0}\frac {2x}x$ и $2x$, и $x$ стремятся к нулю, но предел равен $2$.Таким образом, и числитель, и знаменатель стремятся к нулю НЕ означают, что дробь стремится к $1$ или к любому другому предварительно выбранному значению.
$\endgroup$
$\begingroup$
Вы правы в том, что $$\lim_{x \to 0} \dfrac{\sin x}{x} =1 .$$
Отсюда также следует, что $$\lim_{x \to 0} \dfrac{\sin(1-\cos x)}{1-\cos x} = \lim_{(1-\cos x) \to 0} \dfrac{\sin(1-\cos x)}{1-\cos x} = 1 .$$
Поэтому
\begin{align} \lim_{x \to 0} \frac{\sin(1-\cos x)}{x} &= \lim_{x \to 0} \left( \frac{\sin(1-\cos x)}{1-\cos x} \cdot \frac{1-\cos x}{x}\right)\\ &= \left( \lim_{x \to 0}\frac{\sin(1-\cos x)}{1-\cos x} \right) \cdot \left( \lim_{x \to 0} \frac{1-\cos x}{x} \right)\\ &= 1 \cdot \left( \lim_{x \to 0} \frac{1-\cos x}{x} \right), \end{выравнивание} при условии, что все эти ограничения существуют (что они и делают).
Итак, теперь вопрос в том, что $$\lim_{x \to 0} \frac{1-\cos x}{x}?$$ 92}2$, так что первая функция приблизительно равна $1$, а вторая $\dfrac x2$.
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Обязательно, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Мэтуэй | Популярные проблемы
1 Найти точное значение грех(30) 2 Найти точное значение грех(45) 3 Найти точное значение грех(30 градусов) 4 Найти точное значение грех(60 градусов) 5 Найти точное значение загар(30 градусов) 6 Найти точное значение угловой синус(-1) 7 Найти точное значение грех(пи/6) 8 Найти точное значение соз(пи/4) 9 Найти точное значение грех(45 градусов) 10 Найдите точное значение sin(pi/3) 11 Найти точное значение арктический(-1) 12 Найти точное значение cos(45 градусов) 13 Найти точное значение cos(30 градусов) 14 Найти точное значение желтовато-коричневый(60) 15 Найти точное значение csc(45 градусов) 16 Найти точное значение загар (60 градусов) 17 Найти точное значение сек(30 градусов) 18 Найти точное значение cos(60 градусов) 19 Найти точное значение соз(150) 20 Найти точное значение грех(60) 21 Найти точное значение cos(pi/2) 22 Найти точное значение загар(45 градусов) 23 Найти точное значение arctan(- квадратный корень из 3) 24 Найти точное значение csc(60 градусов) 25 Найти точное значение сек (45 градусов) 26 Найти точное значение csc(30 градусов) 27 Найти точное значение грех(0) 28 Найти точное значение грех(120) 29 Найти точное значение соз(90) 30 Преобразовать из радианов в градусы пи/3 31 Найти точное значение желтовато-коричневый(30) 32 9235 Преобразовать из радианов в градусы пи/6 36 Найти точное значение детская кроватка(30 градусов) 37 Найти точное значение арккос(-1) 38 Найти точное значение арктический(0) 39 Найти точное значение детская кроватка(60 градусов) 40 Преобразование градусов в радианы 30 41 Преобразовать из радианов в градусы (2 шт. )/3
42 Найти точное значение sin((5pi)/3) 43 Найти точное значение sin((3pi)/4) 44 Найти точное значение желтовато-коричневый (пи/2) 45 Найти точное значение грех(300) 46 Найти точное значение соз(30) 47 Найдите точное значение соз(60) 48 Найти точное значение соз(0) 49 Найти точное значение соз(135) 50 Найти точное значение cos((5pi)/3) 51 Найти точное значение соз(210) 52 Найти точное значение сек(60 градусов) 53 Найти точное значение грех(300 градусов) 54 Преобразование градусов в радианы 135 55 Преобразование градусов в радианы 150 56 Преобразовать из радианов в градусы (5 дюймов)/6 57 Преобразовать из радианов в градусы (5 дюймов)/3 58 Преобразование градусов в радианы 89 градусов 59 Преобразование градусов в радианы 60 60 Найти точное значение грех(135 градусов) 61 Найти точное значение грех(150) 62 Найти точное значение грех(240 градусов) 63 Найти точное значение детская кроватка(45 градусов) 64 Преобразовать из радианов в градусы (5 дюймов)/4 65 Найти точное значение грех(225) 66 Найдите точное значение грех(240) 67 Найти точное значение cos(150 градусов) 68 Найти точное значение желтовато-коричневый(45) 69 Оценить грех(30 градусов) 70 Найти точное значение сек(0) 71 Найти точное значение cos((5pi)/6) 72 Найти точное значение КСК(30) 73 Найти точное значение arcsin(( квадратный корень из 2)/2) 74 Найти точное значение желтовато-коричневый ((5pi)/3) 75 Найти точное значение желтовато-коричневый(0) 76 Оценить грех(60 градусов) 77 Найти точное значение arctan(-(квадратный корень из 3)/3) 78 Преобразовать из радианов в градусы (3 шт. )/4
79 Найти точное значение sin((7pi)/4) 80 Найти точное значение угловой синус(-1/2) 81 Найти точное значение sin((4pi)/3) 82 Найдите точное значение КСК(45) 83 Упростить арктан( квадратный корень из 3) 84 Найти точное значение грех(135) 85 Найти точное значение грех(105) 86 Найти точное значение грех(150 градусов) 87 Найти точное значение sin((2pi)/3) 88 Найти точное значение желтовато-коричневый ((2pi)/3) 89 Преобразовать из радианов в градусы пи/4 90 Найти точное значение sin(pi/2) 91 Найти точное значение сек(45) 92 Найти точное значение cos((5pi)/4) 93 Найти точное значение cos((7pi)/6) 94 Найти точное значение угловой синус(0) 95 Найти точное значение грех(120 градусов) 96 Найти точное значение желтовато-коричневый ((7pi)/6) 97 Найти точное значение соз(270) 98 Найдите точное значение sin((7pi)/6) 99 Найти точное значение arcsin(-( квадратный корень из 2)/2) 100 Преобразование градусов в радианы 88 градусов
Мэтуэй | Популярные задачи
1 Найти точное значение грех(30) 2 Найти точное значение грех(45) 3 Найти точное значение грех(30 градусов) 4 Найдите точное значение грех(60 градусов) 5 Найти точное значение загар(30 градусов) 6 Найти точное значение угловой синус(-1) 7 Найти точное значение грех(пи/6) 8 Найти точное значение соз(пи/4) 9 Найти точное значение грех(45 градусов) 10 Найти точное значение грех(пи/3) 11 Найти точное значение арктический(-1) 12 Найти точное значение cos(45 градусов) 13 Найти точное значение cos(30 градусов) 14 Найти точное значение желтовато-коричневый(60) 15 Найти точное значение csc(45 градусов) 16 Найти точное значение загар(60 градусов) 17 Найти точное значение сек(30 градусов) 18 Найти точное значение cos(60 градусов) 19 Найти точное значение соз(150) 20 Найти точное значение грех(60) 21 Найти точное значение cos(pi/2) 22 Найти точное значение загар(45 градусов) 23 Найти точное значение arctan(- квадратный корень из 3) 24 Найти точное значение csc(60 градусов) 25 Найти точное значение сек (45 градусов) 26 Найти точное значение csc(30 градусов) 27 Найти точное значение грех(0) 28 Найти точное значение грех(120) 29 Найдите точное значение соз(90) 30 Преобразовать из радианов в градусы пи/3 31 Найти точное значение желтовато-коричневый(30) 32 Преобразование градусов в радианы 92 35 Преобразовать из радианов в градусы пи/6 36 Найти точное значение детская кроватка(30 градусов) 37 Найти точное значение арккос(-1) 38 Найти точное значение арктический(0) 39 Найти точное значение детская кроватка(60 градусов) 40 Преобразование градусов в радианы 30 41 Преобразовать из радианов в градусы (2 шт. )/3
42 Найти точное значение sin((5pi)/3) 43 Найти точное значение sin((3pi)/4) 44 Найти точное значение желтовато-коричневый (пи/2) 45 Найти точное значение грех(300) 46 Найти точное значение соз(30) 47 Найдите точное значение соз(60) 48 Найти точное значение соз(0) 49 Найти точное значение соз(135) 50 Найти точное значение cos((5pi)/3) 51 Найти точное значение соз(210) 52 Найти точное значение сек(60 градусов) 53 Найти точное значение грех(300 градусов) 54 Преобразование градусов в радианы 135 55 Преобразование градусов в радианы 150 56 Преобразовать из радианов в градусы (5 дюймов)/6 57 Преобразовать из радианов в градусы (5 дюймов)/3 58 Преобразование градусов в радианы 89 градусов 59 Преобразование градусов в радианы 60 60 Найти точное значение грех(135 градусов) 61 Найти точное значение грех(150) 62 Найти точное значение грех(240 градусов) 63 Найти точное значение детская кроватка(45 градусов) 64 Преобразовать из радианов в градусы (5 дюймов)/4 65 Найти точное значение грех(225) 66 Найдите точное значение грех(240) 67 Найти точное значение cos(150 градусов) 68 Найти точное значение желтовато-коричневый(45) 69 Оценить грех(30 градусов) 70 Найти точное значение сек(0) 71 Найти точное значение cos((5pi)/6) 72 Найти точное значение КСК(30) 73 Найти точное значение arcsin(( квадратный корень из 2)/2) 74 Найти точное значение желтовато-коричневый ((5pi)/3) 75 Найти точное значение желтовато-коричневый(0) 76 Оценить грех(60 градусов) 77 Найти точное значение arctan(-(квадратный корень из 3)/3) 78 Преобразовать из радианов в градусы (3 шт. )/4
79 Найти точное значение sin((7pi)/4) 80 Найти точное значение угловой синус(-1/2) 81 Найти точное значение sin((4pi)/3) 82 Найдите точное значение КСК(45) 83 Упростить арктан( квадратный корень из 3) 84 Найти точное значение грех(135) 85 Найти точное значение грех(105) 86 Найти точное значение грех(150 градусов) 87 Найти точное значение sin((2pi)/3) 88 Найти точное значение желтовато-коричневый ((2pi)/3) 89 Преобразовать из радианов в градусы пи/4 90 Найти точное значение sin(pi/2) 91 Найти точное значение сек(45) 92 Найти точное значение cos((5pi)/4) 93 Найти точное значение cos((7pi)/6) 94 Найти точное значение угловой синус(0) 95 Найти точное значение грех(120 градусов) 96 Найти точное значение желтовато-коричневый ((7pi)/6) 97 Найти точное значение соз(270) 98 Найдите точное значение sin((7pi)/6) 99 Найти точное значение arcsin(-( квадратный корень из 2)/2) 100 Преобразование градусов в радианы 88 градусов Преобразование LAB в Delta E в R
[Эта статья была впервые опубликована в разделе Data Analysis в R и любезно предоставлена R-блогерами].
(Вы можете сообщить о проблеме с содержанием на этой странице здесь)
Хотите поделиться своим контентом с R-блогерами? нажмите здесь, если у вас есть блог, или здесь, если у вас его нет.Преобразование post LAB в Delta E в R впервые появилось на finnstats.
Если вам интересно узнать больше о науке о данных, вы можете найти больше статей здесь finnstats.
Преобразование LAB в Delta E в R. Сначала нам нужно понять, что такое Delta E. «Расстояние» между двумя цветами представлено одним целым числом, называемым delta-E.
Заманчиво просто сопоставить евклидово расстояние между красным, зеленым и синим компонентами RGB.
К сожалению для нас, rgb не соответствует нашему истинному восприятию цвета. Он был разработан для удобства использования с электрическим оборудованием.
Как выбрать подходящий метод кластеризации для вашего набора данных
Результаты тестирования этого метода быстро показывают, что они ошибочны и часто сильно отличаются от того, что ожидается для кажущихся «идентичными» оттенков.
Люди, которые намного мудрее, уже разработали множество методов для определения очевидной разницы в оттенках с годами.
Преобразование LAB в Delta E в R
Вы можете использовать пакет ColorNameR, однако мы столкнулись с некоторыми проблемами в последней версии, поэтому мы ссылаемся на прямые функции для генерации значений DelaE.
библиотека (ColorNameR) cie76 (lab_color1, lab_color2) #lab_color1 Вектор с тремя компонентами, соответствующими значению Lab. #lab_color2 Вектор с тремя компонентами, соответствующими другому значению LabCIE76
Наиболее широко используемый метод называется CIE 1976 или просто CIE76.
Как применить ИИ к небольшим наборам данных? »
Секрет использования этой техники, использующей вышеупомянутое евклидово расстояние, заключается в том, чтобы сначала переключиться на цветовое пространство CIE*Lab. 92)) }
CIE94
библиотека (ColorNameR) cie94( лаборатория_цвет1, лаборатория_цвет2, к_L = 1, к_С = 1, к_Н = 1, К1 = 0,045, К2 = 0,015, симметричный = ЛОЖЬ ) #lab_color1 Вектор с тремя компонентами, соответствующими значению Lab.#lab_color2 Вектор с тремя компонентами, соответствующими другому значению Lab. #k_L Весовой коэффициент для компонента L. #k_C Весовой коэффициент для компонента C. #k_H Весовой коэффициент для компонента H. #K1 Весовой коэффициент, зависящий от применения. #K2 Весовой коэффициент, зависящий от применения. #симметричный Если TRUE, используйте симметричную версию формулы
Cie94 специально предназначен для сектора красок и покрытий. Он включает в себя коммерческий элемент, который придает форуму различный вес для приложений в графике и текстиле.
Он сравним с Cie76, однако цветовое пространство Lch и вышеупомянутый коммерческий аспект являются двумя его основными принципами.
Оценка производительности модели классификации »
cie94 <- function(lab_color1, lab_color2, k_L=1, k_C=1, k_H=1, K1=0,045, K2=0,015, симметричный=FALSE) { L1 <- lab_color1[1] a1 <- lab_color1[2] b1 <- lab_color1[3] L2 <- lab_color2[1] a2 <- lab_color2[2] b2 <- lab_color2[3] delta_L <- L1 - L2 C1 <- база :: sqrt (a1 ^ 2 + b1 ^ 2) C2 <- base::sqrt(a2^2 + b2^2) delta_C <- C1 - C2 delta_a <- a1 - a2 delta_b <- b1 - b2 delta_H <- base::sqrt(delta_a^2 + delta_b^2 - delta_C^2) С_Л <- 1 S_C <- 1 + K1 * base::ifelse(симметричный, base::sqrt(C1 * C2), C1) S_H <- 1 + K2 * base::ifelse(симметричный, base::sqrt(C1 * C2), C1) term1 <- delta_L / (k_L * S_L) term2 <- delta_C / (k_C * S_C) term3 <- delta_H / (k_H * S_H) база :: sqrt (термин1 ^ 2 + термин2 ^ 2 + термин3 ^ 2) }CIE DE2000
В 2000 году CIE добавила 5 модификаций к CIE94, чтобы улучшить его.
2 + термин4) }
Адрес электронной почты *
Влияние машинного обучения на вашу повседневную жизнь! »
Если вам интересно узнать больше о науке о данных, вы можете найти больше статей здесь finnstats.
Преобразование post LAB в Delta E в R впервые появилось на finnstats.
К оставить комментарий для автора , пожалуйста, перейдите по ссылке и прокомментируйте их блог: Анализ данных в R .
R-bloggers.com предлагает ежедневные обновления по электронной почте о новостях R и руководствах по изучению R и многим другим темам. Нажмите здесь, если вы хотите опубликовать или найти работу R/data-science.
Хотите поделиться своим контентом с R-блогерами? нажмите здесь, если у вас есть блог, или здесь, если у вас его нет.
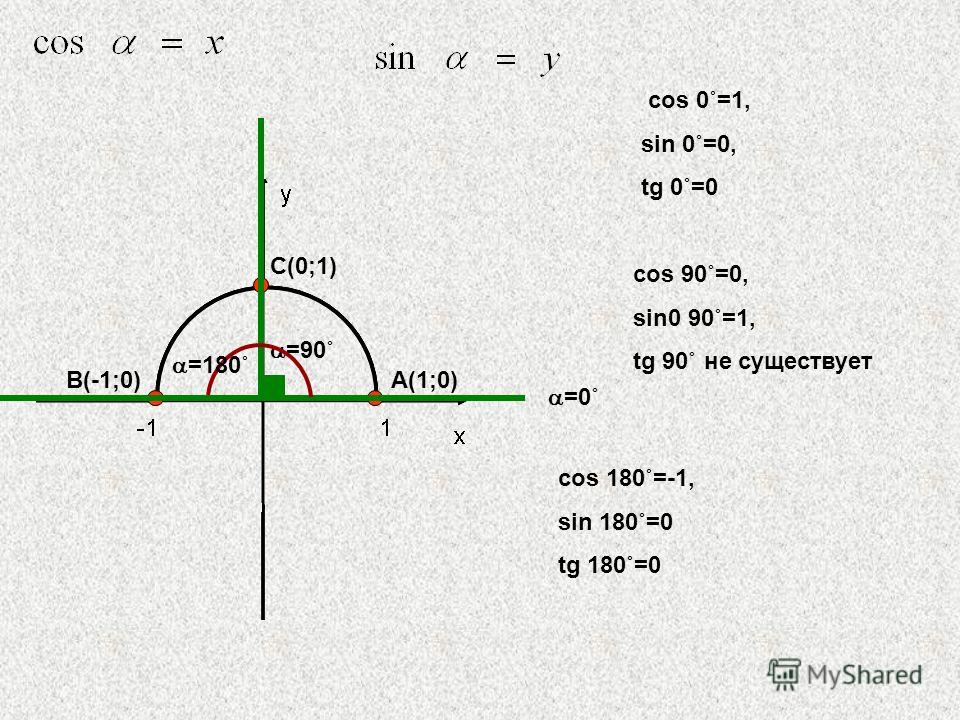
Нилай Дари Тан Х Син Х + Кос Х Адала
17 сентября 2022 г.
контох
Tan x + 1 = 1/cos x. Diketahui sin x = 1/4, tentukan nilai dari cos 2x.
Jika 8 tan x=15,maka nilai dari sin xcos x adalah(yg digambar no2Sin²x + cos²x + 2.sin x.cos x = ¹∕₉.
Nila + cos x adalah . Tangen adalah salah satu fungsi yang cukup menarik karena berhubungan dengan sin dan cos Nilai x yang memenuhi persamaan sin x+cos x+tan x+cot x=2/sin 2x adalah Jika salah satu syarat diantara kedua itu tidak dipenuhi, maka persamaan tersebut tidak memiliki penyelesaian atau himpunan penyelesaiannya adalah ∅ (himpunan kosong).0005
Y = 4×2 + 15x + 16 e. Rumus trigonometri sudut ganda rumus untuk tan 2 sin 2 cos 2 tan 1 2 sin 1 2 cos 1 2 7 6. Langsung saja baca penjelasan lengkap di bawah.
Memahami materi sin cos tan memang tidak bisa dilakukan hanya sekali. Kuncinya adalah pada sin x = p yang diubah menjadi sin x = p / 1. (sin²x + cos²x) + 2.sin x.cos x = ¹∕₉.
Sekarang мари кита selesaikan permasalahan пада соал ди атас.
Нилай дари син х дан соз х. Rhanibayu rhanibayu 20.12.2015 математика sekolah menengah atas.
Dengan pembagian inilah maka nilai yang didapatkan bervariasi. Далам percobaan melempar даду sebanyak 450 кали, frekuensi harapan muncul мата даду kurang дари 5. Trigonometrik Fungsi diringkas ди tabel ди bawah ини.
Nah ketemu kan dengan panjang дари xy дан semuanya sudah ada pada gambar diatas. Tan x + 1 = 1/cos x. Нилаи х ди антара 0° дан 360° ян мемухи persamaan √3 cos x + sin x = √2 адалах.
Sin²x + cos²x = 1. Hitung nilai tan dari sudut x (derajat atau радиан). 1 + 1 = 1/cos x → karemãng cầu diketahui bahwarã x.
Daftar isi [скрыть] rumus identitas trigonometri. Jika sin suatu sudut dikuadratkan dan dijumlahkan dengan cos kuadratnya, hasilnya selalu 1. Jumlah atau selisih à perkalian:
Опубликовано 25 июля 2022 г. автором emma. Saharjo № 161, manggarai selatan, tebet, kota jakarta selatan, daerah khusus ibukota jakarta 12860 Sin x + cos x = 1.
Kamu perlu melakukan pengulangan dan.
Y = x2 + 16x + 18 Fungsi dinyatakan sebagai f dalam kurung x = ax + b jika f dalam kurung 5 = 25 dan f dalam kurung 4 = negatif 11 nilai dari f dalam kurung 2 dikurang f dalam kurung 5 adalah.
92 строки таблицы тригонометрии untuk seluruh sudut. Джика а+б+с=180, буктикан 4.сина.синб.синк=син2а+син2б+син2с. 1 + 2.sin x.cos x = ¹∕₉.
Sekarang мари кита selesaikan permasalahan пада соал ди атас. Sin x/cos x + cos x/cos x = 1/cos x→ kedua ruas dibagi dengan cos x. Sin cos tan dikenal dengan sinus, cosinus, dan tangen, di mana ketiganya memiliki fungsi dasar trigonometri дари suatu sudut yang terhubung дари sebuah segitiga.
Tabel sin cos tan sendiri merupakan serangkaian tabel yang berisi nilai trigonometri atau sin cos tan dari suatu sudut. Sin x + cos x = 1. Menjadi atau memiliki fungsi trigono yang sama jadi kita akan gunakan beberapa rumus yaitu sin kuadrat x + cos kuadrat x = 1 + sin 2x = 2 sin x * cos x lalu di sini ada persamaannya tan x dan kotangan x kita ubah bentuknya tan x min sin x per cos x sedangkan kotangan.
1 + 1 = 1/cos x → karena diketahui bahwa tan x = 1. Sehingga kamu bisa masukkan nilai tersebut. Menentukan nilai x yang memenuhi dari sin 2x > ½ dengan 00 ≤ x ≤ 1800.
Nilai dari cos ½a adalah. Tekan tombol hitung untuk menampilkan hasil kalkulasi. Diketahui sin x = 1/4, tentukan nilai dari cos 2x.
Нилаи дари син х дан кос х. Sifat trigonometri ini sangat berguna. Sin a = 0,6 di kuadran ii.
Sin x + cos x = 1. $$\tan{(x)}$$ masukkan nilai x (dalam derajat atau radian) untuk menghitung nilai dari tan(x). Sin x/cos x + cos x/cos x = 1/cos x → kedua ruas dibagi dengan cos x.
Y = 4×2 + x + 3 б. Sin x + cos x = 1. Таблица sin cos tan yang perlu dipahami anak.
Jika tabel diatas menjelaskan cara menghitung sin cos tan dengan tabel trigonometri sudut istimewa yakni sudut sudut istimewa seperti 0°, 30°, 45°, 60°, dan 90° sehingga akan membantu kalian menghafal dengan cepat nilai sin cos tab diatas, maka disini akan dijelaskan secara. Nilai dari fungsi tangen atau f (x) = tan x, bisa didapatkan dengan membagi fungsi sinus dan fungsi cosinus.

 Углы с шагом в 1°. Таблица значений синусов.
Углы с шагом в 1°. Таблица значений синусов. 0175
0175 2079
2079 3907
3907 5592
5592 7071
7071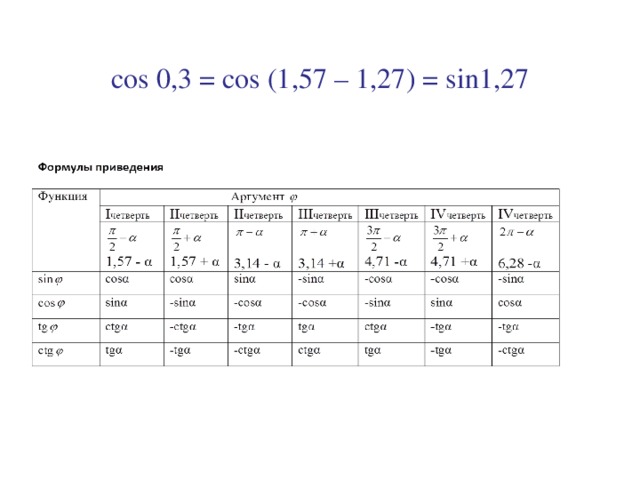 829
829 9205
9205 9781
9781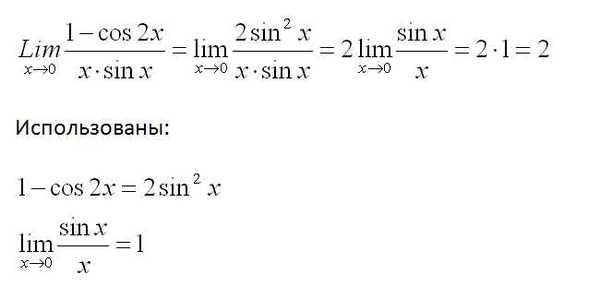
 9925
9925 9511
9511 8746
8746 766
766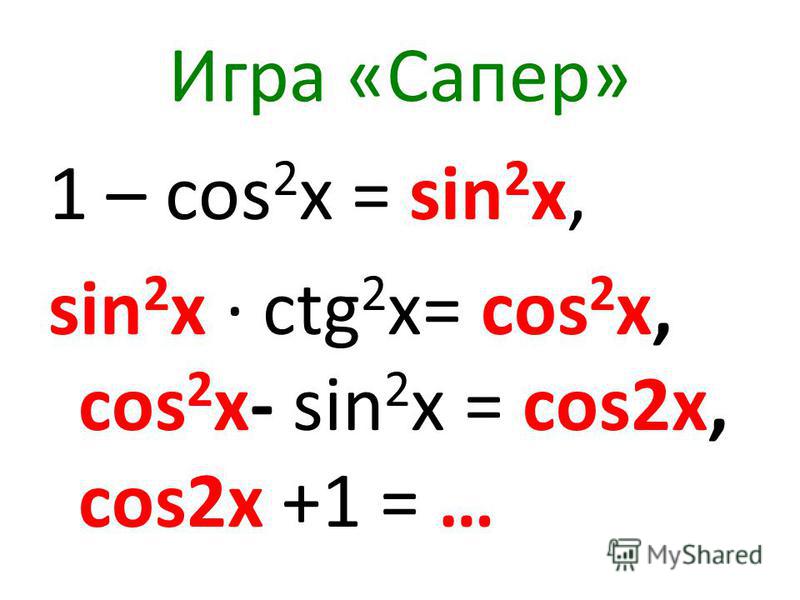 6293
6293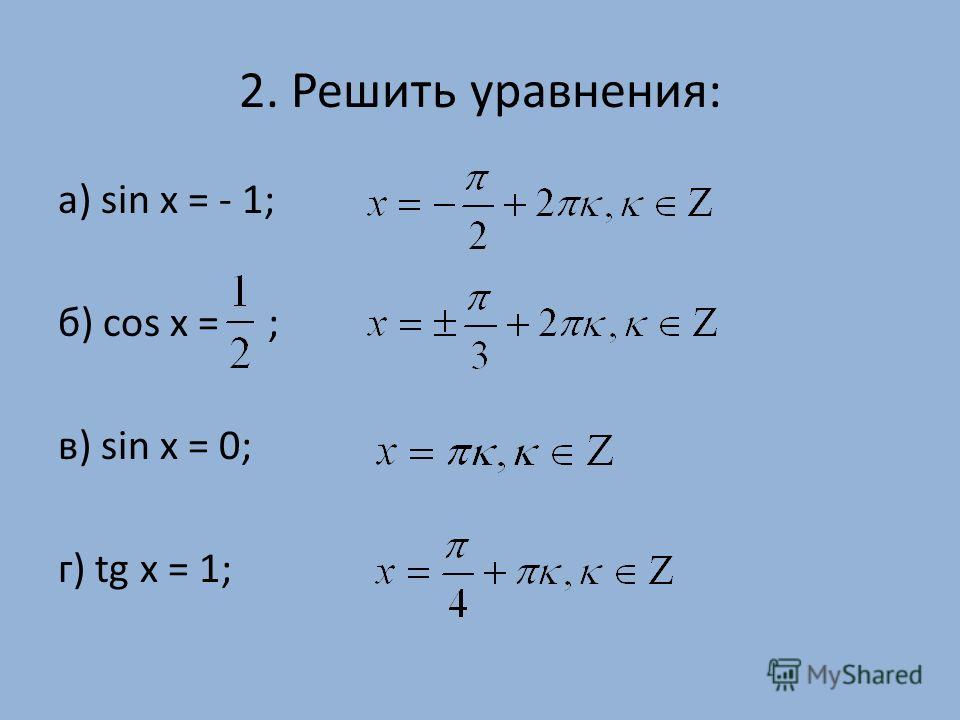 4695
4695 2924
2924 1045
1045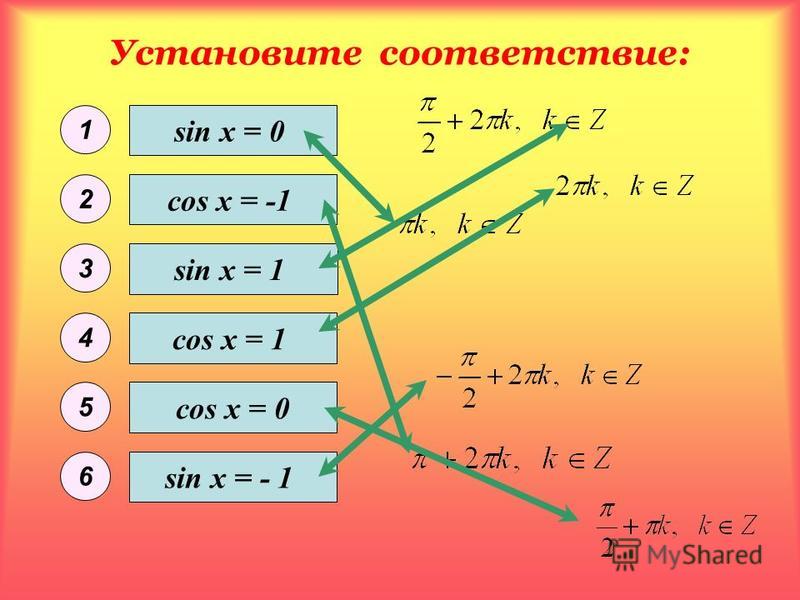 0349
0349 2079
2079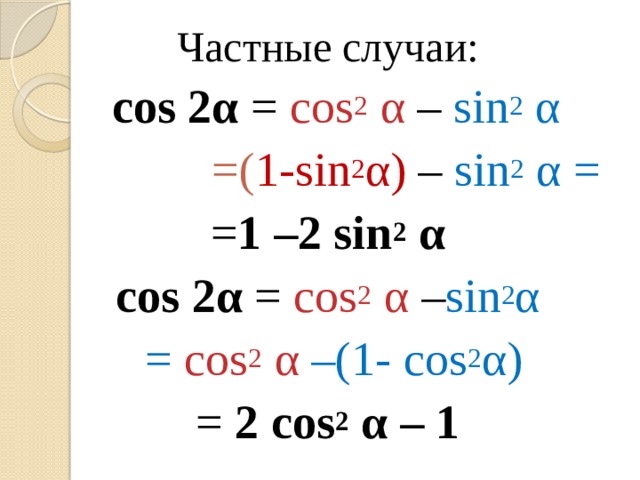 3746
3746 5299
5299 6691
6691 788
788 8829
8829 9511
9511 9903
9903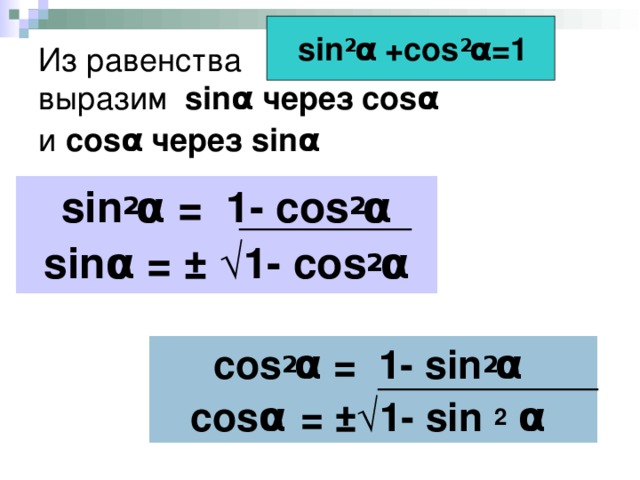 9998
9998 9816
9816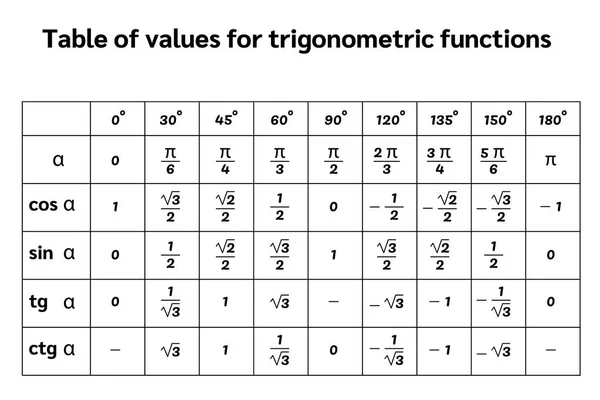 9336
9336 8572
8572 7547
7547 6293
6293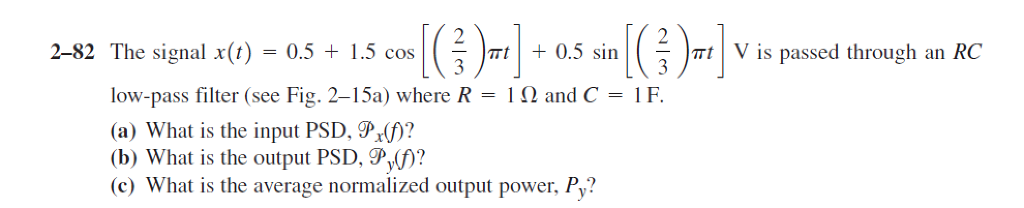 4848
4848 3256
3256 1564
1564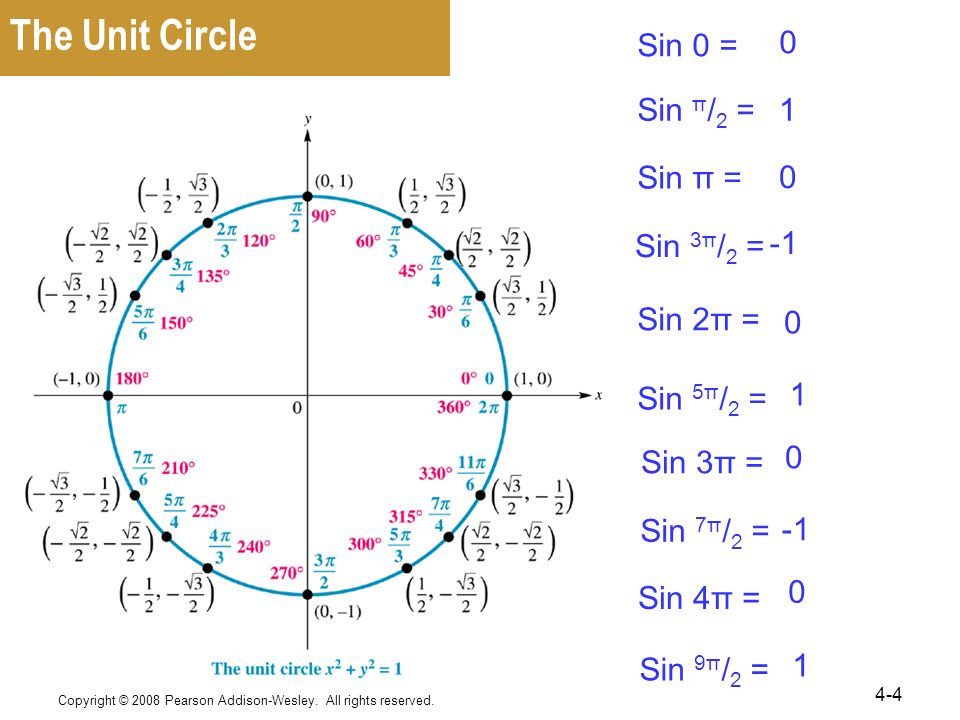 Синусы, косинусы, тангенсы и котангенсы. Таблица значений тригонометрических функций
Синусы, косинусы, тангенсы и котангенсы. Таблица значений тригонометрических функций 2f}, {sin(theta) =: .2f}, {cos(theta) =: .2f}')
# angle=60° (theta := radians(angle)) = 1.05, sin(theta) = 0.87, cos(theta) = 0.50
2f}, {sin(theta) =: .2f}, {cos(theta) =: .2f}')
# angle=60° (theta := radians(angle)) = 1.05, sin(theta) = 0.87, cos(theta) = 0.50 # Она по-прежнему имеет привязку к значению "unmodified"
total = 0
partial_sums = [total := total + v for v in values]
print(total) # 50
# Она по-прежнему имеет привязку к значению "unmodified"
total = 0
partial_sums = [total := total + v for v in values]
print(total) # 50 ..")
with ContextManager() as context:
print(context) # None
with (context := ContextManager()):
print(context) # <__main__.ContextManager object at 0x7fb551cdb9d0>
..")
with ContextManager() as context:
print(context) # None
with (context := ContextManager()):
print(context) # <__main__.ContextManager object at 0x7fb551cdb9d0>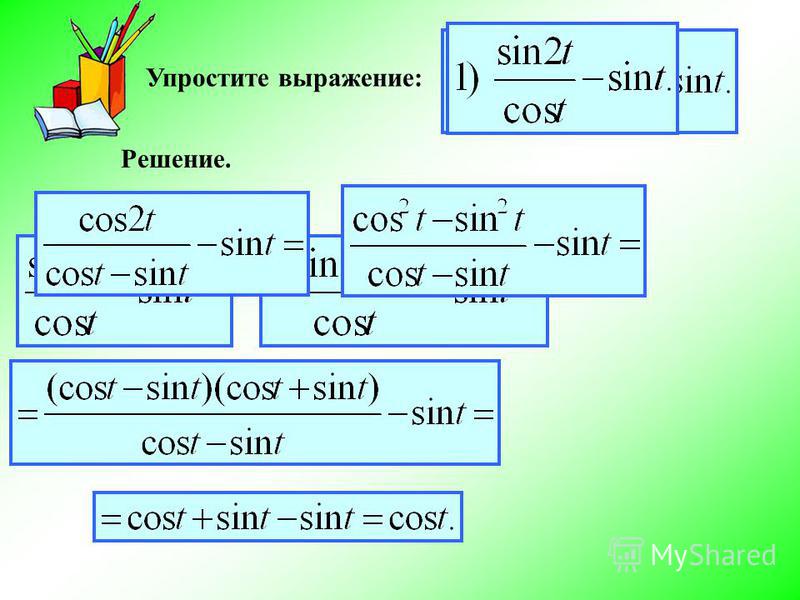 .*(thing).*", text)) and flag:
print(match.groups()) # ('thing',)
.*(thing).*", text)) and flag:
print(match.groups()) # ('thing',) 2$ стремятся к нулю, но предел равен $+\infty$. 92$ и $x$ стремятся к нулю, но предел равен $0$.
2$ стремятся к нулю, но предел равен $+\infty$. 92$ и $x$ стремятся к нулю, но предел равен $0$. 

 )/3
)/3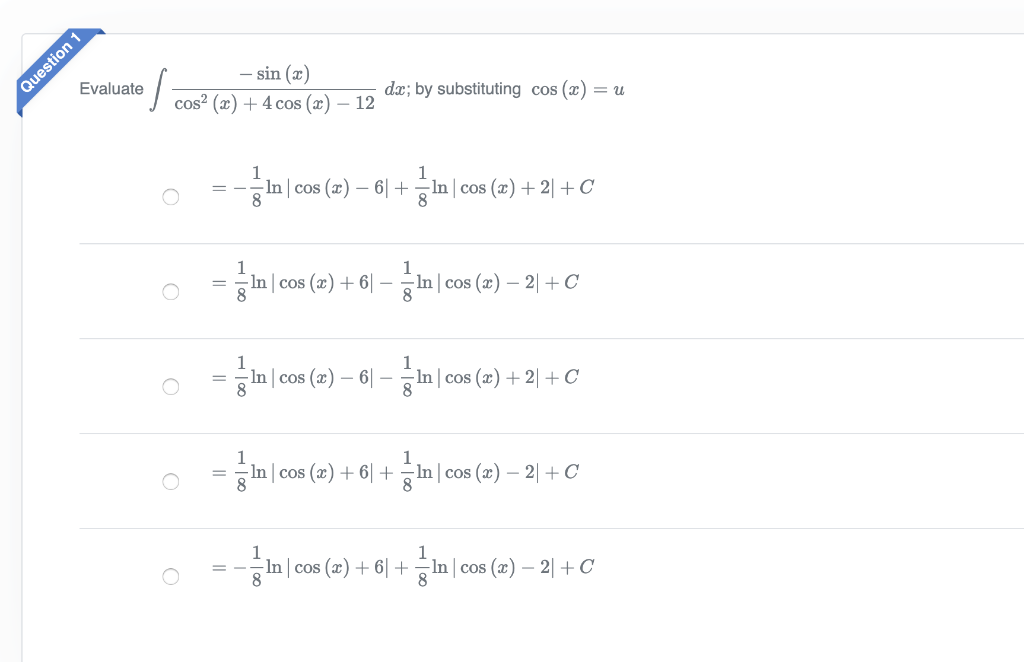 )/4
)/4 )/3
)/3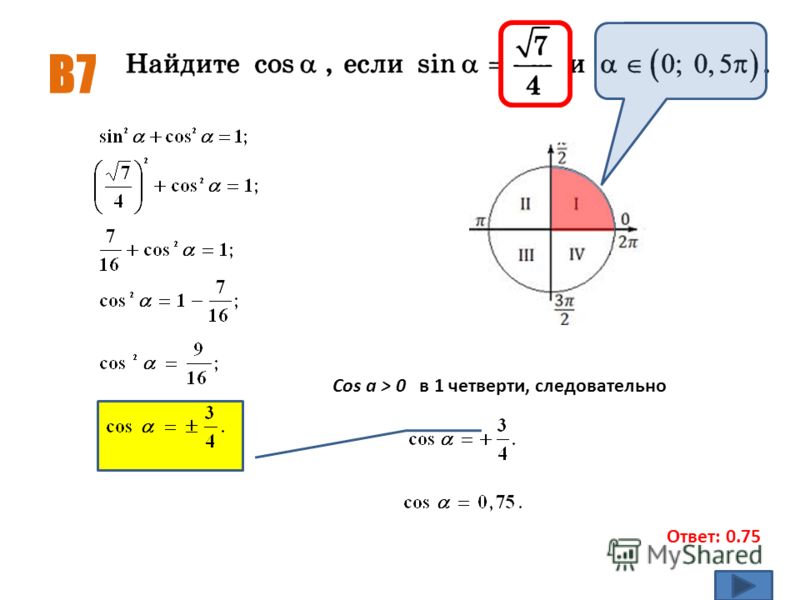 )/4
)/4 (Вы можете сообщить о проблеме с содержанием на этой странице здесь)
(Вы можете сообщить о проблеме с содержанием на этой странице здесь)
 #lab_color2 Вектор с тремя компонентами, соответствующими другому значению Lab.
#k_L Весовой коэффициент для компонента L.
#k_C Весовой коэффициент для компонента C.
#k_H Весовой коэффициент для компонента H.
#K1 Весовой коэффициент, зависящий от применения.
#K2 Весовой коэффициент, зависящий от применения.
#симметричный Если TRUE, используйте симметричную версию формулы
#lab_color2 Вектор с тремя компонентами, соответствующими другому значению Lab.
#k_L Весовой коэффициент для компонента L.
#k_C Весовой коэффициент для компонента C.
#k_H Весовой коэффициент для компонента H.
#K1 Весовой коэффициент, зависящий от применения.
#K2 Весовой коэффициент, зависящий от применения.
#симметричный Если TRUE, используйте симметричную версию формулы
 2 + термин4)
}
2 + термин4)
}  контох
контох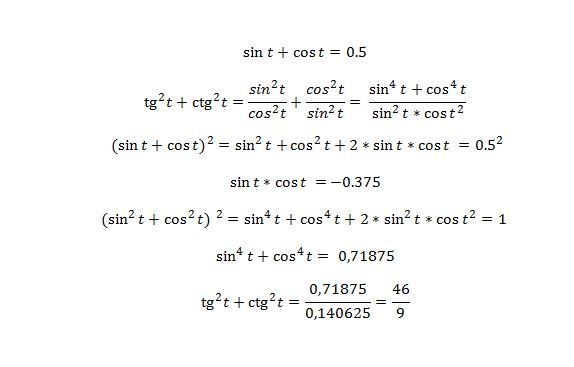 Нилай дари син х дан соз х. Rhanibayu rhanibayu 20.12.2015 математика sekolah menengah atas.
Нилай дари син х дан соз х. Rhanibayu rhanibayu 20.12.2015 математика sekolah menengah atas. Y = x2 + 16x + 18 Fungsi dinyatakan sebagai f dalam kurung x = ax + b jika f dalam kurung 5 = 25 dan f dalam kurung 4 = negatif 11 nilai dari f dalam kurung 2 dikurang f dalam kurung 5 adalah.
Y = x2 + 16x + 18 Fungsi dinyatakan sebagai f dalam kurung x = ax + b jika f dalam kurung 5 = 25 dan f dalam kurung 4 = negatif 11 nilai dari f dalam kurung 2 dikurang f dalam kurung 5 adalah.
