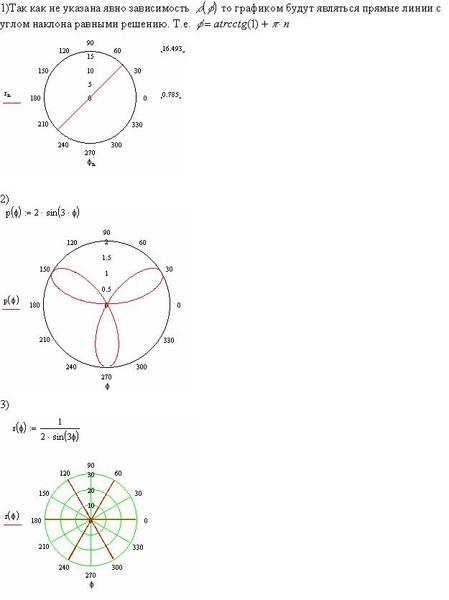
Как построить линию в полярных координатах?
Собственно:
– Сначала нужно построить полярную систему координат: отметить полюс, изобразить полярную ось и указать масштаб. Впрочем, этот пункт можно выполнить позже.
– Определяем область определения функции – угловые секторы, в которых линия существует, и в которых нет. Тонко прочерчиваем соответствующие угловые направления (прямые и / или лучи, разграничивающие эти секторы). Лучше пунктиром.
– В большинстве случаев потребуется найти десяток-другой точек, принадлежащих линии. Но иногда можно обойтись меньшим количеством, а то и вовсе отделаться схематическим чертежом.
– На следующем шаге следует прочертить угловые направления точек (тонкие прямые) и отметить на них найденные точки. Как это сделать с помощью
каменного топора транспортира, циркуля и линейки, я подробнейшим образом объяснил выше.
– И, наконец, отложенные точки нужно аккуратно-аккуратно соединить линией (линиями).
Отработаем алгоритм на более основательных типовых задачах:
Задача 120
Построить по точкам линию, заданную в полярной системе координат уравнением , рассматривая значения угла с интервалом в рад. Найти уравнение линии в прямоугольной системе координат.
Решение: найдём область определения. Поскольку полярный радиус неотрицателен, то:
Неравенство опять же удобно решить графически. Мысленно либо на черновике изобразите график косинуса (см. Приложение
Тригонометрия) и прямой . Что означает неравенство ? Оно означает, что нас
устраивает та часть косинусоиды, которая не ниже прямой .
График косинуса полностью удовлетворяет этому условию, поэтому может принимать
любые значения, и нам предстоит «перепахать» весь круг от 0 до , причём, по
условию сделать это требуется строго с интервалом в рад.
и так далее, пока не будет пройден весь оборот до «двух пи»…., но хочется ли вам сидеть с калькулятором… и ложкой? J Используйте Приложение Геометрический Калькулятор, который позволит буквально в пару щелчков вычислить все значения !
Вычисления, как правило, не расписывают подробно, а сразу заносят их результаты в таблицу:
Изобразим на чертеже полярную систему координат и угловые направления – тонкие прямые, соответствующие
вышеуказанным углам. Здесь можно опять воспользоваться Геометрическим Калькулятором
Если у вас под рукой нет ни программы, ни транспортира, ни даже линейки, то используйте мой handmade-продукт – выполните этот чертёж,
ориентируясь по клеточкам:
(углы проставлены для удобства, и на чистовике их записывать не надо)
До сих пор бережно храню этот листок бумаги, чтобы лет через 10-20 продать его антикварном аукционе J
… Шутки шутками, а оперативная память моего первого компьютера ZX Spectrum составляла 32 килобайта.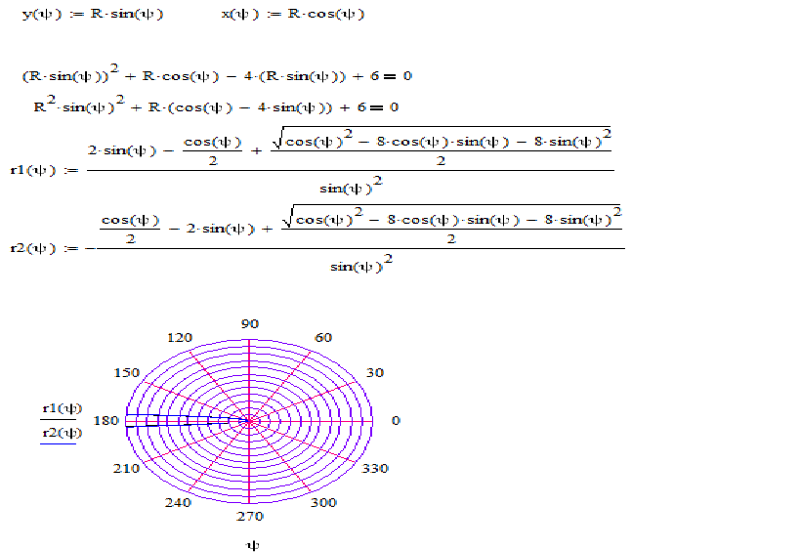 КИЛОбайта. При этом программисты умудрялись
заталкивать туда аркадные игры с сотнями экранов и отличной графикой (по меркам 8-разрядных машин, конечно). …А ведь с той поры прошло немногим
больше двух десятилетий.
КИЛОбайта. При этом программисты умудрялись
заталкивать туда аркадные игры с сотнями экранов и отличной графикой (по меркам 8-разрядных машин, конечно). …А ведь с той поры прошло немногим
больше двух десятилетий.
После ностальгических воспоминаний отметим найденные точки на чертеже и аккуратно соединим их линией:
Напоминаю, что одинаковые значения радиуса эффективнее засекать циркулем,
а слишком малые значения для углов допустимо отметить и «на глазок».
Данная кривая называется кардиоидой. Найдём её уравнение в декартовой системе координат. Для этого используем знакомый приём – домножим обе части
уравнения на «эр»:
И по формулам перехода к прямоугольным координатам , получим:
Перенесём «икс» налево и возведём обе части в квадрат:
Дальнейшее возведение левой части в квадрат только усложнит запись, поэтому результат целесообразнее оставить в таком виде.
Из полученного уравнения следует, что кардиоида – это алгебраическая линия 4-го порядка, и обратите
внимание, насколько сложной получилась её формула по сравнению с полярной системой координат. Алгебраическим линиям 3-го, 4-го, 5-го, 6-го и высших
порядков посвящены серьёзные исследования, и желающие без труда могут отыскать море информации по данной теме. Хорошая тема для курсовика, кстати,
или реферата. Ну а я, как обычно, предлагаю полезную и здоровую пищу на каждый день:
Задача 121
Линия задана уравнением в полярной системе координат. Треба:
1) построить линию по точкам, придавая значения через интервал , начиная
с и заканчивая ;
2) найти уравнение линии в декартовой системе координат;
3) определить вид кривой.
Типовая формулировка, предвещающая час (а то и больше) усердного пыхтения,
а нередко и чертыханья студента.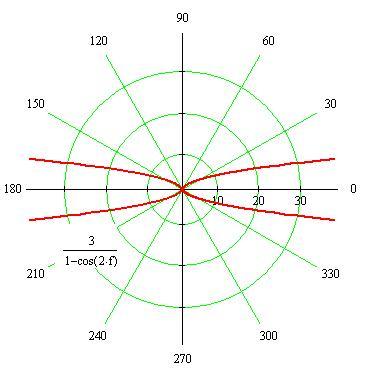
Рассмотрим ряд других важных особенностей решения:
Задача 122
Линия задана уравнением в полярной системе координат. Требуется:
1) построить линию по точкам, начиная от до и придавая значения через промежуток ;
2) найти уравнение данной линии в прямоугольной системе координат;
3) назвать линию, найти координаты фокусов и эксцентриситет.
Решение: 1) найдём область определения: .
Заметьте, что ноль в знаменателе нас тоже не устраивает, и поэтому неравенство строгое. Перенесём косинус направо: и развернём избушку – к нам передом, а к лесу задом:
Неравенство несложно решить аналитически, но для лучшего
понимания я опять воспользуюсь графическим методом. Мысленно или на черновике изобразим графики , при этом нас будет интересовать только один период – от до :
Условию удовлетворяет та часть синусоиды, которая расположена ПОД прямой .
То есть, в нашем распоряжении оказываются почти все значения угла за исключением «макушки», расположенной на симметричном отрезке .
Таким образом, . Арккосинус составляет примерно , поэтому из
рассмотрения исключаем углы и . Заполним расчётную таблицу с прочерками в соответствующих ячейках:
Изобразим полярную систему координат и лучи , между которыми нет точек линии. Прочертим угловые направления найденных точек и с помощью циркуля сделаем засечки. Аккуратно соединим отмеченные
точки линией (точки, соответствующие углам , не вместились на
чертёж):
2)
Используем формулы перехода
и дальнейшее знакомо из задач с линиями второго порядка:
– искомое
уравнение.
3) Данная линия представляется собой гиперболу с центром симметрии в точке , действительной полуосью , мнимой полуосью .
Вы спрОсите: «но в полярной же системе координат прорисовалась только одна ветвь гиперболы, поэтому не ошибочно ли сейчас говорить
о целой гиперболе?». Не ошибочно! И вот по какой причине: если подразумевать обобщённую полярную систему координат с отрицательными значениями «эр», то при значениях угла из интервала прорисуется левая ветвь! Желающие могут провести самостоятельную проверку и анализ этого факта. Я не сторонник и даже
противник обобщенных полярных координат, но в данном случае всё получается ловко и очень хитро – можно как бы и не оговариваться о том, что на
чертеже только одна ветвь гиперболы.
Вычислим координаты фокусов и эксцентриситет. По условию уравнение не нужно приводить к каноническому виду, а значит, требуемые вещи проще найти напрямую – с учётом параллельного переноса гиперболы, к тому же, она не повёрнута.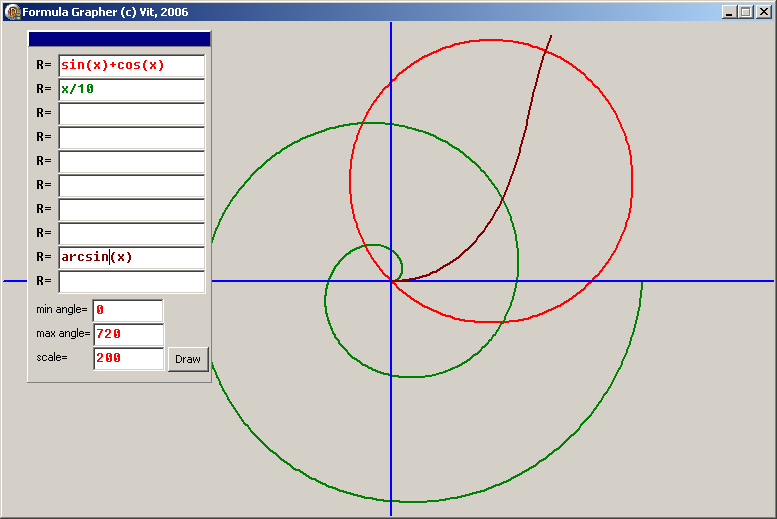
Вычислим значение и поправкой на параллельный перенос в точку найдём фокусы:
Эксцентриситет:
Готово. Педантичные люди могут ещё записать развёрнутый ответ.
Заключительное задание для самостоятельного решения:
Задача 123
Линия задана уравнением в полярной системе координат. Требуется:
1) построить линию по точкам, начиная от до и придавая значения через промежуток ;
2) найти уравнение данной линии в прямоугольной системе координат и определить её вид;
3) привести уравнение к каноническому виду и выполнить чертёж в прямоугольной системе координат. Найти фокусы кривой и её эксцентриситет.
Внимательно проанализируйте, что и в каком порядке требуется выполнить по условию. Сам много раз «налетал» – краем
глаза показалось одно, а нужно совсем другое. В образце решения приведение уравнения линии 2-го порядка к
каноническому виду выполнено строгим академическим способом.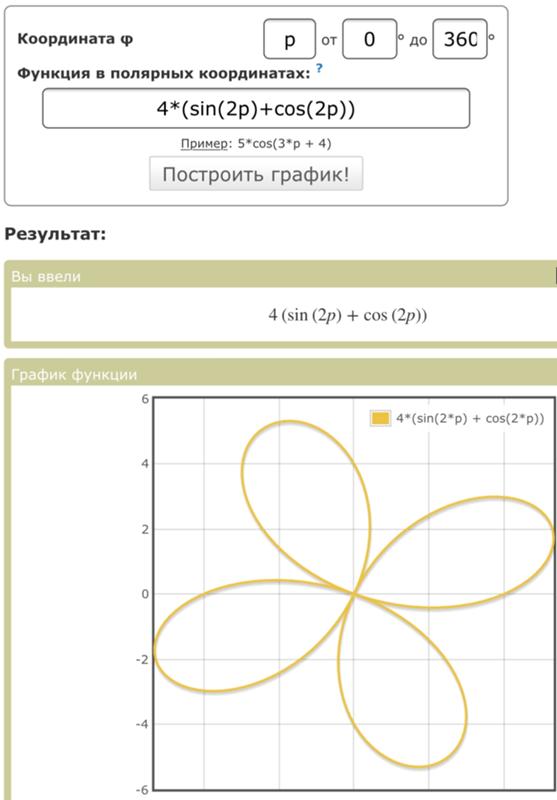
Когда удобно использовать полярные координаты? Ну, конечно, когда мы имеем дело со всевозможными окружностям, дугами, кругами, эллипсами, спиралями и т.д. А причина простА – уравнения получаются простые.
На основе полярных координат плоскости базируются цилиндрические и сферические координаты пространства. В частности, угловые величины широко используются в воздушной навигации и астрономии. Действительно, представьте земной шар (а если строго, эллипсоид), эллиптические орбиты планет и вы поймёте, что «распиаренная» прямоугольная система координат как-то здесь совсем «не в тему».
5.1.1. Понятие плоскости в пространстве
4.5. Полярная роза
| Оглавление |
Автор: Aлeксaндр Eмeлин
Линия в полярной системе координат. Связь между полярными и декартовыми координатами. Решение задач и контрольных работ по высшей математике онлайн
Краткая теория
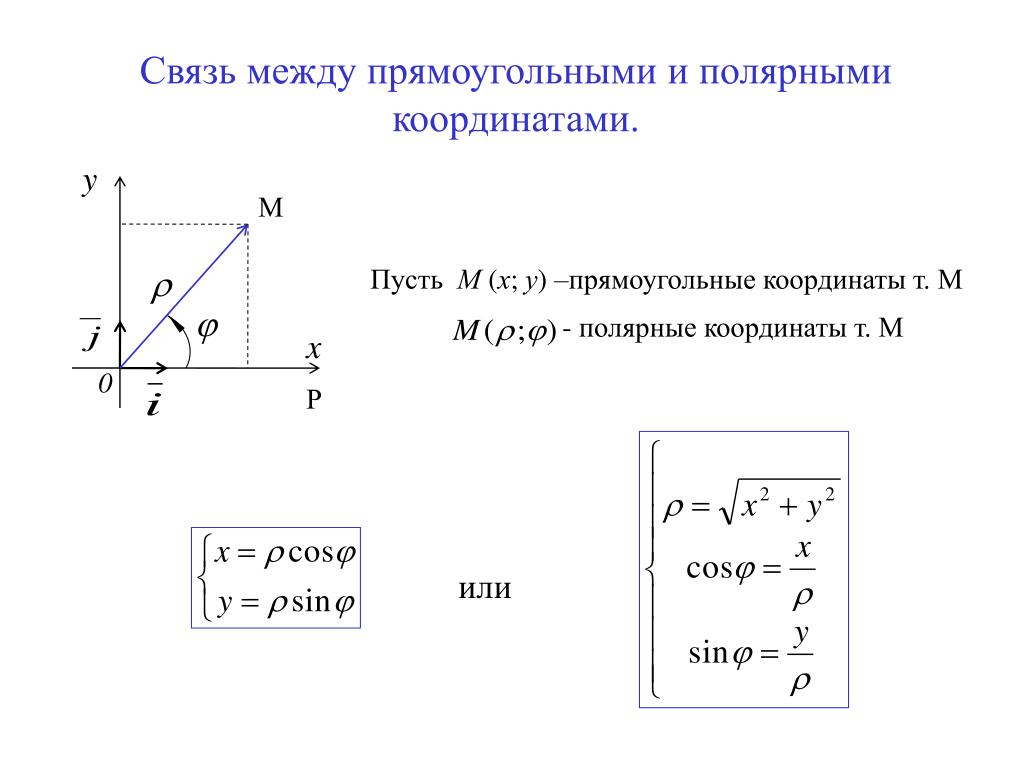
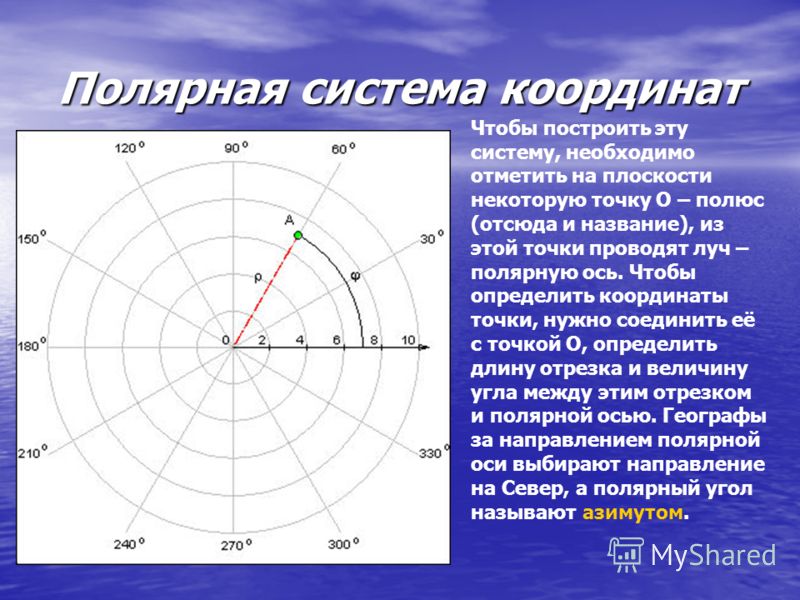
В полярной системе координат точка задается полярным углом φ и полярным радиусом r.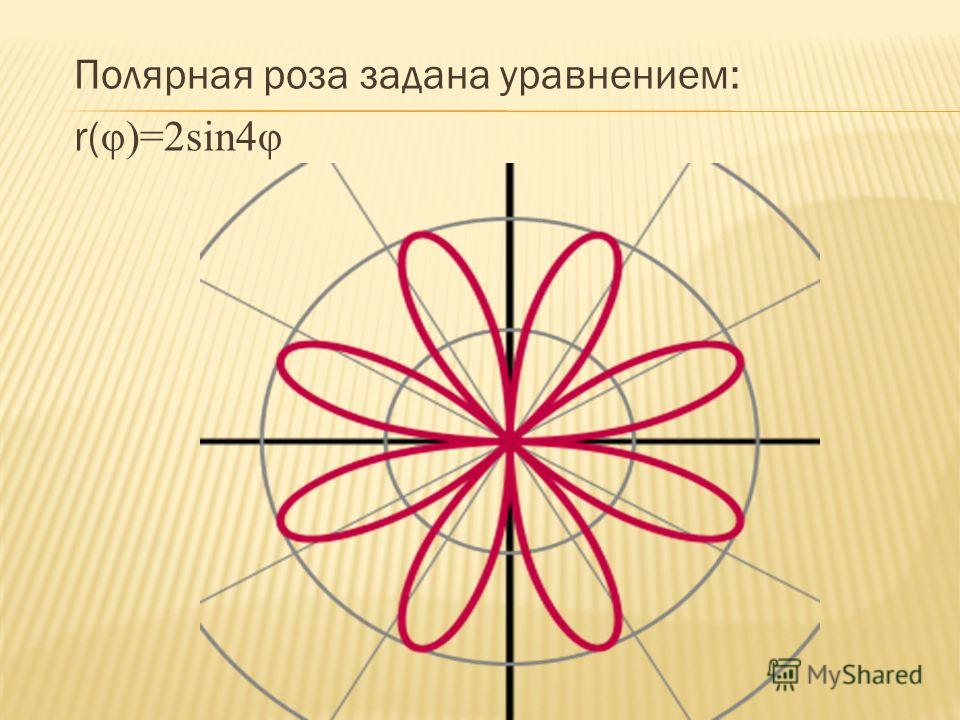
φ — угол, отсчитываемый от полярной оси в положительном направлении (против часовой стрелки)
r — расстояние от заданной точки до полюса
Если совместить начало декартовых координат с полюсом, а ось абсцисс с полярной осью, то между полярной и декартовой системой координат может быть установлена однозначная связь.
Пример решения задачи
Линия задана уравнением в полярной системе координат. Требуется:
- Построить линию по точкам начиная с до и придавая значения через промежуток ;
- Найти уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью;
- По уравнению в декартовой прямоугольной системе координат определить, какая это линия.
Решение
Построение линии по точкам
Построим линию по точкам, предварительно заполнив таблицу значений r и j:
| 1 | 0 | 1 | 9 | 0,556 |
| 2 | 0,924 | 8,772 | 0,570 | |
| 3 | 0,707 | 8,121 | 0,616 | |
| 4 | 0,383 | 7,148 | 0,699 | |
| 5 | 0,000 | 6,000 | 0,833 | |
| 6 | -0,383 | 4,852 | 1,031 | |
| 7 | -0,707 | 3,879 | 1,289 | |
| 8 | -0,924 | 3,228 | 1,549 | |
| 9 | -1 | 3 | 1,667 | |
| 10 | -0,924 | 3,228 | 1,549 | |
| 11 | -0,707 | 3,879 | 1,289 | |
| 12 | -0,383 | 4,852 | 1,031 | |
| 13 | 0,000 | 6,000 | 0,833 | |
| 14 | 0,383 | 7,148 | 0,699 | |
| 15 | 0,707 | 8,121 | 0,616 | |
| 16 | 0,924 | 8,772 | 0,570 | |
| 17 | 1 | 9 | 0,556 |
Используя данные
таблицы, строим линию.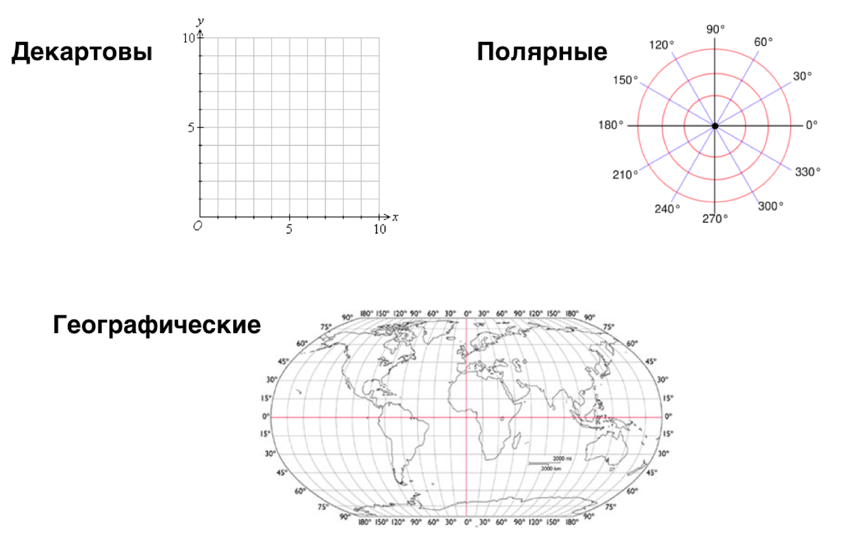
- Отмечаем полюс и указываем масштаб.
- С помощью транспортира прочерчиваем угловые направления
- Циркулем и линейкой отмечаем найденные точки
- Отложенные точки соединяем линией
Если не находите примера, аналогичного вашему, если сами не успеваете выполнить работу, если впереди экзамен по предмету и нужна помощь — свяжитесь со мной:
ВКонтакте
WhatsApp
Telegram
Я буду работать с вами, над вашей проблемой, пока она не решится.
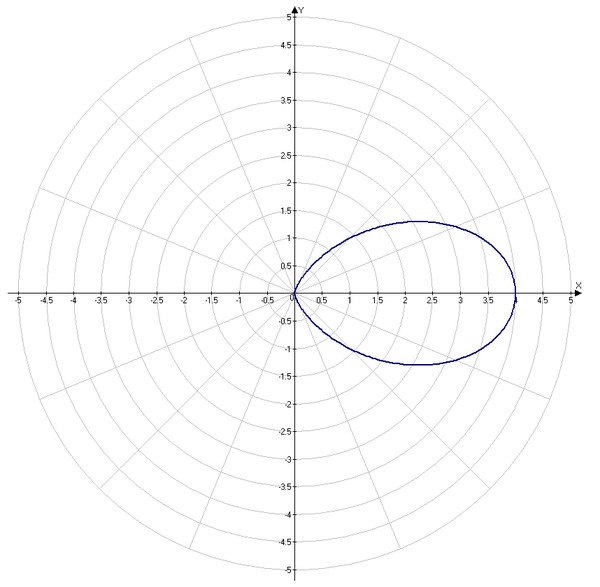
График в полярной системе координат имеет вид:
Уравнение линии в декартовой прямоугольной системе координат
Найдем уравнение данной линии в декартовой системе координат:
Подставляя в исходное уравнение в полярных координатах, получаем:
Полученная линия -эллипс
| 3.2.4. Кривые в полярной системе координат |
Высшая математика > 3. Аналитическая геометрия > 3.2. Аналитическая геометрия на плоскости > 3.2.4. Кривые в полярной системе координат Аналитическая геометрия > 3.2. Аналитическая геометрия на плоскости > 3.2.4. Кривые в полярной системе координат
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
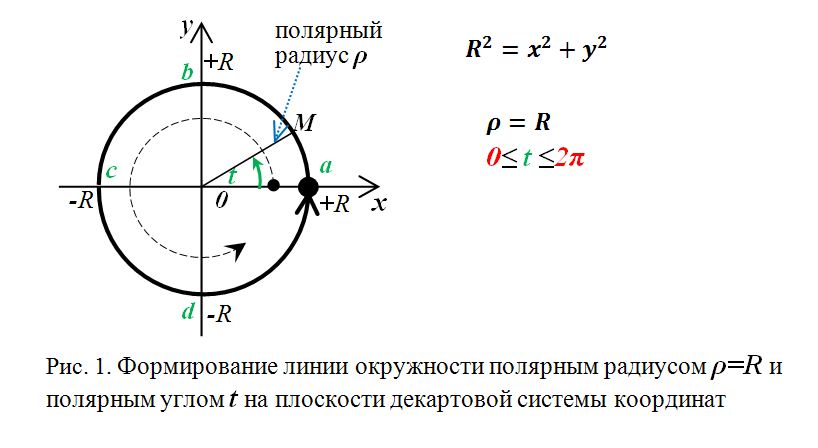
Полярная система координат задана, если задана точка , называемая полюсом, и исходящий из полюса луч , который называется полярной осью. Положение любой точки в полярной системе координат однозначно определяется ее
полярными координатами: полярным радиусом — расстоянием от полюса до точки и полярным углом — углом поворота полярной оси до совпадения с вектором
(рис.31). В полюсе полярный радиус , а полярный угол не определен. Полярный угол измеряется в радианах и считается положительным, если
отсчитывается от полярной оси против часовой стрелки. Полярный угол определяется
с точностью до , где — целое число. Это означает, что точки с полярными координатами
и при целом совпадают. Если задана полярная система координат, то каждой паре чисел , из которых , соответствует точка плоскости, для которой эти числа являются
ее полярными координатами. Если , то эта точка расположена на луче, составляющим угол с полярной осью , и на расстоянии от полюса. Если , то эта точка совпадает с полюсом. Из определения полярных координат следует, что уравнение задает на плоскости окружность с центром в полюсе и
радиусом , а уравнение задает на плоскости луч, проходящий через полюс и
составляющий с полярной осью угол , в частности уравнения полярной оси .
Если задать на плоскости прямоугольную декартову систему координат, поместив
ее начало в полюс и совместив ось абсцисс с полярной осью, то, как легко видеть
из рис. 32, декартовы координаты и выражаются через полярные координаты из
соотношений Если каждое уравнение системы возвести в квадрат и сложить их, то получим
уравнение , из которого по заданным декартовым координатам можно
определить полярный радиус.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Как строить полярные графики в mathcad
Как построить полярный график по точкам?
Построить полярный график
в задании педагог написaл то не полный графиk r<0 не понимаю в чем ошибка
Построить полярный график в декартовых координатах
Построить полярный график в декартовых координатах Скрин
Как построить график по точкам
Забыл. Давно пользовался MathCad . Как построить график чтобы получился как на скриншоте. Ну.
Давно пользовался MathCad . Как построить график чтобы получился как на скриншоте. Ну.
Как построить график по точкам в полярном графике?
Необходимо перевести треугольник с точками (0,0) (-1,-1) (0,-2) в декартовых координатах в полярные.
5.2. Построение графиков в полярной системе координат при помощи MathCad
Определить как дискретную переменную (в пределах области определения).
Задать функцию () .
Щелкнуть мышью в свободном месте. Выбрать из меню «Графика» PolarPlot (Полярный график).
В появившемся шаблоне напечатать в нижнем поле, напечатать () в левом поле.
Щелкнуть мышью вне графика.
Пример 2. Построим график функции (спираль Архимеда) при помощиMathCAD.
График в полярных координатах можно форматировать.
Чтобы открыть окно форматирования графика поступают также как при форматировании декартово графика. Аналогично декартовому графику, для полярного графика можно задать стиль оформления осей (в частности, для наглядности удобно отразить вспомогательные угловые линии), изменить параметры кривой, создать надписи.
Аналогично декартовому графику, для полярного графика можно задать стиль оформления осей (в частности, для наглядности удобно отразить вспомогательные угловые линии), изменить параметры кривой, создать надписи.
5.3. Задания для самостоятельного решения
1. Построить (в тетради) в полярной системе координат линию по точкам, придавая значения от 0 до с шагом (для вычисления значений можно использовать возможности MathCAD):
,,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
,,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
2. При помощи MathCAD построить кривые в полярной системе координат, придавая различные значения параметру а:
Лабораторная работа № 6 Тема: Символьные вычисления
Цель работы: Научиться производить символьные вычисления: преобразовывать выражения, вычислять пределы.
MathCAD позволяет получить значение некоторого выражения в численном виде (при помощи обычного знака равенства) или в символьном виде (при помощи знака символьного равенства, о котором будет рассказано ниже). В первом случае после знака равенства появляется одно или несколько чисел. Во втором случае результатом вычислений является некоторое выражение.
Прежде, чем производить символьные вычисления, необходимо убедиться, что символьный процессор включен в работу: в меню «Math» должны быть отмечены команды «Live Symbolics» («Использовать символику») и «Automatic Mode» («Автоматический режим»).
Знак символьного равенства представляет собой стрелку вправо () и набирается сочетанием клавиш [Ctrl] и [.], либо с палитры «Преобразования».
Чтобы произвести символьные вычисления, необходимо:
Ввести выражение, которое надо вычислить или преобразовать.
Выделить выражение синей выделительной рамкой и набрать знак символьного равенства.
Щелкнуть мышью вне выражения.
Проиллюстрируем разницу между численным и символьным результатом на простом примере. Вычислим двумя способами:
Следует отметить, что для одних выражений можно произвести как численные, так и символьные вычисления, для других – только численные, для третьих – только символьные.
При помощи символьных вычислений можно вычислять пределы, решать неопределенные системы уравнений (т.е. системы, которые имеют множество решений), преобразовывать выражения, находить производные и т.д.
Графика
В MathCAD полярные графики рисуются с использованием стандартных преобразований и . Предполагается, что r и могут принимать и положительные, и отрицательные значения. Типичный полярный график показывает зависимость выражения для радиуса от угла.
Построение графика
Полярный график строится с использованием шаблона полярного графика на панели Графика. Выражение для функции и угла вводятся в соответствующие шаблоны графика. Можно построить несколько графиков на одном и том же чертеже. Все выражения должны использовать одну и ту же переменную. Угол вводится в радианах (по умолчанию) или в градусах (указываются единицы – deg).
Все выражения должны использовать одну и ту же переменную. Угол вводится в радианах (по умолчанию) или в градусах (указываются единицы – deg).
- Определить как функцию ,
- заполнить шаблоны,
- отобразить график в полярных координатах (Рис.3.13).
Форматирование графика
Используется команда меню Format/Graph/Plar Plot (Формат/Графика/Полярный график) или двойной щелчок на графике. Окно форматирования такое же, как и для декартовых графиков.
Установка границ на осях координат
По умолчанию устанавливаются верхние и нижние границы на радиальной оси. Для линейного масштаба верхняя граница — максимальное значение радиуса, нижняя граница — ноль. Чтобы вручную установить максимальное значение на радиальной оси, щёлкнуть на числе в верхнем поле ввода и впечатать новое число.
Так же, как и для декартовых графиков, можно использовать индексную переменную, отобразить в полярных координатах один вектор значений относительно другого.
Пример 3.6
Построить график функций , в полярных координатах с разным шагом по углу, разной сеткой (Рис.3.14, Рис.3.15).
- задан автомасштаб, автосетка. Пределы изменения радиуса от 0 до 4 .
- задан угол в радианах с шагом ?/5. Заданы пределы угла Пределы изменения радиуса от 0 до 4 .
- функция задана как индексная переменная. Угол задан в градусах, от 0 до 90. Пределы изменения радиуса от 1 до 2 . Введена сетка 2х8.
a)
b)
c)
Построение графика в Maple 14 в полярной системе координат : Околонаучный софт
| Boris143 |
| ||||
23/06/13 |
| ||||
| |||||
| Ms-dos4 |
| |||
25/02/08 |
| |||
| ||||
| Boris143 |
| ||
23/06/13 |
| ||
| |||
| Ms-dos4 |
| |||
25/02/08 |
| |||
| ||||
| Boris143 |
| ||
23/06/13 |
| ||
| |||
| Boris143 |
| ||
23/06/13 |
| ||
| |||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 6 ] |
Модераторы: Toucan, PAV, Karan, maxal, Супермодераторы
| 1 | Множитель | x^2-4 | |
| 2 | Множитель | 4x^2+20x+16 | |
| 3 | График | y=-x^2 | |
| 4 | Вычислить | 2+2 | |
| 5 | Множитель | x^2-25 | |
| 6 | Множитель | x^2+5x+6 | |
| 7 | Множитель | x^2-9 | |
| 8 | Множитель | x^3-8 | |
| 9 | Вычислить | квадратный корень из 12 | |
| 10 | Вычислить | квадратный корень из 20 | |
| 11 | Вычислить | квадратный корень из 50 | |
| 12 | Множитель | x^2-16 | |
| 13 | Вычислить | квадратный корень из 75 | |
| 14 | Множитель | x^2-1 | |
| 15 | Множитель | x^3+8 | |
| 16 | Вычислить | -2^2 | |
| 17 | Вычислить | квадратный корень из (-3)^4 | |
| 18 | Вычислить | квадратный корень из 45 | |
| 19 | Вычислить | квадратный корень из 32 | |
| 20 | Вычислить | квадратный корень из 18 | |
| 21 | Множитель | x^4-16 | |
| 22 | Вычислить | квадратный корень из 48 | |
| 23 | Вычислить | квадратный корень из 72 | |
| 24 | Вычислить | квадратный корень из (-2)^4 | |
| 25 | Множитель | x^3-27 | |
| 26 | Вычислить | -3^2 | |
| 27 | Множитель | x^4-1 | |
| 28 | Множитель | x^2+x-6 | |
| 29 | Множитель | x^3+27 | |
| 30 | Множитель | x^2-5x+6 | |
| 31 | Вычислить | квадратный корень из 24 | |
| 32 | Множитель | x^2-36 | |
| 33 | Множитель | x^2-4x+4 | |
| 34 | Вычислить | -4^2 | |
| 35 | Множитель | x^2-x-6 | |
| 36 | Множитель | x^4-81 | |
| 37 | Множитель | x^3-64 | |
| 38 | Вычислить | 4^3 | |
| 39 | Множитель | x^3-1 | |
| 40 | График | y=x^2 | |
| 41 | Вычислить | 2^3 | |
| 42 | Вычислить | (-12+ квадратный корень из -18)/60 | |
| 43 | Множитель | x^2-6x+9 | |
| 44 | Множитель | x^2-64 | |
| 45 | График | y=2x | |
| 46 | Множитель | x^3+64 | |
| 47 | Вычислить | (-8+ квадратный корень из -12)/40 | |
| 48 | Множитель | x^2-8x+16 | |
| 49 | Вычислить | 3^4 | |
| 50 | Вычислить | -5^2 | |
| 51 | Множитель | x^2-49 | |
| 52 | Вычислить | (-20+ квадратный корень из -75)/40 | |
| 53 | Множитель | x^2+6x+9 | |
| 54 | Множитель | 4x^2-25 | |
| 55 | Вычислить | квадратный корень из 28 | |
| 56 | Множитель | x^2-81 | |
| 57 | Вычислить | 2^5 | |
| 58 | Вычислить | -8^2 | |
| 59 | Вычислить | 2^4 | |
| 60 | Множитель | 4x^2-9 | |
| 61 | Вычислить | (-20+ квадратный корень из -50)/60 | |
| 62 | Вычислить | (-8+ квадратный корень из -20)/24 | |
| 63 | Множитель | x^2+4x+4 | |
| 64 | Множитель | x^2-10x+25 | |
| 65 | Вычислить | квадратный корень из -16 | |
| 66 | Множитель | x^2-2x+1 | |
| 67 | Вычислить | -7^2 | |
| 68 | График | f(x)=2^x | |
| 69 | Вычислить | 2^-2 | |
| 70 | Вычислить | квадратный корень из 27 | |
| 71 | Вычислить | квадратный корень из 80 | |
| 72 | Множитель | x^3+125 | |
| 73 | Вычислить | -9^2 | |
| 74 | Множитель | 2x^2-5x-3 | |
| 75 | Вычислить | квадратный корень из 40 | |
| 76 | Множитель | x^2+2x+1 | |
| 77 | Множитель | x^2+8x+16 | |
| 78 | График | y=3x | |
| 79 | Множитель | x^2+10x+25 | |
| 80 | Вычислить | 3^3 | |
| 81 | Вычислить | 5^-2 | |
| 82 | График | f(x)=x^2 | |
| 83 | Вычислить | квадратный корень из 54 | |
| 84 | Вычислить | (-12+ квадратный корень из -45)/24 | |
| 85 | Множитель | x^2+x-2 | |
| 86 | Вычислить | (-3)^3 | |
| 87 | Множитель | x^2-12x+36 | |
| 88 | Множитель | x^2+4 | |
| 89 | Вычислить | квадратный корень из (-8)^2 | |
| 90 | Множитель | x^2+7x+12 | |
| 91 | Вычислить | квадратный корень из -25 | |
| 92 | Множитель | x^2-x-20 | |
| 93 | Вычислить | 5^3 | |
| 94 | Множитель | x^2+8x+15 | |
| 95 | Множитель | x^2+7x+10 | |
| 96 | Множитель | 2x^2+5x-3 | |
| 97 | Вычислить квадратный корень | квадратный корень из 116 | |
| 98 | Множитель | x^2-x-12 | |
| 99 | Множитель | x^2-x-2 | |
| 100 | Вычислить | 2^2 |
Введение в полярные координаты
В некотором смысле может показаться странным, что первый способ, которым нас учат представлять положение объектов в математике, — это использование декартовых координат, тогда как этот метод определения местоположения не самый естественный или самый удобный.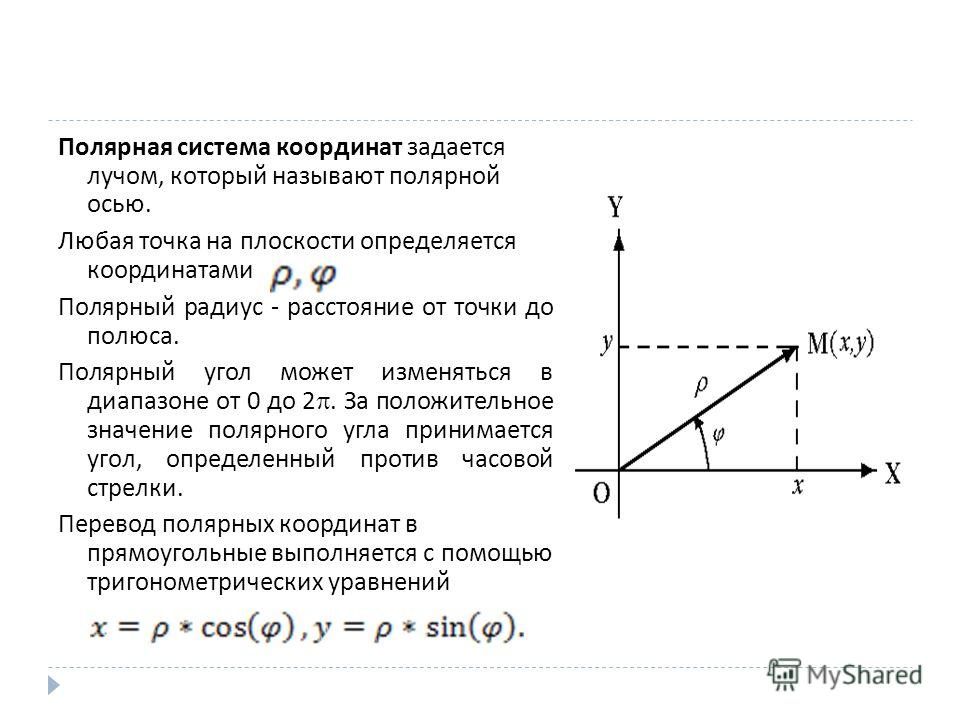 . Для начала вам нужно использовать как положительные, так и отрицательные числа для описания всех точек на плоскости, и вы должны создать сетку (оси скважин), чтобы использовать ее в качестве
ссылка.
. Для начала вам нужно использовать как положительные, так и отрицательные числа для описания всех точек на плоскости, и вы должны создать сетку (оси скважин), чтобы использовать ее в качестве
ссылка.
Когда вы спросите ребенка, где он оставил свой мяч, он ответит: «вон там» и покажет пальцем. Он описывает (хотя и очень приблизительно) расстояние «вон там» и направление «вон там» или кивок головой). Когда вы спрашиваете кого-то, где находится их город, они часто говорят что-то вроде «примерно в 30$ милях к северу от Лондона». Опять же, расстояние и направление. Не так уж часто кто-то дает широту и долготу своего города!
Таким образом, использование расстояния и направления в качестве средства описания положения гораздо более естественно, чем использование двух расстояний на сетке. Это средство определения местоположения используется в полярных координатах и пеленгах.
Полярные координаты точки описывают ее положение с точки зрения расстояния от фиксированной точки (начала координат) и угла, измеренного от фиксированного направления, которое, что интересно, не «север» (или вверх на странице), а «восток» (вправо). c$ .. , под углом и все равно в конечном итоге указывают в том же направлении! В приведенном выше примере общие координаты для $A$ будут $(90,2n\pi + \frac{\pi}{2})$, где $n$ — целое число.
c$ .. , под углом и все равно в конечном итоге указывают в том же направлении! В приведенном выше примере общие координаты для $A$ будут $(90,2n\pi + \frac{\pi}{2})$, где $n$ — целое число.
Это также означает, что полярные координаты полюса $O$ равны $(0,\theta)$, где $\theta$ может быть любым углом.
Связь между полярными и декартовыми координатами
Представьте себе точку $P$ с полярными координатами $(r,\theta)$. Попробуем использовать эту информацию для получения декартовых координат $P$. Мы можем опустить перпендикуляр из точки $P$ на $Ox$, пересекающий $Ox$ в точке $Q$. Длины $OQ$ и $OP$ представляют собой координаты $x$ и $y$ в декартовой форме, поэтому нам просто нужно найти эти два расстояния.
$$\begin{eqnarray} PQ &=& r \sin \theta \\ OQ &=& r \cos \theta \end{eqnarray}$$
Следовательно, декартовы координаты $P$ равны $ (r \sin \theta, r \cos \theta)$
Теперь пойдем по другому пути:
Начнем с декартовой системы координат.
Мы возьмем декартовы координаты $P$ как $(x,y)$.
Теперь попробуем найти $r$ и $\theta$ через $x$ и $y$. 9в)$!!
Используя знаки $\sin\theta$ и $\cos\theta$, вы можете быть уверены, что угол находится в правильном квадранте.
Итак, давайте закончим с использованием этой системы координат. Было бы неплохо попробовать некоторые уравнения и посмотреть на их графики (полярные диаграммы).
Рассмотрим несколько примеров:
Рассмотрим график:
$r= \theta$
Он имеет форму спирали (каждая точка смещается от центра по мере увеличения угла).
На приведенной ниже диаграмме показаны графики $r= a\theta$ для различных значений $a$. Сможете ли вы определить, что это такое?
Теперь ваша очередь. Графический калькулятор или графический пакет были бы очень полезны!
Как будет выглядеть серия графиков
$r=1, r=2, r=3, $…?
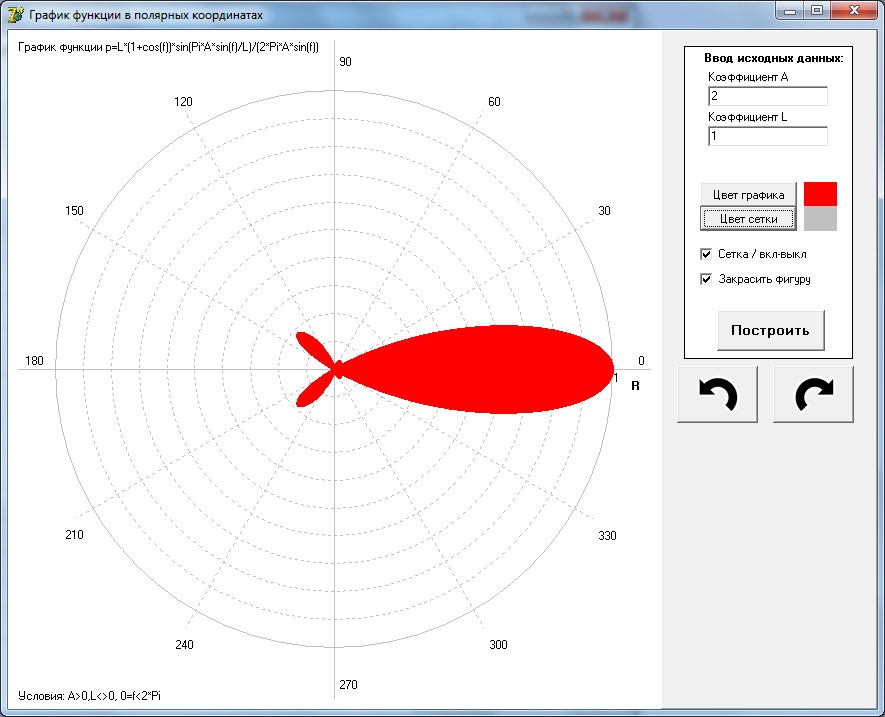
Как насчет $r = 2a(1 + \cos\theta )$ для разных значений $a$? Кстати, эти графики называются кардиоидами.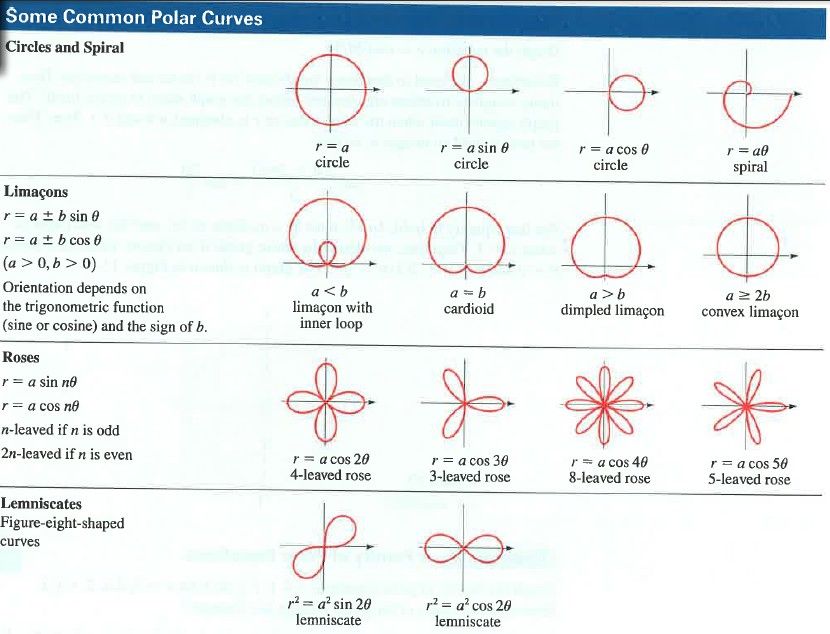
Ответы:
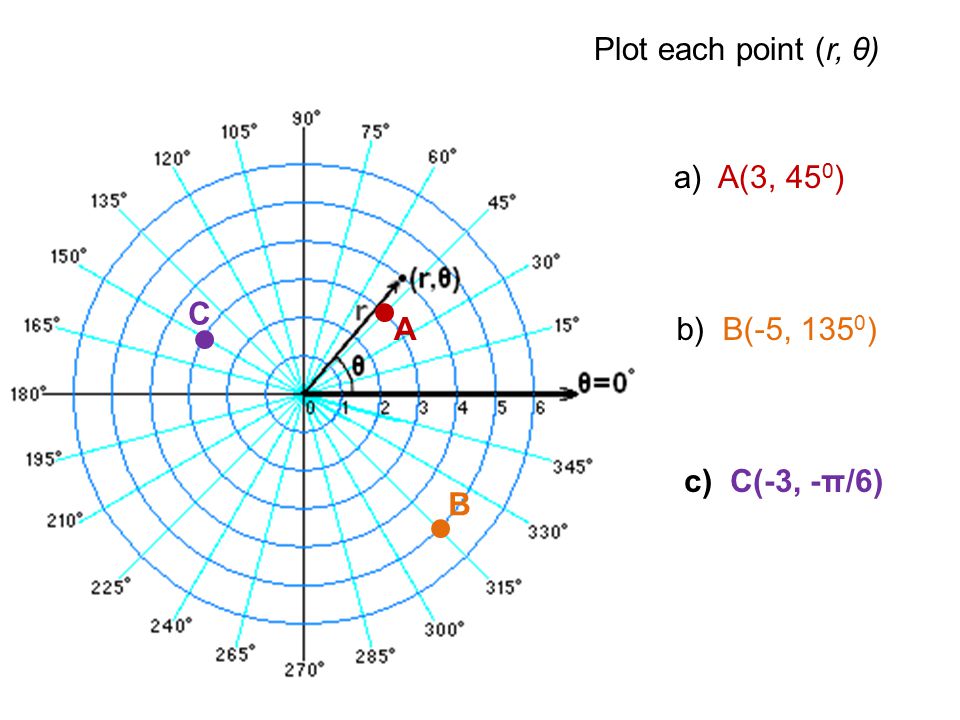
$$\begin{eqnarray} \mbox{D }\rightarrow(60,0)\\ \mbox{E }\rightarrow(30, 270)\\ \mbox{C }\rightarrow(120 , 225)\\ \mbox{A }\стрелка вправо(90, 90)\\ \mbox{F}\rightarrow(60,60)\\ \mbox{B}\rightarrow(120, 180) \end{eqnarray}$$ И $$\begin{eqnarray} (60, 0)\стрелка вправо(60,0)\\ (30, 270)\стрелка вправо(30, \frac{3\pi}{2})\\ (120, 225)\стрелка вправо(120, \frac{5\pi {4})\\ (90, 90)\стрелка вправо(90, \frac{\pi}{2})\\ (60,60)\rightarrow(60,\frac{\pi}{3})\\ (120, 180)\rightarrow(120,\pi) \end{eqnarray}$$
Сожмите это вверх, чтобы сделать веер вокруг точки, или . . . .
. . . . как использовать график xy, чтобы помочь визуализировать полярный график
Когда вы пытаетесь представить себе, как будет выглядеть полярный график функции, иногда бывает полезно сначала посмотреть на декартов (xy) график этой функции, используя значения от $0$ до $2\pi$ (от $0$ до $360). $ градусов), а затем представьте, что график превратился в веер.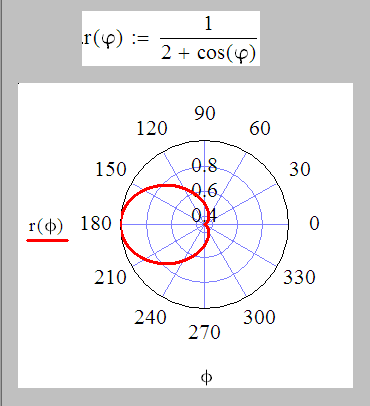
Изобразите ось X, втянутую в точку, вокруг которой расположены веером значения функции.
Например: $y = 5 \sin 2x$ выглядит как декартовский график.
Но как полярный график $r = 5\sin 2\theta$: $4$ регионов
В районе $1$ функция возрастает до максимального значения $5$, а затем симметрично падает до нуля.
В области $2$ функция падает до минимального значения $-5$, после чего возвращается к нулю.
Обратите внимание на положение области $2$ на полярном графике: когда $\theta$ перемещает второй квадрант от $\pi/2$ до $\pi$, все значения r отрицательны, проецируя каждую точку графика назад в четвертый квадрант.
Область $3$ прямолинейна, как и область $1$, а область $4$, как и область $2$, также имеет отрицательные значения $r$ и поэтому находится во втором квадранте.
Теперь попробуйте $r = 5 + 5 \sin 2\theta$ :
Сначала нарисуйте график xy, затем сожмите его, чтобы сделать веер вокруг точки.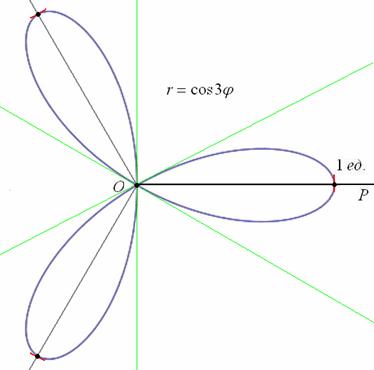 После того, как вы нарисовали полярную диаграмму, используйте графический калькулятор или графопостроитель, чтобы подтвердить свой рисунок.
После того, как вы нарисовали полярную диаграмму, используйте графический калькулятор или графопостроитель, чтобы подтвердить свой рисунок.
Придумайте несколько собственных функций, чтобы поиграть с ними. Например, предположим, что я остаюсь с формой $r = A + 5 \sin 2\theta$ , $A$ изначально было $0$, а затем $5$. Как повлияет изменение значений $A$ на появление полярной диаграммы?
Получайте удовольствие.
Дженнифер Пигготт и Грэм Браун
Построение полярных кривых в Python
Точка в полярных координатах представляется как ( r , тета ). Здесь r — это расстояние от начала координат, а тета — это угол, под которым r следует измерять от начала координат. Любая математическая функция в декартовой системе координат также может быть построена с использованием полярных координат.
- Matplotlib : Matplotlib — это обширная библиотека Python для создания статических и интерактивных графиков и визуализаций. Чтобы установить этот модуль, введите следующую команду в терминале.
pip установить matplotlib
- Numpy : Numpy — это основная библиотека для вычислений массивов в Python. Чтобы установить этот модуль, введите следующую команду в терминале.
pip установить numpy
- математика : математика — это встроенный модуль, используемый для решения различных математических задач.
Модуль matplotlib.pyplot содержит функцию polar() , которую можно использовать для построения кривых в полярных координатах.
Синтаксис : matplotlib.pyplot.polar (Theta, R, ** Kwargs)
Параметры :
- THETA — Угла
- THETA –ANGEL
- THETA — ANGLE
- THETA —
- .
0241
В каждом из приведенных ниже примеров
- Создается список значений в радианах. Эти значения охватывают домен соответствующей функции.
- Каждому значению тета в радианах соответствует значение r по специальной формуле для каждой кривой.
1. Окружность: Окружность – это фигура, состоящая из всех точек на плоскости, которые находятся на заданном расстоянии (радиусе) от данной точки, центра. Следовательно, r является константой 9Значение 0241 равно радиусу .
Example :
Python3
importnumpy as np
importmatplotlib.pyplot as plt
plt.axes( проекция
=«полярная»)
r=2
rads=np.arange(0, (2*np.pi),0.01)
forradinrads:
plt.polar(rad, r,'g.')
plt.show()Выход:
Here, r is defined as :
Where,
- a = length of semi major axis
- b = length of semi minor axis
Example :
Python3
importnumpy as np
importmatplotlib.pyplot as plt
importmath
plt.axes(projection='polar')
a=4
b=3
rads=np.arange(0, (2*np.pi),0.01)
forradinrads:
r=(a*b)/math.sqrt((a
*np.sin(rad))**2+(b*np.cos(rad))**2)
plt.polar(rad, r,'g.')
plt.show()Output :
3. Кардиоида : Кардиоида — это геометрическое место точки на окружности окружности, когда она катится по другой такой же окружности. Здесь r определяется как:
Where, a = length of axis of cardioid
Example :
Python3
importnumpy as np
importmatplotlib.pyplot as plt
ИмпортMATH
PLT.Axes (Программа=44444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444440345
a=4
rads=np.arange(0, (2*np. pi),0.01)
forradinrads:
r=a+(a*np.cos(rad))
plt.polar(rad,r,'g.')
plt.show()Вывод:
из его конечных точек. Здесь r определяется как:
Example:
Python3
importnumpy as np
importmatplotlib.pyplot as plt
plt. Оси (Проекция='Polar')
RADS=444.ARNGE
=444.ARNGE=444.0344 ,2*np.pi,0.001)
forradinrads:
r=rad
plt.polar(rad, r,'g.')
plt.show()Вывод:
5. Rhodonea : Кривая Rhodonea или Rose представляет собой синусоиду в форме розы, построенную в полярных координатах. Here, r is defined as :
Where,
- a = length of petals
- n = number of petals
Example:
Python3
importnumpy как np
импортmatplotlib.pyplot as plt
plt.axes(projection='polar')
a=1
N=6
RADS=NP.Arne0345np.pi,0.001)
forradinrads:
r=a*np .cos(n
*rad)
plt.polar(rad, r,'g.')
plt.show()Вывод:
Полярные и декартовы координаты
... и как конвертировать между ними.
Спешите? Прочитайте резюме. Но сначала прочтите, почему:
Чтобы определить, где мы находимся на карте или графике, есть две основные системы:
Декартовы координаты
Используя декартовы координаты, мы отмечаем точку с помощью , как далеко вдоль и , как далеко вверх это:
Полярные координаты
Используя полярные координаты, мы отмечаем точку как далеко и какой угол это:
Преобразование
Преобразование из декартовых координат в полярные
Когда мы знаем точку в декартовых координатах (x,y) и хотим, чтобы она была в полярных координатах (r, θ ), мы решаем прямоугольный треугольник с двумя известными сторонами .
Пример. Что такое (12,5) в полярных координатах?
Используйте теорему Pythagoras, чтобы найти длинную сторону (гипотенуза):
R 2 = 12 2 + 5 2
R = √ (12 2 + 5 2)
)))))))))))))).г = √ (144 + 25)
г = √ (169) = 13
Используйте функцию касательной, чтобы найти угол:
тангенс( θ ) = 5 / 12
θ = тангенс -1 ( 5 / 12 ) = 22,6° (до одного десятичного знака)
Ответ : точка (12,5) равна (13, 22,6°) в полярных координатах.
Что такое
тан -1 ?Функция арктангенса:
- Тангенс берет угол и дает нам отношение,
- Арктангенс принимает отношение (например, "5/12") и дает нам угол.
Резюме : преобразовать декартовы координаты (x, y) в полярные координаты (r, θ):
- r = √ ( x 2 + y 2 )
- θ = тангенс -1 (г/х)
Примечание.
Калькуляторы могут дать неверное значение tan -1 () , когда значения x или y отрицательны... подробнее см. ниже.
Преобразование полярных координат в декартовы
Когда мы знаем точку в полярных координатах (r, θ ), и мы хотим, чтобы это было в декартовых координатах (x,y) мы решаем прямоугольный треугольник с известной длинной стороной и углом :
Пример: Что такое (13, 22,6°) в декартовых координатах?
Используйте функцию косинуса для x: cos( 22,6° ) = х / 13 Перестановка и решение: х = 13 × cos( 22,6° ) х = 13 х 0,923 х = 12,002... Использовать функцию синуса для y: sin( 22,6° ) = у / 13 Перестановка и решение: y = 13 × sin(22,6°) у = 13 × 0,391 г = 4,996. ..
Ответ: точка (13, 22,6°) равна почти точно (12, 5) в декартовых координатах.
Резюме : преобразование полярных координат (r, θ ) в декартовы координаты (x,y):
- x = r × потому что ( θ )
- y = r × sin( θ )
Как запомнить?
(x,y) в алфавитном порядке,
(cos,sin) также в алфавитном порядке Х и Y?Четыре квадранта
Когда мы включаем отрицательные значения, оси x и y делят
разделите пробел на 4 части:Квадранты I, II, III и IV
(они нумеруются против часовой стрелки)
При преобразовании полярных координат в декартовы все работает хорошо :
Пример: Что такое (12, 195°) в декартовых координатах?
r = 12 и θ = 195°
- x = 12 × cos(195°)
x = 12 × −0,9659...
x = −11,59 к 2 десятичные разряды- y = 12 × sin(195°)
y = 12 × −0,2588...
y = −3,11 до 2 десятичные разрядыИтак, точка находится на (-11,59, -3,11) , что находится в квадранте III
Но при переводе из декартовых координат в полярные ...
... калькулятор может дать неправильное значение тангенса -1
Все зависит от того, в каком квадранте находится точка! Используйте это, чтобы исправить вещи:
Квадрант Значение тангенса -1 я Использование значение калькулятора II Добавить 180° к значению калькулятора III Добавить 180° к значению калькулятора IV Добавить 360° к значению калькулятора Пример: P = (−3, 10)
P находится в квадранте II
- r = √((−3) 2 + 10 2 )
r = √109 = 10,4 десятичный разряд- θ = тангенс -1 (10/−3)
θ = тангенс -1 (-3,33...)
Значение tan -1 (−3,33...) равно −73,3°
Правило для квадранта II: сложить 180° к значению калькулятора
θ = −73,3° + 180° = 106,7°
Таким образом, полярные координаты точки (−3, 10) равны 9.1097 (10,4, 106,7°)
Пример: Q = (5, −8)
Q находится в квадранте IV
- r = √(5 2
7 + (−46) 291 р = √89 = 9,4 до 1 знака после запятой
- θ = тангенс -1 (-8/5)
θ = тангенс -1 (-1,6)Значение калькулятора для тангенса -1 (-1,6) равно -58,0°
Правило для квадранта IV: Сложить 360° к значению калькулятора
θ = −58,0° + 360° = 302,0°
Таким образом, полярные координаты точки (5, −8) составляют , θ ) в Декартовы координаты (x,y):
- x = r × cos( θ )
- y = r × sin( θ )
Для преобразования декартовых координат (x, y) в полярные координаты (r, θ):
- г = √ ( х 2 + у 2 )
- θ = тангенс -1 (г/х)
Значение tan -1 ( y/x ) , возможно, необходимо скорректировать:
- Квадрант Я использую значение калькулятора
- Квадрант II: Добавить 180°
- Квадрант III: Добавить 180°
- Квадрант IV: Добавить 360°
Упражнение: Прогулка в пустыне 2
Департамент математического образования J.
Департамент математического образования J.
Департамент математического образования
Дж. Уилсон, ЭМАП 6680Введение в Полярные уравнения
Дэвид УайзЭто исследование служит введением в полярные координаты система и полярные уравнения. Мы начнем с обсуждения полярную систему координат и развивать понимание основных полярные уравнения, которые производят несколько «знаменитых» семейств кривых, особенно спиралей, кардиоид и n-листных роз. Есть много других «знаменитых» кривых, которые нужно изучить. и каждый аспект этого расследования можно было бы изучить более подробно. глубина. Это исследование должно служить хорошим справочным инструментом и плацдарм для других расследований.
Эти демонстрационные графики были созданы с использованием программа-калькулятор, графический калькулятор 2.
2.1. Если вы этого не сделаете Если у вас есть это программное обеспечение, вы можете использовать демо-версию или приобрести программное обеспечение через Интернет по адресу http://www.pacifict.com. Эти демонстрации также могут быть созданы с использованием других графических программное обеспечение или графические калькуляторы.
Полярная система координат
Полярные уравнения основаны на полярной системе координат, который строится следующим образом.
- Начните с точки О, называемой полярной точкой отсчета или полюс , а луч, исходящий из О, называется полярная ось . Полярную ось обычно рисуют горизонтально и простираясь вправо (точно так же, как положительная часть оси x в прямоугольной системе координат).
- Каждая точка P затем помечается парой координат (р, к) .
- r это направленное расстояние от O до P и может быть любым действительным числом.
- q угол , направленный от полярной оси к отрезку OP. Следуйте законам тригонометрии, установить вращение против часовой стрелки как положительную меру угла и повороты по часовой стрелке как мера отрицательного угла.
- Полярная точка не уникальна (как и прямоугольная точка). Каждая полярная точка имеет бесконечное число пар координат, так как добавление или вычитание на кратное 2p обеспечивает вращение в одну и ту же сторону терминала. Значение, (р, к) и (р, к) д + 2кп) , где k — любое целое число, — координаты одной и той же точки. В кроме того, (r, q) и (-r, q + p) и (-r, q - р) - координаты одной и той же точки.
Связь между полярными координатами и прямоугольными координаты следующие.
- Для преобразования полярных координат в прямоугольные, учитывая (r, q) , тогда x = r cos д и y = r sin q .
- Чтобы преобразовать прямоугольные координаты в полярные, учитывая (x, у) , затем р 2 = х 2 + y 2 и желтовато-коричневый д = у/х .
Взгляд на полярные уравнения
Спирали:
Семейство кривых спирали производится общее уравнение r = aq.
Следующий график представляет собой уравнения:
r = 0,2q, r = 0,5q и r = д с qmin = 0 и qmax = 2p. и контролирует «размер» или «герметичность» и скаляр спирали. Диапазон q на графике представляет 1 положительное и, следовательно, вращение против часовой стрелки. Как qmax увеличивается до +бесконечности, r увеличивается до +бесконечности.
Регулировка диапазон q производит следующий график:
г = 0,5q с qmin = -2p и qmax = 2p График теперь включает 1 отрицательный и следовательно, вращение по часовой стрелке. При приближении qmin к -бесконечности r приближается к -бесконечности. Результат отрицательного и положительного вращения в «зеркальном отображении» или «перевороте» о вертикальная ось. Возвращаясь к и , когда и отрицательные, получается следующий график.
r = 0,5q и r = -0,5q с qмин = 0 и qmax = 2п Негатив производит поворот на p (или -p) графа +a .
Чтобы изучить семейство спиральных кривых подробнее об использовании Graphing Calculator 2.2.1 в качестве вспомогательного приложения, нажмите здесь .
Кардиоиды:
Семейство кардиоидных кривых названы в честь их формы сердца и производятся следующие общие уравнения.
r = а(cosq+1), r=a(cosq-1), r = a(sin q + 1) и r = a(sin q - 1) Сходство кардиоид:
- Для получения любой кардиоиды диапазон д должно равняться расстоянию 2п. Диапазон может включать любую комбинацию qmin и qmax, если расстояние вращения равно 2п. Поэтому стандартно установить qmin = 0 и qmax = 2р.
- Графики, созданные r = a(cos q + 1) и r = a(cos q - 1) идентичны друг другу.
- Графики, созданные r = а (грех q + 1) и r = a(sin q - 1) идентичны друг другу.
Следующий график представляет собой два наиболее основные кардиоиды.
r = cos q + 1 и r = sin q + 1 Замена косинуса на синус приводит к р / 4 вращение кардиоиды. Обратите внимание на перехваты каждого из графики по отношению к соответствующим уравнениям. Смотря на только косинусные кардиоиды, эффект и показан на следующий график.
r = cos q + 1, r = 2 (cos q + 1), и r = 0,5 (cos q + 1) и управляет «размером» и является скаляром кардиоиды. Опять же, обратите внимание на точки пересечения каждого из графиков в отношении к соответствующим уравнениям. Горизонтальные пересечения 0 и 2 и , а вертикальные точки пересечения и и -а . и имеют такое же влияние на синусоидальные кардиоиды, но не забудьте принять во внимание вращение p/4. Следовательно, горизонтальные пересечения и и - и вертикальные пересечения равны 0 и 2 а . Если и отрицательные, следующие результаты графика:
r = cos q + 1 и r = -cos q + 1 -а производит «переворот» вокруг вертикальной оси. - оказывает такое же влияние на синусоидальные кардиоиды, но "флип" находится относительно горизонтальной оси.
Чтобы изучить семейство кардиоидных кривых подробнее об использовании Graphing Calculator 2.
2.1 в качестве вспомогательного приложения, нажмите здесь .
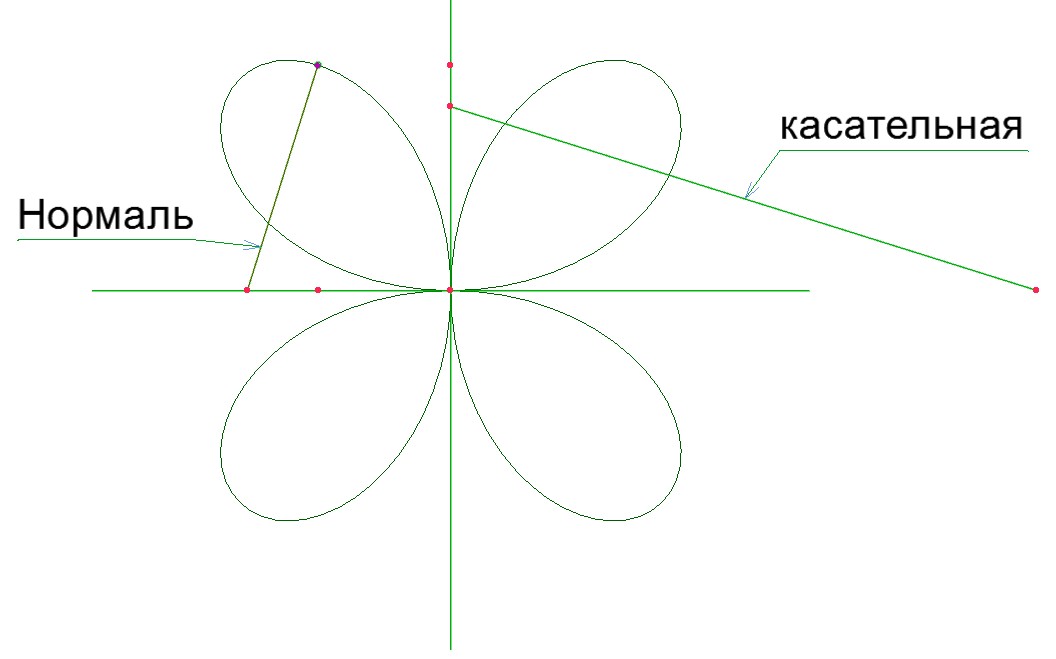
Розы без листьев:
роза семейство кривых названы в честь их формы цветка и производятся следующими общие уравнения.
r = a cos (nq) и r = a sin (nq) Сходства между розой и кардиоидой уравнения:
- и управляет «размером» и является скаляром розы. Однако для роз горизонтальные и/или вертикальные точки пересечения находятся в 0 и .
- Замена косинуса синусоидой в повороте р/4 розы. Поэтому все горизонтальные перехваты становятся вертикальными перехватами и все вертикальные перехваты становятся горизонтальными перехватами.
- -а производит «переворот» относительно вертикальной оси для косинуса розы и «флип» вокруг горизонтальной оси для синуса розы.
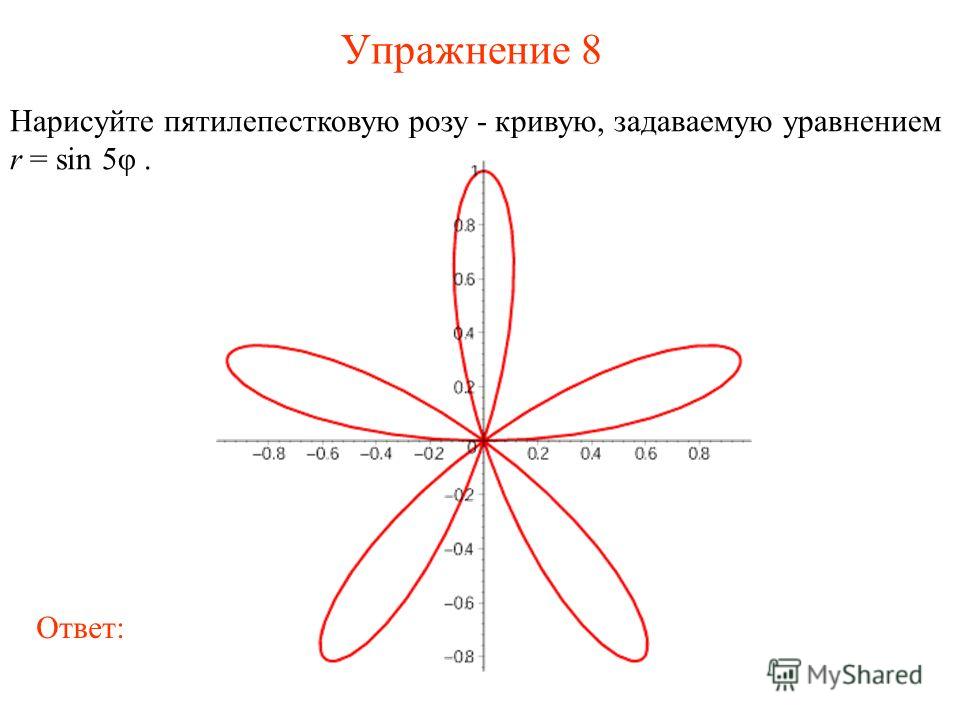
На следующем графике показана роза с n листами, когда n нечетно.
r = 2 cos q, r = 2 cos (3q) и г = 2 потому что (5q) Для получения нечетной n-листной розы диапазон из q должно равняться расстоянию p.
Диапазон может включать любую комбинацию qmin и qmax, пока расстояние вращения равно p. Следовательно стандартное значение по умолчанию qmin = 0 и qmax = 2p дважды отображает множество всех точек вокруг кривой. n = количество листьев розы . При n = 1 возникает частный случай, однолистная роза представляет собой круг. Обратите внимание, что перехваты находятся на 0 и и .
Чтобы больше узнать о разнолистных розах, используйте Графический калькулятор 2.2.1 в качестве вспомогательного приложения, нажмите здесь .
Следующий граф представляет розы с n листами, когда n четно.
r = 2 cos (2q) и r = 2 cos (4q) Чтобы получить ровную n-листную розу, диапазон q должен равняться расстоянию 2p. Ассортимент может включать любая комбинация qmin и qmax, пока расстояние вращения равно 2п. Поэтому стандартно установить qmin = 0 и qmax = 2р. п = 1/2 количества листьев розы . Уведомление что точки пересечения находятся на 0, a, и -a .
Для более подробного изучения однолистных роз с помощью Графический калькулятор 2.2.1 в качестве вспомогательного приложения, нажмите здесь .
Если у вас есть какие-либо комментарии относительно этого расследования, которые было бы полезно, особенно для использования на уровне средней школы, пожалуйста, отправьте электронное письмо по адресу [email protected] .
Возврат на мою домашнюю страницу.
Системы координат
Системы координатСистемы координат
О системах координат
COMSOL Multiphysics по умолчанию использует глобальную декартову систему координат для указания свойств материалов, нагрузок и ограничений во всех физических интерфейсах и на всех уровнях геометрических объектов (точки, ребра, границы и домены). В граничных условиях и областях жидкости глобальная система обычно интерпретируется как имеющая фиксированные направления осей в пространстве; то есть это система пространственного каркаса.
При задании свойств твердых материалов глобальные системные оси вместо этого фиксируются в материале. Другими словами, в этом контексте это система материального каркаса.
Таким образом, не только глобальная система координат, но и системы координат, определенные как поворот относительно глобальной системы, зависят от контекста. Такие системы в совокупности называются относительными системами координат, чтобы отличить их от абсолютных систем координат.
Координаты пространственной декартовой системы координат по умолчанию имеют следующие имена в 2D и 3D (в 2D осесимметричных геометриях COMSOL Multiphysics использует цилиндрические координаты):
Геометрия
Имя по умолчанию пространственных координат
2D
х у
3D
х у г
Осевая симметрия 2D
r z
В 3D изображение отображается в левом нижнем углу графического окна, чтобы указать ориентацию глобальной системы координат.
Определяемые пользователем системы координат могут использоваться на всех уровнях геометрического объекта для упрощения процесса моделирования. В физических интерфейсах вы можете использовать эти системы координат для определения ортотропных и анизотропных свойств материала, которые не выровнены с глобальной декартовой системой координат. Чтобы выбрать систему координат, выберите ее из списка Система координат в разделе Выбор системы координат. Список содержит глобальную систему координат (по умолчанию) и любые другие системы координат, которые вы добавили, например, см. рис. 5-3.
Рисунок 5-3: Пример параметров, доступных в списке Система координат. По умолчанию используется глобальная система координат.
См. Таблицу 5-17 для обзора доступных систем координат. В частности, обратите внимание, что некоторые системы координат задают абсолютные направления в пространстве, в то время как другие задают поворот относительно глобальной системы по умолчанию, как указано в столбце «Тип» в таблице.
Чтобы добавить систему координат к любому компоненту:
•
На панели инструментов «Определения» выберите элементы системы координат в меню «Системы координат» или
.
•
Щелкните правой кнопкой мыши узел Определения () и выберите параметр в подменю Системы координат.
Таблица 5-17: Описание системы координат
Имя и ссылка
значок Тип
Описание
Базовая векторная система
Родственник
1D, 2D и 3D.
Задайте это, используя набор базовых векторов, чтобы сформировать систему координат.
Пограничная система
Абсолют
2D и 3D. Локальная система базовых векторов на двумерных границах (t, n) и трехмерных границах (t1, t2, n). Используйте его для приложения нагрузок, которые действуют в нормальном или тангенциальном направлении на границу, которая не выровнена с глобальной декартовой системой координат. Эта система координат всегда доступна. Вы можете добавить подузлы Reverse Normal и Domain Normal, чтобы изменить направление нормали для некоторых границ и изменить направление нормали на внешней стороне некоторых доменов, соответственно.
Комбинированная система
1D, 2D и 3D.
Используйте комбинированную систему, когда вам нужно использовать разные системы координат в разных областях, например, для представления некоторого свойства материала. Вы можете добавить применимые системы координат в качестве подузлов, каждый с выбором геометрического объекта.
Композитная система
То же, что и базовая система
1D, 2D и 3D. Создайте составную систему координат из базовой системы и системы, определяющей оси относительно базовой системы.
Цилиндрическая система
Абсолют
2D и 3D. Используйте цилиндрическую систему, когда требуется вращательная симметрия относительно оси.
Недоступно в геометриях с двумерной осевой симметрией, где цилиндрическая система координат является системой координат по умолчанию.
Сопоставленная система
Абсолют
1D, 2D и 3D. Сопоставленная система может иметь дело с перемещенными и повернутыми системами координат. Используйте это, чтобы создать систему, которая определяет отображение из системы координат фрейма.
Повернутая система
Родственник
2D и 3D. Используйте повернутую систему, чтобы определить вращение относительно направления вне плоскости или углов Эйлера в 2D и углов Эйлера в 3D.
Масштабирующая система
Абсолют
Только для физики, поддерживающей бесконечные элементы или идеально согласованные слои.
Используйте эту систему координат, похожую на систему координат с картой, для произвольной деформации домена.
Сферическая система
Абсолют
Только 3D. Используйте сферическую систему, когда необходимо задать поле или свойство с использованием сферических координат.
Система из геометрии
Абсолют
Только 3D. Используйте систему координат из рабочей плоскости в 2D-геометрической или 3D-геометрической детали.
•
Группировка узлов по пространственному размеру и типу
•
Переменные пространственных координат
Использование эффекта «Полярные координаты»
Эффект «Полярные координаты» в After Effects — это полезный инструмент, который можно использовать для создания эффекта искажения изображения или анимации.
Он переключает положение пикселя по осям X и Y в полярной системе координат.
Например, если вы начнете с длинного тонкого прямоугольника и увеличите интерполяцию до 100%, прямоугольник превратится в круг. С другой стороны, если вы начнете с круглого изображения, оно развернется в линию. Добавление движения и других эффектов может создать психоделические эффекты, которые выглядят профессионально.
В этом уроке вы узнаете, как использовать эффект «Полярные координаты» в After Effects.
Как использовать эффект полярных координат в After EffectsЧтобы использовать эффект «Полярные координаты» в After Effects, выполните следующие действия:
Импорт видеоматериала
Чтобы использовать эффект «Полярные координаты», вы можете импортировать существующее изображение, ввести текст с помощью инструмента «Текст» или использовать базовую форму, например звезду или прямоугольник.
Добавление эффекта полярных координат
Выделив слой с изображением, текстом или фигурой, перейдите к Эффект > Искажение > Полярные координаты.
После этого на панели управления эффектами появятся настройки полярных координат.
Отрегулируйте настройки
Существует две настройки полярных координат:
Как выглядит эффект полярных координат при использовании?
- Интерполяция: Эта настройка определяет степень искажения изображения. При 0% искажения отсутствуют. Вы можете изменить настройку до 100%, что полностью изменит координаты с прямоугольных на полярные и наоборот.
- Тип преобразования: Можно выбрать между полярной и прямоугольной (прямоугольной) и прямоугольной полярной. Это изменит координаты каждого пикселя либо с прямоугольной координаты по осям X и Y, либо на полярные координаты с радиусом и градусом. Например, если у вас есть прямоугольная координата (5, 7), она изменится на полярную координату с радиусом 5 и степенью 7. Горизонтальные линии станут кругами, а вертикальные линии станут радиальными линиями.
Эффект «Полярные координаты» может придать объектам вид, будто их выворачивают наизнанку.
Верх вашего изображения становится центром круга, если вы измените настройку интерполяции на 100%.
Вот пример из руководства пользователя After Effects.
Другой пример, взятый из учебника School of Motion, показывает, как можно превратить прямоугольный графический дизайн в вращающийся круг, похожий на шестеренку.
При включении эффекта «Полярные координаты» изображение может создавать закрученные, искаженные изображения, из-за которых вам может показаться, что вы падаете в туннель.
Как еще можно использовать эффект полярных координат?Для создания еще более потрясающей графики эффект «Полярные координаты» можно комбинировать с другими эффектами.
Полярные координаты и жалюзи
Одним из популярных вариантов является эффект жалюзи. Это добавляет равномерно расположенные разрезы по всему изображению. В сочетании с полярными координатами он создает закрученный, звездообразный вид линий вместо простых вертикальных разрезов.
Еще один интересный эффект — сочетание полярных координат с эффектом шахматной доски. Это создает искривленный радиальный вид шахматной доски вместо горизонтальных и вертикальных линий.
Вы можете увидеть обе комбинации в этом видео на YouTube от Jake in Motion.
Эффект деформации в Photoshop
Полярные координаты аналогичны другим типам эффектов деформации или искажения, которые можно найти в других программах для редактирования видео и фотографий, таких как Photoshop. Например, эффект «Деформация» в Photoshop позволяет накладывать одно изображение на другое.
Полярные координаты с текстом
Вы также можете использовать полярные координаты с текстом. Если текст расположен горизонтально, эффект «Полярные координаты» заставит его вращаться по кругу. Если вы ориентируете текст вертикально, полярные координаты сделают его спиральным в виде звезды.
Полярные координаты с компенсацией оптики
Если вам нравится внешний вид анимации с полярными координатами, но вы хотите, чтобы она заполнила весь экран, вы можете комбинировать ее с компенсацией оптики.
Когда это применяется, изображение искажается, как если бы оно было снято широкоугольным объективом. Это также может помочь создать эффект туннеля, если вы используете настройку Rect to Polar. Если вы хотите, чтобы центр вашего круга полярных координат был пуст, вы можете создать слой Matte и замаскировать верхнюю часть изображения. Вы можете растушевать край, чтобы создать плавный переход.
Векторизация изображения
Если у вас есть изображение, к которому вы хотите добавить эффект полярных координат, может быть полезно сначала векторизовать изображение. Векторная графика имеет множество преимуществ перед другими типами изображений.
Это:
- Легко управляемый
- Масштабируемый
- Многоразовый
- Легко анимированный
- Интерактивный
- Многоцелевой
- Редактируется с кодом
- Независимое разрешение
С векторным изображением вы можете получить лучшие результаты при использовании полярных координат.
Полярные координаты с панорамными изображениями
Популярное использование полярных координат — создание панорамных снимков, например, городских пейзажей, и преобразование их в круглые изображения. Для этого вам нужно добавить небольшой дубликат участка левого края картинки и переместить его на правый край. Это гарантирует, что края плавно выровняются, когда они соединены. Вам также нужно перевернуть изображение вверх ногами, чтобы небо стало центром изображения. Когда вы включите полярные координаты, вы должны получить круговой городской пейзаж.
Используйте шаблоны Storyblocks для простого создания видеоконтентаЧтобы улучшить рабочий процесс создания видеоконтента, вы можете попробовать несколько готовых шаблонов. Шаблон избавляет вас от необходимости создавать эффект самостоятельно. Storyblocks предлагает широкий выбор шаблонов, включая шаблоны Adobe After Effects и шаблоны Adobe Premiere Pro.
Вы можете попробовать добавить эффект полярных координат к некоторым из этих шаблонов, чтобы посмотреть, какие результаты вы получите.

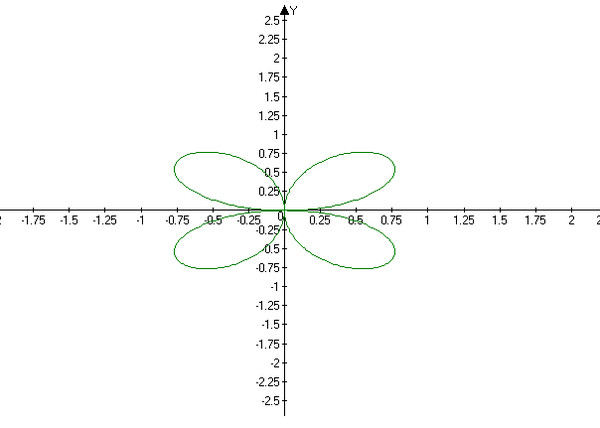 2.4. Кривые в полярной системе координат
2.4. Кривые в полярной системе координат Для всех точек плоскости, не
совпадающих с полюсом .
Для всех точек плоскости, не
совпадающих с полюсом . 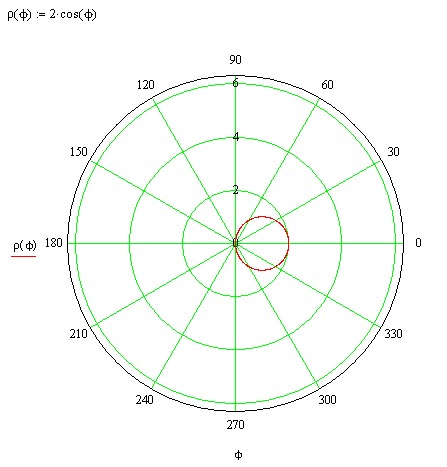 32
32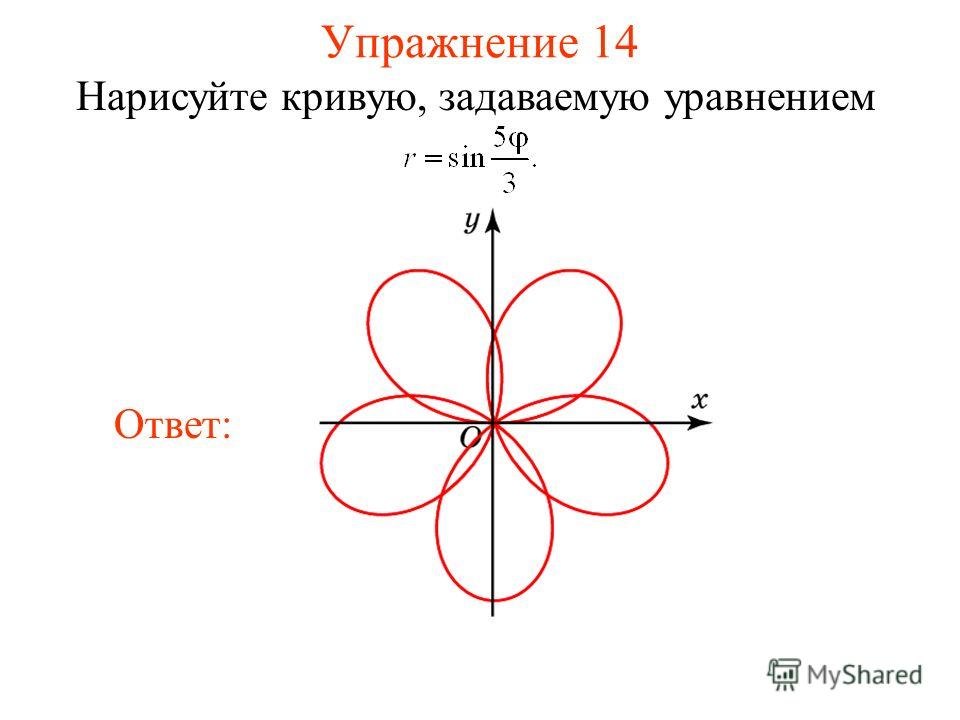 Из уравнения кривой следует, что если мы будем
увеличивать , то будет возрастать. Кривая построена на рисунке
33.
Из уравнения кривой следует, что если мы будем
увеличивать , то будет возрастать. Кривая построена на рисунке
33.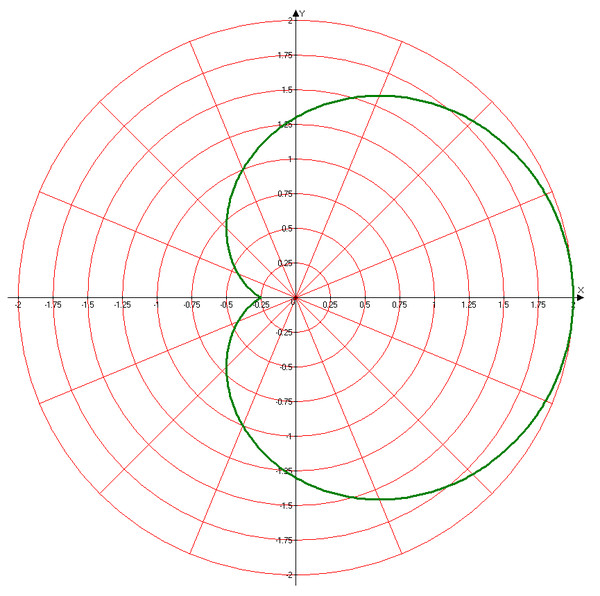 34
34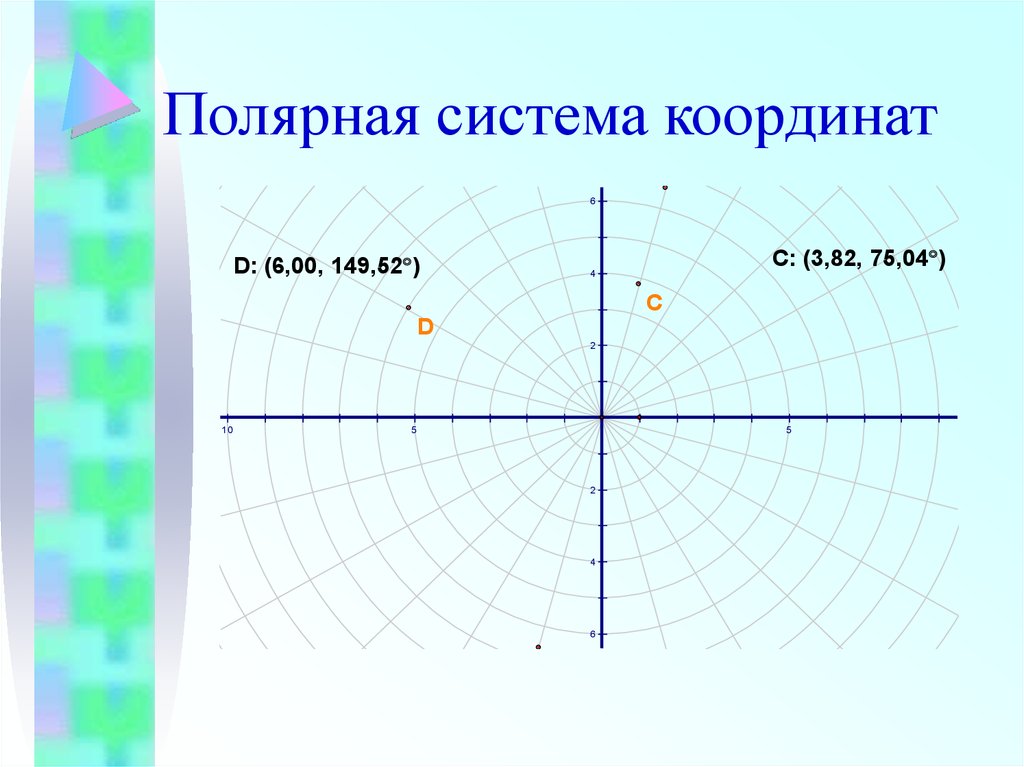 Поэтому найдем
несколько точек на кривой при из промежутка и нанесем их на плоскость в полярной системе
координат.
Поэтому найдем
несколько точек на кривой при из промежутка и нанесем их на плоскость в полярной системе
координат.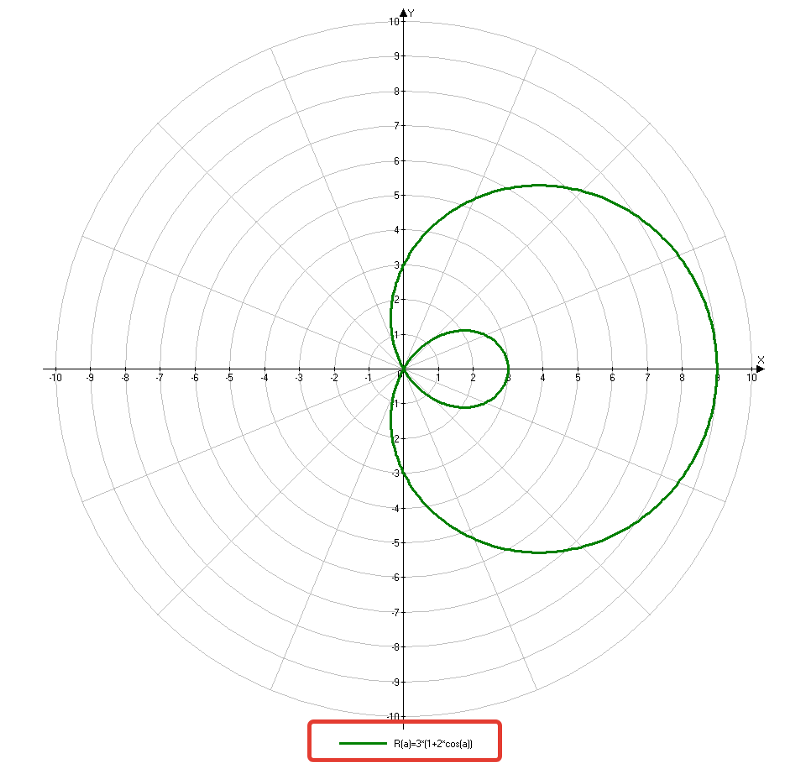 36
36 05.2014, 18:40
05.2014, 18:40 
 . 2*Pi, coords = polar)
. 2*Pi, coords = polar) Но выбирая даже между, все равно ничего не показывается. Какая тут может быть ошибка?
Но выбирая даже между, все равно ничего не показывается. Какая тут может быть ошибка?  Как я понимаю это (а может ?). В любом случае ошибка в том, что это иностранные пакеты, и у них тангенс обозначается . Поэтому например для первой функции график строится так
Как я понимаю это (а может ?). В любом случае ошибка в том, что это иностранные пакеты, и у них тангенс обозначается . Поэтому например для первой функции график строится так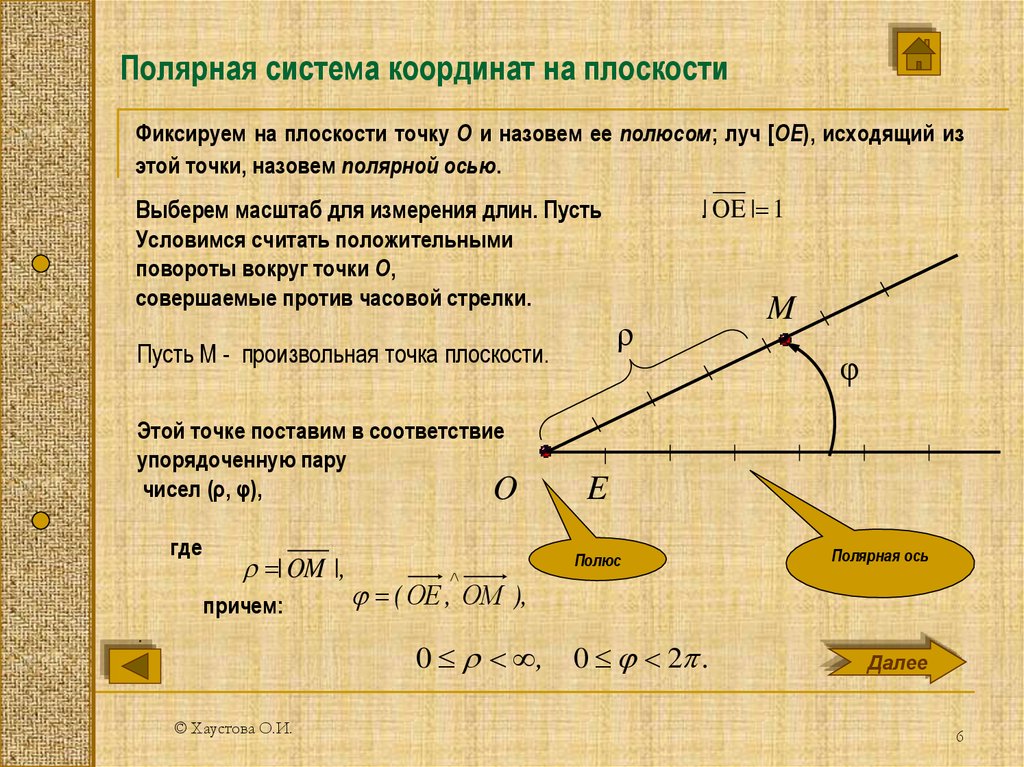 (2*tan((x/2))-x)}, x = (Pi/4) .. (Pi/3), coords = polar, color = red)
(2*tan((x/2))-x)}, x = (Pi/4) .. (Pi/3), coords = polar, color = red)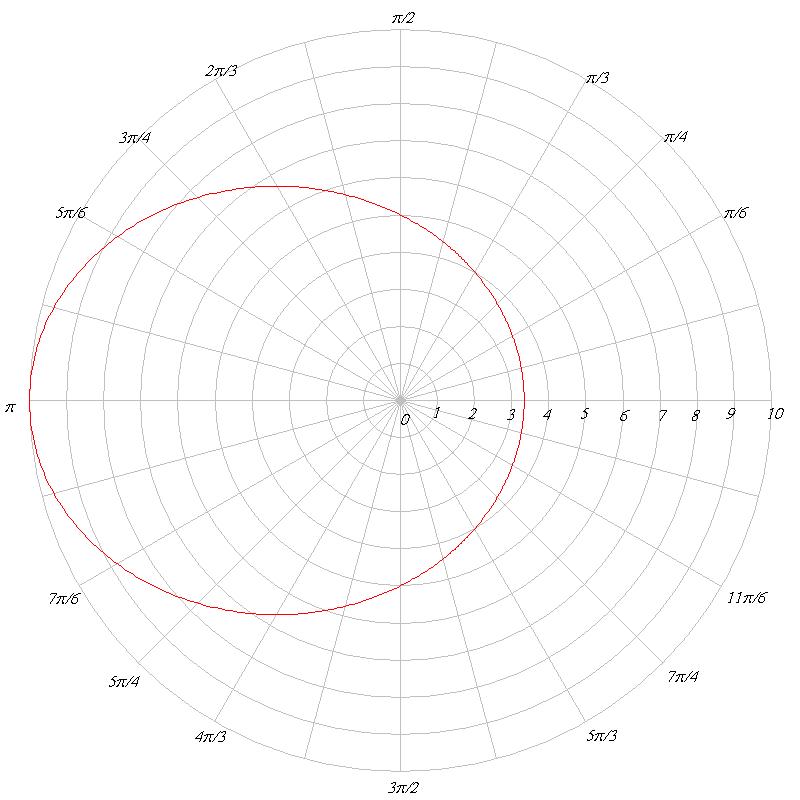 0241
0241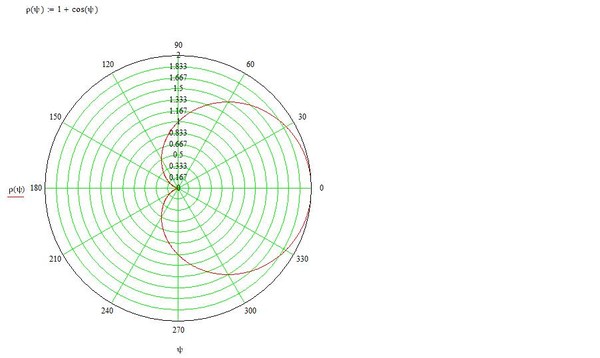 axes( проекция
axes( проекция  pyplot as plt
pyplot as plt 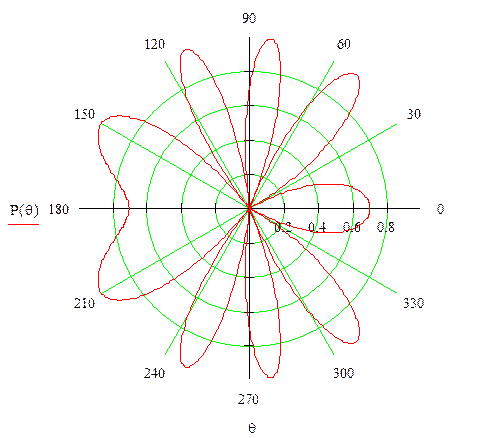 sqrt((a
sqrt((a 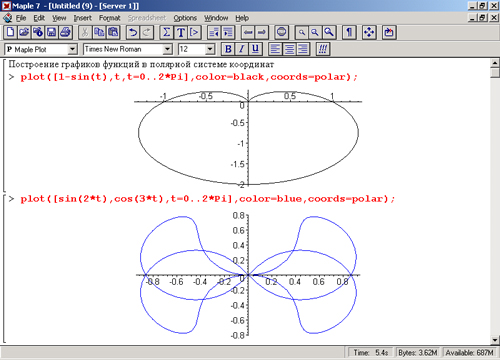 pyplot as plt
pyplot as plt  cos(rad))
cos(rad)) 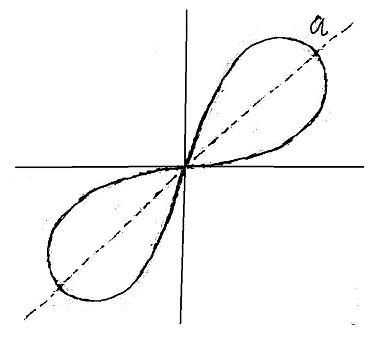 ARNGE
ARNGE 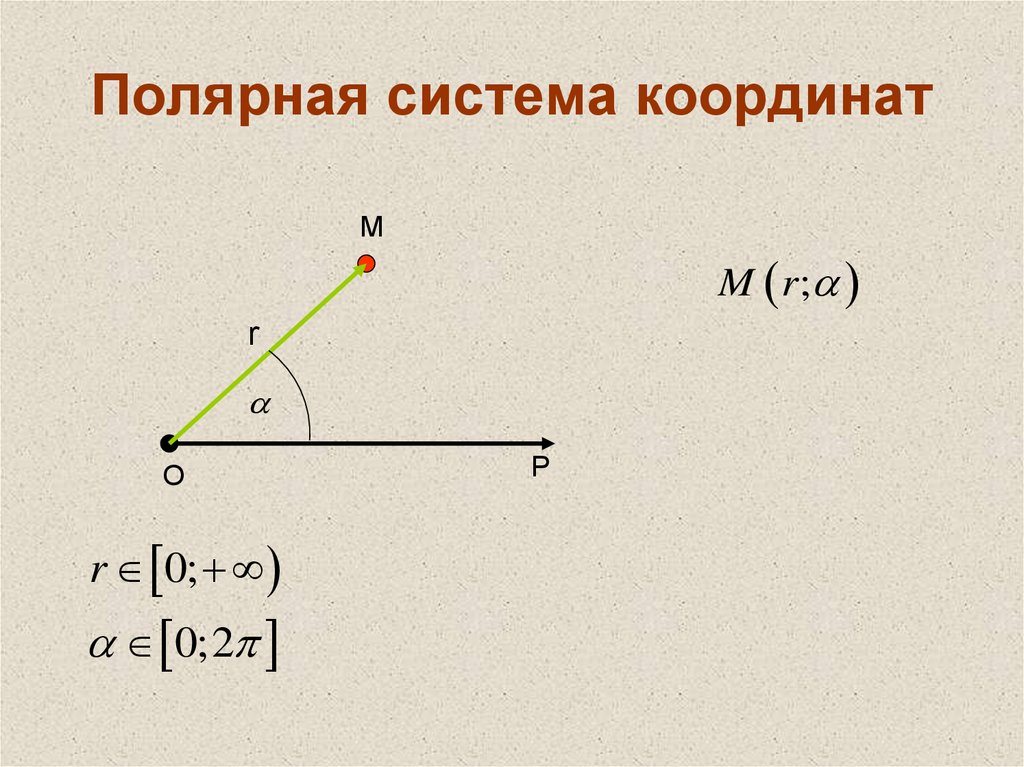 pyplot as plt
pyplot as plt 
 Калькуляторы могут дать неверное значение tan -1 () , когда значения x или y отрицательны... подробнее см. ниже.
Калькуляторы могут дать неверное значение tan -1 () , когда значения x или y отрицательны... подробнее см. ниже.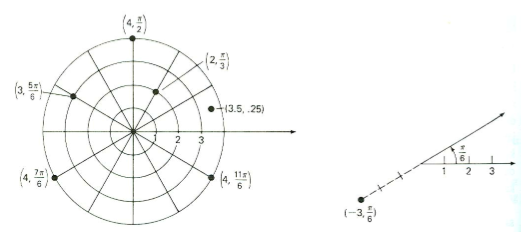 ..
..  ..
..  ..)
..) Департамент математического образования J.
Департамент математического образования J.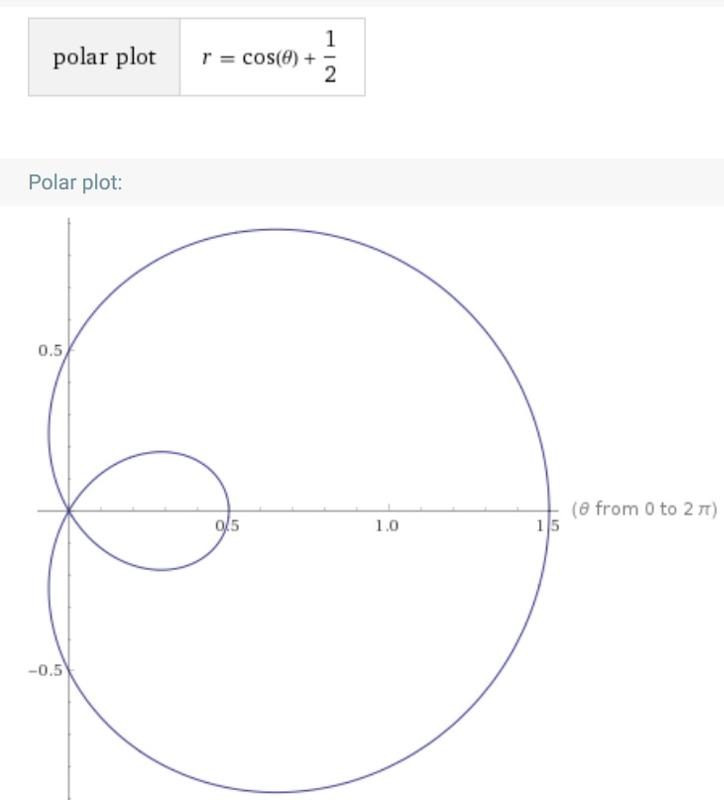 2.1. Если вы этого не сделаете
Если у вас есть это программное обеспечение, вы можете использовать демо-версию или приобрести
программное обеспечение через Интернет по адресу http://www.pacifict.com. Эти демонстрации также могут быть созданы с использованием других графических
программное обеспечение или графические калькуляторы.
2.1. Если вы этого не сделаете
Если у вас есть это программное обеспечение, вы можете использовать демо-версию или приобрести
программное обеспечение через Интернет по адресу http://www.pacifict.com. Эти демонстрации также могут быть созданы с использованием других графических
программное обеспечение или графические калькуляторы.
 Регулировка
диапазон q производит
следующий график:
Регулировка
диапазон q производит
следующий график:
 2.1 в качестве вспомогательного приложения, нажмите здесь .
2.1 в качестве вспомогательного приложения, нажмите здесь .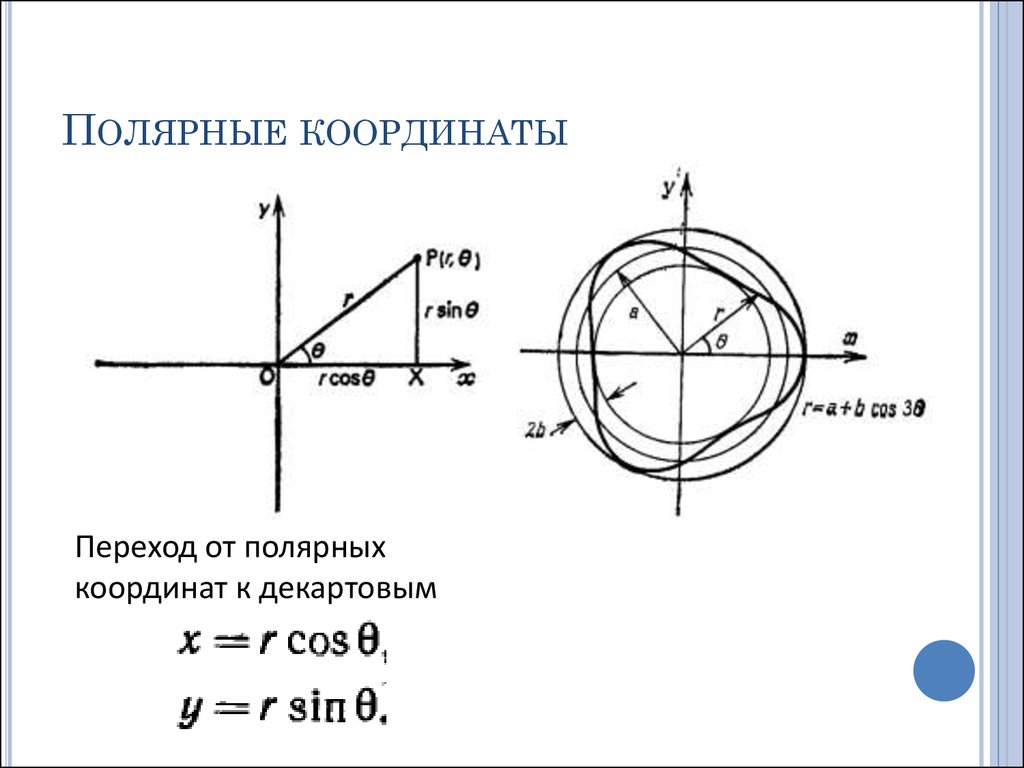 Диапазон может включать любую комбинацию qmin
и qmax,
пока расстояние вращения равно p. Следовательно
стандартное значение по умолчанию qmin = 0 и qmax = 2p
дважды отображает множество всех точек
вокруг кривой. n = количество листьев розы .
При n = 1 возникает частный случай, однолистная роза представляет собой круг.
Обратите внимание, что перехваты находятся на 0 и и .
Диапазон может включать любую комбинацию qmin
и qmax,
пока расстояние вращения равно p. Следовательно
стандартное значение по умолчанию qmin = 0 и qmax = 2p
дважды отображает множество всех точек
вокруг кривой. n = количество листьев розы .
При n = 1 возникает частный случай, однолистная роза представляет собой круг.
Обратите внимание, что перехваты находятся на 0 и и .
 При задании свойств твердых материалов глобальные системные оси вместо этого фиксируются в материале. Другими словами, в этом контексте это система материального каркаса.
При задании свойств твердых материалов глобальные системные оси вместо этого фиксируются в материале. Другими словами, в этом контексте это система материального каркаса.
 Задайте это, используя набор базовых векторов, чтобы сформировать систему координат.
Задайте это, используя набор базовых векторов, чтобы сформировать систему координат. Используйте комбинированную систему, когда вам нужно использовать разные системы координат в разных областях, например, для представления некоторого свойства материала. Вы можете добавить применимые системы координат в качестве подузлов, каждый с выбором геометрического объекта.
Используйте комбинированную систему, когда вам нужно использовать разные системы координат в разных областях, например, для представления некоторого свойства материала. Вы можете добавить применимые системы координат в качестве подузлов, каждый с выбором геометрического объекта.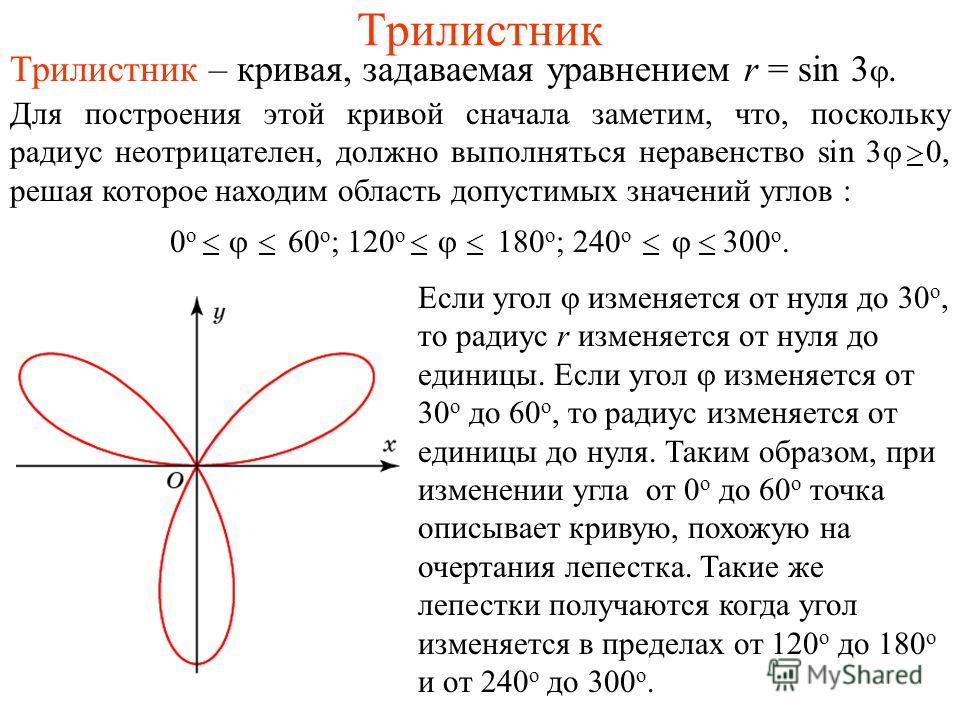 Недоступно в геометриях с двумерной осевой симметрией, где цилиндрическая система координат является системой координат по умолчанию.
Недоступно в геометриях с двумерной осевой симметрией, где цилиндрическая система координат является системой координат по умолчанию. Используйте эту систему координат, похожую на систему координат с картой, для произвольной деформации домена.
Используйте эту систему координат, похожую на систему координат с картой, для произвольной деформации домена.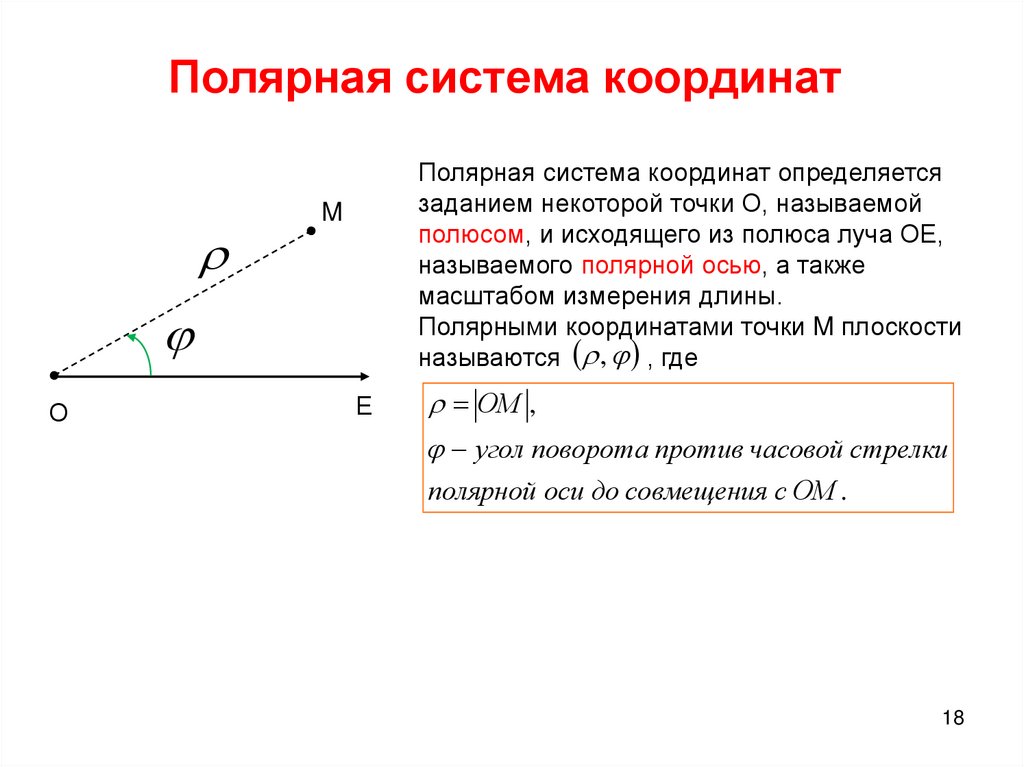 Он переключает положение пикселя по осям X и Y в полярной системе координат.
Он переключает положение пикселя по осям X и Y в полярной системе координат.
 Верх вашего изображения становится центром круга, если вы измените настройку интерполяции на 100%.
Верх вашего изображения становится центром круга, если вы измените настройку интерполяции на 100%.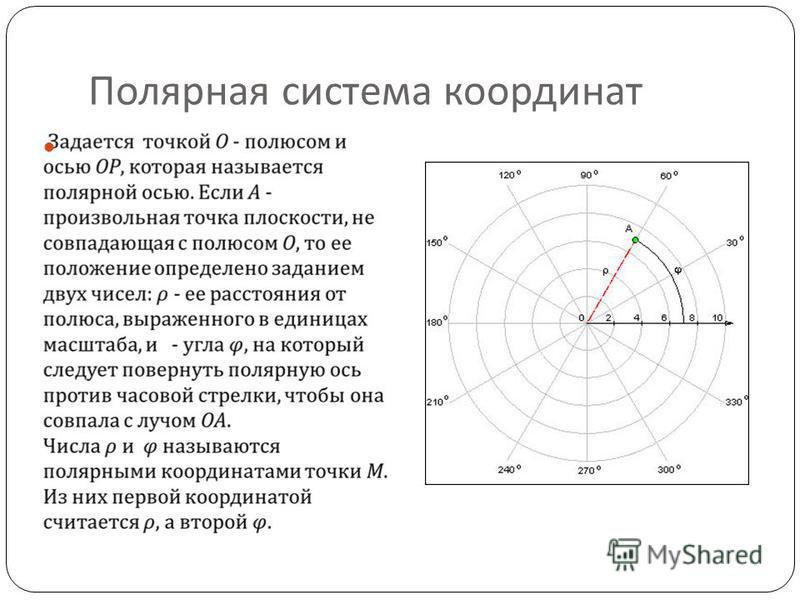
 Когда это применяется, изображение искажается, как если бы оно было снято широкоугольным объективом. Это также может помочь создать эффект туннеля, если вы используете настройку Rect to Polar. Если вы хотите, чтобы центр вашего круга полярных координат был пуст, вы можете создать слой Matte и замаскировать верхнюю часть изображения. Вы можете растушевать край, чтобы создать плавный переход.
Когда это применяется, изображение искажается, как если бы оно было снято широкоугольным объективом. Это также может помочь создать эффект туннеля, если вы используете настройку Rect to Polar. Если вы хотите, чтобы центр вашего круга полярных координат был пуст, вы можете создать слой Matte и замаскировать верхнюю часть изображения. Вы можете растушевать край, чтобы создать плавный переход.