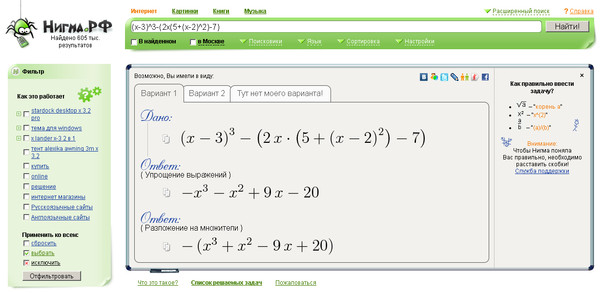
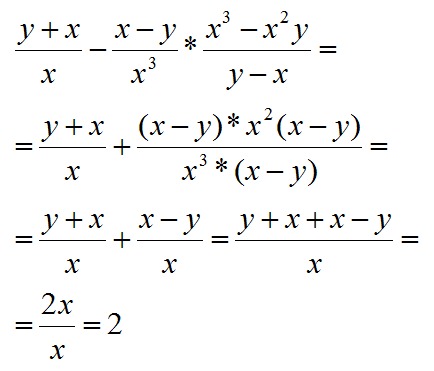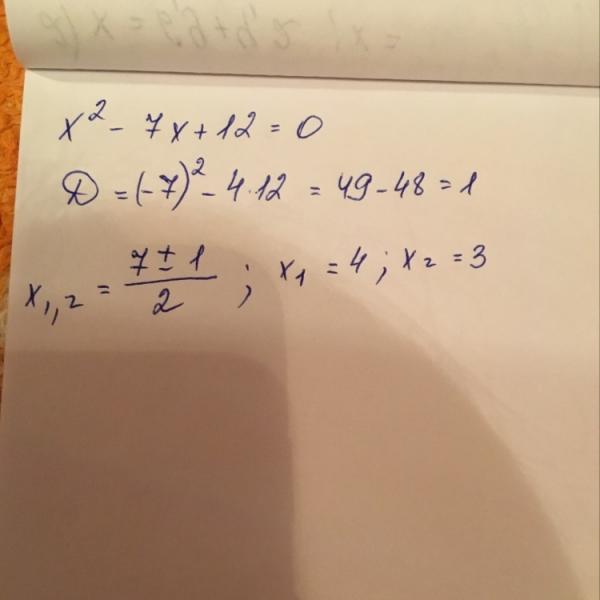Как ты помнишь, \( \displaystyle t\) не является конечным решением уравнения. Возвращаемся к изначальной переменной:
Дробно-рациональная замена в общем виде
\( \displaystyle t=\frac{{{P}_{n}}\left( x \right)}{{{Q}_{m}}\left( x \right)}\)
\( \displaystyle {{P}_{n}}\left( x \right)\) и \( \displaystyle {{Q}_{m}}\left( x \right)\) − многочлены степеней \( \displaystyle n\) и \( \displaystyle m\) соответственно.
Например, при решении возвратных уравнений, то есть уравнений вида
\( \displaystyle a{{x}^{4}}+b{{x}^{3}}+c{{x}^{2}}+bx+a=0,\text{ }a\ne 0\),
обычно используется замена \( \displaystyle t=x+\frac{1}{x}\). {2}}-10x+7>0\) при всех \( \displaystyle x\), так как \( \displaystyle D=100-4\cdot 4\cdot 7=-12<0\).
{2}}-10x+7>0\) при всех \( \displaystyle x\), так как \( \displaystyle D=100-4\cdot 4\cdot 7=-12<0\).
Значит, неравенство равносильно следующему: \( \displaystyle \frac{1}{x}<0\Rightarrow x<0\).
Итак, неравенство оказывается равносильно совокупности:
\( \displaystyle \left[ \begin{array}{l}\left\{ \begin{array}{l}y\ge -16;\\y<8;\end{array} \right.\\\left\{ \begin{array}{l}y\ge 9;\\y<10;\end{array} \right.\end{array} \right.\Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x\in \left[ -\frac{7}{2};-\frac{1}{2} \right]\cup \left( 0;+\infty \right)\\x<0\end{array} \right.\\\left\{ \begin{array}{l}x>0\\x<0\end{array} \right.\end{array} \right.\Rightarrow x\in \left[ -\frac{7}{2};-\frac{1}{2} \right].\)
Ответ: \( \displaystyle \left[ -\frac{7}{2};-\frac{1}{2} \right]\).
Замена переменных – один из важнейших методов решения уравнений и неравенств.
Решение квадратных уравнений
youtube.com/embed/_8kCIRbOpsQ» frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.
Квадратное уравнение — это уравнение вида ax2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, причем a ≠ 0.
Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:
- Не имеют корней;
- Имеют ровно один корень;
- Имеют два различных корня.
В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант.
Дискриминант
Пусть дано квадратное уравнение ax2 + bx + c = 0.
Тогда дискриминант — это просто число D = b2 − 4ac.
Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:
- Если D < 0, корней нет;
- Если D = 0, есть ровно один корень;
- Если D > 0, корней будет два.
Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:
Задача. Сколько корней имеют квадратные уравнения:
- x2 − 8x + 12 = 0;
- 5x2 + 3x + 7 = 0;
- x2 − 6x + 9 = 0.
Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a = 1, b = −8, c = 12;
D = (−8)2 − 4 · 1 · 12 = 64 − 48 = 16
Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
Аналогично разбираем второе уравнение:
a = 5; b = 3; c = 7;
D = 32 − 4 · 5 · 7 = 9 − 140 = −131.
Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a = 1; b = −6; c = 9;
D = (−6)2 − 4 · 1 · 9 = 36 − 36 = 0.
Дискриминант равен нулю — корень будет один.
Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.
Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.
Корни квадратного уравнения
Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:
Основная формула корней квадратного уравненияКогда D = 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D < 0, корней нет — ничего считать не надо.
Наконец, если D < 0, корней нет — ничего считать не надо.
Задача. Решить квадратные уравнения:
- x2 − 2x − 3 = 0;
- 15 − 2x − x2 = 0;
- x2
+ 12x + 36 = 0.
Первое уравнение:
x2 − 2x − 3 = 0 ⇒ a = 1; b = −2; c = −3;
D = (−2)2 − 4 · 1 · (−3) = 16.
D > 0 ⇒ уравнение имеет два корня. Найдем их:
Второе уравнение:
15 − 2x − x2 = 0 ⇒ a = −1; b = −2; c = 15;
D = (−2)2 − 4 · (−1) · 15 = 64.
D > 0 ⇒ уравнение снова имеет два корня. Найдем их
\[\begin{align} & {{x}_{1}}=\frac{2+\sqrt{64}}{2\cdot \left( -1 \right)}=-5; \\ & {{x}_{2}}=\frac{2-\sqrt{64}}{2\cdot \left( -1 \right)}=3. \\ \end{align}\]
Наконец, третье уравнение:
x2 + 12x + 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 122 − 4 · 1 · 36 = 0.
D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:
Например, первую:
\[x=\frac{-12+\sqrt{0}}{2\cdot 1}=-6\]
Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.
Неполные квадратные уравнения
Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:
- x2 + 9x = 0;
- x2 − 16 = 0.
Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:
Уравнение ax2 + bx + c = 0 называется неполным квадратным уравнением, если b = 0 или c = 0, т.е. коэффициент при переменной x или свободный элемент равен нулю.
Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид ax
Рассмотрим остальные случаи. Пусть b = 0, тогда получим неполное квадратное уравнение вида ax2 + c = 0. Немного преобразуем его:
Решение неполного квадратного уравненияПоскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−c/a) ≥ 0. Вывод:
- Если в неполном квадратном уравнении вида ax2 + c = 0 выполнено неравенство (−c/a) ≥ 0, корней будет два. Формула дана выше;
- Если же (−c/a) < 0, корней нет.
Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c/a) ≥ 0. Достаточно выразить величину x2 и посмотреть, что стоит с другой стороны от знака равенства.
Теперь разберемся с уравнениями вида ax2 + bx = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:
Вынесение общего множителя за скобкуПроизведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:
Задача. Решить квадратные уравнения:
- x2 − 7x = 0;
- 5x2 + 30 = 0;
- 4x2 − 9 = 0.
x2 − 7x = 0 ⇒ x · (x − 7) = 0 ⇒ x1 = 0; x2 = −(−7)/1 = 7.
5x2 + 30 = 0 ⇒ 5x2 = −30 ⇒ x2 = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.
4x
Смотрите также:
- Теорема Виета
- Следствия из теоремы Виета
- Тест на тему «Значащая часть числа»
- Метод коэффициентов, часть 1
- Однородные тригонометрические уравнения: общая схема решения
- Задача B4: строительные бригады
ГДЗ по математике 3 класс учебник Моро, Волкова 1 часть
- Тип: ГДЗ, Решебник.
- Автор: Моро М. И., Волкова С. И., Бантова М. А.
- Год: 2020.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
❤️️Ответ к странице 93. Математика 3 класс учебник 1 часть. Автор: М.И. Моро.
Решебник — страница 93Готовое домашнее задание
Номер 3.
Масса одного ящика с мандаринами 8 кг. Найди массу 9 коробок с бананами, если одна коробка с бананами на 3 кг легче одного ящика с мандаринами.
Ответ:
1) 8 − 3 = 5 (кг) – масса ящика с бананами. 2) 5 ∙ 9 = 45 (кг)
Ответ: 45 кг масса 9 коробок с бананами.
2) 5 ∙ 9 = 45 (кг)
Ответ: 45 кг масса 9 коробок с бананами.
Номер 4.
Реши уравнения, подбирая значения х.
Ответ: 72 : х = 9 8 ∙ х = 64 х : 7 = 4 х = 72 : 9 х = 64 : 8 х = 4 ∙ 7 х = 8 х = 8 х = 28
Номер 5.
Реши уравнения с устным объяснением.
Ответ:
Номер 6.
Найди значение выражения.
Ответ:
1) а : 7
если а = 49, то 49 : 7 = 7
если а = 35, то 35 : 7 = 5
если а = 56, то 56 : 7 = 8
если а = 63, то 63 : 7 = 9
2) b ∙ 8
если b = 9, то 9 ∙ 8 = 72
если b = 8, то 8 ∙ 8 = 64
если b = 7, то 7 ∙ 8 = 56
Номер 7.
Ответ:
Номер 8.
Рассмотри рисунок и определи, кто из девочек какую долю закрасил, если Таня закрасила большую долю, чем Оля, а Лена закрасила большую долю, чем Таня.
Ответ:
Лена закрасила одну третью долю (рис. 1).
Таня закрасила одну шестую (рис.3).
А Оля закрасила одну двенадцатую (рис. 2).
1).
Таня закрасила одну шестую (рис.3).
А Оля закрасила одну двенадцатую (рис. 2).
Номер 9.
Начерти квадрат со стороной 4 см. Раздели его на 2 равных прямоугольника и закрась один из них красным цветом. Другой прямоугольник раздели на 2 равных квадрата и закрась один из них синим цветом. Другой квадрат раздели на 2 равных треугольника и закрась один из них зеленым цветом. Какая доля большого квадрата осталась незакрашенной?
Ответ:
Осталась не закрашенной одна восьмая доля. Это хорошо видно, если незакрашенный квадрат разделить на одинаковые части.
Задание внизу страницы
Начерти квадрат, длина стороны которого 3 см. Раздели его на равные части так, чтобы можно было закрасить одну девятую его часть; одну третью.
Ответ: Одна девятая часть:
Одна третья часть:
Рейтинг
Выберите другую страницу
1 часть
| Учебник Моро | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 | 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 |
|---|
2 часть
| 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 | 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 |
|---|
Ваше сообщение отправлено!
+
Apple Watch Series 7 – Apple (RU)
5″>Показывают максимум.- Большой продвинутый дисплей.
- Самые прочные Apple Watch в истории.
- Мощные инновации для заботы о здоровье.
- Более быстрая зарядка: до 33% быстрее.
Пять абсолютно новых
цветов алюминия.
Посмотрите в дополненной
реальности
- Зелёный
- Синий
- Сияющая звезда
- Тёмная ночь
Встречайте
Apple Watch
с самым большим
дисплеем.

Большой экран. Огромная польза.
Мы поставили себе задачу сделать дисплей больше, почти не увеличивая размер корпуса. И нашли решение. Конструкция дисплея была фундаментально переосмыслена, что позволило уменьшить рамку на 40%. В итоге область просмотра увеличилась по сравнению с Series 6 и Series 3. Есть повод порадоваться.
Более чем на 50% увеличена область просмотра по сравнению с Series 3.
Простор
для касаний.
Комфортнее глазам.
Комфортнее пальцам.
По всему интерфейсу у кнопок изменился дизайн. Это было сделано, чтобы выгодно задействовать возможности увеличенного дисплея. Поэтому пользоваться приложениями, например «Калькулятором» и «Таймером», стало ещё удобнее.
Отмечайте отрезки времени в приложении для круговых тренировок. На увеличенном дисплее ещё проще рассмотреть всё необходимое.
Всегда включённый дисплей Retina.
 Данные ярче яркого.
Данные ярче яркого.Вам не придётся специально поднимать запястье или прикасаться к дисплею, чтобы увидеть на циферблате время или другие данные и расширения — дисплей всегда включён. А ещё он теперь светится на 70% ярче в помещении, в неактивном режиме, когда рука с часами внизу.
Ударный факт: Series 7 — самая прочная модель Apple Watch.
Фундаментальные изменения в дизайне были необходимы, потому что стояла задача создать всегда включённый дисплей Retina увеличенного размера. Специально для этого были разработаны инновационные решения. Затем с их же помощью удалось сделать фронтальное стекло дисплея сверхвысокой прочности с защитой от трещин.
Пришло время невиданной прочности.
Фронтальное стекло толще на 50%.
Это стекло повышенной толщины. Особенно в центре дисплея. В этой области оно в 2 раза толще, чем у Apple Watch Series 6, что делает его более прочным.
Геометрия надёжности.
У фронтального стекла теперь совершенно другой дизайн. Основание стало плоским. За счёт этого стекло приобрело более надёжную форму с повышенной устойчивостью к трещинам.
Основание стало плоским. За счёт этого стекло приобрело более надёжную форму с повышенной устойчивостью к трещинам.
Дисплей OLED.
Сенсорный датчик интегрирован прямо в панель OLED и образует с ней единый компонент. Это позволило уменьшить толщину дисплея и сделать его рамку тоньше.
Технологии
на пользу.
Дисплей на максимум.
Измеряйте уровень кислорода в крови с помощью инновационного датчика и передового приложения. Делайте ЭКГ, когда удобно и где угодно. Проверяйте частоту сокращений сердца. Вам также доступно много других инноваций, в том числе для повышения осознанности и отслеживания сна. Эти часы заботятся о вас с головы до ног. Другими словами, Series 7 приносят заметно больше пользы.
Измерение уровня кислорода в крови. Дыхание инноваций.
Уровень кислорода в крови — это очень важный показатель общего состояния организма. Он помогает оценить, насколько хорошо кровь насыщается кислородом и сколько кислорода поступает в организм. А измерить этот показатель теперь можно с помощью потрясающего датчика и специального приложения на Apple Watch Series 7. Они даже умеют делать это в фоновом режиме днём и ночью.3
А измерить этот показатель теперь можно с помощью потрясающего датчика и специального приложения на Apple Watch Series 7. Они даже умеют делать это в фоновом режиме днём и ночью.3
Подробнее о приложении «Кислород в крови»
Делайте ЭКГ когда угодно.
С помощью приложения «ЭКГ» ваши Apple Watch Series 7 способны сделать ЭКГ, сопоставимую с электрокардиограммой в одном отведении. Это исключительно важное достижение для носимого устройства. Оно даёт возможность медицинским специалистам получать важные данные, а вам придаёт больше спокойствия.4
Проверьте состояние сердца одним касанием.
Приложение «ЭКГ» задействует электроды, встроенные в колёсико Digital Crown и в заднюю поверхность часов, и с их помощью собирает данные об электрической активности вашего сердца. Просто приложите палец к Digital Crown на 30 секунд, и вы получите результат измерений в виде графика ЭКГ. Приложение «ЭКГ» способно выявить в вашем сердечном ритме наличие признаков мерцательной аритмии, то есть серьёзных нарушений ритма сердца. Или, наоборот, может определить, что у вас синусовый ритм, а значит, сердце бьётся в нормальном режиме.5
Или, наоборот, может определить, что у вас синусовый ритм, а значит, сердце бьётся в нормальном режиме.5
Подробнее о приложении «ЭКГ»
Устройство вашего сна.
Приложение «Сон» не просто отслеживает продолжительность сна. Оно позволяет настроить режим дня и ночи, а также создать набор действий, необходимых вам перед сном. Всё, чтобы вы ложились спать вовремя. А ещё это приложение отслеживает частоту вашего дыхания во сне. Спокойной вам ночи и бодрого дня.
Набирают заряд моментально.
Система зарядки для Apple Watch Series 7 была полностью переосмыслена. Теперь часы получают электропитание быстрее быстрого, чтобы вы мгновенно включались в жизнь. Благодаря обновлённой архитектуре зарядных компонентов и кабелю USB-C для быстрой зарядки, достаточно около 45 минут, чтобы часы набрали энергию с 0 до 80%.6
Обретите баланс. Двигайтесь дальше.
Возьмите небольшую паузу в течение дня и подышите — это может снизить уровень вашего стресса. А новая функция «Размышление» в приложении «Осознанность» поможет привести в порядок мысли и обрести баланс. И всё это с невероятно красивой анимацией. Кроме того, в Apple Fitness+ вас ждут медитации с сопровождением — видеосеансы и аудио.9 С их помощью можно улучшить общее самочувствие, фокусируясь на таких темах, как спокойствие, доброта или благодарность.
А новая функция «Размышление» в приложении «Осознанность» поможет привести в порядок мысли и обрести баланс. И всё это с невероятно красивой анимацией. Кроме того, в Apple Fitness+ вас ждут медитации с сопровождением — видеосеансы и аудио.9 С их помощью можно улучшить общее самочувствие, фокусируясь на таких темах, как спокойствие, доброта или благодарность.
Могучая
мотивация.
Выбирайте из десятков вариантов тренировок. Стартуйте одним касанием. Отслеживайте все физические активности. Прокачивайте свои цели в фитнесе с Apple Fitness+. Для этого у Apple Watch Series 7 есть всё. И даже увеличенный дисплей, на котором ещё удобнее следить за своим прогрессом и показателями — на суше и в воде.
Вперёд, к мощным возможностям.
Фитнес по вашим запросам.
Скалолазание, сквош, сноубординг и столько всего другого — список тренировок на Apple Watch впечатляет. А теперь можно отслеживать даже тайцзицюань и пилатес.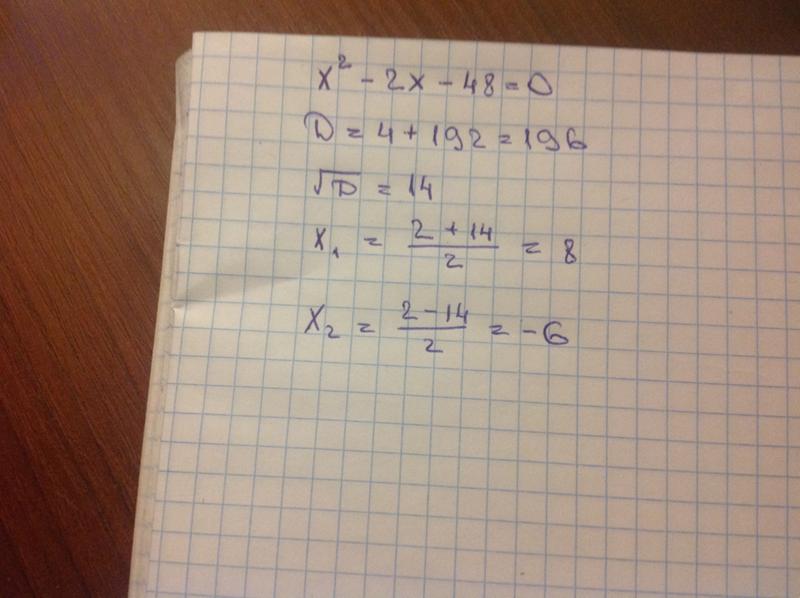 Больше движения, больше эндорфинов. Стартуйте. Прямо с запястья.
Больше движения, больше эндорфинов. Стартуйте. Прямо с запястья.
Новый поворот для велосипедистов.
Теперь Apple Watch могут автоматически определить, что вы начали крутить педали, и тогда предложат включить тренировку. А функция обнаружения падения теперь оптимизирована для велосипедных и других тренировок.10 Она поможет вызвать экстренные службы, если вы упадёте.11 И, чтобы вы не отвлекались от дороги, функция аудиоотзывов будет вам сообщать голосовыми уведомлениями об изменении ключевых показателей — скорости, расстояния и других. Кроме того, был улучшен алгоритм для электровелосипедов, который стал ещё точнее подсчитывать
сожжённые калории.
H
2O. В воду смело.Apple Watch выдерживают погружение на глубину до 50 метров. Поэтому можно спокойно плавать в море или отслеживать количество проплытых дорожек в бассейне.2
5″>Мотивацияот старта до финиша.
Кольца Активности.
«Подвижность», «Упражнения», «С разминкой» —
эти три кольца наглядно показывают вашу физическую активность в течение дня.
Доступ к Активности.
Обменяйтесь с друзьями или близкими доступом к своим кольцам Активности, чтобы мотивировать друг друга вести более подвижный образ жизни.
Соревнования.
Бросьте вызов в Активности друзьям или близким. Из пары участников выигрывает тот, кто за семь дней наберёт больше баллов за свою активность.
Музыка, подкасты и аудиокниги.
Коллекция Apple Music насчитывает миллионы треков — это бесконечный заряд мотивации у вас на запястье. А ещё прямо с часов можно слушать подкасты и аудиокниги, чтобы погружаться в увлекательные истории, пока сжигаешь калории.12
Первый фитнес‑сервис на технологиях Apple Watch.
Apple Fitness+ — это совершенно особенный фитнес-сервис. Там каждую неделю появляются новые тренировки длительностью от 5 до 45 минут на выбор. Вас ждут 11 видов тренировок: например HIIT, пилатес, силовой тренинг, йога. И медитации с сопровождением, которые помогут вам уделить внимание общему самочувствию. При этом ваши личные показатели с Apple Watch бегут прямо перед вами на экране
iPhone, iPad или Apple TV.
Получите три месяца бесплатной подписки при покупке Apple Watch.13
Подробнее об Apple Fitness+
Всё, что вам нужно.
Повсюду с вами.
Когда у вас Apple Watch Series 7 и iPhone, то все важные связи, полезная информация и любимый контент всегда у вас под рукой на большом дисплее часов, куда бы вы ни отправились.
В курсе важного. В любой момент.
Всё самое нужное всегда с вами, где бы вы ни оказались. Позвоните в офис, ответьте на срочное письмо, определите верное направление по встроенному компасу, отправьте своим детям сообщение с эмодзи. Когда Apple Watch подключены к iPhone, все важные связи, полезная информация и любимый контент у вас под рукой.
Позвоните в офис, ответьте на срочное письмо, определите верное направление по встроенному компасу, отправьте своим детям сообщение с эмодзи. Когда Apple Watch подключены к iPhone, все важные связи, полезная информация и любимый контент у вас под рукой.
Приложение Wallet для всего ценного.
Вы можете прямо с часов показать посадочный талон в аэропорту, использовать свою бонусную карту в магазине или кафе, оплатить практически любую покупку и сделать ещё многое другое. Всё благодаря приложению Wallet, где хранится вместе самое важное. Это очень удобно, когда на вас сваливаются все дела сразу.14
Siri. Главный ответ на грандиозные вопросы.
Какая столица у Острова Рождества? Где ближайшая заправка? Что это за песня? Спрашивайте всё подряд. Голосовой помощник Siri даже умеет переводить слова и фразы на иностранные языки в режиме реального времени. Просто fantástico.
Карты. Направят на путь.
Идти пешком или ехать на машине особенно удобно с приложением «Карты». Потому что лёгкие тактильные сигналы, которые генерирует встроенный в часы привод Taptic Engine, подскажут вам, когда повернуть налево или направо. И смотреть на часы не придётся.
Приложения специально для того и этого.
Самые разные приложения можно найти в App Store прямо с запястья. Вот почему Apple Watch — это персональное устройство, которое идеально подходит для самых разных занятий. Сёрфинг, фотография, астрономия, всё что угодно. Просто скачайте подходящее приложение прямо на Apple Watch, открывайте и пользуйтесь на здоровье.
Циферблаты в персонально вашем стиле.
Создавайте собственные циферблаты с расширениями специально для своих увлечений. Например, если вы занимаетесь сёрфингом, добавьте показатели приливов, ветра и температуры воды. А ещё такими циферблатами можно делиться с родными и друзьями — по электронной почте и в текстовых сообщениях.
Окружающая среда
Мы несём ответственность за воздействие наших продуктов на окружающую среду в течение всего их жизненного цикла. В будущем мы перейдём на использование полностью переработанных и возобновляемых материалов при производстве всех своих устройств и упаковки для них. Apple Watch созданы таким образом, чтобы воздействие на окружающую среду было минимальным.
Подробнее об Apple и окружающей среде
Какие Apple Watch
вам подходят?
Корпус 45 мм или 41 мм
Защита от воды при плавании2
Сверхпрочное фронтальное стекло с защитой от трещин
Защита от пыли: рейтинг IP6X2
Всегда включённый дисплей Retina
По сравнению с Apple Watch SE
увеличен примерно на 20%
По сравнению с Series 3
увеличен более чем на 50%
Приложение
«Кислород в крови»3
Приложение «ЭКГ»4
Уведомления о слишком
низком и высоком пульсе
Уведомления о нерегулярном
ритме сердца5
Экстренный
вызов — SOS11
Функция обнаружения падения
Корпус 44 мм или 40 мм
Защита от воды при плавании2
Дисплей
Retina
По сравнению с Series 3
увеличен более чем на 30%
Уведомления о слишком
низком и высоком пульсе
Уведомления о нерегулярном
ритме сердца5
Экстренный
вызов — SOS11
Функция обнаружения падения
Корпус 42 мм или 38 мм
Защита от воды при плавании2
Дисплей
Retina
Уведомления о слишком
низком и высоком пульсе
Уведомления о нерегулярном
ритме сердца5
Экстренный
вызов — SOS11
Сравните все модели
Series 7
Более чем на 50% увеличена область просмотра по сравнению с Series 3.
396×484 пикселя
Площадь дисплея 1143 мм²
SE
Более чем на 30% увеличена область просмотра по сравнению с Series 3.
368×448 пикселей
Площадь дисплея 977 мм²
Series 3
312×390 пикселей
Площадь дисплея 740 мм²
Общий тест обновления 1.18.1 | Обновления
Танкисты!
У нас для вас ряд приятных новостей. Теперь навык «Шестое чувство» будет доступен всем экипажам. В игре появится новый режим «Натиск», который предложит множество оригинальных игровых механик и прогрессионный 2D-стиль в качестве награды. Вас также ждут переработанные личные резервы и несколько доработанных карт.
Общий тест 1.18.1 будет доступен для пользователей до 21 сентября 10:00 (МСК).
Доступный всем навык «Шестое чувство»
В обновлении 1.18.1 «Шестое чувство» станет особенностью командира! Это значит, что навык по умолчанию будет изучен каждым командиром на вашей технике (включая тех, которых ещё вы не рекрутировали в Казарме, и всех командиров, которых получите или будете рекрутировать в будущем). Это изменение сделает сражения более комфортными для всех игроков, особенно для новых.
Это изменение сделает сражения более комфортными для всех игроков, особенно для новых.
Если кто-то из командиров вашей техники уже изучил навык «Шестое чувство», вы сможете бесплатно выбрать для него другое умение или навык.
В редких случаях, когда навык «Шестое чувство» был «нулевым», вместо него можно будет выбрать другой «нулевой» навык или умение (но только один раз для каждого командира машины). Можно выбрать любой навык командира.
Наконец, в интерфейсе экипажа особенность командира и «нулевые» умения/навыки будут отображаться отдельно.
Обновлено 16.09.2022 в 11:38 (МСК)
Режим «Натиск»
Возможно, во время Общего теста вы сразу захотите опробовать «Натиск». В этом совершенно новом режиме есть специальные правила и уникальные механики, в том числе:
- бои в формате 7 на 7 только на исследуемой и коллекционной технике X уровня;
- подбор игроков по рейтингу в режиме;
- улучшаемые навыки, зависящие от роли машины;
- ключевые позиции, которые можно захватывать для получения тактических преимуществ, таких, как огневая поддержка или полное обнаружение противника для вашей команды;
- возможность играть супервзводом из семи игроков.

И многое другое! Вы можете ознакомиться с детальной информацией в подробной статье о режиме «Натиск».
Конечно, мы должны упомянуть ещё одну важную особенность режима «Натиск» — награды. Впервые у вас появится возможность получить прогрессионный 2D-стиль. 2D-стиль «Крыло и коготь» будет отображать ваши достижения в режиме «Натиск».
По мере вашего продвижения в режиме будут открываться новые сочетания камуфляжных схем и декалей. Кроме того, вы в любое время сможете переключиться на более «раннюю» версию, если захотите.
Стиль останется на вашем аккаунте навсегда, даже после окончания режима «Натиск», и его можно будет наносить на любую технику X уровня.
Новые личные резервы
Вам обязательно захочется оценить переработанные личные резервы. Оптимизированные резервы с возможностью активации даже в бою — это долгожданное изменение. В двух абзацах невозможно описать все доработки, поэтому мы предлагаем прочитать об этом в специальной статье.
В ней приведены правила конвертации прежних резервов в новые, а также калькулятор конвертации. Если кратко, то при конвертации вы ничего не потеряете.
Больше карт для ребаланса
Мы продолжаем дорабатывать карты. В обновлении 1.18 в некоторые из них были внесены балансные правки. Проанализировав огромное количество отзывов и данных, в версии 1.18.1 мы планируем доработать ещё четыре боевые локации.
Малиновка
Небольшой холм в квадрате E7 станет менее крутым, и вы сможете заехать на его вершину незаметно для противника. Кроме того, он обеспечит более надёжную защиту от снарядов противника.
Рельеф в районе круга захвата для верхней базы станет более плоским. Расположенная рядом ферма будет смещена с линии огня для техники, спускающейся с горы и проезжающей через лес.
На обеих базах будет по одному кусту внутри круга захвата.
Песчаная река
Новое каменное образование в квадрате A6 защитит технику, подъезжающую к этому холму, и позволит ей вести ответный огонь по противнику, занявшему позицию в квадрате D7.
В квадрате K0 будет добавлена новая точка пересечения каньона, позволяющая легко добраться до назойливого противника, засевшего между скалами.
Центральное направление для атаки будет существенно преобразовано. Изменится ландшафт, и появятся новые позиции с различной дальностью ведения огня.
Добавлены новые позиции для отхода, если центральная долина будет потеряна.
Центральная долина будет лучше защищена от огня с позиций для СТ и ПТ-САУ нижней команды.
Рыбацкая бухта
Подход к центру городской части карты с верхней базы станет безопаснее. Ключевые позиции станут более удобными для игры «от борта».
Расположение строений в центральном квартале города будет изменено. Новое строение будет перекрывать линию огня с холма в центре карты.
Чтобы уравнять шансы сторон, нижняя команда больше не сможет скрываться за густыми кустами и вести огонь по технике верхней команды в центральном квартале городка. Квартал зданий в квадрате F9 будет иметь форму, аналогичную кварталу с северной стороны, чтобы обеспечить обеим командам равные возможности для удержания позиций.
Квартал зданий в квадрате F9 будет иметь форму, аналогичную кварталу с северной стороны, чтобы обеспечить обеим командам равные возможности для удержания позиций.
В центральной части карты с обеих сторон (квадраты D6 и F6) появится больше укрытий.
Проблемная огневая позиция с северной стороны в квадрате С9 будет обладать меньшим пространством для укрытия и, соответственно, давать меньшее преимущество.
В квадрате F5 будет добавлена складка местности, чтобы нижняя команда могла безопаснее перемещаться вблизи центра карты так же, как это может делать команда противника.
Химмельсдорф
У нижней команды всегда было два заезда на вершину горы. В обновлении 1.18.1 верхняя команда получит свой второй заезд, который будет безопаснее основного.
Известные проблемы
Личные резервы
Во время первой итерации общего теста обновления 1. 18.1 вместо значений бонусов личного резерва будет отображаться строка текста с надписью «bonus%». Во второй итерации общего теста это будет исправлено. Приносим свои извинения за доставленные неудобства.
18.1 вместо значений бонусов личного резерва будет отображаться строка текста с надписью «bonus%». Во второй итерации общего теста это будет исправлено. Приносим свои извинения за доставленные неудобства.
Натиск
В настоящее время игра во взводах на два игрока недоступна в режиме «Натиск». Мы знаем о проблеме и решим ее в ближайшее время.
Как участвовать в тестировании
- Используйте эту ссылку. Wargaming.net Game Center загрузит все дополнительные файлы.
- Начинайте играть.
Участвовать в тесте могут только игроки, которые зарегистрировались в World of Tanks до 5 сентября 23:59 (МСК).
Подробнее о Wargaming.net Game Center
- Из-за большого количества танкистов на тестовом сервере установлено ограничение на вход пользователей. Все новые игроки, желающие поучаствовать в тестировании обновления, будут поставлены в очередь и смогут зайти на сервер, когда он освободится.
- Если пользователь изменил пароль после 4 сентября 23:59 (МСК), авторизация на тестовом сервере будет доступна только по паролю, который использовался до указанного времени.

- Платежи на тестовом сервере не производятся.
- На этом тестировании не увеличивается заработок опыта и кредитов.
- Достижения на тестовом сервере не перейдут на основной.
- В ходе тестирования версии 1.18.1 на тестовых серверах проходят плановые технические работы (по 25 минут на каждом сервере начиная с 7:00 (МСК)).
- Обратите внимание: на тестовом сервере действуют те же правила, что и на основном игровом. Следовательно, существуют и наказания за нарушение этих правил в соответствии с Лицензионным соглашением.
- Центр поддержки пользователей не рассматривает заявки, связанные с общим тестом.
- Напоминаем: скачивать клиент World of Tanks, а также его тестовые версии и обновления надёжнее всего в специальном разделе на официальном портале игры. Скачивая игру из иных источников, вы подвергаете свой компьютер риску заражения вредоносным ПО. Команда разработчиков не несёт ответственности за ссылки на игровой клиент и обновления (а также за их содержимое) на сторонних ресурсах.

Бойцы, заходите на Общий тест и делитесь своим мнением обо всех нововведениях в рамках обновления 1.18.1!
3-8множитель x в квадрате-7x-30 полностью | Wyzant Спросите эксперта
Алгебра 2
Майра А.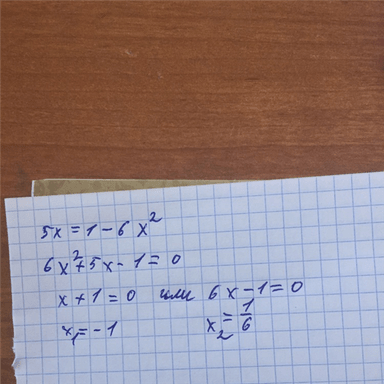
а. (x-1)(x+30)
б. (x-5)(x+6)
в. (x-10)(x+3)
d. (х+2)(х-15)
Подписаться І 4
Подробнее
Отчет
4 ответа от опытных наставников
г. Лучший Новейшие Самый старыйАвтор: ЛучшийНовыйСамый старый
Роберт Дж. ответил 08.08.13
Репетитор
4.6 (13)
Сертифицированный учитель исчисления и физики средней школы AP
См. таких репетиторов
Смотрите таких репетиторов
x 2 — 7x — 30 = (x-10)(x+3), так как -30 = -10*3 и -10+3 = -7, коэффициент при x.
Ответ: с. (х-10)(х+3)
Голосовать за 1 Понизить
Подробнее
Отчет
Пьета С. ответил 10.12.14
ответил 10.12.14
Репетитор
5,0 (1148)
Учитель английского языка, специализирующийся на подготовке к экзаменам, чтении и письме!
г.Об этом репетиторе ›
Об этом репетиторе ›
просто тестирую этот сайт
Голосовать за 0 Понизить
Подробнее
Отчет
Рамеш В. ответил 08.08.13
Репетитор
4 (1)
Индивидуальное и эффективное обучение математике и естественным наукам
Смотрите таких репетиторов
Смотрите таких репетиторов
X 2 -10X+3X-30
= X(X-10)+3(X-10)
= (X-10) (X+3)
Голосовать за 0 Понизить
Подробнее
Отчет
Феличе Р. ответил 08.08.13
ответил 08.08.13
Репетитор
4 (1)
Нужна помощь по математике и естественным наукам — инженер готов помочь
См. таких репетиторов
Смотрите таких репетиторов
Самый простой способ разложить квадратное уравнение на множители a x 2 + b x + c — использовать формулу квадратного уравнения. Что вы делаете, так это предполагаете, что уравнение установлено равным нулю, а затем решаете для разных значений x, которые сделают это утверждение верным. Это даст вам факторы квадратного уравнения
Итак, если A x 2 + B x + C = 0, и квадратичное уравнение
x 1 = ( B + SQRT (999877987878781111111198879.71118711118711111111989. 7. ac ))/2 a
7. ac ))/2 a
x 2 =(- b — sqrt( b 2 — 4 ac ))/2 a
Which would give us the разложение (x-x 1 )(x-x 2 )
В многочлене x 2 — 7x -30
a =1. B = -7 и C = -30
Если мы заменим эти значения, мы получаем
x 1 = ( — B + SQRT ( B 9 291911350 — B 9 29191. ))/2 a = (-(-7) + sqrt((7 2 — 4 * (1)*(-30))/(2*1) = (7+sqrt(49+120) )/2 = (7+sqrt(169))/2 = (7+13)/2 = 20/2 = 10
x 2 = (- b — sqrt( b 2 — 4 ac ))/2 a = (-(-7) — sqrt((7 2 + 4 * (1)*(-30))/(2*1)= (7 — sqrt(169 ))/2 = (7-13)/2 = (-6)/2 = -3
Теперь, если мы подставим значения x 1 и x 2 , мы получим
(x-x 1 )(x-x 2 ) = (x-10)(x-(-3)) = (x-10)(x+3) — Что равно ОТВЕТ C
Примечание : вы можете проверьте свой ответ, умножив полученный ответ
(x-10)(x+3) = x 2 + 3x -10x — 30 = x 2 -7x -30
Голосовать за 0 Понизить
Подробнее
Отчет
Все еще ищете помощи? Получите правильный ответ, быстро.
Задайте вопрос бесплатно
Получите бесплатный ответ на быстрый вопрос.
Ответы на большинство вопросов в течение 4 часов.
ИЛИ
Найдите онлайн-репетитора сейчас
Выберите эксперта и встретьтесь онлайн. Никаких пакетов или подписок, платите только за то время, которое вам нужно.
Системы линейных и квадратных уравнений
| Линейное уравнение — это уравнение линии . | |
| Квадратное уравнение представляет собой уравнение параболы и имеет по крайней мере одну переменную в квадрате (например, х 2 ) | |
| И вместе они образуют Систему Линейного и Квадратного уравнения |
A Система из этих двух уравнений может быть решена (найти место их пересечения) одним из следующих способов:
- Графически (построив их оба на графике функций и увеличив масштаб)
- или используя Алгебра
Как решить с помощью алгебры
- Преобразовать оба уравнения в формат «y =»
- Установить их равными друг другу
- Упростить до формата «= 0» (как стандартное квадратное уравнение)
- Решите квадратное уравнение!
- Используйте линейное уравнение для вычисления совпадающих значений «y», чтобы получить (x,y) баллов в качестве ответов
Пример поможет:
Пример: Решите эти два уравнения:
- у = х 2 — 5х + 7
- у = 2х + 1
Превратите оба уравнения в формат «y=»:
Они оба в формате «y=», поэтому сразу переходите к следующему шагу
Приравняйте их друг к другу + 7 = 2x + 1
Упростить до формата «= 0» (как стандартное квадратное уравнение)
Вычесть 2x с обеих сторон: x 2 — 7x + 7 = 1
Вычтите 1 из обеих сторон: x 2 — 7x + 6 = 0
Решите квадратное уравнение!
(самая сложная часть для меня)
Вы можете прочитать, как решать квадратные уравнения, но здесь мы будем учитывать квадратное уравнение:
Начните с: x 2 — 7x + 6 = 0
Перепишите — 7x как -x-6x: x 2 — x — 6x + 6 = 0
Тогда: x(x-1) — 6(x-1) = 0
Тогда: (x- 1)(х-6) = 0
Что дает нам решения x=1 и x=6
Используйте линейное уравнение для вычисления совпадающих значений «y», таким образом, мы получаем (x,y) точек в качестве ответов
Соответствующие значения y (см. также график):
также график):
- для x= 1 : y = 2x+1 = 3
- для х= 6 : у = 2х+1 = 13
Наше решение: две точки равны (1,3) и (6,13)
Я рассматриваю это как три этапа:
Объединить в квадратное уравнение ⇒ Решить квадратное уравнение ⇒ Вычислить точки
Решения
Возможны три случая:
- Нет реального решения (возникает, когда они никогда не пересекаются)
- Одно действительное решение (когда прямая только касается квадрата)
- Два реальных решения (как в примере выше)
Время для другого примера!
Пример: Решите эти два уравнения:
- y — x 2 = 7 — 5x
- 4г — 8х = -21
Превратите оба уравнения в формат «y=»:
Первое уравнение: y — x 2 = 7 — 5x
Прибавьте x 2 к обеим сторонам: y = x 7 +
0 2 — 5xВторое уравнение: 4y — 8x = -21
Добавьте 8x к обеим сторонам: 4y = 8x — 21
Divide All на 4: y = 2x — 5,25
Установите их, равную каждому другу
x 2 — 5x + 7 = 2x — 5,25
Simplify Into «= 0».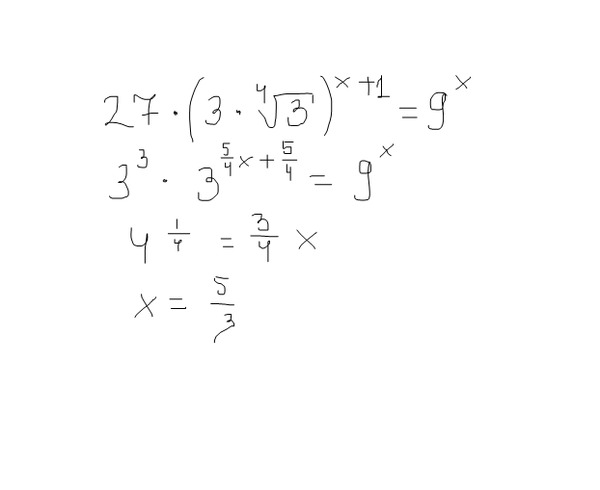 как стандартное квадратное уравнение)
как стандартное квадратное уравнение)
Вычесть 2x с обеих сторон: x 2 — 7x + 7 = -5,25
Прибавить 5,25 к обеим сторонам: x 2 — 7x + 12,25 = 0
1 1 1 Уравнение!
Использование квадратичной формулы из квадратных уравнений:
- x = [-b ± √(b 2 -4ac)] / 2a
- х = [7 ± √((-7) 2 -4×1×12,25)] / 2×1
- х = [7 ± √(49 -49)] / 2
- х = [7 ± √0] / 2
- х = 3,5
Только одно решение! («Дискриминант» равен 0)
Используйте линейное уравнение для вычисления совпадающих значений «y», чтобы мы получили (x,y) баллов в качестве ответов
Совпадающее значение y равно:
- для x= 3,5 : y = 2x-5,25 = 1,75
Наше решение: (3.5,1.75)
Реальный пример
Бум!
Пушечное ядро летит по воздуху по параболе: y = 2 + 0,12x — 0,002x 2
Земля наклонена вверх: y = 0,15x
Куда приземляется пушечное ядро?
Оба уравнения уже имеют формат «y =», поэтому приравняем их друг к другу:
0,15x = 2 + 0,12x — 0,002x 2
Упростить до формата «= 0»:
Перенести все члены влево: 0,002x 2 + 0,15x — 1 8 = 1 0,10x — 9 9 Упростить: 0,002x 2 + 0,03x — 2 = 0
Умножить на 500: x 2 + 15x — 1000 = 0
-25x + 40x — 1000 = 0
Тогда: x(x-25) + 40(x-25) = 0
Тогда: (x+40)(x-25) = 0
x = -40 или 25
Отрицательный ответ можно игнорировать, поэтому x = 25
Используйте линейное уравнение для вычисления соответствующего значения «y»:
y = 0,15 x 25 = 3,75
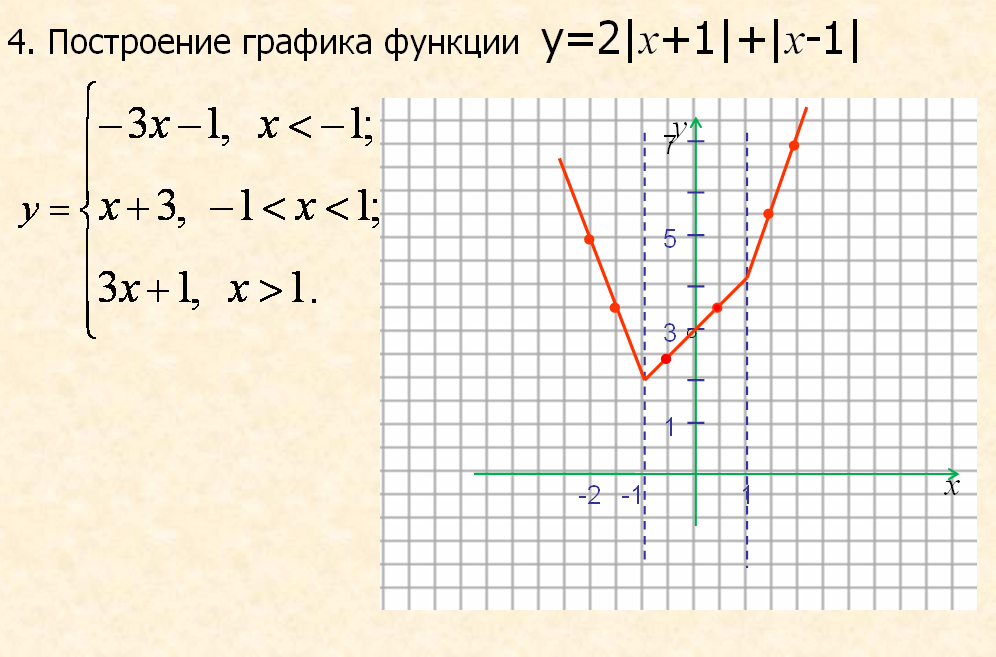
Таким образом, пушечное ядро ударяет по склону с координатами (25, 3,75)
Вы также можете найти ответ графически с помощью графического редактора функций:
.
Квадрат обеих переменных
Иногда ОБА члена квадратного уравнения могут быть возведены в квадрат:
Пример: Найдите точки пересечения
Круг x 2 + Y 2 = 25
и прямая линия 3Y — 2x = 6
— 2x = 6
— 2x = 6
— 2x = 6
. y=» формат:
Переместить 2x вправо: 3y = 2x + 6
Разделить на 3: y = 2x/3 + 2
СЕЙЧАС. Вместо того, чтобы делать круг в формате «y=», мы можем используйте замену (замените «у» в квадратичном выражении линейным):
Поместите y = 2x/3 + 2 в уравнение окружности: x 2 + (2x/3 + 2) 2 = 25
Разверните: x 2 + 4x 2 /9 + 2(2x /3)(2) + 2 2 = 25
Умножить все на 9: 9x 2 + 4x 2 + 2(2x)(2)(3) + (9)(2 2 ) = (9)(25)
Упростить: 13x 2 + 24x + 36 = 225
Вычесть 225 с обеих сторон: 13x 2 + 24x — 189 = 0
Теперь это в стандартной квадратичной форме решить это:
13x 2 + 24x — 189 = 0
Разделить 24x на 63x-39x: 13x 2 + 63x — 39x — 189 = 0
— 3 x 6(1×3) ) = 0
Тогда: (x — 3)(13x + 63) = 0
Итак: x = 3 или -63/13
Теперь вычислим значения y:
Подставим x = 3 в линейное уравнение:
- 3г — 6 = 6
- 3г = 12
- г = 4
- Таким образом, одна точка равна (3, 4)
Подставьте x = -63/13 в линейное уравнение:
- 3 года + 126/13 = 6
- г + 42/13 = 2
- г = 2 — 42/13 = 26/13 — 42/13 = -16/13
- Значит другая точка (-63/13, -16/13)
Нестандартные размеры фоторамки | Майклз
В вашем браузере отключены функции Javascript. Пожалуйста, включите его, чтобы вы могли испытать все возможности этого сайта.
Пожалуйста, включите его, чтобы вы могли испытать все возможности этого сайта.
- Дом
- /
- Рамки /
- Магазин по размеру кадра /
- Нестандартные размеры
Фильтровать результаты 373 Результаты
Сортировать по: Магазин по
Сортировать по
Коллекция рамок
Количество отверстий
Отделка
Размер отверстия
Дополнительные способы совершения покупок
Дополнительные способы совершения покупок
- Распродажа (80)
- Отличная покупка (12)
- MichaelsPro™ — купить оптом (84)
Сортировать по:
Быстро
Бесплатный самовывоз из магазина
Категории
- Магазин по размеру кадра
- 4×6 кадров
- 5×7 кадров
- 8×10 кадров
- 11×14 кадров
- 16×20 кадров
- Кадры 18×24
- Нестандартные размеры
- Маленькие фоторамки
- Большие фоторамки
- Мини фоторамки
- Квадратные фоторамки
- Круглые фоторамки
- Рамки для плакатов
- Настенные рамы
- Настенные рамы галереи
- Коллаж фоторамки
- Теневые ящики
- Рамки стола
- Подставки для картин
- Мультиупаковки и наборы рамок
- Коллекции кадров
- Оборудование для обрамления
- Рамочные коврики
- Пользовательские рамки
Больше возможностей для покупок
Распродажа Отличная покупка MichaelsPro™ — купить оптом
Все элементы
Быстрый просмотр
Быстрый просмотр
Быстрый просмотр
Быстрый просмотр
6 размеров
Быстрый просмотр
Самовывоз из магазина
черная рама с паспарту, lifestyles™ by studio decor®
14,99 $ $19,99
Калькулятор средней точки
Создано Матеушем Мухой и Петром Малеком
Отзыв от Джека Боуотера
Последнее обновление: 25 марта 2022 г.
- Как найти среднюю точку
- Формула средней точки
- Другие связанные темы точка прямо между ними обоими. Эта точка часто используется в геометрии. В качестве дополнения к этому калькулятору мы написали статью ниже, в которой обсуждается, как найти среднюю точку и что такое формула средней точки.
Если вы хотите понять, как меняется одна координата относительно другой, рекомендуем воспользоваться калькулятором средней скорости изменения.
Как найти середину
- Обозначьте координаты
(x₁,y₁) и (x₂,y₂). - Введите значения в формулу.
- Сложите значения в скобках и разделите каждый результат на 2.
- Новые значения образуют новые координаты средней точки.
- Проверьте свои результаты с помощью калькулятора средней точки.
Предположим, у нас есть отрезок, и мы хотим разрезать его на две равные части. Для этого нам нужно знать центр. Мы можем добиться этого, найдя среднюю точку.
 Вы можете измерить с помощью линейки или просто использовать формулу, включающую координаты каждой конечной точки сегмента. Средняя точка — это просто среднее значение каждой координаты сечения, образующее новую точку координат. Мы проиллюстрируем это ниже.
Вы можете измерить с помощью линейки или просто использовать формулу, включающую координаты каждой конечной точки сегмента. Средняя точка — это просто среднее значение каждой координаты сечения, образующее новую точку координат. Мы проиллюстрируем это ниже.Формула средней точки
Если у нас есть координаты
(x₁,y₁) и (x₂,y₂), то середина этих координат определяется как(x₁ + x₂)/2, (y₁ + y₂)/2. Это формирует новую координату, которую вы можете назвать(x₃,y₃). Калькулятор средней точки решит это мгновенно, если вы введете координаты. Выполните шаги, описанные выше, если рассчитываете вручную.Для небольших чисел легко вычислить среднюю точку вручную, но для больших и десятичных значений калькулятор является самым простым и удобным способом вычисления средней точки.
Отрезок можно разделить в любом соотношении, а не только 1:1. Используйте наш калькулятор соотношений направленных отрезков, чтобы узнать, как это сделать.

Как в геометрии часто требуется найти среднюю точку, так и найти расстояние между двумя точками. Расстояние между двумя точками на горизонтальной или вертикальной линии легко вычислить, но процесс усложняется, если точки не выровнены как таковые. Это часто имеет место при работе со сторонами треугольника. Поэтому калькулятор расстояний является удобным инструментом для выполнения этой задачи.
В некоторых геометрических случаях мы хотим вписать треугольник внутрь другого треугольника, где вершины вписанного треугольника лежат в середине исходного треугольника. Калькулятор средней точки чрезвычайно полезен в таких случаях.
Часто задаваемые вопросы
Как найти середину класса?
- Найдите нижний предел класса . Для диапазона 2-5 это 2.
- Найдите верхний предел класса . Для того же диапазона это 5,
- Сложите два числа вместе. Для нас это дает 7,
- Разделите результат на 2. Среднее значение класса 2-5 равно 3,5.

Как найти конечную точку со средней и другой конечной точкой?
- Удвойте среднюю точку.
- Вычтите известную конечную точку, чтобы получить другую. не имеет значения, верхняя это или нижняя граница .
- Поразитесь своим математическим способностям!
Как найти середину треугольника?
Чтобы найти середину треугольника, технически известного как его центроид , выполните следующие действия:
- Найдите середины сторон треугольника. Если вы знаете, как это сделать, перейдите к шагу 5 .
- Измерьте расстояние между двумя конечными точками и разделите результат на 2. Это расстояние от любого конца является серединой этой линии.
- Можно также добавить две координаты x конечных точек и разделить на 2. Сделайте то же самое для координат y. Результаты дают вам координаты средней точки.
- Проведите линию между средней точкой и ее противоположным углом.

- Повторить по крайней мере для еще одной средней точки и пары углов или для обеих наивысшей степени точности .
- Место пересечения всех линий находится в центре треугольника.
Что такое середина круга?
Чтобы найти середину или центр окружности, следуйте этим инструкциям:
- Найдите две точки на окружности, которые полностью противоположны друг другу , т. е. разделены диаметром окружности.
- Если вы знаете их координаты, сложите две координаты x вместе и разделите результат на 2. Это координата x центра.
- Сделайте то же самое для двух координат по оси Y, что даст вам координату по оси Y.
- Объедините их, чтобы получить координаты центроида .
- Если вы не знаете координат, измерьте расстояние между двумя точками и половину его.
- : Эта половина расстояния между одной конечной точкой и другой является средней точкой.

Как найти середину квадрата?
Чтобы найти середину или центроид квадрата, следуйте этому простому руководству:
- Если у вас есть координаты двух противоположных углов квадрата, сложите 2 x координаты вместе и разделите результат на 2.
- Сделайте то же самое для координаты y.
- Используйте эти два рассчитанных числа, чтобы найти центр квадрата, поскольку они являются его координатами x и y соответственно.
- В качестве альтернативы проведите линию от одного угла к противоположному углу и еще одну для оставшейся пары.
- Место пересечения этих двух точек является центром тяжести квадрата.
Вы округляете середину?
В общем, вы не округляете середины . Вы определенно не делаете для непрерывных данных , так как эта точка является реальной точкой в наборе данных. Для дискретных данных вы обычно не делаете , вместо этого отмечая, что средняя точка является значением обоих значений по обе стороны от вычисления средней точки.

Что такое середина чисел 0 и 5?
2,5 . Чтобы найти середину любого диапазона, сложите два числа вместе и разделите на 2. В этом случае 0 + 5 = 5, 5 / 2 = 2,5.
Как найти середину трапеции?
Вы можете найти середину или центр тяжести трапеции одним из двух способов:
- Проведите линию от одного угла трапеции к ее противоположному углу.
- Сделайте то же самое для оставшейся пары углов.
- Там, где эти две линии пересекаются, находится центр тяжести .
- Идеально сбалансируйте трапецию на ее центроиде!
Альтернативно:
- Возьмите координаты двух противоположных сторон.
- Сложите координаты x этих точек вместе и разделите на 2. Это координата x средней точки .
- Повторите для 2-х координат y, получив координату y средней точки .
Что такое середина 0,2 и 2,8?
- Сложите 0 и 2, чтобы получить 2.

- Обозначьте координаты

 Тогда дискриминант — это просто число D = b2 − 4ac.
Тогда дискриминант — это просто число D = b2 − 4ac.



 Вы можете измерить с помощью линейки или просто использовать формулу, включающую координаты каждой конечной точки сегмента. Средняя точка — это просто среднее значение каждой координаты сечения, образующее новую точку координат. Мы проиллюстрируем это ниже.
Вы можете измерить с помощью линейки или просто использовать формулу, включающую координаты каждой конечной точки сегмента. Средняя точка — это просто среднее значение каждой координаты сечения, образующее новую точку координат. Мы проиллюстрируем это ниже.