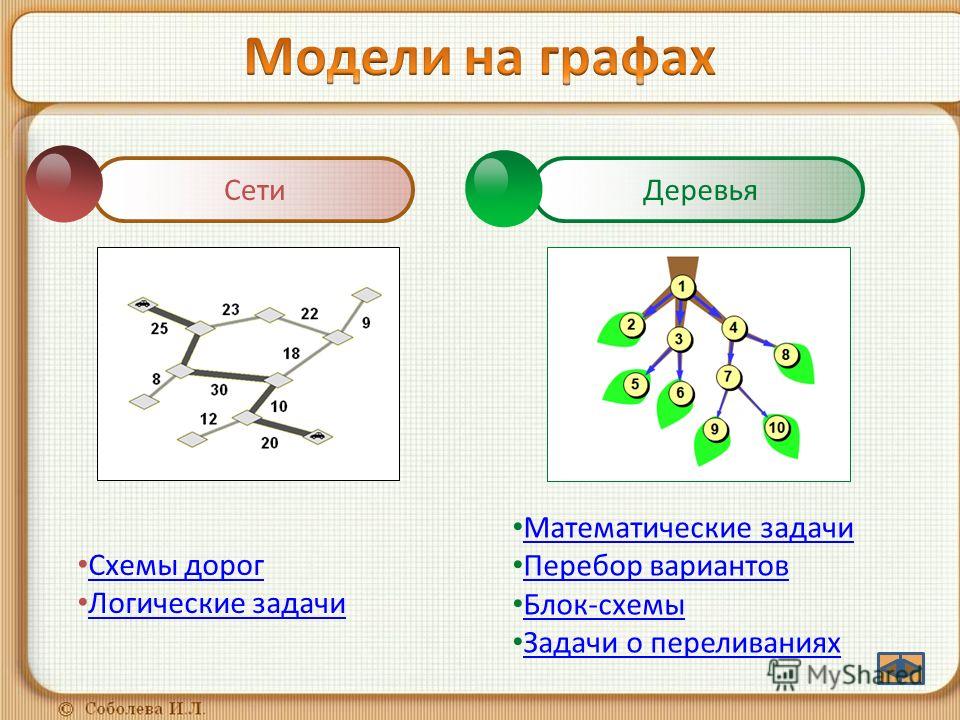
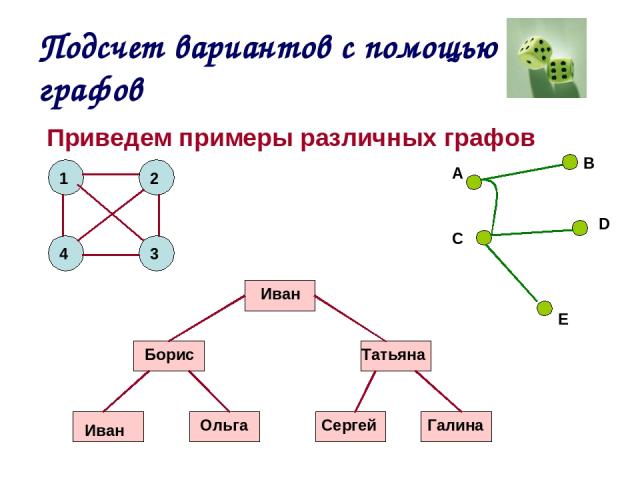
Решение задач с помощью графа
Теория графов применяется при решении задач из многих предметных областей: математика, биология, информатика
1736 год, г.Кёнигсберг. Через город протекает река Прегеля. В городе — семь мостов, расположенных так, как показано на рисунке выше. С давних времен жители Кенигсберга бились над загадкой: можно ли пройти по всем мостам, пройдя по каждому только один раз? Эту задачу решали и теоретически, на бумаге, и на практике, на прогулках — проходя по этим самым мостам. Никому не удавалось доказать, что это неосуществимо, но и совершить такую «загадочную» прогулку по мостам никто не мог.
Разрешить проблему удалось знаменитому математику Леонарду Эйлеру. Причем, он решил не только эту конкретную задачу, но придумал общий метод решения подобных задач. При решении задачи о Кенигсбергских мостах Эйлер поступил следующим образом: он «сжал» сушу в точки, а мосты «вытянул» в линии. Такую фигуру, состоящую из точек и линий, связывающих эти точки, называют ГРАФОМ

Граф – это совокупность непустого множества вершин и связей между вершинами. Кружки называются вершинами графа, линии со стрелками – дугами, без стрелок – ребрами.
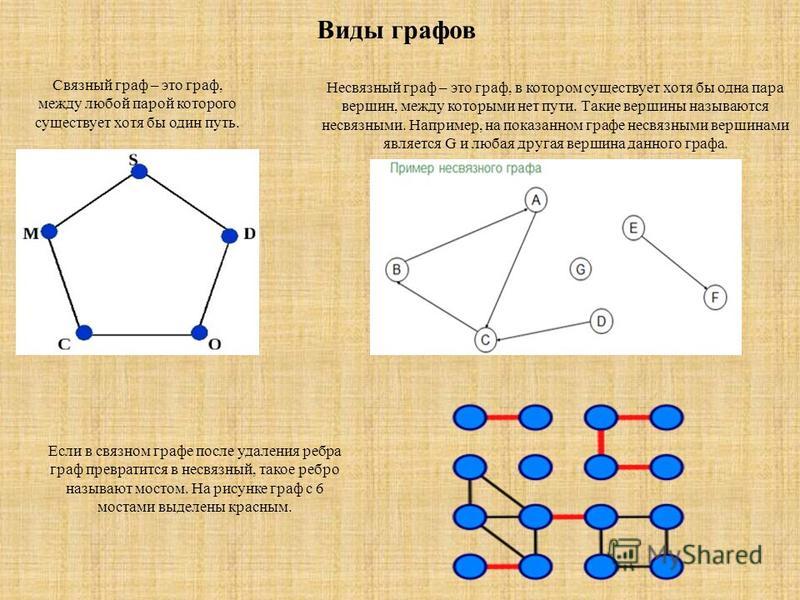
Виды графов:
1. Ориентированный граф (кратко орграф) — рёбрам которого присвоено направление.
2. Неориентированный граф — это граф, в котором нет направления линий.
3. Взвешенный граф – дуги или ребра имеют вес (дополнительная информация).
Решение задач с помощью графов:
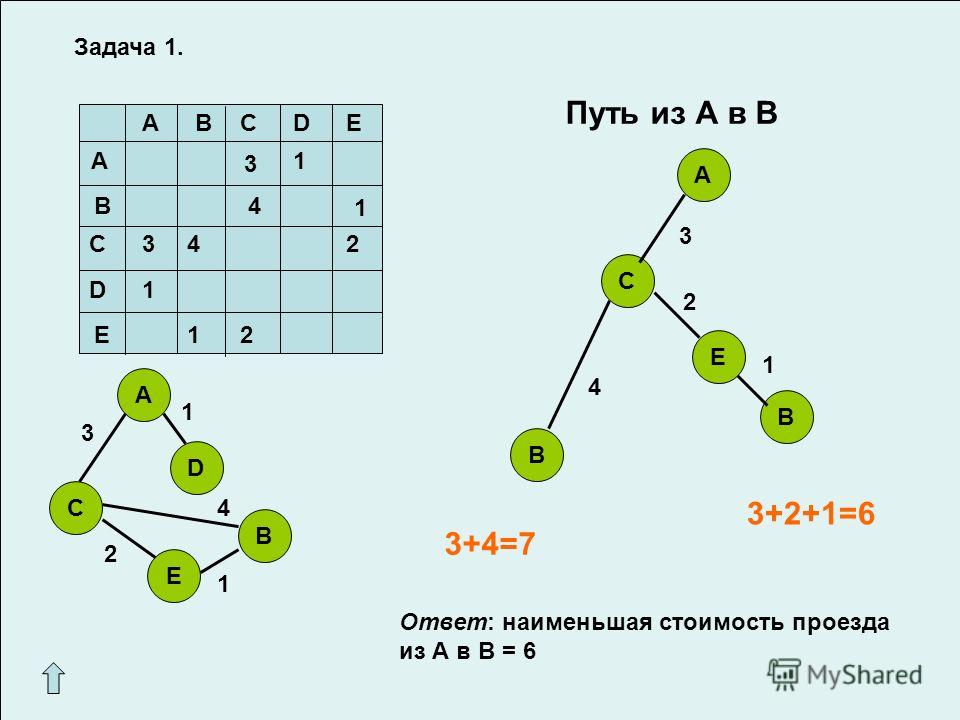
Задача 1.
Решение: Обозначим ученых вершинами графа и проведем от каждой вершины линии к четырем другим вершинам. Получаем 10 линий, которые и будут считаться рукопожатиями.
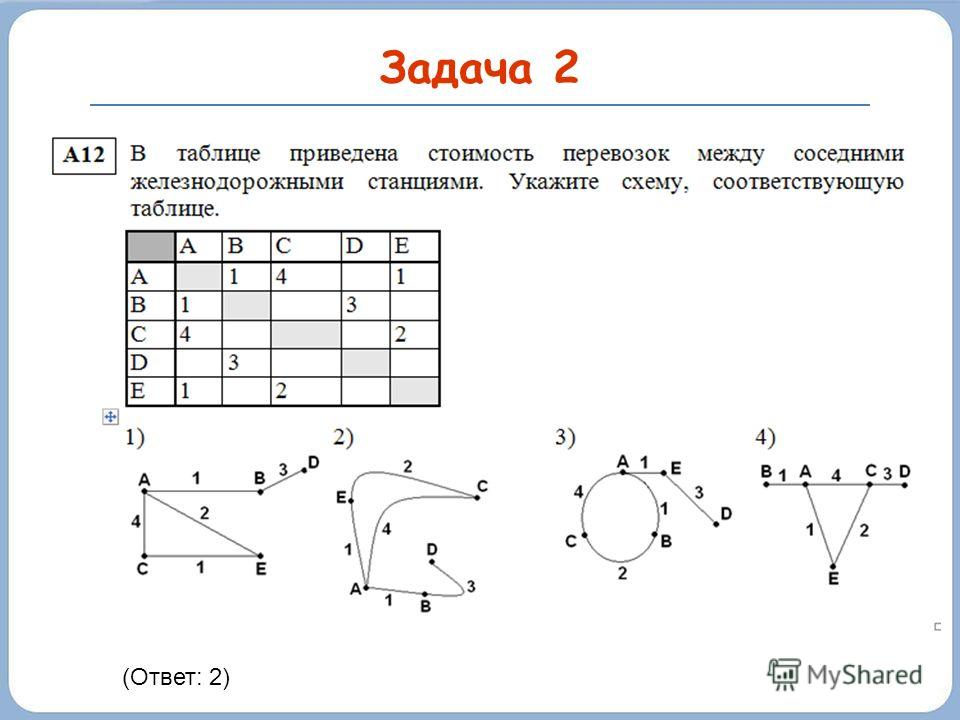
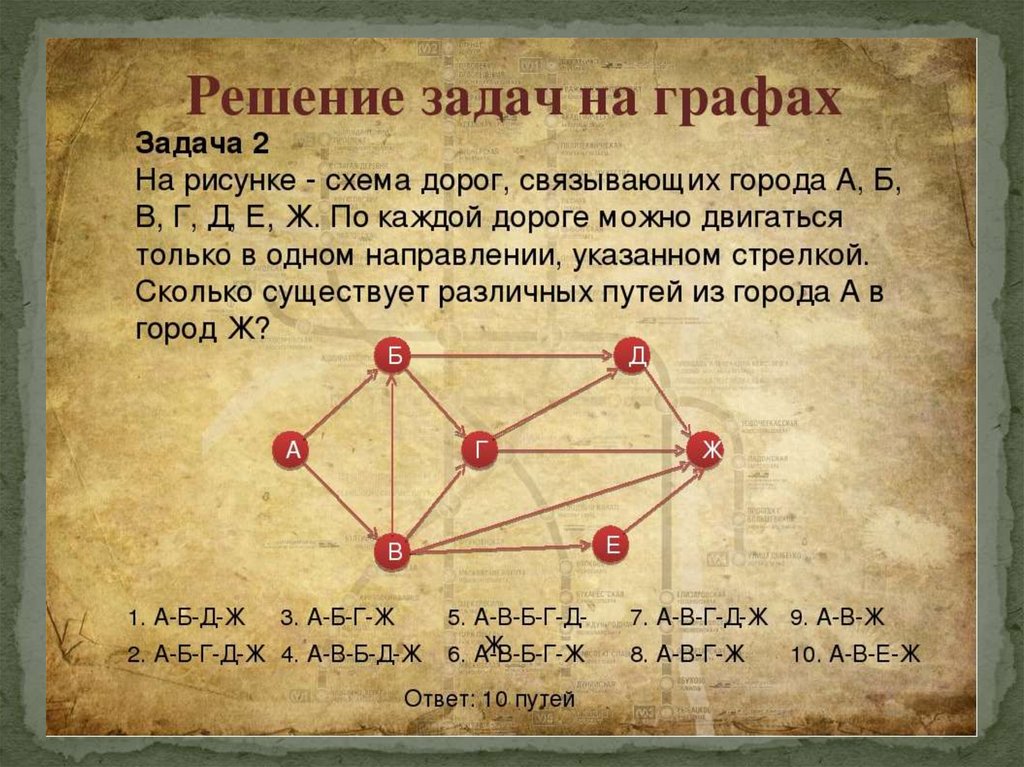
Задача 2.
На пришкольном участке растут 8 деревьев: яблоня,
тополь, береза, рябина, дуб, клен, лиственница и сосна.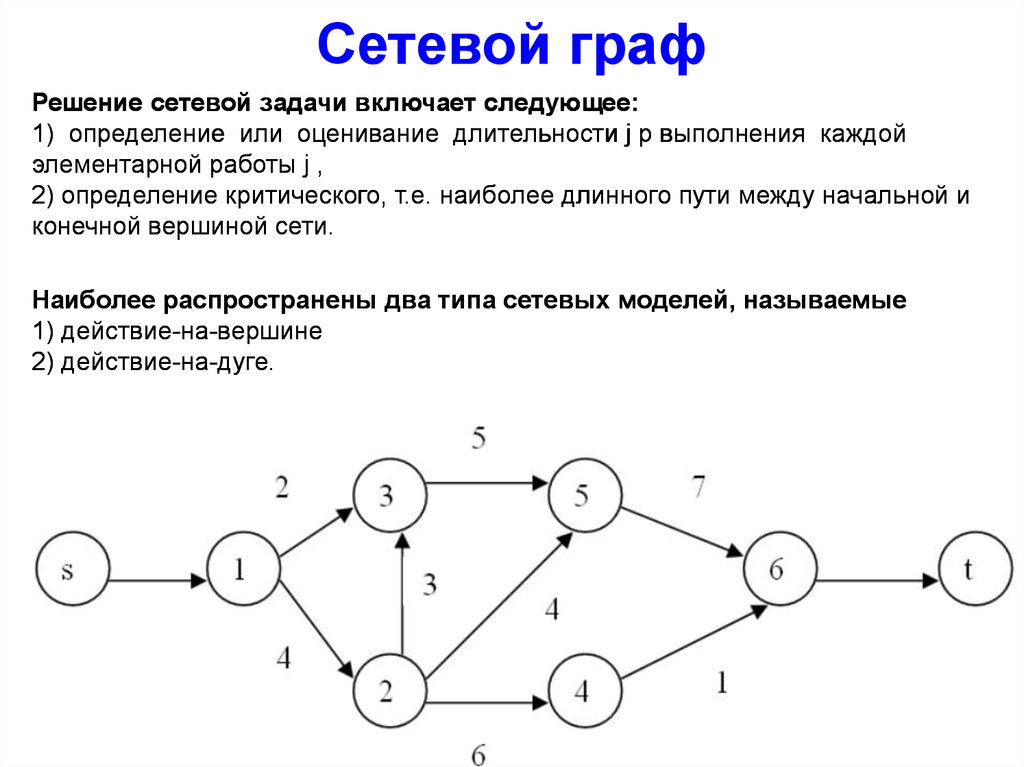
Решение:
Вершины графа — это деревья, обозначенный первой буквой названия дерева. В данной задача два отношения: “быть ниже” и “быть выше”. Рассмотрим отношение “быть ниже” и проведем стрелки от более низкого дерева к более высокому. Если в задаче сказано, что рябина выше лиственницы, то стрелку ставим от лиственницы к рябине и т.д. Получаем граф, на котором видно, что самое низкое дерево – клен, затем идут яблоня, лиственница, рябина, сосна, дуб, береза и тополь.
Задача 3.
У Наташи есть 2 конверта: обычный и авиа, и 3 марки: прямоугольная, квадратная и треугольная. Сколькими способами Наташа может выбрать конверт и марку, чтобы отправить письмо?
Решение:
Ниже представлен разбор задач.
Теория графов в информатике: примеры
Графы в информатике являются способом определения отношений в совокупности элементов. Это основные объекты изучения теории графов.
Это основные объекты изучения теории графов.
Базовые определения
Из чего состоит граф в информатике? Он включает множество объектов, называемых вершинами или узлами, некоторые пары которых связаны т. н. ребрами. Например, граф на рисунке (а) состоит из четырех узлов, обозначенных А, В, С, и D, из которых B соединен с каждой из трех других вершин ребрами, а C и D также соединены. Два узла являются соседними, если они соединены ребром. На рисунке показан типичный способ того, как строить графы по информатике. Круги представляют вершины, а линии, соединяющие каждую их пару, являются ребрами.
Какой граф называется неориентированным в информатике? У него отношения между двумя концами ребра являются симметричными. Ребро просто соединяет их друг с другом. Во многих случаях, однако, необходимо выразить асимметричные отношения – например, то, что A указывает на B, но не наоборот. Этой цели служит определение графа в информатике, по-прежнему состоящего из набора узлов вместе с набором ориентированных ребер. Каждое ориентированное ребро представляет собой связь между вершинами, направление которой имеет значение. Направленные графы изображают так, как показано на рисунке (b), ребра их представлены стрелками. Когда требуется подчеркнуть, что граф ненаправленный, его называют неориентированным.
Каждое ориентированное ребро представляет собой связь между вершинами, направление которой имеет значение. Направленные графы изображают так, как показано на рисунке (b), ребра их представлены стрелками. Когда требуется подчеркнуть, что граф ненаправленный, его называют неориентированным.
Модели сетей
Графы в информатике служат математической моделью сетевых структур. На следующем рисунке представлена структура интернета, тогда носившего название ARPANET, в декабре 1970 года, когда она имела лишь 13 точек. Узлы представляют собой вычислительные центры, а ребра соединяют две вершины с прямой связью между ними. Если не обращать внимания на наложенную карту США, остальная часть изображения является 13-узловым графом, подобным предыдущим. При этом действительное расположение вершин несущественно. Важно, какие узлы соединены друг с другом.
Применение графов в информатике позволяет представить, как вещи либо физически, либо логически связаны между собой в сетевой структуре. 13-узловой ARPANET является примером коммуникационной сети, в которой вершины-компьютеры или другие устройства могут передавать сообщения, а ребра представляют собой прямые линии связи, по которым информация может быть передана.
13-узловой ARPANET является примером коммуникационной сети, в которой вершины-компьютеры или другие устройства могут передавать сообщения, а ребра представляют собой прямые линии связи, по которым информация может быть передана.
Примеры информационных моделей объектов
Услышав такие слова, как «моделирование», «модель», человек представляет себе образы из своего…
Маршруты
Хотя графы применяются во многих различных областях, они обладают общими чертами. Теория графов (информатика) включает, возможно, важнейшую из них – идею о том, что вещи часто перемещаются по ребрам, последовательно переходя от узла к узлу, будь то пассажир нескольких авиарейсов или информация, передаваемая от человека к человеку в социальной сети, либо пользователь компьютера, последовательно посещающий ряд веб-страниц, следуя по ссылкам.
Эта идея мотивирует определение маршрута как последовательности вершин, связанных между собой ребрами. Иногда возникает необходимость рассматривать маршрут, содержащий не только узлы, но и последовательность ребер, их соединяющих. Например, последовательность вершин MIT, BBN, RAND, UCLA является маршрутом в графе интернета ARPANET. Прохождение узлов и ребер может быть повторным. Например, SRI, STAN, UCLA, SRI, UTAH, MIT также является маршрутом. Путь, в котором ребра не повторяются, называется цепью. Если же не повторяются узлы, то он носит название простой цепи.
Например, последовательность вершин MIT, BBN, RAND, UCLA является маршрутом в графе интернета ARPANET. Прохождение узлов и ребер может быть повторным. Например, SRI, STAN, UCLA, SRI, UTAH, MIT также является маршрутом. Путь, в котором ребра не повторяются, называется цепью. Если же не повторяются узлы, то он носит название простой цепи.
Графическая информация и текстовая информация. Графическая…
Графическая информация используется сегодня в множестве областей визуальной коммуникации, однако…
Циклы
Особенно важные виды графов в информатике – это циклы, которые представляют собой кольцевую структуру, такую как последовательность узлов LINC, CASE, CARN, HARV, BBN, MIT, LINC. Маршруты с, по крайней мере, тремя ребрами, у которых первый и последний узел одинаковы, а остальные различны, представляют собой циклические графы в информатике.
Примеры: цикл SRI, STAN, UCLA, SRI является самым коротким, а SRI, STAN, UCLA, RAND, BBN, UTAH, SRI значительно больше.
Фактически каждое ребро графа ARPANET принадлежит к циклу. Это было сделано намеренно: если какое-либо из них выйдет из строя, останется возможность перехода из одного узла в другой. Циклы в системах коммуникации и транспорта присутствуют для обеспечения избыточности – они предусматривают альтернативные маршруты по другому пути цикла. В социальной сети тоже часто заметны циклы. Когда вы обнаружите, например, что близкий школьный друг кузена вашей жены на самом деле работает с вашим братом, то это является циклом, который состоит из вас, вашей жены, ее двоюродного брата, его школьного друга, его сотрудника (т. е. вашего брата) и, наконец, снова вас.
Связный граф: определение (информатика)
Естественно задаться вопросом, можно ли из каждого узла попасть в любой другой узел. Граф связный, если между каждой парой вершин существует маршрут. Например, сеть ARPANET – связный граф. То же можно сказать и о большинстве коммуникационных и транспортных сетей, так как их цель состоит в том, чтобы направлять трафик от одного узла к другому.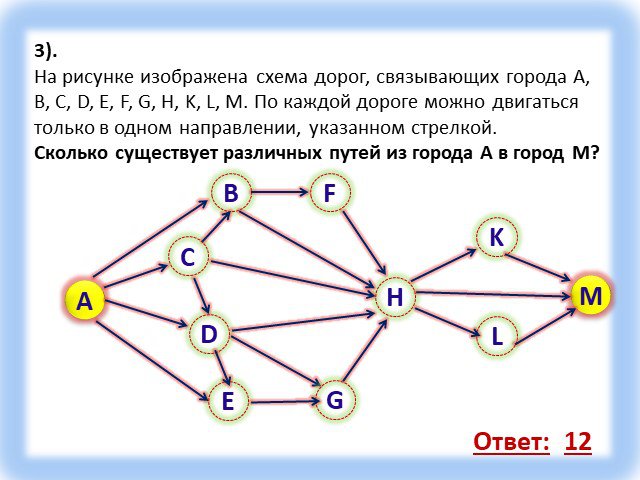
С другой стороны, нет никаких априорных оснований ожидать того, что данные виды графов в информатике широко распространены. Например, в социальной сети несложно представить двух людей, не связанных между собой.
Компоненты
Если графы в информатике не связаны, то они естественным образом распадаются на набор связанных фрагментов, групп узлов, которые являются изолированными и не пересекающимися. Например, на рисунке изображены три таких части: первая – А и В, вторая – C, D и Е, и третья состоит из оставшихся вершин.
Компоненты связности графа представляют собой подмножество узлов, у которых:
- каждая вершина подгруппы имеет маршрут к любой другой;
- подмножество не является частью некоторого большего набора, в котором каждый узел имеет маршрут к любому другому.
Когда графы в информатике разделяются на их компоненты, то это является лишь начальным способом описания их структуры. В рамках данного компонента может быть богатая внутренняя структура, важная для интерпретации сети. Например, формальным методом определения важности узла является определение того, на сколько частей разделится граф, если узел будет убран.
Например, формальным методом определения важности узла является определение того, на сколько частей разделится граф, если узел будет убран.
Максимальная компонента
Существует метод качественной оценки компонентов связности. Например, есть всемирная социальная сеть со связями между двумя людьми, если они являются друзьями.
Связная ли она? Вероятно, нет. Связность – довольно хрупкое свойство, и поведение одного узла (или небольшого их набора) может свести ее на нет. Например, один человек без каких-либо живых друзей будет компонентом, состоящим из единственной вершины, и, следовательно, граф не будет связным. Или отдаленный тропический остров, состоящий из людей, которые не имеют никакого контакта с внешним миром, также будет небольшой компонентой сети, что подтверждает ее несвязность.
Глобальная сеть друзей
Но есть еще кое-что. Например, читатель популярной книги имеет друзей, выросших в других странах, и составляет с ними одну компоненту. Если принять во внимание родителей этих друзей и их друзей, то все эти люди также находятся в той же компоненте, хотя они никогда не слышали о читателе, говорят на другом языке и рядом с ним никогда не были. Таким образом, хотя глобальная сеть дружбы — не связная, читатель будет входить в компонент очень большого размера, проникающий во все части мира, включающий в себя людей из самых разных слоев и, фактически, содержащий значительную часть населения земного шара.
Таким образом, хотя глобальная сеть дружбы — не связная, читатель будет входить в компонент очень большого размера, проникающий во все части мира, включающий в себя людей из самых разных слоев и, фактически, содержащий значительную часть населения земного шара.
То же имеет место и в сетевых наборах данных – большие, сложные сети часто имеют максимальную компоненту, которая включает значительную часть всех узлов. Более того, когда сеть содержит максимальную компоненту, она почти всегда только одна. Чтобы понять, почему, следует вернуться к примеру с глобальной сетью дружбы и попробовать вообразить наличие двух максимальных компонент, каждая из которых включает миллионы людей. Потребуется наличие единственного ребра от кого-то из первой компоненты ко второй, чтобы две максимальные компоненты слились в одну. Так как ребро единственное, то в большинстве случаев невероятно, чтобы оно не образовалось, и, следовательно, две максимальные компоненты в реальных сетях никогда не наблюдаются.
В некоторых редких случаях, когда две максимальные компоненты сосуществовали в течение длительного время в реальной сети, их объединение было неожиданным, драматическим, и, в конечном итоге, имело катастрофические последствия.
Катастрофа слияния компонент
Например, после прибытия европейских исследователей в цивилизации Западного полушария примерно полтысячелетия назад произошел глобальный катаклизм. С точки зрения сети это выглядело так: пять тысяч лет глобальная социальная сеть, вероятно, состояла из двух гигантских компонент — одной в Северной и Южной Америке, а другой — в Евразии. По этой причине технологии развивалась независимо в двух компонентах, и, что еще хуже, так же развивались и болезни человека и т. д. Когда две компоненты, наконец, вошли в контакт, технологии и заболевания одной быстро и катастрофически переполнили вторую.
Американская средняя школа
Понятие максимальных компонент полезно для рассуждений о сетях и в гораздо меньших размерах. Интересный пример представляет собой граф, иллюстрирующий романтические отношения в американской средней школе за 18-месячный период. Тот факт, что он содержит максимальную компоненту, имеет важное значение, когда речь заходит о распространении заболеваний, передаваемых половым путем, что и являлось целью проведенного исследования. Ученики, возможно, имели лишь одного партнера за этот период времени, но, тем не менее, не осознавая этого, были частью максимальной компоненты и, следовательно, частью многих маршрутов потенциальной передачи. Эти структуры отражают отношения, которые, возможно, давно закончилась, но они связывают индивидуумов в цепях слишком долго, чтобы стать предметом пристального внимания и сплетен. Тем не менее, они реальны: как социальные факты это невидимые, но логически вытекающие макроструктуры, возникшие как продукт индивидуального посредничества.
Интересный пример представляет собой граф, иллюстрирующий романтические отношения в американской средней школе за 18-месячный период. Тот факт, что он содержит максимальную компоненту, имеет важное значение, когда речь заходит о распространении заболеваний, передаваемых половым путем, что и являлось целью проведенного исследования. Ученики, возможно, имели лишь одного партнера за этот период времени, но, тем не менее, не осознавая этого, были частью максимальной компоненты и, следовательно, частью многих маршрутов потенциальной передачи. Эти структуры отражают отношения, которые, возможно, давно закончилась, но они связывают индивидуумов в цепях слишком долго, чтобы стать предметом пристального внимания и сплетен. Тем не менее, они реальны: как социальные факты это невидимые, но логически вытекающие макроструктуры, возникшие как продукт индивидуального посредничества.
Расстояние и поиск в ширину
В дополнение к сведениям о том, связаны ли два узла маршрутом, теория графов в информатике позволяет узнать и о его длине – в транспорте, связи или при распространении новостей и заболеваний, а также о том, проходит ли он через несколько вершин или множество.
Для этого следует определить длину маршрута, равную числу шагов, которые он содержит от начала до конца, т. е. число ребер в последовательности, которая его составляет. Например, маршрут MIT, BBN, RAND, UCLA имеет длину 3, а MIT, UTAH – 1. Используя длину пути, можно говорить о том, расположены ли два узла в графе близко друг к другу или далеко: расстояние между двумя вершинами определяется как длина самого короткого пути между ними. Например, расстояние между LINC и SRI равно 3, хотя, чтобы убедиться в этом, следует удостовериться в отсутствии длины, равной 1 или 2, между ними.
Алгоритм поиска в ширину
Для небольших графов расстояние между двумя узлами подсчитать легко. Но для сложных появляется необходимость в систематическом методе определения расстояний.
Самым естественным способом это сделать и, следовательно, наиболее эффективным, является следующий (на примере глобальной сети друзей):
- Все друзья объявляются находящимися на расстоянии 1.

- Все друзья друзей (не считая уже отмеченных) объявляются находящимися на расстоянии 2.
- Все их друзья (опять же, не считая помеченных людей) объявляются удаленными на расстояние 3.
Продолжая таким образом, поиск проводят в последующих слоях, каждый из которых — на единицу дальше предыдущего. Каждый новый слой составляется из узлов, которые еще не участвовали в предыдущих, и которые входят в ребро с вершиной предыдущего слоя.
Эта техника называется поиском в ширину, так как она выполняет поиск по графу наружу от начального узла, в первую очередь охватывая ближайшие. В дополнение к предоставлению способа определения расстояния, она может служить полезной концептуальной основой для организации структуры графа, а также того, как построить граф по информатике, располагая вершины на основании их расстояния от фиксированной начальной точки.
Поиск в ширину может быть применен не только к сети друзей, но и к любому графу.
Мир тесен
Если вернуться к глобальной сети друзей, можно увидеть, что аргумент, объясняющий принадлежность к максимальной компоненте, на самом деле утверждает нечто большее: не только у читателя есть маршруты к друзьям, связывающие его со значительной долей населения земного шара, но эти маршруты на удивление коротки.
Эта идея получила название «феномена тесного мира»: мир кажется маленьким, если думать о том, какой короткий маршрут связывает любых двух людей.
Теория «шести рукопожатий» впервые экспериментально исследовалась Стенли Милгрэмом и его коллегами в 1960-е годы. Не имея какого-либо набора данных социальных сетей и с бюджетом в 680 долларов он решил проверить популярную идею. С этой целью он попросил 296 случайно отобранных инициаторов попробовать отослать письмо биржевому брокеру, который жил в пригороде Бостона. Инициаторам были даны некоторые личные данные о цели (включая адрес и профессию), и они должны были переслать письмо лицу, которого они знали по имени, с теми же инструкциями, чтобы оно достигло цели как можно быстрее. Каждое письмо прошло через руки ряда друзей и образовало цепочку, замыкавшуюся на биржевом брокере за пределами Бостона.
Среди 64 цепочек, достигших цели, средняя длина равнялась шести, что подтвердило число, названное два десятилетия ранее в названии пьесы Джона Гэра.
Несмотря на все недочеты этого исследования, эксперимент продемонстрировал один из важнейших аспектов нашего понимания социальных сетей. В последующие годы из него был сделан более широкий вывод: социальные сети, как правило, имеют очень короткие маршруты между произвольными парами людей. И даже если такие опосредованные связи с руководителями предприятий и политическими лидерами не окупаются на ежедневной основе, существование таких коротких маршрутов играет большую роль в скорости распространения информации, болезней и других видов заражения в обществе, а также в возможностях доступа, которые социальная сеть предоставляет людям с совершенно противоположными качествами.
графиков в информатике
график в информатикеВведение
Графики — это математические концепции, которые нашли множество применений.
в информатике. Графики бывают разных видов, многие из
которые нашли применение в компьютерных программах. Некоторые вкусы:
Некоторые вкусы:
- Простой график
- Неориентированные или ориентированные графы
- Циклические или ациклические графы
- помеченные графики
- Взвешенные графики
- Бесконечные графы
- … и многие другие, которых невозможно перечислить.
Большинство графиков определяются как небольшое изменение следующего правила.
- Граф состоит из двух наборов, называемых Вершинами и Ребрами.
- Вершины взяты из некоторого базового типа, и набор может быть конечным или бесконечным.
- Каждый элемент набора Edge представляет собой пару, состоящую из двух элементов из набора вершин.
- Графики часто изображают визуально, рисуя элементы
вершин, установленных в виде прямоугольников или кругов, и рисование элементов
край, установленный как линии или дуги между прямоугольниками или кругами. Есть дуга
между v1 и v2, если (v1,v2) является элементом множества ребер.

Смежность. Если (u,v) находится в наборе ребер, мы говорим, что u смежно с v (что мы иногда пишем как u ~ v ).
Например, график, нарисованный ниже:
Имеет следующие части.
- Базовым набором для набора Verticies являются целые числа.
- Набор вершин = {1,2,3,4,5,6}
- Набор ребер = {(6,4),(4,5),(4,3),(3,2),(5,2),(2,1),(5,1)}
Виды графиков
Различные разновидности графов имеют следующие специализации и подробности о том, как они обычно рисуются.Неориентированные графы.
В неориентированном графе порядок вершин в парах набора ребер не имеет значения. Таким образом, если мы рассмотрим выборку выше, мы могли бы записать набор ребер как {(4,6),(4,5),(3,4),(3,2),(2,5)),(1,2)),( 1,5)}. Неориентированные графы обычно рисуются с прямыми линиями между вершины.Отношение смежности симметрично в неориентированном графе, поэтому, если u ~ v , то также имеет место v ~ u .

Направленные графы.
В ориентированном графе порядок вершин в парах в наборе ребер имеет значение. Таким образом u смежно с v, только если пара (u,v) находится в наборе ребер. Для ориентированных графов мы обычно используем стрелки для дуг между вершины. Стрелка от u к v рисуется, только если (u,v) находится в наборе ребер. Ориентированный граф нижеИмеет следующие части.
- Базовый набор для набора Verticies — заглавные буквы.
- Набор вершин = {A,B,C,D,E}
- Набор ребер = {(A,B),(B,C),(D,C),(B,D),(D,B),(E,D),(B,E)}
Обратите внимание, что и (B,D), и (D,B) находятся в наборе ребер, поэтому дуга между B и D является стрелкой в обоих направлениях.
Графики с метками вершин.
В размеченном графе каждая вершина помечен некоторыми данными в дополнение к данным, которые идентифицируют вершина. В файле присутствуют только идентификационные данные. пара в наборе Edge. Это относится к (ключевым, спутниковым) данным
различие для сортировки.
Это относится к (ключевым, спутниковым) данным
различие для сортировки.Здесь у нас есть следующие части.
- Базовым набором ключей набора вершин являются целые числа.
- Базовым набором для спутниковых данных является Цвет.
- Набор вершин = {(2,Синий),(4,Синий),(5,Красный),(7,Зеленый),(6,Красный),(3,Желтый)}
- Набор ребер = {(2,4),(4,5),(5,7),(7,6),(6,2),(4,3),(3,7)}
Циклические графики.
Циклический граф — это ориентированный граф хотя бы с одним циклом. Цикл — это путь по направленным ребрам от вершины к самой себе. Вершина, помеченная графом выше, как несколько циклов. Один из них 2 » 4 » 5 » 7 » 6 » 2Графики с маркировкой Edge.
Граф с меткой Edge представляет собой граф, где ребра связаны с метками. Можно указать, что это делая набор Edge набором троек. Таким образом, если (u,v,X) находится в набор ребер, далее идет ребро от u до v с меткой XГрафы с метками ребер обычно рисуются с метками, нарисованными рядом с дуги, определяющие ребра.

Здесь у нас есть следующие части.
- Базовым набором для набора Vertices является Color.
- Базовым набором для меток ребер являются наборы цветов.
- Набор вершин = {красный, зеленый, синий, белый}
- Набор Edge = {(красный, белый, {белый, зеленый}) ,(белый,красный,{синий}) ,(белый,синий,{зеленый,красный}) ,(красный,синий,{синий}) ,(зеленый,красный,{красный,синий,белый}) ,(синий,зеленый,{белый,зеленый,красный})}
Взвешенные графики.
Взвешенный граф является ребром помеченный граф, над метками которого может работать обычные арифметические операторы, включая сравнения, такие как используя меньше чем и больше чем. В Haskell мы бы сказали, что метки ребер — это класс Num. Обычно это целые числа или плавает. Идея состоит в том, что некоторые ребра могут быть больше (или менее) дорого, и эта стоимость представлена краем этикетки или вес.
Здесь у нас есть следующие части.
- Базовым набором для набора Vertices является Integer.
- Базовым набором весов является Integer.
- Набор вершин = {1,2,3,4,5}
- Набор краев = {(1,4,5) ,(4,5,58) ,(3,5,34) ,(2,4,5) ,(2,5,4) ,(3,2,14) ,(1,2,2)}
Направленные ациклические графы.
A Dag — ориентированный граф без циклов. Они постоянно появляются как частные случаи в приложениях CS.Здесь у нас есть следующие части.
- Базовым набором для набора Vertices является Integer.
- Набор вершин = {1,2,3,4,5,6,7,8}
- Набор ребер = {(1,7) ,(2,6) ,(3,1),(3,5) ,(4,6) ,(5,4),(5,2) ,(6,8) ,(7,2),(7,8)}
Отключенные графики
Вершины графа не обязательно должны быть связаны с другими вершинами. Граф может иметь несвязанные компоненты и даже одиночные вершины.
без единого подключения.
Граф может иметь несвязанные компоненты и даже одиночные вершины.
без единого подключения.Вершины (например, 5,7 и 8) только с стрелками внутри называются стоками. Вершины только с стрелками наружу (например, 3 и 4) называются источниками.
Здесь у нас есть следующие части.
- Базовым набором для набора Vertices является Integer.
- Набор вершин = {1,2,3,4,5,6,7,8}
- Набор ребер = {(1,7) ,(3,1),(3,8) ,(4,6) ,(6,5)}
Представление графов на компьютере
Графики часто используются для представления физических объектов.
(сеть дорог, отношения между людьми и т.д.) внутри
компьютер. Используется множество механизмов. Хороший выбор
механизм зависит от операций, которые компьютерная программа должна выполнять на графе
для достижения своих потребностей . Возможные операции включают.
- Вычислить список всех вершин
- Вычислить список всех ребер.
- Для каждой вершины u вычислить список ребер (u,v). Это часто называют функцией смежности.
- Если граф помечен (помечены либо вершины, либо ребра) вычислить метку для каждой вершины (или ребра).
Не всем программам потребуются все эти операции, поэтому для некоторых программы, эффективное представление, которое может вычислить только необходимых операций (но не других), будет достаточно.
Преимущества представления графиков в виде функций
- Просто и понятно
- Легко адаптируется к различным типам графиков
Недостатки использования графиков в качестве функций
- Не может быть расширен для размещения запросов о набор вершин или набор ребер.
- В зависимости от компилятора, компилирующего функции
может быть не очень эффективным. На самом деле время в худшем случае может быть пропорционально количеству вершин.

- График должен быть известен статически во время компиляции.
Графы как массивы смежных вершин.
Один механизм, который может смягчить недостатки использования функций в качестве способа представления графиков следует использовать вместо них массивы. Используя это механизм требует, чтобы базовый домен Vertices был некоторым тип, который можно использовать в качестве индекса в массиве.В оставшейся части этой заметки мы будем предполагать, что вершины имеют тип Int , и что набор вершин представляет собой конечный диапазон типа Int . Таким образом, граф можно представить следующим образом:
введите ArrGraph = Массив [Int]Теперь мы можем быстро и эффективно ответить на ряд вопросов о графиках.
введите ArrGraph i = Массив [i]
вершины:: ArrGraph i -> IO[Int]
ребра:: ArrGraph i -> IO[(Int,i)]
дети:: ArrGraph i -> i -> IO[i]
вершины г =
делать { (ло, привет)
Преимущества представления графов в виде массивов
Недостатки представления графиков в виде массивов
- Требует, чтобы доступ к графу был командой, а не вычислением.

- Домен Vertices должен быть такого типа, который можно использовать в качестве индекса в массиве.
Алгоритмы на графиках
Алгоритмов на графах очень много. В этой заметке мы будем посмотрите на некоторые из них. Они включают:
- Поиск графиков
- Обнаружение циклов на графиках
- Алгоритмы кратчайшего пути
Вернемся к ежедневной записи.
Вернуться на страницу класса.
Типы графиков с примерами
График представляет собой нелинейную структуру данных, состоящую из узлов и ребер . Узлы иногда также называют вершинами, а ребра — линиями или дугами, соединяющими любые два узла в графе. Более формально граф можно определить как граф, состоящий из конечного набора вершин (или узлов) и набора ребер, соединяющих пару узлов 9.
0008
- Неориентированные графы : Граф, в котором ребра не имеют направления, т. е. ребра не имеют стрелок, указывающих направление обхода. Пример: граф социальной сети, где дружеские отношения не являются направленными.
- Направленные графы : Граф, в котором ребра имеют направление, т. е. ребра имеют стрелки, указывающие направление обхода. Пример: граф веб-страницы, где ссылки между страницами являются направленными.
- Взвешенные графики: Граф, в котором ребра имеют вес или стоимость, связанные с ними. Пример: граф дорожной сети, где веса могут представлять расстояние между двумя городами.
- Невзвешенный граф s: Граф, в котором ребра не имеют весов или связанных с ними затрат. Пример: граф социальной сети, где ребра представляют собой дружеские отношения.
- Полные графы: Граф, в котором каждая вершина соединена с каждой другой вершиной.
 Пример: график турнира, где каждый игрок играет против каждого другого игрока.
Пример: график турнира, где каждый игрок играет против каждого другого игрока. - Двудольные графы: Граф, в котором вершины можно разделить на два непересекающихся множества так, что каждое ребро соединяет вершину одного множества с вершиной другого множества. Пример: граф кандидатов на работу, вершины которого можно разделить на кандидатов на работу и вакансии.
- Деревья : Связный граф без циклов. Пример: Генеалогическое древо, в котором каждый человек связан со своими родителями.
- Циклы : Граф с хотя бы одним циклом. Пример: граф совместного использования велосипедов, где циклы представляют маршруты, по которым ездят велосипеды.
- Разреженные графы: Граф с относительно небольшим количеством ребер по сравнению с количеством вершин. Пример: граф химической реакции, где каждая вершина представляет собой химическое соединение, а каждое ребро представляет собой реакцию между двумя соединениями.

- Плотный граф s: граф с большим количеством ребер по сравнению с количеством вершин. Пример: Граф социальной сети, где каждая вершина представляет человека, а каждое ребро представляет дружбу.
Граф называется конечным, если он имеет конечное число вершин и конечное число ребер. Конечный граф — это граф с конечным числом вершин и ребер. Другими словами, и количество вершин, и количество ребер в конечном графе ограничено и может быть подсчитано. Конечные графы часто используются для моделирования реальных ситуаций, когда существует ограниченное количество объектов и отношений между
2. Бесконечный граф:Граф называется бесконечным, если он имеет бесконечное количество вершин, а также бесконечное количество ребер.
3. Тривиальный граф: Граф называется тривиальным, если конечный граф содержит только одну вершину и не содержит ребер. Тривиальный граф — это граф, имеющий только одну вершину и не имеющий ребер. Он также известен как одноэлементный граф или граф с одной вершиной. Тривиальный граф — это простейший тип графа, который часто используется в качестве отправной точки для построения более сложных графов. В теории графов тривиальные графы считаются вырожденным случаем и обычно подробно не изучаются
Тривиальный граф — это граф, имеющий только одну вершину и не имеющий ребер. Он также известен как одноэлементный граф или граф с одной вершиной. Тривиальный граф — это простейший тип графа, который часто используется в качестве отправной точки для построения более сложных графов. В теории графов тривиальные графы считаются вырожденным случаем и обычно подробно не изучаются
Простой граф — это граф, который не содержит более одного ребра между парой вершин. Простой железнодорожный путь, соединяющий разные города, является примером простого графа.
5. Мультиграф:
Любой граф, содержащий несколько параллельных ребер, но не содержащий ни одной петли, называется мультиграфом. Например, Дорожная карта.
- Параллельные кромки: Если две вершины соединены более чем одним ребром, то такие ребра называются параллельными ребрами, у которых много маршрутов, но один пункт назначения.

- Петля: Ребро графа, которое начинается с вершины и заканчивается в той же вершине, называется петлей или самопетлей.
Граф порядка n и нулевого размера — это граф, в котором есть только изолированные вершины без ребер, соединяющих любую пару вершин. Нулевой граф — это граф без ребер. Другими словами, это граф только с вершинами и без связей между ними. Нулевой граф также может называться графом без ребер, изолированным графом или дискретным графом 9.0008
7. Полный граф:Простой граф с n вершинами называется полным графом, если степень каждой вершины равна n-1, то есть одна вершина соединена с n-1 ребрами или остальными вершин в графе. Полный граф также называется полным графом.
8. Псевдограф:
Граф G с петлей и несколькими кратными ребрами называется псевдографом. Псевдограф — это тип графа, который допускает существование петель (ребер, соединяющих вершину с самой собой) и множественных ребер (более одного ребра, соединяющих две вершины). Напротив, простой граф — это граф, который не допускает петель или множественных ребер.
Напротив, простой граф — это граф, который не допускает петель или множественных ребер.
Простой граф называется регулярным, если все вершины графа G имеют одинаковую степень. Все полные графы регулярны, но наоборот невозможно. Регулярный граф — это тип неориентированного графа, в котором каждая вершина имеет одинаковое количество ребер или соседей. Другими словами, если граф правильный, то все вершины имеют одинаковую степень.
10. Двудольный граф:Граф G = (V, E) называется двудольным, если его множество вершин V(G) можно разбить на два непустых непересекающихся подмножества. V1(G) и V2(G) таким образом, что каждое ребро e ребра E(G) имеет один конец в V1(G), а другой конец в V2(G). Разбиение V1 U V2 = V называется двудольным G. Здесь на рисунке: V1(G)={V5, V4, V3} и V2(G)={V1, V2}
11. Размеченный граф: Если вершины и ребра графа помечены именем, датой или весом, то он называется размеченным графом. Его также называют взвешенным графиком.
Его также называют взвешенным графиком.
Граф G = (V, E) с отображением f таким, что каждое ребро отображается на некоторую упорядоченную пару вершин (Vi, Vj), называется орграфом. Его также называют Directed Graph . Упорядоченная пара (Vi, Vj) означает ребро между Vi и Vj со стрелкой, направленной из Vi в Vj. Здесь на рисунке: e1 = (V1, V2) e2 = (V2, V3) e4 = (V2, V4)
13. Подграф:Граф G1 = (V1, E1) называется подграфом графа G(V, E), если V1(G) является подмножеством V(G) и E1( G) является подмножеством E(G) таким, что каждое ребро G1 имеет те же концевые вершины, что и в G.
вершин (Vi, Vj) графа G достижимы друг из друга. Или граф называется связным, если существует хотя бы один путь между каждой и каждой парой вершин в графе G, в противном случае он несвязен. Нулевой граф с n вершинами — это несвязный граф, состоящий из n компонент. Каждый компонент состоит из одной вершины и не содержит ребер. 15. Циклический граф:
15. Циклический граф: Граф G, состоящий из n вершин и n> = 3, то есть V1, V2, V3- – – – Vn и ребер (V1, V2), (V2, V3) , (V3, V4)- – – – (Vn, V1) называются циклическими графами.
16. Типы подграфов:- Вершинный непересекающийся подграф: Любые два графа G1 = (V1, E1) и G2 = (V2, E2) называются вершинно непересекающимися графа г = (V, E), если пересечение V1(G1) V2(G2) = null. На рисунке нет общей вершины между G1 и G2.
- Реберно непересекающийся подграф: Подграф называется реберно непересекающимся, если E1(G1) пересечение E2(G2) = null. На рисунке нет общего ребра между G1 и G2.
Примечание: Реберный непересекающийся подграф может иметь общие вершины, но вершинный непересекающийся граф не может иметь общего ребра, поэтому вершинный непересекающийся подграф всегда будет реберно непересекающимся подграфом.
17.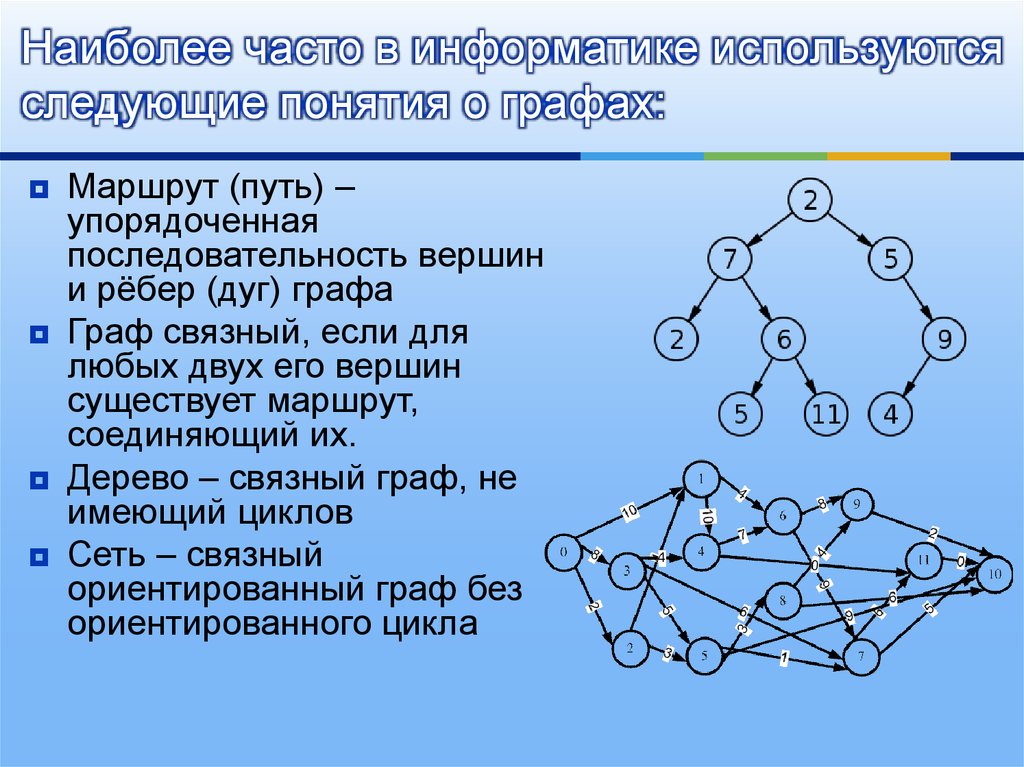 Охватывающий подграф
Охватывающий подграф Рассмотрим граф G(V,E), как показано ниже. Остовный подграф — это подграф, содержащий все вершины исходного графа G, то есть G'(V’,E’) является остовным, если V’=V и E’ является подмножеством E.
Таким образом, один из связующих подграфов может быть таким, как показано ниже G'(V’,E’). Он имеет все вершины исходного графа G и некоторые ребра графа G.
Это всего лишь один из многих остовных подграфов графа G. Мы можем различать другие остовные подграфы с помощью различных комбинаций ребер. Заметим, что если мы рассмотрим граф G'(V’,E’), где V’=V и E’=E, то граф G’ является остовным подграфом графа G(V,E).
Преимущества графиков:
- Графики можно использовать для моделирования и анализа сложных систем и взаимосвязей.
- Они полезны для визуализации и понимания данных.
- Графовые алгоритмы широко используются в компьютерных науках и других областях, таких как анализ социальных сетей, логистика и транспорт.



 Это относится к (ключевым, спутниковым) данным
различие для сортировки.
Это относится к (ключевым, спутниковым) данным
различие для сортировки.

 Граф может иметь несвязанные компоненты и даже одиночные вершины.
без единого подключения.
Граф может иметь несвязанные компоненты и даже одиночные вершины.
без единого подключения.
 0008
0008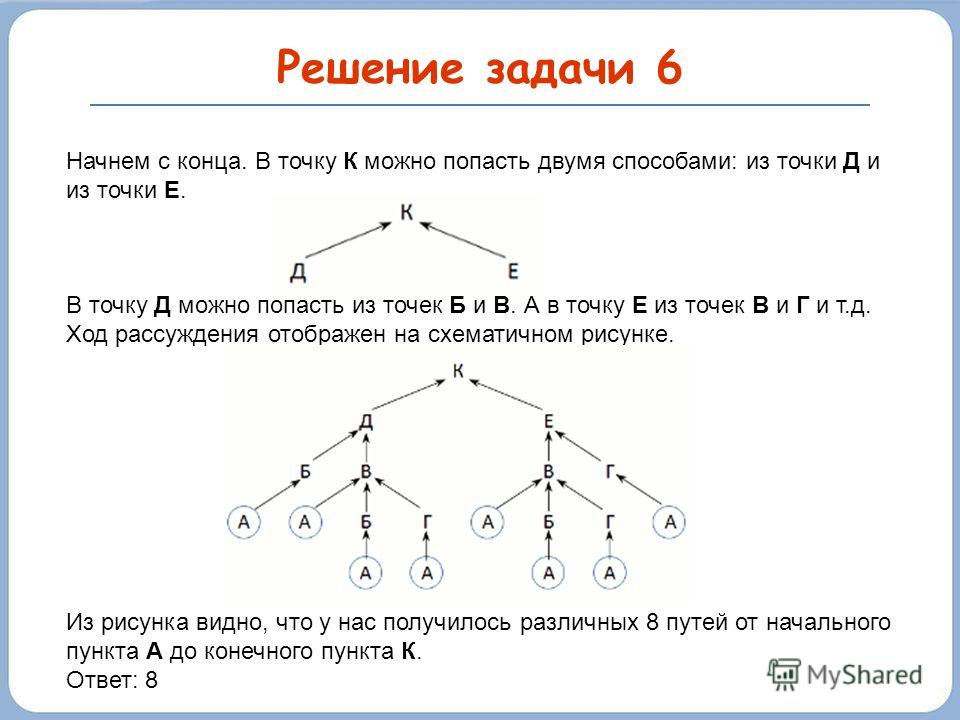 Пример: график турнира, где каждый игрок играет против каждого другого игрока.
Пример: график турнира, где каждый игрок играет против каждого другого игрока.