Как выглядит четная функция. Четность функции
Исследование функции.
1) D(y) – Область опрделения: множество всех тех значений переменной х. при которых алгебраические выражения f(x) и g(x) имеют смысл.
Если функция задана формулой, то область определения состоит из всех значений независимой переменной, при которых формула имеет смысл.
2) Свойства функции: четность/нечетность, периодичность:
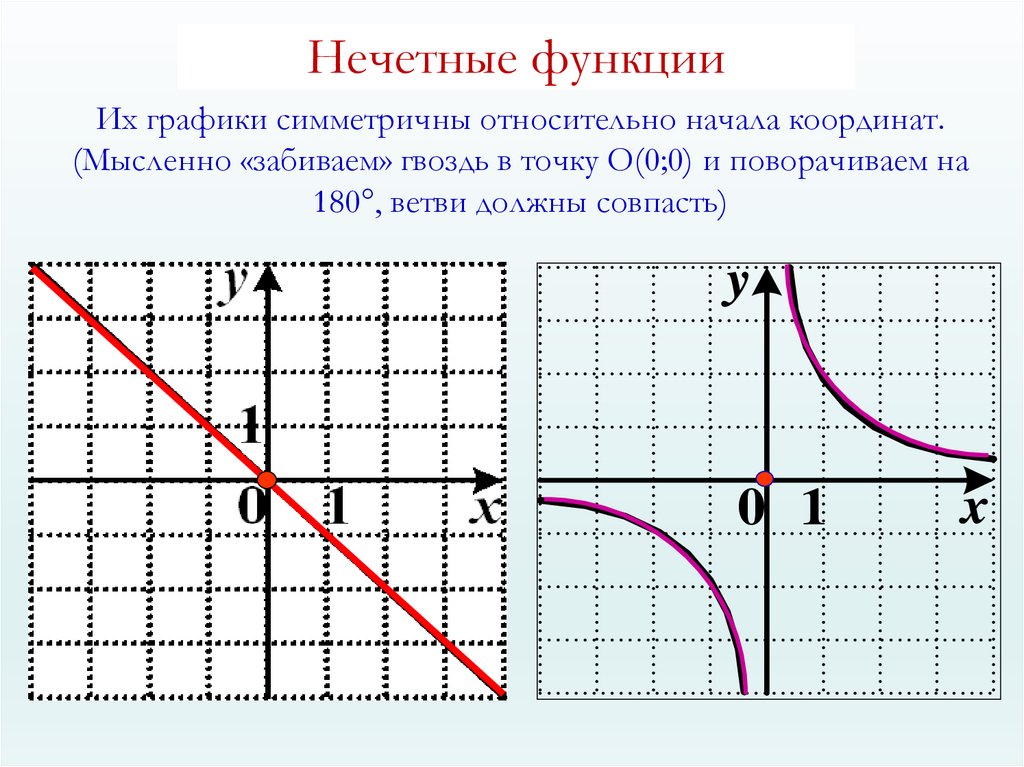
Нечётными и чётными называются функции, графики которых обладают симметрией относительно изменения знака аргумента.
Нечётная функция — функция, меняющая значение на противоположное при изменении знака независимой переменной (симметричная относительно центра координат).
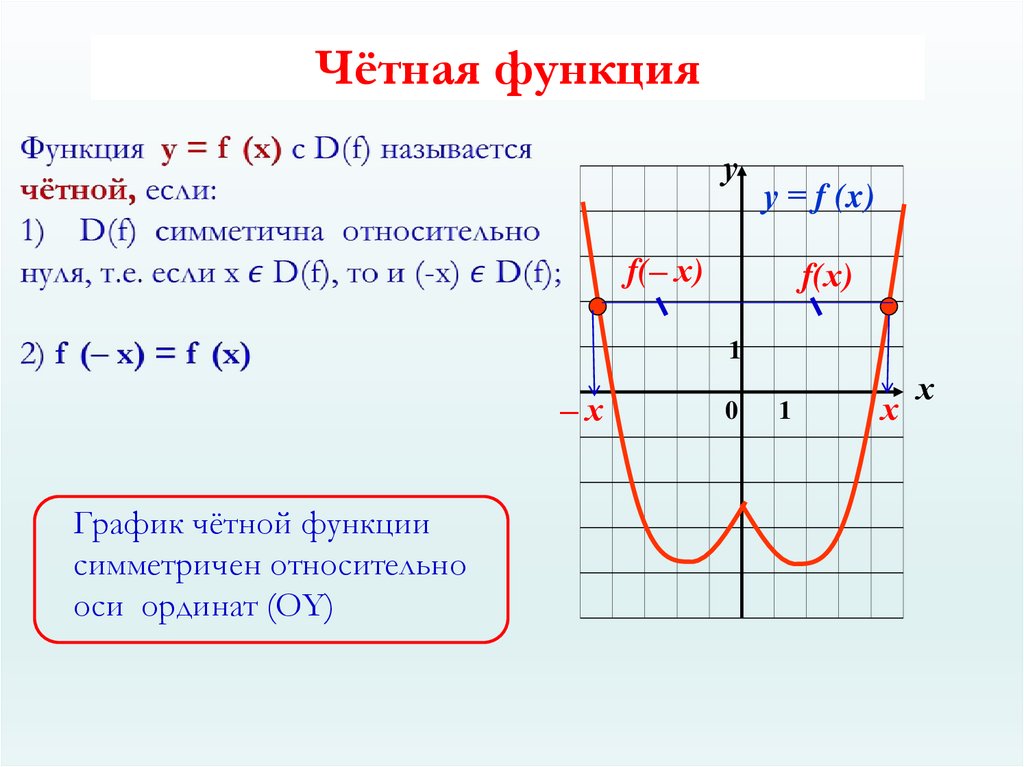
Чётная функция — функция, не изменяющая своего значения при изменении знака независимой переменной (симметричная относительно оси ординат).
Ни
чётная ни нечётная функция (функция
общего вида) —
функция, не обладающая симметрией. В
эту категорию относят функции, не
подпадающие под предыдущие 2 категории.
В
эту категорию относят функции, не
подпадающие под предыдущие 2 категории.
Функции, не принадлежащие ни одной из категорий выше, называются ни чётными ни нечётными (или функциями общего вида).
Нечётные функции
Нечётная степень где — произвольное целое число.
Чётные функции
Чётная степень где — произвольное целое число.
Периоди́ческая фу́нкция ― функция, повторяющая свои значения через некоторый регулярный интервал аргумента, то есть не меняющая своего значения при добавлении к аргументу некоторого фиксированного ненулевого числа (пери́ода функции) на всей области определения.
3) Нули (корни) функции — точки, где она обращается в ноль.
Нахождение
точки пересечения графика с осью Oy . Для
этого нужно вычислить значение f (0).
Найти также точки пересечения графика
с осью Ox ,
для чего найти корни уравнения f (x )
= 0 (или
убедиться в отсутствии корней).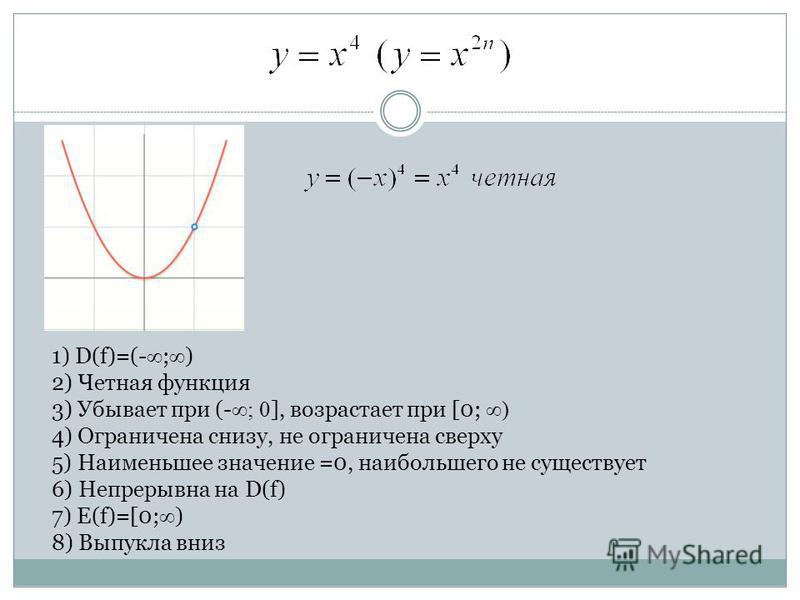
Точки, в которых график пересекает ось , называют нулями функции . Чтобы найти нули функции нужно решить уравнение , то есть найти те значения «икс» , при которых функция обращается в ноль.
4) Промежутки постоянства знаков, знаки в них.
Промежутки, где функция f(x) сохраняет знак.
Интервал знакопостоянства – это интервал, в каждой точке которого функция положительна либо отрицательна.
ВЫШЕ оси абсцисс.
НИЖЕ оси .
5) Непрерывность (точки разрыва, характер разрыва, ассимптоты).
Непрерывная функция — функция без «скачков», то есть такая, у которой малые изменения аргумента приводят к малым изменениям значения функции.
Устранимые точки разрыва
Если предел функции существует , но функция не определена в этой точке, либо предел не совпадает со значением функции в данной точке:
,
то точка называется
Если «поправить» функцию в точке устранимого разрыва и положить , то получится функция, непрерывная в данной точке. Такая операция над функцией называется доопределением функции до непрерывной или доопределением функции по непрерывности , что и обосновывает название точки, как точки устранимого разрыва.
Точки разрыва первого и второго рода
Если функция имеет разрыв в данной точке (то есть предел функции в данной точке отсутствует или не совпадает со значением функции в данной точке), то для числовых функций возникает два возможных варианта, связанных с существованием у числовых функций односторонних пределов :
если оба односторонних предела существуют и конечны, то такую точку называют точкой разрыва первого рода . Точки устранимого разрыва являются точками разрыва первого рода;
если
хотя бы один из односторонних пределов
не существует или не является конечной
величиной, то такую точку называют точкой
разрыва второго рода .
Аси́мпто́та — прямая , обладающая тем свойством, что расстояние от точки кривой до этой прямой стремится к нулю при удалении точки вдоль ветви вбесконечность.
Вертикальная
Вертикальная асимптота — прямая предела .
Как правило, при определении вертикальной асимптоты ищут не один предел, а два односторонних (левый и правый). Это делается с целью определить, как функция ведёт себя по мере приближения к вертикальной асимптоте с разных сторон. Например:
Горизонтальная
Горизонтальная асимптота — прямая вида при условии существования предела
.
Наклонная
Наклонная
асимптота — прямая вида при
условии существования
Замечание: функция может иметь не более двух наклонных (горизонтальных) асимптот.
Замечание: если хотя бы один из двух упомянутых выше пределов не существует (или равен ), то наклонной асимптоты при (или ) не существует.
если в
п. 2.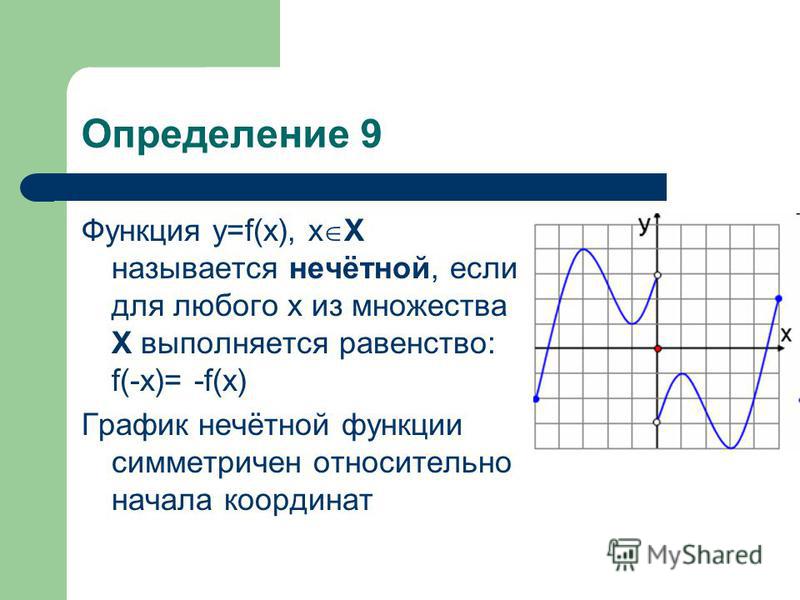 ), то ,
и предел находится
по формуле горизонтальной асимптоты, .
), то ,
и предел находится
по формуле горизонтальной асимптоты, .
6) Нахождение промежутков монотонности. Найти интервалы монотонности функции f (x )(то есть интервалы возрастания и убывания). Это делается с помощью исследования знака производной f (x ). Для этого находят производную f (x ) и решают неравенство f (x )0. На промежутках, где это неравенство выполнено, функция f (x )возрастает. Там, где выполнено обратное неравенство f (x )0, функция f (x )убывает.
Нахождение
локального экстремума. Найдя
интервалы монотонности, мы можем сразу
определить точки локального экстремума
там, где возрастание сменяется убыванием,
располагаются локальные максимумы, а
там, где убывание сменяется возрастанием
— локальные минимумы. Вычислить значение
функции в этих точках. Если функция
имеет критические точки, не являющиеся
точками локального экстремума, то
полезно вычислить значение функции и
в этих точках.
Нахождение наибольшего и наименьшего значений функции y = f(x) на отрезке (продолжение)
1. Найти производную функции: f (x ). 2. Найти точки, в которых производная равна нулю: f (x )=0x 1, x 2 ,… 3. Определить принадлежность точек х 1 , х 2 , … отрезку [a ; b ]: пусть x 1a ;b |
Четность и нечетность функции являются одним из основных ее свойств, и на четность занимает внушительную часть школьного курса по математике. Она во много определяет характер поведения функции и значительно облегчает построение соответствующего графика.
Определим четность функции. Вообще говоря, исследуемую функцию считают четной, если для противоположных значений независимой переменной (x), находящихся в ее области определения, соответствующие значения y (функции) окажутся равными.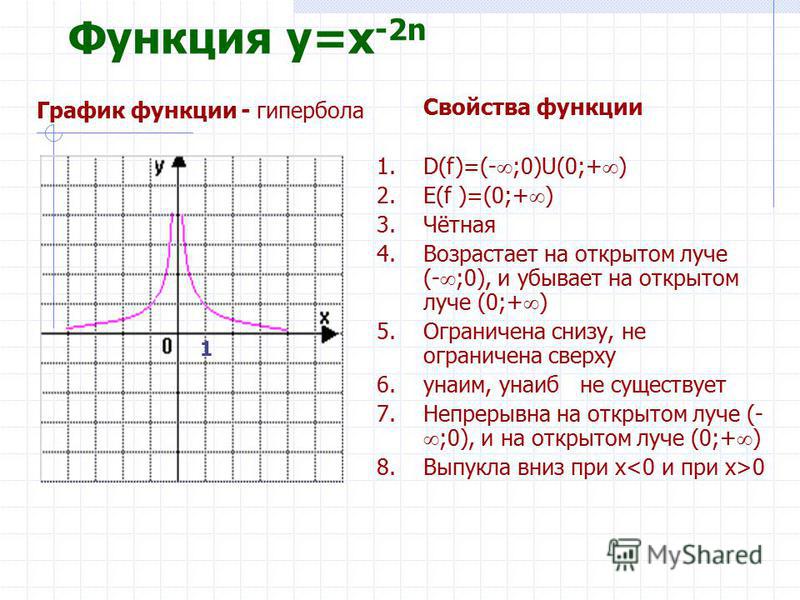 (-x))=- h(x). Следовательно, h(x) — нечетная.
(-x))=- h(x). Следовательно, h(x) — нечетная.
Кстати, следует напомнить, что есть функции, которые невозможно классифицировать по этим признакам, их называют ни четными, ни нечетными.
Четные функции обладают рядом интересных свойств:
- в результате сложения подобных функций получают четную;
- в результате вычитания таких функций получают четную;
- четной, также четная;
- в результате умножения двух таких функций получают четную;
- в результате умножения нечетной и четной функций получают нечетную;
- в результате деления нечетной и четной функций получают нечетную;
- производная такой функции — нечетная;
- если возвести нечетную функцию в квадрат, получим четную.
Четность функции можно использовать при решении уравнений.
Чтобы решить уравнение типа g(x) = 0, где левая часть уравнения представляет из себя четную функцию, будет вполне достаточно найти ее решения для неотрицательных значений переменной. Полученные корни уравнения необходимо объединить с противоположными числами. 2+2 может быть нечетным, причем для любого значения параметра. Действительно, легко проверить, что множество корней данного уравнения содержит решения «парами». Проверим, является ли 0 корнем. При подстановке его в уравнение, получаем 2=2 . Таким образом, кроме «парных» 0 также является корнем, что и доказывает их нечетное количество.
2+2 может быть нечетным, причем для любого значения параметра. Действительно, легко проверить, что множество корней данного уравнения содержит решения «парами». Проверим, является ли 0 корнем. При подстановке его в уравнение, получаем 2=2 . Таким образом, кроме «парных» 0 также является корнем, что и доказывает их нечетное количество.
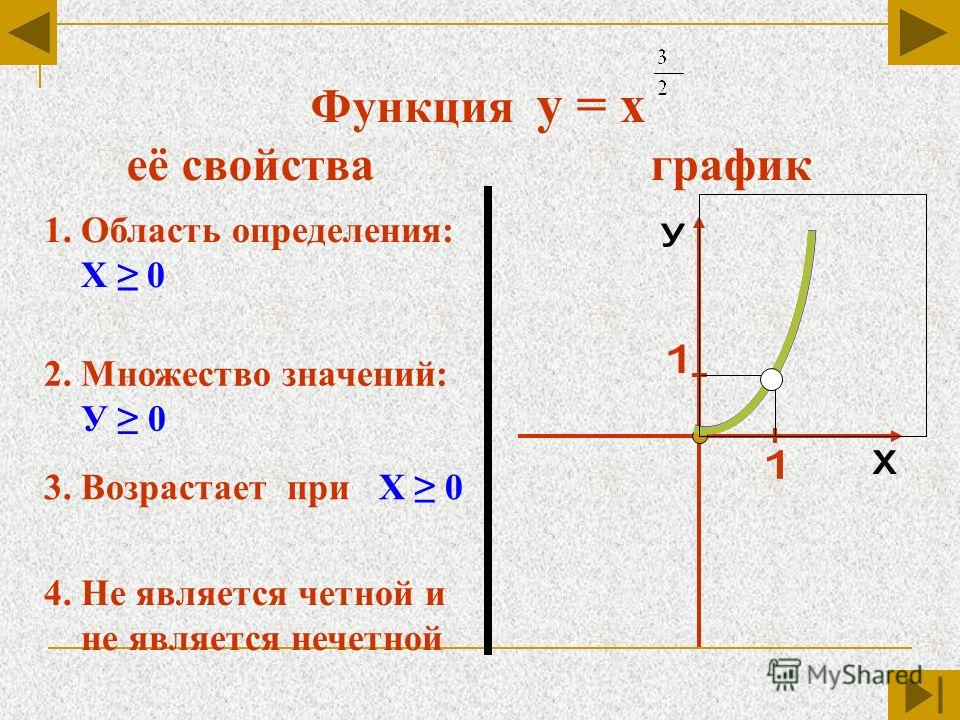
Функция — это одно из важнейших математических понятий. Функция — зависимость переменной у от переменной x , если каждому значению х соответствует единственное значение у . Переменную х называют независимой переменной или аргументом. Переменную у называют зависимой переменной. Все значения независимой переменной (переменной x ) образуют область определения функции. Все значения, которые принимает зависимая переменная (переменная y ), образуют область значений функции.
Графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции, тоесть по оси абсцисс откладываются значения переменной x , а по оси ординат откладываются значения переменной y .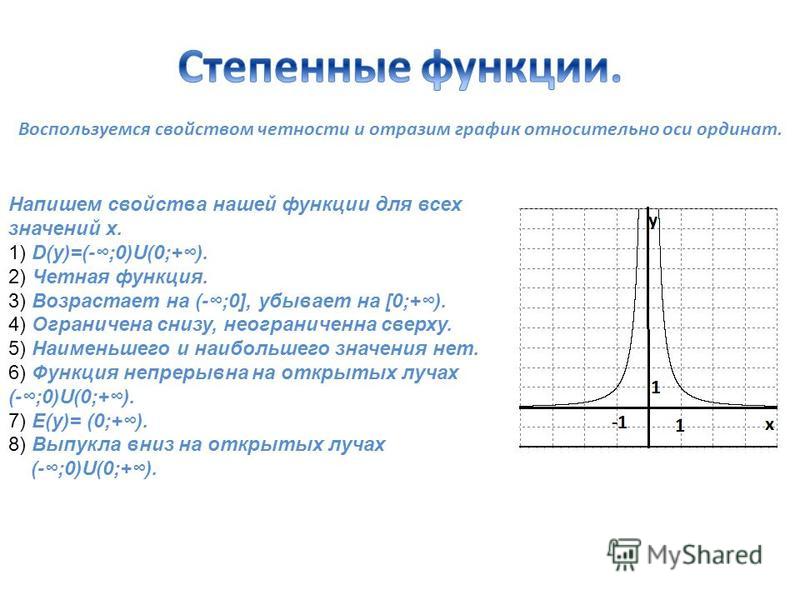
Для построения графика функции советуем использовать нашу программу — Построение графиков функций онлайн. Если при изучении материала на данной странице у Вас возникнут вопросы, Вы всегда можете задать их на нашем форуме. Также на форуме Вам помогут решить задачи по математике, химии, геометрии, теории вероятности и многим другим предметам!
Основные свойства функций.
1) Область определения функции и область значений функции .
Область определения функции — это множество всех допустимых действительных значений аргумента x (переменной x ), при которых функция y = f(x) определена.
Область значений функции — это множество всех действительных значений y , которые принимает функция.
В элементарной математике изучаются функции только на множестве действительных чисел.
2) Нули функции .
Значения х , при которых y=0 , называется нулями функции .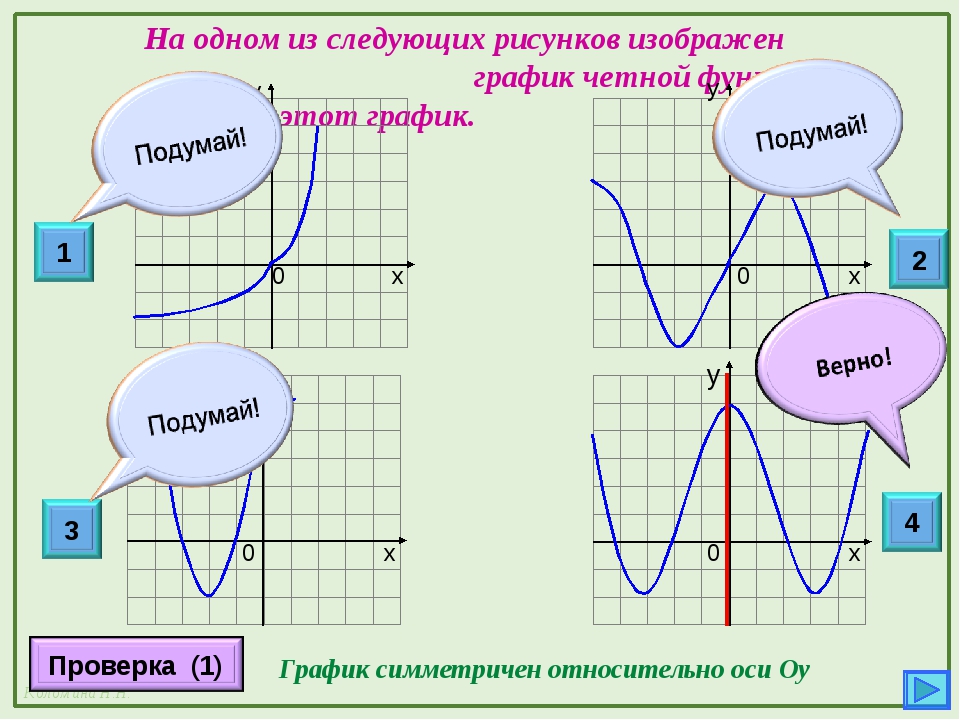 Это абсциссы точек пересечения графика функции с осью Ох.
Это абсциссы точек пересечения графика функции с осью Ох.
3) Промежутки знакопостоянства функции .
Промежутки знакопостоянства функции – такие промежутки значений x , на которых значения функции y либо только положительные, либо только отрицательные, называются промежутками знакопостоянства функции.
4) Монотонность функции .
Возрастающая функция (в некотором промежутке) — функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции.
Убывающая функция (в некотором промежутке) — функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.
5) Четность (нечетность) функции .
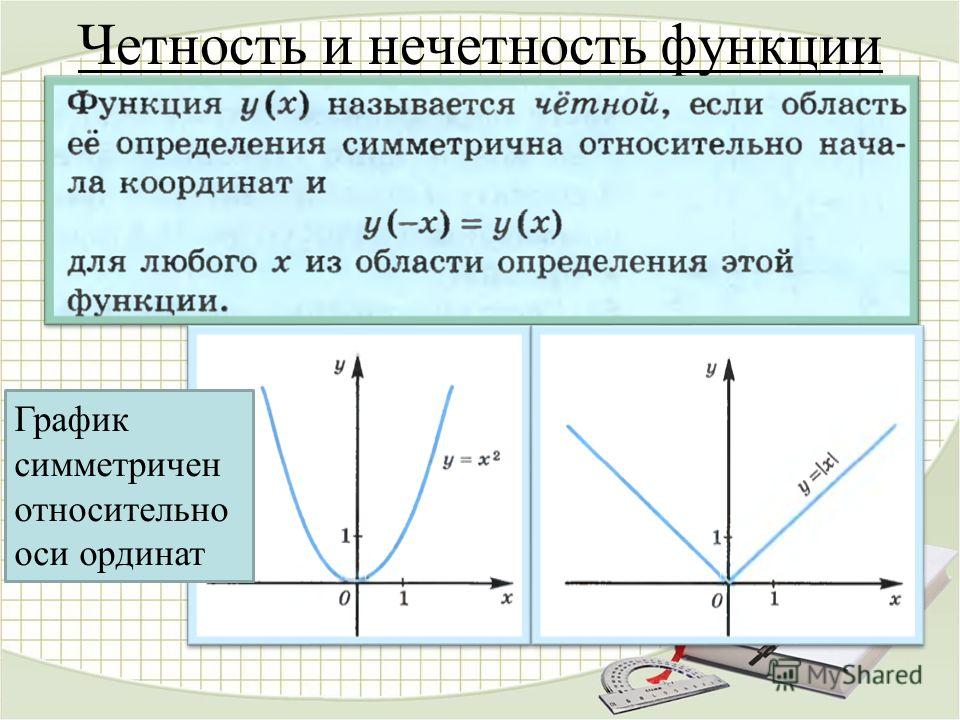
Четная функция — функция, у которой область определения симметрична относительно начала координат и для любого х f(-x) = f(x) . График четной функции симметричен относительно оси ординат.
Нечетная функция — функция, у которой область определения симметрична относительно начала координат и для любогох из области определения справедливо равенство f(-x) = — f(x ).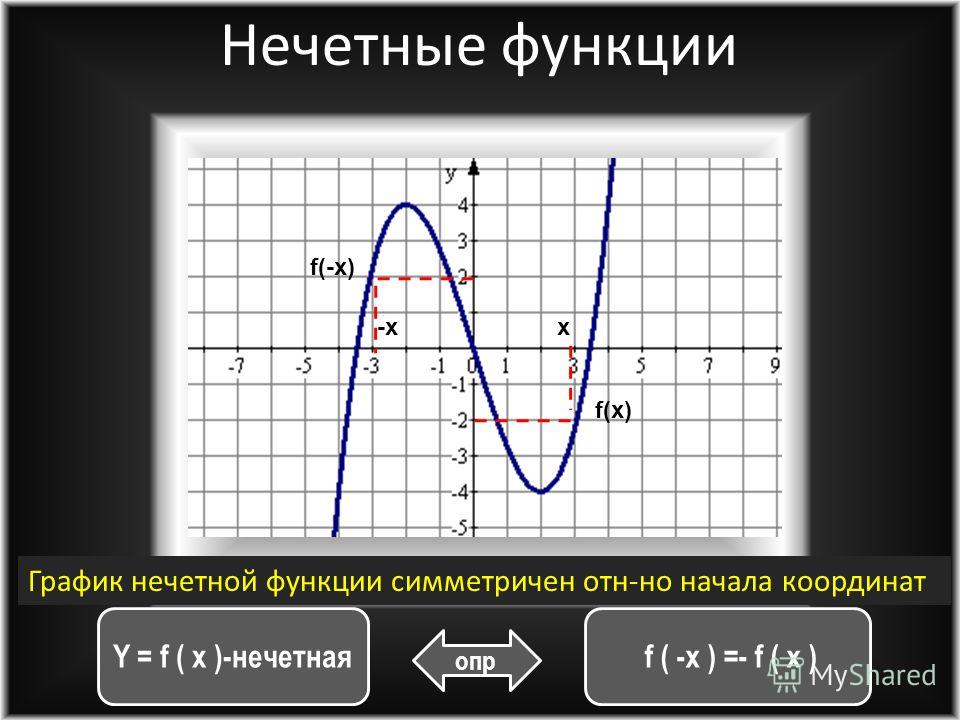 График нечетной функции симметричен относительно начала координат.
График нечетной функции симметричен относительно начала координат.
Четная функция
1) Область определения симметрична относительно точки (0; 0), то есть если точка a принадлежит области определения, то точка -a также принадлежит области определения.
2) Для любого значения x f(-x)=f(x)
3) График четной функции симметричен относительно оси Оу.
Нечетная функция обладает следующими свойствами:
1) Область определения симметрична относительно точки (0; 0).
2) для любого значения x , принадлежащего области определения, выполняется равенство f(-x)=-f(x)
3) График нечетной функции симметричен относительно начала координат (0; 0).
Не всякая функция является четной или нечетной. Функции общего вида не являются ни четными, ни нечетными.
6) Ограниченная и неограниченная функции .
Функция называется ограниченной, если существует такое положительное число M, что |f(x)| ≤ M для всех значений x . {2}-3
, можно вычислить только одно значение функции, которое ему соответствует. Функцию можно представить в виде таблицы:
{2}-3
, можно вычислить только одно значение функции, которое ему соответствует. Функцию можно представить в виде таблицы:
| x | −2 | −1 | 0 | 1 | 2 | 3 |
| y | −4 | −3 | −2 | −1 | 0 | 1 |
Пользуясь данной таблицей, можно разобрать, что для значения аргумента −1 будет соответствовать значение функции −3 ; а значению x=2 будет соответствовать y=0 и т.д. Также важно знать, что каждому значению аргумента в таблице соответствует лишь одно значение функции.
Еще функции возможно задать, используя графики. С помощью графика устанавливается какое значение функции соотносится с определенным значением x . Наиболее часто, это будет приближенное значение функции.
Четная и нечетная функция
Функция является четной функцией , когда f(-x)=f(x)
для любого x
из области определения. Такая функция будет симметрична относительно оси Oy
. {2}} \neq 1
для любого x \in [-1;1]
.
{2}} \neq 1
для любого x \in [-1;1]
.
Ограниченной принято называть функцию y=f(x), x \in X тогда, когда существует такое число K > 0 , для которого выполняется неравенство \left | f(x) \right | \neq K для любого x \in X .
Пример ограниченной функции: y=\sin x ограничена на всей числовой оси, так как \left | \sin x \right | \neq 1 .
Возрастающая и убывающая функция
О функции, что возрастает на рассматриваемом промежутке принято говорить как о возрастающей функции тогда, когда большему значению x будет соответствовать большее значение функции y=f(x) . Отсюда выходит, что взяв из рассматриваемого промежутка два произвольных значения аргумента x_{1} и x_{2} , причем x_{1} > x_{2} , будет y(x_{1}) > y(x_{2}) .
Функция, что убывает на рассматриваемом промежутке, называется убывающей функцией тогда, когда большему значению x будет соответствовать меньшее значение функции y(x) . Отсюда выходит, что взяв из рассматриваемого промежутка два произвольных значений аргумента x_{1} и x_{2} , причем x_{1} > x_{2} , будет y(x_{1})
Корнями функции принято называть точки, в которых функция F=y(x)
пересекает ось абсцисс (они получаются в результате решения уравнения y(x)=0
).
а) Если при x > 0 четная функция возрастает, то убывает она при x
б) Когда при x > 0 четная функция убывает, то возрастает она при x
в) Когда при x > 0 нечетная функция возрастает, то возрастает она и при x
г) Когда нечетная функция будет убывать при x > 0 , то она будет убывать и при x
Экстремумы функции
Точкой минимума функции y=f(x) принято называть такую точку x=x_{0} , у которой ее окрестность будет иметь остальные точки (кроме самой точки x=x_{0} ), и для них тогда будет выполняться неравенство f(x) > f(x_{0}) . y_{min} — обозначение функции в точке min.
Точкой максимума функции y=f(x) принято называть такую точку x=x_{0} , у которой ее окрестность будет иметь остальные точки (кроме самой точки x=x_{0} ), и для них тогда будет выполняется неравенство f(x)
Необходимое условие
Согласно теореме Ферма: f»(x)=0
тогда, когда у функции f(x)
, что дифференцируема в точке x_{0}
, появится экстремум в этой точке.
Достаточное условие
- Когда у производной знак меняется с плюса на минус, то x_{0} будет точкой минимума;
- x_{0} — будет точкой максимума только тогда, когда у производной меняется знак с минуса на плюс при переходе через стационарную точку x_{0} .
Наибольшее и наименьшее значение функции на промежутке
Шаги вычислений:
- Ищется производная f»(x) ;
- Находятся стационарные и критические точки функции и выбирают принадлежащие отрезку ;
- Находятся значения функции f(x) в стационарных и критических точках и концах отрезка. Меньшее из полученных результатов будет являться наименьшим значением функции , а большее — наибольшим .
Преобразование графиков.
Словесное описание функции.
Графический способ.
Графический способ задания функции является наиболее наглядным и часто применяется в технике. В математическом анализе графический способ задания функций используется в качестве иллюстрации.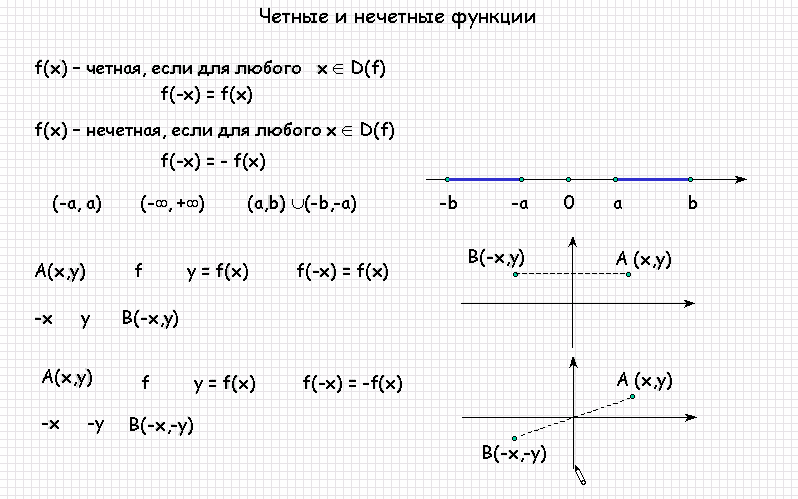
Графиком функции f называют множество всех точек (x;y) координатной плоскости, где y=f(x), а x «пробегает» всю область определения данной функции.
Подмножество координатной плоскости является графиком какой-либо функции, если оно имеет не более одной общей точки с любой прямой, параллельной оси Оу.
Пример. Является ли графиками функций фигуры, изображенные ниже?
Преимуществом графического задания является его наглядность. Сразу видно, как ведёт себя функция, где возрастает, где убывает. По графику сразу можно узнать некоторые важные характеристики функции.
Вообще, аналитический и графический способы задания функции идут рука об руку. Работа с формулой помогает построить график. А график частенько подсказывает решения, которые в формуле и не заметишь.
Почти любой ученик знает три способа задания функции, которые мы только что рассмотрели.
Попытаемся ответить на вопрос: «А существуют ли другие способы задания функции?»
Такой способ есть.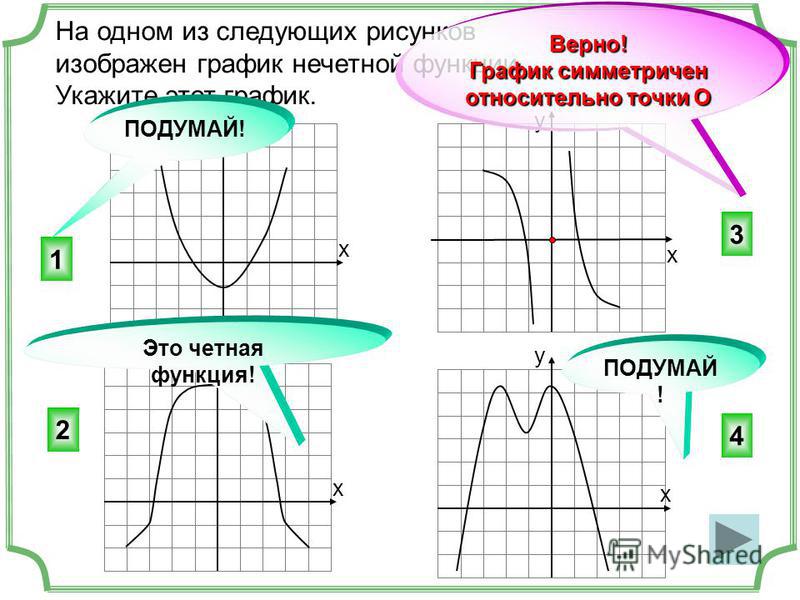
Функцию можно вполне однозначно задать словами.
Например, функцию у=2х можно задать следующим словесным описанием: каждому действительному значению аргумента х ставится в соответствие его удвоенное значение. Правило установлено, функция задана.
Более того, словесно можно задать функцию, которую формулой задать крайне затруднительно, а то и невозможно.
Например: каждому значению натурального аргумента х ставится в соответствие сумма цифр, из которых состоит значение х. Например, если х=3, то у=3. Если х=257, то у=2+5+7=14. И так далее. Формулой это записать проблематично. А вот табличку легко составить.
Способ словесного описания — достаточно редко используемый способ. Но иногда встречается.
Если есть закон однозначного соответствия между х и у — значит, есть функция. Какой закон, в какой форме он выражен — формулой, табличкой, графиком, словами – сути дела не меняет.
Рассмотрим функции, области определения которых симметричны относительно начала координат, т. е. для любого х из области определения число (-х ) также принадлежит области определения. Среди таких функций выделяют четные и нечетные .
е. для любого х из области определения число (-х ) также принадлежит области определения. Среди таких функций выделяют четные и нечетные .
Определение. Функция f называется четной , если для любого х из ее области определения
Пример. Рассмотрим функцию
Она является четной. Проверим это.
Для любого х выполнены равенства
Таким образом, у нас выполняются оба условия, значит функция четная. Ниже представлен график этой функции.
Определение. Функция f называется нечетной , если для любого х из ее области определения
Пример. Рассмотрим функцию
Она является нечетной. Проверим это.
Область определения вся числовая ось, а значит, она симметрична относительно точки (0;0).
Для любого х выполнены равенства
Таким образом, у нас выполняются оба условия, значит функция нечетная. Ниже представлен график этой функции.
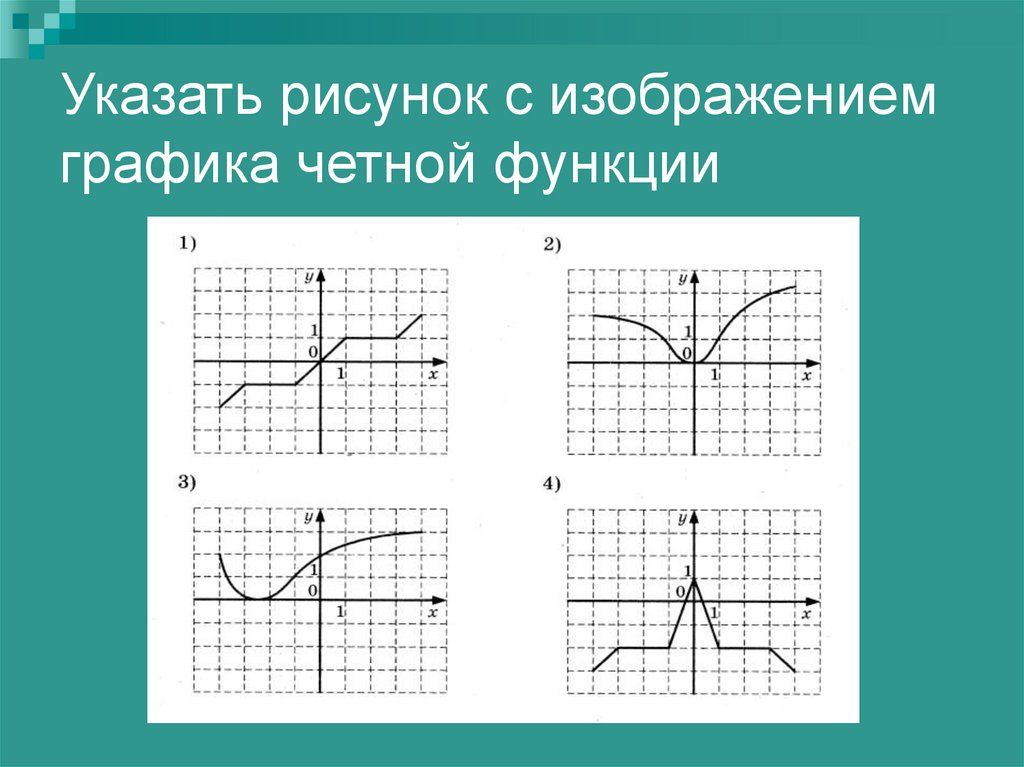
Графики, изображенные на первом и третьем рисунках симметричны относительно оси ординат, а графики, изображенные на втором и четвертом рисункам симметричны относительно начала координат.
Какие из функций, графики которых изображены на рисунках являются четными, а какие нечетными?
свойства функции ограниченная неограниченная монотонная возрастающая убывающая четная нечетная периодическая непериодическая график гиперболические функции
| Справочник по математике | Элементы математического анализа | Функции |
Содержание
| Ограниченные и неограниченные функции |
| Монотонные и строго монотонные функции |
| Четные и нечетные функции |
| Периодические и непериодические функции. Период функции |
| График функции. Свойства графиков четных, нечетных, периодических функций |
Ограниченные и неограниченные функции
Обозначим буквой X некоторое множество чисел, входящих в область определения D ( f ) функции y = f (x).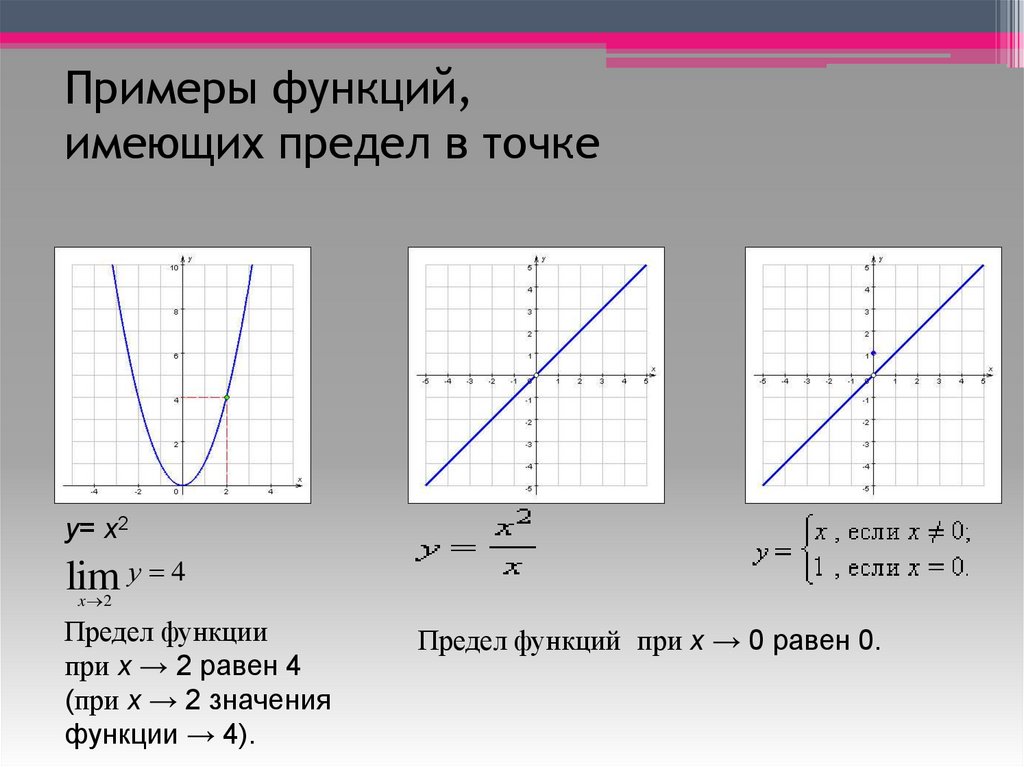
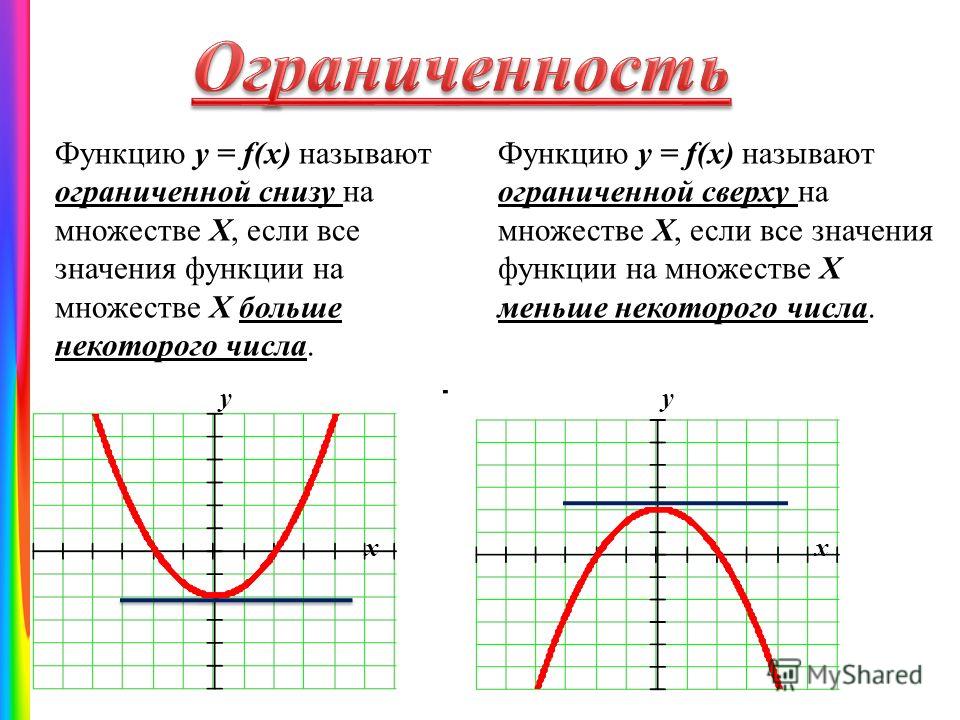
ОПРЕДЕЛЕНИЕ 1. Функцию y = f (x) называют ограниченной сверху на множестве X , если существует такое число a , что для любого x из множества X выполнено неравенство
ОПРЕДЕЛЕНИЕ 2. Функцию y = f (x) называют ограниченной снизу на множестве X , если существует такое число b , что для любого x из множества X выполнено неравенство
ОПРЕДЕЛЕНИЕ 3. Функцию y = f (x) называют ограниченной на множестве X , если существуют такие числа a и b , что для любого x из множества X выполнено неравенство
ОПРЕДЕЛЕНИЕ 4. Функцию y = f (x) называют неограниченной сверху на множестве X , если для любого числа a существует такой x из множества X , для которого выполнено неравенство
ОПРЕДЕЛЕНИЕ 5.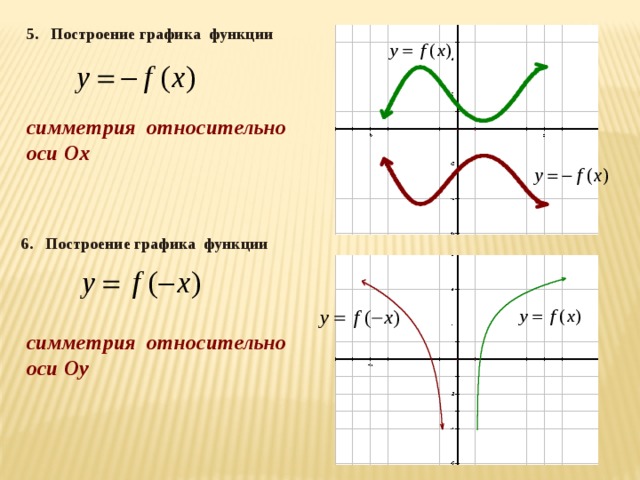 Функцию y = f (x) называют неограниченной снизу на множестве X , если для любого числа b существует такой x из множества X , для которого выполнено неравенство
Функцию y = f (x) называют неограниченной снизу на множестве X , если для любого числа b существует такой x из множества X , для которого выполнено неравенство
ОПРЕДЕЛЕНИЕ 6. Функцию y = f (x) называют неограниченной на множестве X , если эта функция или неограничена сверху, или неограничена снизу, или неограничена и сверху, и снизу.
Проиллюстрируем эти определения следующими примерами.
ПРИМЕР 1. Функция y = x2 (рис. 1) является ограниченной снизу и неограниченной сверху на множестве
Рис.1
ПРИМЕР 2. Функция y = – x2 (рис. 2) является ограниченной сверху и неограниченной снизу на множестве
Рис.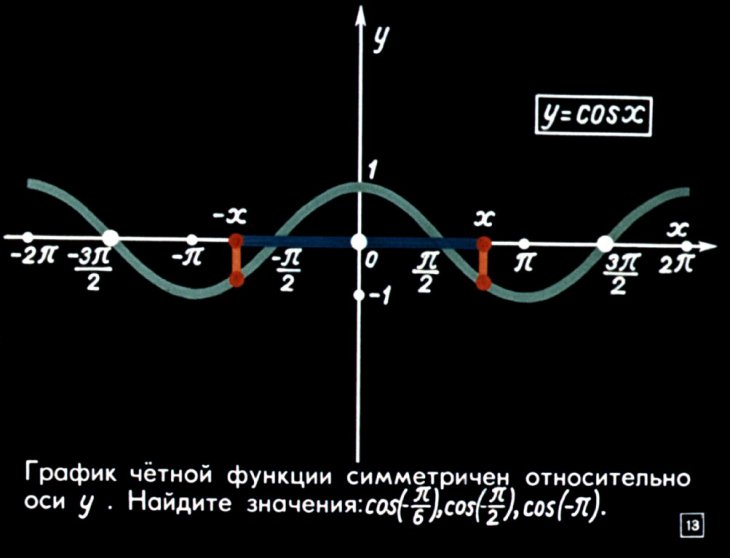 2
2
ПРИМЕР 3. Функция y = x (рис. 3) неограничена сверху и неограничена снизу на множестве
Рис.3
ПРИМЕР 4. Функция y = arctg x (рис. 4) ограничена на множестве
Рис.4
Монотонные и строго монотонные функции
ОПРЕДЕЛЕНИЕ 7. Функцию y = f (x) называют возрастающей на множестве X , если для любых чисел и , удовлетворяющих неравенству x1 < x2 , выполнено неравенство
ЗАМЕЧАНИЕ 1. Возрастающие функции также называют неубывающими функциями.
ОПРЕДЕЛЕНИЕ 8. Функцию y = f (x) называют убывающей на множестве X , если для любых чисел и , удовлетворяющих неравенству x1 < x2 , выполнено неравенство
Функцию y = f (x) называют убывающей на множестве X , если для любых чисел и , удовлетворяющих неравенству x1 < x2 , выполнено неравенство
ЗАМЕЧАНИЕ 2. Убывающие функции также называют невозрастающими функциями.
ОПРЕДЕЛЕНИЕ 9. Функцию y = f (x) называют строго возрастающей на множестве X , если для любых чисел и , удовлетворяющих неравенству x1 < x2 , выполнено неравенство
f (x1) < f (x2)
ОПРЕДЕЛЕНИЕ 10. Функцию y = f (x) называют строго убывающей на множестве X , если для любых чисел и , удовлетворяющих неравенству x1 < x2 , выполнено неравенство
f (x1) > f (x2)
ОПРЕДЕЛЕНИЕ 11.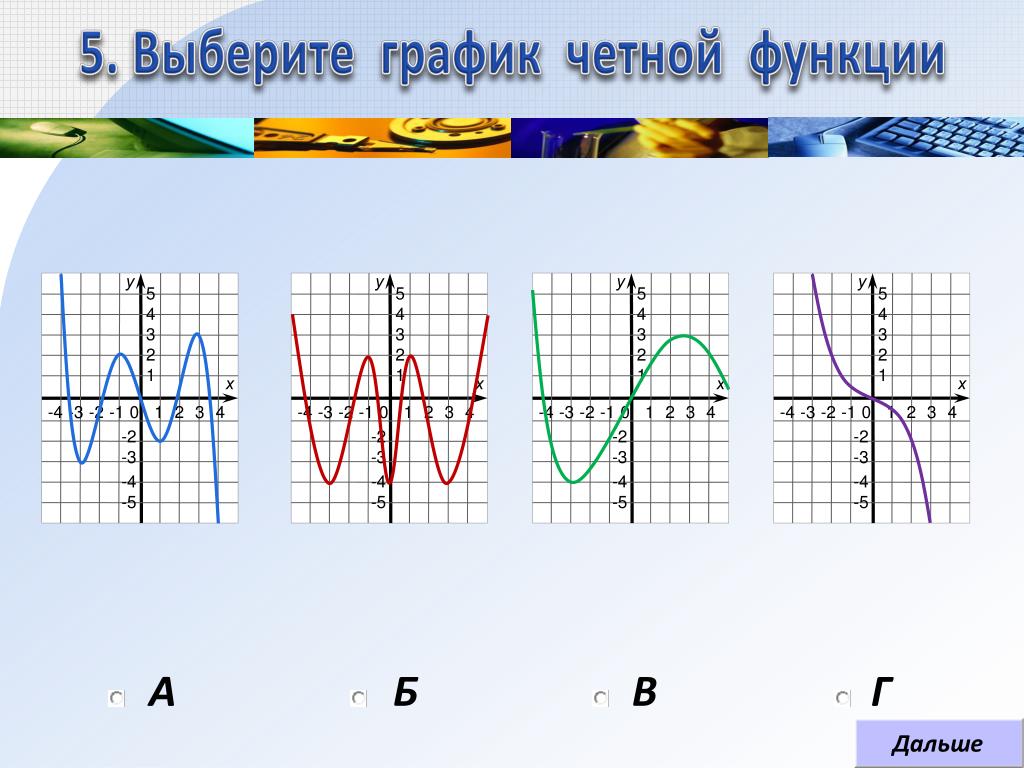 Возрастающие и убывающие функции называют монотонными, строго возрастающие и строго убывающие функции называют строго монотонными.
Возрастающие и убывающие функции называют монотонными, строго возрастающие и строго убывающие функции называют строго монотонными.
ПРИМЕР 5. Функция y = x2 (рис. 1) является строго убывающей функцией на множестве и строго возрастающей на множестве
ПРИМЕР 6. Функция y = – x2 (рис. 2) является строго возрастающей функцией на множестве и строго убывающей на множестве
ПРИМЕР 7. Функция y = x (рис. 3) является строго возрастающей функцией на множестве
ПРИМЕР 8. Функция y = arctg x (рис. 4) является строго возрастающей на множестве
Четные и нечетные функции
ОПРЕДЕЛЕНИЕ 12. Функцию y = f (x) , определенную на множестве X , называют четной функцией, если для любого числа x из множества X число – x также принадлежит множеству X и выполняется равенство
Функцию y = f (x) , определенную на множестве X , называют четной функцией, если для любого числа x из множества X число – x также принадлежит множеству X и выполняется равенство
f (– x) = f (x)
ОПРЕДЕЛЕНИЕ 13. Функцию y = f (x) , определенную на множестве X , называют нечетной функцией, если для любого числа x из множества X число – x также принадлежит множеству X и выполняется равенство
f (– x) = – f (x)
ПРИМЕР 9. Функции y = x2 и y = – x2 являются четными функциями (рис. 1 и рис. 2), а функции y = x и y = arctg x являются нечетными функциями (рис. 3 и рис. 4).
ПРИМЕР 10. Примерами функций, которые не являются ни четными, ни нечетными функциями, являются показательные и логарифмические функции.
УТВЕРЖДЕНИЕ. Любую функцию y = f (x) , определенную на симметричном относительно точки x = 0 множестве X , можно представить в виде суммы четной и нечетной функций.
ДОКАЗАТЕЛЬСТВО. Рассмотрим две функции:
сумма которых равна f (x) , и заметим, что функция g1 (x) является четной функцией, а функция g2 (x) является нечетной функцией. Действительно,
что и завершает доказательство утверждения.
ЗАМЕЧАНИЕ 3. Раскладывая функцию y = e x в сумму четной и нечетной функций, получаем:
Функцию g1 (x) называют гиперболическим косинусом и обозначают ch x :
Функцию g2 (x) называют гиперболическим синусом и обозначают sh x :
Таким образом, справедливо равенство
e x= sh x + ch x
Периодические и непериодические функции.
 Период функции
Период функцииОПРЕДЕЛЕНИЕ 14. Число называют периодом функции y = f (x) , если для любого числа числа x + T и x – T также принадлежат области определения D ( f ) и справедливы равенства
f ( x + T ) = f (x) ,
f ( x – T ) = f (x)
ОПРЕДЕЛЕНИЕ 15. Если функция имеет период, то ее называют периодической. Если же у функции периода нет, то ее называют непериодической.
ЗАМЕЧАНИЕ 4. Если число T является периодом некоторой функции, то и число kT , где k – любое целое число, отличное от нуля, также является периодом этой функции.
ПРИМЕР 11. Функции y = sin x и y = cos x являются периодическими функциями с периодом 2π , функции y = tg x и y = ctg x являются периодическими функциями с периодом π .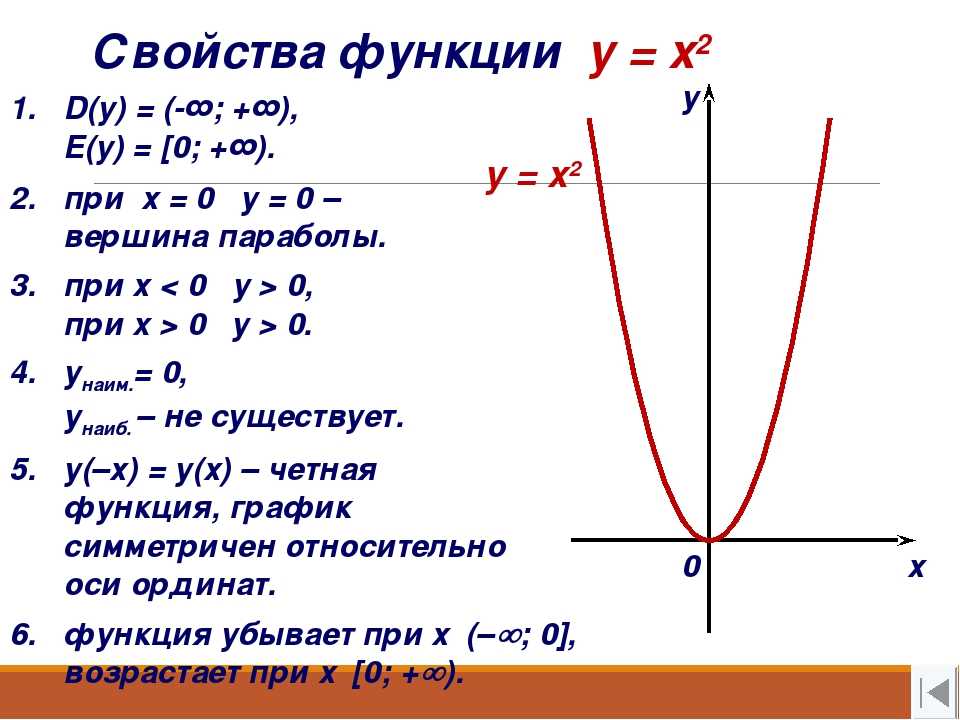
Подробнее об этом можно прочитать в разделе «Свойства тригонометрических функций» → «Периодичность тригонометрических функций. Полупериодичность синуса и косинуса» нашего справочника.
ПРИМЕР 12. Показательные, логарифмические и степенные функции являются непериодическими функциями.
График функции. Свойства графиков четных, нечетных, периодических функций
Рассмотрим плоскость с заданной прямоугольной системой координат Oxy .
ОПРЕДЕЛЕНИЕ 16. Графиком функции y = f (x) называют множество всех точек, координаты которых имеют вид (x; f (x)) , где .
ЗАМЕЧАНИЕ 5. График четной функции симметричен относительно оси ординат Oy (см., например, рис. 1 и рис. 2), график нечетной функции симметричен относительно начала координат (см., например, рис. 3 и рис.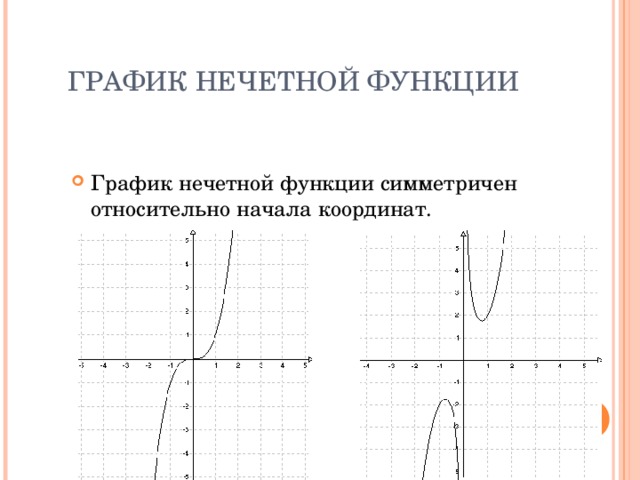 4).
4).
ЗАМЕЧАНИЕ 6. График периодической функции не изменяется при сдвиге вдоль оси абсцисс Ox на период вправо или влево (см., например, раздел «Графики тригонометрических функций» нашего справочника). Поэтому для того, чтобы построить график периодической функции с периодом T, достаточно построить график этой функции на любом отрезке оси абсцисс Ox длины T, а затем сдвигать его влево и вправо на расстояния nT , где n – любое натуральное число.
график, как определить четность, доказательство
Содержание:
-
Понятие четности и нечетности функции
- Четная функция
- Нечетная функция
- Произведение четной и нечетной функции
- Исследование функций в примерах
Содержание
-
Понятие четности и нечетности функции
- Четная функция
- Нечетная функция
- Произведение четной и нечетной функции
- Исследование функций в примерах
Понятие четности и нечетности функции
Главное условие при исследовании функции на четность/нечетность — это симметричность области определения относительно 0.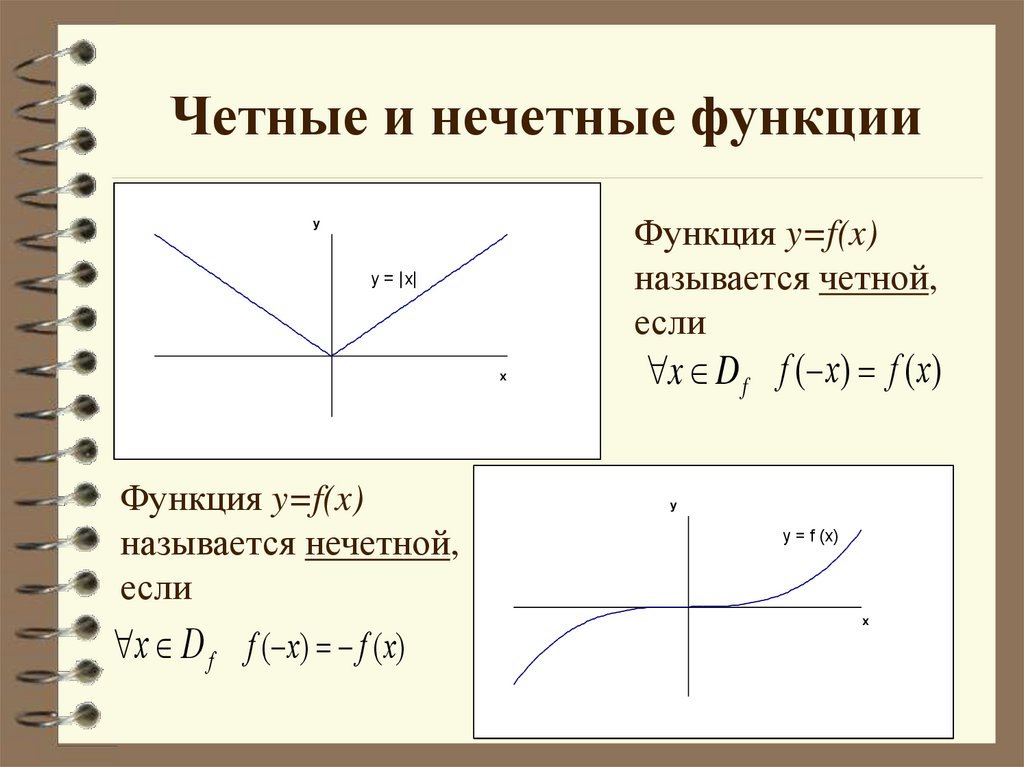 Если она не симметрична, то функция не является ни четной, ни нечетной, и дальнейшее исследование производить не нужно. Например, \(D(y)\in(-\infty;+\infty)\) симметрична относительно 0, а \(D(y):x\in(-5;9)\) — нет.
Если она не симметрична, то функция не является ни четной, ни нечетной, и дальнейшее исследование производить не нужно. Например, \(D(y)\in(-\infty;+\infty)\) симметрична относительно 0, а \(D(y):x\in(-5;9)\) — нет.
Четная функция
Функцию \(f(x)\) называют четной, если для любого значения х из области определения функции \(f(x)\) соблюдается равенство \(f(-x)=f(x).\)
Источник: myshared.ruСвойство:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
График четной функции симметричен относительно оси Ох.
Доказательство:
Возьмем произвольную точку \(M(x,\;f(x))\) из области определения \(f(x)\), тогда точка \(M_1(-x,\;f(x))\) так же будет принадлежать графику, что следует из определения. Значит график данной функции будет симметричен относительно оси ординат.
Нечетная функция
Функцию \(f(x)\) называют нечетной, если для любого значения х из области определения функции \(f(x)\) соблюдается равенство \(f(-x)=-f(x).\)
Источник: myshared.ruСвойство:
График нечетной функции симметричен относительно начала координат (точки (0;0)).
Доказательство:
Возьмем произвольную точку \(M(x,\;f(x))\) из области определения \(f(x)\), тогда точка \(M_1(-x,\;-f(x))\) также будет принадлежать графику, что следует из определения. Значит график данной функции будет симметричен относительно начала координат.
Произведение четной и нечетной функции
Теорема
Произведение четной и нечетной функций есть нечетная функция.
Доказательство:
Пусть \(f(x)\) — четная функция, а \(g(x)\) — нечетная. Тогда \(f(x)=f(-x), а g(-x)=-g(x).\)
\(f(x)\cdot g(x)=(f\cdot g)(x)\)
\((f\cdot g)(-x)=f(-x)\cdot g(-x)=f(x)\cdot(-g(x))=-f(x)\cdot g(x)=-(f\cdot g)(x)\)
Значит, \((f\cdot g)(-x)=-(f\cdot g)(x)\), т.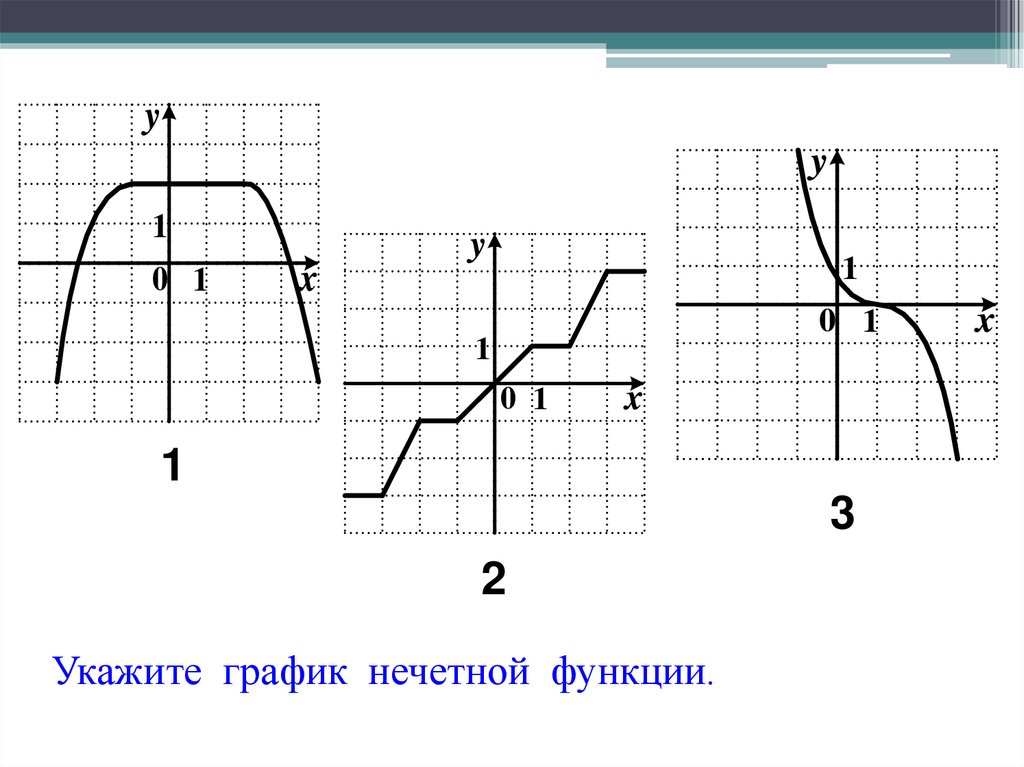 2-1}\)
2-1}\)
\(f_1(x)=f_1(-x)\), значит функция четная.
Насколько полезной была для вас статья?
У этой статьи пока нет оценок.
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Поиск по содержимому
Как понять четность нечетность функции. График четной и нечетной функций
Преобразование графиков.
Словесное описание функции.
Графический способ.
Графический способ задания функции является наиболее наглядным и часто применяется в технике. В математическом анализе графический способ задания функций используется в качестве иллюстрации.
Графиком функции f называют множество всех точек (x;y) координатной плоскости, где y=f(x), а x «пробегает» всю область определения данной функции.
Подмножество координатной плоскости является графиком какой-либо функции, если оно имеет не более одной общей точки с любой прямой, параллельной оси Оу.
Пример. Является ли графиками функций фигуры, изображенные ниже?
Преимуществом графического задания является его наглядность. Сразу видно, как ведёт себя функция, где возрастает, где убывает. По графику сразу можно узнать некоторые важные характеристики функции.
Вообще, аналитический и графический способы задания функции идут рука об руку. Работа с формулой помогает построить график. А график частенько подсказывает решения, которые в формуле и не заметишь.
Почти любой ученик знает три способа задания функции, которые мы только что рассмотрели.
Попытаемся ответить на вопрос: «А существуют ли другие способы задания функции?»
Такой способ есть.
Функцию можно вполне однозначно задать словами.
Например, функцию у=2х можно задать следующим словесным описанием: каждому действительному значению аргумента х ставится в соответствие его удвоенное значение. Правило установлено, функция задана.
Более того, словесно можно задать функцию, которую формулой задать крайне затруднительно, а то и невозможно.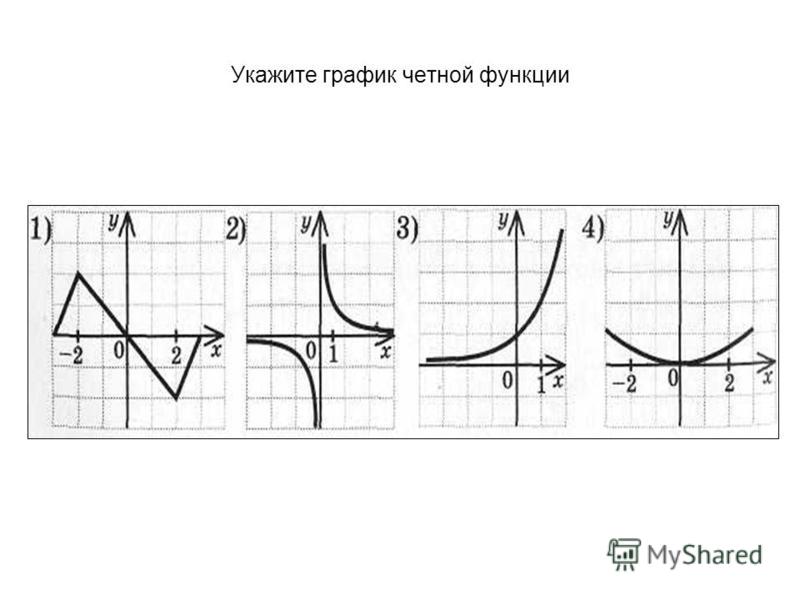
Например: каждому значению натурального аргумента х ставится в соответствие сумма цифр, из которых состоит значение х. Например, если х=3, то у=3. Если х=257, то у=2+5+7=14. И так далее. Формулой это записать проблематично. А вот табличку легко составить.
Способ словесного описания — достаточно редко используемый способ. Но иногда встречается.
Если есть закон однозначного соответствия между х и у — значит, есть функция. Какой закон, в какой форме он выражен — формулой, табличкой, графиком, словами – сути дела не меняет.
Рассмотрим функции, области определения которых симметричны относительно начала координат, т.е. для любого х из области определения число (-х ) также принадлежит области определения. Среди таких функций выделяют четные и нечетные .
Определение. Функция f называется четной , если для любого х из ее области определения
Пример. Рассмотрим функцию
Она является четной. Проверим это.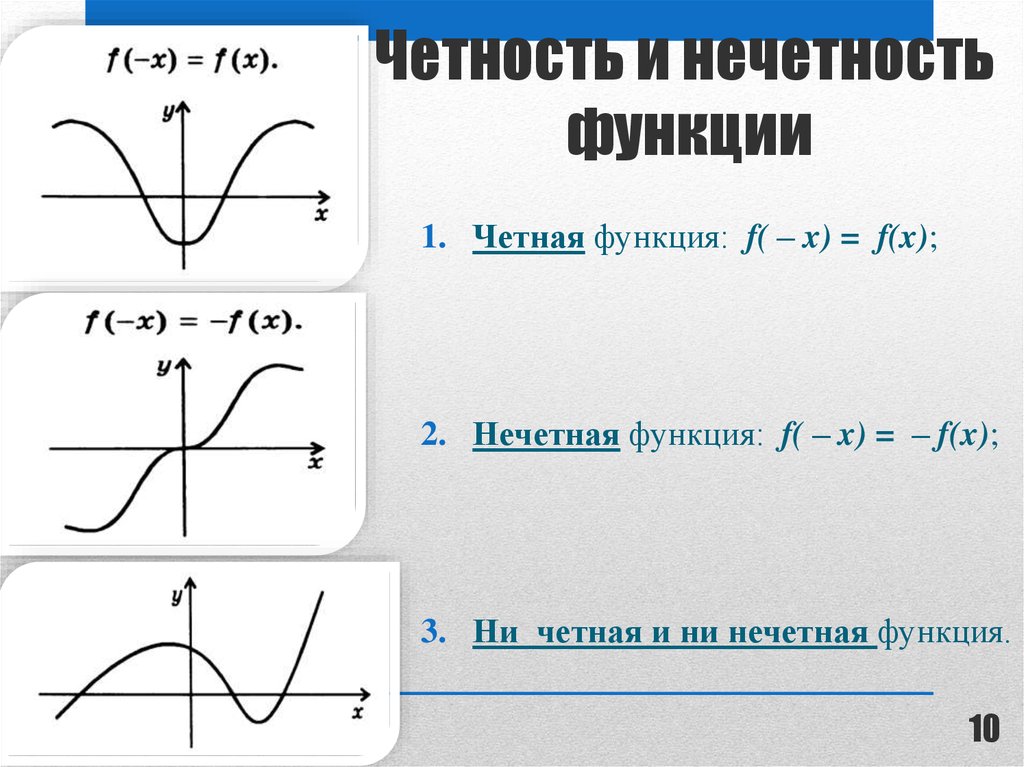
Для любого х выполнены равенства
Таким образом, у нас выполняются оба условия, значит функция четная. Ниже представлен график этой функции.
Определение. Функция f называется нечетной , если для любого х из ее области определения
Пример. Рассмотрим функцию
Она является нечетной. Проверим это.
Область определения вся числовая ось, а значит, она симметрична относительно точки (0;0).
Для любого х выполнены равенства
Таким образом, у нас выполняются оба условия, значит функция нечетная. Ниже представлен график этой функции.
Графики, изображенные на первом и третьем рисунках симметричны относительно оси ординат, а графики, изображенные на втором и четвертом рисункам симметричны относительно начала координат.
Какие из функций, графики которых изображены на рисунках являются четными, а какие нечетными?
Исследование функции.
1) D(y)
– Область опрделения: множество всех
тех значений переменной х.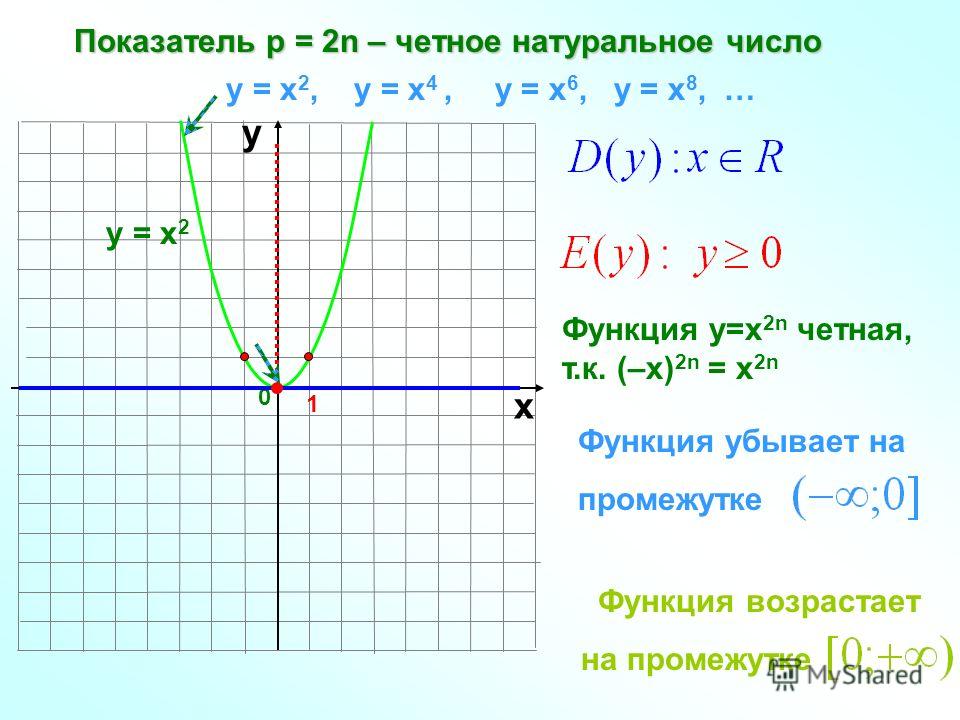 при которых
алгебраические выражения f(x)
и g(x)
имеют смысл.
при которых
алгебраические выражения f(x)
и g(x)
имеют смысл.
Если функция задана формулой, то область определения состоит из всех значений независимой переменной, при которых формула имеет смысл.
2) Свойства функции: четность/нечетность, периодичность:
Нечётными и чётными называются функции, графики которых обладают симметрией относительно изменения знака аргумента.
Нечётная функция — функция, меняющая значение на противоположное при изменении знака независимой переменной (симметричная относительно центра координат).
Чётная функция — функция, не изменяющая своего значения при изменении знака независимой переменной (симметричная относительно оси ординат).
Ни чётная ни нечётная функция (функция общего вида) — функция, не обладающая симметрией. В эту категорию относят функции, не подпадающие под предыдущие 2 категории.
Функции,
не принадлежащие ни одной из категорий
выше, называются ни
чётными ни нечётными (или
функциями общего вида).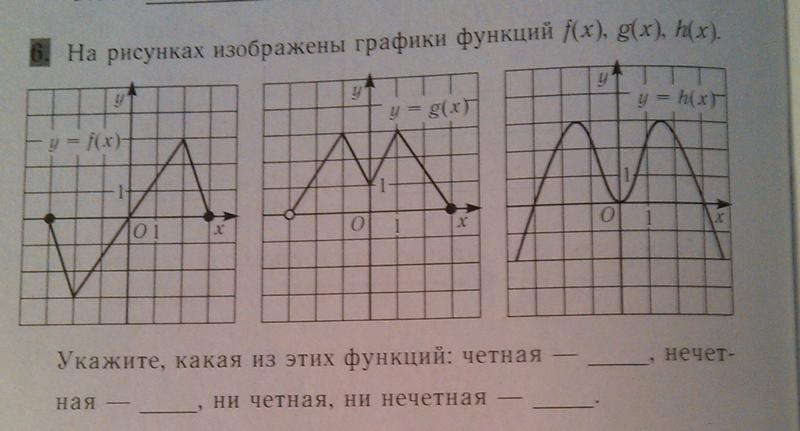
Нечётные функции
Нечётная степень где — произвольное целое число.
Чётные функции
Чётная степень где — произвольное целое число.
Периоди́ческая фу́нкция ― функция, повторяющая свои значения через некоторый регулярный интервал аргумента, то есть не меняющая своего значения при добавлении к аргументу некоторого фиксированного ненулевого числа (пери́ода функции) на всей области определения.
3) Нули (корни) функции — точки, где она обращается в ноль.
Нахождение точки пересечения графика с осью Oy . Для этого нужно вычислить значение f (0). Найти также точки пересечения графика с осью Ox , для чего найти корни уравнения f (x ) = 0 (или убедиться в отсутствии корней).
Точки, в которых график пересекает ось , называют нулями функции . Чтобы найти нули функции нужно решить уравнение , то есть найти те значения «икс» , при которых функция обращается в ноль.
4)
Промежутки
постоянства знаков, знаки в них.
Промежутки, где функция f(x) сохраняет знак.
Интервал знакопостоянства – это интервал, в каждой точке которого функция положительна либо отрицательна.
ВЫШЕ оси абсцисс.
НИЖЕ оси .
5) Непрерывность (точки разрыва, характер разрыва, ассимптоты).
Непрерывная функция — функция без «скачков», то есть такая, у которой малые изменения аргумента приводят к малым изменениям значения функции.
Устранимые точки разрыва
Если предел функции существует , но функция не определена в этой точке, либо предел не совпадает со значением функции в данной точке:
,
то точка называется точкой устранимого разрыва функции (в комплексном анализе -устранимая особая точка).
Если
«поправить» функцию в
точке устранимого разрыва и положить ,
то получится функция, непрерывная в
данной точке. Такая операция над функцией
называется доопределением
функции до непрерывной или доопределением
функции по непрерывности ,
что и обосновывает название точки, как
точки устранимого разрыва.
Точки разрыва первого и второго рода
Если функция имеет разрыв в данной точке (то есть предел функции в данной точке отсутствует или не совпадает со значением функции в данной точке), то для числовых функций возникает два возможных варианта, связанных с существованием у числовых функций односторонних пределов :
если оба односторонних предела существуют и конечны, то такую точку называют точкой разрыва первого рода . Точки устранимого разрыва являются точками разрыва первого рода;
если хотя бы один из односторонних пределов не существует или не является конечной величиной, то такую точку называют точкой разрыва второго рода .
Аси́мпто́та — прямая , обладающая тем свойством, что расстояние от точки кривой до этой прямой стремится к нулю при удалении точки вдоль ветви вбесконечность.
Вертикальная
Вертикальная асимптота — прямая предела .
Как
правило, при определении вертикальной
асимптоты ищут не один предел, а два
односторонних (левый и правый).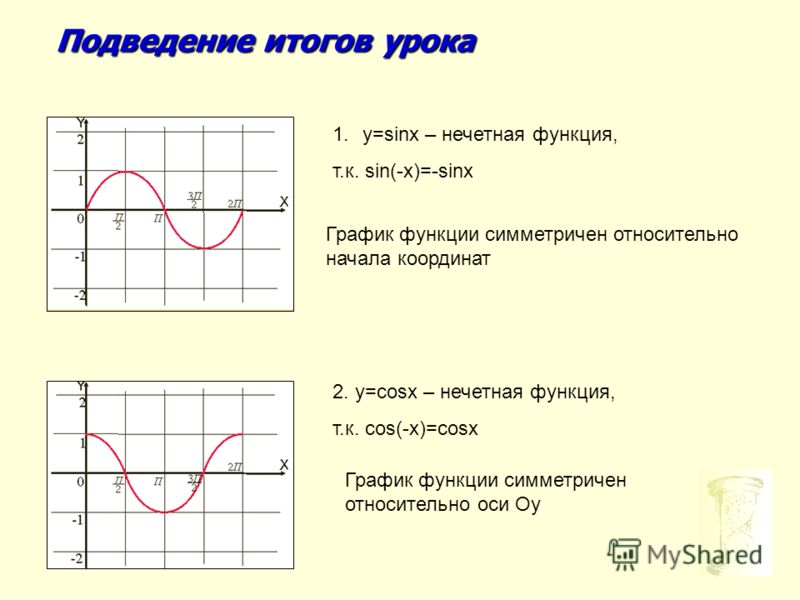 Это
делается с целью определить, как функция
ведёт себя по мере приближения к
вертикальной асимптоте с разных сторон.
Например:
Это
делается с целью определить, как функция
ведёт себя по мере приближения к
вертикальной асимптоте с разных сторон.
Например:
Горизонтальная
Горизонтальная асимптота — прямая вида при условии существования предела
.
Наклонная
Наклонная асимптота — прямая вида при условии существования пределов
Замечание: функция может иметь не более двух наклонных (горизонтальных) асимптот.
Замечание: если хотя бы один из двух упомянутых выше пределов не существует (или равен ), то наклонной асимптоты при (или ) не существует.
если в п. 2.), то , и предел находится по формуле горизонтальной асимптоты, .
6) Нахождение
промежутков монотонности. Найти
интервалы монотонности функции f (x )(то
есть интервалы возрастания и убывания).
Это делается с помощью исследования
знака производной f (x ).
Для этого находят производную f (x ) и
решают неравенство f (x )0. На промежутках, где это неравенство
выполнено, функция f (x )возрастает.
Там, где выполнено обратное неравенство f (x )0,
функция f (x )убывает.
На промежутках, где это неравенство
выполнено, функция f (x )возрастает.
Там, где выполнено обратное неравенство f (x )0,
функция f (x )убывает.
Нахождение локального экстремума. Найдя интервалы монотонности, мы можем сразу определить точки локального экстремума там, где возрастание сменяется убыванием, располагаются локальные максимумы, а там, где убывание сменяется возрастанием — локальные минимумы. Вычислить значение функции в этих точках. Если функция имеет критические точки, не являющиеся точками локального экстремума, то полезно вычислить значение функции и в этих точках.
Нахождение наибольшего и наименьшего значений функции y = f(x) на отрезке (продолжение)
1. Найти производную функции: f (x ). 2. Найти точки, в которых производная равна нулю: f (x )=0x 1, x 2 ,… 3. |
Функция — это одно из важнейших математических понятий. Функция — зависимость переменной у от переменной x , если каждому значению х соответствует единственное значение у . Переменную х называют независимой переменной или аргументом. Переменную у называют зависимой переменной. Все значения независимой переменной (переменной x ) образуют область определения функции. Все значения, которые принимает зависимая переменная (переменная y ), образуют область значений функции.
Графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции, тоесть по оси абсцисс откладываются значения переменной x , а по оси ординат откладываются значения переменной y . Для построения графика функции необходимо знать свойства функции. Основные свойства функции будут рассмотрены далее!
Для построения графика функции необходимо знать свойства функции. Основные свойства функции будут рассмотрены далее!
Для построения графика функции советуем использовать нашу программу — Построение графиков функций онлайн. Если при изучении материала на данной странице у Вас возникнут вопросы, Вы всегда можете задать их на нашем форуме. Также на форуме Вам помогут решить задачи по математике, химии, геометрии, теории вероятности и многим другим предметам!
Основные свойства функций.
1) Область определения функции и область значений функции .
Область определения функции — это множество всех допустимых действительных значений аргумента x (переменной x ), при которых функция y = f(x) определена.
Область значений функции — это множество всех действительных значений y , которые принимает функция.
В элементарной математике изучаются функции только на множестве действительных чисел.
2) Нули функции .
Значения х , при которых y=0 , называется нулями функции . Это абсциссы точек пересечения графика функции с осью Ох.
Это абсциссы точек пересечения графика функции с осью Ох.
3) Промежутки знакопостоянства функции .
Промежутки знакопостоянства функции – такие промежутки значений x , на которых значения функции y либо только положительные, либо только отрицательные, называются промежутками знакопостоянства функции.
4) Монотонность функции .
Возрастающая функция (в некотором промежутке) — функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции.
Убывающая функция (в некотором промежутке) — функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.
5) Четность (нечетность) функции .
Четная функция — функция, у которой область определения симметрична относительно начала координат и для любого х f(-x) = f(x) . График четной функции симметричен относительно оси ординат.
Нечетная функция — функция, у которой область определения симметрична относительно начала координат и для любогох из области определения справедливо равенство f(-x) = — f(x ). График нечетной функции симметричен относительно начала координат.
График нечетной функции симметричен относительно начала координат.
Четная функция
1) Область определения симметрична относительно точки (0; 0), то есть если точка a принадлежит области определения, то точка -a также принадлежит области определения.
2) Для любого значения x f(-x)=f(x)
3) График четной функции симметричен относительно оси Оу.
Нечетная функция обладает следующими свойствами:
1) Область определения симметрична относительно точки (0; 0).
2) для любого значения x , принадлежащего области определения, выполняется равенство f(-x)=-f(x)
3) График нечетной функции симметричен относительно начала координат (0; 0).
Не всякая функция является четной или нечетной. Функции общего вида не являются ни четными, ни нечетными.
6) Ограниченная и неограниченная функции .
Функция называется ограниченной, если существует такое положительное число M, что |f(x)| ≤ M для всех значений x .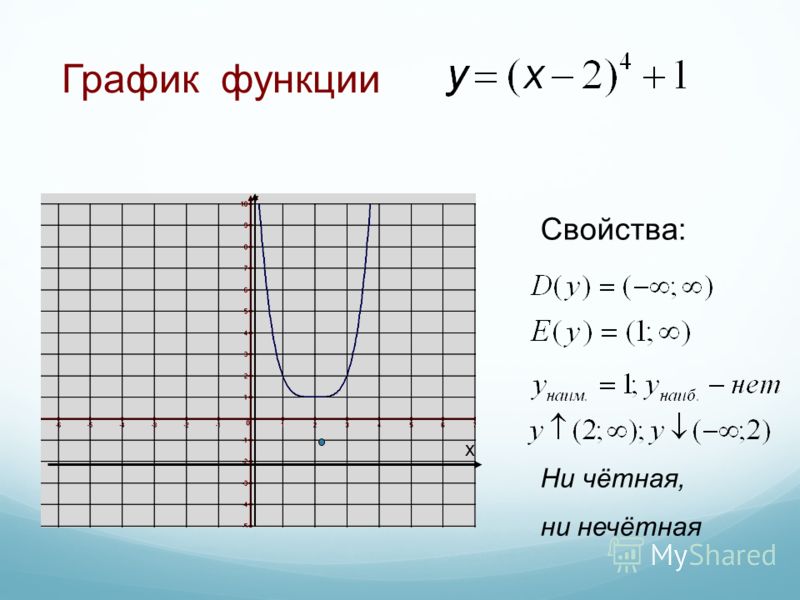 {2}-3
, можно вычислить только одно значение функции, которое ему соответствует. Функцию можно представить в виде таблицы:
{2}-3
, можно вычислить только одно значение функции, которое ему соответствует. Функцию можно представить в виде таблицы:
| x | −2 | −1 | 0 | 1 | 2 | 3 |
| y | −4 | −3 | −2 | −1 | 0 | 1 |
Пользуясь данной таблицей, можно разобрать, что для значения аргумента −1 будет соответствовать значение функции −3 ; а значению x=2 будет соответствовать y=0 и т.д. Также важно знать, что каждому значению аргумента в таблице соответствует лишь одно значение функции.
Еще функции возможно задать, используя графики. С помощью графика устанавливается какое значение функции соотносится с определенным значением x . Наиболее часто, это будет приближенное значение функции.
Четная и нечетная функция
Функция является четной функцией , когда f(-x)=f(x)
для любого x
из области определения. Такая функция будет симметрична относительно оси Oy
. {2}} \neq 1
для любого x \in [-1;1]
.
{2}} \neq 1
для любого x \in [-1;1]
.
Ограниченной принято называть функцию y=f(x), x \in X тогда, когда существует такое число K > 0 , для которого выполняется неравенство \left | f(x) \right | \neq K для любого x \in X .
Пример ограниченной функции: y=\sin x ограничена на всей числовой оси, так как \left | \sin x \right | \neq 1 .
Возрастающая и убывающая функция
О функции, что возрастает на рассматриваемом промежутке принято говорить как о возрастающей функции тогда, когда большему значению x будет соответствовать большее значение функции y=f(x) . Отсюда выходит, что взяв из рассматриваемого промежутка два произвольных значения аргумента x_{1} и x_{2} , причем x_{1} > x_{2} , будет y(x_{1}) > y(x_{2}) .
Функция, что убывает на рассматриваемом промежутке, называется убывающей функцией тогда, когда большему значению x будет соответствовать меньшее значение функции y(x) . Отсюда выходит, что взяв из рассматриваемого промежутка два произвольных значений аргумента x_{1} и x_{2} , причем x_{1} > x_{2} , будет y(x_{1})
Корнями функции принято называть точки, в которых функция F=y(x)
пересекает ось абсцисс (они получаются в результате решения уравнения y(x)=0
).
а) Если при x > 0 четная функция возрастает, то убывает она при x
б) Когда при x > 0 четная функция убывает, то возрастает она при x
в) Когда при x > 0 нечетная функция возрастает, то возрастает она и при x
г) Когда нечетная функция будет убывать при x > 0 , то она будет убывать и при x
Экстремумы функции
Точкой минимума функции y=f(x) принято называть такую точку x=x_{0} , у которой ее окрестность будет иметь остальные точки (кроме самой точки x=x_{0} ), и для них тогда будет выполняться неравенство f(x) > f(x_{0}) . y_{min} — обозначение функции в точке min.
Точкой максимума функции y=f(x) принято называть такую точку x=x_{0} , у которой ее окрестность будет иметь остальные точки (кроме самой точки x=x_{0} ), и для них тогда будет выполняется неравенство f(x)
Необходимое условие
Согласно теореме Ферма: f»(x)=0
тогда, когда у функции f(x)
, что дифференцируема в точке x_{0}
, появится экстремум в этой точке.
Достаточное условие
- Когда у производной знак меняется с плюса на минус, то x_{0} будет точкой минимума;
- x_{0} — будет точкой максимума только тогда, когда у производной меняется знак с минуса на плюс при переходе через стационарную точку x_{0} .
Наибольшее и наименьшее значение функции на промежутке
Шаги вычислений:
- Ищется производная f»(x) ;
- Находятся стационарные и критические точки функции и выбирают принадлежащие отрезку ;
- Находятся значения функции f(x) в стационарных и критических точках и концах отрезка. Меньшее из полученных результатов будет являться наименьшим значением функции , а большее — наибольшим .
Четность и нечетность функции являются одним из основных ее свойств, и на четность занимает внушительную часть школьного курса по математике. Она во много определяет характер поведения функции и значительно облегчает построение соответствующего графика.
Определим четность функции.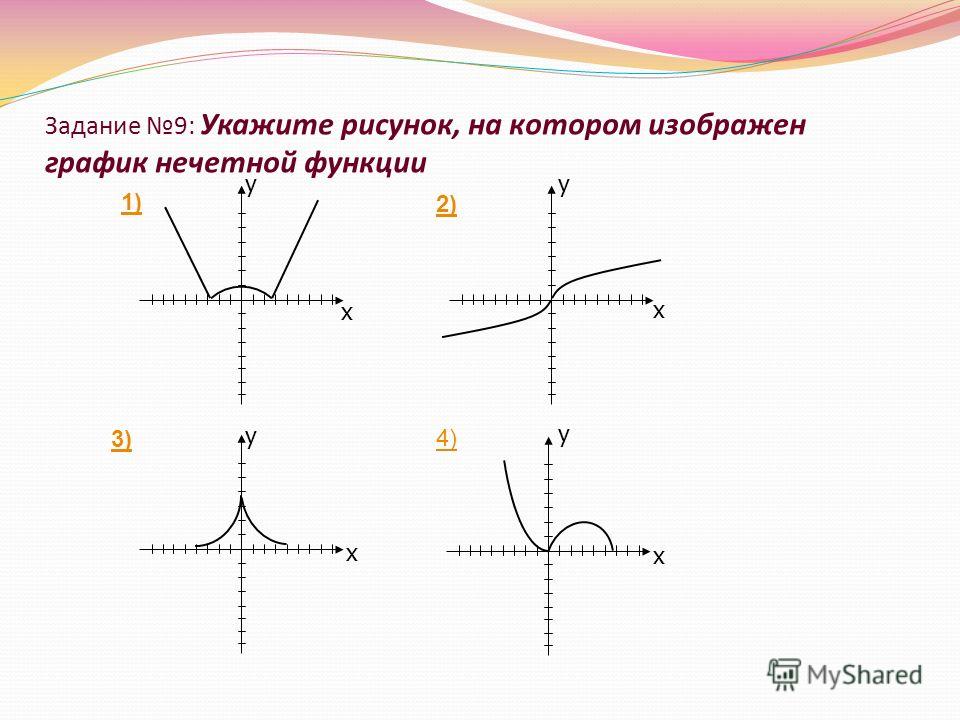 Вообще говоря, исследуемую функцию считают четной, если для противоположных значений независимой переменной (x), находящихся в ее области определения, соответствующие значения y (функции) окажутся равными.
Вообще говоря, исследуемую функцию считают четной, если для противоположных значений независимой переменной (x), находящихся в ее области определения, соответствующие значения y (функции) окажутся равными.
Дадим более строгое определение. Рассмотрим некоторую функцию f (x), которая задана в области D. Она будет четной, если для любой точки x, находящейся в области определения:
- -x (противоположная точка) также лежит в данной области определения,
- f (-x) = f (x).
Из приведенного определения следует условие, необходимое для области определения подобной функции, а именно, симметричность относительно точки О, являющейся началом координат, поскольку если некоторая точка b содержится в области определения четной функции, то соответствующая точка — b тоже лежит в этой области. Из вышесказанного, таким образом, вытекает вывод: четная функция имеет симметричный по отношению к оси ординат (Oy) вид.
Как на практике определить четность функции?
Пусть задается с помощью формулы h(x)=11^x+11^(-x).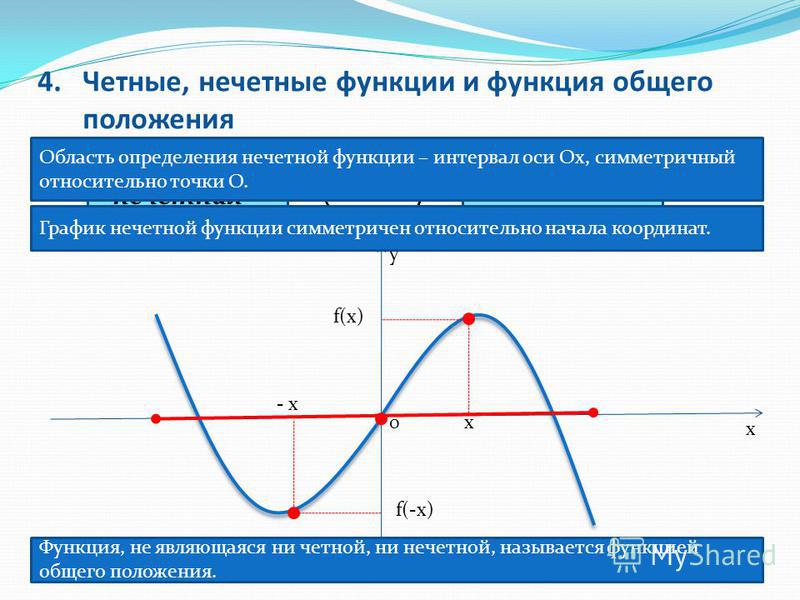 (-x))=- h(x). Следовательно, h(x) — нечетная.
(-x))=- h(x). Следовательно, h(x) — нечетная.
Кстати, следует напомнить, что есть функции, которые невозможно классифицировать по этим признакам, их называют ни четными, ни нечетными.
Четные функции обладают рядом интересных свойств:
- в результате сложения подобных функций получают четную;
- в результате вычитания таких функций получают четную;
- четной, также четная;
- в результате умножения двух таких функций получают четную;
- в результате умножения нечетной и четной функций получают нечетную;
- в результате деления нечетной и четной функций получают нечетную;
- производная такой функции — нечетная;
- если возвести нечетную функцию в квадрат, получим четную.
Четность функции можно использовать при решении уравнений.
Чтобы решить уравнение типа g(x) = 0, где левая часть уравнения представляет из себя четную функцию, будет вполне достаточно найти ее решения для неотрицательных значений переменной. Полученные корни уравнения необходимо объединить с противоположными числами. 2+2 может быть нечетным, причем для любого значения параметра. Действительно, легко проверить, что множество корней данного уравнения содержит решения «парами». Проверим, является ли 0 корнем. При подстановке его в уравнение, получаем 2=2 . Таким образом, кроме «парных» 0 также является корнем, что и доказывает их нечетное количество.
2+2 может быть нечетным, причем для любого значения параметра. Действительно, легко проверить, что множество корней данного уравнения содержит решения «парами». Проверим, является ли 0 корнем. При подстановке его в уравнение, получаем 2=2 . Таким образом, кроме «парных» 0 также является корнем, что и доказывает их нечетное количество.
Четные и нечетные функции. Периодические функции
Определение 1. Функция называется четной (нечетной), если вместе с каждым значением переменной значение –х также принадлежит и выполняется равенство
(11.1)
Таким образом, функция может быть четной или нечетной только тогда, когда ее область определения симметрична относительно начала координат на числовой прямой (числа х и –х одновременно принадлежат ). Например, функция не является четной и нечетной, так как ее область определения не симметрична относительно начала координат.
Функция четная, так как симметрична относительно начала координат и .
Функция нечетная, так как и .
Функция не является четной и нечетной, так как хотя и симметрична относительно начала координат, равенства (11.1) не выполняются. Например, .
График четной функции симметричен относительно оси Оу, так как если точка принадлежит графику, то и точка тоже принадлежит графику. График нечетной функции симметричен относительно начала координат, так как если принадлежит графику, то и точка тоже принадлежит графику.
При доказательстве четности или нечетности функции бывают полезны следующие утверждения.
Теорема 1. а) Сумма двух четных (нечетных) функций есть функция четная (нечетная).
б) Произведение двух четных (нечетных) функций есть функция четная.
в) Произведение четной и нечетной функций есть функция нечетная.
г) Если f – четная функция на множестве Х, а функция g определена на множестве , то функция – четная.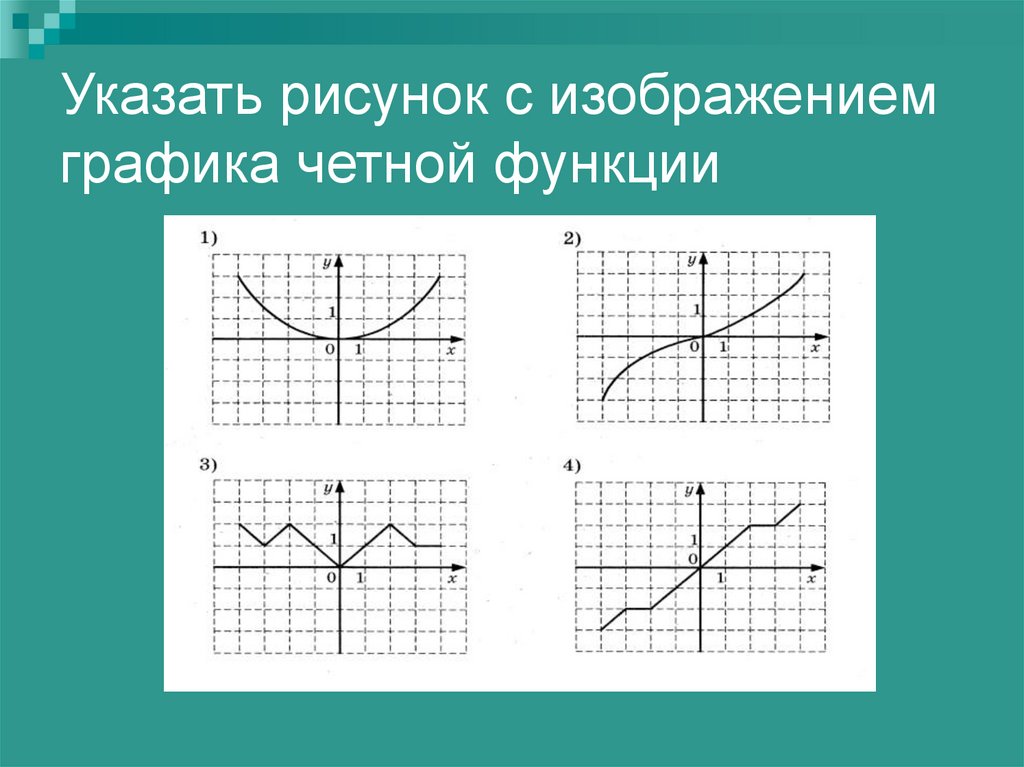
д) Если f – нечетная функция на множестве Х, а функция g определена на множестве и четная (нечетная), то функция – четная (нечетная).
Доказательство. Докажем, например, б) и г).
б) Пусть и – четные функции. Тогда , поэтому . Аналогично рассматривается случай нечетных функций и .
г) Пусть f – четная функция. Тогда .
Остальные утверждения теоремы доказываются аналогично. Теорема доказана.
Теорема 2. Любую функцию , заданную на множестве Х, симметричном относительно начала координат, можно представить в виде суммы четной и нечетной функций.
Доказательство. Функцию можно записать в виде
.
Функция – четная, так как , а функция – нечетная, поскольку . Таким образом, , где – четная, а – нечетная функции. Теорема доказана.
Определение 2. Функция называется периодической, если существует число , такое, что при любом числа и также принадлежат области определения и выполняются равенства
.
Такое число T называется периодом функции .
Из определения 1 следует, что если Т – период функции , то и число –Т тожеявляется периодом функции (так как при замене Т на –Т равенство сохраняется). С помощью метода математической индукции можно показать, что если Т – период функции f, то и , тоже является периодом. Отсюда следует, что если функция имеет период, то она имеет бесконечно много периодов.
Определение 3. Наименьший из положительных периодов функции называется ее основным периодом.
Теорема 3. Если Т – основной период функции f, то остальные периоды кратны ему.
Доказательство. Предположим противное, то есть что существует период функции f ( >0), не кратный Т. Тогда, разделив на Т с остатком, получим , где . Поэтому
,
то есть – период функции f, причем , а это противоречит тому, что Т – основной период функции f.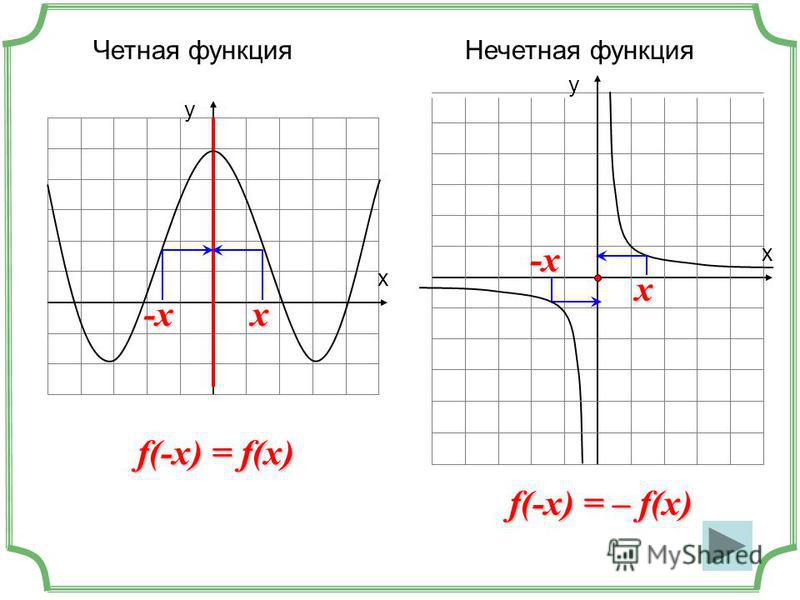 Из полученного противоречия следует утверждение теоремы. Теорема доказана.
Из полученного противоречия следует утверждение теоремы. Теорема доказана.
Хорошо известно, что тригонометрические функции являются периодическими. Основной период и равен , и . Найдем период функции . Пусть — период этой функции. Тогда
(так как .
Отсюда
или или или .
Значение T, определяемое из первого равенства, не может быть периодом, так как зависит от х, т.е. является функцией от х, а не постоянным числом. Период определяется из второго равенства: . Периодов бесконечно много, при наименьший положительный период получается при : . Это – основной период функции .
Примером более сложной периодической функции является функция Дирихле
Заметим, что если T – рациональное число, то и являются рациональными числами при рациональном х и иррациональными при иррациональном х. Поэтому
при любом рациональном числе T.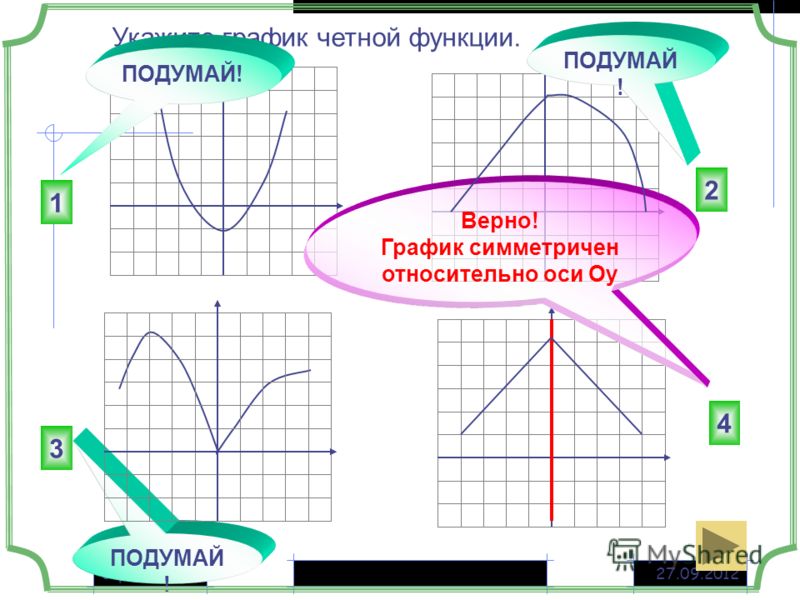 Следовательно, любое рациональное число T является периодом функции Дирихле. Ясно, что основного периода у этой функции нет, так как есть положительные рациональные числа, сколь угодно близкие к нулю (например, рациональное число можно сделать выбором n сколь угодно близким к нулю).
Следовательно, любое рациональное число T является периодом функции Дирихле. Ясно, что основного периода у этой функции нет, так как есть положительные рациональные числа, сколь угодно близкие к нулю (например, рациональное число можно сделать выбором n сколь угодно близким к нулю).
Теорема 4. Если функция f задана на множестве Х и имеет период Т, а функция g задана на множестве , то сложная функция тоже имеет период Т.
Доказательство. Имеем , поэтому
,
то есть утверждение теоремы доказано.
Например, так как cos x имеет период , то и функции имеют период .
Определение 4. Функции, не являющиеся периодическими, называются непериодическими.
Обратная функция
Пусть – некоторая функция, и — ее область определения и область значений соответственно.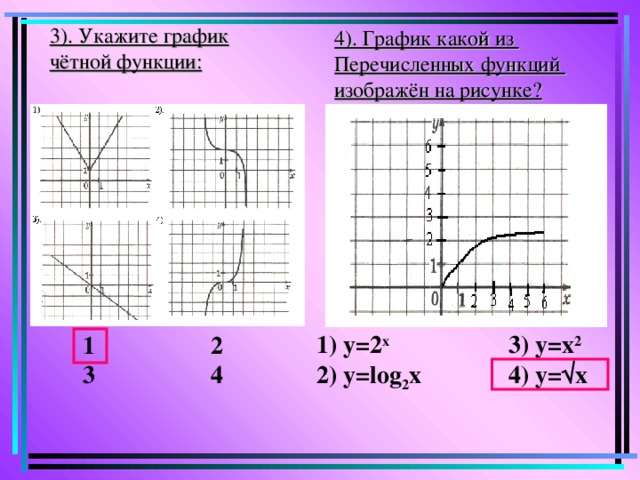 Если любым различным значениям аргумента соответствуют различные значения функции, то есть из , , то, как известно из § 8, отображение f, определяемое этой функцией, обратимо, и для него существует обратное отображение множества на множество . Это отображение называется обратной функцией к функции , то есть обратная функция такова, что . Функция и обратная для нее функция называются взаимно-обратными функциями. Заметим, что , а графики взаимно-обратных функций и симметричны относительно прямой – биссектрисы первого и третьего координатных углов. Обратная функция всегда существует для строго монотонной функции, которая каждое свое значение принимает только один раз.
Если любым различным значениям аргумента соответствуют различные значения функции, то есть из , , то, как известно из § 8, отображение f, определяемое этой функцией, обратимо, и для него существует обратное отображение множества на множество . Это отображение называется обратной функцией к функции , то есть обратная функция такова, что . Функция и обратная для нее функция называются взаимно-обратными функциями. Заметим, что , а графики взаимно-обратных функций и симметричны относительно прямой – биссектрисы первого и третьего координатных углов. Обратная функция всегда существует для строго монотонной функции, которая каждое свое значение принимает только один раз.
Чтобы найти аналитическое выражение для функции , обратной к функции , нужно решить уравнение относительно х, и если при этом получается несколько значений х, то выбрать те значения, которые принадлежат . Таким образом получают равенство , в котором обычно заменяют у на х и х на у.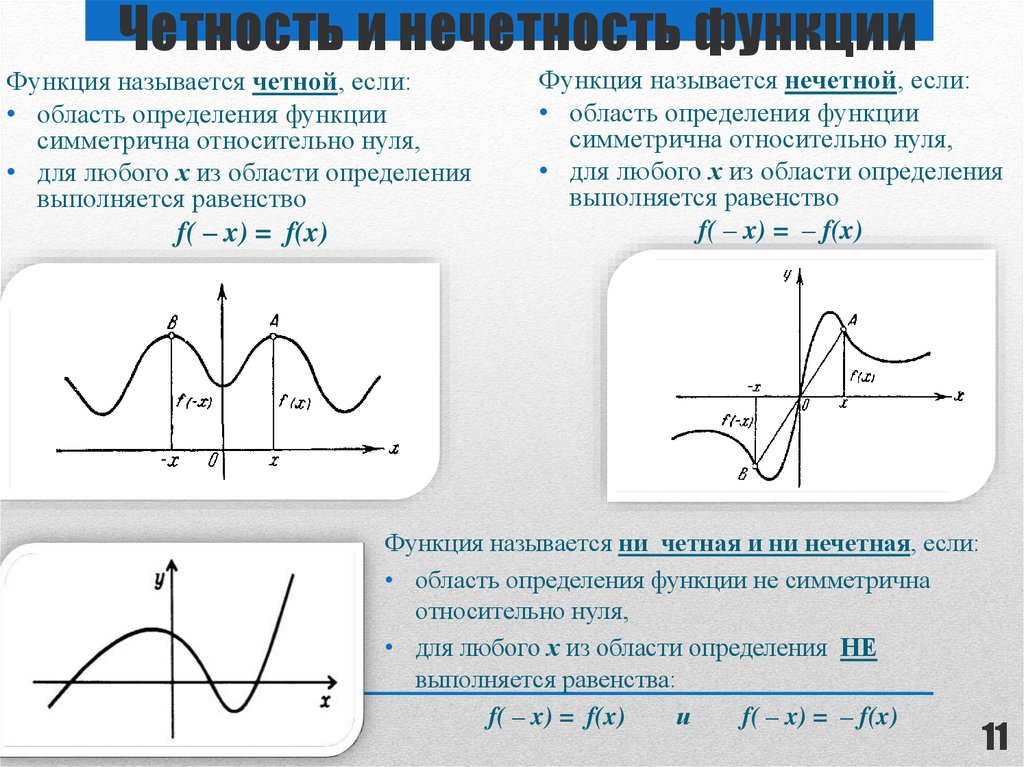
Обратные функции для функций нужно рассмотреть на практических занятиях.
|
значение функция принимает только один раз (такие функции называются инъективными).
Дата добавления: 2016-06-09; просмотров: 8033; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Четные и нечетные функции
Используй поиск, чтобы найти научные материалы и собрать список литературы
База статей справочника включает в себя статьи написанные экспертами Автор24, статьи из научных журналов и примеры студенческих работ из различных вузов страны
Содержание статьи
1. Четные функции
Четные функции
2. Нечетные функции
3. Функция общего вида
4. Пример задачи
Четные функции
Определение 1
Функцию $y=f(x)$, которая имеет своей областью определения множество $X$, будем называть четной, если для всех точек из множества $X$ будет выполняться
\[f\left(x\right)=f(-x)\]
Так как при выборе равных по модулю с обоими знаками значений независимых переменных для любой четной функции значения самой функции будет совпадать, то график этих функции будет подчиняться закону осевой симметрии по отношению к оси ординат (рис. 1).
Рисунок 1.
Для исследования функции на четность необходимо в его аналитической записи заменить переменную $x$ на переменную $-x$, произвести, при необходимости элементарные преобразования, и проверить условие определения 1.
Нечетные функции
Определение 2
Функцию $y=f(x)$, которая имеет своей областью определения множество $X$, будем называть нечетной, если для всех точек из множества $X$ будет выполняться
\[f\left(-x\right)=-f(x)\]
Так как при выборе равных по модулю с обоими знаками значений независимых переменных для любой четной функции значения самой функции будут также совпадать по модулю и отрицательны по знакам, то график этих функции будет подчиняться закону центральной симметрии по отношению к началу координат (рис. 2).
2).
Рисунок 2.
Для исследования функции на нечетность необходимо в его аналитической записи заменить переменную $x$ на переменную $-x$, произвести, при необходимости элементарные преобразования, и проверить условие определения 2.
Функция общего вида
Определение 3
Функцию $y=f(x)$, которая имеет своей областью определения множество $X$, будем называть функцией общего вида, если она не будет ни четной, ни нечетной.
Для того чтобы понять, что данная функция является функцией общего вида, необходимо в его аналитической записи заменить переменную $x$ на переменную $—x$, произвести, при необходимости элементарные преобразования, и проверить невыполнение условий определений 1 и 2.
Функция общего вида никогда не будет симметрична оси ординат и началу координат. Пример функции общего вида изображен на рисунке 3.
Рисунок 3.
Пример задачи
Пример 1
Исследовать функцию на четность и нечетность и построить их графики.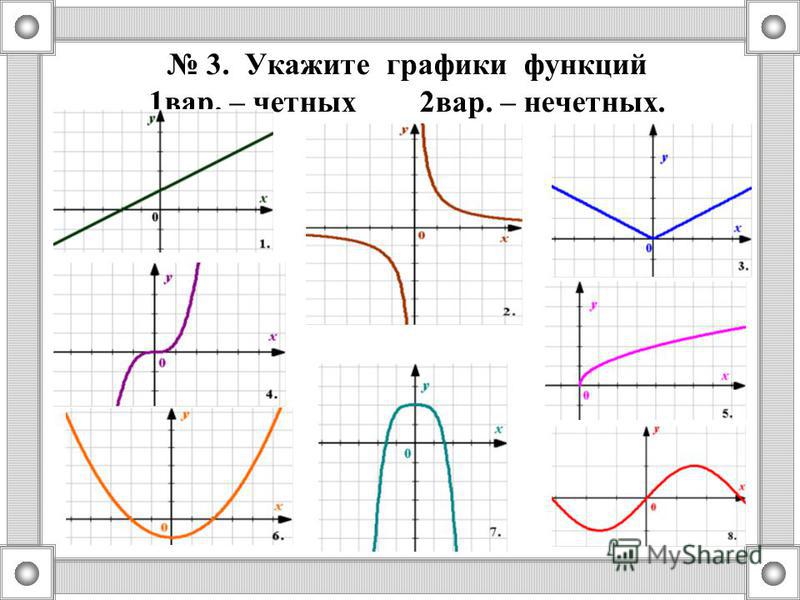 2+4}{x}$ следовательно, $f(x)$ — нечетная функция.
2+4}{x}$ следовательно, $f(x)$ — нечетная функция.
Изобразим её на графике:
Рисунок 5.
в) $f\left(x\right)=sinx+cosx$
$f\left(-x\right)={\sin \left(-x\right)\ }+{\cos \left(-x\right)\ }=cosx-sinx$ следовательно, $f\left(x\right)$ — функция общего вида.
Изобразим её на графике:
Рисунок 6.
Сообщество экспертов Автор24
Автор этой статьи Дата последнего обновления статьи: 04.07.2022
Выполнение любых типов работ по математике
Решение задач по комбинаторике на заказ Решение задачи Коши онлайн Математика для заочников Контрольная работа на тему числовые неравенства и их свойства Контрольная работа на тему умножение и деление рациональных чисел Контрольная работа на тему действия с рациональными числами Дипломная работа на тему числа Курсовая работа на тему дифференциальные уравнения Контрольная работа на тему приближенные вычисления Решение задач с инвариантами
Подбор готовых материалов по теме
Дипломные работы Курсовые работы Выпускные квалификационные работы Рефераты Сочинения Доклады Эссе Отчеты по практике Решения задач Контрольные работы
Четная функция — определение, свойства, график, примеры
LearnPracticeDownload
Функция является четной, если f от x равно f от −x для всех значений x.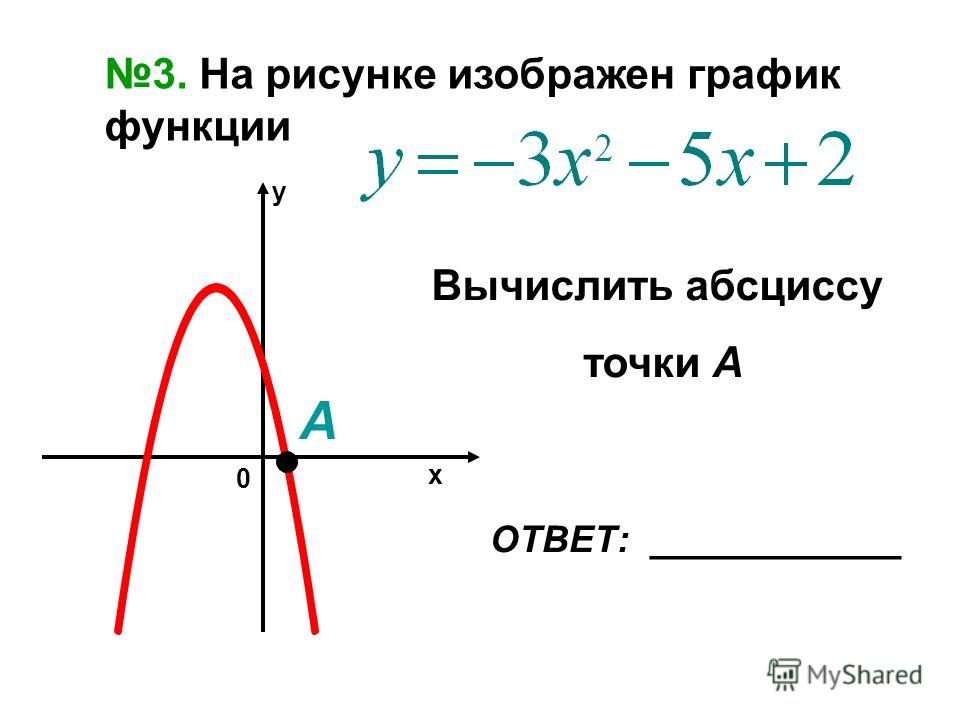 Это означает, что функция одинакова для положительной оси x и отрицательной оси x или графически симметрична относительно оси y. Примером четной функции являются тригонометрическая четная функция, секущая функция и т. д. Давайте подробно рассмотрим четную функцию, а также ее графическое представление и свойства.
Это означает, что функция одинакова для положительной оси x и отрицательной оси x или графически симметрична относительно оси y. Примером четной функции являются тригонометрическая четная функция, секущая функция и т. д. Давайте подробно рассмотрим четную функцию, а также ее графическое представление и свойства.
| 1. | Что такое четная функция? |
| 2. | Графическое представление четной функции |
| 3. | Свойства четной функции |
| 4. | Часто задаваемые вопросы о функции Even |
Что такое четная функция?
Давайте сначала поймем значение четных функций алгебраически. Функция четная, если f(x) = f(-x) для всех значений x. Теперь давайте посмотрим, что это значит. Для четной функции f(x), если мы подставим -x вместо x, то значение f(-x) будет равно значению f(x). Точно так же такие функции, как \(x^4, x^6, x^8, x^{10}\) и т. д., являются четными функциями.
д., являются четными функциями.
Интересно, что указанные выше функции имеют равные силы. Обратите внимание на график ниже y = x 2 , график четной функции.
Пример четной функции
Рассмотрим тригонометрическую функцию (f(x) = cos x. Определите значение f(-x) и определите, является ли она четной функцией или нет.
Решение: f(-x) = cos (-x) = cos x = f(x)
cos (-x) = cos x для всех значений x
Следовательно, f(x) = cos x равно четная функция
Графическое представление четной функции
Теперь посмотрим, как графически ведет себя четная функция. Приведенный выше график четной функции симметричен относительно оси y. Другими словами, график четной функции остается прежним после отражения относительно оси у.
Вот несколько примеров четных функций, соблюдайте симметрию относительно оси Y.
Посмотрим график для f(x) = cos x
Свойства четной функции
Поняв значение четной функции, мы собираемся исследовать ее свойства. Несколько основных свойств четной функции перечислены ниже.
Несколько основных свойств четной функции перечислены ниже.
- Сумма двух четных функций четна.
- Разница между двумя четными функциями четна.
- Произведение двух четных функций четно.
- Частное от деления двух четных функций четно.
- Состав двух четных функций четный.
- Композиция четной и нечетной функций четна.
☛Статьи о четной функции
Ниже приведен список тем, тесно связанных с четной функцией. Эти темы также дадут вам представление о том, как такие понятия рассматриваются в Cuemath.
- Экспоненциальная функция
- Полиномиальные функции
- Квадратичные функции
- Линейные функции
- Постоянные функции
Примеры четных функций
Пример 1: Сэм хочет алгебраически определить, является ли функция f(x) = 4x 4 − 7x 2 четной функцией или нет.
Решение: Подставьте -x вместо x в f(x) = 4x 4 — 7x 2 .

f(−x) = 4(−x) 4 −7(−x) 2
= 4x 4 − 7x 2
= f(x)Поскольку f(−x) = f(x), функция f(x) является четной функцией.
Пример 2. Рассмотрим функцию f(x) = x 2 . Определите значение f(−x). Определите, является ли это четной функцией или нет.
Решение: f(−x) = (−x) 2 = x 2 = f(x)
Следовательно, f(x) = x 2 — четная функция.
Мы можем проверить, взяв определенное значение x.
Для x = 2 значение f(x) определяется по формуле:
f(2) = 2 2 = 4
Значение f(−x) определяется по формуле:
f(− 2) = (−2) 2 = 4 = f(2)
Пример 3: Определите, является ли функция f(x) = 6x 4 − x 12 четной или нет.
Решение: Подставьте −x вместо x в f(x) = 6x 4 − x 12 .

f(−x) = 6(−x) 4 − (−x) 12
= 6x 4 − x 12
= f(x)
Поскольку f(−x) = f(x), функция f(x) является четной функцией.
f(x) = 6x 4 − x 12 — четная функция.
перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по четной функции
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о функции Even
Что такое четные функции в исчислении?
Четные функции — это те функции в исчислении, которые одинаковы для +ve оси x и -ve оси x или графически симметричны относительно оси y. Он представлен как f (x) = f (-x) для всех x.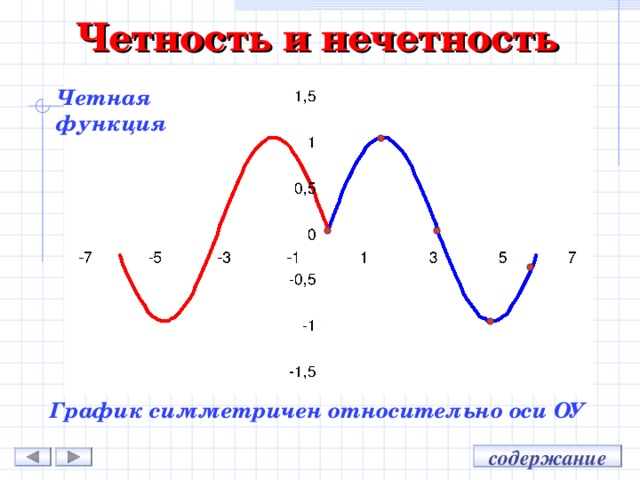 Несколько примеров четных функций: x 4 , cos x, y = x 2 и т. д.
Несколько примеров четных функций: x 4 , cos x, y = x 2 и т. д.
Что такое уравнение четной функции?
Уравнение четной функции, математически выраженное как f(-x) = f(x) для всех x.
Как определить, является ли функция четной функцией или нет?
Если функция удовлетворяет условию f(−x) = f(x) для всех x, она называется четной функцией. Это означает, что он одинаков для +ve оси x и -ve оси x или графически симметричен относительно оси y.
- Если значение f(−x) совпадает со значением f(x) для каждого значения x, функция четная.
- Если значение f(−x) НЕ совпадает со значением f(x) для любого значения x, функция не является четной.
- Если функция имеет четную степень, функция не обязательно должна быть четной.
Является ли Cos x четной функцией?
Уравнение четной функции, математически выраженное как f(−x) = f(x) для всех x. При подстановке значения имеем cos(−x) = cosx.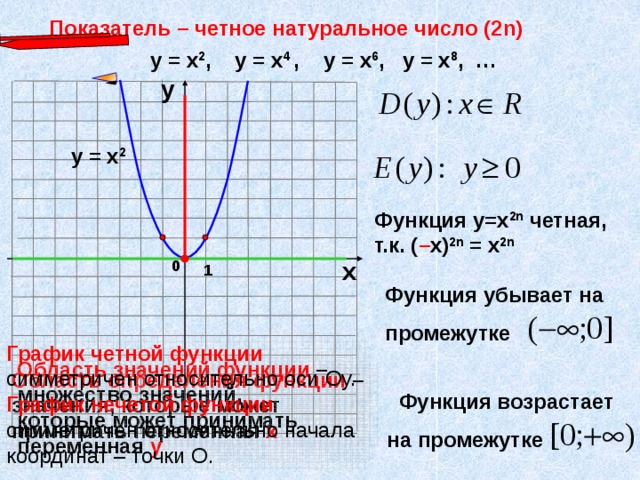 Следовательно, cos x — четная функция.
Следовательно, cos x — четная функция.
Как определить, имеет ли построенный график четную функцию?
Существуют определенные правила, позволяющие определить, является ли построенный график четной функцией или нет. Правила перечислены ниже.
- Если график симметричен относительно оси Y, функция четная.
- Если график симметричен относительно начала координат, функция нечетная.
- Если график несимметричен относительно оси Y или начала координат, функция не является ни четной, ни нечетной.
Константы даже функционируют?
Постоянная функция f(x) = k является четной функцией, поскольку f(−x) = k = f(x).
Запишите два основных свойства четной функции.
Существуют различные свойства, определяющие четную функцию. Вот два основных свойства:
- Когда мы вычитаем две четные функции, получается четная разница.
- Когда мы умножаем две четные функции, получается четное произведение.
Скачать БЕСПЛАТНЫЕ учебные материалы
Рабочие листы по четной функции
Рабочие листы по математике и визуальный учебный план
Как определить, является ли функция четной, нечетной или ни одной из них
Я подготовил восемь (8) рабочих примеров, чтобы проиллюстрировать процедуру или шаги, как определить, является ли заданная функция четной, нечетной или ни той, ни другой. Математика, связанная с вычислением, проста, если вы внимательны на каждом этапе своего решения.
Математика, связанная с вычислением, проста, если вы внимательны на каждом этапе своего решения.
Чтобы проникнуть в «сердце» этой темы, изучите иллюстрацию ниже.
Как определить, является ли функция четной, нечетной или ни одной из них
Давайте поговорим о каждом случае.
СЛУЧАЙ 1: Четная функция
Учитывая некоторую «начальную» функцию f\left( x \right):
- Если мы вычислим или подставим \color{red}-x в f\left( x \right) и получим исходную или «начальную» снова функция, это означает, что f\left( x \right) является четной функцией .
СЛУЧАЙ 2: нечетная функция
Дана некоторая «начальная» функция f\left( x \right):
- \right) и получить отрицательную или противоположную «начальной» функции, это означает, что f\left( x \right) является нечетная функция .
СЛУЧАЙ 3: ни четная, ни нечетная функция x \right) и мы не получаем ни случая 1, ни случая 2, из которого следует, что f\left( x \right) не является ни четным, ни нечетным . Другими словами, оно не подпадает под классификацию четных или нечетных.
Другими словами, оно не подпадает под классификацию четных или нечетных. Примеры алгебраического определения, является ли функция четной, нечетной или ни одной из них 92} — 3, подставьте значение \color{red}-x и затем упростите. Что я могу получить? Давайте решим это алгебраически.
Поскольку f\left( { {\color{red}- x}} \right) = f\left( x \right), это означает, что f\left( x \right) является четной функцией !
График четной функции симметричен относительно оси y или относительно вертикальной линии x = 0. Обратите внимание, что график функции разрезается равномерно по оси y, и каждая половина является точным зеркалом еще один. Другой способ описать это состоит в том, что каждая половина функции является отражением по оси Y. 93} + 2x, а затем упростите.
Как определить нечетную функцию
Важные советы:
- Если вы когда-нибудь придете к другой функции после вычисления \color{red}–x в заданном f\left( x \right), немедленно попробуйте вынесите из него -1 и посмотрите, появится ли исходная функция.
 Если это так, то у нас есть нечетная функция .
Если это так, то у нас есть нечетная функция .
- Эффект вынесения на множитель -1 приводит к переключению знаков членов внутри скобок. Это ключевой шаг для определения нечетной функции.
Теперь, поскольку f\left( { {\color{red}- x}} \right) = — f\left( x \right), это означает, что исходная функция f\left( x \right) равна нечетная функция !
График нечетной функции имеет вращательную симметрию относительно начала координат или в точке \left( {0,0} \right). Это означает, что мы разрезаем его график по оси y, а затем отражаем его четную половину сначала по оси x, а затем по оси y.
См. анимированную иллюстрацию.
90}}, который имеет четную степень нуля.
Эта характеристика функции, содержащей только четные степени, может привести к четной функции. Однако мы должны показать это алгебраически. Итак, вот оно.
Вычисляя \color{red}-x в f\left( x \right), мы получаем следующий расчет. 3} + 6x
3} + 6x
В отличие от примера 3, где у функции четные степени, у этого есть нечетные степени: 7, 5, 3 и 1. Надеюсь, вы уже видите закономерность. Скорее всего, это странная функция, но мы проверим.
Подставляя \color{red}-x в данное f\left( x \right) и упрощая, мы получаем:
После вынесения на множитель -1 многочлен в скобках равен начальной функции. Это показывает, что это нечетная функция !
Пример 5 : Определить, является ли заданная функция четной, нечетной или ни одной:
На этот раз я покажу вам пример функции, которая не является ни четной, ни нечетной. Вы готовы?
- Сначала проверьте, четно ли оно. Имеем ли мы случай f\left( {\color{red}{ — x}} \right) = f\left( x \right)?
Определенно не является четной функцией , поскольку f\left( {\color{red}{ — x}} \right) \ne f\left( x \right).
- Во-вторых, проверьте, является ли оно нечетным, показав f\left( {\color{red}{ — x}} \right) = — f\left( x \right).

Даже после вычета −1 я все еще не получаю исходную функцию.
Это не нечетная функция , так как f\left( {\color{red}{ — x}} \right) \ne — f\left( x \right).
- Вывод: Поскольку мы достигли случая, когда f\left( {\color{red}{ — x}} \right) \ne f\left( x \right) и f\left( {\color{red} { — x}} \right) \ne — f\left( x \right), эта функция ни четная, ни нечетная !
Пример 6 : Определить, является ли заданная функция четной, нечетной или ни одной:
Решение:
Следовательно, функция g\left( x \right) является нечетной функцией !
Пример 7 : Определить, является ли заданная функция четной, нечетной или ни одной:
Решение:
Следовательно, функция h\left( x \right) не равна и не !
Пример 8 : Определить, является ли заданная функция четной, нечетной или ни одной:
Решение:
Следовательно, функция k\left( x \right) равна даже функция !
Объяснение урока: Четные и нечетные функции
В этом объяснении мы узнаем, как определить, является ли функция четной, нечетной,
или ни по графику функции, ни по ее правилу.
Четность функции описывает, является ли функция четной или нечетной.
Определение: нечетные и четные функции
Функция 𝑓(𝑥) является
- четной функцией, если 𝑓(−𝑥)=𝑓(𝑥),
- нечетной функцией, если 𝑓(−𝑥)=−𝑓( 𝑥),
для каждого 𝑥 в области определения функции.
Обратите внимание, что единственная функция, определенная на множестве действительных чисел, и четное, и нечетное равно 𝑓(𝑥)=0; таким образом, как только мы определили четность функции, нам не нужно проверять ее снова.
Графики четных и нечетных функций также обладают некоторыми ключевыми свойствами, которые могут чтобы их было легко идентифицировать. Рассмотрим графики функции 𝑓(𝑥)=𝑥+4 и 𝑔(𝑥)=𝑥.
Мы можем проверить четность 𝑓(𝑥) вычислением 𝑓(−𝑥): 𝑓(−𝑥)=(−𝑥)+4=𝑥+4=𝑓(𝑥).
𝑓(𝑥) является четной функцией. Обратите внимание, как график
𝑓(𝑥)=𝑥+4 имеет отражательную симметрию относительно
к оси 𝑦 или прямой 𝑥=0.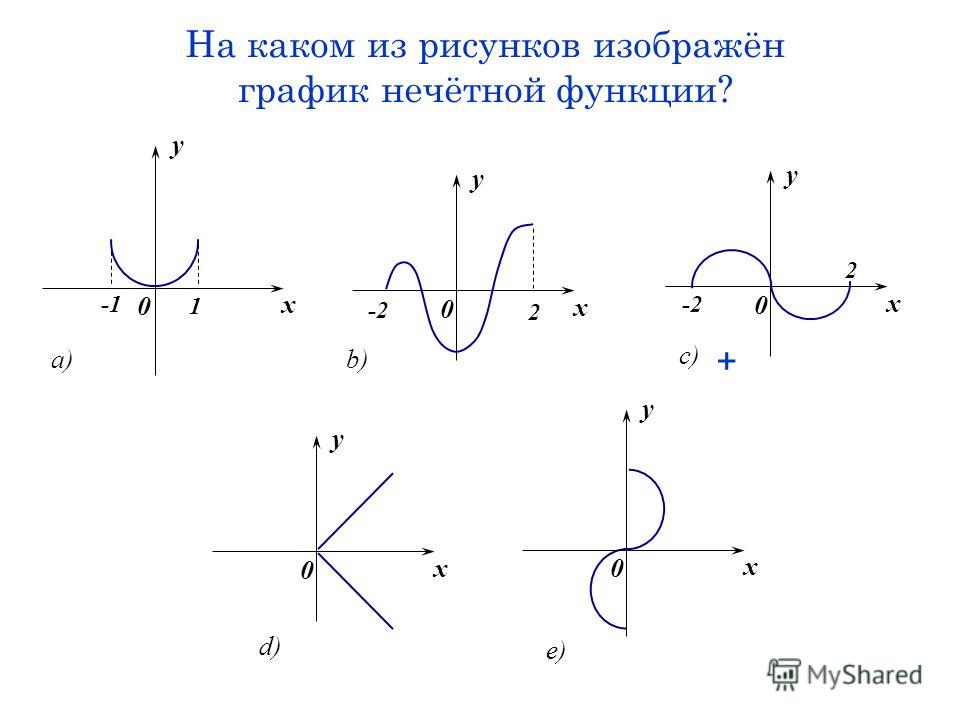 Это связано с тем, что вывод функции будет таким же, если мы введем 𝑥 или −𝑥. Например, точки (2,8) и (−2,8) лежат на кривой
𝑦=𝑓(𝑥).
Это связано с тем, что вывод функции будет таким же, если мы введем 𝑥 или −𝑥. Например, точки (2,8) и (−2,8) лежат на кривой
𝑦=𝑓(𝑥).
Фактически, 𝑓(−𝑥)=𝑓(𝑥) подразумевает, что график функции будет иметь отражательную симметрию относительно 𝑦-ось для каждого значения 𝑥 в области определения функции. Эти функции называются даже функций, так как функция 𝑓(𝑥)=𝑥 будет обладать этим свойством, если 𝑛 — любое четное целое число.
Теперь рассмотрим функцию 𝑔(𝑥)=𝑥. Чтобы проверить четность этой функции, мы оценим 𝑔(−𝑥): 𝑔(−𝑥)=(−𝑥)=−𝑥=−𝑔(𝑥).
𝑔(𝑥) — нечетная функция. На этот раз граф 𝑔(𝑥) имеет вращательную симметрию порядка 2 относительно начала координат, что означает, что его график остается неизменным после
поворот на 180∘ о (0,0). Это потому, что если точка с координатами
(𝑥,𝑦) лежит на кривой, то
поскольку 𝑔(−𝑥)=−𝑔(𝑥), соответствующая точка с координатами (−𝑥,−𝑦) также должна лежать на кривой.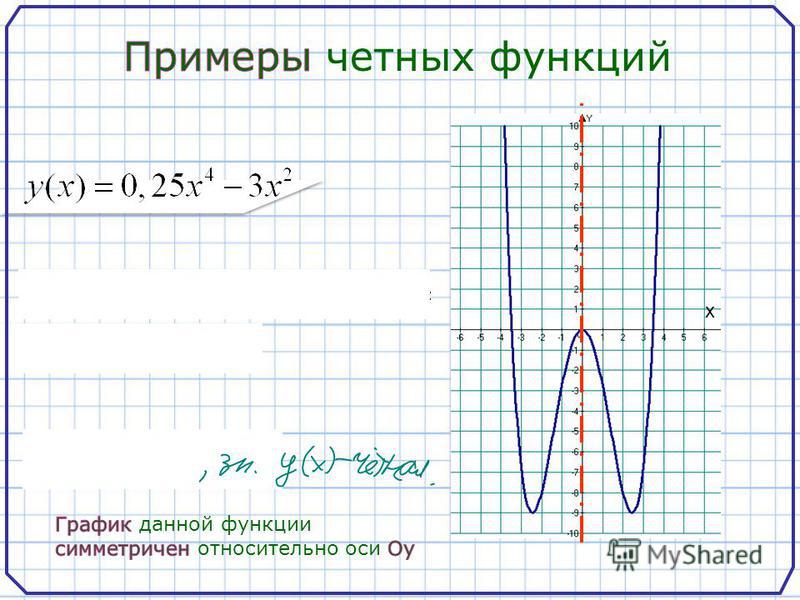 Например, с момента
с координатами (2,8) лежит на кривой 𝑦=𝑔(𝑥),
тогда точка с координатами (−2,−8) также должна лежать на кривой.
Например, с момента
с координатами (2,8) лежит на кривой 𝑦=𝑔(𝑥),
тогда точка с координатами (−2,−8) также должна лежать на кривой.
𝑔(−𝑥)=−𝑔(𝑥) означает, что график функция будет иметь порядок вращательной симметрии 2 относительно начала координат для каждого значения 𝑥 в области определения функции. Эти функции называются нечетными функциями, поскольку функция 𝑔(𝑥)=𝑥 будет обладать этим свойством, если 𝑛 — любое нечетное целое число.
Если нечетная функция определена в нуле, то ее график должен проходить через начало координат. Мы можем продемонстрировать это, положив 𝑥=0 в определении нечетной функции, 𝑔(𝑥)=−𝑔(𝑥). Заметим, что 𝑔(0)=−𝑔(0), что соответствует вращению интерпретация нечетной функции.
Поскольку для нечетной функции 𝑔(−𝑥)=−𝑔(𝑥),
мы можем сделать вывод, что абсолютное значение
на самом деле эта функция должна быть четной; для любой нечетной функции
𝑔(𝑥), если
ℎ(𝑥)=|𝑔(𝑥)|, то ℎ четно.
Определение: графики четных и нечетных функций
График любой четной функции имеет отражательную симметрию относительно оси 𝑦.
График любой нечетной функции имеет вращательную симметрию порядка 2 относительно начала координат.
Мы можем использовать как определение функции, так и ее график, чтобы определить четность функции. В нашем первом примере мы покажем, как использовать определение функции, чтобы определить, является ли функция четной, нечетной или ни той, ни другой.
Пример 1. Определение четности линейной функции
Является ли функция 𝑓(𝑥)=4𝑥−3 четной, нечетной или ни одной?
Ответ
Напомним, что функция 𝑓(𝑥) является
- четной функцией, если 𝑓(−𝑥)=𝑓(𝑥),
- нечетной функцией, если 𝑓(−𝑥)=−𝑓(𝑥) ,
для каждого 𝑥 в области определения функции.
Поскольку 𝑓(𝑥) — линейная функция, ее область определения равна ℝ. Это симметрично относительно 0, поэтому мы знаем, что симметрично
применяются свойства четных и нечетных функций. Чтобы проверить четность 𝑓(𝑥), мы оценим 𝑓(−𝑥):
𝑓(−𝑥)=4(−𝑥)−3=−4𝑥−3.
Чтобы проверить четность 𝑓(𝑥), мы оценим 𝑓(−𝑥):
𝑓(−𝑥)=4(−𝑥)−3=−4𝑥−3.
Заметим, что 𝑓(−𝑥)≠𝑓(𝑥), и равно как и 𝑓(−𝑥)=−𝑓(𝑥).
Функция не является ни четной, ни нечетной.
В наших следующих двух примерах мы рассмотрим, как определение четных и нечетных функций (относительно симметрии их графиков) может помочь нам определить четность функции.
Пример 2. Определение того, является ли построенная на графике функция четной, нечетной или ни одной из них
Определите, является ли функция, представленная на следующем рисунке, четной, нечетной или ни одной из них.
Ответ
Напомним, что график четной функции имеет отражательную симметрию с
относительно оси 𝑦, а график нечетной функции имеет вращательную симметрию порядка 2 о происхождении. Важно понимать, что это должно выполняться
истинно для 90 527 для каждого 90 528 значения 𝑥 в области определения функции, и поэтому мы должны
убедитесь, что область определения функции симметрична относительно 0.
Область определения функции — это множество возможных 𝑥-значений, которые можно заменить в функцию; это можно вывести из графика функции, посмотрев на разброс 𝑥-значений слева направо.
Областью определения этой функции являются значения 𝑥 в интервале [−8,8], не считая 𝑥=0. Используя обозначение набора, домен задается [−8,8]−{0}.
Так как эта область симметрична относительно 0, мы можем теперь проверить, является ли функция четное, нечетное или ни то, ни другое.
Мы наблюдаем, что график имеет отражательную симметрию относительно оси 𝑦, или линия 𝑥=0. Это означает, что для любого значения 𝑥 в области определения функция, 𝑓(−𝑥)=𝑓(𝑥).
Функция четная.
В нашем предыдущем примере мы продемонстрировали, как определить четность функции, заданной в ограниченной области, по ее графику. В примере 3 мы увидим, как этот процесс можно применить к функциям, определенным в неограниченной области.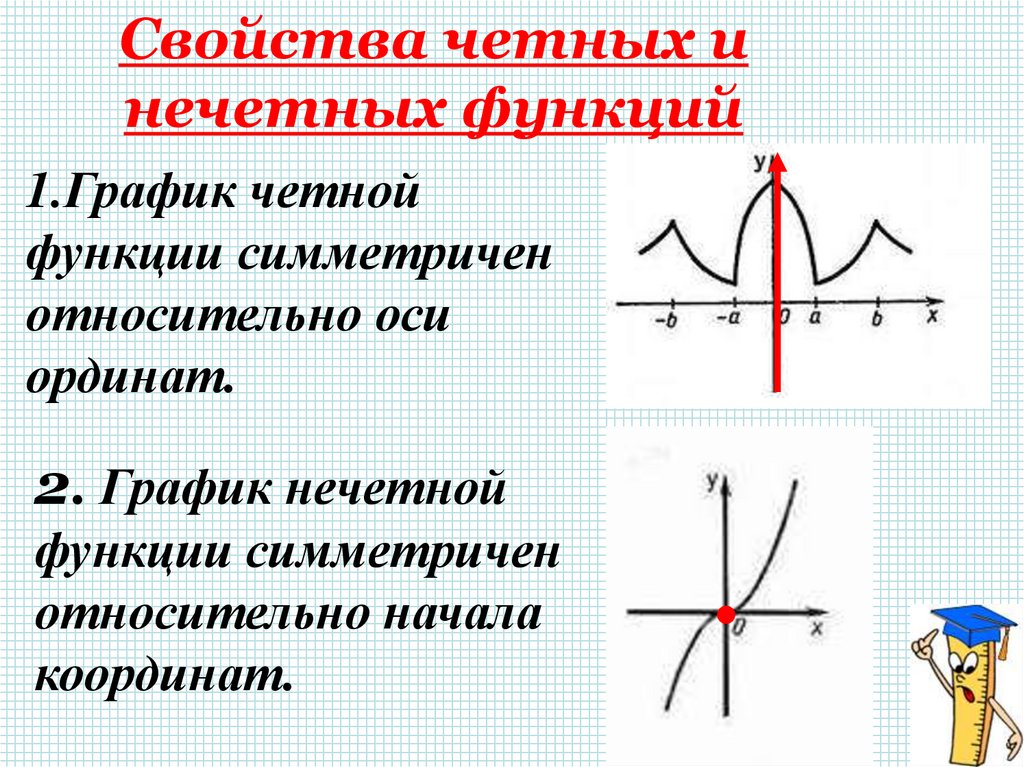
Пример 3. Определение четности построенной на графике рациональной функции
Является ли функция, представленная цифрой, четной, нечетной или ни одной?
Ответ
Напомним, что график нечетной функции имеет вращательная симметрия порядка 2 относительно начала координат, а график четной функции имеет 90 527 отражательную симметрию 90 528 относительно начала координат. 𝑦-ось. Важно понимать, что это должно быть верным для 90 527 каждого 90 528 значения 𝑥 в домен функции, и поэтому мы должны убедиться, что домен функции симметрична относительно 0.
График функции имеет вертикальную асимптоту, заданную при 𝑥=0. Это единственное значение 𝑥, где функция не определена; следовательно, его область определения определяется выражением ℝ−{0}.
Так как эта область симметрична относительно 0, мы можем теперь проверить, является ли функция
является четным, нечетным или ни тем, ни другим.
Мы видим, что граф не имеет отражательных симметрия задается осью 𝑦, поэтому эта функция не может быть четной.
Однако график остается неизменным после поворота на 180° вокруг начала координат.
Следовательно, функция нечетная.
В наших предыдущих двух примерах мы начали с проверки того, что домен функции был симметричен относительно 0. Поскольку четность функции зависит от ее симметричные свойства относительно оси 𝑦 или начала координат, следует, что функция, область определения которой не симметрична относительно 0, будет ни четным, ни нечетным.
В следующем примере мы увидим, как подтверждение этого элемента определение может сэкономить нам время при определении, является ли функция четной, странно, или ни то, ни другое.
Пример 4. Определение того, является ли изображенная на графике функция четной, нечетной или ни той, ни другой
Является ли функция, представленная цифрой, четной, нечетной или ни той, ни другой?
Ответ
График четной функции имеет отражательную симметрию относительно
𝑦-ось, а график нечетной функции имеет вращательная симметрия г.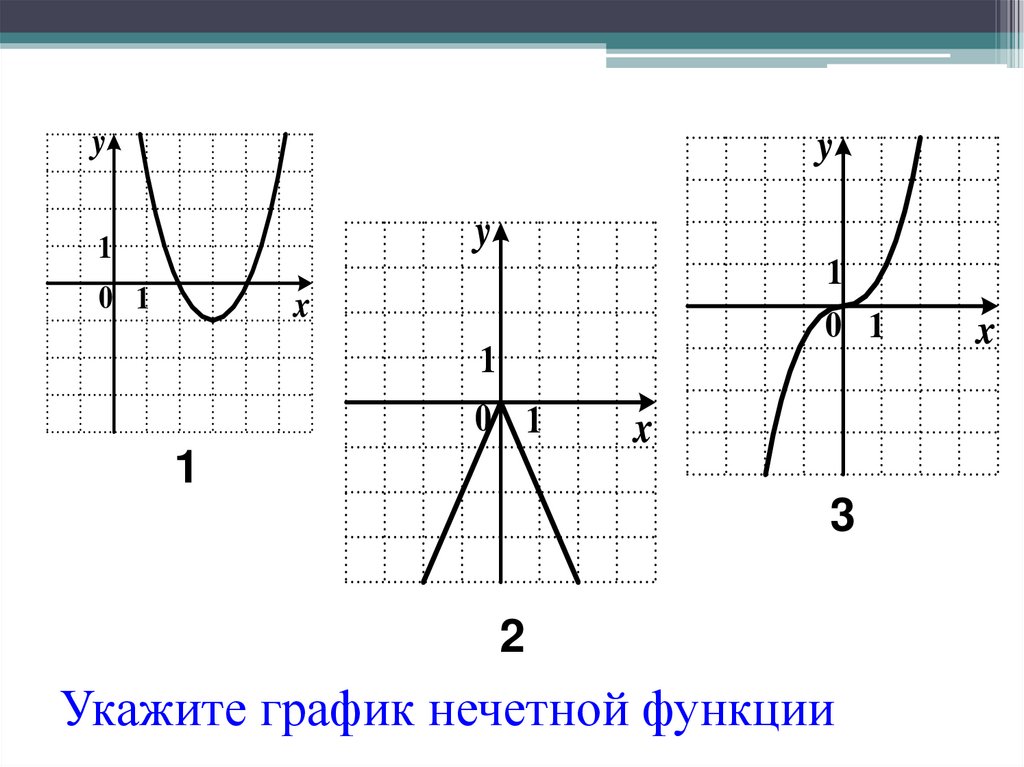 порядок 2 о происхождении. Важно понимать, что это должно выполняться
истинно для 90 527 для каждого 90 528 значения 𝑥 в области определения функции, и поэтому мы должны
убедитесь, что область определения функции симметрична относительно 0.
порядок 2 о происхождении. Важно понимать, что это должно выполняться
истинно для 90 527 для каждого 90 528 значения 𝑥 в области определения функции, и поэтому мы должны
убедитесь, что область определения функции симметрична относительно 0.
Область определения функции — это набор возможных входных данных или 𝑥-значений, что мы можем подставить в эту функцию.
Областью определения этой функции является интервал 2≤𝑥≤6. Этот домен не симметричный около 0,
Поскольку область определения этой функции не симметрична относительно 0, мы можем вывести что функция не четная и не нечетная.
В нашем следующем примере мы рассмотрим, как определить четность тригонометрической функции из ее уравнения, используя следующие определения.
Определение: четность тригонометрических функций
𝑓(𝑥)=𝑥cos и 𝑓(𝑥)=𝑥sec являются четными функциями.
𝑓(𝑥)=𝑥sin, 𝑓(𝑥)=𝑥csc,
𝑓(𝑥)=𝑥tan и 𝑓(𝑥)=𝑥cot — нечетные функции.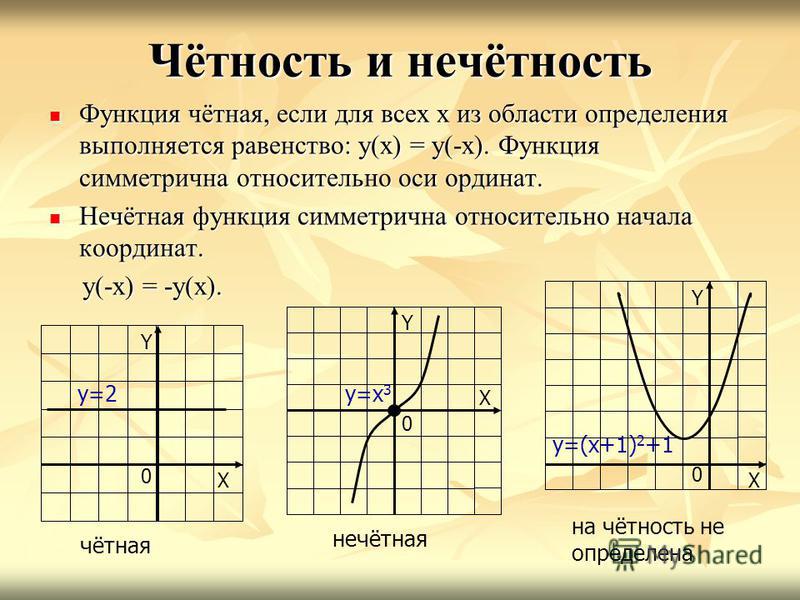
Пример 5. Определение четности функции
Является ли функция 𝑓(𝑥)=𝑥6𝑥tan четной, странно или нет?
Ответ
Функция 𝑦=𝑓(𝑥) является
- четной функцией, если 𝑓(−𝑥)=𝑓(𝑥),
- нечетной функцией, если 𝑓(−𝑥)=−𝑓),(𝑓
для каждого 𝑥 в области определения функции.
Начнем с определения области определения функции. Нам нужно убедиться, что это симметричный относительно 0; в противном случае симметричные свойства четных и нечетных функций не будет применяться.
𝑥6𝑥tan является произведением двух функций, поэтому его домен будет пересечением доменов каждой функции.
Поскольку 𝑥 — многочлен, мы знаем, что его областью определения является множество действительных чисел.
Область определения функции тангенса представляет собой множество действительных чисел, кроме тех,
где cos(𝑥)=0. Это означает, что область определения функции tan6𝑥 равна
множество действительных чисел, за исключением тех, что делают cos6𝑥=0.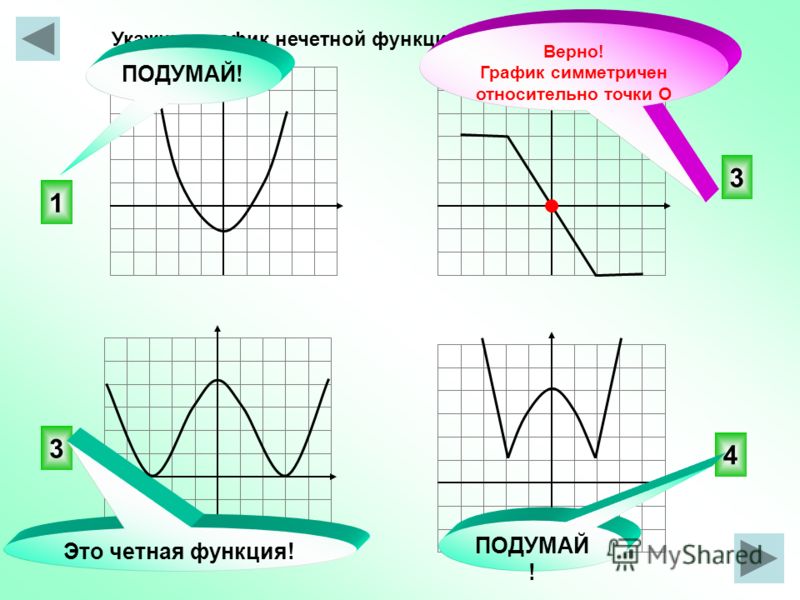 Значения 𝑥, которые
make cos6𝑥=0
𝑥=𝜋12,3𝜋12,−𝜋12,−3𝜋12 и так далее. Эти значения симметричны относительно оси 𝑦, что означает, что домен tan6𝑥 должен быть симметричным.
около 0,
Значения 𝑥, которые
make cos6𝑥=0
𝑥=𝜋12,3𝜋12,−𝜋12,−3𝜋12 и так далее. Эти значения симметричны относительно оси 𝑦, что означает, что домен tan6𝑥 должен быть симметричным.
около 0,
Таким образом, пересечение двух доменов также симметрично относительно 0, поэтому теперь мы можем проверить четность, оценив 𝑓(−𝑥): 𝑓(−𝑥)=(−𝑥)(−6𝑥).tan
И мы перепишем (−𝑥) как (−𝑥)=(−1×𝑥)=(−1)×𝑥=−𝑥.
Чтобы вычислить тангенс(−6𝑥), мы можем рассмотреть график функции tan6𝑥; это горизонтальный участок график 𝑦=(𝑥)tan с масштабным коэффициентом 16.
Мы видим, что tan6𝑥 нечетно, так как график нечетного функция имеет вращательная симметрия порядка 2 относительно начала координат.
Следовательно, тантан(−6𝑥)=−(6𝑥) и мы можем написать 𝑓(−𝑥) как 𝑓(−𝑥)=(−𝑥)×(−6𝑥)=−𝑥×6𝑥=−𝑥6𝑥=−𝑓(𝑥).тантантан
Теперь мы можем видеть, для каждого 𝑥 в домене из 𝑓,
𝑓(−𝑥)=−𝑓(𝑥).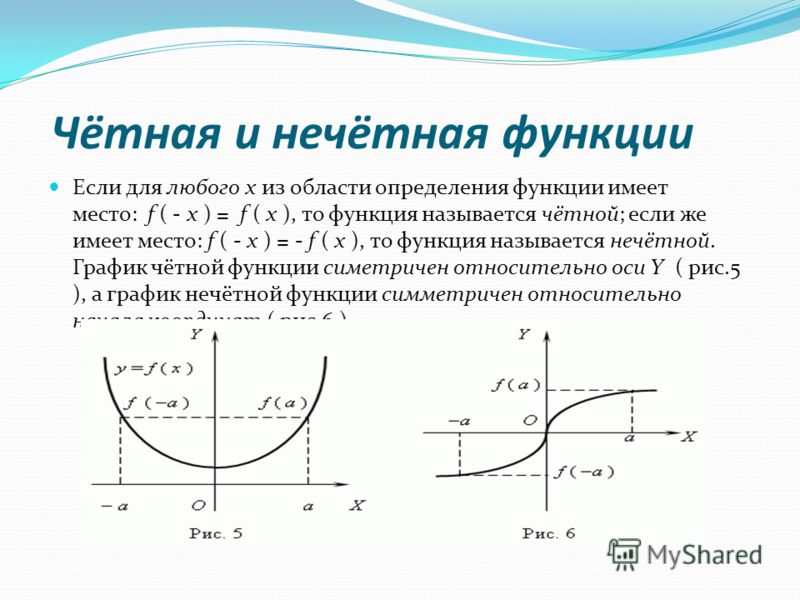
Следовательно, функция 𝑓(𝑥)=𝑥6𝑥tan нечетна.
В примере 5 мы умножили нечетную функцию 𝑥 на четную функцию tan(6𝑥), что привело к нечетной функции. Фактически, произведение четной и нечетной функций всегда будет нечетным. Мы можем обобщить этот результат наряду с некоторыми другими свойствами комбинирования функций.
Определение: Комбинация четных и нечетных функций
Пусть 𝑓 и 𝑓 — четные функции а 𝑔 и 𝑔 — нечетные функции:
- 𝑓±𝑓 четно, а 𝑔±𝑔 нечетно,
- 𝑓±𝑔 не четно и не нечетно, 𝑔⋅𝑔 и 𝑔𝑔 четные,
- 𝑓⋅𝑔 и 𝑓𝑔 нечетные.
Теперь мы узнаем, как применять эту концепцию для определения четности кусочно определенной функции.
Пример 6. Определение четности кусочно-определенной функции
Определить, является ли функция 𝑓 четной, нечетной или ни одной, учитывая, что 𝑓(𝑥)=−9𝑥−8𝑥0,9𝑥−8𝑥≥0.ifif
Ответ
Функция 𝑓(𝑥) является
- четной функцией, если нечетная функция, если 𝑓(−𝑥)=−𝑓(𝑥),
для каждого 𝑥 в области определения функции.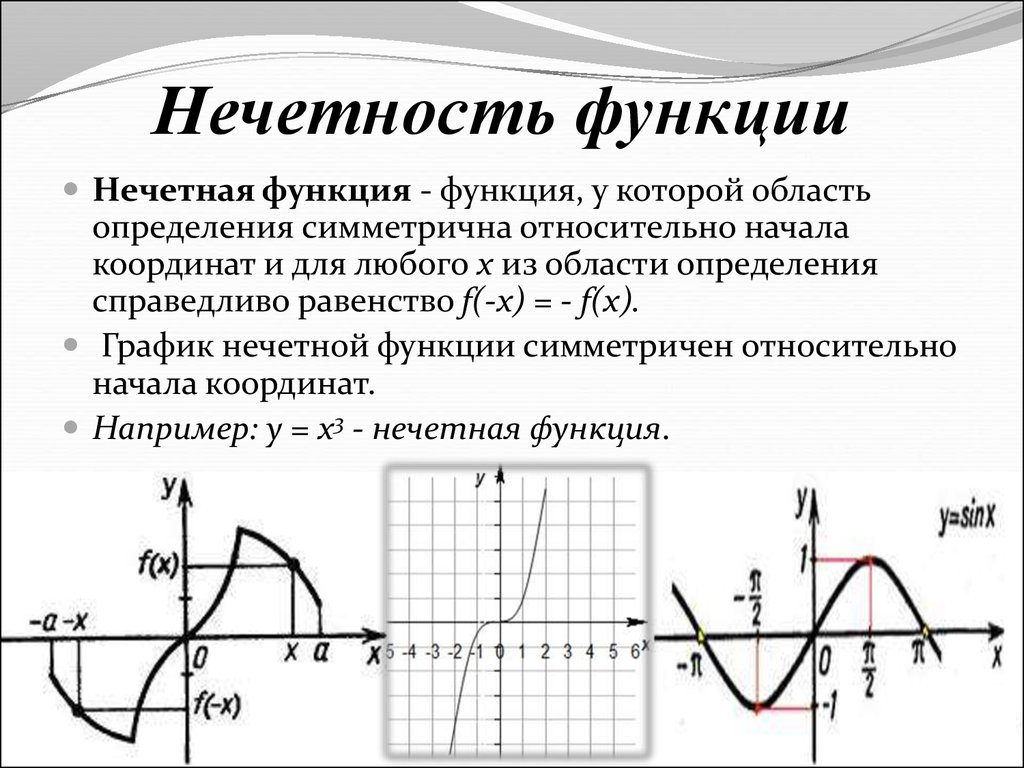
Нам нужно убедиться, что область определения функции симметрична относительно 0; в противном случае симметричные свойства четных и нечетных функций не будут применяться.
Область определения кусочно определенной функции есть объединение подобластей различных подфункции. В этом вопросе у нас есть подфункция, −9𝑥–8, определенный на интервале ]−∞,0[ и другое, 9𝑥–8, определенные на интервале [0,∞[. Обе подфункции линейны, поэтому они определены на всем своем протяжении. поддомен. Следовательно, объединение этих интервалов есть множество действительных чисел. Домен 𝑓(𝑥) можно записать как ℝ.
Это симметрично относительно 0, поэтому теперь мы можем проверить четность функции, оценив 𝑓(−𝑥). Нам нужно будет сделать это для отрицательных и положительных входных данных отдельно, чтобы определить отображает ли функция отражательную симметрию относительно оси 𝑦.
Для 𝑥0, −𝑥 будет положительным:
𝑓(−𝑥)=9×(−𝑥)−8=−9𝑥−8.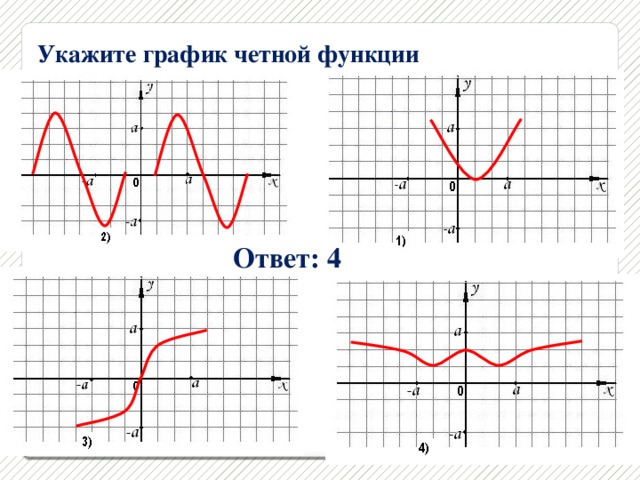
Это равно другой части кусочной функции, подфункции, используемой для отрицательных значений 𝑥.
Тогда для 𝑥>0 −𝑥 будет отрицательным: 𝑓(−𝑥)=−9×(−𝑥)−8=9𝑥−8.
Опять же, это равно другой части кусочной функции, подфункция, используемая для положительных значений 𝑥.
Мы можем подтвердить наши выводы и проверить, что происходит при 𝑥=0, рисуя эскиз графика.
График имеет отражательную симметрию относительно оси 𝑦.
Поскольку 𝑓(−𝑥)=−𝑓(𝑥) для всех 𝑥 в области 𝑓, функция четная.
Теперь мы исследуем, как на четность функции может влиять ее область определения.
Пример 7. Определение четности функций
Определите, является ли функция 𝑓(𝑥)=9𝑥 четный, нечетный или ни один из них 𝑓∶]−7,7]→ℝ.
Ответ
Функция 𝑓(𝑥) является
- четной функцией, если 𝑓(−𝑥)=𝑓(𝑥),
- нечетной функцией, если 𝑓(−𝑥)=−𝑓(𝑥), ,
для каждого 𝑥 в области определения функции.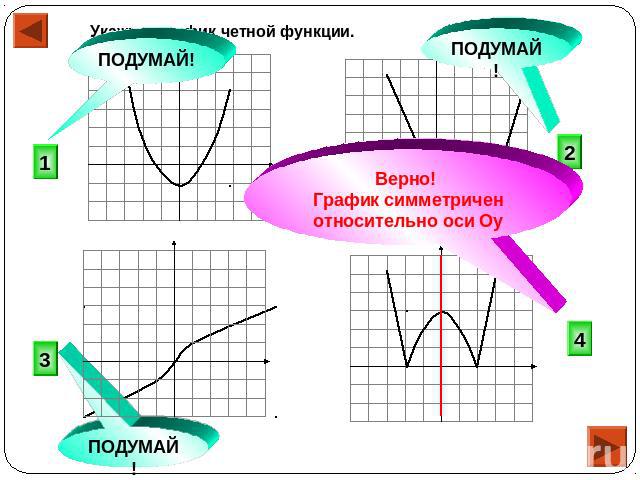
Нам нужно убедиться, что область определения функции симметрична относительно 0; в противном случае симметричные свойства четных и нечетных функций не будут применяться.
Нам дано, что 𝑓∶]−7,7]→ℝ. Мы можем прочитать это как «функция 𝑓 отображает числа слева, справа и слева». замкнутый интервал от −7 до 7 на множество действительных чисел». Областью определения является интервал ]−7,7], а областью определения является множество действительных чисел.
Может показаться, что этот домен симметричен относительно 0; однако нам говорят, что 𝑥 может быть равно 7, но не может быть равным −7. Это означает, что он не симметричен относительно 0,
Поскольку область определения 𝑓(𝑥) не симметрична относительно 0, функция не четная и не нечетная.
В нашем последнем примере мы покажем, как знание четности функции может помочь нам получить информацию о ее переменных.
Пример 8. Нахождение неизвестного в рациональной функции по заданной четности
Найдите значение 𝑎, если 𝑓 является четным
функция, где 𝑓(𝑥)=68𝑥+𝑎𝑥−3
и 𝑥≠0.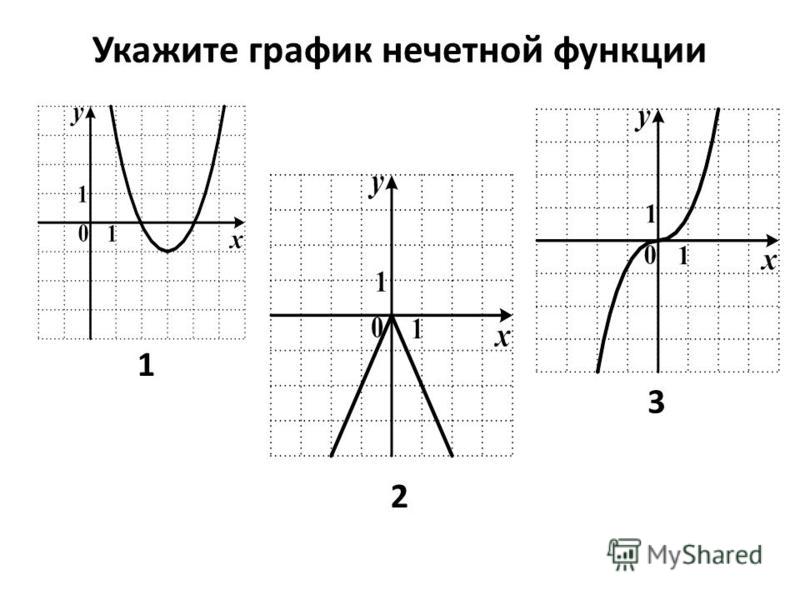
Ответ
Мы знаем, что если 𝑓 и 𝑓 четные функции, их частное 𝑓𝑓 тоже четный. Точно так же говорят, что функция 𝑓(𝑥) быть четным, если 𝑓(−𝑥)=𝑓(𝑥) для каждого 𝑥 в области определения функции.
Поскольку функция числителя не зависит от 𝑥, это даже. Это означает, что функция в знаменателе также должна быть четной. Пусть функция 𝑓(𝑥)=8𝑥+𝑎𝑥−3 так, что 𝑓(−𝑥)=8(−𝑥)+𝑎(−𝑥)−3=8𝑥−𝑎𝑥−3.
Чтобы функция была четной, 𝑓(−𝑥)=𝑓(𝑥) для каждого значения 𝑥 в домене 𝑓: 8𝑥−𝑎𝑥−3=8𝑥+𝑎𝑥−3.
Вычитая 8𝑥 и добавляя 3 к обеим частям, это уравнение упрощается до −𝑎𝑥=𝑎𝑥.
Поскольку 𝑥≠0, мы можем разделить на 𝑥: −𝑎=𝑎.
Это уравнение может быть истинным только в том случае, если 𝑎=0.
Чтобы 𝑓 была четной функцией, 𝑎=0.
Теперь мы повторим ключевые моменты этого объяснения. Функция
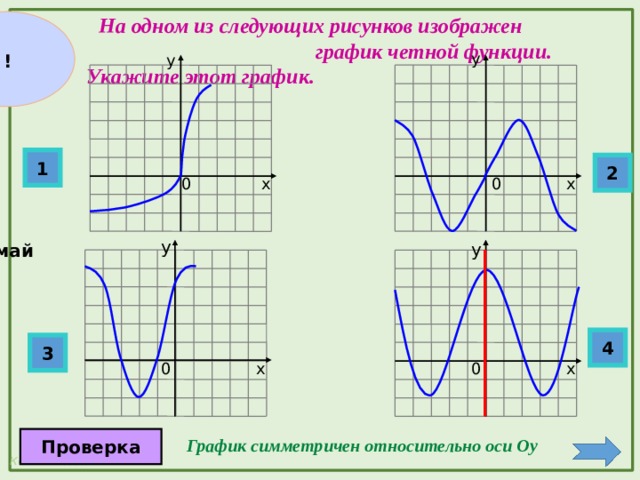 Точно так же функция, график которой имеет отражательную
симметрия относительно оси 𝑦 является четной функцией.
Точно так же функция, график которой имеет отражательную
симметрия относительно оси 𝑦 является четной функцией.Как вы должны различать четные и нечетные функции?
Защита и оценка. at NumbersОценка выражений
Purplemath
Как алгебраически определить, является ли функция четной, нечетной или ни одной?
Чтобы «алгебраически определить», является ли функция четной, нечетной или ни одной, вы берете функцию и подставляете − x вместо x , упрощаете и сравниваете результаты с тем, с чего вы начали.
Содержание продолжается ниже
MathHelp.
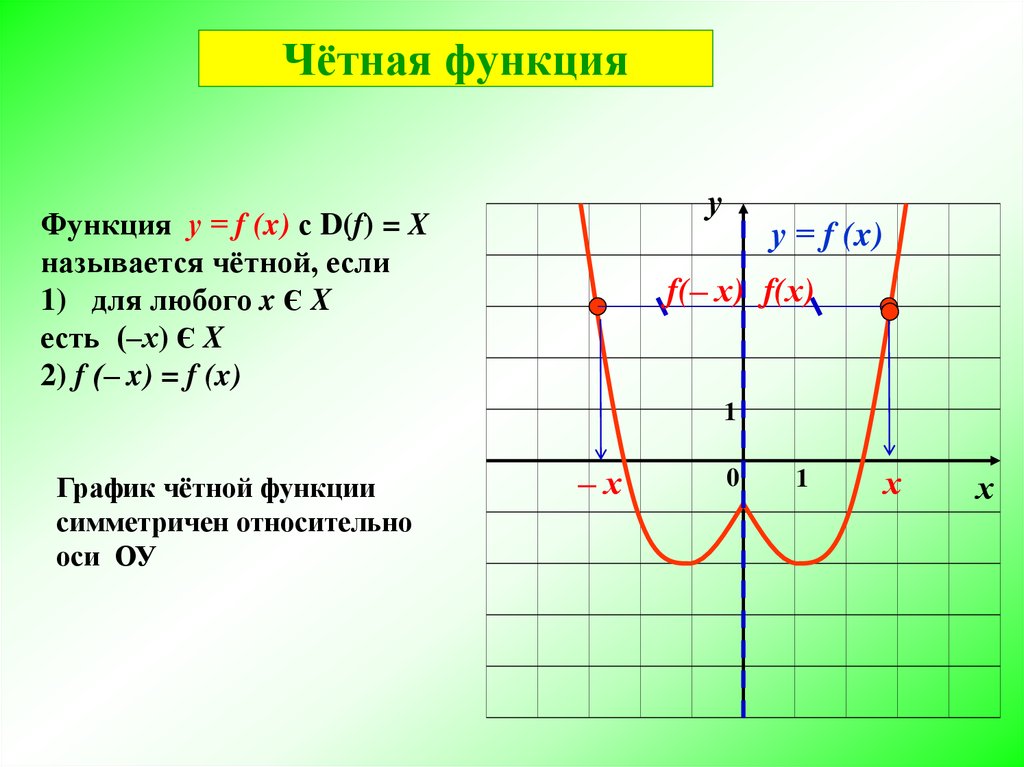 com
comЕсли вы получите точно такую же функцию, с которой начали (то есть, если f (− x ) = f ( x ), поэтому все знаки одинаковы), то функция четная; если вы получите полную противоположность тому, с чего начали (то есть, если f (− x ) = − f ( x ), поэтому все знаки меняются местами), то функция странно.
Если результат не является ни точно таким же, ни прямо противоположным (т. е. не имеет всех одинаковых членов, но с обратными знаками), то функция не является ни четной, ни нечетной.
Что является примером определения того, является ли функция четной, нечетной или ни той, ни другой?
Если я нарисую это, я увижу, что это «симметрично относительно оси и «; другими словами, все, что график делает на одной стороне оси y , отражается на другой стороне:
Это отражение относительно оси y является отличительной чертой четных функций.
Также отмечу, что показатели степени всех членов четные — показатель степени постоянного члена равен нулю: 4 x 0 = 4 × 1 = 4. Это полезные подсказки, которые убедительно говорят мне, что у меня здесь четная функция.
Но вопрос просит меня сделать определение алгебраически , а это значит, что мне нужно сделать алгебру.
Итак, я подставлю — x вместо x и упрощу:
f (- x ) = -3(- x )1 2 40094 ( x 2 ) + 4
= −3 x 2 + 4
Я вижу, сравнивая исходную функцию с моим окончательным результатом выше, что у меня есть совпадение, что означает, что:
Если я построю это на графике, то увижу, что он «симметричен относительно начала координат»; то есть, если я начну с точки на графике по одну сторону оси y и проведу линию из этой точки через начало координат и продолжаю ту же длину по другую сторону y -ось, я попаду в другую точку на графике.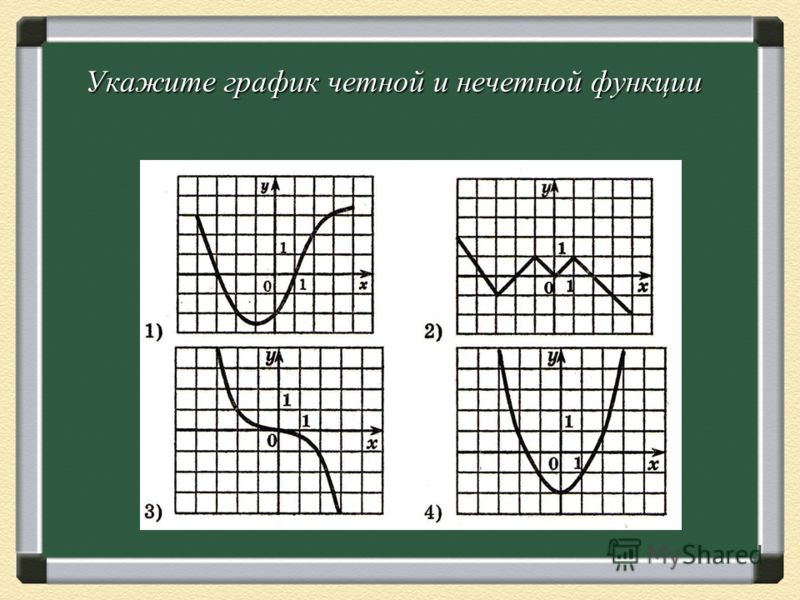
Вы также можете думать об этом как о половине графика на одной стороне оси y , которая является перевернутой версией половины графика на другой стороне оси y . Эта симметрия является отличительной чертой нечетных функций.
Также обратите внимание, что все показатели степени в правиле функции нечетные, так как второй член может быть записан как 4 x = 4 x 1 . Это полезная подсказка. Я должен ожидать, что эта функция будет странной.
Вопрос требует от меня определить алгебраически, поэтому я подставлю − x вместо x и упрощу:
f (− x ) = 2 (− x ) 3 — 4 ( — x ) = 2 ( — x 3 ) + 4 x = −2 x 3 + 4 x 3 + 4 x . чтобы быть нечетным, мне нужно, чтобы приведенный выше результат имел все противоположные знаки исходной функции. Оригинал: F ( x ) = 2 ( x ) 3 — 4 ( x ) : — F (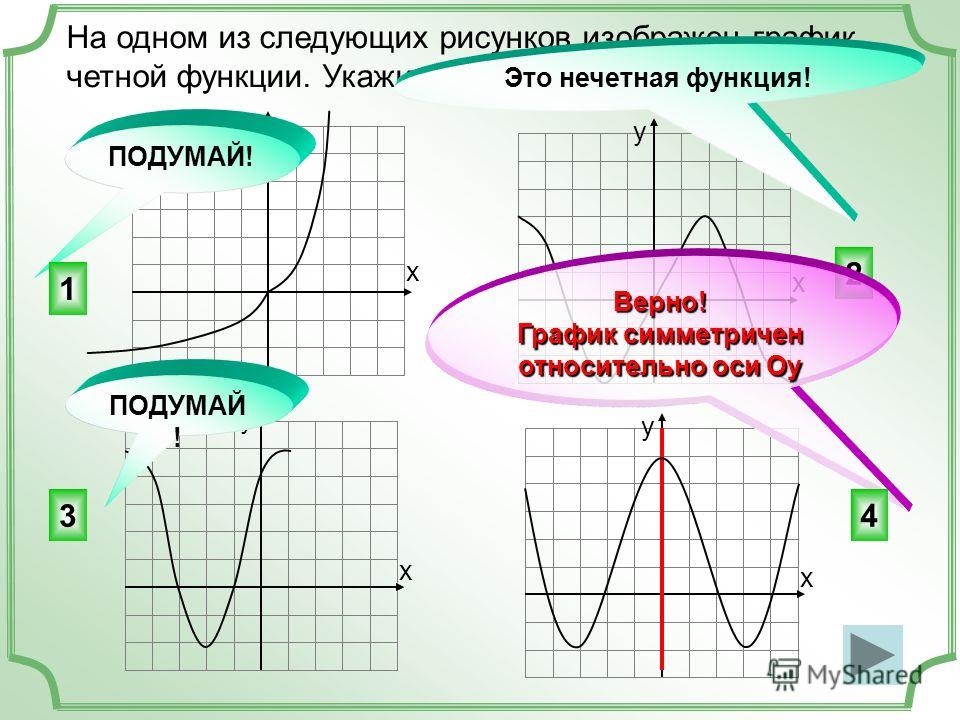 Так что напишу исходную функцию, а потом поменяю местами все знаки:
Так что напишу исходную функцию, а потом поменяю местами все знаки:
Сравнивая это с тем, что я получил, я вижу, что они совпадают. Когда я подключил — x вместо x , все знаки поменялись местами. Это означает, что, как я и ожидал,
f ( x ) нечетно.
Эта функция является суммой двух предыдущих функций. Но, хотя сумма нечетного и четного числа есть нечетное число, я не могу заключить то же самое о сумме нечетной и четной функции.
Обратите внимание, что график этой функции не имеет симметрии ни с одной из предыдущих:
…и все ее показатели не четные или нечетные.
Основываясь на показателях, а также на графике, я бы ожидал, что эта функция будет ни , ни четные и нечетные.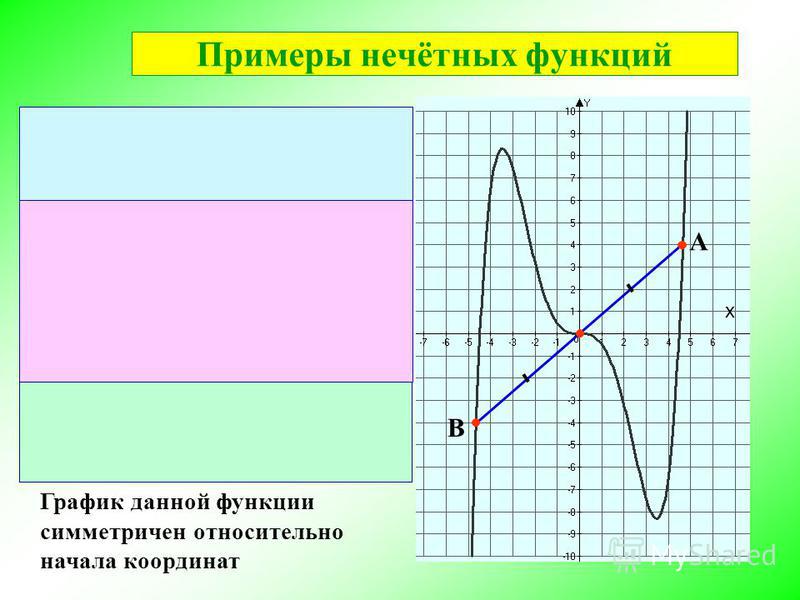 Однако, чтобы быть уверенным (и чтобы получить полное признание за мой ответ), мне нужно заняться алгеброй.
Однако, чтобы быть уверенным (и чтобы получить полное признание за мой ответ), мне нужно заняться алгеброй.
Я подключаю — x в для x и упрощает:
F ( — x ) = 2 ( — x ) 3 — 3 ( x ) 3 — 3 ( x ) 3 — 3 ( x ) 3 — 3 ( x ) 3 — 3 ( x ) 3 — 3 ( x ) 2 — 4 ( — x ) + 4
= 2 ( — x 3 ) — 3 ( x 2 ) + 4 x + 4 9003
= 2 1 x + 4 9003
= 2 1 x + 4 9003
= 2 1 x + 4 9003
= 1 x + 4 9003
= ). 3 − 3 x 2 + 4 x + 4
При быстром сравнении я вижу, что это не соответствует тому, с чего я начал, поэтому эта функция неравномерна. А как насчет странного?
Для проверки я запишу прямо противоположное тому, с чего начал, т.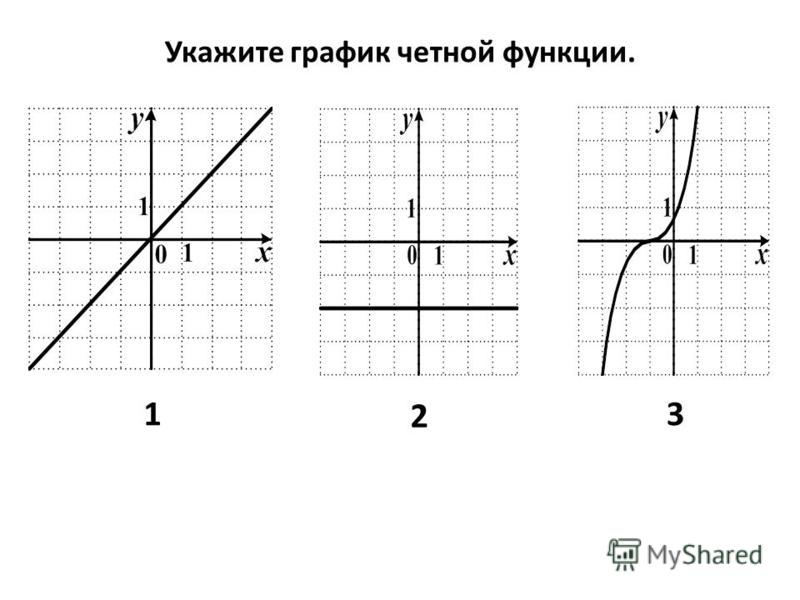 е. исходную функцию, но со всеми измененными знаками: x 3 + 3 x 2 + 4 x − 4
е. исходную функцию, но со всеми измененными знаками: x 3 + 3 x 2 + 4 x − 4
Это тоже не соответствует тому, что я придумал. Так что исходная функция тоже не является странной. Затем, как я и ожидал:
f ( x ) не является ни четным, ни нечетным.
Как видите, сумма или разность четной и нечетной функций , а не нечетная функция. На самом деле вы обнаружите, что сумма или разность двух четных функций — это еще одна четная функция, а сумма или разность двух нечетных функций — еще одна нечетная функция.
Есть ли функция, которая одновременно является четной *и* нечетной?
Существует (ровно) одна функция, которая одновременно является четной и нечетной; это нулевая функция, f ( x ) = 0.
Другими словами, «четные» и «нечетные» в контексте функций означают нечто отличное от того, как эти термины используются с целыми числами.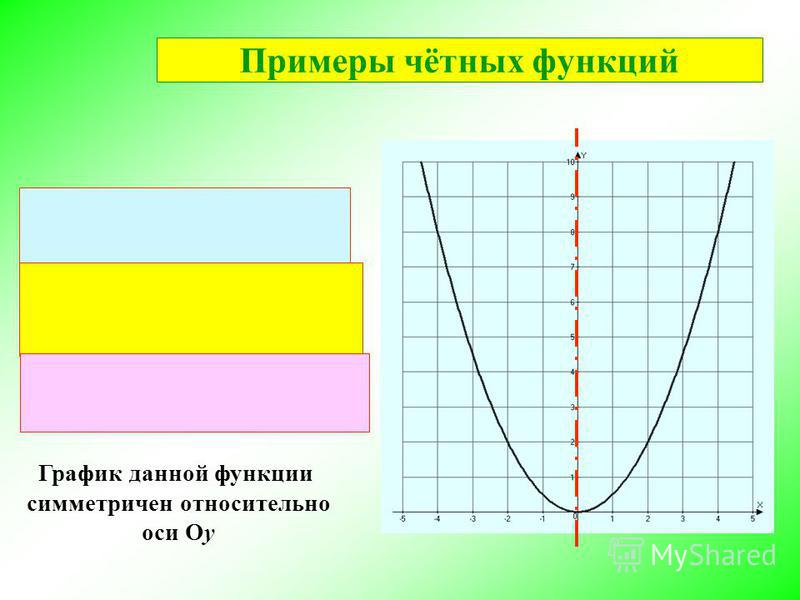 . Не пытайтесь смешивать два набора определений; это только смутит вас.
. Не пытайтесь смешивать два набора определений; это только смутит вас.
Только потому, что все примеры до сих пор включали полиномиальные функции, не думайте, что концепция четных и нечетных функций ограничивается полиномами. Это не. Тригонометрия полна функций, которые являются четными или нечетными, и другие типы функций также могут рассматриваться.
Определите, является ли
г ( x ) = 3/( x 2 + 2) четным, нечетным или ни тем, ни другим.
Это рациональная функция. Процесс проверки четности, нечетности или отсутствия такой же, как всегда. Я начну с подстановки − x вместо x :
g (− x ) = 3/[(− x ) 2 + 2]
= 3/[( x 2 ) + 2]
= 3/( x 2 + 2)
I Conta что это то же самое, с чего я начал.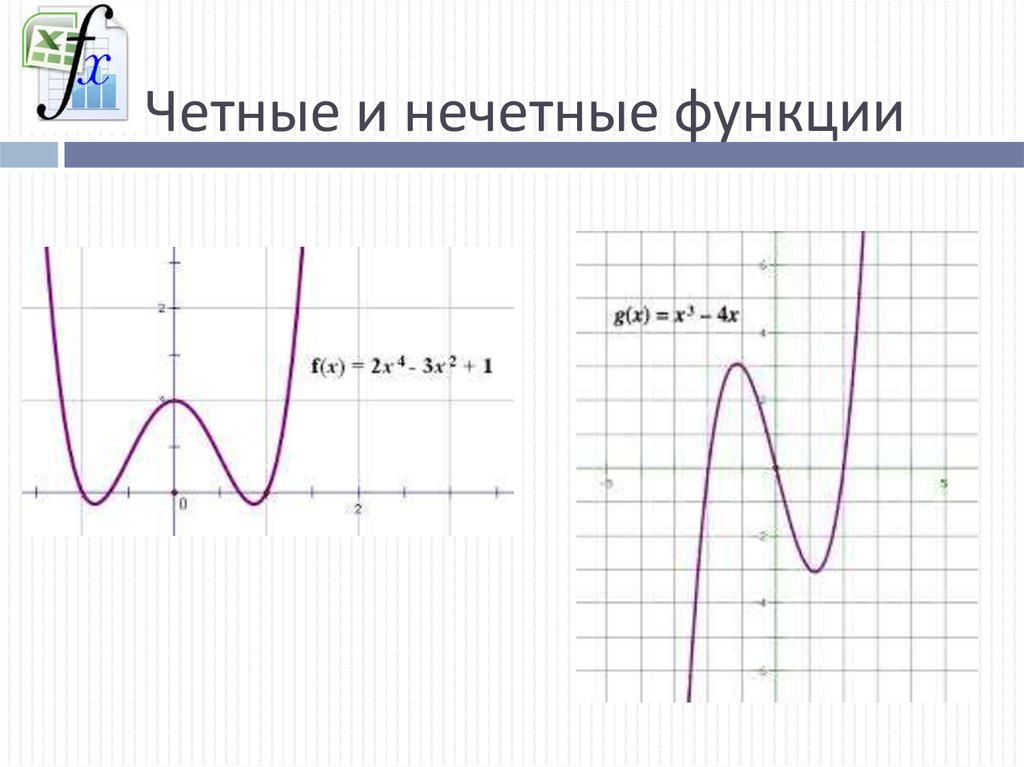 Итак:
Итак:
g ( x ) равно четному
При ответе на этот вопрос типа «четный или нечетный» вам может оказаться полезным записать − f ( x ) явно, и затем сравните это с тем, что вы получаете за f (− x ). Это может помочь вам уверенно определить правильный ответ.
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в определении того, является ли функция четной, нечетной или ни одной из них. Попробуйте введенное упражнение или введите свое собственное упражнение. Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway.
Пожалуйста, примите куки-файлы настроек, чтобы включить этот виджет.
(Нажав «Нажмите, чтобы просмотреть шаги» на экране ответов виджета, вы перейдете на сайт Mathway для платного обновления.)
URL: https://www.purplemath.com/modules/fcnnot3.htm
Страница 1 Страница 2 случаи, когда функции описываются как четные или нечетные.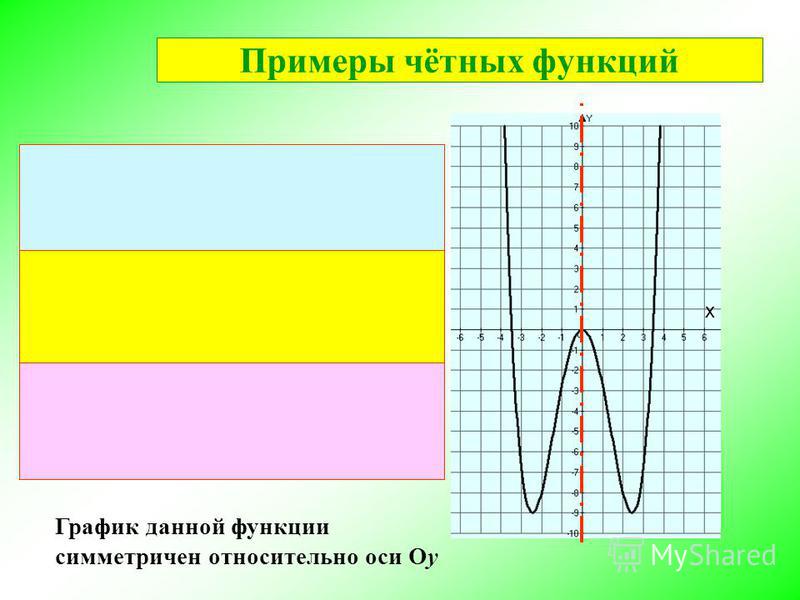 Если вам интересно узнать о четных и нечетных функциях , вы только что нашли нужную статью. Начнем с их определения:
Если вам интересно узнать о четных и нечетных функциях , вы только что нашли нужную статью. Начнем с их определения:
Четные и нечетные функции — это специальные функции, обладающие особой симметрией относительно оси Y и начала координат соответственно.
Зачем нам знать, является ли функция четной или нечетной? Знание этого важного свойства функции может помочь нам:
- Знать поведение графика функции.
- Сэкономьте время на построении графиков функций и вместо этого применяйте свойства нечетных и четных функций.
- Предсказать природу произведения и суммы двух функций.
Видя, что это может помочь нам работать над следующими темами намного быстрее, мы должны убедиться, что охватываем все аспекты нечетных и четных функций. Начнем с последнего!
Что такое четная функция?
В этом разделе будет подробно изучена даже функция, включая ее определение, свойства и график. Ниже приведены некоторые функции, широко известные как четные функции:
- Функции абсолютного значения
- Функции косинуса
- Большинство функций с четной степенью
Мы сможем понять, почему приведенные выше функции являются четными функциями после следующие два раздела.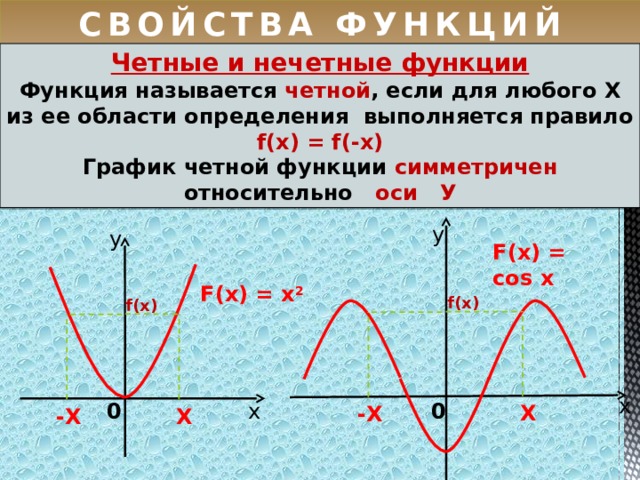 Итак, как мы узнаем, является ли данная функция четной?
Итак, как мы узнаем, является ли данная функция четной?
Определение функции четности
Функции четности — это функции, которые возвращают одно и то же выражение как для x , так и для -x . Это означает, что если f(x) является четной функцией, когда f(-x) = f(x) . Таблица значений четной функции также будет иметь симметричные значения. Квадратичная функция f(x) = x 2 , является четной функцией. Обратите внимание, как это соответствует определению четных функций:
f(-x) = (-x) 2
= x 2
Мы можем видеть, что [x, f(x)] → [-x, f(x)], показывая, как f(x) удовлетворяет определению четной функции. Теперь взгляните на его таблицу значений.
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| f(x) | 9 | 4 | 1 | 0 | 1 | 4 | 9 |
Как видно, x и его отрицательное значение будут иметь одинаковые значения, что делает каждую половину таблицы идентичной.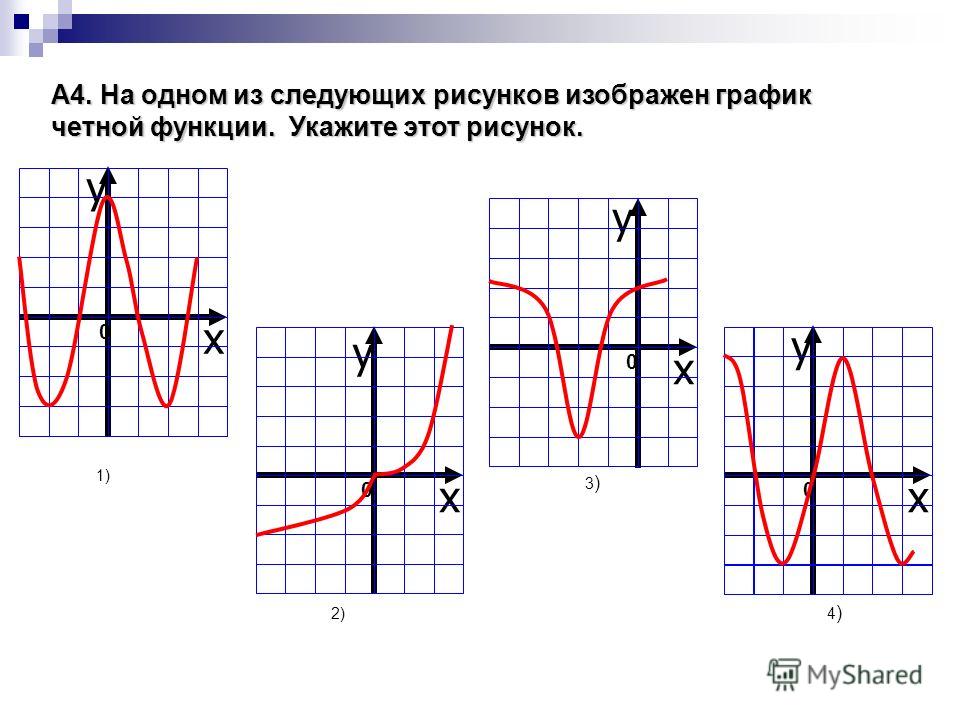
График четной функции и понимание ее симметрии
Поскольку у нас уже есть таблица значений для f(x) = x 2 , , почему бы нам не использовать их для построения графика функции?
На приведенном выше графике показано, что квадратичная функция также симметрична относительно оси Y. Что это значит для нашего движения вперед?
Вы можете построить график половины любых четных функций, а затем отразить его по оси Y. Это экономит нам много времени, поскольку нам нужны только упорядоченные пары для построения графика левой или правой части четной функции.
Почему бы нам не попробовать, построив половину функции абсолютного значения, f(x) = |x| , первый?
| x | 0 | 1 | 2 | 3 | 4 |
| F (x) | 0 | 1 | 4 | 9 | 16 |
После того, как мы построили правую часть f(x) = |x| , давайте отразим его относительно оси, чтобы показать завершенный график функции.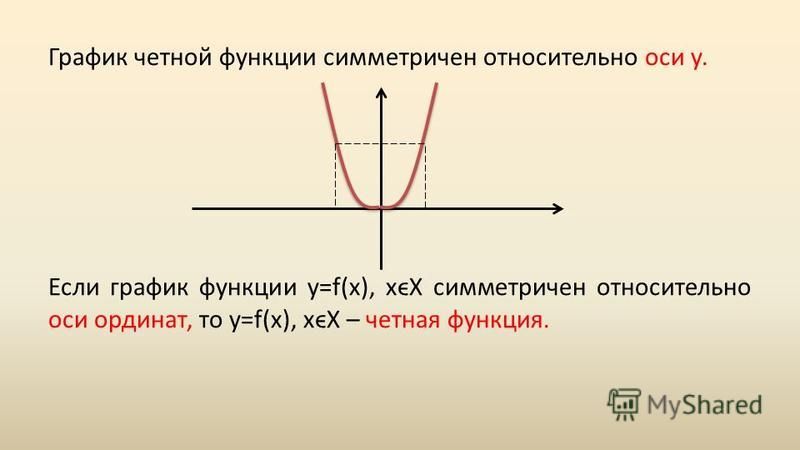
Этот метод построения графиков сэкономит ваше время, особенно при работе с более сложными выражениями. Не забудьте, однако, перепроверить и убедиться, что функция даже.
Что такое нечетная функция?
Теперь, когда мы узнали о четных функциях, пришло время освежить наши знания о нечетных функциях. Вот некоторые из хорошо известных нечетных функций, с которыми вы, возможно, уже сталкивались:
- Обратные функции
- Синусоидальные и тангенциальные функции
- Большинство функций с нечетной степенью
После следующих двух разделов мы поймем, почему упомянутые выше функции являются нечетными. Итак, что делает нечетные функции особенными?
Определение нечетной функции
Нечетные функции — это функции, которые возвращают свою отрицательную инверсию при замене x на –x . Это означает, что f(x) — это число 9.0049 нечетная функция, когда f(-x) = -f(x) .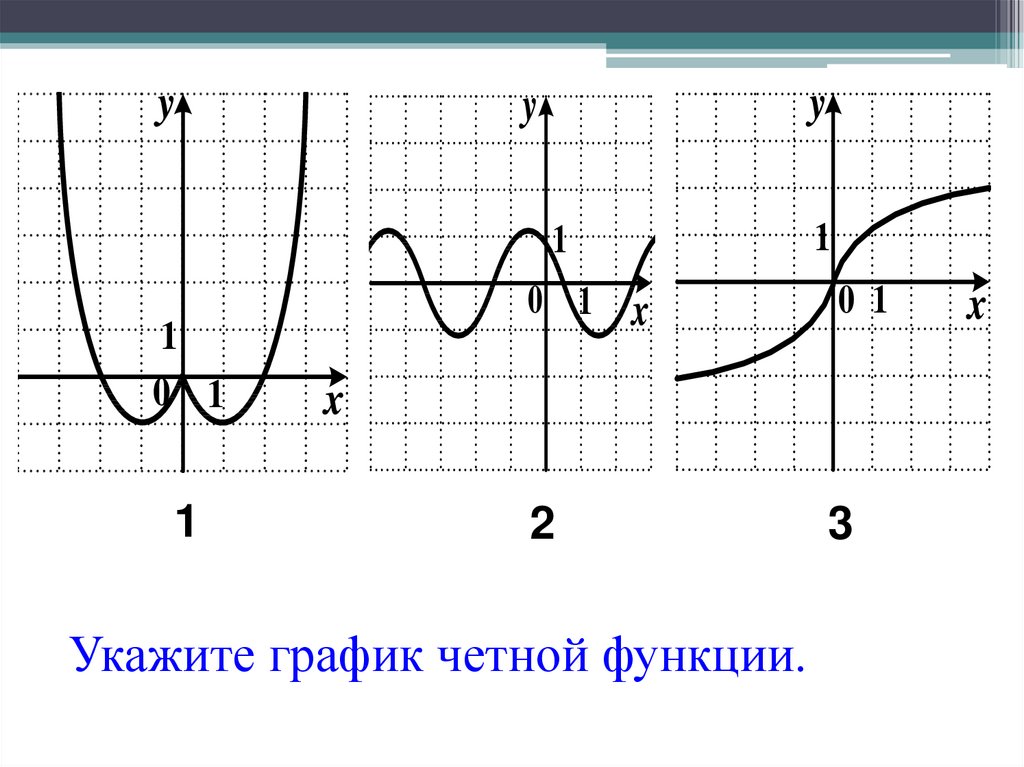 Давайте попробуем наблюдать f(x) = x 3 , нечетную функцию и посмотрим, как это повлияет на ее таблицу значений.
Давайте попробуем наблюдать f(x) = x 3 , нечетную функцию и посмотрим, как это повлияет на ее таблицу значений.
f(-x) = (-x) 3
= – x 3
Это подтверждает, что [x, f(x)] → [-x, -f ]. Таблица значений для f(x) = x 3 показана ниже. Заметили некоторые закономерности?
| х | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| f(x) | -27 | -8 | -1 | 0 | 1 | 8 | 27 |
Видите, как f(1) = -f(1)? Эта закономерность согласуется с остальными значениями. В левой части таблицы показаны отрицательные значения его аналога с правой стороны.
График нечетной функции и понимание его симметрии
Мы также можем наблюдать, как нечетные функции ведут себя на xy -координата по графику f(x) = x 3 .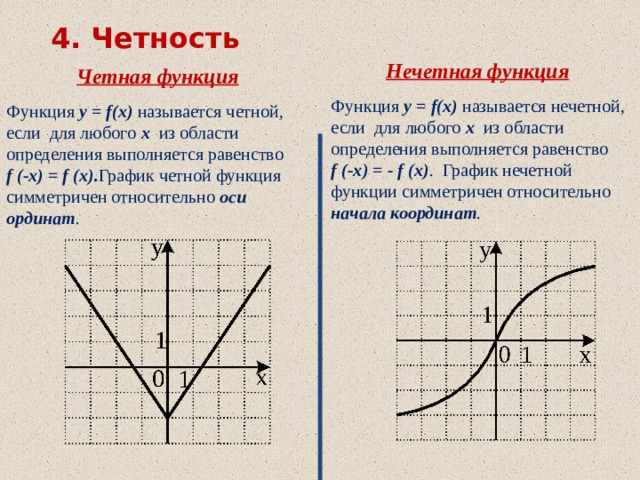 Используйте таблицу значений, показанную в предыдущем разделе, для построения точек, которые соединят кривую f(x) = x 3 .
Используйте таблицу значений, показанную в предыдущем разделе, для построения точек, которые соединят кривую f(x) = x 3 .
Этот график ясно показывает нам, насколько нечетные функции симметричны относительно начала координат. Мы также можем использовать это свойство, чтобы сократить время, необходимое для построения графика нечетных функций. Хотите увидеть пример? Давайте попробуем изобразить f(x) = 1/x .
| x | 1/4 | 1/2 | 1 | 2 | 4 | |
| F (x) | 4 | 2 | 1 | 1/2 | 9009 1/41 | 1/2 | 9009 1/4
После построения верхней части обратной функции мы можем отразить ее в начале координат, чтобы завершить график. Посмотрите на пунктирную линию как на руководство того, как мы отражаем графики о происхождении.
При большей практике и примерах вы определенно сможете легко строить графики четных и нечетных функций.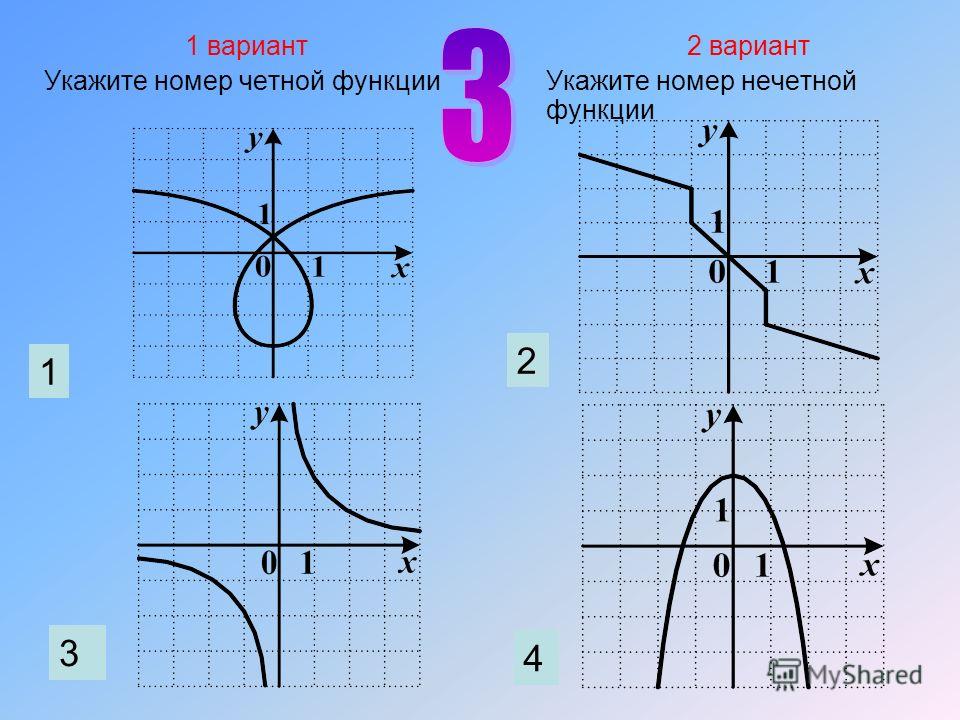 Давайте всегда не забывать проверять, является ли график нечетным или четным, прежде чем применять соответствующую технику.
Давайте всегда не забывать проверять, является ли график нечетным или четным, прежде чем применять соответствующую технику.
Какими свойствами обладают четные и нечетные функции?
Теперь, когда мы узнали о нечетных и четных функциях, какие еще свойства мы можем наблюдать у этих типов функций?
- Сумма, разность, частное или произведение двух четных функций будут четными. То же самое касается нечетных функций.
- Пример: f(x) = sin x и g(x) = tan x нечетны, поэтому h(x) = sin x + tan x также будет нечетным.
- Состав двух четных функций будет четным. То же правило применимо и к нечетным функциям.
- Пример: f(x) = x 2 и g(x) = cos x четны, поэтому f(g(x)) = (cos x)2 также будет нечетным.
Что, если нам дана функция, и мы не знаем, четная она или нечетная? Это не будет проблемой! Давайте воспользуемся тем, что мы уже узнали, чтобы определить, является ли функция четной или нечетной.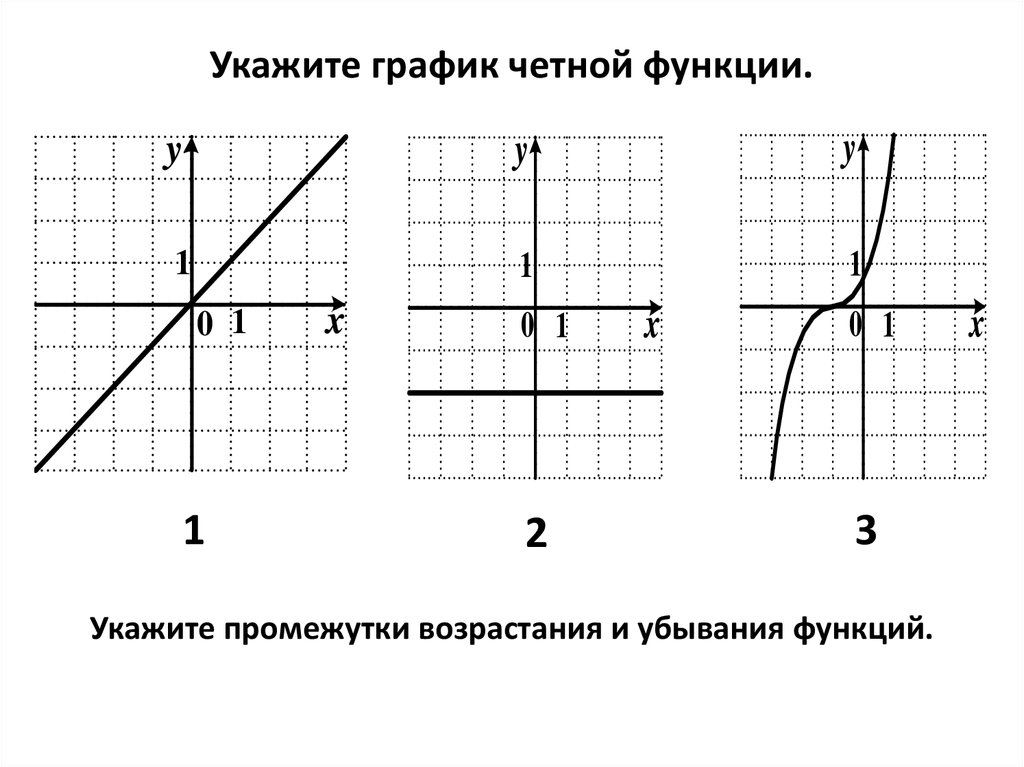
При задании функции : посмотрите, что произойдет, если мы заменим х с – х .
- Когда вы подставили –x в f(x), функция осталась прежней? Если да, то f(x) четно.
- Когда вы подставили –x в f(x), изменился ли знак коэффициента функции? Если да, то f(x) нечетно.
При наличии графика : определить, является ли график симметричным относительно начала координат или оси Y.
- Если график симметричен относительно оси y , функция равна даже . как нам это сделать?
- Представьте, что сложите график по вертикали и посмотрите, будут ли два графика лежать рядом друг с другом.
- Вы также можете указать несколько точек и посмотреть, имеют ли x и –x одну и ту же координату.
- Если график симметричен относительно начала координат , функция нечетная .
 как нам это сделать?
как нам это сделать?- Представьте, что сложите график по диагонали (проверьте оба направления) и посмотрите, будут ли два графика лежать рядом друг с другом.
- Вы также можете найти несколько точек и посмотреть, разделяют ли x и –x y-
Существуют ли функции, которые не являются ни нечетными, ни четными?
Должны ли все функции быть четными или нечетными? Нет. Бывают случаи, когда функция не соответствует ни четным, ни нечетным функциям. Функция f(x) = (x + 1) 2 является примером функции, которая не является ни нечетной, ни четной.
Давайте продолжим и посмотрим на выражение для f(-x) :
f(x) = (x + 1) 2
f(-x) = (-x + 1) 2
= (1 – x) 2
= 1 – 2x + x 2
Сравните это выражение с расширенной формой f(x) и –f(x).
| Проверка нечетной функции: f(-x) = -f(x) | Проверка четной функции: f(-x) = f(x) |
-f(x) = — (х + 1) 2 =-(х 2 + 2х + 1) =-x 2 – 2x – 1 f(-x) ≠ -f(x) | f(x) = (x + 1) 2 =x 2 + 2 + 1 f(-x) ≠ f(x) |
Это показывает, что такая функция, как f(x) = (x + 1) 2 , не может быть ни нечетной, ни четной.
Если вы посмотрите на график f(x) , вы увидите, что он не симметричен относительно начала координат или оси Y. Это еще раз подтверждает, что функция не является ни нечетной, ни четной.
Вот так мы рассмотрели все основные темы по четным и нечетным функциям. Со всеми свойствами, правилами и определениями, которые мы только что изучили, мы теперь готовы работать над дополнительными примерами, чтобы понять еще больше и странные функции.
Пример 1
Заполните пропуск либо нечетным , либо четным , чтобы сделать следующие утверждения верными.
- Функции f(x) и g(x) являются четными функциями, поэтому их сумма также будет _________ функцией.
- Композиция f(x) и g(x) возвращает нечетную функцию, поэтому и f(x), и g(x) являются _________ функциями.
- Абсолютное значение нечетной функции является _____________ функцией.
Решение
- Сумма двух четных функций также будет четным .

- Композиция двух нечетных функций также будет нечетной .
- Предположим, что f(x) нечетно, поэтому f(-x) равно -f(x). Взятие абсолютного значения этой функции возвращает f(x) обратно. Это означает, что функция даже .
Пример 2
Определить, F (x) , G (x) и ч (x) — даже или нечетные функции, использующие таблицы. значения, показанные ниже.
а.
| x | -4 | -2 | 0 | 2 | 4 | ||
| F (x) | 17 | 5 | 1 | 17 | 5 | 1 | 0009 517 |
б.
| x | -3 | -1 | 0 | 1 | 3 |
| f(x) | 18 | 4 | 1 | 4 | 18 |
в.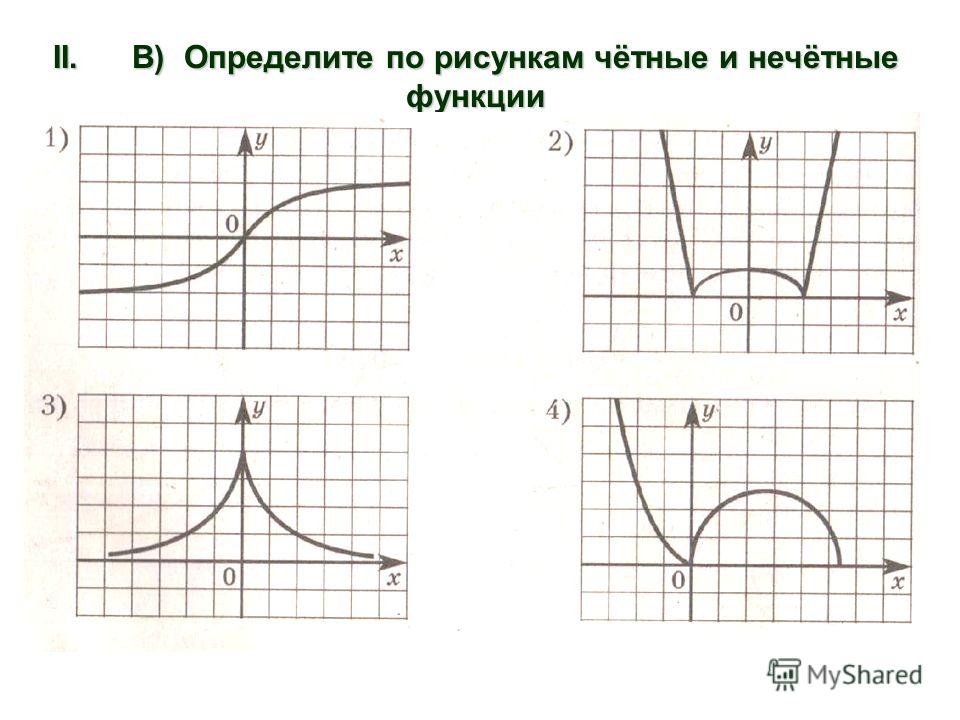
| x | -4 | -2 | -1/2 | 0 | 1/2 | 2 | 4 |
| H (x) | |||||||
| H (x) | 4|||||||
| H (x) | 0009 -64-8 | -1/8 | 0 | 1/8 | 8 | 64 |
Решение
ОБСЛУЖИВАЕТСЯ. Равны ли соответствующие значения? Являются ли значения слева отрицательными значениями справа?
- Мы видим, что таблица значений для f(x) показывает одинаковые значения для f(-x) и f(x), функция четная.
- То же самое можно сказать и о значениях, показанных для g(x), так что функция четная.
- В левой части таблицы отрицательные значения той, что сбоку, поэтому функция нечетная.
Пример 3
Определите, являются ли следующие функции четными, нечетными или ни теми, ни другими.
- f(x) = x 2 – 1
- g(x) = |x -1|
- h(x) = -3x 5
Решение
Замените x на -x и проверьте выражение функции. Если f(-x) возвращает ту же функцию, мы можем сделать вывод, что функция четная. Если он возвращает ту же функцию, но с коэффициентами, имеющими разные знаки, он нечетный.
Если f(-x) возвращает ту же функцию, мы можем сделать вывод, что функция четная. Если он возвращает ту же функцию, но с коэффициентами, имеющими разные знаки, он нечетный.
- Проверим первую функцию, f(x) = x 2 – 1.
f(-x) = (-x) 2 – 1
= 2
1
Так как f(-x) возвращает то же самое выражение для f(x), , функция четна .
Используя тот же процесс для b и c, мы получаем следующие результаты.
2.
g(-x) = |x – 1|
= |-х – 1|
= |-(х + 1)|
=|х + 1|
Поскольку g(-x) не равно ни g(x), ни -g(x), g(x) равно ни нечетному, ни четному .
3.
H (-x) = -3 (-x) 5
= -3 (-x 5 )
= 3x 5
=-(3x 5 )
Мы видим, что h(-x) = -h(x), поэтому h(x) является нечетной функцией .
Пример 4
Определите, являются ли следующие функции четными, нечетными или ни тем, ни другим, изучив графики следующих функций.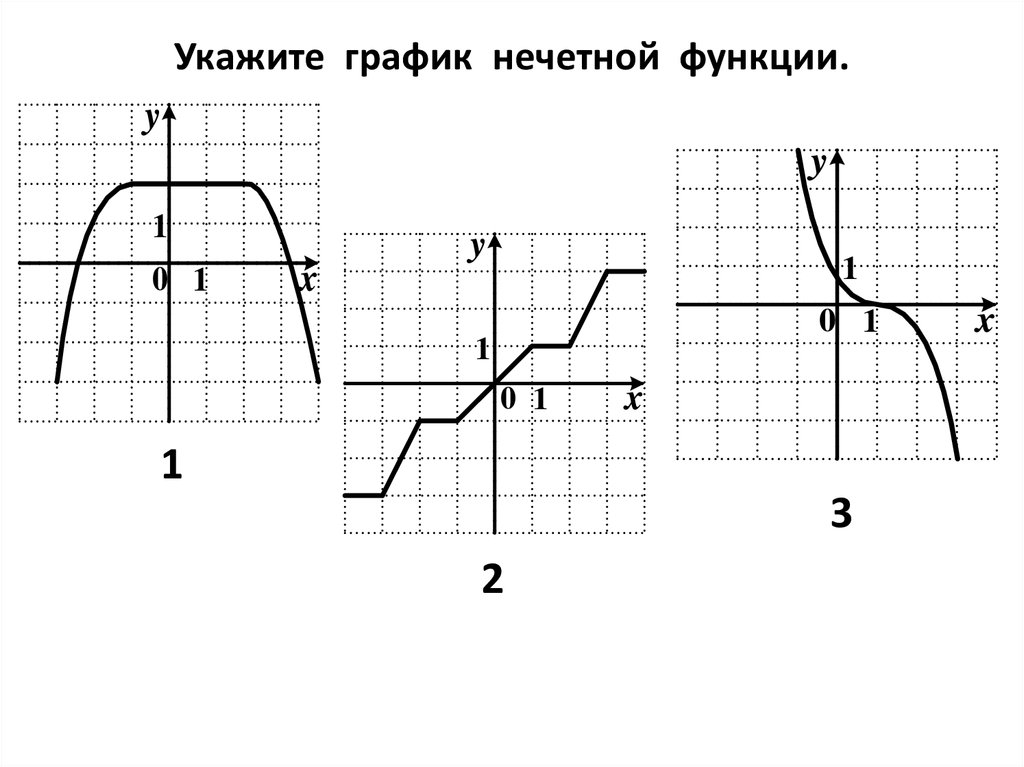
а.
б.
в.
Решение
Имея график, мы можем идентифицировать нечетные и четные функции на основе симметрии графика.
- Первый график показывает, что он симметричен относительно оси Y , поэтому это четная функция .
- Второй график показывает, что он симметричен относительно начала координат , поэтому это нечетная функция .
- Поскольку третий граф равен не симметричен относительно начала координат или оси Y , это ни нечетное, ни четное .
Пример 5
Заполните приведенную ниже таблицу, используя свойства функций.
- Функция f(x) нечетная.
| x | -1 | -1/2 | -1/4 | 1/2 | 1/4 | 1 |
| f(x) | -2 | -4 | -8 |
2.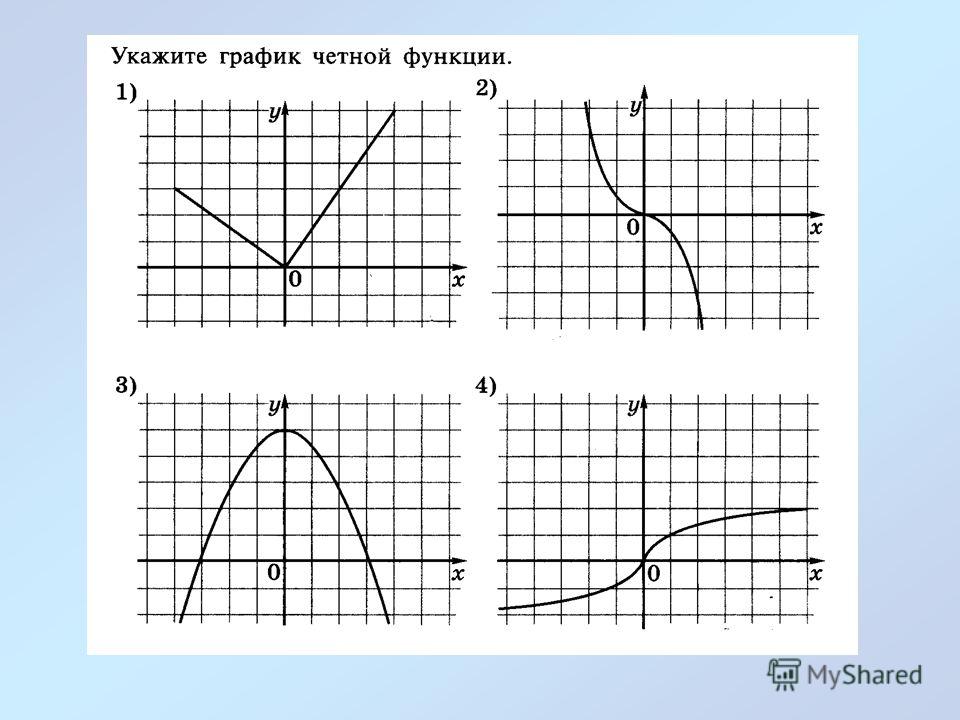 Функция f(x) четна.
Функция f(x) четна.
| x | -3 | -1 | 0 | 1 | 3 |
| f(x) | -6 | -5 | -3 |
Решение
- Поскольку функция нечетная, мы заполняем незаполненные значения отрицательными обратными значениями -2, -4 и -8. Следовательно, у нас есть 2, 4 и 8.
- Поскольку функция четная, мы заполняем незаполненные значения, которые будут такими же, как f(1) и f(3). Следовательно, у нас есть 3 и 1.
Пример 6
Используйте приведенную ниже таблицу значений и тот факт, что f(x) четно графику f(x).
| x | -3 | -2 | -1 | 0 |
| F (x) | 0 | 9000 -2-4 | -6 | -4 | -6 | 9000-4 | -6 | -4 | -6 | -4 | -6 | -4 | -6 | -4 | -2 | .
Решение
Сначала нанесем точки. Соедините их, чтобы построить график части f(x).
Помните, что f(x) — четная функция. Его график будет симметричен относительно оси Y. Это означает, что для завершения графика f(x) мы отражаем график относительно оси y.
График выше показывает полный график f(x). Вы также можете убедиться в этом, визуализировав оставшуюся половину графика функции, «свернув» график по оси Y.
Это показывает, что понимание свойств нечетных и четных функций может сэкономить нам время при решении задач и построении графиков функций.
Симметрия графов. Темы предварительного исчисления
Темы в
ПРЕДВАРИТЕЛЬНАЯ РАБОТА
Содержание | Дом
16
Тест на симметрию: четные и нечетные функции
ПУСТЬ ЭТО БУДЕТ ПРАВАЯ СТОРОНА графика функции:
Теперь нарисуем левую сторону — так, чтобы график был симметричен относительно оси y :
В данном случае
f (− x ) = f ( x ).
Высота кривой при −90 527 x 90 528 равна 90 527, равной 90 528 высоте кривой при 90 527 x 90 528 — для каждых 90 527 x 90 528 в области ф .
Опять же, пусть это будет правая часть:
Теперь нарисуем левую сторону — так, чтобы график был симметричен относительно начала координат:
Каждая точка справа отражается через начало координат. В данном случае
f (− x ) = − f ( x ).
Значение f at − x — это минус значения at x .
(Отражение через начало координат эквивалентно отражению вокруг оси y , за которым следует отражение вокруг оси x .)
Тест на симметрию: четные и нечетные функции
Таким образом, симметриязависит от поведения f ( x ) по другую сторону оси y — на минус x : 90 527 f 90 528 (− 90 527 x 90 528).
Вот тест:
Если f (− x ) = f ( x ),
, то график f ( x ) симметричен относительно оси y .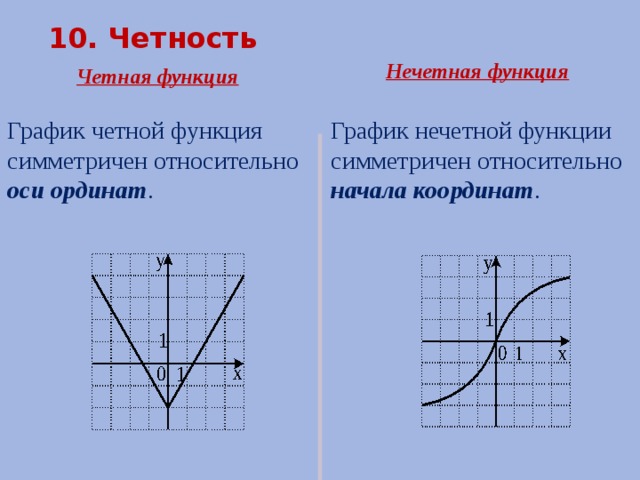
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы перекрыть ответ, нажмите «Обновить» («Reload»).
Если f (- х ) = — f ( х ),
, то график f ( x ) симметричен относительно начала координат.
Функция, симметричная относительно оси y , называется четной функцией.
Функция, симметричная относительно начала координат, называется нечетной функцией.
Пример 1. Проверить эту функцию на симметрию:
f ( x ) = x 4 + x 2 + 3
Решение . Мы должны посмотреть на f (− x ):
| f (− x ) | = | (- x ) 4 + (- x ) 2 + 3 |
| = | x 4 + x 2 + 3 | |
| = | f ( x ).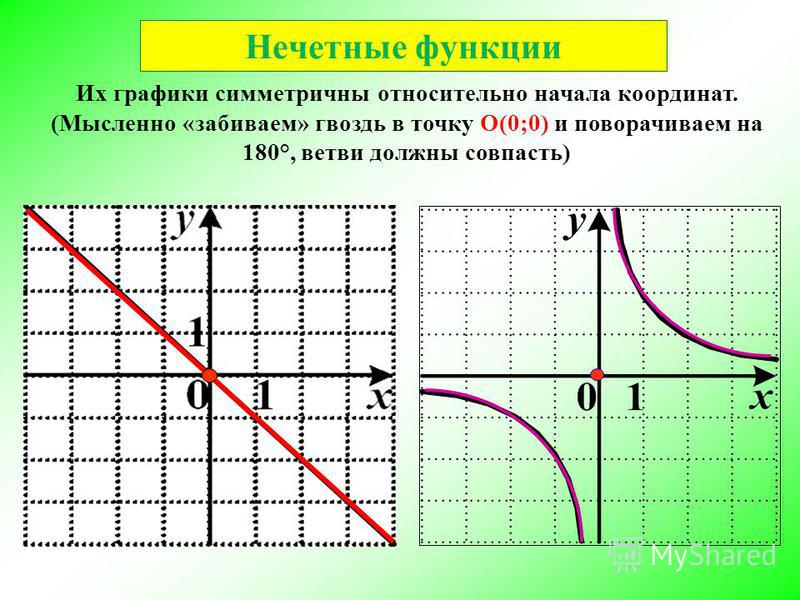 | |
Так как f (− x ) = f ( x ), эта функция симметрична относительно оси y . Это четная функция.
Пример 2. Проверить эту функцию на симметрию:
f ( x ) = x 5 + x 3 + x
Решение . Опять же, мы должны посмотреть на 90 527 f 90 528 (− 90 527 x 90 528): 90 003
| f (− x ) | = | (- x ) 5 + (- x ) 3 + (- x ) |
| = | − х 5 − х 3 − х | |
| = | −( х 5 + х 3 + х ) | |
| = | − f ( x ).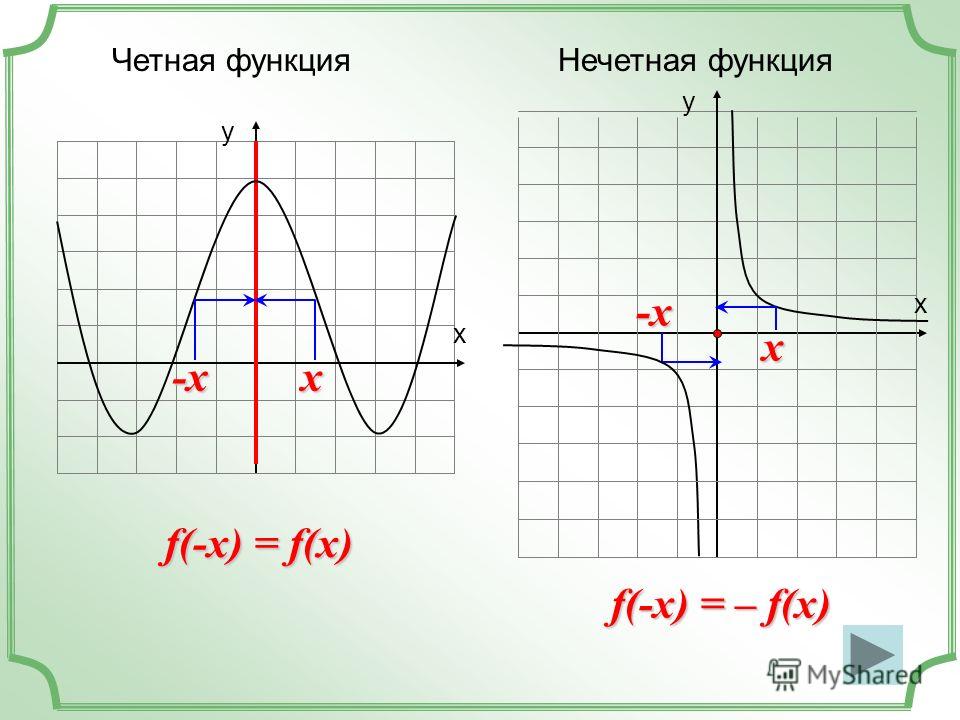 | |
Поскольку f (− x ) = − f ( x ), эта функция симметрична относительно начала координат. Это странная функция.
Проблема. Проверьте каждое из следующих на симметрию. Является ли f ( x ) четным, нечетным или ни тем, ни другим?
а) f ( x ) = x 3 + x 2 + х + 1
Ответ. Ни то, ни другое, потому что f (− x ) ≠ f ( x ) и f (− x ) ≠ − f ( x 9).
b) f ( x ) = 2 x 3 − 4 x
Ответ. f ( x ) нечетно — оно симметрично относительно начала координат — потому что ф (- х ) = — ф ( х ).
c) f ( x ) = 7 x 2 − 11
Ответ. f ( x ) является четным — оно симметрично относительно оси y — потому что f (− x ) = f ( x ).

 Определить
принадлежность точек х 1 , х 2 , … отрезку
[a ; b ]:
пусть x 1a ;b ,
а x 2a ;b .
Определить
принадлежность точек х 1 , х 2 , … отрезку
[a ; b ]:
пусть x 1a ;b ,
а x 2a ;b .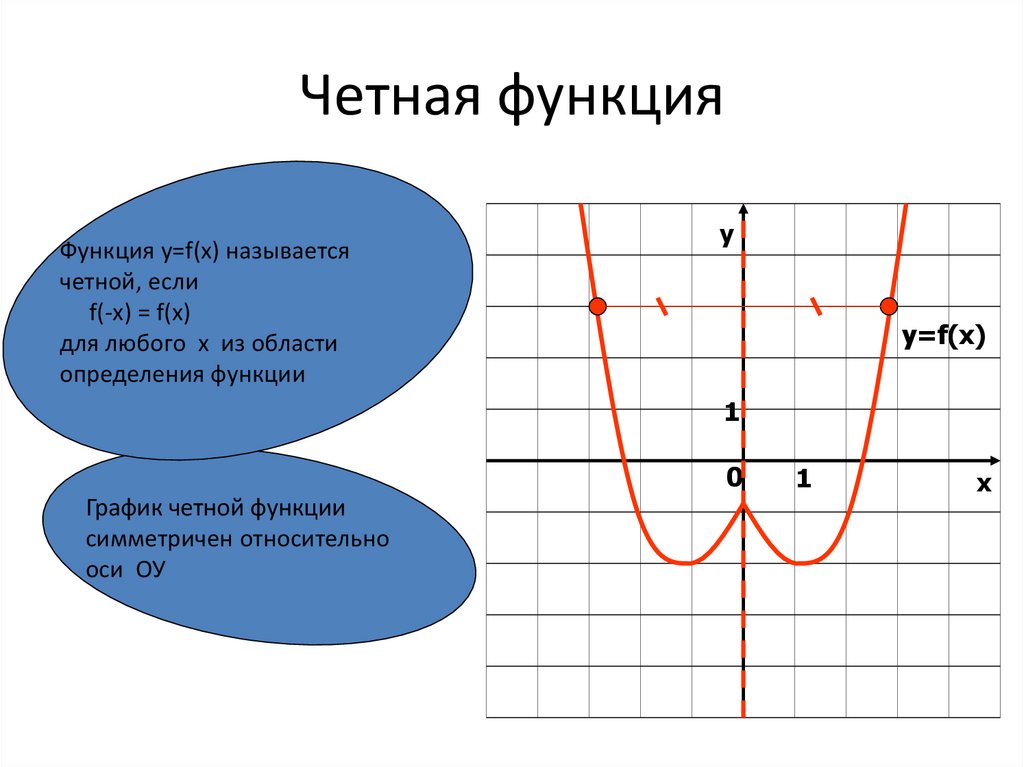
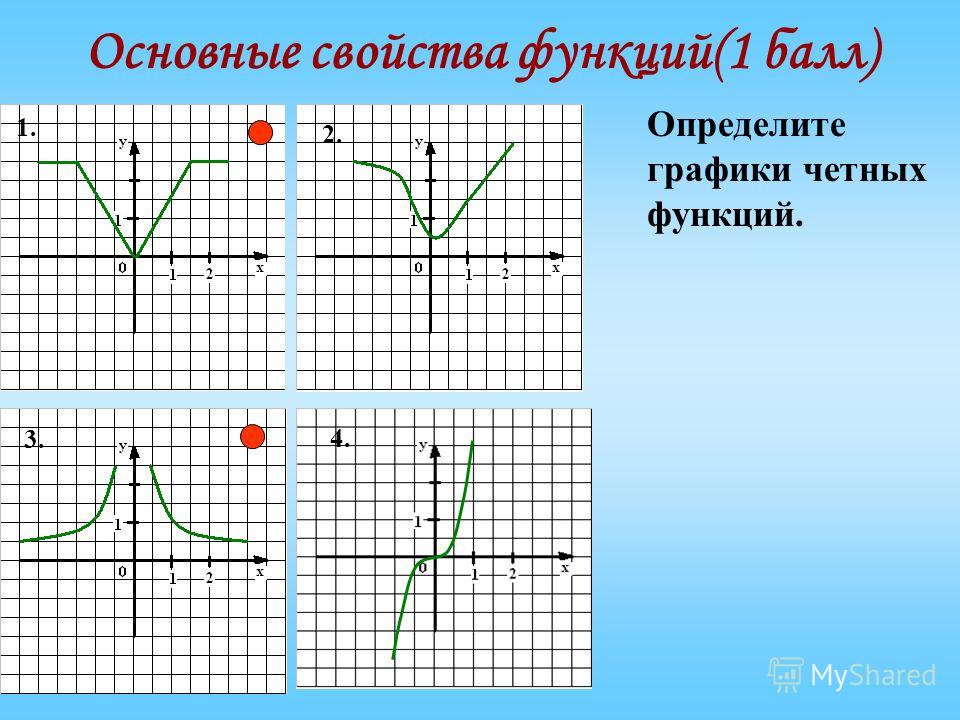
 Если это так, то у нас есть нечетная функция .
Если это так, то у нас есть нечетная функция .
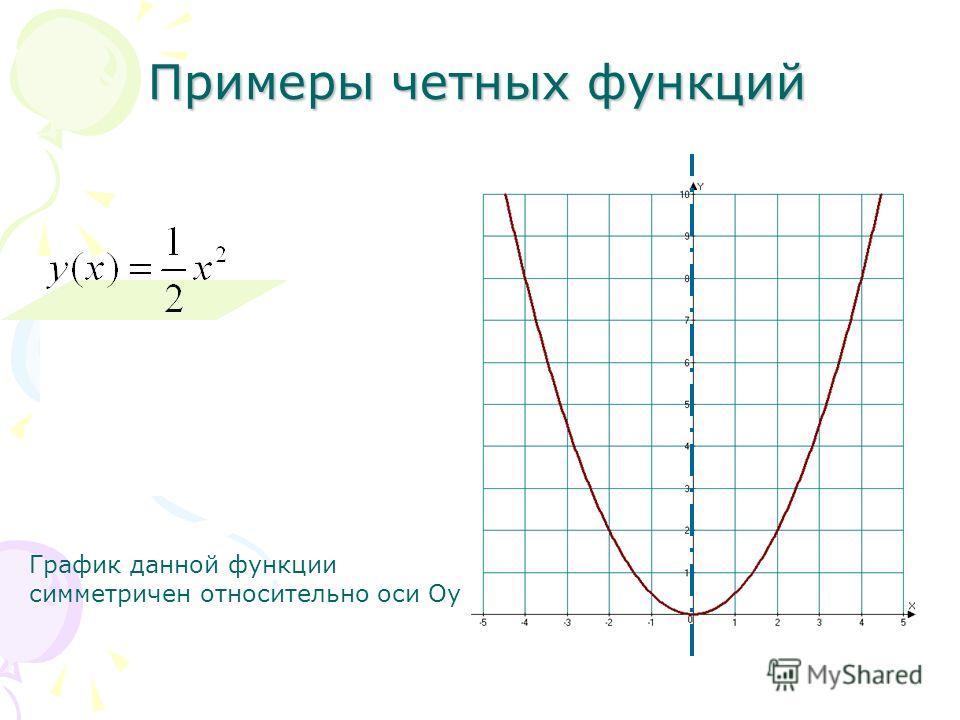 как нам это сделать?
как нам это сделать?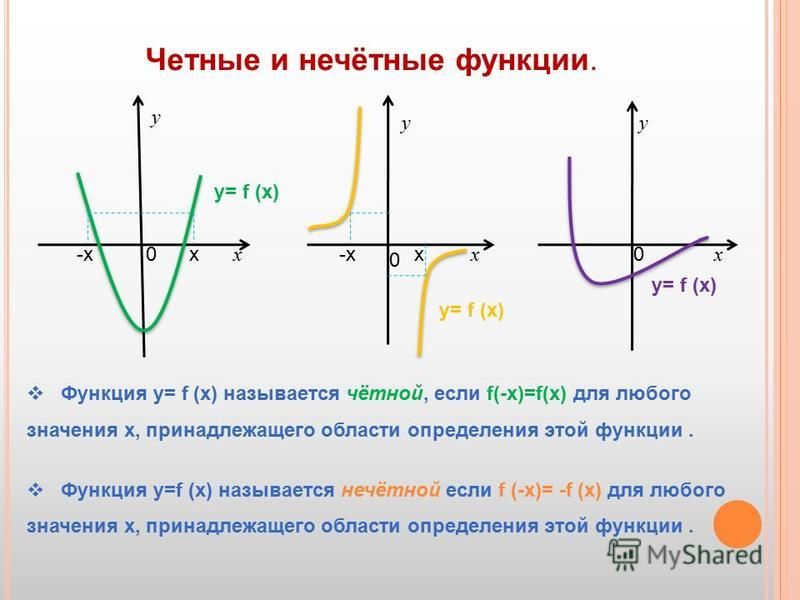
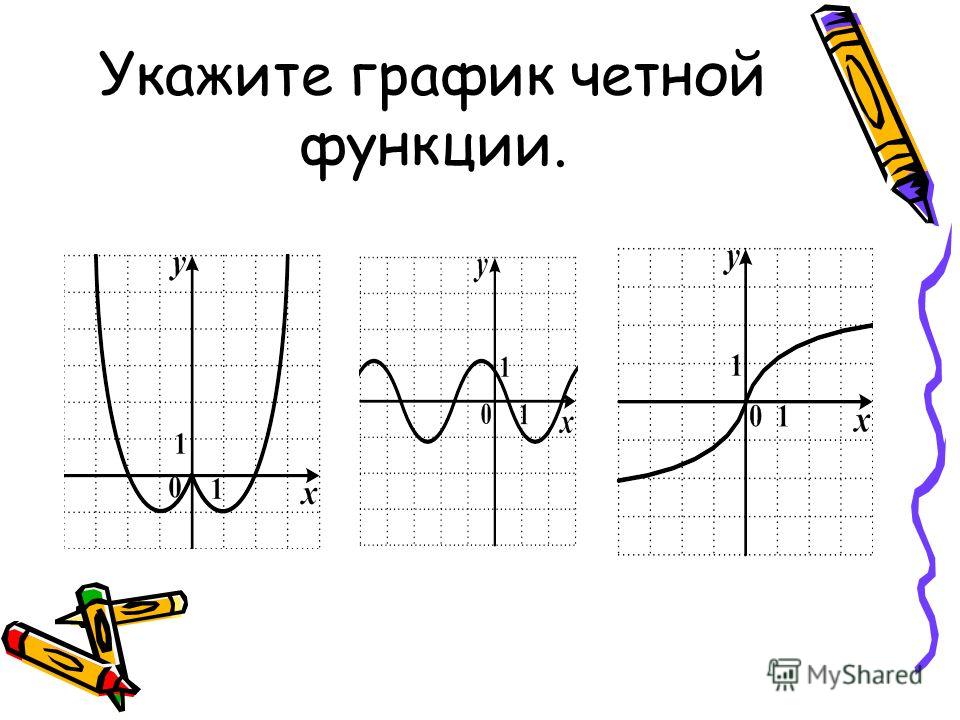 0032
0032