| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град.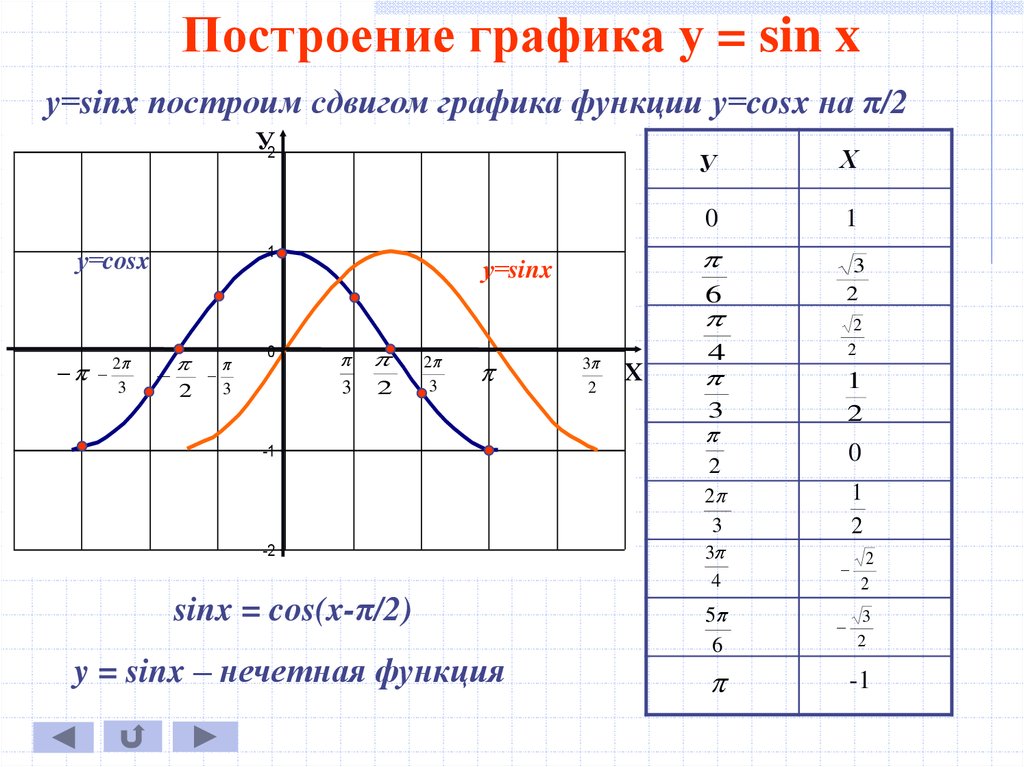 ) ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град.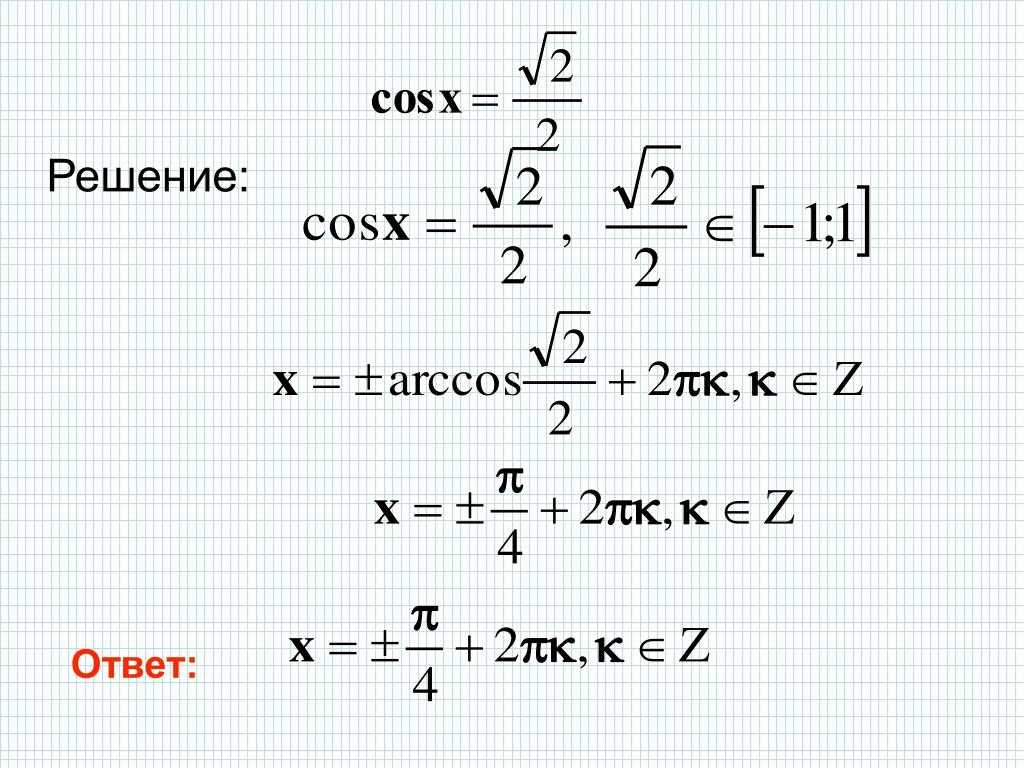 ) ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град.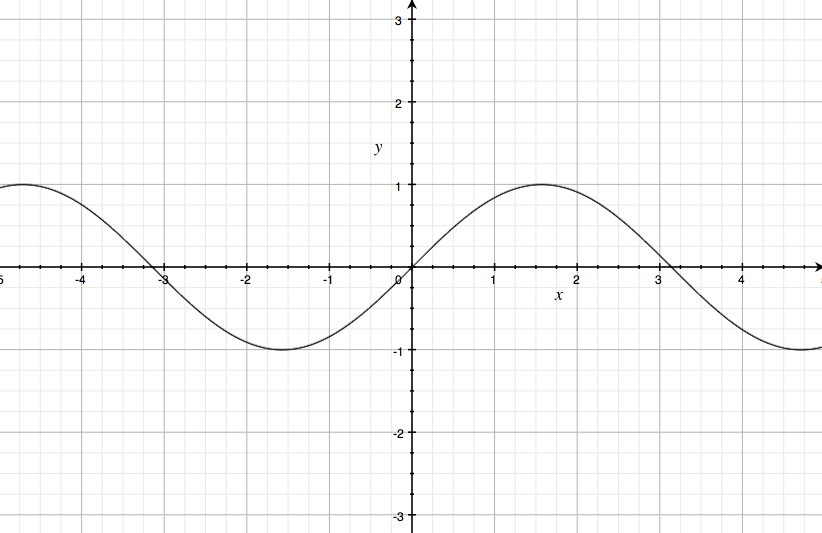 ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град.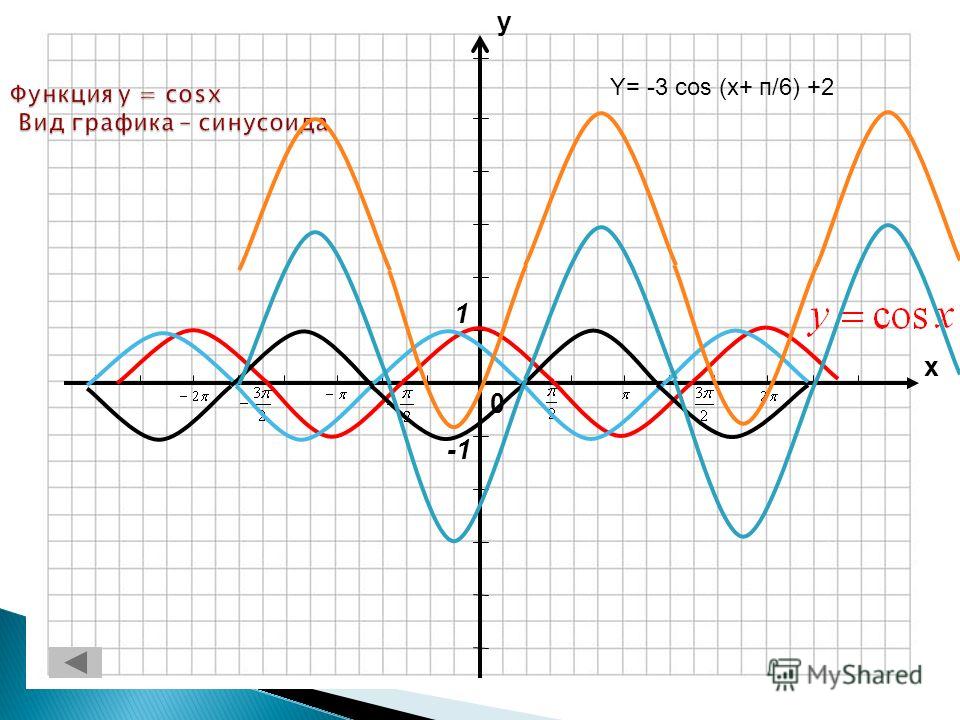 ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град.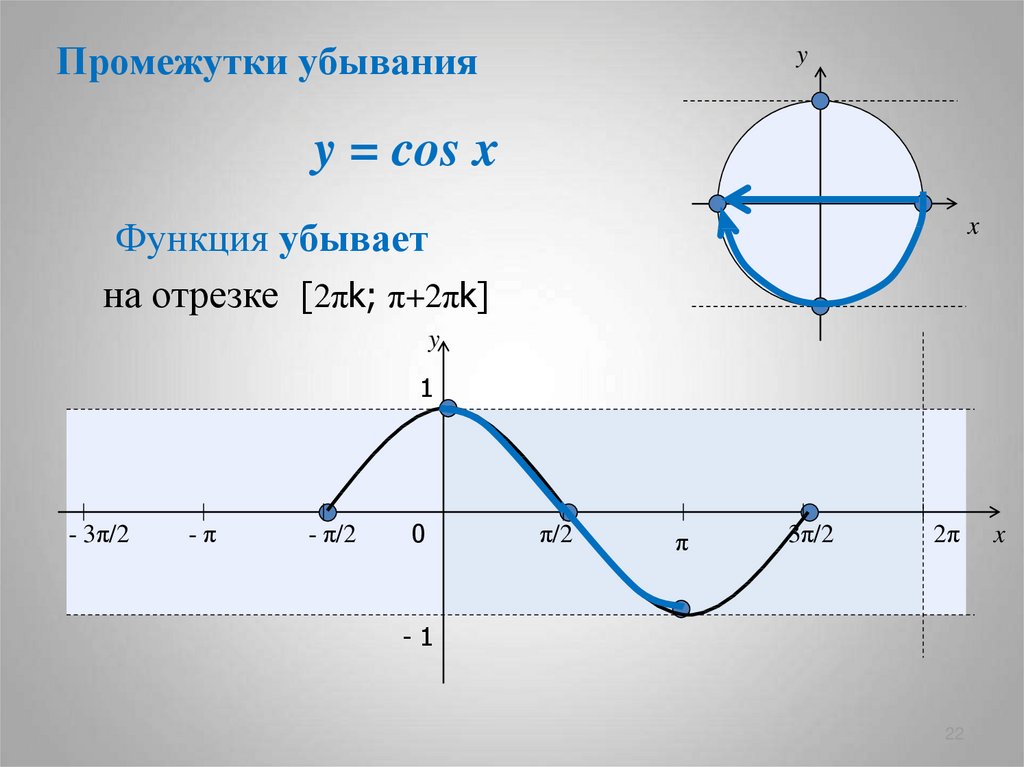 ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | ||
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град.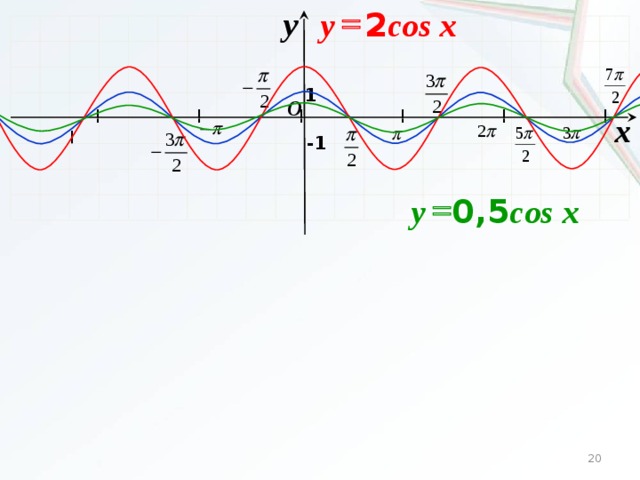 ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Построить график у cosx 2. Графики тригонометрических функций кратных углов
«Графики функций и их свойства» — y = ctg x. 4) Ограниченность функции. 3) Нечётная функция. (График функции симметричен относительно начала координат).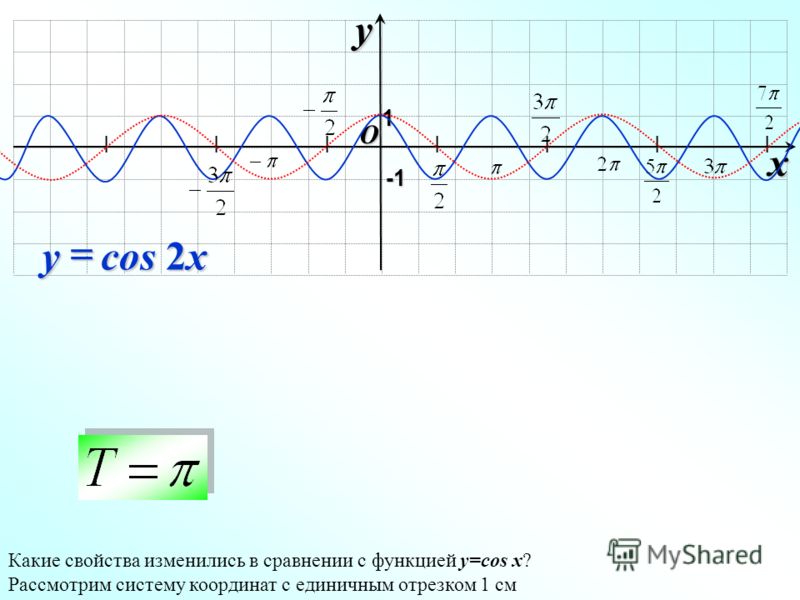 y = tg x. 7) Функция непрерывна на любом интервале вида (?k; ? + ?k). Функция y = tg x непрерывна на любом интервале вида. 4) Функция убывает на любом интервале вида (?k; ? + ?k). График функции y = tg x называется тангенсоидой.
y = tg x. 7) Функция непрерывна на любом интервале вида (?k; ? + ?k). Функция y = tg x непрерывна на любом интервале вида. 4) Функция убывает на любом интервале вида (?k; ? + ?k). График функции y = tg x называется тангенсоидой.
«График функции Y X» — Шаблон параболы у = х2. Чтобы увидеть графики, щелкни мышкой. Пример 2. Построим график функции y = x2 + 1, опираясь на график функции y=x2 (щелчок мышкой). Пример 3. Докажем, что графиком функции у = х2 + 6х + 8 является парабола, и построим график. График функции y=(x — m)2 является параболой с вершиной в точке (m; 0).
«Математика графики» — Как можно строить графики? Наиболее естественно функциональные зависимости отражаются с помощью графиков. Интересное применение: рисунки,… Зачем мы изучаем графики? Графики элементарных функций. Что вы можете нарисовать с помощью графиков? Рассматриваем применение графиков в учебных предметах: математике, физике,…
«Построение графиков с помощью производной» — Обобщение. Построить эскиз графика функции.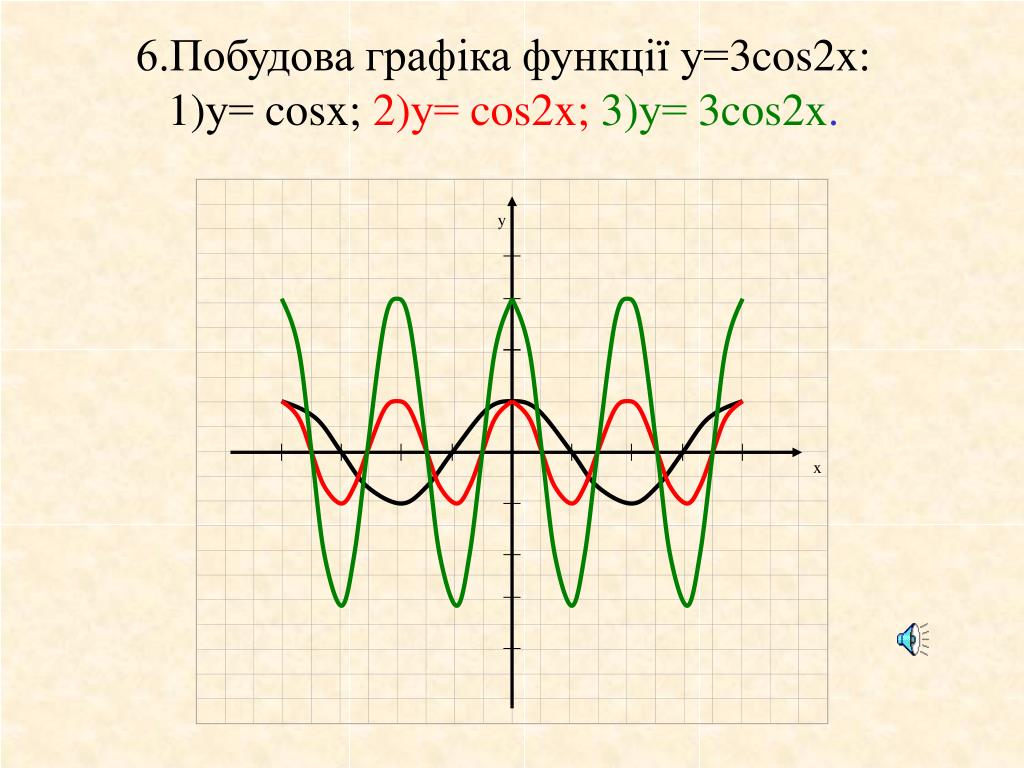 Найти асимптоты графика функции. График производной функции. Дополнительное задание. Исследовать функцию. Назвать промежутки убывания функции. Самостоятельная работа учащихся. Расширить знания. Урок закрепления изученного материала. Оцените свои умения. Точки максимума функции.
Найти асимптоты графика функции. График производной функции. Дополнительное задание. Исследовать функцию. Назвать промежутки убывания функции. Самостоятельная работа учащихся. Расширить знания. Урок закрепления изученного материала. Оцените свои умения. Точки максимума функции.
«Графики с модулем» — Отобрази «нижнюю» часть в верхнюю полуплоскость. Модуль действительного числа. Свойства функции y = |x|. |x|. Числа. Алгоритм построения графика функции. Алгоритм построения. Функция y= lхl. Свойства. Самостоятельная работа. Нули функции. Советы великих. Решение самостоятельной работы.
«Уравнение касательной» — Уравнение касательной. Уравнение нормали. Если,то и кривые пересекаются под прямым углом. Условия параллельности и перпендикулярности двух прямых. Угол между графиками функций. Уравнение касательной к графику функции в точке. Пусть функция дифференцируема в точке. Пусть прямые заданы уравнениями и.
Всего в теме 25 презентаций
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания.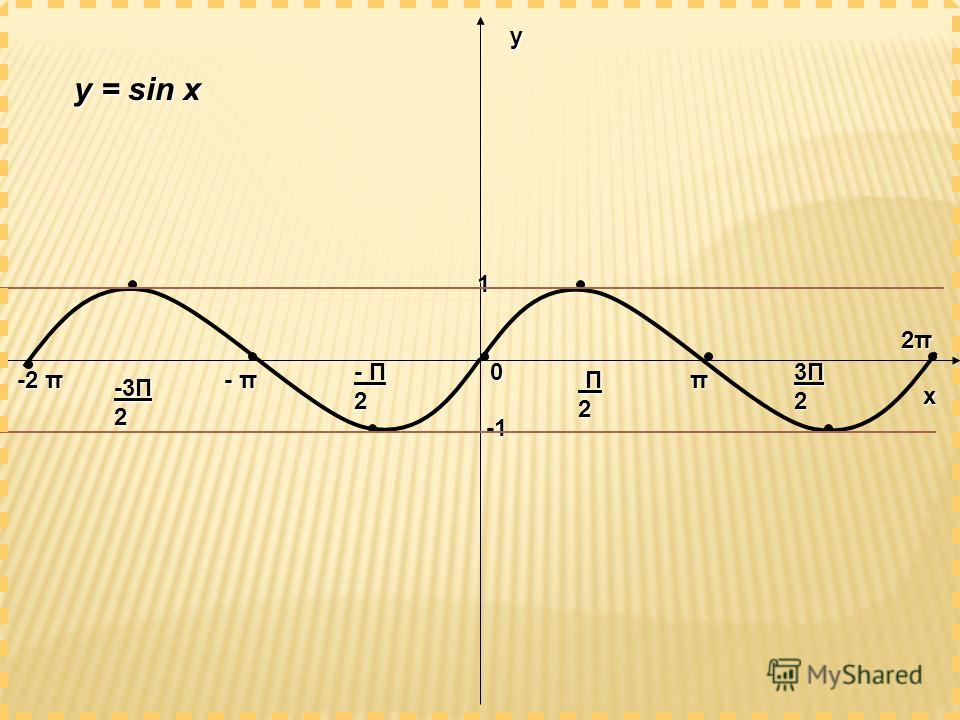 Все материалы проверены антивирусной программой.
Все материалы проверены антивирусной программой.
Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 10 класса
Алгебраические задачи с параметрами, 9–11 классы
Программная среда «1С: Математический конструктор 6.1»
Что будем изучать:
1. Определение.
2. График функции.
3. Свойства функции Y=cos(X).
4. Примеры.
Определение функции косинуса у=cos(x)
Ребята, мы уже познакомились с функцией Y=sin(X).
Давайте вспомним одну из формул привидения : sin(X + π/2) = cos(X).
Благодаря этой формуле, мы можем утверждать, что функции sin(X + π/2) и cos(X) тождественны, и их графики функций совпадают.
График функции sin(X + π/2) получается из графика функции sin(X) параллельным переносом на π/2 единиц влево. Это и будет график функции Y=cos(X).
График функции Y=cos(X) так же называют синусоидой.
Свойства функции cos(x)
- Запишем свойства нашей функции:
- Область определения – множество действительных чисел.

- Функция четная. Давайте вспомним определение четной функции. Функция называется четной, если выполняется равенство y(-x)=y(x). Как мы помним из формул привидения: cos(-x)=-cos(x), определение выполнилось, тогда косинус – четная функция.
- Функция Y=cos(X) убывает на отрезке и возрастает на отрезке [π; 2π]. В этом мы можем убедиться на графике нашей функции.
- Функция Y=cos(X) ограничена снизу и сверху. Данное свойство следует из того, что
-1 ≤ cos(X) ≤ 1 - Наименьшее значение функции равно -1 (при х = π + 2πk). Наибольшее значение функции равно 1 (при х = 2πk).
- Функция Y=cos(X) является непрерывной функцией. Посмотрим на график и убедимся, что у нашей функции нет разрывов, это и означает непрерывность.
- Область значений отрезок [- 1; 1]. Это также хорошо видно из графика.
- Функция Y=cos(X) — периодическая функция. Посмотрим опять на график и увидим, что функция принимает одни и те же значения через некоторые промежутки.
Примеры с функцией cos(x)
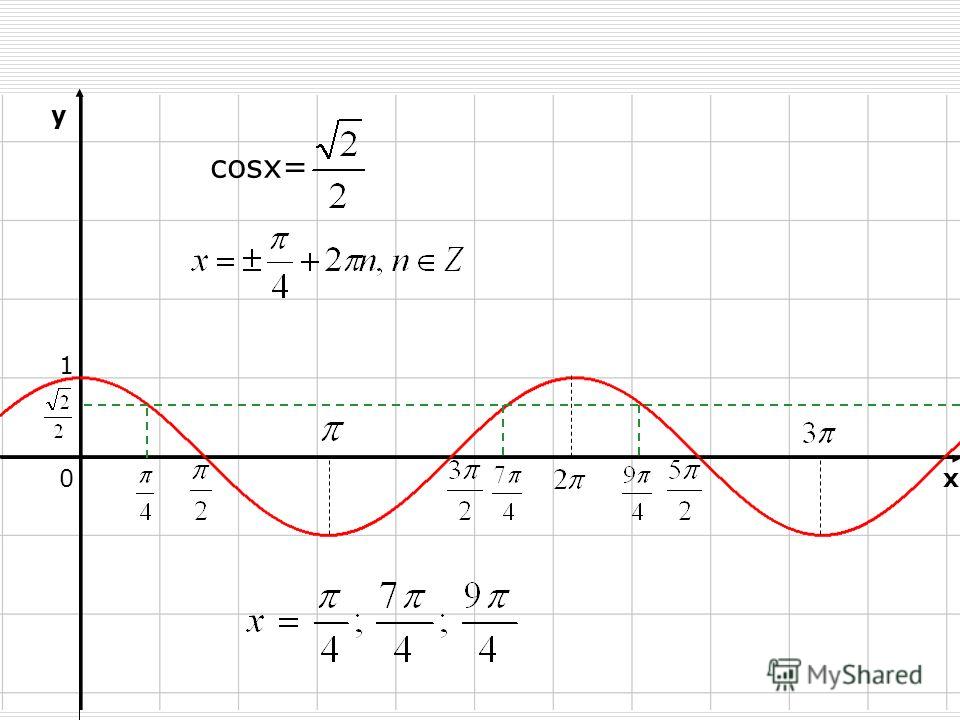
1. Решить уравнение cos(X)=(x — 2π) 2 + 1
Решить уравнение cos(X)=(x — 2π) 2 + 1
Решение: Построим 2 графика функции: y=cos(x) и y=(x — 2π) 2 + 1 (см. рисунок).
y=(x — 2π) 2 + 1 — это парабола, смещенная вправо на 2π и вверх на 1. Наши графики пересекаются в одной точке А(2π;1), это и есть ответ: x = 2π.
2. Построить график функции Y=cos(X) при х ≤ 0 и Y=sin(X) при x ≥ 0
Решение: Чтобы построить требуемый график, давайте построим два графика функции по «кусочкам». Первый кусочек: y=cos(x) при х ≤ 0. Второй кусочек: y=sin(x)
при x ≥ 0. Изобразим оба «кусочка» на одном
графике.
3. Найти наибольшее и наименьшее значение функции Y=cos(X) на отрезке [π; 7π/4]
Решение: Построим график функции и рассмотрим наш отрезок [π; 7π/4]. На графике видно, что наибольшие и наименьшие значения достигаются на концах отрезка: в точках π и 7π/4 соответственно.
Ответ: cos(π) = -1 – наименьшее значение, cos(7π/4) = наибольшее значение.
4. Построить график функции y=cos(π/3 — x) + 1
Решение: cos(-x)= cos(x), тогда искомый график получится путем переноса графика функции y=cos(x) на π/3 единиц вправо и 1 единицу вверх.
Задачи для самостоятельного решения
1)Решить уравнение: cos(x)= x – π/2.
2) Решить уравнение: cos(x)= — (x – π) 2 — 1.
3) Построить график функции y=cos(π/4 + x) — 2.
4) Построить график функции y=cos(-2π/3 + x) + 1.
5) Найти наибольшее и наименьшее значение функции
y=cos(x) на отрезке .
6) Найти наибольшее и наименьшее значение функции
y=cos(x) на отрезке [- π/6; 5π/4].
Теперь мы рассмотрим вопрос о том, как строить графики тригонометрических функций кратных углов ωx , где ω — некоторое положительное число.
Для построения графика функции у = sin ωx сравним эту функцию с уже изученной нами функцией у = sin x . Предположим, что при х = x 0 функция у = sin х принимает значение, равное у 0 . Тогда
у 0 = sin x 0 .
Преобразуем это соотношение следующим образом:
Следовательно, функция у = sin ωx при х = x 0 / ω принимает то же самое значение у 0 , что и функция у = sin х при х = x 0 .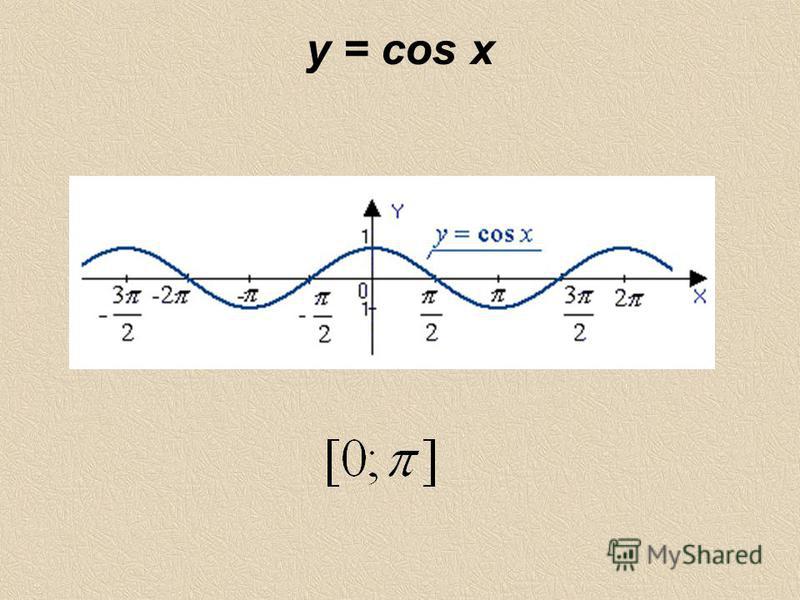 А это означает, что функция у = sin ωx повторяет свои значения в ω раз чаще, чем функция у
= sin x . Поэтому график функции у = sin ωx получается путем «сжатия» графика функции у = sin x в ω раз вдоль оси х.
А это означает, что функция у = sin ωx повторяет свои значения в ω раз чаще, чем функция у
= sin x . Поэтому график функции у = sin ωx получается путем «сжатия» графика функции у = sin x в ω раз вдоль оси х.
Например, график функции у = sin 2х получается путем «сжатия» синусоиды у = sin x вдвое вдоль оси абсцисс.
График функции у = sin x / 2 получается путем «растяжения» синусоиды у = sin х в два раза (или «сжатия» в 1 / 2 раза) вдоль оси х.
Поскольку функция у = sin ωx повторяет свои значения в ω раз чаще, чем функция
у = sin x , то период ее в ω раз меньше периода функции у = sin x . Например, период функции у = sin 2х равен 2π / 2 = π , а период функции у = sin x / 2 равен π
/ x / 2 = 4π .
Интересно провести исследование поведения функции у = sin аx на примере анимации, которую очень просто можно создать в программе Maple :
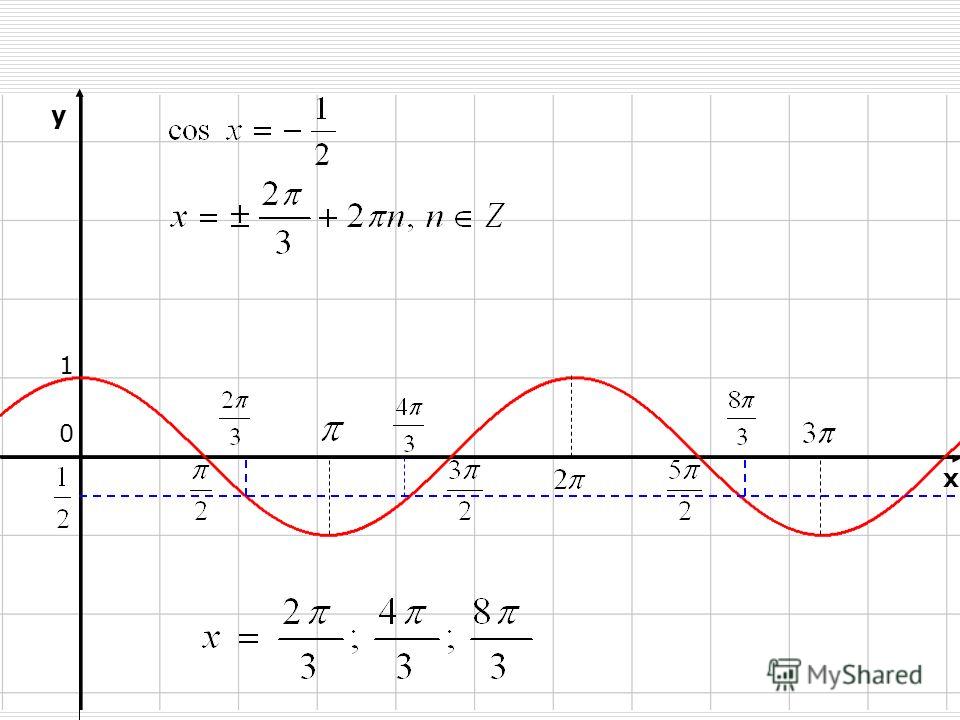
Аналогично строятся графики и других тригонометрических функций кратных углов.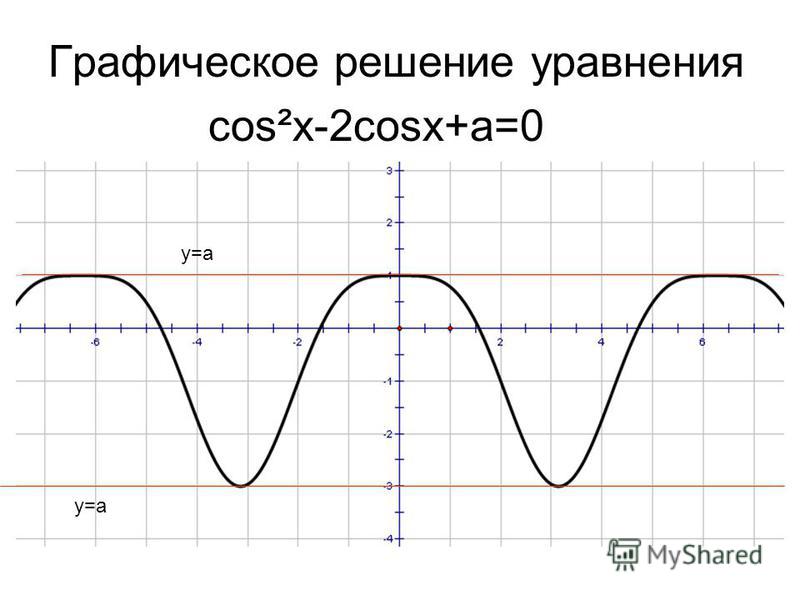 На рисунке представлен график функции у = cos 2х , который получается путем «сжатия» косинусоиды у = cos х в два раза вдоль оси абсцисс.
На рисунке представлен график функции у = cos 2х , который получается путем «сжатия» косинусоиды у = cos х в два раза вдоль оси абсцисс.
График функции у = cos x / 2 получается путем «растяжения» косинусоиды у = cos х вдвое вдоль оси х.
На рисунке вы видите график функции у = tg 2x , полученный «сжатием» тангенсоиды у = tg x вдвое вдоль оси абсцисс.
График функции у = tg x / 2 , полученный «растяжением» тангенсоиды у = tg x вдвое вдоль оси х.
И, наконец, анимация, выполненная программой Maple:
Упражнения
1. Построить графики данных функций и указать координаты точек пересечения этих графиков с осями координат. Определить периоды данных функций.
а). y = sin 4x / 3 г). y = tg 5x / 6 ж). y = cos 2x / 3
б). у= cos 5x / 3 д). у = ctg 5x / 3 з). у= ctg x / 3
у= ctg x / 3
в). y = tg 4x / 3 е). у = sin 2x / 3
2. Определить периоды функций у = sin (πх) и у = tg ( πх / 2 ).
3. Приведите два примера функции, которые принимают все значения от -1 до +1 (включая эти два числа) и изменяются периодически с периодом 10.
4 *. Приведите два примера функций, которые принимают все значения от 0 до 1 (включая эти два числа) и изменяются периодически с периодом π / 2 .
5. Приведите два примера функций, которые принимают все действительные значения и изменяются периодически с периодом 1.
6 *. Приведите два примера функций, которые принимают все отрицательные значения и нуль, но не принимают положительные значения и изменяются периодически с периодом 5.
Функция у=cos x
Функция
y = cos x
её свойства и график
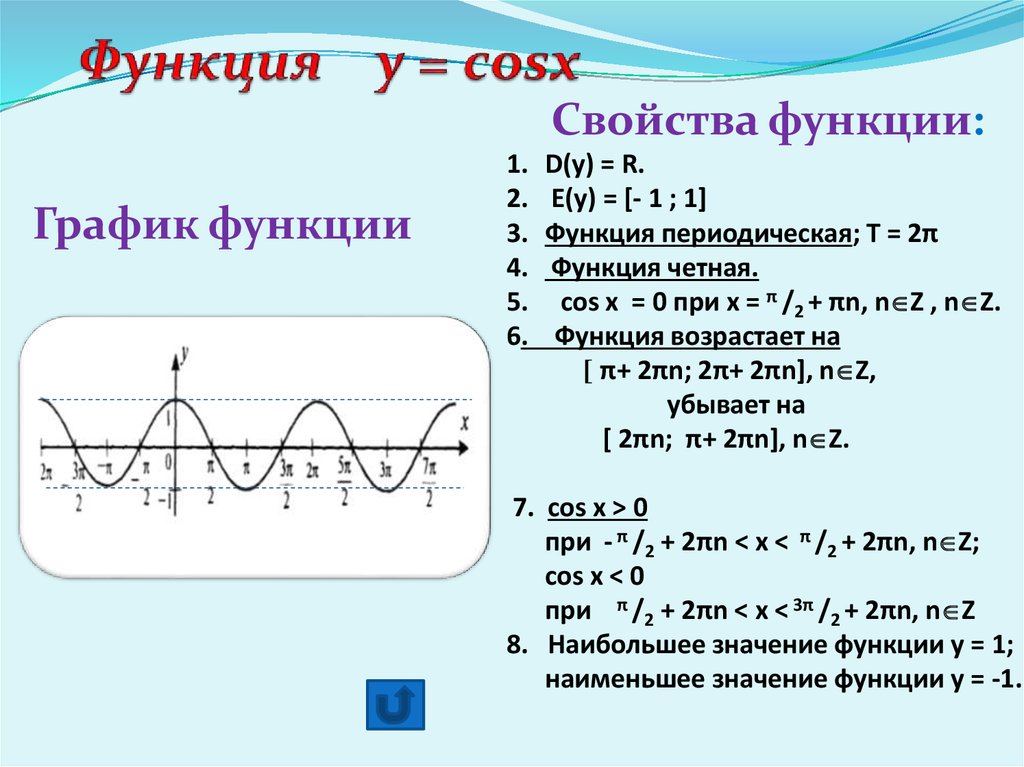
Функция y = cos x определена на всей числовой прямой, и множеством её значений является отрезок [−1;1].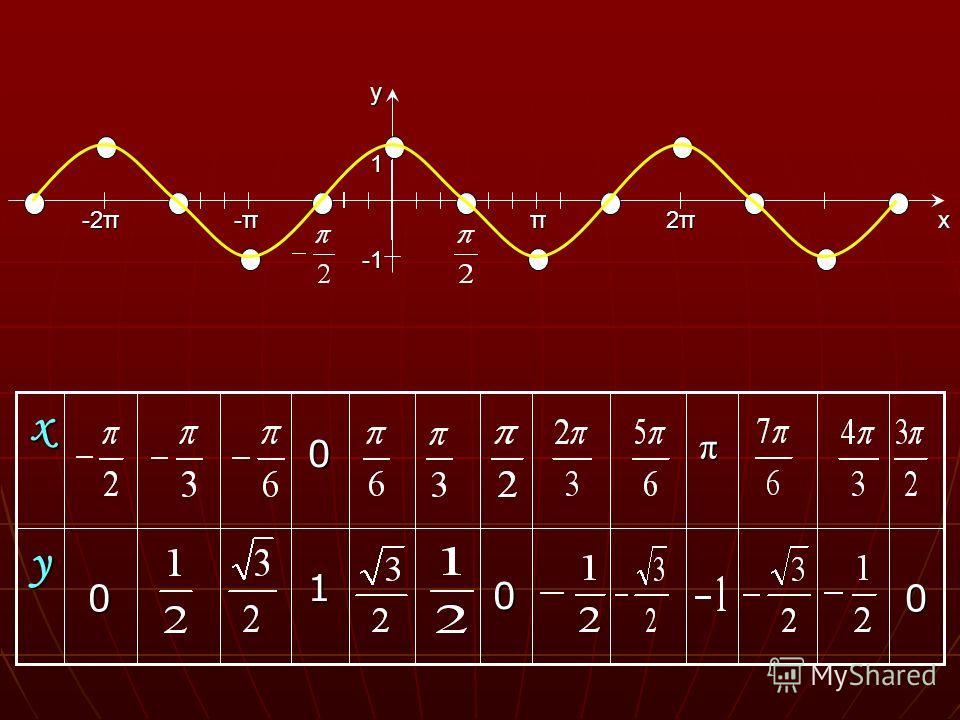
Следовательно, график этой функции расположен в полосе между прямыми y= −1 и y=1.
Так как функция y = cos x периодическая с периодом 2π , то достаточно построить её график на каком-нибудь промежутке длиной 2π , тогда на промежутках, получаемых сдвигами выбранного отрезка на 2πn, n∈Z, график будет таким же.
Рассмотрим поведение функции и отметим важнейшие точки на промежутке [0; ]
В координатной плоскости
На числовой окружности
Функция y = cos x является чётной. Поэтому её график симметричен относительно оси ОУ
Для построения графика на отрезке — π≤x≤π достаточно построить его для 0≤x≤π , а затем симметрично отразить его относительно оси ОУ
График функции y = cos x
Кривая, являющаяся графиком функции y= cos x, называется косинусоидой .
Свойства функции y = cos x
1. Область определения — множество R всех действительных чисел. D(y) = (-∞ ; + ∞ )
2. Множество значений Е(у) = [−1;1]
3. Функция периодическая с периодом T= 2π .
4. Функция чётная cos(-x) = cos x
(график симметричен относительно оси ОУ ).
5 . Функция ограничена и сверху, и снизу.
6. Функция y= cos x принимает: — значение, равное 0 , при x=π /2+ πn,n∈Z; — наибольшее значение, равное 1 , при x=2πn,n∈Z ; — наименьшее значение, равное −1 , при x=π+2πn,n∈Z;
7. Промежутки, на которых функция принимает положительные значения при
x ∈ ( -π/2+2π n; π/2+2π n), n ∈ Z
Промежутки, на которых функция принимает отрицательные значения при
x ∈ ( π /2+2 π n; 3 π / 2+2 π n), n ∈ Z
- Функция возрастает на x ∈ [ π + 2 π n; 2 π n ] , n ∈ Z
функция убывает на x ∈ [ 2 π n ; π + 2 π n ] , n ∈ Z
Решение задач
Задача №1
Найти пределы изменения функции y = cos t на данном отрезке [ /6; /2]
Решение
Функция монотонно убывает на указанном промежутке, значит, наибольшее значение принимает на левом конце отрезка у( /6)= 3/2, а наименьшее значение принимает на его правом конце у( /2) = 0
Задача №2
Найти наибольшее и наименьшее значение функции y = cos t на данном отрезке [ / 3 ; 7 / 6 ]
Решение
На данном промежутке функция немонотонна.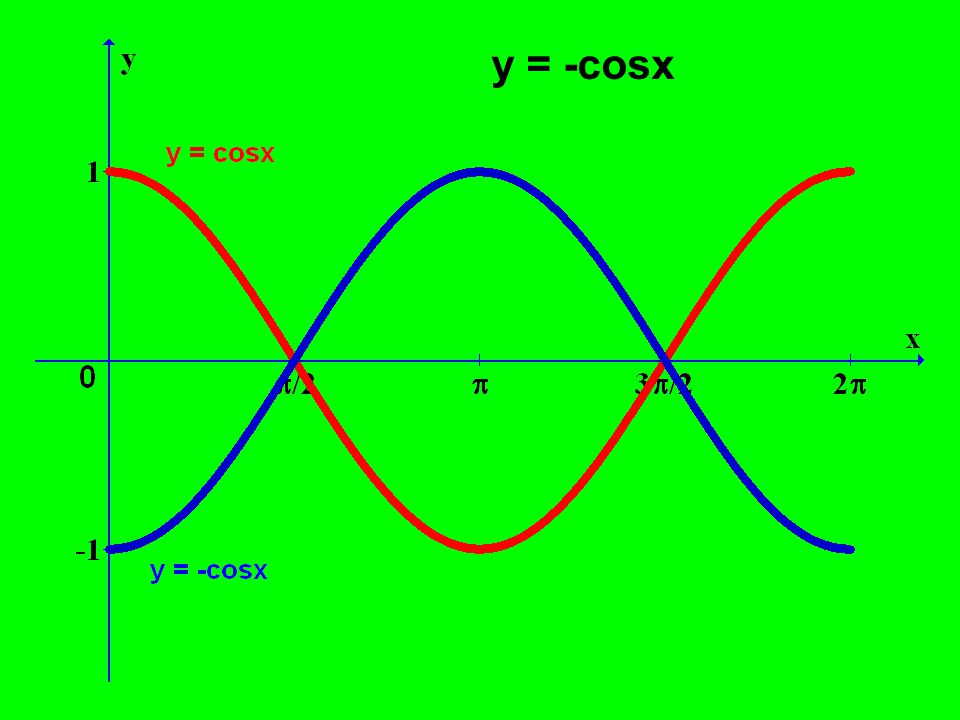
Наибольшее значение принимает на левом конце отрезка у( /3)=1/2, а наименьшее значение у( ) = -1
Задача №3
Задача 2. Найти все значения параметра а, при каждом из которых уравнение имеет хотя бы одно решение: 1 + cos t = a
Решение
Построим график функции y = 1 + cos t
Уравнение
1 + cos t = a
имеет хотя бы одно решение при a Є [0;2]
В данном случае множество значений параметра совпадает со множеством значений функции.
Ответ: а Є [0; 2]
Задача №4
Решить уравнение
Решение
Построим в одних координатных осях графики функций
Графики имеют только одну общую точку
А(0; 1)
Ответ: х=0
Задача №5
Найти число корней уравнения
Решение
На промежутке [- π ; 0] функция у= cosx монотонно возрастает, функция у=х 2 монотонно убывает. Это значит, что на данном промежутке графики имеют только одну общую точку.
Это значит, что на данном промежутке графики имеют только одну общую точку.
На промежутке [ 0; π ] функция у= cosx монотонно убывает, функция у=х 2 монотонно возрастает. Значит, и на этом промежутке графики имеют только одну общую точку.
Ответ: два корня
Задача №5
Построить график функции y=cos3x
Решение
Косинус – четная функция, строим график на участке
[0; π /3] , затем симметрично отображаем относительно оси y и получаем график на промежутке [- π /3; π /3] длина которого равна периоду. График сжимается к оси Оу в 3 раза.
Задания для самостоятельного решения
1) Постройте графики функций
1) у = cos x + 1;
2) у = cos x – 1;
3) у = cos (x + π /2)
4) у = cos (x – π /3)
2 ) Найти наибольшее и наименьшее значение функции y= cos (x) на отрезке [0; 4π/3]
3) Определить область значений функции y=−8cosx+3.
4) Определить чётность или нечётность функции:
f(x)=x5⋅cos6x.
5) Определить, возрастает или убывает функция y=cosx на отрезке: [−4π;−3π].
6) Найти наибольшее и наименьшее значения функции:
y=cos 4 2x−sin 4 2x+4.
7) Определить наименьшее и наибольшее значения функции y=cosx
на полуинтервале (−4π / 3;−π / 3].
Заключение.
Мы рассмотрели график функции
y = cos x ,
изучили особенности ее поведения, использовали их и свойства функции при решении задач, в том числе и задач с параметром
Функция y = cosx её свойства и график доклад, проект
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация на тему Функция y = cosx её свойства и график, предмет презентации: Алгебра.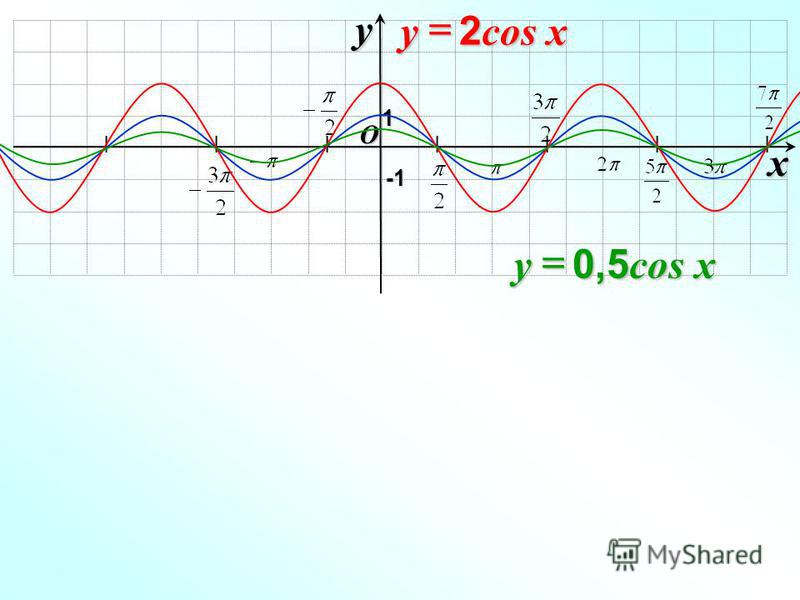 Этот материал в формате pptx (PowerPoint) содержит 16 слайдов, для просмотра воспользуйтесь проигрывателем. Презентацию на заданную тему можно скачать внизу страницы, поделившись ссылкой в социальных сетях! Презентации взяты из открытого доступа или загружены их авторами, администрация сайта не отвечает за достоверность информации в них, все права принадлежат авторам презентаций и могут быть удалены по их требованию.
Этот материал в формате pptx (PowerPoint) содержит 16 слайдов, для просмотра воспользуйтесь проигрывателем. Презентацию на заданную тему можно скачать внизу страницы, поделившись ссылкой в социальных сетях! Презентации взяты из открытого доступа или загружены их авторами, администрация сайта не отвечает за достоверность информации в них, все права принадлежат авторам презентаций и могут быть удалены по их требованию.
Функция
y = cosx
её свойства и график
Цель:
Изучить функцию y = cos x
Задачи:
1. Изучить свойства функции у = cos x.
2. Уметь применять свойства функции у = cos x и читать график.
3. Формировать практические навыки построения графика функции у = cos x на основе изученного теоретического материала.
4. Закрепить понятия с помощью выполнения заданий.
Функция y = cos x определена на всей числовой прямой, и множеством её значений является отрезок [−1;1].
Следовательно, график этой функции расположен в полосе между прямыми y= −1 и y=1.
Так как функция y = cos x периодическая с периодом 2π, то достаточно построить её график на каком-нибудь промежутке длиной 2π, тогда на промежутках, получаемых сдвигами выбранного отрезка на 2πn, n∈Z, график будет таким же.
Рассмотрим поведение функции и отметим важнейшие точки на промежутке [0;π]
В координатной плоскости
На числовой окружности
Функция y = cos x является чётной. Поэтому её график симметричен относительно оси ОУ
Для построения графика на отрезке — π≤x≤π достаточно построить его для 0≤x≤π, а затем симметрично отразить его относительно оси ОУ
График функции y = cos x
Кривая, являющаяся графиком функции y=cos x, называется косинусоидой.
Свойства функции y = cos x
1.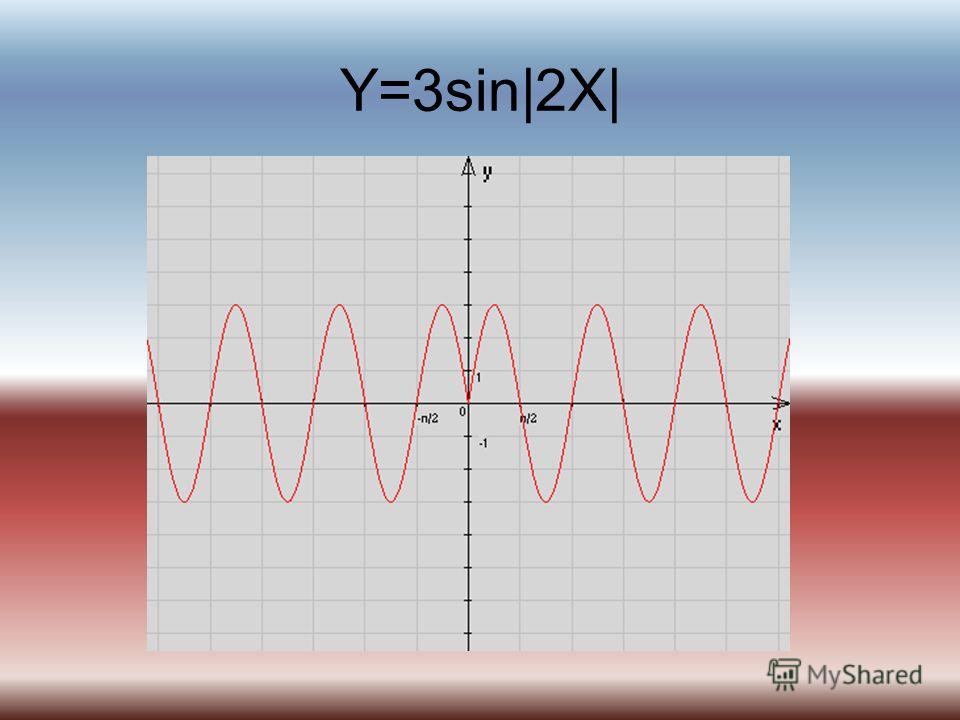 Область определения — множество R всех действительных чисел. D(y) = (-∞; + ∞)
Область определения — множество R всех действительных чисел. D(y) = (-∞; + ∞)
2. Множество значений Е(у) = [−1;1]
3. Функция периодическая с периодом T= 2π.
4. Функция чётная cos(-x) = cos x
(график симметричен относительно оси ОУ).
5. Функция ограничена и сверху, и снизу.
6. Функция y=cos x принимает:
— значение, равное 0, при x=π/2+πn,n∈Z;
— наибольшее значение, равное 1, при x=2πn,n∈Z;
— наименьшее значение, равное −1, при x=π+2πn,n∈Z;
7. Промежутки, на которых функция принимает положительные значения при
x ∈ (-π/2+2πn; π/2+2πn), n ∈ Z
Промежутки, на которых функция принимает отрицательные значения при
x ∈ (π/2+2πn; 3π/2+2πn), n ∈ Z
Функция возрастает на x ∈ [π + 2 πn; 2 πn], n ∈ Z
функция убывает на x ∈ [2 πn; π+ 2 πn], n ∈ Z
Решение задач
Задача №1
Найти пределы изменения функции y = cos t на данном отрезке [π/6; π/2]
Функция монотонно убывает на указанном промежутке, значит, наибольшее значение принимает на левом конце отрезка у(π/6)=√3/2, а наименьшее значение принимает на его правом конце у(π/2) = 0
Решение
Задача №2
Найти наибольшее и наименьшее значение функции y = cos t на данном отрезке [π/3; 7π/6]
На данном промежутке функция немонотонна.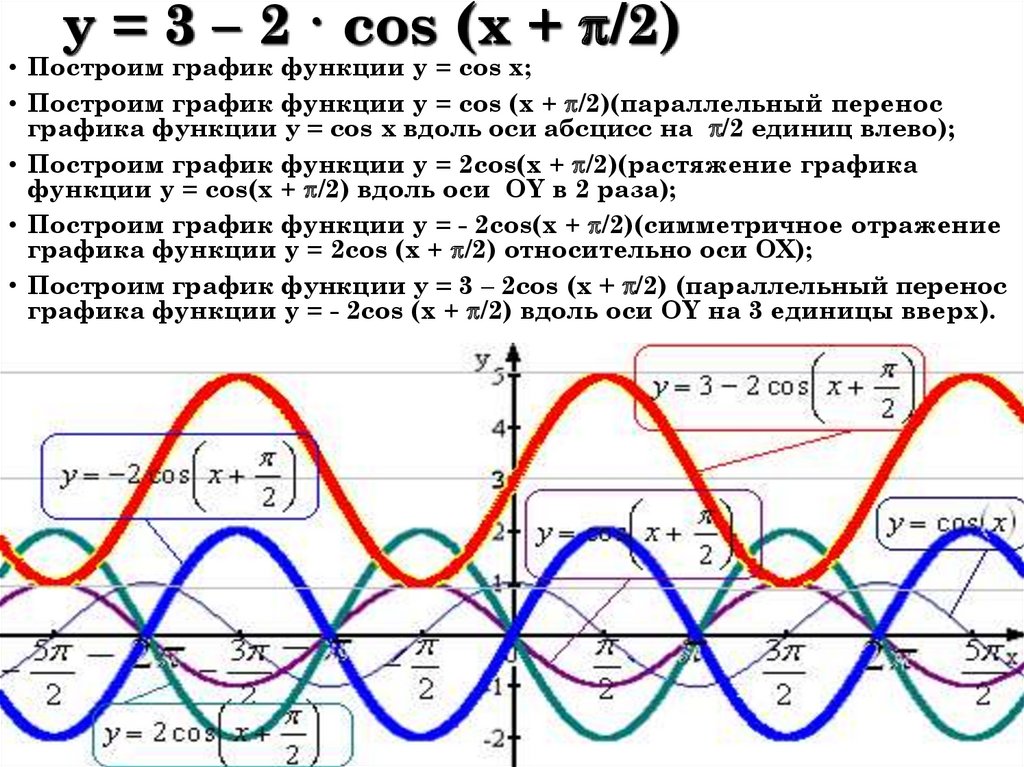
Решение
Наибольшее значение принимает на левом конце отрезка у(π/3)=1/2, а наименьшее значение у(π) = -1
Задача 2. Найти все значения параметра а, при каждом из которых уравнение имеет хотя бы одно решение: 1 + cos t = a
Задача №3
Решение
Построим график функции y = 1 + cos t
Уравнение
1 + cos t = a
имеет хотя бы одно решение при aЄ [0;2]
В данном случае множество значений параметра совпадает со множеством значений функции.
Ответ: аЄ[0; 2]
Задача №4
Решить уравнение
Построим в одних координатных осях графики функций
Решение
Графики имеют только одну общую точку
А(0; 1)
Ответ: х=0
Задача №5
Найти число корней уравнения
Решение
На промежутке [-π; 0] функция у=cosx монотонно возрастает, функция у=х2 монотонно убывает.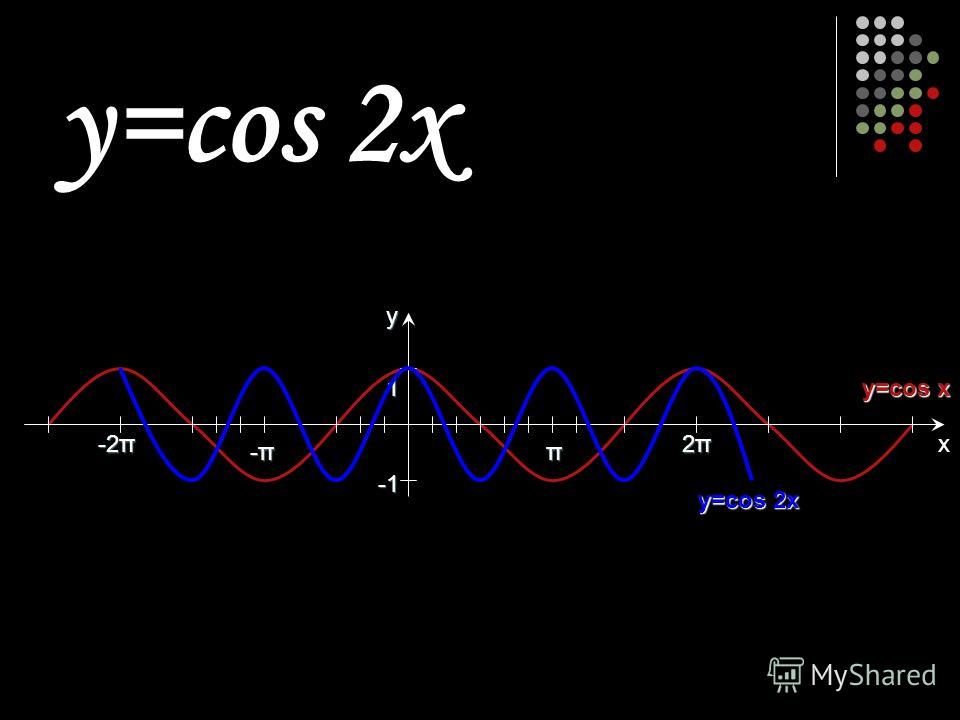 Это значит, что на данном промежутке графики имеют только одну общую точку.
Это значит, что на данном промежутке графики имеют только одну общую точку.
На промежутке [0; π] функция у=cosx монотонно убывает, функция у=х2 монотонно возрастает. Значит, и на этом промежутке графики имеют только одну общую точку.
Ответ: два корня
Построить график функции y=cos3x
Задача №5
Косинус – четная функция, строим график на участке
[0; π/3], затем симметрично отображаем относительно оси y и получаем график на промежутке [-π/3; π/3] длина которого равна периоду. График сжимается к оси Оу в 3 раза.
Решение
Задания для самостоятельного решения
1) Постройте графики функций
1) у = cosx + 1;
2) у = cosx – 1;
3) у = cos (x + π/2)
4) у = cos (x – π/3)
2) Найти наибольшее и наименьшее значение функции y=cos (x) на отрезке [0; 4π/3]
3) Определить область значений функции y=−8cosx+3.
4) Определить чётность или нечётность функции:
f(x)=x5⋅cos6x.
5) Определить, возрастает или убывает функция y=cosx на отрезке: [−4π;−3π].
6) Найти наибольшее и наименьшее значения функции:
y=cos42x−sin42x+4.
7) Определить наименьшее и наибольшее значения функции y=cosx
на полуинтервале (−4π/3;−π/3].
Заключение.
Мы рассмотрели график функции
y = cos x ,
изучили особенности ее поведения, использовали их и свойства функции при решении задач, в том числе и задач с параметром
Скачать презентацию
Это сайт презентаций, где можно хранить и обмениваться своими презентациями, докладами, проектами, шаблонами в формате PowerPoint с другими пользователями. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами.
Для правообладателей
Обратная связь
Email: Нажмите что бы посмотреть
Cos x п 2 график.
 Графики тригонометрических функций кратных углов
Графики тригонометрических функций кратных угловДополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.
Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 10 класса
Алгебраические задачи с параметрами, 9–11 классы
Программная среда «1С: Математический конструктор 6.1»
Что будем изучать:
1. Определение.
2. График функции.
3. Свойства функции Y=cos(X).
4. Примеры.
Определение функции косинуса у=cos(x)
Ребята, мы уже познакомились с функцией Y=sin(X).
Давайте вспомним одну из формул привидения : sin(X + π/2) = cos(X).
Благодаря этой формуле, мы можем утверждать, что функции sin(X + π/2) и cos(X) тождественны, и их графики функций совпадают.
График функции sin(X + π/2) получается из графика функции sin(X) параллельным переносом на π/2 единиц влево. Это и будет график функции Y=cos(X).
График функции Y=cos(X) так же называют синусоидой.
Свойства функции cos(x)
- Запишем свойства нашей функции:
- Область определения – множество действительных чисел.
- Функция четная. Давайте вспомним определение четной функции. Функция называется четной, если выполняется равенство y(-x)=y(x). Как мы помним из формул привидения: cos(-x)=-cos(x), определение выполнилось, тогда косинус – четная функция.
- Функция Y=cos(X) убывает на отрезке и возрастает на отрезке [π; 2π]. В этом мы можем убедиться на графике нашей функции.
- Функция Y=cos(X) ограничена снизу и сверху. Данное свойство следует из того, что
-1 ≤ cos(X) ≤ 1 - Наименьшее значение функции равно -1 (при х = π + 2πk). Наибольшее значение функции равно 1 (при х = 2πk).
- Функция Y=cos(X) является непрерывной функцией. Посмотрим на график и убедимся, что у нашей функции нет разрывов, это и означает непрерывность.
- Область значений отрезок [- 1; 1]. Это также хорошо видно из графика.

- Функция Y=cos(X) — периодическая функция. Посмотрим опять на график и увидим, что функция принимает одни и те же значения через некоторые промежутки.
Примеры с функцией cos(x)
1. Решить уравнение cos(X)=(x — 2π) 2 + 1
Решение: Построим 2 графика функции: y=cos(x) и y=(x — 2π) 2 + 1 (см. рисунок).
y=(x — 2π) 2 + 1 — это парабола, смещенная вправо на 2π и вверх на 1. Наши графики пересекаются в одной точке А(2π;1), это и есть ответ: x = 2π.
2. Построить график функции Y=cos(X) при х ≤ 0 и Y=sin(X) при x ≥ 0
Решение: Чтобы построить требуемый график, давайте построим два графика функции по «кусочкам». Первый кусочек: y=cos(x) при х ≤ 0. Второй кусочек: y=sin(x)
при x ≥ 0. Изобразим оба «кусочка» на одном
графике.
3. Найти наибольшее и наименьшее значение функции Y=cos(X) на отрезке [π; 7π/4]
Решение: Построим график функции и рассмотрим наш отрезок [π; 7π/4]. На графике видно, что наибольшие и наименьшие значения достигаются на концах отрезка: в точках π и 7π/4 соответственно.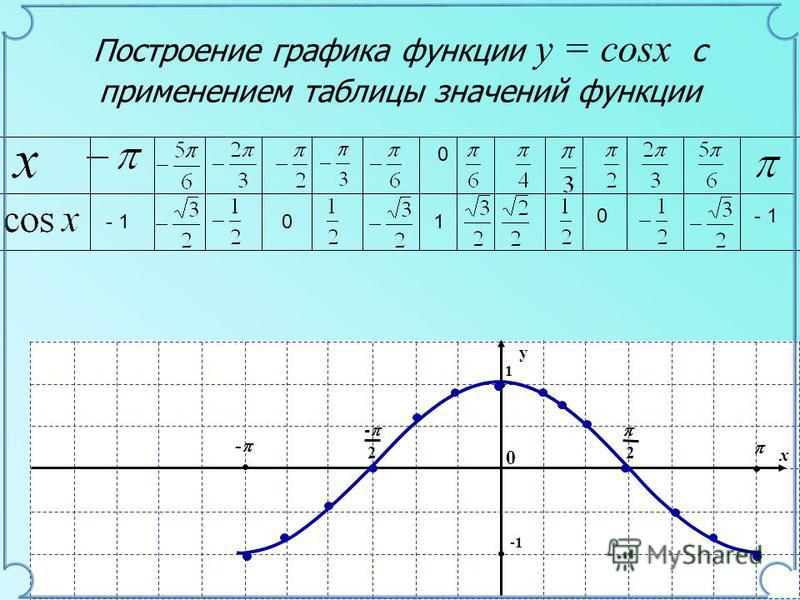
Ответ: cos(π) = -1 – наименьшее значение, cos(7π/4) = наибольшее значение.
4. Построить график функции y=cos(π/3 — x) + 1
Решение: cos(-x)= cos(x), тогда искомый график получится путем переноса графика функции y=cos(x) на π/3 единиц вправо и 1 единицу вверх.
Задачи для самостоятельного решения
1)Решить уравнение: cos(x)= x – π/2.
2) Решить уравнение: cos(x)= — (x – π) 2 — 1.
3) Построить график функции y=cos(π/4 + x) — 2.
4) Построить график функции y=cos(-2π/3 + x) + 1.
5) Найти наибольшее и наименьшее значение функции
y=cos(x) на отрезке .
6) Найти наибольшее и наименьшее значение функции
y=cos(x) на отрезке [- π/6; 5π/4].
«Графики функций и их свойства» — y = ctg x. 4) Ограниченность функции. 3) Нечётная функция. (График функции симметричен относительно начала координат). y = tg x. 7) Функция непрерывна на любом интервале вида (?k; ? + ?k). Функция y = tg x непрерывна на любом интервале вида. 4) Функция убывает на любом интервале вида (?k; ? + ?k). График функции y = tg x называется тангенсоидой.
4) Функция убывает на любом интервале вида (?k; ? + ?k). График функции y = tg x называется тангенсоидой.
«График функции Y X» — Шаблон параболы у = х2. Чтобы увидеть графики, щелкни мышкой. Пример 2. Построим график функции y = x2 + 1, опираясь на график функции y=x2 (щелчок мышкой). Пример 3. Докажем, что графиком функции у = х2 + 6х + 8 является парабола, и построим график. График функции y=(x — m)2 является параболой с вершиной в точке (m; 0).
«Математика графики» — Как можно строить графики? Наиболее естественно функциональные зависимости отражаются с помощью графиков. Интересное применение: рисунки,… Зачем мы изучаем графики? Графики элементарных функций. Что вы можете нарисовать с помощью графиков? Рассматриваем применение графиков в учебных предметах: математике, физике,…
«Построение графиков с помощью производной» — Обобщение. Построить эскиз графика функции. Найти асимптоты графика функции. График производной функции. Дополнительное задание. Исследовать функцию.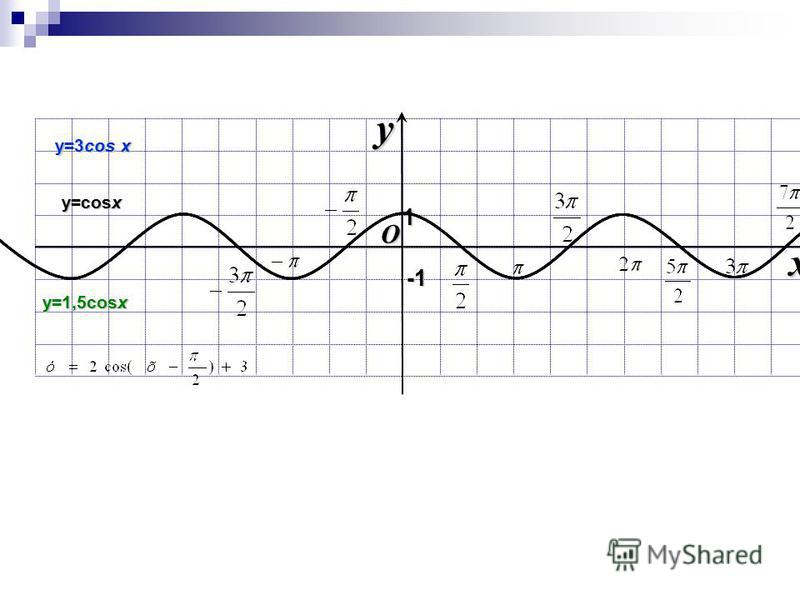 Назвать промежутки убывания функции. Самостоятельная работа учащихся. Расширить знания. Урок закрепления изученного материала. Оцените свои умения. Точки максимума функции.
Назвать промежутки убывания функции. Самостоятельная работа учащихся. Расширить знания. Урок закрепления изученного материала. Оцените свои умения. Точки максимума функции.
«Графики с модулем» — Отобрази «нижнюю» часть в верхнюю полуплоскость. Модуль действительного числа. Свойства функции y = |x|. |x|. Числа. Алгоритм построения графика функции. Алгоритм построения. Функция y= lхl. Свойства. Самостоятельная работа. Нули функции. Советы великих. Решение самостоятельной работы.
«Уравнение касательной» — Уравнение касательной. Уравнение нормали. Если,то и кривые пересекаются под прямым углом. Условия параллельности и перпендикулярности двух прямых. Угол между графиками функций. Уравнение касательной к графику функции в точке. Пусть функция дифференцируема в точке. Пусть прямые заданы уравнениями и.
Всего в теме 25 презентаций
Теперь мы рассмотрим вопрос о том, как строить графики тригонометрических функций кратных углов ωx , где ω — некоторое положительное число.
Для построения графика функции у = sin ωx сравним эту функцию с уже изученной нами функцией у = sin x . Предположим, что при х = x 0 функция у = sin х принимает значение, равное у 0 . Тогда
у 0 = sin x 0 .
Преобразуем это соотношение следующим образом:
Следовательно, функция у = sin ωx при х = x 0 / ω принимает то же самое значение у 0 , что и функция у = sin х при х = x 0 . А это означает, что функция у = sin ωx повторяет свои значения в ω раз чаще, чем функция у = sin x . Поэтому график функции у = sin ωx получается путем «сжатия» графика функции у = sin x в ω раз вдоль оси х.
Например, график функции у = sin 2х получается путем «сжатия» синусоиды у = sin x вдвое вдоль оси абсцисс.
График функции у = sin x / 2 получается путем «растяжения» синусоиды у = sin х в два раза (или «сжатия» в 1 / 2 раза) вдоль оси х.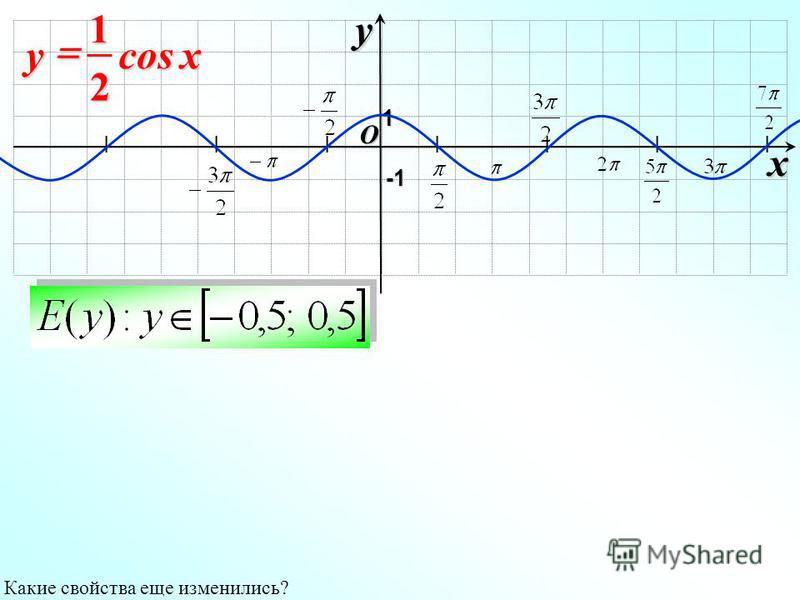
Поскольку функция у = sin ωx повторяет свои значения в ω раз чаще, чем функция
у = sin x , то период ее в ω раз меньше периода функции у = sin x . Например, период функции у = sin 2х равен 2π / 2 = π , а период функции у = sin x / 2 равен π
/ x / 2 = 4π .
Интересно провести исследование поведения функции у = sin аx на примере анимации, которую очень просто можно создать в программе Maple :
Аналогично строятся графики и других тригонометрических функций кратных углов. На рисунке представлен график функции у = cos 2х , который получается путем «сжатия» косинусоиды у = cos х в два раза вдоль оси абсцисс.
График функции у = cos x / 2 получается путем «растяжения» косинусоиды у = cos х вдвое вдоль оси х.
На рисунке вы видите график функции у = tg 2x , полученный «сжатием» тангенсоиды у = tg x вдвое вдоль оси абсцисс.
График функции у = tg x / 2 , полученный «растяжением» тангенсоиды у = tg x вдвое вдоль оси х.
И, наконец, анимация, выполненная программой Maple:
Упражнения
1. Построить графики данных функций и указать координаты точек пересечения этих графиков с осями координат. Определить периоды данных функций.
а). y = sin 4x / 3 г). y = tg 5x / 6 ж). y = cos 2x / 3
б). у= cos 5x / 3 д). у = ctg 5x / 3 з). у= ctg x / 3
в). y = tg 4x / 3 е). у = sin 2x / 3
2. Определить периоды функций у = sin (πх) и у = tg ( πх / 2 ).
3. Приведите два примера функции, которые принимают все значения от -1 до +1 (включая эти два числа) и изменяются периодически с периодом 10.
4 *. Приведите два примера функций, которые принимают все значения от 0 до 1 (включая эти два числа) и изменяются периодически с периодом π / 2 .
5. Приведите два примера функций, которые принимают все действительные значения и изменяются периодически с периодом 1.
6 *. Приведите два примера функций, которые принимают все отрицательные значения и нуль, но не принимают положительные значения и изменяются периодически с периодом 5.
Преобразование графиков элементарных функций
Основные элементарные функции в чистом виде без преобразования встречаются редко, поэтому чаще всего приходится работать с элементарными функциями, которые получили из основных с помощью добавления констант и коэффициентов. Такие графики строятся при помощи геометрических преобразований заданных элементарных функций.
Рассмотрим на примере квадратичной функции вида y=-13x+232+2, графиком которой является парабола y=x2, которая сжата втрое относительно Оу и симметрична относительно Ох, причем сдвинутую на 23 по Ох вправо, на 2 единицы по Оу вверх. На координатной прямой это выглядит так:
Геометрические преобразования графика функции
Применяя геометрические преобразования заданного графика получаем, что график изображается функцией вида ±k1·f(±k2·(x+a))+b, когда k1>0, k2>0 являются коэффициентами сжатия при 0<k1<1, 0<k2<1 или растяжения при k1>1, k2>1 вдоль Оу и Ох.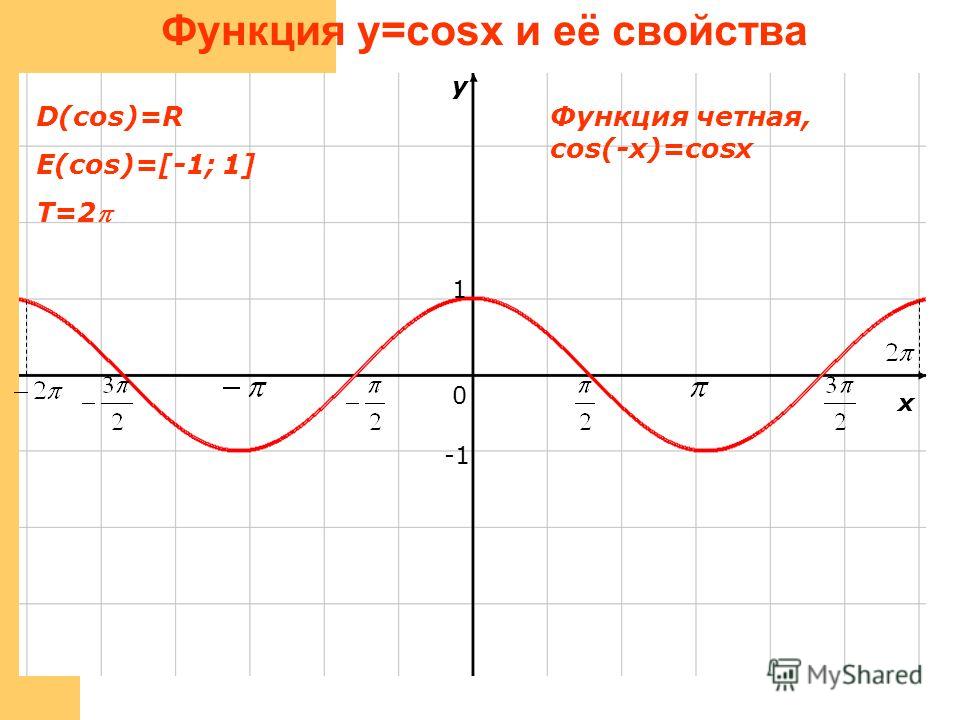 Знак перед коэффициентами k1 и k2 говорит о симметричном отображении графика относительно осей, a и b сдвигают ее по Ох и по Оу.
Знак перед коэффициентами k1 и k2 говорит о симметричном отображении графика относительно осей, a и b сдвигают ее по Ох и по Оу.
Существует 3 вида геометрических преобразований графика:
- Масштабирование вдоль Ох и Оу. На это влияют коэффициенты k1 и k2 при условии не равности 1, когда 0<k1<1, 0<k2<1, то график сжимается по Оу, а растягивается по Ох, когда k1>1, k2>1, то график растягивается по Оу и сжимается по Ох.
- Симметричное отображение относительно координатных осей. При наличии знака «-» перед k1 симметрия идет относительно Ох, перед k2 идет относительно Оу. Если «-» отсутствует, тогда пункт при решении пропускается;
- Параллельный перенос (сдвиг) вдоль Ох и Оу. Преобразование производится при наличии коэффициентов a и b неравных 0. Если значение a положительное, до график сдвигается влево на |а|единиц, если отрицательное a, тогда в право на такое же расстояние. Значение b определяет движение по оси Оу, что значит при положительном b функция движется вверх, при отрицательном – вниз.

Степенная функция
Рассмотрим решения на примерах, начиная со степенной функции.
Пример 1Преобразовать y=x23 и построить график функции y=-12·8x-423+3.
Решение
Представим функции таким образом:
y=-12·8x-423+3=-12·8x-1223+3=-2x-1223+3
Где k1=2, стоит обратить внимание на наличие «-», а=-12 , b=3. Отсюда получаем, что геометрические преобразования производятся с растяжения вдоль Оу вдвое, отображается симметрично относительно Ох, сдвигается вправо на 12 и вверх на 3 единицы.
Если изобразить исходную степенную функцию, получим, что
при растягивании вдвое вдоль Оу имеем, что
Отображение, симметричное относительно Ох, имеет вид
а движение вправо на 12
движение на 3 единицы вверх имеет вид
Показательная функция
Преобразования показательной функции рассмотрим на примерах.
Пример 2Произвести построение графика показательной функции y=-1212(2-x)+8.
Решение.
Преобразуем функцию, исходя из свойств степенной функции. Тогда получим, что
y=-1212(2-x)+8=-12-12x+1+8=-12·12-12x+8
Отсюда видно, что получим цепочку преобразований y=12x:
y=12x→y=12·12x→y=12·1212x→→y=-12·1212x→y=-12·12-12x→→y=-12·12-12x+8
Получаем, что исходная показательная функция имеет вид
Сжимание вдвое вдоль Оу дает
Растягивание вдоль Ох
Симметричное отображение относительно Ох
Отображение симметрично относительно Оу
Сдвигание на 8 единиц вверх
Логарифмическая функция
Рассмотрим решение на примере логарифмической функции y=ln(x).
Пример 3Построить функцию y=lne2·-12×3 при помощи преобразования y=ln(x).
Решение
Для решения необходимо использовать свойства логарифма, тогда получаем:
y=lne2·-12×3=ln(e2)+ln-12×13=13ln-12x+2
Преобразования логарифмической функции выглядят так:
y=ln(x)→y=13ln(x)→y=13ln12x→→y=13ln-12x→y=13ln-12x+2
Изобразим график исходной логарифмической функции
Производим сжимание строе по Оу
Производим растягивание вдоль Ох
Производим отображение относительно Оу
Производим сдвигание вверх на 2 единицы, получаем
Для преобразования графиков тригонометрической функции необходимо подгонять под схему решения вида ±k1·f(±k2·(x+a))+b. Необходимо , чтобы k2 приравнивался к Tk2. Отсюда получаем, что 0<k2<1 дает понять, что график функции увеличивает период по Ох, при k1 уменьшает его. От коэффициента k1 зависит амплитуда колебаний синусоиды и косинусоиды.
Необходимо , чтобы k2 приравнивался к Tk2. Отсюда получаем, что 0<k2<1 дает понять, что график функции увеличивает период по Ох, при k1 уменьшает его. От коэффициента k1 зависит амплитуда колебаний синусоиды и косинусоиды.
Преобразования y = sin x
Рассмотрим примеры решения заданий с преобразованиями y=sinx.
Пример 4Построить график y=-3sin12x-32-2 с помощью преобразований функции y=sinx.
Решение
Необходимо привести функцию к виду ±k1·f±k2·x+a+b. Для этого:
y=-3sin12x-32-2=-3sin12(x-3)-2
Видно, что k1=3, k2=12, a=-3, b=-2. Так как перед k1 имеется «-», а перед k2 — нет, тогда получим цепочку преобразований вида:
y=sin(x)→y=3sin(x)→y=3sin12x→y=-3sin12x→→y=-3sin12x-3→y=-3sin12(x-3)-2
Подробное преобразование синусоиды. При построении графика исходной синусоиды y=sin(x) получаем, что наименьшим положительным периодом считается T=2π. Нахождение максимума в точках π2+2π·k; 1, а минимума — -π2+2π·k; -1, k∈Z.
Производится растягивание по Оу втрое, значит возрастание амплитуды колебаний возрастет в 3 раза.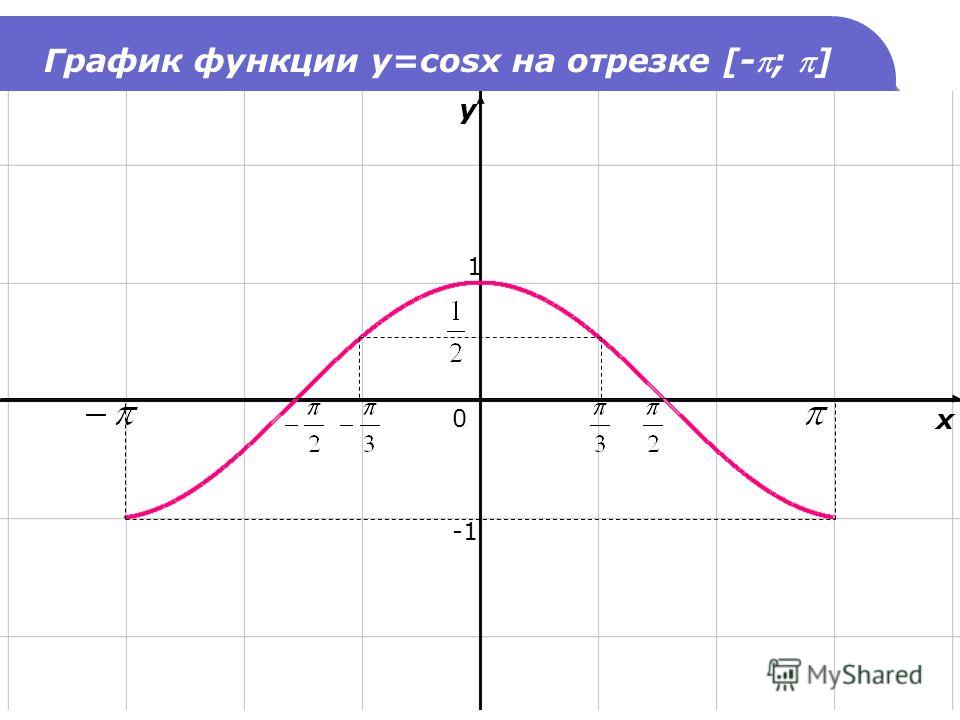 T=2π — это наименьший положительный период. Максимумы переходят в π2+2π·k; 3, k∈Z , минимумы — -π2+2π·k; -3, k∈Z.
T=2π — это наименьший положительный период. Максимумы переходят в π2+2π·k; 3, k∈Z , минимумы — -π2+2π·k; -3, k∈Z.
При растягивании по Ох вдвое получаем, что наименьший положительный период увеличивается в 2 раза и равняется T=2πk2=4π. Максимумы переходят в π+4π·k; 3, k∈Z, минимумы – в -π+4π·k; -3, k∈Z.
Изображение производится симметрично относительно Ох. Наименьший положительный период в данном случае не меняется и равняется T=2πk2=4π. Переход максимума выглядит как -π+4π·k; 3, k∈Z, а минимума – π+4π·k; -3, k∈Z.
Производится сдвижение графика вниз на 2 единицы. Изменение наименьшего общего периода не происходит. Нахождение максимумов с перехождением в точки -π+3+4π·k; 1, k∈Z, минимумов — π+3+4π·k; -5, k∈Z.
На данном этапе график тригонометрической функции считается преобразованным.
Преобразование функции y = cos x
Рассмотрим подробное преобразование функции y=cosx.
Пример 5Построить график функции y=32cos2-2x+1 при помощи преобразования функции вида y=cosx.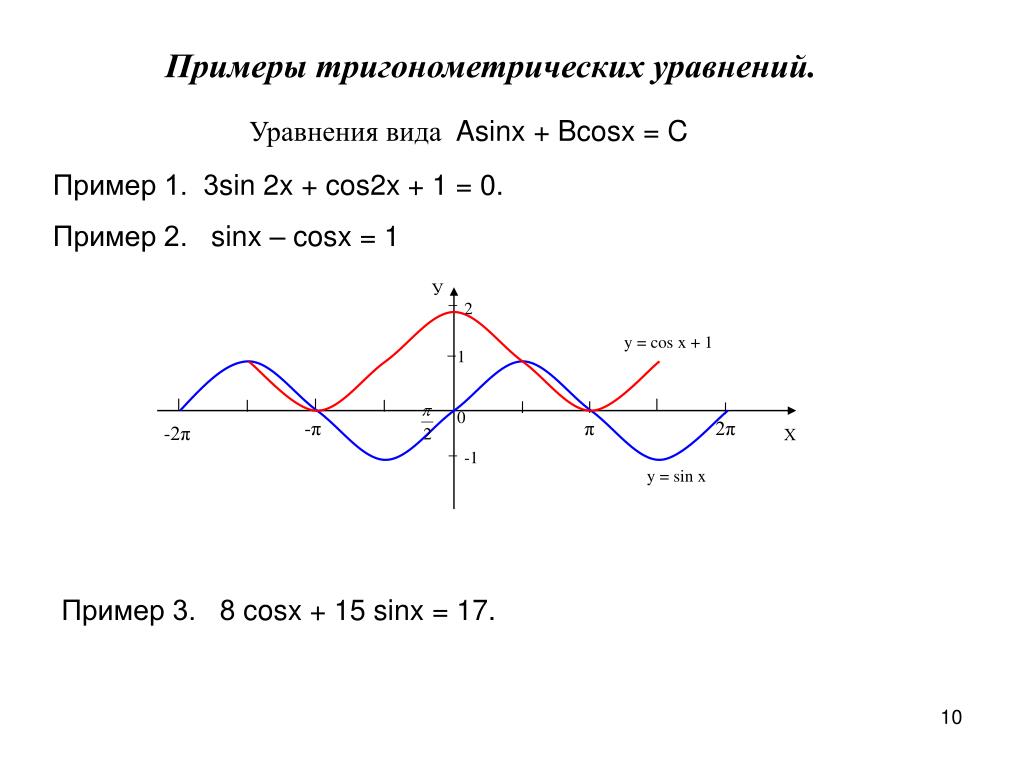
Решение
По алгоритму необходимо заданную функцию привести к виду ±k1·f±k2·x+a+b. Тогда получаем, что
y=32cos2-2x+1=32cos(-2(x-1))+1
Из условия видно, что k1=32, k2=2, a=-1, b=1, где k2 имеет «-», а перед k1 он отсутствует.
Отсюда получаем, что получится график тригонометрической функции вида:
y=cos(x)→y=32cos(x)→y=32cos(2x)→y=32cos(-2x)→→y=32cos(-2(x-1))→y=32cos-2(x-1)+1
Пошаговое преобразование косинусоиды с графической иллюстрацией.
При заданной графике y=cos(x) видно, что наименьший общий период равняется T=2π. Нахождение максимумов в 2π·k; 1, k∈Z, а минимумов π+2π·k; -1, k∈Z.
При растягивании вдоль Оу в 32 раза происходит возрастание амплитуды колебаний в 32 раза.T=2π является наименьшим положительным периодом. Нахождение максимумов в 2π·k; 32, k∈Z, минимумов в π+2π·k; -32, k∈Z.
При сжатии вдоль Ох вдвое получаем, что наименьшим положительным периодом является число T=2πk2=π. Производится переход максимумов в π·k; 32, k∈Z,минимумов — π2+π·k; -32, k∈Z.
Симметричное отображение относительно Оу. Так как график нечетный, то он не будет изменяться.
При сдвигании графика на 1. Отсутствуют изменения наименьшего положительного периода T=π. Нахождение максимумов в π·k+1; 32, k∈Z, минимумов — π2+1+π·k; -32, k∈Z.
При сдвигании на 1 наименьший положительный период равняется T=π и не изменен. Нахождение максимумов в π·k+1; 52, k∈Z, минимумов в π2+1+π·k; -12, k∈Z.
Преобразования функции косинуса завершено.
Преобразования y = tgx
Рассмотрим преобразования на примере y=tgx.
Пример 6Построить график функции y=-12tgπ3-23x+π3 при помощи преобразований функции y=tg(x).
Решение
Для начала необходимо привести заданную функцию к виду ±k1·f±k2·x+a+b, после чего получаем, что
y=-12tgπ3-23x+π3=-12tg-23x-π2+π3
Отчетливо видно, что k1=12, k2=23, a=-π2, b=π3, а перед коэффициентами k1 и k2 имеется «-». Значит, после преобразования тангенсоиды получаем
y=tg(x)→y=12tg(x)→y=12tg23x→y=-12tg23x→→y=-12tg-23x→y=-12tg-23x-π2→→y=-12tg-23x-π2+π3
Поэтапное преобразование тангенсоиды с графическим изображением.
Имеем, что исходный график – это y=tg(x). Изменение положительного периода равняется T=π. Областью определения считается -π2+π·k; π2+π·k, k∈Z.
Сжимаем в 2 раза вдоль Оу. T=π считается наименьшим положительным периодом, где область определения имеет вид -π2+π·k; π2+π·k, k∈Z.
Растягиваем вдоль Ох в 32 раза. Вычислим наименьший положительный период, причем равнялся T=πk2=32π. А область определения функции с координатами -3π4+32π·k; 3π4+32π·k, k∈Z , меняется только область определения.
Симметрия идет по сторону Ох. Период не изменится в этот момент.
Необходимо симметрично отображать оси координат. Область определения в данном случае неизменна. График совпадает с предыдущим. Это говорит о том, что функция тангенса нечетная. Если к нечетной функции задать симметричное отображение Ох и Оу, тогда преобразуем до исходной функции.
При движении вправо на π2 видим, что наименьшим положительным периодом является T=32π. А изменения происходят внутри области определения -π4+32π·k; 5π4+32π·k, k∈Z.
При сдвигании графика на π3 получаем, что изменение области определения отсутствует.
Преобразование тангенса завершено.
Тригонометрическая функция вида y=arccosx
Рассмотрим на примере тригонометрической функции вида y=arccosx.
Пример 7Построить график функции y=2arcsin13(x-1) при помощи преобразования y=arccosx.
Решение
Для начала необходимо перейти от арккосинуса к арксинусу при помощи обратных тригонометрических функций arcsin x+arcocos x=π2. Значит, получим, что arcsinx=π2-arccosx.
Видно, что y=arccosx→y=-arccosx→y=-arccosx+π2.
Поэтапное преобразование арккосинуса и графическое изображение.
График, данный по условию
Производим отображение относительно Ох
Производим движение вверх на π2.
Таким образом, осуществляется переход от арккосинуса к косинусу. Необходимо произвести геометрические преобразования арксинуса и его графика.
Видно, что k1=2, k2=13, a=-1, b=0, где отсутствует знак «-» у k1 и k2.
Отсюда получаем, что преобразования y=arcsinx примет вид:
y=arcsin(x)→y=2arcsin(x)→→y=2arcsin13x→y=2arcsin13(x-1)
Поэтапное преобразование графика арксинуса и графическое изображение.
График y=arcsinx имеет область определения вида x∈-1; 1, тогда интервал y∈-π2; π2 относится к области значений.
Необходимо растянуть вдвое по Оу, причем область определения останется неизменной x∈-1; 1, а область значений y∈-π; π.
Растягивание по Ох строе. Происходит расширение области определения x∈-3; 3, но область значений остается неизменной y∈-π; π.
Производим сдвигание вправо на 1, причем область определения становится равной x∈-2; 4. Без изменений остается область значений y∈-π; π.
Задача преобразования графика обратной тригонометрической функции завершена. Если по условию имеются сложные функции, тогда необходимо прибегнуть к полному исследованию функция.
Решение задач
от 1 дня / от 150 р. Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Автор: Ирина Мальцевская
Преподаватель математики и информатики.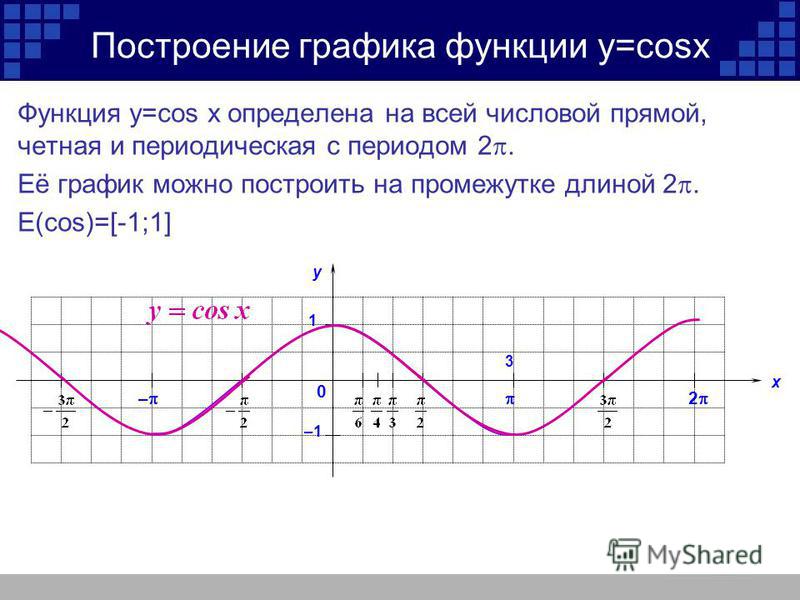 Кафедра бизнес-информатики Российского университета транспорта
Кафедра бизнес-информатики Российского университета транспорта
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт.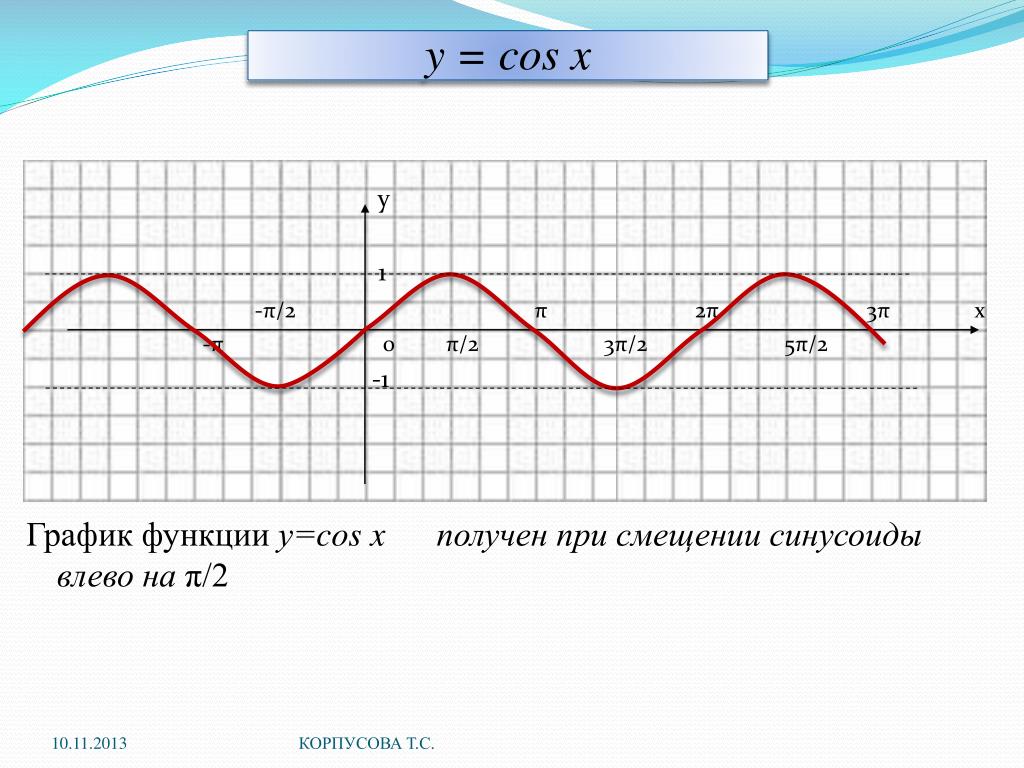 )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан( квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | соз(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | Преобразование градусов в радианы 92 | ||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан( квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
Лучшая математика
Навигация
- Home
- Год 12 (13 NZ, KS 5)
- Год 12 Темы
- ТРИГОМОМОМОМАТИЧЕСКИЙ Уравнение
- потому что 0 = 1 ⇒ 0 = потому что -1 (1)
- , потому что π/3 = 1/2 ⇒ π/3 = потому что -1 (1/2)
- , потому что π/2 = 0 ⇒ π/2 = потому что -1 (0)
- , потому что π = -1 ⇒ π = потому что -1 (-1)
- Когда x = 0, y = π/2
- Когда x = 1/2, y = π/3
- Когда х = 1, у = 0
- Когда x = -1, y = π г.
- Когда x = -1/2, y = 2π/3
- cos(cos -1 x) = x, только если x ∈ [-1, 1] (когда x ∉ [-1, 1], cos(cos -1 x) НЕ определено)
- cos -1 (cos x) = x, только когда x ∈ [0, π] (когда x ∉ [0, π], примените тригонометрические тождества, чтобы найти эквивалентный угол x, лежащий в [0, π ])
- , потому что -1 (-x) = π — потому что -1 x
- cos -1 (1/x) = сек -1 x, когда |x| ≥ 1
- грех -1 x + cos -1 x = π/2, когда x ∈ [-1, 1]
- d(cos -1 x)/dx = -1/√(1 — x 2 ), -1 < x < 1
- ∫cos -1 x dx = x cos -1 x — √(1 — x²) + C
- Инверсный косинус НЕ совпадает с (cos x) -1 как (cos x) -1 = 1/(cos x) = sec x.

- θ = cos -1 [ (прилежащая сторона) / (гипотенуза) ], θ ∈ [0, π] г.
- d(cos -1 x)/dx = -1/√(1 — x 2 ), -1 < x < 1
- ∫cos -1 x dx = x cos -1 x — √(1 — x²) + C
- , потому что -1 (-x) = π — потому что -1 x
- sin cos tan
- Тригонометрические функции
- Закон синусов
- Тригонометрическая таблица
- у = грех х
- Корни или нули y = sin x кратны π
- График sin проходит ось x одинаково sin x = 0 в этом месте
- Менструация синуса функции 2π
- г. Высота кривой в каждой точке равна линейному значению синуса
- Оба принимают один и тот же изгиб, сдвинутый вперед по оси x.

- Оба имеют амплитуду 1
- Примите за
йод 360
° или 2π радиан - г = загар х
- График касательной имеет неопределённую амплитуду, если изгиб стремится к бесконечности
- У него также есть менструация o
f 180
°, т.е. на восток. № - Синус
- Косинус
- Тангенс
- Косеканс
- секанс
- Котангенс
- Это ударенное значение любого числа, умноженное на информатику на тригонометрическую часть.

- Высота от средней линии до пика (или впадины) выбирается по амплитуде. г.
- Вы также можете измерить высоту от самых высоких до обычных точек, а затем разделить информационные технологии на 2.
- Это в основном говорит о том, насколько альпийским или коротким является поворот.
- Также обратите внимание, что функция находится в обычной ориентации или перевернута в зависимости от знака минус или плюс значения амплитуды.
- Максимальная и минимальная точки поворота.
Выберите All Front Matter
Полный текст
13.
 Выберите All Front Matter
Выберите All Front Matter.
Copyright
ПРЕДИСЛОВИЕ
ПРЕПОДАВАТЕЛЮ
Выберите ОДИН — ПРЕДВАРИТЕЛЬНЫЕ ЗАДАНИЯ
Глава книгиТолько реферат
ОДИН — ПРЕДВАРИТЕЛЬНЫЕ ЗАДАНИЯ
Страницы 1-52
Выбрать два — ограничения и производные
Книга Глава.
ТРИ — ЕЩЕ О ПРОИЗВОДНЫХ
Страницы 134-183
Выбрать ЧЕТЫРЕ — ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ
Глава книгиТолько реферат
ЧЕТЫРЕ — ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ
Страницы 184-249
SELECT FIVE — Интегральная
Книга Глава. — ЭКСПОНЕНТЫ И ЛОГАРИФМЫ
Страницы 324-383
Выберите СЕМЬ — ТРИГОНОМЕТРИЧЕСКИЕ И ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
Глава книгиТолько реферат
2805
Страницы 384-425
Выбрать восемь — методы интеграции
Книга Глава. только главаAbstract
ДЕВЯТЬ — ДОПОЛНИТЕЛЬНЫЕ ПРИМЕНЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Страницы 482-525
Выберите ДЕСЯТЬ — ТЕМЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ
Книга Глава.
 — НЕОПРЕДЕЛЕННЫЕ ФОРМЫ И СОБСТВЕННЫЕ ИНТЕГРАЛЫ
— НЕОПРЕДЕЛЕННЫЕ ФОРМЫ И СОБСТВЕННЫЕ ИНТЕГРАЛЫГлава книгиТолько реферат
ДВЕНАДЦАТЬ — НЕОПРЕДЕЛЕННЫЕ ФОРМЫ И СОБСТВЕННЫЕ ИНТЕГРАЛЫ
Страницы 576-598
Выбор тринадцать — полиномов Тейлора и приближения
Книга Глава.
Страницы 614-667
Выбрать ПЯТНАДЦАТЬ — ВЕКТОРЫ НА ПЛОСКОСТИ
Глава книгиТолько реферат
ПЯТНАДЦАТЬ — ВЕКТОРЫ НА ПЛОСКОСТИ
Страницы 668-688
Выбрать шестнадцать — векторные функции, векторная дифференциация и параметрические уравнения
ГЛАВА ГЛАВА Выберите СЕМНАДЦАТЬ — ВЕКТОРЫ В ПРОСТРАНСТВЕ
Глава книгиТолько реферат
СЕМНАДЦАТЬ — ВЕКТОРЫ В ПРОСТРАНСТВЕ
Страницы 739-792
1831
Книга Глава Абстракт только
Восемнадцать — дифференциация функций двух и трех переменных
Страницы 793-876
SELECT NINETEEN — Несколько интеграций
ГЛАВА ГЛАВА.

Выберите ДВАДЦАТЬ — ВВЕДЕНИЕ В ВЕКТОРНЫЙ АНАЛИЗ
Глава книгиТолько реферат
ДВАДЦАТЬ — ВВЕДЕНИЕ В ВЕКТОРНЫЙ АНАЛИЗ
Страниц 928-989
Выбрать двадцать один-обычные дифференциальные уравнения
Глава. доступ
ПРИЛОЖЕНИЕ 1 — ОБЗОР ТРИГОНОМЕТРИИ
Страницы A1-A14
Выбрать ПРИЛОЖЕНИЕ 2 — МАТЕМАТИЧЕСКАЯ ИНДУКЦИЯ
Глава книги Нет доступа
APPENDIX 2 — MATHEMATICAL INDUCTION
Pages A15-A18
Select APPENDIX 3 — DETERMINANTS
Book chapterNo access
APPENDIX 3 — DETERMINANTS
Pages A19-A28
Select APPENDIX 4 — THE BINOMIAL THEOREM
Глава книги Нет доступа
ПРИЛОЖЕНИЕ 4. ТЕОРЕМА О БИНОМЕ
Страницы A29-A31
Выбрать ПРИЛОЖЕНИЕ 5.1831
Книга Capterno Access
Приложение 5 — Доказательства некоторых теорем о пределах, непрерывности и дифференциации
Страницы A32 -A38
Select Appendix 6 — Комплексные номера
КОНФЕРСА.

- 1818181818 гг.
 х и загар х.
х и загар х.Их можно решить с помощью тригонометрических графиков и, при необходимости, калькулятора. Можно использовать другой метод, использующий общие решения.
Поскольку тригонометрические функции являются периодическими и продолжаются вечно, эти тригонометрические уравнения часто имеют бесконечное число решений, если область определения (значения x) не фиксирована. Обычно домен предоставляется.
Для иллюстрации различных методов, которые можно использовать, будет приведено несколько различных типов примеров. Решения даны в тех же единицах, в которых написан вопрос. Градусы или радианы.
Углы, используемые в особых треугольниках, часто встречаются в тригонометрических уравнениях и снова показаны ниже в качестве напоминания.
Особые треугольники
Такие углы, как 30 ° ( ), 45 ° ( ) и 60 ° ( ), используются часто, и тригонометрические отношения этих углов получаются из двух специальных треугольников (см.
 Блок 38, 12 год). Они приведены ниже:
Блок 38, 12 год). Они приведены ниже:sin 30°
cos 30°
желтовато-коричневый 30°
sin 45°
cos 45°
желтовато-коричневый 45°
sin 60°
cos 60°
желтовато-коричневый 60°
1
√3
Если ответы могут быть даны с использованием точных значений из специальных треугольников, они должны быть даны.
 Калькулятор следует использовать только в том случае, если не используются специальные углы треугольника.
Калькулятор следует использовать только в том случае, если не используются специальные углы треугольника.Тригонометрические уравнения
Пример 1
Решите sin x = 0,5 для 0° ≤ x ≤ 360°. Дайте ответы в градусах.
Рассмотрим функции y = sin x и прямую y = 0,5. Там, где встречаются линия и кривая, и будут решения. Калькулятор можно использовать, чтобы найти первое значение, найдя sin -1 (0,5)
Калькулятор можно использовать для первого решения 30° и второе решение, найденное из симметрии график (180 ° — 30° = 150°).
Набор решений {30°, 150°}
Аналогичные методы можно использовать для уравнений, содержащих косинус и тангенс.
Пример 2
Решите 2sin 2 x + sin x = 0 для 0 ≤ x ≤ 2π .
 Дайте ответы в радианах.
Дайте ответы в радианах. Это квадратное уравнение, поэтому, если возможно, разложите его на множители.
sin x(2sin x + 1) = 0
Имеется два набора решений:
sin x = 0 и 2sin x + 1 = 0, что дает sin x = -0,5Решения sin x = 0 равны 0, 3,14π и 2π
Решения sin x = -0,5 равны 7π/6 и 11π/6Набор решений составляет {0, π, 7π/6, 11π/6, 2π}
Пример 3
43 Solve nember 2x 218. Дайте ответы в терминах π .
Функция косинуса изолируется делением обеих частей на √2. Потому что 2 x необходимо изучить график cos x от 0 до 4π, чтобы найти все корни.
√ 2, потому что 2x = 1
потому что 2x = 1 / √ 2
Первое решение можно найти с помощью специальных треугольников выше или с помощью калькулятора.
 Остальные решения находятся из симметрии графа:
Остальные решения находятся из симметрии графа:2x = ,
2x = 2π − =
г.2x = 2π + =
2x = 4π − =
х =
х =
х =
х =
Набор решений {, , }
Пример 4
Решите sin 3x + sin x = 0 для 0 ≤ x ≤ 2π . Дайте ответы в терминах π .
Здесь используется формула суммы в произведение.

2sin 2x cos x = 0
Следовательно, sin 2x = 0 или cos x = 0
2x = {0, π, 2π, 3π, 4π} или x = { , }
Набор решений равен {0, , π , , 2π }
Обратный косинус – формула, график, примеры
Арккосинус — важная обратная тригонометрическая функция. Математически это записывается как cos -1 (x) и является обратной функцией тригонометрической функции косинуса, cos(x). Важно отметить, что арккосинус не является обратной величиной cos x. Существует 6 обратных тригонометрических функций: sin -1 x, cos -1 x, tan -1 x, csc -1 x, sec -1 x, cot -1 x.
Арккосинус используется для определения меры угла по значению тригонометрического отношения cos x. В этой статье мы разберемся с формулами функции арккосинуса, ее областью определения и диапазоном и, следовательно, с ее графиком.
 Мы также определим производную и интеграл от cos, обратный x, чтобы лучше понять его свойства.
Мы также определим производную и интеграл от cos, обратный x, чтобы лучше понять его свойства.1. Что такое арккосинус? 2. Домен и диапазон арккосинуса 3. График арккосинуса 4. Производная обратного косинуса x 5. Интеграл арккосинуса 6. Свойства арккосинуса 7. Часто задаваемые вопросы об арккосинусе Что такое арккосинус?
Арккосинус — это функция, обратная функции косинуса. Это одна из важных обратных тригонометрических функций. Cos, обратный x, также может быть записан как arccos x. Если y = cos x ⇒ x = cos -1 (y). Давайте рассмотрим несколько примеров, чтобы увидеть, как работает функция арккосинуса.
В прямоугольном треугольнике косинус угла (θ) равен отношению его прилежащей стороны к гипотенузе, то есть cos θ = (прилежащая сторона) / (гипотенуза).
 Используя определение арккосинуса, θ = cos -1 [(прилегающая сторона) / (гипотенуза)].
Используя определение арккосинуса, θ = cos -1 [(прилегающая сторона) / (гипотенуза)].Таким образом, арккосинус используется для нахождения неизвестных углов в прямоугольном треугольнике.
Домен и диапазон арккосинуса
Мы знаем, что областью определения функции косинуса является R, то есть все действительные числа, и ее диапазон [-1, 1]. Функция f(x) имеет обратную тогда и только тогда, когда она биективна (один-один и один). Поскольку cos x не является биективной функцией, поскольку она не является взаимно однозначной, арккосинус не может иметь R в качестве своего диапазона. Следовательно, нам нужно сделать функцию косинуса взаимно однозначной, ограничив ее область определения. Область определения функции косинуса можно ограничить до [0, π], [π, 2π], [-π, 0] и т. д. и получить соответствующую ветвь арккосинуса.
Область определения функции косинуса обычно ограничена [0, π], а ее диапазон остается равным [-1, 1]. Следовательно, ветвь cos, обратная x со значением [0, π], называется главной ветвью.
 Поскольку область определения и область значений функции становятся областью значений и областью значений ее обратной функции, соответственно, область определения арккосинуса равна [-1, 1], а ее область значений равна [0, π], то есть cos, обратная x, равна функция из [-1, 1] → [0, π].
Поскольку область определения и область значений функции становятся областью значений и областью значений ее обратной функции, соответственно, область определения арккосинуса равна [-1, 1], а ее область значений равна [0, π], то есть cos, обратная x, равна функция из [-1, 1] → [0, π].График арккосинуса
Поскольку область определения и область значений функции арккосинуса равны [-1, 1] и [0, π] соответственно, мы построим график косинуса, обратного х, в пределах главной ветви. Поскольку мы знаем значения функции косинуса для конкретных углов, мы будем использовать те же значения для построения точек и, следовательно, графика арккосинуса. Для y = cos -1 x имеем:
Cos, обратный x производная
Теперь определим производную функции арккосинуса, используя некоторые тригонометрические формулы и тождества.
 Предположим, что y = cos -1 x ⇒ cos y = x. Дифференцируйте обе части уравнения, потому что y = x по x, используя цепное правило. (1)
Предположим, что y = cos -1 x ⇒ cos y = x. Дифференцируйте обе части уравнения, потому что y = x по x, используя цепное правило. (1)Так как cos 2 y + sin 2 y = 1, то sin y = √(1 — cos 2 y) = √(1 — x 2 ) [Поскольку cos y = x]
Подставив sin y = √(1 — x 2 ) в (1), мы получим
dy/dx = -1/√(1 — x 2 )
знаменатель √(1 — x 2 ) равен 0, и, следовательно, производная не определена, поэтому x не может быть -1 и 1.
Следовательно, производная cos, обратная x, равна -1/√(1 — x 2 ), где -1 < x < 1
Интегрирование арккосинуса
Найдем интеграл арккосинуса, то есть ∫cos -1 x dx, используя интегрирование по частям (ILATE).
∫cos -1 x = ∫cos -1 x · 1 dx
Используя интегрирование по частям,
∫f(x) . g(x) dx = f(x) ∫g(x) dx − ∫(f′(x) ∫g(x) dx) dx + C
Здесь f(x) = cos -1 x и g (x) = 1,
∫cos -1 x · 1 dx = cos -1 x ∫1 dx — ∫ [d(cos -1 x)/dx ∫1 dx]dx + C
∫cos -1 x dx = cos — 1 х .
 (x) — ∫ [-1/√(1 — x²)] x dx + C
(x) — ∫ [-1/√(1 — x²)] x dx + CМы вычислим этот интеграл ∫ [-1/√(1 — x²)] x dx методом подстановки. Предположим 1-x 2 = u. Тогда -2x dx = du (или) x dx = -1/2 du.
∫cos -1 x dx = x cos -1 x — ∫(-1/√u) (-1/2) du + C
= x cos -1 x — 1/2 ∫u -1/2 du + C
= x cos -1 x — (1/2) (u 1/2 /(1/2)) + C
= x cos -1 x — √u + C
= x cos -1 x — √(1 — x²) + C
Следовательно, ∫cos -1 x dx = x cos -1 x — √(1 — x²) + C
Свойства арккосинуса
Некоторые свойства или формулы функции арккосинуса приведены ниже. Они очень полезны при решении задач, связанных с cos, обратным x, в тригонометрии.
Важные замечания по инверсному косинусу x
Связанные темы об арккосинусе
Часто задаваемые вопросы об арккосинусе
Что такое арккосинус в тригонометрии?
Обратный косинус — функция, обратная косинусу. Арккосинус x также может быть записан как cos -1 x или arccos x. Тогда по определению арккосинуса θ = cos -1 [(прилежащая сторона)/(гипотенуза)].
Что такое формула арккосинуса?
По определению арккосинуса θ = cos -1 [(прилежащая сторона)/(гипотенуза)].
 Здесь θ — угол между прилежащей стороной и гипотенузой и лежит между 0 и π.
Здесь θ — угол между прилежащей стороной и гипотенузой и лежит между 0 и π.Что такое производная арккосинуса?
Производная cos, обратная x, равна -1/√(1 — x 2 ), где -1 < x < 1. Ее можно вычислить с помощью цепного правила.
Что такое домен и диапазон арккосинуса?
Область определения арккосинуса – [-1, 1], поскольку диапазон функции косинуса – [-1, 1]. Диапазон cos, обратный x, cos – 1 x , равен [0, π]. Нам нужно сделать косинус функцией один-один, ограничив его область определения R главной ветвью [0, π], что делает диапазон арккосинуса равным [0, π].
Как вычислить интеграл арккосинуса?
Интеграл от cos, обратного х, можно вычислить с помощью интегрирования по частям. Интеграл арккосинуса задается выражением ∫cos -1 x dx = x cos -1 x — √(1 — x²) + C
Что такое косинус косинуса, обратный x?
Cos от cos, обратного x, равен x, то есть cos(cos -1 x) = x, если x ∈ [-1, 1].
 Если x ∉ [-1, 1], то cos(cos -1 x) не определен.
Если x ∉ [-1, 1], то cos(cos -1 x) не определен.Что такое арккосинус для Cos x?
Арккосинус cos x равен x, то есть cos -1 (cos x) = x, если x ∈ [0, π]. Если x ∉ [0, π], то примените тригонометрические тождества, чтобы найти эквивалентный угол x, лежащий в [0, π].
Sin X Cos X Tan X
Чтобы набросать тригонометрические графики функций – синуса, косинуса и тангенса, нам нужно знать поток, стадию, амплитуду, максимальную и минимальную точки поворота. Эти графики используются во многих областях техники и науки. Несколько примеров — рост животных и растений, двигателей и волн и т. д. Кроме того, у нас есть графики для всех
тригонометрические функции
.Графическое представление функций синуса, косинуса и тангенса здесь кратко объясняется с помощью соответствующего графика. Студенты могут узнать, как построить график тригонометрической функции здесь и далее с практическими вопросами, основанными на этом.
Графики тригонометрических функций
Синус, косинус и тангенс являются важными тригонометрическими соотношениями, на основании которых функции различаются.
 Ниже приведены графики трех тригонометрических функций sin x, cos x и tan x.
Ниже приведены графики трех тригонометрических функций sin x, cos x и tan x.На этих тригонометрических графиках центральные по оси x значения углов выражены в радианах, а по оси y берется ее f(x) — значение функции при каждом заданном угле.
График грехов
График CosМаксимальное значение графика Минимальное значение графика 1 в
π/2-1 в (три
π/2)Максимальное значение графика Минимальное значение графика один в 0, четыре π -один на 2
πМежду графиками синуса и косинуса есть несколько сходств:
Комбинированный график функции синуса и косинуса может быть представлен через каждый бит.
г.График загара
Управление загаром полностью отличается от функции sin and cos. Функция здесь проходит между отрицательной и положительной бесконечностью, пересекая 0 за период π радиан.
Графики тригонометрических функций
Тригонометрические функции vi:
Тригонометрические графики для этих тригонометрических функций можно построить, если вы знаете следующее:
Амплитуда
Период
Menstruum
переходит от любого сигнала (один пик) к следующему указанию совпадения.Ниже приведено графическое изображение потока и амплитуды роли.
г.Фаза
Насколько функция сдвинута от обычного положения
по горизонтали
называется Фазой.Приведенные выше условия слишком важны, чтобы использовать
график тригонометрических формул
.
Как нарисовать график тригонометрической части?
Для описания графика тригонометрической функции можно использовать различные методы. Подробное объяснение одного из эффективных методов приведено ниже.
г.Пока рисуете график синусоидальной функции, преобразуйте данную функцию в общую форму как
a sin (bx – c) + d
в золоте, чтобы обнаружить различные параметры, такие как амплитуда каждого бита, фазовый сдвиг, вертикальный сдвиг и менструации.
Где,
|а| = Амплитуда
2π/|b| = период
c/b = фазовый сдвиг
d = вертикальное смещение
Точно так же для функции косинуса мы можем использовать формулу
а cos (bx – c) + d
.Таким образом, графики всех шести тригонометрических функций выглядят так, как показано на рисунке ниже.
видео урок
Максимальное и минимальное значение тригонометрических функций
График функций триггера Упражнение
Позвольте попрактиковаться в том, что мы узнали в предыдущих параграфах, с несколькими вопросами графических функций тригонометрии.

1) Нарисуйте график
у = v sin 2x
°
+ 4два) Нарисуйте график числа
y = 4 cos 3x° + 7Чтобы получить больше, чем просто тригонометрию и связанные с ней понятия, зарегистрируйтесь на сайте BYJU’Southward.
Исчисление | ScienceDirect
ScienceDirectРегистрацияВойти
Книга • Второе издание • 1981
Авторы:
Стэнли И. Гроссман
Книга • Второе издание • 1981
Стрелка.
Исчисление, второе издание обсуждает методы и теоремы исчисления. В этом издании представлены функции синуса и косинуса, распределяются ?-? материал в течение нескольких глав, а … прочитать полное описание
Поиск в этой книге
Просмотр содержания
Соглашение
Действия для выбранных главах
Выберите All / Deselect All
- Год 12 Темы
- Год 12 (13 NZ, KS 5)




 х и загар х.
х и загар х.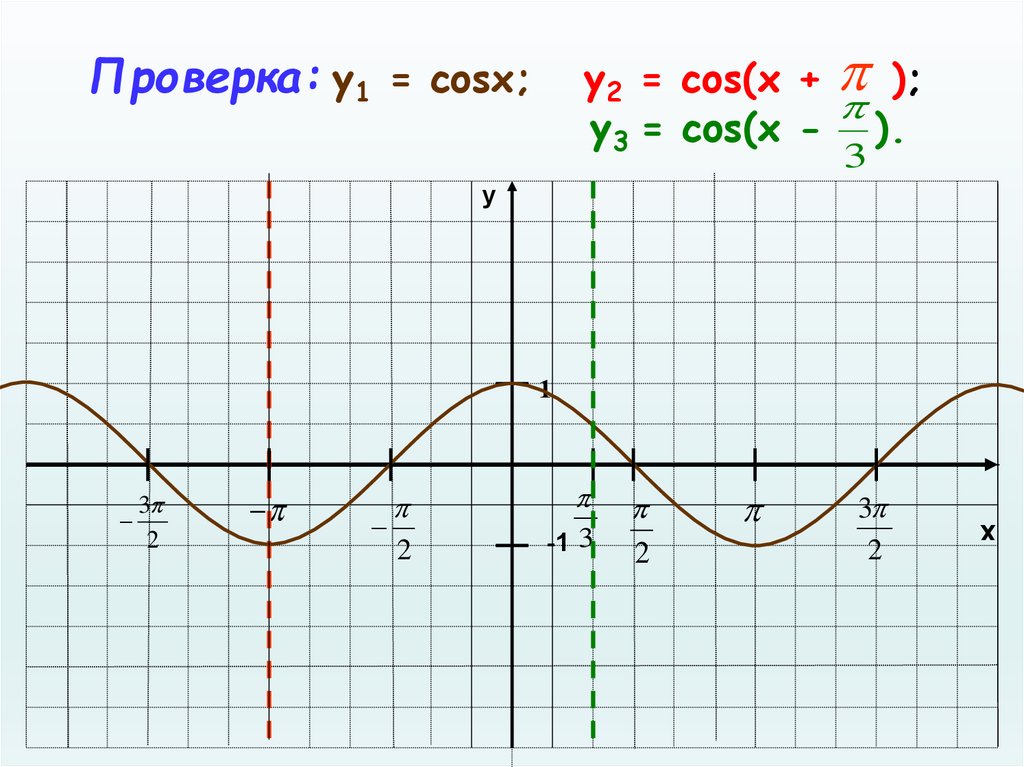 Блок 38, 12 год). Они приведены ниже:
Блок 38, 12 год). Они приведены ниже: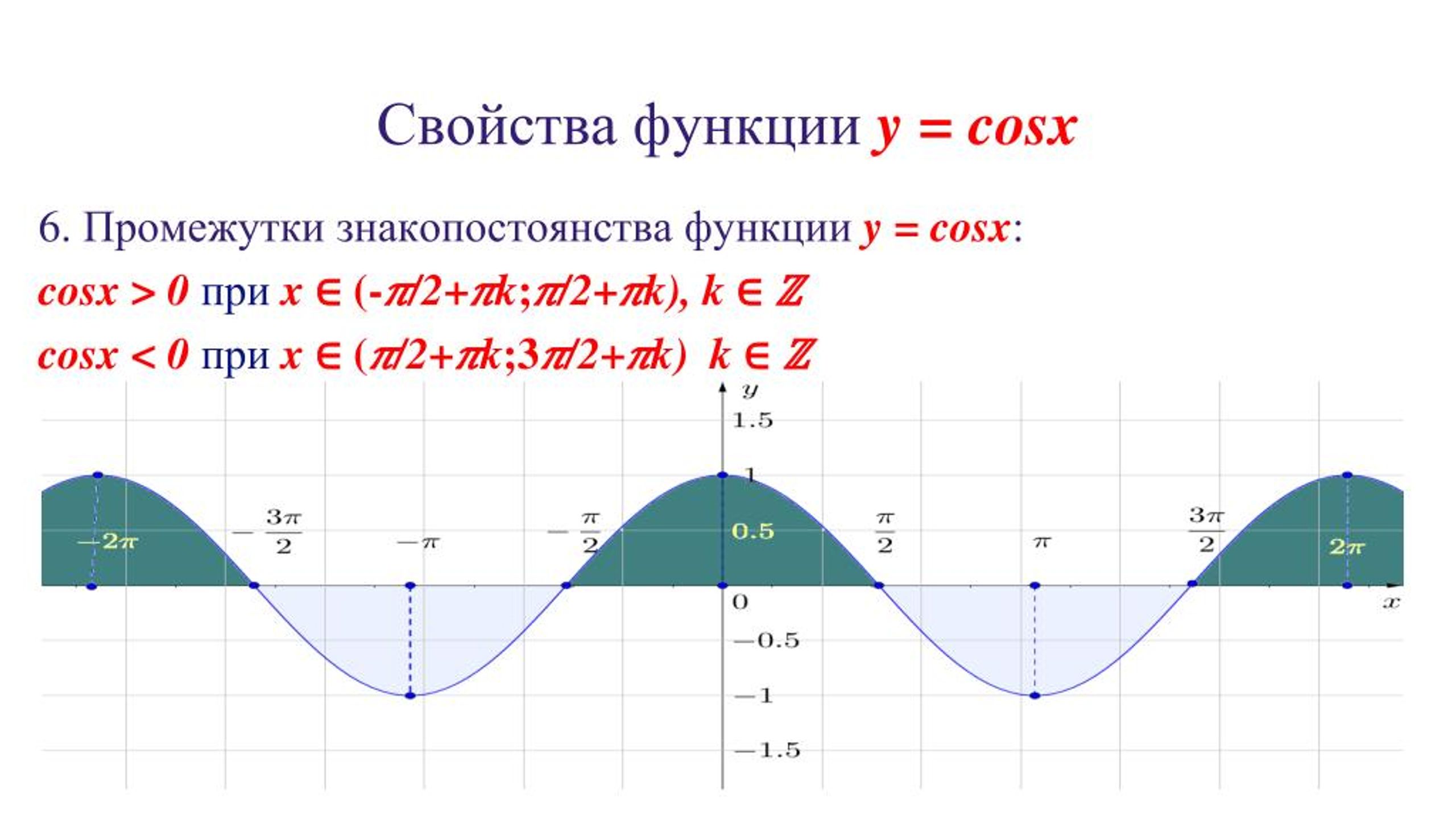 Калькулятор следует использовать только в том случае, если не используются специальные углы треугольника.
Калькулятор следует использовать только в том случае, если не используются специальные углы треугольника.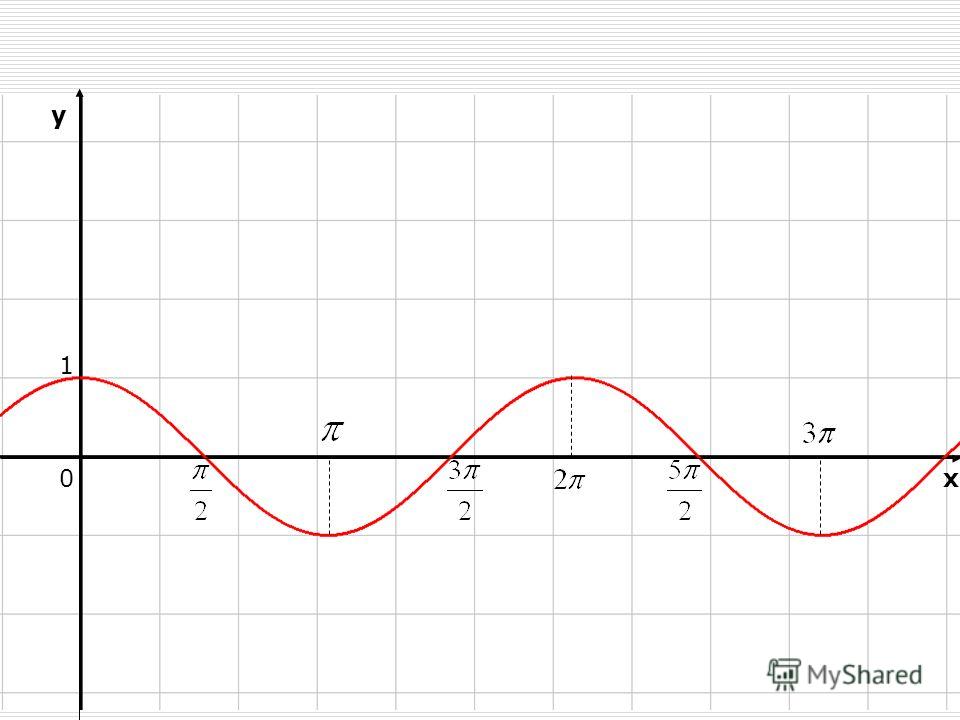 Дайте ответы в радианах.
Дайте ответы в радианах. 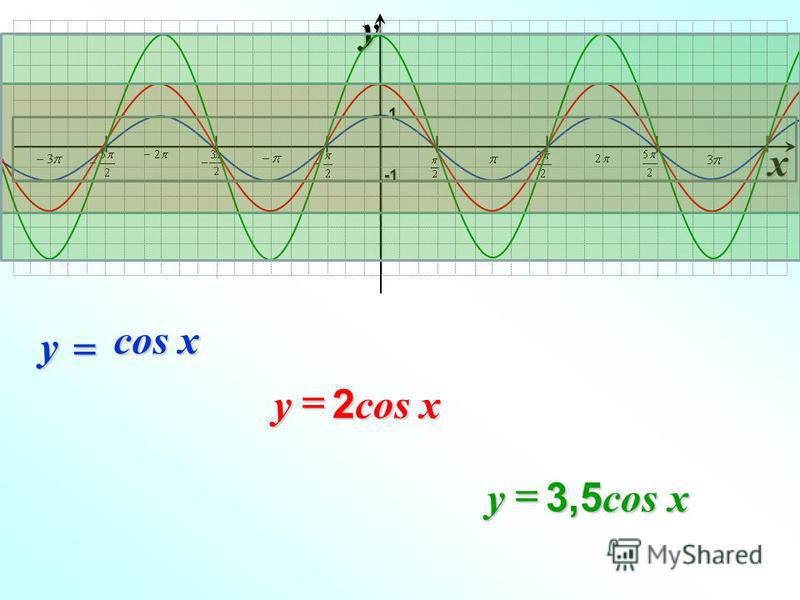 Остальные решения находятся из симметрии графа:
Остальные решения находятся из симметрии графа:
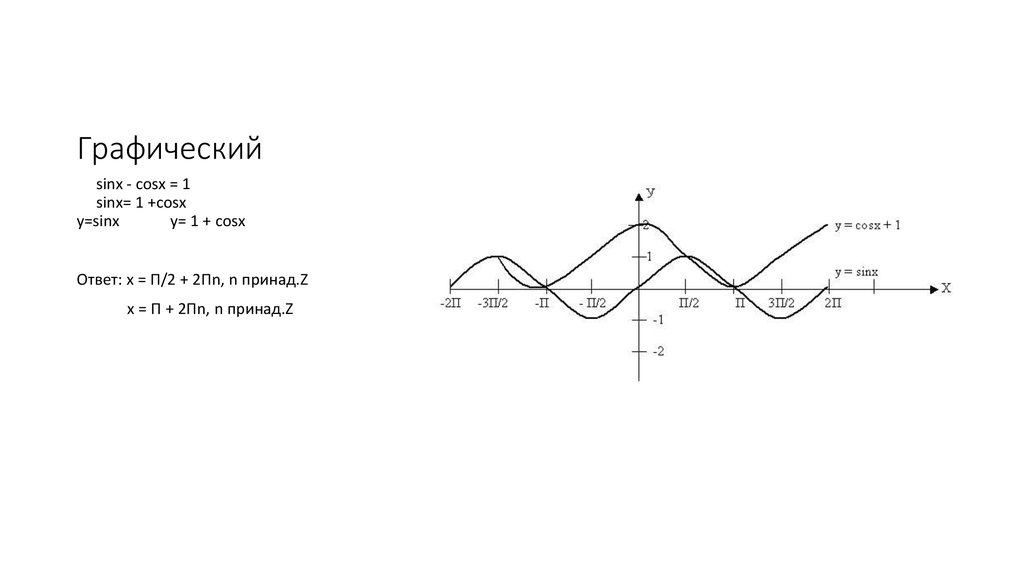 Мы также определим производную и интеграл от cos, обратный x, чтобы лучше понять его свойства.
Мы также определим производную и интеграл от cos, обратный x, чтобы лучше понять его свойства.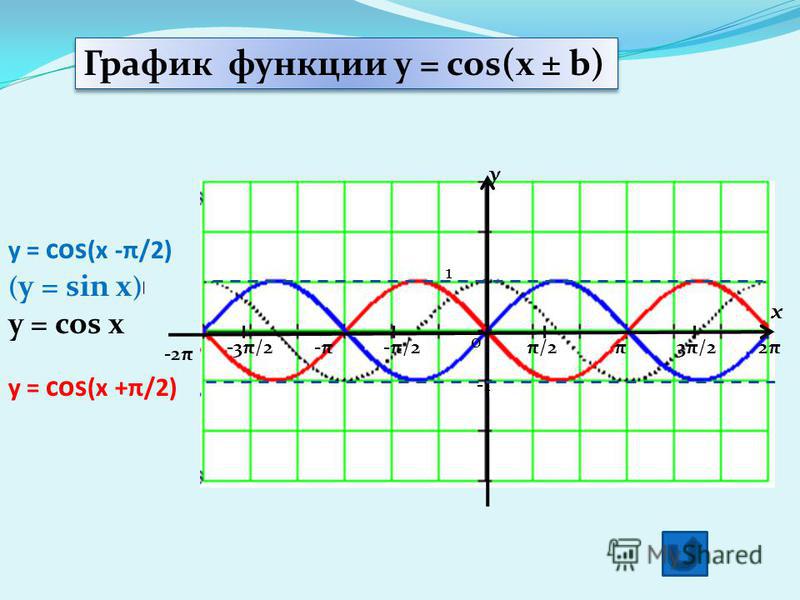 Используя определение арккосинуса, θ = cos -1 [(прилегающая сторона) / (гипотенуза)].
Используя определение арккосинуса, θ = cos -1 [(прилегающая сторона) / (гипотенуза)]. Поскольку область определения и область значений функции становятся областью значений и областью значений ее обратной функции, соответственно, область определения арккосинуса равна [-1, 1], а ее область значений равна [0, π], то есть cos, обратная x, равна функция из [-1, 1] → [0, π].
Поскольку область определения и область значений функции становятся областью значений и областью значений ее обратной функции, соответственно, область определения арккосинуса равна [-1, 1], а ее область значений равна [0, π], то есть cos, обратная x, равна функция из [-1, 1] → [0, π].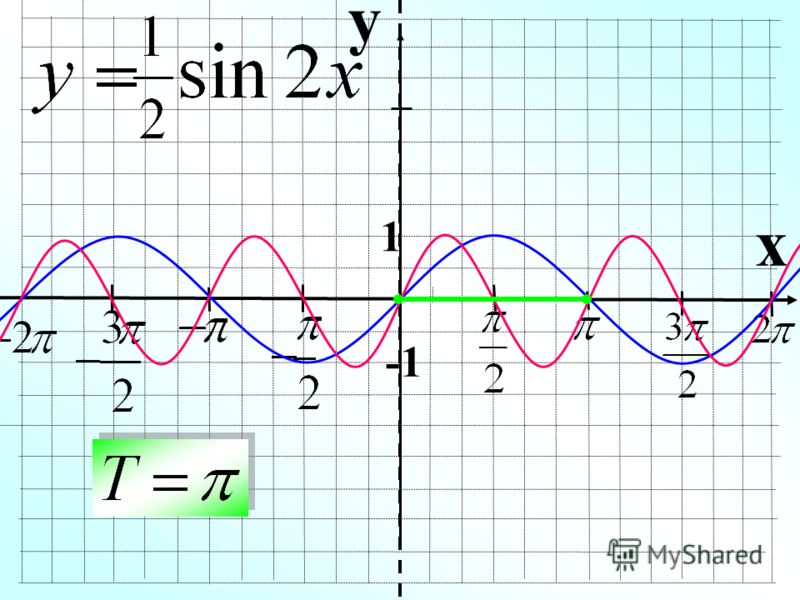 Предположим, что y = cos -1 x ⇒ cos y = x. Дифференцируйте обе части уравнения, потому что y = x по x, используя цепное правило. (1)
Предположим, что y = cos -1 x ⇒ cos y = x. Дифференцируйте обе части уравнения, потому что y = x по x, используя цепное правило. (1) (x) — ∫ [-1/√(1 — x²)] x dx + C
(x) — ∫ [-1/√(1 — x²)] x dx + C
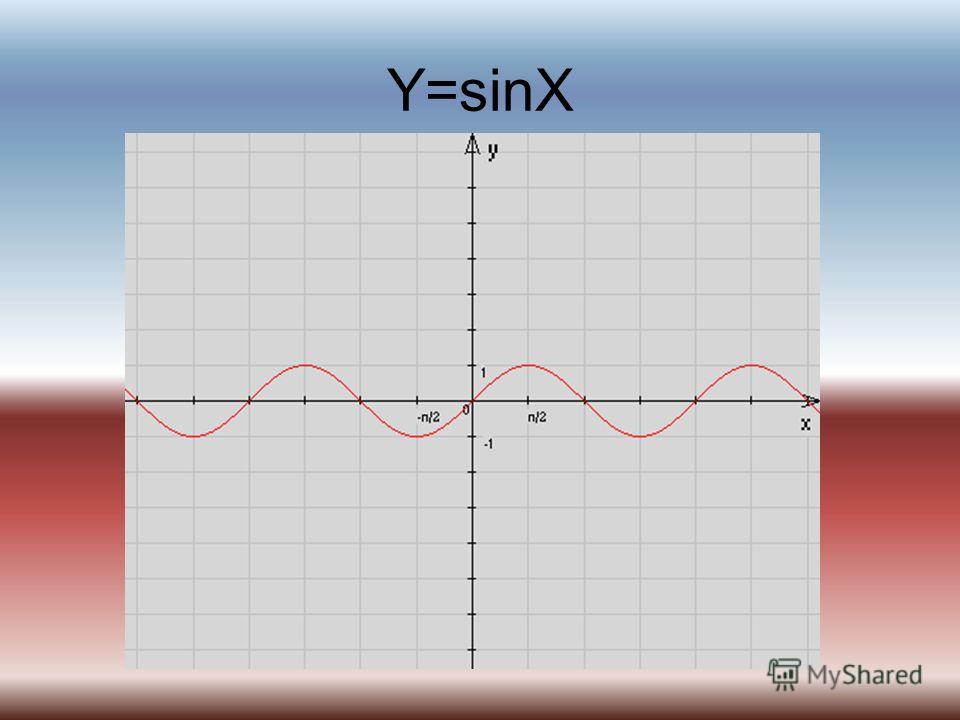 Здесь θ — угол между прилежащей стороной и гипотенузой и лежит между 0 и π.
Здесь θ — угол между прилежащей стороной и гипотенузой и лежит между 0 и π.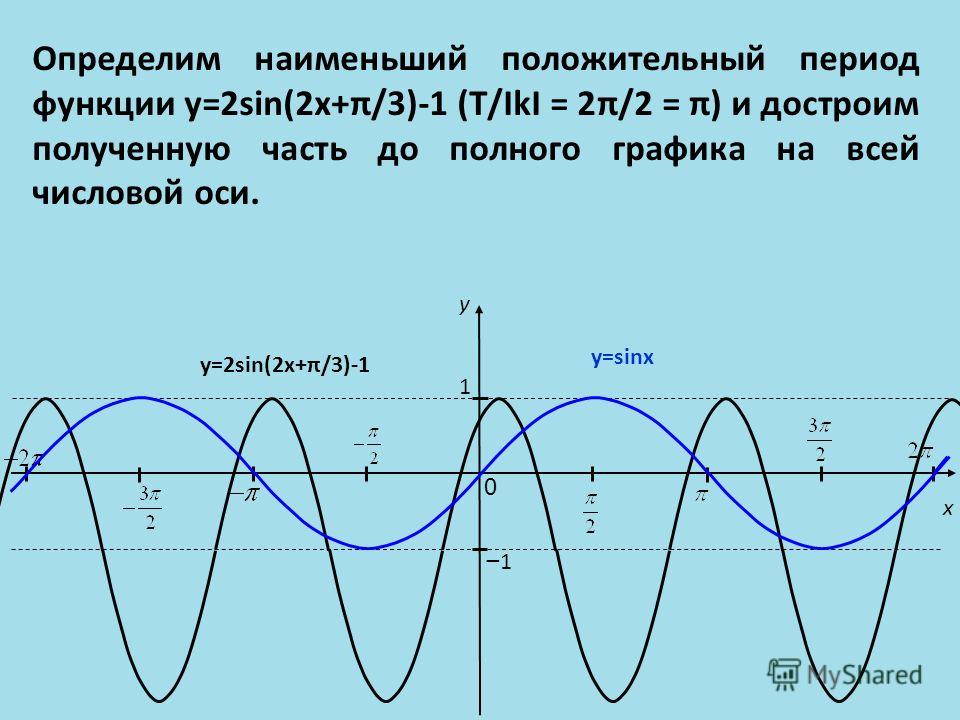 Если x ∉ [-1, 1], то cos(cos -1 x) не определен.
Если x ∉ [-1, 1], то cos(cos -1 x) не определен.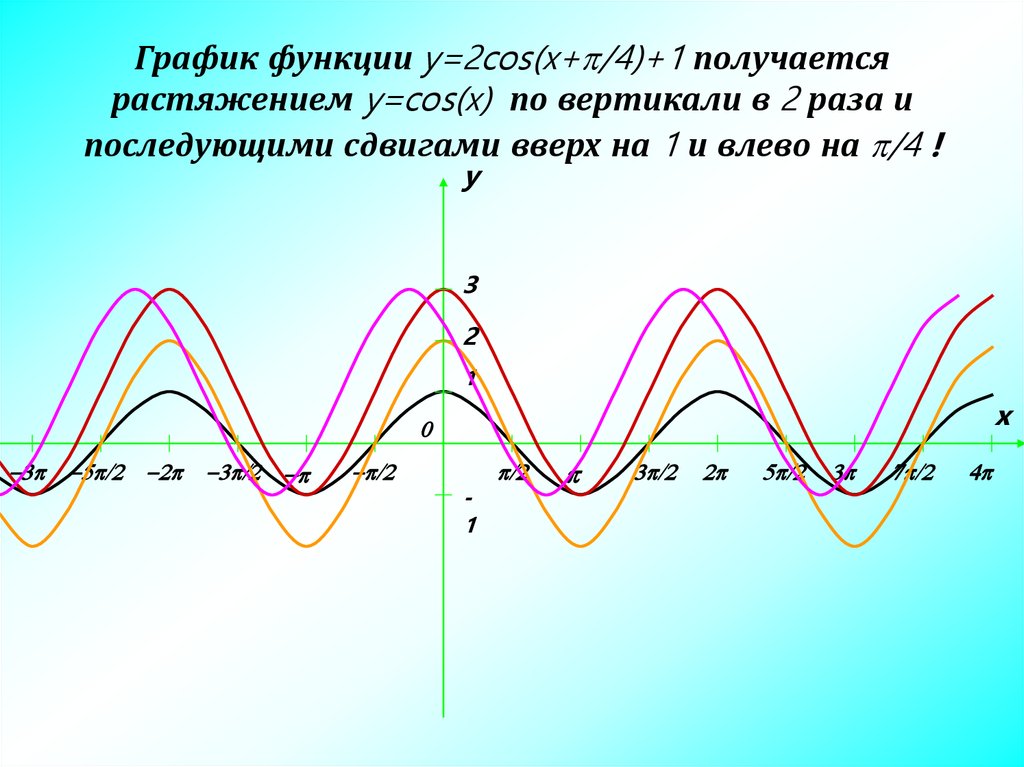 Ниже приведены графики трех тригонометрических функций sin x, cos x и tan x.
Ниже приведены графики трех тригонометрических функций sin x, cos x и tan x.

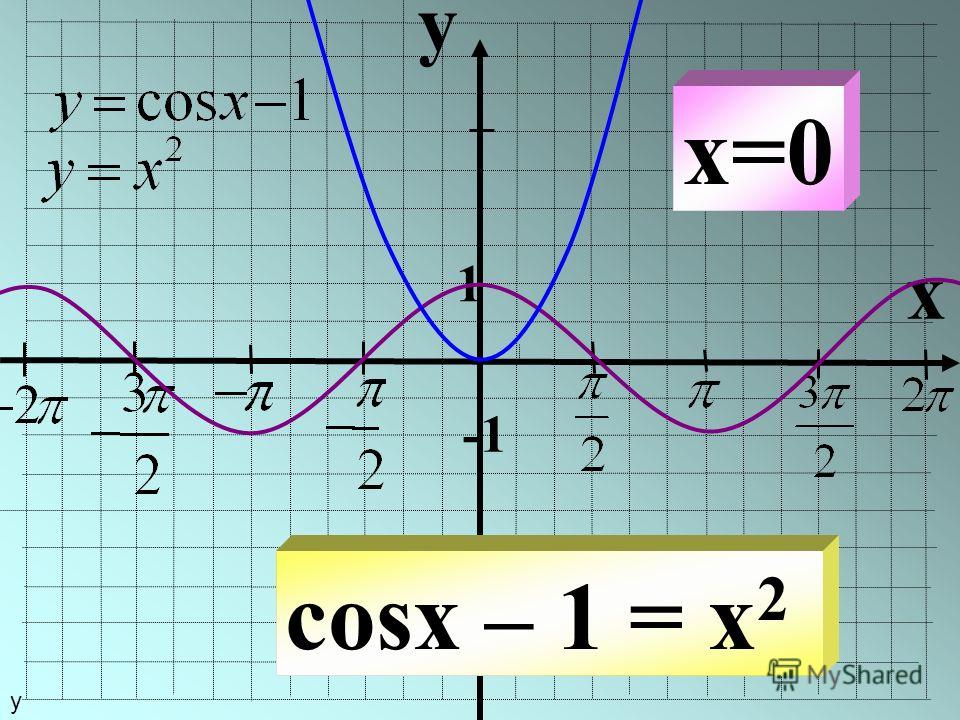
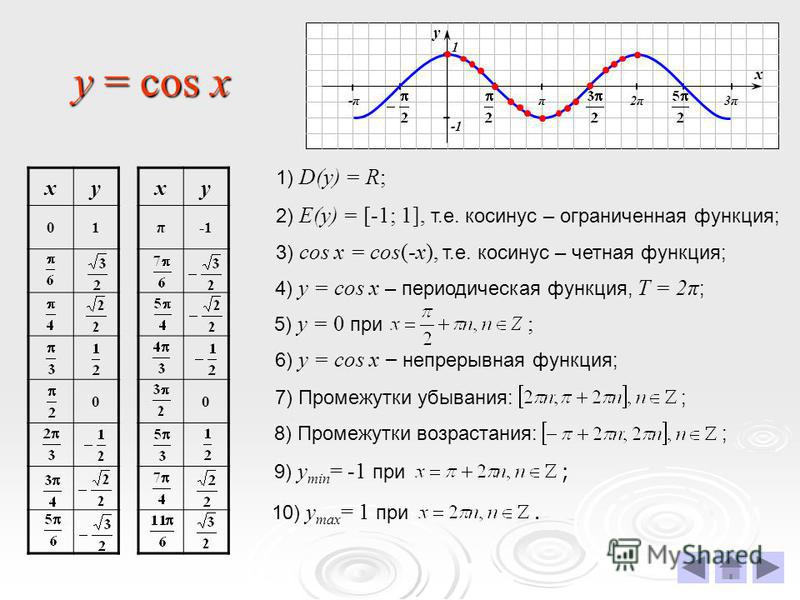
 Выберите All Front Matter
Выберите All Front Matter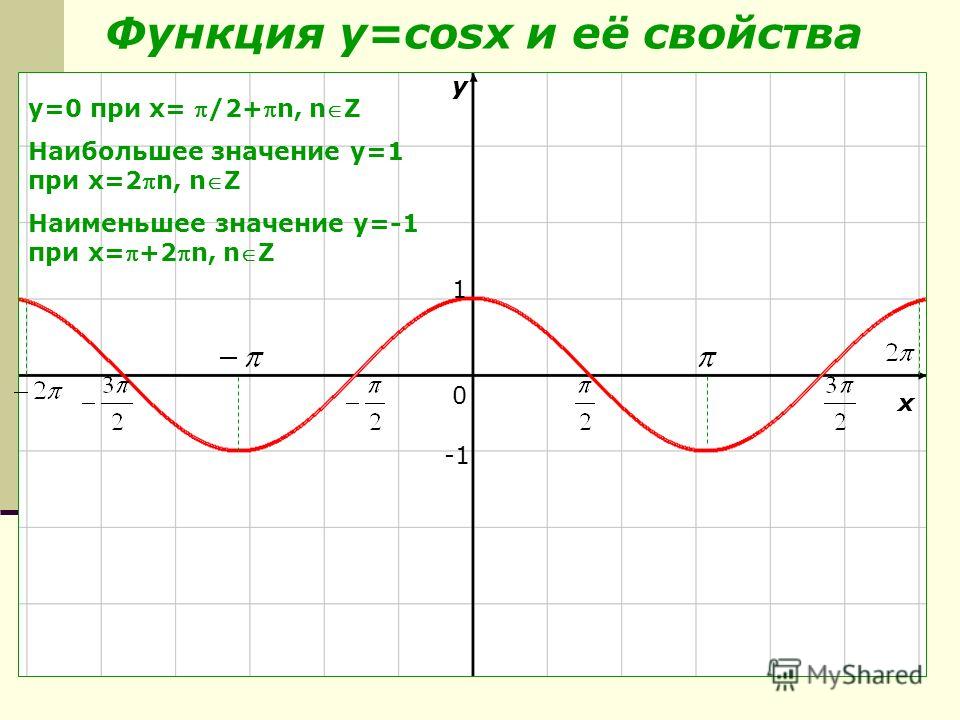 — НЕОПРЕДЕЛЕННЫЕ ФОРМЫ И СОБСТВЕННЫЕ ИНТЕГРАЛЫ
— НЕОПРЕДЕЛЕННЫЕ ФОРМЫ И СОБСТВЕННЫЕ ИНТЕГРАЛЫ