Комбинаторика — основные формулы. Перестановки, размещения, сочетания. Теория вероятностей
- Правило умножения
- Правило сложения
- Размещения и перестановки
- Сочетания
- Разбиение множества на группы
- Задачи контрольных и самостоятельных работ
Основные понятия и формулы
Комбинаторикой называется раздел математики, изучающий вопрос о том, сколько комбинаций определенного типа можно составить из данных предметов (элементов).
Правило умножения (основная формула комбинаторики)
Общее число способов, которыми можно выбрать по одному элементу из каждой группы и расставить их в определенном порядке (то есть получить упорядоченную совокупность ), равно:
Пример 1
Монету подбросили 3 раза. Сколько различных результатов бросаний можно ожидать?
Решение
Первая монета имеет
альтернативы – либо орел, либо решка. Для
второй монеты также есть
альтернативы
и т.д., т.е.
.
Для
второй монеты также есть
альтернативы
и т.д., т.е.
.
Искомое количество способов:
Правило сложения
Если любые две группы и не имеют общих элементов, то выбор одного элемента или из , или из , …или из можно осуществить способами.
Пример 2
На полке 30 книг, из них 20 математических, 6 технических и 4 экономических. Сколько существует способов выбора одной математической или одной экономической книги.
Решение
Математическая книга может быть выбрана способами, экономическая — способами.
По правилу суммы существует способа выбора математической или экономической книги.
Размещения и перестановки
Размещения – это
упорядоченные совокупности элементов, отличающиеся друг от друга либо составом,
либо порядком элементов.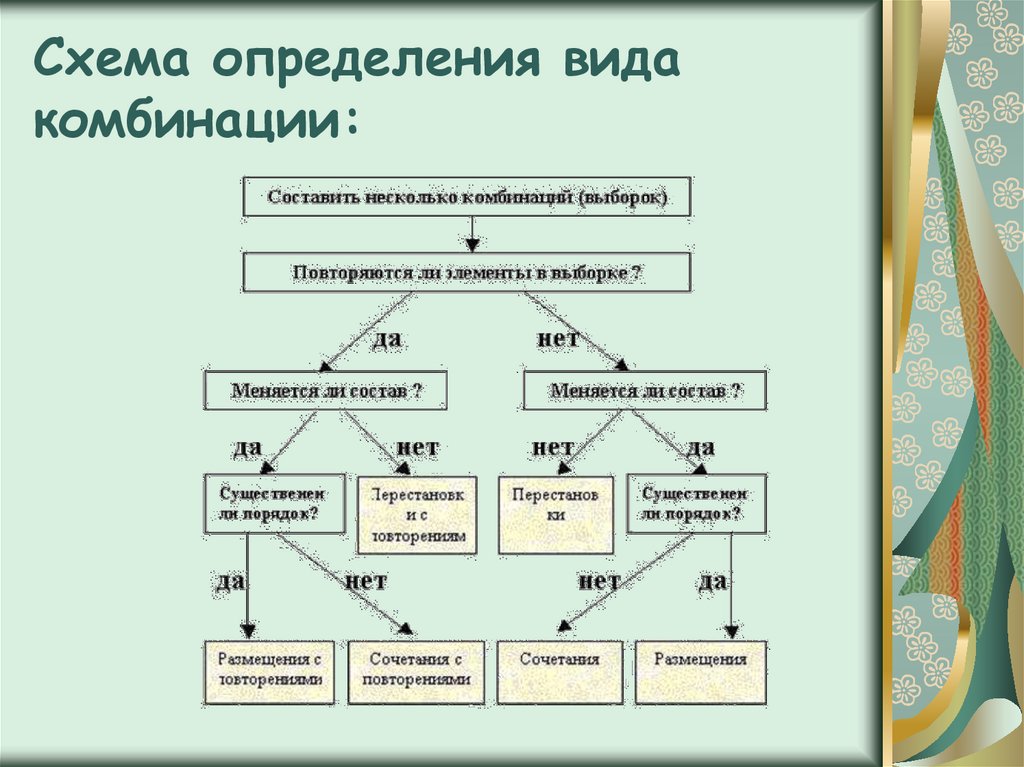
Размещения без повторений, когда отобранный элемент перед отбором следующего не возвращается в генеральную совокупность. Такой выбор называется последовательным выбором без возвращения, а его результат – размещением без повторений из элементов по .
Число различных способов, которыми можно произвести последовательный выбор без возвращения элементов из генеральной совокупности объема , равно:
Пример 3
Расписание дня состоит из 5 различных уроков. Определите число вариантов расписания при выборе из 11 дисциплин.
Решение
Каждый вариант расписания представляет набор 5 дисциплин из 11, отличающихся от других вариантов как составом, так и порядком следования. поэтому:
Перестановки – это упорядоченные совокупности, отличающиеся друг от друга только порядком элементов. Число всех перестановок множества из элементов равно
Пример 4
Сколькими способами можно рассадить 4 человек за одним столом?
Решение
Каждый вариант рассадки отличается только порядком участников, то есть является перестановкой из 4 элементов:
Размещения с повторениями,
когда отобранный элемент перед отбором следующего возвращается в генеральную
совокупность. Такой выбор называется последовательным выбором с возвращением, а
его результат — размещением с
повторениями из
элементов по
.
Такой выбор называется последовательным выбором с возвращением, а
его результат — размещением с
повторениями из
элементов по
.
Общее число различных способов, которыми можно произвести выбор с возвращением элементов из генеральной совокупности объема , равно
Если не находите примера, аналогичного вашему, если сами не успеваете выполнить работу, если впереди экзамен по предмету и нужна помощь — свяжитесь со мной:
ВКонтакте
WhatsApp
Telegram
Я буду работать с вами, над вашей проблемой, пока она не решится.
Пример 5
Лифт останавливается на 7 этажах. Сколькими способами могут выйти на этих этажах 6 пассажиров, находящихся в кабине лифта?
Решение
Каждый из способов
распределения пассажиров по этажам представляет собой комбинацию 6 пассажиров
по 7 этажам, отличающуюся от других комбинаций как составом, так и их порядком.
Так как одном этаже может выйти как
один, так и несколько пассажиров, то одни и те же пассажиры могут
повторяться. Поэтому число таких комбинаций равно числу размещений с
повторениями из 7 элементов по 6:
Поэтому число таких комбинаций равно числу размещений с
повторениями из 7 элементов по 6:
Сочетания
Сочетаниями из n элементов по k называются неупорядоченные совокупности, отличающиеся друг от друга хотя бы одним элементом.
Пусть из генеральной совокупности берется сразу несколько элементов (либо элементы берут последовательно, но порядок их появления не учитывается). В результате такого одновременного неупорядоченного выбора элементов из генеральной совокупности объема получаются комбинации, которые называются сочетаниями без повторений из элементов по .
Число сочетаний из элементов по равно:
Пример 6
В ящике 9 яблок. Сколькими способами можно выбрать 3 яблока из ящика?
Решение
Каждый вариант выбора состоит из 3 яблок и отличается от других только составом, то есть представляет собой сочетания без повторений из 9 элементов:
Количество способов, которыми можно выбрать 3 яблока из 9:
Пусть из генеральной совокупности объема
выбирается
элементов, один за другим, причем каждый
отобранный элемент перед отбором следующего возвращается в генеральную
совокупность. При этом ведется запись, какие элементы появились и сколько раз,
однако порядок их появления не учитывается. Получившиеся совокупности
называются сочетаниями с повторениями
из
элементов по
.
При этом ведется запись, какие элементы появились и сколько раз,
однако порядок их появления не учитывается. Получившиеся совокупности
называются сочетаниями с повторениями
из
элементов по
.
Число сочетаний с повторениями из элементов по :
Если не находите примера, аналогичного вашему, если сами не успеваете выполнить работу, если впереди экзамен по предмету и нужна помощь — свяжитесь со мной:
ВКонтакте
WhatsApp
Telegram
Я буду работать с вами, над вашей проблемой, пока она не решится.
Пример 7
На почте продают открытки 3 видов. Сколькими способами можно купить 6 открыток?
Решение
Это задача на отыскание числа сочетаний с повторениями из 3 по 6:
Разбиение множества на группы
Пусть множество из
различных элементов разбивается на
групп так, то в первую группу попадают
элементов, во вторую —
элементов, в
-ю
группу —
элементов, причем
. Такую ситуацию называют разбиением множества на группы.
Такую ситуацию называют разбиением множества на группы.
Число разбиений на групп, когда в первую попадают элементов, во вторую — элементов, в k-ю группу — элементов, равно:
Пример 8
Группу из 16 человек требуется разбить на три подгруппы, в первой из которых должно быть 5 человек, во второй – 7 человек, в третьей – 4 человека. Сколькими способами это можно сделать?
Решение
Здесь
Число разбиений на 3 подгруппы:
Задачи контрольных и самостоятельных работ
Задача 1
Монету подбросили 3 раза. Сколько различных результатов бросаний можно ожидать?
Задача 2
Доступ к файлу открывается, только если введен правильный пароль – определенный трехзначный номер из нечетных цифр. Какова максимальное число возможных попыток угадать пароль?
Задача 3
Группу из
10 человек требуется разбить на две непустые подгруппы
и
. Сколькими способами можно
это сделать?
Сколькими способами можно
это сделать?
Задача 4
Два наборщика должны набрать 16 текстов. Сколькими способами они могут распределить эту работу между собой.
Задача 5
Шесть студентов-переводников нужно распределить по трем группам. Сколькими способами это можно сделать?
Если не находите примера, аналогичного вашему, если сами не успеваете выполнить работу, если впереди экзамен по предмету и нужна помощь — свяжитесь со мной:
ВКонтакте
WhatsApp
Telegram
Я буду работать с вами, над вашей проблемой, пока она не решится.
Задача 6
Лифт останавливается на 7 этажах. Сколькими способами могут выйти на этих этажах 6 пассажиров, находящихся в кабине лифта?
Задача 7
В ящике 5 красных и 4 зеленых яблока. Сколькими способами можно выбрать 3 яблока из ящика?
Задача 8
Из ящика,
в котором лежат 10 красных и 5 зеленых яблок, выбирают одно красное и два
зеленых яблока. Сколькими способами можно это сделать.
Сколькими способами можно это сделать.
Задача 9
В группе из 25 студентов нужно выбрать старосту и 3 членов студенческого комитета. Сколькими способами можно это сделать.
Задача 10
Акционерное собрание компании выбирает из 50 человек президента компании, председателя совета директоров и 10 членов совета директоров. Сколькими способами это можно сделать?
Задача 11
В телевизионной студии работают 3 режиссера, 4 звукорежиссера, 5 операторов, 7 корреспондентов и 2 музыкальных редактора. Сколькими способами можно составить съемочную группу, состоящую из одного режиссера, двух операторов, одного звукорежиссера и двух корреспондентов.
Задача 12
На группу из 25 человек выделены 3 пригласительных билета на вечер. Сколькими способами они могут быть распределены (не более одного билета в руки).
Задача 13
Имеются 7
билетов: 3 в один театр и 4 – в другой.
Задача 14
Группу из 16 человек требуется разбить на три подгруппы, в первой из которых должно быть 5 человек, во второй – 7 человек, в третьей – 4 человека. Сколькими способами это можно сделать?
- Правило умножения
- Правило сложения
- Размещения и перестановки
- Сочетания
- Разбиение множества на группы
- Задачи контрольных и самостоятельных работ
Формулы по комбинаторике: Формулы комбинаторики с примерами. Основные формулы комбинаторики: сочетания, размещения, перестановки — ЭкоДом: Дом своими руками
Содержание
Формулы комбинаторики с примерами. Основные формулы комбинаторики: сочетания, размещения, перестановки
Учитесь решать задачи по комбинаторике? На самом начальном этапе нужно изучить основные формулы комбинаторики: сочетания, размещения, перестановки (смотрите подробнее ниже) и научиться их применять для решения задач.
Как выбрать формулу комбинаторики?
Мы подготовили для вас наглядную схему с примерами решений по каждой формуле комбинаторики:
- алгоритм выбора формулы (сочетания, перестановки, размещения с повторениями и без),
- рекомендации по изучению комбинаторики,
- 6 задач с решениями и комментариями на каждую формулу.
Нужна помощь в решении задач по комбинаторике?
Перестановки
Пусть имеется $n$ различных объектов.
Будем переставлять их всеми возможными способами (число объектов остается неизменными, меняется только их порядок). Получившиеся комбинации называются перестановками, а их число равно
$$P_n=n!=1\cdot 2\cdot 3 \cdot … \cdot (n-1) \cdot n$$
Символ $n!$ называется факториалом и обозначает произведение всех целых чисел от $1$ до $n$. По определению, считают, что $0!=1, 1!=1$.
Пример всех перестановок из $n=3$ объектов (различных фигур) — на картинке справа. m=\frac{n!}{(n-m)!}=n\cdot (n-1)\cdot . m \cdot P_m.$$
m=\frac{n!}{(n-m)!}=n\cdot (n-1)\cdot . m \cdot P_m.$$
Удобный и бесплатный онлайн калькулятор сочетаний.
Решебник задач по комбинаторике
Изучаем комбинаторику: полезные ссылки
Комбинаторика: основные правила и формулы.
КОМБИНАТОРИКА
Комбинаторика – раздел математики, который изучает задачи выбора и расположения элементов из некоторого основного множества в соответствии с заданными правилами. Формулы и принципы комбинаторики используются в теории вероятностей для подсчета вероятности случайных событий и, соответственно, получения законов распределения случайных величин. Это, в свою очередь, позволяет исследовать закономерности массовых случайных явлений, что является весьма важным для правильного понимания статистических закономерностей, проявляющихся в природе и технике.
Правила сложения и умножения в комбинаторике
Правило суммы. Если два действия А и В взаимно исключают друг друга, причем действие А можно выполнить m способами, а В – n способами, то выполнить одно любое из этих действий (либо А, либо В) можно n + m способами.
Пример 1.
В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить одного дежурного?
Решение
Дежурным можно назначить либо мальчика, либо девочку, т.е. дежурным может быть любой из 16 мальчиков, либо любая из 10 девочек.
По правилу суммы получаем, что одного дежурного можно назначить 16+10=26 способами.
Правило произведения. Пусть требуется выполнить последовательно k действий. Если первое действие можно выполнить n1 способами, второе действие n2 способами, третье – n3 способами и так до k-го действия, которое можно выполнить nk способами, то все k действий вместе могут быть выполнены:
способами.
Пример 2.
В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить двух дежурных?
Решение
Первым дежурным можно назначить либо мальчика, либо девочку. Т.к. в классе учится 16 мальчиков и 10 девочек, то назначить первого дежурного можно 16+10=26 способами.
Т.к. в классе учится 16 мальчиков и 10 девочек, то назначить первого дежурного можно 16+10=26 способами.
После того, как мы выбрали первого дежурного, второго мы можем выбрать из оставшихся 25 человек, т.е. 25-ю способами.
По теореме умножения двое дежурных могут быть выбраны 26*25=650 способами.
Сочетания без повторений. Сочетания с повторениями
Классической задачей комбинаторики является задача о числе сочетаний без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать m из n различных предметов?
Пример 3.
Необходимо выбрать в подарок 4 из 10 имеющихся различных книг. Сколькими способами можно это сделать?
Решение
Нам из 10 книг нужно выбрать 4, причем порядок выбора не имеет значения. Таким образом, нужно найти число сочетаний из 10 элементов по 4:
.
Рассмотрим задачу о числе сочетаний с повторениями: имеется по r одинаковых предметов каждого из n различных типов; сколькими способами можно выбрать m () из этих (n*r) предметов?
.
Пример 4.
В кондитерском магазине продавались 4 сорта пирожных: наполеоны, эклеры, песочные и слоеные. Сколькими способами можно купить 7 пирожных?
Решение
Т.к. среди 7 пирожных могут быть пирожные одного сорта, то число способов, которыми можно купить 7 пирожных, определяется числом сочетаний с повторениями из 7 по 4.
.
Размещения без повторений. Размещения с повторениями
Классической задачей комбинаторики является задача о числе размещений без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n различных предметов?
Пример 5.
В некоторой газете 12 страниц. Необходимо на страницах этой газеты поместить четыре фотографии. Сколькими способами можно это сделать, если ни одна страница газеты не должна содержать более одной фотографии?
Решение.
В данной задаче мы не просто выбираем фотографии, а размещаем их на определенных страницах газеты, причем каждая страница газеты должна содержать не более одной фотографии. Таким образом, задача сводится к классической задаче об определении числа размещений без повторений из 12 элементов по 4 элемента:
Таким образом, 4 фотографии на 12 страницах можно расположить 11880 способами.
Также классической задачей комбинаторики является задача о числе размещений с повторениями, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n предметов, среди которых есть одинаковые?
Пример 6.
У мальчика остались от набора для настольной игры штампы с цифрами 1, 3 и 7. Он решил с помощью этих штампов нанести на все книги пятизначные номера– составить каталог. Сколько различных пятизначных номеров может составить мальчик?
Сколько различных пятизначных номеров может составить мальчик?
Решение
Можно считать, что опыт состоит в 5-кратном выборе с возращением одной из 3 цифр (1, 3, 7). Таким образом, число пятизначных номеров определяется числом размещений с повторениями из 3 элементов по 5:
.
Перестановки без повторений. Перестановки с повторениями
Классической задачей комбинаторики является задача о числе перестановок без повторения, содержание которой можно выразить вопросом: сколькими способами можно разместить n различных предметов на n различных местах?
Пример 7.
Сколько можно составить четырехбуквенных «слов» из букв слова«брак»?
Решение
Генеральной совокупностью являются 4 буквы слова «брак» (б, р, а, к). Число «слов» определяется перестановками этих 4 букв, т. е.
е.
Для случая, когда среди выбираемых n элементов есть одинаковые (выборка с возвращением), задачу о числе перестановок с повторениями можно выразить вопросом: сколькими способами можно переставить n предметов, расположенных на n различных местах, если среди n предметов имеются k различных типов (k < n), т. е. есть одинаковые предметы.
Пример 8.
Сколько разных буквосочетаний можно сделать из букв слова «Миссисипи»?
Решение
Здесь 1 буква «м», 4 буквы «и», 3 буквы «c» и 1 буква «п», всего 9 букв. Следовательно, число перестановок с повторениями равно
ОПОРНЫЙ КОНСПЕКТ ПО РАЗДЕЛУ «КОМБИНАТОРИКА»
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра
При решении задач по комбинаторике используют следующие важные понятия
Размещения
Рассмотрим следующую задачу.
Задача. 9 карточек пронумерованы числами 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 . Из этих карточек четыре наугад взятых карточки выкладываем в ряд. Сколько при этом можно получить различных четырехзначных чисел?
Решение.Сначала слева направо пронумеруем места в ряду, куда выкладываем карточки: первое место, второе, третье, четвертое.
На первое место можно положить одну из 9 карточек. Для этого есть 9 способов. В каждом из этих 9 способов на второе место можно положить одну из оставшихся 8 карточек. Таким образом, существует
способа, чтобы положить карточки на первое и второе места. В каждом из этих 72 способов на третье место можно положить одну из оставшихся 7 карточек. Следовательно, существует
Следовательно, существует
способа, чтобы положить карточки на первое, второе и третье места. В каждом из этих 504 способов на четвертое место можно положить одну из оставшихся 6 карточек. Отсюда вытекает, что существует
различных способа, чтобы выложить в ряд 4 карточки из набора, состоящего из 9 пронумерованных карточек. Таким образом, при выкладывании карточек можно получить 3024 различных четырехзначных числа.
Ответ: 3024.
При решении задачи мы провели подсчет числа способов раскладывания карточек, который является частным случаем общего метода подсчета числа размещений и заключается в следующем.
Определение 1. Рассмотрим множество, содержащее n элементов, и все его упорядоченные подмножества, содержащие k элементов. Каждое из этих подмножеств называют размещением из n элементов по k элементов.
Каждое из этих подмножеств называют размещением из n элементов по k элементов.
Если обозначить символом число размещений из n элементов по k элементов, то будет справедлива формула:
В соответствии с определением факториала, формулу (1) можно также записать в виде:
В задаче множеством из n элементов является исходный набор из 9 пронумерованных карточек, а упорядоченным подмножеством из k элементов – 4 карточки, выложенные в ряд.
Таким образом, при решении задачи мы на частном примере подсчитали, чему равно число размещений из 9 элементов по 4 элемента, т.е. число
В соответствии с формулой (1),
что и было получено в задаче.
Замечание 1. Введенные в данном разделе размещения также называют размещениями без повторений.
Замечание 2. Из формул для числа перестановок и числа размещений вытекает формула
смысл которой заключается в следующем.
Утверждение. Размещение из n элементов по n элементов является перестановкой из n элементов.
Сочетания
Определение 2. Рассмотрим множество, состоящее из n элементов. Каждое его подмножество, содержащее k элементов, называют сочетанием из n элементов по k элементов.
Число сочетаний из n элементов по k элементов обозначается символом
Замечание 3. Важно отметить, что, в отличие от определения размещений, рассмотренные в определении сочетаний подмножества, содержащие k элементов, не являются упорядоченными. Поэтому, если в каждом подмножестве, содержащем k элементов (из определения 2), совершить всевозможные перестановки, количество которых равно k ! , то мы получим все размещения.
Поэтому, если в каждом подмножестве, содержащем k элементов (из определения 2), совершить всевозможные перестановки, количество которых равно k ! , то мы получим все размещения.
Таким образом, справедлива формула:
Следовательно,
откуда вытекает формула
Теперь рассмотрим несколько примеров подсчета числа сочетаний, которые непосредственно вытекают из формулы (2):
В заключение приведем часто используемое равенство, также непосредственно вытекающее из формулы (2):
Замечание 4. С разделом справочника «Сочетания» близко связан раздел «Бином Ньютона», где приведены и доказаны свойства чисел сочетаний.
С понятиями факториала числа n и перестановок из n элементов можно познакомиться в разделе «Комбинаторика: факториалы и перестановки» нашего справочника.
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.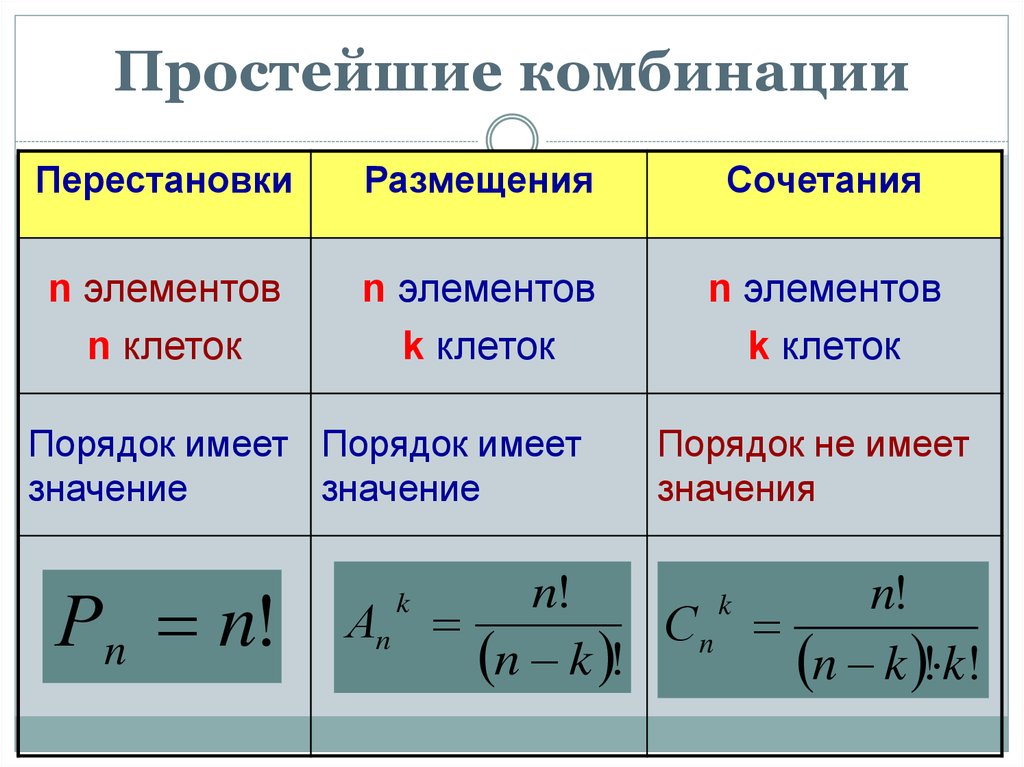
Комбинаторика. Размещения, перестановки, сочетания | Математика, которая мне нравится
В комбинаторике изучают вопросы о том, сколько комбинаций определенного типа можно составить из данных предметов (элементов).
Рождение комбинаторики как раздела математики связано с трудами Б. Паскаля и П. Ферма по теории азартных игр. Большой вклад в развитие комбинаторных методов внесли Г.В. Лейбниц, Я. Бернулли и Л. Эйлер.
Французский философ, писатель, математик и физик Блез Паскаль (1623–1662) рано проявил свои выдающиеся математические способности. Круг математических интересов Паскаля был весьма разнообразен. Паскаль доказал одну
из основных теорем проективной геометрии (теорема Паскаля), сконструировал суммирующую машину (арифмометр Паскаля), дал способ вычисления биномиальных коэффициентов (треугольник Паскаля), впервые точно определил и применил для доказательства метод математической индукции, сделал существенный шаг в развитии анализа бесконечно малых, сыграл важную роль в зарождении теории вероятности. В гидростатике Паскаль установил ее основной закон (закон Паскаля). “Письма к провинциалу” Паскаля явились шедевром французской классической прозы.
В гидростатике Паскаль установил ее основной закон (закон Паскаля). “Письма к провинциалу” Паскаля явились шедевром французской классической прозы.
Готфрид Вильгельм Лейбниц (1646–1716) — немецкий философ, математик, физик и изобретатель, юрист, историк, языковед. В математике наряду с И. Ньютоном разработал дифференциальное и интегральное исчисление. Важный вклад внес в комбинаторику. С его именем, в частности, связаны теоретико-числовые задачи.
Готфрид Вильгельм Лейбниц имел мало внушительную внешность и поэтому производил впечатление довольно невзрачного человека. Однажды в Париже он зашел в книжную лавку в надежде приобрести книгу своего знакомого философа. На вопрос посетителя об этой книге книготорговец, осмотрев его с головы до ног, насмешливо бросил: “Зачем она вам? Неужели вы способны читать такие книги?” Не успел ученый ответить, как в лавку вошел сам автор книги со словами: “Великому Лейбницу привет и уважение!” Продавец никак не мог взять втолк, что перед ним действительно знаменитый Лейбниц, книги которого пользовались большим спросом среди ученых.
В дальнейшем важную роль будет играть следующая
Лемма. Пусть в множестве элементов, а в множестве — элементов. Тогда число всех различных пар , где будет равно .
Доказательство. Действительно, с одним элементом из множества мы можем составить таких различных пар, а всего в множестве элементов.
Размещения, перестановки, сочетания
Пусть у нас есть множество из трех элементов . Какими способами мы можем выбрать из этих элементов два? .
Определение. Размещениями множества из различных элементов по элементов называются комбинации, которые составлены из данных элементов по > элементов и отличаются либо самими элементами, либо порядком элементов.
Число всех размещений множества из элементов по элементов обозначается через (от начальной буквы французского слова “arrangement”, что означает размещение), где и .
Теорема. Число размещений множества из элементов по элементов равно
Доказательство. Пусть у нас есть элементы . Пусть — возможные размещения. Будем строить эти размещения последовательно. Сначала определим — первый элемент размещения. Из данной совокупности элементов его можно выбрать различными способами. После выбора первого элемента для второго элемента остается способов выбора и т.д. Так как каждый такой выбор дает новое размещение, то все эти выборы можно свободно комбинировать между собой. Поэтому имеем:
Пусть у нас есть элементы . Пусть — возможные размещения. Будем строить эти размещения последовательно. Сначала определим — первый элемент размещения. Из данной совокупности элементов его можно выбрать различными способами. После выбора первого элемента для второго элемента остается способов выбора и т.д. Так как каждый такой выбор дает новое размещение, то все эти выборы можно свободно комбинировать между собой. Поэтому имеем:
Пример. Сколькими способами можно составить флаг, состоящий из трех горизонтальных полос различных цветов, если имеется материал пяти цветов?
Решение. Искомое число трехполосных флагов:
Определение. Перестановкой множества из элементов называется расположение элементов в определенном порядке.
Так, все различные перестановки множества из трех элементов — это
Очевидно, перестановки можно считать частным случаем размещений при >.
Число всех перестановок из элементов обозначается (от начальной буквы французского слова “permutation”, что значит “перестановка”, “перемещение”). Следовательно, число всех различных перестановок вычисляется по формуле
Следовательно, число всех различных перестановок вычисляется по формуле
Пример. Сколькими способами можно расставить ладей на шахматной доске так, чтобы они не били друг друга?
Решение. Искомое число расстановки ладей
по определению!
Определение. Сочетаниями из различных элементов по элементов называются комбинации, которые составлены из данных элементов по элементов и отличаются хотя бы одним элементом (иначе говоря, -элементные подмножества данного множества из элементов).
Как видим, в сочетаниях в отличие от размещений не учитывается порядок элементов. Число всех сочетаний из элементов по элементов в каждом обозначается (от начальной буквы французского слова “combinasion”, что значит “сочетание”). k
1. .
Действительно, каждому -элементному подмножеству данного -элементного множества соответствует одно и только одно -элементное подмножество того же множества.
2. .
Действительно, мы можем выбирать подмножества из элементов следующим образом: фиксируем один элемент; число -элементных подмножеств, содержащих этот элемент, равно ; число -элементных подмножеств, не содержащих этот элемент, равно .
Треугольник Паскаля
В этом треугольнике крайние числа в каждой строке равны 1, а каждое не крайнее число равно сумме двух чисел предыдущей строки, стоящих над ним. Таким образом, этот треугольник позволяет вычислять числа .
.
Теорема.
Доказательство. Рассмотрим множество из элементов и решим двумя способами следующую задачу: сколько можно составить последовательностей из элементов данного
множества, в каждой из которых никакой элемент не встречается дважды?
1 способ. Выбираем первый член последовательности, затем второй, третий и т.д. член
2 способ. Выберем сначала элементов из данного множества, а затем расположим их в некотором порядке
Домножим числитель и знаменатель этой дроби на :
Пример. Сколькими способами можно в игре “Спортлото” выбрать 5 номеров из 36?
Сколькими способами можно в игре “Спортлото” выбрать 5 номеров из 36?
Искомое число способов
Задачи.
1. Номера машин состоят из 3 букв русского алфавита (33 буквы) и 4 цифр. Сколько существует различных номеров автомашин?
2. На рояле 88 клавиш. Сколькими способами можно извлечь последовательно 6 звуков?
3. Сколько есть шестизначных чисел, делящихся на 5?
4. Сколькими способами можно разложить 7 разных монет в три кармана?
5. Сколько можно составить пятизначных чисел, в десятичной записи которых хотя бы один раз встречается цифра 5?
6. Сколькими способами можно усадить 20 человек за круглым столом, считая способы одинаковыми, если их можно получить один из другого движением по кругу?
7. Сколько есть пятизначных чисел, делящихся на 5, в записи которых нет одинаковых цифр?
8. На клетчатой бумаге со стороной клетки 1 см нарисована окружность радиуса 100 см, не проходящая через вершины клеток и не касающаяся сторон клеток. Сколько клеток может пересекать эта окружность?
Сколько клеток может пересекать эта окружность?
9. Сколькими способами можно расставить в ряд числа так, чтобы числа стояли рядом и притом шли в порядке возрастания?
10. Сколько пятизначных чисел можно составить из цифр , если каждую цифру можно использовать только один раз?
11. Из слова РОТ перестановкой букв можно получить еще такие слова: ТОР, ОРТ, ОТР, ТРО, РТО. Их называют анаграммами. Сколько анаграмм можно составить из слова ЛОГАРИФМ?
12. Назовем разбиением натурального числа представление его в виде суммы натуральных чисел. Вот, например, все разбиения числа :
Разбиения считаются разными, если они отличаются либо числами, либо порядком слагаемых.
Сколько существует различных разбиений числа на слагаемых?
13. Сколько существует трехзначных чисел с невозрастающим порядком цифр?
14. Сколько существует четырехзначных чисел с невозрастающим порядком цифр?
15. Сколькими способами можно рассадить в ряд 17 человек, чтобы и оказались рядом?
Сколькими способами можно рассадить в ряд 17 человек, чтобы и оказались рядом?
16. девочек и мальчиков рассаживаются произвольным образом в ряду из мест. Сколькими способами можно их рассадить так, чтобы никакие две девочки не сидели рядом?
17. девочек и мальчиков рассаживаются произвольным образом в ряду из мест. Сколькими способами можно их рассадить так, чтобы все девочки сидели рядом?
Основные формулы комбинаторики — презентация онлайн
1. Основные формулы комбинаторики
• Комбинаторика изучает количества
комбинаций, подчиненных
определенным условиям, которые
можно составить из элементов,
безразлично какой природы, заданного
конечного множества.
Размещения с повторениями.
Кортеж-множество где каждый элемент стоит на своем месте и не повторяется.
Кортежи длины k, составленные из элементов m – элементного множества х,
называют размещениями с повторениями из m элементов по k. Число этих
кортежей обозначают Ākm. Рассчитывают по формуле:
Рассчитывают по формуле:
Ākm =mk.
Задача:
Сколько пятизначных номеров можно составить из девяти цифр
1,2,3,4,5,6,7,8,9?
Решение:
Такие номера являются кортежами длины 5, составляем из этих элементов
множества X={ 1,2,3,4,5,6,7,8,9}. По формуле
Аkm=mk рассчитываем:
А59=95=6561.
Размещения без повторений.
Упорядоченное множество длины k, составленное из элементов m – элементного
множества X, называют размещениями без повторений из m элементов множества
Х по k. Рассчитывают по формуле:
N!=1*2*3*…*n, где 0!=1.
m!
k
Аm=
(m k )!
Задача:
Сколькими способами можно выбрать из класса, насчитывающего 40 учеников,
старосту, комсорга и физорга.
Решение:
Любой такой выбор является размещением без повторений из 40 элементов по
3 (он задается кортежем длины 3 без повторений, составленным из элементов
множества учеников). Значит, число способов выбора равно
А340=40! / 37! = 59280.
Ответ:59280.
Перестановки с повторениями.
Перестановки с повторениями состава (k1,…,km) из букв (a1,…,am) называют
любой кортеж длины k= k1+k2+…+km, в которой буква a1 входит в k1 раз, …, буква
am – km раз. Число таких перестановок обозначается P(k1,…,km). Рассчитывается
по формуле:
(k1 k 2 …kn)!
P(k1,…,km) =
k1!k 2!..kn!
Задача:
Сколько слов можно получить, переставляя буквы в слове «математика»?
Решение:
Слово «математика» является кортежем длины 10, имеющим состав (2, 3, 2, 1,
1, 1) (буква «м» входит 2 раза, буква «а» — раза, буква «т» — 2 раза, буквы «е»,
«и», «к» — по одному разу).
10!
P (2, 3, 2, 1, 1, 1) =
= 151200.
2!3!2!1!1!1!
Ответ: 151200
Перестановка без повторений.
Перестановка без повторений из m – элементов называют размещением без
повторений из этих элементов по m. Число перестановок обозначают Рm.
Рассчитывают по формуле:
Pm = m!
Задача:
Сколькими способами 6 человек могут сесть в 6 машин?
Решение:
Пронумеруем машины числами 1, 2, 3, 4, 5, 6 и обозначим человека, севшего в k
–тую машину через Xk. Тогда (х1,…,х6) – перестановка из имен этих шести
Тогда (х1,…,х6) – перестановка из имен этих шести
людей, причем каждой такой перестановке соответствует один и только один
способ размещения в машинах, следовательно:
Р6 = 6!=720
Ответ: 720.
5
2
4
1
3
6
Сочетание с повторениями.
Имеются предметы m видов и из них составляется набор, содержащие k элементов. Два
таких набора считаются одинаковыми в том и только в том случае, когда они имеют
одинаковый состав. Такие наборы называются сочетаниями с повторениями из m
элементов по k. Рассчитываются по формуле:
Сkm = Ckk+m-1
Задача:
Сколько наборов из 7 пирожных можно составить, если в продаже имеются 4
сорта пирожных?
Решение:
Искомое число равно: С74 т.е. C77+4-1 следовательно:
С710 = C310 = (10*9*8) / (1*2*3)=120
Ответ: 120.
Сочетания без повторений.
K – элементные подмножества m-элементного множества x называют
сочетаниями без повторений из элементов этого множества по K. Их число
обозначают Ckm. Рассчитывают по формуле:
Рассчитывают по формуле:
m!
Ckm =
k!(m k )!
Задача:
Сколькими способами можно выбрать один цветок из 5 роз и 3 водяных
лилий?
5!
С = 1!4! =5
3!
1
С 3= 1!2! =3
1
5
Решение:
С13+С15=3+5=8 способов
Ответ: 8 способов.
Бином Ньютона.
Формула: (x-a)n=xn-naxn-1+C2na2xn-2-C3na3xn-3+…+(-1)kCkrakxn-k+…+(-1)nan.
Пример: Найдите разложения: а) (2y2-3y) 5 ; б) (1- 2)6
Решение: а) y5(2y – 3)5 = y5(32y5 – 16y4*5*3 + 8y3*10*9 – 4y2*10*27 + 2y*5*81 –
— 243) = 32y10 — 240y9 + 720y8 — 1080y7 + 810y6 – 243y5;
б) 1 — 6 2 + 15*2 – 20*2 2 +15*4 – 6*4 2 + 8 = 99 — 70 2.
Для нахождения коэффициентов в биноме Ньютона удобно использовать
треугольник Паскаля.
0-я степень
1
1
1
1
1
1
1
2
3
3
4
5
1
6
10
1
4
10
1
5
1
5-я степень
Коэффициент в разложении многочлена легко искать с
помощью треугольника Паскаля.
(х-а)3=х3-3х2а+3а2х-а3
1
1
1
1
1
1
2
3
4
1
3
6
1
4
1
Элементы комбинаторики.
 Перестановки, размещения, сочетания
Перестановки, размещения, сочетанияНиже калькулятор, подсчитывающий число перестановок, размещений и сочетаний. Под ним, как водится, ликбез, если кто подзабыл.
Элементы комбинаторики. Перестановки, размещения, сочетания
Число перестановок из n
Число размещений из n по m
Число размещений из n по m с повторениями
Число сочетаний из n по m
content_copy Ссылка save Сохранить extension Виджет
Итак, есть множество из n элементов.
Вариант упорядочивания данного множества называется перестановкой (permutation).
Например, есть множество, состоящее из 3 элементов — А, В, и С. Пример перестановки — СВА. Число всех перестановок из n элементов:
Пример: Для случая А, В, С число всех перестановок 3! = 6. Перестановки: АВС, АСВ, ВАС, ВСА, САВ, СВА
Если из множества n элементов выбирают m в определенном порядке, это называется размещением (arrangement).
Пример размещения из 3 по 2: АВ или ВА — это два разных размещения. Число всех размещений из n по m
Пример: Для случая А, В, С число всех размещений из 3 по 2 равно 3!/1! = 6. Размещения: АВ, ВА, АС, СА, ВС, СВ
Также бывают размещения с повторениями, как ясно из названия, элементы на определенных позициях могут повторяться.
Число всех размещений из n по m с повторениями:
Пример: Для случая А, В, С число всех размещений из 3 по 2 с повторениями равно 3*3 = 9. Размещения: AA, АВ, АС, ВА, BB, ВС, СА, СВ, CC
Если из множества n элементов выбирают m, и порядок не имеет значения, это называется сочетанием (combination).
Пример сочетания из 3 по 2: АВ. Число всех сочетаний из n по m
Пример: Для случая А, В, С число всех сочетаний из 3 по 2 равно 3!/(2!*1!) = 3. Сочетания: АВ, АС, СВ
Приведем до кучи формулу соотношения между перестановками, размещениями и сочетаниями:
Обратите внимание, что внизу
основные формулы. Перестановки, размещения, сочетания.
 Задачи по теории вероятностей с решением онлайн. Помощь студентам
Задачи по теории вероятностей с решением онлайн. Помощь студентамОсновные понятия и формулы
Комбинаторикой называется раздел математики, изучающий вопрос о
том, сколько комбинаций определенного типа можно составить из данных предметов
(элементов).
Правило умножения (основная формула комбинаторики)
Общее число
способов, которыми можно выбрать по одному
элементу из каждой группы и расставить их в определенном порядке (то есть
получить упорядоченную совокупность
),
равно:
Пример 1
Монету подбросили 3 раза.
Сколько различных результатов бросаний можно ожидать?
Решение
Первая монета имеет
альтернативы – либо орел, либо решка. Для
второй монеты также есть
альтернативы
и т.д., т.е.
.
Искомое количество
способов:
Правило сложения
Если любые две группы
и
не имеют общих элементов, то выбор одного
элемента или из
,
или из
,
…или из
можно осуществить
способами.
Пример 2
На полке 30 книг, из них 20 математических, 6 технических и 4
экономических. Сколько существует способов
выбора одной математической или одной экономической книги.
Решение
Математическая книга может быть выбрана
способами, экономическая —
способами.
По правилу суммы существует
способа выбора математической или
экономической книги.
Размещения и перестановки
Размещения – это
упорядоченные совокупности элементов, отличающиеся друг от друга либо составом,
либо порядком элементов.
Размещения без повторений,
когда отобранный элемент перед отбором следующего не возвращается в генеральную
совокупность. Такой выбор называется последовательным выбором без возвращения,
а его результат – размещением без повторений из
элементов по
.
Число различных способов, которыми можно произвести
последовательный выбор без возвращения
элементов из генеральной совокупности объема
,
равно:
Пример 3
Расписание дня состоит из 5 различных уроков. Определите число
Определите число
вариантов расписания при выборе из 11 дисциплин.
Решение
Каждый вариант расписания представляет набор 5 дисциплин из 11,
отличающихся от других вариантов как составом, так и порядком следования.
поэтому:
Перестановки – это
упорядоченные совокупности, отличающиеся друг от друга только порядком
элементов. Число всех перестановок множества из
элементов равно
Пример 4
Сколькими способами можно рассадить 4 человек за одним столом?
Решение
Каждый вариант рассадки отличается только порядком участников, то
есть является перестановкой из 4 элементов:
Размещения с повторениями,
когда отобранный элемент перед отбором следующего возвращается в генеральную
совокупность. Такой выбор называется последовательным выбором с возвращением, а
его результат — размещением с
повторениями из
элементов по
.
Общее число различных способов, которыми можно произвести выбор с
возвращением
элементов из генеральной совокупности объема
,
равно
Если вам сейчас не требуется платная помощь с решением задач, контрольных работ и типовых расчетов, но может потребоваться в дальнейшем, то, чтобы не потерять контакт
вступайте в группу ВК
сохраните контакт WhatsApp (+79688494598)
сохраните контакт Телеграм (@helptask) .
Пример 5
Лифт останавливается на 7
этажах. Сколькими способами могут выйти на этих этажах 6 пассажиров,
находящихся в кабине лифта?
Решение
Каждый из способов
распределения пассажиров по этажам представляет собой комбинацию 6 пассажиров
по 7 этажам, отличающуюся от других комбинаций как составом, так и их порядком.
Так как одном этаже может выйти как
один, так и несколько пассажиров, то одни и те же пассажиры могут
повторяться. Поэтому число таких комбинаций равно числу размещений с
Поэтому число таких комбинаций равно числу размещений с
повторениями из 7 элементов по 6:
Сочетания
Сочетаниями
из n элементов по k называются
неупорядоченные совокупности, отличающиеся друг от друга хотя бы одним
элементом.
Пусть из генеральной совокупности берется сразу несколько элементов
(либо элементы берут последовательно, но порядок их появления не учитывается).
В результате такого одновременного неупорядоченного выбора
элементов из генеральной совокупности объема
получаются комбинации, которые называются сочетаниями без повторений из
элементов по
.
Число сочетаний из
элементов по
равно:
Пример 6
В ящике 9 яблок. Сколькими
способами можно выбрать 3 яблока из ящика?
Решение
Каждый вариант выбора
состоит из 3 яблок и отличается от других только составом, то есть представляет
собой сочетания без повторений из 9 элементов:
Количество способов,
которыми можно выбрать 3 яблока из 9:
Пусть из генеральной совокупности объема
выбирается
элементов, один за другим, причем каждый
отобранный элемент перед отбором следующего возвращается в генеральную
совокупность. При этом ведется запись, какие элементы появились и сколько раз,
При этом ведется запись, какие элементы появились и сколько раз,
однако порядок их появления не учитывается. Получившиеся совокупности
называются сочетаниями с повторениями
из
элементов по
.
Число сочетаний с повторениями из
элементов по
:
Если вам сейчас не требуется платная помощь с решением задач, контрольных работ и типовых расчетов, но может потребоваться в дальнейшем, то, чтобы не потерять контакт
вступайте в группу ВК
сохраните контакт WhatsApp (+79688494598)
сохраните контакт Телеграм (@helptask) .
Пример 7
На почте продают открытки 3 видов. Сколькими способами можно купить
6 открыток?
Решение
Это задача на отыскание числа сочетаний с повторениями из 3 по 6:
Разбиение множества на группы
Пусть множество из
различных элементов разбивается на
групп так, то в первую группу попадают
элементов, во вторую —
элементов, в
-ю
группу —
элементов, причем
.
Такую ситуацию называют разбиением множества на группы.
Число разбиений на
групп, когда в первую попадают
элементов, во вторую —
элементов, в k-ю группу —
элементов, равно:
Пример 8
Группу из 16 человек
требуется разбить на три подгруппы, в первой из которых должно быть 5 человек,
во второй – 7 человек, в третьей – 4 человека. Сколькими способами это можно
сделать?
Решение
Здесь
Число разбиений на 3 подгруппы:
Задачи контрольных и самостоятельных работ
Задача 1
Монету
подбросили 3 раза. Сколько различных результатов бросаний можно ожидать?
Задача 2
Доступ к
файлу открывается, только если введен правильный пароль – определенный
трехзначный номер из нечетных цифр. Какова максимальное число возможных попыток
угадать пароль?
Задача 3
Группу из
10 человек требуется разбить на две непустые подгруппы
и
. Сколькими способами можно
Сколькими способами можно
это сделать?
Задача 4
Два
наборщика должны набрать 16 текстов. Сколькими способами они могут распределить
эту работу между собой.
Задача 5
Шесть
студентов-переводников нужно распределить по трем группам. Сколькими способами
это можно сделать?
Если вам сейчас не требуется платная помощь с решением задач, контрольных работ и типовых расчетов, но может потребоваться в дальнейшем, то, чтобы не потерять контакт
вступайте в группу ВК
сохраните контакт WhatsApp (+79688494598)
сохраните контакт Телеграм (@helptask) .
Задача 6
Лифт
останавливается на 7 этажах. Сколькими способами могут выйти на этих этажах 6
пассажиров, находящихся в кабине лифта?
Задача 7
В ящике 5
красных и 4 зеленых яблока. Сколькими способами можно выбрать 3 яблока из
ящика?
Задача 8
Из ящика,
в котором лежат 10 красных и 5 зеленых яблок, выбирают одно красное и два
зеленых яблока. Сколькими способами можно это сделать.
Сколькими способами можно это сделать.
Задача 9
В группе
из 25 студентов нужно выбрать старосту и 3 членов студенческого комитета.
Сколькими способами можно это сделать.
Задача 10
Акционерное
собрание компании выбирает из 50 человек президента компании, председателя совета
директоров и 10 членов совета директоров. Сколькими способами это можно
сделать?
Задача 11
В
телевизионной студии работают 3 режиссера, 4 звукорежиссера, 5 операторов, 7
корреспондентов и 2 музыкальных редактора. Сколькими способами можно составить съемочную
группу, состоящую из одного режиссера, двух операторов, одного звукорежиссера и
двух корреспондентов.
Задача 12
На группу
из 25 человек выделены 3 пригласительных билета на вечер. Сколькими способами
они могут быть распределены (не более одного билета в руки).
Задача 13
Имеются 7
билетов: 3 в один театр и 4 – в другой. Сколькими способами они могут быть
Сколькими способами они могут быть
распределены между студентами группы из 25 человек?
Задача 14
Группу из
16 человек требуется разбить на три подгруппы, в первой из которых должно быть
5 человек, во второй – 7 человек, в третьей – 4 человека. Сколькими способами
это можно сделать?
Если вам сейчас не требуется платная помощь с решением задач, контрольных работ и типовых расчетов, но может потребоваться в дальнейшем, то, чтобы не потерять контакт
вступайте в группу ВК
сохраните контакт WhatsApp (+79688494598)
сохраните контакт Телеграм (@helptask) .
На цену сильно влияет срочность решения (от суток до нескольких часов). Онлайн-помощь на экзамене/зачете (срок решения 1,5 часа и меньше) осуществляется по предварительной записи.
Заявку можно оставить прямо в чате ВКонтакте, WhatsApp или Telegram, предварительно сообщив необходимые вам сроки решения и скинув условие задач.
Калькулятор комбинаций и перестановок
Узнайте, сколько разных способов выбирать предметы.
Для более подробного объяснения формул, пожалуйста, посетите «Комбинации и перестановки».
Примечание. Здесь находится старая версия Flash.
Для более подробного объяснения, пожалуйста, посетите «Комбинации и перестановки».
Опытные пользователи!
Теперь вы можете добавить «Правила», которые уменьшат список:
Правило «имеет» , которое гласит, что определенные элементы должны быть включены (чтобы запись была включена).
Пример: имеет 2, a, b, c. означает, что запись должна иметь как минимум две из букв a, b и c.
Правило «нет» , которое означает, что некоторые элементы из списка не должны встречаться вместе.
Пример: no 2, a, b, c означает, что запись должна содержать , а не , две или более букв a, b и c.
Правило «шаблона» используется для наложения некоторого шаблона для каждой записи.
Пример: шаблон c, * означает, что буква c должна быть первой (может следовать все остальное)
Поместите правило в отдельной строке:
Пример: правило «имеет»
a, b, c, d, e, f, g
имеет 2, a, b
Комбинации a, b, c, d, e, f, g, которые имеют по крайней мере 2 из a, b или c
Правила в деталях
Правило «имеет»
За словом «имеет» следует пробел и число. Затем запятая и список элементов, разделенных запятыми.
Затем запятая и список элементов, разделенных запятыми.
Число говорит, сколько (минимум) из списка необходимо для того, чтобы этот результат был разрешен.
Пример имеет 1, a, b, c
Допускается, если есть a , или b , или c , или a и b , или a и c , или b и c , или все три a, b и с .
Другими словами, он настаивает на том, чтобы в результате присутствовали a, b или c.
Итак, {a, e, f} принято, но {d, e, f} отклонено.
Пример имеет 2, a, b, c
Допустим, если есть a и b , или a и c , или b и c , или все три a, b и c .
Другими словами, он настаивает на том, чтобы в результате было как минимум 2 из a, b или c.
Итак, {a, b, f} принято, но {a, e, f} отклонено.
Правило «нет»
Слово «нет», за которым следует пробел и число. Затем запятая и список элементов, разделенных запятыми.
Число указывает, сколько (минимум) из списка необходимо для отклонения.
Пример: n = 5, r = 3, Order = no, Replace = no
Что обычно дает:
{a, b, c} {a, b, d} {a, b, e} {a, c, d} {a, c, e} {a, d, e} {b, c, d } {b, c, e} {b, d, e} {c, d, e}
Но когда мы добавляем такое правило «нет»:
а, б, в, г, д, е, г
№ 2, а, б
Получаем:
{a, c, d} {a, c, e} {a, d, e} {b, c, d} {b, c, e} {b, d, e} {c, d, e }
Записи {a, b, c}, {a, b, d} и {a, b, e} отсутствуют, потому что правило говорит, что у нас не может быть 2 из списка a, b (имеющего a или b нормально, но не вместе)
Пример: № 2, а, б, в
Разрешает только это:
{a, d, e} {b, d, e} {c, d, e}
Он отклонил любые с a и b , или a и c , или b и c , или даже все три a, b и c .
Итак, {a, d, e) разрешено (в нем только один из a, b и c)
Но {b, c, d} отклоняется (у него 2 из списка a, b, c)
Пример: № 3, а, б, в
Разрешает все:
{a, b, d} {a, b, e} {a, c, d} {a, c, e} {a, d, e} {b, c, d} {b, c, e } {b, d, e} {c, d, e}
Отсутствует только {a, b, c}, потому что это единственный, у которого 3 из списка a, b, c
Правило «шаблона»
Слово «шаблон», за которым следует пробел и список элементов, разделенных запятыми.
Вы можете включить эти «особые» предметы:
- ? (вопросительный знак) означает любой предмет. Это похоже на «подстановочный знак».
- * (звездочка) означает любое количество элементов (0, 1 или более). Как «супер-шаблон».
Пример: узор?, C, *, f
Означает «любой элемент, за которым следует c, за которым следует ноль или более элементов, затем f»
Итак, {a, c, d, f} разрешено
И {b, c, f, g} также разрешены (между c и f нет элементов, и это нормально)
Но {c, d, e, f} нет, потому что перед c нет элемента.
Пример: сколькими способами можно выстроить Алекса, Бетти, Кэрол и Джона в ряд, с Джоном после Алекса.
Используйте: n = 4, r = 4, order = yes, replace = no.
Алекс, Бетти, Кэрол, Джон
узор *, Алекс, *, Джон
Результат:
{Алекс, Бетти, Кэрол, Джон} {Алекс, Бетти, Джон, Кэрол} {Алекс, Кэрол, Бетти, Джон} {Алекс, Кэрол, Джон, Бетти} {Алекс, Джон, Бетти, Кэрол} {Алекс, Джон , Кэрол, Бетти} {Бетти, Алекс, Кэрол, Джон} {Бетти, Алекс, Джон, Кэрол} {Бетти, Кэрол, Алекс, Джон} {Кэрол, Алекс, Бетти, Джон} {Кэрол, Алекс, Джон, Бетти} {Кэрол, Бетти, Алекс, Джон}
Лотереи
Лотерея — это разновидность азартных игр, при которой люди покупают билеты, а затем выигрывают, если выберут их числа.
«Лот» — это то, что происходит случайно. Возможно, вы слышали, как люди говорят: «Давайте решим жеребьевкой» или «Так что это мой удел».
Правила
У разных лотерей разные правила.
Здесь мы будем использовать типичную лотерею, в которой игрок выбирает 6 различных чисел из 49 .
Пример:
Вы участвуете в лотерее, купив билет и выбрав свои шесть чисел.
Вы выбираете: 1, 2, 12, 14, 20 и 21
В субботу проводится розыгрыш лотереи, и выигрышных номеров составляют:
3, 12, 18, 20, 32 и 43
Вы сопоставили два чисел (12 и 20):
- Этого достаточно, чтобы выиграть что-нибудь? №
- Обычно вы должны угадать не менее трех чисел , чтобы получить небольшой приз.
- Если угадать четырех номеров , вы получите больший приз,
- Соответствие пяти еще больше.
- Но если вы угадаете ВСЕ ШЕСТЬ чисел, вы можете выиграть миллионов .

Шансы на выигрыш всех 6 номеров равны 1 из 13 983 816 (рассчитано ниже).
Выбор чисел
Они могут выиграть.
Цифры не знают, какие они!
Лотерея — это с такой же вероятностью, что выпадет «1,2,3,4,5,6», как «9,11,16,23,27,36»
Серьезно!
Вместо чисел это могут быть символы или цвета, лотерея все равно будет работать.
На самом деле получился результат ниже (Florida Fantasy 5 от 21 марта 2011 г.):
Так что неважно, какие числа вы выберете, шансы одинаковы.
Более вероятные номера?
Значит, вы читали, что одни числа встречаются чаще, чем другие? Ну, конечно, есть, это случайный случай.
У организаторов лотерей есть строгие правила, запрещающие «фальсификацию» результатов. Но случайный случай может иногда приводить к странным результатам.
Например, используя Spinner, я сделал 1000 вращений на 10 чисел и получил следующее:
Ух ты! 7 выпало 115 раз, ,
и 8 только 81 раз.
Означает ли это, что 7 теперь будет появляться чаще или реже ? На самом деле это ничего не значит, 7 с такой же вероятностью, как и любое число, будет выбрано.
Попробуйте сами и посмотрите, какие результаты вы получите.
Популярные номера
Но есть хитрость! У людей есть любимые числа, поэтому, когда выпадают популярные числа, вы делитесь выигрышем с множеством людей.
дней рождения — популярный выбор, поэтому люди выбирают 1–12 и 1–31 чаще. Также счастливые числа.
Так что, возможно, вам стоит выбрать непопулярных номеров , чтобы, когда вы действительно выиграете, вы получите больше денег.
(Предполагается, что в вашей лотерее призы распределяются между победителями.)
Сожаление
Не выбирайте одни и те же номера каждую неделю . Это ловушка! Если вы забыли неделю, вы беспокоитесь, что выпадут ваши числа , и это заставит вас покупать билет каждую неделю (даже если у вас есть другие более важные дела).
Мой совет:
Составьте список из множества непопулярных номеров.
Выбирать случайным образом из этого списка каждый раз.
Синдикаты
«Синдикат» — это группа людей, которые все вкладывают небольшие деньги, чтобы группа могла купить много билетов. Шансы на выигрыш повышаются, но каждый раз ваша выплата меньше (потому что вы делитесь).
Синдикаты могут быть интересными, потому что они общительны … способ завести и сохранить дружеские отношения. К тому же некоторые синдикаты любят тратить небольшие выигрыши на всех, кто собирается вместе пообедать.
Еще одна веская причина для присоединения к синдикату заключается в том, что ваши шансы на выигрыш повышаются (а то, что вы выигрываете, снижается).
Подумайте об этом … выигрыш Десяти миллионов действительно изменит вашу жизнь, но Один миллион также значительно улучшит вашу жизнь. Вы можете предпочесть десятикратный шанс выиграть миллион.
Вероятность выиграть большой приз
ОК. Каковы шансы выиграть большой приз?
Каковы шансы выиграть большой приз?
Шансы на выигрыш всех 6 номеров равны 1 из 13 983816
Вы можете использовать калькулятор комбинаций и перестановок, чтобы вычислить это (используйте n = 49 , r = 6 , «Нет» для параметра «Важен ли порядок?» И «Нет» для параметра «Разрешено ли повторение?»)
Фактический расчет таков:
49 С 6 = 49! / (43! X 6!) = 13983816
Итак, сколько раз вам нужно сыграть, чтобы выиграть?
1 неделя
Предположим, вы играете каждую неделю
Вероятность выигрыша через 1 неделю:
1
13983816
= 0.0000000715 …
Таким образом, вероятность того, что не выиграют через 1 неделю, составляет:
1 —
1
13983816
= 0,9999999285 …
50 лет
Допустим, вы играете 50 лет, это 2600 недель.
Вероятность того, что не выиграют за 2600 недель, составляет:
(1 —
1
13983816
) 2600 = 0,999814 …
Это означает, что вероятность выигрыша (через 50 лет) составляет: 1 — 0. 999814 … = 0,000186 …
999814 … = 0,000186 …
Еще только около 0,02%
И вы бы потратили тысячи на этот маленький шанс.
Вы могли хорошо провести отпуск за эти деньги.
НО это весело думать: «Я могу выиграть на этой неделе!»
Просто оставь это забавой , хорошо?
Твоя очередь
Теперь ваша очередь:
- Узнайте правила выигрыша в лотерею в вашем регионе.
- Сколько номеров вам нужно выбрать и из скольких номеров вы выбираете?
- Рассчитайте вероятность выигрыша в любую неделю.
- Подсчитайте вероятность выигрыша, если вы будете играть каждую неделю в течение 50 лет.
- Сколько денег вы сэкономите, не играя? Что можно купить за эти деньги?
Биномиальное распределение
«Би» означает «два» (как у велосипеда два колеса) … | |
Подбрасывание монеты:
- Получили ли мы головы (H) или
- Хвосты (Т)
Мы говорим, что вероятность выпадения монеты H составляет ½
А вероятность выпадения монеты T составляет ½
Бросок кубика:
- Мы получили четверку…?
- … или нет?
Мы говорим, что вероятность четыре равна 1/6 (одна из шести граней равна четверке)
И вероятность того, что не четыре составляет 5/6 (пять из шести граней не четыре)
Обратите внимание, что матрица имеет 6 сторон, но здесь мы рассмотрим только два корпуса : «четыре: да» или «четыре: нет»
Подбросим монетку!
Подбросьте справедливую монету трижды … каков шанс получить две головы ?
Подбрасывая монету три раза ( H для орла, T для решки) можно получить любой из этих 8 результатов :
Какие результаты мы хотим?
«Две головы» могут быть в любом порядке: «HHT», «THH» и «HTH» имеют две головы (и один хвост).
Итак, 3 результата дают «Две головы».
Какова вероятность каждого исхода?
Каждый исход одинаково вероятен, а их 8, поэтому каждый исход имеет вероятность 1/8
Таким образом, вероятность события «Две головы» составляет:
| Количество желаемых результатов | Вероятность каждого исхода | ||
| 3 | × | 1/8 | = 3/8 |
Таким образом, шанс получить две головы составляет 3/8
Мы использовали специальные слова:
- Результат : любой результат трех подбрасываний монеты (8 различных возможностей)
- Событие : «Две головы» из трех подбрасываний монеты (3 исхода имеют это)
3 головы, 2 головы, 1 голова, нет
Расчеты (P означает «Вероятность»):
- P (три головки) = P ( HHH ) = 1/8
- P (две головки) = P ( HHT ) + P ( HTH ) + P ( THH ) = 1/8 + 1/8 + 1/8 = 3/8
- P (одна головка) = P ( HTT ) + P ( THT ) + P ( TTH ) = 1/8 + 1/8 + 1/8 = 3/8
- P (нулевой напор) = P ( TTT ) = 1/8
Мы можем записать это в терминах случайной переменной, X, = «Количество голов при 3 подбрасываниях монеты»:
- P (X = 3) = 1/8
- P (X = 2) = 3/8
- P (X = 1) = 3/8
- P (X = 0) = 1/8
А вот как это выглядит в виде графика:
Он симметричный!
Создание формулы
А теперь представьте, что нам нужны шансы 5 решек за 9 бросков : перечисление всех 512 исходов займет много времени!
Итак, давайте составим формулу.
В нашем предыдущем примере, как мы можем получить значения 1, 3, 3 и 1?
Что ж, они действительно находятся в Треугольнике Паскаля!
Можем ли мы сделать их по формуле?
Конечно, можем, и вот он:
Его часто называют «n choose k»
- n = общее количество
- k = число, которое мы хотим
- знак «!» означает «факториал», например 4! = 1 × 2 × 3 × 4 = 24
Подробнее …
об этом в Комбинации и Перестановки.
Попробуем:
Пример: при 3 бросках, каковы шансы на 2 решки?
У нас есть n = 3 и k = 2 :
н! к! (Н-к)! = 3! 2! (3-2)!
= 3 × 2 × 1 2 × 1 × 1
= 3
Итак, есть 3 исхода с «2 головами»
(Мы это уже знали, но теперь у нас есть формула.)
Давайте ответим на более сложный вопрос:
Пример: при 9 бросках, каковы шансы на 5 бросков?
У нас есть n = 9 и k = 5 :
н! к! (Н-к)! = 9! 5! (9-5)!
= 9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1 5 × 4 × 3 × 2 × 1 × 4 × 3 × 2 × 1
= 126
Значит, у 126 исходов будет 5 голов
А для 9 бросков всего 2 9 = 512 исходов, поэтому получаем вероятность:
| Количество желаемых результатов | Вероятность каждого исхода | |||
| 126 | × | 1 512 | = | 126 512 |
Итак:
P (X = 5) = 126 512 = 0. 24609375
24609375
Примерно с вероятностью 25% .
(Легче, чем перечислить их все.)
Смещение!
До сих пор шансы на успех или неудачу равнялись и равны .
Но что, если монеты смещены (больше на одну сторону, чем на другую) или выбор не равен 50/50.
Пример: вы продаете бутерброды. 70% выбирают курицу, остальные выбирают что-то другое.
Какова вероятность продать 2 бутерброда с курицей следующим 3 покупателям?
Это похоже на пример орла и решки, но с 70/30 вместо 50/50.
Нарисуем древовидную диаграмму:
Ящики «Две курицы» выделены.
Вероятности для «двух цыплят» равны 0,147 , потому что мы умножаем два 0,7 и один 0,3 в каждом случае. Другими словами
0,147 = 0,7 × 0,7 × 0,3
Или, используя экспоненты:
= 0,7 2 × 0,3 1
0,7 — это вероятность каждого выбора, который мы хотим, назовем это p
2 — это количество вариантов, которое мы хотим, назовем его k
А у нас (пока):
= p k × 0. 3 1
3 1
0,3 — вероятность противоположного выбора, так что это: 1 − p
1 — это количество противоположных вариантов, так что это: n − k
Что дает нам:
= p k (1-p) (n-k)
Где
- p — вероятность каждого желаемого нами выбора
- k — это количество вариантов, которое мы хотим
- n — общее количество вариантов
Пример: (продолжение)
- р = 0.7 (шанс курицы)
- k = 2 (выбор курицы)
- n = 3 (всего вариантов)
Получаем:
п к (1-р) (н-к) = 0,7 2 (1-0,7) (3-2)
= 0,7 2 (0,3) (1)
= 0,7 × 0,7 × 0,3
= 0,147
, что у нас было раньше, но теперь используется формула
Теперь мы знаем, что вероятность каждого исхода равна 0,147
Но мы должны указать, что существует три таких способов: (курица, курица, другое) или (курица, другое, курица) или (другое, курица, курица)
Пример: (продолжение)
Общее количество исходов «два цыпленка»:
н! к! (Н-к)! = 3! 2! (3-2)!
= 3 × 2 × 1 2 × 1 × 1
= 3
И получаем:
| Количество желаемых результатов | Вероятность каждого исхода | |||
| 3 | × | 0. 147 147 | = | 0,441 |
Таким образом, вероятность события «2 человека из 3 выбирают курицу» = 0,441
ОК. Это был большой труд для того, что мы уже знали, но теперь у нас есть формула, которую мы можем использовать для более сложных вопросов.
Пример: Сэм говорит: «70% выбирают курицу, поэтому 7 из следующих 10 клиентов должны выбрать курицу» … каковы шансы, что Сэм прав?
Итак имеем:
И получаем:
п к (1-п) (н-к) = 0.7 7 (1-0,7) (10-7)
= 0,7 7 (0,3) (3)
= 0,0022235661
Это вероятность каждого исхода.
И общее количество этих исходов:
н! к! (Н-к)! = 10! 7! (10-7)!
= 10 × 9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1 7 × 6 × 5 × 4 × 3 × 2 × 1 × 3 × 2 × 1
= 10 × 9 × 8 3 × 2 × 1
= 120
И получаем:
| Количество желаемых результатов | Вероятность каждого исхода | |||
| 120 | × | 0. 0022235661 0022235661 | = | 0,266827932 |
Таким образом, вероятность того, что 7 из 10 выберут курицу, составляет всего около 27%
Мораль истории: даже при том, что долгосрочное среднее значение составляет 70%, не ожидайте 7 из следующих 10.
Собираем вместе
Теперь мы знаем, как вычислить , сколько :
н! к! (Н-к)!
И вероятность каждого :
п к (1-р) (н-к)
При умножении получаем:
Вероятность k из n способов:
П (k из n) = n! к! (Н-к)! п к (1-р) (н-к)
Общая формула биномиальной вероятности
Важные примечания:
- Испытания независимые,
- В каждом испытании есть только два возможных исхода,
- Вероятность «успеха» в каждом испытании постоянна.
Quincunx
Поиграйте с Quincunx (затем прочтите Quincunx Explained), чтобы увидеть биномиальное распределение в действии.
Брось кубик
Честный кубик бросается четыре раза. Рассчитайте вероятности получения:
- 0 двоек
- 1 Два
- 2 двоих
- 3 двоих
- 4 двойки
В данном случае n = 4 , p = P (Два) = 1/6
X — это случайная переменная «Количество двоек из четырех бросков».
Подставьте x = от 0 до 4 в формулу:
P (k из n) = n! к! (Н-к)! п к (1-р) (н-к)
Вот так (до 4 знаков после запятой):
- P (X = 0) = 4! 0! 4! × (1/6) 0 (5/6) 4 = 1 × 1 × (5/6) 4 = 0,4823
- P (X = 1) = 4! 1! 3! × (1/6) 1 (5/6) 3 = 4 × (1/6) × (5/6) 3 = 0.3858
- P (X = 2) = 4! 2! 2! × (1/6) 2 (5/6) 2 = 6 × (1/6) 2 × (5/6) 2 = 0,1157
- P (X = 3) = 4! 3! 1! × (1/6) 3 (5/6) 1 = 4 × (1/6) 3 × (5/6) = 0,0154
- P (X = 4) = 4! 4! 0! × (1/6) 4 (5/6) 0 = 1 × (1/6) 4 × 1 = 0,0008
Резюме: «для 4 бросков существует 48% вероятность отсутствия двоек, 39% вероятность 1 два, 12% вероятность 2 двоек, 1. Вероятность 5% на 3 двойки и крошечная вероятность 0,08% того, что все броски будут двойками (но это все равно может случиться!) »
Вероятность 5% на 3 двойки и крошечная вероятность 0,08% того, что все броски будут двойками (но это все равно может случиться!) »
На этот раз график несимметричный:
Это несимметрично!
Перекошено, потому что p не равно 0,5
Спортивные мотоциклы
Ваша компания занимается производством спортивных мотоциклов. 90% проходят окончательную проверку (а 10% не проходят и требуют исправления).
Каково ожидаемое среднее значение и отклонение от 4 следующих проверок?
Сначала посчитаем все вероятности.
X — случайная переменная «Количество проходов из четырех проверок».
Подставьте x = от 0 до 4 в формулу:
P (k из n) = n! к! (Н-к)! п к (1-р) (н-к)
Как это:
- P (X = 0) = 4! 0! 4! × 0,9 0 0,1 4 = 1 × 1 × 0,0001 = 0,0001
- P (X = 1) = 4! 1! 3! × 0,9 1 0.
 1 3 = 4 × 0,9 × 0,001 = 0,0036
1 3 = 4 × 0,9 × 0,001 = 0,0036 - P (X = 2) = 4! 2! 2! × 0,9 2 0,1 2 = 6 × 0,81 × 0,01 = 0,0486
- P (X = 3) = 4! 3! 1! × 0,9 3 0,1 1 = 4 × 0,729 × 0,1 = 0,2916
- P (X = 4) = 4! 4! 0! × 0,9 4 0,1 0 = 1 × 0,6561 × 1 = 0,6561
Резюме: «для следующих 4 велосипедов есть крошечный 0.Вероятность отсутствия передач 01%, вероятность отсутствия передач 0,36%, вероятность 2 передач 5%, вероятность 3 передач 29% и колоссальная вероятность 66%, что все они пройдут проверку «.
Среднее значение, дисперсия и стандартное отклонение
Давайте рассчитаем среднее значение, дисперсию и стандартное отклонение для проверок спортивных велосипедов.
Для них существуют (относительно) простые формулы. Их немного сложно доказать, но они работают!
Среднее или «ожидаемое значение»:
мк = np
Для спортивных мотоциклов:
μ = 4 × 0. 9 = 3,6
9 = 3,6
Итак, можно ожидать, что 3,6 мотоцикла (из 4) пройдут техосмотр.
На самом деле имеет смысл … 0,9 шанс для каждого велосипеда умножить на 4 велосипеда равняется 3,6
Формула дисперсии:
Отклонение: σ 2 = np (1-p)
Стандартное отклонение — это квадратный корень из дисперсии:
σ = √ (np (1-p))
Для спортивных мотоциклов:
Разница: σ 2 = 4 × 0,9 × 0,1 = 0,36
Стандартное отклонение:
σ = √ (0.36) = 0,6
Примечание: мы также можем вычислить их вручную, составив такую таблицу:
| X | П (Х) | X × P (X) | X 2 × P (X) |
| 0 | 0,0001 | 0 | 0 |
| 1 | 0.0036 | 0,0036 | 0,0036 |
| 2 | 0,0486 | 0,0972 | 0,1944 |
| 3 | 0,2916 | 0,8748 | 2,6244 |
| 4 | 0,6561 | 2,6244 | 10,4976 |
| СУММ: | 3. 6 6 | 13,32 |
Среднее значение — это Сумма (X × P (X)) :
мк = 3,6
Дисперсия равна сумме (X 2 × P (X)) минус Среднее 2 :
Разница: σ 2 = 13,32 — 3,6 2 = 0,36
Стандартное отклонение:
σ = √ (0,36) = 0,6
И мы получили те же результаты, что и раньше (ура!)
Сводка
Треугольник Паскаля
Одним из самых интересных шаблонов чисел является треугольник Паскаля (названный в честь Блеза Паскаля , известного французского математика и философа).
Чтобы построить треугольник, начните с «1» вверху, затем продолжайте размещать числа под ним в виде треугольника.
Каждое число — это числа непосредственно над ним, сложенные вместе.
(Здесь я выделил, что 1 + 3 = 4)
Узоры внутри треугольника
Диагонали
Первая диагональ, конечно же, всего «1» с
На следующей диагонали расположены счетные числа (1,2,3 и т. Д.).
Д.).
На третьей диагонали расположены треугольные числа
(Четвертая диагональ, не выделенная, имеет четырехгранные числа.)
Симметричный
Треугольник тоже симметричный. Цифры на левой стороне имеют одинаковые совпадающие числа на правой стороне, как в зеркальном отображении.
Суммы по горизонтали
Что вы заметили в горизонтальных суммах?
Есть узор?
Они удваивают каждый раз (степени двойки).
Показатели из 11
Каждая строка также является степенью (показателем) 11:
- 11 0 = 1 (первая строка — просто «1»)
- 11 1 = 11 (вторая строка — «1» и «1»)
- 11 2 = 121 (третья строка — «1», «2», «1»)
- и т. Д.!
Но что происходит с 11 5 ? Простой! Цифры просто перекрываются, вот так:
То же самое происходит с 11 6 и т. Д.
Квадраты
Для второй диагонали квадрат числа равен сумме чисел рядом с ним и под ними обоими.
Примеры:
- 3 2 = 3 + 6 = 9,
- 4 2 = 6 + 10 = 16,
- 5 2 = 10 + 15 = 25,
- …
Есть и веская причина … ты можешь придумать это?
(Подсказка: 4 2 = 6 + 10, 6 = 3 + 2 + 1 и 10 = 4 + 3 + 2 + 1)
Последовательность Фибоначчи
Попробуйте следующее: сделайте узор, двигаясь вверх, а затем вдоль, затем сложите значения (как показано на рисунке)… вы получите последовательность Фибоначчи.
(Последовательность Фибоначчи начинается с «0, 1», а затем продолжается добавлением двух предыдущих чисел, например 3 + 5 = 8, затем 5 + 8 = 13 и т. Д.)
Шансы и эвены
Если вы раскрасите четные и нечетные числа, вы получите узор, такой же, как треугольник Серпинского
Использование треугольника Паскаля
Голова и решка
Треугольник Паскаля может показать вам, сколько способов совмещения орла и решки.Это может показать вам вероятность любой комбинации.
Например, если вы подбрасываете монету три раза, есть только одна комбинация, которая даст вам три решки (HHH), но есть три, которые дадут две решки и одну решку (HHT, HTH, THH), а также три, которые дают одну голову и два решки (HTT, THT, TTH) и по одному для всех решек (TTT). Это образец «1,3,3,1» в Треугольнике Паскаля.
| Боссы | Возможные результаты (сгруппированы) | Треугольник Паскаля |
|---|---|---|
| 1 | H T | 1, 1 |
| 2 | HH HT TH TT | 1, 2, 1 |
| 3 | HHH HHT, HTH, THH HTT, THT, TTH TTT | 1, 3, 3, 1 |
| 4 | HHHH HHHT, HHTH, HTHH, THHH HHTT, HTHT, HTTH, THHT, THTH, TTHH HTTT, THTT, TTHT, TTTH TTTT | 1, 4, 6, 4, 1 |
… и т. д … д … |
Пример: Какова вероятность выпадения ровно двух орлов при подбрасывании 4 монет?
Есть 1 + 4 + 6 + 4 + 1 = 16 (или 2 4 = 16) возможных результатов, и 6 из них дают ровно две решки. Таким образом, вероятность составляет 6/16, или 37,5%
Комбинации
Треугольник также показывает, сколько комбинаций объектов возможно.
Пример: у вас есть 16 бильярдных шаров.Сколько разных способов вы можете выбрать только 3 из них (игнорируя порядок, в котором вы их выбираете)?
Ответ: спуститесь в начало строки 16 (верхняя строка — 0), а затем по трем разрядам (первое место — 0) и там значение будет вашим ответом, 560 .
Вот отрывок из строки 16:
1 14 ... 1 15 105 455 1365 ... 1 16120 560 1820 4368 ...
Формула для любого входа в треугольник
На самом деле существует формула из Комбинации для вычисления значения в любом месте треугольника Паскаля:
Обычно его называют «n выберите k» и пишут так: |
Обозначение: «n выберите k» также можно написать C (n, k) , n C k или даже n C k .
Знак «!» является «факториалом» и означает умножение ряда убывающих натуральных чисел. Примеры:
|
Таким образом, треугольник Паскаля также может быть
треугольником «n выбрать k» , подобным этому.
(обратите внимание, что верхняя строка — это , нулевая строка
, а также крайний левый столбец — нулевой)
Пример: строка 4, член 2 в треугольнике Паскаля равен «6» …
… посмотрим, работает ли формула:
Да, работает! Попробуйте другое значение для себя.
Это может быть очень полезно … теперь вы можете вычислить любое значение в треугольнике Паскаля непосредственно (без вычисления всего треугольника над ним).
Полиномы
Треугольник Паскаля также может показать вам коэффициенты в биномиальном разложении:
| Мощность | Биномиальное разложение | Треугольник Паскаля |
|---|---|---|
| 2 | (x + 1) 2 = 1 x 2 + 2 x + 1 | 1, 2, 1 |
| 3 | (x + 1) 3 = 1 x 3 + 3 x 2 + 3 x + 1 | 1, 3, 3, 1 |
| 4 | (x + 1) 4 = 1 x 4 + 4 x 3 + 6 x 2 + 4 x + 1 | 1, 4, 6, 4, 1 |
… и т. д … д … |
Первые 15 строк
Для справки я включил строки с 0 по 14 треугольника Паскаля
.
1
10
45
120
210
252
210
120
45
10
1
1
11
55
165
330
462
462
330
165
55
11
1
1
12
66
220
495
792
924
792
495
220
66
12
1
1
13
78
286
715
1287
1716
1716
1287
715
286
78
130009 13
1
14
91
364
1001
2002
3003
3432
3003
2002
1001
364
91
364
91
Китайцы знали об этом
Этот рисунок называется «Схема семи квадратов умножения по старинному методу».Просмотр полного изображения
Это с лицевой стороны книги Чу Ши-Чи « Ssu Yuan Yü Chien» (Драгоценное зеркало четырех элементов) , написанной в году нашей эры 1303 (более 700 лет назад и более чем на 300 лет до Паскаля!) В книге говорится, что треугольник был известен более чем за два столетия до этого.
Квинканкс
Удивительная маленькая машина, созданная сэром Фрэнсисом Гальтоном, представляет собой треугольник Паскаля, сделанный из колышков. Он называется Quincunx.
Шарики падают на первый колышек, а затем отскакивают до нижней части треугольника, где они собираются в маленькие ящики.
Сначала это выглядит совершенно случайным (и это так), но затем вы обнаруживаете, что шары складываются в красивый узор: нормальное распределение.
перестановок и комбинаций (алгебра 2, дискретная математика и вероятность) — Mathplanet
Прежде чем мы обсудим перестановки, мы собираемся взглянуть на то, что означает сочетание слов и перестановка.Вальдорфский салат — это смесь сельдерея, грецких орехов и салата. Неважно, в каком порядке мы добавляем наши ингредиенты, но если у нас есть комбинация для нашего замка, которая составляет 4-5-6, то порядок чрезвычайно важен.
Если порядок не имеет значения, то у нас есть комбинация, если порядок имеет значение, то у нас есть перестановка. Можно сказать, что перестановка — это упорядоченная комбинация.
Можно сказать, что перестановка — это упорядоченная комбинация.
Число перестановок n объектов, взятых r за раз, определяется по следующей формуле:
$$ P (n, r) = \ frac {n!} {(N-r)!} $$
Пример
Код состоит из 4 цифр в определенном порядке, цифры от 0 до 9.Сколько существует различных перестановок, если одну цифру можно использовать только один раз?
Четырехзначный код может быть любым от 0000 до 9999, следовательно, существует 10000 комбинаций, если каждая цифра может использоваться более одного раза, но поскольку в вопросе нам сказано, что можно использовать только одну цифру, если она ограничивает наше количество комбинаций . Чтобы определить правильное количество перестановок, мы просто подставляем наши значения в нашу формулу:
$$ P (n, r) = \ frac {10!} {(10-4)!} = \ Frac {10 \ cdot9 \ cdot8 \ cdot 7 \ cdot 6 \ cdot 5 \ cdot 4 \ cdot 3 \ cdot 2 \ cdot 1} {6 \ cdot5 \ cdot 4 \ cdot 3 \ cdot 2 \ cdot 1} = 5040 $$
В нашем примере порядок цифр был важен, если бы порядок не имел значения, у нас было бы определение комбинации. Количество комбинаций из n объектов, взятых r за раз, определяется по следующей формуле:
Количество комбинаций из n объектов, взятых r за раз, определяется по следующей формуле:
$$ C (n, r) = \ frac {n!} {(N-r)! R!} $$
Видеоурок
Четверо друзей сядут за стол с 6 стульями. Какими способами могут сидеть друзья?
Мир математики — Mathigon
Введение
Леонард Эйлер (1707 — 1783)
Комбинаторика — это раздел математики, который насчитывает примерно , считая , и мы откроем для себя множество захватывающих примеров «вещей», которые вы можете сосчитать.
Первые комбинаторные задачи изучали математики Древней Индии, Арабских стран и Греции. Интерес к этому предмету возрос в XIX и XX веках, вместе с развитием теории графов и таких проблем, как теорема о четырех цветах. Среди ведущих математиков — Блез Паскаль (1623–1662), Якоб Бернулли (1654–1705) и Леонард Эйлер (1707–1783).
Комбинаторика имеет множество приложений в других областях математики, включая теорию графов, кодирование и криптографию, а также вероятность.
Факториалы
Комбинаторика может помочь нам подсчитать количество приказов , в которых что-то может случиться. Рассмотрим следующий пример:
В классе стоят в ряд учеников V.CombA1 и стульев V.CombA1 . В скольких различных порядках ученики могут сидеть на этих стульях?
Перечислим возможности — в этом примере V.CombA1 разных зрачков представлены V.CombA1 разных цветов стульев.
Существует {2: 2, 3: 6, 4: 24, 5: 120} [V.CombA1] различных возможных порядка. Обратите внимание, что количество возможных порядков очень быстро увеличивается по мере увеличения количества учеников. У 6 учеников есть 720 различных возможностей, и перечислять их все становится непрактично. Вместо этого нам нужна простая формула, которая говорит нам, сколько имеется заказов на n человек, чтобы сесть на n стулья. Затем мы можем просто заменить 3, 4 или любое другое число на n , чтобы получить правильный ответ.
Затем мы можем просто заменить 3, 4 или любое другое число на n , чтобы получить правильный ответ.
Предположим, у нас есть стульев V.CombB1 и мы хотим разместить V.CombB1 == 1? ‘Один ученик’: V.CombB1 == 2? ‘Два ученика’: V.CombB1 == 3? ‘Три ученика ‘: V.CombB1 == 4?’ Четыре ученика ‘: V.CombB1 == 5?’ Пять учеников ‘: V.CombB1 == 6?’ Шесть учеников ‘:’ семь учеников ‘ на них.
{7: «Семь учеников могут сесть на первый стул. Затем есть 6 учеников, которые могли бы сесть на второй стул. Есть 5 вариантов для третьего стула, 4 варианта для четвертого стула, 3 варианта для пятого стула, 2 варианта для шестого стула и только один вариант для последнего стула.’,
6: «Есть 6 учеников, которые могли бы сесть на первый стул. Затем есть 5 учеников, которые могли бы сесть на второй стул. Есть 4 варианта для третьего стула, 3 варианта для четвертого стула, 2 варианта для пятого стула и только один вариант для последнего стула. ‘,
‘,
5: «Пятеро учеников могли бы сесть на первый стул. Затем есть 4 ученика, которые могут сесть на второй стул. Есть 3 варианта для третьего стула, 2 варианта для четвертого стула и только один вариант для последнего стула.’,
4: «Есть 4 ученика, которые могли бы сесть на первый стул. Затем есть 3 ученика, которые могут сесть на второй стул. Есть 2 варианта для третьего стула и только один вариант для последнего стула. ‘,
3: «Есть 3 ученика, которые могут сесть на первый стул. Затем есть 2 ученика, которые могут сесть на второй стул. Наконец, остался только один ученик, чтобы сесть на третий стул. ‘,
2: «Есть 2 ученика, которые могут сесть на первый стул. Затем остается только один ученик, который может сесть на второй стул.’,
1: ‘Это только один вариант для одиночного стула.’} [V.CombB1]
Всего
возможностей. Чтобы упростить обозначения, математики используют знак «!» называется факториалом. Например, 5! («Пять факториалов») то же самое, что 5 × 4 × 3 × 2 × 1. Выше мы только что показали, что существует n ! возможности заказать н объекта.
Выше мы только что показали, что существует n ! возможности заказать н объекта.
Насколько разными способами 23 ребенка могли сесть на 23 стула в классе математики? Если у вас 4 урока в неделю, а в году 52 недели, сколько лет нужно, чтобы изучить все возможности? Примечание: Возраст Вселенной составляет около 14 миллиардов лет.
Для 23 детей, чтобы сесть на 23 стула, их 23! = 25 852 016 738 884 800 000 000 возможностей (это число слишком велико для отображения на экране калькулятора). Испытание всех возможностей потребует
23! 4 × 52 = 124 288 542 000 000 000 000 лет.
Это почти в 10 миллионов раз больше нынешнего возраста Вселенной!
Перестановки
Вышеупомянутый метод требовал, чтобы у нас было столько же учеников, сколько стульев, на которых можно было бы сидеть.Но что будет, если стульев не хватит?
Сколько различных возможностей существует для любых Math.min (V.CombC1, V.CombC2) из V.
CombC1 учеников, чтобы сесть на Math.min (V.CombC1, V.CombC2) стульев? Обратите внимание, что Math.max (0, V.CombC1-V.CombC2) останется включенным, и мы не должны включать его при перечислении возможностей.
Давайте начнем снова, перечислив все возможности:
Чтобы найти простую формулу, подобную приведенной выше, мы можем думать о ней очень похожим образом.
«Есть ученики« + V.CombC1 + », которые могут сесть на первый стул. ‘+
(((Math.min (V.CombC1, V.CombC2)) == 2 || (Math.min (V.CombC1, V.CombC2)) == 3 || (Math.min (V.CombC1, V .CombC2)) == 4)? ‘Тогда есть’ + (V.CombC1-1) + ‘ученики, которые могли бы сесть на второй стул.’: ») +
(((Math.min (V.CombC1, V.CombC2)) == 3 || (Math.min (V.CombC1, V.CombC2)) == 4)? ‘Тогда есть’ + (V.CombC1 -2) + ‘ученики, которые могли бы сесть на третий стул.’: ») +
(((Math.min (V.CombC1, V.CombC2)) == 4)? ‘Наконец, остался один ученик, который сядет на последний стул. ’:’ ‘) +
’:’ ‘) +
((V.CombC1- (Math.min (V.CombC1, V.CombC2)) == 1 || V.CombC1- (Math.min (V.CombC1, V.CombC2)) == 2 || V. CombC1- (Math.min (V.CombC1, V.CombC2)) == 3)? ‘Нас не волнуют оставшиеся’ + (V.CombC1-V.CombC2) + ‘дети, оставшиеся стоять.’: ‘ ‘)
Всего
возможностей. Мы снова должны подумать об обобщении этого. Мы начинаем, как и делали бы с факториалами, но останавливаемся, не дойдя до 1. Фактически мы останавливаемся, как только достигаем числа студентов без стула. При размещении 7 студентов на 3 стульях их
7 × 6 × 5 = 7 × 6 × 5 × 4 × 3 × 2 × 17 × 6 × 5 × 4 × 3 × 2 × 1 = 7 ! 4! = 7 ! ( 7 — 3 )!
возможностей, так как 4 × 3 × 2 × 1 будут компенсировать друг друга.Опять же, для этого есть более простое обозначение: 7 P 3 . Если мы хотим разместить n объектов на m позиций, то будет
n P m = n ! ( n — m )!
возможностей. P означает « p ermutations», поскольку мы подсчитываем количество перестановок (порядков) объектов. Если m и n такие же, как и в задаче в начале этой статьи, мы имеем
P означает « p ermutations», поскольку мы подсчитываем количество перестановок (порядков) объектов. Если m и n такие же, как и в задаче в начале этой статьи, мы имеем
n P n = n ! ( n — n )! = n ! 0 !.
Чтобы понять это, мы определяем 0! = 1. Теперь n P n = n ! как и следовало ожидать от нашего решения первой проблемы.
К сожалению, вы не можете вспомнить код своего четырехзначного замка. Вы только знаете, что не использовали ни одну цифру более одного раза. Сколько разных способов вы должны попробовать? Что вы делаете о безопасности этих замков?
Имеется 10 цифр (0, 1,…, 9), каждая из которых встречается не более одного раза.Число порядков этих цифр составляет 10 P 4 = 5040. Проверка такого количества комбинаций займет очень много времени, поэтому 4-значные блокировки очень безопасны.
Комбинации
Перестановки используются, когда вы выбираете предметы и заботитесь об их порядке — например, о порядке детей на стульях. Однако в некоторых задачах вы не заботитесь о порядке и просто хотите знать, сколько есть способов выбрать определенное количество объектов из большего набора.
В магазине есть пять разных футболок, которые вам нравятся: красного, синего, зеленого, желтого и черного цветов.К сожалению, у вас достаточно денег, чтобы купить три из них. Сколько существует способов выбрать три футболки из пяти, которые вам нравятся?
Здесь нас не волнует порядок (неважно, покупаем ли мы сначала черный, а затем красный или сначала красный, а затем черный), а только количество комбинаций футболок. Возможностей
, итого их 10. Если бы мы вычислили 5 P 3 = 60, мы бы дважды подсчитали некоторые возможности, как показано в следующей таблице:
При перестановках мы считаем каждую комбинацию из трех футболок 6 раз, потому что их 3! = 6 способов заказать три футболки. Чтобы получить количество комбинаций из количества перестановок, нам просто нужно разделить на 6. Мы пишем
Чтобы получить количество комбинаций из количества перестановок, нам просто нужно разделить на 6. Мы пишем
5 C 3 = 5 P 33! = 606 = 10.
Здесь C означает « c комбинаций». В общем, если мы хотим выбрать r объекта из n , то будет
n C r = n P r r ! = n ! r ! ( n — r )!
различных комбинаций.Вместо n C r математики часто пишут n C r = ( n r ), как дробь в скобках, но без промежуточной линии. (Для упрощения набора мы продолжим использовать первую строчную нотацию.)
(a) В вашем классе 10 детей, но вы можете пригласить только пятерых на свой день рождения. Сколько разных комбинаций друзей вы могли бы пригласить? Объясните, следует ли использовать комбинации или перестановки.
(б) На вечеринке 75 человек. Каждый раз всем пожимает руку. Как часто в целом рукопожатие? Подсказка: сколько человек участвует в рукопожатии?
(a) Количество комбинаций друзей, которых вы можете пригласить, составляет 10 C 5 = 252. Мы использовали комбинации, потому что не имеет значения, в каком порядке мы приглашаем друзей, а на какие мы приглашаем.
(b) Вы хотите найти количество всех возможных пар гостей вечеринки.Это просто 75 C 2 = 2775. (Это много рукопожатий!)
Комбинаторика и треугольник Паскаля
Рассчитаем некоторые значения n C r . Начнем с 0 C 0. Затем находим 1 C 0 и 1 C 1. Затем 2 C 0, 2 C 1 и 2 C 2. Затем 3 C 0 , 3 C 1, 3 C 2 и 3 C 3. Мы можем записать все эти результаты в таблицу:
| 0 С 0 = 1 | |||||||||||
| 1 С 0 = 1 | 1 С 1 = 1 | ||||||||||
| 2 С 0 = 1 | 2 С 1 = 2 | 2 С 2 = 1 | |||||||||
| 3 С 0 = 1 | 3 С 1 = 3 | 3 С 2 = 3 | 3 С 3 = 1 | ||||||||
| 4 С 0 = 1 | 4 С 1 = 4 | 4 С 2 = 6 | 4 С 3 = 4 | 4 С 4 = 1 | |||||||
| 5 С 0 = 1 | 5 С 1 = 5 | 5 С 2 = 10 | 5 С 3 = 10 | 5 С 4 = 5 | 5 С 5 = 1 | ||||||
Это в точности треугольник Паскаля, который мы исследовали в статье о последовательностях. Его можно создать более легко, если учесть, что любая ячейка представляет собой сумму двух ячеек, указанных выше. В треугольнике Паскаля скрыто бесчисленное множество узоров и числовых последовательностей.
Его можно создать более легко, если учесть, что любая ячейка представляет собой сумму двух ячеек, указанных выше. В треугольнике Паскаля скрыто бесчисленное множество узоров и числовых последовательностей.
Теперь мы также знаем, что номер r в строке n также задается как n C r (но мы всегда должны начинать отсчет с 0, поэтому первая строка или столбец фактически нулевой ряд). Если мы применим то, что мы знаем о создании треугольника Паскаля, к нашим комбинациям, мы получим
( n r )
+
( n r + 1)
знак равно
( № + 1 № + 1)
.
Это известно как идентификатор Паскаля . Вы можете получить его, используя определение n C r в терминах факториалов, или вы можете думать об этом следующим образом:
Мы хотим выбрать r + 1 объектов из набора n + 1 объектов.
Это в точности то же самое, что пометить один объект из n + 1 , который будет называться X, и либо выбрать X плюс r других (из оставшихся n), либо не выбрать X и r + 1 другие ( от оставшихся n).
Многие задачи комбинаторики имеют простое решение, если вы думаете о нем правильно, и очень сложное решение, если вы просто пытаетесь использовать алгебру…
Звезды и решетки
Решение
Пример
Зеленщик на рынке хранит большое количество из из различных видов фруктов. Какими способами мы можем собрать мешок из или фруктов? Обратите внимание, что r может быть меньше, равно или больше n .
Обратите внимание, что с r ≤ n существует n C r способов выбрать по одному фрукту каждого вида. Однако мы также можем съесть более одного фрукта каждого вида, например, два яблока, одну клубнику и один банан.
Мы можем представить любой допустимый выбор фруктов цепочкой звезд и полосок, как показано в этом примере:
| ★★★ | | | ★★ | | | | | ★★ | | | ★ | |
| 3 типа 1 | 2 типа 2 | 0 типа 3 | 2 типа 4 | 1 типа 5 |
Всего есть r звезды (что соответствует r фруктам, которые нам разрешено есть) и n — 1 столбик (деление n различных фруктов). Это составляет r + n — всего 1 место. Любой заказ r звезды и n — 1 батончик соответствует ровно одному действительному выбору фруктов.
Это составляет r + n — всего 1 место. Любой заказ r звезды и n — 1 батончик соответствует ровно одному действительному выбору фруктов.
Теперь мы можем применить наши комбинаторные инструменты: есть r + n — 1 мест, и мы хотим выбрать n — 1 из них как столбцы (все остальные — звездочки). Что есть ровно ( r + n — 1) C ( n — 1) возможностей для этого!
Предположим, есть пять видов фруктов, и мы хотим взять десять штук.Исходя из того, что мы подсчитали выше, всего
(10 + 5-1) C (5-1) = 14 C 4 = 24 024
возможностей. Подумайте об этом в следующий раз, когда пойдете за покупками!
Комбинаторика и вероятность
Комбинаторика имеет множество приложений в теории вероятностей. Вы часто хотите найти вероятность одного конкретного события, и вы можете использовать уравнение
P ( X ) = вероятность того, что X произойдет = количество исходов, при которых произошло X , общее количество возможных исходов
Вы можете использовать комбинаторику, чтобы вычислить «общее количество возможных результатов». Вот пример:
Вот пример:
Четверо детей, которых зовут A, B, C и D, случайным образом сидят на четырех стульях. Какова вероятность того, что А сядет на первый стул?
Мы уже показали, что всего существует 24 способа сесть на четыре стула. Если вы посмотрите на наше решение, вы также обнаружите, что А сидит на первом стуле в шести случаях. Следовательно,
P (A сидит на первом стуле) = количество результатов, где A сидит на первом стуле, общее количество возможных результатов = 624 = 14.
Этот ответ был ожидаемым, поскольку каждый из четырех детей с одинаковой вероятностью сядет на первый стул. Но в других случаях все не так просто…
(a) Почтальон должен доставить четыре письма в четыре разных дома на улице. К сожалению, дождь стер адреса, поэтому он просто раздает их случайным образом, по одной букве на дом. Какова вероятность, что каждый дом получит нужную букву? (☆ Какова вероятность, что каждый дом получит неправильную букву?)
(b) В лотерее нужно угадать 6 номеров из 49. Какова вероятность того, что вы все сделаете правильно? Если каждую неделю отправлять 100 предположений, сколько времени в среднем вам понадобится, чтобы выиграть?
Какова вероятность того, что вы все сделаете правильно? Если каждую неделю отправлять 100 предположений, сколько времени в среднем вам понадобится, чтобы выиграть?
(а) Всего 4! = 24 способа случайного распределения букв и только один способ получить их все правильно. Таким образом, вероятность того, что каждое письмо будет доставлено в нужный дом, составляет 1/24 = 0,0417 = 4,17%.
Определить вероятность того, что каждое письмо будет доставлено не в тот дом, немного сложнее.Это не просто 1 — 0,0417, так как во многих случаях один или два, но не , все домов получают правильную букву. В этом простом случае самым простым решением было бы записать все 24 варианта. Вы обнаружите, что в 9 из 24 случаев каждый дом получает неправильную букву, что дает вероятность 0,375 = 37,5%. Если домов слишком много, чтобы записать все возможности, вы можете использовать идею, называемую принцип включения исключения .
(b) Существует 49 C 6 = 13 983 816 возможных результатов лотереи, поэтому вероятность получить правильное решение составляет 1/49 C 6 = 0. 000000072.
000000072.
В среднем также потребуется 13 983 816 попыток, чтобы выиграть. Если мы отправляем 100 предположений каждую неделю, это соответствует 139 838 неделям, что равняется 2689 годам. Урок, который нужно усвоить: не играйте в лото!
Комбинаторика: формулы и примеры — урок математики [видео 2021]
Типичные комбинаторные вычисления
Факториал выражается как n !. Мы читаем это как: n факториал.
Некоторые факты о факторике включают:
Например:
Факториал появится в наших расчетах.Вот одна из этих формул:
Левая часть читается как: n взять k . Предположим, что n равно 5, а k равно 2. Затем мы получаем формулу с подключенными значениями, которые вы видите ниже, и которая в конечном итоге равна 10.
Кстати, верно и то, что:
Мы можем показать это в следующей формуле:
Наш последний тип математических вычислений выражается в двойных скобках, как вы можете видеть здесь:
Вот пример этого разыгрывания, которое, как вы можете видеть, в конечном итоге равняется 15.
Теперь мы можем изучить, как использовать эту математику для подсчета возможностей.
Подсчет возможностей
Прежде чем мы начнем использовать формулы, давайте посчитаем возможности для нашей ситуации рецепта. Затем мы можем использовать формулы и проверить результаты.
Для краткости мы будем использовать C для тмина, O для орегано и B для базилика.
При определении количества возможных вариантов выбора, когда мы выбираем k из n , мы сначала решаем, имеет значение порядок или нет.
Допустим, у нас есть эти три специи, и мы можем выбрать любые две для рецепта. Одна специя добавляется в начале процесса приготовления. Другая специя добавляется в конце. Здесь порядок имеет значение.
Теперь решаем, разрешено ли повторение. Предположим, что одна и та же переменная не повторяется (в нашем случае это пряность). Это называется перестановкой с недопустимым повторением . Формула имеет следующий вид:
Перечислим фактически возможные рецепты: ( C, O ), ( O, C ), ( C, B ), ( B, C ), ( O, B ) , ( Б, О ). Есть шесть возможных рецептов при выборе 2 из 3, где порядок имеет значение и нет повторений.
Есть шесть возможных рецептов при выборе 2 из 3, где порядок имеет значение и нет повторений.
Что дает формула? Как видим, получается:
Мы можем думать об этом как о трех вариантах для первой специи и двух вариантах для второй. Это дает 3 x 2 = 6 возможных рецептов.
Перестановка с допустимыми повторениями имеет формулу:
В примере рецепта перестановки с повторениями могут произойти, если вы можете использовать одну и ту же специю в начале и в конце.Список комбинаций специй увеличился: ( C, C ), ( O, O ), ( B, B ), ( C, O ), ( O, C ), ( C, B ), ( B, C ), ( O, B ), ( B, O ). Есть 9 возможных рецептов.
Наша формула для перестановок с допустимыми повторениями будет:
Мы можем думать об этой ситуации как о том, что есть 3 варианта для первой специи и 3 варианта для второй специи.Тогда 3 x 3 = 9 возможных рецептов.
А теперь перейдем к случаям, когда порядок не имеет значения. Когда порядок не имеет значения и повторение не допускается, у нас есть комбинация без повторения . Формула:
Формула:
Допустим, в этом рецепте мы можем использовать любые 2 из 3 специй. Если выбранные специи объединяются и добавляются один раз, то заказ не имеет значения. Кроме того, если мы не повторим одну и ту же специю для нашего выбора из двух специй, то у нас будет комбинация без повторения.
Вот список возможных рецептов: ( C, O ), ( C, B ), ( O, B ). Есть 3 возможных рецепта.
Давайте проверим это с помощью нашей формулы, которая, как мы видим, выглядит так:
Наша четвертая возможная группировка — это когда порядок не имеет значения и допускается повторение. Это называется комбинацией с повторением . Формула:
Что, если наш рецепт позволяет использовать две столовые ложки из трех доступных специй, и мы можем использовать одну и ту же специю дважды? Выбранные специи смешиваются и добавляются за один раз.Здесь порядок не имеет значения, повторение разрешено. Это сочетание с повторением.
Список рецептов: ( C, C ), ( O, O ), ( B, B ), ( C, O ), ( C, B ), ( О, В ). Есть 6 возможных рецептов.
Есть 6 возможных рецептов.
Как видите, наша формула в конечном итоге дает нам:
Дополнительные примеры
Пример 1
Допустим, у вас есть класс с 15 учениками.Из этого класса мы хотели бы сформировать меньшую группу из трех учеников, которые будут представлять весь класс. Будет капитан, первый помощник и второй помощник. Сколько способов мы можем выбрать эту меньшую группу?
Решение 1. Здесь порядок имеет значение, и одно и то же лицо не повторяется. Это перестановка с недопустимым повторением. Как мы видим, это становится:
Пример 2
Мы хотели бы выбрать три шарика мороженого для смешивания с нашим молочным коктейлем.Доступные вкусы: шоколад, ваниль, фисташки и клубника. Сколько вариантов мы могли сделать?
Решение 2: Здесь порядок не имеет значения, повторение разрешено. Это сочетание с повторением. Мы видим, что это превращается в:
Итоги урока
Давайте кратко рассмотрим. Выбор количества доступных возможностей — это область комбинаторики . Когда порядок имеет значение, у нас есть так называемая перестановка .Если порядок не имеет значения, у нас комбинация . Мы также должны учитывать, разрешены ли повторений или нет. Это приводит к четырем формулам в этом исследовании комбинаторики.
Когда порядок имеет значение, у нас есть так называемая перестановка .Если порядок не имеет значения, у нас комбинация . Мы также должны учитывать, разрешены ли повторений или нет. Это приводит к четырем формулам в этом исследовании комбинаторики.
Сочетанием из n элементов по k называют. Сочетания и теория вероятностей
В данной статье речь пойдет об особом разделе математики под названием комбинаторика. Формулы, правила, примеры решения задач — все это вы сможете найти здесь, прочитав статью до самого конца.
Итак, что же это за раздел? Комбинаторика занимается вопросом подсчета каких-либо объектов. Но в данном случае объектами выступают не сливы, груши или яблоки, а нечто иное. Комбинаторика помогает нам находить вероятность какого-либо события. Например, при игре в карты — какова вероятность того, что у противника есть козырная карта? Или такой пример — какова вероятность того, что из мешка с двадцатью шариками вы достанете именно белый? Именно для подобного рода задач нам и нужно знать хотя бы основы данного раздела математики.
Комбинаторные конфигурации
Рассматривая вопрос основных понятий и формул комбинаторики, мы не можем не уделить внимание комбинаторным конфигурациям. Они используются не только для формулировки, но и для решения различных Примерами таких моделей служат:
- размещение;
- перестановка;
- сочетание;
- композиция числа;
- разбиение числа.
О первых трех мы поговорим более подробно далее, а вот композиции и разбиению мы уделим внимание в данном разделе. Когда говорят о композиции некого числа (допустим, а), то подразумевают представление числа а в виде упорядоченной суммы неких положительных чисел. А разбиение — это неупорядоченная сумма.
Разделы
Прежде чем мы перейдем непосредственно к формулам комбинаторики и рассмотрению задач, стоит обратить внимание на то, что комбинаторика, как и другие разделы математики, имеет свои подразделы. К ним относятся:
- перечислительная;
- структурная;
- экстремальная;
- теория Рамсея;
- вероятностная;
- топологическая;
- инфинитарная.

В первом случае речь идет об исчисляющей комбинаторике, задачи рассматривают перечисление или подсчет разных конфигураций, которые образованы элементами множеств. На данные множества, как правило, накладываются какие-либо ограничения (различимость, неразличимость, возможность повтора и так далее). А количество этих конфигураций подсчитывается при помощи правила сложения или умножения, о которых мы поговорим немного позже. К структурной комбинаторике относятся теории графов и матроидов. Пример задачи экстремальной комбинаторики — какова наибольшая размерность графа, который удовлетворяет следующим свойствам… В четвертом пункте мы упомянули теорию Рамсея, которая изучает в случайных конфигурациях наличие регулярных структур. Вероятностная комбинаторика способна нам ответить на вопрос — какова вероятность того, что у заданного множества присутствует определенное свойство. Как нетрудно догадаться, топологическая комбинаторика применяет методы в топологии. И, наконец, седьмой пункт — инфинитарная комбинаторика изучает применение методов комбинаторики к бесконечным множествам.
Правило сложения
Среди формул комбинаторики можно найти и довольно простые, с которыми мы достаточно давно знакомы. Примером является правило суммы. Предположим, что нам даны два действия (С и Е), если они взаимоисключаемы, действие С выполнимо несколькими способами (например а), а действие Е выполнимо b-способами, то выполнить любое из них (С или Е) можно а+b способами.
В теории это понять достаточно трудно, постараемся донести всю суть на простом примере. Возьмем среднюю численность учеников одного класса — допустим, это двадцать пять. Среди них пятнадцать девочек и десять мальчиков. Ежедневно в классе назначается один дежурный. Сколько есть способов назначить дежурного по классу сегодня? Решение задачи достаточно простое, мы прибегнем к правилу сложения. В тексте задачи не сказано, что дежурными могут быть только мальчики или только девочки. Следовательно, им может оказаться любая из пятнадцати девочек или любой из десяти мальчиков. Применяя правило суммы, мы получаем достаточно простой пример, с которым без труда справится школьник начальных классов: 15 + 10. Подсчитав, получаем ответ: двадцать пять. То есть существует всего двадцать пять способов назначить на сегодня дежурного класса.
Подсчитав, получаем ответ: двадцать пять. То есть существует всего двадцать пять способов назначить на сегодня дежурного класса.
Правило умножения
К основным формулам комбинаторики относится и правило умножения. Начнем с теории. Допустим, нам необходимо выполнить несколько действий (а): первое действие выполняется с1 способами, второе — с2 способами, третье — с3 способами и так далее до последнего а-действия, выполняемого са способами. Тогда все эти действия (которых всего у нас а) могут быть выполнены N способами. Как высчитать неизвестную N? В этом нам поможет формула: N = с1 * с2 * с3 *…* са.
Опять же, в теории ничего не понятно, переходим к рассмотрению простого примера на применение правила умножения. Возьмем все тот же класс из двадцати пяти человек, в котором учится пятнадцать девочек и десять мальчиков. Только на этот раз нам необходимо выбрать двух дежурных. Ими могут быть как только мальчики или девочки, так и мальчик с девочкой. Переходим к элементарному решению задачи. Выбираем первого дежурного, как мы решили в прошлом пункте, у нас получается двадцать пять возможных вариантов. Вторым дежурным может быть любой из оставшихся человек. У нас было двадцать пять учеников, одного мы выбрали, значит вторым дежурным может быть любой из оставшихся двадцати четырех человек. Наконец, применяем правило умножения и получаем, что двоих дежурных можно избрать шестью сотнями способов. Мы данное число получили умножением двадцати пяти и двадцати четырех.
Выбираем первого дежурного, как мы решили в прошлом пункте, у нас получается двадцать пять возможных вариантов. Вторым дежурным может быть любой из оставшихся человек. У нас было двадцать пять учеников, одного мы выбрали, значит вторым дежурным может быть любой из оставшихся двадцати четырех человек. Наконец, применяем правило умножения и получаем, что двоих дежурных можно избрать шестью сотнями способов. Мы данное число получили умножением двадцати пяти и двадцати четырех.
Перестановка
Сейчас мы рассмотрим еще одну формулу комбинаторики. В данном разделе статьи мы поговорим о перестановках. Рассмотреть проблему предлагаем сразу же на примере. Возьмем бильярдные шары у нас их n-ое количество. Нам нужно подсчитать: сколько есть вариантов расставить их в ряд, то есть составить упорядоченный набор.
Начнем, если у нас нет шаров, то и вариантов расстановки у нас так же ноль. А если у нас шар один, то и расстановка тоже одна (математически это можно записать следующим образом: Р1 = 1). Два шара можно расставить двумя разными способами: 1,2 и 2,1. Следовательно, Р2 = 2. Три шара можно расставить уже шестью способами (Р3=6): 1,2,3; 1,3,2; 2,1,3; 2,3,1; 3,2,1; 3,1,2. А если таких шаров не три, а десять или пятнадцать? Перечислять все возможные варианты очень долго, тогда нам на помощь приходит комбинаторика. Формула перестановки поможет нам найти ответ на интересующий нас вопрос. Pn = n *P (n-1). Если попытаться упростить формулу, то получаем: Pn = n* (n — 1) *…* 2 * 1. А это и есть произведение первых натуральных чисел. Такое число называется факториалом, а обозначается как n!
Два шара можно расставить двумя разными способами: 1,2 и 2,1. Следовательно, Р2 = 2. Три шара можно расставить уже шестью способами (Р3=6): 1,2,3; 1,3,2; 2,1,3; 2,3,1; 3,2,1; 3,1,2. А если таких шаров не три, а десять или пятнадцать? Перечислять все возможные варианты очень долго, тогда нам на помощь приходит комбинаторика. Формула перестановки поможет нам найти ответ на интересующий нас вопрос. Pn = n *P (n-1). Если попытаться упростить формулу, то получаем: Pn = n* (n — 1) *…* 2 * 1. А это и есть произведение первых натуральных чисел. Такое число называется факториалом, а обозначается как n!
Рассмотрим задачу. Вожатый каждое утро выстраивает свой отряд в шеренгу (двадцать человек). В отряде есть три лучших друга — Костя, Саша и Леша. Какова вероятность того, что они будут стоять рядом? Чтобы найти ответ на вопрос, нужно вероятность «хорошего» исхода поделить на общее количество исходов. Общее число перестановок составляет 20! = 2,5 квинтиллиона. Как посчитать количество «хороших» исходов? Предположим, что Костя, Саши и Леша — это один сверхчеловек. Тогда мы имеем всего восемнадцать субъектов. Число перестановок в данном случае равняется 18 = 6,5 квадриллионов. При всем этом, Костя, Саша и Леша могут произвольно перемещаться между собой в своей неделимой тройке, а это еще 3! = 6 вариантов. Значит всего «хороших» расстановок у нас 18! * 3! Нам остается только найти искомую вероятность: (18! * 3!) / 20! Что равняется примерно 0,016. Если перевести в проценты, то это получается всего 1,6%.
Тогда мы имеем всего восемнадцать субъектов. Число перестановок в данном случае равняется 18 = 6,5 квадриллионов. При всем этом, Костя, Саша и Леша могут произвольно перемещаться между собой в своей неделимой тройке, а это еще 3! = 6 вариантов. Значит всего «хороших» расстановок у нас 18! * 3! Нам остается только найти искомую вероятность: (18! * 3!) / 20! Что равняется примерно 0,016. Если перевести в проценты, то это получается всего 1,6%.
Размещение
Сейчас мы рассмотрим еще одну очень важную и необходимую формулу комбинаторики. Размещение — это наш следующий вопрос, который предлагаем вам рассмотреть в данном разделе статьи. Мы идем на усложнение. Предположим, что мы хотим рассмотреть возможные перестановки, только не из всего множества (n), а из меньшего (m). То есть мы рассматриваем перестановки из n предметов по m.
Основные формулы комбинаторики стоит не просто заучивать, а понимать их. Даже несмотря на то, что они усложняются, так как у нас не один параметр, а два. Предположим, что m = 1, то и А = 1, m = 2, то А = n * (n — 1). Если далее упрощать формулу и перейти на запись при помощи факториалов, то получится вполне лаконичная формула: А = n! / (n — m)!
Предположим, что m = 1, то и А = 1, m = 2, то А = n * (n — 1). Если далее упрощать формулу и перейти на запись при помощи факториалов, то получится вполне лаконичная формула: А = n! / (n — m)!
Сочетание
Мы рассмотрели практически все основные формулы комбинаторики с примерами. Теперь перейдем к заключительному этапу рассмотрения базового курса комбинаторики — знакомство с сочетанием. Сейчас мы будем выбирать m предметов из имеющихся у нас n, при этом всем мы будем выбирать всеми возможными способами. Чем же тогда это отличается от размещения? Мы не будем учитывать порядок. Этот неупорядоченный набор и будет являться сочетанием.
Сразу введем обозначение: С. Берем размещения m шариков из n. Мы перестаем обращать внимание на порядок и получаем повторяющиеся сочетания. Чтобы получить число сочетаний нам надо поделить число размещений на m! (m факториал). То есть С = А / m! Таким образом, способов выбрать из n шаров немножко, равняется примерно столько, сколько выбрать почти все. Этому есть логическое выражение: выбрать немножко все равно, что выкинуть почти все. Еще в данном пункте важно упомянуть и то, что максимальное число сочетаний можно достигнуть при попытке выбрать половину предметов.
Этому есть логическое выражение: выбрать немножко все равно, что выкинуть почти все. Еще в данном пункте важно упомянуть и то, что максимальное число сочетаний можно достигнуть при попытке выбрать половину предметов.
Как выбрать формулу для решения задачи?
Мы подробно рассмотрели основные формулы комбинаторики: размещение, перестановка и сочетание. Теперь наша задача — облегчить выбор необходимой формулы для решения задачи по комбинаторике. Можно воспользоваться следующей довольно простой схемой:
- Задайте себе вопрос: порядок размещения элементов учитывается в тексте задачи?
- Если ответ нет, то воспользуйтесь формулой сочетания (С = n! / (m! * (n — m)!)).
- Если ответ нет, то необходимо ответить на еще один вопрос: все ли элементы входят в комбинацию?
- Если ответ да, то воспользуйтесь формулой перестановки (Р = n!).
- Если ответ нет, то воспользуйтесь формулой размещения (А = n! / (n — m)!).
Пример
Мы рассмотрели элементы комбинаторики, формулы и некоторые другие вопросы. Теперь перейдем к рассмотрению реальной задачи. Представьте, что перед вами лежат киви, апельсин и банан.
Теперь перейдем к рассмотрению реальной задачи. Представьте, что перед вами лежат киви, апельсин и банан.
Вопрос первый: сколькими способами их можно переставить? Для этого воспользуемся формулой перестановок: Р = 3! = 6 способов.
Вопрос второй: сколькими способами можно выбрать один фрукт? Это очевидно, у нас всего три варианта — выбрать киви, апельсин или банан, но применим формулу сочетаний: С = 3! / (2! * 1!) = 3.
Вопрос третий: сколькими способами можно выбрать два фрукта? Какие есть у нас вообще варианты? Киви и апельсин; киви и банан; апельсин и банан. То есть три варианта, но это легко проверить при помощи формулы сочетания: С = 3! / (1! * 2!) = 3
Вопрос четвертый: сколькими способами можно выбрать три фрукта? Как видно, выбрать три фрукта можно одним-единственным способом: взять киви, апельсин и банан. С = 3! / (0! * 3!) = 1.
Вопрос пятый: сколькими способами можно выбрать хотя бы один фрукт? Это условие подразумевает, что мы можем взять один, два или все три фрукта. Следовательно, мы складываем С1 + С2 + С3 =3 + 3 + 1 = 7. То есть у нас есть семь способов взять со стола хотя бы один фрукт.
Следовательно, мы складываем С1 + С2 + С3 =3 + 3 + 1 = 7. То есть у нас есть семь способов взять со стола хотя бы один фрукт.
КОМБИНАТОРИКА
Комбинаторика — раздел математики, который изучает задачи выбора и расположения элементов из некоторого основного множества в соответствии с заданными правилами. Формулы и принципы комбинаторики используются в теории вероятностей для подсчета вероятности случайных событий и, соответственно, получения законов распределения случайных величин. Это, в свою очередь, позволяет исследовать закономерности массовых случайных явлений, что является весьма важным для правильного понимания статистических закономерностей, проявляющихся в природе и технике.
Правила сложения и умножения в комбинаторике
Правило суммы. Если два действия А и В взаимно исключают друг друга, причем действие А можно выполнить m способами, а В — n способами, то выполнить одно любое из этих действий (либо А, либо В) можно n + m способами.
Пример 1.
В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить одного дежурного?
Решение
Дежурным можно назначить либо мальчика, либо девочку, т.е. дежурным может быть любой из 16 мальчиков, либо любая из 10 девочек.
По правилу суммы получаем, что одного дежурного можно назначить 16+10=26 способами.
Правило произведения. Пусть требуется выполнить последовательно k действий. Если первое действие можно выполнить n 1 способами, второе действие n 2 способами, третье — n 3 способами и так до k-го действия, которое можно выполнить n k способами, то все k действий вместе могут быть выполнены:
способами.
Пример 2.
В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить двух дежурных?
Решение
Первым дежурным можно назначить либо мальчика, либо девочку. Т.к. в классе учится 16 мальчиков и 10 девочек, то назначить первого дежурного можно 16+10=26 способами.
После того, как мы выбрали первого дежурного, второго мы можем выбрать из оставшихся 25 человек, т.е. 25-ю способами.
По теореме умножения двое дежурных могут быть выбраны 26*25=650 способами.
Сочетания без повторений. Сочетания с повторениями
Классической задачей комбинаторики является задача о числе сочетаний без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать m из n различных предметов ?
Пример 3.
Необходимо выбрать в подарок 4 из 10 имеющихся различных книг. Сколькими способами можно это сделать?
Решение
Нам из 10 книг нужно выбрать 4, причем порядок выбора не имеет значения. Таким образом, нужно найти число сочетаний из 10 элементов по 4:
.
Рассмотрим задачу о числе сочетаний с повторениями: имеется по r одинаковых предметов каждого из n различных типов; сколькими способами можно выбрать m () из этих (n*r) предметов?
.
Пример 4.
В кондитерском магазине продавались 4 сорта пирожных: наполеоны, эклеры, песочные и слоеные. Сколькими способами можно купить 7 пирожных?
Решение
Т.к. среди 7 пирожных могут быть пирожные одного сорта, то число способов, которыми можно купить 7 пирожных, определяется числом сочетаний с повторениями из 7 по 4.
.
Размещения без повторений. Размещения с повторениями
Классической задачей комбинаторики является задача о числе размещений без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n различных предметов?
Пример 5.
В некоторой газете 12 страниц. Необходимо на страницах этой газеты поместить четыре фотографии. Сколькими способами можно это сделать, если ни одна страница газеты не должна содержать более одной фотографии?
Решение.
В данной задаче мы не просто выбираем фотографии, а размещаем их на определенных страницах газеты, причем каждая страница газеты должна содержать не более одной фотографии. Таким образом, задача сводится к классической задаче об определении числа размещений без повторений из 12 элементов по 4 элемента:
Таким образом, 4 фотографии на 12 страницах можно расположить 11880 способами.
Также классической задачей комбинаторики является задача о числе размещений с повторениями, содержание которой можно выразить вопросом: сколькими способами можно вы б рать и разместить по m различным местам m из n предметов, с реди которых есть одинаковые?
Пример 6.
У мальчика остались от набора для настольной игры штампы с цифрами 1, 3 и 7. Он решил с помощью этих штампов нанести на все книги пятизначные номера- составить каталог. Сколько различных пятизначных номеров может составить мальчик?
Сколько различных пятизначных номеров может составить мальчик?
Перестановки без повторений . Перестановки с повторениями
Классической задачей комбинаторики является задача о числе перестановок без повторения, содержание которой можно выразить вопросом: сколькими способами можно разместить n различных предметов на n различных местах?
Пример 7.
Сколько можно составить четырехбуквенных «слов» из букв слова«брак»?
Решение
Генеральной совокупностью являются 4 буквы слова «брак» (б, р, а, к). Число «слов» определяется перестановками этих 4 букв, т. е.
Для случая, когда среди выбираемых n элементов есть одинаковые (выборка с возвращением), задачу о числе перестановок с повторениями можно выразить вопросом: сколькими способами можно переставить n предметов, расположенных на n различных местах, если среди n предметов имеются k различных типов (k
Пример 8.
Сколько разных буквосочетаний можно сделать из букв слова «Миссисипи»?
Решение
Здесь 1 буква «м», 4 буквы «и», 3 буквы «c» и 1 буква «п», всего 9 букв. Следовательно, число перестановок с повторениями равно
ОПОРНЫЙ КОНСПЕКТ ПО РАЗДЕЛУ «КОМБИНАТОРИКА»
Число сочетаний
Сочетанием из n по k называется набор k элементов, выбранных из данных n элементов. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания отличаются от размещений .
Явные формулы
Число сочетаний из n по k равно биномиальному коэффициенту
При фиксированном значении n производящей функцией чисел сочетаний с повторениями из n по k является:
Двумерной производящей функцией чисел сочетаний с повторениями является:
Ссылки
- Р. Стенли Перечислительная комбинаторика.
 — М.: Мир, 1990.
— М.: Мир, 1990. - Вычисление числа сочетаний онлайн
Wikimedia Foundation . 2010 .
Смотреть что такое «Число сочетаний» в других словарях:
70 семьдесят 67 · 68 · 69 · 70 · 71 · 72 · 73 40 · 50 · 60 · 70 · 80 · 90 · 100 Факторизация: 2×5×7 Римская запись: LXX Двоичное: 100 0110 … Википедия
Световое число, условное число, однозначно выражающее внеш. условия при фотосъёмке (обычно яркость объекта съёмки и светочувствительность применяемого фотоматериала). Любому значению Э. ч. можно подобрать неск. сочетаний диафрагменное число… … Большой энциклопедический политехнический словарь
Форма числа, выделяющая два предмета как по отношению к единичному предмету, так и по отношению к множеству предметов. В современном русском языке эта форма не существует, но остатки ее влияния сохранились. Так, сочетания два стола (ср. мн. ч.… … Словарь лингвистических терминов
Комбинаторная математика, комбинаторика, раздел математики, посвященный решению задач выбора и расположения элементов нек рого, обычно конечного, множества в соответствии с заданными правилами. Каждое такое правило определяет способ построения… … Математическая энциклопедия
Каждое такое правило определяет способ построения… … Математическая энциклопедия
В комбинаторике сочетанием из по называется набор элементов, выбранных из данного множества, содержащего различных элементов. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания… … Википедия
Занимается изучением событий, наступление которых достоверно неизвестно. Она позволяет судить о разумности ожидания наступления одних событий по сравнению с другими, хотя приписывание численных значений вероятностям событий часто бывает излишним… … Энциклопедия Кольера
1) то же, что математический Комбинаторный анализ. 2) Раздел элементарной математики, связанный с изучением количества комбинаций, подчинённых тем или иным условиям, которые можно составить из заданного конечного множества объектов… … Большая советская энциклопедия
— (греч. paradoxos неожиданный, странный) в широком смысле: утверждение, резко расходящееся с общепринятым, устоявшимся мнением, отрицание того, что представляется «безусловно правильным»; в более узком смысле два противоположных утверждения, для… … Философская энциклопедия
— (или принцип включений исключений) комбинаторная формула, позволяющая определить мощность объединения конечного числа конечных множеств, которые в общем случае могут пересекаться друг с другом … Википедия
Математическая теория, занимающаяся определением числа различных способов распределения данных предметов в известном порядке; имеет особенно важное значение в теории уравнений и в теории вероятностей. Простейшие задачи этого рода заключаются в… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Простейшие задачи этого рода заключаются в… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Книги
- Число судьбы. Гороскоп совместимости. Желания. Страсти. Фантазии (количество томов: 3) , Майер Максим. Число судьбы. Как составить индивидуальный нумерологический прогноз. Нумерология — одна из самых древних эзотерических систем. Невозможно точно установить времяее возникновения. Однако в…
На первом месте в ряду может стоять любой из N элементов, следовательно, получается N вариантов. На втором месте — любой, кроме того, который уже был использован для первого места. Следовательно, для каждого из N уже найденных вариантов есть (N — 1) вариантов второго места, и общее количество комбинаций становится N*(N — 1).
Это же можно повторить для остальных элементов ряда. Для самого последнего места остается только один вариант — последний оставшийся элемент. Для предпоследнего — два варианта, и так далее.
Следовательно, для ряда из N неповторяющихся элементов возможных перестановок равно произведению всех целых от 1 до N. Это произведение называется N и N! (читается «эн факториал»).
Это произведение называется N и N! (читается «эн факториал»).
В предыдущем случае количество возможных элементов и количество мест ряда совпадали, и их число было равно N. Но возможна ситуация, когда в ряду меньше мест, чем имеется возможных элементов. Иными словами, количество элементов в выборке равно некоторому числу M, причем M возможных комбинаций может иметь два различных варианта.
Во-первых, может потребоваться сосчитать общее количество возможных способов, которыми можно выстроить в ряд M элементов из N. Такие способы размещениями.
Во-вторых, исследователя может интересовать число способов, которыми можно выбрать M элементов из N. При этом порядок расположения элементов уже не важен, но любые два варианта должны различаться между собой хотя бы одним элементом. Такие способы называются сочетаниями.
Чтобы найти количество размещений по M элементов из N, можно прибегнуть к такому же способу рассуждений, как и в случае с перестановками. На первом месте здесь по-прежнему может стоять N элементов, на втором (N — 1), и так далее. Но для последнего места количество возможных вариантов равняется не единице, а (N — M + 1), поскольку, когда размещение будет закончено, останется еще (N — M) неиспользованных элементов.
Но для последнего места количество возможных вариантов равняется не единице, а (N — M + 1), поскольку, когда размещение будет закончено, останется еще (N — M) неиспользованных элементов.
Таким образом, число размещений по M элементов из N равняется произведению всех целых чисел от (N — M + 1) до N, или, что то же самое, частному N!/(N — M)!.
Очевидно, что количество сочетаний по M элементов из N будет меньше количества размещений. Для каждого возможного сочетания есть M! возможных размещений, зависящих от порядка элементов этого сочетания. Следовательно, чтобы найти это количество, нужно разделить число размещений по M элементов из N на N!. Иными словами, количество сочетаний по M элементов из N равно N!/(M!*(N — M)!).
Источники:
- количество сочетаний
Факториал натурального числа – это произведение всех предыдущих натуральных чисел, включая само число. Факториал нуля равен единице. Кажется, что посчитать факториал числа очень просто – достаточно перемножить все натуральные числа, не превышающие заданное. Однако, значение факториала настолько быстро возрастает, что некоторые калькуляторы не справляются с этой задачей.
Однако, значение факториала настолько быстро возрастает, что некоторые калькуляторы не справляются с этой задачей.
Вам понадобится
- калькулятор, компьютер
Инструкция
Чтобы посчитать факториал натурального числа перемножьте все , не превосходящие данное. Каждое число учитывается только один раз. В виде формулы это можно записать следующим образом:n! = 1*2*3*4*5*…*(n-2)*(n-1)*n, гдеn – натуральное число, факториал которого требуется посчитать.
0! принимается равным единице (0!=1).При возрастании аргумента значение факториала очень быстро увеличивается, поэтому обычный (бухгалтерский) уже для факториала 15-ти вместо результата может выдать об ошибке.
Чтобы посчитать факториал большого натурального числа, возьмите инженерный калькулятор. То есть, такой калькулятор на клавиатуре которого имеются обозначения математических функций (cos, sin, √). Наберите на калькуляторе исходное число, а затем нажмите кнопку вычисления факториала. Обычно такая кнопка как «n!» или аналогично (вместо «n» может стоять «N» или «х», но восклицательный знак «!» в обозначении факториала должен присутствовать в любом случае).
При больших значениях аргумента результаты вычислений начинают отображаться в «экспоненциальном» (показательном) виде. Так, например, факториал 50 будет представлен в форме: 3,0414093201713378043612608166065e+64 (или похожем). Чтобы получить результат вычислений в обычном виде, припишите к числу, показанному до символа «е», столько нулей, сколько указано после «е+» (если, конечно, хватит места).
Мы иногда делаем выбор из множества без учета порядка . Такой выбор называется комбинацией . Если вы играете в карты, например, вы знаете, что в большинстве ситуаций порядок, в котором вы держите карты, не имеет значения.
Пример 1 Найдите все комбинации 3-х букв, взятых из набора в 5 букв {A, B, C, D, E}.
Решение Эти комбинации следующие:
{A, B, C}, {A, B, D},
{A, B, E}, {A, C, D},
{A, C, E}, {A, D, E},
{B, C, D}, {B, C, E},
{B, D, E}, {C, D, E}.
Существует 10 комбинаций из трех букв, выбранных из пяти букв.
Когда мы находим все комбинации из набора с 5 объектами, если мы берем 3 объекта за один раз, мы находим все 3-элементные подмножества. В таком случае порядок объектов не рассматривается. Тогда,
В таком случае порядок объектов не рассматривается. Тогда,
{A, C, B} называется одним и тем же набором как и {A, B, C}.
Подмножество
Множество A есть подмножеством B, и означает что A это подмножество и/или совпадает с B если каждый элемент A является элементом B.
Элементы подмножество не упорядочены. Когда рассматриваются комбинации, не рассматривается порядок!
Комбинация
Комбинация, содержащая k объектов является подмножеством, состоящим из k объектов.
Мы хотим записать формулу для вычисления число сочетаний из n объектов, если взято к объектов одновременно.
Обозначения комбинации
Число сочетаний из n объектов, если взято к объектов одновременно, обозначается n C k .
Мы называем n C k число сочетаний . Мы хотим записать общую формулу для n C k для любого k ≤ n. Во-первых, это верно, что n C n = 1, потому что множество с n элементами имеет только одно подмножестов с n элементами, есть само множество. Во-вторых, n C 1 = n, потому что множество с n элементами имеет только n подмножеств с 1 элементом в каждом. Наконец, n C 0 = 1, потому что множество с n элементами имеет только одно подмножество с 0 элементами, то есть пустое множество ∅. Чтобы рассмотреть другие сочетания, давайте вернемся к примеру 1 и сравним число комбинаций с числом перестановок.
Во-вторых, n C 1 = n, потому что множество с n элементами имеет только n подмножеств с 1 элементом в каждом. Наконец, n C 0 = 1, потому что множество с n элементами имеет только одно подмножество с 0 элементами, то есть пустое множество ∅. Чтобы рассмотреть другие сочетания, давайте вернемся к примеру 1 и сравним число комбинаций с числом перестановок.
Обратите внимание, что каждая комбинация из 3-х элементов имеет 6, или 3!, перестановок.
3! . 5 C 3 = 60 = 5 P 3 = 5 . 4 . 3,
so
.
В общем, число сочетаний из k элементов, выбранных из n объектов, n C k раз перестановок этих элементов k!, должно быть равно числу перестановок n элементов по k элементов:
k!. n C k = n P k
n C k = n P k /k!
n C k = (1/k!). n P k
n C k =
Комбинации k объектов из n объектов
Общее число комбинаций к элементов из n объектов обозначается n C k , определяется
(1) n C k = ,
или
(2) n C k =
Другой тип обозначения для n C k это биноминальный коэффициент . Причина для такой терминологии будет понятна ниже.
Причина для такой терминологии будет понятна ниже.
Биноминальный коэффициент
Пример 2 Вычислите , используя формулы (1) и (2).
Решение
a) Согласно (1),
.
b) Согласно (2),
Имейте в виду, что не означает n/k.
Пример 3 Вычислите и .
Решение Мы используем формулу (1) для первого выражения и формулу (2) для второго. Тогда
,
используя (1), и
,
испоьлзуя формулу (2).
Обратите внимание, что
,
и используя результат примера 2 дает нам
.
Отсюда вытекает, что число 5-ти элементного подмножества из множества 7 элементов то же самое, что и число 2-элементного подмножества множества из 7 элементов. Когда 5 элементов выбираются из набора, они не включают в себя 2 элемента. Чтобы увидеть это, рассмотрим множество {A, B, C, D, E, F, G}:
В целом, мы имеем следующее. Этот результат дает альтернативный способ вычисления комбинации.
Подмножества размера k и размера
и n C k = n C n-k
Число подмножеств размера к множества с n объектами такое же, как и число подмножеств размера n — к. Число сочетаний k объектов из множества n объектов, такое же как и число сочетаний из n объектов, взятых одновременно.
Число сочетаний k объектов из множества n объектов, такое же как и число сочетаний из n объектов, взятых одновременно.
Теперь мы будем решать задачи с комбинациями.
Пример 4 Мичиганская лотерея. Проводящаяся в штате Мичиган два раза в неделю лотерея WINFALL имеет джек-пот, который, по крайней мере, равен 2 млн. долларов США. За один доллар игрок может зачеркнуть любые 6 чисел от 1 до 49. Если эти числа совпадают с теми, которые выпадают при проведении лотереи, игрок выигрывает. (
4.2.3. Сочетания
Глава 4. Комбинаторика
4.2.
4.2.3.
Допустим теперь, что нас не интересует порядок, в котором идут выбранные элементы. Например, нужно из десяти человек выбрать троих дежурных. Такая операция называется неупорядоченной выборкой, или сочетанием, в отличие от упорядоченной выборки – размещений.
Например, нужно из десяти человек выбрать троих дежурных. Такая операция называется неупорядоченной выборкой, или сочетанием, в отличие от упорядоченной выборки – размещений.
|
Всякая неупорядоченная выборка объёма k из множества, состоящего из n элементов, (k ≤ n) называется сочетанием из n элементов по k. Количество сочетаний обозначается и вычисляется по формуле |
||
Символ читается «це из эн по ка».
Формулу для можно получить из следующих соображений.
Из любого набора, содержащего k элементов, можно получить k! перестановок. Поэтому упорядоченных выборок объёма k существует
 Значит,
Значит,
|
Модель 4.4. Сочетания |
Пример 1
Для проведения письменного экзамена нужно составить 3 варианта по 5 задач в каждом. Сколькими способами можно разбить 15 задач на 3 варианта?
Показать решение
Пример 2
Сколькими способами можно разместить 10 различных шаров по 4 ящикам так, чтобы в первом ящике оказалось 2 шара, во втором – 3, в третьем – 3 и в четвёртом снова два?
Показать решение
Для числа сочетаний справедливы некоторые тождества, в частности:
Пример 3
Докажите тождество
Показать решение
Запишем в «нулевой» строке число
В первой строке напишем значения чисел
и
каждое из которых тоже равно 1, так, чтобы значение
оказалось над промежутком между этими двумя числами. Во второй строке запишем числа
и
тоже равные 1, а между ними – число
Обратим внимание, что число равно сумме двух чисел, стоящих над ним:
Продолжим построение, записывая в n-й строке числа от
до
включительно.
Во второй строке запишем числа
и
тоже равные 1, а между ними – число
Обратим внимание, что число равно сумме двух чисел, стоящих над ним:
Продолжим построение, записывая в n-й строке числа от
до
включительно.
|
|
| Рисунок 4.2.3.1. Треугольник Паскаля |
Полученный числовой треугольник называется треугольником Паскаля. Согласно свойству любое число в этом треугольнике равно сумме двух чисел, расположенных над ним в предыдущей строке.
При помощи треугольника Паскаля удобно доказывать различные комбинаторные тождества.
Пример 4
Доказать, что
Показать решение
На языке множеств утверждение, доказанное в задаче, выглядит по-другому.
Число подмножеств множества из n элементов равно 2n. |
Еще один интересный факт, связанный с треугольником Паскаля, мы приведём здесь без доказательства:
| Бином Ньютона |
Приведённое тождество называется биномом Ньютона.
Как и в случае с размещениями, существует понятие числа сочетаний с повторениями. Рассмотрим его на следующем примере.
Пример 5
В палитре художника 8 различных красок. Художник берет кистью наугад любую из красок и ставит цветное пятно на ватмане. Затем берет следующую кисть, окунает её в любую из красок и делает второе пятно по соседству. Сколько различных комбинаций существует для шести пятен? Порядок пятен на ватмане не важен.
Затем берет следующую кисть, окунает её в любую из красок и делает второе пятно по соседству. Сколько различных комбинаций существует для шести пятен? Порядок пятен на ватмане не важен.
|
|
Показать решение
Вообще, можно сформулировать следующее правило.
|
Если из множества, содержащего n элементов, выбирается поочередно m элементов, причём выбранный элемент каждый раз возвращается обратно, то количество способов произвести неупорядоченную выборку – число сочетаний с повторениями – составляет |
||
Главная Онлайн учебники База репетиторов России Тренажеры по математике Подготовка к ЕГЭ 2017 онлайн |
||||||||
|
||||||||
|
|
||||||||
формулы, правила и примеры с решением задач и заданий
Оглавление:
Комбинаторика — это область математики, прежде всего связанная с подсчетом, как средство и цель получения результатов, так и с определением свойств конечных структур. Она тесно связана со многими другими областями математики — алгеброй, геометрией, теорией вероятностей и применяется в различных областях знаний (например, в генетике, информатике, статистической физике).
Комбинаторика (или комбинаторный анализ) — раздел математики, объектом исследования которого являются дискретные множества произвольной природы. Основной задачей комбинаторики является определение числа способов выполнения некоторых точно определенных операций, или, другими словами, определение числа подчиненных тем или иным условиям комбинаций, которые можно составить из заданной совокупности объектов.
Основной задачей комбинаторики является определение числа способов выполнения некоторых точно определенных операций, или, другими словами, определение числа подчиненных тем или иным условиям комбинаций, которые можно составить из заданной совокупности объектов.
Подмножества и выборки: Пусть задано произвольное множество из -объектов, которое мы обозначим за А, с элементами Последовательность произвольных элементов
называется выборкой объема r из А, причем каждый элемент из множества А может встречаться в выборке произвольное число раз. Объем выборки может превосходить объем исходного множества А. Если же все компоненты r-выборки
из -множества А различны, то и r-выборка представляет cобой r-подмножество А. Выборки подразумевают возможность наличия в них одинаковых элементов, а подмножество не допускает повторений элементов. Для отличия подмножеств от выборок в формулах для выборок введем подчеркивание сверху.
Если свойства выборки изменяются при транспозиции элементов (т.е. при перемене местами двух элементов), то выборка называется упорядоченной, в противном случае — неупорядоченной. Число появлений одного и того же элемента называется его кратностью и обозначается Типичным примером выборки может являться слово в фиксированном алфавите. Следовательно, если каждый элемент m-выборки Имеет кратность то выборка является просто m-подмножеством множества А. Упорядоченное m-подмножество n-множества называется m-перестановкой из n-элементов (или размещением из n-элементов по m).
Неупорядоченное m-подмножество n-множества называется m-сочетанием из m-элементов (или сочетанием из n-элементов по m). Число упорядоченных m-подмножеств n-множества равно
Если то число таких подмножеств есть
т. е. равно произведению всех первых n- натуральных чисел, так как по определению
читается: «n — факториал». Размещения из n элементов по n называются просто перестановками. Чтобы показать очень быстрый рост числа перестановок с ростом числа n, сравним числа Вычисляя, получим: Величина принимается равной единице, хотя она и не имеет комбинаторного смысла. Кроме того, по определению при значениях или если Имеет место рекуррентное (возвратное) соотношение
Размещения из n элементов по n называются просто перестановками. Чтобы показать очень быстрый рост числа перестановок с ростом числа n, сравним числа Вычисляя, получим: Величина принимается равной единице, хотя она и не имеет комбинаторного смысла. Кроме того, по определению при значениях или если Имеет место рекуррентное (возвратное) соотношение
Подсчет при больших значениях n становится затруднительным. В этих случаях можно рекомендовать) использовать приближенную формулу Стирлинга:
Пример:
Сколько вариантов расположения слов допускает предложение: «Редактор вчера внимательно прочитал рукопись»? Так как в данном предложении нет никаких грамматических ограничений на порядок слов, то на первое место можно поставить любое слово (5 вариантов), на второе -любое другое, кроме выбранного (4 варианта) и т. д.; всего
Если рассматривается произведение первых натуральных только четных или только нечетных чисел, то такие произведения называются двойными факториалами и обозначаются так:
Число упорядоченных m-выборок из n-множеств равно
Пример:
Сколько всего телефонных номеров можно иметь в городе, если номер имеет шесть цифр? Решение. Каждый телефонный номер может содержать любые шесть цифр из десяти (0, 1, 2, …, 9). При этом одинаковые цифры могут повторяться до шести раз, и, кроме того, телефонные номера различны, даже если они отличаются лишь порядком цифр. На основании этого задача сводится к подсчету количества 6-выборок 10-множества, т. е.
Каждый телефонный номер может содержать любые шесть цифр из десяти (0, 1, 2, …, 9). При этом одинаковые цифры могут повторяться до шести раз, и, кроме того, телефонные номера различны, даже если они отличаются лишь порядком цифр. На основании этого задача сводится к подсчету количества 6-выборок 10-множества, т. е.
Число неупорядоченных m-подмножеств n-множества (число сочетаний) равно
Сочетания — это соединения из n-элементов по m-элементов, которые отличаются друг от друга только самими элементами. Числа обычно называют биномиальными коэффициентами. Если в этой формуле заменить m на разность n — m, то получим »отношение
Рекуррентная формула для сочетаний
Принято считать, что при или при
Числа часто условно записывают в следующем виде:
Хотя величина не имеет комбинаторного смысла, понятие чисел можно распространить на отрицательные значения n, а именно:
Пример:
Абонент забыл последние три цифры телефонного номера. Какое наибольшее число вариантов номеров ему нужно перебрать, чтобы дозвониться (в этом случае необходимый номер набирается последним)? Очевидно, что таких номеров столько, сколько можно составить размещений из десяти цифр
Какое наибольшее число вариантов номеров ему нужно перебрать, чтобы дозвониться (в этом случае необходимый номер набирается последним)? Очевидно, что таких номеров столько, сколько можно составить размещений из десяти цифр
по три, т. е.
Пример:
Требуется составить колонну из пяти автомашин. Сколькими способами это можно сделать? По условиям задачи порядок следования автомобилей может быть любым, поэтому количество способов составить автоколонну из пяти машин есть число перестановок из пяти:
Пример:
Читатель отобрал по каталогу 8 книг. Однако в библиотеке выдают одному читателю не более 5 книг. Сколько альтернатив взять книги есть у этого читателя? Решение. Поскольку читатель отобрал книг больше разрешенного числа, то он должен выбрать из них 5 книг. Естественно, что все книги, разные и все равно, в каком порядке их взять. Следовательно, каждая альтернатива есть неупорядоченное 5 — подмножество из 8 и число вариантов в выборе книг (число альтернатив) равно
Число неупорядоченных m-выборок из n-множества равно
Пример:
Кости домино можно рассматривать как сочетания с повторениями по два из семи цифр: 0,1,2,3,4, 5,6. Число всех таких сочетаний равно
Число всех таких сочетаний равно
Набор целых чисел называется разбиением числа n, если например 6=1+2+3.
Число разбиений. Число R упорядоченных — разбиений n-множества равно.
Замечание:
Числа R в (2.4) называют также полиномиальными коэффициентами. Это название обусловлено тем, что они являются коэффициентами при произведениях степеней переменных в разложении полинома по степеням
В частном случае, когда имеем соотношение
Число (m, n — m) — разбиений n-множества равно числу его упорядоченных m-подмножеств.
Пример:
Число различных слов, которое получим, переставляя буквы слова «математика», равно
так как кратность букв м равна двум, а — трем, т- двум, остальные буквы встречаются по одному разу.
Число неупорядоченных подмножеств. Число всех неупорядоченных подмножеств n-множества равно
Пример:
В комнате 4 различных светильника. Сколько вариантов включения светильников может быть реализовано?
Сколько вариантов включения светильников может быть реализовано?
Так как в задаче речь идет лишь о том, горит светильник или нет, то мы рассматриваем неупорядоченные разбиения, т. е. применима формула (вариантов).
Основные правила комбинаторикиКомбинаторика – раздел математики, который изучает задачи выбора и расположения элементов из некоторого основного множества в соответствии с заданными правилами.
Правило суммыПусть существует разбиение множества изучаемых комбинаций на классы, т. е. каждая комбинация входит в один и только в один класс. Тогда полное число комбинаций равно сумме количества комбинаций, входящих в каждый из классов. Иными словами, если некоторый объект типа а можно выбрать m-способами, а объект типа b можно выбрать n-способами, то выбор одного из этих объектов можно осуществить — способами:
Это правило сумм справедливо лишь в том случае, если классы разбиения не пересекаются. Если же классы разбиения пересекаются, т. е. способы выбора объекта типа а совпадают со способами выбора объекта типа b, то из формулы (1.4) следует вычесть число k таких совпадений:
е. способы выбора объекта типа а совпадают со способами выбора объекта типа b, то из формулы (1.4) следует вычесть число k таких совпадений:
Пример:
Пусть а — число, делящееся на два; b — число, делящееся на три. Сколькими способами можно выбрать или а, или b, если задано множество Решение. Согласно формуле (1.4), имеем: (числа 2 и 4) и (число 3), т. е.
Если подобный выбор осуществляется из множества то необходимо использовать уже формулу (1.5), т.к. 6 делится и на 2 и на 3:
Обобщая формулы на случай i классов, получим формулу сумм
где — число способов выбора объектов i-го типа; — число совпадений способов выбора объектов i-го и j-го типа.
Правило произведенияЕсли объект типа а можно выбрать m способами и если после каждого такого выбора объект типа b можно выбрать n способами, то выбор в указанном порядке пары можно осуществить -способами:
Если же при i-м способе выбора объекта типа а объект b может быть выбран -способами, то число способов такого выбора пары равно
Пример:
Сколько существует целых четырехзначных чисел, не делящихся на 5? Целое число не делится на 5, если оно не заканчивается на 5 или на 0. Поэтому первую значащую цифру можно выбирать девятью способами (все цифры, кроме нуля), вторую и третью — десятью способами, а четвертую лишь восемью (все цифры, кроме 0 и 5). Следовательно, искомое число есть
Поэтому первую значащую цифру можно выбирать девятью способами (все цифры, кроме нуля), вторую и третью — десятью способами, а четвертую лишь восемью (все цифры, кроме 0 и 5). Следовательно, искомое число есть
Размещения с повторениями — это упорядоченные m-выборки из n-множества. Таких выборок будет штук.
Перестановки с повторениями — это упорядоченные разбиения п-множества , т. е. мы имеем
где — число повторений в перестановке элементов i-го типа.
Очевидно, что
Пример:
Сколько различных слов можно составить, переставляя буквы в слове «перепел»?
Решение:
Поскольку в слове имеются три буквы е и две буквы п, перестановки будут происходить с повторениями.
Поэтому искомое число есть
Сочетания с повторениями — это неупорядоченные m-выборки из n-множества. Поэтому число таких сочетаний, согласно теореме о числе неупорядоченных выборок, равно
Имеет место также следующее рекуррентное соотношение:
Пример:
Число целых неотрицательных решений уравнениях, равно числу сочетаний из m-элементов по n-элементов с повторениями. Это, в частности, означает, что уравнение имеет решений.
Это, в частности, означает, что уравнение имеет решений.
Комбинаторные задачи
Среди различных задач, которые приходится решать математикам, встречаются такие, где нужно ответить на вопрос: каким числом различных способов можно осуществить требуемое? Такие задачи принято называть комбинаторными задачами. Для решения таких задач созданы общие методы и выведены готовые формулы. Однако для того чтобы лучше ознакомиться с методами их решения, мы начнем не с общих методов и готовых формул, а с рассмотрения конкретных примеров.
Пример:
Каким числом способов можно обить 12 раз личных стульев, если есть 12 образцов обивочного материала, причем каждый материал имеется в любом количестве?
Решение:
Поскольку имеется 12 различных образцов обивочного материала, то один стул можно обить двенадцатью различными способами. То же самое справедливо и для второго стула, так как каждый обивочный материал имеется в любом количестве. Но каждый способ обивки первого стула можно соединить с любым способом обивки второго, так что число различных способов обивки двух стульев равно
Но каждый способ обивки первого стула можно соединить с любым способом обивки второго, так что число различных способов обивки двух стульев равно
При этом важно, что имеющиеся стулья различны. Если бы они были одинаковыми, то число различных способов обивки было бы меньшим, так как способы, при которых первый стул обит матералом а, а второй — материалом b, или, наоборот, первый стул обит материалом b, а второй—материалом а, нельзя было бы считать различными способами.
Итак, для двух различных стульев мы получили различных способов их обивки. Очевидно, что для каждого следующего стула остается в силе приведенное выше рассуждение: для каждого стула существует двенадцать возможных способов обивки, и каждый способ обивки данного стула можно соединить с любым способом обивки предыдущих. Отсюда следует, что для трех стульев число различных способов обивки составляет для четырех — и т. д. Для двенадцати стульев это число составляет
Пример:
Каким числом способов можно рассадить 12 гостей на имеющихся 12 различных стульях?
Решение:
Представим себе, что гости входят в комнату по одному. Первому из входящих гостей предоставляется выбор из 12 различных стульев, т. е. 12 возможностей, как и в предыдущем примере. Однако уже для следующего гостя остаются не те же две надцать возможностей, что и для первого, а всего лишь одиннадцать, поскольку один из стульев оказывается уже занятым. По-прежнему каждое место, занятое первым гостем, может комбинироваться с любым другим местом, занятым вторым; поэтому общее число различных способов, с помощью которых можно рассадить двух гостей, равно 12 • 11 = 132.
Первому из входящих гостей предоставляется выбор из 12 различных стульев, т. е. 12 возможностей, как и в предыдущем примере. Однако уже для следующего гостя остаются не те же две надцать возможностей, что и для первого, а всего лишь одиннадцать, поскольку один из стульев оказывается уже занятым. По-прежнему каждое место, занятое первым гостем, может комбинироваться с любым другим местом, занятым вторым; поэтому общее число различных способов, с помощью которых можно рассадить двух гостей, равно 12 • 11 = 132.
Дальнейший ход решения теперь уже ясен. Для гостя, входящего третьим, останется только 10 различных возможностей, так как из 12 мест два места окажутся уже занятыми. Поэтому для трех гостей число различных способов рассадить их составляет 12 • 11 • 10 = 1320. Продолжая аналогичные рассуждения, найдем, что общее число различных способов рассадить 12 гостей на 12 стульях составляет 12 • 11 • … • 2 • 1 = 12!= 479001600.
Пример:
В отделении 12 солдат. Каким числом способов можно составить наряд из двух человек, если один из них должен быть назначен старшим?
Каким числом способов можно составить наряд из двух человек, если один из них должен быть назначен старшим?
Решение этой задачи очень похоже на решение предыдущей. Действительно, если назначить сначала старшего по наряду, то для его выбора у нас имеется 12 различных возможностей: каждый солдат отделения может быть назначен старшим наряда. После того как старший наряда назначен, вторым в наряд может быть назначен любой из оставшихся одиннадцати. Как и во всех предыдущих случаях, общее число различных нарядов составляет 12- И = 132.
Пример:
Какое число различных парных нарядов можно назначить из 12 солдат отделения, если не требуется назначать старшего по наряду?
Решение:
Легко понять, что число таких нарядов должно быть меньше, чем в предыдущем примере. Действительно, наряды —Иванов (старший) и Петров или Петров (старший) и Иванов — различны, тогда как, если не требуется назначать старшего, эти два солдата в обоих случаях составляют один и тот же наряд. Каждый парный наряд без старшего можно превратить в два различных наряда со старшим. Поэтому число различных парных нарядов со старшим в два раза больше, чем нарядов без старших. Отсюда следует, что интересующее нас в данном примере число различных парных нарядов из 12 солдат отделения в два раза меньше, чем получено в предыдущем примере, т. е. равно
Каждый парный наряд без старшего можно превратить в два различных наряда со старшим. Поэтому число различных парных нарядов со старшим в два раза больше, чем нарядов без старших. Отсюда следует, что интересующее нас в данном примере число различных парных нарядов из 12 солдат отделения в два раза меньше, чем получено в предыдущем примере, т. е. равно
Пример:
Клавиатура пианино состоит из 88 клавиш. Сколько различных музыкальных фраз можно составить из 6 нот, допуская повторения одних и тех же нот в одной фразе?
Решение:
Как и в примере 1, в качестве первой ноты для музыкальной фразы можно взять любую из 88 нот, т. е. для первой ноты мы имеем 88 возможностей. Так как повторения допускаются, то для второй ноты мы снова имеем те же 88 возможностей, и поэтому музыкальных фраз из двух нот существует Продолжая рассуждения, как в примере 1, найдем, что число различных музыкальных фраз из 6 нот составляет
Пример:
Сколько различных музыкальных фраз можно составить из 6 нот, если не допускать в одной фразе повторений уже встречавшихся звуков?
Решение этой задачи так же отличается от решения предыдущей, как решение задачи примера 2 от примера 1. Действительно, при составлении произвольной музыкальной фразы для первой ноты мы имеем по-прежнему 88 возможностей. Для второй ноты число возможностей уменьшится уже до 87, так как нота, использованная первой, не должна больше употребляться. После того как выбрана вторая нота, для третьей остается уже только 86 возможностей. Теперь ясно, что общее число различных музыкальных фраз из 6 нот без повторений равно произведению 88 • 87 • 86 • 85 • 84 • 83 = 390 190489920.
Действительно, при составлении произвольной музыкальной фразы для первой ноты мы имеем по-прежнему 88 возможностей. Для второй ноты число возможностей уменьшится уже до 87, так как нота, использованная первой, не должна больше употребляться. После того как выбрана вторая нота, для третьей остается уже только 86 возможностей. Теперь ясно, что общее число различных музыкальных фраз из 6 нот без повторений равно произведению 88 • 87 • 86 • 85 • 84 • 83 = 390 190489920.
Пример:
Сколько существует различных аккордов из шести нот?
Решение:
Аккорд отличается от музыкальной фразы тем, что все ноты, в него входящие, звучат одновременно. Отсюда следует, что все ноты аккорда должны быть различными. Кроме того, различные музыкальные фразы могут приводить к одному и тому же аккорду, если они состоят из одних и тех же нот, но расположенных в фразе в различном порядке. Поэтому, подобно примеру 4, так как число различных музыкальных фраз уже известно, нам остается определить, сколько различных музыкальных фраз могут «склеиваться» в один и тот же аккорд, или, наоборот, сколько различных фраз получается из одного и того же аккорда.
Мы приходим, таким образом, к задаче, аналогичной рассмотренной в примере 6: имеется аккорд из шести различных нот, сколько различных музыкальных фраз можно из него составить? В качестве первой ноты для составляемой музыкальной фразы можно взять любую из входящих в аккорд нот, то есть мы имеем для нее шесть различных возможностей. Для второй ноты остается уже только пять возможностей, для третьей — четыре и т. д.
Теперь уже ясно, что число различных музыкальных фраз, которые можно получить из одного аккорда из шести нот, равно 6 • 5 • 4 • 3 • 2 • 1 =6!= 720. Это означает, что 6! различных музыкальных фраз склеиваются в один и тот же аккорд, так что число возможных аккордов будет в 61 раз меньше, чем число различных музыкальных фраз. Итак, мы получаем, что число различных возможных аккордов из 6 нот равно:
Пример:
Из города А в город В ведет k дорог, а в город С — l дорог. В город D из города В ведет m дорог, а из города С — n дорог. Города В и С дорогами не соединяются. Сколько различных автобусных маршрутов можно провести между городами А и D?
Сколько различных автобусных маршрутов можно провести между городами А и D?
Решение:
Число автобусных маршрутов определяется числом различных дорог между городами. Всего из города А выходит k + l дорог, а в город D входит m + n дорог. Мы не можем, однако, сказать, что общее число дорог равно произведению этих чисел, так как здесь невозможно комбинировать любую дорогу, выходящую из A, с любой дорогой, входящей в D . Если же рассматривать отдельно дороги, проходящие через В или через С, то такая комбинация возможна.
Рассмотрим всевозможные маршруты, идущие из A в D через В. Из A в В ведет k дорог, а из В в D —m дорог. Каждую из таких дорог, выходящих из A, можно комбинировать с любой дорогой,, входящей в D поэтому общее число различных маршрутов, как и во всех предыдущих задачах, получается перемножением числа возможностей и равно km, Следовательно, число различных маршрутов, идущих из A в D через В, равно km.
Аналогично подсчитывается число различных маршрутов, идущих из A в D через С; оно равно ln. Далее, мы замечаем, что всякий автобусный маршрут, соединяющий города A и D, должен проходить или через В, или через С, и, значит, он должен входить либо в число km маршрутов, идущих через В, либо в число ln маршрутов, идущих через С. Общее число различных маршрутов равнo тогда сумме km + ln.
Далее, мы замечаем, что всякий автобусный маршрут, соединяющий города A и D, должен проходить или через В, или через С, и, значит, он должен входить либо в число km маршрутов, идущих через В, либо в число ln маршрутов, идущих через С. Общее число различных маршрутов равнo тогда сумме km + ln.
Прежде чем перейти к следующим примерам, подведем некоторые итоги. Рассмотренные в предыдущем параграфе примеры имели между собой много общего и решались по существу одинаковыми приемами. Главная мысль, которая лежит в основе всех решений, может быть сформулирована в виде следующего общего правила: если некоторый выбор может быть сделан т различными способами, а для каждого из этих способов некоторый второй выбор может быть сделан п различными способами, то число способов для осуществления последовательности двух этих выборов равно произведению mn.
Фактически при решении всех задач мы пользовались этим общим правилом, и нужно было только определить число различных возможностей в том или ином случае. Это число менялось в зависимости от условий задачи.
Это число менялось в зависимости от условий задачи.
Другое общее правило имеет следующий вид: если некоторый выбор может быть сделан т различными способами, а другой выбор—n различными способами {отличными от предыдущих), то общее число способов, которыми можно осуществить какой-нибудь один из этих выборов, равен сумме m +n.
Это правило также применялось нами в предыдущем параграфе (см. пример 8).
При внимательном рассмотрении задач предыдущего параграфа можно заметить, что мы имеем дело с очень небольшим числом различных типов задач. Чтобы сделать этот вывод более наглядным, рассмотрим еще несколько примеров.
Пример:
Во взводе 5 сержантов и 50 солдат. Сколькими способами можно составить наряд из одного сержанта и трех солдат?
Решение:
Очевидно, что одного сержанта из пяти можно выбрать пятью различными способами. В соответствии с приведенным выше правилом остается определить число возможностей выбора трех солдат, а затем числа возможностей выбора солдат и выбора сержантов между собой перемножить, поскольку каждого сержанта можно отправить в наряд с любой группой солдат.
Для определения числа возможностей выбора трех солдат нам придется снова воспользоваться первым правилом, как мы это уже и делали все время, не формулируя его явно. Нам придется при этом действовать в два приема.
Представим себе сначала, что назначаемых в наряд солдат мы вызываем по одному и строим в шеренгу. Тогда легко подсчитать, что при вызове первого солдата у нас есть 50 различных возможностей; после того как один солдат уже вызван, для выбора второго остается 49 возможностей, а для выбора третьего — лишь 48. Таким образом, применяя правило умножения, находим, что всего для выбора трех солдат в определенном порядке число возможностей равно произведению 50 • 49 • 48. На этом и заканчивается первая часть решения, но отнюдь не все решение.
В предыдущем абзаце совсем не зря выделены слова «в определенном порядке». Полученное произведение не равно числу возможностей выбора трех солдат, а больше этого числа, причем выделенные слова как раз и объясняют, почему. Дело в том, что мы можем получить один и тот же наряд, вызывая солдате различном порядке. Поэтому необходимо подсчитать, какое число раз может получиться один и тот же наряд, и разделить полученное выше произведение на это число.
Поэтому необходимо подсчитать, какое число раз может получиться один и тот же наряд, и разделить полученное выше произведение на это число.
Остается, следовательно, определить, в каком числе случаев будет получаться один и тот же наряд. Это можно подсчитать, решая в каком-то смысле обратную задачу: каким числом способов можно расставить в шеренгу трех солдат уже выбранного наряда. Очевидно, что это число равно требуемому. Но это число легко под считать, пользуясь обычным приемом: чтобы поставить какого-либо солдата на первое место, есть три различные возможности, на второе место остается два солдата и на третье — только один Поэтому общее число возможных перестановок трех солдат в шеренге равно 3 • 2 • 1 = 3! = 6.
Итак, каждый наряд из трех солдат можно расставить в шеренгу 3! различными способами, а, значит, в произведении 50 • 49 • 48, показывающем число возможностей при выборе трех человек в определенном порядке, каждый наряд считается ровно 3! раз. Поэтому общее число различных способов, которыми можно назначить в наряд трех солдат из пятидесяти, равно
Число различных нарядов из одного сержанта и трех солдат равно теперь
Пример:
Сколько членов, содержащих две буквы, получится после раскрытия скобок в выражении
Решение:
После раскрытия всех скобок мы получим сумму некоторого числа слагаемых (нетрудно подсчитать, что общее число слагаемых равно но для решения поставленной задачи это не существенно), каждое из которых состоит из шести множителей. Различные множители, входящие в одно и то же произведение, берутся из различных скобок. При этом для каждого множителя есть две различные возможности — он может быть либо буквой, либо единицей.
Различные множители, входящие в одно и то же произведение, берутся из различных скобок. При этом для каждого множителя есть две различные возможности — он может быть либо буквой, либо единицей.
Вопрос, поставленный в условии, состоит в том, чтобы определить, каким числом способов можно из шести множителей выбрать две буквы. В такой постановке он решается уже совсем просто. Пользуясь уже часто употреблявшимися рассуждениями, мы можем сразу написать, что число различных слагаемых, содержащих две буквы, равно
Действительно, для выбора первой буквы у нас есть шесть возможностей, а для выбора второй — пять. Кроме того, каждую пару букв мы считаем дважды, один раз полагая первой одну из них, а другой раз — вторую.
Пример:
Подсчитаем, сколько в рассмотренном в предыдущем примере произведении слагаемых, содержащих четыре буквы.
Решение этой задачи аналогично решению предыдущей. Тем же методом можно подсчитать, что выбор четырех букв в определенном порядке может быть сделан 6 • 5 • 4 • 3 = 360 различными способами. С другой стороны, каждая четверка считается здесь несколько раз, именно столько, каким числом способов можно ее упорядочить. Число способов упорядочить четверку букв равно произведению 4 • 3 • 2 • 1 = 24. Поэтому число слагаемых, содержащих четыре буквы, равно
С другой стороны, каждая четверка считается здесь несколько раз, именно столько, каким числом способов можно ее упорядочить. Число способов упорядочить четверку букв равно произведению 4 • 3 • 2 • 1 = 24. Поэтому число слагаемых, содержащих четыре буквы, равно
Этот ответ совпадает с ответом, полученным в предыдущем примере. Про это можно было бы догадаться заранее и, следовательно, обойтись без всяких вычислений, сославшись на предыдущий результат. В самом деле, легко понять, что комбинаций пар букв столько же, сколько комбинаций четверок: каждой паре букв соответствует одна-единственная определенная четверка, которая остается, когда мы удалим выбранную пару. Разным парам соответствуют разные четверки и, наоборот, разным четверкам соответствуют разные пары. Поэтому число различных пар и различных четверок букв одинаково.
Пример:
В классе m мест. Каким числом способов можно рассадить в нем n учеников (n < m)?
Решение:
Если в этой задаче и есть что-либо новое по сравнению с предыдущими, то только то, что в ней нет конкретных числовых данных. Способ решения задачи от этого, естественно, не изменяется.
Способ решения задачи от этого, естественно, не изменяется.
Представим себе, что ученики входят в класс по одному. Тогда для первого из них имеется m возможностей выбрать место. После того как первый выбрал какое-то место, для второго остается m — 1 возможностей. Далее, для третьего будет m — 2 различных возможностей и т. д. Искомое число способов рассадить всех учеников выразится произведением
Найдем последний сомножитель этого произведения. Его можно определить по-разному, например так: каждый сомножитель на единицу меньше предыдущего и получается вычитанием из m числа, на единицу меньшего, чем номер сомножителя. Поэтому сомножитель с номером п получается вычитанием из т числа n — 1, то есть равен m — (n — 1) = m — n + 1.
Можно рассуждать и иначе: после того как все ученики рассядутся, в классе должно остаться m — n свободных мест. Перед входом последнего ученика свободных мест было на 1 больше, то есть m — n + 1. Таково же число возможностей для выбора мест последним учеником, то есть последний сомножитель в произведении.
Итак, искомое число различных способов рассадить n учеников на m местах равно произведению п последовательных целых чисел от m до m — n + 1 включительно:
Пример:
В комнате имеется пять лампочек. Сколько существует различных способов освещения?
Решение:
После всех рассмотренных примеров читатель уже самостоятельно справится с несложным подсчетом того, сколько существует способов освещения, при которых горит данное число лампочек. Сложив все полученные результаты для каждого числа лампочек (от нуля до пяти включительно), мы и получим ответ на поставленный вопрос. Однако этот способ решения, при всей своей простоте, потребует сравнительно длинных рассуждений и вычислений.
Между тем задача допускает простое и короткое решение, если проводить рассуждение в другом порядке. Рассмотрим сначала случай, когда в комнате имеется всего лишь одна лампочка. Тогда, очевидно, возможны ровно два различных способа освещения: лампочка либо горит, либо не горит.
Теперь присоединим к первой лампочке вторую. Она тоже может находиться в одном из двух состояний: гореть, либо не гореть. Так как каждое состояние второй лампочки можно комбинировать с любым состоянием первой, то для двух лампочек число различных состояний, то есть различных способов освещения, равно
Дальнейшие рассуждения теперь уже совершенно очевидны. Каждая из лампочек может находиться в двух состояниях. Поэтому, присоединяя новую лампочку к уже рассмотренным предыдущим, мы увеличиваем число возможных способов освещения вдвое. Следовательно, при трех лампочках будет различных способов освещения, при четырех — и, наконец, при пяти лампочках = 32 способа освещения.
Пример:
Чему равен коэффициент при и при в выражении после раскрытия скобок.
Решение:
Внимательный читатель сразу заметит, что этот пример очень похож на только что разобранный выше пример 4. Еще большую похвалу заслужит тот, кто заметит связь этого примера с примером 7 из предыдущего параграфа.
Выражение можно рассматривать как произведение 88 скобок; из каждой нужно выбрать в качестве множителя одно из слагаемых: либо а, либо b. Если мы ищем коэффициент при то нужно определить, каким числом способов можно выбрать из 88 букв а и b ровно шесть букв а. Но именно этот вопрос мы решали в примере 7 предыдущего параграфа, когда нужно было определить число различных аккордов из 6 нот.
Благодаря замеченной общности задач мы могли бы воспользоваться уже готовым результатом; но мы повторим совсем коротко приведенные там рассуждения в новых терминах, относящихся уже к данной задаче.
Шесть букв а можно разместить на 88 возможных местах числом способов, равным произведению
если выбрать эти буквы в определенном порядке. Поскольку порядок выбора букв нам безразличен, то каждая комбинация считается в этом произведении несколько раз: столько же, каким число способов можно переставлять между собой уже выбранные буквы на определенных шести местах.
Число возможных способов переставлять между собой шесть букв на шести местах, как мы уже видели, равно 6! Поэтому число различных способов выбрать шесть букв а из 88, а значит, и коэффициент при члене в разложении равно
Легко догадаться, что коэффициент при равен тому же числу. Соответствующее рассуждение уже приводилось в примере 4: способов выбрать по 82 буквы а из 88 равно столько же, сколько способов выбрать по 6, так как каждой группе по 6 букв соответствует определенная группа по 82 буквы, состоящая из оставшихся 82 мест. Но мы можем и не обращаться к этому рассуждению, рассматривая для члена не выбор 82 букв а, а, наоборот, выбор шести букв b. Отсюда снова вытекает, что коэффициенты при и а одинаковы.
Соответствующее рассуждение уже приводилось в примере 4: способов выбрать по 82 буквы а из 88 равно столько же, сколько способов выбрать по 6, так как каждой группе по 6 букв соответствует определенная группа по 82 буквы, состоящая из оставшихся 82 мест. Но мы можем и не обращаться к этому рассуждению, рассматривая для члена не выбор 82 букв а, а, наоборот, выбор шести букв b. Отсюда снова вытекает, что коэффициенты при и а одинаковы.
Определения и формулы
Примеров, рассмотренных в двух предыдущих параграфах, вполне достаточно, чтобы заметить некоторые общие закономерности и поставить общие задачи. Заметим прежде всего, что во всех рассмотренных примерах нам приходилось иметь дело с некоторыми конечными множествами и различными их под множествами.
Нас интересовало или число всех возможных подмножеств (пример 5 из § 2), или число подмножеств, обладающих определенным количеством элементов (примеры 4, 7 из § 1, примеры 1, 2, 3, 6 из § 2). В других случаях нужно было рассматривать упорядоченные подмножества, в которых элементы были расположены определенным образом (примеры 3, 6 из § 1, пример 4 из § 2). Здесь нам нужно было знать число различных упорядоченных подмножеств, считая различным образом упорядоченные подмножества различными. Наконец, встречалась и задача, в которой нужно было определить количество различных способов упорядочить данное конечное множество, то есть расположить его элементы в определенном порядке (пример 2, § 1). Все эти задачи можно теперь рассмотреть в общем виде.
Здесь нам нужно было знать число различных упорядоченных подмножеств, считая различным образом упорядоченные подмножества различными. Наконец, встречалась и задача, в которой нужно было определить количество различных способов упорядочить данное конечное множество, то есть расположить его элементы в определенном порядке (пример 2, § 1). Все эти задачи можно теперь рассмотреть в общем виде.
Рассмотрим прежде всего точное определение упоминавшегося выше термина упорядоченное множество.
Конечное множество, состоящее из n элементов, называется упорядоченным, если его элементы каким-либо образом занумерованы, числами 1, 2, …, n.
«Номера», которые при этом приписываются элементам множества, позволяют мыслить элементы этого множества «расположенными» в каком-то «порядке»: первый элемент «предшествует» второму (а второй «следует» за первым), второй предшествует третьему и т. д.
Одно и то же конечное множество можно, разумеется, упорядочить разными способами. Например, множество учеников данного класса можно упорядочить по росту (опять-таки двумя противоположными способами), по весу, по возрасту, по алфавиту фамилий и т. д. и т. п.
Например, множество учеников данного класса можно упорядочить по росту (опять-таки двумя противоположными способами), по весу, по возрасту, по алфавиту фамилий и т. д. и т. п.
Не следует, однако, думать, что каждый такой «порядок» связан непременно с каким-либо «естественным правилом» упорядочения. Скажем, множество шахматных фигур (каждого цвета по отдельности или все 32) можно, конечно, упорядочить слева направо в порядке их расстановки на доске или по силе (а фигуры одинаковой силы — слева направо или еще как угодно), но можно считать «упорядочением» и «беспорядочную» последовательность, в которой мы случайно поставили их на доску для данной партии. А можно было бы их просто расставить в ряд в произвольном «порядке». Аналогично множество учеников данного класса можно считать упорядоченным в соответствии с тем (в достаточной мере случайным!) порядком, в котором они сегодня пришли в школу.
Короче говоря, «нумерация», о которой говорится в определении упорядоченного множества, не предполагает, вообще говоря, никакого заранее известного «закона» — упорядочивая конечное множество, мы просто приписываем каким-либо образом номера его элементам. И если в приведенных примерах легко было все же указать некоторые «естественные» способы упорядочения, то для упорядочения, например, множества муравьев в муравейнике или рыб в озере трудно указать более «естественный» способ, чем переловить их всех по очереди и перенумеровать в порядке попадания их в банку или на удочку…
И если в приведенных примерах легко было все же указать некоторые «естественные» способы упорядочения, то для упорядочения, например, множества муравьев в муравейнике или рыб в озере трудно указать более «естественный» способ, чем переловить их всех по очереди и перенумеровать в порядке попадания их в банку или на удочку…
Таким образом, речь, как правило, идет лишь о теоретическом, мысленном упорядочении, которое для конечного множества всегда возможно.
В отличие от соглашений, принятых нами выше (Введение, п. 1 и п. 6) для множеств неупорядоченных, упорядоченные множества мы будем считать совпадающими (или равными) лишь тогда, когда они не только состоят из одних и тех же элементов, но и упорядочены (расположены, занумерованы и т. п.) одинаковым образом.
Говоря о различных упорядоченных множествах, состоящих из одних и тех же элементов, мы уже несколько раз называли их различными упорядочениями какого-либо множества. Этим термином нам будет удобно пользоваться и в дальнейшем.
Поскольку в этой главе нам придется иметь дело только с конечными множествами и их подмножествами, мы не будем много говорить о распространении понятия упорядоченности на общий случай бесконечных множеств, ограничившись определением и парой примеров.
Множество (безразлично — конечное или бесконечное) называется упорядоченным, если между его элементами установлено некоторое отношение, называемое отношением предшествования, обладающее следующими свойствами.
1) Для любых двух различных элементов а и b данного множества либо а предшествует b, либо b предшествует а.
2) Для любых элементов а, b и с данного множества из того, что а предшествует Ь, а Ь предшествует с, следует, что а предшествует с.
Примером упорядоченного множества может служить множество N натуральных чисел, «естественным» образом упорядоченное по величине: мы считаем, что n предшествует m , если n < m (можно, конечно, было бы выбрать и упорядочение, обратное «естественному», то есть считать, что n предшествует m , когда n > m ). Точно так же упорядочивается множество D всех действительных чисел. Множество K комплексных чисел, не обладающее никаким «естественным» порядком, можно, например, упорядочить, положив, что а+bi предшествует с+di, если а< с, а при а = с, если b < d. Все эти множества можно, разумеется, упорядочить и иными способами.
Точно так же упорядочивается множество D всех действительных чисел. Множество K комплексных чисел, не обладающее никаким «естественным» порядком, можно, например, упорядочить, положив, что а+bi предшествует с+di, если а< с, а при а = с, если b < d. Все эти множества можно, разумеется, упорядочить и иными способами.
Введем теперь следующее
Определение:
Пусть дано конечное множество М, состоящее из m элементов. Размещением из m элементов по n элементов называют всякое упорядоченное подмножество множества М, состоящее из n элементов.
Из этого определения следует, что и что различные размещения отличаются друг от друга составом входящих в них элементов или порядком их расположения. Как видно из предыдущих параграфов, в комбинаторных задачах требуется знать число различных размещений из т элементов по n элементов. Это число принято обозначать символом (А — первая буква французского слова аrrаngement, что означает размещение, приведение в порядок).
Теорема:
Число различных размещений из т элементов по n элементов равно произведению п последовательных натуральных чисел, начиная от m и до m — n + 1 включительно:
Доказательство:
Формула (1) была уже получена нами при разборе примера 4 в § 2. Здесь мы дадим вывод этой формулы, основанный на методе полной математической индукции. Индукцию будем вести по индексу n.
Пусть дано множество М, состоящее из т элементов. Очевидно, что число различных подмножеств этого множества, содержащих по одному элементу, равно числу m элементов М, то есть (подмножества из одного элемента автоматически упорядочены, так как содержат только первый элемент).
Далее, из каждого размещения по одному элементу можно получить различные размещения по два элемента, присоединяя к выбранному первому элементу второй. Так как для выбора второго элемента мы имеем уже m — 1 возможностей (один из элементов уже использован!), то
Предположим теперь, что для некоторого значения n — k справедлива формула
и докажем, что такая же формула имеет место и для n = k + 1. Пусть образованы все размещения из m элементов по k элементов. Размещения по k + 1 элементу могут быть получены присоединением к каждому из полученных еще одного элемента на (k + 1)-е место.
Пусть образованы все размещения из m элементов по k элементов. Размещения по k + 1 элементу могут быть получены присоединением к каждому из полученных еще одного элемента на (k + 1)-е место.
Из одного размещения по к элементов получится столько размещений по k + 1 элементу, сколько различных элементов можно присоединить, то есть m — k. Все получающиеся размещения будут различными, так как они отличаются последним элементом. Размещения по k + 1 элементу, получающиеся из различных размещений по k элементов, также не могут совпасть, поскольку их первые k элементов не совпадают. Остается добавить, что таким способом будут получены все размещения по k + 1 элементу. Отсюда следует, что число размещений по k + 1 элементу удовлетворяет равенству
Воспользовавшись предположенной по индукции формулой для , найдем:
что и утверждалось. Справедливость этой формулы для n = 1 и n =2 была уже установлена выше; из принципа математической индукции следует, что формула (1) верна для всех
Определение:
Перестановками из n элементов называют различные упорядочения данного конечного множества, состоящего из n элементов.
Таким образом, различные перестановки отличаются друг от друга лишь порядком элементов. Число возможных различных перестановок из п элементов обозначается символом (от французского слова permutation— перестановка, перемещение).
Теорема:
Число различных перестановок из n элементов равно произведению всех последовательных целых чисел, начиная от n и до 1 включительно:
Доказательство этой теоремы окажется излишним, если мы заметим, что перестановки являются частным случаем размещений, а именно, при m = n. Значит, согласно формуле (1),
Впрочем, нетрудно доказать эту теорему и независимо от понятия размещения. Рассмотрим всевозможные перестановки из n элементов и подсчитаем, сколько из них начинаются одним и тем же определенным элементом. Если поставить выделенный элемент перед каждой из перестановок из остальных элементов, то мы получим все возможные перестановки, начинающиеся данным элементом. Следовательно, число всех перестановок из n элементов, начинающихся одним определенным элементом, равно . Но тогда для числа всех возможных перестановок из n элементов находим:
Но тогда для числа всех возможных перестановок из n элементов находим:
так как любой из п элементов может оказаться выделенным.
Формулу (3) можно использовать для доказательства нашей теоремы, пользуясь индукцией по числу элементов множества. Очевидно, что так как один элемент может находиться только на первом месте. Допустим, что формула (2) верна для множества, содержащего n — 1 элемент, то есть что
На основании формулы (3) найдем, что
Таким образом, формула (2) верна для любого n.
Теорема:
Число различных размещений из m элементов по n элементов равно числу перестановок из m элементов, деленному на число перестановок из m — n элементов:
Доказательство:
Формулу (4) легко получить из формул (1) и (2). Действительно,
Это доказательство, несмотря на простоту и очевидность, часто вызывает чувство неудовлетворенности, так как сводится к формальным выкладкам и не показывает существа дела. Поэтому мы приведем еще одно доказательство, опирающееся только на определения размещений и перестановок.
Пусть дано некоторое множество из т элементов и все размещения его элементов по n. Из каждого такого размещения можно получить перестановку элементов множества, присоединив к нему в произвольном порядке остальные m — n элементов. В результате мы получим в с е перестановки из m элементов множества.
Следовательно, каждое размещение из m элементов по n элементов порождает столько перестановок по m элементов, сколькими различными способами к нему можно присоединить m — n оставшихся элементов. Так как это можно сделать различными способами, то общее число перестановок из m элементов равно
откуда и следует равенство (4).
Определение:
Пусть дано конечное множество M, состоящее из m элементов. Сочетанием из m элементов по n элементов называется любое подмножество УИ, содержащее п элементов.
Таким образом, сочетания являются неупорядоченным и подмножествами, и различные сочетания различаются между собой только составом элементов. Число всех возможных сочетаний из m элементов по n обозначают через (от французского combinaison — сочетание, комбинация), а также через или С (m, n).
Число всех возможных сочетаний из m элементов по n обозначают через (от французского combinaison — сочетание, комбинация), а также через или С (m, n).
Теорема:
Число всех возможных сочетаний из m элементов по n элементов равно произведению n последовательных натуральных чисел от m до m — n + 1, деленному на произведение n последовательных натуральных чисел от n до 1:
Доказательство этой теоремы сводится к доказательству следующего утверждения: число сочетаний из m элементов по n элементов равно числу размещений из m элементов по n элементов, деленному на число перестановок из n элементов. В самом деле, из этого утверждения, пользуясь формулами (1) и (2), легко получаем формулу (5).
Чтобы доказать теперь это утверждение, заметим, что каждое размещение из m элементов по n элементов может быть получено из такого же сочетания путем различных перестановок его элементов. Следовательно, каждое сочетание порождает столько размещений, сколько возможно различных перестановок его элементов. Отсюда следует, что или
Отсюда следует, что или
что и требовалось доказать.
Формулу (5) обычно приводят к более удобному для записи симметричному виду, умножая числитель и знаменатель на произведение всех натуральных чисел от m — n до 1 включительно. Тогда мы приходим к формуле:
Формула (7) означает, что
Рекомендуем читателю самостоятельно разобраться в комбинаторном смысле этого равенства, доказавши его непосредственно, исходя лишь из определения перестановок и сочетаний.
Как было указано в формулировке теоремы 4, символ имеет смысл при и означает количество подмножеств множества М , содержащих ровно по n элементов. Ясно, что это следует и из формулы (5), но формулу (7) в этом случае приме нить нельзя, так как она будет содержать бессмысленный символ О!. Для общности принято полагать 0! = 1. В этом случае формула (7) дает для то же значение 1.
Удобно также ввести в рассмотрение символ , что означает число пустых подмножеств множества М, то есть = 1. То же самое получится и из формулы (7), если воспользоваться принятым условием 0! = 1.
Принимаемое условие 0! = 1 имеет на самом деле более глубокий смысл, чем просто возможность вычислять или по формуле (7).
Более существенное основание для того, чтобы считать выражение 0! равным единице, состоит в следующем. Выражение n! можно рассматривать как функцию, определенную лишь для натурального аргумента В своей области определения она удовлетворяет функциональному уравнению справедливость которого легко проверяется для всех натуральных Действительно, Если же в этом равенстве положить n = 1, то мы получим
Однако все эти соображения являются не слишком убедительными, так как нельзя быть уверенным в том, что нам не встретится другая формула, в которой будет удобно полагать 0! равным какому-нибудь другому числу. Окончательное решение можно получить, идя вот каким путем. Естественно поставить вопрос: можно ли построить непрерывную функцию, определенную для всех значений х, и такую, которая для целых значений аргумента совпадает с то есть доопределить функцию расширив ее область определения? Напомним, что в математическом анализе такое расширение производится, например, для показательной функции которая вначале была определена лишь для натурального показателя степени.
Поставленный вопрос был решен Эйлером и Гауссом. С помощью различных формул (Эйлер — через интеграл, а Гаусс — через бесконечное произведение) они определили функцию, обладающую нужным свойством, и доказали единственность такой функции при некоторых естественных предположениях. Эта функция называется гамма-функцией и обозначается Г(х). Она определена для всех х > 0 и удовлетворяет функциональному уравнению Г(х)= хГ(х — 1), а для натуральных n принимает значения Г(n) = (n — 1)!.
Обе формулы, определяющие функцию Г(х), имеют смысл при х=1 и определяют значение Г(1) = 1. Но в силу равенства Г(n) = (n — 1)! под выражением 0! следует понимать именно значение Г(1).
Все выведенные нами в настоящем параграфе формулы для числа размещений, перестановок и сочетаний фактически уже не однократно выводились нами ранее для различных частных конкретных случаев при рассмотрении примеров в § 1, 2. Рассмотрим еще некоторые свойства сочетаний, которые потребуются в дальнейшем.
Теорема:
Число сочетаний из т элементов по п элементов равно числу сочетаний из m элементов по m — n элементов:
Доказательство:
Формально равенство (9) легко получить из формулы для числа сочетаний, записанной в виде (7). Действительно,
Комбинаторный смысл этого равенства также достаточно ясен. Каждому подмножеству из n элементов соответствует единственное определенное подмножество из m — n элементов—именно, тех, которые не вошли в первоначальное. Поэтому количество тех и других возможных подмножеств одинаково. При рассмотрении примеров (см. примеры 3 и 6 из § 2) мы фактически уже пользовались этим соображением.
Равенство (9) позволяет сокращать вычисления в тех случаях, когда n > m — n.
Теорема:
Число сочетаний из т элементов по п элементов равно сумме числа сочетаний из (m — 1) элементов по n элементов и по (n — 1) элементов:
Доказательство, как и в предыдущем случае, проведем двумя различными способами. Прежде всего, пользуясь формулой (7) для числа сочетаний, находим:
Прежде всего, пользуясь формулой (7) для числа сочетаний, находим:
Второе доказательство состоит в следующем. Выделим некоторый фиксированный элемент а множества М и рассмотрим сочетания из m элементов по n элементов, содержащие или не содержащие этот элемент. Число сочетаний по n элементов, не содержащих элемента а, равно, очевидно, так как здесь рассматриваются подмножества по n элементов, образованные из элементов множества, содержащего m — 1 элемент (множество М без элемента а). Сочетания, содержащие а, можно получить так: образовать всевозможные сочетания по n — 1 элементу из того же множества М без элемента а и к каждому из них присоединить а. Отсюда ясно, что число таких сочетаний равно Так как каждое сочетание по n элементов либо содержит данный элемент а, либо не содержит его, то оно принадлежит либо одной, либо другой группе. Поэтому
что и утверждалось
Размещения, перестановки и сочетания вместе часто называют одним словом — соединения.
Соединения с повторениями
Если рассмотреть теперь снова задачи, разобранные в §§ 1 и 2, то мы увидим, что решение почти всех из них не требует уже никаких рассуждений, а получается непосредственным применением нужной формулы из выведенных в предыдущем параграфе. Собственно говоря, все рассуждения, которые приводились при решении задач, были не чем иным, как именно выводом соответствующей формулы, но только для данного конкретного случая. Формулы § 3 потому и являются общими, что они применимы ко всем соединениям одного типа, и рассуждения, проведенные при выводе формул, освобождают нас от необходимости повторять их при решении каждой отдельной задачи.
Собственно говоря, все рассуждения, которые приводились при решении задач, были не чем иным, как именно выводом соответствующей формулы, но только для данного конкретного случая. Формулы § 3 потому и являются общими, что они применимы ко всем соединениям одного типа, и рассуждения, проведенные при выводе формул, освобождают нас от необходимости повторять их при решении каждой отдельной задачи.
Однако в числе приведенных там примеров есть и такие, которые не укладываются в уже рассмотренные схемы. К ним относятся, скажем, примеры 1 и 5 из § 1. Дело в том, что при определении различных видов соединений в предыдущем параграфе мы брали некоторое определенное множество, элементы которого существо вали «в единственном экземпляре» и в каждое данное соединение могли входить только один раз. Между тем в некоторых случаях элементы в соединении могут повторяться, как например ноты в музыкальной фразе в примере 5 из § 1. Для того чтобы охватить общей теорией и такие задачи, необходимо рассмотреть соединения с повторениями, которым и посвящен настоящий параграф.
Пусть имеется m непересекающихся множеств каждое из которых содержит не менее чем n элементов. Для простоты мы будем называть элементы множества элементами 1-го сорта, элементы множества — элементами 2-го сорта, …, элементы множества — элементами m-го сорта. Иначе говоря, мы рассматриваем разбиение (см. п. 7 Введения) некоторого множества на непересекающиеся подмножества состоящие из элементов различных «сортов». Все элементы каждого подмножества, то есть элементы одного и того же сорта, будем считать одинаковыми, или совпадающими между собой.
Слова «одинаковые» или «совпадающие» употребляются здесь в том смысле, в каком одинаковыми являются, например, 12 белых или 12 черных шашек. Именно в таком смысле понимается распространенное выражение «множество с повторяющимися элементами», хотя оно и не согласуется с описанным во Введении пониманием терминов «множество» и «элемент» (согласно которому множества, содержащие одни и те же элементы, считаются совпадающими).
Вообще, в таких случаях правильнее говорить о множестве различных вхождений «одинаковых» (точнее — одноименных) эле ментов. Так, слово «алгебра» состоит из ш е с т и букв, но содержит семь вхождений букв (буква «а» входит дважды, остальные — по одному разу). С совершенно аналогичной по существу ситуацией мы уже имели дело о гл. I, говоря о «кратных» корнях многочленов.
Из элементов множества A, то есть элементов, входящих в различные его подмножества можно составлять различные упорядоченные множества, содержащие по n элементов в каждом. Такие упорядоченные множества принято называть размещениями с повторениями из элементов m сортов по n элементов, или, более коротко, просто размещениями с повторениями из m элементов по n.
В первом из этих терминов (более точном, но менее употребительном из-за своей громоздкости) явным образом указывается, что имеется не т различных элементов, а m различных сортов элементов; число же элементов любого сорта в размещении может быть каким угодно.
Для наглядности будем представлять себе, что элементами рассматриваемых множеств являются буквы. Если, например, m=3, то это могут быть буквы а, b, с. Тогда возможны следующие размещения с повторениями этих трех элементов по n = 2:
Размещения с повторениями можно рассматривать и в случае n > m, то есть неравенство которое считалось необходимым в предыдущем параграфе, здесь необходимым уже не является. На пример, из m = 2 элемента а, b можно образовать размещения по n = 3 элемента. Они будут иметь вид:
Число различных возможных размещений с повторениями из m элементов по n элементов будем обозначать
Теорема:
Число различных размещений с повторениями из m элементов по n элементов определяется по формуле:
Доказательство:
Прежде всего заметим, что размещения с повторениями по n элементов могут быть получены из размещений по (n — 1) элементу присоединением еще одного элемента. Так как к каждому размещению по (n — 1) элементу можно присоединить любой из имеющихся m элементов, то каждое размещение по (n — 1) элементу порождает т различных размещений по n элементов, то есть
Проведем теперь доказательство формулы (1) по индукции. Ясно, что при n = 1 число размещений равно m:
Ясно, что при n = 1 число размещений равно m:
Допустим, что для некоторого числа n справедливо равенство
и найдем число размещений с повторениями из m элементов по n. Пользуясь формулой (2), получаем:
Таким образом, формула (1) справедлива для n — 1 и из ее справедливости для некоторого п следует и справедливость для n+1. Теорема доказана.
Для определения перестановки с повторениями рассмотрим множество, состоящее из п элементов, среди которых есть одинаковые. Как и раньше, мы можем представлять себе, что элементами этого множества являются буквы.
Определение:
Перестановкой с повторениями из n элементов называется любое упорядочение конечного множества, состоящего из n элементов, среди которых имеются совпадающие.
Пусть рассматриваемое множество состоит из букв букв букв букв l. Подсчитаем число возможных перестановок с повторениями для такого множества.
Занумеруем сначала все элементы а номерами буквы b — номерами …, и т. д. и будем считать все эти элементы различными. Тогда мы имеем множество, состоящее из
д. и будем считать все эти элементы различными. Тогда мы имеем множество, состоящее из
n различных элементов, и число перестановок этого множества, в силу теоремы 2 предыдущего параграфа, равно n!, причем
Теперь мы заметим, что элементы множества фактически не различаются между собой и поэтому среди всех n! перестановок имеются совпадающие, так что каждая перестановка с повторениями считается здесь несколько раз. Подсчитаем, сколько именно.
Ясно, что две перестановки, отличающиеся друг от друга лишь расположением элементов а, совпадают между собой. Таких перестановок существует столько, сколько возможно различных перестановок элементов между собой, то есть . Но то же самое относится и к элементу b: перестановки, отличающиеся лишь расположением элементов , совпадают между собой, и таких перестановок существует ровно и т. д.
Следовательно, в числе n! перестановок всех элементов каждая считается раз. Отсюда следует, что число различных перестановок с повторениями в нашем случае равно
Обозначая число перестановок через мы можем сформулировать полученный результат в виде следующей теоремы.
Теорема:
Число различных перестановок из п элементов, в ко торых элементы а, b, с, …, l повторяются соответственно раз, выражается формулой
Определение:
Сочетанием с повторениями из m элементов по n элементов называется всякое множество, содержащее n элементов, каждый из которых является элементом одного из данных m сортов.
Как видно из этого определения, сочетания с повторениями являются неупорядоченными множествами, так что расположение эле ментов в них несущественно. Различные сочетания отличаются друг от друга входящими в них элементами, причем каждый элемент может входить в сочетание несколько раз.
Например, из трех элементов а, b, с можно образовать такие сочетания с повторениями по два элемента:
Из тех же трех элементов сочетания с повторениями по три эле мента будут следующими:
Ясно, что из элементов а, b, с можно составлять сочетания с повторениями и по четыре элемента и вообще по любому числу n элементов, так что для сочетаний с повторениями неравенство не является необходимым, а можно рассматривать и случай m < n.
Число различных возможных сочетаний с повторениями из m элементов по n элементов мы будем обозначать символом Для его нахождения можно воспользоваться следующей теоремой.
Теорема:
Число различных возможных сочетаний с повторения ми из т элементов по п элементов может быть найдено по формуле
Доказательство:
Как уже говорилось выше, сочетания, в том числе с повторениями, являются неупорядоченными множествами. Поэтому всякое сочетание однозначно определяется тем, сколько элементов каждого сорта в него входит.
Например, если имеются элементы четырех сортов, то сочетание вполне определится, если сказать, что оно содержит два эле мента первого сорта, четыре элемента второго, ни одного элемента третьего и один элемент четвертого сорта. Это есть одно из возможных сочетаний с повторениями из четырех элементов по семи. Такое сочетание можно условно записать комбинацией четырех чисел (2, 4, 0, 1), показывающей, сколько элементов каждого сорта берется.
Другие сочетания определятся, например, комбинациями (3, 0, 0, 4) или (1, 1,2, 3). Первая из них определяет сочетание, состоящее из трех элементов первого сорта и четырех элементов четвертого. Элементы второго и третьего сорта в это сочетание не входят. Вторая комбинация определяет сочетание, содержащее один элемент первого сорта, один — второго, два — третьего и три элемента четвертого сорта. Заметим еще, что, пока мы рассматриваем сочетания из четырех элементов по семи, условная запись представляет комбинацию всегда четырех чисел — по одному числу на каждый имеющийся сорт элементов, и сумма этих чисел всегда равна семи, то есть общему числу элементов, входящих в сочетание.
В общем случае, если мы захотим условной комбинацией чисел изобразить некоторое сочетание с повторением из m элементов по n элементов, то придется написать уже m целых неотрицательных чисел, снова по одному числу на каждый имеющийся сорт элементов, обозначив их, скажем, причем сумма этих чисел должна равняться числу элементов в сочетании, то есть n:
Такую комбинацию мы будем записывать в виде
Комбинацию , определяющую сочетание, можно записать, пользуясь только цифрами 1 и 0. Сделаем это следующим образом. Вместо числа а 4, означающего количество элементов первого сорта в сочетании, напишем такое же число единиц. Затем таким же способом запишем число элементов второго сорта, а между этими двумя группами единиц поставим нуль для их разделения. Так же будем поступать и дальше. Комбинация (1, 1, 2, 3) изобразится тогда как (1010110111), а комбинация (2, 1, 2, 2) — как (1101011011). Запись (1011011101) соответствует комбинации (1, 2, 3, 1).
Сделаем это следующим образом. Вместо числа а 4, означающего количество элементов первого сорта в сочетании, напишем такое же число единиц. Затем таким же способом запишем число элементов второго сорта, а между этими двумя группами единиц поставим нуль для их разделения. Так же будем поступать и дальше. Комбинация (1, 1, 2, 3) изобразится тогда как (1010110111), а комбинация (2, 1, 2, 2) — как (1101011011). Запись (1011011101) соответствует комбинации (1, 2, 3, 1).
Если какое-либо из чисел равно нулю, то есть элементы данного сорта в сочетание не входят, то единиц на этом месте писать не будем, и два или несколько нулей могут тогда оказаться рядом. Например, комбинация (2, 4, 0, 1) запишется в виде (1101111001). Запись (1111000111) соответствует комбинации (4, 0, 0, 3).
Запись из нулей и единиц, соответствующая сочетанию из m элементов по n элементов, будет содержать ровно n единиц и m — 1 нулей. Действительно, количество единиц равно числу элементов в сочетании, а количество нулей на единицу меньше числа сортов элементов, поскольку нуль употребляется лишь для их разделения. Поэтому число сочетаний с повторениями из m элементов по n элементов равно числу перестановок из n единиц и m — 1 нулей. Как уже известно из теоремы 2, это число равно
Поэтому число сочетаний с повторениями из m элементов по n элементов равно числу перестановок из n единиц и m — 1 нулей. Как уже известно из теоремы 2, это число равно
Теорема доказана.
Если сравнить полученное выражение с формулой (7) для числа сочетаний без повторений, выведенной в предыдущем параграфе, то мы заметим, что
Таким образом, число сочетаний с повторениями из m элементов по n элементов равно числу сочетаний без повторений из n + m — 1 элементов по m — 1 элементов.
В этом параграфе мы рассмотрим еще несколько комбинаторных задач, при решении которых будем пользоваться установленными выше формулами и правилами.
Пример:
В некотором государстве каждые два человека отличаются набором зубов. Каково максимально возможное число жителей этого государства, если наибольшее число зубов у человека равно 32?
Решение:
Эту задачу можно решить двумя способами. Первый способ заключается в том, что мы сначала ищем, сколько людей может иметь k зубов, а потом просуммируем полученные результаты от k= 0 до k=32. Ясно, что k мест из 32 можно выбрать способами. Поэтому ровно кkзубов имеют не более чем жителей. А тогда общее число жителей не превосходит
Ясно, что k мест из 32 можно выбрать способами. Поэтому ровно кkзубов имеют не более чем жителей. А тогда общее число жителей не превосходит
Полученный этим способом ответ оказался очень громоздким. Выгоднее избрать другой путь, которым мы уже пользовались при решении примера 5 в § 2, — применить метод индукции.
Если речь идет об одном зубе, то возможны только два человека—один с зубом и второй без него. При двух зубах число возможных наборов зубов становится равным четырем: нет ни одного зуба, есть первый, есть второй и есть оба.
Увеличив число зубов до трех, мы удвоим число возможностей и получим восемь различных наборов. Действительно, каждый из рассмотренных наборов двух зубов может встретиться дважды — когда нет третьего зуба и когда он есть.
Обозначим число возможных наборов k зубов через Предыдущими рассуждениями мы доказали, что Допустим, что для некоторого k справедливо равенство и докажем, что аналогичное равенство справедливо и для случая k + 1 зубов. Среди всех различных наборов, входящих в имеется ровно наборов, в которых отсутствует (k+1)-й зуб, и столько же наборов, в которых (k+1)-й зуб имеется. Поэтому
Среди всех различных наборов, входящих в имеется ровно наборов, в которых отсутствует (k+1)-й зуб, и столько же наборов, в которых (k+1)-й зуб имеется. Поэтому
Таким образом, при возможных n зубах число всех людей, отличающихся набором зубов, равно . В нашем случае n = 32, поэтому мы получаем Как известно, Поэтому так что возможное население этого государства больше нынешнего населения всего земного шара.
Заметим, что полученный нами результат на самом деле дает больше, чем только оценку возможного населения забавного государства. Сравнивая полученное значение N с написанным выше выражением N как суммы сочетаний, мы приходим к формуле:
Более того, из приведенного выше доказательства по индукции вытекает, что аналогичное равенство справедливо при любом n, то есть что имеет место формула
Пример:
Дана прямоугольная сетка квадратов размером m х n. Каково число различных дорог на этой сетке, ведущих из левого верхнего угла в правый нижний (рис. 46)? (Все звенья дороги предполагаются идущими или вправо, или вниз — без возвращений; сходная ситуация возникает, скажем, при выборе одного из кратчайших маршрутов между двумя городскими перекрестками.)
46)? (Все звенья дороги предполагаются идущими или вправо, или вниз — без возвращений; сходная ситуация возникает, скажем, при выборе одного из кратчайших маршрутов между двумя городскими перекрестками.)
Решение:
Всякая дорога представляет собой ломаную, содержащую m горизонтальных и n вертикальных звеньев, то есть состоящую из m + n звеньев. Различные дороги отличаются одна от другой лишь порядком чередования горизонтальных и вертикальных звеньев. Поэтому число возможных дорог равно числу способов, которыми можно выбрать n вертикальных отрезкoв из общего числа m + n отрезков, а следовательно, есть
Можно было бы рассматривать число способов выбора не n вертикальных, а m горизонтальных отрезков и тогда мы получили бы ответ Но формула (9) из § 3 показывает, что
Полученный результат можно использовать для вывода еще одной интересной формулы. Пусть наша сетка является квадрат ной, то есть имеет размеры n х n. Тогда из приведенного выше решения следует, что число различных дорог, соединяющих левый верхний угол с правым нижним, равно
Вместе с тем число этих дорог можно подсчитать иначе. Рассмотрим диагональ, идущую из нижнего левого угла в верхний правый, и обозначим вершины, лежащие на этой диагонали, через Так как каждая дорога обязательно проходит через одну — и притом единственную—точку этой диагонали, то общее число дорог есть сумма числа дорог, идущих через точку через точку через точку через точку
Рассмотрим диагональ, идущую из нижнего левого угла в верхний правый, и обозначим вершины, лежащие на этой диагонали, через Так как каждая дорога обязательно проходит через одну — и притом единственную—точку этой диагонали, то общее число дорог есть сумма числа дорог, идущих через точку через точку через точку через точку
Найдем число возможных дорог, идущих через точку Если нумерация точек произведена снизу вверх, ка это показано на рис. 47, то точка отстоит от нижней горизонтали на расстоянии k, считая за единицу измерения длину стороны квадрата сетки. От правой вертикали ее отделяют тогда n— k горизонтальных отрезка.
Дорог, соединяющих верхний левый угол с точкой , будет тогда , а дорог, соединяющих точку с нижним правым углом, будет (это видно из рассмотрения равных прямоугольников, противоположными вершинами которых служат верхний левый угол исходного квадрата и точка и соответственно точка и нижний правый угол квадрата). Поэтому общее число дорог, соединяющих верхний левый угол с нижним правым и проходящих через , равно Но тогда общее число всех дорог равно сумме
Сравнивая полученную сумму с найденным выше выражением для числа дорог, мы придем к формуле:
Пример:
Шесть пассажиров садятся на остановке в трамвайный поезд, состоящий из трех трамвайных вагонов. Каким числом различных способов могут они распределиться в вагонах?
Каким числом различных способов могут они распределиться в вагонах?
Решение:
Прежде всего необходимо указать, что задача сформулирована недостаточно точно и допускает два различных толкования. Нас может интересовать или только число пассажиров в каждом вагоне или же кто именно в каком вагоне находится. Рассмотрим обе возможные формулировки.
Сначала рассмотрим случай, когда учитывается, кто в каком вагоне находится, то есть когда случаи «пассажир А в первом вагоне, а пассажир В — во втором» и «пассажир В в первом вагоне, а пассажир А — во втором» считаются различными.
Здесь мы имеем размещения с повторениями из трех элементов по шесть элементов: для каждого из шести пассажиров имеются три возможности. Пользуясь формулой (1) из § 4, получаем, что число различных способов, которыми шесть пассажиров могут распределиться в трех вагонах, равно:
Иной результат получится в том случае, если нас интересует лишь число пассажиров в каждом вагоне, так что случай «один пассажир в первом вагоне и один во втором» является единственным, независимо от того, кто из пассажиров где находится. Здесь нужно подсчитывать уже не размещения, а Сочетания с повторениями. По формуле (4) из §4 находим, что число различных способов распределения пассажиров в этом случае равно
Здесь нужно подсчитывать уже не размещения, а Сочетания с повторениями. По формуле (4) из §4 находим, что число различных способов распределения пассажиров в этом случае равно
Пример:
Сколькими способами можно распределить 28 костей домино между 4 игроками так, чтобы каждый получил 7 костей?
Решение:
Первый игрок может выбрать 7 костей способами. После этого второй игрок должен выбрать 7 костей из оставшихся 21 кости. Это можно сделать способами. Третий игрок может выбрать кости способами, а четвертый — способом. Всего получаем
способов раздела костей.
Эту задачу можно решить иначе. Упорядочим все кости и отдадим первые 7 костей первому игроку, вторые 7 костей — второму игроку и т. д. Так как 28 костей можно упорядочить 28! способами, то получаем 28! способов раздела. Но некоторые из этих способов приводят к одинаковым результатам — игрокам неважно, в каком порядке приходят к ним кости, а важно лишь, какие именно кости они получат. Поэтому результат не изменится, если мы как угодно переставим друг с другом первые 7 костей, потом вторые 7 костей и т. д. Первые 7 костей можно переставить 7! способами, вторые 7 костей — тоже 7! способами и т. д. Всего получим перестановок, дающих то же распределение костей, что и данная. Поэтому число способов раздела костей равно
Поэтому результат не изменится, если мы как угодно переставим друг с другом первые 7 костей, потом вторые 7 костей и т. д. Первые 7 костей можно переставить 7! способами, вторые 7 костей — тоже 7! способами и т. д. Всего получим перестановок, дающих то же распределение костей, что и данная. Поэтому число способов раздела костей равно
Пример:
Сколькими способами можно разделить 40 яблок между 4 мальчиками (все яблоки считаются одинаковыми)?
Решение:
Возьмем три одинаковые перегородки и рассмотрим всевозможные перестановки 43 предметов: 40 яблок и 3 пере городок. Каждой такой перестановке соответствует свой способ раздела: первый мальчик получает все яблоки от начала до первой перегородки, второй — все яблоки между первой и второй перегородками, третий — все яблоки между второй и третьей перегородками, а четвертый — все остальные яблоки. (Если, например, первая и вторая перегородки оказались рядом, то второй мальчик ничего не получает. ) Значит, число способов раздела равно числу перестановок 40 яблок и 3 перегородок. По формуле числа перестановок с повторениями получаем, что это число равно
) Значит, число способов раздела равно числу перестановок 40 яблок и 3 перегородок. По формуле числа перестановок с повторениями получаем, что это число равно
Пример:
Сколькими способами можно разделить 40 яблок между 4 мальчиками так, чтобы каждый получил по крайней мере 3 яблока (все яблоки по-прежнему считаются одинаковыми)?
Решение:
Сначала дадим каждому мальчику по 3 яблока. А потом разделим оставшиеся 28 яблок так, как было сделано в предыдущей задаче. Всего получаем
способов раздела.
Пример:
Имеется m различных сигнальных флагов и k мачт, на которых их вывешивают. Значение сигнала зависит от того, в каком порядке развешаны флаги. Сколько сигналов можно передать этими флагами, если все флаги должны быть использованы, но некоторые из мачт могут оказаться пустыми?
Решение:
Добавим к m флагам k — 1 перегородку и рассмотрим всевозможные перестановки из m различных флагов и k одинаковых перегородок. Как ив примере 5, каждой перестановке соответствует свой сигнал (на первую мачту вывешиваются по порядку все флаги от начала до первой перегородки и т. д.). Поэтому число сигналов равно числу таких перестановок, то есть равно
Как ив примере 5, каждой перестановке соответствует свой сигнал (на первую мачту вывешиваются по порядку все флаги от начала до первой перегородки и т. д.). Поэтому число сигналов равно числу таких перестановок, то есть равно
Если бы мы не потребовали, чтобы все флаги были использованы, то число сигналов оказалось бы больше. В этом случае задача решалась бы в два этапа. Сначала выберем, какие флаги будут участвовать в сигнале. Если число выбираемых флагов равно s, то выбор можно сделать способами. Как мы уже знаем, с помощью данных s флагов можно передать сигналов. По этому всего имеем сигналов, передаваемых s флагами. А общее число сигналов равно
Бином Ньютона и его обобщения
В главе I (§ 1, п. 8) была выведена формула бинома Ньютона:
Через мы обозначили коэффициент при в разложении Для было получено соотношение которое позволяет вычислять эти коэффициенты один за другим. Сейчас мы получим явную формулу для — для этого мы покажем, что коэффициенты — не что иное, как число сочетаний из n элементов по k (именно поэтому в гл. I и было выбрано обозначение
I и было выбрано обозначение
В самом деле, запишем в виде произведения n сомножителей:
— и раскроем скобки в этом произведении, причем будем записывать все множители в том порядке, в котором они нам встретятся. Например, запишем
или
Видно, что в формулу (3) входят все размещения с повторениями из букв х и а, по две буквы в каждом размещении , а в формулу (4) — размещения с повторениями из тех же букв, содержащие по три буквы. То же самое будет в общем случае — после раскрытия скобок в формуле (2) получаются все размещения с повторениями из букв х и а, по n букв в каждом размещении.
Приведем подобные члены. Подобными будут члены, содержащие одинаковое количество букв а (тогда и букв х в них будет поровну). Найдем число членов, содержащих k букв а (и, следовательно, n — k букв х). Эти члены являются всевозможными перестановками с повторениями, составленными из k букв а и n — k букв Их число равно
Отсюда вытекает, что после приведения подобных членов коэффициент при окажется равным , то есть числу сочетаний из n элементов по k. Тем самым доказано, что числа в формуле (1) действительно являются числами сочетаний из n элементов по k .
Тем самым доказано, что числа в формуле (1) действительно являются числами сочетаний из n элементов по k .
Рассмотрим несколько задач, связанных с формулой бинома Ньютона.
Пример:
Определить коэффициент при в разложении
Решение:
Запишем данное нам выражение в виде:
где Отсюда видно, что может получиться только из члена, содержащего . В соответствии с формулой (1) этот член имеет вид:
Для получения нужно при раскрытии скобок взять член, содержащий в первой степени. Этот член имеет вид поэтому искомый коэффициент при равен произведению
Пример:
С каким коэффициентом входит в разложение
Решение:
Выясним сначала, каким числом способов можно представить в виде произведений для чего надо знать, какими способами можно представить число 30 в виде суммы слагаемых 3 и 7. Очевидно, что 30 можно представить в виде суммы десяти троек, и без участия слагаемого 7 других представлений нет. С участием 7 возможно только одно представление 30 = 7+7+7+3+3+3, так как число семерок, входящих в сумму, должно быть кратно трем, иначе сумма не будет делиться на 3.
С участием 7 возможно только одно представление 30 = 7+7+7+3+3+3, так как число семерок, входящих в сумму, должно быть кратно трем, иначе сумма не будет делиться на 3.
Итак, для нахождения коэффициента при в нам нужно определить коэффициенты при членах
Как и в предыдущем примере, перепишем наше выражение в виде и воспользуемся формулой (1):
Слагаемое есть только в последнем из выписанных нами членов, и коэффициент при нем равен Еще одно слагаемое вида входит в слагаемое
при раскрытии произведения
Так как в этой последней скобке коэффициент при равен то коэффициент при члене равен произведению
Окончательно, искомый коэффициент при есть сумма
Подставляя в (1) х=1, получим другой вывод формулы (1) из § 5. Аналогично, приняв в (1) х = — 1, получим еще одну любопытную формулу:
или, иначе,
то есть для любого n сумма сочетаний из n элементов по четному числу элементов равна сумме сочетаний из п элементов по нечетному числу элементов.
Формулу, аналогичную формуле бинома Ньютона, можно получить и для возведения в степень суммы нескольких слагаемых. Если число слагаемых невелико, то ее легко получить, применяя несколько раз формулу бинома Ньютона. Например, для трех слагаемых можно написать:
раскрывая, в свою очередь, каждое слагаемое справа по формуле (2). При небольших n это нетрудно сделать.
Пусть, например, n = 2. Тогда получаем:
При n = 3 находим:
Таким образом, мы получили формулы для квадрата и куба суммы трех слагаемых, которые имеют вид:
Однако для больших n, не говоря уже о большом числе слагаемых , такой способ вывода формулы потребует уже чересчур сложных и громоздких вычислений.
Формулу для возведения в степень суммы нескольких слагаемых можно получить и непосредственно, подобно тому как мы это делали для формулы бинома Ньютона.
Действительно, n-я степень суммы есть произведение n одинаковых слагаемых вида Перемножив все скобки, мы получим сумму произведений, причем в каждом слагаемом будет n сомножителей. Общее число слагаемых равно числу размещений с повторениями из m элементов по n элементов, то есть так как множители, взятые из различных скобок, могут совпадать. Вследствие этого каждое отдельное слагаемое будет иметь вид
Общее число слагаемых равно числу размещений с повторениями из m элементов по n элементов, то есть так как множители, взятые из различных скобок, могут совпадать. Вследствие этого каждое отдельное слагаемое будет иметь вид
Показатели степени а удовлетворяют, очевидно, условиям и
то есть все они суть целые неотрицательные числа и их сумма равна n.
Чтобы определить коэффициент, который будет стоять у произведения после приведения подобных членов, нужно подсчитать, сколько раз такое произведение может встретиться. Это можно сделать следующим образом.
Каждому произведению (до приведения подобных членов) поставим в соответствие перестановку из элементов 1, 2, …, m . При этом если из первой скобки берется, например, множитель из второй — из третьей — и т. д., то перестановка имеет вид 2, 3, 1 … . Иначе говоря, в перестановке на первом месте ставится номер элемента, взятого из первой скобки, на втором — номер элемента из второй скобки и т.д. Например, произведению соответствует перестановка 1, 2, 4, 1, 4, 3.
Ясно, что произведению ставится в соответствие такая перестановка, в которой элемент 1 повторяется на различных местах ровно раз, элемент 2— ровно раз и т. д. В том случае, когда что возможно, соответствующий элемент к не входит в рассматриваемую перестановку вовсе.
Из сказанного вытекает, что произведение встречается среди слагаемых столько раз, сколько существует различных перестановок с повторениями из п элементов, в которых элемент 1 повторяется раз, элемент 2 повторяется раз,…, элемент m повторяется раз, то есть
(см. формулу (3) из § 4). Это же число служит коэффициентом при произведении в разложении n-й степени суммы m слагаемых.
Полученное можно выразить в виде следующей теоремы.
Теорема:
Результат возведения суммы m слагаемых в n-ю степень имеет вид:
где суммирование распространяется на все возможные системы целых неотрицательных чисел, удовлетворяющие условию
Эту теорему называют полиномиальной, а коэффициенты (5) — полиномиальными коэффициентами.
Легко убедиться в том, что формула бинома Ньютона является частным случаем полиномиальной формулы (6).
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
Сочетания из n по k онлайн.
 Формулы комбинаторики
Формулы комбинаторикиКомбинаторика — это раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов. Основы комбинаторики очень важны для оценки вероятностей случайных событий, т.к. именно они позволяют подсчитать принципиальновозможное количество различных вариантов развития событий.
Основная формула комбинаторики
Пусть имеется k групп элементов, причем i-я группа состоит из n i элементов. Выберем по одному элементу из каждой группы. Тогда общее число N способов, которыми можно произвести такой выбор, определяется соотношением N=n 1 *n 2 *n 3 *…*n k .
Пример 1. Поясним это правило на простом
примере. Пусть имеется две группы элементов, причем первая группа состоит из
n 1 элементов, а вторая — из n 2 элементов. Сколько
различных пар элементов можно составить из этих двух групп, таким образом,
чтобы в паре было по одному элементу от каждой группы? Допустим, мы взяли
первый элемент из первой группы и, не меняя его, перебрали все возможные
пары, меняя только элементы из второй группы. Таких пар для этого элемента
можно составить n 2 . Затем мы берем второй элемент из первой группы
и также составляем для него все возможные пары. Таких пар тоже будет n 2 .
Так как в первой группе всего n 1 элемент, всего возможных
вариантов будет n 1 *n 2 .
Таких пар для этого элемента
можно составить n 2 . Затем мы берем второй элемент из первой группы
и также составляем для него все возможные пары. Таких пар тоже будет n 2 .
Так как в первой группе всего n 1 элемент, всего возможных
вариантов будет n 1 *n 2 .
Пример 2. Сколько
трехзначных четных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, 6, если
цифры могут повторяться?
Решение: n 1 =6
(т.к. в качестве первой цифры можно взять любую цифру из 1, 2, 3, 4, 5, 6), n 2 =7
(т.к. в качестве второй цифры можно взять любую цифру из 0, 1, 2, 3, 4, 5,
6), n 3 =4 (т.к. в качестве третьей цифры можно взять любую цифру из 0, 2, 4,
6).
Итак, N=n 1 *n 2 *n 3 =6*7*4=168.
В том случае, когда все группы состоят из одинакового числа элементов, т.е. n 1 =n 2 =…n k =n
можно считать, что каждый выбор производится из одной и той же группы, причем
элемент после выбора снова возвращается в группу. Тогда число всех способов
выбора равно n k . Такой способ выбора в комбинаторики носит название выборки с возвращением.
Пример 3. Сколько всех четырехзначных чисел
можно составить из цифр 1, 5, 6, 7, 8?
Решение. Для каждого разряда
четырехзначного числа имеется пять возможностей, значит N=5*5*5*5=5 4 =625.
Рассмотрим множество, состоящие из n элементов. Это множество в комбинаторике называется генеральной совокупностью .
Число размещений из n элементов по m
Определение 1. Размещением из n элементов по m в комбинаторике называется любой упорядоченный набор из m различных элементов, выбранных из генеральной совокупности в n элементов.
Пример 4. Различными размещениями из трех элементов {1, 2, 3} по два будут наборы (1, 2), (2, 1), (1, 3), (3, 1), (2, 3),(3, 2). Размещения могут отличаться друг от друга как элементами, так и их порядком.
Число размещений в комбинаторике обозначается A n m и вычисляется по формуле:
Замечание: n!=1*2*3*…*n (читается: «эн факториал»), кроме того
полагают, что 0!=1.
Пример 5 . Сколько существует двузначных
чисел, в которых цифра десятков и цифра единиц различные
и нечетные?
Решение: т.к. нечетных цифр
пять, а именно 1, 3, 5, 7, 9, то эта задача сводится к выбору и размещению на
две разные позиции двух из пяти различных цифр, т.е. указанных чисел будет:
Определение 2. Сочетанием из n элементов по m в комбинаторике называется любой неупорядоченный набор из m различных элементов, выбранных из генеральной совокупности в n элементов.
Пример 6 . Для множества {1, 2, 3}сочетаниями являются {1, 2}, {1, 3}, {2, 3}.
Число сочетаний из n элементов по m
Число сочетаний обозначается C n m и вычисляется по формуле:
Пример 7. Сколькими способами читатель может выбрать две книжки из шести имеющихся?
Решение: Число способов равно числу сочетаний из шести книжек по две, т.е. равно:
Перестановки из n элементов
Определение 3. Перестановкой из n элементов
называется любой упорядоченный набор этих элементов.
Перестановкой из n элементов
называется любой упорядоченный набор этих элементов.
Пример 7a. Всевозможными перестановками множества, состоящего из трех элементов {1, 2, 3} являются: (1, 2, 3), (1, 3, 2), (2, 3, 1), (2, 1, 3), (3, 2, 1), (3, 1, 2).
Число различных перестановок из n элементов обозначается P n и вычисляется по формуле P n =n!.
Пример 8. Сколькими способами семь книг разных авторов можно расставить на полке в один ряд?
Решение: эта задача о числе перестановок семи разных книг. Имеется P 7 =7!=1*2*3*4*5*6*7=5040 способов осуществить расстановку книг.
Обсуждение. Мы видим, что число возможных комбинаций можно посчитать по разным правилам (перестановки, сочетания, размещения) причем результат получится различный, т.к. принцип подсчета и сами формулы отличаются. Внимательно посмотрев на определения, можно заметить, что результат зависит от нескольких факторов одновременно.
Во-первых, от того, из какого количества элементов мы можем комбинировать их
наборы (насколько велика генеральная совокупность элементов).
Во-вторых, результат зависит от того, какой величины наборы элементов нам нужны.
И последнее, важно знать, является ли для нас существенным порядок элементов в наборе. Поясним последний фактор на следующем примере.
Пример 9. На родительском собрании
присутствует 20 человек. Сколько существует различных вариантов состава
родительского комитета, если в него должны войти 5 человек?
Решение: В этом примере нас
не интересует порядок фамилий в списке комитета. Если в результате в его
составе окажутся одни и те же люди, то по смыслу для нас это один и тот же
вариант. Поэтому мы можем воспользоваться формулой для подсчета числа сочетаний из 20 элементов по 5.
Иначе будут обстоять дела, если каждый член комитета изначально отвечает за
определенное направление работы. Тогда при одном и том же списочном составе
комитета, внутри него возможно 5! вариантов перестановок , которые имеют значение. Количество
разных (и по составу, и по сфере ответственности) вариантов определяется в
этом случае числом размещений из 20 элементов по 5.
Задачи для самопроверки
1. Сколько трехзначных четных чисел можно составить из цифр 0, 1, 2, 3, 4, 5,
6, если цифры могут повторяться?
2. Сколько существует пятизначных чисел, которые одинаково читаются слева направо и справа налево?
3. В классе десять предметов и пять уроков в день. Сколькими способами можно составить расписание на один день?
4. Сколькими способами можно выбрать 4 делегата на конференцию, если в группе 20 человек?
5. Сколькими способами можно разложить восемь различных писем по восьми различным конвертам, если в каждый конверт кладется только одно письмо?
6. Из трех математиков и десяти экономистов надо составить комиссию, состоящую из двух математиков и шести экономистов. Сколькими способами это можно сделать?
На первом месте в ряду может стоять любой из N элементов, следовательно, получается N вариантов. На втором месте — любой, кроме того, который уже был использован для первого места. Следовательно, для каждого из N уже найденных вариантов есть (N — 1) вариантов второго места, и общее количество комбинаций становится N*(N — 1).
Это же можно повторить для остальных элементов ряда. Для самого последнего места остается только один вариант — последний оставшийся элемент. Для предпоследнего — два варианта, и так далее.
Следовательно, для ряда из N неповторяющихся элементов возможных перестановок равно произведению всех целых от 1 до N. Это произведение называется N и N! (читается «эн факториал»).
В предыдущем случае количество возможных элементов и количество мест ряда совпадали, и их число было равно N. Но возможна ситуация, когда в ряду меньше мест, чем имеется возможных элементов. Иными словами, количество элементов в выборке равно некоторому числу M, причем M Во-первых, может потребоваться сосчитать общее количество возможных способов, которыми можно выстроить в ряд M элементов из N. Такие способы размещениями.
Во-вторых, исследователя может интересовать число способов, которыми можно выбрать M элементов из N. При этом порядок расположения элементов уже не важен, но любые два варианта должны различаться между собой хотя бы одним элементом. Такие способы называются сочетаниями.
Такие способы называются сочетаниями.
Чтобы найти количество размещений по M элементов из N, можно прибегнуть к такому же способу рассуждений, как и в случае с перестановками. На первом месте здесь по-прежнему может стоять N элементов, на втором (N — 1), и так далее. Но для последнего места количество возможных вариантов равняется не единице, а (N — M + 1), поскольку, когда размещение будет закончено, останется еще (N — M) неиспользованных элементов.
Таким образом, число размещений по M элементов из N равняется произведению всех целых чисел от (N — M + 1) до N, или, что то же самое, частному N!/(N — M)!.
Очевидно, что количество сочетаний по M элементов из N будет меньше количества размещений. Для каждого возможного сочетания есть M! возможных размещений, зависящих от порядка элементов этого сочетания. Следовательно, чтобы найти это количество, нужно разделить число размещений по M элементов из N на N!. Иными словами, количество сочетаний по M элементов из N равно N!/(M!*(N — M)!).
Источники:
- количество сочетаний
Факториал натурального числа – это произведение всех предыдущих натуральных чисел, включая само число. Факториал нуля равен единице. Кажется, что посчитать факториал числа очень просто – достаточно перемножить все натуральные числа, не превышающие заданное. Однако, значение факториала настолько быстро возрастает, что некоторые калькуляторы не справляются с этой задачей.
Вам понадобится
- калькулятор, компьютер
Инструкция
Чтобы посчитать факториал натурального числа перемножьте все , не превосходящие данное. Каждое число учитывается только один раз. В виде формулы это можно записать следующим образом:n! = 1*2*3*4*5*…*(n-2)*(n-1)*n, гдеn – натуральное число, факториал которого требуется посчитать.
0! принимается равным единице (0!=1).При возрастании аргумента значение факториала очень быстро увеличивается, поэтому обычный (бухгалтерский) уже для факториала 15-ти вместо результата может выдать об ошибке.
Чтобы посчитать факториал большого натурального числа, возьмите инженерный калькулятор. То есть, такой калькулятор на клавиатуре которого имеются обозначения математических функций (cos, sin, √). Наберите на калькуляторе исходное число, а затем нажмите кнопку вычисления факториала. Обычно такая кнопка как «n!» или аналогично (вместо «n» может стоять «N» или «х», но восклицательный знак «!» в обозначении факториала должен присутствовать в любом случае).
При больших значениях аргумента результаты вычислений начинают отображаться в «экспоненциальном» (показательном) виде. Так, например, факториал 50 будет представлен в форме: 3,0414093201713378043612608166065e+64 (или похожем). Чтобы получить результат вычислений в обычном виде, припишите к числу, показанному до символа «е», столько нулей, сколько указано после «е+» (если, конечно, хватит места).
В комбинаторике изучают вопросы о том, сколько комбинаций определенного типа можно составить из данных предметов (элементов).
Рождение комбинаторики как раздела связано с трудами Б. Паскаля и П. Ферма по теории азартных игр. Большой вклад в развитие комбинаторных методов внесли Г.В. Лейбниц, Я. Бернулли и Л. Эйлер.
Паскаля и П. Ферма по теории азартных игр. Большой вклад в развитие комбинаторных методов внесли Г.В. Лейбниц, Я. Бернулли и Л. Эйлер.
Французский философ, писатель, математик и физик Блез Паскаль (1623–1662) рано проявил свои выдающиеся математические способности. Круг математических интересов Паскаля был весьма разнообразен. Паскаль доказал одну
из основных теорем проективной геометрии (теорема Паскаля), сконструировал суммирующую машину (арифмометр Паскаля), дал способ вычисления биномиальных коэффициентов (треугольник Паскаля), впервые точно определил и применил для доказательства метод математической индукции, сделал существенный шаг в развитии анализа бесконечно малых, сыграл важную роль в зарождении теории вероятности. В гидростатике Паскаль установил ее основной закон (закон Паскаля). “Письма к провинциалу” Паскаля явились шедевром французской классической прозы.
Готфрид Вильгельм Лейбниц (1646–1716) — немецкий философ, математик, физик и изобретатель, юрист, историк, языковед. В математике наряду с И. Ньютоном разработал дифференциальное и интегральное исчисление. Важный вклад внес в комбинаторику. С его именем, в частности, связаны теоретико-числовые задачи.
В математике наряду с И. Ньютоном разработал дифференциальное и интегральное исчисление. Важный вклад внес в комбинаторику. С его именем, в частности, связаны теоретико-числовые задачи.
Готфрид Вильгельм Лейбниц имел мало внушительную внешность и поэтому производил впечатление довольно невзрачного человека. Однажды в Париже он зашел в книжную лавку в надежде приобрести книгу своего знакомого философа. На вопрос посетителя об этой книге книготорговец, осмотрев его с головы до ног, насмешливо бросил: “Зачем она вам? Неужели вы способны читать такие книги?” Не успел ученый ответить, как в лавку вошел сам автор книги со словами: “Великому Лейбницу привет и уважение!” Продавец никак не мог взять втолк, что перед ним действительно знаменитый Лейбниц, книги которого пользовались большим спросом среди ученых.
В дальнейшем важную роль будет играть следующая
Лемма. Пусть в множестве элементов, а в множестве — элементов. Тогда число всех различных пар , где будет равно .
Доказательство. Действительно, с одним элементом из множества мы можем составить таких различных пар, а всего в множестве элементов.
Размещения, перестановки, сочетания
Пусть у нас есть множество из трех элементов . Какими способами мы можем выбрать из этих элементов два? .
Определение. Размещениями множества из различных элементов по элементов называются комбинации, которые составлены из данных элементов по > элементов и отличаются либо самими элементами, либо порядком элементов.
Число всех размещений множества из элементов по элементов обозначается через (от начальной буквы французского слова “arrangement”, что означает размещение), где и .
Теорема. Число размещений множества из элементов по элементов равно
Доказательство. Пусть у нас есть элементы . Пусть — возможные размещения. Будем строить эти размещения последовательно. Сначала определим — первый элемент размещения. Из данной совокупности элементов его можно выбрать различными способами. После выбора первого элемента для второго элемента остается способов выбора и т.д. Так как каждый такой выбор дает новое размещение, то все эти выборы можно свободно комбинировать между собой. Поэтому имеем:
После выбора первого элемента для второго элемента остается способов выбора и т.д. Так как каждый такой выбор дает новое размещение, то все эти выборы можно свободно комбинировать между собой. Поэтому имеем:
Пример. Сколькими способами можно составить флаг, состоящий из трех горизонтальных полос различных цветов, если имеется материал пяти цветов?
Решение. Искомое число трехполосных флагов:
Определение. Перестановкой множества из элементов называется расположение элементов в определенном порядке.
Так, все различные перестановки множества из трех элементов — это
Число всех перестановок из элементов обозначается (от начальной буквы французского слова “permutation”, что значит “перестановка”, “перемещение”). Следовательно, число всех различных перестановок вычисляется по формуле
Пример. Сколькими способами можно расставить ладей на шахматной доске так, чтобы они не били друг друга?
Решение. Искомое число расстановки ладей
По определению!
Определение. k
k
Действительно, каждому -элементному подмножеству данного -элементного множества соответствует одно и только одно -элементное подмножество того же множества.
Действительно, мы можем выбирать подмножества из элементов следующим образом: фиксируем один элемент; число -элементных подмножеств, содержащих этот элемент, равно ; число -элементных подмножеств, не содержащих этот элемент, равно .
Треугольник Паскаля
В этом треугольнике крайние числа в каждой строке равны 1, а каждое не крайнее число равно сумме двух чисел предыдущей строки, стоящих над ним. Таким образом, этот треугольник позволяет вычислять числа .
Теорема.
Доказательство. Рассмотрим множество из элементов и решим двумя способами следующую задачу: сколько можно составить последовательностей из элементов данного
множества, в каждой из которых никакой элемент не встречается дважды?
1 способ. Выбираем первый член последовательности, затем второй, третий и т. д. член
д. член
2 способ. Выберем сначала элементов из данного множества, а затем расположим их в некотором порядке
Домножим числитель и знаменатель этой дроби на :
Пример. Сколькими способами можно в игре “Спортлото” выбрать 5 номеров из 36?
Искомое число способов
Задачи.
1. Номера машин состоят из 3 букв русского алфавита (33 буквы) и 4 цифр. Сколько существует различных номеров автомашин?
2. На рояле 88 клавиш. Сколькими способами можно извлечь последовательно 6 звуков?
3. Сколько есть шестизначных чисел, делящихся на 5?
4. Сколькими способами можно разложить 7 разных монет в три кармана?
5. Сколько можно составить пятизначных чисел, в десятичной записи которых хотя бы один раз встречается цифра 5?
6. Сколькими способами можно усадить 20 человек за круглым столом, считая способы одинаковыми, если их можно получить один из другого движением по кругу?
7. Сколько есть пятизначных чисел, делящихся на 5, в записи которых нет одинаковых цифр?
8. На клетчатой бумаге со стороной клетки 1 см нарисована окружность радиуса 100 см, не проходящая через вершины клеток и не касающаяся сторон клеток. Сколько клеток может пересекать эта окружность?
На клетчатой бумаге со стороной клетки 1 см нарисована окружность радиуса 100 см, не проходящая через вершины клеток и не касающаяся сторон клеток. Сколько клеток может пересекать эта окружность?
9. Сколькими способами можно расставить в ряд числа так, чтобы числа стояли рядом и притом шли в порядке возрастания?
10. Сколько пятизначных чисел можно составить из цифр , если каждую цифру можно использовать только один раз?
11. Из слова РОТ перестановкой букв можно получить еще такие слова: ТОР, ОРТ, ОТР, ТРО, РТО. Их называют анаграммами. Сколько анаграмм можно составить из слова ЛОГАРИФМ?
12. Назовем разбиением натурального числа представление его в виде суммы натуральных чисел. Вот, например, все разбиения числа :
Разбиения считаются разными, если они отличаются либо числами, либо порядком слагаемых.
Сколько существует различных разбиений числа на слагаемых?
13. Сколько существует трехзначных чисел с невозрастающим порядком цифр?
14. Сколько существует четырехзначных чисел с невозрастающим порядком цифр?
Сколько существует четырехзначных чисел с невозрастающим порядком цифр?
15. Сколькими способами можно рассадить в ряд 17 человек, чтобы и оказались рядом?
16. девочек и мальчиков рассаживаются произвольным образом в ряду из мест. Сколькими способами можно их рассадить так, чтобы никакие две девочки не сидели рядом?
17. девочек и мальчиков рассаживаются произвольным образом в ряду из мест. Сколькими способами можно их рассадить так, чтобы все девочки сидели рядом?
Число сочетаний
Сочетанием из n по k называется набор k элементов, выбранных из данных n элементов. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания отличаются от размещений .
Явные формулы
Число сочетаний из n по k равно биномиальному коэффициенту
При фиксированном значении n производящей функцией чисел сочетаний с повторениями из n по k является:
Двумерной производящей функцией чисел сочетаний с повторениями является:
Ссылки
- Р.
 Стенли Перечислительная комбинаторика. — М.: Мир, 1990.
Стенли Перечислительная комбинаторика. — М.: Мир, 1990. - Вычисление числа сочетаний онлайн
Wikimedia Foundation . 2010 .
Смотреть что такое «Число сочетаний» в других словарях:
70 семьдесят 67 · 68 · 69 · 70 · 71 · 72 · 73 40 · 50 · 60 · 70 · 80 · 90 · 100 Факторизация: 2×5×7 Римская запись: LXX Двоичное: 100 0110 … Википедия
Световое число, условное число, однозначно выражающее внеш. условия при фотосъёмке (обычно яркость объекта съёмки и светочувствительность применяемого фотоматериала). Любому значению Э. ч. можно подобрать неск. сочетаний диафрагменное число… … Большой энциклопедический политехнический словарь
Форма числа, выделяющая два предмета как по отношению к единичному предмету, так и по отношению к множеству предметов. В современном русском языке эта форма не существует, но остатки ее влияния сохранились. Так, сочетания два стола (ср. мн. ч.… … Словарь лингвистических терминов
Комбинаторная математика, комбинаторика, раздел математики, посвященный решению задач выбора и расположения элементов нек рого, обычно конечного, множества в соответствии с заданными правилами. Каждое такое правило определяет способ построения… … Математическая энциклопедия
Каждое такое правило определяет способ построения… … Математическая энциклопедия
В комбинаторике сочетанием из по называется набор элементов, выбранных из данного множества, содержащего различных элементов. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания… … Википедия
Занимается изучением событий, наступление которых достоверно неизвестно. Она позволяет судить о разумности ожидания наступления одних событий по сравнению с другими, хотя приписывание численных значений вероятностям событий часто бывает излишним… … Энциклопедия Кольера
1) то же, что математический Комбинаторный анализ. 2) Раздел элементарной математики, связанный с изучением количества комбинаций, подчинённых тем или иным условиям, которые можно составить из заданного конечного множества объектов… … Большая советская энциклопедия
— (греч. paradoxos неожиданный, странный) в широком смысле: утверждение, резко расходящееся с общепринятым, устоявшимся мнением, отрицание того, что представляется «безусловно правильным»; в более узком смысле два противоположных утверждения, для… … Философская энциклопедия
— (или принцип включений исключений) комбинаторная формула, позволяющая определить мощность объединения конечного числа конечных множеств, которые в общем случае могут пересекаться друг с другом … Википедия
Математическая теория, занимающаяся определением числа различных способов распределения данных предметов в известном порядке; имеет особенно важное значение в теории уравнений и в теории вероятностей. Простейшие задачи этого рода заключаются в… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Простейшие задачи этого рода заключаются в… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Книги
- Число судьбы. Гороскоп совместимости. Желания. Страсти. Фантазии (количество томов: 3) , Майер Максим. Число судьбы. Как составить индивидуальный нумерологический прогноз. Нумерология — одна из самых древних эзотерических систем. Невозможно точно установить времяее возникновения. Однако в…
Мы иногда делаем выбор из множества без учета порядка . Такой выбор называется комбинацией . Если вы играете в карты, например, вы знаете, что в большинстве ситуаций порядок, в котором вы держите карты, не имеет значения.
Пример 1 Найдите все комбинации 3-х букв, взятых из набора в 5 букв {A, B, C, D, E}.
Решение Эти комбинации следующие:
{A, B, C}, {A, B, D},
{A, B, E}, {A, C, D},
{A, C, E}, {A, D, E},
{B, C, D}, {B, C, E},
{B, D, E}, {C, D, E}.
Существует 10 комбинаций из трех букв, выбранных из пяти букв.
Когда мы находим все комбинации из набора с 5 объектами, если мы берем 3 объекта за один раз, мы находим все 3-элементные подмножества. В таком случае порядок объектов не рассматривается. Тогда,
{A, C, B} называется одним и тем же набором как и {A, B, C}.
Подмножество
Множество A есть подмножеством B, и означает что A это подмножество и/или совпадает с B если каждый элемент A является элементом B.
Элементы подмножество не упорядочены. Когда рассматриваются комбинации, не рассматривается порядок!
Комбинация
Комбинация, содержащая k объектов является подмножеством, состоящим из k объектов.
Мы хотим записать формулу для вычисления число сочетаний из n объектов, если взято к объектов одновременно.
Обозначения комбинации
Число сочетаний из n объектов, если взято к объектов одновременно, обозначается n C k .
Мы называем n C k число сочетаний . Мы хотим записать общую формулу для n C k для любого k ≤ n. Во-первых, это верно, что n C n = 1, потому что множество с n элементами имеет только одно подмножестов с n элементами, есть само множество. Во-вторых, n C 1 = n, потому что множество с n элементами имеет только n подмножеств с 1 элементом в каждом. Наконец, n C 0 = 1, потому что множество с n элементами имеет только одно подмножество с 0 элементами, то есть пустое множество ∅. Чтобы рассмотреть другие сочетания, давайте вернемся к примеру 1 и сравним число комбинаций с числом перестановок.
Во-первых, это верно, что n C n = 1, потому что множество с n элементами имеет только одно подмножестов с n элементами, есть само множество. Во-вторых, n C 1 = n, потому что множество с n элементами имеет только n подмножеств с 1 элементом в каждом. Наконец, n C 0 = 1, потому что множество с n элементами имеет только одно подмножество с 0 элементами, то есть пустое множество ∅. Чтобы рассмотреть другие сочетания, давайте вернемся к примеру 1 и сравним число комбинаций с числом перестановок.
Обратите внимание, что каждая комбинация из 3-х элементов имеет 6, или 3!, перестановок.
3! . 5 C 3 = 60 = 5 P 3 = 5 . 4 . 3,
so
.
В общем, число сочетаний из k элементов, выбранных из n объектов, n C k раз перестановок этих элементов k!, должно быть равно числу перестановок n элементов по k элементов:
k!. n C k = n P k
n C k = n P k /k!
n C k = (1/k!). n P k
n C k =
Комбинации k объектов из n объектов
Общее число комбинаций к элементов из n объектов обозначается n C k , определяется
(1) n C k = ,
или
(2) n C k =
Другой тип обозначения для n C k это биноминальный коэффициент . Причина для такой терминологии будет понятна ниже.
Причина для такой терминологии будет понятна ниже.
Биноминальный коэффициент
Пример 2 Вычислите , используя формулы (1) и (2).
Решение
a) Согласно (1),
.
b) Согласно (2),
Имейте в виду, что не означает n/k.
Пример 3 Вычислите и .
Решение Мы используем формулу (1) для первого выражения и формулу (2) для второго. Тогда
,
используя (1), и
,
испоьлзуя формулу (2).
Обратите внимание, что
,
и используя результат примера 2 дает нам
.
Отсюда вытекает, что число 5-ти элементного подмножества из множества 7 элементов то же самое, что и число 2-элементного подмножества множества из 7 элементов. Когда 5 элементов выбираются из набора, они не включают в себя 2 элемента. Чтобы увидеть это, рассмотрим множество {A, B, C, D, E, F, G}:
В целом, мы имеем следующее. Этот результат дает альтернативный способ вычисления комбинации.
Подмножества размера k и размера
и n C k = n C n-k
Число подмножеств размера к множества с n объектами такое же, как и число подмножеств размера n — к. Число сочетаний k объектов из множества n объектов, такое же как и число сочетаний из n объектов, взятых одновременно.
Число сочетаний k объектов из множества n объектов, такое же как и число сочетаний из n объектов, взятых одновременно.
Теперь мы будем решать задачи с комбинациями.
Пример 4 Мичиганская лотерея. Проводящаяся в штате Мичиган два раза в неделю лотерея WINFALL имеет джек-пот, который, по крайней мере, равен 2 млн. долларов США. За один доллар игрок может зачеркнуть любые 6 чисел от 1 до 49. Если эти числа совпадают с теми, которые выпадают при проведении лотереи, игрок выигрывает. (
Биномиальное распределение
«Би» означает «два» (как у велосипеда два колеса) … | |
Подбрасывание монеты:
- Выпали ли мы орлом (H) или
- Хвосты (Т)
Мы говорим вероятность выпадения монеты H равно ½
И вероятность выпадения монеты T равна ½
Бросание игральной кости:
- Получили ли мы четыре .
 .. ?
.. ? - … или нет?
Мы говорим, что вероятность четыре равна 1/6 (одна из шести граней является четверкой)
И вероятность того, что не четыре равна 5/6 (пять из шести граней не четыре)
Обратите внимание, что у игральной кости 6 граней, но здесь мы рассматриваем только 9.0007 два корпуса: «четыре: да» или «четыре: нет»
Подбросим монетку!
Подбросьте правильную монету трижды … какова вероятность того, что выпадет ровно два орла ?
Используя H для орла и T для решки, мы можем получить любой из этих 8 исходов :
| ЧЧЧ | ||
| ННТ | ||
| ХТХ | ||
| ХТТ | ||
| ТХХ | ||
| ТГТ | ||
| ТТХ | ||
| ТТТ |
Каких результатов мы хотим?
«Две головы» могут быть в любом порядке: «HHT», «THH» и «HTH» имеют две головы (и один хвост).
Итак, 3 исхода дают «Две головы».
Какова вероятность каждого исхода?
Все исходы равновероятны, а их 8, поэтому вероятность каждого исхода равна 1/8
Значит, вероятность события «Две головы» равна:
| Количество исходов, которые мы хотим | Вероятность каждого исхода | ||
| 3 | × | 1/8 | = 3/8 |
Таким образом, шанс выпадения двух голов равен 3/8
Мы использовали специальные слова:
- Результат : любой результат трех подбрасываний монеты (8 различных вариантов)
- Событие : «Два орла» из трех подбрасываний монеты (это 3 исхода)
3 головки, 2 головки, 1 головка, нет
Вычисления (P означает «Вероятность»):
- P(три головки) = P( ЧЧЧ ) = 1/8
- P(две головки) = P( HHT ) + P( HTH ) + P( THH ) = 1/8 + 1/8 + 1/8 = 3/8
- P(одна головка) = P( HTT ) + P( THT ) + P( TTH ) = 1/8 + 1/8 + 1/8 = 3/8
- P(Ноль головок) = P( TTT ) = 1/8
Мы можем записать это в терминах случайной переменной «X» = «Количество орлов при 3-х подбрасываниях монеты»:
- Р(Х = 3) = 1/8
- Р(Х = 2) = 3/8
- Р(Х = 1) = 3/8
- Р(Х = 0) = 1/8
А вот как это выглядит на графике:
Симметрично!
Создание формулы
А теперь представьте, что нам нужны шансы 5 голов за 9 бросков : чтобы перечислить все 512 исходов, потребуется много времени!
Давайте составим формулу.
Как в нашем предыдущем примере получить значения 1, 3, 3 и 1?
На самом деле они в Треугольнике Паскаля!
Можем ли мы сделать их по формуле?
Конечно можем, и вот оно:
Формула может показаться пугающей, но ее легко использовать. Нам нужны только два числа:
- n = общее количество
- k = номер, который нам нужен
«!» означает «факториал», например 4! = 1×2×3×4 = 24
Примечание: его часто называют «n select k» , и вы можете узнать больше здесь.
Давайте попробуем:
Пример: при 3 бросках, каковы шансы на 2 орла?
У нас есть n=3 и k=2 :
n! к!(н-к)! = 3! 2!(3-2)!
= 3×2×1 2×1 × 1
= 3
Таким образом, есть 3 исхода, которые имеют «2 орла»
(мы это уже знали, но теперь у нас есть формула для это. )
)
Давайте использовать его для более сложного вопроса:
Пример: при 9 бросках, каковы шансы на 5 орлов?
У нас n=9 и k=5 :
n! к!(н-к)! = 9! 5!(9-5)!
= 9×8×7×6×5×4×3×2×1 5×4×3×2×1 × 4×3×2×1
=126
Итак, 126 из исходов выпадет 5 орлов
И за 9 бросков всего 2 9 = 512 исходов, поэтому мы получаем вероятность:
| Число 1 исходов | Вероятность каждого исхода | |||
| 126 | × | 1 512 | = | 126 512 |
Итак:
P(X=5) = 126 512 = 0,24609375
Примерно 25% шанс .
(Легче, чем перечислить их все.)
Предвзятость!
До сих пор шансы на успех или неудачу были равновероятными .
Но что, если монеты смещены (выпадают больше с одной стороны, чем с другой) или выбор не 50/50.
Пример: Вы продаете бутерброды. 70% людей выбирают курицу, остальные выбирают что-то другое.
Какова вероятность того, что 2 сэндвича с курицей будут проданы следующим 3 покупателям?
Это похоже на пример с орлом и решкой, но с 70/30 вместо 50/50.
Нарисуем древовидную диаграмму:
Кейсы «Два цыпленка» выделены.
Все вероятности для «двух цыплят» составляют 0,147 , потому что мы умножаем два 0,7 и одно 0,3 в каждом случае. Другими словами
0,147 = 0,7 х 0,7 х 0,3
Или, используя экспоненты:
= 0,7 2 × 0,3 1
0,7 — это вероятность каждого выбора, который мы хотим, назовем это р
2 — это количество вариантов, которые мы хотим, назовем их k
И у нас есть (пока):
= р к × 0,3 1
0,3 — это вероятность противоположного выбора, поэтому она равна: 1−p
1 — это количество противоположных вариантов, поэтому оно равно: n−k
Что дает нам:
= р к (1-п) (н-к)
Где
- p вероятность каждого выбора, который мы хотим
- k количество вариантов, которые мы хотим
- n общее количество вариантов
Пример: (продолжение)
- p = 0,7 (вероятность курицы)
- k = 2 (выбор курицы)
- n = 3 (всего вариантов)
Получаем:
р к (1-р) (n-k) =0. 7 2 (1-0.7) (3-2)
7 2 (1-0.7) (3-2)
=0.7 2 (0.3) (1)
=0.7 × 0.7 × 0.3
=0.147
то, что мы получили раньше, но теперь используем формулу
Теперь мы знаем, что вероятность каждого исхода равна 0,147
Но надо учесть, что есть три таких способов, как это может произойти: (курица, курица, прочее) или (курица, прочее, курица) или (другое, курица, курица)
Пример: (продолжение)
Общее количество исходов «два цыпленка»:
n! к!(н-к)! = 3! 2!(3-2)!
= 3×2×1 2×1 × 1
=3
.
каждого исхода
Значит, вероятность события «2 человека из 3 выбирают курицу» = 0,441
ОК. Это было много работы для того, что мы уже знали, но теперь у нас есть формула, которую мы можем использовать для более сложных вопросов.
Это было много работы для того, что мы уже знали, но теперь у нас есть формула, которую мы можем использовать для более сложных вопросов.
Пример: Сэм говорит: «70% выбирают курицу, поэтому 7 из следующих 10 покупателей должны выбрать курицу»… каковы шансы, что Сэм прав?
Итак, имеем:
- р = 0,7
- n = 10
- к = 7
И получаем:
р к (1-р) (н-к) =0,7 7 (1-0,7) (10-7)
=0,17 7 9093 (3)
= 0,0022235661
Это вероятность каждого исхода.
И общее количество этих исходов:
n! к!(н-к)! = 10! 7!(10-7)!
= 10×9×8×7×6×5×4×3×2×1 7×6×5×4×3×2×1 × 3×2×1
= 10×9×8 3×2×1
= 120
Получаем:
| Количество исходов, которые мы хотим | Вероятность каждого исхода | |||
| 120 | × | 0,0022235661 | = | 0,266827932 |
Таким образом, вероятность того, что 7 из 10 выберут курицу, составляет всего около 27%
Мораль этой истории: хотя долгосрочное среднее значение составляет 70%, не ожидайте, что 7 из следующие 10.
Собираем вместе
Теперь мы знаем, как посчитать сколько :
н! к!(н-к)!
И вероятность каждого :
стр к (1-п) (н-к)
При перемножении получаем:
Вероятность k из n способов:
P(k из n) = n! к!(н-к)! p k (1-p) (n-k)
Общая биномиальная формула вероятности
Важные примечания:
- Испытания независимые,
- В каждом испытании возможны только два исхода,
- Вероятность «успеха» в каждом испытании постоянна.
Квинконс
Поиграйте с Quincunx (затем прочитайте «Объяснение Quincunx»), чтобы увидеть биномиальное распределение в действии.
Бросьте кубик
Правильная игральная кость подбрасывается четыре раза. Рассчитайте вероятности получения:
- 0 Двойки
- 1 Два
- 2 двойки
- 3 Двойки
- 4 двойки
В этом случае n=4 , p = P(Two) = 1/6
X — это случайная переменная «Количество двоек из четырех бросков».
Подставьте x = от 0 до 4 в формулу:
P(k из n) = n! к!(н-к)! п к (1-п) (н-к)
Вот так (до 4 знаков после запятой):
- Р(Х = 0) = 4! 0!4! × (1/6) 0 (5/6) 4 = 1 × 1 × (5/6) 4 = 0,4823
- Р(Х = 1) = 4! 1!3! × (1/6) 1 (5/6) 3 = 4 × (1/6) × (5/6) 3 = 0,3858
- Р(Х = 2) = 4! 2!2! × (1/6) 2 (5/6) 2 = 6 × (1/6) 2 × (5/6) 2 = 0,1157
- Р(Х = 3) = 4! 3!1! × (1/6) 3 (5/6) 1 = 4 × (1/6) 3 × (5/6) = 0,0154
- Р(Х = 4) = 4! 4!0! × (1/6) 4 (5/6) 0 = 1 × (1/6) 4 × 1 = 0,0008
Резюме: «для 4 бросков существует вероятность 48% не выпадения двойки, 39% вероятность 1 двойки, 12% вероятность 2 двойки, 1,5% вероятность 3 двойки и крошечная 0,08% вероятность всех бросков быть двойкой (но это все еще может случиться!)»
На этот раз график несимметричен:
Не симметрично!
Он искажен, потому что p не 0,5
Спортивные велосипеды
Ваша компания производит спортивные велосипеды. 90% проходят окончательную проверку (а 10% не проходят и требуют исправления).
90% проходят окончательную проверку (а 10% не проходят и требуют исправления).
Каково ожидаемое среднее значение и отклонение от 4 следующих проверок?
Сначала посчитаем все вероятности.
- n = 4,
- p = P(прошел) = 0,9
X — Случайная переменная «Количество проходов из четырех проверок».
Подставьте x = от 0 до 4 в формулу:
P(k из n) = n! к!(н-к)! п к (1-п) (н-к)
Вот так:
- Р(Х = 0) = 4! 0!4! × 0,9 0 0,1 4 = 1 × 1 × 0,0001 = 0,0001
- Р(Х = 1) = 4! 1!3! × 0,9 1 0,1 3 = 4 × 0,9 × 0,001 = 0,0036
- Р(Х = 2) = 4! 2!2! × 0,9 2 0,1 2 = 6 × 0,81 × 0,01 = 0,0486
- Р(Х = 3) = 4! 3!1! × 0,9 3 0,1 1 = 4 × 0,729 × 0,1 = 0,2916
- Р(Х = 4) = 4! 4!0! × 0,9 4 0,1 0 = 1 × 0,6561 × 1 = 0,6561
Резюме: «для 4 следующих велосипедов есть крошечный шанс 0,01% не пройти, 0,36% шанс 1 прохода, 5% шанс 2 прохода, 29% шанс 3 проходов и колоссальный 66% шанс, что все они пройдут проверку. »
»
Среднее значение, дисперсия и стандартное отклонение
Давайте рассчитаем среднее значение, дисперсию и стандартное отклонение для проверок спортивных велосипедов.
Для них есть (относительно) простые формулы. Их немного трудно доказать, но они работают!
Среднее или «ожидаемое значение»:
мк = np
Для спортивных велосипедов:
μ = 4 × 0,9 = 3,6
Таким образом, мы можем ожидать, что 3,6 велосипеда (из 4) пройдут проверку.
Действительно имеет смысл… Шанс 0,9 для каждого велосипеда умножить на 4 велосипеда равно 3,6
Формула дисперсии:
Дисперсия: σ 2 = np(1-p)
Стандартное отклонение равно квадратному корню из дисперсии:
σ = √(np(1-p))
Для спортивных мотоциклов:
Отклонение: σ 2 = 4 × 0,9 × 0,1 = 0,36
Стандартное отклонение:
σ = √(0,36) = 0,6
Примечание: мы также можем рассчитать их вручную, составив такую таблицу:
| X | П(Х) | Х × Р(Х) | Х 2 × Р(Х) |
| 0 | 0,0001 | 0 | 0 |
| 1 | 0,0036 | 0,0036 | 0,0036 |
| 2 | 0,0486 | 0,0972 | 0,1944 |
| 3 | 0,2916 | 0,8748 | 2,6244 |
| 4 | 0,6561 | 2,6244 | 10. 4976 4976 |
| СУММА: | 3,6 | 13,32 |
Среднее значение равно сумме (X × P(X)) :
μ = 3,6
Дисперсия равна сумме (X 2 9072 × P008) минус 9 Среднее 2 :
Дисперсия: σ 2 = 13,32 − 3,6 2 = 0,36
Стандартное отклонение:
σ = √(0,36) = 0,6
И мы получили те же результаты, что и раньше (ура!)
Резюме
8815, 8816, 8820, 8821, 8828, 8829, 8609, 8610, 8612, 8613, 8614, 8615
Треугольник Паскаля
Одной из самых интересных числовых моделей является треугольник Паскаля (названный в честь Блеза Паскаля , известного французского математика и философа).
Чтобы построить треугольник, начните с «1» вверху, затем продолжайте размещать числа под ним в виде треугольника.
Каждое число представляет собой сложенные вместе числа, находящиеся непосредственно над ним.
(Здесь я подчеркнул, что 1+3 = 4)
Узоры внутри треугольника
Диагонали
Первая диагональ это, конечно же, просто «1»
На следующей диагонали находятся Счетные числа (1,2,3 и т.д.).
Третья диагональ имеет треугольные числа
(Четвертая диагональ, не выделенная, имеет четырехгранные числа.)
Симметричный
Треугольник также симметричен. Числа на левой стороне имеют одинаковые совпадающие числа на правой стороне, как зеркальное отражение.
Горизонтальные суммы
Что вы заметили в горизонтальных суммах?
Есть образец?
Они удваивают каждый раз (степень двойки).
Экспоненты числа 11
Каждая строка также представляет собой степени (показатели) числа 11:
- 11 0 =1 (первая строка просто «1»)
- 11 1 =11 (вторая строка «1» и «1»)
- 11 2 =121 (третья строка «1», «2», «1»)
- и т.
 д.!
д.!
Но что происходит с 11 5 ? Простой! Цифры просто перекрываются, вот так:
То же самое происходит с 11 6 и т. д.
Квадраты
Для второй диагонали квадрат числа равен сумме чисел рядом с ним и под обоими из них.
Примеры:
- 3 2 = 3 + 6 = 9,
- 4 2 = 6 + 10 = 16,
- 5 2 = 10 + 15 = 25,
- …
Есть и веская причина… ты можешь подумать? (Подсказка: 4 2 =6+10, 6=3+2+1 и 10=4+3+2+1)
Последовательность Фибоначчи
Попробуйте следующее: создайте фигуру, двигаясь вверх и вниз, затем сложите значения (как показано на рисунке)… вы получите последовательность Фибоначчи.
(Последовательность Фибоначчи начинается с «0, 1», а затем продолжается добавлением двух предыдущих чисел, например, 3+5=8, затем 5+8=13 и т. д.)
д.)
Шансы и четы
Если мы раскрасим нечетные и четные числа, мы получим узор, аналогичный треугольнику Серпинского
Пути
Каждая запись также содержит число различных путей сверху вниз.
Пример: есть только один путь сверху вниз к любой «1»
И мы видим, что есть 2 разных пути к «2»
То же самое вверх, есть 3 разных пути от 3:
Ваша очередь, посмотрите, сможете ли вы найти все пути вниз к «6»:
Использование треугольника Паскаля
Орел и решка
Треугольник Паскаля показывает нам, сколько способов может сочетаться орел и решка. Затем это может показать нам вероятность любой комбинации.
Например, если вы подбросите монету три раза, только одна комбинация даст три орла (HHH), но есть три комбинации, которые дадут два орла и одну решку (HHT, HTH, THH), а также три комбинации, которые дадут одна голова и две решки (HTT, THT, TTH) и одна для всех решек (TTT). Это паттерн «1,3,3,1» в треугольнике Паскаля.
Это паттерн «1,3,3,1» в треугольнике Паскаля.
| Подбрасывает | Возможные результаты (сгруппированные) | Треугольник Паскаля |
|---|---|---|
| 1 | Х Т | 1, 1 |
| 2 | HH HT TH TT | 1, 2, 1 |
| 3 | HHH HHT, HTH, THH HTT, THT, TTH TTT | 1, 3, 3, 1 |
| 4 | HHHH HHHT, HHTH, HTHH, THHH HHTT, HTHT, HTTH, THHT, THTH, TTHH HTTT, THTT, TTHT, TTTH TTTT | 1, 4, 6, 4, 1 |
. .. и т. д. … .. и т. д. … |
Пример. Какова вероятность того, что при 4 подбрасываниях монеты выпадет ровно два орла?
Существует 1+4+6+4+1 = 16 (или 2 4 =16) возможных результатов, и 6 из них дают ровно два орла. Таким образом, вероятность равна 6/16, или 37,5%
.Комбинации
Треугольник также показывает нам, сколько комбинаций объектов возможно.
Пример: У вас есть 16 шаров для пула. Сколькими способами можно выбрать только 3 из них (игнорируя порядок их выбора)?
Ответ: спуститься к началу 16 ряда (верхний ряд 0), а потом по 3 местам (первое место 0) и значение там ваш ответ, 560 .
Вот выдержка из строки 16:
1 14 91 364 ... 1 15 105 455 1365 ... 1 16 120 560 1820 4368 ...
Формула для любого входа в треугольник
На самом деле существует формула из Комбинаций для определения значения в любом месте треугольника Паскаля:
Это обычно называется «n выбрать k» и пишется так: | н! к!(н-к)! = ( п к ) |
Обозначение: «n выбирает k» также может быть записано как C(n,k) , n C k или n 4 C k 9. 0008
0008
| ! | «!» является «факториалом» и означает умножение ряда убывающих натуральных чисел. Примеры:
|
Таким образом, Треугольник Паскаля также может быть
треугольником «n выбрать k» , подобным этому.
(Обратите внимание, что верхняя строка — это нулевая строка
, а также крайний левый столбец — ноль)
Пример: Строка 4, член 2 в треугольнике Паскаля равен «6» …
… посмотрим, работает ли формула:
( 4 2 ) = 4! 2!(4−2)! = 4! 2!2! = 4×3×2×1 2×1×2×1 = 6
Да, это работает! Попробуйте другое значение для себя.
Это может быть очень полезно… теперь мы можем найти любое значение в Треугольнике Паскаля непосредственно (без вычисления всего треугольника над ним).
Многочлены
Треугольник Паскаля также показывает нам коэффициенты в биномиальном разложении:
| Мощность | Биномиальное разложение | Треугольник Паскаля |
|---|---|---|
| 2 | (х + 1) 2 = 1 х 2 + 2 х + 1 | 1, 2, 1 |
| 3 | (x + 1) 3 = 1 x 3 + 3 x 2 + 3 x + 1 | 1, 3, 3, 1 |
| 4 | (x + 1) 4 = 1 x 4 + 4 x 3 + 6 x 2 + 4 x + 1 9. 0013 0013 | 1, 4, 6, 4, 1 |
| … и т. д. … |
Первые 15 строк
Для справки я включил строки с 0 по 14 треугольника Паскаля
.1
5
10
10
5
1
1
6
15
20
15
6
1
1
7
21
35
35
21
7
1
1
8
28
56
70
56
28
8
1 11
9
36
84
126
126
84
36 9 1
1
10
45
120
210
252
210
120
45
10
21
1
11
55
165
330
462
462
330
165
55
11
1
55
11
1
55
11
1
1
12
66
220
495
792
924
792
495
220
495
220
0006 6612
1
1
13
78
286
715
1287
1716
1716
1287
715
286
78
13
1
1
14
91
364
1001
2002
3003
3432
3003
2002
1001
364
91
14
1
Китайцы знали об этом
Этот рисунок называется «Таблица старого метода семи умножающих квадратов». Просмотреть полное изображение
Просмотреть полное изображение
Это обложка книги Чу Ши-Чие « Ссу Юань Юй Цзянь» (Драгоценное Зеркало Четырех Элементов) , написанной в году нашей эры 1303 (более 700 лет назад и более 300 лет до Паскаля!) , а в книге написано, что треугольник был известен примерно за два с лишним века до этого.
Квинконс
Удивительная маленькая машина, созданная сэром Фрэнсисом Гальтоном, представляет собой треугольник Паскаля, сделанный из колышков. Называется Квинканкс.
Мячи падают на первый стержень, а затем отскакивают к нижней части треугольника, где собираются в маленькие корзины.
Сначала это выглядит совершенно случайным (и это так), но затем мы обнаруживаем, что шары складываются в красивый узор: нормальное распределение.
1297, 2467, 2468, 1298, 8366, 8367, 8368, 8369, 8370, 8371, 8372
Деятельность: Подмножества
Лотереи
Лотерея — это вид азартной игры, в которой люди покупают билеты, а затем выигрывают, если выпадают их номера.
«Много» — это то, что происходит случайно. Возможно, вы слышали, как люди говорят: «давайте решим по жребию» или «это мой жребий».
Правила
В разных лотереях действуют разные правила.
Здесь мы будем использовать обычную лотерею, в которой игрок выбирает 6 разных номеров из 49 .
Пример:
Вы участвуете в лотерее, покупая билет и выбирая шесть номеров.
Вы выбираете: 1, 2, 12, 14, 20 и 21
В субботу проводится лотерея, и выигрышных номеров :
3, 12, 18, 20, 32 и 2 Вы угадали с двумя числами (12 и 20):
- Этого достаточно, чтобы выиграть? №
- Обычно вы должны угадать как минимум три числа , чтобы получить небольшой приз.
- Угадав четыре числа , вы получите больший приз,
- Соответствует пять еще больше.
- Но если вы угадаете ВСЕ ШЕСТЬ чисел, вы можете выиграть миллионы .

Вероятность совпадения со всеми 6 числами составляет 1 к 13 983 816 (рассчитано ниже).
Выбор чисел
Они могут победить.
Числа не знают, что они такое!
Лотерея с такой же вероятностью, что выпадет «1,2,3,4,5,6», как и «9,11,16,23,27,36»
Серьезно!
На самом деле приведенный ниже результат действительно имел место (Florida Fantasy 5, 21 марта 2011 г.):
Вместо чисел они могут быть цветами или символами, и лотерея все равно будет работать:
Так что неважно, какие числа вы выберете, шансы все одинаковы.
Более вероятные числа?
Итак, вы читали, что одни числа выпадают чаще, чем другие? Ну, конечно, они есть, это случайность.
У людей, которые проводят лотереи, есть строгие правила, запрещающие «фальсификацию» результатов. Но случайность иногда может привести к странным результатам.
Например, с помощью The Spinner я сделал 1000 вращений для 10 номеров и получил вот это:
Вау! 7 встречалось 115 раз ,
и 8 только 81 раз.
Значит ли это, что 7 теперь будет встречаться чаще или реже ? На самом деле это ничего не значит, 7 так же вероятно, как и любое другое число, будет выбрано.
Попробуйте сами и посмотрите, какие результаты вы получите.
Популярные номера
Но есть хитрость! У людей есть любимые номера, поэтому, когда выпадают популярные номера, вы делите выигрыш со многими людьми.
День рождения — популярный выбор, поэтому люди чаще выбирают 1-12 и 1-31. Также счастливые числа.
Так что, возможно, вам следует выбрать непопулярных номеров , чтобы, когда вы ДЕЙСТВИТЕЛЬНО выигрывали, вы получали больше денег.
(Предполагается, что в вашей лотерее призы распределяются между победителями.)
Сожаление
Не выбирать одни и те же номера каждую неделю . Это ловушка! Если вы забудете неделю, вы будете беспокоиться, что ваши номера выпадут на , и это вынуждает вас покупать билет каждую неделю (даже если вы очень заняты).
Это ловушка! Если вы забудете неделю, вы будете беспокоиться, что ваши номера выпадут на , и это вынуждает вас покупать билет каждую неделю (даже если вы очень заняты).
Мой совет:
Составьте список из множества непопулярных номеров.
Каждый раз случайным образом выбирать из этого списка.
Синдикаты
«Синдикат» — это группа людей, которые вложили немного денег, чтобы группа могла купить много билетов. Шанс на выигрыш увеличивается, но ваша выплата с каждым разом меньше (потому что вы делитесь).
Синдикаты могут быть забавными, потому что они общительны… способ заводить и поддерживать дружеские отношения. Кроме того, некоторые синдикаты любят тратить небольшие выигрыши на то, чтобы все вместе пообедали.
А выиграть меньшую сумму не так уж и плохо.
Подумайте об этом… выигрыш в десять миллионов действительно изменит вашу жизнь, но и в один миллион она тоже улучшится. Вы можете предпочесть десятикратный шанс выиграть миллион.
Шанс выиграть большой приз
ОК. Каковы шансы, что вы выиграете главный приз?
Шансы на выигрыш все 6 номеров 1 из 13 983 816
Для расчета можно использовать Калькулятор комбинаций и перестановок (используйте n=49 , r=6 , «Нет» для Важен ли порядок? и «Нет» для «Разрешено ли повторение?»)
Фактический расчет таков:
49 С 6 = 49! 43! × 6! = 13983816
Так сколько раз нужно сыграть, чтобы выиграть?
1 неделя
Предположим, вы играете в каждую неделю
Вероятность выигрыша через 1 неделю:
1 13983816 = 0,0000000715…
Таким образом, вероятность того, что не выиграют через 1 неделю, составляет:
1 — 1 13983816 = 0,9999999285…
50 лет
Допустим, вы играете 50 лет, это 2600 недель.
Вероятность того, что не выиграет за 2600 недель, составляет:
(1 – 1 13983816 ) 2600 = 0,999814…
Это означает Вероятность выигрыша (через 50 лет): 1 − 0,999814… = 0,000186…
Еще только около 0,02%
И ты бы потратил тысячи на этот маленький шанс.
За эти деньги вы могли хорошо отдохнуть.
НО это забавно думать: «Я могу выиграть на этой неделе!»
Просто пусть это будет забавным занятием, хорошо?
Ваша очередь
Теперь ваша очередь:
- Узнайте правила выигрыша в лотерею в вашем регионе.
- Сколько номеров вам нужно выбрать и из скольких номеров вы выбираете?
- Рассчитайте вероятность выигрыша в любую неделю.
- Рассчитайте вероятность выигрыша, если играть каждую неделю в течение 50 лет.
- Сколько денег вы бы сэкономили, не играя? Что можно купить на эти деньги?
Простые перестановки и комбинации – BetterExplained
Я всегда путал «перестановку» и «комбинацию» — какая из них какая?
Вот простой способ запомнить: перестановка звучит сложно , не так ли? И это. В перестановках важна каждая мелочь. Алиса, Боб и Чарли отличаются от Чарли, Боба и Алисы (вставьте сюда имена ваших друзей).
В перестановках важна каждая мелочь. Алиса, Боб и Чарли отличаются от Чарли, Боба и Алисы (вставьте сюда имена ваших друзей).
Комбинации, с другой стороны, довольно просты. Детали не имеют значения. Алиса, Боб и Чарли такие же, как Чарли, Боб и Алиса.
Перестановки для списков (порядок имеет значение), а комбинации для групп (порядок не имеет значения).
Вы знаете, «кодовый замок» действительно должен называться «замком перестановки». Порядок, в котором вы ставите числа, имеет значение.
Настоящий «кодовый замок» будет принимать как 10-17-23, так и 23-17-10 как правильные.
Перестановки: Волосатые детали
Начнем с перестановок, или всех возможных способов что-то сделать. Мы используем модный термин «перестановка», поэтому мы позаботимся о каждой детали, включая порядок каждого элемента. Допустим, у нас есть 8 человек:
Допустим, у нас есть 8 человек:
1: Алиса 2: Боб 3: Чарли 4: Дэвид 5: Ева 6: Фрэнк 7: Джордж 8: Горацио
Сколькими способами мы можем присудить 1-е, 2-е и 3-е место среди восьми участников? (Золото / Серебро / Бронза)
Мы собираемся использовать перестановки, поскольку порядок, в котором мы раздаем эти медали, имеет значение. Вот как это выглядит:
- Золотая медаль: 8 вариантов: A B C D E F G H (умно, как я сопоставил имена с буквами, а?). Допустим, А выигрывает золото.
- Серебряная медаль: 7 вариантов: B C D E F G H. Допустим, B выиграет серебро.
- Бронзовая медаль: 6 вариантов: C D E F G H. Скажем… C выигрывает бронзу.
Мы выбрали определенных людей, чтобы выиграть, но детали не имеют значения: у нас было сначала 8 вариантов, затем 7, затем 6. Общее количество вариантов было 8 $ * 7 * 6 = 336 $.
Давайте посмотрим на детали. Пришлось заказывать 3 человека из 8. Для этого мы начинали со всех вариантов (8) потом забирали их по одному (7, потом 6) пока не кончились медали.
Мы знаем, что факториал:
К сожалению, это слишком много! Мы хотим только $8 * 7 * 6$. Как мы можем «остановить» факториал на 5?
Вот где перестановки становятся крутыми: обратите внимание, как мы хотим избавиться от $5 * 4 * 3 * 2 * 1$. Какое другое название для этого? 5 факториал!
Итак, если мы сделаем 8!/5! получаем:
А почему мы использовали цифру 5? Потому что она осталась после того, как мы взяли 3 медали из 8. Таким образом, лучше записать это так:
, где 8!/(8-3)! — это просто причудливый способ сказать: «Используйте первые 3 числа из 8!». Если у нас есть 9Всего 0319 n элементов и вы хотите выбрать k в определенном порядке, мы получаем:
И это причудливая формула перестановки: У вас есть n элементов и вы хотите найти количество способов k элементов можно заказать:
Комбинации, Хо!
Комбинации несложные. Порядок не имеет значения. Вы можете смешать это, и это будет выглядеть так же. Допустим, я скряга и не могу позволить себе отдельные золотые, серебряные и бронзовые медали. На самом деле, я могу позволить себе только пустые жестяные банки.
Порядок не имеет значения. Вы можете смешать это, и это будет выглядеть так же. Допустим, я скряга и не могу позволить себе отдельные золотые, серебряные и бронзовые медали. На самом деле, я могу позволить себе только пустые жестяные банки.
Сколькими способами я могу раздать 3 консервные банки 8 людям?
Ну, в данном случае порядок, в котором мы выбираем людей, не имеет значения. Если я даю банку Алисе, Бобу, а затем Чарли, это то же самое, что дать Чарли, Алисе, а затем Бобу. В любом случае, они одинаково разочарованы.
Это поднимает интересный момент — у нас есть некоторые излишества. Элис Боб Чарли = Чарли Боб Элис. На минутку давайте просто выясним, сколькими способами мы можем переставить 3 человек.
Итак, у нас есть 3 варианта для первого человека, 2 для второго и только 1 для последнего. Итак, у нас есть $3 * 2 * 1 $ способов переставить 3 человек.
Минуточку… это немного похоже на перестановку! Ты обманул меня!
Действительно. Если у вас есть N человек, и вы хотите знать, сколько аранжировок существует для 90 319 всех 90 320 из них, это просто N факториал или N!
Итак, если у нас есть 3 жестяных банки для раздачи, их будет 3! или 6 вариантов для каждого выбора, который мы выбираем. Если мы хотим выяснить, сколько комбинаций у нас есть, мы просто создаем все перестановки и делим на все избыточности . В нашем случае мы получаем 336 перестановок (сверху), делим на 6 избыточностей для каждой перестановки и получаем 336/6 = 56,9.0012
Если мы хотим выяснить, сколько комбинаций у нас есть, мы просто создаем все перестановки и делим на все избыточности . В нашем случае мы получаем 336 перестановок (сверху), делим на 6 избыточностей для каждой перестановки и получаем 336/6 = 56,9.0012
Общая формула:
, что означает «Найдите все способы выбрать k людей из n и разделите на k! варианты». Записав это, мы получим нашу формулу комбинации , или количество способов объединить k элементов из набора n:
Иногда C(n,k) записывается как: биномиальный коэффициент.
Несколько примеров
Вот несколько примеров комбинаций (порядок не имеет значения) из перестановок (порядок имеет значение).
Комбинация: Выбор команды из 3 человек из группы 10. $C(10,3) = 10!/(7! * 3!) = 10 * 9 * 8 / (3 * 2 * 1) = 120$.
Перестановка: выбор президента, вице-президента и мальчика-водителя из группы из 10 человек. $P(10,3) = 10!/7! = 10 * 9 * 8 = 720$.

Комбинация: выбор 3 десертов из меню из 10. C(10,3) = 120.
Перестановка: Перечислите 3 ваших любимых десерта по порядку из меню из 10. P(10,3) = 720.
Не запоминайте формулы, поймите, почему они работают. Комбинации звучат проще, чем перестановки, и это так. У вас меньше комбинаций, чем перестановок.
Другие сообщения из этой серии
- Простые перестановки и комбинации
- Навигация по сетке с использованием комбинаций и перестановок
- Как понимать комбинации с помощью умножения
- Почему мы умножаем комбинации?
Мир математики – Mathigon
Введение
Леонард Эйлер (1707 – 1783)
Комбинаторика — это раздел математики, которому около считает — и мы обнаружим много интересных примеров «вещей», которые можно считать.
Первые комбинаторные задачи изучались древнеиндийскими, арабскими и греческими математиками. Интерес к этому предмету возрос в 19-м и 20-м веках вместе с развитием теории графов и таких проблем, как теорема о четырех цветах. Некоторые из ведущих математиков включают Блеза Паскаля (1623–1662), Якоба Бернулли (1654–1705) и Леонарда Эйлера (1707–1783).
Комбинаторика имеет множество приложений в других областях математики, включая теорию графов, кодирование и криптографию, а также вероятность.
Факториалы
Комбинаторикаможет помочь нам подсчитать количество порядков , в которых что-то может произойти. Рассмотрим следующий пример:
В классе стоят V.CombA1 учеников и V.CombA1 стульев, стоящих в ряд. В скольких различных порядках ученики могут сесть на эти стулья?
Давайте перечислим возможности – в этом примере V.CombA1 разных учеников представлены V. CombA1 разных цветов стульев.
CombA1 разных цветов стульев.
Есть {2: 2, 3: 6, 4: 24, 5: 120}[V.CombA1] различных возможных порядков. Обратите внимание, что количество возможных заказов очень быстро увеличивается по мере увеличения числа учеников. С 6 учениками у нас есть 720 различных возможностей, и перечислить их все становится нецелесообразно. Вместо этого нам нужна простая формула, которая говорит нам, сколько заказов на n человек сидят на n стульях. Тогда мы можем просто заменить 3, 4 или любое другое число на n , чтобы получить правильный ответ.
Предположим, у нас есть V.CombB1 стульев, и мы хотим разместить V.CombB1==1?’один ученик’:V.CombB1==2?’два ученика’:V.CombB1==3?’три ученика. ‘:V.CombB1==4?’четыре ученика’:V. CombB1==5?’пять учеников’:V.CombB1==6?’шесть учеников’:’семь учеников’ на них. { 7: ‘На первый стул могут сесть 7 учеников. Тогда есть 6 учеников, которые могут сесть на второй стул. Есть 5 вариантов для третьего стула, 4 варианта для четвертого стула, 3 варианта для пятого стула, 2 варианта для шестого стула и только один вариант для последнего стула.’,
6: «На первый стул могут сесть 6 учеников. Тогда есть 5 учеников, которые могут сесть на второй стул. Есть 4 варианта для третьего стула, 3 варианта для четвертого стула, 2 варианта для пятого стула и только один вариант для последнего стула.’,
5: «На первый стул могут сесть 5 учеников. Тогда есть 4 ученика, которые могут сесть на второй стул. Есть 3 варианта выбора третьего стула, 2 варианта выбора четвертого стула и только один вариант выбора последнего стула.’,
4: «На первый стул могут сесть 4 ученика. Тогда есть 3 ученика, которые могут сесть на второй стул. Есть 2 варианта выбора третьего стула и только один вариант выбора последнего стула.
CombB1==5?’пять учеников’:V.CombB1==6?’шесть учеников’:’семь учеников’ на них. { 7: ‘На первый стул могут сесть 7 учеников. Тогда есть 6 учеников, которые могут сесть на второй стул. Есть 5 вариантов для третьего стула, 4 варианта для четвертого стула, 3 варианта для пятого стула, 2 варианта для шестого стула и только один вариант для последнего стула.’,
6: «На первый стул могут сесть 6 учеников. Тогда есть 5 учеников, которые могут сесть на второй стул. Есть 4 варианта для третьего стула, 3 варианта для четвертого стула, 2 варианта для пятого стула и только один вариант для последнего стула.’,
5: «На первый стул могут сесть 5 учеников. Тогда есть 4 ученика, которые могут сесть на второй стул. Есть 3 варианта выбора третьего стула, 2 варианта выбора четвертого стула и только один вариант выбора последнего стула.’,
4: «На первый стул могут сесть 4 ученика. Тогда есть 3 ученика, которые могут сесть на второй стул. Есть 2 варианта выбора третьего стула и только один вариант выбора последнего стула. ‘,
3: «На первый стул могут сесть 3 ученика. Затем есть 2 ученика, которые могут сесть на второй стул. Наконец, на третьем стуле остался только один ученик.’,
2: «Есть 2 ученика, которые могут сесть на первый стул. Далее на втором стуле остается только один ученик.’,
1: «Это только один вариант для одного стула».}[V.CombB1] Всего
‘,
3: «На первый стул могут сесть 3 ученика. Затем есть 2 ученика, которые могут сесть на второй стул. Наконец, на третьем стуле остался только один ученик.’,
2: «Есть 2 ученика, которые могут сесть на первый стул. Далее на втором стуле остается только один ученик.’,
1: «Это только один вариант для одного стула».}[V.CombB1] Всего
возможностей. Для упрощения записи математики используют «!» называется факториалом. Например, 5! («пять факториалов») — это то же самое, что 5 × 4 × 3 × 2 × 1. Выше мы только что показали, что существует n ! возможности заказать n предметов.
Упражнение
Решение
Сколькими способами 23 ребенка могут сесть на 23 стула на уроке математики? Если у вас 4 урока в неделю, а в году 52 недели, сколько лет потребуется, чтобы освоить все различные возможности? Примечание. Возраст Вселенной составляет около 14 миллиардов лет.
Для 23 детей, чтобы сидеть на 23 стульях есть 23! = 25 852 016 738 884 800 000 000 возможностей (это число слишком велико для отображения на экране калькулятора). Перепробование всех возможностей заняло бы
Перепробование всех возможностей заняло бы
23,4 × 52 = 124 288 542 000 000 000 000 лет.
Это почти в 10 миллионов раз больше текущего возраста Вселенной!
Перестановки
Приведенный выше метод требовал, чтобы у нас было столько учеников, сколько стульев для сидения. Но что делать, если стульев не хватает?
Сколько существует различных возможностей для любого Math.min(V.CombC1,V.CombC2) из V.CombC1 учеников сесть на Math.min(V.CombC1,V.CombC2) стульев? Обратите внимание, что Math.max(0,V.CombC1-V.CombC2) останется в силе, что нам не нужно включать при перечислении возможностей.
Давайте начнем снова, перечислив все возможности:
min(V.CombC1,V.CombC2))==1)?29:(V.CombC1==2&&(Math.min(V.CombC1,V.CombC2))==1)?92:(V.CombC1==2&&(Math.min(V.CombC1,V.CombC2))==2)?156:(V.CombC1==3&&(Math.min(V.CombC1,V.CombC2))==1)?154:(V.CombC1==3&&(Math.min(V.CombC1,V.CombC2))==2)?250:(V.CombC1==3&&(Math.min(V.CombC1,V.CombC2))==3)?336:(V.CombC1==4&&(Math.min(V.CombC1,V.CombC2))==1)?216:(V.CombC1==4&&(Math.min(V.CombC1,V.CombC2))==2)?480:(V.CombC1==4&&(Math.min(V.CombC1,V.CombC2))==3)?532:586)»>
Чтобы найти простую формулу, подобную приведенной выше, мы можем думать об этом очень похожим образом. ‘Есть ученики ‘+V.CombC1+’, которые могли сесть на первый стул. ‘+
(((Math.min(V.CombC1,V.CombC2))==2||(Math.min(V.CombC1,V.CombC2))==3||(Math.min(V.CombC1,V .CombC2))==4)?’Тогда есть ‘+(V.CombC1-1)+’ учеников, которые могли бы сесть на второй стул. ‘:»)+
(((Math.min(V.CombC1,V.CombC2))==3||(Math.min(V.CombC1,V.CombC2))==4)?’Тогда есть ‘+(V.CombC1 -2)+’ ученики, которые могли сесть на третий стул. ‘:»)+
(((Math.min(V.CombC1,V.CombC2))==4)?’На последнем стуле остался один ученик. ‘:»)+
((V.CombC1-(Math.min(V.CombC1,V.CombC2))==1||V.CombC1-(Math.min(V.CombC1,V.CombC2))==2||V. CombC1-(Math.min(V.CombC1,V.CombC2))==3)?’Нас не волнуют оставшиеся ‘+(V.CombC1-V.CombC2)+’ дочерние элементы, оставшиеся стоять. ‘:’ ‘) Всего
‘:»)+
(((Math.min(V.CombC1,V.CombC2))==4)?’На последнем стуле остался один ученик. ‘:»)+
((V.CombC1-(Math.min(V.CombC1,V.CombC2))==1||V.CombC1-(Math.min(V.CombC1,V.CombC2))==2||V. CombC1-(Math.min(V.CombC1,V.CombC2))==3)?’Нас не волнуют оставшиеся ‘+(V.CombC1-V.CombC2)+’ дочерние элементы, оставшиеся стоять. ‘:’ ‘) Всего
возможностей. Опять же, мы должны подумать об обобщении этого. Мы начинаем, как и с факториалов, но останавливаемся до того, как достигнем 1. На самом деле мы останавливаемся, как только достигаем количества студентов без стульев. При размещении 7 студентов на 3 стульев их становится
7 × 6 × 5 = 7 × 6 × 5 × 4 × 3 × 2 × 17 × 6 × 5 × 4 × 3 × 2 × 1 = 7 !4! = 7 !( 7 – 3 )!
возможностей, так как 4 × 3 × 2 × 1 аннулируют друг друга. Опять же, для этого есть более простое обозначение: 7 Р 3 . Если мы хотим разместить n объектов в м позиций, то есть
Если мы хотим разместить n объектов в м позиций, то есть
n P m = n !( n – m )!
возможностей. P означает «перестановки p », так как мы подсчитываем количество перестановок (порядков) объектов. Если m и n такие же, как были в задаче в начале статьи, то имеем
n P n = n !( n – n )! = n !0!.
Чтобы понять это, мы определяем 0! = 1. Теперь n P n = n ! как и следовало ожидать от нашего решения первой проблемы.
Упражнение
Решение
К сожалению, вы не можете вспомнить код своего четырехзначного замка. Вы только знаете, что не использовали ни одну цифру более одного раза. Сколько разных способов нужно попробовать? Что вы можете сказать о безопасности этих замков?
Имеется 10 цифр (0, 1, …, 9), каждая из которых встречается не более одного раза. Количество порядков этих цифр равно 10 P 4 = 5040. Тестирование такого количества комбинаций заняло бы очень много времени, поэтому замки с 4 цифрами очень безопасны.
Количество порядков этих цифр равно 10 P 4 = 5040. Тестирование такого количества комбинаций заняло бы очень много времени, поэтому замки с 4 цифрами очень безопасны.
Комбинации
Перестановки используются, когда вы выбираете объекты и заботитесь об их порядке — например, о порядке детей на стульях. Однако в некоторых задачах вам не важен порядок, и вы просто хотите знать, сколько существует способов выбрать определенное количество объектов из большего набора.
В магазине есть пять разных футболок, которые вам нравятся, красного, синего, зеленого, желтого и черного цветов. К сожалению, у вас есть только достаточно денег, чтобы купить три из них. Сколькими способами можно выбрать три футболки из пяти понравившихся?
Здесь нас не волнует порядок (неважно, покупаем ли мы сначала черную, а затем красную или сначала красную, а затем черную), только количество комбинаций футболок. Возможности
Возможности
, так что всего 10. Если бы мы вычислили 5 P 3 = 60, мы бы дважды посчитали некоторые возможности, как показано в следующей таблице:
С перестановками каждую комбинацию из трех футболок считаем 6 раз, потому что их 3! = 6 способов заказать три футболки. Чтобы получить количество комбинаций из количества перестановок, нам просто нужно разделить на 6. Пишем
5 C 3 = 5 P 33! = 606 = 10,
Здесь C означает « c комбинации». В общем, если мы хотим выбрать r объектов из общего числа n , то есть
n C r = n P r r ! = n ! р ! ( n – r )!
различных комбинаций. Вместо n C r математики часто пишут n C r = ( n r ), как дробь в скобках, но без черты между ними. (Чтобы упростить набор текста, мы продолжим использовать первое встроенное обозначение.)
(Чтобы упростить набор текста, мы продолжим использовать первое встроенное обозначение.)
Упражнения
Решения
(a) В вашем классе 10 детей, но вы можете пригласить только 5 на свой день рождения. Сколько различных комбинаций друзей вы могли бы пригласить? Объясните, следует ли использовать комбинации или перестановки.
(б) На вечеринке 75 человек. Все пожимают всем руку один раз. Как часто в целом пожимают руки? Подсказка: Сколько человек участвует в рукопожатии?
(a) Количество комбинаций друзей, которых вы можете пригласить, равно 10 C 5 = 252. Мы использовали комбинации, потому что не имеет значения в каком порядке мы приглашаем друзей, на каких мы приглашаем.
(b) Вы хотите найти количество всех возможных пар гостей вечеринки. Это просто 75 C 2 = 2775. (Много рукопожатий!)
Комбинаторика и треугольник Паскаля
Давайте посчитаем некоторые значения n C r . Начинаем с 0 C 0. Затем находим 1 C 0 и 1 C 1. Далее 2 C 0, 2 C 1 и 2 C 2. Затем 3 C 2. , 3 C 1, 3 C 2 и 3 C 3. Запишем все эти результаты в таблицу:
Начинаем с 0 C 0. Затем находим 1 C 0 и 1 C 1. Далее 2 C 0, 2 C 1 и 2 C 2. Затем 3 C 2. , 3 C 1, 3 C 2 и 3 C 3. Запишем все эти результаты в таблицу:
| 0 С 0 = 1 | |||||||||||
| 1 С 0 = 1 | 1 С 1 = 1 | ||||||||||
| 2 С 0 = 1 | 2 С 1 = 2 | 2 С 2 = 1 | |||||||||
| 3 С 0 = 1 | 3 С 1 = 3 | 3 С 2 = 3 | 3 С 3 = 1 | ||||||||
| 4 С 0 = 1 | 4 С 1 = 4 | 4 С 2 = 6 | 4 С 3 = 4 | 4 С 4 = 1 | |||||||
| 5 С 0 = 1 | 5 С 1 = 5 | 5 С 2 = 10 | 5 С 3 = 10 | 5 С 4 = 5 | 5 С 5 = 1 | ||||||
Это и есть треугольник Паскаля, который мы исследовали в статье о последовательностях. Его можно легко создать, заметив, что любая ячейка является суммой двух ячеек выше. В треугольнике Паскаля скрыты бесчисленные закономерности и числовые последовательности.
Его можно легко создать, заметив, что любая ячейка является суммой двух ячеек выше. В треугольнике Паскаля скрыты бесчисленные закономерности и числовые последовательности.
Теперь мы также знаем, что r -е число в n -й строке также задается как n C r (но мы всегда должны начинать отсчет с 0, поэтому первая строка или столбец на самом деле является нулевой строкой). Если мы применим то, что мы знаем о построении треугольника Паскаля, к нашим комбинациям, мы получим
.( н р ) + ( п р + 1) знак равно ( n + 1 r + 1) .
Это известно как Личность Паскаля . Вы можете получить его, используя определение n C r в терминах факториалов, или вы можете думать об этом следующим образом:
Мы хотим выбрать r + 1 объектов из набора n + 1 объектов.
Это точно так же, как пометить один объект из n + 1 как X и либо выбрать X плюс r других (из оставшихся n), либо не выбрать X и r + 1 других ( из оставшихся n).
Многие задачи по комбинаторике имеют простое решение, если правильно подумать, и очень сложное решение, если просто попробовать использовать алгебру…
Stars and Bars
Solution
Пример
Зеленщик на рынке хранит большое количество n различных видов фруктов. Сколькими способами можно составить мешок из и фруктов? Обратите внимание, что r может быть меньше, равно или больше, чем n .
Обратите внимание, что при r ≤ n существует n C r способов выбрать по одному фрукту каждого вида. Однако нам также разрешено брать более одного фрукта каждого вида, например, два яблока, одну клубнику и один банан.
Мы можем представить любой допустимый выбор фруктов с помощью цепочки звездочек и полос, как показано в этом примере:
| ★★★ | | | ★★ | | | | | ★★ | | | ★ | |
| 3 типа 1 | 2 типа 2 | 0 типа 3 | 2 типа 4 | 1 типа 5 |
Всего имеется r звездочек (представляющих r фруктов, которые нам разрешено брать) и n – 1 полоска (разделяющих n различных видов фруктов). Получается r + n – всего 1 место. Любой заказ r звездочек и n – 1 бруска соответствует только одному допустимому набору фруктов.
Получается r + n – всего 1 место. Любой заказ r звездочек и n – 1 бруска соответствует только одному допустимому набору фруктов.
Теперь мы можем применить наши комбинаторные инструменты: есть r + n – 1 место, и мы хотим выбрать n – 1 из них в качестве баров (все остальные – звезды). Что есть ровно ( r + n – 1) C ( n – 1) возможности сделать это!
Предположим, есть пять видов фруктов, и мы хотим взять десять штук. Из того, что мы подсчитали выше,
(10 + 5 – 1) C (5 – 1) = 14 C 4 = 24 024
возможностей. Подумайте об этом в следующий раз, когда пойдете за покупками!
Комбинаторика и Вероятность
Комбинаторика имеет множество приложений в теории вероятностей. Вы часто хотите найти вероятность одного конкретного события, и вы можете использовать уравнение
P ( X ) = вероятность того, что произойдет X = количество исходов, при которых произойдет X , общее количество возможных исходов
Вы можете использовать комбинаторику для вычисления «общего количества возможных исходов». Вот пример:
Вот пример:
Четверо детей, которых зовут A, B, C и D, произвольно сидят на четырех стульях. Какова вероятность того, что А сядет на первый стул?
Мы уже показали, что всего есть 24 способа сесть на четыре стула. Если вы вернетесь к нашему решению, вы также обнаружите, что А сидит на первом стуле в шести случаях. Поэтому
P (A сидит на первом стуле) = количество исходов, где A сидит на первом стуле, общее количество возможных исходов = 624 = 14,
Этот ответ был ожидаем, так как каждый из четырех детей с равной вероятностью сядет на первый стул. Но в других случаях все не так однозначно…
Упражнения
Решения
(a) Почтальон должен доставить четыре письма в четыре разных дома на улице. К сожалению, дождь стер адреса, поэтому он просто раздает их случайным образом, по одной букве на дом. Какова вероятность того, что каждый дом получит нужную букву? (☆ Какова вероятность того, что каждый дом получит неправильную букву?)
(b) В лотерее нужно угадать 6 номеров из 49.
