Что такое экспонента: определение, формула, свойства, график
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Математика Алгебра Экспонента: определение, формула, свойства, график
В данной публикации мы рассмотрим, что такое экспонента, как выглядит ее график, приведем формулу, с помощью которой задается экспоненциальная функция, а также перечислим ее основные свойства.
- Определение и формула экспоненты
- График экспоненты
- Свойства экспоненциальной функции
Определение и формула экспоненты
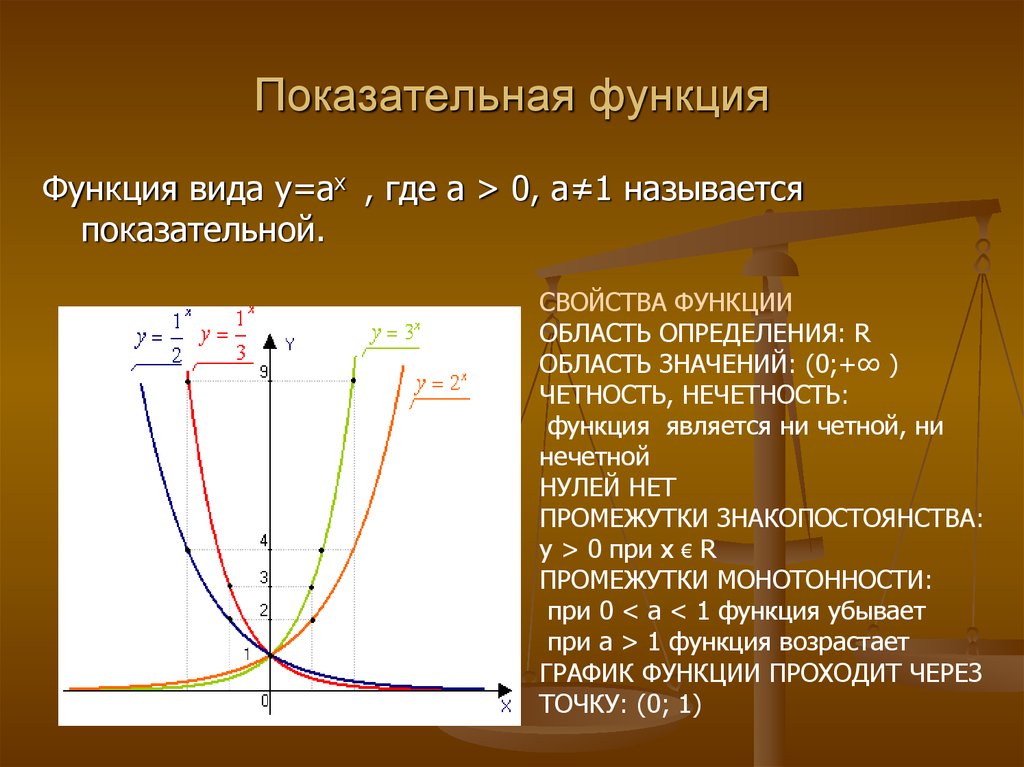
Экспонента – это показательная функция, формула которой выглядит следующим образом:
f (x) = exp(x) = e x
где e – число Эйлера.
Экспоненциальная функция (так часто называют экспоненту) может быть определена:
Через предел (lim):
Через степенной ряд Тейлора:
График экспоненты
Ниже представлен график экспоненциальной функции y = e x.
Как мы видим график (синяя линия) является выпуклым, строго возрастающим, т.е. при увеличении x увеличивается значение y.
Асимптотой является ось абсцисс, т.е. график во II четверти координатной плоскости стремится к оси Ox, но никогда не пересечет и не коснется ее.
Пересечение с осью ординат Oy – в точке (0, 1), так как e0 = 1.
Касательная (зеленая линия) к экспоненте проходит под углом 45 градусов в точке касания.
Свойства экспоненциальной функции
- Экспонента определена для всех x, причем функция везде возрастает, и ее значение всегда больше нуля. То есть:
- область определения: – ∞ < x + ∞;
- область значений: 0 < y < + ∞.
- Обратная к экспоненте функция – это натуральный логарифм (ln x).
- ln e x = x;
- e ln x = x, где x > 0.
- Для экспоненты применимы правила операций с показателями, например: e (a + b) = e a ⋅ e b.
- Производная экспоненты:
- (e x)‘ = e x.
- если вместо x – сложная функция u: (e u)‘ = e u + u‘.
- Интеграл экспоненты: ∫ e x dx = e x + C, где C – константа интегрирования.
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
доказательство, графики, примеры решения задач
Производная экспоненциальной функции
Экспонентой называют показательную функцию со степенным основанием, которое соответствует значению е, то есть такому пределу: \(е=\lim\limits_{n\to \infty} (1+\frac{1}{n})^{n} = 2,718281828459045…\)
В данном случае n допустимо взять из множества натуральных или действительных чисел.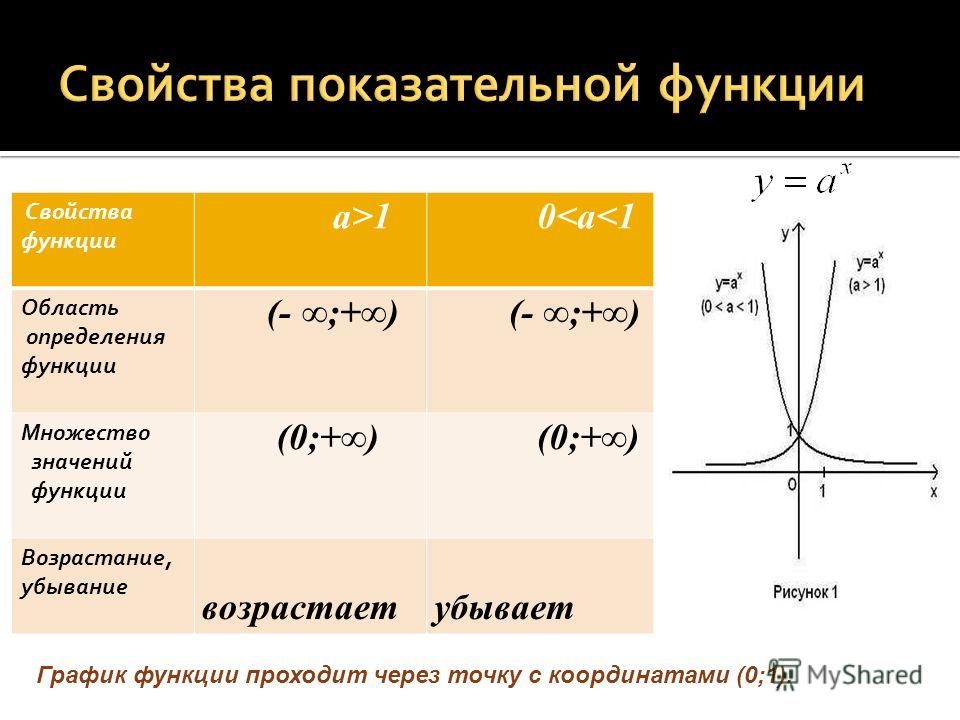
{x}\).
Экспоненциальный график — рост, спад, примеры
LearnPracticeDownload
Экспоненциальный график — это график экспоненциальной функции. Он всегда имеет горизонтальную асимптоту, но не имеет вертикальной асимптоты. График экспоненциальной функции можно построить, нанеся на нее горизонтальную асимптоту, точки пересечения и несколько точек.
Давайте посмотрим, как подробно нарисовать экспоненциальный график, и посмотрим, как будет выглядеть график экспоненциального роста и график экспоненциального затухания.
| 1. | Что такое экспоненциальный график? |
| 2. | График экспоненциальной функции |
| 3. | График экспоненциального роста и график экспоненциального затухания |
| 4. | Часто задаваемые вопросы об экспоненциальном графике |
Что такое экспоненциальный график?
Экспоненциальный график — это кривая, представляющая экспоненциальную функцию.
График экспоненциальной функции
График экспоненциальной функции — это процесс рисования кривой, представляющей ее. Экспоненциальная функция имеет вид f(x) = a x , где a – константа, а a > 0. Значение a x никогда не равно 0 ни при каком значении x, поэтому y = 0 равно горизонтальная асимптота показательной функции f(x) = a x . Горизонтальная асимптота играет важную роль в процессе построения графика показательной функции.
Горизонтальная асимптота экспоненциальной функции есть не что иное, как ее сдвиг по вертикали (т.е. это число, которое прибавляется к x ). Например, горизонтальная асимптота f(x) = 2 x равна y = 0, а горизонтальная асимптота g(x) = 2 x — 3 равна y = -3. Вот шаги, чтобы нарисовать экспоненциальный график самым простым способом.
- Шаг 1: Найдите горизонтальную асимптоту.
- Шаг 2: Найдите точку пересечения с осью y, подставив x = 0 в функцию. Каждый экспоненциальный график имеет горизонтальную асимптоту.
- Шаг 3: Найдите точку пересечения по оси x, подставив y = 0 в функцию. Экспоненциальный график может иметь или не иметь точку пересечения по оси x.
- Шаг 4: Создайте таблицу с двумя столбцами x и y; возьмем несколько случайных чисел для x, скажем -1, 0 и 1; подставьте каждое из этих чисел в функцию, чтобы получить соответствующие значения y.
- Шаг 5: Нанесите на график всю приведенную выше информацию и соедините все точки, полученные выше, кривой, не касаясь, но достигая горизонтальной асимптоты.
Вот пример построения графика экспоненциальной функции.
Пример: Постройте график экспоненциальной функции f(x) = 2 x — 3.
Решение:
Горизонтальная асимптота y = -3.
Для точки пересечения по оси y положим x = 0. Тогда получим y = 2 0 — 3 = 1 — 3 = -2. Таким образом, y-перехват равен (0, -2).
Для пересечения по оси x положим y = 0. Тогда мы получим 0 = 2 x — 3 ⇒ 2 x = 3 ⇒ x = log 2 3 ≈ 1,6. Таким образом, x-перехват равен (1.6, 0).
Теперь создадим таблицу экспоненциальной функции.
| х | г |
|---|---|
| -1 | 2 -1 — 3 = (1/2) — 3 = -2,5 |
| 1 | 2 1 — 3 = 2 — 3 = -1 |
| 2 | 2 2 — 3 = 4 — 3 = 1 |
Давайте построим всю эту информацию, чтобы получить экспоненциальный график.
Здесь график имеет отрицательную точку пересечения оси Y и положительный наклон (возрастающая кривая).
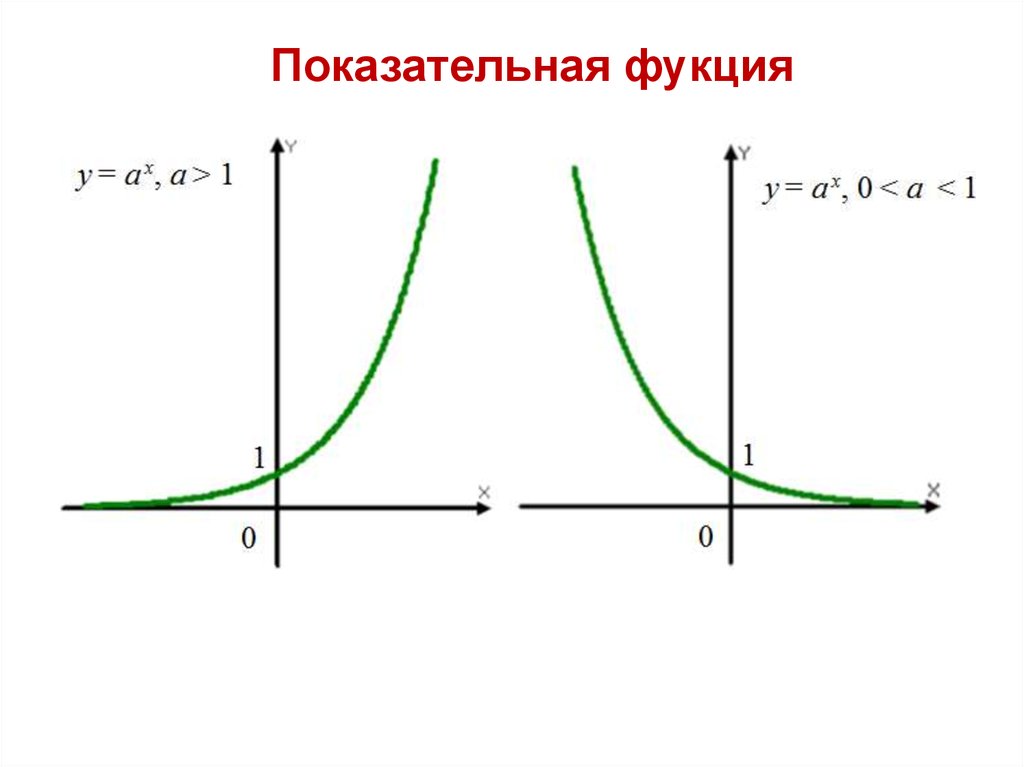
График экспоненциального роста и график экспоненциального затухания
Приведенный выше график является возрастающим (всегда смотрите слева направо) и, следовательно, этот график представляет собой экспоненциальный рост. Обратите внимание, что функция, которая представляет приведенный выше график, равна f(x) = 2
- экспоненциальный график показывает рост при a > 1
- экспоненциальный график показывает затухание, когда 0 < a < 1.
Например,
- f(x) = 2 x показывает экспоненциальный рост при 2 > 1.
- g(x) = 0,5 x показывает экспоненциальное затухание как 0 < 0,5 < 1.
Оба графика показаны на рисунке ниже.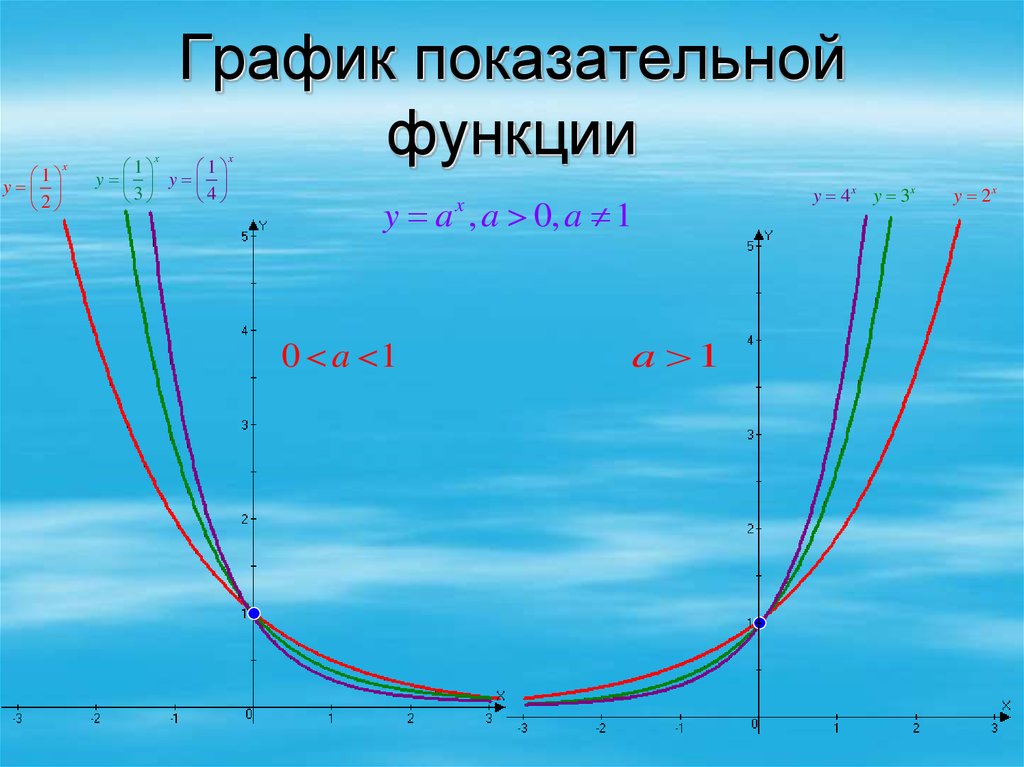
Обратите внимание на некоторые другие случаи.
- Означает ли f(x) = -2 x рост или распад?
Его затухание как g(x) = 2 x представляет собой экспоненциальный рост. - Представляет ли f(x) = 2 -x рост или распад?
Он представляет собой экспоненциальное затухание, поскольку мы можем представить его как f(x) = (2 -1 ) x (по степени степенного свойства показателей) = (1/2) x = 0,5 x . - Представляет ли f(x) = -2 -x рост или распад?
Он представляет собой экспоненциальный рост, поскольку 2 -x представляет собой распад.
Важные замечания по экспоненциальному графику:
- Для построения графика экспоненциальной функции постройте ее горизонтальную асимптоту, точки пересечения и несколько точек на ней.
- f(x) = a x является экспоненциальным ростом, если a > 1, и является экспоненциальным убыванием, когда 0 < a < 1.
- (0, 1) и (1, a) всегда являются двумя точками на f (x) = a x , и они помогают в построении экспоненциального графика.
- Показательная функция никогда не имеет вертикальной асимптоты (поскольку она определена для всех значений x).
☛ Связанные темы:
- Логарифмические функции
- Экспоненциальные уравнения
- Калькулятор экспоненциальной функции
Примеры экспоненциального графика
Пример 1: Каковы горизонтальные асимптоты экспоненциальных графиков следующих экспоненциальных функций? а) f(x) = (1/3) x — 2 + 5 b) g(x) = (-0,5) x + 2 — 8.
Решение:
Вертикальный сдвиг экспоненциальной функции сам по себе дает горизонтальную асимптоту. т. е. мы должны просто смотреть на число, которое добавляется к экспоненциальной части.
а) Горизонтальная асимптота f(x) = (1/3) x — 2 + 5 равно y = 5.
b) Горизонтальная асимптота g(x) = (-0,5) x + 2 — 8 равно у = -8.
Ответ: а) у = 5 б) у = -8.
Пример 2: Объясните процесс построения графика показательной функции f(x) = -6 (1/2) x . Также нарисуйте экспоненциальный график.
Решение:
Мы следуем приведенным ниже шагам для построения графика данной экспоненциальной функции.
Его горизонтальная асимптота равна y = 0.
Для нахождения точки пересечения с y y = -6 (1/2) 0 = -6(1) = -6. Таким образом, его точка пересечения по оси y равна (0, -6).
Для нахождения точки пересечения, 0 = -6 (1/2) х . Но нет x, удовлетворяющего этому уравнению. Так что никакого х-перехвата нет.
Теперь найдем на нем несколько точек.
х г 1 -6 (1/2) 1 = -3 2 -6 (1/2) 2 = -1,5 3 -6 (1/2) 3 = -0,75 Просто нанесите всю информацию, не пересекая и не касаясь горизонтальной асимптоты.
Ответ: Объясняется процесс построения графика экспоненциальной функции, а также рисуется экспоненциальный график.
Пример 3: Каждая из следующих экспоненциальных функций представляет рост или спад? а) f(x) = 3 х — 5 + 7 б) g(x) = 0,5 3x — 2 — 8.
Решение:
В общем случае экспоненциальная функция f(x) = a x демонстрирует рост, если a >
0, и убывание, если 0 < a < 1.а) В функции f(x) = 3 x — 5 + 7, a = 3 > 1. Следовательно, он представляет собой график экспоненциального роста.
b) В функции g(x) = 0,5 3x — 2 — 8, a = 0,5, которая лежит между 0 и 1. Следовательно, она представляет собой график экспоненциального затухания.
Ответ: а) Экспоненциальный рост б) Экспоненциальный спад.
перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по экспоненциальному графику
перейти к слайдуперейти к слайду
Часто задаваемые вопросы об экспоненциальном графике
Что такое экспоненциальный график?
Экспоненциальный график — это график экспоненциальной функции. Он всегда имеет горизонтальную асимптоту, но не имеет вертикальной асимптоты. График экспоненциальной функции — это процесс рисования кривой, представляющей ее.
Как построить график экспоненциальной функции?
Чтобы нарисовать экспоненциальный график , выполните шаги, указанные ниже:
- Найдите горизонтальную асимптоту.
- Найдите точку пересечения по оси Y и по оси X (если есть).
- Найдите на нем несколько точек, взяв несколько случайных значений x.
- Нанесите их все на график и соедините все точки.
Как бы выглядел экспоненциальный график роста?
График экспоненциального роста всегда увеличивается, если рассматривать его слева направо. т. е. всегда имеет положительный наклон. Экспоненциальная функция f(x) = a x показывает рост, если a > 1.
Каковы асимптоты экспоненциального графика?
Экспоненциальный график имеет горизонтальную асимптоту (HA). HA экспоненциальной функции f(x) = a x + b равно y = b. Он не имеет вертикальной асимптоты.
Является ли экспоненциальный график параболой?
Нет, парабола — это уравнение квадратичной функции. График экспоненциальной функции либо начинается медленно и быстро растет, либо наоборот.
В чем разница между экспоненциальным графиком и логарифмическим графиком?
Математически экспоненциальная функция и логарифмическая функция являются обратными друг другу. Таким образом, их графики являются отражением друг друга относительно прямой y = x.
Как бы выглядел экспоненциальный график распада?
График экспоненциального распада всегда уменьшается, если мы видим его слева направо.
т. е. всегда имеет отрицательный наклон. Экспоненциальная функция f(x) = a x показывает затухание, если 0 < a < 1.
Скачать БЕСПЛАТНО учебные материалы
ЛИСТКИ
Рабочие листы по математике и
визуальные учебные программы
Exponents by Amanda
1
Мы видим, что график с основанием e больше похож на график с основанием 3, чем на график с основанием 2. Теперь, когда мы увидели родительский график и то, как он выглядит по сравнению с другими экспоненциальными функциями, давайте рассмотрим свойства экспоненциального графика. с основанием е. Сначала посмотрим, как меняется график в зависимости от значения константы «с» в уравнении. Из наших знаний по алгебре мы могли бы предсказать, что график будет сдвигаться вверх на единицу при каждом увеличении c. «Сдвинут вверх» относится более непосредственно к точке пересечения по оси y, поэтому форма графика, сохраняемая точкой пересечения с осью y, будет увеличиваться по мере увеличения c.
Поскольку родительский граф имеет точку пересечения по оси y, равную 1, мы можем предположить, что точка пересечения по оси y будет равна c+1. Графики ниже подтверждают наши прогнозы. Однако асимптота увеличивается на 1 при каждом увеличении c на 1. Родительский граф или когда c=0 имеет асимптоту y=0, но когда c=1, асимптота равна y=1. Это связано с тем, что значение y=0 может быть получено только тогда, когда a=0 и c=0. В противном случае график никогда не будет пересекать ось X.
Теперь, вернувшись к нашему уравнению, мы видим, что точка пересечения с осью y, когда коэффициент при e равен 1, всегда будет равна c+1. Y-пересечение происходит из уравнения, когда x = 0. Мы имеем дело с экспоненциальным уравнением, где все в степени 0 равно 1. Так почему же тогда коэффициент при e должен быть равен 1? Давайте посмотрим на график, когда a=2 и c=1.
Отрезок по оси y увеличился на 1 по сравнению с нашим предыдущим уравнением, где a=1.
Почему и как это могло быть? Как было сказано ранее, все в степени 0 равно 1. Таким образом, когда мы ищем точку пересечения по оси y в этом экспоненциальном уравнении, мы на самом деле смотрим на уравнение y=a(1)+c, где y представляет нашу точку пересечения по оси y. , a представляет собой коэффициент e, а c представляет константу уравнения. На графике выше точка пересечения с осью y выглядит равной 3. Давайте используем наше новое уравнение для проверки: y=2(1)+1=3. 3 действительно является точкой пересечения с осью y, и мы видим, что уравнение y=a+c порождает эту точку пересечения с осью y. Но изменяет ли значение «а» форму графика или оно влияет только на y-пересечение графика? 9x)+c, следовательно, y=c. Но как быть, когда a<0?
Мы можем видеть, что обратное действительно имеет место, когда c<0. Принятие противоположного «с» отражает график по оси x, но асимптота y = 0 не затрагивается. В приведенных выше случаях c = 0, но случай, когда c не равен нулю, был бы еще одним замечательным исследованием, которое могли бы попробовать как ученики, так и учителя, но для общих случаев мы рассмотрим константы отдельно.