x=\frac{-8±\sqrt{64-4\left(-2\right)\left(-y-6\right)}}{2\left(-2\right)}
Возведите 8 в квадрат.
x=\frac{-8±\sqrt{64+8\left(-y-6\right)}}{2\left(-2\right)}
Умножьте -4 на -2.
x=\frac{-8±\sqrt{64-8y-48}}{2\left(-2\right)}
Умножьте 8 на -6-y.
x=\frac{-8±\sqrt{16-8y}}{2\left(-2\right)}
Прибавьте 64 к -48-8y.
x=\frac{-8±2\sqrt{4-2y}}{2\left(-2\right)}
Извлеките квадратный корень из 16-8y.
x=\frac{-8±2\sqrt{4-2y}}{-4}
Умножьте 2 на -2.
x=\frac{2\sqrt{4-2y}-8}{-4}
Решите уравнение x=\frac{-8±2\sqrt{4-2y}}{-4} при условии, что ± — плюс. Прибавьте -8 к 2\sqrt{4-2y}.
x=-\frac{\sqrt{4-2y}}{2}+2
Разделите -8+2\sqrt{4-2y} на -4.
x=\frac{-2\sqrt{4-2y}-8}{-4}
Решите уравнение x=\frac{-8±2\sqrt{4-2y}}{-4} при условии, что ± — минус. Вычтите 2\sqrt{4-2y} из -8.
x=\frac{\sqrt{4-2y}}{2}+2
Разделите -8-2\sqrt{4-2y} на -4.
x=-\frac{\sqrt{4-2y}}{2}+2 x=\frac{\sqrt{4-2y}}{2}+2
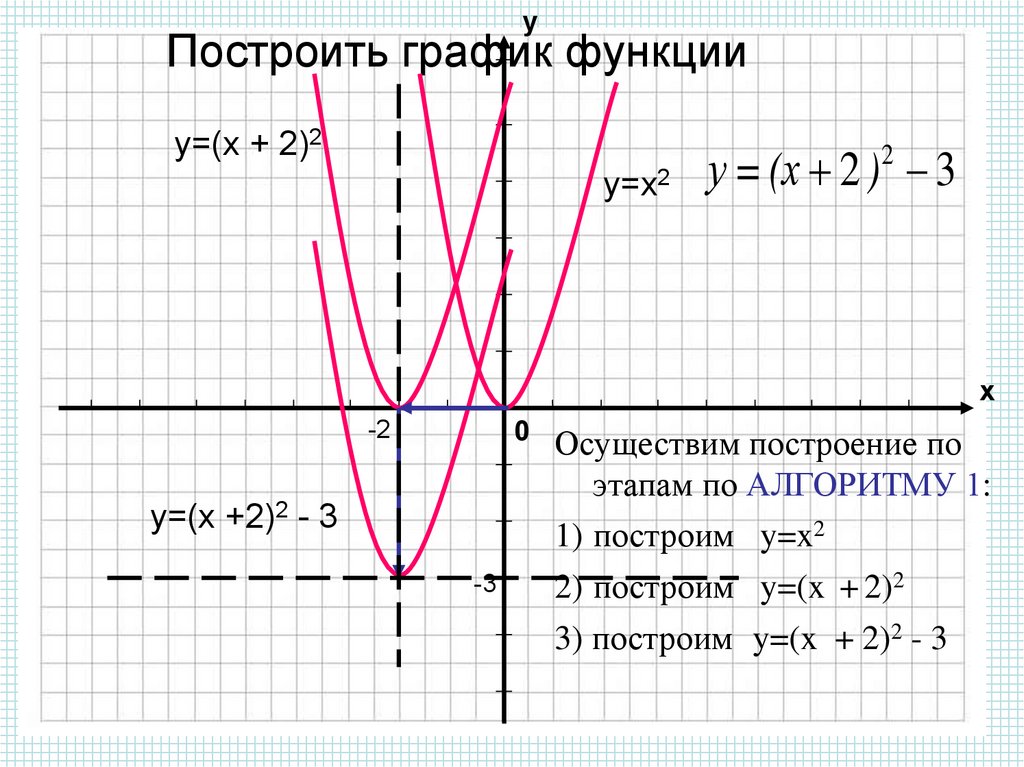
Уравнение решено.
{2}+2 x-3}
Преобразования функций: Сжатие и растяжение
Переводы Отражения Перемещение точек Работа в обратном направлении
Purplemath
Есть еще два преобразования, но их труднее «увидеть» с какой-либо степенью точности.
Первым из этих преобразований является умножение на всю функцию. Чтобы увидеть, как это выглядит, сравните графики 2 × f ( x ) = 2 x 2 , f ( x ) = x 2 и ½ × f ( x ) = (½) x 2 , ниже:
график 2 x f0 010 ) = 2 х 2 :
(Это более тонкий график, чем график обычной функции в поле ниже.)
Содержание продолжается ниже х ) = х 2 :
(Это график обычной функции.)
график ½ × f ( x ) = (½) x 0 0 9:0015 2 6 02 (Это толще, чем график регулярной функции, который был показан в предыдущем блоке.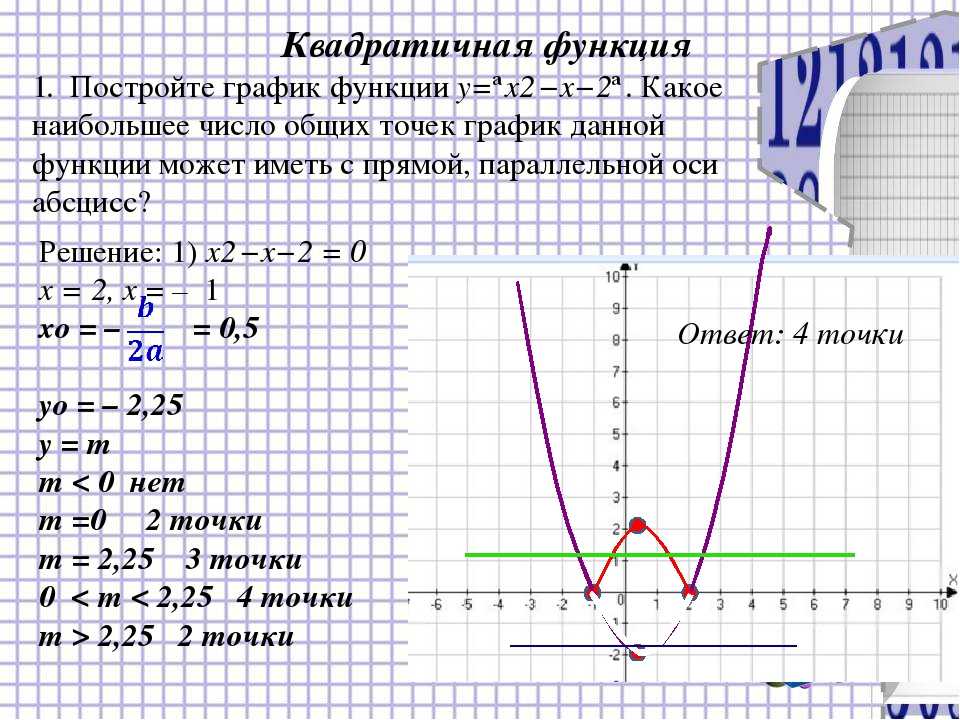
)
Первая парабола, та, что для 2 x 2 , растет в два раза быстрее, чем x 2 (средняя график), поэтому его график высокий и худой. С другой стороны, третья парабола для функции (½) x 2 растет вдвое быстрее, чем x 2 , поэтому его график короткий и толстый.
Вы можете сказать, грубо говоря, что первый график, более тонкий, умножается на нечто большее, чем 1, поэтому он растет быстрее, чем обычно, и что третий график, более квадратный, умножается на что-то меньшее, чем 1, поэтому он растет медленнее, чем обычно. Но, как правило, довольно сложно точно сказать, на что был умножен график, просто взглянув на картинку.
Например, можете ли вы сказать, что на графике ниже показано 1,4 × f ( x ) = 1,4 x 2 ?
Маловероятно.
Другим более сложным типом преобразования является умножение на аргумент функции. Это часто очень похоже на умножение всей функции.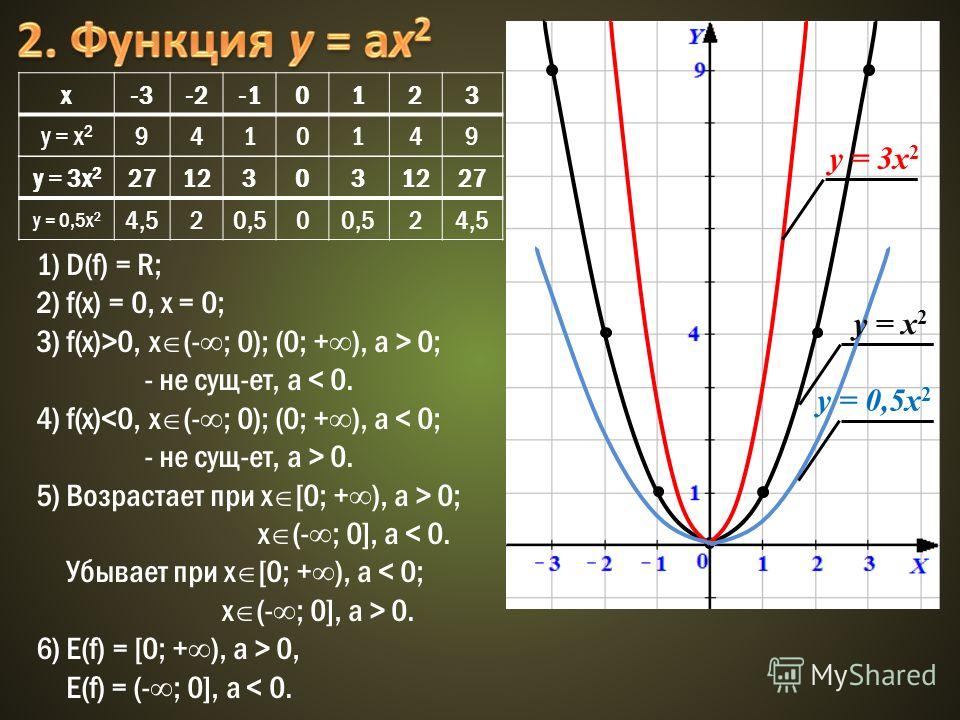
Например, рассмотрим графики f (2 x ) = (2 x ) 2 , f ( x ) = x 2 и f (½ x ) = (½ x) 2 , ниже:
график f (2 9 9 x 90 = 90) 0010 ) 2 :
(Этот график растет в два раза быстрее, чем график обычной функции, показанный в следующей рамке.) (Это график обычной функции.) график f (½ x ) = (½ x ) 2 : (Этот график растет вдвое медленнее, чем график обычной функции, показанный в предыдущей рамке.) Как видите, умножение внутри функции (внутри аргумента функции) приводит к тому, что график становится тоньше или толще. Это очень похоже на другое преобразование умножения, но это преобразование является умножением вне всей функции или над ней. И обычно практически невозможно идентифицировать это преобразование по графику или отличить его от другого мультипликативного преобразования. Иногда, однако, полезно посмотреть на нули графика (если их больше одного) или поворотные точки, так как они будут разбросаны дальше (если аргумент умножается на нечто большее, чем 1) или сгруппированы к оси y (если аргумент умножается на что-то меньшее, чем 1). Например, глядя на y = x 2 − 4, вы можете видеть, что умножение вне функции не меняет положение нулей, но умножение внутри функции меняет: график x 2 − 4: (Это график f ( x ), с нулями при x = −2, 2) 9001 × f ( x ) = 2( x 2 − 4): (Этот график выше, но нули совпадают с нулями исходной функции, показанной в предыдущем поле.) график (2 x ) 2 − 4: (Этот график не только выше, но и нули сместились внутрь, до x = -1, 1.) Напомним, что преобразования «влево», «вправо», «вверх», «вниз», «перевернуть» и «отразить» довольно просты, но » умножить», также называемые «растягиванием» и «сжатием», могут немного запутаться.
В типичных домашних заданиях по этой теме вас просят изобразить преобразование функции с учетом исходной функции или вычислить преобразование с учетом сравнительных графиков.
График f ( x ) = x 4 выглядит следующим образом: будет перемещен вверх на одну единицу. И «-2» внутри аргумента говорит мне, что график будет сдвинут на две единицы ВПРАВО. (Помните, что смещение влево-вправо происходит в обратную сторону от ожидаемого.)
Обычно лучше работать изнутри наружу. Поэтому сначала я сдвину график вправо на две единицы. Затем я подниму результат на одну единицу вверх.
Тогда мой переведенный график выглядит так:
Когда они заставляют вас рисовать, перемещая другие графики, они не могут быть ужасно критичны к вашему рисунку, так как вы не должны делать Т-диаграмму и вычисление точных точек. Но постарайтесь, чтобы ваш график выглядел разумным.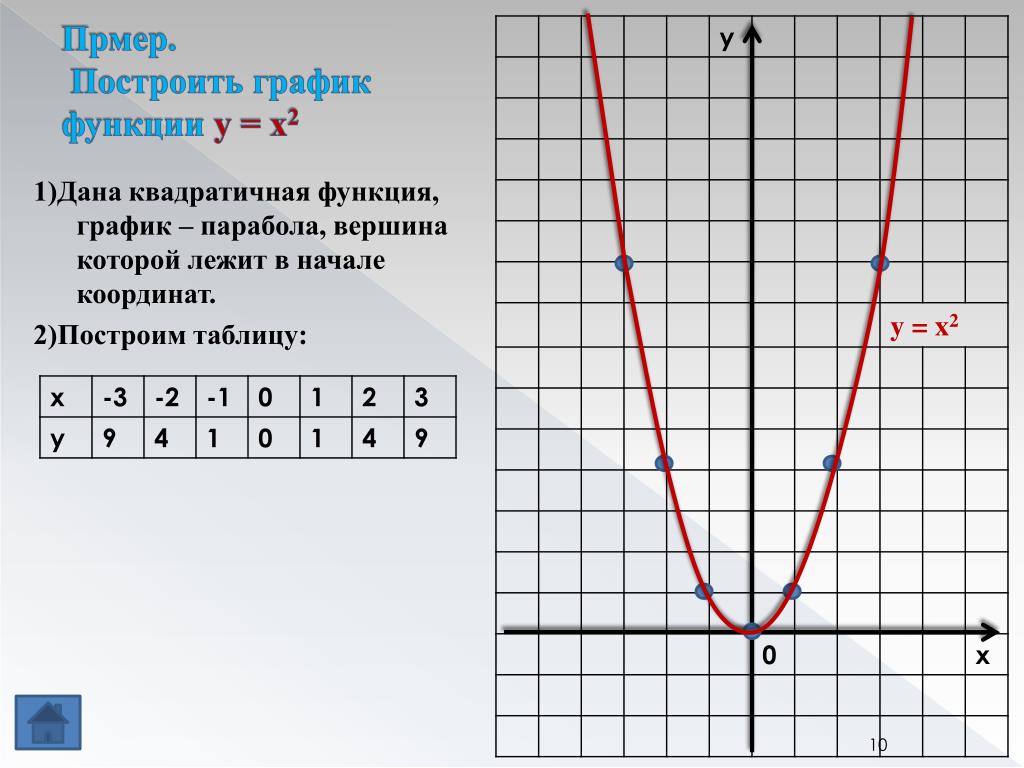
Кстати, вы всегда можете «обмануть», особенно если у вас есть графический калькулятор, быстро построив график y = ( x − 2) 4 + 1 и убедившись, что он соответствует тому, что вы нарисовали . Но вам нужно знать, как выполнять преобразования функций, потому что есть способы задавать вопросы, которые не позволяют вам обманывать, как мы увидим в следующем разделе.
URL: https://www.purplemath.com/modules/fcntrans3.htm
Страница 1Страница 2Страница 4Страница 5
| 2008 Расмус Эф и Джанн Сак | Уравнения III |
Урок 3 Перекресток точки графиков
Как мы найдем точки, в которых два графика y = f(x) и y = g(x) пересекаются?
Мы уже знаем, как найти, где график
f(x) пересекает ось x. Вот где y = 0. Мы вычисляем его, решая
уравнение f(x) = 0 .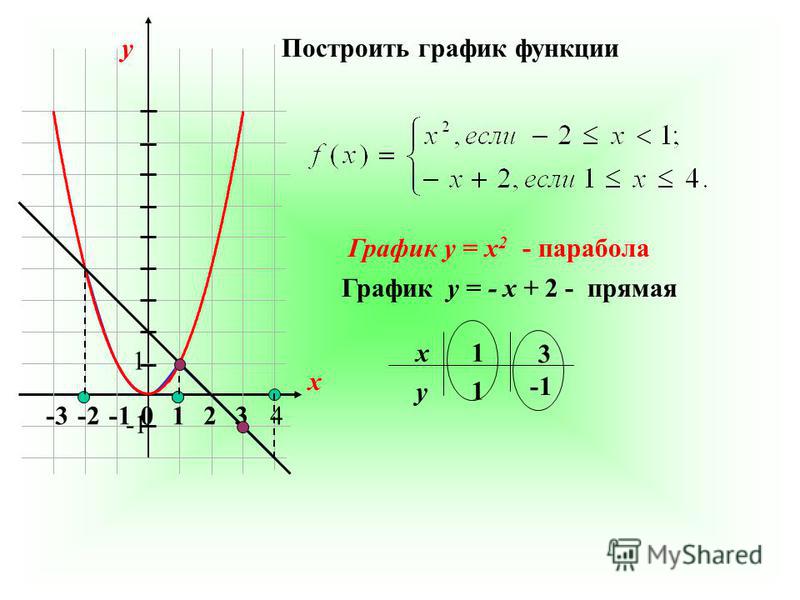
Когда графики y = f(x) и y =
g(x) пересекаются, оба графика имеют
точно такие же значения x и y. Таким образом, мы можем найти точку или точки
пересечение путем решения уравнения f(x)
= г(х). Решение этого уравнения даст нам значение(я) x
точка (точки) пересечения. Затем мы можем найти значение y, подставив значение для
x, которые мы нашли, в одно из исходных уравнений. то есть по расчету
либо f(x), либо g(x).
Пример 1
Рассчитать точку пересечение двух прямых f(x) = 2x − 1 и g(x) = x + 1. Первая давайте посмотрим на график двух функций. Мы можем видеть точку пересечение (2, 3).
Вычисляем точку пересечения по решение уравнения f(x) = g(x). То есть:
2x − 1 = x + 1
2x − x = 1 + 1
х = 2
Координата y теперь может быть найдена вычисление f(2):
f(2) = 2×2 − 1 = 3
Точка пересечения (2, 3) .
Пример показывает, что мы можем найти точку
пересечения двумя способами.
Либо графически, рисуя два графика в одной системе координат, либо
алгебраически, решая уравнение, такое как в приведенном выше примере.
Некоторые уравнения не могут быть решены алгебраически, но мы можем найти решения, которые исправить столько значащих цифр, сколько мы хотим, используя компьютеры и калькуляторы.
Пример 2
Решите уравнение x
Рисуем графики f(x) = x 2 − 2x — 3 и g (x) = 2x — 3, составив таблицу значений и построив график точки. Мы видим, как из графика, так и из таблицы значений, что графики пересекаются, когда x = 0 и х = 4 .
Алгебраическое решение:
x 2 − 2x − 3 = 2x − 3
x 2 − 4x = 0
х(х — 4) = 0
Получение решений x = 0 и x = 4 .
Пример 3
Решите уравнение x 2 — 1 = 2x — 3
Сначала переместите все условия перейти к левой части уравнения и упростить.
Это дает x 2 − 2x + 2 = 0
Используем квадратичную формулу с a = 1, b = −2 и с = 2,
Число под знаком квадратного корня
отрицательное, что означает, что это уравнение не имеет решения.
Чтобы понять, почему это так, нарисуем графики левой части исходного
уравнение
f(x) = x 2 − 1 и правая часть g(x) = 2x − 3,
Мы видим, что парабола f(x) и прямая g(x) не пересекаются. Легко видеть, что мы не может вычислить точку пересечения просто потому, что такой точки нет.
Пример 4
Решите уравнение x 3 − 3x + 2 = x 2 − 2x + 1
Как и в предыдущем примере, мы перемещаем все
члены в левой части уравнения.
х 3 — 3х + 2 = х 2 — 2х + 1
x 3 − x 2 − x + 1 = 0
(х 3 — х 2 ) — (х — 1) = 0
х 2 (х — 1) — (х — 1) = 0
(х — 1)(х 2 — 1) = 0
(х — 1) (х — 1) (х + 1) = 0
Расчеты показывают, что есть только два решения, x = 1 и x = -1, но кубическое уравнение может иметь три решения. График показывает нам, что происходит.
Графики f(x) = x 2 − 2x + 1 и g(x) = x 3 — 3x + 2 пересекаются только в двух местах, где x = −1 и x = 1, которые были решениями уравнение.
Пример 5
Решите уравнение x 2 = x
Легко видеть, что x = 0 и x = 1 равны
решения уравнения, но есть ли еще решения? Это не очень
вероятно, но давайте посмотрим на графики.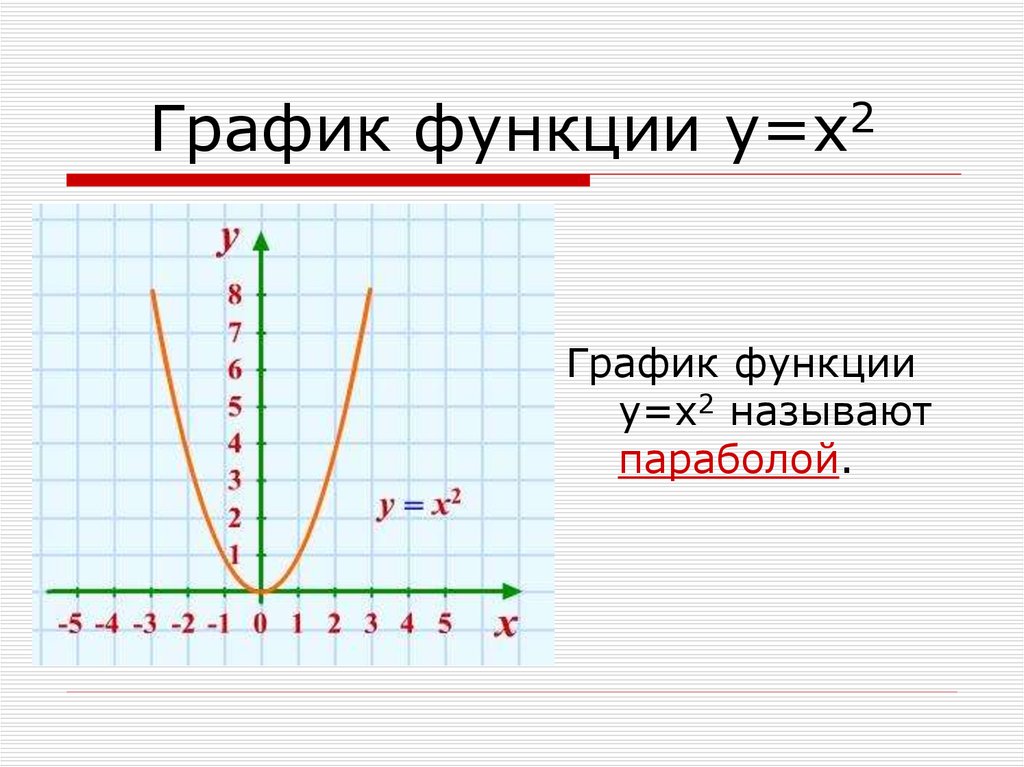
Назовем левую часть f(x) = x 2 , а правую часть g(x) = x. Помните, что g(x) не может принимать отрицательные значения x, поэтому не может быть никаких отрицательные точки пересечения.
На графике видно, что точек всего две
пересечения и, следовательно, только два решения уравнения. х = 0 и х =
1.
Вот как решить уравнение вычислением:
| х 2 = х x 4 = x х 4 — х = 0 х(х 3 — 1) = 0 | Квадрат обе части уравнения, чтобы избавиться от квадратного корня . |
Это дает решение x = 0 и x = 1 .
Пример 6
Решите уравнение ln x = x 2 − 1
Это уравнение не так просто решить.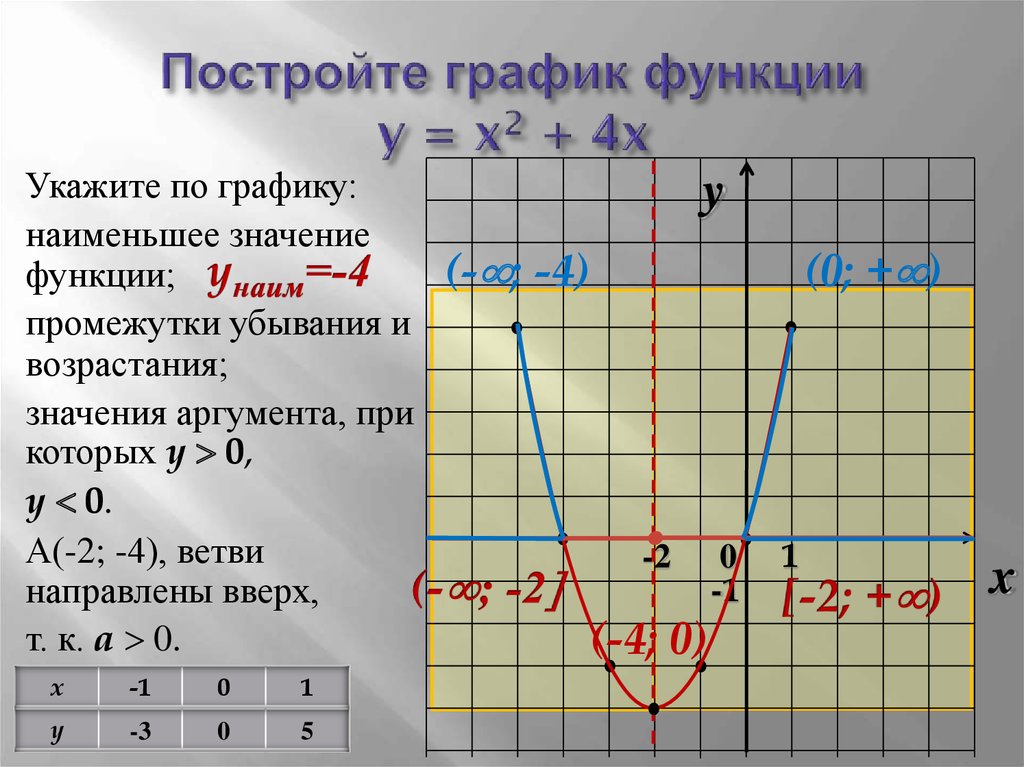
Если мы
помните определение логарифма, мы можем видеть, что x = 1 делает обе части
уравнение равно 0 и, следовательно, является одним решением уравнения. Мы рисуем
графики, чтобы увидеть, есть ли какие-либо другие решения.
График показывает нам, что есть два решения. Одно решение равно x = 1, потому что e 0 =1.
Обратите внимание, что мы выбираем значения x так, чтобы значения y становятся все ближе и ближе друг к другу в таблице ценностей. Таким образом мы можно выбрать значение x, чтобы получить желаемую точность.| Пример 7 | EXCEL |
Если мы используем графический калькулятор, мы можем найти решение уравнения ln x = x 2 − 1 намного проще.
Рисуем графики обеих сторон
уравнение и используйте Zoom (Shift F2), а затем Trace (Shift F1), чтобы найти
точка пересечения.
Еще проще использовать G-Solve ( F5) и затем функция пересечения ISCT (F5) . Это дает нам первую точку пересечение. Затем мы нажимаем стрелку вправо, и калькулятор переходит к вторая точка пересечения.
Программа электронных таблиц EXCEL есть инструмент под названием цель искать для решения уравнений, которые не могут быть легко решается алгебраически.
Начните с изменения уравнения, как показано на рисунке.
ln x = x 2 − 1
1 = х 2 — ln х
Откройте EXCEL и начните с выбора или угадывания
начальное значение для х. Введите это в ячейку B2. Мы можем, например, выбрать 0,1.
Затем мы помещаем формулу, которая у нас есть в правой части уравнения, x 2 — ln x , в ячейку D2.
Формула будет выглядеть так: 92-пер(В2)
Теперь выберите Инструменты а затем «Поиск цели» в строке меню. на экране появляется следующее:
Пишем D2,
1 и B2 в местах, как показано.