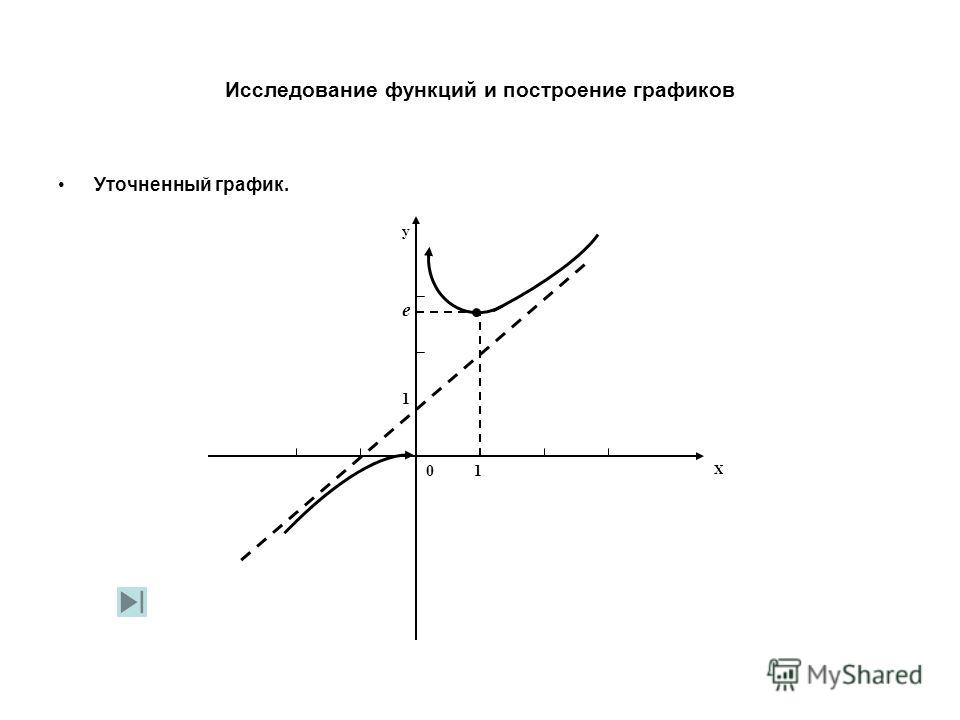
13. Общая схема исследования функций и построения графиков.
Общее исследование функции следует проводить по приведенной ниже схеме:
1.Определить область существования функции, область непрерывности, точки разрыва.
2. Найти асимптоты функции.
3. Выяснить вопрос о периодичности.
4. Выяснить вопрос о четности или нечетности.
В случае, если функция окажется четной или нечетной достаточно исследовать функцию только при положительных значениях аргумента. При построении графика следует учесть, что график четной функции симметричен относительно оси ординат; график нечетной функции симметричен относительно начала координат.
5.Найти точки пересечения графика функции с осями координат:
с осью абсцисс — точки , где -решение уравнения ;
с осью ординат- точки , где .
6.
Найти промежутки
монотонности и локальные экстремумы.
7.Найти интервалы выпуклости и вогнутости, точки перегиба.
8. Составить таблицу
Возрастает или убывает, Выпукла или вогнута | Возрастает или убывает, Выпукла или вогнута | Возрастает или убывает, Выпукла или вогнута | Возрастает или убывает, Выпукла или вогнута | ||||
знак | знак | знак | знак | ||||
знак | знак | знак | знак |
Точки -все найденные в п.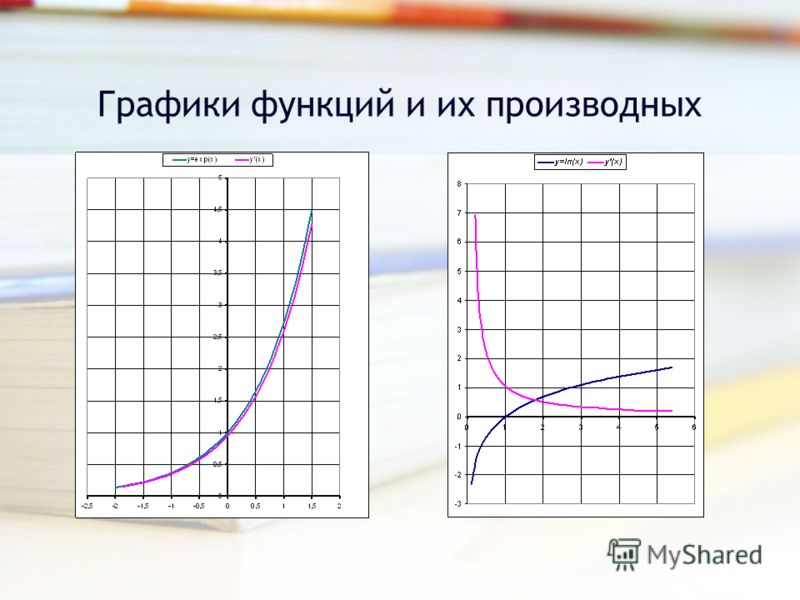
9.На основании проведенного исследования построить график заданной функции.
Пример 26
Провести полное исследование и построить график функции .
Решение:
Область определения функции
Точка разрыва функции , функция непрерывна на и .
2. Асимптоты.
Вертикальная асимптота .
Поведение функции в окрестности :
Найдем наклонную асимптоту:
Прямая является наклонной асимптотой заданной кривой.
3. Функция не является периодической.
4. Четность функции
Условие четности
или нечетности не выполнено.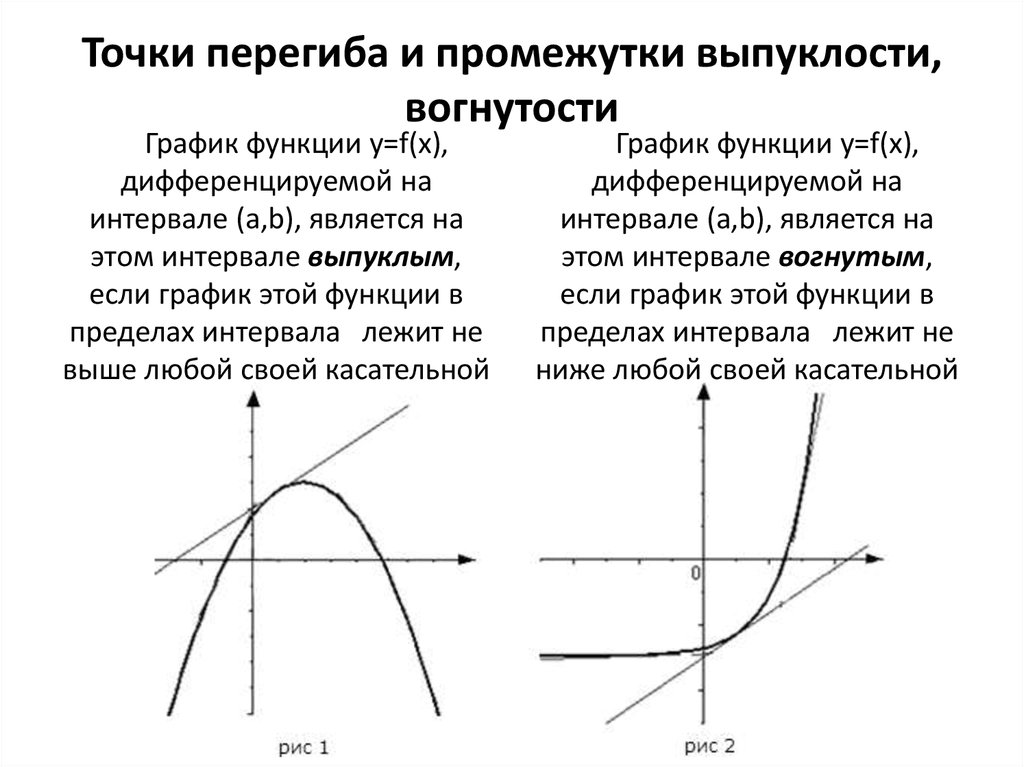
Заданная
функция –функция общего вида.
5. Точки пересечения с осями.
График функции проходит через начало координат.
6. Промежутки монотонности, локальные экстремумы.
Найдем критические точки:
И
знак
сследуем знак производной методом интервалов:
Найдем значения функции в критических точках:
7.Промежутки выпуклости и вогнутости. Точки перегиба.
Найдем вторую производную.
Точки, в которых равна нулю или несуществует:
Исследуем знак второй производной методом интервалов:
8. Составляем таблицу.
0 | — | ||||||
+ | 0 | + | — | — | 0 | + | |
— | 0 | + | — | + | + | ||
перегиб | разрыв | Мин. |
ТЕСТ. Исследование функции и построение графика | Материал для подготовки к ЕГЭ (ГИА) по алгебре:
ТЕСТ. Исследование функции и построение графика.
Вариант 1
1. Функция задана формулой: f (x) = x3 – 4x +1. Найдите f (-2).
1) 1 2) 17 3) 3 4) 12
2. Для каждой функции, заданной формулой, укажите её график ( см. рис.1 )
а) б)
в)г)
Рис. 1
1) y =3x + 2 2 ) –x+1 3) y = (x-1)2 4) –x2 + 2x + 3
Ответ:
3. Функция f (x) определена на . Пользуясь графиком функции (см. рис. 2), укажите промежутки убывания.
1) 2) (- ; 2) 3) (2; — ) 4) [0; +)
4.
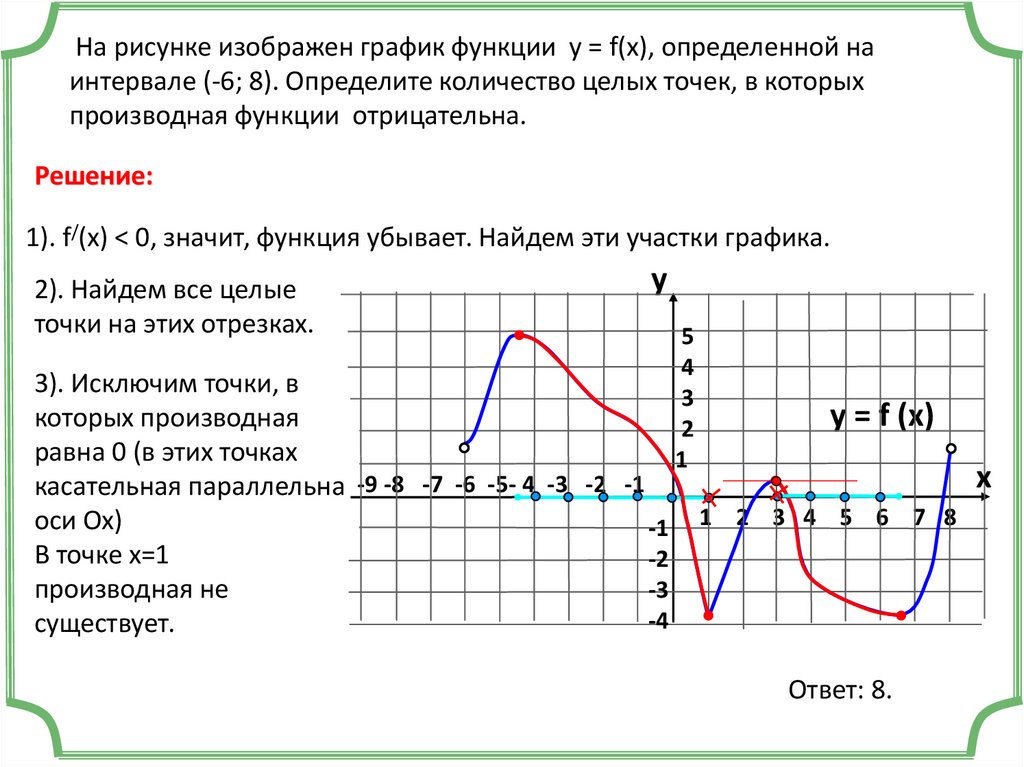На рисунке 3 изображён график функции y = ax2 + c. Определите знаки a и c.
Ответ:_______
Рис. 3Рис. 2
5. Среди функций: y = 5×5; y = │x│; y = (x+3)5; y = x5 + 3 укажите нечётную.
1) y = 5×5 2) y = (x+3)5 3) y = x5 + 3 4) y = │x│
6. Найдите координаты точек пересечения графика функции
у = + 1 c осью абсцисс.
1) (0; 1) 2) (1;0) 3) (;0) 4) 0;)
7. Найдите, при каком значении a точка А(а;3) принадлежит графику функции y=-2
1) 5 2) 29 3) 9 4) 1
8. Соотнесите функции
А) y = x2 + 1, Б) y = , В) y =
с их графиками (см. рис. 4)
Ответ:
1)2)
3)4)
Рис. 4
Исследование функции и построение графика
Вариант 2
1.
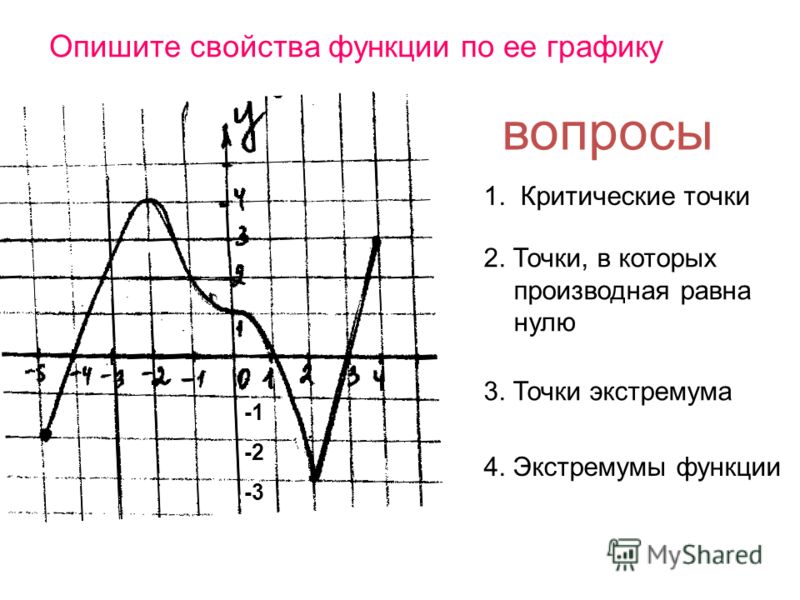Найдите область определения функции у =+7.
1) (-;4) 2) (-;4] 3) [4;+) 4) (4; +)
2. Соотнесите рисунок, изображающий график функции y = kx + b, с одним из условий (см. рис. 1)
А) Б)
В)
Рис. 1
1) k0;b>0 3) k=0; b>0
Ответ:
3. Найдите область определения функции y = 2 /
1) [;+) 2) ( -;] 3) ,25; +) 4) (-;) (;+)
4. На рисунке 2 изображён график функции y=ax2+c. Определите знаки a и c.
Рис. 2
Ответ: _______
5. На рисунке 3 изображена кубическая парабола. Какая из перечисленных формул задаёт эту функцию?
Рис. 3
1) y = (x-3)3 + 1 2) y = ()3 + 2 3) y = ()3 4) y =
6. Найдите абсциссу точки пересечения графика функции y = — 1 с осью Ox/
Ответ: ______
7. Найдите количество точек пересечения графиков функций y = — и y = -3x.
Ответ: ______
8.
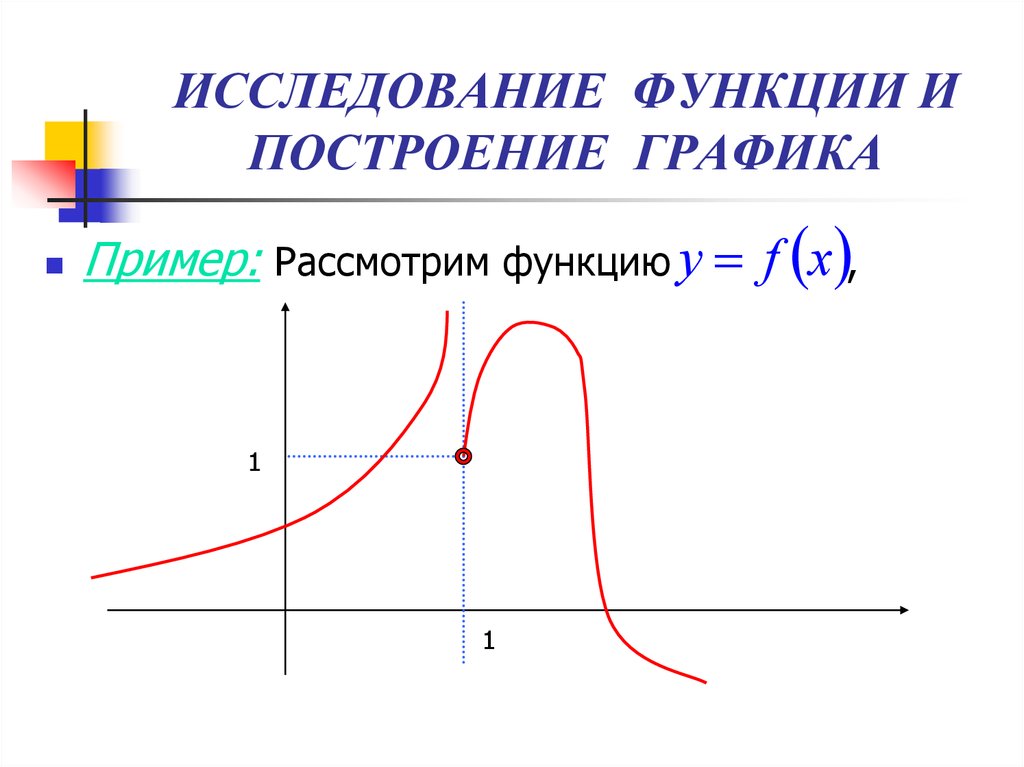По графику функции (см. рис. 4) найдите все значения x, при котором значения функции положительны.
А) Б)
В)
Ответ:
Как построить график функции
- Войти
- Биографии репетитора
- Подготовка к тесту
СРЕДНЯЯ ШКОЛА
- ACT Репетиторство
- SAT Репетиторство
- Репетиторство PSAT
- ASPIRE Репетиторство
- ШСАТ Репетиторство
- Репетиторство STAAR
ВЫСШАЯ ШКОЛА
- Репетиторство MCAT
- Репетиторство GRE
- Репетиторство по LSAT
- Репетиторство по GMAT
К-8
- Репетиторство AIMS
- Репетиторство по HSPT
- Репетиторство ISEE
- Репетиторство ISAT
- Репетиторство по SSAT
- Репетиторство STAAR
Поиск 50+ тестов
- Академическое обучение
репетиторство по математике
- Алгебра
- Исчисление
- Элементарная математика
- Геометрия
- Предварительный расчет
- Статистика
- Тригонометрия
репетиторство по естественным наукам
- Анатомия
- Биология
- Химия
- Физика
иностранные языки
- французский
- немецкий
- Латинский
- Китайский мандарин
- Испанский
начальное обучение
- Чтение
- Акустика
- Элементарная математика
прочие
- Бухгалтерия
- Информатика
- Экономика
- Английский
- Финансы
- История
- Письмо
- Лето
Поиск по 350+ темам
- О
- Обзор видео
- Процесс выбора наставника
- Онлайн-репетиторство
- Мобильное обучение
- Мгновенное обучение
- Как мы работаем
- Наша гарантия
- Влияние репетиторства
- Обзоры и отзывы
- Освещение в СМИ
- О преподавателях университета
Звоните прямо сейчас, чтобы записаться на обучение:
(888) 888-0446
Все ресурсы по алгебре 1
10 Диагностические тесты 557 практических тестов Вопрос дня Карточки Learn by Concept
Алгебра 1 Помощь » Функции и линии » График » Как построить график функции
На каком графике изображена функция?
Правильный ответ:
Объяснение:
Функция может иметь только одно значение y для каждого значения x.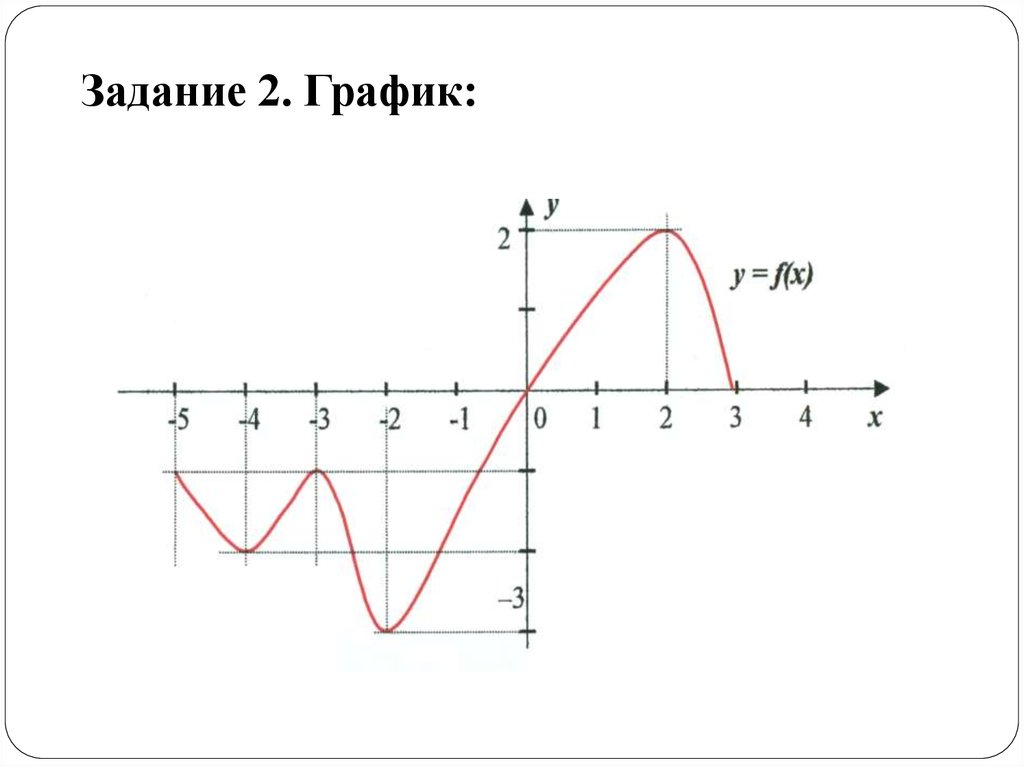
Проверка вертикальной линии может использоваться для определения функции. Если в любой точке графика прямая вертикальная линия пересекает кривую более чем в одной точке, кривая не является функцией.
Сообщить об ошибке
График ниже представляет собой график кусочной функции на некотором интервале. Определите, в записи интервала, убывающий интервал.
Возможные ответы:
Правильный ответ:
Объяснение:
Как видно из графика, в промежутке между ( включено) и постоянная при , а затем от ( не включено) до ( не включено) является убывающей функцией.
Сообщить об ошибке
Какое уравнение лучше всего представляет следующий график?
Возможные ответы:
Ничего из перечисленного
Пояснение:
У нас есть следующие варианты ответов.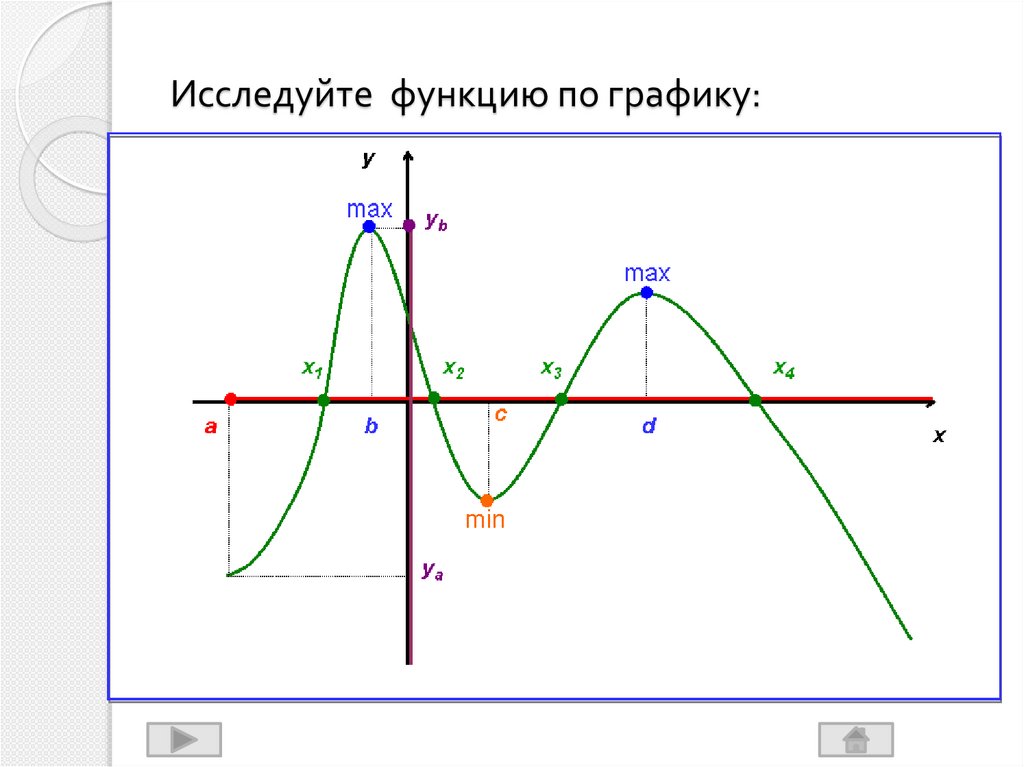
Первое уравнение представляет собой кубическую функцию, которая дает функцию, похожую на график. Второе уравнение является квадратным и, таким образом, является параболой. График не похож на праболу, поэтому 2-е уравнение будет неверным. Третье уравнение описывает линию, но график нелинейный; третье уравнение неверно. Четвертое уравнение неверно, потому что оно экспоненциальное, а график не экспоненциальный. Так что остается первое уравнение как наилучший возможный выбор.
Сообщить об ошибке
Уведомление об авторских правах
Посмотреть репетиторов по алгебре
Лорен
Сертифицированный репетитор
Центральный Мичиганский университет, бакалавр искусств, человеческого развития и семейных исследований.
Посмотреть Репетиторы по алгебре
Ингрид
Сертифицированный репетитор
Университет Северного Иллинойса, бакалавр наук, начальное образование. Университет Северного Иллинойса, магистр наук, к.
..
Просмотреть репетиторов по алгебре
Рут А.
Сертифицированный преподаватель
Университет Альфреда, бакалавр наук, керамических наук и техники.
Все ресурсы по алгебре 1
10 Диагностические тесты 557 практических тестов Вопрос дня Карточки Learn by Concept
Изучение графиков функций
Процесс рисования графика (кривой) соответствующей функции известен как построение графиков функций. Графики основных функций, таких как линейные, квадратичные, кубические и т. д., довольно просты; однако для построения графиков сложных функций, таких как рациональные, логарифмические и т. д., требуются определенные навыки и знание математических понятий.
График функции — это совокупность всех точек функции, нанесенных на график. Тест вертикальной линии можно использовать для определения графика функции. Просто нарисуйте вертикальные линии (линии, параллельные оси y) для каждого значения x.
Поскольку функция имеет только один выход для каждого входа, если вертикальная линия пересекает значение x более одного раза, график не является функцией. Если вертикальная линия пересекает каждое значение x только один раз.
Как графики представляют функции
Графики функций — это процесс рисования кривой, представляющей функцию на координатной плоскости. Если функция представлена кривой (графиком), то каждая точка на кривой удовлетворяет уравнению функции. Например, на графике ниже изображена линейная функция f(x) = -x+ 2.
Возьмем любую точку на этой прямой, например (-1, 3). Заменим (-1, 3) = (x, y), т. е. x = -1 и (y = 3) в функции f(x) = -x + 2 (заметим, что ее можно записать и в виде y = -х + 2). Затем
3 = -(-1) + 2,
3 = 1 + 2,
3 = 1 + 2
3 = 3, поэтому (-1, 3) выполняет функцию. Точно так же вы можете поэкспериментировать с разными точками, чтобы увидеть, удовлетворяют ли они функции.
Каждая точка на линии, которую обычно называют «кривой», выполняет эту функцию. Графические функции — это процесс рисования таких кривых для представления функций.
Графики основных функций
Построить график основных функций, таких как линейные функции и квадратичные функции, очень просто. Фундаментальная концепция графических функций
Если возможно, определите форму. Если это линейная функция вида f(x) = ax + b, ее график представляет собой линию; если это квадратичная функция вида . Его график представляет собой параболу.
Нахождение некоторых точек на ней путем подстановки некоторых случайных значений x и нахождение соответствующих значений y путем подстановки каждого значения в функцию , x и y-пересечения, дыры и несколько точек на нем. Затем просто присоединитесь к точке, избегая асимптот и отмечая домен и диапазон функции.
Ниже приведены шаги для построения графика функции:
Убедитесь, что функция имеет вид y=mx+b.
b теперь откладывается по оси Y.
м сокращается до дроби.
Наклон теперь используется для продолжения линии от b.
Линия может быть дополнительно расширена с помощью мм в качестве ориентира.
Итак, нам нужны только две точки на линейной функции, чтобы построить ее график. Чтобы построить график, просто создайте таблицу значений с двумя столбцами x и y, выберите несколько случайных чисел для x и вычислите соответствующие значения y, подставив каждое из них в функцию. Затем просто нанесите точки на график, соедините их линией и бесконечно продлите линию с обеих сторон.
Типы графиков функций
График функций помогает визуализировать функцию, заданную в алгебраической форме. Глядя на уравнение, вы можете сказать, будет ли график нечетным или четным, возрастающим или убывающим, и представляет ли уравнение график вообще.