Чему равен периметр 4см? – Обзоры Вики
Периметр P = 4 * с. Таким образом, периметр P = 16 см.
Аналогично, что такое квадратная формула? В геометрии квадрат — это фигура с четырьмя равными сторонами. Площадь квадрата определяется как количество квадратных единиц, составляющих полный квадрат. Он рассчитывается по формуле площади квадрата Площадь = s × s = s2 в квадратных единицах.
Чему равен периметр 3см? Периметр — это общая длина контура фигуры. У квадрата 4 стороны одинаковой длины. Ответ на вопрос: длина стороны квадрата 3 см, если длина стороны удвоена, чему равен новый периметр? Если у нас есть 4 стороны по 3 см каждая, то периметр равен 12 cms.
Какова площадь 7см и 6см? Площадь = 21 единиц.
Во-вторых Какова площадь 6см и 4см? Чтобы вычислить площадь, мы просто умножаем основание (ширину) на высоту (как прямоугольник). Площадь = 6 см x 4 см = 24 см2 = 22cm2 Page 5 Начальная школа Netherbrook 1. На схеме показан прямоугольник, нарисованный на квадратной сетке.
0.5 = 25 единиц. Периметр квадрата = 100 единиц.
Чему равен периметр 8 см? Периметр — это расстояние вокруг прямоугольника. У прямоугольника 4 стороны: 2 из них будут длиной (8 см) и 2 из них шириной (3 см). Чтобы получить периметр, нужно сложить 2 длины и 2 ширины: 2 х 8 + 2 х 3. Следовательно, ответ таков: 22cm (не забудьте единицы измерения!)
Каков периметр 5 см?
Так как сторона квадрата 5 см. Его периметр равен 5×4=20см.
Чему равен периметр квадрата со стороной 4 см? Следовательно, периметр квадрата = 16 см.
Как рассчитать периметр?
Прямоугольник имеет две равные длины и две равные ширины. Чтобы найти периметр или расстояние вокруг прямоугольника, нам нужно сложить длины всех четырех сторон. Это можно сделать эффективно, просто сложив длину и ширину, а затем умножив эту сумму на два, поскольку каждой стороны по две.
см2 это периметр? Для квадрата 2 см периметр равен 8 см, а площадь 4 см2. Периметр вдвое больше площади.
Чему равен периметр 8 см и 3 см?
Периметр — это расстояние вокруг прямоугольника. У прямоугольника 4 стороны: 2 из них будут длиной (8 см) и 2 из них шириной (3 см). Чтобы получить периметр, нужно сложить 2 длины и 2 ширины: 2 х 8 + 2 х 3. Следовательно, ответ таков: 22cm (не забудьте единицы измерения!)
Чему равен периметр фигуры В?
Ответ: Периметр двумерной фигуры равен расстояние вокруг формы. Он находится путем сложения всех сторон (если они все равны).
Что такое периметр площади? Периметр. Площадь относится к пространству, занимаемому формой, предметом или поверхностью. Периметр относится к мере длины контура или границы формы, объекта или поверхности. Площадь измеряется в квадратных единицах.
Как посчитать периметр из квадратных метров? Периметр будет 2 x один фактор + 2 x другой фактор. Допустим, площадь прямоугольника равна 96 квадратных футов. Тогда прямоугольник может быть 8 футов на 12 футов, поэтому периметр будет равен 2 x 8 футов + 2 x 12 футов, или 40 футов.
Но прямоугольник также может быть 6 футов на 16 футов, поэтому периметр будет равен 44.
Чему равен периметр квадрата, площадь которого 625 квадратных метров?
Периметр равен 100 метров.
Какой идеальный квадрат между 40 и 50? Итак, совершенный квадрат числа между 40 и 50 равен 49.
Чему равна сторона квадрата, площадь которого равна 625 мм 2 ?
100 есть ответ.
Чему равен периметр 3 и 8? Периметр это сумма сторон. а если каждая сторона 38 см. тогда периметр равен 38+38+38 или 3×38=98 см.
Каков периметр квадрата 6 см?
Периметр квадрата 6 см равен 24.
Чему равен периметр квадрата 80см? Эй!!! Дан периметр = 80 см. Как мы знаем, периметр = 4 х сторона. = 80/4 = 20 см.
Задачи «Нахождение периметра и площади прямоугольника» | Тренажёр по математике (3 класс):
Опубликовано 02.04.2021 — 17:54 — Зотова Наталья Анатольевна
Дополнительный материал на отработку задач по математике на нахождение периметра и площади прямоугольника.
Скачать:
Предварительный просмотр:
Задачи на нахождение
периметра и площади прямоугольника.
- Длина прямоугольника равна 28 см, а периметр равен 86 см. Чему равна ширина?
- Периметр квадрата равен 64 см. Чему равна его сторона?
- Ширина прямоугольника равна 13 см, а периметр равен 70 см. Чему равна длина?
- Периметр прямоугольника 80 см. Длина его стороны 26 см. Узнайте ширину прямоугольника.
- Участок земли имеет форму прямоугольника, длина которого 69 м, а ширина 31 м. Какой длины забор окружает этот участок?
- Длина прямоугольника 18 см, а ширина в 2 раза короче. Чему равна площадь данного прямоугольника?
- Площадь прямоугольника 130 см², ширина его равна 26 см. Чему равна длина прямоугольника?
- Периметр прямоугольника 120 см, ширина его равна 20 см. Найдите площадь этого прямоугольника.
- Периметр квадрата 80 см. Найдите площадь этого квадрата.
- Длина клумбы прямоугольной формы 20 м, ширина в 2 раза меньше.
Найдите площадь клумбы. - Ширина участка 10 м, а периметр равен 78 м. Найдите площадь этого участка.
- Периметр квадрата равен периметру треугольника со сторонами 6 см, 3 см и 7 см. Чему равна длина стороны квадрата?
- Дачный участок прямоугольной формы имеет длину 25 м и ширину 12 м. Какой длины забор надо поставить вокруг участка?
- Периметр прямоугольника 90 см. Одна сторона 10 см. Чему равна его площадь?
- Площадь прямоугольника 114 см², его длина 19 см. Чему равна ширина прямоугольника?
- Периметр квадрата равен 136 см. Чему равна его сторона?
- Площадь прямоугольника 120 см², его длина 24 см. Чему равна ширина прямоугольника?
- Часть участка прямоугольной формы площадью 60 м² засажена картофелем, другая часть, квадратной формы, отведена под лук. Длина участка, отведенного под лук, 4 м. Чему равна площадь участка занятая картофелем?
- Четвёртая часть участка длиной 10 м, шириной 8 м, отведена под землянику, а остальная часть — под цветник. Какая площадь занята цветником?
- Под цветы отведено 2 клумбы. Длина прямоугольной клумбы 10 м, ширина 5 м. Сторона квадратной клумбы 6 м. Площадь какой клумбы больше и на сколько?
Найдите площадь клумбы.
Какая площадь занята цветником?По теме: методические разработки, презентации и конспекты
Презентация по математике «Периметр и Площадь прямоугольника»
Решение задач на нахождение Периметра и Площади прямоугольника…
Методическая разработка урока математики «Нахождение периметра и площади прямоугольника» с презентацией
повторить изученное, вспомнить нахождение периметра и площади прямоугольника как фигуры на плоскости, провести сравнительный анализ…
Презентация к уроку: «Формулы периметра и площади прямоугольника»
Тема: Формулы периметра и площади прямоугольника.Цели: сформировать у детей понятие о формуле, учить записывать с помощью формул правила нахождения периметра, площади, выражать зависимость между велич…
Конспект урока: «Формулы периметра и площади прямоугольника»
Тема: Формулы периметра и площади прямоугольника.
Цели: сформировать у детей понятие о формуле, учить записывать с помощью формул правила нахождения периметра, площади, выражать зависимость между велич…
Конспект урока математики по теме «Периметр и площадь прямоугольника.Закрепление»
Цели и задачи: 1. повторить и закрепить и расширить знания о прямоугольнике и квадрате; совершенствовать умение решать задачи на нахождение периметра и площади прямоугольников; продолжать формирование…
Конспект урока математики по теме «Периметр и площадь прямоугольника.Закрепление»
Цели и задачи: 1. повторить и закрепить и расширить знания о прямоугольнике и квадрате; совершенствовать умение решать задачи на нахождение периметра и площади прямоугольников; продолжать формирование…
Методическая разработка урока математики по теме «Формулы периметра и площади прямоугольника».
Тема урока «Формулы периметра и площади прямоугольника» 3 класс УМК «Перспектива»Автор учебника Петерсон Л.Г….
Поделиться:
Домашняя страница | Институт периметра
Разгадка величайших тайн Вселенной, от квантов до космоса.
Учить больше
ТРЕНИНГ
PSI Открыты стартовые приложения
ПОДКАСТ
Старт 2 сезона «Беседы на периметре»
НОВОСТИ
Космический взрыв привел к первому в своем роде обнаружению гамма-всплеска4 HER 900 NOET03 MY 900 NOET03 ИНИЦИАТИВЫ
Принимаются заявки на участие в программе Simons EN Fellowship Program
НОВОСТИ
Вселенная до появления атомов
Мероприятия
Ищете конкретное исследование, обучение или просветительскую деятельность? Начните здесь.
Все
Семинар
Искусство и культура
Публичная лекция
24–29 июля
Конференция
Струны 2023
Театр
14 декабря
Семинар
Дискретный сдвиг и квантованная поляризация заряда: новые инварианты в кристаллических топологических состояниях
Нарен Манджунат, University System of Maryland
14 декабря
Семинар
Аргумент против квантовых компьютеров
Гил Калай, Еврейский университет в Иерусалиме
15 декабря
Семинар
Возникновение классической калибровочной симметрии из квантовой запутанности
Джошуа Кирклин, Окинавский институт науки и технологий (OIST)
15 декабря
Семинар
Гравитационно-волновые зонды экстремальной гравитации: от черных дыр до космологии
Банафше Ширалилу, Университет Амстердама
Кто мы
«Периметр — это грандиозный эксперимент в теоретической физике.
Я надеюсь и ожидаю, что здесь произойдут великие дела». Стивен Хокинг,
Заслуженный научный руководитель Института периметра
Чем мы занимаемся
Perimeter — это зарегистрированная некоммерческая благотворительная организация, занимающаяся фундаментальными исследованиями, обучением и просветительской деятельностью в области теоретической физики.
Исследования
Магнит для самых талантливых исследователей мира, мы вместе решаем важные вопросы.
Обучение
Инновационные программы обучения для талантливой молодежи.
Outreach
Творческие программы для учителей, учащихся и широкой публики.
Служба поддержки PI
Perimeter — зарегистрированная некоммерческая благотворительная организация. Ваша поддержка жизненно важна для нашего успеха.
Пожертвовать
В центре внимания исследования
Периметр создает специальные исследовательские инициативы, направленные на дальнейшее развитие новых идей.
Эти инициативы выбираются стратегически и выполняются в течение определенных периодов.Event Horizon Telescope Initiative
Perimeter Institute Quantum Intelligence Lab (PIQuIL)
Clay Riddell Center for Quantum Matter
Quantum Causal Inference Initiative
Quantum Simulations of Fundamental Interactions (QFun)
Центр Вселенной
Посмотреть все исследования
Исследователи
Мы верим, что прорывы осуществляются через столкновение интеллекта, воображения и вдохновения.
Узнать больше
Будущие пионеры
Мы разработали инновационные и пользующиеся большим спросом программы обучения исследователям, чтобы помочь начинающим ученым совершенствовать свои идеи и интересы посредством активного академического и исследовательского взаимодействия.
Магистерская программа PSI
Другой вид магистерской программы по физике, предназначенный для амбициозных и целеустремленных молодых людей.
PSI Start
Возможности онлайн-обучения и личных исследований для студентов, которые намерены продолжить обучение в аспирантуре по теоретической физике.
Аспиранты
Возможности для общения с руководителями научных исследований, закладывая основу для карьеры в области физики.
Посмотреть все курсы
Исследуйте науку
Узнайте о наших мероприятиях, лекциях, курсах и других способах изучения науки здесь.
Беседы на периметре
Познакомьтесь с некоторыми блестящими учеными, пытающимися разгадать самые глубокие тайны природы, в этом подкасте Perimeter.
Quantum to Cosmos
Используйте нашу интерактивную шкалу, чтобы углубиться в атом, или уменьшите масштаб, чтобы увидеть пределы нашей вселенной.
Публичные лекции
Присоединяйтесь к нам лично и онлайн, чтобы услышать, как великие мыслители делятся своими идеями о передовой науке.
Узнать больше
Свяжитесь с нами
Подпишитесь на электронные письма от Perimeter Institute, чтобы быть в курсе всего, что здесь происходит.
Имя
Фамилия
Электронная почта
Ресурсы
PIRSA
PIRSA — это постоянный, бесплатный, доступный для поиска и цитирования архив записей семинаров соответствующих физических организаций.
Образовательные ресурсы
Загрузите бесплатные образовательные ресурсы для 5–12 классов, которые помогут вам объяснить ряд важных понятий физики и науки.
Беседы на периметре
Этот подкаст познакомит вас с исследователями, работающими на переднем крае науки и стремящимися разгадать самые глубокие тайны природы.
Галерея постеров
Просмотрите нашу библиотеку, наполненную прекрасными научными плакатами, и загрузите свои бесплатно!
Канал Периметра на YouTube
Просмотрите некоторые из замечательных видео, которые доступны на нашем канале YouTube, включая публичные лекции, материалы для занятий и многое другое!
SCITALKS
Единый сайт, который позволяет пользователям находить научные доклады из многих учреждений с помощью инструмента поиска в метарепозитории.
Викторины по естествознанию
Проверьте свои знания по физике, истории науки и случайным занудным мелочам.
Что такое периметр? Найдите периметр для различных фигур
- Автор Шротасвини Мохапатра
- Последнее изменение 02-12-2022
Слово «периметр» происходит от греческого слова «пери», что означает «вокруг», и «метрон», что означает «мера». Периметр — это замкнутый путь, очерчивающий двухмерную форму или одномерную длину. Периметр круга или эллипса называется окружностью.
Есть несколько приложений, где важно найти периметр. Это может варьироваться от расчета стоимости ограждения сада на заднем дворе до измерения нити, необходимой для обозначения границы футбольного поля. Итак, давайте лучше поймем концепцию периметра.
Сумма длин границ замкнутой формы называется ее периметром. Давайте попробуем понять это на примере.
Пример 1 : У нас есть огромная квадратная ферма.
Теперь, чтобы спасти нашу ферму от уличных животных, мы решаем огородить ее. Итак, если мы знаем длину одной стороны фермы, умножьте ее на \(4\), чтобы найти периметр фермы.
Пример 2 : Если нам нужно найти длину границы квадратного парка, мы должны найти его периметр.
Есть много таких вещей, где мы можем найти периметр.
Площадь и периметр
Площадь — это область или поверхность, ограниченная формой объекта. Полное пространство, занимаемое фигурой или геометрической фигурой, называется ее площадью. Площадь фигуры зависит от ее размеров и свойств. Разные формы имеют разную площадь. Например, площадь квадрата отличается от площади круга.
Площадь прямоугольного поля \( = \) Длина \( × \) Ширина 9{\г{2}}}\).
Периметр формы определяется как общая длина вокруг формы. Это длина фигуры, если она развернута в линейную форму.
Периметр прямоугольного поля \( = {\rm{ }}2\)(Длина \( + \) Ширина)
Что такое периметр треугольника?
Треугольник представляет собой двумерную замкнутую фигуру, имеющую три стороны и три угла.
Сумма длин всех сторон есть периметр любого многоугольника. В случае треугольника периметр треугольника \(=\) Сумма длин всех трех сторон.
Периметр любой замкнутой формы равен общей длине ее внешних линий.
Если треугольник имеет \(3\) сторон a , b и c ,
Периметр треугольника \({\rm{(P) = a + b + c}}\)
Что такое периметр прямоугольника?
Четырехугольник, у которого две пары параллельных и равных сторон и все четыре угла при вершинах прямые, называется прямоугольником .
Периметр прямоугольника равен общей длине его границы.
Периметр прямоугольника \(=\) Сумма всех четырех сторон. Если a — это длина двух противоположных сторон, а b — ширина (ширина) двух противоположных сторон.
Тогда периметр прямоугольника \({\rm{(P) = a + a + b + b = 2(a + b)}}\)
Что такое периметр квадрата?
Квадрат – это четырехугольник с четырьмя равными сторонами, и все четыре угла при вершинах прямые.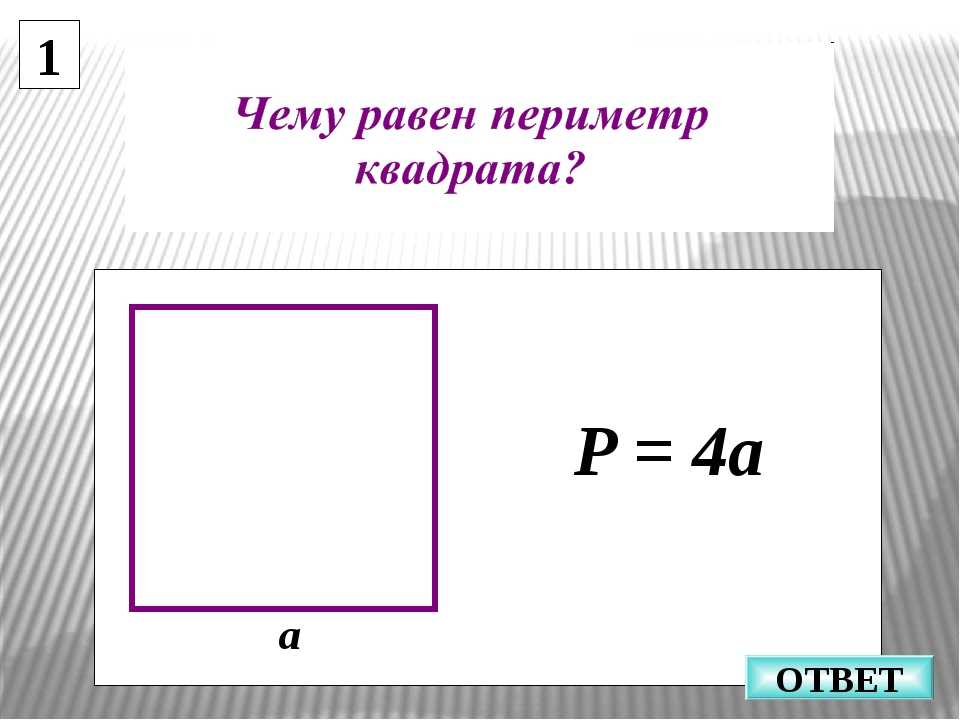
Периметр квадрата определяется как длина его границы.
Периметр \(=\) Сумма длин четырех сторон \(=a+a+a+a=4 \times a\).
Итак, периметр квадрата \({\rm{(P) = 4 a}}\) единиц, где a — длина стороны квадрата.
Что такое периметр круга?
Окружность представляет собой замкнутую двумерную круглую фигуру без угла и с центром, равноудаленным от любой точки на ее границе.
Периметр круга также называется его окружностью . Это измерение границы круга. Если мы раскроем круг и сделаем из него прямую линию, то его длина будет равна длине окружности этого круга.
Когда мы используем формулу для вычисления длины окружности, требуется радиус окружности. Итак, нам нужно знать значение радиуса \((r)\) или диаметра \((d = 2r)\), чтобы вычислить периметр круга.
Теперь периметр/длина окружности \(= 2πr\), когда радиус \(r\) известен. \(=\pi d\), когда диаметр \(d\) известен, где значение \(\pi=\frac{22}{7}\) (прибл.
)
Что такое формула периметра ?
Периметр любой двумерной фигуры равен сумме ее сторон. Формула для нахождения периметра приведена ниже:
Периметр \(=\) Сумма всех его сторон
Сведем все формулы периметра в одну таблицу. Это будет легко запомнить.
| Shape | Perimeter | Terms |
| Triangle | \(P = a + b + c\) | \(a, b\) and \(c\ ) три стороны |
| Прямоугольник | \(P = 2 \times \left( {a + b} \right)\) | \(a =\) длина \(b =\) ширина (ширина) |
| Квадрат | \(P = 4a\) | \(a =\) длина стороны |
| Окружность | Окружность \(= 2 Окружность r\) | \(r =\) радиус окружности |
Как найти периметр неправильной формы?
Периметр \(=\) Сумма всех его сторон
Чтобы получить периметр приведенной выше фигуры, сложите длины всех его сторон.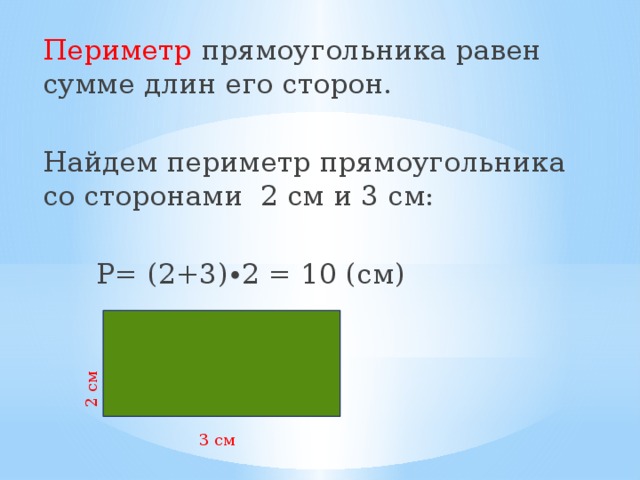
Таким образом, периметр \(=1 \mathrm{~см}+1 \mathrm{~см}+1 \mathrm{~см}+1 \mathrm{~см}+3 \mathrm{~см}+3 \mathrm{~см}+3 \mathrm{~см}+3 \mathrm{~см}\)
\(+2,5 \mathrm{~см}+2,5 \mathrm{~см}+2,5 \mathrm{~см}+2,5 \mathrm{~см}=26 \mathrm{~см}\)
Следовательно, периметр приведенной выше фигуры равен \(26 \mathrm{~cm}\).
Периметр и площадь
Площадь — это пространство, занимаемое фигурой, тогда как периметр — это общее расстояние, пройденное вокруг края фигуры.
Мы определяем площадь как количество пространства, покрытого плоской поверхностью определенной формы. Он измеряется в «количестве» квадратных единиц (квадратных сантиметров, квадратных метров, квадратных футов и т. д.). Периметр измеряется в единицах «количества» (сантиметр, метр, фут и т. д.).
Теперь взгляните на изображение, приведенное ниже, чтобы понять, что означают площадь и периметр любой формы. 1 . Если длина стороны квадрата \(12 \mathrm{~cm}\), Тогда найдите общую длину его границы .
Ans : Учитывая, что длина стороны квадрата \(=12 \mathrm{~см}\). Мы знаем, что общая длина границы называется периметром.
Периметр квадрата \(=4 \times\) стороны
Итак, периметр квадрата \(=4 \times 12 \mathrm{~cm}=48 \mathrm{~cm}\)
Следовательно, общая длина границы \(48 \mathrm{~cm}\).
Q . 2 . Если радиус окружности равен \(28 \mathrm{~cm}\). Найдите длину окружности.
Ответ : Учитывая радиус (r) окружности \(= 28 \mathrm{~cm}\).
Длина окружности называется периметром окружности.
Мы знаем, что длина окружности \(=2 \pi r\)
Теперь длина окружности \(=2 \times \frac{22}{7} \times 28 \mathrm{~cm}= 176 \mathrm{~см}\).
Следовательно, длина окружности равна \(176 \mathrm{~cm}\).
Q.3. Найдите периметр прямоугольника, если его длина \({\rm{12\,m}}\) , а ширина \({\rm{7\,m}}\) .
Ответ : Дано,
Длина прямоугольника \({\rm{= 12\,m}}\)
Ширина прямоугольника \({\rm{= 7\,m}}\)
Мы знаем, что периметр прямоугольника \( = 2 \times ({\rm{ длина }} + {\rm{ ширина }})\)
Теперь периметр прямоугольника \( = 2 \times (12\ ;{\rm{m}} + 7\;{\rm{m}}) = 2 \times 19\;{\rm{m}} = 38\;{\rm{m}}\).
Следовательно, периметр прямоугольника равен \({\rm{38\,m}}\).
Вопрос 4. Найдите периметр нижеприведенного треугольника.
Ответ: Учитывая, что три стороны треугольника равны \(5 \mathrm{~cm}, 5 \mathrm{~cm}\) и \(3 \mathrm{~cm}\) .
Мы знаем, что периметр равен сумме всех сторон
Теперь периметр треугольника \(=5 \mathrm{~cm}+5 \mathrm{~cm}+4 \mathrm{~cm}=14 \ mathrm{~cm}\)
Следовательно, периметр данного треугольника ABC равен \(14 \mathrm{~cm}\).
Q.5. Если ширина прямоугольника равна \(80\;{\rm{m}}\), а периметр равен \({\rm{360\,m}}\) .
Найдите его длину .
Ответ: Дано,
Ширина прямоугольника \({\rm{ = 80\,m}}\)
Периметр прямоугольника \({\rm{ = 360\,m}}\)
Здесь нам нужно найти его длину.
Мы знаем, что
Периметр прямоугольника \( = 2 \times ({\rm{Длина}} + {\rm{Ширина}})\)
\( \Rightarrow 360\;{\rm{m}} = 2 \times ({\rm{Длина}} + 80\;{\rm{m}})\)
\( \Rightarrow \frac{{ 360}}{2} = {\rm{Длина}} + 80\;{\rm{m}}\)
\( \Rightarrow 180 = {\rm{Длина}} + 80\;{\rm{m }}\)
\( \Rightarrow {\rm{Длина}} = 180\;{\rm{m}} – 80\;{\rm{m}} = 100\;{\rm{m}}\ )
Следовательно, длина прямоугольника равна \(100\;{\rm{m}}\).
Резюме
Эта статья поможет всесторонне научиться вычислять периметр различных геометрических фигур, таких как треугольник, круг, прямоугольник, квадрат, в зависимости от имеющейся информации о фигурах. Зная это, можно вычислить периметр любой правильной, неправильной формы, земли и т.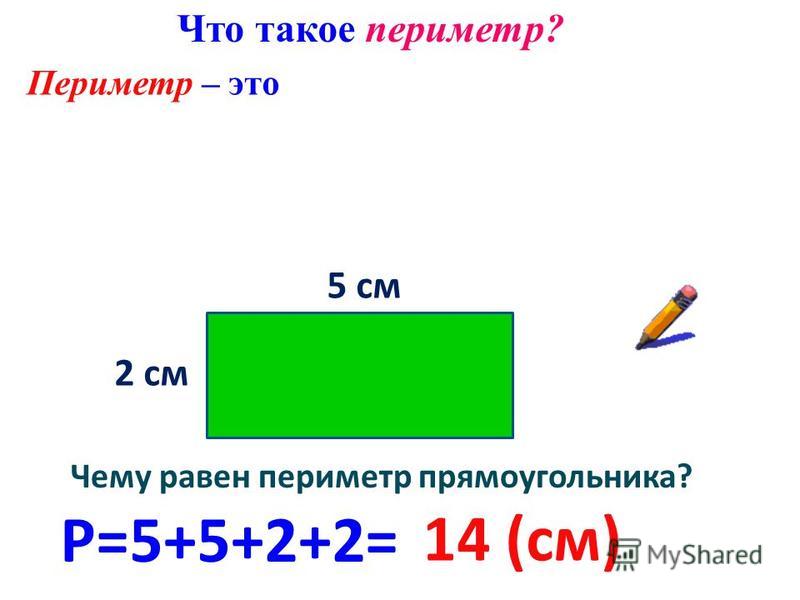
д.
Ознакомьтесь с полным списком геометрических формул
Часто задаваемые вопросы (FAQ) – Perimeter
Q.1. Чему равен периметр ABCD?
Ответ: Дано
Длина фигуры ABCD \(=4 \mathrm{~cm}\)
Так как противоположные стороны замкнутой поверхности плоскости равны, то это прямоугольник.
Мы знаем, что периметр прямоугольника \( = 2({\rm{длина}} + {\rm{ширина}})\).
Итак, периметр прямоугольника \(ABCD=2\)\((4 \mathrm{~cm}+2 \mathrm{~cm})=2 \times 6 \mathrm{~cm}=12 \mathrm{~ см}\)
Следовательно, периметр \(ABCD\) равен \(12 \mathrm{~см}\).
Q.2. Чему равен периметр фигуры B?
Ответ : Дана фигура,
Нам нужно найти периметр фигуры выше.
Здесь длина одной стороны (по вертикали) \(=14 \mathrm{~cm}\)
Остальные две части \(B\) имеют вид полукруга.
Две полукруглые части \(B\) образуют круг.
Здесь диаметр окружности \( = \frac{{14}}{2} = 7\;{\rm{см}}\)
Теперь радиус \( = \frac{7}{2} \,{\rm{cm}}\)
Теперь периметр \(B=14 \mathrm{~см}+22 \mathrm{~см}= 36 \mathrm{~см}\)
Следовательно, периметр формы \(B\) равен \(36 \mathrm{~cm}\)
Q.3. Что такое периметр в математике?
Ответ: Периметр — это длина вокруг плоскости или двумерной фигуры, ограниченной отрезками линий или кривыми.
Q.4. Как найти периметр и площадь?
Ответ: Периметр — это длина контура любой формы. Площадь – это измерение поверхности фигуры.
Мы используем формулы для нахождения периметра и площади, где форма представляет собой стандартные геометрические фигуры, такие как треугольник, квадрат, прямоугольник, круг и т.