Решение транспортной задачи в Excel (сбалансированная задача)
36047
Транспортная задача — математическая задача линейного программирования специального вида о поиске оптимального распределения однородных объектов из аккумулятора к приемникам с минимизацией затрат на перемещение.
Цитата взята с википедии.
Решение транспортной задачи рассматривается практически на всех специальностях, где хоть как-то присутствует курс математики. Решить транспортную задачу можно различными способами и программными средствами. Причем если решение такой задачи в математических пакетах типа Mathcad или MATLAB обыденное дело, то решение такой задачи в программе 1С:Предприятие 8.2 уже интересная диковинка.
Смотрите также видео версию статьи «Решение транспортной задачи в Excel (сбалансированная задача)».
Сегодня мы рассмотрим решение сбалансированной транспортной задачи в табличном процессоре MS Excel.
Есть запасы однотипной продукции у поставщиков A1, A2, A3, A4.
Существует потребность в этой продукции B1, B2, B3
Стоимость доставки единицы продукции от поставщиков к потребителям представлена в таблице.
Поставщик | Потребитель | Запас | ||
| В1 | В2 | В2 | ||
| А1 | 6 | 5 | 2 | 250 |
| А2 | 3 | 7 | 4 | 100 |
| А3 | 7 | 8 | 1 | 80 |
| А4 | 2 | 2 | 3 | 120 |
Потребность | 150 | 150 | 250 | |
Необходимо составить такой план перевозок, который бы удовлетворил все потребности и имел минимальную стоимость.
Для решения данной задачи в табличном процессоре необходимо составить две таблицы, приведенные выше, но вторую таблицу не заполнять данными.
Для решения транспортной задачи потребуются функции: СУММПРОИЗВ, СУММ и надстройка «Поиск решения».
Для отображения формул необходимо на вкладке «Формулы» в группе «Зависимости формул» выбрать «Показать формулы» либо горячее сочетание клавиш «Ctrl+` (тильда)».
Дальше выбираем команду «Поиск решения» на вкладке «Данные»
Кстати, если дать имена диапазонам ячеек, то окно поиска решения будет выглядеть следующим образом:
Решение поставленной задачи представлено ниже.
Еще записей в тему?
Если честно, некоторые могут быть не свежие:)
БОЛЬШЕ МАТЕРИАЛОВ
Решение транспортной задачи в Excel — Блог Анатолия Бузова
В этом материале попробуем разобраться, как 
Среда решения – Excel. Данный материал подходит для версий программы: 2007, 2010, 2013, 2016.
Постановка задачи и подготовка таблиц
Цель задачи сводится к математическому моделированию минимизации грузопотоков. Довольно часто студенты пишут рефераты на тему поиска решения транспортной задачи. Этот пример можно взять за основу реферата. Рассмотрим решение на конкретном примере.
Задача
В хозяйстве имеются 5 складов минеральных удобрений и 4 пункта, в которые необходимо доставить удобрения. Потребность каждого пункта в удобрениях различна, а так же запасы на каждом складе ограничены. Требуется определить, с какого склада, в какой пункт поставлять, сколько удобрений для минимализации грузооборота перевозок.
Исходные данные:
Наличие минеральных удобрений (либо иной продукции) на складах.
| Склады | Наличие удобрений, т. |
| Склад № 1 | 200 |
| Склад № 2 | 190 |
| Склад № 3 | 220 |
| Склад № 4 | 145 |
| Склад № 5 | 280 |
Потребность в минеральных удобрениях на различных пунктах.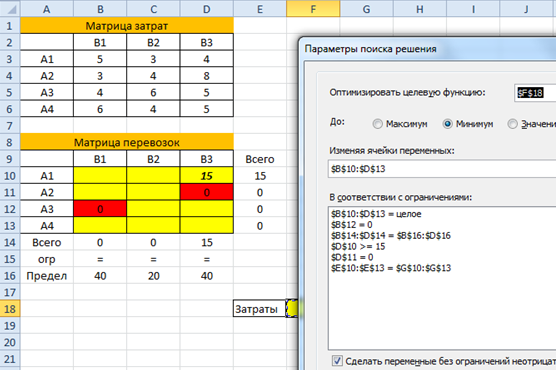
| Пункты | Потребность в удобрениях |
| 1 пункт | 200 |
| 2 пункт | 150 |
| 3 пункт | 220 |
| 4 пункт | 330 |
Расстояние между складами и пунктами доставки
| Пункт 1 | Пункт 2 | Пункт 3 | Пункт 4 | |
| Склад № 1 | 6 | 4 | 5 | 11 |
| Склад № 2 | 12 | 6 | 4 | |
| Склад № 3 | 15 | 7 | 10 | 4 |
| Склад № 4 | 9 | 5 | 12 | 5 |
| Склад № 5 | 3 | 7 | 12 | 11 |
Данные в таблицах. На пересечении столбца конкретного пункта доставки со строкой склада находится информация о расстоянии между этим пунктом доставки и складом. Например, расстояние между 3 пунктом и складом № 3 равно 10 километрам.
Пошаговое решение в Excel
Подготовим таблицы для решения задачи.
Рисунок 1. Изменяемые ячейки.Значения ячеек в столбце B с третьей по седьмую определяют сумму значения соответствующих строк со столбца C до столбца F.
Например, значение ячейки B3=СУММ(C4:F4)
Аналогично значения в восьмой строке, складываются из суммы соответствующих столбцов. Далее создадим еще одну таблицу.
Рисунок 2. Исходная информация в Excel
В строке 16 по столбцам C-F определим грузооборот по каждому пункты доставки. Например, для пункта 1 (ячейка С16) это рассчитывается по формуле:
C16==C3*C11+C4*C12+C5*C13+C6*C14+C7*C15
Либо, это можно рассчитать с помощью функции СУММПРОИЗВ:
C16 =СУММПРОИЗВ(C3:C7;C11:C15)
В ячейке B4 находится количество минеральных удобрений, перевозимых со склада № 1 в 1 пункт доставки, а в ячейке C11 — расстояние от склада №1 до 1 пункта доставки. Соответственно первое слагаемое в формуле означает полный грузооборот по данному маршруту.
Вся же формула вычисляет полный грузооборот перевозок минеральных удобрений в 1 пункт доставки.
В ячейке B16 по формуле =СУММ(C16:F16) будет вычисляться общий объем грузооборота минеральных удобрений. Рабочий лист примет следующий вид.
Рисунок 3. Рабочий лист, приготовленный для решения транспортной задачи.Для решения транспортной задачи воспользуемся процедурой Поиск решения, которая находится на вкладке Данные. Если у вас нет процедуры Поиск решения, необходимо зайти в Параметры Excel -> Надстройки — > Поиск решения.
После выбора данной процедуры на вкладке Данные откроется диалоговое окно.
Выберем целевую ячейку $B$16, установим ее равной минимальному значению, что бы минимизировать значение конечной ячейки, путем изменения влияющих ячеек, изменяя ячейки, выберем диапазон с единицами $C$3:$F$7.
Рисунок 5. Условия для решения транспортной задачи.Если запустить процесс, то мы получим параметры равные нулям. Для получения необходимых значений установим некоторые ограничения:
- $B$3:$B$7 <= $B$11:$B$15
- $C$3:$F$7 >= 0
- $C$8:$F$8 >= $C$10:$F$10
После всех установок нажмем «Выполнить» и получаем результат.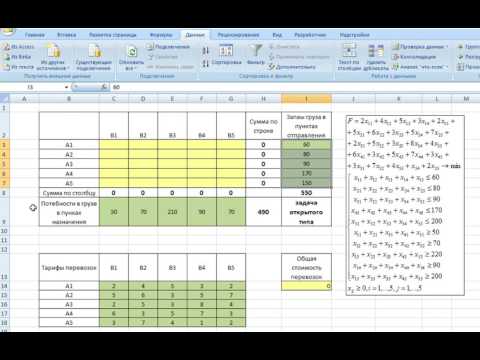
Транспортная задача в Excel (простой учебник)
Формулировка модели | Проб и ошибок | Решите модель
Используйте решатель в Excel , чтобы найти количество единиц, отправляемых с каждого завода каждому клиенту, которое минимизирует общую стоимость.
Формулировка модели
Модель, которую мы собираемся решить, выглядит в Excel следующим образом.
1. Чтобы сформулировать эту транспортную задачу , ответьте на следующие три вопроса.
а. Какие решения предстоит принять? Для решения этой задачи нам понадобится Excel, чтобы узнать, сколько единиц продукции нужно отправить с каждой фабрики каждому покупателю.
б. Каковы ограничения для этих решений? Каждая фабрика имеет фиксированное предложение, а каждый клиент имеет фиксированный спрос.
в. Какова общая мера эффективности этих решений? Общая мера производительности — это общая стоимость поставок, поэтому цель состоит в том, чтобы минимизировать это количество.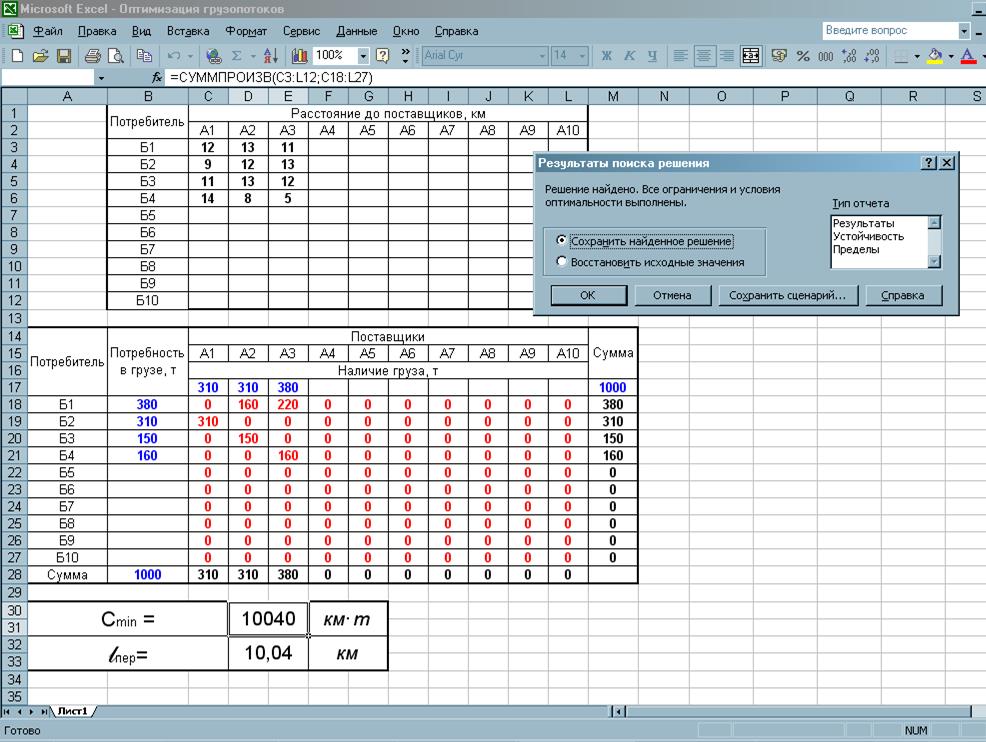
2. Чтобы упростить понимание модели, создайте следующие именованные диапазоны.
| Название диапазона | Ячейки |
|---|---|
| Стоимость единицы | С4:Е6 |
| Отгрузки | С10:Е12 |
| Итого | С14:Е14 |
| Спрос | С16:Е16 |
| Итого | G10:G12 |
| Поставка | И10:И12 |
| Общая стоимость | И16 |
3. Вставьте следующие функции.
Объяснение: Функции СУММ вычисляют общее количество, отгруженное с каждого завода (Всего на выходе) каждому клиенту (Всего на входе).
Общая стоимость равна сумме Удельной стоимости и Отгрузок.
Пробы и ошибки
Благодаря этой формулировке становится легко анализировать любое пробное решение.
Например, если мы отправляем 100 единиц с завода 1 заказчику 1, 200 единиц с завода 2 заказчику 2, 100 единиц с завода 3 заказчику 1 и 200 единиц с завода 3 заказчику 3, общий объем поставки равен поставке и общему объему. В равном спросе. Это решение имеет общую стоимость 27800.
Нет необходимости использовать метод проб и ошибок. Далее мы опишем, как Excel Solver можно использовать для быстрого поиска оптимального решения.
Решение модели
Чтобы найти оптимальное решение, выполните следующие шаги.
1. На вкладке Данные в группе Анализ щелкните Решатель.
Примечание: не можете найти кнопку Решатель? Нажмите здесь, чтобы загрузить надстройку Solver.
Введите параметры решателя (читайте дальше). Результат должен соответствовать картинке ниже.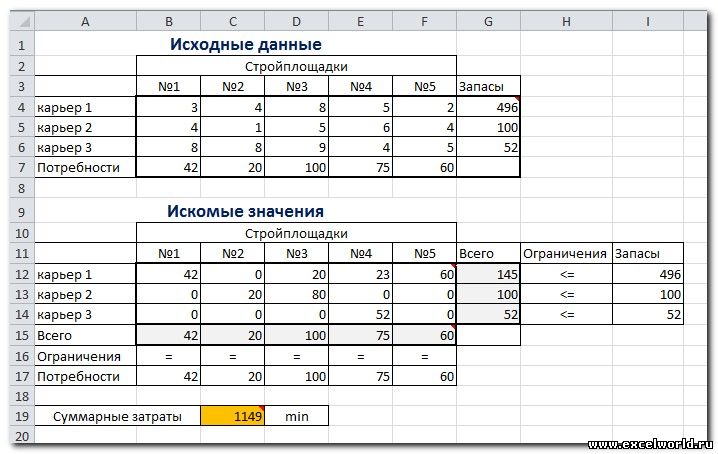
У вас есть выбор: ввести имена диапазонов или щелкнуть ячейки в электронной таблице.
2. Введите TotalCost для цели.
3. Щелкните Мин.
4. Введите отгрузки для меняющихся переменных ячеек.
5. Щелкните Добавить, чтобы ввести следующее ограничение.
6. Щелкните Добавить, чтобы ввести следующее ограничение.
7. Установите флажок «Сделать переменные без ограничений неотрицательными» и выберите «Симплекс LP».
8. Наконец, нажмите «Решить».
Результат:
Оптимальное решение:
Вывод: оптимально отгрузить 100 шт. с завода 1 заказчику 2, 100 шт. с завода 2 заказчику 2, 100 шт. с завода 2 заказчику 3, 200 шт. с завода 3 заказчику 1 и 100 шт. Заказчику 3. Это решение дает минимальную стоимость 26000. Все ограничения соблюдены.
Как решить транспортную задачу с помощью Microsoft Excel
Логистика — важная функция в обрабатывающей промышленности, поскольку она влияет на общую эффективность и конкурентоспособность вовлеченных фирм.
Подготовка оптимальных планов транспортировки может рассматриваться как отправная точка в достижении эффективности управления логистикой. Различные инструменты и методы, связанные с промышленным проектированием и исследованием операций, используются для улучшения планирования логистики и транспортировки. В этой статье объясняется, как можно решить базовую транспортную задачу с помощью довольно распространенного инструмента анализа Microsoft Excel. Статья ориентирована на специалистов-практиков в области логистики и представлена без углубления в теорию и математические формулировки, связанные с проблемой.
Предположим, что у компании есть три завода в точках X, Y и Z, которые производят определенный тип продукта. Этот продукт должен быть доставлен четырем покупателям в четырех разных точках A, B, C и D. Нам известны затраты на транспортировку единицы продукции от каждой фабрики к каждому покупателю. Транспортные расходы на единицу продукции (в индийских рупиях) приведены в таблице 1.
Ежедневная поставка с завода является фиксированной из-за ограничений его мощности. Поставки с заводов X, Y и Z составляют 150, 250 и 100 единиц соответственно. Далее, у каждого заказчика есть определенный спрос. Здесь спрос клиентов в точках A, B, C и D равен 50, 100, 200 и 150 соответственно.
Задача состоит в том, чтобы определить количество единиц продукта, которое необходимо транспортировать с каждой фабрики каждому покупателю, чтобы минимизировать общие транспортные расходы. Здесь мы предполагаем, что общее предложение от разных фабрик и общий спрос покупателей равны. Этот тип задачи известен как сбалансированная транспортная задача. Проблема может быть легко решена с помощью Microsoft Excel и описана ниже.
Откройте Microsoft Excel и введите указанные данные. На рис. 1 представлен скриншот шаблона Excel, который можно использовать для решения настоящей проблемы. Вводятся удельные затраты на транспортировку продукта, поставка с разных заводов и спрос в разных местах клиентов.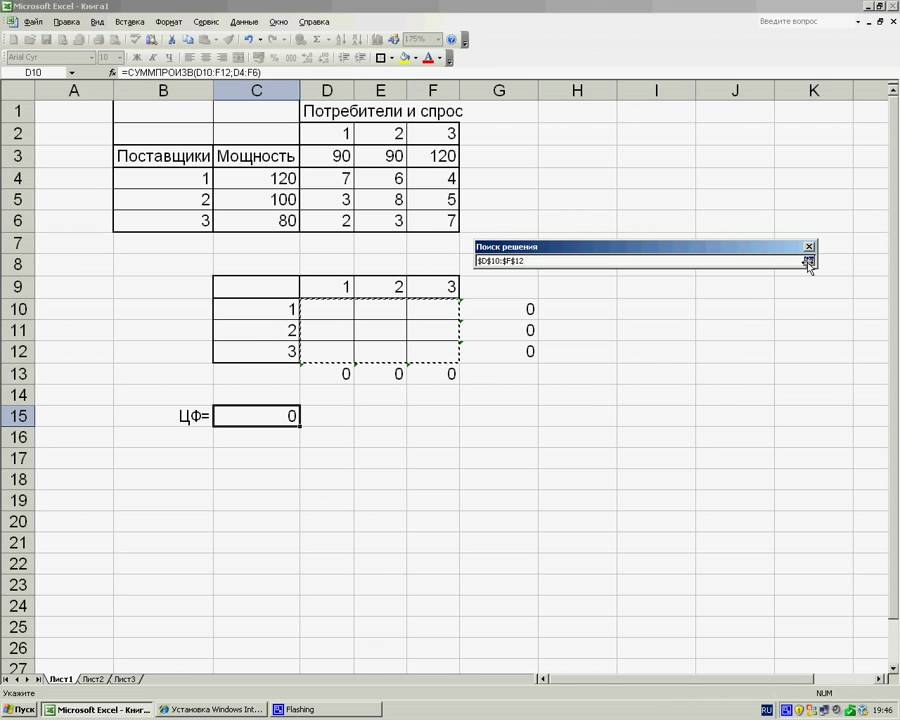
Для удобства пользователя диапазоны ячеек различных входных данных представлены следующим образом:
Ячейки в разделе «Распределение» предназначены для отображения решения задачи. В ячейках, заштрихованных оранжевым цветом, отображается количество единиц продукта, которое необходимо транспортировать с каждого завода до каждого места клиента. Сумма строк и сумма столбцов ячеек распределения также вычисляются. Сумма в строке дает общее предложение, произведенное с каждой фабрики (ячейки со светло-голубым цветом), а сумма в столбце показывает спрос, удовлетворяемый в каждом местоположении клиента (ячейки со светло-зеленым цветом). Далее общая стоимость будет отображаться в ячейке, заштрихованной желтым цветом. Ячейки, предназначенные для отображения решения, следующие:
Теперь давайте посмотрим, как определены ячейки для представления общей стоимости, произведенного предложения и удовлетворенного спроса.
После ввода этих формул в соответствующих ячейках будет отображаться значение «0», пока проблема не будет решена.
Чтобы решить проблему, перейдите к параметру «Поиск решения» в «Данные» (надстройка «Поиск решения» должна быть загружена в Excel)
Затем откроется диалоговое окно «Параметры решения». Данные, которые необходимо ввести в диалоговое окно, приведены ниже. Он также показан на рис. 2.
«С учетом ограничений»: ограничения связаны со спросом и предложением. Сумма строк ячеек распределения должна быть равна поставке каждой фабрики, а сумма столбцов ячеек распределения должна быть равна спросу в каждом местоположении клиента. Чтобы указать это, нажмите на опцию «Добавить». Затем появляется диалоговое окно для ввода ограничения (рис. 3). В опции «Ссылка на ячейку» выберите ячейку со значением суммы столбца (требование выполнено). Выберите знак равенства «=» из следующего выпадающего списка. В опции «Ограничение» выберите ячейку со значением Спроса. Затем нажмите «ОК». Повторите процедуру, чтобы добавить все ограничения, связанные со спросом и предложением. Обратитесь к рисунку 2, чтобы увидеть полный список ограничений.
Решатель решит проблему, и откроется диалоговое окно «Результаты решателя», как показано на рисунке 4. В нем выберите «Сохранить решение решателя» и нажмите «ОК».
Теперь решение будет отображаться в файле Excel. См. рис. 5. Из решения можно узнать количество единиц продукта, которое необходимо транспортировать с каждого завода к каждому клиенту. Также отображается соответствующая общая стоимость (45 000 индийских рупий). Можно заметить, что значения «Сделано предложения» (сумма строки) и «Предложение» и «Удовлетворенный спрос» (сумма столбца) и «Спрос» равны во всех ячейках. Это гарантирует соблюдение ограничений, связанных со спросом и предложением, при создании решения. Таким образом, получается оптимальное решение.
Если вы знаете какой-либо предмет, который может быть связан с обрабатывающей промышленностью или промышленным проектированием, вы можете получить некоторый доход, став автором статей на этом веб-сайте. Чтобы узнать больше об этом, пожалуйста, посетите страницу Присоединяйтесь к нам.