Графики функции, производной, первообразной — Умскул Учебник
На этой странице вы узнаете- Где проходит граница между теплом и холодом?
- Почему успех фильма не всегда зависит от наличия экшн-сцен?
- Чем кофе похож на функцию, ее первообразную и производную?
Многие из нас чем-то похожи на родителей. Не являясь их точной копией, мы перенимаем определенные черты. То же самое происходит и с графиками. О том, какие особенности “наследуют” друг у друга графики функции, производной и первообразной, поговорим в статье.
Связь графика функции и производнойПодготовим карандаши и линейки, мы начинаем погружение в мир графиков. Почему графики — это круто? Они дают нам наглядное представление о функции. Мы можем проанализировать ее, не прибегая к сложным формулам и трудоемким вычислениям.
Воспринимать визуальную информацию всегда легче. А графики — это как раз визуальное описание функции.
А графики — это как раз визуальное описание функции.
Возьмем график произвольной функции.
Прежде чем приступать к дальнейшему изучению материала, рекомендуем ознакомиться с «Определением и графиком функции», а также «Производной».
Мы точно видим, на каких промежутках график будет возрастать, а на каких убывать. Если представить, что мы пойдем по направлению оси х, то график будет возрастать на подъемах в горку и убывать на спусках с нее. Отметим промежутки возрастания зеленым фоном, а промежутки убывания красным.
В зеленых промежутках производная будет положительна, а в красных отрицательна. Пока что просто запомним этот факт.
Обратим внимание на границы между зелеными и красными зонами. В этих точках функция будет менять свой знак с положительного на отрицательный или обратно. Такие точки называются точками экстремума.
Экстремум — это точка, в которой достигается максимальное или минимальное значение функции на заданном отрезке.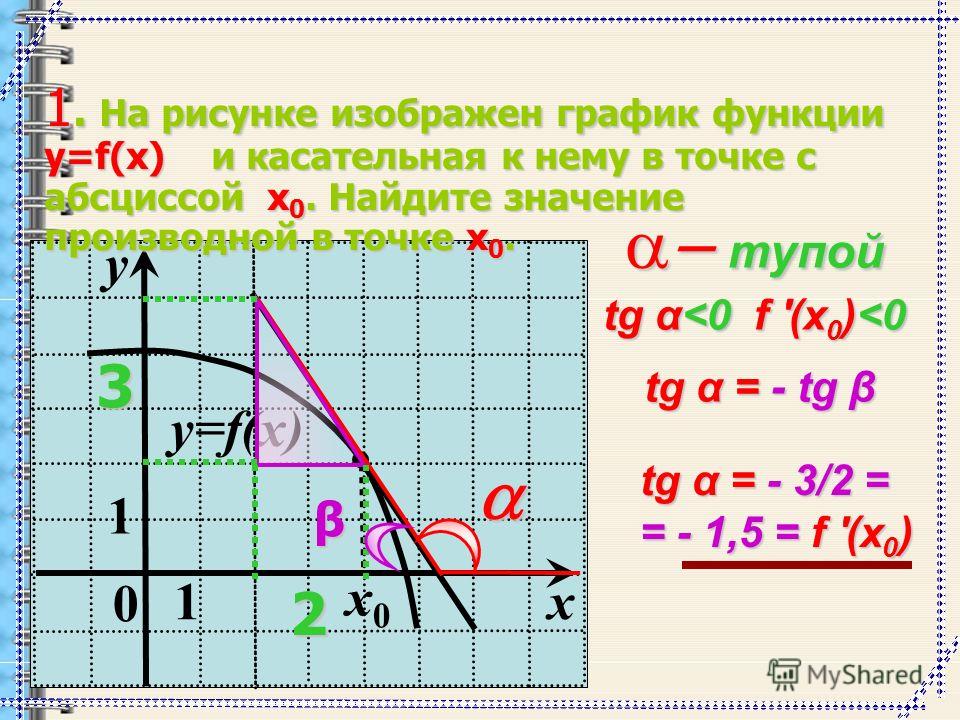
Точки экстремума — точки, в которых достигается экстремум.
В точках экстремума производная равна 0.
Теперь попробуем построить примерный график производной. Для начала опустим точки экстремума. Где они будут лежать на графике производной? На оси х.
Вспомним, что в точках экстремума производная функции будет равна 0. Пусть график будет задан
y = f'(x), тогда в точках экстремума получаем y = 0. Это и есть ось х.
Так мы получили целых 9 точек, через которые пройдет производная. Осталось провести через них примерный график.
Вспомним, что:
- производная положительна на промежутках возрастания функции;
- производная отрицательна на промежутках убывания функции.
Как понять, что все точки на графике производной будут положительны или отрицательны? Достаточно посмотреть на то, с какой стороны от оси х они располагаются.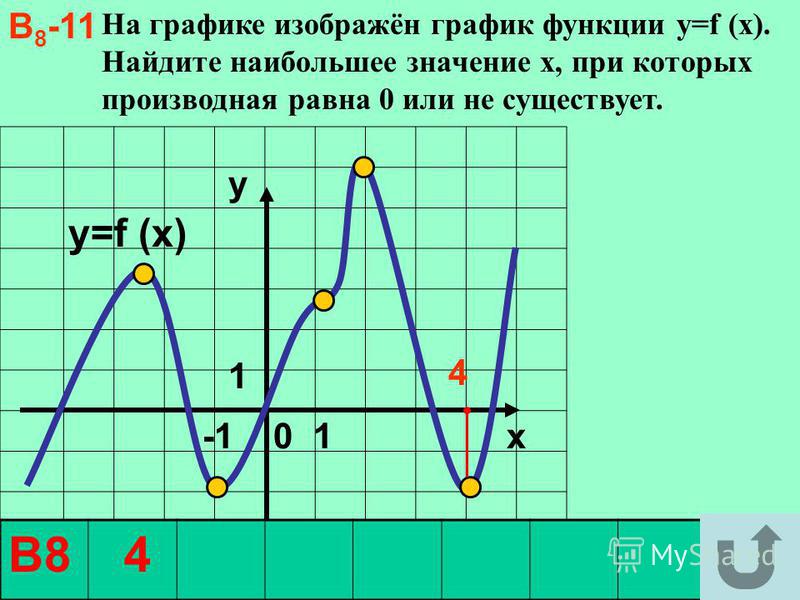
Положительные значения всегда будут лежать выше оси х. Это связано со значением y: значения функции будут положительны при положительных значениях у, и отрицательны при отрицательных значениях у.
| Где проходит граница между теплом и холодом? Можно представить, что ось х — это полюс, который разделяет тропики и льды. Над осью х всегда будет светить солнце, а температура будет положительной. А вот под осью х всегда будут льды и снега, и температура — отрицательной. Следовательно, знак производной на ее графике будет совпадать со знаком температуры в тропиках или льдах. |
Итак, как нам нарисовать график производной? На зеленых участках ее график будет лежать над осью х, а на красных участках — под ней.
Подведем итоги:
- В точках экстремума функции график производной будет проходить через ось х.

- На промежутках возрастания функции график производной будет лежать выше оси х.
- На промежутках убывания функции график производной будет лежать ниже оси х.
Эти зависимости можно отследить на любых графиках функции и ее производной.
Если провести обратные рассуждения, то по графику производной можно восстановить примерный график функции. В этом случае:
- В точках, где график производной пересекает ось х, будут лежать точки экстремума. При этом если в точке производная меняет значение с положительного на отрицательное, то это точка максимума, а если с отрицательного на положительное, то это точка минимума.
- На промежутках, где график производной будет лежать выше оси х, функция будет возрастать.
- На промежутках, где график производной будет лежать ниже оси х, функция будет убывать.
Разберем несколько примеров, где можно применить эти знания.
Пример 1. На рисунке изображен график функции f(x) и отмечены пять точек на оси абсцисс: x1, x2, x3, x4, x5. В скольких из этих точек производная функции отрицательна?
Решение. Производная отрицательна на промежутках убывания функции. Отметим такие промежутки.
В точках, которые попали в эти промежутки, производная отрицательная. Всего таких точек 2.
Ответ: 2
Пример 2. На рисунке изображен график функции y = f'(x) — производной функции f(x), определенной на интервале (-5; 3). Найдите точку максимума функции f(x).
Решение. Точки экстремума на графике производной лежат на оси х. На данном графике таких точки две: x = -2, x = 2.
Точка максимума — это точка, в которой производная меняет знак с положительного на отрицательный. По графику определяем, что это точка x = -2.
Ответ: -2
| Почему успех фильма не всегда зависит от наличия экшн-сцен? Представим, что мы составили графики “Заинтересованность зрителей фильмом” и “Наличие в фильме экшн-сцен”. Экшн-сцены могут вызывать интерес у зрителей, равно как и романтические сцены или смешные повороты сюжета. Получается, что наличие экшн-сцен и заинтересованность фильмом — это разные величины в кинематографе, хотя и связаны между собой. Также и графики производной и функции: они зависят друг от друга, но иллюстрируют совсем разные свойства функции, поэтому сильно отличаются. |
Мы разобрались, как связаны графики функции и ее производной. Есть ли связь между графиком функции и «Первообразной»?
Вспомним один важный факт: если взять производную от первообразной, то получим функцию.
F'(x) = f(x)
Похоже на функцию и ее производную, верно? На самом деле, ситуации ничем не отличаются.
В этом случае изначальной функцией будет первообразная, а ее производной — функция. Для наглядности составим таблицу.
| Было | Взяли производную | Стало | |
| Функция и производная | f(x) | f'(x) | f'(x) |
| Функция и первообразная | F(x) | F'(x) | f(x) |
Получается, для функции и первообразной будут действовать почти те же правила, что и для функции и ее производной.
При решении заданий с графиками первообразной достаточно проанализировать уравнение F'(x) = f(x). Рассмотрим несколько примеров.
Пример 3. На рисунке изображен график функции y = F(x) — одной из первообразных функции f(x) и отмечены шесть точек на оси абсцисс x1, x2, x3, x4, x5, x6. В скольких из этих точек функция f(x) отрицательна?
Решение. Поскольку F'(x) = f(x), то функция f(x) будет отрицательна в тех же точках, в которых будет отрицательна F'(x).
Поскольку на графике изображена функция y = F(x), то ее производная будет отрицательна на промежутках убывания функции. Отметим их красным.
В эти промежутки попадают 3 из 6 точек.
Ответ: 3.
Пример 4. На рисунке изображен график функции y = F(x) — одной из первообразных функции f(x), определенной на интервале (-6; 7). Пользуясь рисунком, определите количество решений уравнения f(x) = 0 на отрезке [-5; 4].
Решение. Вспомним, что F'(x) = f(x). Тогда если f(x) = 0, то и F'(x) = 0. Следовательно, на заданном промежутке нужно найти точки экстремума.
Отметим заданный промежуток красными линиями. На промежутке всего 9 точек экстремума, значит, в 9 точках f(x) будет равна 0.
Ответ: 9
| Чем кофе похож на функцию, ее первообразную и производную? Представим, что в качестве функции у нас выступают кофейные зерна. Тогда производная — то, что мы получаем в результате их переработки — это вкусный напиток. Из чего получаются сами кофейные зерна? Их собирают с кофейного дерева. То есть зерна будут производной от кофейного дерева, а кофейное дерево — это первообразная. Так мы можем отследить следующую цепочку: кофейное дерево → кофейные зерна → кофе. И эта цепочка наглядно иллюстрирует связь первообразной, функции и ее производной. |
- Графики функции, производной и первообразной связаны между собой.

- В точках экстремума функции график производной будет проходить через ось х.
- На промежутках возрастания функции график производной будет лежать выше оси х.
- На промежутках убывания функции график производной будет лежать ниже оси х.
- Для решения задач с первообразной необходимо вспомнить, что F'(x) = f(x). Любой график можно проанализировать с помощью этого уравнения также, как анализируются графики функции и ее производной.
Задание 1.
На каких промежутках будет производная функции будет положительна?
- На промежутках убывания функции.
- На промежутках возрастания функции.
- В точках экстремума.
- Невозможно определить по графику.
Задание 2.
На каких промежутках производная функции будет отрицательна?
- На промежутках возрастания функции.

- На промежутках убывания функции.
- В точках экстремума.
- Невозможно определить по графику.
Задание 3.
На рисунке изображен график производной функции f(x), на котором отмечена точка. Чем будет являться эта точка для функции f(x)?
- Точка максимума функции.
- Точка минимума функции.
- Любая произвольная точка на функции.
- Невозможно определить по графику.
Задание 4.
Выберите верный вариант:
- F(x) = f'(x)
- F(x) = f(x)
- F'(x) = f'(x)
- F'(x) = f(x)
Ответы: 1. — 2 2. — 2 3. — 1 4. — 4
Задание № 7. Производная функции. ЕГЭ . Математика. 2
1. Планиметрия
2. Стереометрия
3. Начала теории вероятностей
4. Теория вероятностей
5. Простейшие уравнения
6. Преобразование выражений
7. Производная функции
Производная функции
8. Практические задачи
9. Текствые задачи
10. Графики функций
11. Исследование функций
12. Уравнения
13. Стереометрия с доказ-вом
14. Неравенства
15. Финансовая математика
16. Планиметрия с доказ-вом
17. Задачи с параметром
18. Задачи на логику
Задание № 7. Производная функции.
26. На рисунке изображён график функции y=f(x). На оси абсцисс отмечены восемь точек: x1, x2, x3, x4, x5, x6, x7, x8. В скольких из этих точек производная функции f(x) отрицательна?
Ответ: 4
27. На рисунке изображён график функции y=f(x). На оси абсцисс отмечены десять точек: x1, x2, x3, x4, x5, x6, x7, x8, x9, x10. В скольких из этих точек производная функции f(x) положительна?
На рисунке изображён график функции y=f(x). На оси абсцисс отмечены десять точек: x1, x2, x3, x4, x5, x6, x7, x8, x9, x10. В скольких из этих точек производная функции f(x) положительна?
Ответ: 3
28. На рисунке изображён график дифференцируемой функции y=f(x) и отмечены девять точек на оси абсцисс: x1, x2, x3, x4, x5, x6, x7, x8, x9. В скольких из этих точек производная функции f(x) положительна?
Ответ: 4
29. На рисунке изображён график дифференцируемой функции y=f(x) и отмеченышесть точек на оси абсцисс: x1, x2, x3, x4, x5, x6.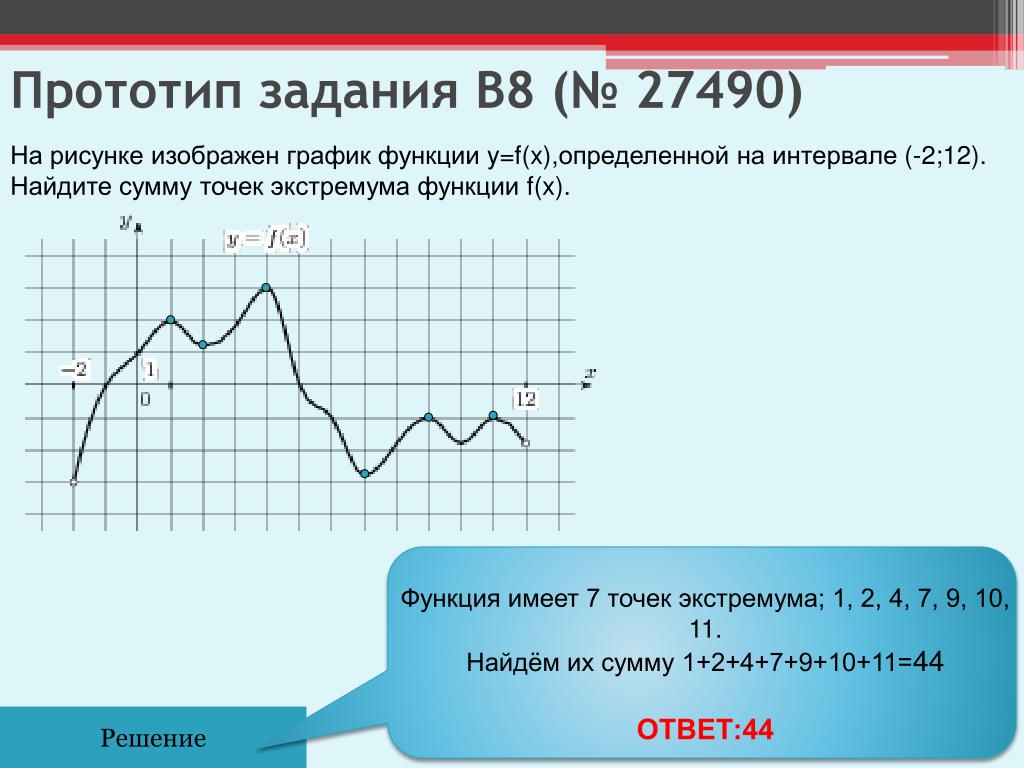 В скольких из этих точек производная функции f(x) отрицательна?
В скольких из этих точек производная функции f(x) отрицательна?
Ответ: 3
30. На рисунке изображён график y=f '(x) — производной функции
Ответ: 3
31. На рисунке изображён график y=f '(x) — производной функции f(x). На оси абсцисс отмечено семь точек: x1, x2, x3, x4, x5, x6, x7. Сколько из этих точек принадлежит промежуткам убывания функции f(x)?
Ответ: 2
32. На рисунке изображён график y=f '(x) — производной функции f(x).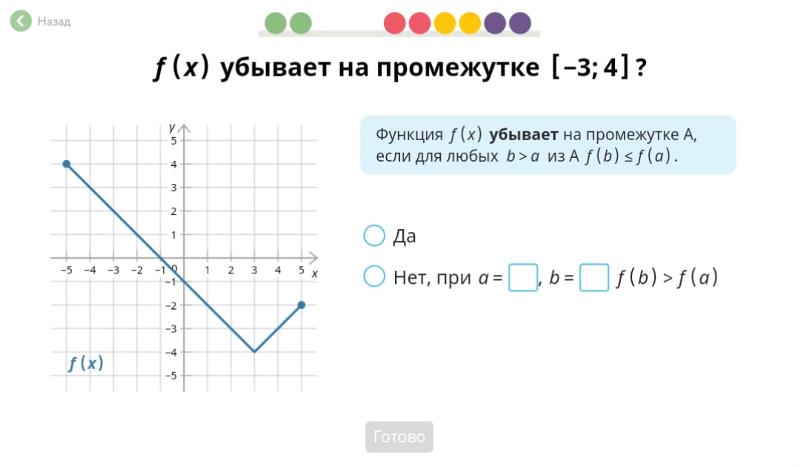 На оси абсцисс отмечено восемь точек: x1, x2, x3, x4, x5, x6, x7, x8. Сколько из этих точек принадлежит промежуткам возрастания функции f(x)?
На оси абсцисс отмечено восемь точек: x1, x2, x3, x4, x5, x6, x7, x8. Сколько из этих точек принадлежит промежуткам возрастания функции f(x)?
Ответ: 4
33. На рисунке изображён график y=f '(x) — производной функции f(x). На оси абсцисс отмечено одиннадцать точек: x1, x2, x3, x4, x5, x6, x7, x8, x9, x10, x11. Сколько из этих точек принадлежит промежуткам убывания функции f(x)?
Ответ: 9
34. На рисунке изображён график функции y=f(x). На оси абсцисс отмечены точки − 1, 2, 3, 4. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.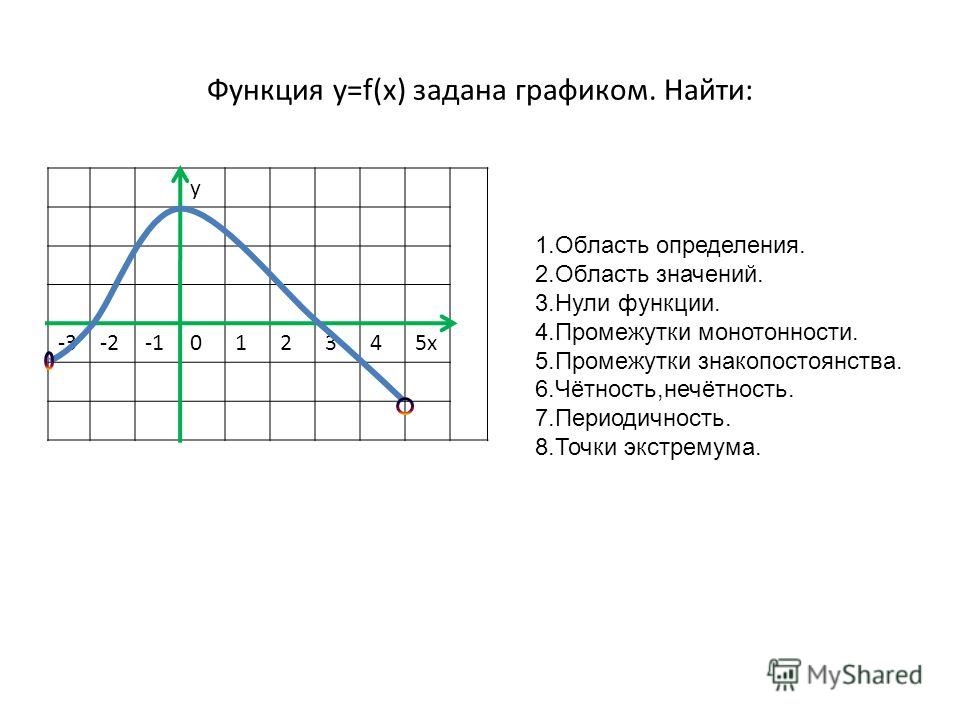
Ответ: -1
35. На рисунке изображён график функции y=f(x). На оси абсцисс отмечены точки − 2, − 1, 3, 4. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.
Ответ: -1
36. На рисунке изображен график функции y=f(x) и отмечены точки -2, -1, 1, 4. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.
Ответ: 4
37. На рисунке изображен график функции y=f(x) и отмечены точки -2, -1, 1, 2. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.
Ответ: -2
38. На рисунке изображён график y=f '(x) — производной функции f(x), определённой на интервале (− 2; 9). В какой точке отрезка [2; 8] функция f(x) принимает наибольшее значение?
Ответ: 8
39.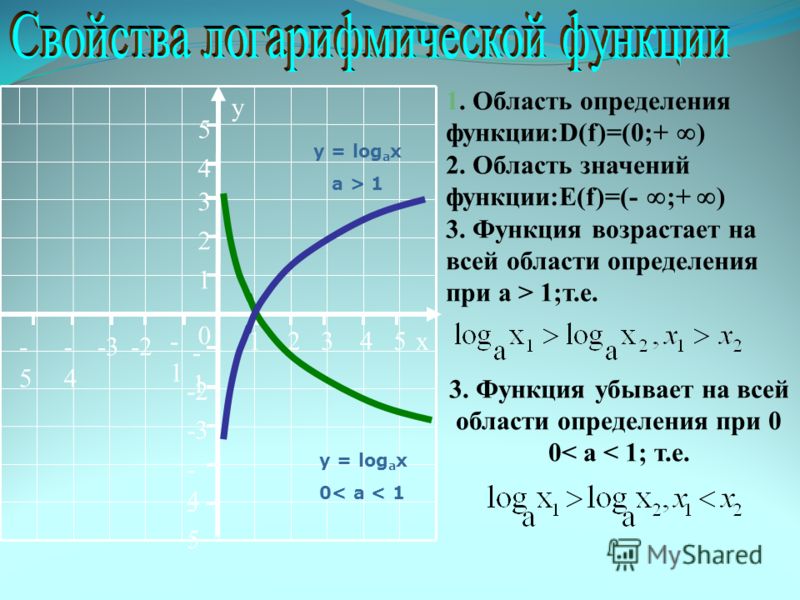 На рисунке изображён график y=f '(x) — производной функции f(x), определённой на интервале (− 8; 4). В какой точке отрезка [− 2; 3] функция f(x) принимает наименьшее значение?
На рисунке изображён график y=f '(x) — производной функции f(x), определённой на интервале (− 8; 4). В какой точке отрезка [− 2; 3] функция f(x) принимает наименьшее значение?
Ответ: -2
40. На рисунке изображён график y=f '(x) — производной функции f(x), определённой на интервале (− 3; 8). В какой точке отрезка [− 2; 3] функция f(x) принимает наименьшее значение?
Ответ: 3
41. На рисунке изображён график y=f '(x) — производной функции
Ответ: -6
42. На рисунке изображён график y=f '(x) — производной функции f(x), определённой на интервале (−9; 8). Найдите точку экстремума функции f(x) на отрезке [−3; 3].
Найдите точку экстремума функции f(x) на отрезке [−3; 3].
Ответ: -2
43. На рисунке изображён график y=f '(x) — производной функции f(x), определенной на интервале (-11;11). Найдите количество точек экстремума функции f(x) на отрезке [-10;10].
Ответ: 5
44. На рисунке изображён график y=f '(x) — производной функции f(x), определённой на интервале (− 11; 6). Найдите количество точек минимума функции f(x), принадлежащих отрезку [− 6; 4].
Ответ: 1
45. На рисунке изображён график y=f '(x) — производной функции f(x), определённой на интервале (− 3; 19). Найдите количество точек максимума функции f(x), принадлежащих отрезку [− 2; 15].
Найдите количество точек максимума функции f(x), принадлежащих отрезку [− 2; 15].
Ответ: 1
46. На рисунке изображён график y=f '(x) — производной функции f(x), определенной на интервале (-11;3). Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.
Ответ: 6
47. На рисунке изображён график y=f '(x) — производной функции f(x), определенной на интервале (-2;12). Найдите промежутки убывания функции f(x). В ответе укажите длину наибольшего из них.
Ответ: 6
48. На рисунке изображён график y=f '(x) — производной функции f(x), определённой на интервале (− 2; 11). Найдите абсциссу точки, в которой касательная к графику функции y=f(x) параллельна оси абсцисс или совпадает с ней.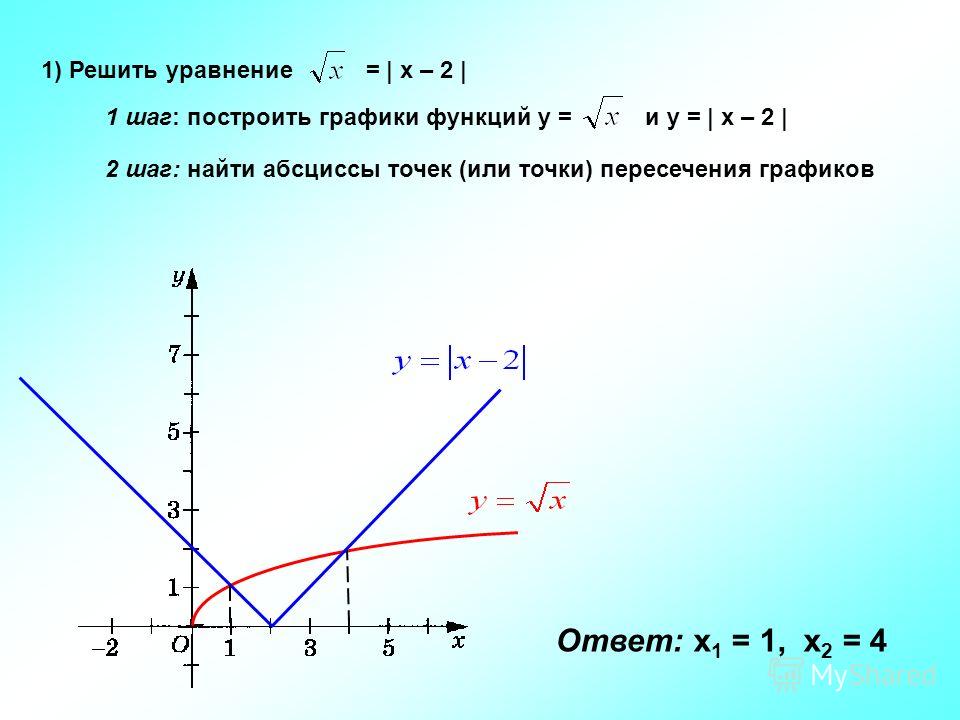
Ответ: 3
49. На рисунке изображён график y=f '(x) — производной функции f(x), определённой на интервале (− 4; 13)
. Найдите количество точек, в которых касательная к графику функции y=f(x) параллельна прямой y=−2x−10 или совпадает с ней.Ответ: 5
50. На рисунке изображён график функции y=f(x), определённой на интервале (− 4; 13). Определите количество точек, в которых касательная к графику функции y=f(x) параллельна прямой y=14.
Ответ: 6
1 2 3
Главная
Ответы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука
| Похожие вопросы |
Боковое ребро правильной треугольной призмы равно 9 см,а диагональ боковой грани равна 15 см. 2 . Найдите радиус соответствующего круга.
2 . Найдите радиус соответствующего круга.
Пользуйтесь нашим приложением
Урок 10. определение производной. физический смысл производной — Алгебра и начала математического анализа — 11 класс
Алгебра и начала математического анализа, 11 класс
Урок №10. Определение производной. Физический смысл производной.
Перечень вопросов, рассматриваемых в теме
1) Определение производной;
2) Физический смысл производной;
2) Приращение функции;
3) Скорость материальной точки в заданный момент времени по данному закону движения.
Глоссарий по теме
Пусть функция y=f(x) определена в точках x0 и x1. Разность x1−x0 называют приращением аргумента (при переходе от точки x0 к точке x1), а разность f(x1)-f(x0) называют приращением функции.
Определение. Производной функции называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
Основная литература:
Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
Дополнительная литература:
Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2017.
Теоретический материал для самостоятельного изучения
Изучая поведение функции y=f(x) около конкретной точки x0, важно знать, как меняется значение функции при изменении значения аргумента. Для этого используют понятия приращений аргумента и функции.
Пусть функция y=f(x) определена в точках x0 и x1. Разность x1−x0 называют приращением аргумента (при переходе от точки x0 к точке x1), а разность f(x1)-f(x0) называют приращением функции.
Приращение аргумента обозначают Δx (читают: дельта икс; Δ — прописная буква греческого алфавита «дельта»; соответствующая строчная буква пишется так: δ). Приращение функции обозначают Δy или Δf.
Итак, x1-x0=Δx, значит, x1=x0+Δx.
f(x1)-f(x0)=Δy, значит,
Δy=f(x0+Δx)-f(x0). (1)
Нельзя истолковывать термин «приращение» как «прирост».
Примеры и разбор решения заданий тренировочного модуля
Пример 1.
Найдем приращение Δx и Δf в точке x0, если f(x)= x2, x0=2 и х=1,9
Решение:
Δx= x1−x0=1,9-2=-0,1
Δf= f(1,9) –f(2)=1,92-22=-0,39
Ответ: Δx=-0,1; Δf =-0,39
Пример 2.
Найдем приращение Δx и Δf в точке x0, если f(x)= x2, x0=2 и х=2,1
Решение:
Δx= x1−x0=2,1-2=0,1
Δf= f(1,9) –f(2)=2,12-22=0,41
Ответ: Δx=0,1; Δf =0,41
Пример 3.
Найдем приращение Δf функции в точке x0,если приращение аргумента равно x0.
Решение:
по формуле (1) находим:
.
Ответ: .
С помощью введенных обозначений приращений удобно также выражать среднюю скорость движения за промежуток времени [t0; t0+∆t]. Если точка движется по прямой и известна ее координата x(t), то
Эта формула верна и для ∆t<0 (для промежутка [t0+∆t; t0]).
Аналогично выражение называют средней скорость изменения функции на промежутке с концами х0 и х0+∆х.
Определение. Производной функции называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
Обозначение: y’ или f’(x)
Если функция f(x) имеет производную в точке х, то эта функция называется дифференцируемой в этой точке. Если функция f(x) имеет производную в каждой точке некоторого промежутка, то эта функция дифференцируема на этом промежутке.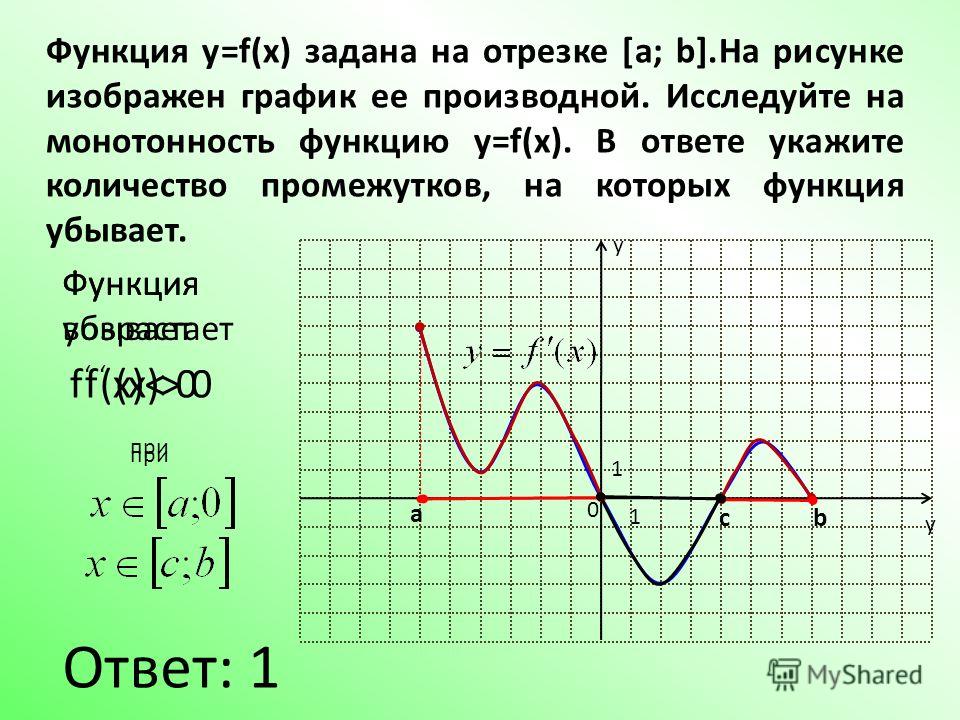 Операция нахождения производной называется дифференцированием.
Операция нахождения производной называется дифференцированием.
Схема вычисления производной функции
- Найти приращение функции на отрезке [x; x+Δx]:
∆y=y(x+∆x)-y(x)
- Разделить приращение функции на приращение аргумента:
- Найти предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
Пример 4.
Вычислить производную функции y=x2
Решение: Используем схему вычисления производной по действиям:
- ∆y=y(x+∆x)-y(x)= (х+∆х)²-х²= х²+2х·∆х+ ∆х²-х²= 2х·∆х+ ∆х²
Ответ: y’=2x.
Физический смысл производной: если положение точки при её движении задаётся функцией пути S(t), где t – время движения, то производная функции S есть мгновенная скорость движения в момент времени t: v(t)=S’(t).
Таким образом, скорость – есть производная от пути по времени.
Пример 5.
Точка движется по закону s(t)=1-2t. Найдите среднюю скорость движения за промежуток времени от t=0,8 до t=1.
Найдите среднюю скорость движения за промежуток времени от t=0,8 до t=1.
Решение:
найдем ∆t= 1-0,8=0,2
S(0,8)= 1-2·0,8= -0,6=S(t)
S(1)= 1-2·1= -1=S(t+∆t)
.
Ответ: .
Необходимое и достаточное условие дифференцируемости
Теорема 1. Для того, чтобы функция f(x) была дифференцируема в точке x0, необходимо и достаточно, чтобы в этой точке она имела конечную производную. Следствие. Функция, дифференцируемая в точке, непрерывна в этой точке.
Замечание. Дифференциалом dx независимой переменной будем считать приращение Δx, т.е. dx ≡ Δx.
Прототипы задания №6 ЕГЭ по математике
16 декабря 2021
В закладки
Обсудить
Жалоба
Видеоуроки ЕГЭ по математике
Pеклaмa Бесплатные уроки для подготовки к ЕГЭ каждый день от MAXIMUM Education →
Готовим к ЕГЭ бесплатно и проводим более 300 уроков в месяц по всем предметам.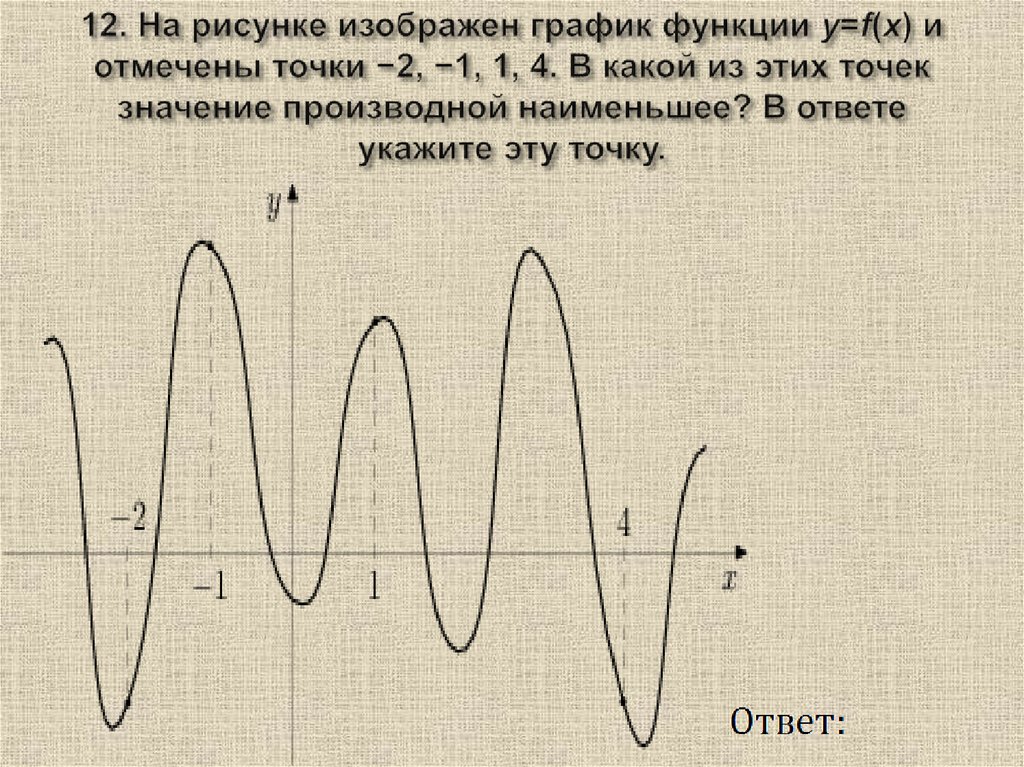 ‘ (x)=0 на отрезке [-4,5;2,5].
‘ (x)=0 на отрезке [-4,5;2,5].
Задача 3 – 03:55
В скольких из этих точек производная функции f(x) положительна?
Задача 4 – 05:09
Определите количество целых точек, в которых производная функции положительна.
Задача 5 – 08:18
В скольких из этих точек производная функции f(x) положительна?
Задача 6 – 09:53
В скольких из этих точек производная функции f(x) отрицательна?
Задача 7 – 11:03
На рисунке изображён график функции y=f(x), определённой на интервале (-7;7). Определите количество целых точек, в которых производная функции отрицательна.
Задача 8 – 12:55
Сколько из этих точек лежит на промежутках возрастания функции f(x)?
Задача 9 – 14:15
Сколько из этих точек лежит на промежутках убывания функции f(x)?
Задача 10 – 15:40
Найдите количество точек экстремума функции f(x), принадлежащих отрезку [-17;-4].
Задача 11 – 17:20
Найдите точку экстремума функции f(x), принадлежащую отрезку [1;6]. ‘ (x) производной функции f(x), определённой на интервале (-2;9). В какой точке отрезка [2;8] функция f(x) принимает наименьшее значение?
‘ (x) производной функции f(x), определённой на интервале (-2;9). В какой точке отрезка [2;8] функция f(x) принимает наименьшее значение?
Задача 17 – 31:03
На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x_0. Найдите значение производной функции f(x) в точке x_0.
Задача 18 – 35:25
На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x_0. Найдите значение производной функции f(x) в точке x_0.
Задача 19 – 37:34
На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x_0. Найдите значение производной функции f(x) в точке x_0.
Задача 20 – 41:30
На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x_0. Найдите значение производной функции f(x) в точке x_0.
Задача 21 – 45:03
На рисунке изображён график функции y=f(x), определённой на интервале (-4;13). Определите количество точек, в которых касательная к графику функции y=f(x) параллельна прямой y=14. ‘ (x)- производной функции f(x), определённой на интервале (-4;6). Найдите абсциссу точки, в которой касательная к графику функции y=f(x) параллельна прямой y=3x или совпадает с ней.
‘ (x)- производной функции f(x), определённой на интервале (-4;6). Найдите абсциссу точки, в которой касательная к графику функции y=f(x) параллельна прямой y=3x или совпадает с ней.
Задача 24 – 55:10
Найдите абсциссу точки, в которой касательная к графику функции y=f(x) параллельна оси абсцисс или совпадает с ней.
Задача 25 – 57:43
На рисунке изображён график функции y=f(x). На оси абсцисс отмечены точки -1, 2, 3, 4. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.
Задача 26 – 01:03:11
На рисунке изображён график функции y=f(x). На оси абсцисс отмечены точки -2, -1, 3, 4. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.
Общие материалы | Сегодня, 16:01
Приём заявок от учеников 8-11-х классов на прохождение бесплатных курсов по программированию стартовал на портале госуслуг. Начать обучение смогут более 100 тыс. школьников в 2022 году, сообщил заместитель председателя правительства РФ Дмитрий Чернышенко.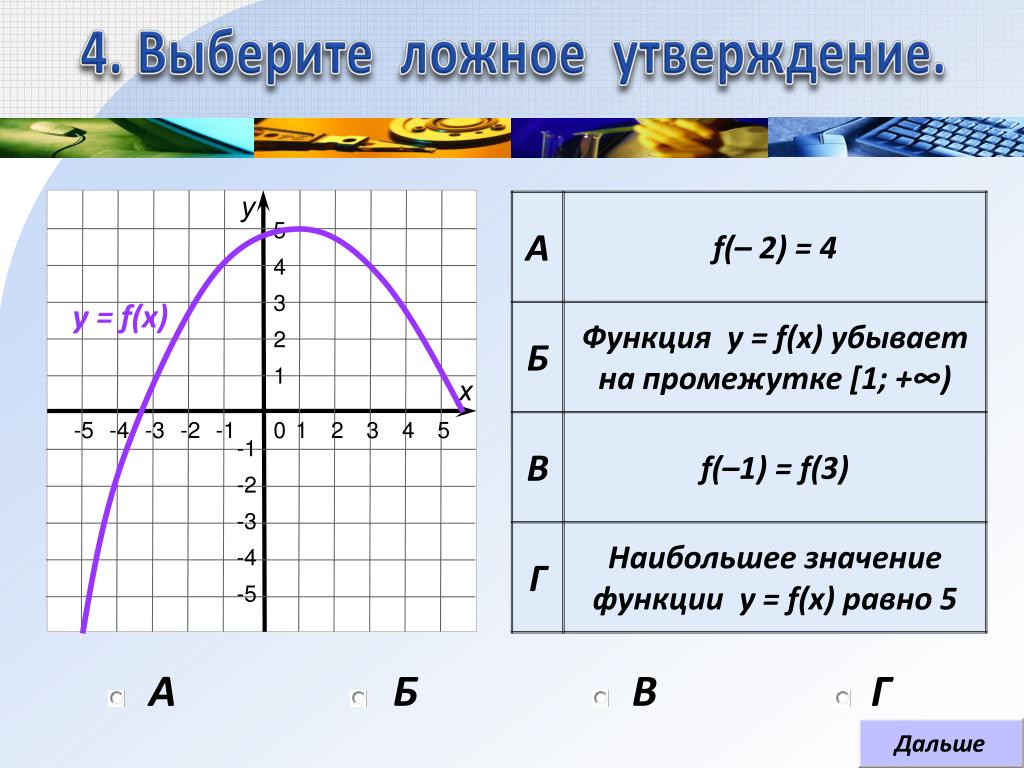
Образование | Сегодня, 15:46
Ответы на самые распространённые вопросы в инфографике от Минпросвещения.
3-8
Функция «один к одному» — объяснение и примеры
Вы понимаете, что изучаете функции, когда слышите «один к одному» чаще, чем когда-либо. Хотите узнать, что делает один к одному особенным с функциями ? Эта статья поможет вам узнать об их свойствах и оценить эти функции. Давайте начнем с этого краткого определения функций «один к одному»:
Хотите узнать, что делает один к одному особенным с функциями ? Эта статья поможет вам узнать об их свойствах и оценить эти функции. Давайте начнем с этого краткого определения функций «один к одному»:
Функции «один к одному» — это функции, которые возвращают уникальный диапазон для каждого элемента в своей области.
Поскольку функции «один к одному» являются особыми типами функций, лучше всего просмотреть наши знания о функциях, их предметной области и диапазоне.
Эта статья поможет нам понять свойства функций один к одному . Мы также узнаем, как идентифицировать функции один к одному на основе их выражений и графиков.
Давайте продолжим и начнем с определения и свойств функций один к одному.
Что такое функция «один к одному»?
Чтобы легко запомнить, что такое функции один к одному, попробуйте вспомнить это утверждение: «для каждого y существует уникальный x». Следующие два раздела покажут вам, почему эта фраза помогает нам вспомнить основную концепцию, лежащую в основе функций one-to-one.
Следующие два раздела покажут вам, почему эта фраза помогает нам вспомнить основную концепцию, лежащую в основе функций one-to-one.
Определение функции «один к одному»
Функция f(x), является функцией «один к одному», когда один уникальный элемент из своего домена возвращает каждый элемент своего диапазона. Это означает, что для каждого значения x будет уникальное значение y или f(x).
Почему бы нам не визуализировать это, сопоставив две пары значений для сравнения функций, которые не находятся в однозначном соответствии?
Давайте сначала посмотрим на g(x), g(4) и g(-4) имеют общее значение y, равное 16. Это также верно для g(-2) и g(2). Вы правильно угадали; g(x) — функция, не имеющая однозначного соответствия.
Теперь обратите внимание на f(x). Обратите внимание, что для каждого значения f(x) существует только одно уникальное значение x? Когда вы наблюдаете функции, имеющие такое соответствие, мы называем эти функции взаимно однозначными функциями.
График функции один к одному
Чтобы лучше понять концепцию функций один к одному, давайте изучим график функции один к одному. Помните, что для функций «один к одному» каждый x должен иметь уникальное значение y.
Поскольку каждый x будет иметь уникальное значение для y, функции один к одному никогда не будут иметь упорядоченные пары, которые имеют одну и ту же координату y.
Теперь, когда мы изучили определение функций «один к одному», теперь вы понимаете, почему полезно запомнить утверждение «для каждого y существует уникальный x»?
Свойства функций «один к одному»
Какие еще важные свойства функций «один к одному» следует помнить? Вот некоторые свойства, которые могут помочь вам понять различные типы функций с однозначным соответствием:
- Если две функции, f(x) и g(x), являются взаимно однозначными, f ◦ g является взаимно однозначным также функционировать.
- Если функция один к одному, ее график будет либо всегда возрастать, либо всегда убывать.

- Если g ◦ f является взаимно однозначной функцией, f(x) также гарантированно является взаимно однозначной функцией.
Попробуйте самостоятельно изучить две пары графиков и посмотреть, сможете ли вы подтвердить эти свойства. Конечно, прежде чем мы сможем применить эти свойства, нам будет важно узнать, как мы можем подтвердить, является ли данная функция однозначной функцией или нет.
Как определить, является ли функция один к одному?
Следующие два раздела покажут вам, как мы можем проверить однозначное соответствие функций. Иногда нам дают выражение или график функции, поэтому мы должны научиться идентифицировать функции «один к одному» алгебраически и геометрически. Давайте продолжим и начнем с последнего!
Тестирование функций один к одному геометрически
Помните, что для функций должно быть однозначное соответствие функций. Каждая координата x должна иметь уникальную координату y? Мы можем проверить функции «один к одному», используя тест горизонтальной линии .
- Когда задана функция, рисует горизонтальные линии вместе с системой координат.
- Проверить, могут ли горизонтальные линии проходить через две точки.
- Если горизонтальные линии проходят только через одна точка по всему графику, функция один к одному функция .
Что делать, если он проходит две или более точек функции? Тогда, как вы уже догадались, они не считаются функциями один в один.
Чтобы лучше понять процесс, давайте продолжим и изучим эти два графика, показанные ниже.
Известно, что обратная функция f(x) = 1/x является функцией один к одному. Мы также можем проверить это, нарисовав горизонтальные линии на его графике.
Посмотрите, как каждая горизонтальная линия каждый раз проходит через уникальную упорядоченную пару? Когда это происходит, мы можем подтвердить, что данная функция является функцией один к одному.
Что происходит тогда, когда функция не один к одному? Например, квадратичная функция f(x) = x 2 не является однозначной функцией. Давайте посмотрим на его график, показанный ниже, чтобы увидеть, как тест горизонтальной линии применим к таким функциям.
Давайте посмотрим на его график, показанный ниже, чтобы увидеть, как тест горизонтальной линии применим к таким функциям.
Как видите, каждая горизонтальная линия, проведенная через график функции f(x) = x 2 проходит через две заказанные пары. Это еще раз подтверждает, что квадратичная функция не является однозначной функцией.
Алгебраическое тестирование функций один к одному
Давайте освежим в памяти то, как мы определяем функции один к одному. Напомним, что функции взаимно однозначны, когда:
- f(x 1 ) = f(x 2 ) тогда и только тогда, когда x 1 = x 2
- f(x 9 1) ≠ f(x 2 ) тогда и только тогда, когда x 1 ≠ x 2
Мы будем использовать это алгебраическое определение, чтобы проверить, является ли функция взаимно однозначной. Как мы это делаем?
- Используйте данную функцию и найдите выражение для f(x 1 ).

- Примените тот же процесс и найдите выражение для f(x 2 ).
- Приравняйте оба выражения и покажите, что x 1 = x 2 .
Почему бы нам не попробовать доказать, что f(x) = 1/x является взаимно однозначной функцией, используя этот метод?
Давайте сначала подставим x 1 и x 2 в выражение. У нас будет f(x 1 ) = 1/x 1 и f(x 2 ) = 1/x 2 . Чтобы подтвердить взаимно однозначное соответствие функции, приравняем f(x 1 ) и f(x 2 ).
1/x 1 = 1/x 2
Перемножьте обе части уравнения, чтобы упростить уравнение.
х 2 = х 1
х 1 = x 2
Мы только что показали, что x 1 = x 2 , когда f(x 1 ) = f(x 2 ), следовательно, есть обратная функция к одной функции.
Пример 1
Заполните пропуски иногда , всегда или никогда , чтобы сделать следующие утверждения верными.
- Отношения могут _______________ быть один к одному.
- Функции «один к одному» — это ______________ функции.
- Когда горизонтальная линия проходит через функцию, не являющуюся функцией один к одному, она ____________ проходит через две упорядоченные пары.
Решение
Отвечая на подобные вопросы, всегда возвращайтесь к только что изученным определениям и свойствам.
- Отношения иногда могут быть функциями и, следовательно, могут иногда представлять функцию один к одному.
- Поскольку функции «один к одному» относятся к особому типу функций, они будут всегда быть, в первую очередь, функциями.
- В нашем примере горизонтальные линии могут проходить через график f(x) = x 2 дважды, но горизонтальные линии могут проходить через большее количество точек. Следовательно, иногда проходит через две упорядоченные пары.
Пример 2
Пусть A = {2, 4, 8, 10} и B = {w, x, y, z}. Какие из следующих наборов упорядоченных пар представляют функцию один к одному?
Какие из следующих наборов упорядоченных пар представляют функцию один к одному?
- {(2, w), (2, x), (2, y), (2,z)}
- {(4,w), (2,x), (10,z), (8 , y)}
- {(4,w), (2,x), (8,x), (10, y)}
Решение
Чтобы функция была взаимно однозначной, каждый элемент из A должен сочетаться с уникальным элементом из B.
- Первый вариант имеет одно и то же значение x для каждого значения y, поэтому это не функция и, следовательно, не взаимооднозначная функция.
- Третий вариант имеет разные значения x для каждой упорядоченной пары, но 2 и 8 имеют одинаковый диапазон x. Следовательно, он не представляет функцию один к одному.
- Второй вариант использует уникальный элемент из A для каждого уникального элемента из B, представляя взаимно-однозначную функцию.
Это означает, что {(4,w), (2,x), (10,z), (8, y)} представляют собой функцию «один к одному».
Пример 3
Какой из следующих наборов значений представляет функцию один к одному?
Решение
Всегда возвращайтесь к утверждению «для каждого y существует уникальный x». Для каждого набора давайте проверим, связан ли каждый элемент справа с уникальным значением слева.
Для каждого набора давайте проверим, связан ли каждый элемент справа с уникальным значением слева.
- Для первого набора f(x) мы видим, что каждый элемент с правой стороны соединяется с уникальным элементом с левой стороны. Следовательно, , f(x) является взаимно однозначной функцией .
- Набор g(x) показывает разное количество элементов на каждой стороне. Уже одно это говорит нам о том, что функция не является функцией один к одному.
- Некоторые значения в левой части соответствуют тому же элементу, что и в правой, поэтому m(x) также не является взаимно однозначной функцией.
- Каждый элемент первого набора соответствует уникальному элементу следующего, поэтому n(x) представляет собой функцию один к одному.
Пример 4
График f(x) = |x| + 1 и определить, является ли f(x) взаимно однозначной функцией.
Решение
Постройте таблицу значений f(x) и начертите сгенерированные упорядоченные пары.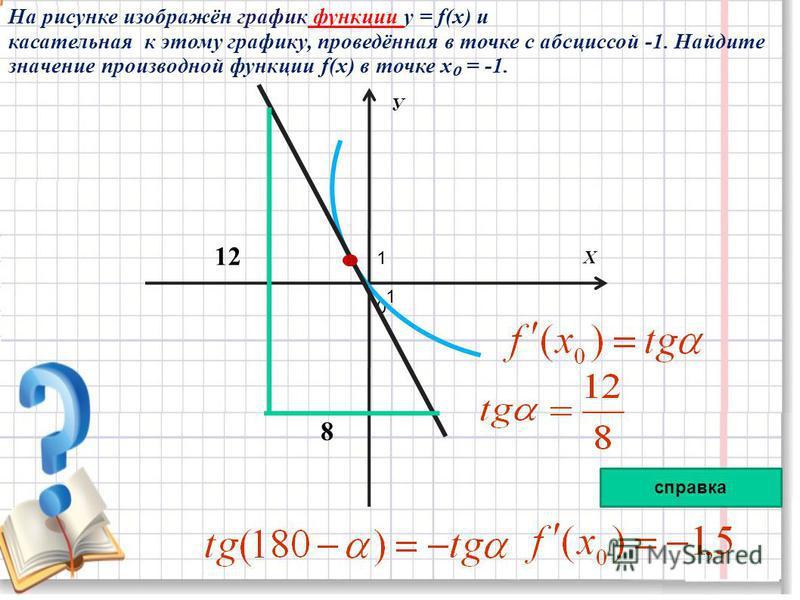 Соединил эти точки с графиком f(x).
Соединил эти точки с графиком f(x).
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3005 |
| F (x) | 4 | 3 | 2 | 1 | 2 | 3 | 4 |
. Только таблица уже может дать вам CLUE на (x). функция один к одному [ Подсказка: f (1) = 2 и f (-1) = 2 ]. Но давайте продолжим и нанесем эти точки на плоскость xy и на график f(x).
После того, как мы построили график f(x) = |x| + 1, проведите через график горизонтальные линии и посмотрите, проходит ли он через одну или несколько точек.
Из графика видно, что построенные нами горизонтальные линии проходят через две точки каждая, поэтому функция не является функцией один к одному .
Пример 5
Определите, является ли f(x) = -2x 3 – 1 однозначной функцией, используя алгебраический подход.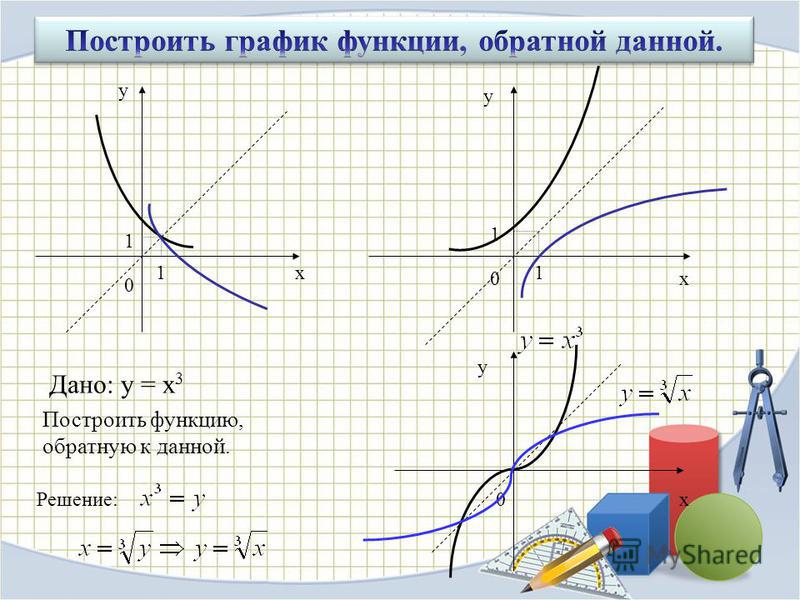
Решение
Напомним, что для того, чтобы функция была взаимно однозначной, f(x 1 ) = f(x 2 ) тогда и только тогда, когда x 1 = х 2 . Чтобы проверить, является ли f(x) функцией один к одному, давайте сначала найдем соответствующие выражения для x 1 и x 2 .
F (x 1 ) = -2 x 1 3 -1
F (x 2 ) = -2 x 2 3 -1
. оно сводится к x 1 = x 2 .
-2 x 1 3 – 1 = -2 x 2 3 – 1
-2 x 1 3 = -2 x 2 3
(x 1 ) 3 = (x 2 ) 9103 3 = (x 2 ) 9103 3 = (x 2 ) стороны уравнения приведут нас к x 1 = x 2 . Следовательно, f(x) = -2x 3 – 1 является однозначной функцией.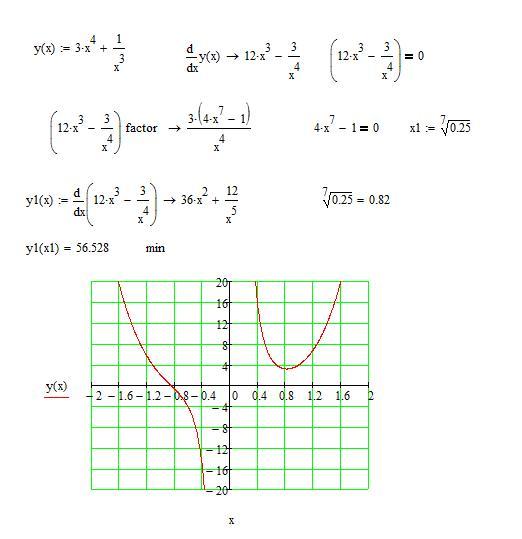
Пример 6
Покажите, что f(x) = -5x 2 + 1 не является взаимно однозначной функцией.
Решение
Другим важным свойством функций один к одному является то, что когда x 1 ≠ x 2 , f(x 1 ) не должно быть равно f(x 2 ).
Быстрый способ доказать, что f(x) не является функцией один к одному, — это представить контрпример, показывающий два значения x, где они возвращают одно и то же значение для f(x).
Посмотрим, что произойдет, если x 1 = -4 и x 2 = 4.
f(x 1 ) = -5(-4) 2 + 1 = -80 + 1 = -79 | f(x 2 ) = -5(4) 2 0 + 96 0 + -80 + 1 = -79 |
Мы можем видеть, что даже когда x 1 не равно x 2 , функция f(x) возвращает одно и то же значение. Это показывает, что функция f(x) = -5x 2 + 1 не является взаимно однозначной функцией.
Это показывает, что функция f(x) = -5x 2 + 1 не является взаимно однозначной функцией.
Пример 7
Учитывая, что a и b не равны 0, покажите, что все линейные функции взаимно однозначны.
Решение
Помните, что общий вид линейных функций может быть выражен как ax + b, где a и b ненулевые константы.
Применим тот же процесс, подставив x 1 и x 2 в общее выражение для линейных функций.
f(x 1 ) = a x 1 + b
f(x 2 ) = a x 2 + b
Приравняйте оба уравнения и посмотрите, можно ли их привести к x 1
019 = х 2 . Поскольку b представляет собой константу, мы можем вычесть b из обеих частей уравнения.a x 1 + b = a x 2 + b
a x 1 = a x 2
. Отсюда можно сделать вывод, что все линейные функции являются взаимно однозначными функциями.
Обратные функции
Обратные функции
|
В комплекте: 9 шт.0908 Эта страница соответствует § 1.7 (стр. 150) текста.
Предполагаемые проблемы из текста
стр.158 #1-4, 5, 8, 9, 12, 13, 15, 18, 21, 22, 27, 31, 34, 37, 46, 48, 51, 71, 74, 83
Определение обратной функции
Графики обратных функций
Существование инверсии
Нахождение инверсий
Определение обратной функции
Прежде чем определить обратную функцию, нам нужно иметь правильный мысленный образ функции.
Рассмотрим функцию f(x) = 2x + 1. Мы знаем, как вычислить f при 3, f(3) = 2*3 + 1 = 7. В этом разделе помогает думать о f как о преобразовании 3 в 7, а f о преобразовании 5 в 11 и т. д.
Теперь, когда мы думаем о f как о «действии» на числа и их преобразовании, мы можем определить обратную функцию f как функцию, которая «отменяет» то, что сделал f. Другими словами, функция, обратная f, должна вернуть 7 к 3, и вернуть -3 обратно в -2 и т.д.
Пусть g(x) = (x — 1)/2. Тогда g(7) = 3, g(-3) = -2 и g(11) = 5, поэтому g, похоже, отменяет то, что сделал f, по крайней мере
для этих трех значений. Чтобы доказать, что g является обратным значением f, мы должны показать, что это верно для любого значения x в
домен ф. Другими словами, g должен вернуть f(x) обратно к x для всех значений x в области определения f. Итак, g(f(x))
= x должно выполняться для всех x в области определения f. Способ проверки этого условия состоит в том, чтобы убедиться, что формула для g(f(x))
упрощается до х.
g(f(x)) = g(2x + 1) = (2x + 1 -1)/2 = 2x/2 = x.
Это упрощение показывает, что если мы выберем любое число и позволим f воздействовать на него, то применение g к результату восстанавливает наш исходный номер. Нам также нужно увидеть, что этот процесс работает в обратном порядке, или что f также отменяет то, что делает g.
f(g(x)) = f((x — 1)/2) = 2(x — 1)/2 + 1 = x — 1 + 1 = x.
Обозначая f -1 , обратную f, мы только что показали, что g = f -1 .
Определение:
Пусть f и g — две функции. Если
f(g(x)) = x и g(f(x)) = x,
, то g является обратным значением f, а f является обратным значением g.
Упражнение 1:
(a) Откройте калькулятор Java и введите формулы для f и g. Обратите внимание, что вы берете куб корень путем повышения до (1/3), и вам нужно ввести показатель степени как (1/3), а не десятичное приближение.
Таким образом, текст для поля g будет 9(1/3)
Используйте калькулятор для вычисления f(g(4)) и g(f(-3)). g является обратным f, но из-за округления ошибка, калькулятор может не вернуть точное значение, с которого вы начали. Попробуйте f(g(-2)). Ответы будут разными для разные компьютеры. Однако на нашей тестовой машине функция f(g(4)) вернула 4; g(f(-3)) вернул 3; но f(g(-2)) вернул -1,9999999999999991, что довольно близко к -2.
Калькулятор может дать нам хорошее представление о том, что g является обратным значением f, но мы не можем проверить все возможные значения х.
(b) Докажите, что g является обратной величиной f, упростив формулы для f(g(x) и g(f(x)).
Вернуться к содержанию
Графики обратных функций
Мы видели примеры отражений на плоскости. Отражение точки (a,b) относительно оси x равно (a,-b),
а отражение (a,b) относительно оси y равно (-a,b). Теперь мы хотим подумать о линии y = x.
Отражение точки (a,b) относительно прямой y = x есть точка (b,a) .
Пусть f(x) = x 3 + 2. Тогда f(2) = 10 и точка (2,10) находится на графике f. Обратное f должно вернуть 10 к 2, т. е. f -1 (10)=2, поэтому точка (10,2) находится на графике f -1 . Смысл (10,2) есть отражение на линии y = x точки (2,10). То же самое можно сделать для всех точек на графики f и f -1 .
График f -1 является отражением относительно линии y = x графика f.
- Видео: x 3 + c Анимированный Gif, Файл MS Avi, или Real Видео файл
- Видео: x 2 + c Анимированный Gif, Файл MS Avi, или Реальный Видео файл
Вернуться к содержанию
Существование инверсии
Некоторые функции не имеют обратных функций. Например, рассмотрим f(x) = x 2 . Есть два числа
что f принимает значение 4, f(2) = 4 и f(-2) = 4. Если бы f было обратным, то тот факт, что f(2) = 4, подразумевал бы, что
обратная функция f возвращает 4 обратно в 2. С другой стороны, поскольку f(-2) = 4, обратная функция f должна преобразовать 4 в -2.
Следовательно, не существует функции, обратной f.
Например, рассмотрим f(x) = x 2 . Есть два числа
что f принимает значение 4, f(2) = 4 и f(-2) = 4. Если бы f было обратным, то тот факт, что f(2) = 4, подразумевал бы, что
обратная функция f возвращает 4 обратно в 2. С другой стороны, поскольку f(-2) = 4, обратная функция f должна преобразовать 4 в -2.
Следовательно, не существует функции, обратной f.
Посмотрите на ту же задачу с точки зрения графиков. Если бы у f была обратная, то ее график был бы отражением график f относительно прямой y = x. График f и его отражение относительно y = x нарисованы ниже.
Обратите внимание, что отраженный график не проходит тест вертикальной линии, так что это не график функции.
Это обобщается следующим образом: функция f имеет обратную тогда и только тогда, когда ее график отражается относительно
линия y = x, результатом является график функции (проходит тест вертикальной линии). Но это можно упростить.
Прежде чем отражать график, мы можем сказать, будет ли какая-либо вертикальная линия пересекаться более одного раза. как горизонтальные линии пересекают исходный график!
как горизонтальные линии пересекают исходный график!
Проверка горизонтальной линии
Пусть f — функция.
Если любая горизонтальная линия пересекает график f более одного раза, то f не имеет обратной.
Если ни одна горизонтальная линия не пересекает график функции f более одного раза, то функция f имеет обратную.
Свойство наличия инверсии очень важно в математике, и у него есть имя.
Определение : Функция f является однозначной тогда и только тогда, когда f имеет обратную.
Следующее определение эквивалентно, и оно чаще всего дается для однозначности.
Альтернативное определение : Функция f является однозначной , если для любых a и b в своей области определения f(a) = f(b) влечет a = b.
Упражнение 2:
9(1/3) (кубический корень из х). Ответ
Вернуться к содержанию
Нахождение инверсий
Пример 1. Сначала рассмотрим простой пример f(x) = 3x + 2 .
Сначала рассмотрим простой пример f(x) = 3x + 2 .
График функции f представляет собой линию с наклоном 3, поэтому он проходит тест горизонтальной линии и имеет обратную сторону.
Для вычисления f по числу x требуется два шага. Сначала умножаем x на 3, затем прибавляем 2.
Думая об обратной функции как об отмене действия f, мы должны отменить эти шаги в обратном порядке.
Шаги, необходимые для вычисления f -1 , состоят в том, чтобы сначала отменить прибавление 2 путем вычитания 2. Затем мы отменяем умножение на 3 делением на 3.
Следовательно, f -1 (х) = (х — 2)/3.
Шаги для нахождения обратной функции f.
- Замените f(x) на y в уравнении, описывающем функцию.
- Развязка x и y. Другими словами, замените каждый x на y и наоборот.
- Решите для y.
- Заменить y на f -1 (x).
Пример 2. f(x) = 6 — x/2
| Шаг 1 | у = 6 — х/2. |
| Шаг 2 | х = 6 — у/2. |
| Шаг 3 | х = 6 — у/2. у/2 = 6 — х. у = 12 — 2х. |
| Шаг 4 | ф -1 (х) = 12 — 2х. |
Шаг 2 часто сбивает учащихся с толку. Мы могли бы пропустить шаг 2 и найти x вместо y, но тогда мы получили бы с формулой в y вместо x. Формула будет та же, но переменная будет другой. Избегать это мы просто меняем роли x и y, прежде чем решить.
Пример 3. f(x) = x 3 + 2
Это функция, с которой мы работали в упражнении 1. Из ее графика (показанного выше) видно, что она имеет обратный. (На самом деле в упражнении 1 дано обратное значение.)
Шаг 1 у = х 3 + 2. Шаг 2 х = у 9(1/3).
Упражнение 3:
График f(x) = 1 — 2x 3 , чтобы увидеть, что у него есть обратный. Найдите f -1 (х). Ответ
Вернуться к содержанию
|
1.7 — Обратные функции
1.7 — Обратные функцииОбозначение
Обратная функция f обозначается как f -1 (если ваш браузер не поддерживает верхние индексы, то выглядит как f
с показателем -1) и произносится как «f inverse». Хотя обратная функция выглядит как
вы возводите функцию в степень -1, это не так. Обратная функция не означает, что
обратная функция.
Обратная функция не означает, что
обратная функция.
Инверсия
Функция обычно говорит вам, что такое y, если вы знаете, что такое x. Обратная функция расскажет каким должен быть x, чтобы получить это значение y.
Функция f -1 является обратной функцией f, если
- для каждого x в области f, f -1 [f(x)] = x и
- для каждого x в области f -1 , f[f -1 (x)] = x
Домен f — это диапазон f -1 , а диапазон f — это домен f -1 .
График обратной функции
Обратная функция отличается от функции тем, что все координаты x и y были переключены. То есть, если (4,6) — точка на графике функции, то (6,4) — точка на график обратной функции.
Точки на функции идентификации (y=x) останутся на функции идентификации при переключении. Все у других точек будут изменены координаты и места перемещения.
График функции и обратная ей функция являются зеркальным отражением друг друга. Они отражаются о
тождественная функция y=x.
Они отражаются о
тождественная функция y=x.
Существование обратной функции
Функция говорит, что для каждого x существует ровно один y. То есть значения y могут дублироваться, но x значения не могут повторяться.
Если функция имеет обратную, которая также является функцией, то для каждого x может быть только один y.
Функция «один к одному» — это функция, в которой для каждого x имеется ровно один y и для каждого y, есть ровно один х. У взаимно однозначной функции есть обратная, которая также является функцией.
Существуют функции, обратные функции которых не являются функциями. Есть также обратные для связи. По большей части мы ими пренебрегаем и имеем дело только с функциями, обратные также функционирует.
Если обратная функция также является функцией, то обратная связь должна проходить через вертикальную линию
тест. Поскольку все координаты x и y меняются местами при нахождении инверсии, говоря
что обратная функция должна пройти тест вертикальной линии, это то же самое, что сказать, что исходная функция должна пройти тест
тест горизонтальной линии.
Если функция проходит как тест вертикальной линии (так что это в первую очередь функция), так и тест горизонтальной линии (чтобы его обратная функция была), то функция является взаимно однозначной и имеет обратная функция.
Неформальное нахождение инверсий
Инверсия некоторых функций, особенно тех, где есть только одно вхождение независимая переменная, может быть решена путем отмены операций. Чтобы отменить операцию, вы должны не только изменить порядок, но и использовать обратную операцию.
Пример 1
Функция f(x) = 5x-2
- Начать с х: х
- Умножить на 5: 5x
- Вычесть 2: 5x-2
Обратная f
-1 (x) = (x+2)/5- Начать с х: х
- Добавить 2: х+2
- Разделить на 5: (х+2) / 5
Пример 2
Функция f(x) = 2(x-3)
2 -5, x≥3 Обратите внимание, что существует ограничение на x.
- Начать с х: х
- Вычесть 3: x-3
- Квадрат: (x-3) 2
- Умножить на 2: 2(x-3) 2
- Вычесть 5: 2(x-3) 2 -5
Обратная f
-1 (x) = 3 + sqrt[(x+5)/2]- Начать с х: х
- Добавить 5: х+5
- Разделить на 2: (х+5)/2
- Извлеките квадратный корень: ± sqrt[(x+5)/2]
- Добавить 3: 3 ± sqrt[(x+5)/2]
- Подожди! Эта обратная функция не является функцией, потому что для каждого x существует два значения y. Это из-за ±, который появился, когда мы взяли квадратный корень из обеих сторон. Теперь вернемся к исходной области определения x≥3. Это означает, что для инверсии диапазон равен y≥3. Поскольку у должно быть не менее 3, нам нужен положительный квадратный корень, а не отрицательный. Без ограничения на x в исходная функция, у него не было бы обратная функция: 3 + sqrt[(x+5)/2]
Пример 3
Функция f(x) = x
2 — 4x + 6, x≤2Уххх????
Что происходит, когда встречается более одного
независимая переменная в функции? Вы не
знаю, что ты сделал с х, потому что ты сделал это с двумя
разные иксы, и вы не сделали то же самое с обоими из
их.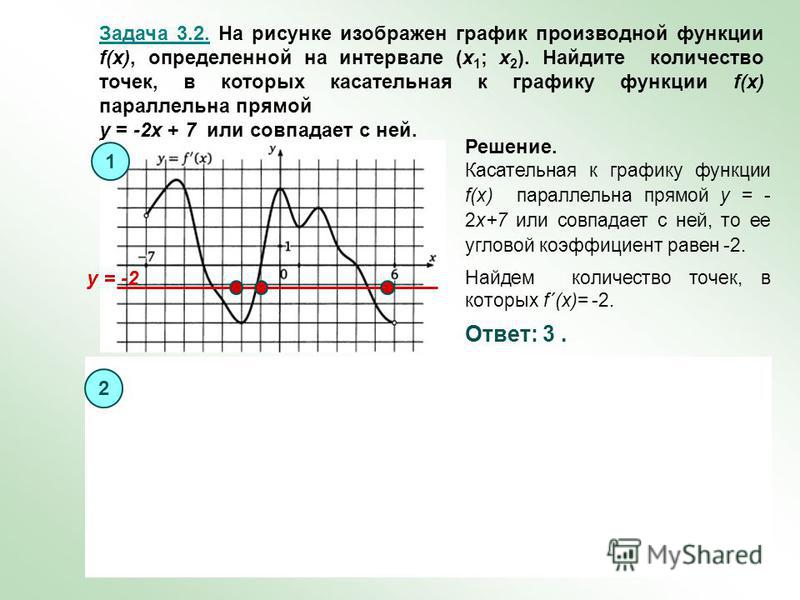
Формальное нахождение инверсий
Нельзя сказать, что последний пример невозможно выполнить, но он включает в себя заполнение квадрата до получить f(x) = (x-2) 2 +2, затем инвертируем его так, чтобы получить f -1 (x) = 2-sqrt(x-2).
Тем не менее, есть другой способ, который не так сильно зависит от неформальности и будет работать независимо от того, не вы можете точно понять, что вы сделали с ровно одним x.
- Запуск с функцией
- При необходимости заменить f(x) на y
- Поменяйте местами x и y. На данный момент вы имеете дело с обратным числом .
- Найдите у
- Заменить у на f -1 (x), если обратная функция также является функцией, в противном случае оставьте как y
Пример 4
Функция f(x) = x
2 / (x 2 +1), x≥0Важно сделать ограничение 1-1.
- Начните с функции: f(x) = x 2 / (x 2 +1), x≥0
- Заменить f(x) на y: y = x 2 / (x 2 +1), x≥0
- Поменяйте местами x и y: x = y 2 / (y 2 +1), у ≥0
- Найдите у:
- Умножить на знаменатель: x(y 2 +1) = y 2
- Распределить: xy 2 + x = y 2
- Переместить y в одну сторону, а все остальное в другую: xy 2 -y 2 = -x
- Коэффициент: у 2 (х-1)=-х
- Разделить на коэффициент при y 2 : y 2 = -x/(x-1)
- Упростить правую часть: y 2 = х/(1-х)
- Извлечение квадратного корня: y = ± sqrt[ x/(1-x)]
- Поскольку y≥0, нам нужен положительный квадратный корень: y = sqrt[ x/(1-x) ]
- Назовите это f -1 (x): f -1 (x) = sqrt[ x/(1-x) ]
Для этой последней функции подразумеваемый домен обратной функции равен [0,1).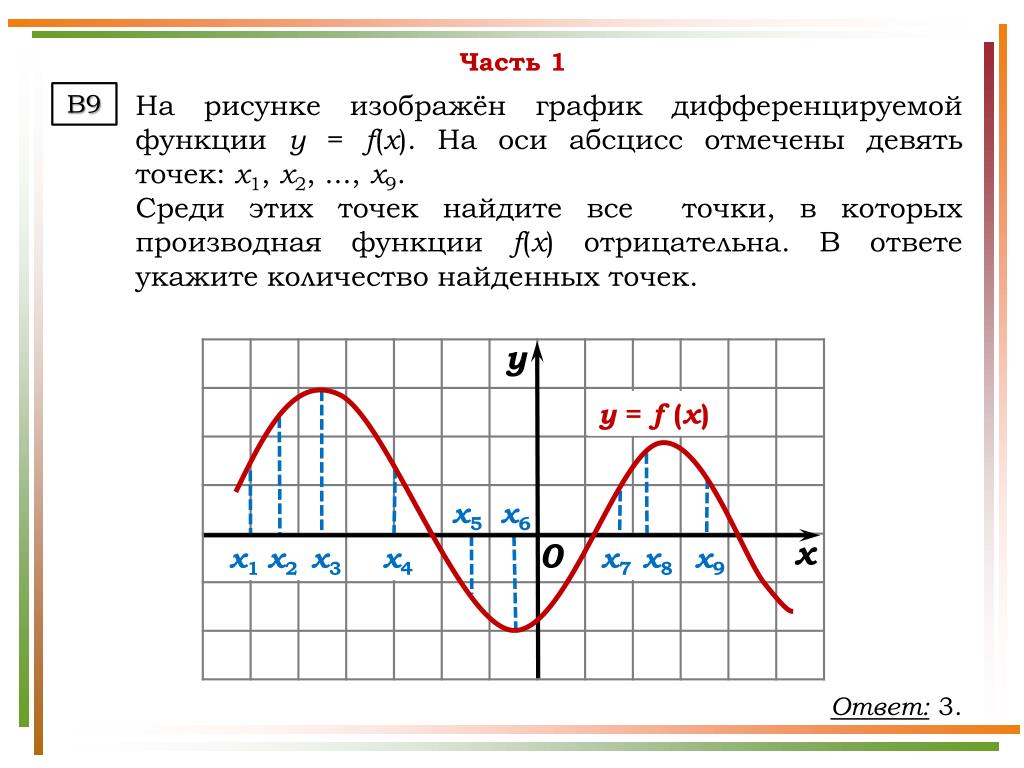 Это означает, что диапазон
исходная функция также должна была быть [0,1). Проверьте это на своем калькуляторе, и вы увидите, что это так.
Это означает, что диапазон
исходная функция также должна была быть [0,1). Проверьте это на своем калькуляторе, и вы увидите, что это так.
Иногда в инструкциях говорят, что если функция не является взаимно однозначной, то не найти обратную функция (потому что ее нет). Поэтому всегда проверяйте, прежде чем тратить время на поиски обратная функция. Теперь, если вы должны найти обратное, независимо от того, является ли оно работать или нет, тогда вперед.
Хороший материал!
Один на один Функции — замечательная штука.
При решении уравнений можно прибавлять одно и то же к обеим частям, вычитать одно и то же из обе стороны, умножить обе стороны на одно и то же ненулевое значение и разделить обе части на одно и то же ненулевое значение и по-прежнему получать то же решение, не беспокоясь о необходимости проверить свой ответ.
Вы также можете применить функцию «один к одному» к обеим частям уравнения, не беспокоясь о введении посторонних решений (решений, которые работают после того, как вы сделали что-то, что раньше не работало). Это не обязательно верно для функций, которые не являются взаимно однозначными, как функция возведения в квадрат, где вы всегда должны проверять ответы после возведения в квадрат обеих частей уравнения. Например, уравнение sqrt(x) = -2 не имеет решения, но если вы возведете в квадрат обе стороны, вы получите x = 4, но это не проверяется исходной задачей. Благодаря функциям «один к одному» вы не будете внедрять никаких посторонних решений.
Это не обязательно верно для функций, которые не являются взаимно однозначными, как функция возведения в квадрат, где вы всегда должны проверять ответы после возведения в квадрат обеих частей уравнения. Например, уравнение sqrt(x) = -2 не имеет решения, но если вы возведете в квадрат обе стороны, вы получите x = 4, но это не проверяется исходной задачей. Благодаря функциям «один к одному» вы не будете внедрять никаких посторонних решений.
Вау! Говорить о мощный. Вы не оцените это сейчас, и книга не рассматривает это должным образом, пока вы не получите к главе 4 и имеют дело с логарифмическими и экспоненциальными функциями, и даже тогда они не делают как бы это ни было важно.
Хорошо, давайте попробуем. Поверьте мне на слово, что exp(x) является взаимно однозначной функцией и обратный ln(x).
- ln(x) = 3
- Найдите x.
- ехр[ln(x)] = ехр[3]
- «Подождите, мистер Джонс» — ваш ответ. Такого зверя вы еще не видели.
 x и находится на странице [2 -й ] Клавиша [ln].
x и находится на странице [2 -й ] Клавиша [ln].
Ничего себе — больше сплоченности. Обратную функцию можно найти, взяв функцию [2 nd ]. Смотреть у него для прочего на калькуляторе.
Квадратный корень является обратным значением квадрата. Если вы посмотрите на три тригонометрических ключа [sin], [cos] и [tan], их обратные значения находятся с помощью клавиши [2 nd ].
Режим Soapbox включен.
Говорю тебе — все сходится. Для тех, кто помнит реплику Ганнибала Смита в A-Team: «Мне нравится, когда складывается план».
Математика — один из самых популярных предметов. Все дополняет все
еще. Я надеюсь, что вы вынесете из этого курса гораздо больше, чем просто механику
математике, а понимание, понимание и понимание того, как работает система.
С таким прочным фундаментом математика может быть менее напряженной и даже приятной. У вас есть
перестать иметь дело с концептами как с отдельными вещами, которые не связаны друг с другом и самостоятельны. Все они связаны друг с другом и переплетены. Их нельзя разделить и понять.
Все они связаны друг с другом и переплетены. Их нельзя разделить и понять.
Режим Soapbox выключен.
Mathscene — Функции 1 — Урок 3
Mathscene — Функции 1 — Урок 3| 2007 Расмус Эф и Джанн Сак | Функции я | Печать |
Урок 3
Функции второй степени
Давайте еще раз посмотрим на многочлены второй степени. Простейшая форма функции – f(x) = х 2 . График представляет собой парабола часто называется основной параболой.
Обратите внимание, что график симметричен относительно y- ось. Ось у называется осью симметрии этой функции.
Теперь посмотрим, как коэффициенты влияют на внешний вид графика.
Коэффициент х 2 есть
обычно называется а.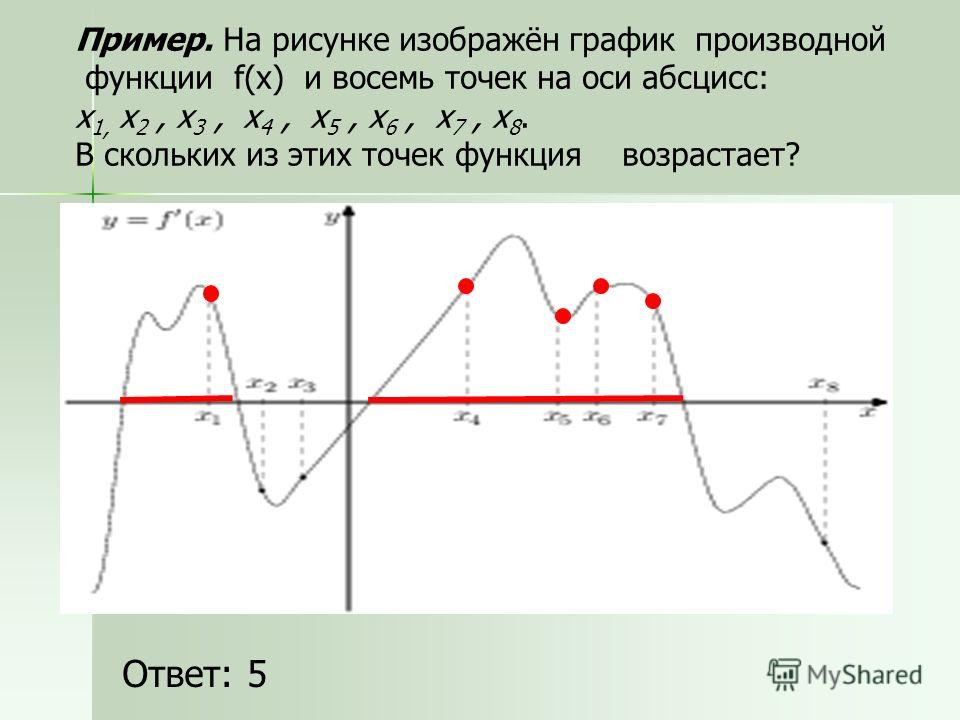 Если мы посмотрим на
парабол с разными значениями a мы видим, что некоторые из них шире, а некоторые
уже, чем основная парабола, где a = 1,
Если мы посмотрим на
парабол с разными значениями a мы видим, что некоторые из них шире, а некоторые
уже, чем основная парабола, где a = 1,
Вот графики парабол, где а = 4, 2, ог .
а = 4 а = 2 а = а =
Вот параболы с отрицательные значения
а = −4 а = -2 а = — а = —
Если значение a равно положительный график изгибается вверх (как улыбка!) Чем больше значение a, тем сузить график.
Как становится мало график становится все более и более плоским, пока, когда a не станет отрицательным, он не повернется вниз ( как хмурый! ).
Пример 1
Теперь нарисуем график f(x) = x 2 + 1 и сравните это с g(x) = x 2 .
| х | ф(х) = х 2 + 1 | |
| -2 | (-2) 2 + 1 = 5 | |
| -1 | (-1) 2 + 1 = 2 | |
| 0 | 0 + 1 = 1 | |
| 1 | 1 2 + 1 = 2 | |
| 2 | 2 2 + 1 = 5 |
Значения функции (
значения y ) в таблице значений для f(x) = x 2 +1 все
на единицу больше соответствующих значений в таблице значений g(x) = x 2 и график сместился по вертикали на 1 единицу.
Обратите внимание, что график f(x) = x 2 + 1 не пересекает ось х. Это говорит нам о том, что уравнение x 2 + 1 = 0 не имеет решения. Мы это уже знаем, поскольку квадрат числа никогда не отрицательный, поэтому x 2 никогда не может быть равен -1.
Пример 2
Нарисуйте график f(x) = x 2 − 1 и сравните его с g(x) = х 2 .
| х | ф(х) = х 2 — 1 | |
| -2 | (-2) 2 — 1 = 3 | |
| -1 | (-1) 2 — 1 = 0 | |
| 0 | 0 — 1 = -1 | |
| 1 | 1 2 — 1 = 0 | |
| 2 | 2 2 — 1 = 3 |
Теперь значения функции в
таблица f(x) на единицу ниже, чем соответствующие значения в таблице для
g(x) = x 2 и график
сместился на одну единицу.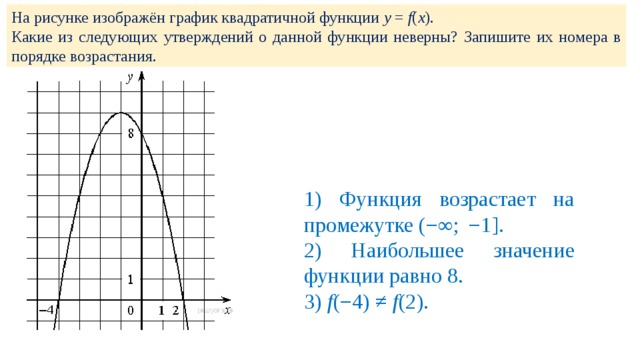
Обратите внимание, что в этом примере график f(x) = x 2 − 1 пересекает ось x в двух местах.
Это означает, что уравнение х 2 − 1 = 0 имеет два решения,
х 2 — 1 = 0
х 2 = 1
х = 1
, которые равны x = −1 и x = 1.
Пример 3
Нарисуйте график f(x) = (x + 1) 2 ( или f(x) = х 2 + 2х + 1) и сравните к основной параболе g(x) = x 2 .
| х | ф(х) = (х+1) 2 | |
| -3 | (-3 + 1) 2 = 4 | |
| -2 | (-2 + 1) 2 = 1 | |
| -1 | (-1 + 1) 2 = 0 | |
| 0 | (0 + 1) 2 = 1 | |
| 1 | (1 + 1) 2 = 4 |
Здесь мы добавили 1 к x
и мы видим, что функция
значения в таблице значений переместились на одну строку вверх по сравнению с базовым
функция.
График функции f(x) представляет собой то же самое, если мы переместим график g(x) = x 2 на одну единицу Слева.
Мы говорим, что базовый граф был переведен на -1 единиц по горизонтали. Ось симметрии теперь x = −1.
Пример 4
Нарисуй график f(x) = (x − 2) 2 − 1 (или f(x) = x 2 − 4x + 3) и сравните его с базовым графом g(x) = x 2 .
Если использовать тот же метод, что и в предыдущем Например, мы можем предположить, что график сместился на две единицы вправо и на одну единица вниз. Теперь проверим это, составив таблицу значения, начиная с x = 0 и рисование графика.
| х | ф(х) = (х — 2) 2 — 1 | |
| 0 | (0–2) 2 — 1= 3 | |
| 1 | (1–2) 2 — 1= 0 | |
| 2 | (2 — 2) 2 — 1 = -1 | |
| 3 | (3 — 2) 2 — 1 = 0 | |
| 4 | (4 — 2) 2 — 1 = 3 |
Обратите внимание, что ось симметрии теперь x = 2.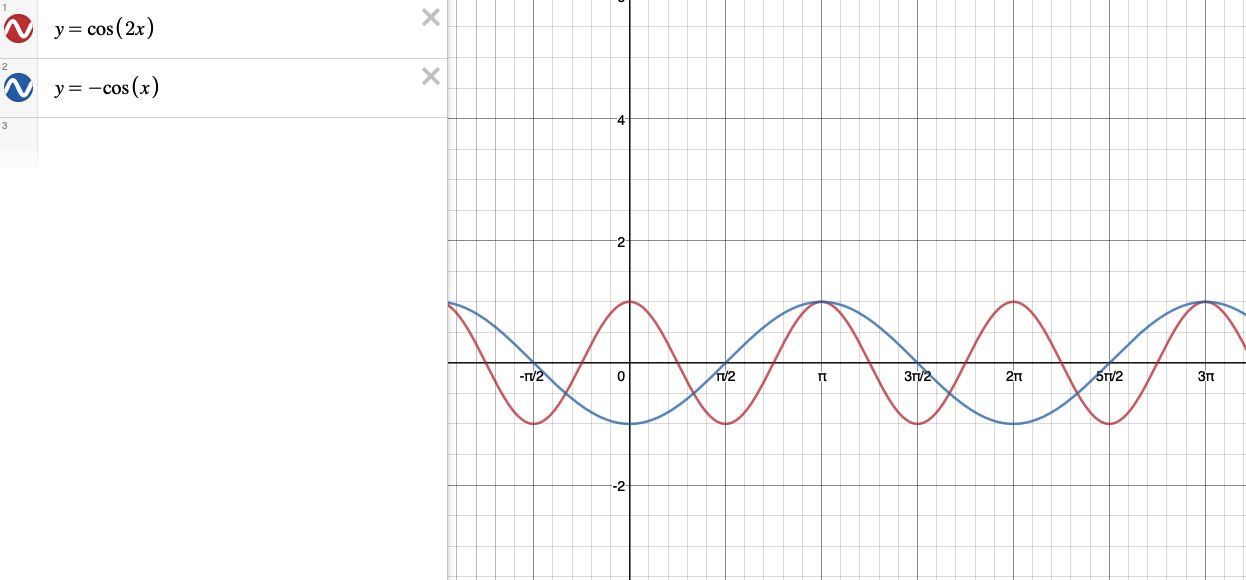
Мы можем найти, где график проходит по оси Y без рисования графика. Мы делаем это, вычисляя f(0) = 3 или путем умножения скобок и видя, что постоянный член (термин без x) равен 3.
f(x) = (x − 2) 2 − 1 = x 2 − 4x + 4 − 1 = x 2 − 4x + 3 или
f(0) = (x − 2) 2 − 1 = 4 − 1 = 3
Пример 5
Найдите график f(x) = (x − 2) 2 − 1 пересекает ось x. Положим y = f(x) = 0 и решим уравнение для х.
| (х — 2) 2 − 1 = 0 | Первый переместите -1 на знак равенства. |
| (х — 2) 2 = 1 | Далее, возьми квадратный корень из обеих частей уравнения. Запомните + и −. |
| х — 2 = 1 = 1 | Наконец
переместите 2 на другую сторону и упростите результат. |
| х = 2 1 |
Точки пересечения х = 2 −1 = 1 и х = 2 + 1 = 3.
Легко видеть, что запись функции в виде f(x) = (x − 2) 2 − 1 дает нам много информации.
Это говорит нам, как переводится базовый график вертикально и горизонтально.
Это также говорит нам, где находится ось симметрии.
Наконец, мы можем легко найти точки пересечение с осями x и y.
Общий вид уравнения, записанного в этом путь:
f(x) = a(x + r) 2 + s
а — коэффициент x 2 как мы уже видели.
ось симметрии имеет уравнение x = −r (или, можно сказать, имеет такое же значение как r, но с обратным знаком).
Из-за этого важно знать, как переписать функцию
ф(х) = топор 2 + bx + c в виде f(x) = a(x + r) 2 + s
Пример 6
Теперь давайте посмотрим, как мы можем изменить секунду
степень функции от одной формы к другой.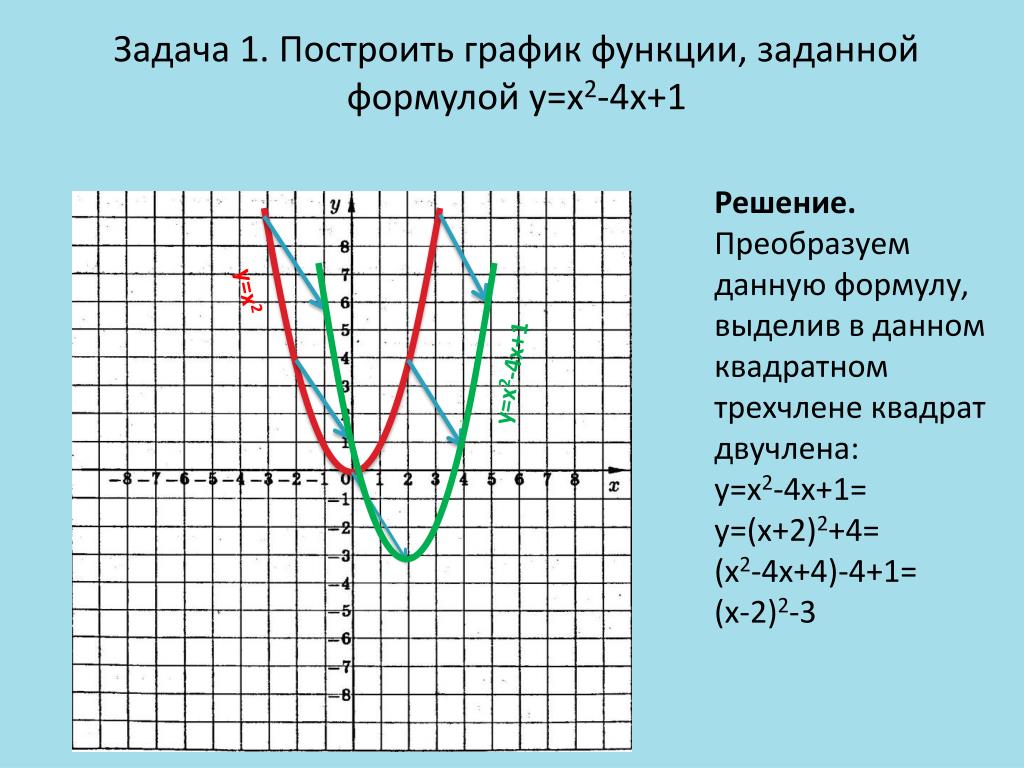
Перепишите f(x) = x 2 − 4x + 3 в виде f(x) = (x − 2) 2 − 1.
По сравнению с общей формой:
f(x) = ах 2 + бх + с
f(x) = x 2 − 4x + 3
Вот = 1
огб = -4
и c = 3 (поэтому график пересекает ось y в 3).
Посмотрите на правило возведения скобки в квадрат:
(x q) 2 = p 2 2xq + q 2 .
Мы видим, что коэффициент x составляет 2 кв.
В нашем примере коэффициент x равен −4, что означает 2q = − 4 и, следовательно, д = -2.
Если мы рассчитаем (х − 2) 2 получаем х 2 − 4x + 4.
(х − 2) 2 = х 2 − 4x + 4.
Если вычесть 1 с обеих сторон мы получаем :
(х — 2) 2 −1 = х 2 − 4х + 4-1 = х 2 — 4х + 3
Подведение итогов метода:
| f(x) = x 2 − 4x + 3 | Половина
коэффициент x равен −4 / 2 = −2, что мы возводим в квадрат (4 ) и
добавить в уравнение. |
| = (x 2 − 4x + 2 2 ) − 2 2 + 3 | |
| = (x − 2) 2 − 4 + 3 | Если мы
добавить 4 к уравнению, мы также должны вычесть 4, так что уравнение
остается без изменений Теперь упростим -4+3 = -1 |
| = (x − 2) 2 − 1 |
Из вышеприведенного примера можно сделать вывод, что график полинома второй степени, где a = 1 (f(x) = x 2 + bx + c) имеет ось симметрии в:
x = −b / 2 и разрезает y ось, где y = c.
Пример 7
Найдите ось симметрии графика f(x) = 2x 2 − 12x + 10.
В этом случае a = 2 , поэтому правило из предыдущего примера не применяется. Ни один
так же легко переписать функцию, как и раньше.
Вместо этого мы переводим функцию вниз на 10 единиц, вычитая 10 из уравнения. Перемещение графика по вертикали не изменить положение оси симметрии.
Мы называем эту новую функцию g(x) и находим, где g(x) пересекает ось x.
2x 2 − 12x = 0
2х(х — 6) = 0
Это уравнение имеет решения x = 0 и 6, поэтому график g(x) пересекает ось x в 0 и 6. Ось симметрии должна быть посередине этих двух точек, т.е. находится в х = 3 .
Пример 8
Перепишите функцию f(x) = 2x 2 − 12x + 10 в виде
f(x) = a(x + r) 2 + с.
| f(x) = 2x 2 − 12x + 10 | Дубль 2
за скобками. Половина коэффициента x
равно −6 / 2 = −3, поэтому в скобках прибавь 3 2 .
Мы действительно добавили 18, так что теперь нам нужно вычесть 23 2 = 18 вне скобок. |
| = 2(x 2 − 6x + 3 2 ) − 2 3 2 + 10 | |
| = 2(x 2 − 6x + 9) − 18 + 10 | |
| = 2 (х — 3) 2 − 8 |
Теперь мы видим, как и прежде, что ось симметрии находится в х = 3,
Коэффициенты x В приведенном выше примере (f(x) = 2x 2 − 12x + 10) a = 2, b = −12 и c = 10. Чтобы найти ось симметрии, мы вынесли множитель 2 за скобки. Это соответствует делению на 2. Тогда мы дополнил квадрат делением коэффициента при x (−6) на 2,
Общая формула для оси симметрии
функция
f(x) = ax 2 + бх + с есть
поэтому:
Пример 9
Найдите вершину параболы f(x) = 2x 2 − 12х + 10.
Вершина (где парабола поворачивается) лежит
на оси симметрии, поэтому мы знаем x-значение вершины (3).
Мы нашли значение y путем вычисления f (3).
f(3) = 23 2 − 123 + 10 = 18 − 36 + 10 = −8.
Вершина параболы (3, −8).
Примечание. Если a>0, вершина является точкой минимума. Если a<0 вершина является точкой максимума.
Попробуйте пройти тест 3 по функциям I.
Не забывайте использовать контрольный список, чтобы отслеживать свою работу.
Исчисление I — обратные функции
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Уведомление для мобильных устройств
Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 1-2: Обратные функции
В последнем примере из предыдущего раздела мы рассмотрели две функции \(f\left( x \right) = 3x — 2\) и \(g\left( x \right) = \frac{x}{ 3} + \frac{2}{3}\) и увидел, что
\[\left( {f \circ g} \right)\left( x \right) = \left( {g \circ f} \right)\left( x \right) = x\]
, и, как отмечалось в этом разделе, это означает, что между этими двумя функциями существует хорошая взаимосвязь. Давайте посмотрим, что это за отношения. Рассмотрим следующие оценки.
\[\require{color} \begin{align*}f\left( {\color{PineGreen} — 1} \right) & = 3\left( { — 1} \right) — 2 = {\color{Red }- 5} \hspace{0. 5in} \Rightarrow \hspace{0.25in} & g\left( {\color{Red} — 5} \right) & = \frac{{ — 5}}{3} + \ frac{2}{3} = \ frac{{ — 3}}{3} = {\color{PineGreen} — 1}\\ & & & & \\ g\left( {\color{PineGreen}2} \right ) & = \ frac {2} {3} + \ frac {2} {3} = {\ color {Red} \ frac {4} {3}} \ hspace {0,5 дюйма} \ Rightarrow \ hspace {0,25 дюйма} & f \ влево ( {\ color {Red} \ frac {4} {3}} \ right) & = 3 \ left ( {\ frac {4} {3}} \ right) — 2 = 4 — 2 = { \color{PineGreen}2}\end{align*}\]
5in} \Rightarrow \hspace{0.25in} & g\left( {\color{Red} — 5} \right) & = \frac{{ — 5}}{3} + \ frac{2}{3} = \ frac{{ — 3}}{3} = {\color{PineGreen} — 1}\\ & & & & \\ g\left( {\color{PineGreen}2} \right ) & = \ frac {2} {3} + \ frac {2} {3} = {\ color {Red} \ frac {4} {3}} \ hspace {0,5 дюйма} \ Rightarrow \ hspace {0,25 дюйма} & f \ влево ( {\ color {Red} \ frac {4} {3}} \ right) & = 3 \ left ( {\ frac {4} {3}} \ right) — 2 = 4 — 2 = { \color{PineGreen}2}\end{align*}\]
В первом случае мы подставили \(x = — 1\) в \(f\left( x \right)\) и получили значение \(-5\). Затем мы развернулись и подставили \(x = — 5\) к \(g\left( x \right)\) и получили значение -1, число, с которого мы начали.
Во втором случае мы сделали нечто подобное. Здесь мы подставили \(x = 2\) к \(g\left( x \right)\) и получили значение \(\frac{4}{3}\), мы развернулись и подставили это к \( f\left( x \right)\) и получил значение 2, которое снова является числом, с которого мы начали.
Обратите внимание, что здесь мы действительно выполняем композицию функций. Первый случай действительно,
Первый случай действительно,
\[\left( {g \circ f} \right)\left( { — 1} \right) = g\left[ {f\left( { — 1} \right)} \right] = g\left[ {- 5} \справа] = — 1\]
и действительно второй случай,
\[\ влево ( {е \ circ g} \ вправо) \ влево ( 2 \ вправо) = е \ влево [ {г \ влево ( 2 \ вправо)} \ вправо] = е \ влево [ {\ гидроразрыва {4} {3}} \справа] = 2\]
Также обратите внимание, что оба они согласуются с формулой композиций, которую мы нашли в предыдущем разделе. Мы получаем обратно из вычисления функции число, которое мы изначально вставили в композицию.
Итак, что здесь происходит? В некотором смысле мы можем думать об этих двух функциях как об отмене того, что другая сделала с числом. В первом случае мы подставили \(x = — 1\) в \(f\left( x \right)\), а затем подставили результат этой функции обратно в \(g\left( x \right)\) и каким-то образом \(g\left( x \right)\) отменил то, что \(f\left( x \right)\) сделал с \(x = — 1\), и вернул нам исходный \(x \), с которого мы начали.
Пары функций, демонстрирующие такое поведение, называются обратные функции . Прежде чем формально определить обратные функции и обозначения, которые мы собираемся использовать для них, нам нужно получить определение.
Функция называется однозначной , если никакие два значения \(x\) не дают одинаковых \(y\). Математически это то же самое, что сказать
. \[f\left( {{x_1}} \right) \ne f\left( {{x_2}} \right)\hspace{0,25 дюйма}\hspace{0,25 дюйма}{\rm{когда}}\hspace{ 0,25 дюйма}\,\,\,\,\,\,{x_1} \ne {x_2}\] 92}\) во взаимно однозначную функцию, если мы ограничимся \(0 \le x < \infty \). Иногда это можно сделать с помощью функций.
Демонстрация однозначности функции часто утомительна и/или сложна. По большей части мы будем предполагать, что функции, с которыми мы будем иметь дело в этом курсе, являются либо взаимно однозначными, либо мы ограничили область определения функции, чтобы сделать ее взаимно однозначной. { — 1}}\left( х \справа)\). 9{ — 1}} \circ f} \right)\left( x \right) = x\) верны. Для всех функций, которые мы будем рассматривать в этом курсе, если одна из них истинна, то и другая тоже будет верна. Однако существуют функции (однако они выходят за рамки этого курса), для которых возможно, что только одно из них будет истинным. Это связано с тем, что во всех задачах здесь мы будем проверять только одну из них. Нам просто нужно всегда помнить, что технически мы должны проверять оба.
{ — 1}}\left( х \справа)\). 9{ — 1}} \circ f} \right)\left( x \right) = x\) верны. Для всех функций, которые мы будем рассматривать в этом курсе, если одна из них истинна, то и другая тоже будет верна. Однако существуют функции (однако они выходят за рамки этого курса), для которых возможно, что только одно из них будет истинным. Это связано с тем, что во всех задачах здесь мы будем проверять только одну из них. Нам просто нужно всегда помнить, что технически мы должны проверять оба.
Давайте рассмотрим несколько примеров. 9{ — 1}}\влево( х \вправо)\).
Показать решение
Теперь мы уже знаем, что является обратной для этой функции, так как мы уже поработали с ней. Тем не менее, было бы неплохо начать с этого, поскольку мы знаем, что мы должны получить. Это будет хорошей проверкой процесса.
Итак, приступим. Сначала мы заменим \(f\left( x \right)\) на \(y\).
\[у = 3x — 2\]
9{ — 1}}\влево( х \вправо)\).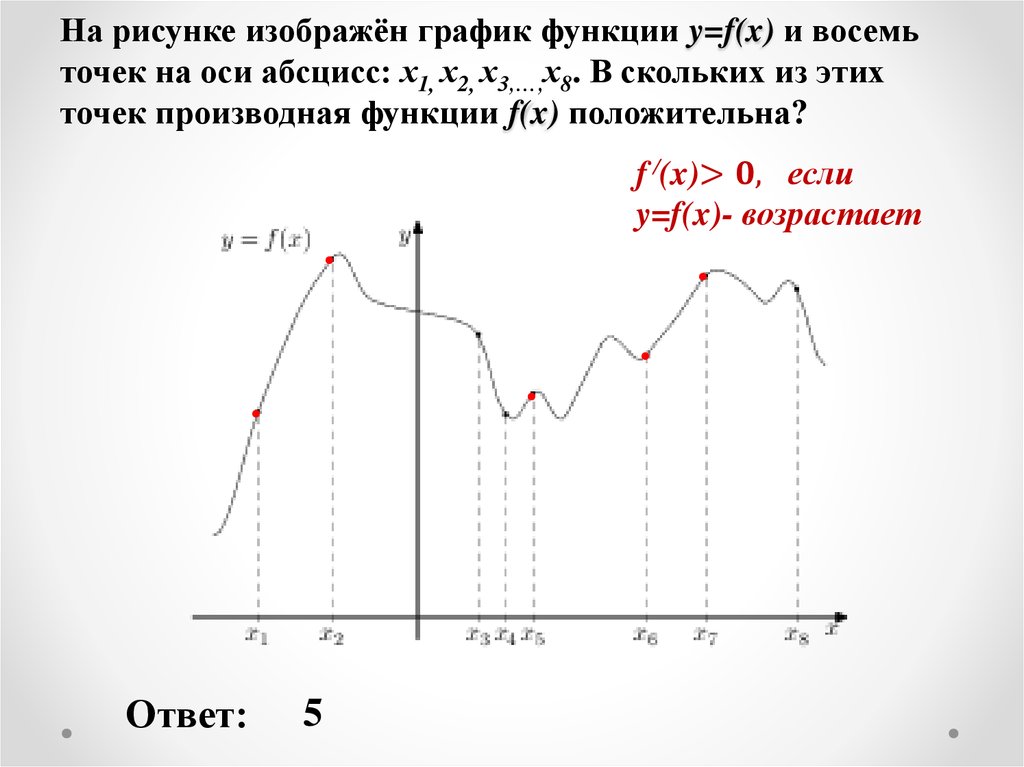
Показать решение
Тот факт, что мы используем \(g\left( x \right)\) вместо \(f\left( x \right)\), не меняет того, как работает процесс. Вот первые несколько шагов.
\[y = \sqrt {x — 3} \hspace{0,25 дюйма}\,\,\,\,\,\, \Rightarrow \hspace{0,25 дюйма}\,\,\,\,\,\,\ ,\,\,х = \sqrt {у — 3} \]
Теперь, чтобы найти \(y\), нам нужно сначала возвести в квадрат обе стороны, а затем действовать как обычно. 9{ — 1}}\влево( х \вправо)\).
Показать решение
Первые несколько шагов почти такие же, как и в предыдущих примерах, так что вот они,
\[y = \frac{{x + 4}}{{2x — 5}}\hspace{0,25 дюйма}\,\,\,\,\,\,\, \Rightarrow \,\,\,\, \,\,\,\,\,\,\,\,\,\,\,\,\,x = \frac{{y + 4}}{{2y — 5}}\]
Теперь будьте осторожны с шагом решения.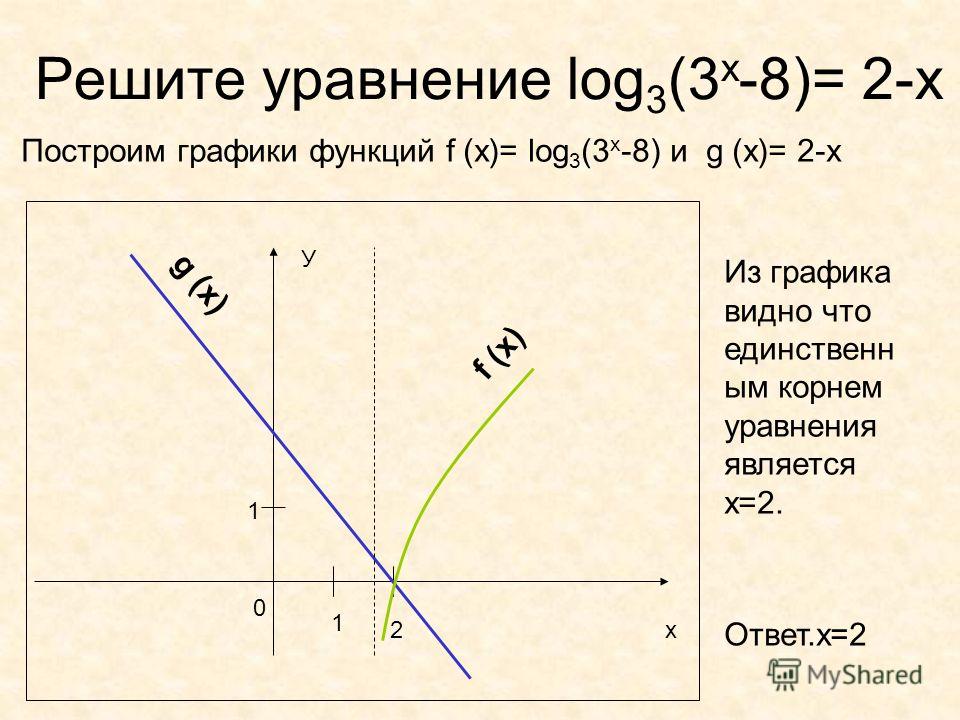 В такой задаче очень легко ошибиться. 9{ — 1}}} \right)\left( x \right) & = \frac{{2x — 1}}{{2x — 1}}\,\,\frac{{\frac{{4 + 5x} }{{2x — 1}} + 4}}{{2\left( {\frac{{4 + 5x}}{{2x — 1}}} \right) — 5}}\\ & = \frac{ {\ влево ( {2x — 1} \ вправо) \ влево ( {\ гидроразрыва {{4 + 5x}} {{2x — 1}} + 4} \ вправо)}} {{\ влево ( {2x — 1} \right)\left( {2\left( {\frac{{4 + 5x}}{{2x — 1}}} \right) — 5} \right)}}\\ & = \frac{{4 + 5x + 4\влево( {2x — 1} \вправо)}}{{2\влево( {4 + 5x} \вправо) — 5\влево( {2x — 1} \вправо)}}\\ & = \ frac{{4 + 5x + 8x — 4}}{{8 + 10x — 10x + 5}}\\ & = \frac{{13x}}{{13}} = x\end{align*}\]
В такой задаче очень легко ошибиться. 9{ — 1}}} \right)\left( x \right) & = \frac{{2x — 1}}{{2x — 1}}\,\,\frac{{\frac{{4 + 5x} }{{2x — 1}} + 4}}{{2\left( {\frac{{4 + 5x}}{{2x — 1}}} \right) — 5}}\\ & = \frac{ {\ влево ( {2x — 1} \ вправо) \ влево ( {\ гидроразрыва {{4 + 5x}} {{2x — 1}} + 4} \ вправо)}} {{\ влево ( {2x — 1} \right)\left( {2\left( {\frac{{4 + 5x}}{{2x — 1}}} \right) — 5} \right)}}\\ & = \frac{{4 + 5x + 4\влево( {2x — 1} \вправо)}}{{2\влево( {4 + 5x} \вправо) — 5\влево( {2x — 1} \вправо)}}\\ & = \ frac{{4 + 5x + 8x — 4}}{{8 + 10x — 10x + 5}}\\ & = \frac{{13x}}{{13}} = x\end{align*}\]
Вау. Было много работы, но в итоге все получилось. Мы сделали всю нашу работу правильно, и на самом деле мы имеем обратное.
Есть еще одна последняя тема, которую нам нужно быстро обсудить, прежде чем мы покинем этот раздел. Между графиком функции и графиком обратной функции существует интересная связь.
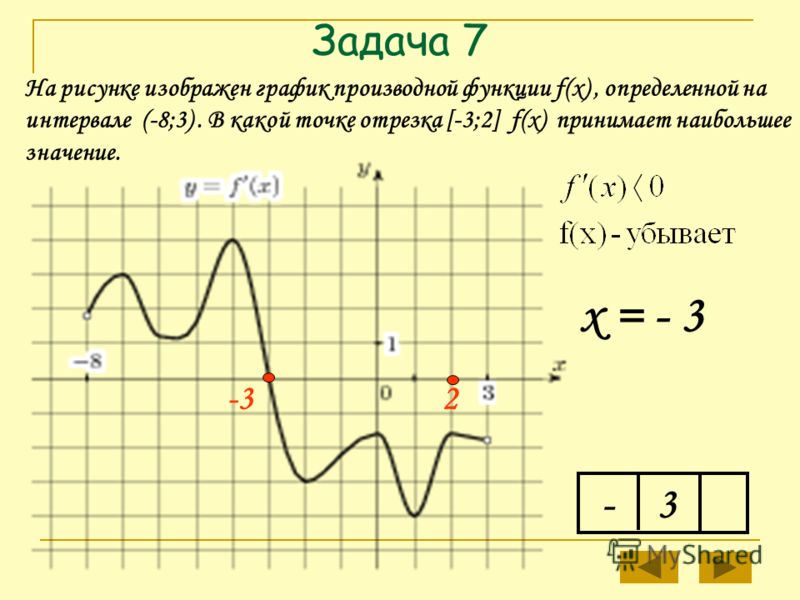
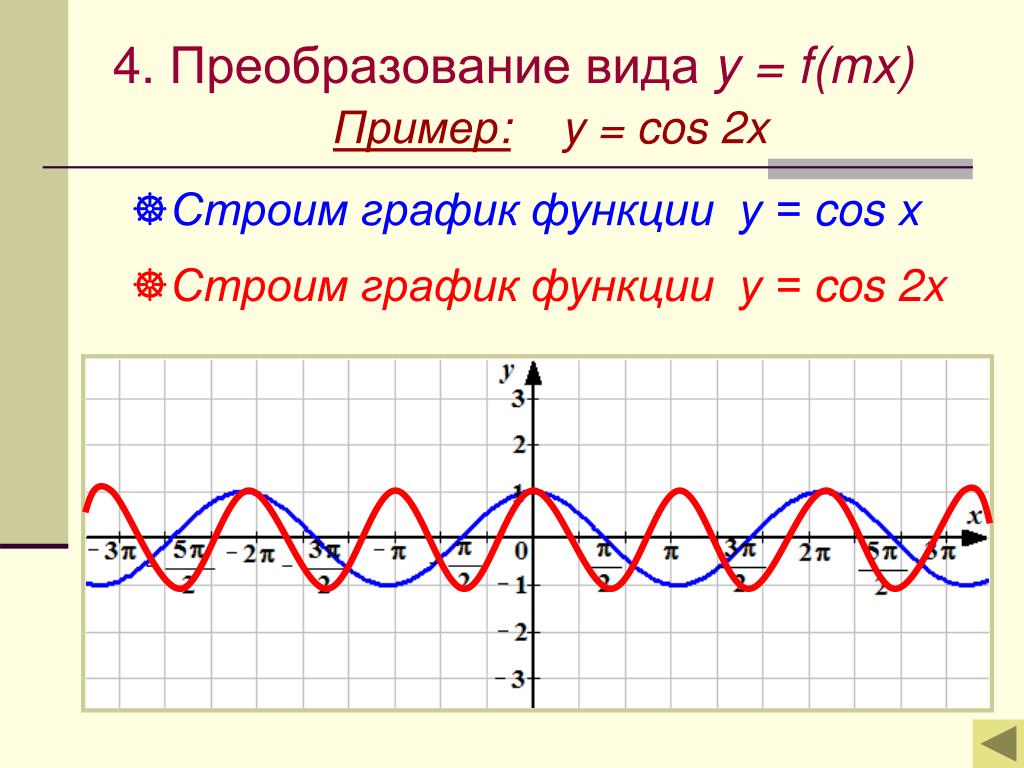
Вот график функции и обратной из первых двух примеров.


 Совпадут ли эти графики? Скорее всего, нет.
Совпадут ли эти графики? Скорее всего, нет. 
 04.18
04.18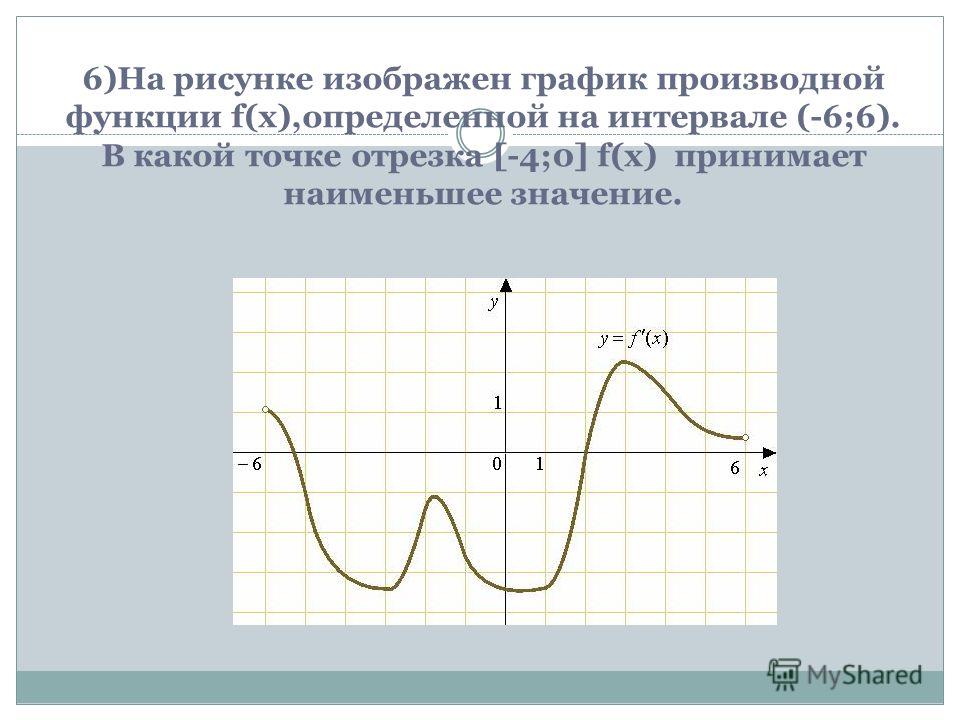

 Таким образом, текст для поля g будет 9(1/3)
Таким образом, текст для поля g будет 9(1/3)
 x и находится на странице [2 -й ] Клавиша [ln].
x и находится на странице [2 -й ] Клавиша [ln].