График функции модуля: Графики функций с модулем

alexxlab / / Разное

Построение графиков, содержащих знак модуля

Построение графиков

с модулем

Выполнила работу:

Ученица 9 В класса

МОУ Гимназии имени А. Л. Кекина

Рогушкина Дарья

Руководитель: Иванченко

Ирина Алексеевна

Понятие «модуль»

Слово « модуль » произошло от латинского слова «modulus»

|x|

Понятие «модуль»

Воспользовавшись определением модуля, можно записать:

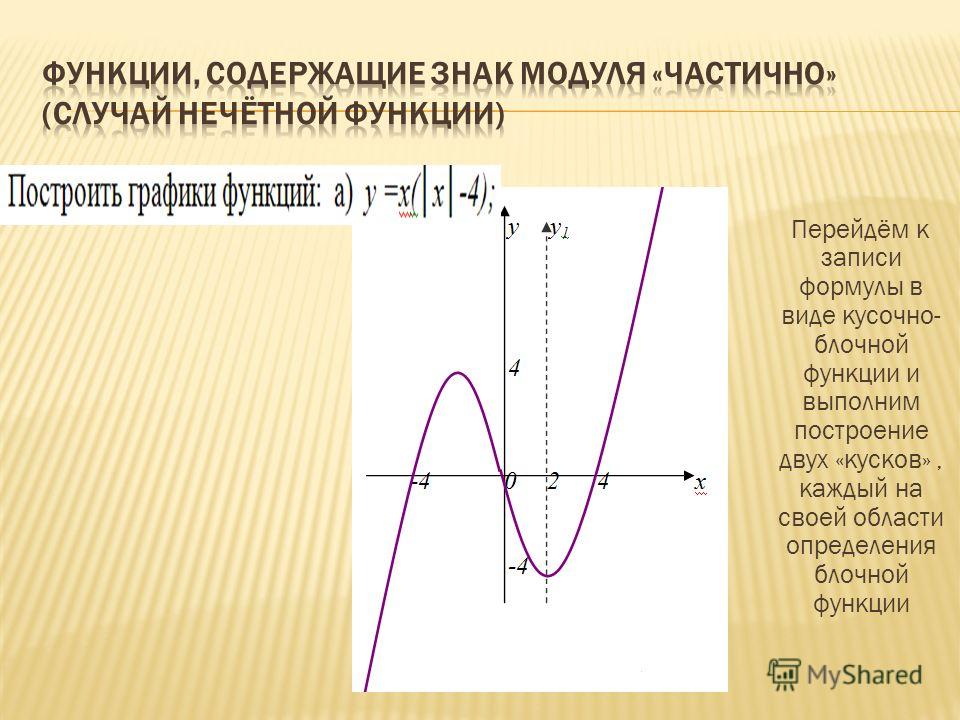
Отсюда можно сделать вывод, что график функции у = f (| x |) при х≥ 0 совпадает с графиком функции у = f ( x ) , а при х 0 — с графиком функции у = f (- x ) .

Алгоритм построения графика функции у = f (| x |)

Тогда построение графика функции

у = f (| x |) можно проводить по следующей схеме.

1) Построить ту часть графика функции у = f ( x ) , все точки которой имеют неотрицательные абсциссы;

2) построить ту часть графика функции у = f (- x ) , все точки которой имеют отрицательные абсциссы.

Объединение этих двух построенных фигур является графиком функции у = f (| x |)

Алгоритм построения графика функции у = f (| x |)

Заметим, что функция у = f (| x |) является чётной. Поэтому ось ординат является осью симметрии её графика. Тогда график функции у = f (| x |) можно получить по следующей схеме.

1) Построить ту часть графика функции у = f ( x ) , все точки которой имеют неотрицательные абсциссы;

2) построить фигуру, симметричную полученной относительно оси ординат.

Объединение двух построенных фигур является графиком функции у = f (| x |)

функция у = f | ( x ) |

Для функции у = f | ( x ) | можно записать:

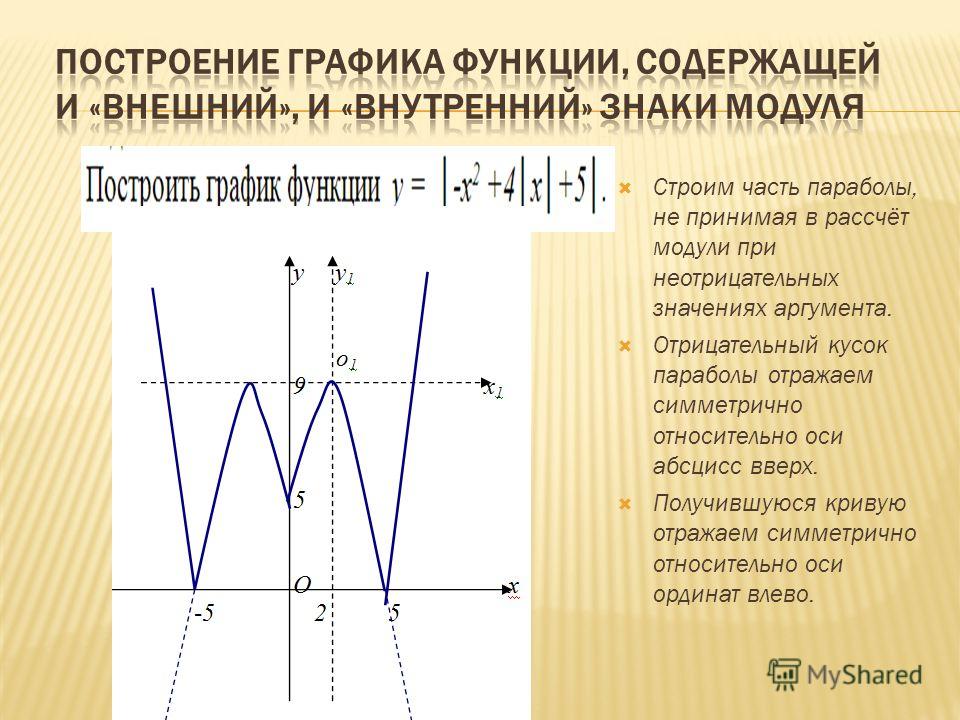
Отсюда можно сделать такой вывод: график функции у = |f(х)| при всех х, для которых f(x) ≥ 0, совпадает с графиком функции у = f(x), а при всех х, для которых f(x)

Алгоритм построения графика функции у = f | (

x ) |

Тогда построение графика функции у = | f (х)| можно проводить по следующей схеме.

1) Построить ту часть графика функции у = f ( x ) , все точки которой

имеют неотрицательные ординаты;

2) построить ту часть графика функции у = — f ( x ) , все точки которой имеют положительные ординаты.

Объединение двух построенных фигур является графиком функции у = | f (х)|

Алгоритм построения графика функции у = f | ( x ) |

Поскольку графики функций у = f ( x ) и у = — f

( x ) симметричны относительно оси абсцисс, то искомый график можно получить по следующей схеме.

1) Ту часть графика функции у = f ( x ) , точки которой имеют неотрицательные ординаты, оставить без изменений;

2) построить фигуру, симметричную относительно оси абсцисс той части графика функции у = f ( x ) , точки которой имеют отрицательные ординаты.

Объединение этих двух построенных фигур и составит график функции у = | f (х)|

Задание №1:

y=I3-xI-2

Задание №1:

y=I3-xI-2

у

1) y=x

х

Задание №1:

y=I3-xI-2

1) y=x

2) y=IxI

Задание №1:

y=I3-xI-2

1) y=x

2) y=IxI

3) y=I3-xI

Задание №1:

y=I3-xI-2

1) y=x

2) y=IxI

3) y=I3-xI

4) y=I3-xI-2

Задание №1:

y=I3-xI-2

1) y=x

2) y=IxI

3) y=I3-xI

4) y=I3-xI-2

Задание №2:

y=I(IxI-2) 2 -3I

Задание №2:

y=I(IxI-2) 2 -3I

1) y=x 2

Задание №2:

y=I(IxI-2) 2 -3I

1) y=x 2

2) y=(x-2) 2

Задание №2:

y=I(IxI-2) 2 -3I

1) y=x 2

2) y=(x-2) 2

3) y=(IxI-2) 2

Задание №2:

y=I(IxI-2) 2 -3I

1) y=x 2

2) y=(x-2) 2

3) y=(IxI-2) 2

4) y=(IxI-2) 2 -3

Задание №2:

y=I(IxI-2) 2 -3I

1) y=x 2

2) y=(x-2) 2

3) y=(IxI-2) 2

4) y=(IxI-2) 2 -3

5) y=I(IxI-2) 2 -3I

Задание №2:

y=I(IxI-2) 2 -3I

1) y=x 2

2) y=(x-2) 2

3) y=(IxI-2) 2

4) y=(IxI-2) 2 -3

5) y=I(IxI-2) 2 -3I

Задание №3:

x+2

y= x-3

x-3 5 5

x-3 + x-3 = 1 + x-3

Задание №3:

x+2

y= x-3

x-3 5 5

x-3 + x-3 = 1 + x-3

5

  • y= x

Задание №3:

x+2

y= x-3

x-3 5 5

x-3 + x-3 = 1 + x-3

5

  • y= x

5

  • y= x-3

Задание №3:

x+2

y= x-3

x-3 5 5

x-3 + x-3 = 1 + x-3

5

  • y= x

5

  • y= x-3

5

3) y=1+x-3

Задание №3:

x+2

y= x-3

x-3 5 5

x-3 + x-3 = 1 + x-3

5

  • y= x

5

  • y= x-3

5

3) y=1+x-3

5

4) y= | 1+x-3 |

Задание №3:

x+2

y= x-3

x-3 5 5

x-3 + x-3 = 1 + x-3

5

  • y= x

5

  • y= x-3

5

3) y=1+x-3

5

4) y= | 1+x-3 |

Задание №4:

y=I √ IxI-1-1 I

Задание №4:

y=I √ IxI-1-1 I

1) y= √ x

Задание №4:

y=I √ IxI-1-1 I

1) y= √ x

2) y= √ x-1

Задание №4:

y=I √ IxI-1-1 I

1) y= √ x

2) y= √ x-1

3) y= √ IxI-1

Задание №4:

y=I √ IxI-1-1 I

1) y= √ x

2) y= √ x-1

3) y= √ IxI-1

4) y= √ IxI-1-1

Задание №4:

y=I √ IxI-1-1 I

1) y= √ x

2) y= √ x-1

3) y= √ IxI-1

4) y= √ IxI-1-1

5) y= I √ IxI-1-1I

Задание №4:

y=I √ IxI-1-1 I

1) y= √ x

2) y= √ x-1

3) y= √ IxI-1

4) y= √ IxI-1-1

5) y= I √ IxI-1-1I

Вывод

Таким образом, мы научились строить графики с модулем.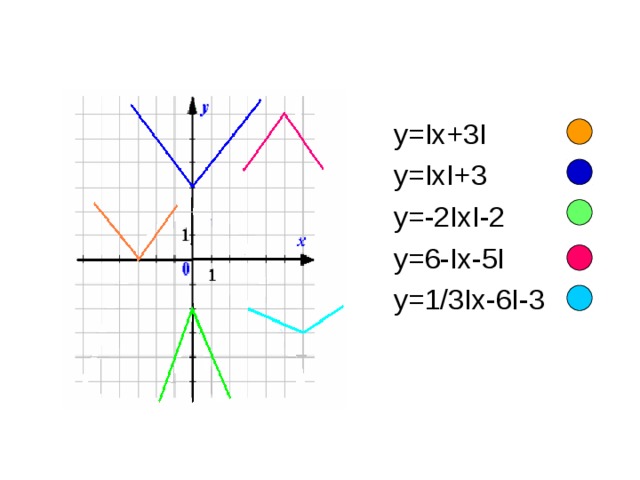 Подробнее изучив алгоритмы их построения, мы сможем применять эти правила на практике.

Спасибо за внимание!

Источники:

  • http://xn--i1abbnckbmcl9fb.xn--p1ai/%D1%81%D1%82%D0%B0%D1%82%D1%8C%D0%B8/524487 /
  • Учебник «Алгебра.9 класс». (авт. А.Г. Мерзляк, В.М. Поляков), 2015

Галерея PowerShell | microsoft.graph.psd1 1.6.1

№
# Манифест модуля для модуля ‘Microsoft.Graph’
№
# Создано: Microsoft
№
# Создано: 12.07.2021
#

@{

# Модуль сценария или файл двоичного модуля, связанный с этим манифестом.
# RootModule = »

# Номер версии этого модуля.
ModuleVersion = ‘1.6.1’

# Поддерживаемые PSEditions
CompatiblePSEditions = ‘Core’, ‘Desktop’

# Идентификатор, используемый для уникальной идентификации этого модуля
GUID = ‘2d708ce1-67c3-40a1-994b-fd69270c3662’

# Автор этого модуля
Автор = ‘Microsoft’

# Компания или поставщик этого модуля
CompanyName = ‘Microsoft’

# Заявление об авторских правах для этого модуля
Авторские права = ‘© Корпорация Microsoft.

Все права защищены.’

# Описание функционала данного модуля
Описание = ‘Модуль Microsoft Graph PowerShell’

# Минимальная версия ядра PowerShell, необходимая для этого модуля
PowerShellVersion = ‘5.1’

# Имя узла PowerShell, необходимого для этого модуля
# PowerShellHostName = »

# Минимальная версия хоста PowerShell, необходимая для этого модуля
# PowerShellHostVersion = »

# Минимальная версия Microsoft .NET Framework, необходимая для этого модуля. Это предварительное условие действительно только для версии PowerShell Desktop.
DotNetFrameworkVersion = ‘4.7.2’

# Минимальная версия общеязыковой среды выполнения (CLR), необходимая для этого модуля. Это предварительное условие действительно только для версии PowerShell Desktop.
# ClrVersion = »

# Архитектура процессора (Нет, X86, Amd64), необходимая для этого модуля

# ProcessorArchitecture = »

# Модули, которые необходимо импортировать в глобальную среду перед импортом этого модуля
RequiredModules = @(@{ModuleName = ‘Microsoft. Graph.Authentication’; ModuleVersion = ‘1.6.0’; }, 
@{ModuleName = ‘Microsoft.Graph.People’; RequiredVersion = ‘1.6.0’; }, 
@{ModuleName = ‘Microsoft.Graph.Users.Functions’; RequiredVersion = ‘1.6.1’; }, 
@{ModuleName = ‘Microsoft.Graph.Users.Actions’; RequiredVersion = ‘1.6.1’; }, 
@{ModuleName = ‘Microsoft.Graph.Users’; RequiredVersion = ‘1.6.1’; }, 
@{ModuleName = ‘Microsoft.Graph.Education’; RequiredVersion = ‘1.6.1’; }, 
@{ModuleName = ‘Microsoft.Graph.Compliance’; RequiredVersion = ‘1.6.1’; }, 
@{ModuleName = ‘Microsoft.Graph.SchemaExtensions’; RequiredVersion = ‘1.6.0’; }, 
@{ModuleName = ‘Microsoft.Graph.Applications’; RequiredVersion = ‘1.6.1’; }, 
@{ModuleName = ‘Microsoft.Graph.DeviceManagement.Functions’; RequiredVersion = ‘1.6.0’; }, 
@{ModuleName = ‘Microsoft.Graph.Mail’; RequiredVersion = ‘1.6.0’; }, 
@{ModuleName = ‘Microsoft.Graph.Files’; RequiredVersion = ‘1.6.1’; }, 
@{ModuleName = ‘Microsoft. Graph.DeviceManagement’; RequiredVersion = ‘1.6.1’; }, 
@{ModuleName = ‘Microsoft.Graph.Groups’; RequiredVersion = ‘1.6.1’; }, 
@{ModuleName = ‘Microsoft.Graph.Reports’; RequiredVersion = ‘1.6.0’; }, 
@{ModuleName = ‘Microsoft.Graph.DeviceManagement.Actions’; RequiredVersion = ‘1.6.1’; }, 
@{ModuleName = ‘Microsoft.Graph.WindowsUpdates’; RequiredVersion = ‘1.6.0’; }, 
@{ModuleName = ‘Microsoft.Graph.Planner’; RequiredVersion = ‘1.6.0’; }, 
@{ModuleName = ‘Microsoft.Graph.Sites’; RequiredVersion = ‘1.6.1’; }, 
@{ModuleName = ‘Microsoft.Graph.DirectoryObjects’; RequiredVersion = ‘1.6.0’; }, 
@{ModuleName = ‘Microsoft.Graph.CloudCommunications’; RequiredVersion = ‘1.6.1’; }, 
@{ModuleName = ‘Microsoft.Graph.Devices.CorporateManagement’; RequiredVersion = ‘1.6.1’; }, 
@{ModuleName = ‘Microsoft.Graph.ChangeNotifications’; RequiredVersion = ‘1.6.0’; }, 
@{ModuleName = ‘Microsoft.Graph.PersonalContacts’; RequiredVersion = ‘1.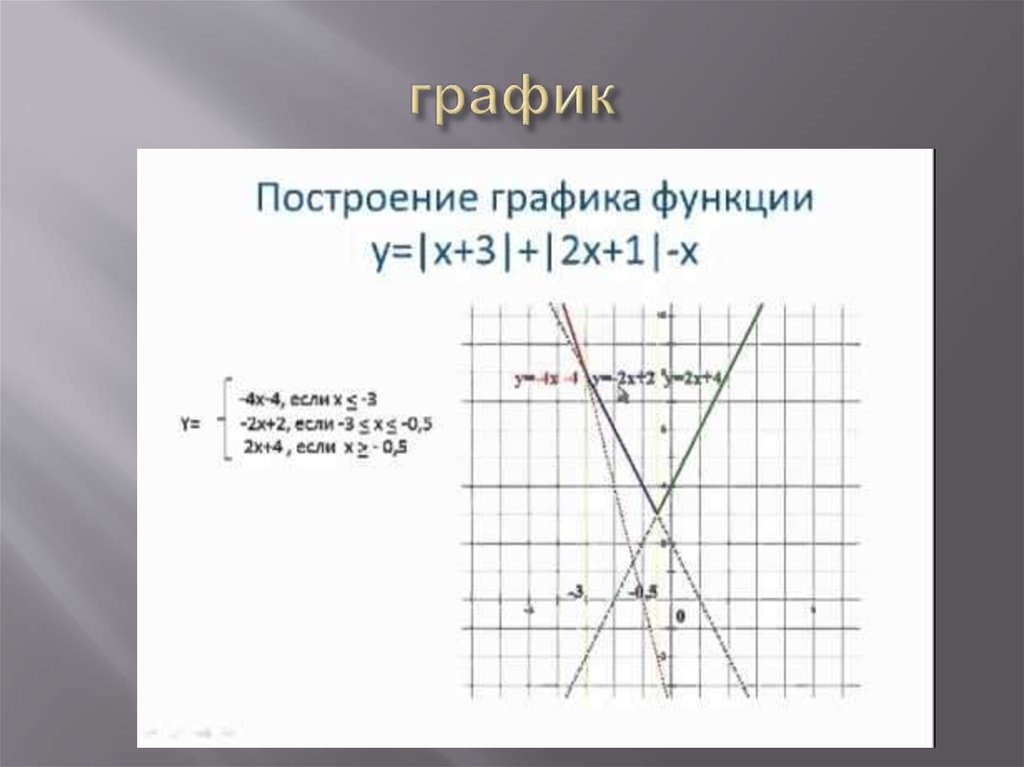 6.0′; }, 
@{ModuleName = ‘Microsoft.Graph.Search’; RequiredVersion = ‘1.6.1’; }, 
@{ModuleName = ‘Microsoft.Graph.Bookings’; RequiredVersion = ‘1.6.0’; }, 
@{ModuleName = ‘Microsoft.Graph.DeviceManagement.Administration’; RequiredVersion = ‘1.6.1’; }, 
@{ModuleName = ‘Microsoft.Graph.DeviceManagement.Enrolment’; RequiredVersion = ‘1.6.0’; }, 
@{ModuleName = ‘Microsoft.Graph.Identity.SignIns’; RequiredVersion = ‘1.6.1’; }, 
@{ModuleName = ‘Microsoft.Graph.CrossDeviceExperiences’; RequiredVersion = ‘1.6.0’; }, 
@{ModuleName = ‘Microsoft.Graph.Identity.Governance’; RequiredVersion = ‘1.6.1’; }, 
@{ModuleName = ‘Microsoft.Graph.Financials’; RequiredVersion = ‘1.6.0’; }, 
@{ModuleName = ‘Microsoft.Graph.Identity.DirectoryManagement’; RequiredVersion = ‘1.6.1’; }, 
@{ModuleName = ‘Microsoft.Graph.Security’; RequiredVersion = ‘1.6.1’; }, 
@{ModuleName = ‘Microsoft.Graph.Teams’; RequiredVersion = ‘1.6.1’; }, 
@{ModuleName = ‘Microsoft. Graph.Devices.CloudPrint’; RequiredVersion = ‘1.6.1’; }, 
@{ModuleName = ‘Microsoft.Graph.Calendar’; RequiredVersion = ‘1.6.0’; }, 
@{ModuleName = ‘Microsoft.Graph.Notes’; RequiredVersion = ‘1.6.0’; })

# Сборки, которые необходимо загрузить перед импортом этого модуля
# RequiredAssemblies = @()

# Файлы сценариев (.ps1), которые запускаются в среде вызывающей стороны перед импортом этого модуля.
# ScriptsToProcess = @()

# Типовые файлы (.ps1xml) для загрузки при импорте этого модуля
# TypesToProcess = @()

# Файлы формата (.ps1xml) для загрузки при импорте этого модуля
# FormatsToProcess = @()

# Модули для импорта как вложенные модули модуля, указанного в RootModule/ModuleToProcess
# NestedModules = @()

# Функции для экспорта из этого модуля, для лучшей производительности не используйте подстановочные знаки и не удаляйте запись, используйте пустой массив, если нет функций для экспорта.
FunctionsToExport = @()

# Командлеты для экспорта из этого модуля, для лучшей производительности не используйте подстановочные знаки и не удаляйте запись, используйте пустой массив, если нет командлетов для экспорта.
CmdletsToExport = @()

# Переменные для экспорта из этого модуля
VariablesToExport = ‘*’

# Псевдонимы для экспорта из этого модуля, для лучшей производительности не используйте подстановочные знаки и не удаляйте запись, используйте пустой массив, если нет псевдонимов для экспорта.
AliasesToExport = @()

# Ресурсы DSC для экспорта из этого модуля
# DscResourcesToExport = @()

# Список всех модулей, упакованных с этим модулем
# ModuleList = @()

# Список всех файлов, упакованных с этим модулем
# FileList = @()

# Частные данные для передачи в модуль, указанный в RootModule/ModuleToProcess. Он также может содержать хэш-таблицу PSData с дополнительными метаданными модуля, используемыми PowerShell.
PrivateData = @{

    PSData = @{

        # Теги, примененные к этому модулю. Они помогают с обнаружением модулей в онлайн-галереях.
Теги = ‘MicrosoftGraph’, ‘Microsoft’, ‘Office365’, ‘Graph’, ‘PowerShell’, 
«Outlook», «OneDrive», «AzureAD», «SharePoint», «Intune»,
‘AzureAutomationNotSupported’

        # URL-адрес лицензии для этого модуля.
LicenseUri = ‘https://aka.ms/devservicesagreement’

        # URL-адрес основного веб-сайта для этого проекта.
ProjectUri = ‘https://github.com/microsoftgraph/msgraph-sdk-powershell’

        # URL-адрес значка, представляющего этот модуль.
IconUri = ‘https://raw.githubusercontent.com/microsoftgraph/msgraph-sdk-powershell/master/documentation/images/graph_color256.png’

        # ReleaseNotes этого модуля
ReleaseNotes = ‘См. https://aka.ms/GraphPowerShell-Release.’

        # Строка предварительной версии этого модуля
# Пререлиз = »

        # Флаг, указывающий, требует ли модуль явного согласия пользователя для установки/обновления/сохранения
# RequireLicenseAcceptance = $false

        # Внешние зависимые модули этого модуля
# ExternalModuleDependencies = @()

    } # Конец хэш-таблицы PSDData

} # Конец хэш-таблицы PrivateData

# URI HelpInfo этого модуля
# HelpInfoURI = »

# Префикс по умолчанию для команд, экспортируемых из этого модуля. Переопределите префикс по умолчанию, используя Import-Module -Prefix.
# DefaultCommandPrefix = »

}

graph — Документация по Alloy

graph — Документация по Alloy

Graph предоставляет предикаты отношений над параметризованной подписью.

 открыть утилиту/граф[узел]
знак узла {
  край: установить узел
}
бег {
  даг [край]
}

Обратите внимание, что граф параметризован по подписи , но предикат принимает отношение . Это сделано для того, чтобы вы могли применять несколько предикатов к нескольким различным отношениям или к разным подмножествам одного и того же отношения. Модуль графика использует определенную терминологию:

Это означает, что в полностью несвязном графе каждый узел является и корнем, и листом.

Функции

весело корни[r: узел->узел]
Тип возврата

комплект Узел

Возвращает набор узлов, которые не соединены с никаким другим узлом.

Предупреждение

это не то же значение корень как в rootedAt предикат! Для предиката корень — это узел, транзитивно покрывающий весь граф. Внутри util/graph использует rootedAt , а не roots .

весело листья[r: узел->узел]
Тип возврата

комплект Узел

Возвращает набор узлов, которые не соединяются с любым другим узлом.

Примечание

Если r пусто, корни[r] = листья[r] = узел . Если r является неориентированным или содержит достаточно петель, корни[r] = листья[r] = нет .

весело innerNodes[r: node-> node]
Возврат

Все узлы, кроме листьев

Тип возврата

комплект Узел

Предикаты

пред ненаправленный [r: узел->узел]

r симметричный .

пред noSelfLoops[r: узел->узел]

r есть иррефлексивное .

пред слабосвязный[r: узел->узел]

Для любых двух узлов A и B существует путь из A в B или путь из B в A. Путь не обязательно может быть двунаправленным.

пред сильно подключен [r: узел-> узел]

Для любых двух узлов A и B существует путь от A до B и путь от B до A.

пред rootedAt[r: узел->узел, корень: узел]

Все узлы доступны из корня .

Предупреждение

это не то же значение корень как в корни функция! Для функции корень — это узел, к которому не подключается ни один узел. Между прочим, util/graph использует rootedAt , а не roots .

пред кольцо [r: узел->узел]

r образует единый цикл.

пред даг [r: узел->узел]

r есть даг : в транзитивном замыкании нет петель.

пред лес [r: узел->узел]

r — это даг, и каждый узел имеет не более одного родителя.

пред дерево [r: узел->узел]

r — это лес с одним корневым узлом.

пред treeRootedAt[r: узел->узел, корень: узел]

r — дерево с узлом корень .

Читать документы v: последний

Версии
последний
Загрузки
При прочтении документов
Дом проекта
Строит

Бесплатный хостинг документов предоставляется Read the Docs.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *