| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) | |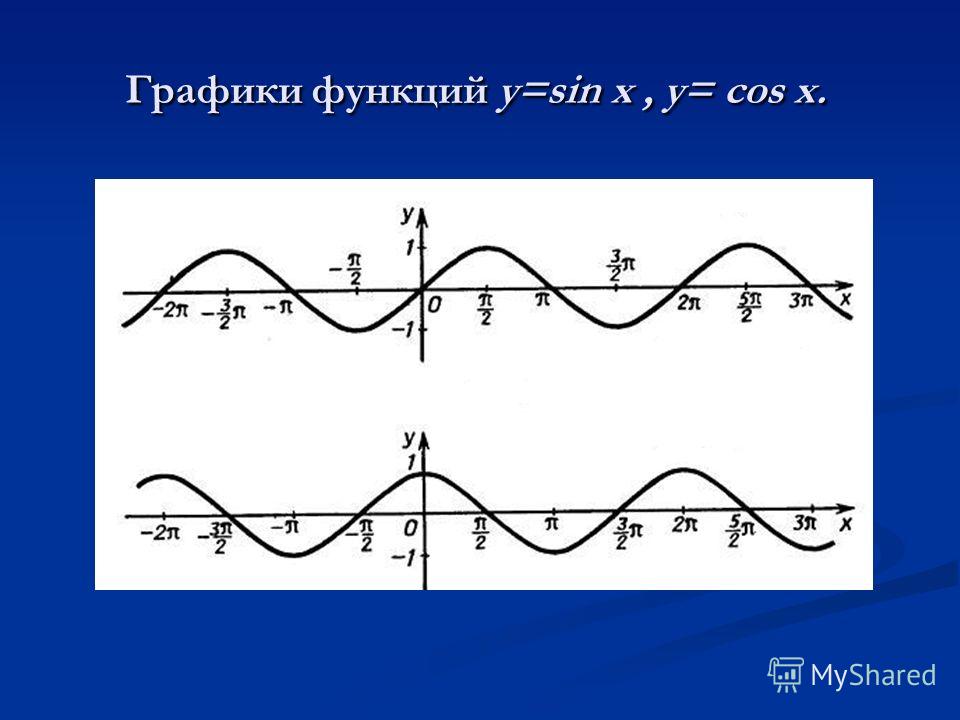
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) | |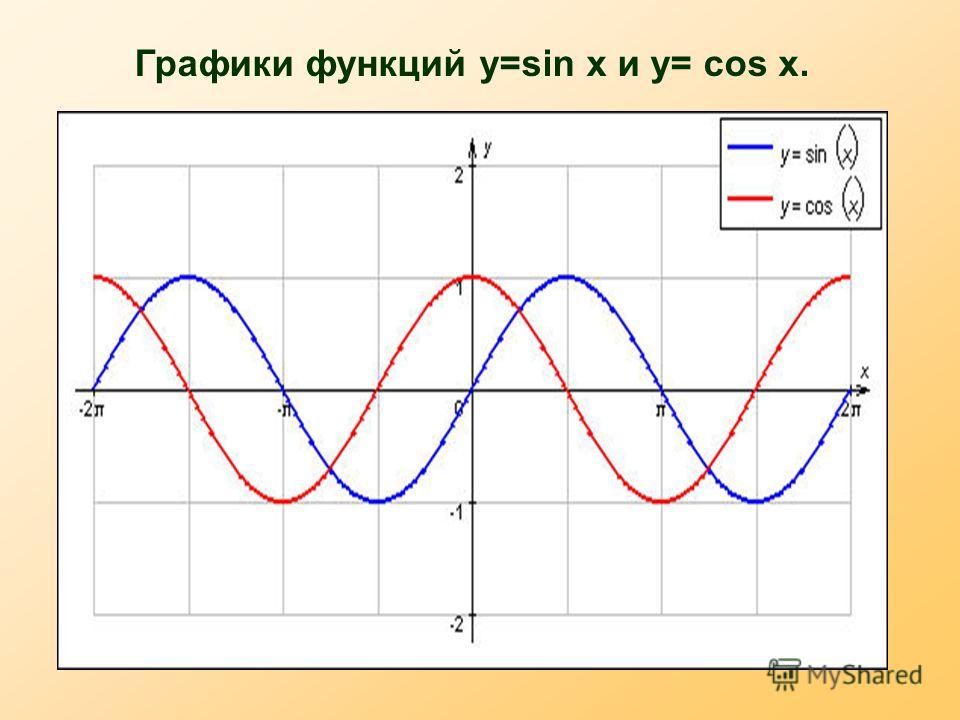
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) | |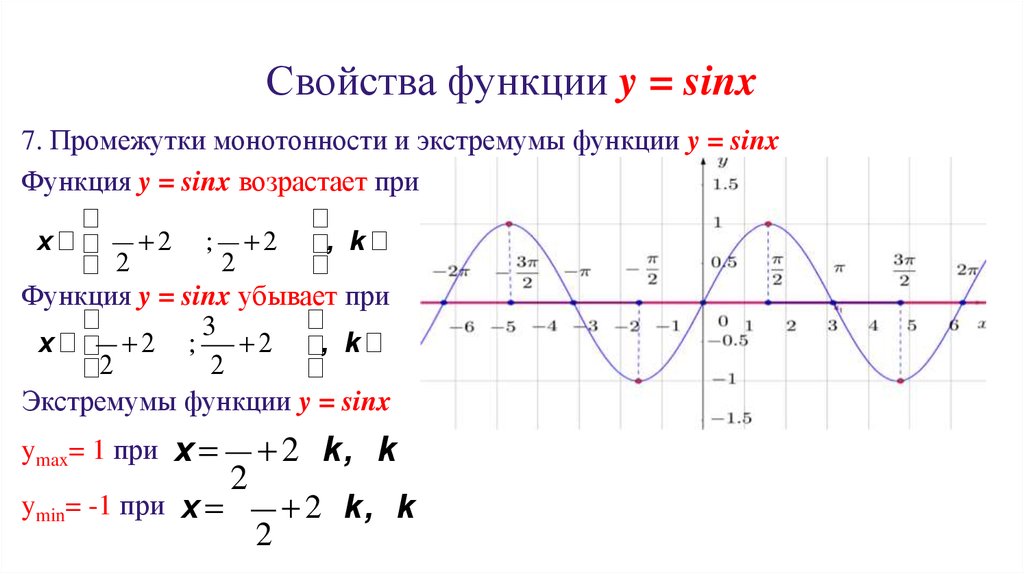
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) | |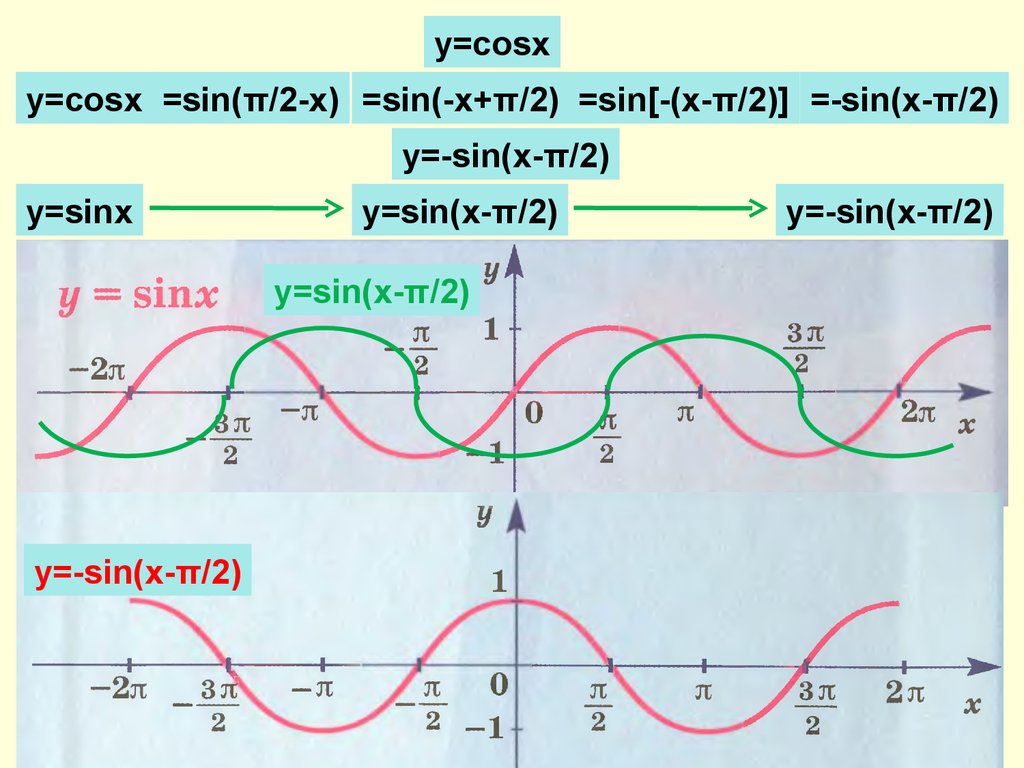
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Функции y=sin x и y=cos x , их свойства и графики | Презентация к уроку по алгебре (10 класс) по теме:
Опубликовано 20.10.2012 — 10:47 — Окорокова Юлия Михайловна
Скачать:
Подписи к слайдам:
Функции y=sin x и y=cos x , их свойства и графики
Алгебра и начала анализа.
10 классОкорокова Ю. М. МБОУ СОШ № 2 имени Короленко В. Г.Г. Ногинск Московской области
1
-1
0
0
0
x
-x
y
-y
1
-1
-1
1
1
-1
0
0
0
x
-x
1
-1
-1
1
y
*
Преобразование графиков функций y=sin x и y=cos x
Параллельный перенос вдоль оси OYПараллельный перенос вдоль оси OXРастяжение (сжатие) в k раз вдоль оси OYРастяжение (сжатие) в k раз вдоль оси OXСимметрия относительно оси абсциссПример построения графика сложной функции
Параллельный перенос вдоль оси OY
y=f(x) y=f(x)+b
Параллельный перенос вдоль оси OX
y=f(x) y=f(x-a)
Растяжение (сжатие) в k раз вдоль оси OY
y=f(x) y=mf(x)
Растяжение (сжатие) в k раз вдоль оси OX
y=f(x) y=f(kx)
Симметрия относительно оси абсцисс
y=f(x) y=-f(x)
Построить график функции
По теме: методические разработки, презентации и конспекты
ФУНКЦИЯ , ЕЁ СВОЙСТВА И ГРАФИК
Сценарий урока по развивающей программе «Школа 2100».
n(nєN), их свойства и графики «. По учебнику «Алгебра, 9» А. Г. Мордкович. Урок получения новых знаний….
Интегрированный урок по алгебре и началам анализа и информатике по теме «Показательная функция, ее свойства и график. Создание моделей графиков функций в среде программирования Visual Basic» (11 класс «А»)
Применение интеграции в учебном процессе как способа развития аналитических и творческих способностей….
Функции, их свойства. Чтение графиков функций
Презентация по теме функции и их свойства, чтение по графику функции…
Функция. Свойства и графики функций
Одним из самых важных вопросов при изучении алгебры является функция. Изучение начинается еще в 7 классе. Однако учащиеся часто воспринимают материал с большим трудом. И даже в 11 классе тема вызывает…
Интегрированный урок по математике и физике по теме «Функция. Применение свойств и графиков некоторых функций в решении задач и при подготовке к ОГЭ».
Разработка интегрированного урока по физике и математике по теме «Функция.
Применение свойств и графиков функций в решении задач при подготовке к ОГЭ»….
Поделиться:
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
Как построить график функции $f(x) = \sqrt{8\sin^2x+4\cos^2x-8\sin{x}\cos{x}}$? 92(x)-8\sin(x)\cos(x).
$$Это однородный тригонометрический полином второй степени, и у нас есть надежда упростить его формулами двойного угла.
Действительно,
$$g(x)=8\frac{1-\cos(2x)}2+4\frac{1+\cos(2x)}2-8\frac{\sin(2x) }2=6-2\cos(2x)-4\sin(2x).$$
Далее можно упростить по формуле для линейных комбинаций
$$g(x)=6-2\sqrt{5} \cos(2x-\arctan(2)).$$
Таким образом, график $g$ является косинусоидой с периодом $\pi$, амплитудой $\приблизительно4,5$, фазовым сдвигом $\arctan(2)$ (смещено влево на $\приблизительно1.1$ радиан), поднято вверх на $6$ единиц. Зная свойства (ко)синусоиды, построить график не составит труда (синяя кривая).
Теперь для $f(x)=\sqrt{g(x)}$ вы берете квадратный корень в каждой точке, в результате чего косинусоида сжимается нелинейно (зеленая кривая). Диапазон ординат: $[\sqrt{6-2\sqrt5},\sqrt{6+2\sqrt5}]\приблизительно[1.24,3.24]$.
$\endgroup$
$\begingroup$
Введите его в wolfram alpha и вы увидите график.
Я думаю, вы не были уверены, что выражение под квадратным корнем никогда не бывает отрицательным. Чтобы проверить это, вычислите минимумы функции. Это помогает, если вы хотите нарисовать функцию вручную без компьютера.
Кстати, $2 \sin x \cos x = \sin(2 x)$ см. здесь. Таким образом, добавление к нему 1 никогда не будет отрицательным. Итак, вы можете видеть, что вы можете построить его, не вычисляя минимумы.
$\endgroup$
7
$\begingroup$
Сначала вас интересует ось $x$:
- из которой $x$ представляет собой интересующую функцию
- к которому $x$
, что дает приблизительную шкалу с точностью до $x$.
Затем на оси $y$ вы хотите охватить как минимум максимальное и минимальное значения на основе диапазона $x$, найденного выше.
В этом случае вы видите «сырой» $x$, переданный нескольким $\sin$ и $\cos$ без дальнейшего искажения $x$; таким образом, вы получаете периодическую функцию, и наличие оси $x$, покрывающей по крайней мере диапазон $[0, 2\pi]$, должно составлять горизонтальную шкалу.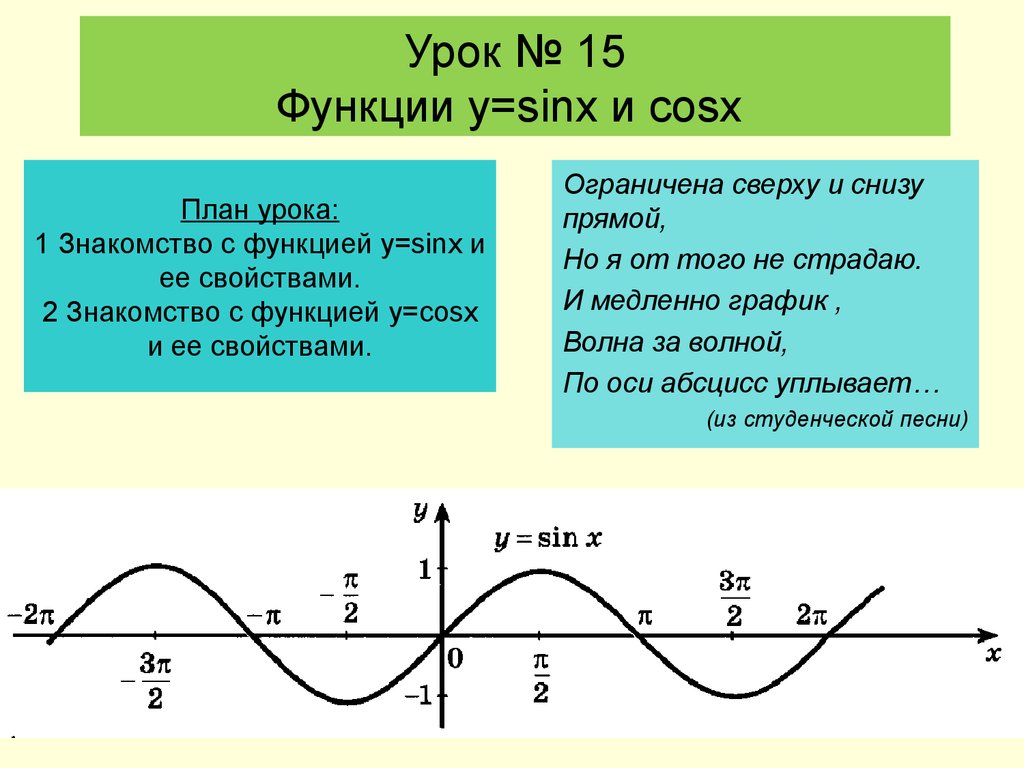
Не пользуясь калькулятором, вы видите, что на $y$ функция грубо не доходит до крайностей и не может быть отрицательной. Итак, для начала вы можете взять $y$ в диапазоне $[0,10]$.
Но в любом случае вам нужно нарисовать график вручную , так что теперь, когда масштаб $x$ примерно определен, вы можете использовать приложение, подобное Excel, и
- иметь столбец с $x$ от $0$, затем ниже это $x$, увеличенное на $2\pi / 100$ и т. д…. чтобы получить $100$ точек
- следующий столбец является результатом функции, к которой применяется левая ячейка
Теперь у вас есть $100$ точек $(x,y)$ для построения графика.
$\endgroup$
$\begingroup$
Я думаю, что это возможно.
При сжатии мы получаем $f(x)=2\sqrt{(\sin x-\cos x)²+\sin² x}$.
Мы видим, что $f$ положительна и $\pi-$периодична. Таким образом, мы можем изучить его на $[0,\pi]$
Поскольку $(\sin x-\cos x)²+\sin² x>0$ и $(\sqrt{u})’=\frac{u ‘}{2\sqrt{u}}$,
, то мы
$f'(x)=\frac{((\sin x-\cos x)²+\sin² x)’}{\sqrt{(\sin x-\cos(x))²+\sin² x}} $.