| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Алгебра и начала анализа 11 класс.
 Углублённый уровень
Углублённый уровеньАлгебра и начала анализа 11 класс. Углублённый уровень
Учебный онлайн курс по предмету Алгебра и начала анализа 11 класс. Углублённый уровень сможет заменить бумажный учебник или дополнить его. Содержание интерактивных онлайн курсов соответствует требованиям федеральных государственных образовательных стандартов (ФГОС).
Онлайн уроки построены таким образом, что перед изучением новой темы, предлагается повторить и закрепить ранее изученный материал Алгебра 10 класса углублённого уровня.
Онлайн уроки учебного онлайн курса по предмету Алгебра и начала анализа 11 класс. Углублённый уровень подходят для самостоятельного изучения. Ребенок познакомится с теорией, проверит полученные знания с помощью онлайн-тренажеров и интерактивных заданий, подготовится к контрольным и проверочным работам, экзаменам, ОГЭ и ЕГЭ.
Такой формат занятий поможет разобраться в новой теме или подтянуть знания по предмету. Доступ к онлайн урокам осуществляется через интернет (24/7). Это позволяет заниматься в дороге и дома, во время соревнований, выездов на олимпиады или в оздоровительный лагерь.
Это позволяет заниматься в дороге и дома, во время соревнований, выездов на олимпиады или в оздоровительный лагерь.
Наш сборник — это способ улучшить успеваемость, начать подготовку к экзаменам, повторить пройденный материал во время каникул.
В качестве одной из составляющей курса, ученикам доступен объемный дополнительный материал, позволяющий углубить имеющиеся знания. Различные типы заданий, представленные в онлайн-учебнике — одна из важных составляющих подготовки к будущим экзаменам.
Темы:
- Элементы логики и теории множеств
- Предел последовательности
- Предел и производная функции
- Применение производной для решения различных задач
- Первообразная и интеграл
- Комбинаторика
- Элементы теории вероятностей
- Уравнения и неравенства, обзор методов решения
- Теория чисел
Главными целями изучения предмета являются:
- обеспечение возможности успешного продолжения образования по специальностям, связанным с прикладным использованием математики;
- формирование представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, об идеях и методах математики;
- развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для будущей профессиональной деятельности, а также последующего обучения в высшей школе;
- овладение математическими знаниями и умениями, необходимыми в повседневной жизни для изучения школьных естественнонаучных дисциплин на базовом уровне, для получения образования в областях, не требующих углублённой математической подготовки;
- воспитание средствами математики культуры личности, понимания значимости математики для научно-технического прогресса, отношения к математике как к части общечеловеческой культуры через знакомство с историей развития математики.

Оглавление
Занятие 1. Элементы логики и теории множеств
Интернет-урок 1. Высказывания и операции над ними. Неопределенные высказывания. Знаки общности и существования
Интернет-урок 2. Некоторые приемы доказательства
Интернет-урок 3. Множества. Операции над множествами. Натуральные, целые, рациональные и иррациональные числа
Интернет-урок 4. Метод математической индукции
Занятие 2. Предел последовательности
Интернет-урок 1. Понятие предела последовательности. Свойства. Арифметика пределов последовательностей. Вычисление пределов
Интернет-урок 2. Бесконечно малые и бесконечно большие последовательности
Интернет-урок 3. Применение пределов числовых последовательностей
Занятие 3. Тематическая контрольная работа № 1. Предел последовательности
Занятие 4. Предел и производная функции
Интернет-урок 1. Определение предела функции в точке. Специальные типы пределов. Теоремы о пределах. Замечательные пределы
Определение предела функции в точке. Специальные типы пределов. Теоремы о пределах. Замечательные пределы
Интернет-урок 2. Непрерывность функции в точке. Точки разрыва функции. Асимптоты графика функции
Интернет-урок 3. Понятие о непрерывности функции на промежутке, основные теоремы о непрерывных функциях. Обратная функция
Интернет-урок 4. Понятие о производной функции, физический смысл производной
Интернет-урок 5. Геометрический смысл производной, касательная
Интернет-урок 6. Дифференциал функции. Непрерывность и дифференцируемость
Интернет-урок 7. Производные суммы, разности, произведения, частного
Интернет-урок 8. Производные основных элементарных функций
Интернет-урок 9. Производная сложной функции вида y = f(ax + b) . Представление о второй производной
Занятие 5. Тематическая контрольная работа № 2. Предел и производная функции
Занятие 6. Применение производной для решения различных задач
Интернет-урок 1. Уравнение касательной к графику функции. Угол между графиками функций
Уравнение касательной к графику функции. Угол между графиками функций
Интернет-урок 2. Производные сложной и обратной функции
Интернет-урок 3. Исследование функций на монотонность. Вторая производная
Интернет-урок 4. Применение производной к исследованию функций и построению графиков. Схема исследования функции и построения графика с помощью производной
Интернет-урок 5. Нахождение наибольших и наименьших значений
Интернет-урок 6. Использование производных для решения уравнений и неравенств, текстовых, физических и геометрических задач
Занятие 7. Тематическая контрольная работа № 3. Применение производной для решения различных задач
Занятие 8. Первообразная и интеграл
Интернет-урок 1. Первообразная. Первообразные элементарных функций. Элементарные свойства первообразной. Вычисления первообразной
Интернет-урок 2. Неопределенный интеграл. Свойства, некоторые приемы и методы вычисления неопределенного интеграла
Интернет-урок 3. Понятие об определённом интеграле. Задачи, приводящие к понятию определенного интеграла
Понятие об определённом интеграле. Задачи, приводящие к понятию определенного интеграла
Интернет-урок 4. Формула Ньютона-Лейбница. Площадь криволинейной трапеции
Интернет-урок 5. Применение определенного интеграла. Примеры применения интеграла в физике и геометрии
Занятие 9. Тематическая контрольная работа № 4. Первообразная и интеграл
Занятие 10. Комбинаторика
Интернет-урок 1. Предмет комбинаторики. 2 правила комбинаторики. Формула включений и исключений. Принцип Дирихле
Интернет-урок 2. Перестановки, число перестановок, инверсия
Интернет-урок 3. Размещения с повторениями и без повторений, формулы
Интернет-урок 4. Сочетания с повторениями и без, формулы
Интернет-урок 5. Треугольник Паскаля и Треугольник Каталана
Занятие 11. Тематическая контрольная работа № 5. Комбинаторика
Занятие 12. Элементы теории вероятностей
Интернет-урок 1. Основные понятия теории вероятностей. Знакомство с предметом теории вероятностей
Знакомство с предметом теории вероятностей
Интернет-урок 2. Противоположные события, полная группа событий; пространство элементарных исходов. Классическая схема, вероятность события
Интернет-урок 3. Операции над событиями. Сумма событий. Теорема сложения вероятностей. Произведение событий, вероятность суммы двух совместных событий
Интернет-урок 4. Геометрические вероятности
Интернет-урок 5. Условная вероятность; независимые события; теорема умножения вероятностей; формула полной вероятности
Интернет-урок 6. Решение задач с применением теорем. Схема Бернулли. Числовые характеристики случайных величин
Занятие 13. Тематическая контрольная работа № 6. Элементы теории вероятностей
Занятие 14. Уравнения и неравенства, обзор методов решения
Интернет-урок 1. Что такое уравнение. Виды уравнений (блок схема) вправо. Равносильные уравнения, равносильные преобразования. Уравнения. Метод разложения на множители
Интернет-урок 2. Уравнения. Метод замены переменной (возвратные уравнения, однородные уравнения, сведение к более простым уравнениям)
Уравнения. Метод замены переменной (возвратные уравнения, однородные уравнения, сведение к более простым уравнениям)
Интернет-урок 3. Функциональный метод решения
Интернет-урок 4. Решение задач на квадратные уравнения с параметром. Метод парабол
Интернет-урок 5. Неравенства. Метод рационализации (идея, замена)
Интернет-урок 6. Применение геометрических соображений при решении алгебраических задач
Интернет-урок 7. Графический способ при исследовании задач с параметрами
Интернет-урок 8. Смешанные и нестандартные задачи с параметром
Занятие 15. Тематическая контрольная работа № 7. Уравнения и неравенства, обзор методов решения
Занятие 16. Теория чисел
Интернет-урок 1. Делимость и ее свойства. Признаки делимости
Интернет-урок 2. Арифметика остатков
Интернет-урок 3. Теория сравнений
Интернет-урок 4. Десятичная запись числа
Интернет-урок 5. Основная теорема арифметики. НОК и НОД. Алгоритм Евклида
Интернет-урок 6. Решение уравнений в целых числах
Решение уравнений в целых числах
Интернет-урок 7. Задача 19 ЕГЭ. Методы решения
Занятие 17. Тематическая контрольная работа № 8. Теория чисел
алгебраических формул для 11 класса: все алгебраические формулы здесь
алгебраические формулы для 11 класса: все алгебраические формулы здесь — Embibe- Автор Принц
- Последнее изменение 14-11-2022
Формулы алгебры для класса 11: Алгебра – это использование букв для представления чисел. Речь идет об установлении связи между различными числами. Алгебра используется в математике, когда мы не знаем точных чисел или значений в расчетах. В алгебре мы используем буквы для обозначения неизвестных значений или значений, которые могут измениться. Алгебру можно использовать в бизнесе для прогнозирования продаж, роста и прибыли.
Мы собрали важные алгебраические формулы для 11-го класса. Эти формулы и алгебраические тождества помогут всем учащимся 11-го класса в учебе, а также на выпускных экзаменах. Главы по алгебре для класса 11 содержат концепции прогрессий, квадратных уравнений, линейных неравенств, биномиальной теоремы, перестановок и комбинаций, а также математической индукции. Мы предоставили все формулы и алгебраические тождества для класса 11, которые важны для этих глав на этой странице. Учащиеся 11 класса CBSE могут скачать эти формулы в формате PDF с этой страницы.
Главы по алгебре для класса 11 содержат концепции прогрессий, квадратных уравнений, линейных неравенств, биномиальной теоремы, перестановок и комбинаций, а также математической индукции. Мы предоставили все формулы и алгебраические тождества для класса 11, которые важны для этих глав на этой странице. Учащиеся 11 класса CBSE могут скачать эти формулы в формате PDF с этой страницы.
Учащиеся, которые ищут полный список математических формул для 11 класса в формате PDF для алгебры, могут обратиться к этой статье. Математика 11 класса содержит 6 глав, связанных с алгеброй. Вы можете проверить формулу по главам в таблице ниже:
| Комплексные числа и квадратные уравнения ★ √-1 = i или i 2 = -1 , что означает, что i можно принять за решение уравнения x 2 + 1 = 0. i называется йота в комплексных числах. ★ i 2 = -1 i 3 = i 2 * i = -i i 4 = i 2 * i 2 = 1 ★ y = ax 2 + bx + c — квадратное уравнение, где a ≠ 0 , b и c могут быть любыми действительными (или комплексными) числами.  Здесь a, b и c называются коэффициентами . ★ Квадратное уравнение имеет два корня: (α, β) = [–b ± √(b 2 – 4ac)]/2ac, где α и β — корни уравнения. (i) Если b 2 − 4ac > 0, то квадратное уравнение имеет два различных действительных корней . (ii) Если b 2 − 4ac < 0, то квадратное уравнение имеет два мнимых корней . (iii) Если b 2 − 4ac = 0, то квадратное уравнение имеет два равных действительных корня . |
| Линейные неравенства ★ График линейного неравенства с одной переменной представляет собой числовую прямую. Используйте открытый кружок для < и > и закрытый кружок для ≤ и ≥. ★ Свойство сложения неравенства: (i) Если x > y, то (x + z) > (y + z) (ii) Если x < y, то (x + z) < (y + z) ) ★ Свойство вычитания неравенства: (i) Если x > y, то (x − z) > (y − z) (ii) Если x < y, то (x − z) < (y − z) ★ Свойство умножения неравенства: (i) Если x > y и z > 0, то xz > yz (ii) Если x< y и z > 0, то xz < yz (iii) Если x > y и z < 0, то xz < yz (iv) Если x < y и z < 0, то xz > yz ★ Свойство неравенства деления: (i) Если x > y и z > 0, то x/z > y/z (ii ) Если x < y и z > 0, то x/z < y/z (iii) Если x > y и z < 0, то x/z < y/z (iv) Если x < y и z < 0, то x/z > y/z |
| Перестановки и комбинации ★ Количество перестановок n объектов, взятых r за раз, определяется по следующей формуле: P(n, r) = n!/(n − r)! ★ Количество сочетаний n предметов, взятых по r за раз, определяется по следующей формуле: C(n, r) = n!/(n − r)!r! |
| Binomial Theorem ★ The Binomial Theorem states that: (a + b) n = a n + ( n C 1 )a n -1 b + ( n C 2 )a n-2 b 2 + … + ( n C n-1 )ab n-1 + b n where n is a positive integer |
| Sequence and Series ★ Arithmetic Progression: ( i) Последовательность: а, а+d, а+2d, ……, а + (n – 1)d, ….  (ii) Общая разница: d = (a 2 – a 1 ), где a 2 и a 1 — это последующий и предшествующий термины соответственно. (iii) Общий срок (n th срок): a n = a + (n – 1)d (iv) n th Срок от последнего срока: a n = l – (n – 1)d (v) Сумма первые n членов: S n = n/2[2a + (n – 1)d] ★ Геометрическая прогрессия: (i) Последовательность: a, ar, ar 2 , …., ar ( n-1) , … (ii) Обычная пропорция: r = ar (n-1) /ar (n-2) , где ar (n-1) и ar (n-2) ) — это последующий термин и предыдущий термин соответственно. (iii) Общий срок (n th термин): a n = ar (n-1) (iv) n th Срок с последнего срока: a n = 1/r (n-1) (v) Сумма первых n членов: S n = a(1 – r n )/(1 – r), если r < 1 S n = a(r n -1)/(r – 1), если r > 1 * Здесь a = первый член, d = обычная разность, r = знаменатель, n = положение члена, l = последний член |
| Принцип математической индукции ★ Математическая индукция – это метод доказательства утверждения, теоремы или формулы, которая утверждается относительно каждого натурального числа.  У него всего 2 шага: Шаг 1: Покажите, что это верно для первого . Шаг 2: Покажите, что если любой истинен, то следующий истинен. Тогда все истинны. |
Ознакомьтесь с другими важными статьями по математике для 11 класса:
Мы предоставили прямую ссылку для загрузки формул алгебры для 11 класса в формате PDF.
Вопросы по алгебре для 11 класса
Мы подготовили несколько важных вопросов по алгебре для 11 класса с решениями, связанными с линейными неравенствами, квадратичными формулами, биномиальной теоремой, математической индукцией и прогрессиями:
| 1) 5 + (√2 − 1) 5 с использованием биномиальной теоремы. |
Решение: . 3 Y 2 + 5C 4 xy 4 ] 3 Y 2 + 5C 4 xy 4 ] = 2 (x 5 + 10 x 3 y 2 + 5xy 4 ) = 58√2 |
| Question 2: Solve the following quadratic equation: (x 2 + 2 x − 35) = 0 using the quadratic формула. |
| Решение: во-первых, мы должны определить, что a , b , и c : a = 1, b = 2, c = −35 Далее нужно подставить эти α, 902 в формулу [–b ± √(b 2 – 4ac)]/2ac = [-2 ± √(2 2 – 4x1x-35)]/2x1x-35 Решив его, получим: (α, β ) = (-2 ± √144)/2 = (-2 ± 12)/2 = 5, -7 Следовательно, корни уравнения равны 5 и -7.  |
| Вопрос 3: Сумма трех чисел в A.P равна 21, а произведение первого и третьего числа последовательности равно 45. Какие три числа? |
| Решение: Пусть числа равны (a – d), a и (a + d) Тогда (a – d) + a + (a + d) = 21 ( Дано) 3a = 21 a = 7 и (a – d)(a + d) = 45 a 2 – d 2 = 45 7 2 – d 2 2 = 4 d = ± 2 Следовательно, числа равны 5, 7 и 9 при d = 2 и 9, 7 и 5 при d = -2. В обоих случаях цифры одинаковые. |
| Вопрос 4: Если резиновый мяч постоянно отскакивает назад на 2/3 высоты, с которой он был брошен, какую долю своей первоначальной высоты отскочит мяч после того, как его бросили и отскочили четыре раза без остановки? |
Решение: Каждый раз, когда мяч падает и отскакивает назад, он достигает 2/3 высоты, с которой он упал. После первого отскока мяч достигнет 2/3 высоты, с которой он был брошен – назовем это исходной высотой. После второго отскока мяч поднимется на 2/3 высоты, которой он достиг бы после первого отскока. Итак, в конце второго отскока мяч достиг бы 2/3 x 2/3 исходной высоты = 4/9 исходной высоты. После третьего отскока мяч поднимется на 2/3 высоты, которой он достиг бы после второго отскока. Таким образом, в конце третьего отскока мяч достиг бы 2/3 x 2/3 x 2/3 = 8/27 исходной высоты. После четвертого и последнего отскока мяч поднимется на 2/3 высоты, которой он достиг бы после третьего отскока. Таким образом, в конце последнего отскока мяч достиг бы 2/3 x 2/3 x 2/3 x 2/3 исходной высоты = 16/81 исходной высоты. |
| Вопрос 5. Сколькими способами можно расположить буквы в слове «КОРПОРАЦИЯ» так, чтобы гласные всегда совпадали? |
Решение: В слове «КОРПОРАЦИЯ» мы рассматриваем гласные OOAIO как одну букву. Итак, у нас есть CRPRTN (OOAIO). В нем 7 (6 + 1) букв, из которых R встречается 2 раза, а остальные разные. Количество способов расстановки этих букв = 7!/2! = 2520. Теперь 5 гласных, в которых О встречается 3 раза, а остальные разные, можно расположить в 5!/3! = 20 способов. ∴ Необходимое количество путей = (2520 x 20) = 50400 |
Проверка формул алгебры для других классов:
Практические вопросы по математическим формулам для класса 11 по алгебре
Здесь мы предоставили некоторые практические вопросы по формуле алгебры для класса 1 для тождеств вам потренироваться:
| В1: Сколько шестизначных чисел можно составить, используя цифры 0, 1, 2, 5, 7 и 9, которые делятся на 11 и ни одна цифра не повторяется. Q2: Найдите наименьшее число, которое нужно добавить к 289279, чтобы оно делилось на 8. Q3: Дедушка в 10 раз старше своей внучки. Q4: Докажите: (2n + 7) < (n + 3) 2 , для n∈N. Q5: Найдите точку (точки) пересечения параболы с уравнением y = x 2 – 5x + 4 и прямой с уравнением y = 2x – 2. Q6: Найдите константу k, чтобы квадратичный уравнение 2x 2 + 5x – k = 0 имеет два действительных решения. Q7: Упростите i 231 где i — мнимая единица, определяемая как: i = √(-1). Q8: Найдите все нули многочлена P(x) = x 3 – 3x 2 – 10x + 24, зная, что x = 2 является нулем многочлена. Q9: Если x является целым числом, какое наибольшее значение x удовлетворяет условию 5 < 2x + 2 < 9? Q10: Разложите выражение на множители 6x 2 – 13x + 5. Q11: Найдите константу k, чтобы система двух уравнений: 2x + ky = 2 и 5x – 3y = 7 не имела решений. Q12: Найдите константу k так, чтобы: -x 2 – (k + 7)x – 8 = -(x – 2)(x – 4). Q13: Найдите квадраты квадратичной функции f, заданной выражением f(x) = 2x 2 – 6x + 4. Q14: Каков остаток, когда f(x) = (x – 2) 54 делится на х – 1? Q15: Упрощение | – х 2 + 4х – 4 | |
Также проверьте
Часто задаваемые вопросы по математическим формулам для класса 11 Алгебра
Здесь мы предоставили некоторые из часто задаваемых вопросов, связанных с формулой алгебры Класс 11.
Q1: Какие различные главы в Классе 11 Алгебра?
A: Блок алгебры для 11-го класса содержит следующие главы:
(i) Глава 1: Принцип математической индукции
(ii) Глава 2: Комплексные числа и квадратные уравнения
(iii) Глава 3: Линейные неравенства
(iv) ) Глава 4: Перестановки и комбинации
(v) Глава 5: Биномиальная теорема
(vi) Глава 6: Последовательность и серия
В2: Где я могу решить вопросы по алгебре для 11 класса?
О: Вы можете решить важные вопросы по алгебре для 11 класса здесь, на этой странице.
Q3: Как скачать формулы алгебры для класса 11 в формате PDF?
О: На этой странице мы разместили прямую ссылку для скачивания формул алгебры для класса 11 в формате PDF. Скачать бесплатно без регистрации.
Q4: Что такое алгебраическое уравнение?
A: Алгебраическое уравнение или тождество состоит из двух или более алгебраических выражений, разделенных знаком равенства. Левая часть (левая часть) уравнения всегда равна правой стороне (правая часть) для любого значения переменных в нем.
Q5: Как получить алгебраические выражения?
A: Алгебраическое выражение представляет собой комбинацию констант, переменных и алгебраических операций (+, -, ×, ÷). Мы можем получить алгебраическое выражение для данной ситуации или условия, используя эти комбинации.
Теперь у вас есть вся необходимая информация о формулах алгебры 11 класса. Мы надеемся, что вы загрузили математические формулы для 11 класса в формате PDF, доступные на этой странице. Учащиеся также могут использовать Решения NCERT для математики, предоставленные Embibe для подготовки к экзаменам.
Мы надеемся, что вы загрузили математические формулы для 11 класса в формате PDF, доступные на этой странице. Учащиеся также могут использовать Решения NCERT для математики, предоставленные Embibe для подготовки к экзаменам.
Мы надеемся, что эта подробная статья о формулах алгебры поможет вам. Если у вас есть какие-либо вопросы относительно этой статьи, свяжитесь с нами через раздел комментариев ниже, и мы свяжемся с вами как можно скорее.
Сокращение глупых ошибок; Пройдите бесплатные пробные тесты, связанные с алгебраическими выражениями
Формулы алгебры для 10-го класса
Алгебра — важный раздел математики, который имеет важное применение в области техники и технологий. Он имеет дело с символами, называемыми переменными, которые представляют значение любой величины в любом случае, и правилами манипулирования этими символами.
Чтобы учащийся преуспел в таких темах, как линейные уравнения с двумя переменными, квадратные уравнения и т. д., необходимо тщательно изучить формулу алгебры для 10-го класса. Алгебраические тождества
д., необходимо тщательно изучить формулу алгебры для 10-го класса. Алгебраические тождества
(a + b)2 = a2 + 2ab + b2
(a − b)2 = a2 − 2ab + b2
(a + b)(a – b) = a2 – b2
(x + a)(x + b) = x2 + (a + b)x + ab
(х + а)(х – Ь) = х2 + (а – Ь)х – аб
(х – а)(х + Ь) = х2 + (б – а)х – аб
(x – a)(x – b) = x2 – (a + b)x + ab
(a + b)3 = a3 + b3 + 3ab(a + b)
(a – b)3 = a3 – b3 – 3ab(a – b)
(x + y + z)2 = x2 + y2 + z2 + 2xy + 2yz + 2xz
(x + y – z)2 = x2 + y2 + z2 + 2xy – 2yz – 2xz
(x – y + z)2 = x2 + y2 + z2 – 2xy – 2yz + 2xz
(х – у – г)2 = х2 + у2 + г2 – 2ху + 2уг – 2хг xy – yz − xz)
(x + a)(x + b)(x + c) = x3 + (a + b + c)x2 + (ab + bc + ca)x + abc
x3 + y3 = (x + y)(x2 – xy + y2)
x3 – y3 = (x – y)(x2 + xy + y2)
x2 + y2 + z2 − xy – yz – zx = 12[(x − y)2 + (y − z)2 + (z − x)2]
x2 + y2 = 1/2[(x + y)2 + (x – y) 2]
Формула для квадратных уравнений
корни уравнения.
Если b2 − 4ac > 0, то квадратное уравнение имеет два различных действительных корня.
Если b2 − 4ac < 0, то квадратное уравнение имеет два мнимых корня.
Если b2 − 4ac = 0, то квадратное уравнение имеет два равных действительных корня.
Формула арифметической прогрессии
n-й член арифметической прогрессии: an = a + (n – 1)d n–1)d
n-й член геометрической прогрессии: an = a.rn-1
Сумма n членов геометрической прогрессии: Sn = a (1 – rn)/ (1 – r) , r≠1
Сумма бесконечных членов геометрической прогрессии: S = a/ (1 – r)
Важные ключевые слова
Некоторые важные понятия, используемые в алгебраических формулах, которые должен знать учащийся, перечислены ниже:
Алгебраическое выражение состоит из различных комбинаций констант и переменных, связанных с помощью различных символов операций сложения, вычитания, деления и умножения.
 (+, -, /, x)
(+, -, /, x)Различные члены составляют алгебраическое выражение
Терм – это произведение, полученное путем умножения двух или более множителей.
Коэффициент относится к числовому коэффициенту, полученному в термине.
Подобные термины — это термины с одинаковыми алгебраическими факторами. Тогда как непохожие термины — это термины, которые имеют разные алгебраические факторы.
Алгебраическое выражение, содержащее всего один член, называется мономом.
Алгебраическое выражение, состоящее всего из двух членов, называется биномиальным выражением.
Алгебраическое выражение, содержащее более двух членов, называется полиномиальным выражением.

При добавлении двух или более одинаковых терминов получается еще один аналогичный термин с числовым коэффициентом. Этот результирующий числовой коэффициент эквивалентен сумме всех числовых коэффициентов всех соответствующих подобных членов.
При вычитании двух или более одинаковых членов получается еще один подобный член с числовым коэффициентом. Этот результирующий числовой коэффициент эквивалентен разности всех числовых коэффициентов всех соответствующих одинаковых членов.
Все одинаковые термины складываются вместе, а все непохожие не включаются и оставляются как есть в алгебраическом выражении.
Класс 10 Алгебраические задачи с решенными решениями
Ниже перечислены некоторые алгебраические задачи с их решенными решениями, чтобы помочь учащимся лучше понять, как разные алгебраические формулы работают в разных задачах.
Выразите следующие утверждения в виде алгебраических выражений, используя соответствующие переменные, константы и арифметические операции.
Вычитание x из y.
Одна треть суммы чисел a и b.
Число r, умноженное само на себя.
Половина произведения чисел s и t.
Числа c и d, возведенные в квадрат и вычтенные.
Число 10 прибавляется к пятикратному произведению чисел v и w
Произведение чисел y и x прибавляется к 20.

Сумма чисел a, b и c, вычтенная из их соответствующего произведения.
Answer:
y – x
1/3 (a +b)
r2
½ (st)
c2 – d2
10 + 5 (VW)
xy + 20
ABC — (A + B + C)
Найти корты уравнения x2 — 10x — n (n + 10) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = №.
 0, где n — константа.
0, где n — константа.
Ответ:
Дано нам такое,
x2 – 10x – n (n + 3) = 0
. Сравнив его с общей формулой алгебраического выражения ax2 + bx + c = 0, получим:
a = 1, b = -10 и c = – n (n + 10)
мы также знаем, что D = (b2 – 4ac)
Итак,
D = (- 10)2 – 4( 1) [-n(n + 10)]
= 100 + 4n (n + 10)
= 4n2 + 40n + 100
= (2n + 10)2
подставив значение D в квадратичную формулу : (α, β) = [–b ± √D]/2ac, получаем:
(α, β) = [–10 ± √(2n + 10)2]/2x1x- n (n + 10)
Решив это уравнение, получим
(α, β) = (n + 10, -n)
Итак, корни данного квадратного уравнения равны (n + 10) и -n.
Практические задачи для учащихся
Найдите корни уравнения y2 – 5y – p (p + 5) = 0, где p – константа.

Если 1 является корнем уравнений az2 + az + 16 = 0 и x2 + x + b = 0, то найдите значение zx.
Найдите значение p, чтобы квадратное уравнение px(x – 4) + 16 = 0 имело два одинаковых корня.
Найдите значение q, чтобы квадратное уравнение qx (x – 10) + 100 = 0 имело два одинаковых корня.
Упростить алгебраическое выражение -2(x – 5) + 4(-3 x + 8)
Развернуть и упростить алгебраическое выражение x + 2) (x – 2) – (-x – 4)
При каких значениях k уравнение -x2 + 3kx – 9 = 0 имеет одно действительное решение?
Если (p2 – q2) = 10 и (p + q) = 2, найти p и q.


 Образцы решения
Образцы решения Свойства и графики степенных функций
Свойства и графики степенных функций Программу можно скачать с официального сайта Microsoft
Программу можно скачать с официального сайта Microsoft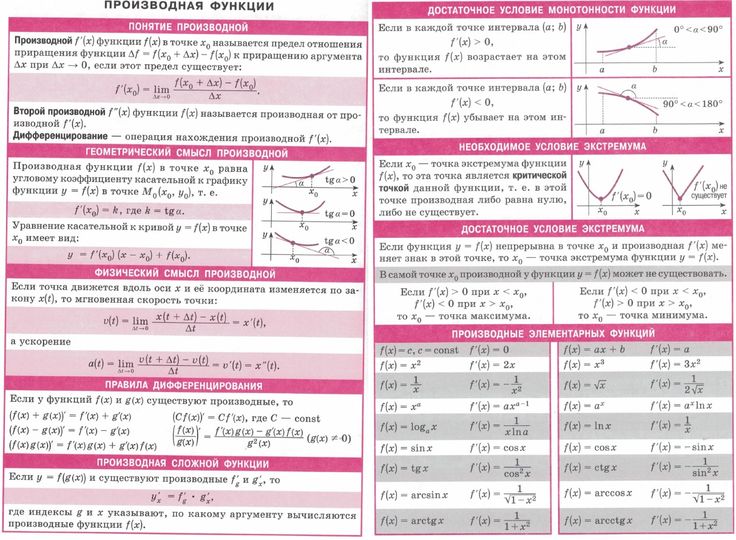
 Он старше ее на 54 года. Найдите их настоящий возраст.
Он старше ее на 54 года. Найдите их настоящий возраст.
 (+, -, /, x)
(+, -, /, x)

 0, где n — константа.
0, где n — константа.
