У cosx 2 график: График y = f(x) = cos(x)-2 (косинус от (х) минус 2) постройте график функции и изобразите его. Исследуйте данную функцию. [Есть ОТВЕТ!]

ФУНКЦИИ y=sinx, y=cosx их свойства и графики

Для начала предлагаю вам посмотреть видео урок

А теперь ещё раз пробежимся по свойствам функцийy=sinx и 
y=cosx


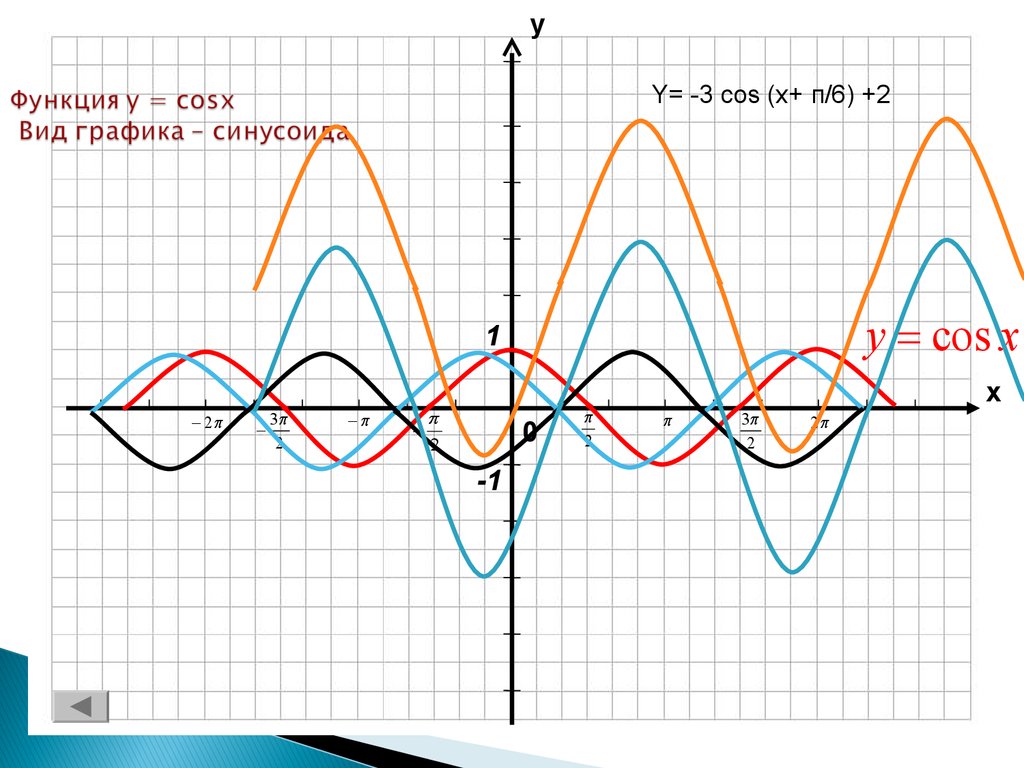
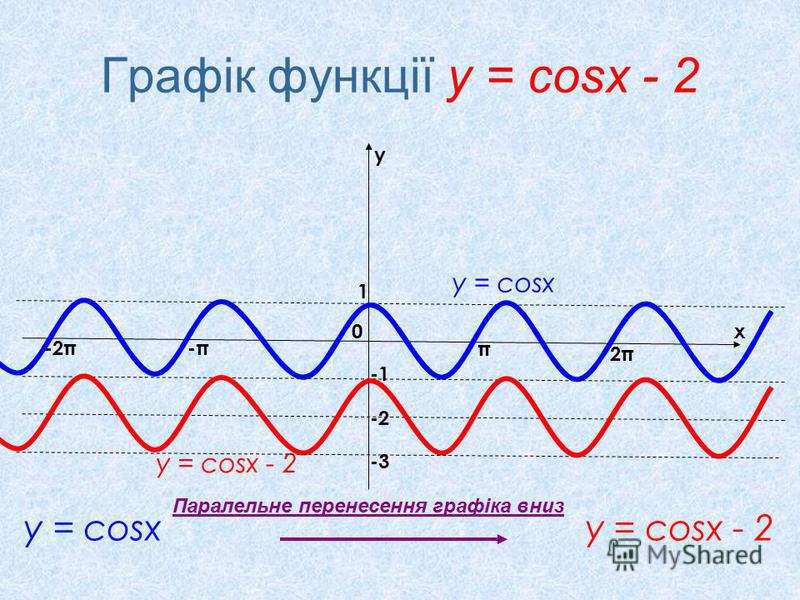
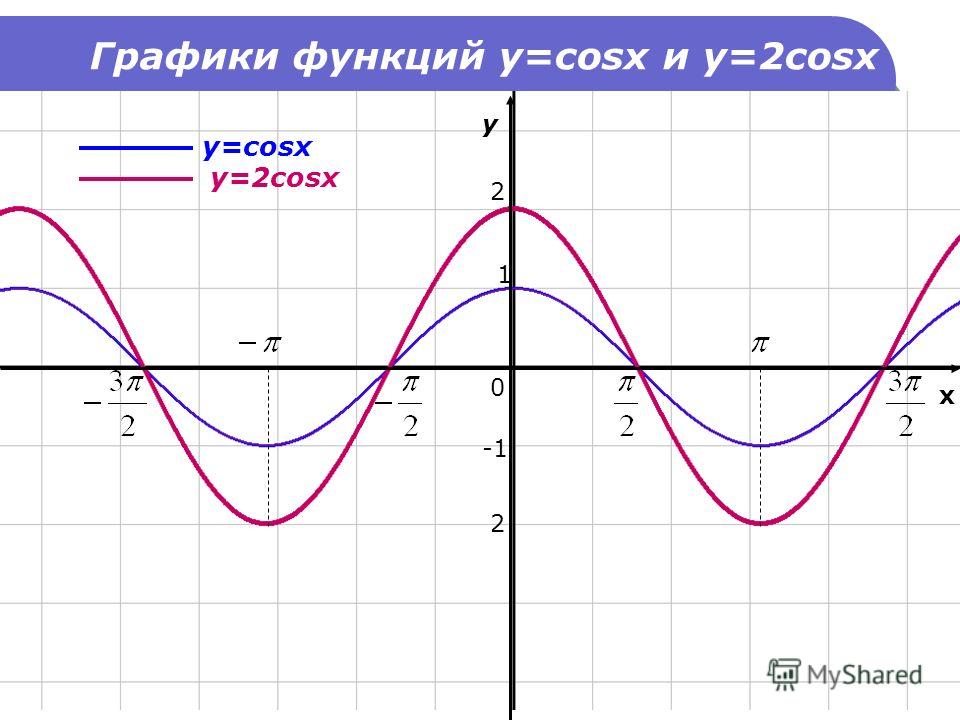
Функция y=cosx

Функция y=cosx определена на всей числовой прямой и множеством её значений является отрезок [−1;1]

Следовательно, график этой функции расположен в полосе между прямыми y=−1 и y=1

Так как функция y=cosx периодическая с периодом 2π, то достаточно построить её график на каком-нибудь промежутке длиной 2π, например на отрезке −π≤x≤π, тогда на промежутках, получаемых сдвигами выбранного отрезка на 2πn,n∈Z, график будет таким же.

Функция y=cosx является чётной. Поэтому её график симметричен относительно оси Oy.

Для построения графика на отрезке −π≤x≤π достаточно построить его для 0≤x≤π, а затем симметрично отразить его относительно оси Oy.

Найдём несколько точек, принадлежащих графику на этом отрезке 0≤x≤π cos0=1;cosπ6=3√2;cosπ4=2√2;cosπ3=12;cosπ2=0;cosπ=−1 

Итак, график функции y=cosx построен на всей числовой прямой.

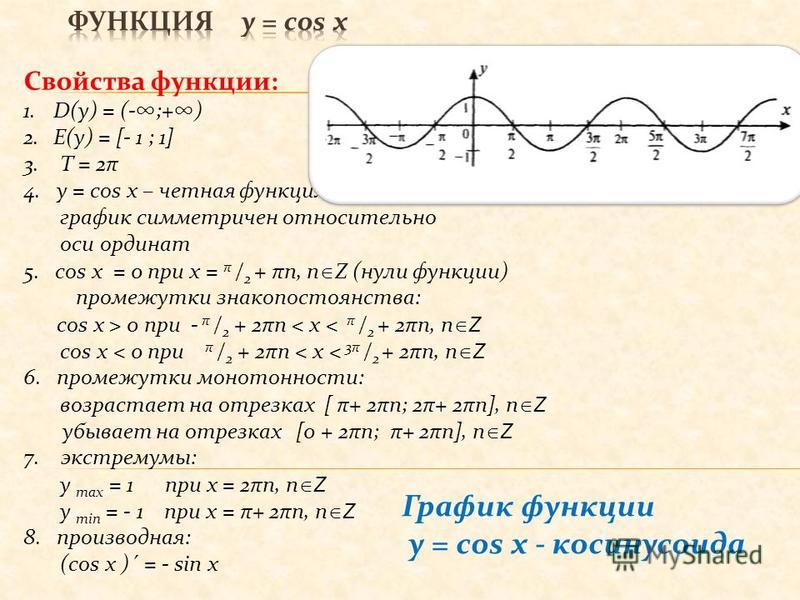
Свойства функции y=cosx

1. Область определения — множество R всех действительных чисел

2. Множество значений — отрезок [−1;1]

3. Функция y=cosx периодическая с периодом 2π 

4. Функция y=cosx — чётная

5. Функция y=cosx принимает:

— значение, равное 0, при x=π2+πn,n∈Z; 

— наибольшее значение, равное 1, при x=2πn,n∈Z 

— наименьшее значение, равное −1, при  x=π+2πn,n∈Z  

— положительные значения на интервале (−π2;π2) и на интервалах, получаемых сдвигами этого интервала на 2πn,n∈Z

— отрицательные значения на интервале (π2;3π2) и на интервалах, получаемых сдвигами этого интервала на 2πn,n∈Z

6. Функция y=cosx

— возрастает на отрезке [π;2π] и на отрезках, получаемых сдвигами этого отрезка на 2πn,n∈Z

— убывает на отрезке [0;π] и на отрезках, получаемых сдвигами этого отрезка на 2πn,n∈Z

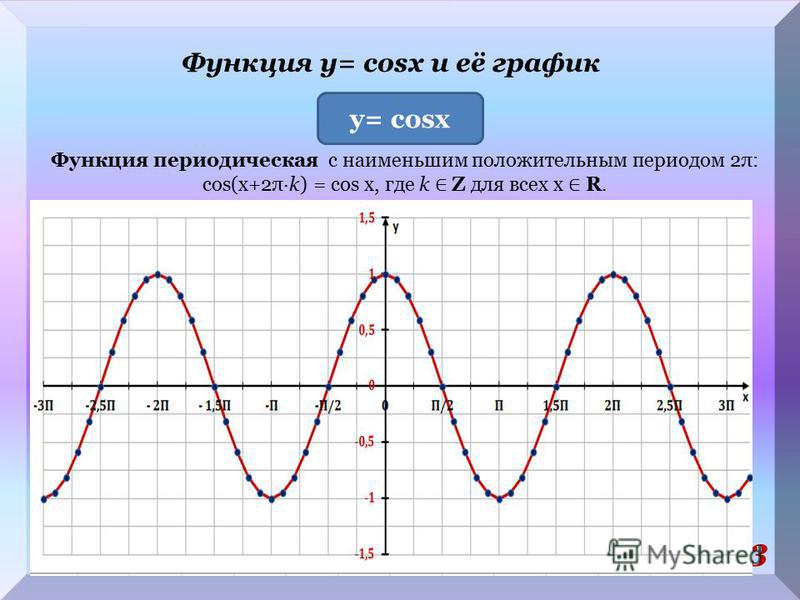
Функция y=sinx

y=sinx

Функция 

y=sinx

 определена на всей числовой прямой, является нечётной и периодической с периодом 

2π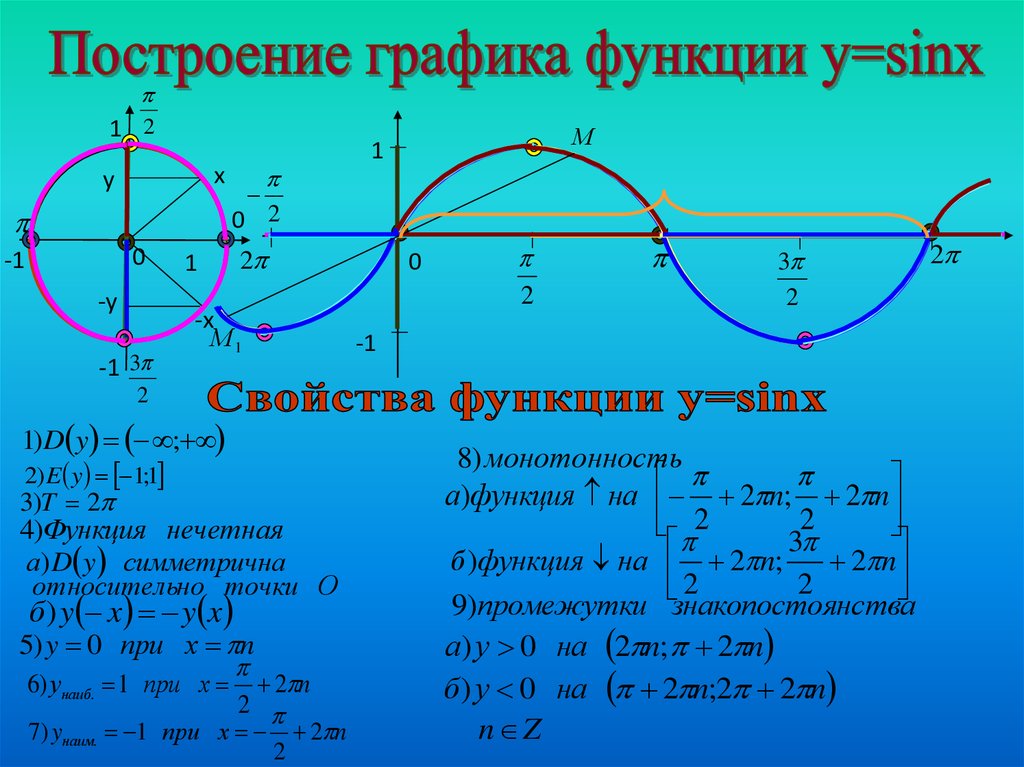

.  

График этой функции можно построить таким же способом, как и график функции y=cosx, начиная с построения, например,  на отрезке [0;π]. 

Однако проще применить формулу sinx=cos(x−π2), которая показывает, что график функции y=sinx можно получить сдвигом графика функции  y=cosx вдоль оси абсцисс вправо на π2 

Свойства функции y=sinx

1. Область определения — множество R всех действительных чисел.

2. Множество значений — отрезок [−1;1]

3. Функция y=sinx периодическая с периодом T=2π 

4. Функция y=sinx- нечётная.

5. Функция y=sinx принимает:
— значение, равное 0, при  x=πn,n∈Z
— наибольшее значение, равное 1, при x=π2+2πn,n∈Z
— наименьшее значение, равное −1, при x=−π2+2πn,n∈Z
— положительные значения на интервале (0;π) и на интервалах, получаемых сдвигами этого интервала на 2πn,n∈Z

— отрицательные значения на интервале (π;2π) и на интервалах, получаемых сдвигами этого интервала на 2πn,n∈Z

6. Функция y=sinx

— возрастает на отрезке

 [−π2;π2] и на отрезках, получаемых сдвигами этого отрезка на 2πn,n∈Z
— убывает на отрезке

 [π2;3π2] и на отрезках, получаемых сдвигами этого отрезка на 2πn,n∈Z

И вновь хочу предложить вам игру, но в этот раз усложним её.  

Вам необходимо из всех предложенных свойств функций  выбрать только те, которые

соответствуют только синусу и косинусу произвольного угла

Готовы? ВПЕРЁД!!!

изобразите схематически график функции y=cosx на промежутке -π/2;2π — Знания.site

• Геометрия

  1 минута назад

  Дано abcd трапеция угол а=16 угол с=121 найти угол b угол d

• Математика

  2 минуты назад

  Помогите решить пожалуйста!!!

• Қазақ тiлi

  2 минуты назад

  мин Тапсырма 1. Берілген үзінді идеясының ұлттық ерекшелiгiн талдап жазыңыз. Жетi журт көшіп кеткен соң,Атамыз қазақ баласы Конып, мекен еткен жер. Мыннан-мыннан жылкы айдап, Жүзден-жүзден нар байлап, Дәулетi калың бiткен жер. .. …Ак борыктай иілген, Кейінгі туған баланың Ұстай ма деп білегін, Шая ма деп журегiн,, Шашын, мұртын қойдырып, Ащы суға тойдырып, Бұза ма деп реңін. Адыра калғыр заманның Мен жаратпаймын сүреңін!.. 2. Жоғарыдағы үзіндіден көркемдегіш құралдарды тауып, колданысын Автордың стилін ажыратыңыз.​

• Литература

  2 минуты назад

  Целевая аудитория: возрастной диапазон широкий (от подростков 15 лет до пожилых людей). Статья привлечет внимание подростков, стоящих перед выбором профессии, и тех, кто заинтересован новыми профессиями, неравнодушен к научным открытиям в области биологии.

• Русский язык

  2 минуты назад

  помоги пожалуйста В восемнадцать лет невозможно быть оседлым, и однажды ты вдруг почувствуешь неодолимое желание соприкоснуться с неизведанным, неизвестным.       Как прекрасно в вечерний час подняться по дрожащему корабельному трапу на празднично освещенную палубу и присоединиться к шумной толпе пассажиров, которые прощаются с землей и уходят в море, в какую-то новую, удивительную, ни с чем не сравнимую жизнь.      Когда пароход загудел трубным голосом и палуба стала содрогаться от работы упрятанных в трюме машин, закипела у бортов темная, с нефтяными оранжевыми пятнами, со световыми бликами вода, вдруг вздрогнул и, медленно разворачиваясь, стал отходить берег с темной толпой провожающих на причале. Поплыли, туманясь, портовые огни, убегая все дальше и дальше в глубь материка, желтея там, вдали, а веселые звезды стали приближаться, иные, казалось, висели прямо на реях, и их можно было, как бабочку, снять рукой.      И вдруг дохнуло свободой, соленой прохладой, и Черное море глянуло прямо в глаза.      Я расхаживал по нижней палубе среди поющих, кричащих, пляшущих пассажиров, гордых и печальных, неподвижно сидящих и вповалку храпящих прямо на палубе.
  Я был один из них в эту ночь, безвестной песчинкой, отправлявшейся в далекое и неизведанное плавание.1. какова основная мысль текста!​

Все предметы

Выберите язык и регион

Русский

Россия

English

United States

How much to ban the user?

1 hour 1 day

2) = \cos(xy)$ так круто?

Вот несколько наблюдений, чтобы попытаться объяснить, что происходит.

Во-первых, почему появляется концентрическое повторение расширяющегося наружу изображения?

Это вызвано периодичностью синуса и косинуса. Каждая пара пересекающихся овалов происходит периодически, но не с постоянным периодом. Поскольку входные данные являются квадратичными по переменным, период сокращается по мере продвижения наружу, что делает повторение более частым. Я займусь этим позже, рассмотрев радиальные срезы и уравнения овалов. 92)$. На самом деле, вы решаете, каким должно быть уравнение для $y=kx$ для любой константы k.

---

Добавлено для полноты:

Действительно ли они эллипсы? Да! Акилле Хуэй объяснил, почему овалы на самом деле являются эллипсами, в комментариях к исходному сообщению. Я повторяю часть этого здесь, чтобы сделать его немного более заметным и долговечным.

Используя эти уравнения:

$$\begin{align} \sin(A) = \cos(B) \iff & B = \pm (\frac{\pi}{2} — A ) + 2m\pi \quad\text{ для некоторых }\; m \in \mathbb{Z}\\ \iff & A \pm B = (2n+\frac{1}{2})\pi\quad\text{ для некоторого }\; n \in \mathbb{Z} \end{align}$$ 92=an+b$ для констант $a,b$ и натурального числа $n$, то мы признали бы, что квадрат радиуса зависит от $n$, поэтому радиус должен изменяться как $\sqrt{n}$, и мы ожидаем, что радиусы будут «замедляться», поскольку значения $\sqrt{n}$ сближаются по мере увеличения $n$.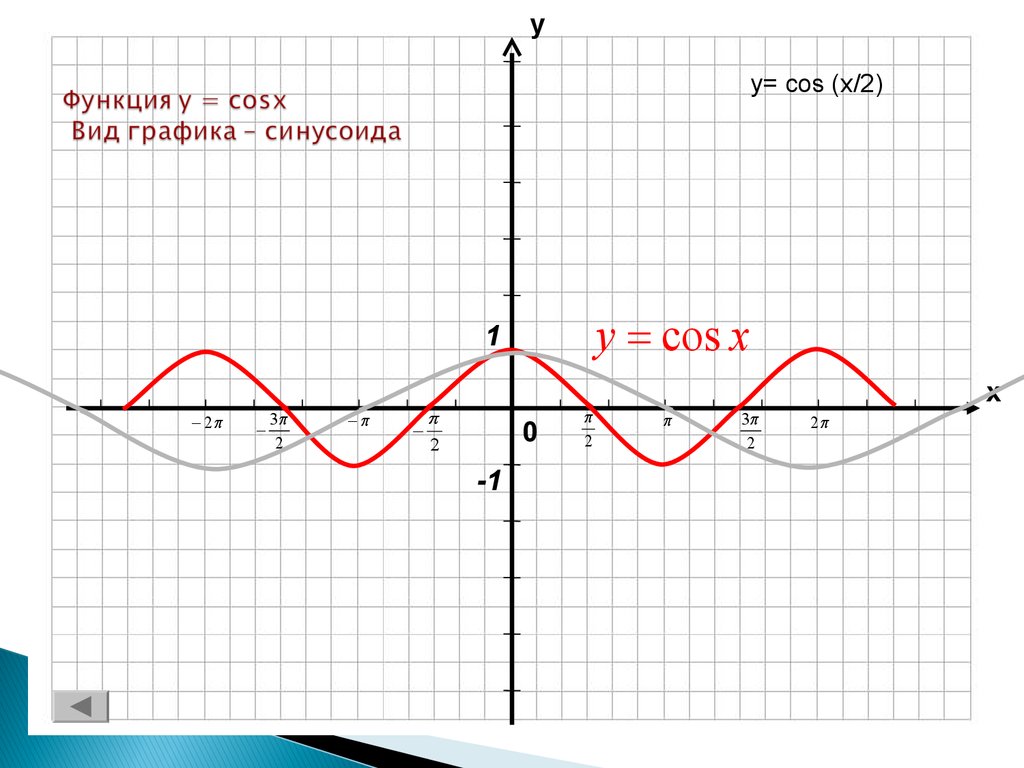

Повернув это семейство уравнений на $\pi/4$, мы можем исключить член $xy$ и рассматривать эллипсы как основные, которые мы используем в исчислении. Вот повернутая версия с использованием $+$ для $\pm$ части уравнения выше: 92}{4\пи н+\пи}=1 $$

Итак, здесь мы видим, что большая и малая главные оси изменяются аналогично $\sqrt{n}$, и, кроме того, большая главная ось в $\sqrt{3}$ раз больше малой оси. Если вы проделаете тот же трюк с «$-$» для $\pm$, вы получите другое семейство эллипсов, повернутое на $\pi/2$ из этих эллипсов.

Ключ к ответу Глава 8 — Алгебра и тригонометрия

Попытайся

8.1 Графики функций синуса и косинуса

1.

6π6π

2.

1212 сжатый

3.

π2;π2; справа

4.

2 шт. до

5.

средняя линия: у=0;у=0; амплитуда: |А|=12;|А|=12; период: P=2π|B|=6π;P=2π|B|=6π; фазовый сдвиг: CB=πCB=π

6.

f(x)=sin(x)+2f(x)=sin(x)+2

7.

две возможности: y=4sin(π5x−π5)+4y=4sin(π5x−π5)+4 или y=−4sin(π5x+4π5)+4y=−4sin(π5x+4π5)+4

8.

средняя линия: у=0;у=0; амплитуда: |А|=0,8;|А|=0,8; период: P=2π|B|=π;P=2π|B|=π; фазовый сдвиг: CB=0CB=0 или нет

9.

средняя линия: у=0;у=0; амплитуда: |А|=2;|А|=2; период: P=2π|B|=6;P=2π|B|=6; фазовый сдвиг: CB=-12CB=-12

10.

7

11.

y=3cos(x)−4y=3cos(x)−4

8.2 Графики других тригонометрических функций

1.

2.

Это отразится на прямой y=−1,y=−1, став возрастающей функцией.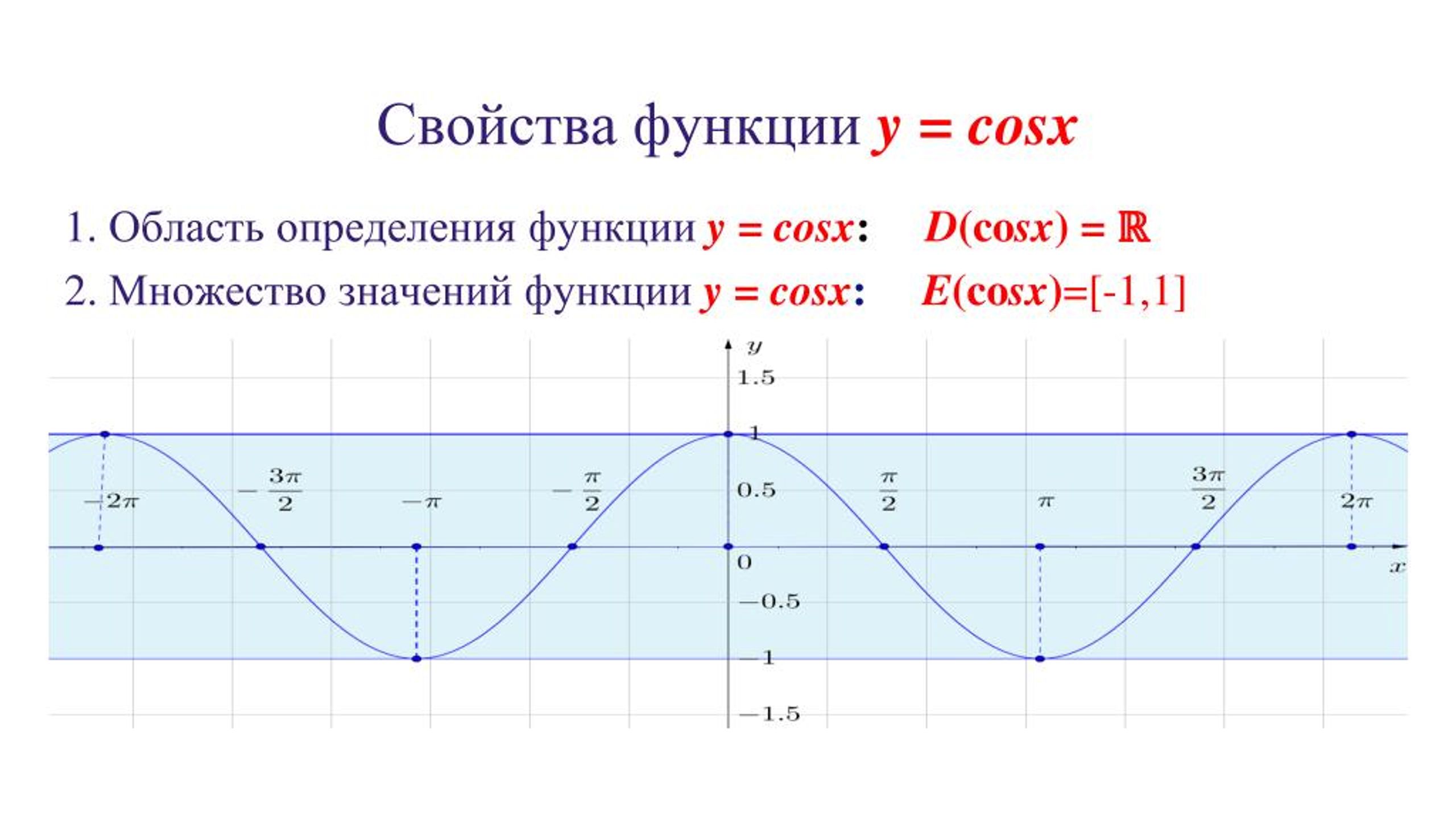

3.

г(х)=4загар(2х)г(х)=4загар(2х)

4.

Это вертикальное отражение предыдущего графика, поскольку AA имеет отрицательное значение.

5.

6.

7.

8.3 Обратные тригонометрические функции

1.

arccos(0,8776)≈0,5arccos(0,8776)≈0,5

2.

1. ⓐ−π2;−π2;
2. ⓑ −π4;−π4;
3. ⓒ π;π;
4. ⓓ π3π3

3.

1,9823 или 113,578°

4.

sin−1(0,6)=36,87°=0,6435sin−1(0,6)=36,87°=0,6435 радиан

5.

π8;2π9π8;2π9

6.

3π43π4

7.

12131213

8.

429429

9.

4x16x2+14x16x2+1

8.1 Секционные упражнения

1.

Функции синуса и косинуса обладают тем свойством, что f(x+P)=f(x)f(x+P)=f(x) для определенного P.P. Это означает, что значения функции повторяются для каждой единицы PP на x — ось.

3.

Абсолютное значение константы AA (амплитуда) увеличивает общий диапазон, а константа DD (вертикальный сдвиг) сдвигает график по вертикали.

5.

В точке, где конечная сторона tt пересекает единичную окружность, можно определить, что sintsint равен y -координате точки.

7.

амплитуда: 23;23; период: 2π;2π; средняя линия: у=0;у=0; максимум: y=23y=23 происходит при x=0;x=0; минимум: y=-23y=-23 происходит при x=π;x=π; за один период график начинается с 0 и заканчивается на 2π2π

9.

амплитуда: 4; период: 2π;2π; средняя линия: у=0;у=0; максимум y=4y=4 приходится на x=π2;x=π2; минимум: y=−4y=−4 происходит при x=3π2;x=3π2; один полный период происходит от x=0x=0 до x=2πx=2π

11.

амплитуда: 1; период: π;π; средняя линия: у=0;у=0; максимум: y=1y=1 происходит при x=π;x=π; минимум: y=−1y=−1 происходит при x=π2;x=π2; один полный период отображается на графике от x=0x=0 до x=πx=π

13.

амплитуда: 4; период: 2; средняя линия: у=0;у=0; максимум: y=4y=4 происходит при x=0;x=0; минимум: y=−4y=−4 происходит при x=1x=1

15.

амплитуда: 3; период: π4;π4; средняя линия: у=5;у=5; максимум: y=8y=8 происходит при x=0,12;x=0,12; минимум: y=2y=2 происходит при x=0,516;x=0,516; сдвиг по горизонтали: −4;−4; вертикальное перемещение 5; один период происходит от x=0x=0 до x=π4x=π4

17.

амплитуда: 5; период: 2π5;2π5; средняя линия: у=-2;у=-2; максимум: y=3y=3 происходит при x=0,08;x=0,08; минимум: y=-7y=-7 происходит при x=0,71;x=0,71; фазовый сдвиг: −4;−4; вертикальный перенос: −2; −2; один полный период можно изобразить на графике от x=0x=0 до x=2π5x=2π5

19.

амплитуда: 1 ; период: 2π;2π; средняя линия: у=1;у=1; максимум: y=2y=2 происходит при x=2,09;x=2,09; максимум: y=2y=2 происходит при t=2,09; t=2,09; минимум: y=0y=0 происходит при t=5,24; t=5,24; фазовый сдвиг: −π3;−π3; вертикальный перевод: 1; один полный период от t=0t=0 до t=2πt=2π

21.

амплитуда: 1; период: 4π;4π; средняя линия: у=0;у=0; максимум: y=1y=1 происходит при t=11,52; t=11,52; минимум: y=-1y=-1 происходит при t=5,24; t=5,24; фазовый сдвиг: −10π3;−10π3; вертикальный сдвиг: 0

23.

амплитуда: 2; средняя линия: у=-3;у=-3; период: 4; уравнение: f(x)=2sin(π2x)−3f(x)=2sin(π2x)−3

25.

амплитуда: 2; период: 5; средняя линия: у=3;у=3; уравнение: f(x)=−2cos(2π5x)+3f(x)=−2cos(2π5x)+3

27.

амплитуда: 4; период: 2; средняя линия: у=0;у=0; уравнение: f(x)=−4cos(π(x−π2))f(x)=−4cos(π(x−π2))

29.

амплитуда: 2; период: 2; средняя линия у=1;у=1; уравнение: f(x)=2cos(πx)+1f(x)=2cos(πx)+1

31.

0,π0,π

33.

sin(π2)=1sin(π2)=1

35.

π2π2

37.

f(x)=sinxf(x)=sinx симметричный

39.

π3,5π3π3,5π3

41.

Максимум: 11 в х=0х=0 ; минимум: -1-1 в х=πx=π

43.

К периодической синусоидальной функции добавляется линейная функция. График не имеет амплитуды, потому что по мере неограниченного возрастания линейной функции комбинированная функция ч(х)=х+sinxh(х)=x+sinx также будет неограниченно увеличиваться. Граф ограничен между графами у=х+1у=х+1 а также у=х-1у=х-1 потому что синус колеблется между -1 и 1.

45.

Амплитуда отсутствует, поскольку функция не ограничена.

47.

График симметричен относительно оси y, амплитуда отсутствует, так как границы функции убывают по мере |х||х| растет. По-видимому, существует горизонтальная асимптота при у=0у=0 .

8.2 Секционные упражнения

1.

Так как y=cscxy=cscx является обратной функцией y=sinx,y=sinx, вы можете построить обратную координату на графике y=sinxy=sinx, чтобы получить y -координаты y=cscx.y=cscx. x точек пересечения графика y=sinxy=sinx являются вертикальными асимптотами графика y=cscx.y=cscx.

3.

Ответы будут разными. Используя единичный круг, можно показать, что tan(x+π)=tanx.tan(x+π)=tanx.

5.

Период тот же: 2π.2π.

9.

III

11.

период: 8; сдвиг по горизонтали: 1 единица влево

13.

1,5

17.

-cotxcosx-sinx-cotxcosx-sinx

19.

коэффициент растяжения: 2; период: π4;π4; асимптоты: x=14(π2+πk)+8, где k — целое число x=14(π2+πk)+8, где k — целое число

21.

коэффициент растяжения: 6; период: 6; асимптоты: x=3k, где k – целое число x=3k, где k – целое число

23.

коэффициент растяжения: 1; период: π;π; асимптоты: x=πk, где k — целое число x=πk, где k — целое число

25.

Коэффициент растяжения: 1; период: π;π; асимптоты: x=π4+πk, где k — целое число x=π4+πk, где k — целое число

27.

коэффициент растяжения: 2; период: 2π;2π; асимптоты: x=πk, где k — целое число x=πk, где k — целое число

29.

коэффициент растяжения: 4; период: 2π3;2π3; асимптоты: x=π6k, где k — нечетное целое число x=π6k, где k — целое нечетное число

31.

коэффициент растяжения: 7; период: 2π5;2π5; асимптоты: x=π10k, где k — нечетное целое числоx=π10k, где k — нечетное целое число

33.

коэффициент растяжения: 2; период: 2π;2π; асимптоты: x=−π4+πk, где k — целое число x=−π4+πk, где k — целое число

35.

коэффициент растяжения: 75;75; период: 2π;2π; асимптоты: x=π4+πk, где k — целое число x=π4+πk, где k — целое число

37.

y=tan(3(x−π4))+2y=tan(3(x−π4))+2

39.

f(x)=csc(2x)f(x)=csc(2x)

41.

f(x)=csc(4x)f(x)=csc(4x)

43.

f(x)=2cscxf(x)=2cscx

45.

f(x)=12tan(100πx)f(x)=12tan(100πx)

47.

49.

51.

53.

55.

1. ⓐ (−π2,π2);(−π2,π2);
2. ⓑ
3. ⓒ x=−π2x=−π2 и x=π2;x=π2; расстояние неограниченно растет как |x||x| приближается к π2π2, т. е. под прямым углом к ​​линии, изображающей точный север, лодка будет так далеко, что рыбак ее не увидит;
4. ⓓ3; при x=−π3,x=−π3 лодка находится на расстоянии 3 км;
5. ⓔ 1,73; когда x=π6,x=π6, лодка находится на расстоянии около 1,73 км;
6. ⓕ 1,5 км; когда х=0х=0

57.

1. ⓐ h(x)=2tan(π120x);h(x)=2tan(π120x);
2. ⓑ
3. ⓒ h(0)=0:h(0)=0: через 0 секунд ракета находится на высоте 0 миль над землей; h(30)=2:h(30)=2: через 30 секунд высота ракет составляет 2 мили;
4. ⓓПоскольку xx приближается к 60 секундам, значения h(x)h(x) становятся все больше. Расстояние до ракеты становится настолько большим, что камера уже не может ее отслеживать.

8.3 Секционные упражнения

1.

Функция y=sinxy=sinx взаимно однозначна на [−π2,π2];[−π2,π2]; таким образом, этот интервал является диапазоном обратной функции y=sinx,y=sinx,f(x)=sin-1x.f(x)=sin-1x. Функция y=cosxy=cosx взаимно однозначна на [0,π];[0,π]; таким образом, этот интервал является диапазоном обратной функции y=cosx,f(x)=cos-1x.y=cosx,f(x)=cos-1x.

3.

π6π6 — мера угла между −π2−π2 и π2π2 в радианах, синус которого равен 0,5.

5.

Для того чтобы любая функция имела обратную, она должна быть взаимно однозначной и должна пройти тест горизонтальной линии. Обычная синусоидальная функция не является взаимно однозначной, если ее область определения каким-либо образом не ограничена. Математики согласились ограничить функцию синуса интервалом [−π2,π2][−π2,π2], чтобы она была взаимно однозначной и имела обратную.

7.

Верно. Угол θ1θ1, равный arccos(−x)arccos(−x), x>0x>0, будет углом второго квадранта с опорным углом θ2θ2, где θ2θ2 равен arccosxarccosx, x>0x>0. Поскольку θ2θ2 является опорным углом для θ1θ1, θ2=π−θ1θ2=π−θ1 и arccos(−x)arccos(−x) = π−arccosxπ−arccosx-

9.

−π6−π6

11.

3π43π4

13.

−π3−π3

15.

π3π3

17.

1,98

19.

0,93

21.

1.41

23.

0,56 радиан

27.

0,71

29.

-0,71

31.

−π4−π4

33.

0,8

35.

513513

37.

х-1-х2+2хх-1-х2+2х

39.

x2-1xx2-1x

41.

х+0,5-х2-х+34х+0,5-х2-х+34

43.

2x+1x+12x+1x+1

45.

2x+1x2x+1x

47.

тт

49.

домен [−1,1];[−1,1]; диапазон [0,π][0,π]

51.

приблизительно х=0,00х=0,00

53.

0,395 радиан

55.

1,11 радиан

57.

1,25 радиан

59.

0,405 радиан

61.

Нет. Угол, который образует лестница с горизонтом, составляет 60 градусов.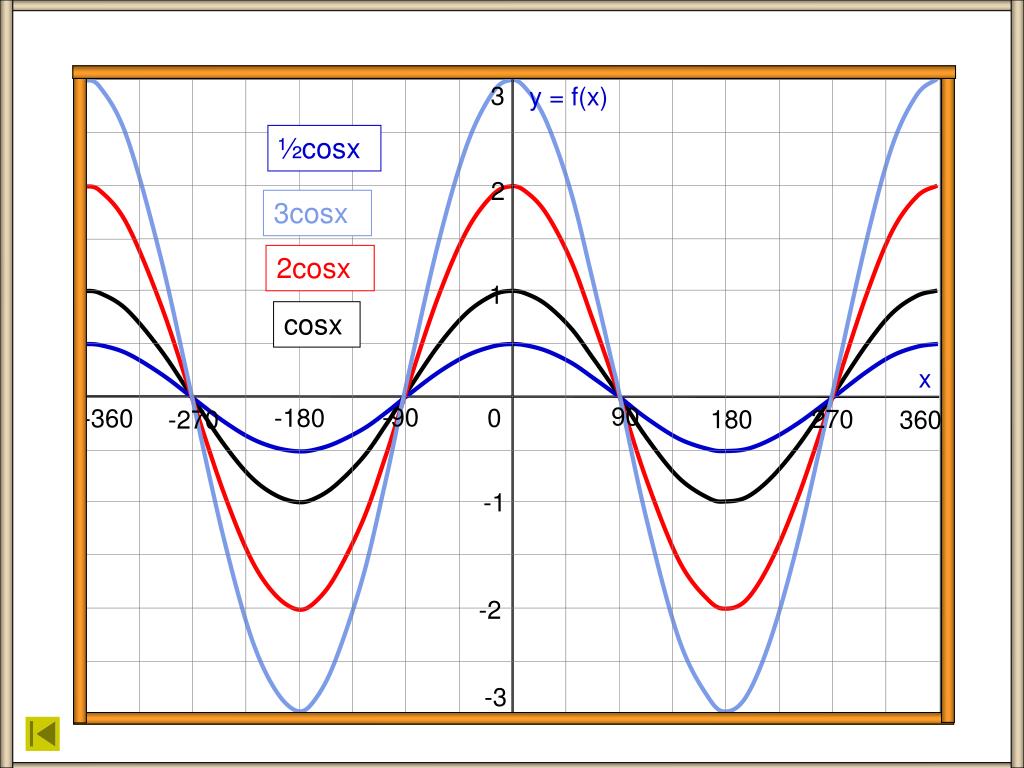

Обзор упражнений

1.

амплитуда: 3; период: 2π;2π; средняя линия: у=3;у=3; нет асимптот

3.

амплитуда: 3; период: 2π;2π; средняя линия: у=0;у=0; нет асимптот

5.

амплитуда: 3; период: 2π;2π; средняя линия: у=-4;у=-4; нет асимптот

7.

амплитуда: 6; период: 2π3;2π3; средняя линия: у=-1;у=-1; нет асимптот

9.

коэффициент растяжения: нет; период: π;π; средняя линия: у=-4;у=-4; асимптоты: x=π2+πk,x=π2+πk, где kk — целое число

11.

коэффициент растяжения: 3; период: π4;π4; средняя линия: у=-2;у=-2; асимптоты: x=π8+π4k,x=π8+π4k, где kk — целое число

13.

амплитуда: нет; период: 2π;2π; нет фазового сдвига; асимптоты: x=π2k,x=π2k, где kk — целое нечетное число

15.

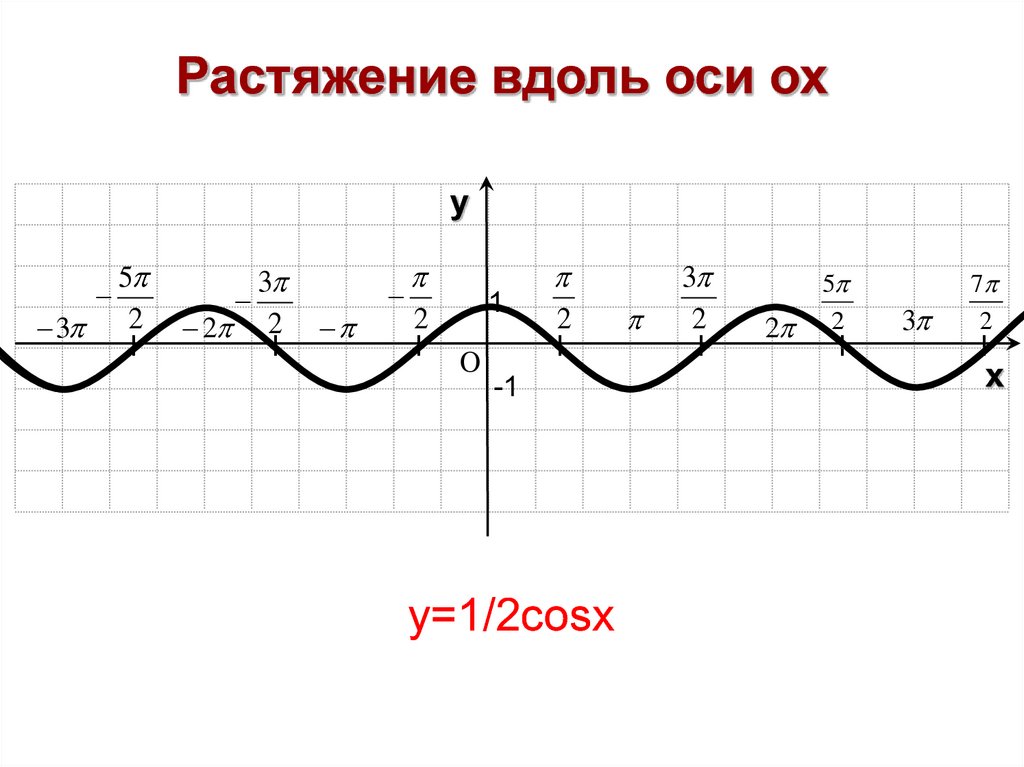
амплитуда: нет; период: 2π5;2π5; нет фазового сдвига; асимптоты: x=π5k,x=π5k, где kk — целое число

17.

амплитуда: нет; период: 4π;4π; нет фазового сдвига; асимптоты: x=2πk,x=2πk, где kk — целое число

19.

самый большой: 20 000; наименьший: 4000

21.

амплитуда: 8000; период: 10; фазовый сдвиг: 0

23.

В 2007 году прогнозируемая численность населения составляет 4413 человек. В 2010 году численность населения составит 11,9 чел.24.

25.

5 дюймов

27.

10 секунд

29.

π6π6

31.

π4π4

33.

π3π3

35.

Нет решения

37.

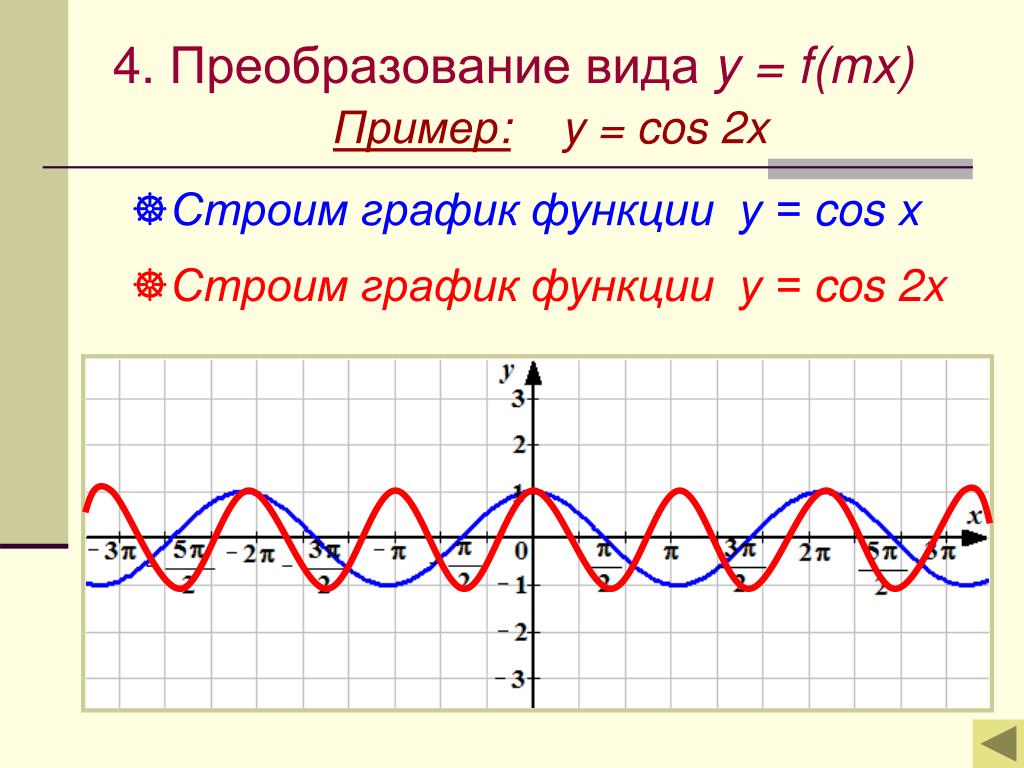
125125

39.

Графики несимметричны относительно прямой y=x.y=x. Они симметричны относительно оси yy.

41.

Графики идентичны.

Практический тест

1.

амплитуда: 0,5; период: 2π;2π; средняя линия y=0y=0

3.

амплитуда: 5; период: 2π;2π; средняя линия: у=0у=0

5.

амплитуда: 1; период: 2π;2π; средняя линия: у=1у=1

7.

амплитуда: 3; период: 6π;6π; средняя линия: у=0у=0

9.

амплитуда: нет; период: π;π; средняя линия: y=0,y=0, асимптоты: x=2π3+πk,x=2π3+πk, где kk — целое число

11.

амплитуда: нет; период: 2π3;2π3; средняя линия: y=0,y=0, асимптоты: x=π3k,x=π3k, где kk — целое число

13.

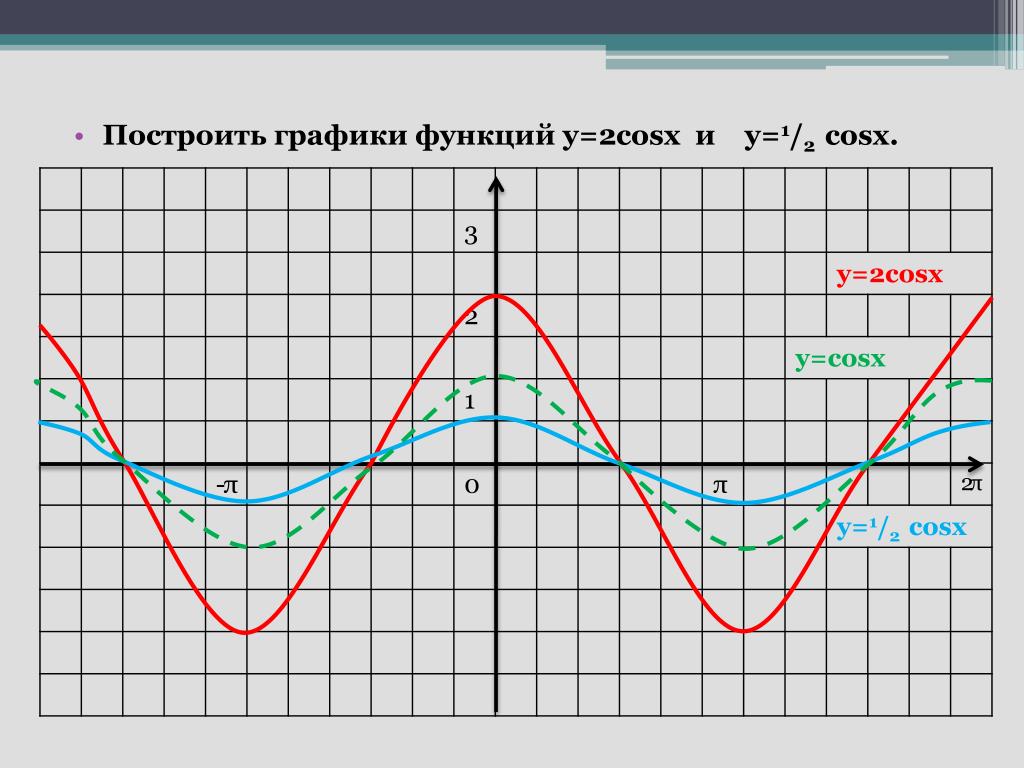
амплитуда: нет; период: 2π;2π; средняя линия: y=−3y=−3

15.

амплитуда: 2; период: 2; средняя линия: y=0;y=0;f(x)=2sin(π(x−1))f(x)=2sin(π(x−1))

17.

амплитуда: 1; период: 12; фазовый сдвиг: −6;−6; средняя линия y=−3y=−3

19.

D(t)=68−12sin(π12x)D(t)=68−12sin(π12x)

21.

период: π6;π6; сдвиг по горизонтали: −7−7

23.

f(x)=sec(πx);f(x)=sec(πx); период: 2; фазовый сдвиг: 0

25.

44

27.

Представления разные, потому что период волны 125,125. В большей области будет больше циклов графа.

29.

3535

31.

На приближенных интервалах (0,5,1),(1,6,2,1),(2,6,3,1),(3,7,4,2),(4,7,5,2),(5,6,6,28)(0,5,1),(1,6, 2.