2+n-72)=1/(n+9)презентация потеме Функция тангенса, ее график и свойства. | Презентация к уроку по алгебре (10 класс) по теме:
Слайд 1
Функция у = tg х и построение ее графика. .
Слайд 3
Определяем цели учебной деятельности 1.Выделите слова и словосочетания, встречаемые впервые. 2.Определите, знаете ли Вы точное значение этих слов, а также тех слов и словосочетаний, которые уже встречались Вам, но точные их значения и определения остаются Вам пока неизвестными.
Слайд 4
Определяем цели учебной деятельности 3 . Какие новые определения и значения каких понятий необходимо будет усвоить в рамках изучения данной темы? 4. Какие умения нужно будет выработать? 5. Какие правила, алгоритмы, способы действий Вам неизвестны , и для решения каких задач они Вам будут нужны?
Слайд 5
Тангенс.
Слайд 6
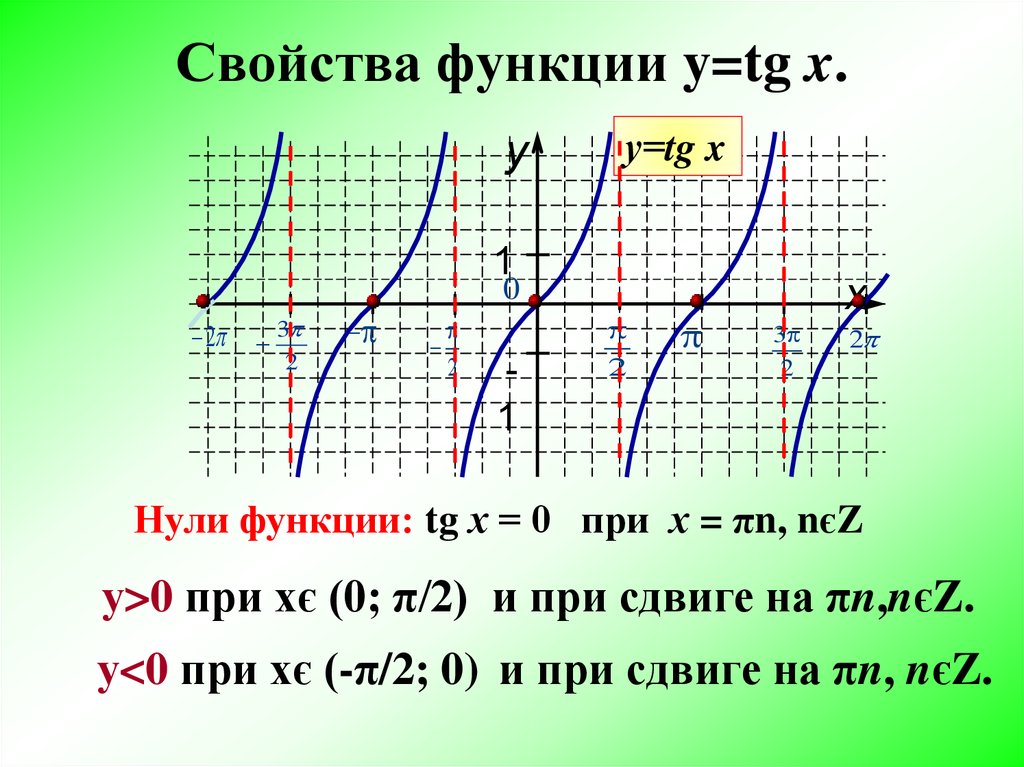
Предполагаемые цели учебной деятельности учеников 1. Определение функции тангенса, свойств этой функции 2.
Построение графика функции тангенс по таблице значений и тем свойствам, которые известны для тангенса (алгоритм построения). Узнать, н а какой линии находятся тангенсы углов.
Слайд 7
Находим ответы на вопросы в учебнике. Стр.17 -стр.18: определение , л иния тангенсов углов, о бласть определения, о бласть значений, с войства тангенса, известные вам на сегодняшний день.
Слайд 8
Рисунок 10 из учебника
Слайд 9
Функция у = tg х. Определение. Числовая функция, заданная формулой у = tg х , называется функцией тангенса. Тангенс угла – отношение ординаты точки на единичной окружности, соответствующей данному углу, к абсциссе этой точки. А где находятся тангенсы углов?
Слайд 10
Тригонометрический круг
Слайд 11
диктант a = 185 градусов a = – 185 градусов a = 102 a = – 102 a = 250 a = – 250 a = 375 a = 145 a = – 145 a = 225 a = – 315 a = 210 a = 590 a = – 15 1Углом какой четверти является угол a , если:
Слайд 12
диктант 2. Вычислите : 1 вариант.
cos 180 + 5sin 90 sin 180 – 3 cos 0 5ctg 90 – 7tg 180 sin 60 + cos 30 2 вариант. cos 0 + 3sin 90 sin 270 – 2cos 180 6tg 180 + 2ctg 90 1 + ctg 270 – 5 tg 360
Слайд 13
Нормы оценок 1.Все задания верны – оценка «5» 2. 1-2 ошибки – оценка «4» 3. 3- 5 ошибок – оценка «3» 4. более 5 ошибок – беру дополнительное домашнее задание. Успехов в учебе!
Слайд 14
Ответы к диктанту. 1вариант. 1. III,II,II,III,III,II,I. 2. 4,-3,0. 2 вариант. 1.II,III,III,I,III,III,IV. 2. 0,2,4. Задание . Заполнить в тетради таблицу значений для построения графика у = tg х. Работа в парах.
Слайд 15
Построение графика. Составляем план построения графика, пользуясь учебником.
Слайд 16
План построения графика. 1 . Правильно выбери единичный отрезок. 2. Н айди область определения. 3 Проведи прямые у = π/ 2 + π n , где n принадлежит целым числам. 4. Построй график. Работаем в парах.
Слайд 17
Линия тангенса
Слайд 18
График функции в 1 четверти у = tg x x y 0 1
Слайд 19
у = tg x х у y = tg x
Слайд 20
Выполнение заданий.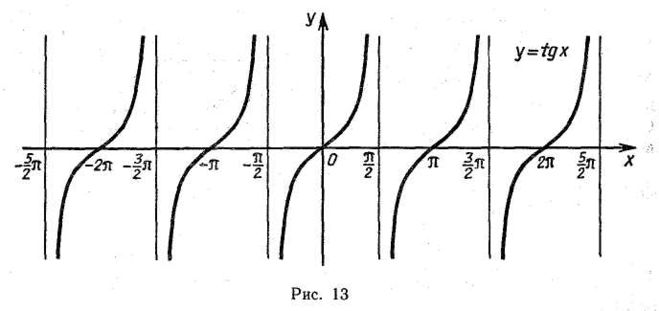
№37(В),33(г). Устно составить план выполнения задания, обговорить в парах. Рефлексия. Ответьте на вопросы: Какие новые знания вы приобрели на этом уроке? Какие новые умения? Все ли цели урока были достигнуты? .
Слайд 21
Домашняя работа. 1. Построить по аналогичному график функции котангенс. 2.Уметь доказывать по рис 10 из учебника, что касательная к числовой окр ., проведенная в точке (1,0), является линией тангенсов. 36( а,б,в ),38(а), 39( а,в,г ) Творческое задание. По рис.11учебника, доказать, что касательная прямая, проведенная в точке (0,1) к числовой окружности, является линией котангесов . Спасибо за урок.
Слайд 22
Спасибо за урок.
3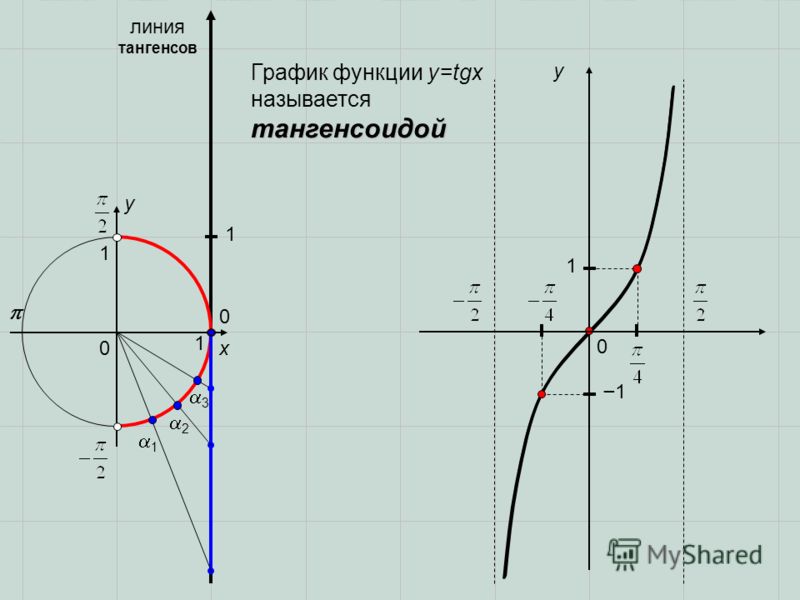
Tangent Graphs
.
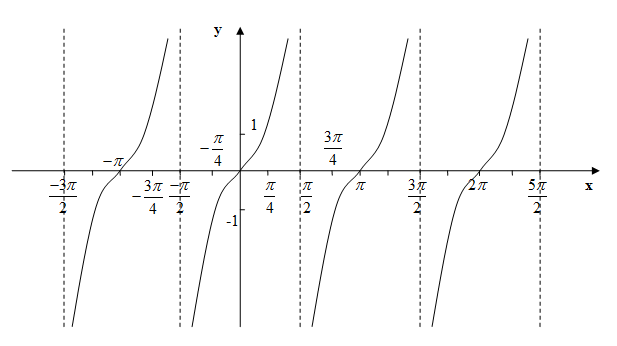бесконечно. Граф
продолжается по вертикали вечно
Синий график — исходный y = tan x. Красный график — это график y = 2 tan x.
Обратите внимание, что единственный эффект изменения значения A должен растянуть график, точки пересечения и точки остаются прежними. одно и тоже.
Период
Период графика — это длина, необходимая для завершения одного шаблона. На красном графике одно повторение от -90 до 90 до полного паттерн, поэтому период составляет 180 градусов. На синем графике одно повторение идет от -45 до 45 для завершения одного шаблона, поэтому период равен 90. значение B равно 2, поэтому период сократился вдвое.
Учитывая уравнение y = A tan B x, значение B определяет период. Чем больше B , тем.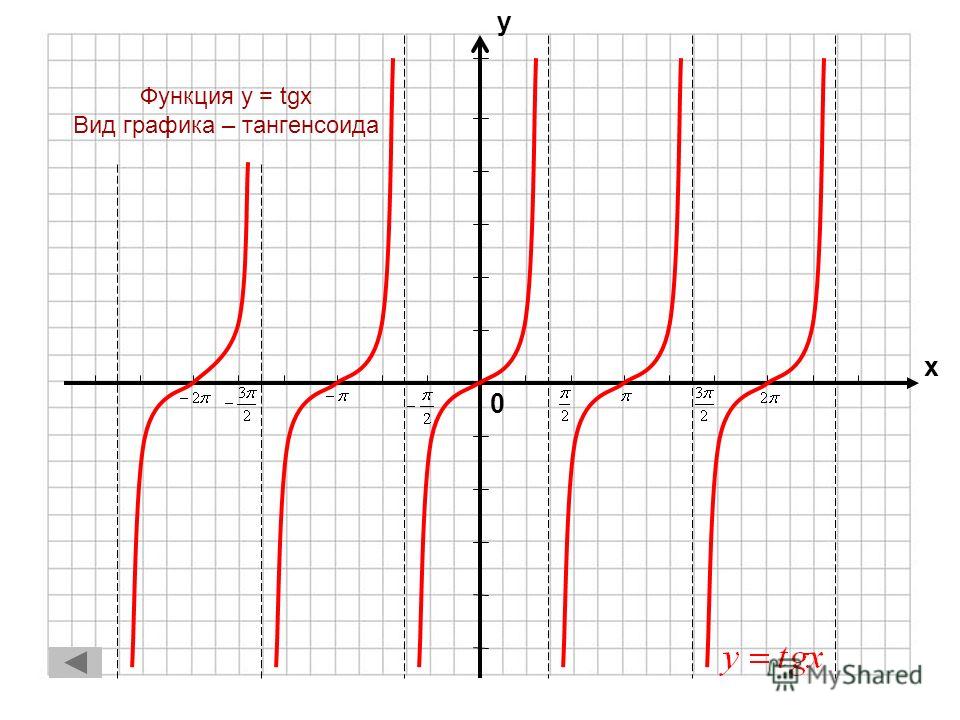
..
меньше становится период.
На приведенном выше графике B = 2, а период сокращен вдвое (т. график сжат). Это приводит к следующему уравнению:
Фазовый сдвиг
Фазовый сдвиг — это расстояние, на которое график сдвигается по горизонтали от его стандартное (y = tan x) положение
Красный график, опять же, является стандартным y = tan x граф. к красному графику применен фазовый сдвиг. единственная разница между уравнениями двух графиков заключается в значении C 45,
Учитывая уравнение y = A tan B (x — C ), значение C диктует
фазовый сдвиг. Обратите внимание, что стандартное уравнение имеет отрицательный знак. в
пример выше, C = 45, а график был сдвинут по горизонтали на 45 градусов.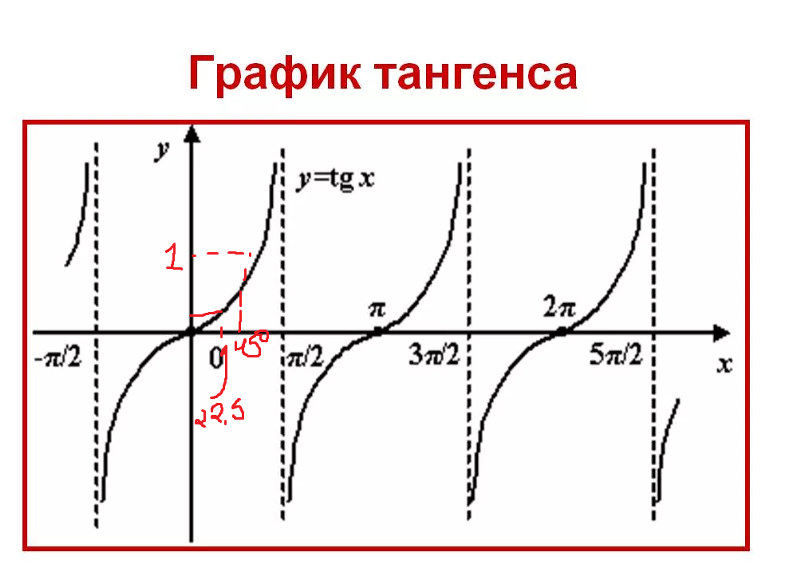
Фаза Сдвиг = С |
Сдвиг по вертикали
Сдвиг по вертикали — это расстояние, на которое график сдвигается по вертикали от его стандартное (y = tan x) положение
Красный график снова является стандартным y = tan x график. Синий график имеет к нему применяется фазовый сдвиг. единственная разница между уравнениями двух графиков заключается в значении D равно 2. В результате график перемещается по вертикали на 2 единицы.
Учитывая уравнение y = A tan B (x — C ) + D , значение D диктует вертикальное смещение. В приведенном выше примере D = -2, и график был сдвинут вниз по вертикали на 2 единицы.
Вертикальный Сдвиг = Д |
Сводка
Фазовый сдвиг = С |
Вертикальное смещение = D |
Следующий сайт позволит вам построить графики нескольких триггеров
за один раз.