Электронный справочник по математике для школьников тригонометрия графики тригонометрических функций синуса косинуса тангенса котангенса
| Справочник по математике | Тригонометрия |
На рисунках 1, 2, 3, 4 приведены графики тригонометрических функций
| y = sin x, | y = cos x, | y = tg x, | y = ctg x. |
y = sin x, y = cos x,
y = tg x, y = ctg x.
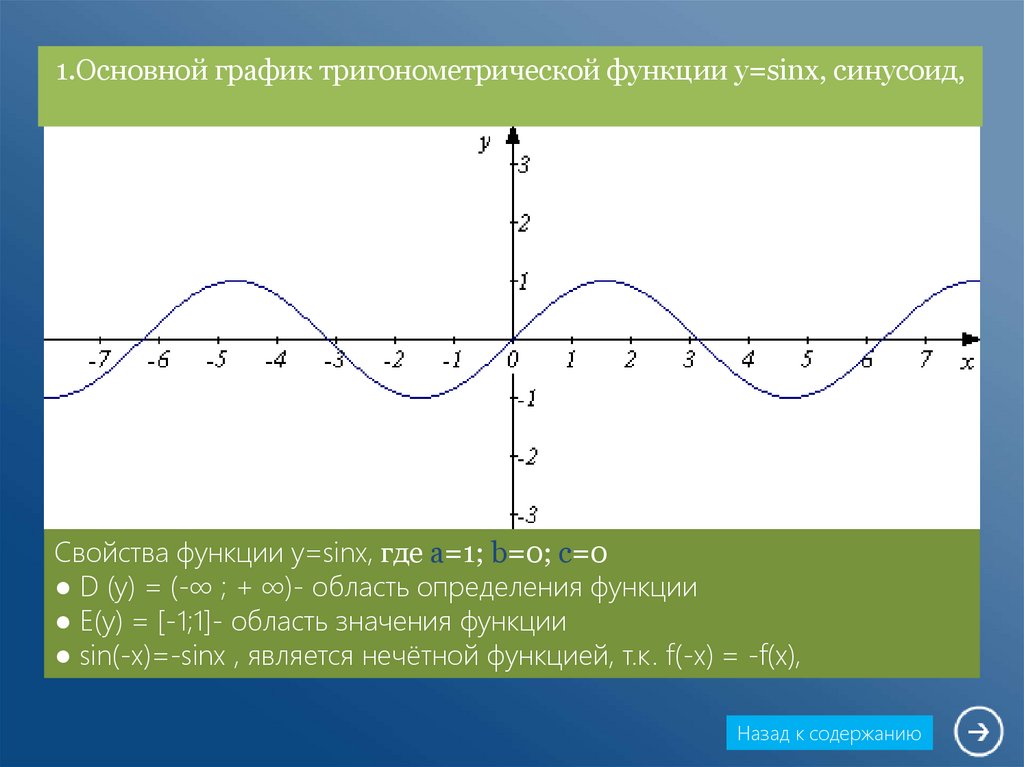
Рис.1. График функции y = sin x
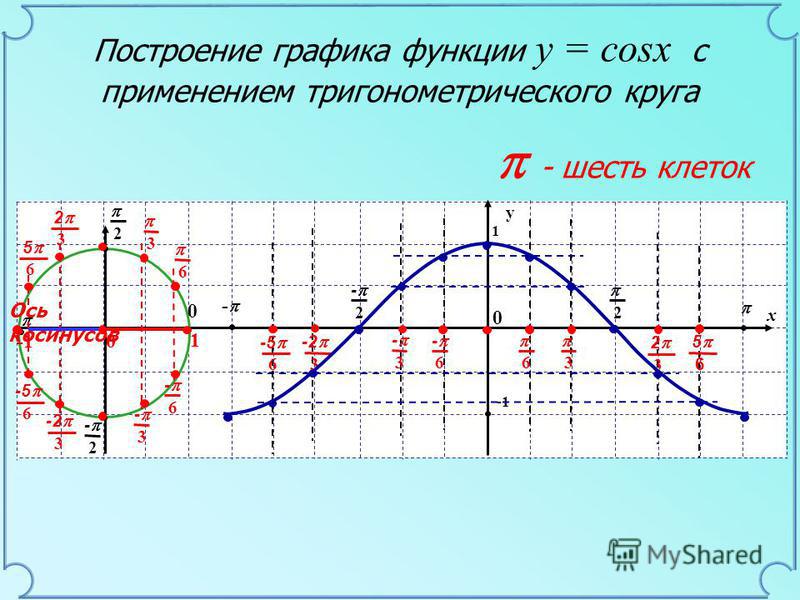
Рис.2. График функции y = cos x
Рис.3. График функции y = tg x
Рис.4. График функции y = ctg x
Наверх
Демонстрационные варианты ЕГЭ и ОГЭ
С демонстрационными вариантами ЕГЭ и ОГЭ по всем предметам, опубликованными на официальном информационном портале Единого Государственного Экзамена, можно ознакомиться на специальной страничке нашего сайта.
Наши учебные пособия для школьников
При подготовке к ЕГЭ и к ОГЭ по математике Вам могут также пригодиться наши учебные пособия.
Решение рациональных неравенств
Задачи на проценты
Решение показательных неравенств
Квадратный трехчлен
Метод координат на плоскости
Решение иррациональных неравенств
Фигуры на координатной плоскости
Решение алгебраических уравнений
Уравнения и неравенства с модулями
Решение показательных уравнений
Арифметическая и геометрическая прогрессии
Решение логарифмических уравнений
Решение логарифмических неравенств
Системы уравнений
Решение тригонометрических уравнений
Тригонометрия в ЕГЭ по математике
Степень с рациональным показателем
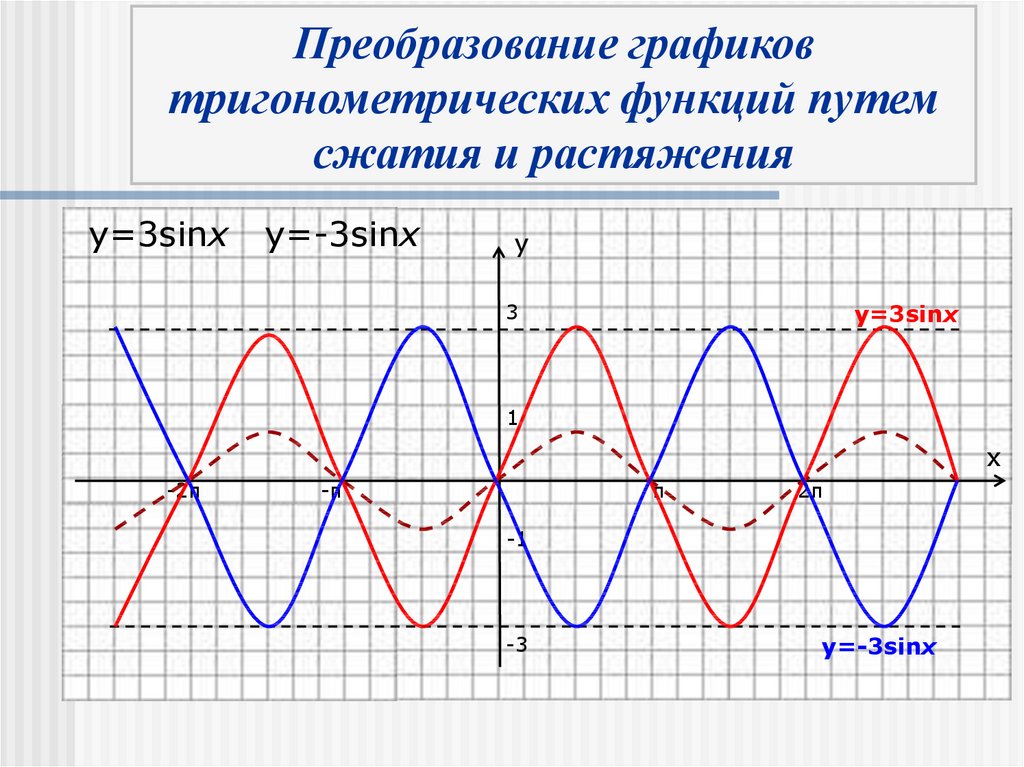
растяжение и сжатие, параллельный перенос, общее уравнение синусоиды, тангенцоиды
- Растяжение и сжатие графиков тригонометрических функций по оси OX
- Растяжение и сжатие графиков тригонометрических функций по оси OY
- Параллельный перенос графиков тригонометрических функций по оси OX
- Параллельный перенос графиков тригонометрических функций по оси OY
- Общее уравнение тангенцоиды
- Примеры
Общие принципы преобразования графиков функций изучались нами в главе 8, (см.
§47, §48, §50 справочника для 8 класса). В этом параграфе мы рассмотрим особенности тригонометрических функций при использовании этих преобразований.
п.1. Растяжение и сжатие графиков тригонометрических функций по оси
OXОбщие принципы растяжения и сжатия графиков по оси OX:
При сравнении графиков двух функций $$ y_1=f(x),\ \ y_2=f(px),\ \ p\gt 1 $$ график второй функции сжимается в p раз по оси OX по сравнению с графиком первой функции.
При сравнении графиков двух функций $$ y_1=f(x),\ \ y_2=f(\frac{x}{p}),\ \ p\gt 1 $$ график второй функции растягивается в p раз по оси OX по сравнению с графиком первой функции.
Эти принципы справедливы и для тригонометрических функций.
Тригонометрические функции являются периодическими: синус и косинус с периодом 2π, тангенс и котангенс – с периодом π. Получаем следствие общих принципов:
При сравнении двух тригонометрических функций $$ y_1=f(x),\ \ y_2=f(px),\ \ p\gt 1 $$ период второй функции уменьшается в p раз: $$ T_2=\frac{T_1}{p} $$
При сравнении двух тригонометрических функций $$ y_1=f(x),\ \ y_2=f(\frac{x}{p}),\ \ p\gt 1 $$ период второй функции увеличивается в p раз: $$ T_2=pT_1 $$
Например:
Построим в одной системе координат три графика: $$ f(x)=sinx,\ \ g(x)=sin2x,\ \ h(x)=sin\frac{x}{2} $$
Период колебаний функции \(g(x)=sin2x\) в 2 раза меньше: \(T_g=\frac{2\pi}{2}=\pi\).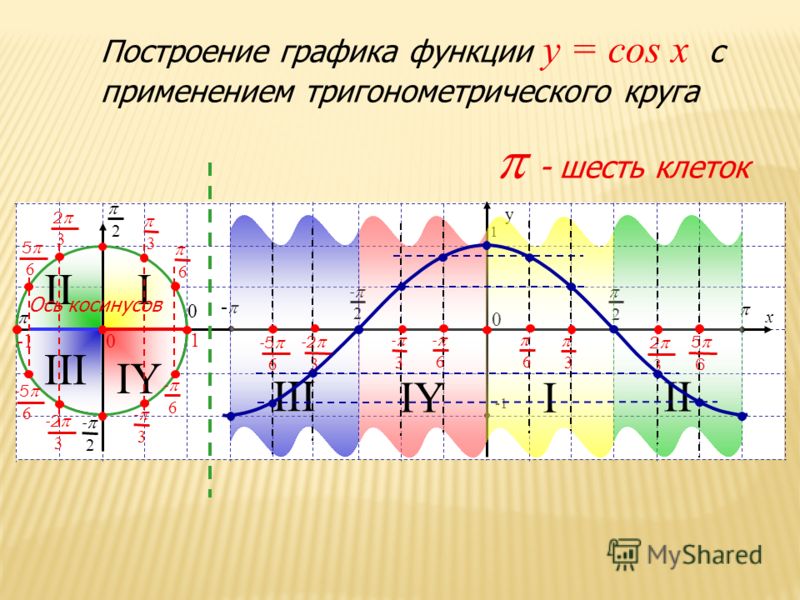
Период колебаний функции \(h(x)=sin\frac{x}{2}\) в 2 раза больше: \(T_h=2\cdot 2\pi=4\pi\).
п.2. Растяжение и сжатие графиков тригонометрических функций по оси
OYОбщие принципы растяжения и сжатия графиков по оси OY:
При сравнении графиков двух функций $$ y_1=f(x),\ \ y_2=Af(x),\ \ A\gt 1 $$ график второй функции растягивается в
Общий принцип сжатия графиков:
При сравнении графиков двух функций $$ y_1=f(x),\ \ y_2=\frac{1}{A}f(x),\ \ A\gt 1 $$ график второй функции сжимается в A раз по оси OY по сравнению с графиком первой функции.
Эти принципы справедливы и для тригонометрических функций.
Т.к. для графиков синуса и косинуса (синусоиды) характерна амплитуда колебаний, то также говорят, что:
- умножение на параметр \(A\gt 1\) увеличивает амплитуду колебаний в \(A\) раз;
- деление на параметр \(A\gt 1\) уменьшает амплитуду колебаний в \(A\) раз.
Например:
1) Построим в одной системе координат три графика: $$ f(x)=cosx,\ \ g(x)=2cosx,\ \ h(x)=\frac{1}{2}cosx $$
Область значений функции \(g(x)=2cosx:\ y\in[-2;2]\). График растягивается по оси OY.
Деление на \(A=2\) уменьшает амплитуду колебаний в 2 раза. Область значений функции \(h(x)=\frac12 cosx:\ y\in\left[-\frac12; \frac12\right]\). График сжимается по оси OY.
2) Теперь построим $$ f(x)=tgx,\ \ g(x)=2tgx,\ \ h(x)=\frac{1}{2}tgx $$
В этом случае хорошей иллюстрацией растяжения по оси OY при умножении и сжатия по оси OY при делении на \(A=2\) служит поведение функции при \(x=\frac\pi4\). $$ f\left(\frac\pi4\right)=tg\left(\frac\pi4\right)=1,\ \ g\left(\frac\pi4\right)=2tg\left(\frac\pi4\right)=2,\ \ h\left(\frac\pi4\right)=\frac12 tg\left(\frac\pi4\right)=\frac12 $$ Аналогично – для любого другого значения аргумента x.
п.3. Параллельный перенос графиков тригонометрических функций по оси
OXОбщие принципы переноса по оси OX:
При сравнении графиков двух функций $$ y_1=f(x),\ \ y_2=f(x+a),\ \ a\gt 0 $$ график второй функции смещается влево на a по оси OX по сравнению с графиком первой функции.
При сравнении графиков двух функций $$ y_1=f(x),\ \ y_2=f(x-a),\ \ a\gt 0 $$ график второй функции смещается вправо на a по оси OX по сравнению с графиком первой функции.
Эти принципы справедливы и для тригонометрических функций.
При этом параметр x называют начальной фазой колебаний.
При сравнении двух тригонометрических функций \(y_1=f(x)\) и \(y_2=f(x\pm a)\) говорят, что у второй функции сдвиг по фазе равен \(\pm a\).
Например:
1) Построим в одной системе координат три графика: $$ f(x)=sinx,\ \ g(x)=sin\left(x+\frac\pi4\right),\ \ h(x)=sin\left(x-\frac\pi4\right) $$
Функция \(g(x)=sin\left(x+\frac\pi4\right)\) сдвинута на \(\frac\pi4\) влево по сравнению с \(f(x)\)
Функция \(h(x)=sin\left(x-\frac\pi4\right)\) сдвинута на \(\frac\pi4\) вправо по сравнению с \(f(x)\)
п.
4. Параллельный перенос графиков тригонометрических функций по оси OYОбщие принципы переноса по оси OY:
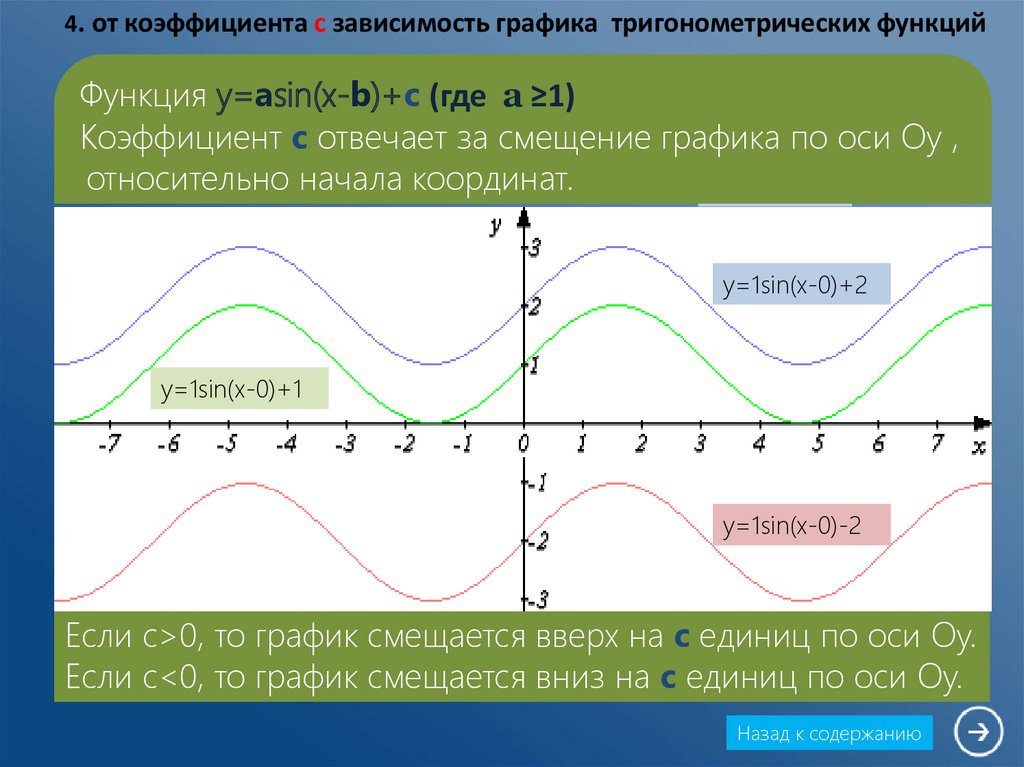
При сравнении графиков двух функций $$ y_1=f(x),\ \ y_2=f(x)+a,\ \ a\gt 0 $$ график второй функции смещается вверх на a по оси OY по сравнению с графиком первой функции.
При сравнении графиков двух функций $$ y_1=f(x),\ \ y_2=f(x)-a,\ \ a\gt 0 $$ график второй функции смещается вниз на a по оси OY по сравнению с графиком первой функции.
Эти принципы справедливы и для тригонометрических функций.
Например:
1) Построим в одной системе координат три графика: $$ f(x)=sinx,\ \ g(x)=sinx+1,\ \ h(x)=sinx-1 $$
Функция \(g(x)=sinx+1\) сдвинута на 1 вверх по сравнению c \(f(x)\)
Функция \(h(x)=sinx-1\) сдвинута на 1 вниз по сравнению с \(f(x)\)
п.5. Общее уравнение синусоиды
Синусоида – плоская кривая, которая задается в прямоугольной системе координат уравнением: $$ y(x)=Asin(cx+d)+B $$ где
B – вертикальный сдвиг, характеризует сдвиг графика по оси OY (вверх/вниз)
c — циклическая частота, характеризует период колебаний и растяжение графика по оси OX
d- начальная фаза, характеризует сдвиг графика по оси OX(влево/вправо)
График \(y(x)=Acos(cx+d)+B\) также называют синусоидой.
Термин «косинусоида» употребляется относительно редко.
Поскольку график косинуса получается из графика синуса сдвигом по фазе на π/2 влево, вводить термин «косинусоида» излишне.
Например:
Построим график \(g(x)=3sin\left(2x+\frac\pi2\right)-1\)
По сравнению с \(f(x)=sinx\):
- \(A=3\) — график растянут по оси OY в 3 раза
- \(c=2\) — период меньше в 2 раза T=π, график сжат в 2 раза по оси OX
- \(d=\frac\pi2\) – начальная фаза положительная, график сдвинут на \(\frac{\pi}{2\cdot 2}=\frac\pi4\) влево
- \(B=-1\) — график сдвинут по оси OY на 1 вниз
п.6. Общее уравнение тангенцоиды
Tангенцоидa – плоская кривая, которая задается в прямоугольной системе координат уравнением: $$ y(x)=Atg(cx+d)+B $$ где
A — амплитуда, характеризует растяжение графика по оси OY
B – вертикальный сдвиг, характеризует сдвиг графика по оси OY (вверх/вниз)
c — циклическая частота, характеризует период колебаний и растяжение графика по оси OX
d- начальная фаза, характеризует сдвиг графика по оси OX(влево/вправо)
График \(y(x)=Actg(cx+d)+B\) также называют тангенцоидой.
Например:
Построим график \(g(x)=\frac12 tg\left(\frac{x}{2}-\frac\pi3\right)+1\)
По сравнению с \(f(x)=tgx\):
- \(A=\frac12\) — график сжат по оси OY в 2 раза
- \(c=\frac12\) — период больше в 2 раза T=2π, расстояние между асимптотами 2π, график растянут в 2 раза по оси OX
- \(d=-\frac\pi3\) – начальная фаза отрицательная, график сдвинут на \(\frac{\pi}{3\cdot 1/2}=\frac{2\pi}{4}\) вправо
- \(B=1\) — график сдвинут по оси OY на 1 вверх
п.7. Примеры
Пример 1.Постройте в одной системе координат графики: $$ f(x)=sinx,\ \ g(x)=-sinx,\ \ h(x)=cosx $$ Найдите сдвиг по фазе для \(g(x)\) и \(h(x)\) в сравнении с \(f(x)\).
Сдвиг по фазе удобно определять по главной арке синусоиды.
Для \(f(x)=sinx\) главная арка определена на отрезке \(0\leq x\leq \pi\)
Для \(g(x)=-sinx\) главная арка определена на отрезке \(-\pi\leq x\leq 0\), т.е. сдвинута на π влево от \(f(x)\).
Это означает, что: $$ f(x)=g(x+\pi),\ \ sinx=-sin(x+\pi) $$ Для \(h(x)=cosx\) главная арка определена на отрезке \(-\frac\pi2\leq x\leq \frac\pi2\), т.е. сдвинута на \(\frac\pi2\) влево от \(f(x)\). Это означает, что: $$ f(x)=h\left(x+\frac\pi2\right),\ \ sinx=cos\left(x+\frac\pi2\right) $$
Пример 2. Найдите наименьшие положительные периоды функций:
a) \(y=sin5x\)
Период синуса \(2\pi\) уменьшается в 5 раз. Получаем: \(T=\frac{2\pi}{5}\)
б) \(y=cos\pi x\)
Период косинуса \(2\pi\) уменьшается в \(\pi\) раз. Получаем: \(T=\frac{2\pi}{\pi}=2\)
в) \(y=tg\frac{x}{4}\)
Период тангенса \(\pi\) увеличивается в 4 раза. Получаем: \(T=4\pi\)
г) \(y=tg\left(2x+\frac{\pi}{3}\right)\)
Период тангенса \(\pi\) уменьшается в 2 раза. Получаем: \(T=\frac\pi2\)
Пример 3. Используя правила преобразования графиков функций, постройте график $$ f(x)=2ctg\left(3x+\frac\pi6\right) $$ По сравнению с \(g(x)=tgx\):
- \(A=2\) — график растянут по оси OY в 2 раза
- \(c=3\) — период меньше в 3 раза \(T=\frac\pi3\), расстояние между асимптотами \(\frac\pi3\), график сжат в 3 раза по оси OX
- \(d=-\frac\pi6\) – начальная фаза положительная, график сдвинут на \(\frac{\pi}{6\cdot 3}=\frac{\pi}{18}\) влево
Расположение нулей: $$ tg\left(3x+\frac\pi6\right)=0\Rightarrow 3x+\frac\pi6=\pi k\Rightarrow 3x=-\frac\pi6+\pi k\Rightarrow x =-\frac{\pi}{18}+\frac{\pi k}{3} $$ Вертикального сдвига нет, нули расположены на оси OX.
Расположение асимптот: $$ 3x+\frac\pi6\ne\frac\pi2+\pi k\Rightarrow 3x\ne\frac\pi3+\pi k\Rightarrow x\ne\frac\pi9+\frac{\pi k}{3} $$ Пересечение главной ветви с осью OY: \(x=0,\ y=2tg\frac\pi6=\frac{2}{\sqrt{3}}\)
С учетом периода \(\frac\pi3\) получаем семейство дополнительных точек для построения графика \(\left(\frac{\pi k}{3}; \frac{2}{\sqrt{3}}\right)\).
Пример 4. Определите графически, сколько корней имеет уравнение на отрезке: a) \(sinx=sin2x\) при \(0\leq x\leq 3\pi\)
Ответ: 7 корней
б) \(cos\frac{x}{2}=cos2x\) при \(-2\pi\leq x\leq 2\pi\)
Ответ: 7 корней
Графики функций синуса и косинуса Видеоруководство и практика
Начните печатать, затем используйте стрелки вверх и вниз, чтобы выбрать вариант из списка.
Этот курс охватывает такие темы, как тригонометрические функции (с графиками и обратными функциями), тождества и уравнения, решения треугольников, комплексные числа и многое другое.
Графики функций синуса и косинуса
Понимание графика y = sin x
ВИДЕО
Предыдущие видео для
Следующие видеоролики для
Графики функций синуса и косинуса
Вариации графиков Y = SIN X
видео
Предыдущие видео для
.
функций синуса и косинуса
Понимание графика y = cos x
ВИДЕО
Предыдущее видео для
Следующее видео для
Графики функций синуса и косинуса
Вариации графиков Y = COS x
Видео
Предыдущие видео для
Следующие видео для
Графики Sine и Cosine Functions
USITIC Кривые синусов и косинусов
ВИДЕО
Предыдущие видео для
Следующие видео для
Графики функций синуса и косинуса
Постройте график суммы двух тригонометрических функций.
Видео
Предыдущие видео для
Следующие видео для
Графики синусов и косинус
Модель периодического поведения
видео
Предыдущие видео для
.
Понять график y = tan x
ВИДЕО
Предыдущие видео для
Следующие видео для
Графики других тригонометрических функций
Вариации графика Y = TAN x
видео
Предыдущие видео для
Следующие видео для
Графики других тригонометрических функций
Понятные графики
.
= кроватка x
ВИДЕО
Предыдущие видео для
Следующие видео для
Графики других тригонометрических функций
Вариации графика Y = COT x
Видео
Предыдущие видео для
Следующие видео для
Графики других тригонометрических функций
Понимают графики Y = CSC x и и и и и и и и и и и и и и и и и и и 11111111111111 годы и и и 2
. y = sec x
ВИДЕО
Предыдущие видео для
Следующие видео для
Графики других тригонометрических функций
Графики вариантов Y = CSC X и Y = SEC x
Видео
Предыдущие видео для
Следующие видео для
.
Предыдущие видео для
Следующие видео для
Обратные тригонометрические функции
Понимание и использование функции обратного косинуса
ВИДЕО
Предыдущие видео для
Следующие видео для
Обратные тригонометрические функции
Понимание и используйте обратную касательную функцию
Видео
Предыдущие видео для
Следующие видео для
Внедренные тригонометрические функции.
для вычисления обратных тригонометрических функций
ВИДЕО
Предыдущие видео для
Следующие видео для
Обратные тригонометрические функции
Найти точные значения композитных функций с обратными тригонометрическими функциями
видео
Предыдущие видео для
Следующие видео для
Приложения тригонометрических функций
Решайте правый треугольник
Videos
Предыдущие видео
. Следующие видео для
Применение тригонометрических функций
Решение задач с подшипниками
ВИДЕО
Предыдущие видео для
Следующие видео для
Приложения тригонометрических функций
Модель простого гармонического движения
видео
Предыдущие видео для
вход для
. и функции секанса
ВИДЕО
Предыдущие видео для
Следующие видео для
Графики тригонометрических функций: Примеры | StudySmarter
Безусловно, лучший способ понять поведение тригонометрических функций — создать визуальное представление их графиков на координатной плоскости.
Это помогает нам определить их ключевые особенности и проанализировать влияние этих функций на внешний вид каждого графика. Однако знаете ли вы, какие шаги нужно выполнить, чтобы построить график тригонометрических функций и их обратных функций? Если ваш ответ отрицательный, не беспокойтесь, мы проведем вас через весь процесс.
В этой статье мы определим, что такое графики тригонометрических функций, обсудим их ключевые особенности и покажем вам, как строить графики тригонометрических функций и их обратных функций на практических примерах.
Графики тригонометрических функций представляют собой графическое представление функций или отношений, определенных на основе сторон и углов прямоугольного треугольника. К ним относятся функции синуса (sin), косинуса (cos), тангенса (tan) и соответствующих им обратных функций косеканса (csc), секанса (sec) и котангенса (cot).
Каковы ключевые особенности графиков тригонометрических функций?
Прежде чем перейти к построению графика тригонометрических функций, нам необходимо определить некоторые ключевые особенности о них:
Амплитуда
Амплитуда тригонометрических функций относится к коэффициенту вертикального растяжения , который можно рассчитать как абсолютное значение половины разницы между его максимальным значением и его минимальным значением.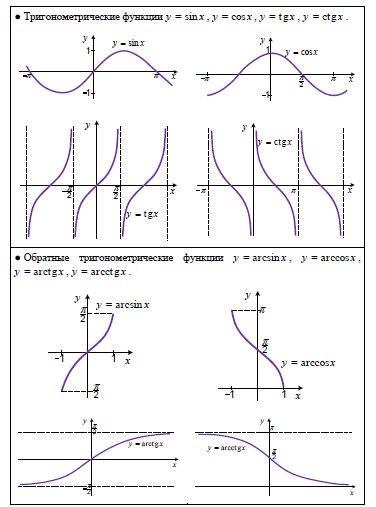
Амплитуда функций и .
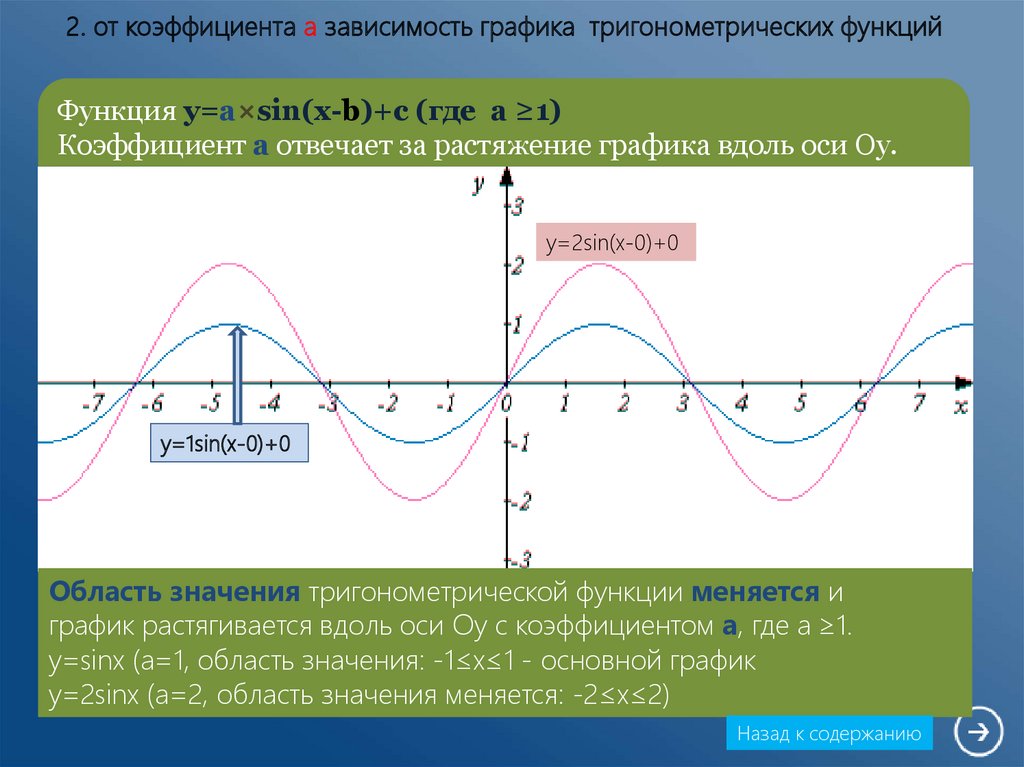
Для функций вида , или , амплитуда равна абсолютному значению a.
Если у вас есть тригонометрическая функция , то амплитуда функции равна 2.
Касательные функции график не имеет амплитуды , так как он не имеет минимального или максимального значения.
Период
Период тригонометрических функций представляет собой расстояние по оси X от начала узора до точки, где он начинается снова.
Период синуса и косинуса равен 2π или 360º.
Для функций в форме , или , b известен как коэффициент горизонтального растяжения , и вы можете рассчитать период следующим образом:
Для функций в форме период рассчитывается следующим образом:
Найдите период следующих тригонометрических функций:
Домен и диапазон
Число domain and range of the main trigonometric functions are as follows:
| Trigonometric function | Domain | Range | |||||||||||||||||||||||||||||||||||||
| Sine | All real numbers | ||||||||||||||||||||||||||||||||||||||
| Cosine | All real numbers | ||||||||||||||||||||||||||||||||||||||
| Тангенс | Все действительные числа, кроме | Все действительные числа | |||||||||||||||||||||||||||||||||||||
| Косеканс | Все действительные числа, кроме | ||||||||||||||||||||||||||||||||||||||
| Secant | Все реальные цифры, кроме | ||||||||||||||||||||||||||||||||||||||
| Cotangent | All Real Number, кроме | All Relate | . потому что их значения повторяются снова и снова после определенного периода.Как построить график тригонометрических функций?Чтобы построить график тригонометрических функций, выполните следующие действия:
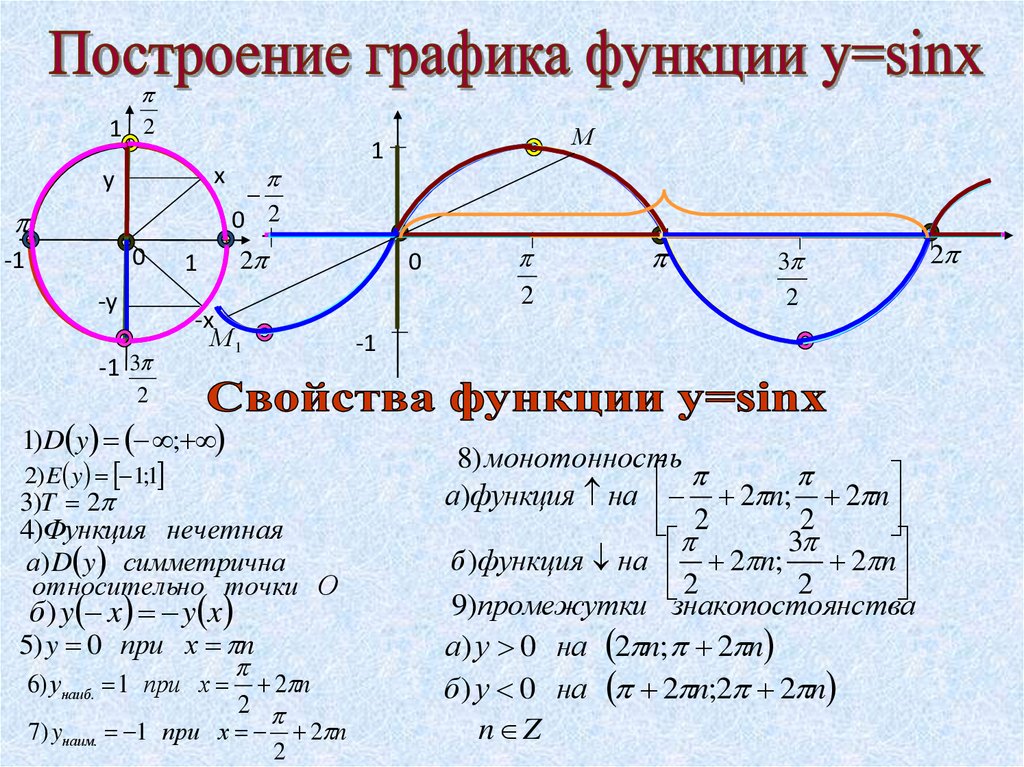
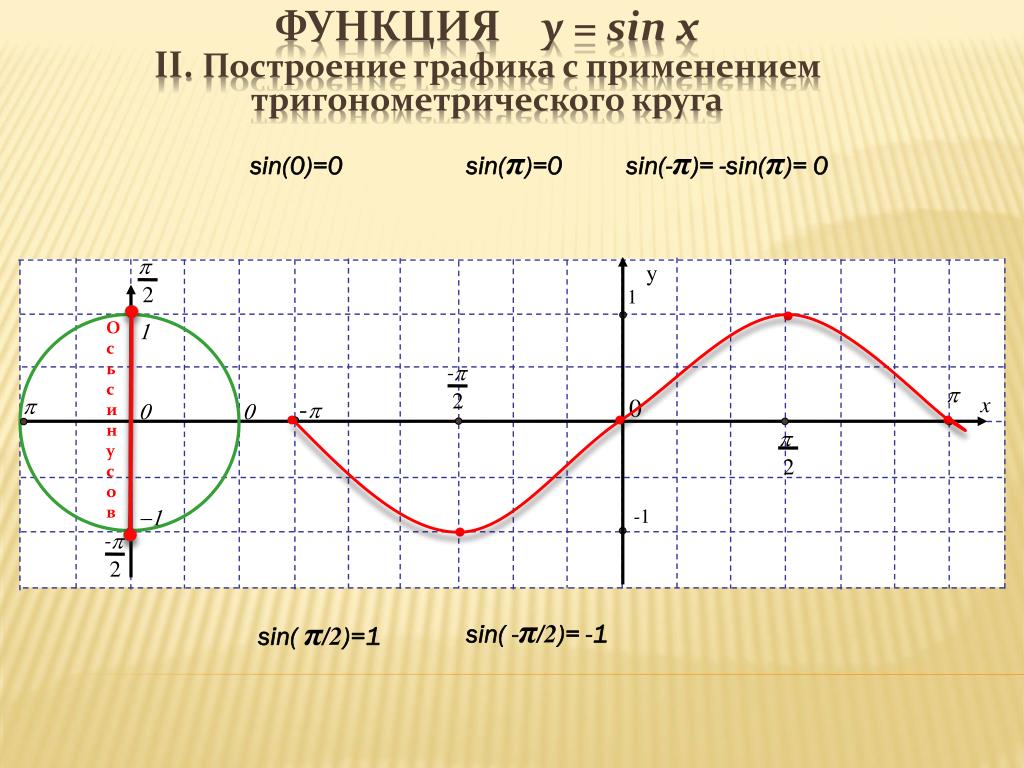
Единичную окружность можно использовать для вычисления значений синуса и косинуса для наиболее часто используемых углов. Пожалуйста, прочитайте о тригонометрических функциях, если вам нужно вспомнить, как это сделать. График синусовСинус представляет собой отношение длины противоположной стороны прямоугольного треугольника к длине гипотенузы. График функции синуса выглядит следующим образом: График синуса, Марилу Гарсия Де Тейлор — StudySmarter Originals На этом графике мы можем наблюдать ключевые особенности функции синуса :
Graph the trigonometric function
Пример графика синуса, Марилу Гарсия Де Тейлор — StudySmarter Originals График косинуса Косинус — это отношение длины прилежащей стороны прямоугольного треугольника к длине гипотенузы. График функции косинуса выглядит точно так же, как график синуса, за исключением того, что он сдвинут влево на π/2 радиана, как показано ниже. График косинуса, Марилу Гарсия Де Тейлор — StudySmarter Originals5 График повторяется каждые 2π радиан или 360°. Минимальное значение косинуса равно -1. Максимальное значение косинуса равно 1. Это означает, что амплитуда графика равна 1, а его период равен 2π (или 360°). График пересекает ось x в точке π/2 и через каждые π радиан до и после этого. Функция косинуса достигает своего максимального значения в 0 и каждые 2π до и после этого. Функция косинуса достигает минимального значения в точке π и каждые 2π до и после этого. Graph the trigonometric function
Пример графика косинуса, Марилу Гарсия Де Тейлор — StudySmarter Originals Диаграмма касательной Тангенс представляет собой отношение длины противоположной стороны прямоугольного треугольника к длине соседней стороны. График функции тангенса, однако, выглядит немного иначе, чем функции косинуса и синуса. Это не волна, а прерывистая функция с асимптотами: Диаграмма тангенса, Марилу Гарсиа Де Тейлор — StudySmarter Originals Наблюдая за этим графиком, мы можем определить ключевые особенности функции тангенса :
ТАНГАНСТВА УГОЛОГО КОГИТЕЛЯ также можно найти с помощью этой формулы: График Тригонометрическая функция
Касательные функции не имеют амплитуды .
Пример касательного графика, Марилу Гарсия Де Тейлор — StudySmarter Originals Какие графики обратных тригонометрических функций?Каждая тригонометрическая функция имеет соответствующую обратную функцию:
Для построения графика обратных тригонометрических функций можно действовать следующим образом: График косекансаГрафик функции косеканса можно получить следующим образом:
График косеканса, Марилу Гарсия Де Тейлор — StudySmarter Originals График функции косеканса имеет тот же период, что и график синуса, т.е. 2π или 360°, и не имеет амплитуды. График Обратной тригонометрической функции
График секущей, Марилу Гарсия Де Тейлор — StudySmarter Originals График функции секущей имеет тот же период, что и график функции косинуса, то есть 2π или 360°, и также не имеет амплитуды. График Обратной тригонометрической функции
График котангенса, Марилу Гарсия Де Тейлор — StudySmarter Originals Период графика котангенса такой же, как и период графика касательной, π радиан или 180°, и он также не имеет амплитуды. График обратной тригонометрической функции
Пример графика котангенса, Марилу Гарсиа Де Тейлор — StudySmarter Originals Каковы графики тригонометрических функций в стихах? Обратные тригонометрические функции относятся к функциям арксинуса, арккосинуса и арктангенса, которые также могут быть записаны как и . Помните, что обратная функция получается путем замены x и y , то есть x становится y и y становится х . Инверсия , и вы можете увидеть ее график ниже: Инверсия графика синуса, Марилу Гарсиа Де Тейлор — StudySmarter Originals их домен . В противном случае обратные функции не являются функциями, поскольку они не проходят тест вертикальной линии. Значения в ограниченных областях тригонометрических функций известны как главных значений , and to identify that these functions have a restricted domain, we use capital letters:
График арксинуса Арксинус Инверсия определяется как или . График арксинуса, Marilu García De Taylor — StudySmarter Originals График арккосинусаАрккосинус является обратной функцией косинуса. Инверсия определяется как или . Домен функции арккосинуса также будет состоять из всех действительных чисел от -1 до 1, а его диапазон — набор мер угла от . График функции арккосинуса показан ниже: График арккосинуса, Марилу Гарсия Де Тейлор — StudySmarter Originals График арктангенса Арктангенс является обратной функцией тангенса. Инверсия определяется как или . Область функции арктангенса будет состоять из действительных чисел, а ее диапазон представляет собой набор мер угла между . Диаграмма арктангенса, Марилу Гарсия Де Тейлор — StudySmarter Originals Если изобразить все обратные функции вместе, они будут выглядеть следующим образом: в статье «Обратные тригонометрические функции», чтобы узнать больше об этой теме. Графики тригонометрических функций. Ключевые выводы
|
Эти функции противоположны функциям синуса, косинуса и тангенса, что означает, что они возвращают угол, когда мы подставляем в них значение sin, cos или tan.
домен функции арксинуса будет состоять из всех действительных чисел от -1 до 1, а его диапазон представляет собой набор мер угла от . График функции арксинуса выглядит следующим образом:
График арктангенса выглядит так: