График функции у sin2x: Решить y=-sin2x | Microsoft Math Solver

Постройте график функции y=sin2x-1 — Знания.site

Последние вопросы

• Литература

  1 минута назад

  Судьба Вани после плена

• Русский язык

  1 минута назад

  Что делать, помогите пжпж

• Физика

  1 минута назад

  Пожалуйста помогите!!! Физика!!!

• Литература

  1 минута назад

  Добрий день, діти, сьогодні останній ривок — *скласти письмовий твір характеристику з використанням цитат* І варіант — Павлуші ІІ варіант — Яви Обсяг — *12- 20 речень, 2-3 цитати* Пам‘ятайте: списане з інтернету оцінюю в 3 б ( за труд переписування) СРОЧНО ДАЮ 40 БАЛІВ

• Физика

  1 минута назад

  ВМЕСТЕ С «ДАНО», ДАЮ 80 баллов 3) Тело плавает в глицерине так, что его погруженная часть составляет 60% от общего объема тела. Найдите плотность тела, если плотность глицерина составляет 1250 кг/м3. Ответ укажите в кг/м3.

• Химия

  1 минута назад

  де в природі трапляються натрій карбонат,кальцій карбонат ,кальцій сульфатСРОЧНОО​

• Математика

  1 минута назад

  Розкрийте дужки і знайдіть значення виразу: -(41-7,8)+(71-12,8)

• Математика

  1 минута назад

  12у – бу, при у = 6​

• Геометрия

  1 минута назад

  Угол между высотой прямоугольного треугольника, опущенной на гипотезу, и одним из катетов равен 30°. Этот катет равен 8см. Найдите гипотенузу​

• Українська мова

  1 минута назад

  3 Перепиши речення в робочий зошит. Постав пропущені розділові знаки. 1. Як то гарно любі діти у вікно вам виглядати! В ньому все тополі квіти сонце й поле біля хати (В. Терен). 2. Степ і лиман озеро усе закуталось у якийсь чарівний світ. Жито пшениця овес усе разом море й присохло. Усе злилось і змішалось докупи і земля і море приспіло (за 1. Нечуєм-Левицьким).​

• Физика

  1 минута назад

  Знать силу струму в колі при напрузі 6кВі опору ділянки кола 0,4к0м. (2 балла)

• География

  1 минута назад

  2. Головна річка з усіма притоками утворює ..​

• Химия

  1 минута назад

  выберите элемент который при взаимодействии с кислородом образует кислотный оксид стронций фосфор кальций магний

• Математика

  6 минут назад

  Золотой ключик 2023

• История

  6 минут назад

  Укажіть характерні риси розвитку Римської республіки в ІІ ст. до н. е.​

Все предметы

Выберите язык и регион

English

United States

Polski

Polska

Português

Brasil

English

India

Türkçe

Türkiye

English

Philippines

Español

España

Bahasa Indonesia

Indonesia

Русский

Россия

How much to ban the user?

1 hour 1 day 100 years

Графік sin 2x.

2/16 \u003d 1)

Можливість зберігати графіки і отримувати на них посилання, яка стає доступною для всіх в інтернеті

Управління масштабом, кольором ліній

Можливість побудови графіків по точках, використання констант

Побудова одночасно декількох графіків функцій

Побудова графіків в полярній системі координат (використовуйте r і θ (\\ theta))

З нами легко в режимі онлайн будувати графіки різної складності. Побудова проводиться миттєво. Сервіс затребуваний для знаходження точок перетину функцій, для зображення графіків для подальшого їх переміщення в Word документ в якості ілюстрацій при вирішенні завдань, для аналізу поведінкових особливостей графіків функцій. Оптимальним браузером для роботи з графіками на даній сторінці сайту є Google Chrome. При використанні інших браузерів коректність роботи не гарантовано.

Додаткові матеріали
Шановні користувачі, не забувайте залишати свої коментарі, відгуки, побажання! Всі матеріали перевірені антивірусною програмою.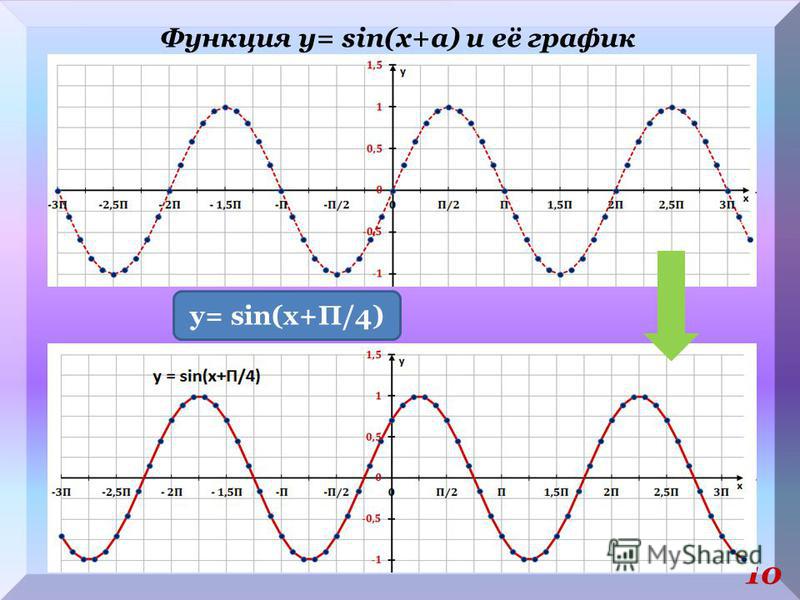

Посібники і тренажери в інтернет-магазині «Інтеграл» для 10 класу від 1С
Вирішуємо завдання з геометрії. Інтерактивні завдання на побудову для 7-10 класів
Програмне середовище «1С: Математичний конструктор 6.1»

Що будемо вивчати:

• Властивості функції Y \u003d sin (X).
• Графік функції.
• Як будувати графік і його масштаб.
• Приклади.

Властивості синуса. Y \u003d sin (X)

Хлопці, ми вже познайомилися з тригонометричними функціями числового аргументу. Ви пам’ятаєте їх?

Давайте познайомимося ближче з функцією Y \u003d sin (X)

Запишемо деякі властивості цієї функції:
1) Область визначення — множина дійсних чисел.
2) Функція непарна. Давайте згадаємо визначення непарної функції. Функція називається непарною якщо виконується рівність: y (-x) \u003d — y (x). Як ми пам’ятаємо з формул привиди: sin (-x) \u003d — sin (x). Визначення виповнилося, значить Y \u003d sin (X) — непарна функція.
3) Функція Y \u003d sin (X) зростає на відрізку і убуває на відрізку [π / 2; π].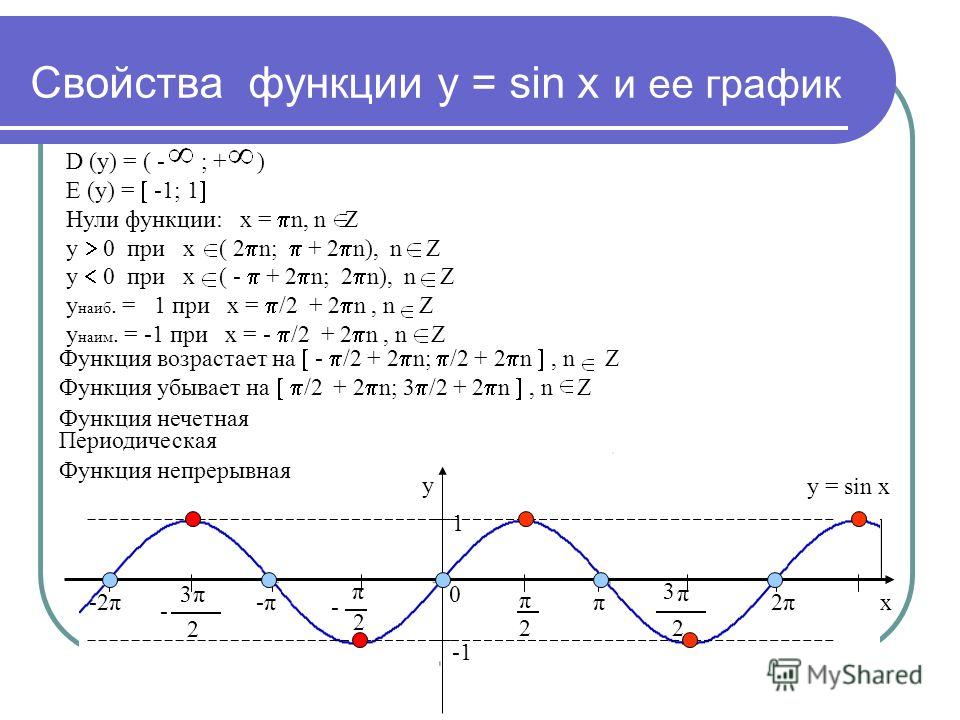 Коли ми рухаємося по першій чверті (проти годинникової стрілки), ордината збільшується, а при русі по другій чверті вона зменшується.

4) Функція Y \u003d sin (X) обмежена знизу і зверху. Дана властивість випливає з того, що
-1 ≤ sin (X) ≤ 1
5) Найменше значення функції дорівнює -1 (при х \u003d — π / 2 + πk). Найбільше значення функції дорівнює 1 (при х \u003d π / 2 + πk).

Давайте, скориставшись властивостями 1-5, побудуємо графік функції Y \u003d sin (X). Будемо будувати наш графік послідовно, застосовуючи наші властивості. Почнемо будувати графік на відрізку.

Особливу увагу варто звернути на масштаб. На осі ординат зручніше прийняти одиничний інтервал рівний 2 клітинам, а на осі абсцис — одиничний інтервал (дві клітинки) прийняти рівним π / 3 (дивіться малюнок).

Побудова графіка функції синус х, y \u003d sin (x)

Порахуємо значення функції на нашому відрізку:

Побудуємо графік по нашим точкам, з урахуванням третього властивості.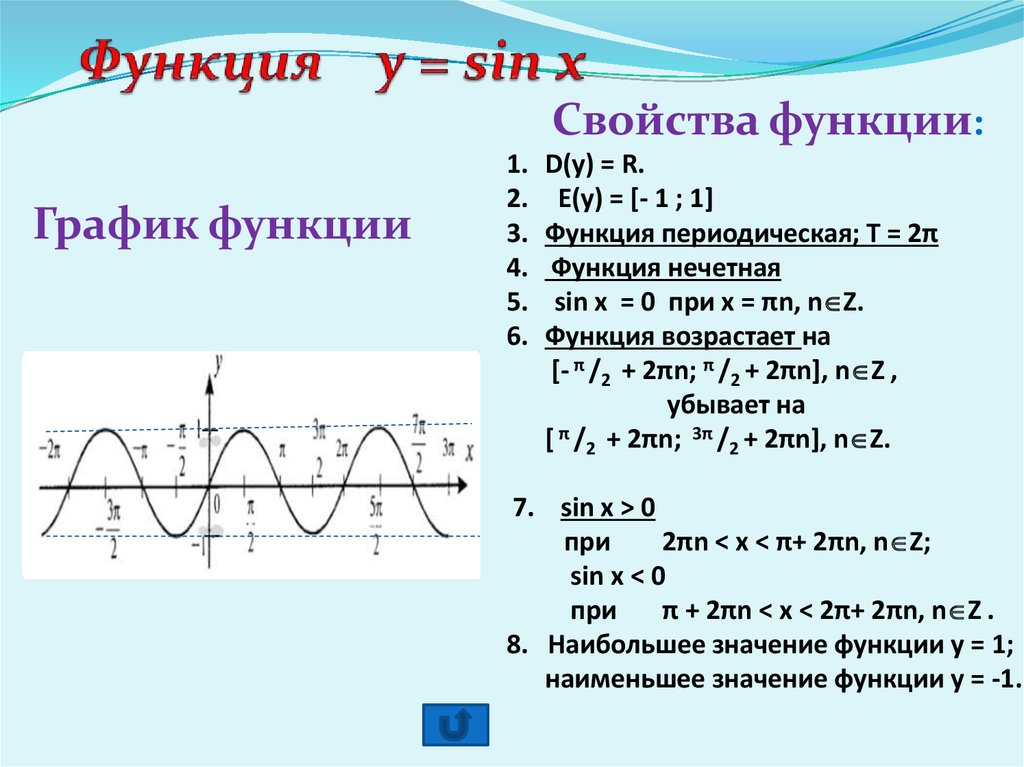

Таблиця перетворень для формул привиди

Скористаємося другою властивістю, яке говорить, що наша функція непарна, а це значить, що її можна відобразити симетрично відносно початок координат:

Ми знаємо, що sin (x + 2π) \u003d sin (x). Це означає, що на відрізку [- π; π] графік виглядає так само, як на відрізку [π; 3π] або або [-3π; — π] і так далі. Нам залишається акуратно перемалювати графік на попередньому малюнку на всю вісь абсцис.

Графік функції Y \u003d sin (X) називають — синусоїдою.

Напишемо ще кілька властивостей згідно побудованому графіку:
6) Функція Y \u003d sin (X) зростає на будь-якому відрізку виду: [- π / 2 + 2πk; π / 2 + 2πk], k — ціле число і убуває на будь-якому відрізку виду: [π / 2 + 2πk; 3π / 2 + 2πk], k — ціле число.
7) Функція Y \u003d sin (X) — безперервна функція. Подивимося на графік функції і переконаємося що у нашої функції немає розривів, це і означає безперервність.
8) Область значень: відрізок [- 1; 1].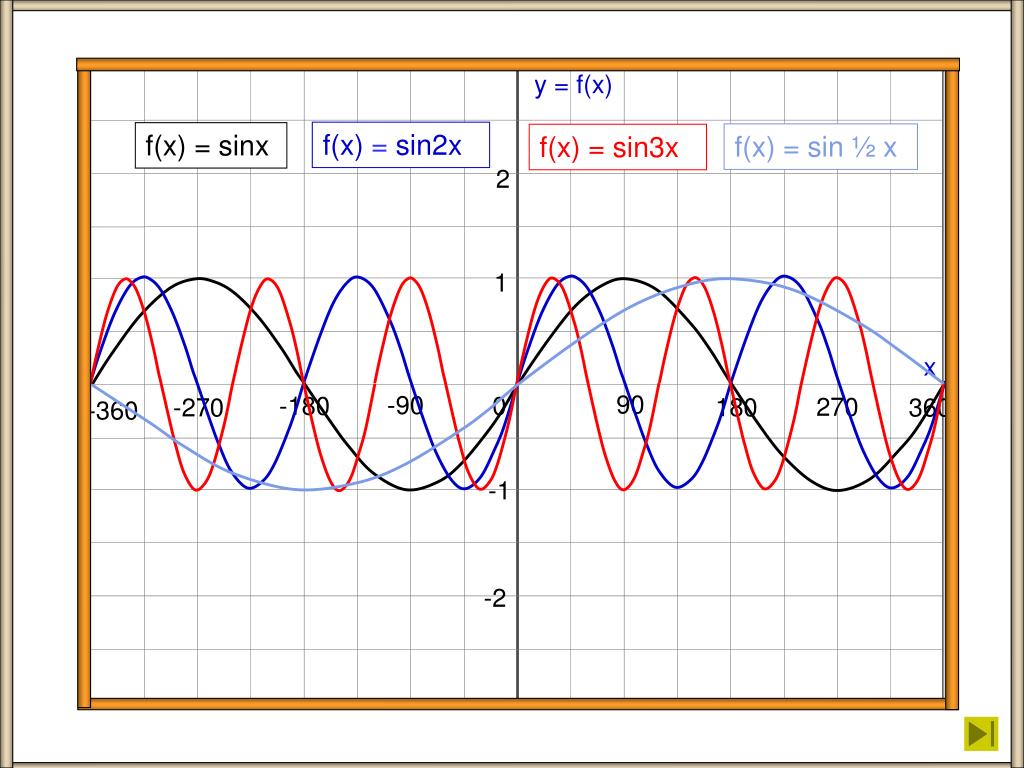 Це також добре видно з графіка функції.
9) Функція Y \u003d sin (X) — періодична функція. Подивимося знову на графік і побачимо, що функція приймає одні і ті ж значення, через деякі проміжки.

Приклади завдань з синусом

1. Вирішити рівняння sin (x) \u003d x-π

Рішення: Побудуємо 2 графіка функції: y \u003d sin (x) і y \u003d x-π (див. Малюнок).
Наші графіки перетинаються в одній точці А (π; 0), це і є відповідь: x \u003d π

2. Побудувати графік функції y \u003d sin (π / 6 + x) -1

Рішення: Бажаємий графік вийде шляхом перенесення графіка функції y \u003d sin (x) на π / 6 одиниць вліво і 1 одиницю вниз.

Рішення: Побудуємо графік функції і розглянемо наш відрізок [π / 2; 5π / 4].
На графіку функції видно, що найбільші і найменші значення досягаються на кінцях відрізка, в точках π / 2 і 5π / 4 відповідно.
Відповідь: sin (π / 2) \u003d 1 — найбільше значення, sin (5π / 4) \u003d найменше значення.

Завдання на синус для самостійного рішення

• Розв’яжіть рівняння: sin (x) \u003d x + 3π, sin (x) \u003d x-5π
• Побудувати графік функції y \u003d sin (π / 3 + x) -2
• Побудувати графік функції y \u003d sin (-2π / 3 + x) +1
• Знайти найбільше і найменше значення функції y \u003d sin (x) на відрізку
• Знайти найбільше і найменше значення функції y \u003d sin (x) на відрізку [- π / 3; 5π / 6]

«Побудова графіка функції з модулем» — Y \u003d lnx.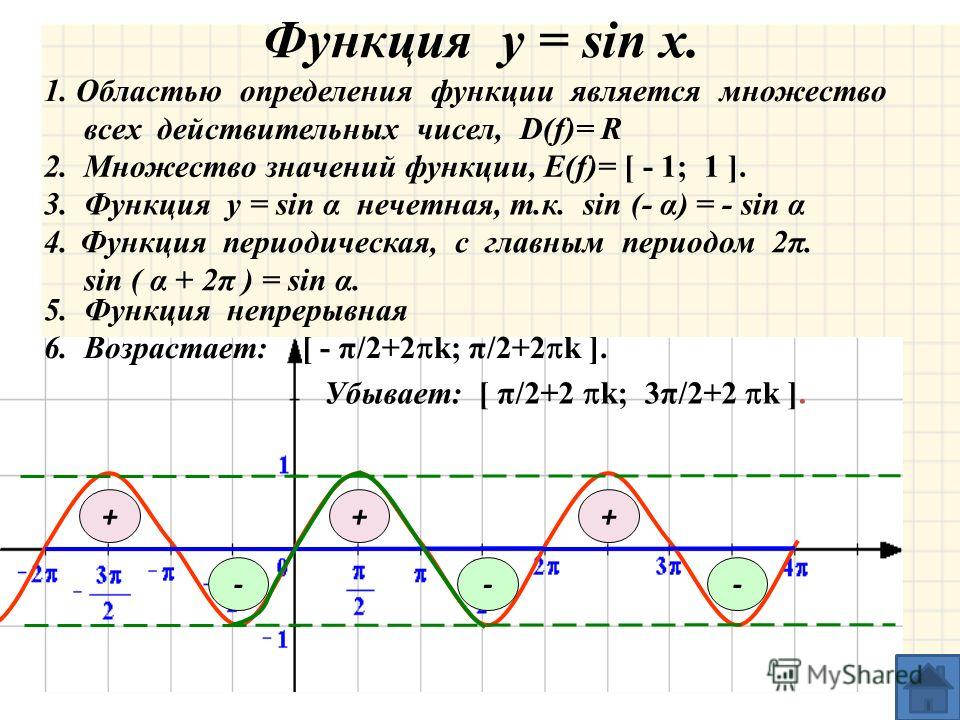 Закріпили знання на раніше вивчених функціях. Побудова графіків функцій. Питання класу. Y \u003d x2 — 2x — 3. Проектна діяльність. Урок узагальнення і систематизації знань. Графік функції. Актуалізація знань про графіки функцій. Узагальнення. Спробуйте самостійно побудувати графіки. Y \u003d f (x).

«« Графіки функцій »9 клас» — Мета уроку. Більшому значенню аргументу відповідає більше значення функції. Нулі функції. Визначення. Заповніть пропуски. Установіть відповідність між функцією і вершиною. Тренажер. Виберіть рівняння, за допомогою якого задана лінійна функція. Встановіть відповідність. Виберіть рівняння. Зворотній пропорційність.

«Графіки функцій з модулями» — Знайдемо вершину функції. Кубічна функція. Негативна сторона. Графіки функцій. Квадратична функція. Складна функція. Функція з модулем. Графіки функцій треба обов’язково вміти будувати. Підготовка до ЄДІ. Графіки функцій з модулями. Парабола. Графік функції.

«Рівняння дотичної до графіка функції» — Похідна в точці. Правила диференціювання. Графік функції. Алгоритм знаходження рівняння. Дайте відповідь на питання. Геометричний зміст похідної. Номери з підручника. Рівняння дотичної до графіка функції. Визначення. Дотична до графіка функції. Основні формули диференціювання. Провести дотичну.

«Побудова графіків функцій» — Побудова графіка функції y \u003d sinx. Лінія тангенсов. Алгебра. Тема: Побудова графіків функцій. Графік функції y \u003d sinx. Виконала: Філіппова Наталія Василівна учитель математики Белоярская середня загальноосвітня школа №1. Побудувати графік функції y \u003d sin (x) + cos (x).

«Графік оберненої пропорційності» — Застосування гіперболи. Гіпербола. Монотонність функції. Парність, непарність. Функція «Зворотній пропорційність». Графік. Побудова графіка оберненої пропорційності. Гіпербола і космічні супутники. Однополостной гіперболоїд. Асимптота. Застосування гіперболоїдів. Визначення оберненої пропорційності.

Всього в темі 25 презентацій

Як побудувати графік функції y \u003d sin x? Для початку розглянемо графік синуса на проміжку.

Одиничний інтервал беремо довжиною 2 клітинки зошити. На осі Oy відзначаємо одиницю.

Для зручності число π / 2 округляємо до 1,5 (а не до 1,6, як потрібно за правилами округлення). В цьому випадку відрізку довжиною π / 2 відповідають 3 клітинки.

На осі Ox відзначаємо непоодинокі відрізки, а відрізки довжиною π / 2 (через кожні 3 клітинки). Відповідно, відрізку довжиною π відповідає 6 клітинок, відрізку довжиною π / 6 — 1 клітинка.

При такому виборі одиничного відрізка графік, зображений на аркуші зошита в клітинку, максимально відповідає графіку функції y \u003d sin x.

Складемо таблицю значень синуса на проміжку:

Отримані точки відзначимо на координатної площині:

Так як y \u003d sin x — непарна функція, графік синуса симетричний відносно початку відліку — точки O (0; 0). З урахуванням цього факту продовжимо побудову графіка вліво, то точки -π:

Функція y \u003d sin x — періодична з періодом T \u003d 2π. Тому графік функції, взятий на на проміжку [-π; π], повторюється нескінченне число разів вправо і вліво.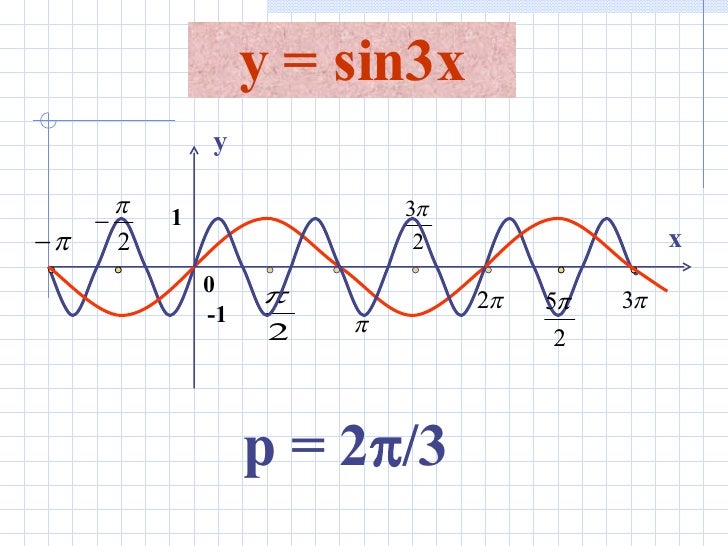

Видео с вопросами: Нахождение уравнения тригонометрической функции по графику

Стенограмма видео

На рисунке показан график функции. Какое из следующих уравнений представляет собой график? Является ли (A) 𝑦 равным греху двух 𝑥? (B) 𝑦 равно греху 𝑥 плюс два. Это (C) 𝑦 равно двум грехам 𝑥? (D) 𝑦 равно греху 𝑥 плюс два. Или (E) 𝑦 равно греху 𝑥 минус два.

Начнем с изучения графика нашей функции. У него действительно узнаваемая форма волны, которая, как мы знаем, обычно соответствует графику функций синуса и косинуса. Но, конечно, в опциях здесь нам даны только синусоидальные функции. По сути, это преобразования синусоидальных функций. Итак, давайте начнем с рисования графика 𝑦 равного греху 𝑥 на том же наборе осей и определения преобразования или преобразований, которые отображают этот график на график, который нам дали.

Мы знаем, что функция 𝑦 равна sin от 𝑥, является периодической и имеет период два 𝜋 радиана. Она достигает максимума и минимума при единице и отрицательной единице соответственно. И он проходит через ось 𝑥 в нуле, 𝜋, двух 𝜋 и так далее. Таким образом, мы можем нарисовать часть функции синуса, как показано на рисунке.

Теперь мы можем рассмотреть некоторые ключевые особенности этого графика, чтобы определить, как он отображается на графике, который нам дали. Например, давайте рассмотрим точку пересечения с 𝑦-осью. На графике 𝑦 равно sin of 𝑥, который имеет координаты ноль, ноль, тогда как на заданном нами графике имеет координаты ноль, два. Несомненно, кажется, что эта точка отображена всего на две единицы вверх одним переносом.

Но давайте проверим, взглянув на некоторые максимумы и минимумы на нашем графике. Например, на графике 𝑦 равно sin of 𝑥 мы имеем относительные максимумы в точке с координатами 𝜋 на два и один. На графике, который нам дали, это, кажется, имеет такое же 𝑥-значение, но 𝑦-значение кажется на две единицы больше. Опять же, это соответствует переводу на две единицы вверх.

Давайте просто трижды проверим это, рассмотрев один из относительных минимумов.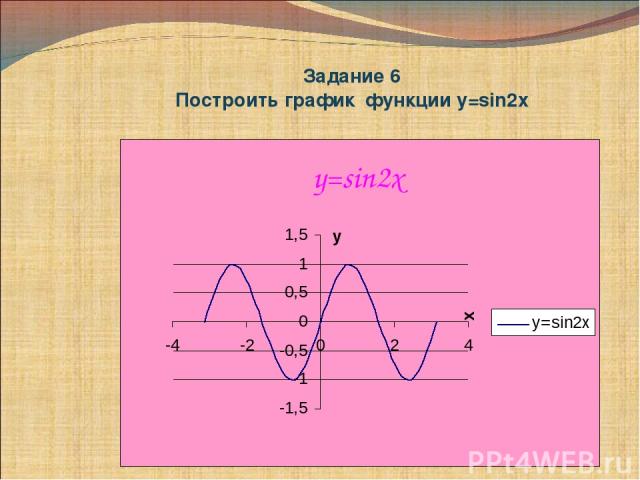 График 𝑦 равен sin 𝑥 имеет относительный минимум при трех 𝜋 больше двух и минус один. На графике функции, который нам дали, эта точка кажется смещенной на две единицы вверх. Он имеет координаты три 𝜋 над двумя и единицей. Таким образом, мы действительно можем предположить, что график 𝑦 равен греху 𝑥, сдвинутому на две единицы вверх или на вектор ноль, два.

Итак, давайте подумаем о том, как мы используем нотацию функций, чтобы описать это. Что ж, мы знаем, что, предположим, у нас есть функция 𝑓 от 𝑥, мы можем отобразить ее на функцию 𝑓 от 𝑥 плюс 𝑎 одним сдвигом на 𝑎 единиц вверх или с помощью нулевого вектора, 𝑎. Итак, давайте определим наш исходный график 𝑦 равно sin of 𝑥, чтобы на самом деле быть 𝑓 of 𝑥 равным sin of 𝑥. Мы знаем, что для перевода этого графика на две единицы вверх нам нужна функция 𝑓 от 𝑥 плюс два. Ну, конечно, если функция 𝑓 от 𝑥 равна sin 𝑥, добавление двух ко всей функции просто дает нам sin 𝑥 плюс два. Итак, график функции, заданной в этом вопросе, имеет уравнение 𝑦, равное греху 𝑥 плюс два.

`f(x) = 2sin(x) + sin(2x), [0, 2pi]` Найдите точки перегиба и обсудите вогнутость графика функции.

Цитата страницы Начать эссе значок-вопрос Задайте вопрос

Начать бесплатную пробную версию

Скачать PDF PDF Цитата страницы Цитировать Поделиться ссылкой Делиться

Ссылайтесь на эту страницу следующим образом:

«`f(x) = 2sin(x) + sin(2x), [0, 2pi]` Найдите точки перегиба и обсудите вогнутость графика функции.» eNotes Editorial , 16 октября 2015 г., https://www.enotes.com/homework-help/f-x-2sin-x-sin-2x-0-2pi-find-points-inflection-529709. По состоянию на 31 марта 2023 г.

Ответы экспертов

Учитывая f(x)=2sin(x)+sin(2x) на интервале [0,2pi], найдите точки перегиба и обсудите вогнутость:

Найдите вторую производную:

f'(x)=2cos(x)+2cos(2x)

f»(x)=-2sin(x)-4sin(2x)

Точки перегиба возникают, когда вторая производная равна нулю (и меняет знак).

-2sinx-4sin(2x)=0

-8sin(x)cos(x)-2sin(x)=0    Используя тождество sin(2x)=2sin(x) cos(x)

-2sin(x)[4cos(x)+1]=0

-2sin(x)=0 ==> x=0,pi,2pi на интервале

4cos(x)+ 1=0 ==> cos(x)=-1/4 ==> x=1,823,4,460

Вторая производная:

положительный слева от 0
отрицательный на (0,1.823)
положительный на (1.823,pi)
отрицательный на (pi,4.460)
положительный на (4.460,2pi)
отрицательный сразу справа от 2pi

————————————————— —————————————

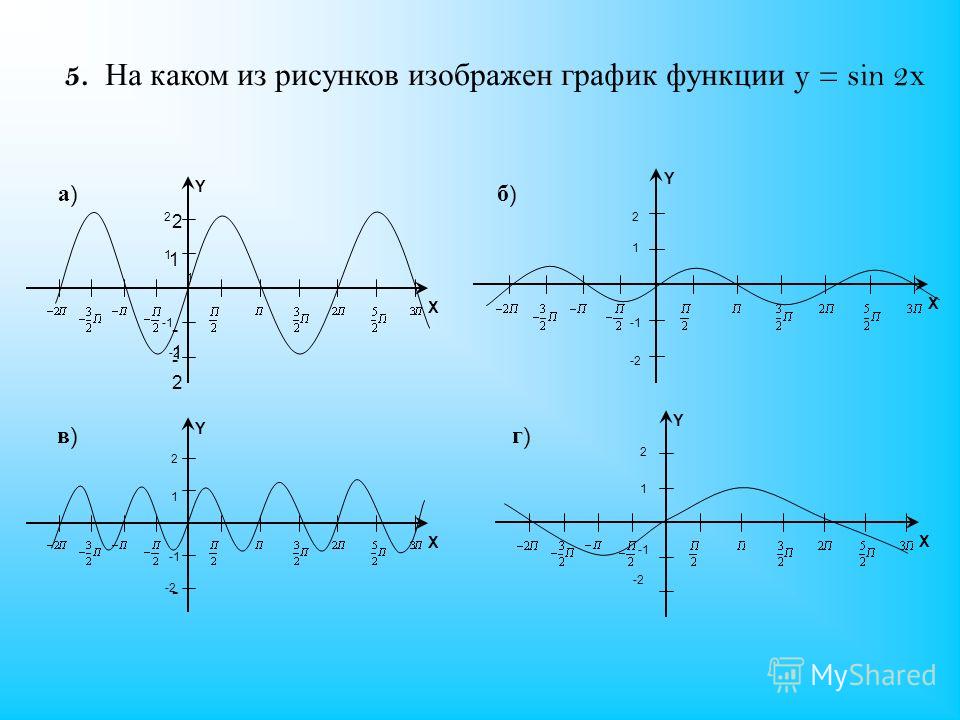
Имеются точки перегиба на 0,1.823,pi ,4.460,2pi

Функция вогнута вниз по (0,1.823), вверх по (1.823,pi), вниз по (pi,4.460) и вверх по (4.460,2pi)

—— ————————————————— ——————————-

График:

 

 

См.

eNotes без рекламы

Начните 48-часовую бесплатную пробную версию , чтобы получить доступ к более чем 30 000 дополнительных руководств и более чем 350 000 вопросов помощи при выполнении домашних заданий, на которые наши эксперты ответили.

Получите 48 часов бесплатного доступа

Уже зарегистрированы? Войдите здесь.

Утверждено редакцией eNotes

Задайте вопрос

Похожие вопросы

Просмотреть все

Математика

Последний ответ опубликован 07 сентября 2010 г. в 12:47:25.

Что означают буквы R, Q, N и Z в математике?

14 Ответы педагога

Математика

Последний ответ опубликован 09 октября 2017 г. в 00:54:39

Добавьте 1 плюс 2 плюс 3 плюс 4. . . вплоть до 100.

3 Ответа учителя

Математика

Последний ответ опубликован 25 февраля 2016 г. в 18:48:45.

Сколько времени (в часах) займет ваше путешествие, если вы проедете 350 км со средней скоростью 80 км/ч? Какова формула с данными: время, расстояние, скорость или скорость?

1 Ответ учителя

Математика

Последний ответ опубликован 3 октября 2011 г. в 14:12:01.

Этот предел представляет собой производную некоторой функции f при некотором числе a. укажите это f и a. lim h->0  [(4-й корень из)(16+h)-2]/h    a=? ф=?

1 Ответ учителя

Математика

Последний ответ опубликован 23 мая 2012 г. в 2:05:32.

Определите, является ли это ростом или спадом.