Алгебра Функция вида у= n√ x, их свойства и график
Материалы к уроку
2. Функция вида у=v(n&x), их свойства и график.ppt
1.55 MBСкачать2. Функция вида у=v(n&x), их свойства и график.doc
778 KBСкачать
Конспект урока
Функция вида у= n√ x, их свойства и график
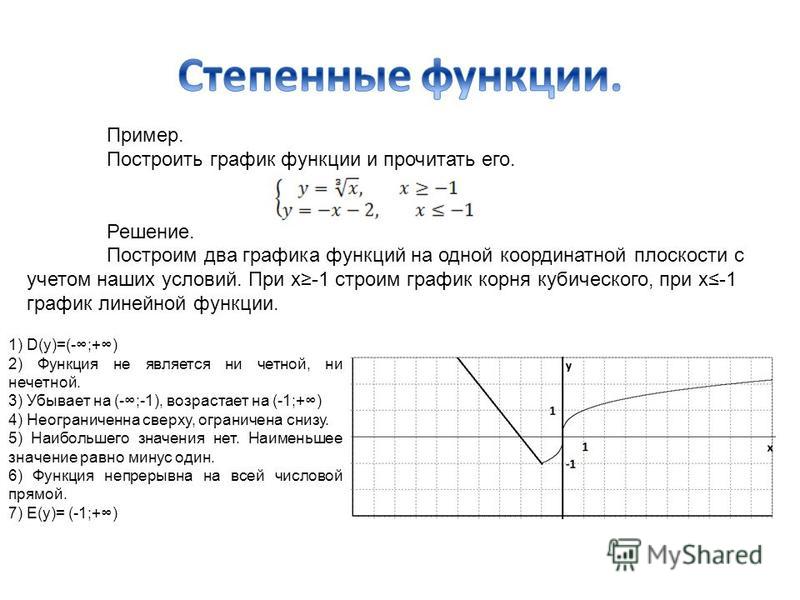
Рассмотрим функцию игрек равняется корень энной степени из икс при условии значение аргумента неотрицательно.
Пусть n=4. Построим в одной системе координат два графика функций игрек равняется икс в четвертой степени и игрек равняется корень четвертой степени из икс
Внимательно рассмотрев графики и таблицы, можно заметить, что графики представляют собой ветвь параболы и симметричны относительно прямой у=х (игрек равен икс), так как на построенных ветвях парабол есть точки, которые симметричны друг другу относительно данной прямой. Так точка А графика функции игрек равен икс в четвертой степени с координатами (1/2;1/16) и точка А1 графика функции.
Так точка А графика функции игрек равен икс в четвертой степени с координатами (1/2;1/16) и точка А1 графика функции.
Если рассмотреть точки с координатами (2;16) и (16;2), (3;81) и (81;3), то заметим, что они также симметричны относительно прямой х=у. А точки с координатами (0;0) и (1;1) лежат на данной прямой и являются общими для парабол.
Значит, для любой точки (m;m в четвертой степени) на графике игрек равно икс в четвертой степени есть ей симметричная точка ( m в четвертой степени; m)на втором графике относительно прямой у=х, справедливо будет и обратное утверждение.
Докажем следующую теорему:
Точки А (a;b) и В (b;a) симметричны относительно прямой у=х.
Доказательство: предположим, что a и b – отрицательные числа. Значит, точки А (a;b) и В (b;a) расположены в третьей координатной четверти. А прямая у=х является биссектрисой первой и третьей координатных четвертей.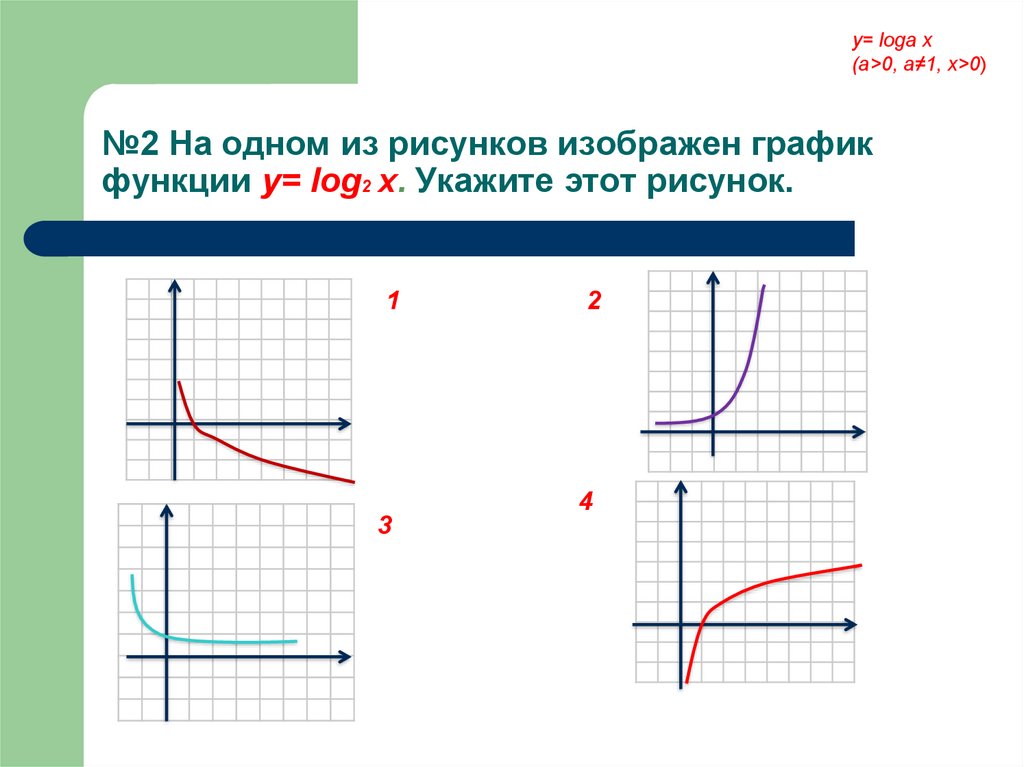 На оси абсцисс отметим точку С (а;0), а на оси ординат точку
На оси абсцисс отметим точку С (а;0), а на оси ординат точку
К (0; а) (рис.6).
Рассмотрим треугольники СОА и КОВ: ОС=ОК=а по построению,
СА=ВК= b по построению,
Угол ACO равен углу BKO равен 90градусам
, следовательно треугольники равны по первому признаку равенства треугольников. Значит, 1)АО=ВО и следавательно треугольник АОВ — равнобедренный.
2) угол COA равен углу KOB , и так как прямая у=х является биссектрисой угла СОК по построению, то и угол AOM равен углу BOM и ОМ является биссектрисой треугольника АОВ, а следовательно и осью симметрии для точек А и В. Аналогично проводится доказательство и при условии если a и b – положительны.
Сделаем вывод: график функции игрек равняется корень кубический из икса можно получить из графика функции игрек равняется икс в третьей степени, при x меньше 0 с помощью преобразования симметрии относительно графика прямой игрек равняется икс. Таким же образом можно построить график функции игрек равняется корень шестой степени из икса при положительном икс с помощью преобразования симметрии графика функции игрек равняется икс в шестой степени, при положительном икс, относительно прямой игрек равняется икс.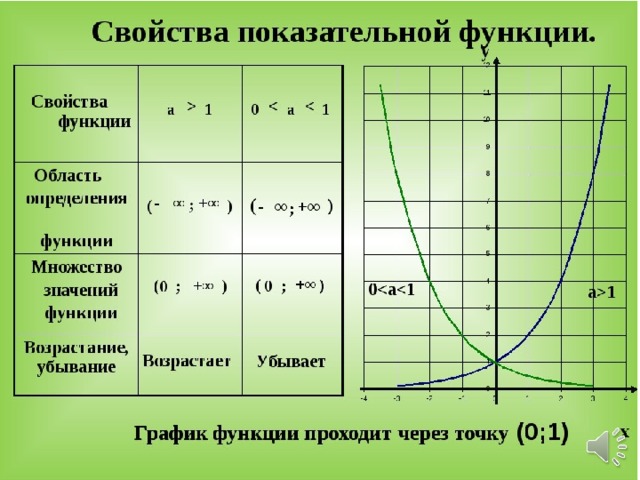
Обобщим полученные результаты: график функции игрек равен корень энной степени из икс, при x меньше или равно 0 и n – нечетное, симметричен относительно прямой у=х графику функции игрек равен икс в энной степени(рис.7)
Пример 1: Построить график функции игрек равняется сумме корня третьей степени из икс минус один и двух
Для построения данного графика функции нам нужна вспомогательная система координат с началом в точке А (1;2) – пунктирные прямые х′=1(икс штрих равен единице) и у′=2 (игрек штрих равен двум) на рис10. В новой системе координат построим график функции игрек равен корень третьей степени из икса).
Таблица
|
х |
-8 |
-1 |
0 |
|
у |
-2 |
-1 |
0 |
Это и будет график данной функции.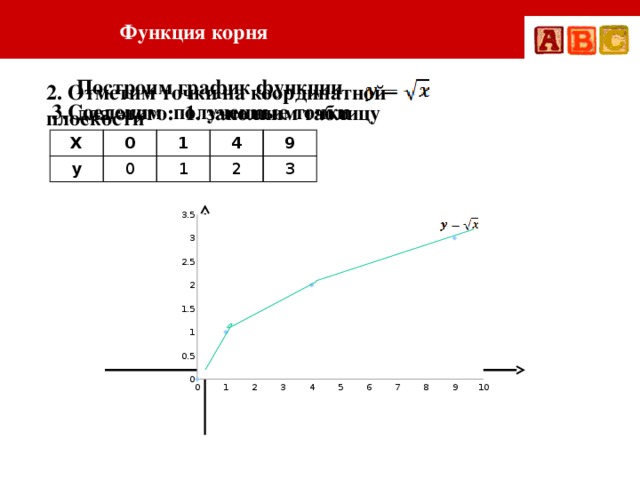
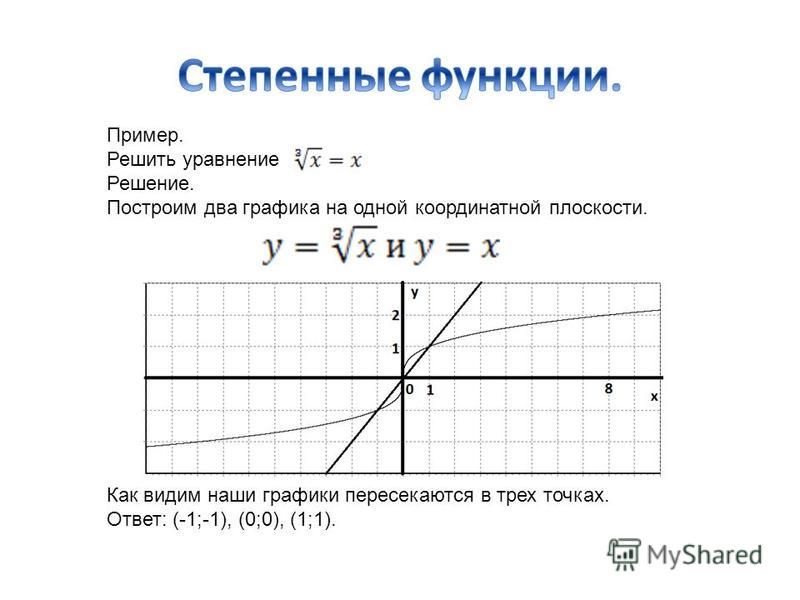
Пример 2.
Решите уравнение корень пятой степени из икса равен минус икс минус два
В одной системе координат построим графики двух функций игрек равняется корень пятой степени из икса
|
х |
-32 |
-1 |
0 |
1 |
32 |
|
у |
-2 |
-1 |
0 |
1 |
2 |
и у=-х-2(игрек равняется минус икс минус два)( графиком является прямая, которую построим по двум точкам)
|
х |
-2 |
0 |
|
у |
0 |
-2 |
(рис.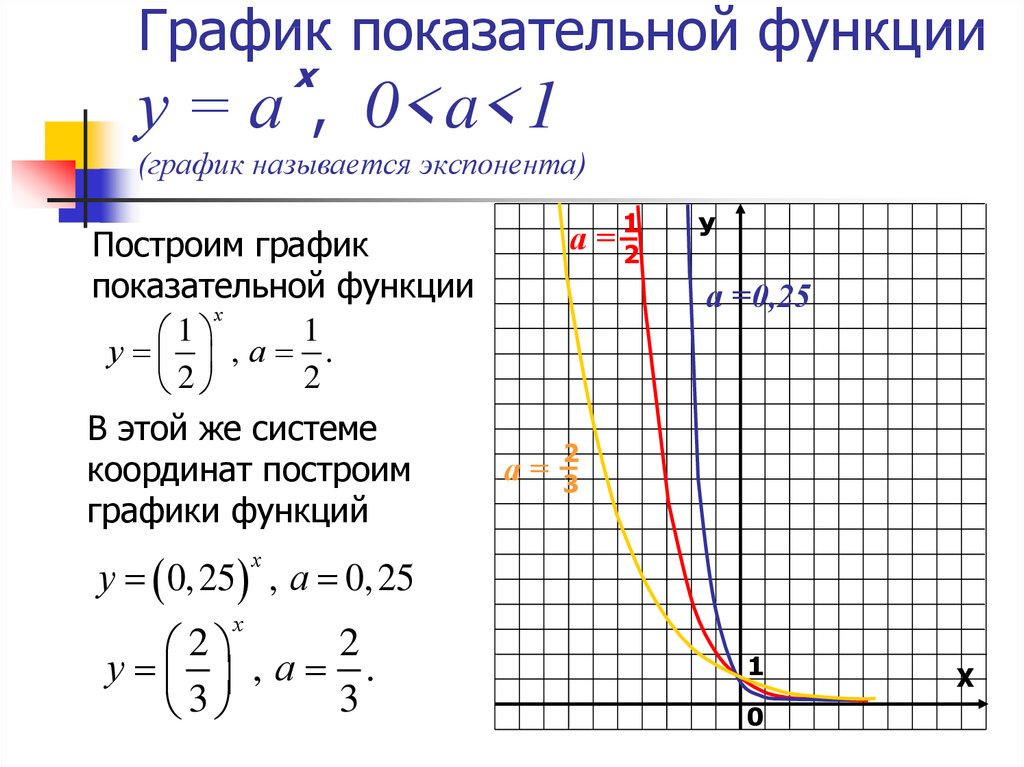 11) графики пересекаются в точке В (-1;-1) (с координатами минус один, минус один). Значит, абсцисса данной точки х= -1 и есть корень данного уравнения.
11) графики пересекаются в точке В (-1;-1) (с координатами минус один, минус один). Значит, абсцисса данной точки х= -1 и есть корень данного уравнения.
Остались вопросы по теме? Наши репетиторы готовы помочь!
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ
Выбрать репетитора
|
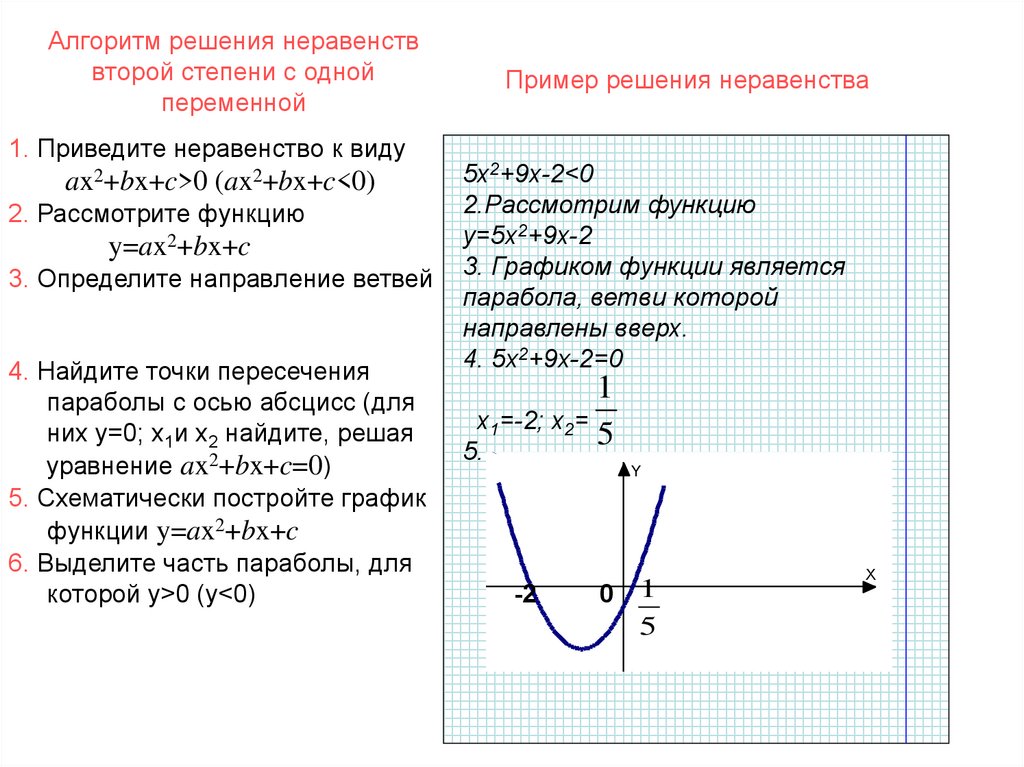
На самом деле эту функцию мы начали разбирать в предыдущем параграфе, где «икс» находился в первой степени. Но степень может быть и больше, и меньше или вообще быть дробной. Рассмотрим наиболее распространенные случаи: Функция вида называется квадратичной функцией, а её
график – параболой. Простейшая парабола вам хорошо известна: (см. ниже).
Обратите внимание, что график этой функции симметричен относительно оси . Такие функции называют чётными. Аналитически чётность выражается условием . Проверим на чётность нашу функцию, для этого ВМЕСТО подставим : В общем случае квадратичная функция чётной не является, но симметрию самой параболы никто не отменял и этим удобно пользоваться на практике. Как быстро построить любую параболу? Очевидно, сначала выгодно найти её вершину, а затем – несколько пар симметричных точек.
Посмотрим, как это происходит на примере функции : Теперь найдём опорные точки (обычно хватает четырёх), при этом используем симметрию параболы и принцип «влево-вправо»: Осталось отметить найденные точки на чертеже и АККУРАТНО соединить их линией.  Рассмотренный алгоритм не является обязательным и в простых
случаях вершину параболы можно обнаружить методом «практического тыка», просто перебирая точки. Особенно, если у вас нелады с производными (их
рассмотрим в курсе вышмата). Рассмотренный алгоритм не является обязательным и в простых
случаях вершину параболы можно обнаружить методом «практического тыка», просто перебирая точки. Особенно, если у вас нелады с производными (их
рассмотрим в курсе вышмата).
График функции представляет собой ветвь параболы, которая «лежит на боку»: График функции называется
кубической параболой График произвольного корня с дробным показателем следует
строить, имея в виду область определения того или иного корня. Так, функция , как и , определена только для
неотрицательных «икс»: и для построения её графика
придётся найти несколько значений приближенно: График функции представляет собой
гиперболу. Да, это тоже степенная функция! Ибо . Как быстро построить график гиперболы? (да и не только её) Принципиально такую же форму имеют графики –
только в первом случае гипербола будет иметь одну ветвь, во втором – две ветви, расположенные в 1-й и 2-й координатных четвертях, и третья
гипербола будет похожа на . Задание 7 г) Дано – уравнение окружности с центром в начале координат Решения и ответы в конце книги. 3.5. Графическое решение уравнений и неравенств 3.3. Линейная функция | Оглавление | |
Свойства функции у 3 в степени х. Функции и графики
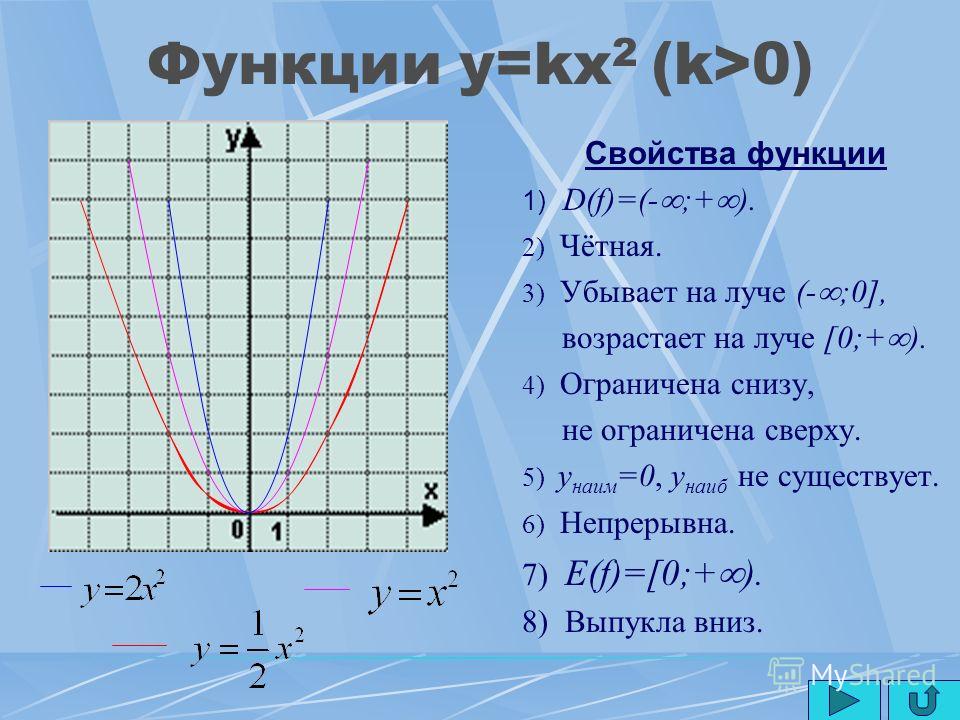
Функция где Х – переменная величина, A – заданное число, называется Степенной функцией .
Если то – линейная функция, ее график – прямая линия (см. параграф 4.3, рис. 4.7).
Если то – квадратичная функция, ее график – парабола (см. параграф 4.3, рис. 4.8).
Если то ее график – кубическая парабола (см. параграф 4.3, рис. 4.9).
Степенная функция
Это обратная функция для
1. Область определения:
2. Множество значений:
3. Четность и нечетность: функция нечетная.
4. Периодичность функции: непериодическая.
5. Нули функции: X = 0 – единственный нуль.
6. наибольшего и наименьшего значений функция не имеет.
7.
8. График функции Симметричен графику кубической параболы относительно прямой Y = X и изображен на рис. 5.1.
Степенная функция
1. Область определения:
2. Множество значений:
3. Четность и нечетность: функция четная.
Четность и нечетность: функция четная.
4. Периодичность функции: непериодическая.
5. Нули функции: единственный нуль X = 0.
6. Наибольшее и наименьшее значения функции: принимает наименьшее значение для X = 0, оно равно 0.
7. Промежутки возрастания и убывания: функция является убывающей на промежутке и возрастающей на промежутке
8. График функции (для каждого N Î N ) «похож» на график квадратичной параболы (графики функций изображены на рис. 5.2).
Степенная функция
1. Область определения:
2. Множество значений:
3. Четность и нечетность: функция нечетная.
4. Периодичность функции: непериодическая.
5. Нули функции: X = 0 – единственный нуль.
6. Наибольшее и наименьшее значения:
7. Промежутки возрастания и убывания: функция является возрастающей на всей области определения.
8. График функции (для каждого ) «похож» на график кубической параболы (графики функций изображены на рис. 5.3).
Степенная функция
1. Область определения:
2. Множество значений:
3. Четность и нечетность: функция нечетная.
4. Периодичность функции: непериодическая.
5. Нули функции: нулей не имеет.
6. Наибольшее и наименьшее значения функции: наибольшего и наименьшего значений функция не имеет при любом
7. Промежутки возрастания и убывания: функция является убывающей в области определения.
8. Асимптоты: (ось Оу ) – вертикальная асимптота;
(ось Ох ) – горизонтальная асимптота.
9. График функции (для любого N ) «похож» на график гиперболы (графики функций изображены на рис. 5.4).
Степенная функция
1. Область определения:
Область определения:
2. Множество значений:
3. Четность и нечетность: функция четная.
4. Периодичность функции: непериодическая.
5. Наибольшее и наименьшее значения функции: наибольшего и наименьшего значений функция не имеет при любом
6. Промежутки возрастания и убывания: функция является возрастающей на и убывающей на
7. Асимптоты: X = 0 (ось Оу ) – вертикальная асимптота;
Y = 0 (ось Ох ) – горизонтальная асимптота.
8. Графиками функций Являются квадратичные гиперболы (рис. 5.5).
Степенная функция
1. Область определения:
2. Множество значений:
3. Четность и нечетность: функция не обладает свойством четности и нечетности.
4. Периодичность функции: непериодическая.
5. Нули функции: X = 0 – единственный нуль.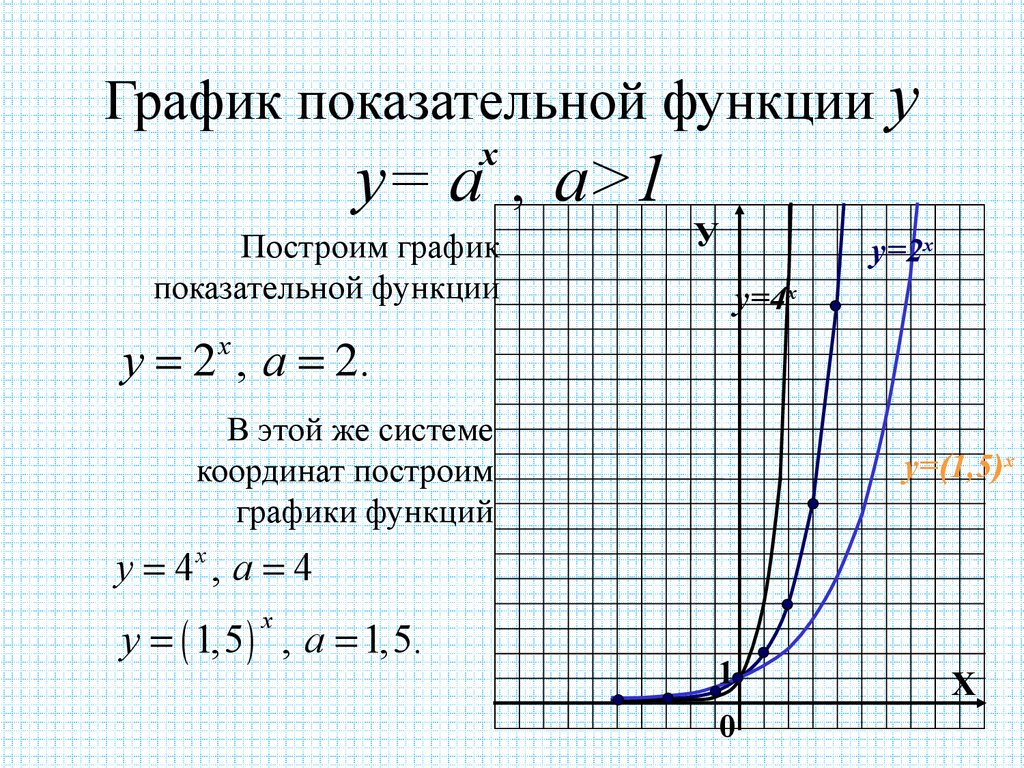
6. Наибольшее и наименьшее значения функции: наименьшее значение, равное 0, функция принимает в точке X = 0; наибольшего значения не имеет.
7. Промежутки возрастания и убывания: функция является возрастающей на всей области определения.
8. Каждая такая функция при определенном показателе является обратной для функции при условии
9. График функции «похож» на график функции при любом N и изображен на рис. 5.6.
Степенная функция
1. Область определения:
2. Множество значений:
3. Четность и нечетность: функция нечетная.
4. Периодичность функции: непериодическая.
5. Нули функции: X = 0 – единственный нуль.
6. Наибольшее и наименьшее значения функции: наибольшего и наименьшего значений функция не имеет при любом
7. Промежутки возрастания и убывания: функция является возрастающей на всей области определения.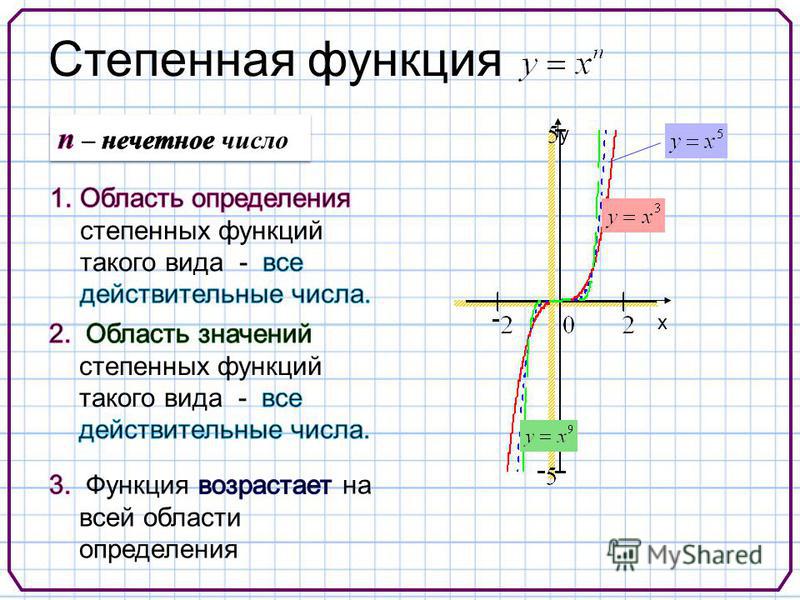
8. График функции Изображен на рис. 5.7.
Степенная функция — это функция вида y = x p , где p — заданное действительное число.
Свойства степенной функции
- Если показатель p = 2n — четное натуральное число:
- область определения — все действительные числа, т. е. множество R;
- множество значений — неотрицательные числа, т. е. y ≥ 0;
- функция четная;
- функция является убывающей на промежутке x ≤ 0 и возрастающей на промежутке x ≥ 0.
- Если показатель p = 2n — 1 — нечетное натуральное число:
- область определения — множество R;
- множество значений — множество R;
- функция нечетная;
- функция является возрастающей на всей действительной оси.

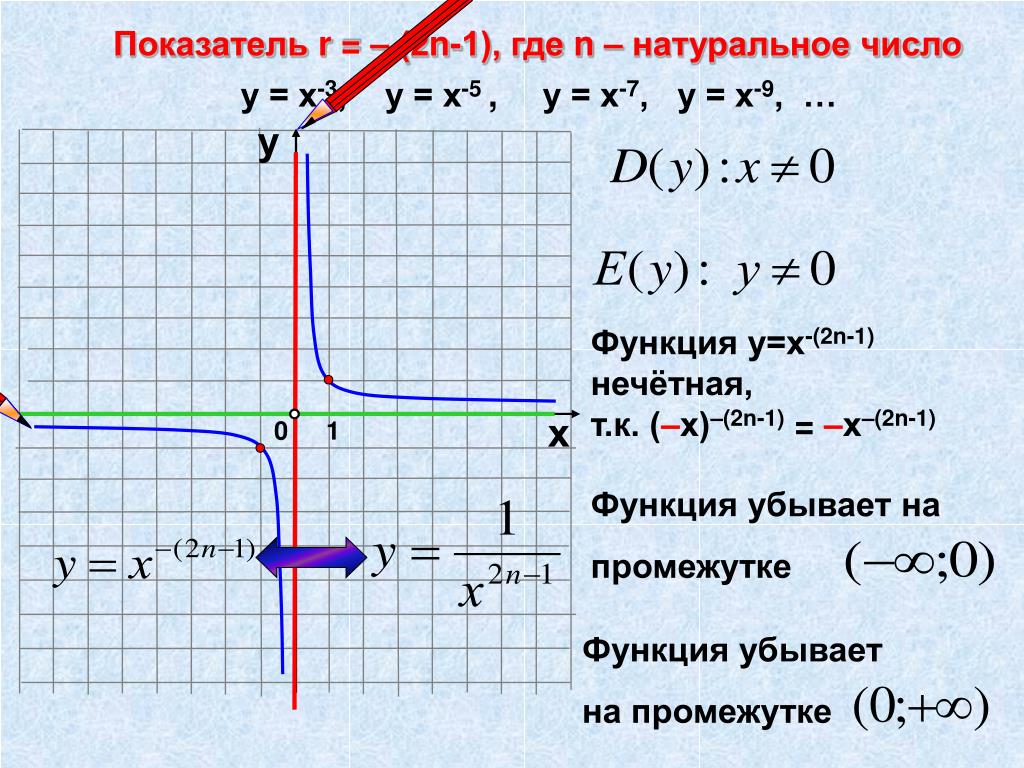
- Если показатель p = -2n , где n — натуральное число:
- множество значений — положительные числа y > 0;
- функция четная;
- функция является возрастающей на промежутке x 0.
- Если показатель p = -(2n — 1) , где n — натуральное число:
- область определения — множество R, кроме x = 0;
- множество значений — множество R, кроме y = 0;
- функция нечетная;
- функция является убывающей на промежутках x 0.
- Если показатель p — положительное действительное нецелое число:
- область определения — неотрицательные числа x ≥ 0;
- множество значений — неотрицательные числа y ≥ 0;
- функция является возрастающей на промежутке x ≥ 0.

- Если показатель p — отрицательное действительное нецелое число:
- область определения — положительные числа x > 0;
- множество значений — положительные числа y > 0;
- функция является убывающей на промежутке x > 0.
Вы знакомы с функциями y=x, y=x 2 , y=x 3 , y=1/x и т. д. Все эти функции являются частными случаями степенной функции, т. е. функции y=x p , где p — заданное действительное число.
Свойства и график степенной функции существенно зависит от свойств степени с действительным показателем, и в частности от того, при каких значениях x и p имеет смысл степень x p .
Перейдем к подобному рассмотрению различных случаев в зависимости от
показателя степени p.
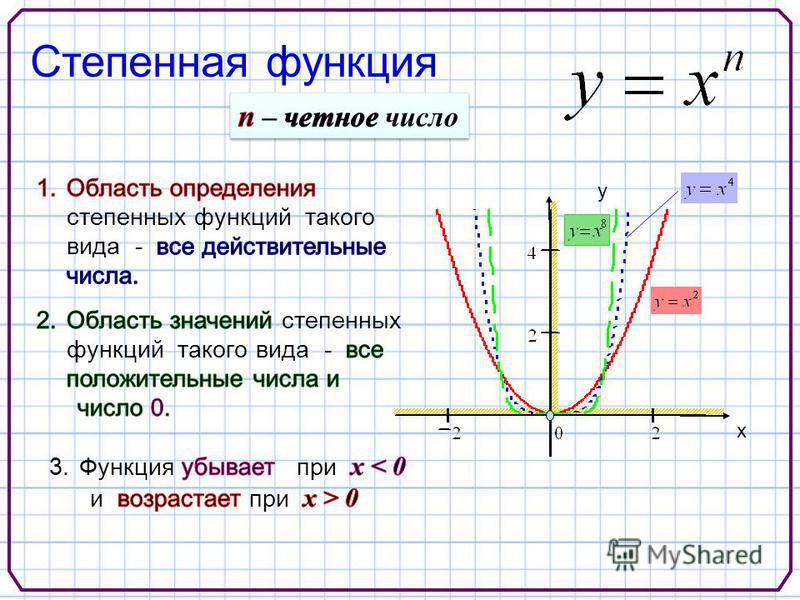
- Показатель p=2n -четное натуральное число.
свойствами:
- область определения — все действительные числа, т.
 е. множество R;
е. множество R; - множество значений — неотрицательные числа, т. е. y больше или равно 0;
- функция y=x 2n четная, так как x 2n =(- x) 2n
- функция является убывающей на промежутке x0.
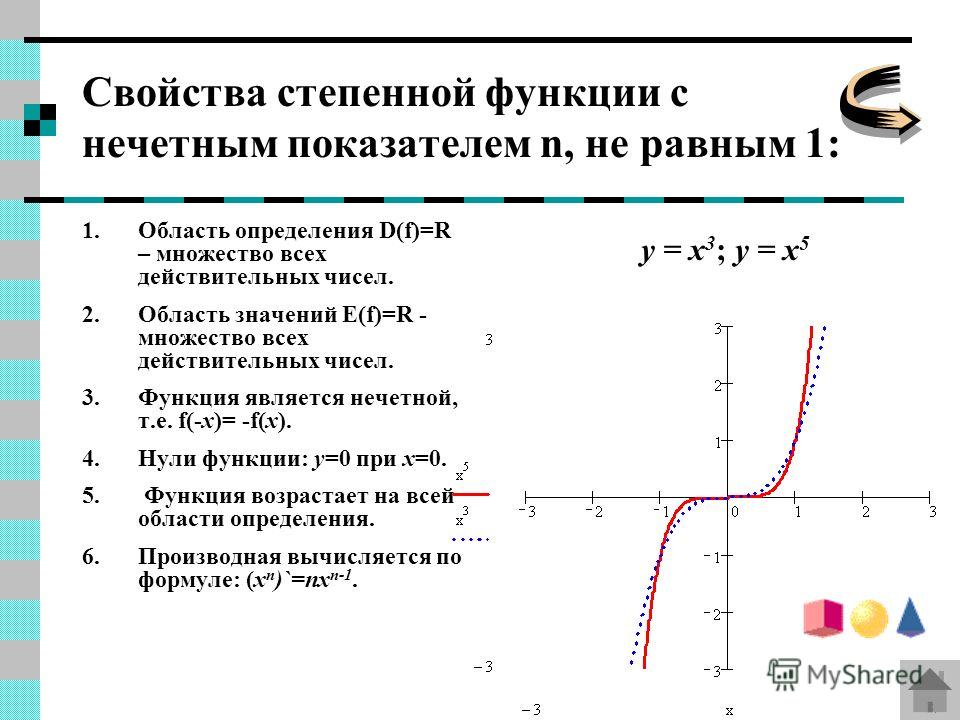
2. Показатель p=2n-1 — нечетное натуральное число
В этом случае степенная функция y=x 2n-1 , где натуральное число, обладает следующими свойствами:
- область определения — множество R;
- множество значений — множество R;
- функция y=x 2n-1 нечетная, так как (-x) 2n-1 =x 2n-1 ;
- функция является возрастающей на всей действительной оси.
3.Показатель p=-2n , где n — натуральное число.
В этом случае степенная функция y=x -2n =1/x 2n обладает следующими свойствами:
- область определения — множество R, кроме x=0;
- множество значений — положительные числа y>0;
- функция y=1/x 2n четная, так как 1/(-x) 2n =1/x 2n ;
- функция является возрастающей на промежутке x0.

Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Тема урока: Степенная функция и ее график.
Как алгебраисты вместо АА, ААА, … пишут А 2 , А 3 , … так я вместо пишу а -1 , а -2 , а -3 , … Ньютон И.
у = х х у у = х 2 х у у = х 3 х у х у Прямая Парабола Кубическая парабола Гипербола Нам знакомы функции: Все эти функции являются частными случаями степенной функции
где р – заданное действительное число Определение: Степенной функцией называется функция вида у = х p Свойства и график степенной функции зависят от свойств степени с действительным показателем, и в частности от того, при каких значениях х и р имеет смысл степень х р.
Функция у=х 2 n четная, т.к. (– х) 2 n = х 2 n Функция убывает на промежутке Функция возрастает на промежутке Степенная функция: Показатель р = 2n – четное натуральное число у = х 2 , у = х 4 , у = х 6 , у = х 8 , … 1 0 х у у = х 2
y x — 1 0 1 2 у = х 2 у = х 6 у = х 4 Степенная функция: Показатель р = 2n – четное натуральное число у = х 2 , у = х 4 , у = х 6 , у = х 8 , …
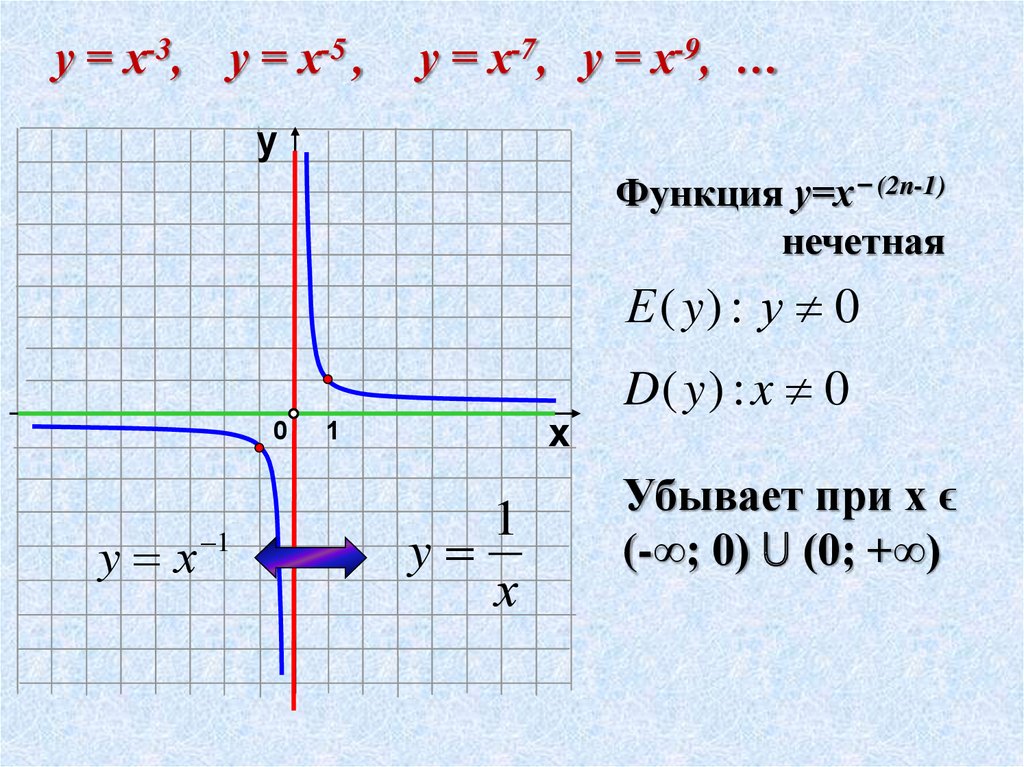
Функция у=х 2 n -1 нечетная, т.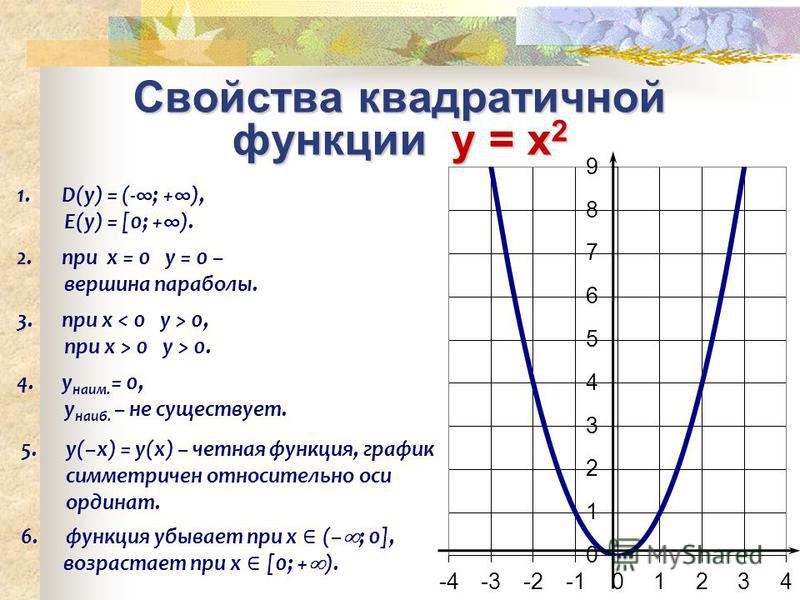 к. (– х) 2 n -1 = – х 2 n -1 Функция возрастает на промежутке Степенная функция: Показатель р = 2n-1 – нечетное натуральное число у = х 3 , у = х 5 , у = х 7 , у = х 9 , … 1 0
к. (– х) 2 n -1 = – х 2 n -1 Функция возрастает на промежутке Степенная функция: Показатель р = 2n-1 – нечетное натуральное число у = х 3 , у = х 5 , у = х 7 , у = х 9 , … 1 0
Степенная функция: y x — 1 0 1 2 у = х 3 у = х 7 у = х 5 Показатель р = 2n-1 – нечетное натуральное число у = х 3 , у = х 5 , у = х 7 , у = х 9 , …
Функция у=х- 2 n четная, т.к. (– х) -2 n = х -2 n Функция возрастает на промежутке Функция убывает на промежутке Степенная функция: Показатель р = -2n – где n натуральное число у = х -2 , у = х -4 , у = х -6 , у = х -8 , … 0 1
1 0 1 2 у = х -4 у = х -2 у = х -6 Степенная функция: Показатель р = -2n – где n натуральное число у = х -2 , у = х -4 , у = х -6 , у = х -8 , … y x
Функция убывает на промежутке Функция у=х -(2 n -1) нечетная, т.к. (– х) –(2 n -1) = – х –(2 n -1) Функция убывает на промежутке Степенная функция: Показатель р = -(2n-1) – где n натуральное число у = х -3 , у = х -5 , у = х -7 , у = х -9 , … 1 0
у = х -1 у = х -3 у = х -5 Степенная функция: Показатель р = -(2n-1) – где n натуральное число у = х -3 , у = х -5 , у = х -7 , у = х -9 , … y x — 1 0 1 2
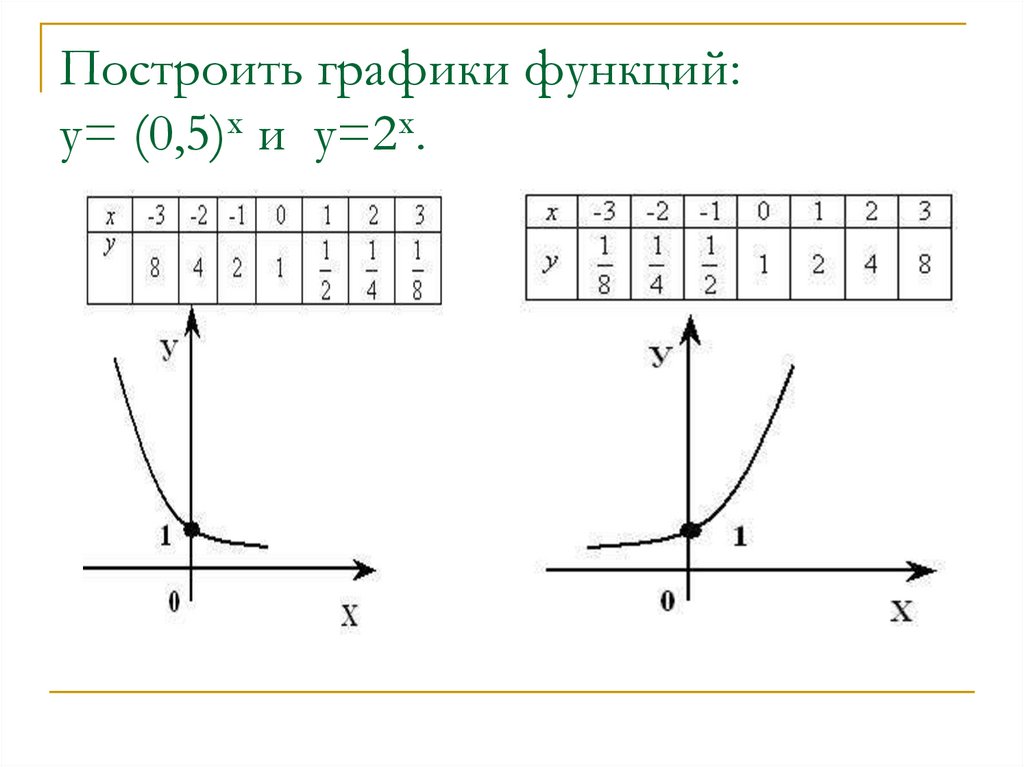
Степенная функция: Показатель р – положительное действительное нецелое число у = х 1,3 , у = х 0,7 , у = х 2,2 , у = х 1/3 ,… 0 1 х у Функция возрастает на промежутке
у = х 0,7 Степенная функция: Показатель р – положительное действительное нецелое число у = х 1,3 , у = х 0,7 , у = х 2,2 , у = х 1/3 ,… y x — 1 0 1 2 у = х 0,5 у = х 0,84
Степенная функция: Показатель р – положительное действительное нецелое число у = х 1,3 , у = х 0,7 , у = х 2,2 , у = х 1/3 ,… y x — 1 0 1 2 у = х 1,5 у = х 3,1 у = х 2,5
Степенная функция: Показатель р – отрицательное действительное нецелое число у= х -1,3 , у= х -0,7 , у= х -2,2 , у = х -1/3 ,… 0 1 х у Функция убывает на промежутке
у = х -0,3 у = х -2,3 у = х -3,8 Степенная функция: Показатель р – отрицательное действительное нецелое число у= х -1,3 , у= х -0,7 , у= х -2,2 , у = х -1/3 ,… y x — 1 0 1 2 у = х -1,3
По теме: методические разработки, презентации и конспекты
Применение интеграции в учебном процессе как способа развития аналитических и творческих способностей.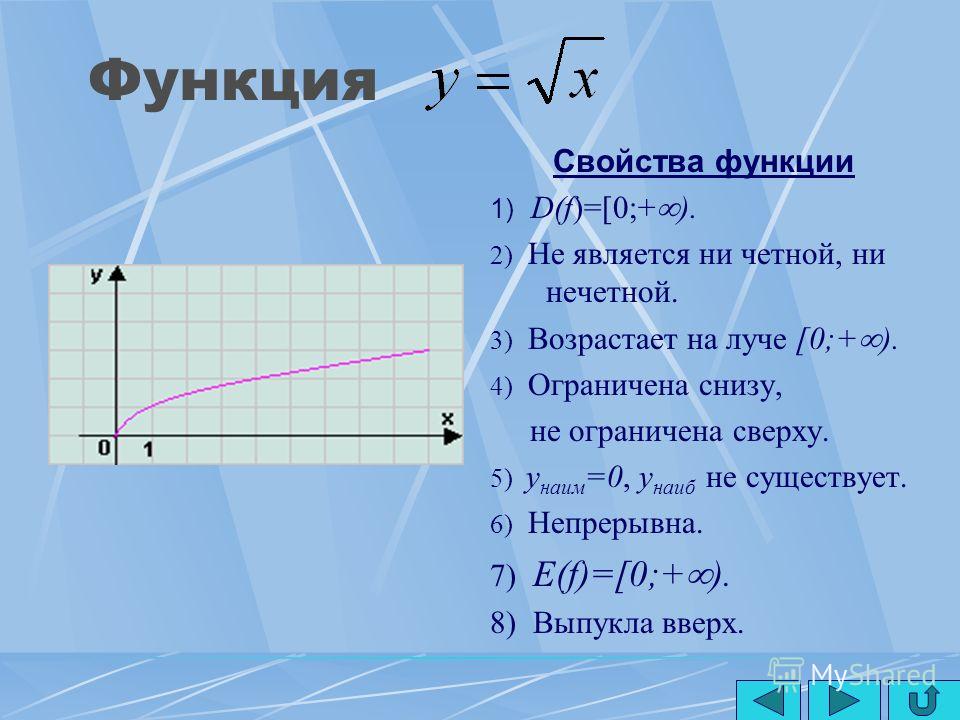 …
…
Лекция: Степенная функция с натуральным показателем, её график
Мы постоянно имеем дело с функциями, в которых аргумент имеет некоторую степень:
у = х 1 , у = х 2 , у = х 3 , у = х -1 и т.д.
Графики степенных функций
Итак, сейчас мы рассмотрим несколько возможных случаев степенной функции.
1) у = х 2 n .
Это означает, что сейчас мы будем рассматривать функции, в которых показатель степени является четным числом.
Характеристика функции:
1. В качестве области значения принимаются все действительные числа.
2. Функция может принимать все положительные значения и число нуль.
3. Функция является четной, поскольку не зависит от знака аргумента, а зависит только от его модуля.
4. Для положительного аргумента функция возрастает, а для отрицательного — убывает.
Графики данных функций напоминают параболу. Например, ниже представлен график функции у = х 4 .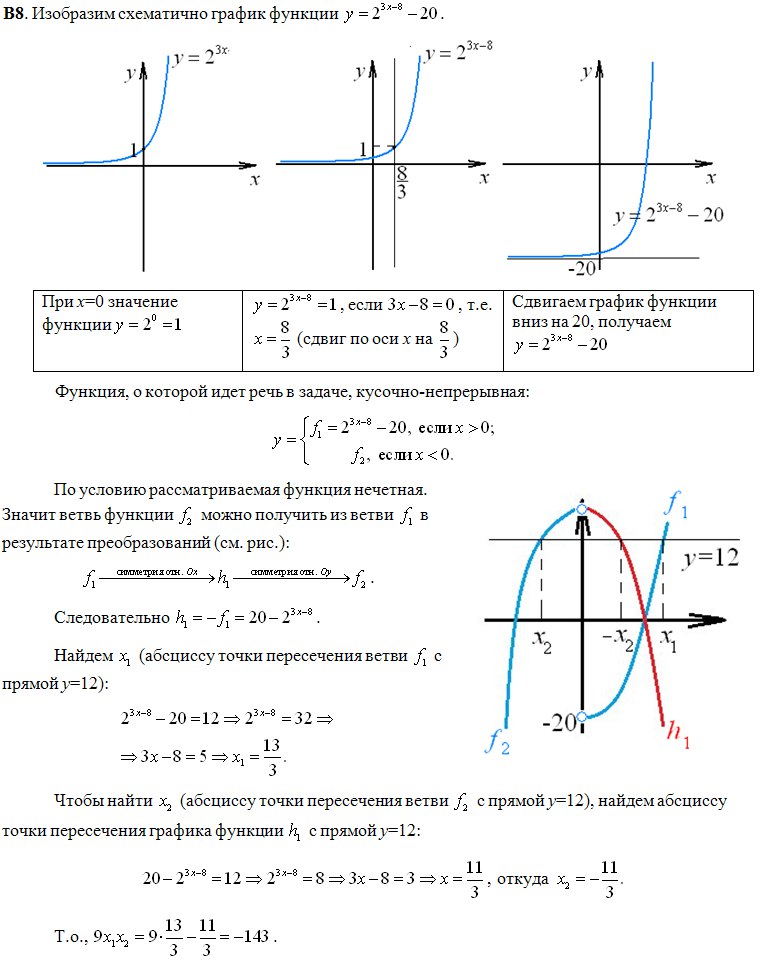
2) Функция имеет нечетный показатель степени: у = х 2 n +1 .
1. Область определения функции — все множество действительных чисел.
2. Область значения функции — может принимать вид любого действительного числа.
3. Данная функция нечетная.
4. Монотонно возрастает на всем промежутке рассмотрения функции.
5. График всех степенных функций с нечетным показателем степени идентичен функции у = х 3 .
3) Функция имеет четный отрицательный натуральный показатель: у = х -2 n .
Все мы знаем, что отрицательный показатель степени позволяет опустить степень в знаменатель и менять знак показателя степени, то есть получится вид у = 1/х 2 n .
1. Аргумент данной функции может принимать любые значения, кроме нуля, поскольку переменная стоит в знаменателе.
2. Так как показатель степени — четное число, то функция не может принимать отрицательные значения.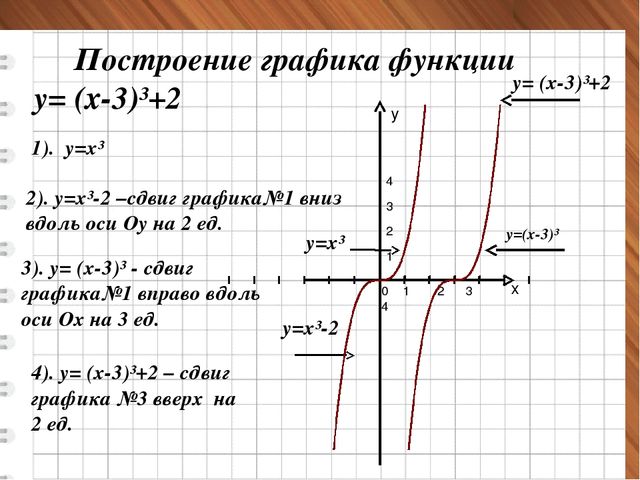 А раз аргумент не может быть равен нулю, то следует исключить и значение функции, равное нулю. Это значит, что функция может принимать только положительные значения.
А раз аргумент не может быть равен нулю, то следует исключить и значение функции, равное нулю. Это значит, что функция может принимать только положительные значения.
3. Данная функция является четной.
4. При отрицательном аргументе функция монотонно возрастает, а при положительном — убывает.
Вид графика функции у = х -2:
4) Функция с отрицательным нечетным показателем степени у = х -(2 n +1) .
1. Данная функция существует при всех значениях аргумента, кроме числа нуль.
2. Функция принимает все действительные значения, кроме числа нуль.
3. Данная функция является нечетной.
4. На двух рассматриваемых промежутках убывает.
Рассмотрим пример графика функции с отрицательным нечетным показателем степени на примере у = х -3 .
Последние материалы раздела:
Значение слова «арабы Даты и времяАрабы
См. Аравия и Мавры.Словарь УшаковаАрабы
ара
бы
, арабов, ед.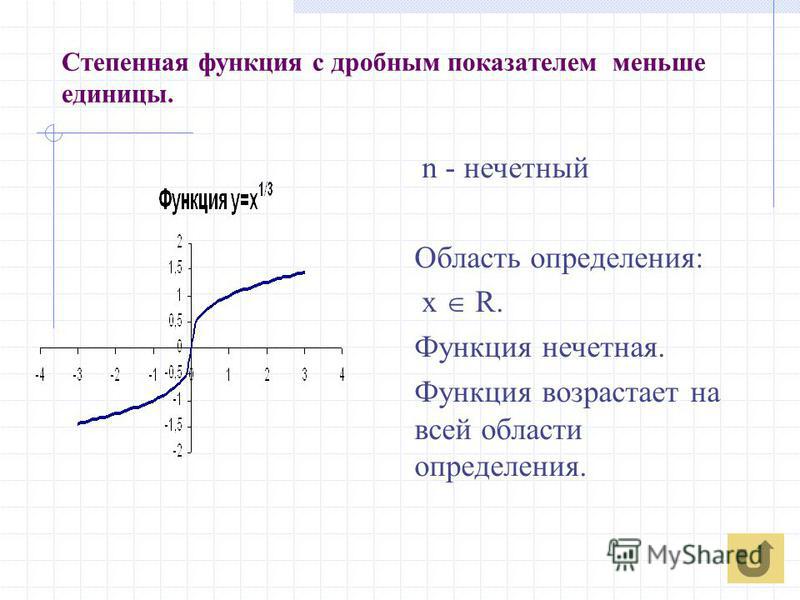 араб, араба, муж.
Народ, населяющий Аравию.Словарь ЕфремовойАрабы
мн. Народы…
араб, араба, муж.
Народ, населяющий Аравию.Словарь ЕфремовойАрабы
мн. Народы…
14 11 319 0Коран – это Святое создание мусульманской религии, основной памятник общества, основой которого является мировоззренческие и…
Суры из Корана: слушать онлайн mp3, читать на русском и арабском языке, скачать Коран суры по порядку на арабском14 11 319 0Коран – это Святое создание мусульманской религии, основной памятник общества, основой которого является мировоззренческие и…
- Рубрики
Конечное поведение степенных функций
Результаты обучения
- Определение степенной функции.

- Опишите конечное поведение степенной функции по ее уравнению или графику.
Три птицы на скале на фоне восходящего солнца. Функции, обсуждаемые в этом модуле, можно использовать для моделирования популяций различных животных, включая птиц. (кредит: Джейсон Бэй, Flickr)
Предположим, что на маленьком острове обитает определенный вид птиц. Его население за последние несколько лет показано ниже. 9{3}+97t+800[/latex], где [latex]P\left(t\right)[/latex] представляет популяцию птиц на острове через t лет после 2009 года. Мы можем использовать эту модель для оценки максимальная популяция птиц и когда это произойдет. Мы также можем использовать эту модель, чтобы предсказать, когда популяция птиц исчезнет с острова.
Идентификация степенных функций
Чтобы лучше понять проблему с птицей, нам нужно понять конкретный тип функции. Степенная функция – это функция с одним членом, являющимся произведением действительного числа 9{x}[/latex] силовая функция?
Нет.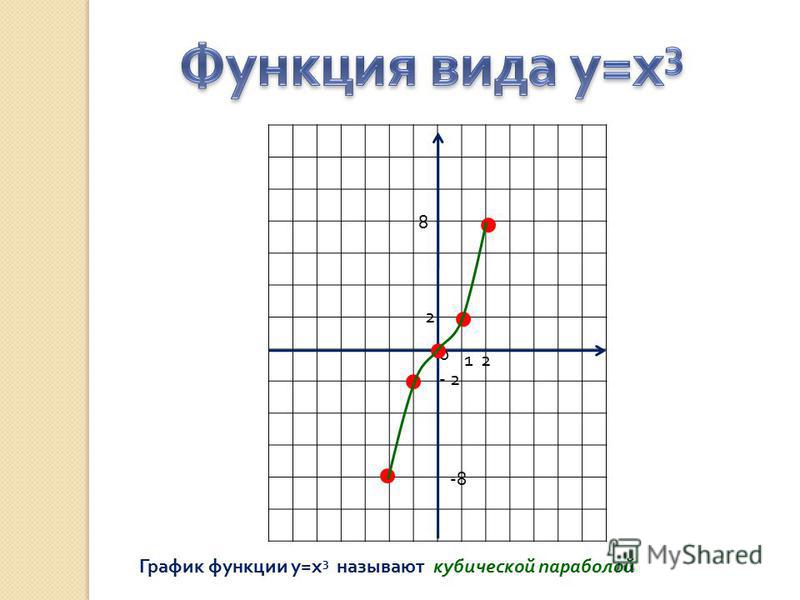 {2}}\hfill & \text{Функция обратного квадрата}\hfill \\ f\left(x\right) =\sqrt{x}\hfill & \text{функция квадратного корня}\hfill \\ f\left(x\right)=\sqrt[3]{x}\hfill & \text{функция кубического корня}\hfill \ конец{массив}[/латекс] 9{10}[/latex], которые являются степенными функциями с четными целыми степенями. Обратите внимание, что эти графики имеют похожие формы, очень похожие на график квадратичной функции. Однако по мере увеличения мощности графики несколько уплощаются вблизи начала координат и становятся более крутыми по мере удаления от начала координат.
{2}}\hfill & \text{Функция обратного квадрата}\hfill \\ f\left(x\right) =\sqrt{x}\hfill & \text{функция квадратного корня}\hfill \\ f\left(x\right)=\sqrt[3]{x}\hfill & \text{функция кубического корня}\hfill \ конец{массив}[/латекс] 9{10}[/latex], которые являются степенными функциями с четными целыми степенями. Обратите внимание, что эти графики имеют похожие формы, очень похожие на график квадратичной функции. Однако по мере увеличения мощности графики несколько уплощаются вблизи начала координат и становятся более крутыми по мере удаления от начала координат.
Чтобы описать поведение по мере того, как числа становятся все больше и больше, мы используем идею бесконечности. Мы используем символ [латекс]\infty[/латекс] для положительной бесконечности и [латекс]-\infty[/латекс] для отрицательной бесконечности. Когда мы говорим, что « x приближается к бесконечности», что можно символически записать как [latex]x\to \infty[/latex], мы описываем поведение; мы говорим, что x неограниченно увеличивается.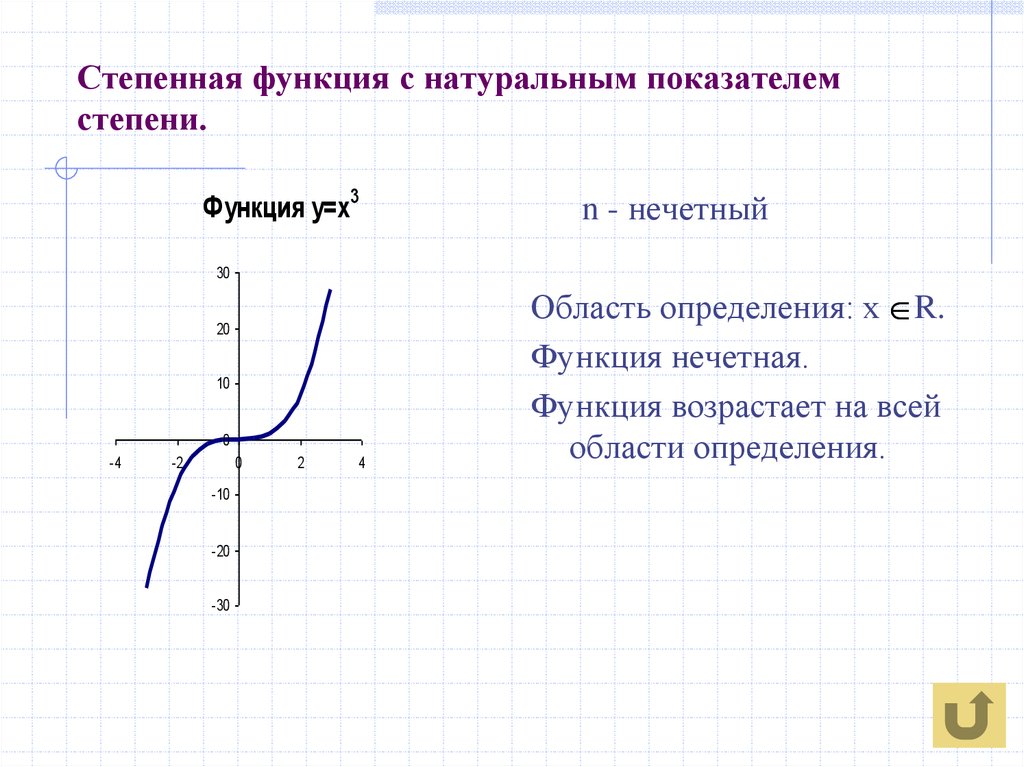
В случае функций мощности с четной мощностью при неограниченном увеличении или уменьшении входных значений выходные значения становятся очень большими, положительными числами. Эквивалентно, мы могли бы описать это поведение, сказав, что по мере того, как [латекс]x[/латекс] приближается к положительной или отрицательной бесконечности, значения [латекс]f\left(x\right)[/латекс] неограниченно возрастают. В символической форме мы могли бы написать 9{n}\text{, }n\text{ нечетные,}[/latex] симметричны относительно начала координат.
Для этих нечетных степенных функций, когда x приближается к отрицательной бесконечности, [латекс]f\left(x\right)[/latex] убывает неограниченно. По мере того, как x приближается к положительной бесконечности, [latex]f\left(x\right)[/latex] безгранично возрастает. В символической форме мы пишем
[латекс]\begin{array}{c}\text{as } x\to -\infty , f\left(x\right)\to -\infty \\ \text{as } x\to \infty , f\left(x\right)\to \infty \end{массив}[/latex] 9{n}[/latex], где [latex]n[/latex] — целое неотрицательное число, зависящее от степени и константы.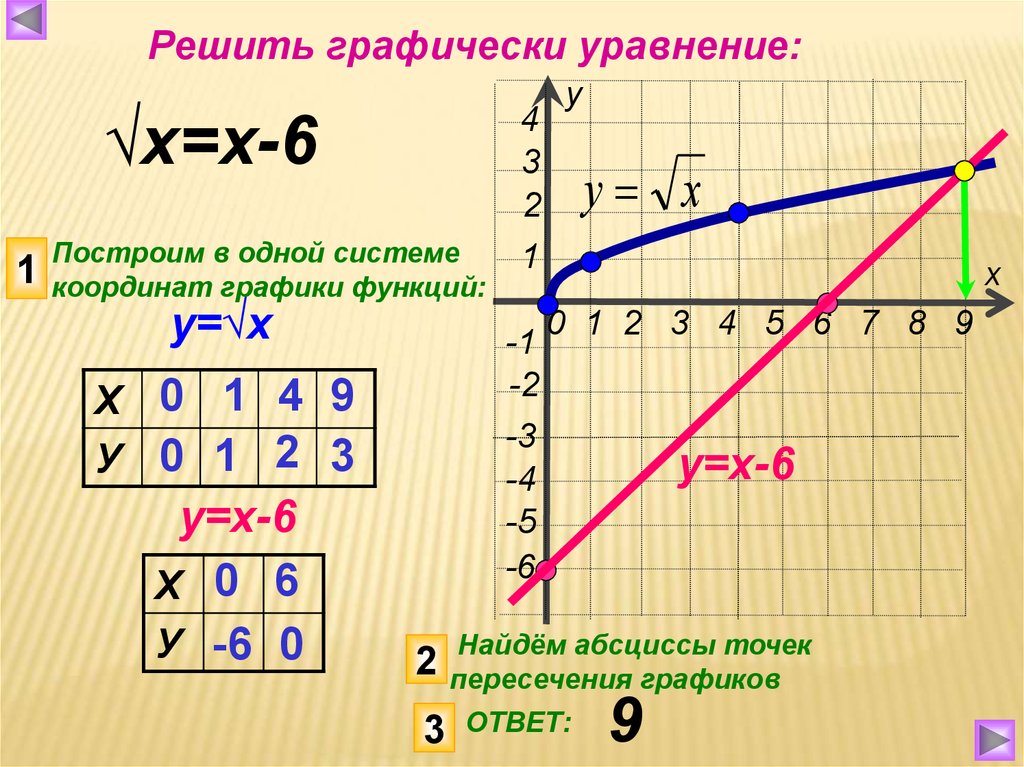
| Равномерная мощность | Нечетная мощность | |
|---|---|---|
| Положительная константа и > 0 | ||
| Отрицательная константа и < 0 |
Показать решение
У вас есть идеи по улучшению этого контента? Мы будем признательны за ваш вклад.
Улучшить эту страницуПодробнее
The Power in the Power Function
- карта |
- < |
- > |
- дом
Итак, вся мощь силовых функций исходит от этой маленькой буквы «б». Давайте посмотрим, какие значения может принимать b и как это меняет форму функция. Для этого давайте снова рассмотрим упрощенную версию нашего уравнение (на этот раз «а» равно 1):
Скорость обмена веществ = 1*Размер b = Размер b
Мы уже знаем, как выглядят отношения для наших четырех млекопитающих:
Для этого мы собираемся исследовать форму силы функция для трех разных диапазонов «b»:
когда b больше 1, между 0 и 1 и меньше нуля. Мы собираемся показать вам, как график функции
внешний вид, определите, что он говорит о связи размера со скоростью метаболизма. Мы будем использовать приведенный выше график в качестве руководства,
но пока мы это делаем, давайте помнить, что приведенный выше график представляет только четырех млекопитающих — и может быть нетипичным — так что
пока мы исследуем поведение функции при изменении значения «b», давайте следить за тем, какое
значения «b» кажутся биологически равными правдоподобно для отношения скорости метаболизма к размеру.
Мы собираемся показать вам, как график функции
внешний вид, определите, что он говорит о связи размера со скоростью метаболизма. Мы будем использовать приведенный выше график в качестве руководства,
но пока мы это делаем, давайте помнить, что приведенный выше график представляет только четырех млекопитающих — и может быть нетипичным — так что
пока мы исследуем поведение функции при изменении значения «b», давайте следить за тем, какое
значения «b» кажутся биологически равными правдоподобно для отношения скорости метаболизма к размеру.
Ниже мы показываем для каждого из трех диапазонов «b» словесное описание того, что это означает для «b» в пределах каждого диапазона, как выглядит функция, опишите, что она означает биологически, затем решите, является ли она правдоподобно полагать, что «b» примет это значение. Помните, поскольку «b» является показателем степени (скорость метаболизма = размер b ), мы действительно исследуем поведение показателей!
б > 1 | 0 < b ≤ 1 | б ≤ 0 |
Что происходит, когда вы увеличиваете число до значения
больше 1? Что произойдет, если возвести число в квадрат или возвести его в степень
5 или 10? Результирующее значение становится все больше и больше со все большей и большей скоростью. | Когда вы возводите число в степень 1, тогда он равен самому себе (и, следовательно, является линейным). Когда его меньше 1 вы эффективно берут «корень» числа (так что X 1/2 то же, что квадратный корень из X). | Когда вы возводите число в нулевую степень, результирующее число = 1. Когда вы возводите число в отрицательную степень, его эквивалент к тому же числу в знаменателе (так, X — b эквивалентно 1/ X b ). |
Итак, если «b» больше 1, это означает, что как размер увеличивается, скорость метаболизма также будет увеличиваться, но все быстрее и быстрее. Например, если вы сравните скорость метаболизма индийского слона с африканским слона (который немного больше), что вы увидите значительное увеличение по скорости метаболизма. Это не имеет никакого смысла! | Когда b равно 1, размер увеличивается линейно с метаболическим
оценивать. | Ни то, ни другое не имеет никакого смысла! Если «b» равно 0, тогда скорость метаболизма всегда равна 1. Совершенно нелепо! Если «b» отрицательно, то по мере того, как организмы становятся больше, скорость их метаболизма все ближе и ближе (но никогда не достигает) 0. Еще одна нелепая закономерность! |
ВЕРДИКТ : НЕТ! | ПРИГОВОР : Это имеет биологический смысл! | ВЕРДИКТ : НЕТ! |
О, немного словарного запаса. Когда b = 1, соотношение остается постоянным для всех классов размеров.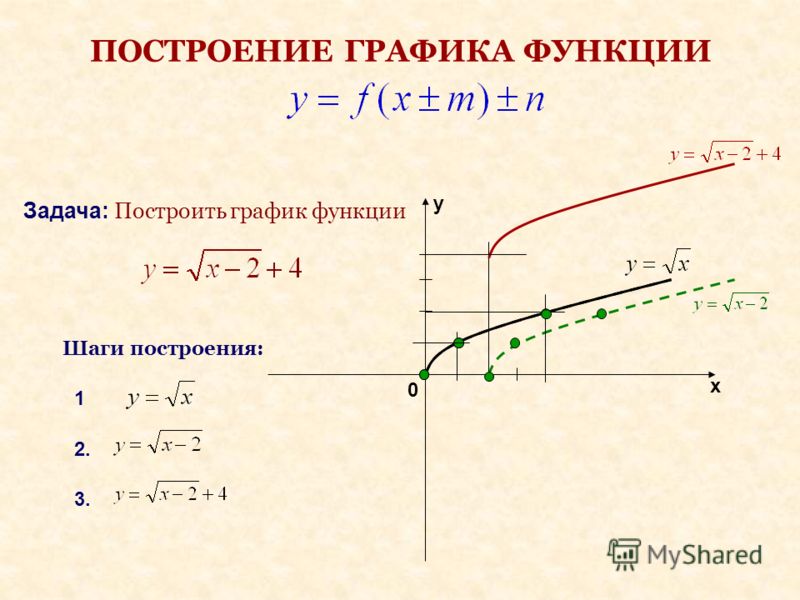 Это называется
«изометрические» отношения. Если отношение меняется между классами размера (так что b ≠ 1), это называется
«аллометрический». Вот почему скейлинговые исследования часто называют областью «аллометрии». Несмотря на то что
(по какой-то причине), когда люди ссылаются на область аллометрии, они обычно имеют в виду изучение формы (т.
меняется ли форма костей по мере того, как динозавры становятся больше?), а не исследования физиологии (т. е. как сердце или
скорость метаболизма меняется по мере того, как млекопитающие становятся больше?).
Это называется
«изометрические» отношения. Если отношение меняется между классами размера (так что b ≠ 1), это называется
«аллометрический». Вот почему скейлинговые исследования часто называют областью «аллометрии». Несмотря на то что
(по какой-то причине), когда люди ссылаются на область аллометрии, они обычно имеют в виду изучение формы (т.
меняется ли форма костей по мере того, как динозавры становятся больше?), а не исследования физиологии (т. е. как сердце или
скорость метаболизма меняется по мере того, как млекопитающие становятся больше?).
Итак, теперь мы знаем, что значение «b» находится в диапазоне от 0 до 1 для нашего примера с млекопитающим. Мы потом покажем
что это верно для всех организмов, и мы потратим много времени на изучение точного значения «b» и его значения.
значит биологически. Но сначала, несмотря на то, что мы только что потратили все это время на изучение поведения степенной функции,
это функция, которая почти всегда используется при изучении отношений масштабирования. Оказывается, есть небольшая хитрость
история — данные для масштабных исследований почти всегда отображаются и анализируются после того, как данные были зарегистрированы.
трансформировался. Итак, мы потратим некоторое время на объяснение того, что это значит, почему это делается, и познакомим вас с
уметь интерпретировать графики и результаты.
Оказывается, есть небольшая хитрость
история — данные для масштабных исследований почти всегда отображаются и анализируются после того, как данные были зарегистрированы.
трансформировался. Итак, мы потратим некоторое время на объяснение того, что это значит, почему это делается, и познакомим вас с
уметь интерпретировать графики и результаты.
Университет штата Мэриленд, 2007 г.
Вы можете ссылаться на этот сайт в образовательных целях.
Пожалуйста, не копируйте без разрешения
запросы/вопросы/отзывы эл. (x + 6)2 (x — 2)2
Математика касается не только чисел, но и работы с различными вычислениями с использованием чисел и переменных. Это то, что в основном известно как алгебра. Алгебра определяется как представление вычислений с использованием математических выражений, состоящих из чисел, операторов и переменных. Цифры могут быть от 0 до 9, операторы — это математические операторы, такие как +, -, ×, ÷, показатели степени и т. д., переменные, такие как x, y, z и т. д.
д.
Экспоненты и степени
используемые для упрощения сложных вычислений, включающих многократное самоумножение, самоумножение — это в основном числа, умноженные сами на себя. Например, 7 × 7 × 7 × 7 × 7 можно просто записать как 7 5 . Здесь 7 — базовое значение, 5 — показатель степени, а значение равно 16807. 11 × 11 × 11 можно записать как 11 3 , здесь 11 — базовое значение, а 3 — показатель степени или степень числа 11. Значение 11 3 равно 1331.
умножается на себя. Если выражение записано как cx y , где c — константа, c — коэффициент, x — основание, а y — показатель степени. Если число, например p, умножить n раз, то n будет показателем степени p. Это будет записано как
p × p × p × p … n раз = p n
Функции
Функцию можно определить как набор правил, относящихся к заданному набору входных данных, которые обеспечивают некоторые возможные выходные данные.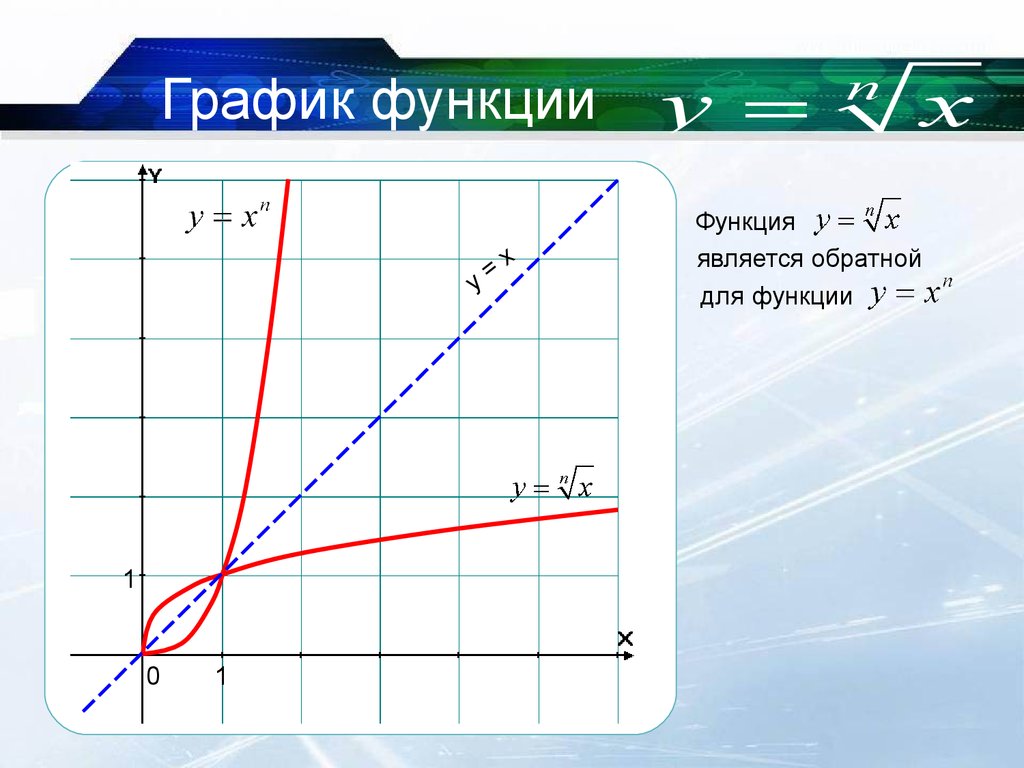 Только те выражения обозначаются как функции, в которых есть один выход для одного входа. Могут ли быть два входа для одного и того же выхода? Да. Однако не может быть двух выходов для одного входа.
Только те выражения обозначаются как функции, в которых есть один выход для одного входа. Могут ли быть два входа для одного и того же выхода? Да. Однако не может быть двух выходов для одного входа.
Функции могут быть представлены как f(x), g(x), h(x) и т. д. Здесь f(x) — результат для заданного входного значения полинома. Например, значение f(x) при x = -2 в функции f(x) = 2x + 20 будет равно 16. Его можно получить, подставив значение x в выражение и решив его.
Функции умножения и деления
Чтобы умножить или разделить две функции, в первую очередь необходимо понять, что умножение и деление являются основными математическими операциями умножения и деления. Точно так же, как числа умножаются или делятся, точно так же умножаются и делятся многочлены. Их можно представить как f(x).g(x) для умножения и f(x)/g(x) для деления.
Степенная функция
Произведение действительного числа, коэффициента и переменной, возведенное в фиксированное действительное или натуральное число, называется степенной функцией. Простыми словами, степенную функцию можно обозначить как переменную, возведенную в действительное число. Степенная функция представлена как y = x R где R — любое действительное число. Например, y = x 2 является степенной функцией, y = 1/x также является степенной функцией и так далее.
Простыми словами, степенную функцию можно обозначить как переменную, возведенную в действительное число. Степенная функция представлена как y = x R где R — любое действительное число. Например, y = x 2 является степенной функцией, y = 1/x также является степенной функцией и так далее.
Вопрос: Найдите степенную функцию, на которую похож график f при больших значениях |x|, учитывая функцию f(x) = (x + 6)
2 (x – 2) 2 .Решение:
Сначала разверните выражение в правой части, используя следующую формулу:
- (a + b) 2 = a 2 + b 2 + 2ab
- (a – b) 2 = a 2 + b 2 – 2ab
f(x) = (6 2 3 x 3 2 2 2 + 4 – 4x)
Now, multiply both terms,
f(x) = (x 4 + 4x 2 – 4x 3 + 36x 2 + 144 – 144x + 12x 3 + 48x – 48x 2 )
f(x) = x 4 + 8x 3 – 18x 2 – 96x + 144)
22 Поскольку ясно, что степень функции равна 4.
Следовательно, степенная функция, на которую похож график f при больших значениях |x| х 4 .
Аналогичные задачи
Вопрос 1. Дана функция f(x) = x 5 + 56x 4 – 78x + 2. Найдите степенную функцию, на которую похож график f.
Решение:
Поскольку функция, указанная в вопросе, уже расширена. Таким образом, нет необходимости в расширении функции.
f(x) = x 5 + 56x 4 – 78x + 2
Поскольку ясно, что степень функции равна 5. Следовательно, степенная функция, на которую похож график f, равна x 5 .
Вопрос 2: Дана функция f(x) = (x + 1) 2 (x – 1) 2 . Найдите степенную функцию, на которую похож график f при больших значениях |x|.
Решение:
Сначала разверните выражение в правой части, используя следующую формулу:
9113 9113 9113 9113 9113 9113 9113 9113 9113 9113 9113 9113 9113 9113 + B .
- (A + B) 2 = A 2 + B 2 + 2AB
- (A — B) 2 = A 2 + B 2 — 2AB
+ B 2 — 2AB + B 2 — 2ABx) = (x 2 + 1 + 2x)(x 2 + 1 – 2x)
Теперь умножьте оба члена,
f(x) = (x 4 + x 2 – 2x 3 + x 2 + 1 – 2x + 2x 3 + 2x – 4x 2 )
f(x) = x 4 – 2x 3 + 911 6
Поскольку ясно, что степень функции равна 4. Следовательно, степенная функция, на которую похож график f при больших значениях |x| х 4 .
Вопрос 3: Дана функция f(x) = (x 5 ) (x + 3) 2 . Найдите степенную функцию, на которую похож график f при больших значениях |x|.
Решение:
Сначала разверните выражение в правой части, используя следующую формулу:
(a + b) 2 = a 2 + b 2 + 2ab
f(x) = (x 2 + 9 + 6x)(x 5 )
, 909 умножить оба члены, f(x) = (x 7 + 9x 5 + 6x 6 )
Поскольку ясно, что степень функции равна 7.
{x}f(x)=bx 9{x+c}+df(x)=bx+c+d
, где
b=2b=2b=2
,
c=1c=1c=1
, и
d=- 3d=-3d=-3
.
Нарисуйте горизонтальную асимптоту
y=dy=dy=d
, поэтому нарисуйте
y=−3y=-3y=−3
.
Идентифицируйте сдвиг как
(−c,d)\left(-c,d\right)(−c,d)
, поэтому сдвиг равен
(−1,−3)\left(- 1,-3\справа)(−1,−3)
.
Сдвиг графика на 9{x+c}+df(x)=bx+c+d
дляxxx
, используйте графический калькулятор для аппроксимации решения.
- Нажмите [Y=] . Введите данное показательное уравнение в строку под названием « Y 1 = ».
- Введите заданное значение для
f(x)f\left(x\right)f(x)
в строку с заголовком « Y 2 = «.- Нажмите [ОКНО] . Отрегулируйте ось y так, чтобы она включала значение, введенное для » Y 2 = ».
- Нажмите [GRAPH] , чтобы просмотреть график экспоненциальной функции вместе с линией для указанного значения
f(x)f\left(x\right)f(x)
.- Чтобы найти значение x , мы вычисляем точку пересечения. Нажмите [2ND] , затем [CALC] . Выберите «пересечение» и нажмите [ENTER] три раза. Точка пересечения дает значение x для указанного значения функции. 9{x}+2,81,2(5)x+2,8
рядом с Y 1 =.
Затем введите 42 рядом с Y2= . Для окна используйте значения от –3 до 3 для x и от –5 до 55 для y . Нажмите [ГРАФИК] . Графики должны пересекаться где-то около x = 2.
Для лучшего приближения нажмите [2ND] , затем [CALC] . Выберите [5: пересечение] и нажмите [ENTER] три раза. Координата точки пересечения x отображается как 2,16619.{x}f(x)=a(b)x
- растягивается по вертикали в a раз, если
∣a∣>1|a|>1∣a∣>1
.- сжимается по вертикали в a раз, если
∣a∣<1|a|<1∣a∣<1
.- имеет y -пересечение
(0,a)\left(0,a\right)(0,a)
.- имеет горизонтальную асимптоту в
y=0y=0y=0
, диапазон(0,∞)\left(0,\infty \right)(0,∞)
и область(-∞ ,∞)\left(-\infty ,\infty \right)(−∞,∞) 9{x}f(x)=4(21)x
.
{x}f (х)=(21)х 9{x}f(x)=4(21)x
32 16 8 4 2 1 0,5 - Постройте точку пересечения y- ,
(0,4)\left(0,4\right)(0,4)
вместе с двумя другими точками. Мы можем использовать(−1,8)\left(-1,8\right)(−1,8)
и(1,2)\left(1,2\right)(1,2)
.Нарисуйте плавную кривую, соединяющую точки.
Рис. 9. Домен 9{x}f(x)=bx
относительно оси y .- имеет y -пересечение
(0,1)\left(0,1\right)(0,1)
, горизонтальную асимптоту наy=0y=0y=0
, диапазон( 0,∞)\left(0,\infty \right)(0,∞)
, и область(−∞,∞)\left(-\infty ,\infty \right)(−∞,∞)
, которые не отличаются от родительской функции.Пример 4. Запись и построение графика экспоненциальной функции
Найдите и начертите уравнение для функции, 9{х}г(х)=-(41)х
–64 –16 –4 –1 –0,25 –0,0625 –0,0156 Постройте точку пересечения y- ,
(0,−1)\left(0,-1\right)(0,−1)
вместе с двумя другими точками.
{x+c}+df(x) =abx+c+d 9{-x}+4\qquad \end{cases}⎩
⎨
⎧f(x)=abx+c+d=2e−x+0+4=2e−x+4
домен
(-∞,∞)\left(-\infty ,\infty \right)(-∞,∞)
; диапазон
(4,∞)\left(4,\infty \right)(4,∞)
; горизонтальная асимптота равна
y=4y=4y=4
.
Попробуйте 6
Напишите уравнение для функции, описанной ниже. Укажите горизонтальную асимптоту, область определения и диапазон.
Раствор
Лицензии и атрибуции
Контент по лицензии CC, совместно используемый ранее
- Precalculus. Автор : Джей Абрамсон и др. Предоставлено : OpenStax. Расположен по адресу : https://openstax.org/books/precalculus/pages/1-introduction-to-functions. Лицензия : CC BY: Attribution .
Условия лицензии : Скачать бесплатно по адресу: http://cnx.org/contents/[email protected]
Экспоненциальные функции и их графики
Экспоненциальная функция в математике — это функция, имеющая постоянное значение, возведенное в степень аргумента (обычно это константа «e», которая приблизительно эквивалентна 2,71828.). Есть несколько реальных применений функции экспоненты. Читайте дальше, чтобы узнать о них и узнать больше о свойствах экспоненциальных функций, о том, как строить графики экспоненциальных функций, формулах, графиках, примерах, практических задачах и многом другом.
Вот что мы рассмотрим в статье:
- Что такое показательная функция? Формула экспоненциальной функции
- Производная экспоненциальной функции
- Свойства экспоненциальных функций
- Экспоненциальные функции графика
- Как найти экспоненциальную функцию на графике?
Что такое показательная функция? Формула экспоненциальной функции
Экспоненциальная функция имеет следующий вид
f (x) = ax.
Здесь
«x» обозначает переменную и является действительным числом.
«a» представляет константу и называется базой функции. Основание должно быть больше 0, т. е. а>0, что не равно 1. Трансцендентное число «е» приблизительно равно 2,71828 и чаще всего используется в качестве основания экспоненциальной функции.
Экспоненциальные функции Примеры
Некоторые примеры экспоненциальных функций:
- f(x) = 3 x+2
- f(x) = 5 x
61 6×9- e(x)
- f(x) = (1/4) x = 4 -x
- f(x) = 0,7 x
Производная экспоненциальной функции
Производная экспоненциальной функции может быть представлена следующим образом:
d(e x )/dx = e x
Кроме того, экспоненциальная функция f(x) =e x обладает особым свойством. Итак, производная показательной функции — это сама функция, как указано ниже:
f ‘(x) = ex = f(x)
Свойства показательных функций
Для выполнения вычислений необходимо понимать свойства экспоненциальных функций.
The key properties are as follows:
- Rule of product
a x a y = a x+y
e.g., 5 2 x 5 3 = 5 2+3 ⇒ 5 5 = 3125
- Правило коэффициента
A x /A Y = A X-Y
E.G.1162 2 = 5 4-2
⇒ 5 2 = 25
- Power rule
(a x ) y = a xy
e.g. (5 2 ) 3 = 5 2×3
⇒ 5 6 = 15,625
- Power of a product
a x b x =(ab) x
⇒ 2 2 3 2 = (2 x 3) 2
⇒ 6 2 = 36
- Power of fractions
(a/b) x = a x /b x
⇒ (6/2) 2 = 6 2 /2 2
⇒ 36/4 =
- Отрицательное правило показания
A -x = 1/ A x
2 -2 = 11166 2
2 -2 = 11166 2
.
- Правило нулевого порядка
a 0 =1
например. 5 0 =1
Здесь a>0 и b>0, x и y — действительные числа.
Пример 1: Решение 4 x = 4 5
Solution : сзади. Ответ: Значение x равно 5.
Пример 2. Решите 5 1-x = 5 5
. , приравняем мощности.
1-x = 5
-x = 5-1
-x = 4
x = -4
Ответ: Значение x равно -4.График экспоненциальных функций
Какой график представляет экспоненциальную функцию? График экспоненциальной функции представляет собой восходящую кривую, как показано на следующем рисунке. Этот график всегда нелинейный, так как его наклоны постоянно меняются.
Здесь, x > 1, значение y = fn(x) будет увеличиваться, когда мы увеличиваем значения (n).
Кроме того, кривая будет становиться круче по мере увеличения показателя степени. Скорость роста тоже увеличится.
Как строить графики экспоненциальных функций?
Теперь мы научимся строить графики экспоненциальных функций. Один из лучших способов построить график экспоненциальной функции — найти несколько точек на графике и нарисовать график на основе этих точек.
Чтобы найти точку на графике, мы сначала выберем входное значение. Теперь вычислите выходное значение из входного значения. Например, для функции f (x) = 2 x +1.
Чтобы найти значение y при x = 1, мы можем использовать f(1)
f (1) = 2 1 + 1
= 3
Итак, у нас есть первая точка на графике, то есть (1, 3).
Используя точки на графике, мы можем определить следующие важные особенности графика:
- Y-отрезок
- Является ли наклон графика положительным или отрицательным?
- Как изменяется значение y при увеличении значения x?
Точка пересечения с осью Y
Точка пересечения с осью Y экспоненциального графика важна, поскольку помогает нам определить ряд других особенностей.
Мы должны оценить функцию при x = 0, чтобы найти значение y-перехвата.
f(x) = 2 x + 1
f(0) = 2 0 +1
= 1+ 1
= 2
Наклон графика3 , мы используем f (0) и f (1). Наклон либо увеличивается, либо уменьшается. Следующие два утверждения помогут вам определить наклон графика экспоненциальной функции.
- Когда f (1) > f (0), то график имеет положительный наклон.
- Когда f (1) < f (0), то график имеет отрицательный наклон.
В приведенном выше примере графика — f (x) = 2 x +1, f(1) = 3 и f(0) = 2. Поскольку f (1) > f(0), наклон графика положительный.
Конечное поведение
Термин конечное поведение относится к отношению между x и y. Мы изучаем, что происходит со значением y, когда x становится очень большим в положительном или отрицательном направлении.
Когда мы рисуем экспоненциальные функции, значение y возрастает до положительной или отрицательной бесконечности к одному концу.
Он приближается, но не достигает горизонтальной линии. Эта горизонтальная линия, к которой график экспоненциальной функции приближается, но не достигает, называется горизонтальной асимптотой.
Чтобы построить экспоненциальную функцию, f (x) = 2 x +1, мы посчитаем еще несколько точек 1) = 2 -1 +1
= 1,5
f (2) = 2 2 +1
= 5
Итак, точки равны (2,5), (-2, 1,25) и (-1, 1,5). Теперь мы можем построить график экспоненциальной функции.
Шаги для построения графика экспоненциальной функции
Следующие шаги помогут вам легко построить график экспоненциальной функции:
- Шаг 1: Мы оценим экспоненциальную функцию для различных значений x. Мы начнем с x = -1, 0, 1 и при необходимости найдем дополнительные точки.
- Шаг 2: Теперь мы будем использовать точки, чтобы нарисовать кривую графика, установив направление наклона и точку пересечения с осью Y.
- Шаг 3: Мы продлим кривую с обоих концов.
В то время как один конец будет достигать горизонтальной асимптоты, другой будет приближаться к отрицательной или положительной бесконечности по оси y.
Как найти экспоненциальную функцию на графике?
Мы можем найти уравнение экспоненциальной функции по заданному графику. Это многоэтапный процесс. Каждый график будет предоставлять различную информацию в зависимости от его типа. Мы можем расшифровать некоторую информацию из самого данного графа, а затем решить другие требования к уравнению экспоненциального графа. Вот список переменных, которые мы должны искать на данном графике:
а — будет задано, или мы можем решить его с помощью алгебры.
b — Будет дано, или мы можем решить его с помощью алгебры.
c — Если мы примем x = 0 и проигнорируем c, то значение y будет равно точке пересечения с осью y. Далее мы подсчитаем количество единиц значения y от оси y. Это число даст нам значение «с».
д — Решаем.
k – равно значению горизонтальной асимптоты.
Давайте рассмотрим пример, чтобы полностью понять процесс извлечения экспоненциальной функции из графика.
Пример: Найдите экспоненциальную функцию ( y = ab x ) по заданному графику.
Решение: Для решения этого графа нам нужно будет найти значения a и b.
Чтобы найти a, мы выберем точку на графике, которая исключает b, так как мы еще не знаем b. Итак, мы возьмем точку пересечения по оси y, т. е. (0,3).
Так как y = ab x (дано)
= 3 = ab 0
= 3 = a1
Итак, a = 3
Чтобы найти b, мы возьмем другую точку на графике, скажем (1,6).
Так как y = ab x (дано)
= 6 = 3b 1 ( Подставим значение a, вычисленное на предыдущем шаге.)
Итак, b = 2
Запишем окончательное уравнение, мы подставим значения, которые мы рассчитали в данной форме уравнения.
As, y = ab x и a = 3, b = 2
Уравнение будет y = 3(2) x
9112 9112. Практические задачи 2 2Вопрос 1: Решайте следующие уравнения:
A.
2x = 6 25 2x = 6 25 9114 91146 2x = 6 25
c.4 1 = 4 + 4 5 – 4
Вопрос 2: Учитывая функцию f(x)= 3x, оцените каждое из следующего.
a.f(3)
b.f(0)
c.f4/5
d.f(1)
Вопрос 3 : Учитывая функцию f (x) = (4/3) x
график для f(x) = e -x + 2
Вопрос 5 : Нарисуйте график для y = 5(2) x
Часто задаваемые вопросы заданная экспоненциальная функция?
Ответ. График слева представляет заданную экспоненциальную функцию. График представляет собой экспоненциальную кривую, потому что он экспоненциально возрастает слева направо. 93, что упрощается до 8.
3. Как определить, является ли график экспоненциальным?
Ответ.

 Если , то ветви параболы «смотрят» вверх, если , то вниз.
Если , то ветви параболы «смотрят» вверх, если , то вниз.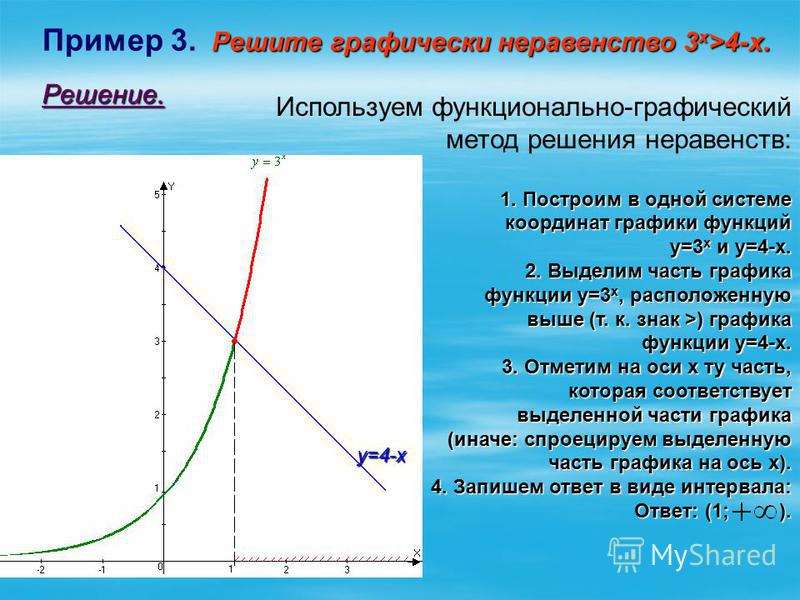
 Если , то ветви гиперболы лежат в 1-й и 3-й координатных четвертях, если , то во 2-й и 4-й (см. примеры на чертеже ниже). Очевидно, что перед нами нечётная функция,
поскольку: .
Если , то ветви гиперболы лежат в 1-й и 3-й координатных четвертях, если , то во 2-й и 4-й (см. примеры на чертеже ниже). Очевидно, что перед нами нечётная функция,
поскольку: .
 е. множество R;
е. множество R;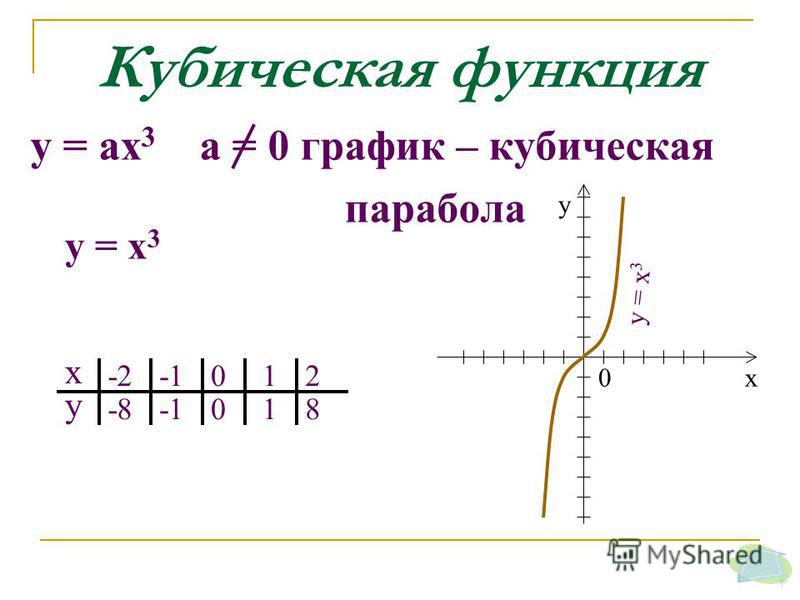


 Когда b меньше 1, это означает, что по мере увеличения размера скорость метаболизма также увеличивается.
увеличивается, но увеличивается все медленнее по мере того, как организмы становятся все больше и больше.
Привет! Это похоже на соотношение для нашего графа млекопитающих (см. выше).
Когда b меньше 1, это означает, что по мере увеличения размера скорость метаболизма также увеличивается.
увеличивается, но увеличивается все медленнее по мере того, как организмы становятся все больше и больше.
Привет! Это похоже на соотношение для нашего графа млекопитающих (см. выше). Следовательно, степенная функция, на которую похож график f при больших значениях |x| х 4 .
Следовательно, степенная функция, на которую похож график f при больших значениях |x| х 4 .  x) = (x 2 + 1 + 2x)(x 2 + 1 – 2x)
x) = (x 2 + 1 + 2x)(x 2 + 1 – 2x)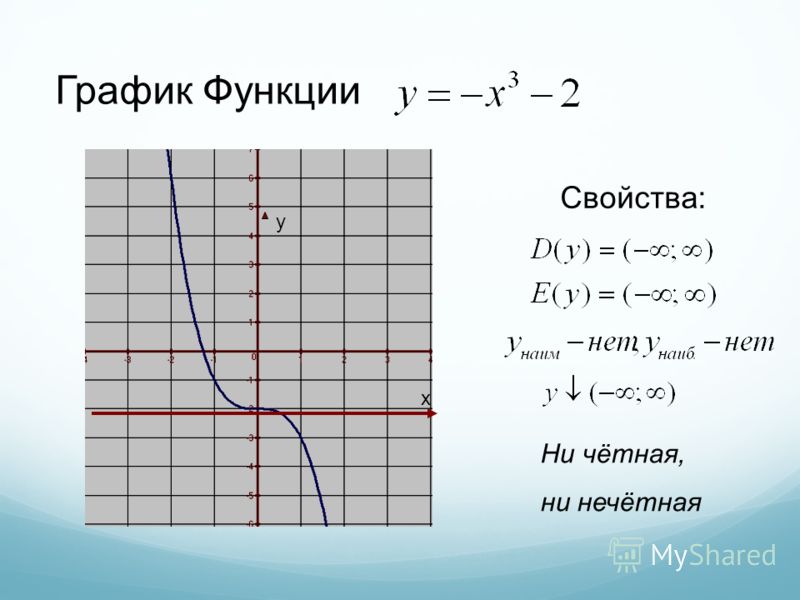 {x}f(x)=bx 9{x+c}+df(x)=bx+c+d
{x}f(x)=bx 9{x+c}+df(x)=bx+c+d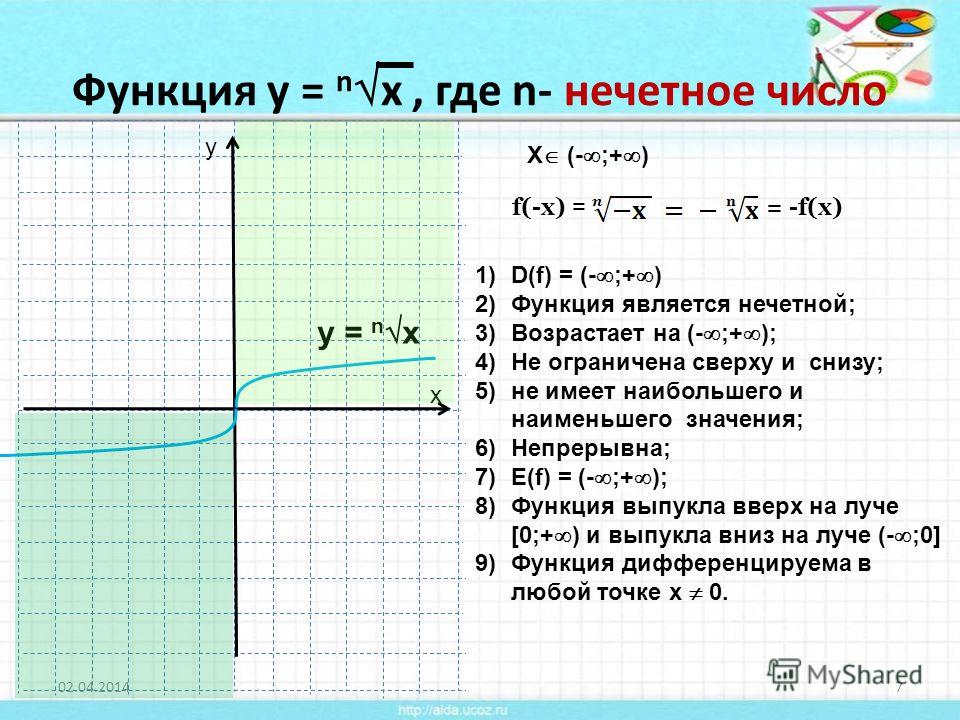
 Затем введите 42 рядом с Y2= . Для окна используйте значения от –3 до 3 для x и от –5 до 55 для y . Нажмите [ГРАФИК] . Графики должны пересекаться где-то около x = 2.
Затем введите 42 рядом с Y2= . Для окна используйте значения от –3 до 3 для x и от –5 до 55 для y . Нажмите [ГРАФИК] . Графики должны пересекаться где-то около x = 2. {x}f (х)=(21)х 9{x}f(x)=4(21)x
{x}f (х)=(21)х 9{x}f(x)=4(21)x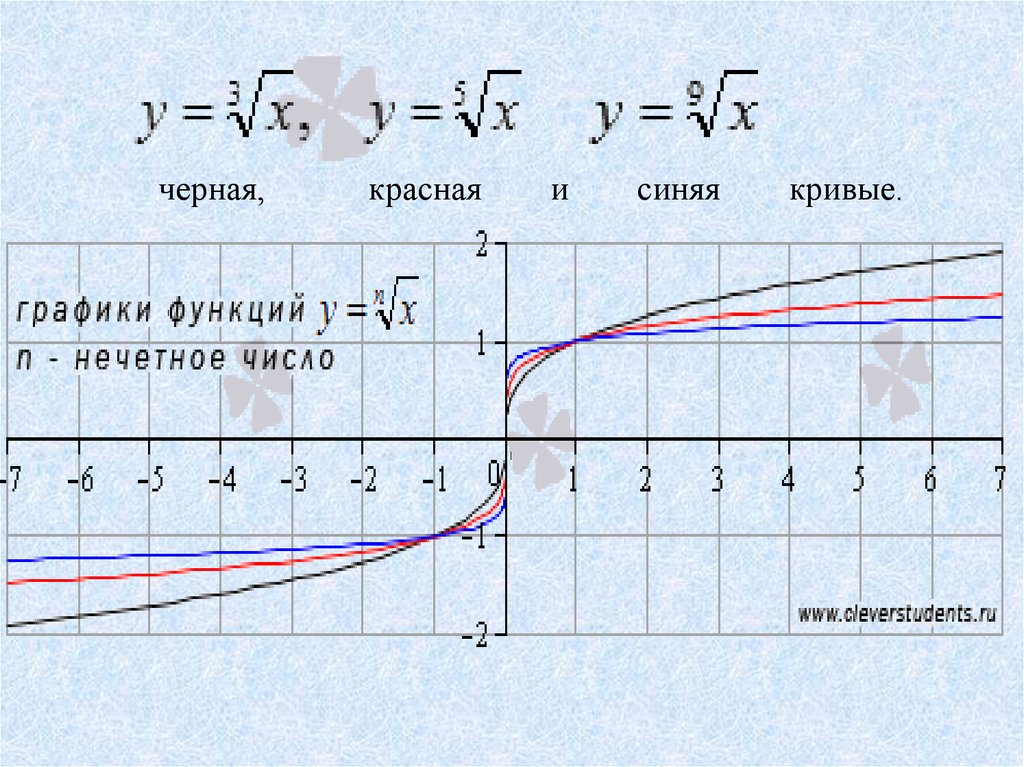 {x+c}+df(x) =abx+c+d 9{-x}+4\qquad \end{cases}⎩
{x+c}+df(x) =abx+c+d 9{-x}+4\qquad \end{cases}⎩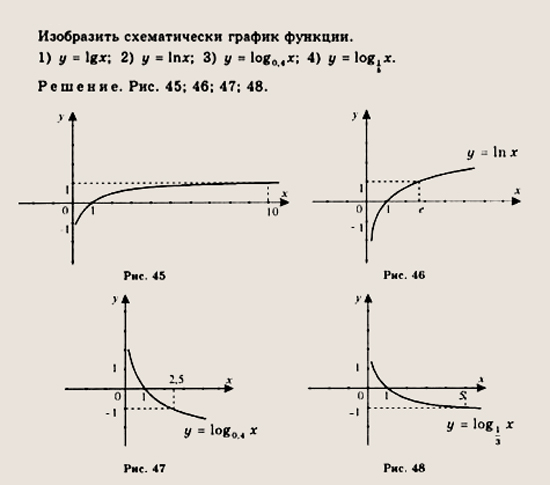 Условия лицензии : Скачать бесплатно по адресу: http://cnx.org/contents/[email protected]
Условия лицензии : Скачать бесплатно по адресу: http://cnx.org/contents/[email protected]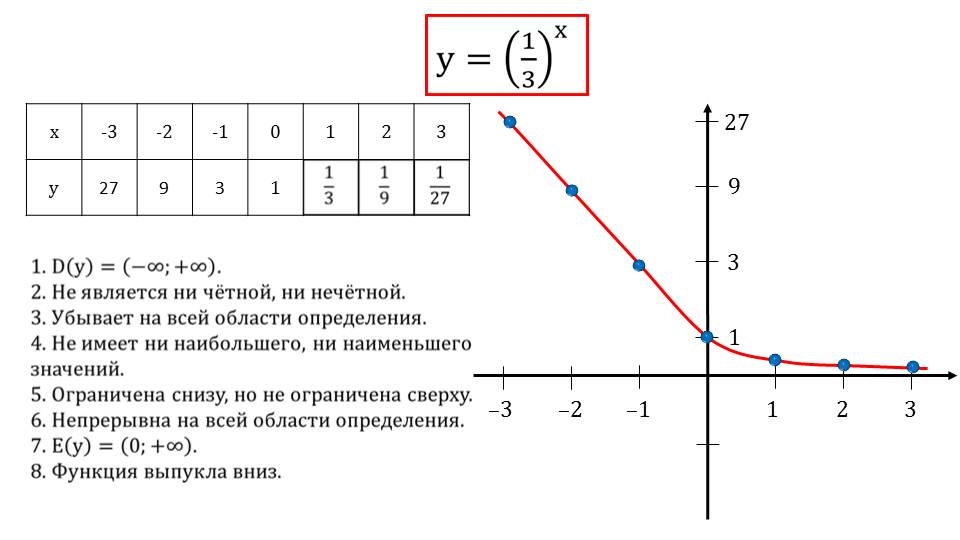
 The key properties are as follows:
The key properties are as follows: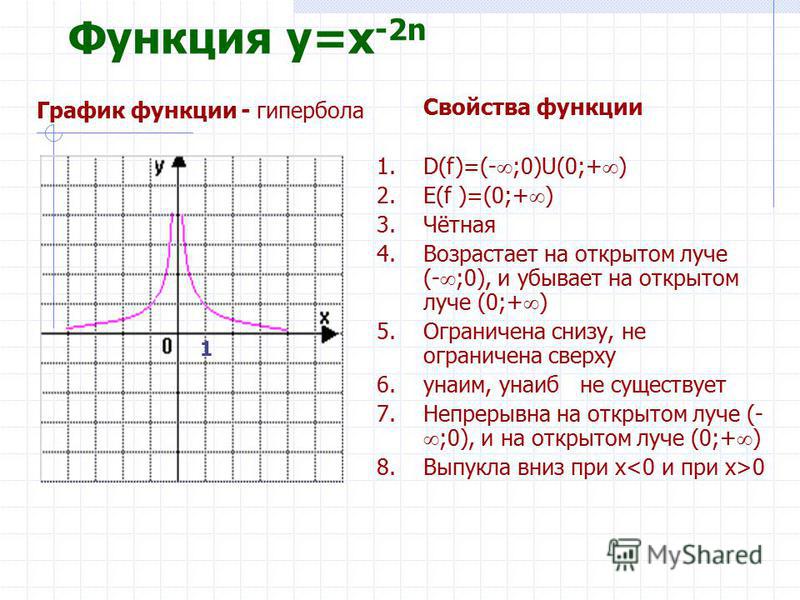
 Кроме того, кривая будет становиться круче по мере увеличения показателя степени. Скорость роста тоже увеличится.
Кроме того, кривая будет становиться круче по мере увеличения показателя степени. Скорость роста тоже увеличится.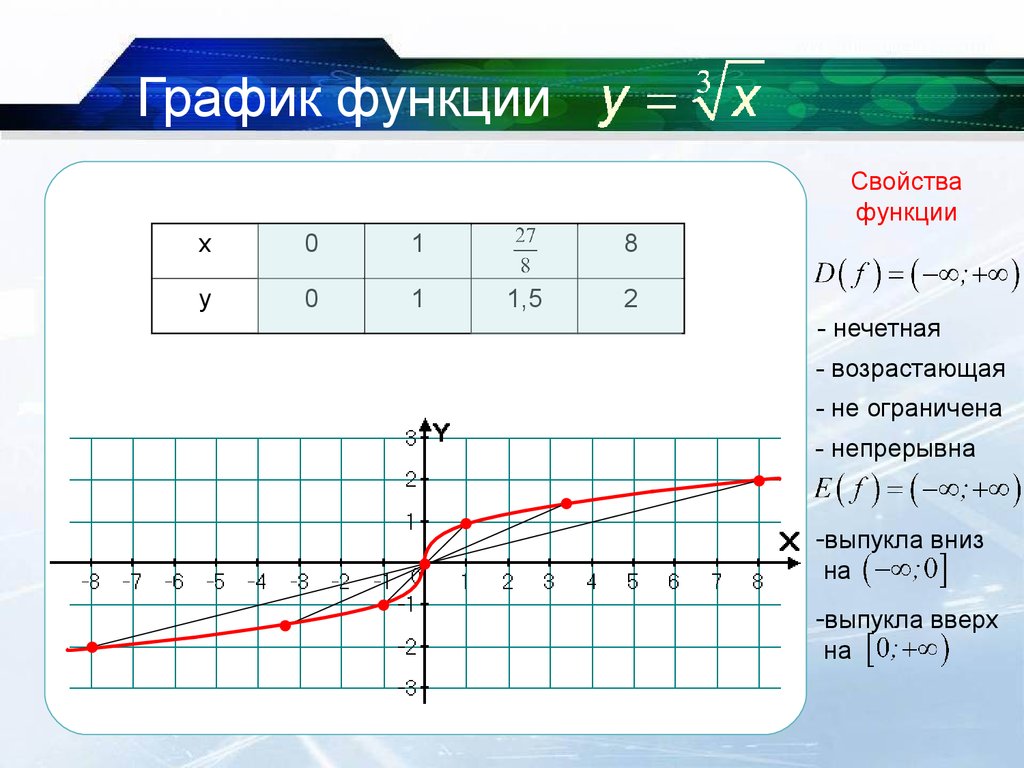 Мы должны оценить функцию при x = 0, чтобы найти значение y-перехвата.
Мы должны оценить функцию при x = 0, чтобы найти значение y-перехвата.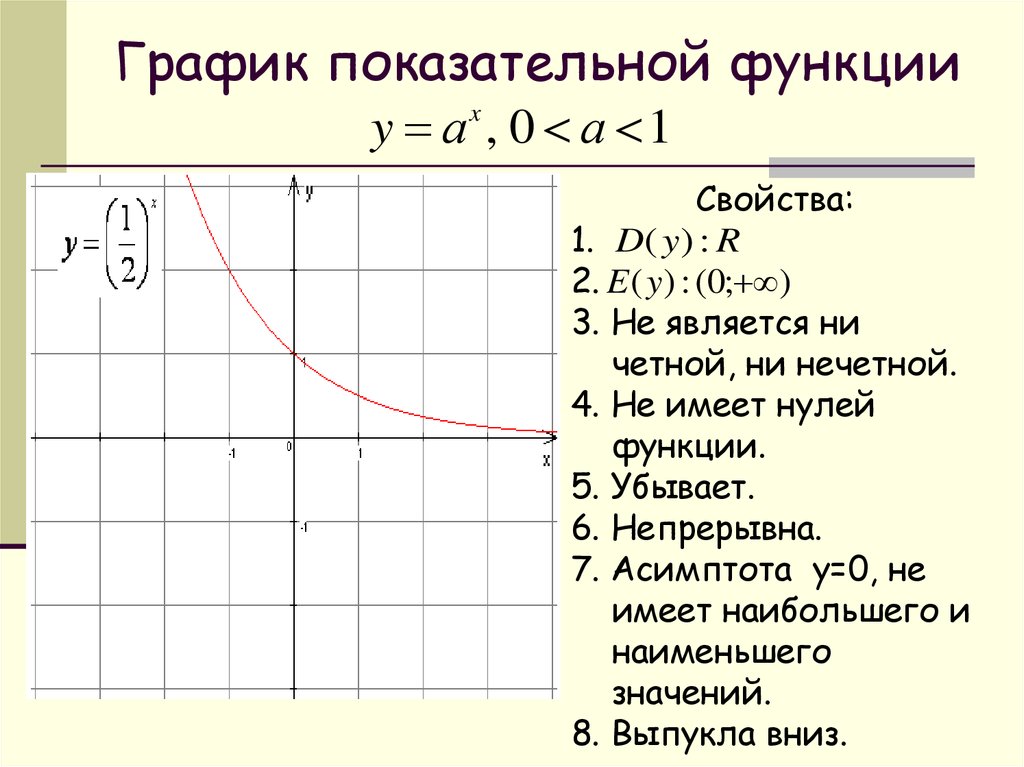 Он приближается, но не достигает горизонтальной линии. Эта горизонтальная линия, к которой график экспоненциальной функции приближается, но не достигает, называется горизонтальной асимптотой.
Он приближается, но не достигает горизонтальной линии. Эта горизонтальная линия, к которой график экспоненциальной функции приближается, но не достигает, называется горизонтальной асимптотой. В то время как один конец будет достигать горизонтальной асимптоты, другой будет приближаться к отрицательной или положительной бесконечности по оси y.
В то время как один конец будет достигать горизонтальной асимптоты, другой будет приближаться к отрицательной или положительной бесконечности по оси y.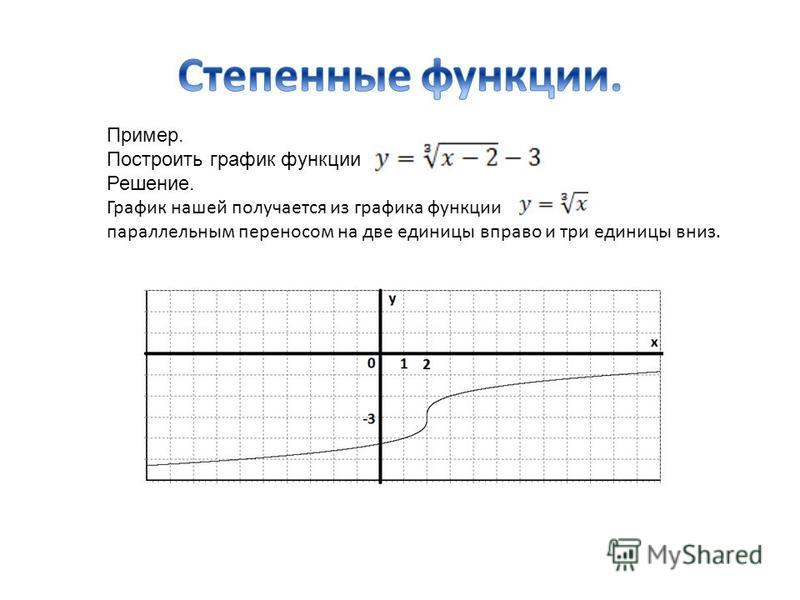
 6 2x = 6 25
6 2x = 6 25