Построение графиков сложных функций на основе свойства монотонности
Похожие презентации:
Исследовательская работа по теме: Построение графиков сложных функций на основе свойства монотонности
Степенные функции, их свойства и графики
Степенные функции, их свойства и графики
Функции, их свойства и графики
Преобразование графиков тригонометрических функций и их свойства
Свойства и графики тригонометрических функций
Логарифмическая функция, ее свойства и график
Функции и их свойства
Функции и их свойства. Предел последовательности и функции. Производная функции и дифференциал
Основные свойства функций и их графики
y
y
k
y
x
k
y
x
k 0
o
k 0
o
x
x
y
y
y sin x
o
y x2
x
o
x
y
y
y
x
y arc tgx
o
o
x
x
y
y
y log a x
o
a 1
0 a 1
a 1
x
0 a 1
o
y ax
x
Итак, рассмотрим функцию :
y arctg 2 x
 Она является композицией двух функций:
Она является композицией двух функций:v 2 x (назовём её внутренней функцией )
y arctgv (назовём её внешней функцией).
Каждая из них является элементарной.
Построим графики этих функций в системе координат.
v
y
v 2x
y
y arctg 2 x
y arctgv
2
2
o
x
o
v
o
2
Внутренняя функция является строго возрастающей: х возрастает от до ;
v возрастает от 0 до .
По графику внешней функции определяем: v возрастает от 0 до ;
y возрастает от 0 до 2 .
Итак, при возрастании х от до ,
у возрастает от 0 до 2 .
Контрольная точка: x = 0; y =
4
x
y 2
Построить график функции
Внутренняя функция v= 1/x. Внешняя функция
Строим графики внутренней и внешней функций.
y
v
1
v
x
y 2
1
x
.
y 2v
.
y
v
y 2
1
x
y(1)=2; y(1/2)=4 ; y(-1)= ½.
o
x
o
v
o
Промежутки монотонности внутренней функции:
x возрастает от до 0; v убывает от 0 до
x возрастает от 0 до ; v убывает от до 0
Такому изменению v соответствует убывание y от 1 до 0 и от до 1
Для более точного построения следует использовать контрольные точки,
выбирая те значения x, при которых легко вычислять точные значения y.

y(1) = 2; y(1/2) = 4 ; y(-1) = ½.
x
Итак, построение графика сложной функции y = f (v(x)) в не которых случаях можно осуществить по следующему плану:
1
Начертить графики:
внутренней v = v(x) функции
внешней y = f(v) функции
И построить систему координат ХОУ.
2
Определить промежутки монотонности внутрен
ней функции
и отметить их на оси ОХ плоскости ХОУ.
3
На каждом промежутке определить границы изме
нения внутренней функции, выбирая те значения
y = v(x), которые попадают в область определения
функции y= f(v).
По графику внешней функции y= f (v) найти харак
тер изменения функции y.
5
В системе координат ХОУ начертить график
y= y(x).
y
Построить график функции
Строим графики
v x2 1 и
v
y
1
x2 1
1
v
y
1
2
1 2
1
y
v
v x 1
o
x
o
y
v
y
o
х возрастает от 0 до ; v возрастает от 1 до
v возрастает от 1 до ; у убывает от 1 до 0.
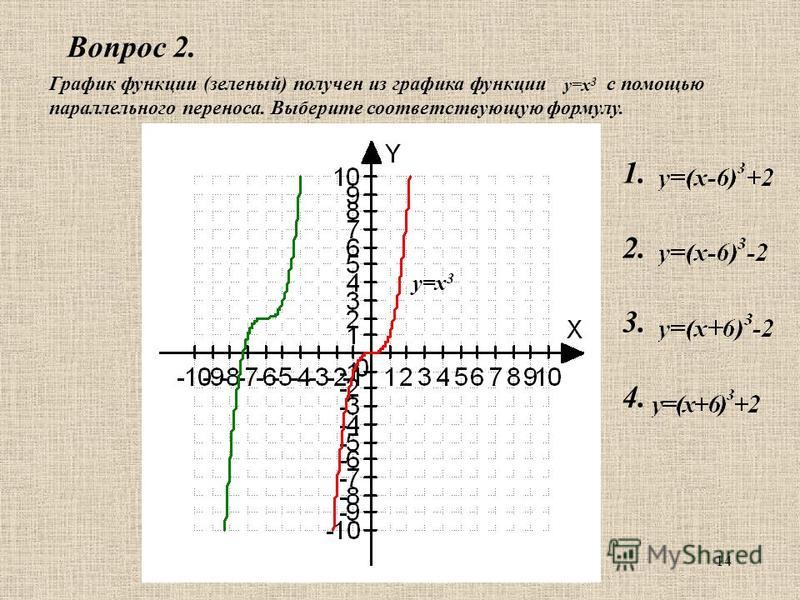
Воспользовавшись чётностью функции, получаем такой график
1
x2 1
x
При построении графиков следует иметь
в виду, что область определения сложной
функции Y = f(v(x)) может быть уже области
определения внутренней функции !
Построить график функции
Строим графики элементарных функций
y ln x 2 3x 2
v x 2 3x 2
и
v
y ln v
y ln x 2 3x 2
v x 3x 2
2
.
y
y
y ln v
o
x
o
v
o
x
х возрастает от до 1; v убывает от до 0.
х возрастает от 2 до ; v возрастает от 0 до
На отрезке [ 1;2 ] функция v(x) = 0 либо v(x)< 0 .
Следовательно, при этих значениях функция y = f (v(x)) не определена
И х = 1, х = 2 — вертикальные асимптоты.
v убывает от до 0; у убывает от до .
v возрастает от 0 до ; у возрастает от до .
Построить график функции
y 2
sin x
.
Достаточно построить график на отрезке , длина которого равна
периоду функции.
v
Строим графики v sin x и y 2 .
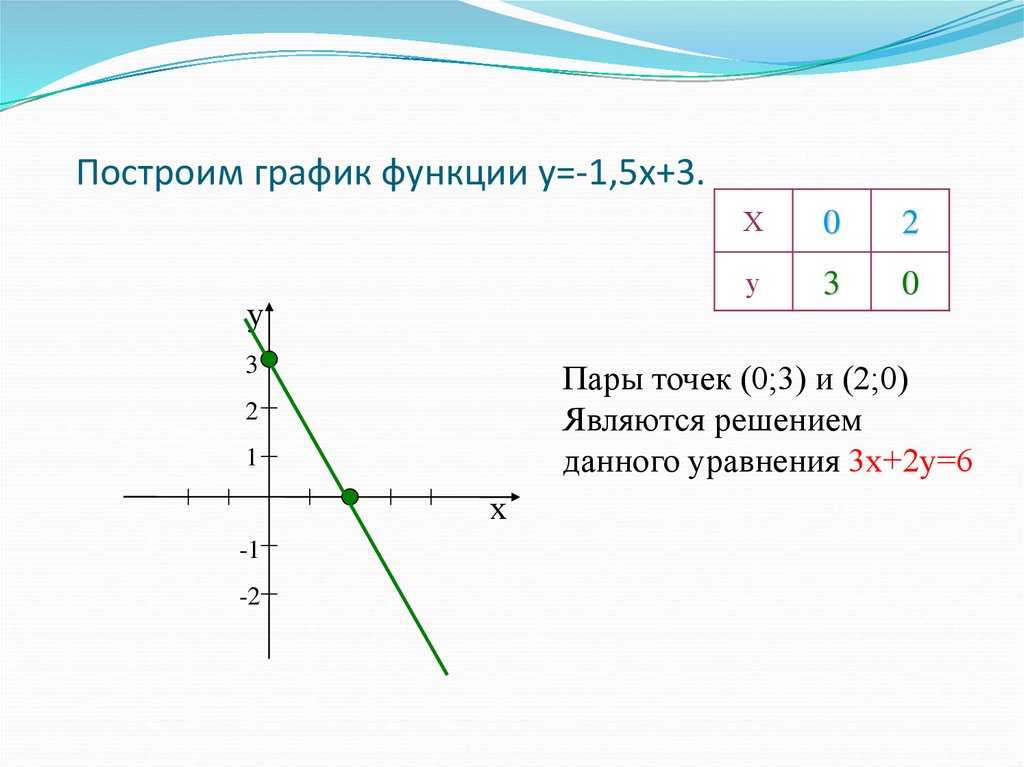
y
v sin x
y
v
y 2 sin x
y 2v
o
x
o
v
o
х возрастает на отрезке ; v возрастает от -1 до 1
2 2
у возрастает от ½ до 2 . .
х убывает на отрезке
у убывает от 2 до ½.
3
2 ; 2 ; v убывает от 1 до -1;
Контрольные точки: х = 0, у = 1; х = -п/2, у = ½ ; х = п/2, у = 2 ;
x
1
2х
Построить график функции
2
4 х 3
Данная функция является композицией трёх функций:
v 1
u x 2 4x 3
y 2v
u
Отсюда последовательно получаем три графика.
u
y
v
1
1
v 2
x 4x 3
y 2 x 4 x 3
2
u x 2 4x 3
o
x
o
x
o
x
Здесь мы обошлись без графиков функций v = 1/u и y = 2 v , свойства
монотонности которых хорошо известны.
Построить график функции
y
1
.
1 2 x
Конечно, при построении графиков сложных функций надо использовать весь
арсенал элементарных средств: переносы, отражения, сложение графиков и т.
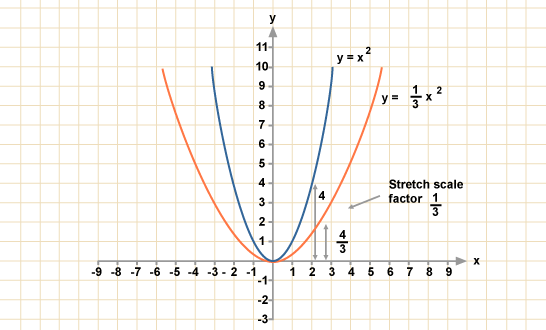 д.
д.Рассмотрим ещё примеры.
y
u
v
v 1 u x
u1 2 x
o
x
y
o
u
1
1 2 x
o
u 2 x
1. Строим график
2. Строим график
x
.
u1 2
u 2 x ,
(симметрия относительно оси ОХ).
3. Строим график v=1+u(x), (смещение на 1 вдоль оси ОУ вверх).
4. Строим график y= 1/v(x), на основании монотонности функций
x
Построить график функции
y lg sin x
Освоив данный метод построения графиков сложных функций,
можно достаточно быстро строить эскизы этих графиков .
v lg u
u sin x
y lg sin x
y
2
o
2
3
x
Итак, на сегодняшнем занятии мы познакомились ещё
с одним из способов построения графиков функций.
Для овладения данной методикой необходима практика.
Этим мы и займёмся на следующих наших занятиях.
Домашнее задание:
Построить графики функций:
1.
2.
3.
4.
y arctg ( x2 4 x 5)
y ln sin x
y 2tgx
y arccos(1 x3 )
?
English Русский Правила
3-8Секция-2,3-линейные функции и слопа-ответы-Google Suce
ALLBILDERVIDEOSBüchermapsNewshopping
SUCOPTIONEN
[PDF] Секция 2.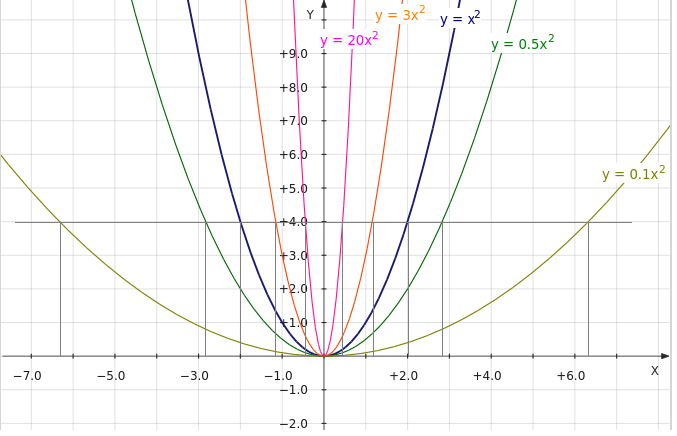 3
3
[PDF] Секция 2.3
[PDF].
Линейные функции и наклон. РАЗДЕЛ 2.3. Цели. Вычислить наклон линии. Запишите уравнение прямой в форме точка-наклон. Напишите и начертите.
[PDF] 2.3 Линейные функции и наклон
Teachers.dadeschools.net › rvancol › Chapter2 › Ch3_Section3
Раздел 2.3 Линейные функции и наклон 229. 116. Я построил график, и одна часть моего графика представляет собой одну точку. 117. Я заметил, что коэффициент разности составляет …
Раздел 2.3. Линейные функции и наклон. линейного уравнения, x-intercept и многое другое.
Алгебра колледжа: Раздел 2.3 (Линейные функции и наклон) — YouTube
www.youtube.com › смотреть
16.09.2019 · Это видео о MAC 1105 — Алгебра колледжа: Раздел 2.3. В этом разделе исследуются линейные …
Dauer: 19:45
Прислан: 16.09.2019
Es fehlt: ответы | Muss Folgendes enthalten:ответы
Раздел 2.3 – Линейные функции и форма пересечения наклона Рассмотрим . ..
..
slideplayer.com › slide
Раздел 2.3 – Линейные функции и форма пересечения наклона. … Решением линейного уравнения является любая упорядоченная пара (x, y), которая делает уравнение верным.
2.3 Линейные функции и форма пересечения наклона Наклон кривой …
slideplayer.com › slide
Линейные функции Функция, графиком которой является линия, является линейной функцией. Вы можете представить линейную функцию линейным уравнением, например, y = 6x – 4.
[PDF] 2.3 Линейные функции
cf.linnbenton.edu › math › storrsm › upload › 2.3 б/у часть 1.pdf
Найдите наклон прямой, проходящей через заданные точки. (Если ответ не определен, введите UNDEFINED.) (−2, 4) и (9, 9).
Es fehlt: раздел- | Muss Folgendes enthalten:section-
Решения для главы 2.3: Линейные функции и наклон — StudySoup
studysoup.com › tsg › math › College-алгебра › Cha…
Bewertung 4,0(303)
Нужна помощь с домашним заданием? Ответ: 2.