График функции y sin 3x: Как построить график функции y=sin 3x — Спрашивалка

Содержание

График функции — определение термина

Термин и определение

линия на плоскости, как множество точек, координаты которых (x, y) связаны соотношением y = f(x) или F(x, y) = 0; графиком функции двух переменных z = f (x, y), в прямоугольной декартовой системе координат в пространстве является в общем случае поверхность

Еще термины по предмету «Высшая математика»

Направляющие углы

углы α, β и γ, образуемые положительными направлениями осей декартовой прямоугольной системы координат с положительным направлением рассматриваемой прямой s

Обратная величина (обратное число)

отношение единицы к рассматриваемому числу a, т. е. a−1 = 1/a; число, произведение которого на рассматриваемое число равно единице; обратный элемент числа относительно умножения

Спрямляемая кривая

кривая, имеющая конечную длину

Научные статьи на тему «График функции»

Пример задачи Пример 1 Построить

графики функций $y=sin3x$ и $y=-sin3x.

$ Решение….
Первым этапом построим график функции $y={\sin x\ }$….
На рисунке 9 данная функция изображена мелким пунктиром….
После этого построим график функции $y=sin3x$ по правилу 3 выше….
Последним этапом из графика функции $y=sin3x$ получаем график функции $y=-sin3x$ по правилу 6, описанном

Статья от экспертов

В статье рассмотрен метод построения графиков сложных функций без помощи производной, если известны графики внутренней и внешней функций. Определяются асимптоты графика, промежутки монотонности, нули функции. По графикам внутренней и внешней функций исследуется «поведение» функции в окрестностях определенных точек и при неограниченном возрастании и убывании аргумента, выясняется характер изменения функции. Составляется таблица зависимости переменных и строятся в координатной плоскости соответ..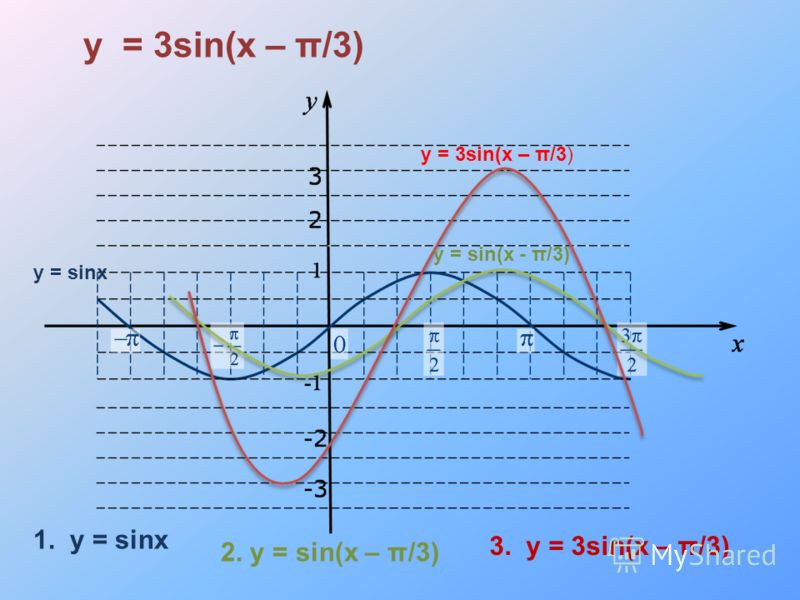

Научный журнал

Creative Commons

Графический способ Введем определение графика функции: Определение 3 График функции $f(x)$…
Задание графика функции называется графическим способом задания функции $f(x)$….
График функции $y=f(x)$….
Схема для построения графика функции Область определения $D(f)$ и область значения $E(f)$….
Пример исследования и построения функции Задача Исследовать функцию и построить её график:

Статья от экспертов

Рассмотрены определения понятия выпуклости (вверх, вниз) графика функции с помощью метода касательных, хорд и аналитического метода. Формулируются признаки и соответствующие способы исследования функций на выпуклость графика с использованием второй производной и функции обобщения.

Научный журнал

Creative Commons

Повышай знания с онлайн-тренажером от Автор24!

📝 Напиши термин
✍️ Выбери определение из предложенных или загрузи свое
🤝 Тренажер от Автор24 поможет тебе выучить термины, с помощью удобных и приятных карточек

Возможность создать свои термины в разработке

Еще чуть-чуть и ты сможешь писать определения на платформе Автор24. Укажи почту и мы пришлем уведомление с обновлением ☺️

Привет! Рады, что термин оказался полезен 🤩

Для копирования текста подпишись на Telegram bot. Удобный поиск по учебным материалам в твоем телефоне

Подписаться и скачать термин

Включи камеру на своем телефоне и наведи на qr-код.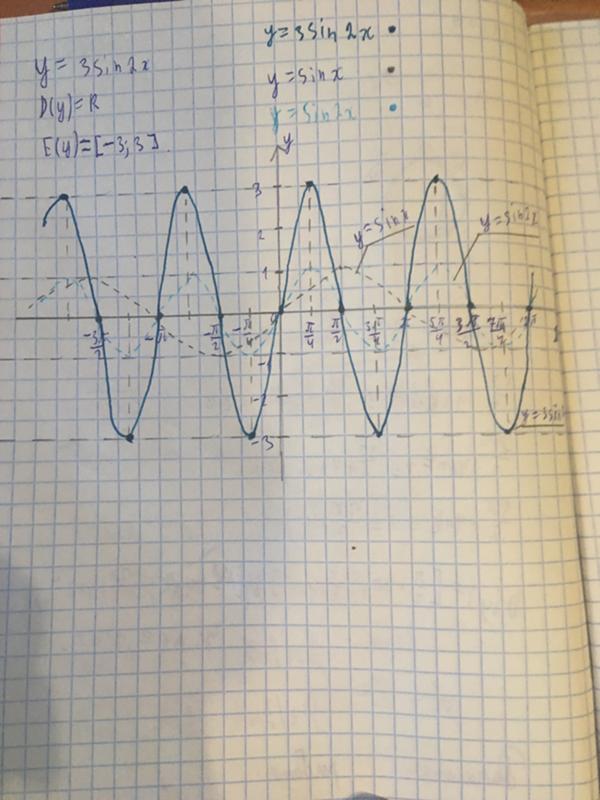 Edu24_bot откроется на устройстве

Привет! Рады, что термин оказался полезен 🤩

Подписчики нашего бота Edu24_bot получают определение прямо в телеграмм! Просто перейди по ссылке ниже

Скачать термин

Включи камеру на своем телефоне и наведи на qr-код. Edu24_bot откроется на устройстве

Новая папка / № 5(1)

№5. Методика изучения тригонометрических функций

Введение тригонометрических функций начинается в старшей школе с введения элементарных понятий: числовая окружность, числовая окружность на координатной плоскости, определения синуса и косинуса числа, основное тригонометрическое тождество, определение тангенса и котангенса, тригонометрические функции числового аргумента, числовые функции углового аргумента, формулы приведения.

И только после этого рассматривают функцию y=sin x, свойства и график.

Свойства:

D(y)=R
y=sin x – нечётная
y=sin x возрастает на [0;П/2], убывает на [П/2;П]
ограничена снизу и сверху
у_наим=-1, у_наиб=1

По этим свойствам строим график, таблично на [0;П], используя свойство симметричности на остальном графике.

После построения: непрерывность

В таком же порядке рассматриваем функцию y=cos x.

Опр: Функцию f(x),xєX называют периодической, если сущ. Т≠0, что для любого xєX выполняется f(x-T)=f(x+T), T – период функции f(x), значит функции y=sin x, y=cos x – периодические.

sin(x-2П)=sinx=sin(x+2П)

cos(x+2П)=sinx= sin(x-2П), 2П – период функций y=sin x, y=cos x.

Периодом является любое число вида kT, где k=±1;±2;±3…

T – наименьший положительный период, нахождение Т по определению.

Пример: Найти период функции y=sin 3x.

Решение: Пусть Т – основной период

f(x)=f(x+T)

f(x)=sin(x)

f(x+T)=sin 3(x+T)=sin (3x+3T)

sin 3x=sin (3x+3T)→3T=2Пn, т.к. нужен основной период n=1

3T=2П, Т=2П/3

Основной период функции y=sin kx (y=cos kx) равен 2П/k.

После изучения функций y=sin x , y=cos x знакомятся с преобразованием графиков функции y=f(x), y=mf(x), y=f(kx).

Далее знакомятся с функциями y=tg x, y=ctg x.

№5 Методика изучения тригонометрических функций

Тригонометрии в школе традиционно уделяется много внимания — сначала в курсе геометрии, затем в курсе алгебры и начал анализа. А.Г.Мордкович предлагает построить изучение темы «Тригонометрия» по следующей схеме: функция – уравнения – преобразования. Объясняется это тем, что сначала целесообразно изучить «простые модели» (таковыми являются элементарные функции), а затем переходить к изучению «сложных моделей» (таковыми в математике являются сложные выражения, которые нужно упрощать, используя формульный аппарат). Таким образом, изучение данной темы следует построить по следующей схеме: 1. рассмотрение тригонометрической формы записи действительного числа и ее свойств. Основной целью является изучить новые математические модели – числовую окружность и числовую окружность на координатной плоскости; познакомить учащихся с первым классом неалгебраических функций – тригонометрическими функциями; научить школьников находить значение тригонометрических функций некоторого аргумента по известному значению другой функции того же аргумента; дать представление о градусной и радианной мерах измерения углов. 2. Собственно тригонометрические уравнения.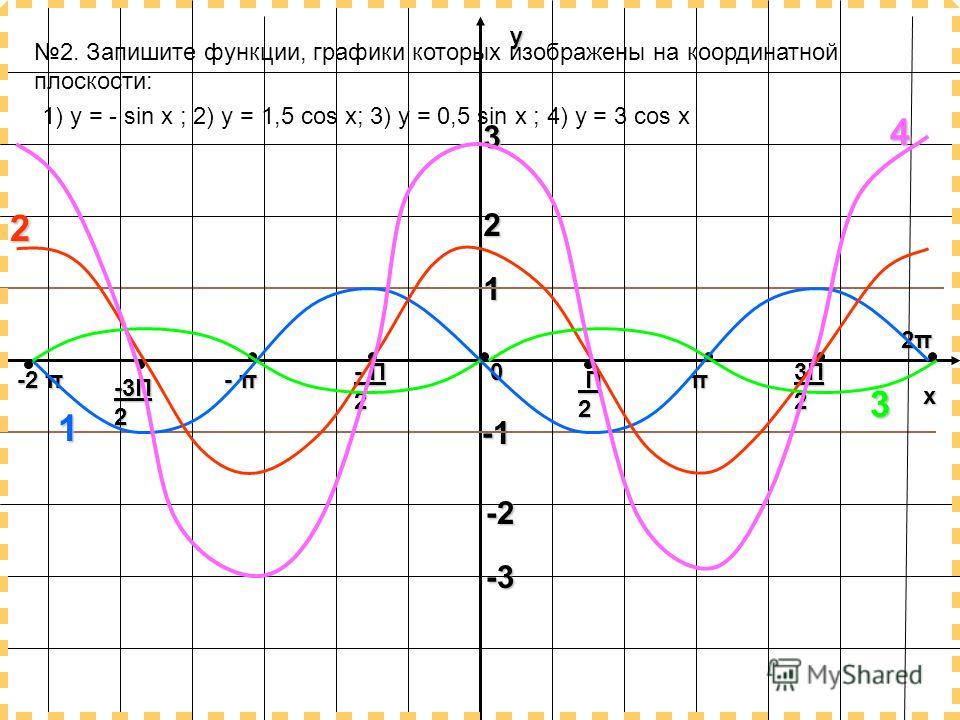 Основная цель – научить школьников решать простейшие тригонометрические уравнения. Сначала надо разобраться с «элементарными моделями», т.е. с простейшими тригонометрическими уравнениями и уравнениями, которые сводятся к простейшим с помощью алгебраических приемов, и только потом переходить к «сложным моделям», т.е. к уравнениям, которые надо сначала долго и упорно «раскручивать, используя рутинный аппарат формул». 3. Тригонометрическими формулами следует заняться после того, как учащиеся овладеют двумя «китами», на которых базируется курс тригонометрии: числовой окружностью и простейшими уравнениями. Основная цель – познакомить учащихся с основными тригонометрическими формулами, научить находить нужную формулу для доказательства тригонометрических тождеств, упрощения тригонометрических выражений. После того, как пройдена тема «Простейшие тригонометрические уравнения», учащимся предлагаются задания с использованием формул тригонометрии. Отсюда и вытекает для учащихся польза от изучения формул: «жуткие» уравнения принимают после преобразований вполне знакомый вид.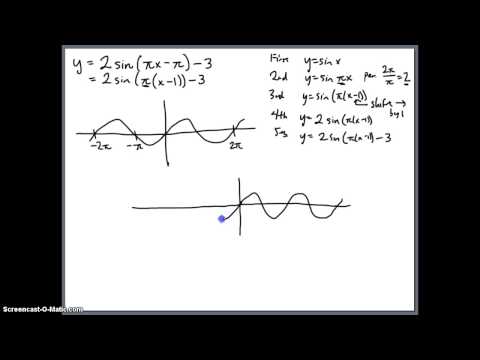

Согласно стандарту полного общего образования в теме «Основы тригонометрии» должны быть рассмотрены следующие темы: синус, косинус, тангенс, котангенс произвольного угла; радианная мера угла; синус, косинус, тангенс, котангенс числа; основные тригонометрические тождества; формулы привидения; синус, косинус, тангенс суммы и разности двух углов; синус, косинус двойного угла; формулы половинного угла; преобразование суммы тригонометрических функций в произведение и произведения в сумму; выражение тригонометрических функций через тангенс половинного аргумента; преобразование простейших тригонометрических выражений; простейшие тригонометрические уравнения; решение тригонометрических уравнений; простейшие тригонометрические неравенства; арксинус, арккосинус, арктангенс числа; тригонометрические функции, их свойства и графики, периодичность, основной период.

Задание 1 Запись

Задание 1 Запись

Проблема:

Изучить графики y = a sin(bx + c) для разных значений а, б и в.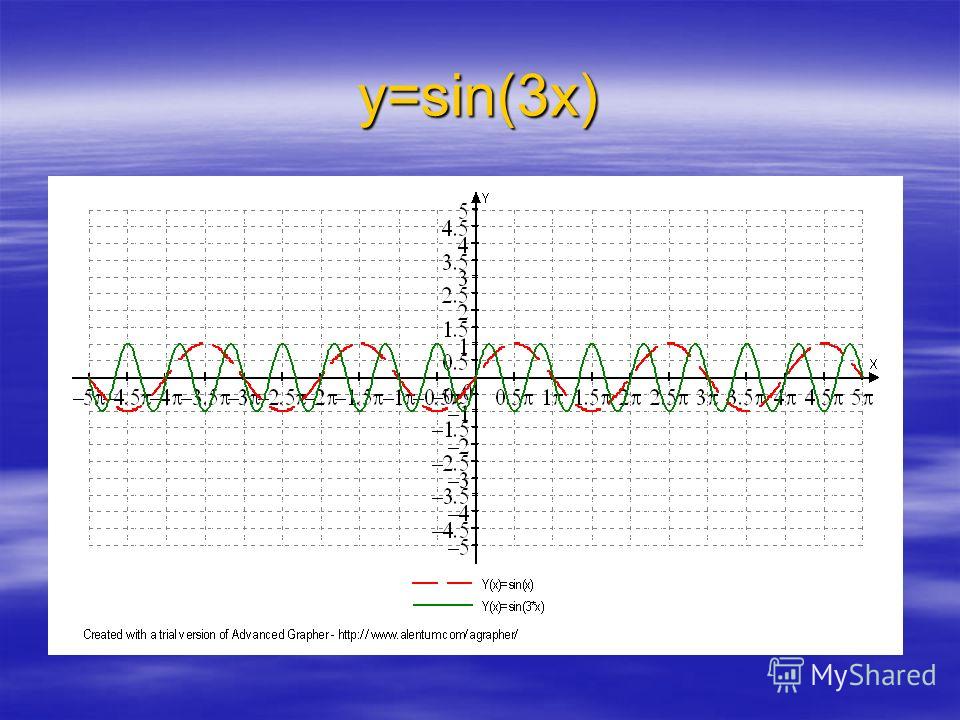

Стратегия:

Для этой задачи мы начнем с проверки различных значений для «а», затем для «б» и, наконец, для «в». Увидев, как каждая переменная взаимодействует по отдельности, мы начинаем менять переменные вместе, проверяя, не изменились ли переменные иметь любое взаимодействие, которое может привести к интересным результатам.

Фонд:

Хорошо, давайте посмотрим, как выглядит график y = sin x ….

График: у = грех х

Ничего подобного мы еще не видели. Для справки мы Держите этот график на экране каждый раз, когда что-то изменяется. (Он всегда будет черным или серым.)

Изменение переменной «а»:

Пришло время поиграть с переменной «a». Мы собираемся построить график у = а грех х и посмотрим, что произойдет, когда мы изменим «а».

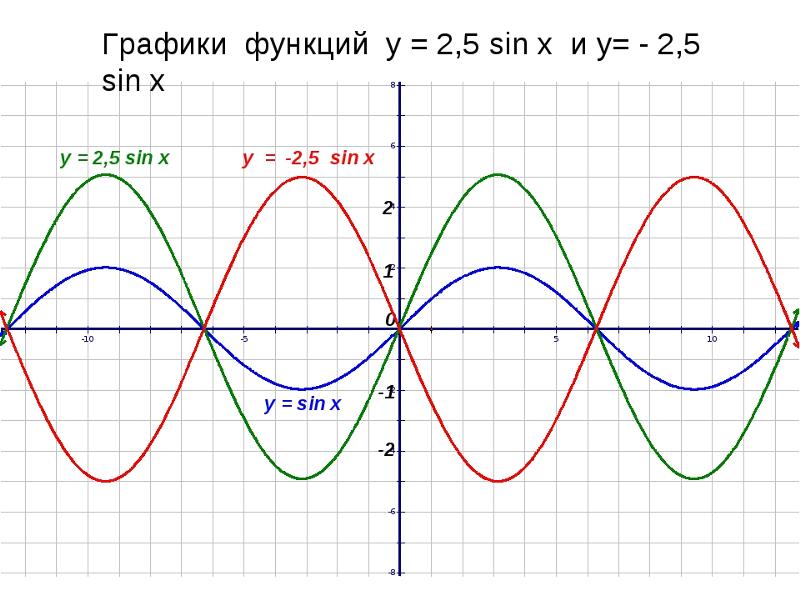
График: y = 2 sin x и у = грех х

Это интересно.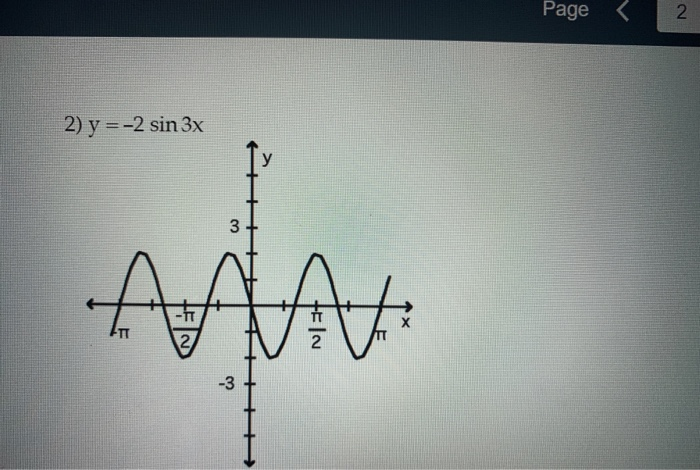 Обратите внимание, как умножение на 2 растянулось график по вертикали. Однако это не изменило ни один из x-перехватов. Я бы предположил (основываясь на моих знаниях об управлении функциями) что умножение на 1/2 сократит график по вертикали, а оставив x-перехваты на том же месте. Посмотрим….

График: у = 1/2 sin x и у = грех х

Я был прав. Изменение значения «а» на 1/2 уменьшилось график, оставляя x-перехваты в покое. Это интересно отметить, что максимум функции равен «а» стоимость. Например, максимум y = 1/2 sin x равен 1/2. Точно так же максимум y = 2 sin x равен 2. Кроме того, минимум функции просто противоположно значению «а» или «-а». Минимум y = 1/2 sin x равно -1/2, а минимум y = 2 sin x равен -2. «а» таким образом, значение определяет амплитуду синусоидальной функции. Однако значение «а» не всегда определяет максимальное или минимальное значение функции синуса. Если параметр «d» добавляется — y = d + a sin (bx + c) (мы не смотрим на параметр «d» в этом исследовании), он сдвинется график по вертикали, что также повлияло бы на максимум и минимум функции.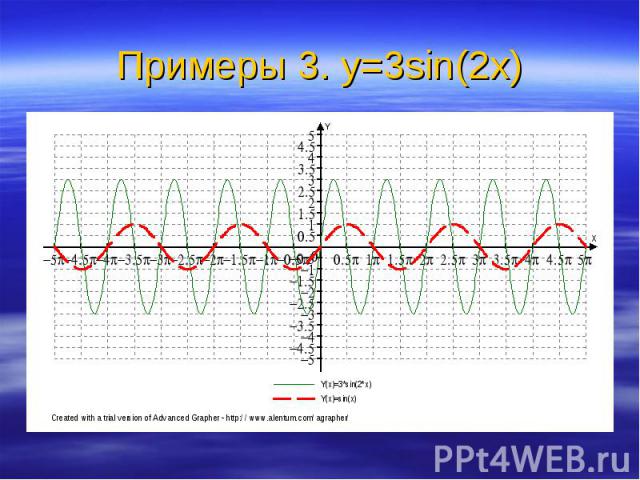

А как насчет отрицательных значений «а»? Посмотрим что делает y = -3 sin x ….

График: y = -3 sin x и y = sin x

Вау! Это немного изменило ситуацию. Как я и думал, умножение на -3 растянуло график. Однако, отрицательный знак немного изменил ситуацию. Теперь график отображается над осью x. Обратите внимание, однако, что x-перехваты по-прежнему имеют не изменился. Мы сделаем еще один: г = -1/4 sin x

График: y = -1/4 sin x и у = грех х

Здесь произошло то же самое. -1/4 уменьшил график и перевернул его по оси X: точно так же, как мы ожидали. Перейдем к переменной «b».

Изменение переменной «b»:

Что ж, изменим переменную «b». мы начнем с чем-то простым, например 2….

График: y = sin (2x) и у = грех х

Как и следовало ожидать, график уменьшился по горизонтали. Так если бы мы сделали «b» 1/2, мы ожидали бы, что график растянуть горизонтально, не так ли? Посмотрим….

График: y = sin (1/2 x) и у = грех х

Мы были правы. Но что конкретно делает переменная «b» делать? Поскольку функция синуса является периодической функцией (или повторяющейся функция), любое горизонтальное растяжение или сжатие повлияет на период функции. В частности, умножение на 1/2 удвоит период, а умножение на 2 даст половину периода. Ты видишь узор? Мы знаем, что период у = грех х есть 2 ИП. В общем случае период равен (1/b)*(2 PI) . Следовательно, период y = sin (1/2 x) равен [1/(1/2)]*(2 PI) или 4 ПИ . Кроме того, период y = sin (2x) равен (1/2)*(2 ИП) или ИП .

Но что произойдет, если переменная «b» будет отрицательной? Мы бы предположили, основываясь на нашем предыдущем опыте с «а» переменной, что если сделать «b» отрицательным, это отразит график по оси Y. Посмотрим….

График: y = sin (-x) и у = грех х

Мы были правы. Здесь есть кое-что интересное. Ранее мы упоминали, что функция синуса является периодической. Отражение график по оси Y такой же, как сдвиг его по горизонтали (в любом направлении) на 1/2 своего периода, или в этом случае ПИ. Помните об этом; это может пригодиться позже.

Давайте сделаем еще несколько примеров манипулирования «b» переменная, а затем мы перейдем к переменной «c».

График: y = sin (-1/3 x) и у = грех х

Как и следовало ожидать, график y = sin (-1/3 x) приводит к горизонтальному растяжению и отражению по оси Y.

График: y = sin (-4x) и у = грех х

И снова у нас есть отражение по оси Y, но теперь также горизонтальная усадка. Каким будет период этой функции, хоть? Помните формулу сверху: (1/b)*(2 ИП) . Следовательно, период y = sin (-4x) равен 1/2 PI . Обратите внимание, что период никогда не бывает отрицательным, поскольку отрицательное значение за период приведет к тому же положительному значению для период. Это показывает, что не имеет значения, в каком направлении (влево справа или справа налево) вы измеряете период в.

Изменение переменной «c»:

И снова мы начнем с чего-то простого. Ну, попробуйте с = 1:

График: y = sin (x + 1) и у = грех х

Похоже, это привело к горизонтальному переводу 1 влево. Давайте попробуем отрицательное значение для «c». Мы ожидать, что это приведет к горизонтальному переводу Направо. Посмотрим, правы ли мы….

График: y = sin (x — 2) и у = грех х

Как мы и ожидали, c = -2 приводит к горизонтальному перемещению из 2 вправо. Помните, что функция синуса периодична. Так как это повторяется, если мы делаем горизонтальный перевод периода (либо влево, либо вправо), мы должны получить точно такое же график.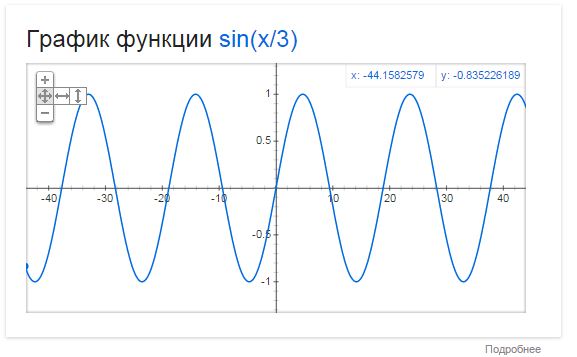 Мы знаем, что период y = sin x равно 2 PI. Так попробуем y = sin (x + (2 PI)) .

График: y = sin (x + (2 PI)) и у = грех х

Мы получили тот же график, что и y = sin x . Это очень интересно. В общем, каждый раз, когда у вас есть периодическая функция, горизонтальная перевод (в любом направлении) периода приведет к график точно такой же, как и в оригинале.

Изменение всех переменных:

Теперь мы собираемся изменить все переменные вместе. Этот не очень жесткий. Все, что нам нужно сделать, это применить каждое из растягиваний/усадок, размышления и переводы.

График: y = 2 sin (2x + 2) и у = грех х

Это вертикальное растяжение на 2, горизонтальное сжатие на 1/2, и горизонтальный перевод -2.

График: y = -1/2 sin (3x — 1) и у = грех х

Это вертикальное сжатие на 1/2, отражение по оси x, горизонтальное сжатие 1/3 и горизонтальное смещение 1.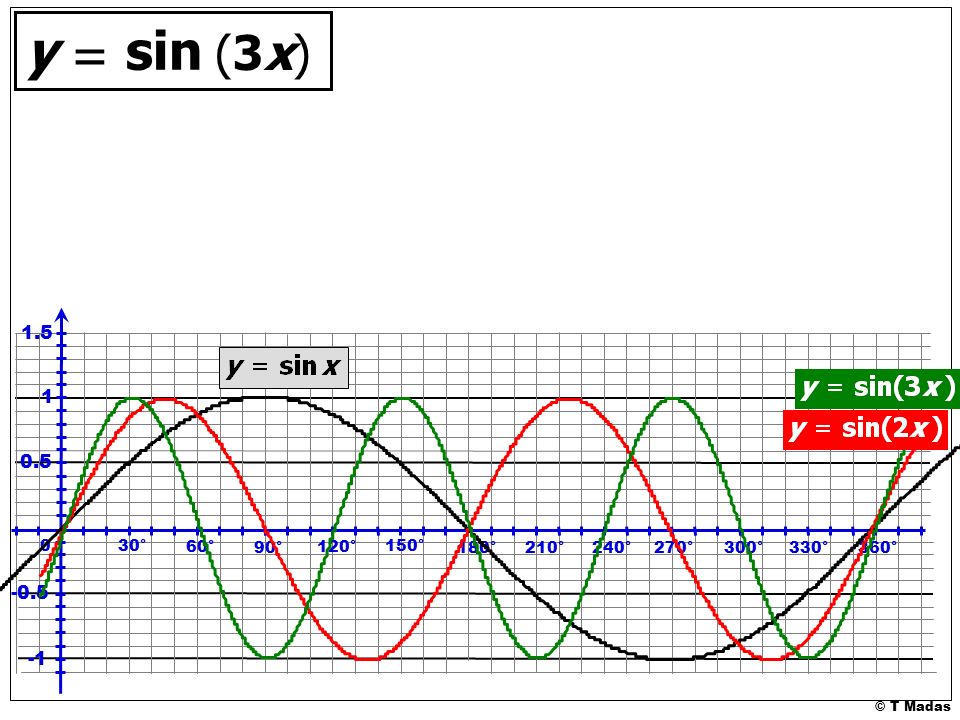

Сейчас мы попробуем кое-что интересное, в результате на графике точно так же, как y = sin x .

График: y = — sin (-x) и у = грех х

Это очень интересно. Отражение по оси Y и отражение по оси x приводит к тому же графику.

График: y = sin (-x + PI) и у = грех х

Отражение по оси Y и последующее горизонтальное смещение результатов PI на том же графике. Это относится к тому, что мы обсуждалось ранее в отношении размышлений и периода.

График: y = — sin (x + PI) и у = грех х

Отражение по оси x и последующее горизонтальное смещение PI также приводит к тому же графику.

Выводы:

Благодаря этому исследованию мы увидели, как разные значения из «а», «б» и «в» могут повлиять график синусоидальной функции. Мы также видели, как переменные взаимодействуют, и как, в некотором смысле, одна переменная может «отменить» Другая.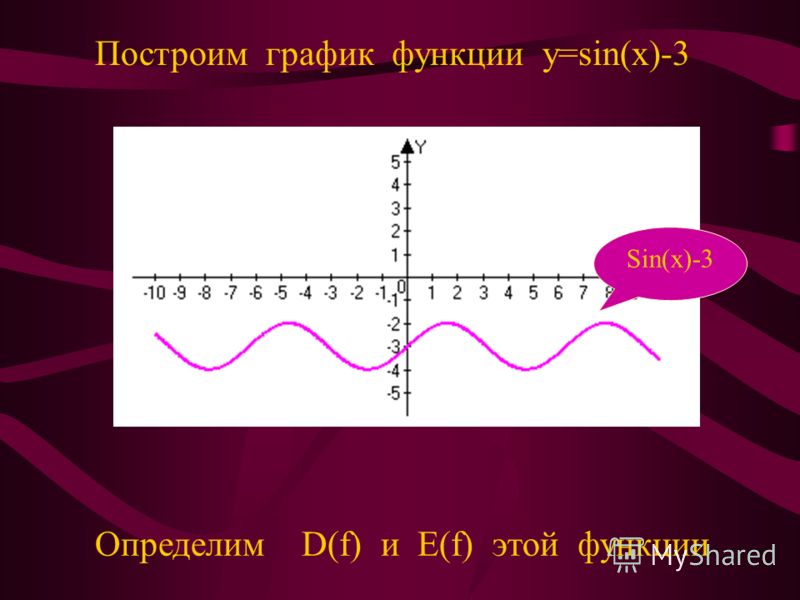 Мы коснулись сжатий и растяжений, отражений, горизонтальных переводы и период. Однако мы ничего не упомянули по поводу вертикального перевода. Было бы интересно проверить о том, как переменная «d» ( 92 (х) .

Вернуться на главную страницу

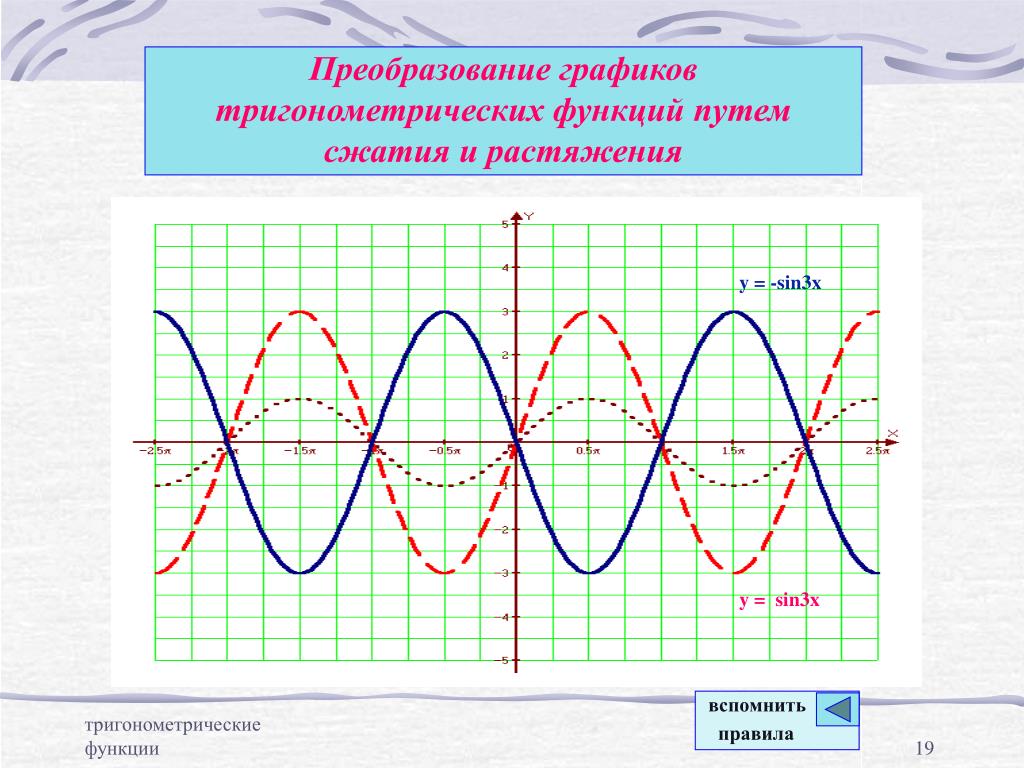
`f(x) = sin(3x), g(x) = sin(-3x)` Опишите взаимосвязь между графиками функций f и g. Учитывайте амплитуду, период и сдвиги.

Цитата страницы Начать эссе значок-вопрос Спросите репетитора

Начать бесплатную пробную версию

Скачать PDF PDF Цитата страницы Цитировать Поделиться ссылкой Делиться

Ссылайтесь на эту страницу следующим образом:

«`f(x) = sin(3x), g(x) = sin(-3x)` Опишите взаимосвязь между графиками f и g. Учитывайте амплитуду, период и сдвиги». eNotes Editorial , 23 июля 2015 г. , https://www.enotes.com/homework-help/f-x-sin-3x-g-x-sin-3x-describe-relationship-483917. По состоянию на 2 января 2023 г.

sin(-b) отражает по оси X только потому, что sin(-b)=-sin(b).

cos(-b) отражает по оси Y. sin(-b) также отражается по оси y, но эффект такой же, как и при отражении по оси x, поскольку синус является нечетной функцией.

В общем, -f(x) отражает график f(x) по горизонтальной оси, а f(-x) отражает график f(x) по вертикальной оси.

Утверждено редакцией eNotes

Обе амплитуды равны 1.

Оба периода равны 2`pi`/3

Отрицательное значение отражает график по оси X.

Графики идентичны, но инвертированы/преобразованы по вертикали из-за использования знака минус.