Основные свойства гиперболического тангенса — Мегаобучалка
Показательные и логарифмические выражения
Показательная функция, гиперболические функции
Показательной функциейназывается функция
,где .
Основные свойства показательной функции.
1. Область определения: .
2. Множество значений: .
3. Четность и нечетность: не обладает свойством четности.
4. Периодичность: не периодическая.
5. Нули функции: нулей не имеет.
6. Промежутки знакопостоянства:функция положительна для .
7. Наибольшее и наименьшее значения: наибольшего и наименьшего значений функция не имеет.
8. Промежутки возрастания и убывания: если функция возрастает для всех ; если –убывает для .
9. Точки пересечения с осями координат: пересекает ось Оу в точке , ось не пересекает.
10. Асимптоты: прямая y = 0 (ось ) является горизонтальной асимптотой.
11. График функции дляa > 1 изображен на рисунке 1, для –на рис. 2.
Из свойств функции следует: неравенство равносильно неравенству:
1) , если ,
2) , если .
Показательная функция с основанием , где иррациональное число , называется экспонентой, пишут или .
Через показательные выражения с основанием определяются гиперболические функции.
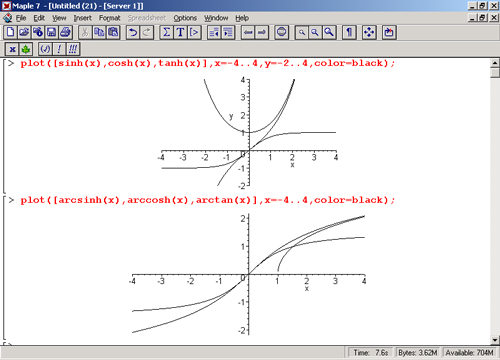
Гиперболическим синусом называется функция
.
Основные свойства гиперболического синуса.
1. Область определения: .
2. Множество значений: .
3. Четность и нечетность: нечётная.
4. Периодичность: не периодическая.
5. Нули функции: .
6. Промежутки знакопостоянства:функция отрицательна для , положительна – для .
7. Наибольшее и наименьшее значения: наибольшего и наименьшего значений функция не имеет.
8. Промежутки возрастания и убывания: функция возрастает для всех .
9. Точки пересечения с осями координат: .
10. Асимптоты: асимптот не имеет.
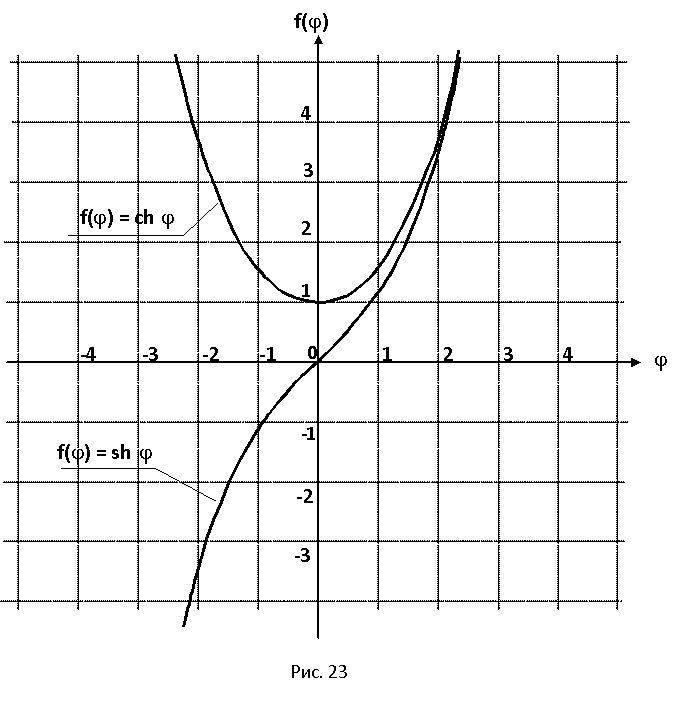
11. График функции изображен на рисунке 3.
Рис. 3.
Гиперболическим косинусом называется функция
Основные свойства гиперболического косинуса.
1. Область определения: .
2. Множество значений: .
3. Четность и нечетность: чётная.
4. Периодичность: не периодическая.
5. Нули функции: нулей не имеет.
6. Промежутки знакопостоянства:функция положительна для .
7. Наибольшее и наименьшее значения: наименьшее значение, равное 1, функция принимает при .
8. Промежутки возрастания и убывания: функция убывает при ; возрастает – при .
9. Точки пересечения с осями координат: пересекает ось в точке , ось не пересекает.
10. Асимптоты: асимптот не имеет.
11. График функции изображен на рисунке 4.
Рис. 4.
Гиперболические тангенс и котангенс определяются через отношение гиперболического синус и косинуса.
Гиперболического тангенсом называется функция
,
.
Основные свойства гиперболического тангенса.
1. Область определения: .
2. Множество значений: .
3. Четность и нечетность: нечётная.
4. Периодичность: не периодическая.
5. Нули функции: .
6. Промежутки знакопостоянства:функция отрицательна для ; положительна – для .
7. Наибольшее и наименьшее значения: наибольшего и наименьшего значений функция не имеет.
8. Промежутки возрастания и убывания: функция возрастает для .
9. Точки пересечения с осями координат: .
10. Асимптоты: имеет горизонтальные асимптоты и .
11. График функции изображен на рисунке 5.
Рис. 5.
Гиперболический котангенсом называется функция
, т.е.
.
Прием задач. Первый курс. Драма в двух частях, часть первая: posic — LiveJournal
Прием задач. Первый курс. Драма в двух частях, часть первая: posic — LiveJournal ?Лёня Посицельский (posic) wrote,
- Образование
- Cancel
б) То же для гиперболических функций sh x, ch x, и t = th x/2.
в) Выразить dx через dt.
— Ну, это школьная задача. Вот решение:
«… cos x = …, sin x = 2 tg x/2.
… ch x = …, sh x = 2 th x/2.»
— Так, так, синус, косинус, хорошо. Гиперболические функции… (Замечая неправильную формулу для гиперболического синуса и глядя одновременно на правильную формулу для гиперболического косинуса.) Скажите, а правда, что гиперболический косинус всегда положителен?
— Я имею ввиду, для вещественного аргумента. Верно ли, что гиперболический косинус вещественного числа всегда положителен? (Переворачиваю страницу, чтобы было видно определение гиперболического косинуса.)
— …
— Ну, ведь экспонента всегда положительна, да? Отсюда не следует, что гиперболический косинус всегда положителен?
— Наверное, да.
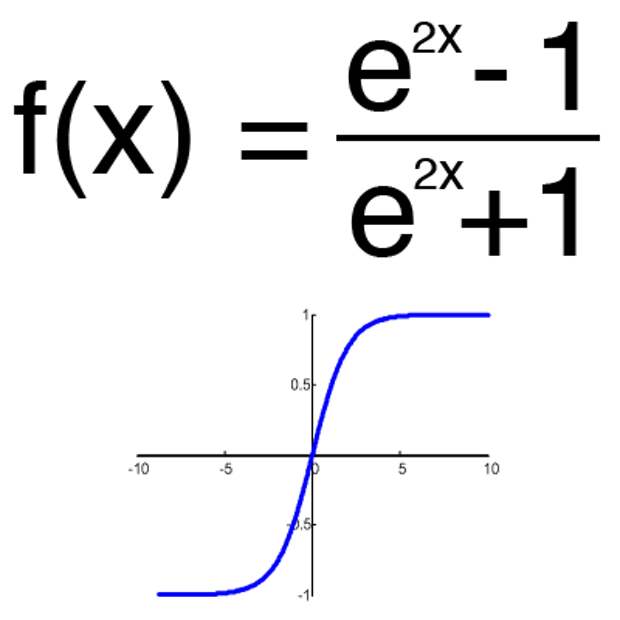 ..
..— А гиперболический тангенс? Вот у вас в выражении для ch x, в знаменателе стоит 1 − th2 x/2. Этот знаменатель может быть отрицательным?
— … Нет, наверное, это зависит от x. При x от −π/2 до π/2 гиперболический косинус положителен, а от π/2 до 3π/2 отрицателен.
— Гиперболический косинус? Вот же формула.
— … Наверное, надо модуль взять. (Рисует знак модуля вокруг 1 − th2 x/2.)
— А нужен ли знак модуля? Верно ли, что гиперболический тангенс всегда по модулю не превосходит единицы? (Имея в виду в итоге указать, что гиперболический тангенс ограничен, а синус нет.)
— …
— (Вдруг замечая, что и формула для обычного синуса тоже неправильная.) А кстати, и обычные тригонометрические функции… Нарисуйте, как примерно выглядит график синуса?
— (Рисует правильную картинку в грубом наброске.)
— А тангенса?
— (Рисует правильную картинку.)
— Так, и может ли быть верна эта формула?
— (Некоторое время напряженно смотрит в свои выкладки, потом дорисовывает правильный знаменатель к выражению для sin x.
 )
)— Так, а гиперболический синус?
— А знак модуля нужен? Все таки, верно ли, что гиперболический тангенс не превосходит по модулю единицы?
— … Да, верно.
— Так что же знаки модуля?
— (Зачеркивает модули.)
— Так. А что такое гиперболический косинус пи?
— Что-то типа е в степени пи… (улыбается)
— Хорошо. (Пункты а и б приняты.)
Subscribe
Вдогонку итогам 2022 года
В ходе написания материалов к отчету по гранту осознал, что в прошедшем году у меня существенно продвинулись четыре больших проекта. I.…
Generalized periodicity theorems
Вторая, теперь уже полная версия — https://arxiv.org/abs/2301.00708 Комментарий см. в постинге https://posic.livejournal.com/2714054.html
Сказавши Б, говори А
В ночь на вторник я сказал «ноль-а», «ноль-б» и «Б», а теперь настала ночь на пятницу, когда я надеюсь сказать А.
 Статья про обобщенные теоремы…
Статья про обобщенные теоремы…
Photo
Hint http://pics.livejournal.com/igrick/pic/000r1edq
- 0 comments
Гиперболическая синусоидальная функция — Статистические инструкции
Типы функций >
Гиперболическая синусоидальная функция , впервые изученная математиком 18-го века Якопо Риккати, представляет собой нечетную функцию, определяемую как половина разности экспоненциальных функций e x и e -x :
Функция определяет гиперболический синус угла. Это похоже на то, как работает синус для единичного круга, за исключением того, что здесь мы работаем с гиперболой вместо единичного круга.
Домен и диапазон включают действительные (-∞, ∞) и комплексные значения. Для сложного аргумента тождество равно
Для сложного аргумента тождество равно
sinh( x ) = − i sin( i x).
Все гиперболические функции можно записать в виде ряда, и гиперболический синус не является исключением. Это может быть записано как:
Знаменатели быстро возрастают, а это означает, что члены более высокого порядка вскоре становятся незначительными. Это приводит к приближению
sh(x) &приблизительно; х, х → 0,
Производная и интегралы
Производной гиперболического синуса является функция гиперболического косинуса, ch(x).
Взяв производную и приравняв ее нулю, мы обычно получаем критические точки функции. Однако e x всегда положительно, а это означает, что производная от sh x никогда не равна нулю. Следовательно, гиперболический синус не имеет критических точек.
Взяв вторую производную и установив ее равной нулю, мы получим точку (точки) перегиба. Вторая производная есть sh(x), которая равна 0, когда e x = e -x , или когда x = 0.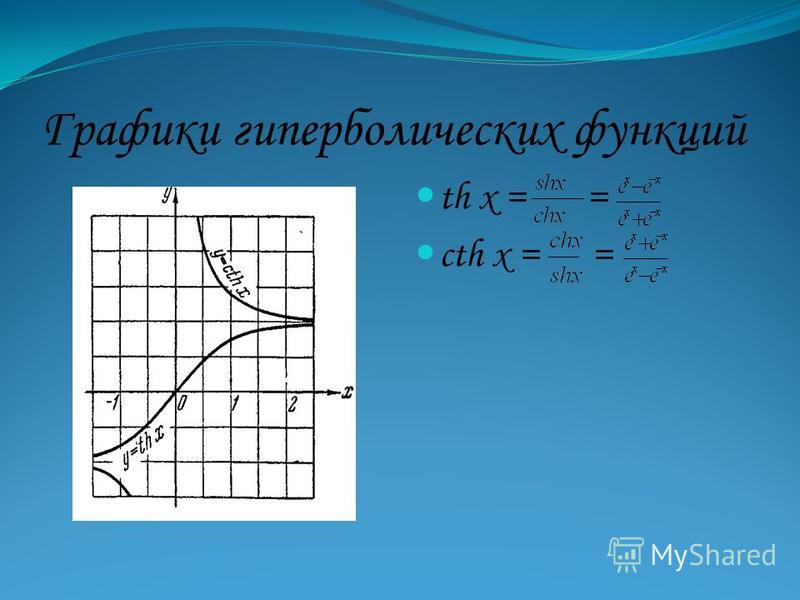 Следовательно, гиперболический синус имеет одну точку перегиба при x = 0.
Следовательно, гиперболический синус имеет одну точку перегиба при x = 0.
Интеграл sin(x) равен ch x + C. функции гиперболического синуса
График гиперболического синуса показан ниже:
График гиперболического синуса, sinh(x).
Это монотонная функция, в отличие от ее тригонометрического аналога синуса, который является периодической функцией.
Личности
Гиперболический синус имеет множество полезных тождеств, в том числе:- sinh(-x) = -sinh (x)
- sin(x + y) = sh(x) ch(y) + ch(x) sh(y)
- sin(x) + ch(x) = e x
- sin(x) – cosh(x) = -e x
- шш 2 (х) – шш 2 (х) = 1
Ссылки
График создан с помощью Desmos.com.
УКАЗЫВАЙТЕ ЭТО КАК:
Стефани Глен . «Функция гиперболического синуса» От StatisticsHowTo.com : Элементарная статистика для всех нас! https://www.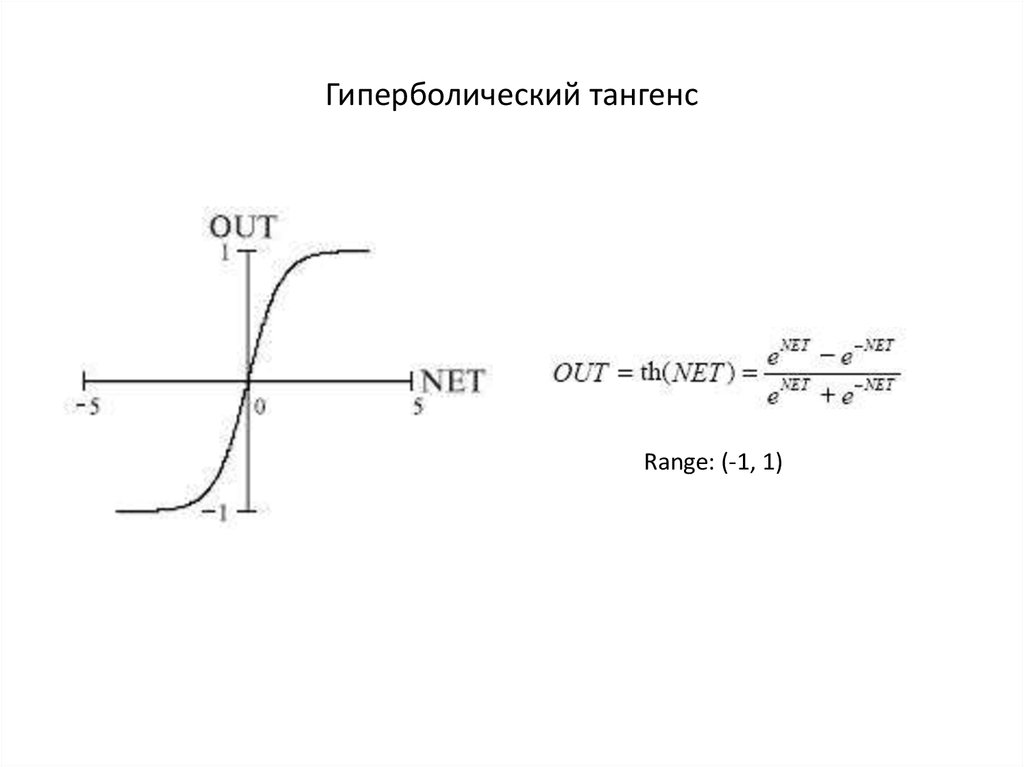 statisticshowto.com/hyperbolic-sine-function/
statisticshowto.com/hyperbolic-sine-function/
————————————————— ————————-
Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на ваши вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста, Свяжитесь с нами .
Гиперболические функции: определение и примеры
В математике существуют определенные четных и нечетных комбинаций натуральных экспоненциальных функций , которые встречаются так часто, что заработали себе особые названия. Они во многом аналогичны тригонометрическим функциям. Например, они имеют такое же отношение к гиперболе , какое ригонометрические функции имеют к окружности .0006 .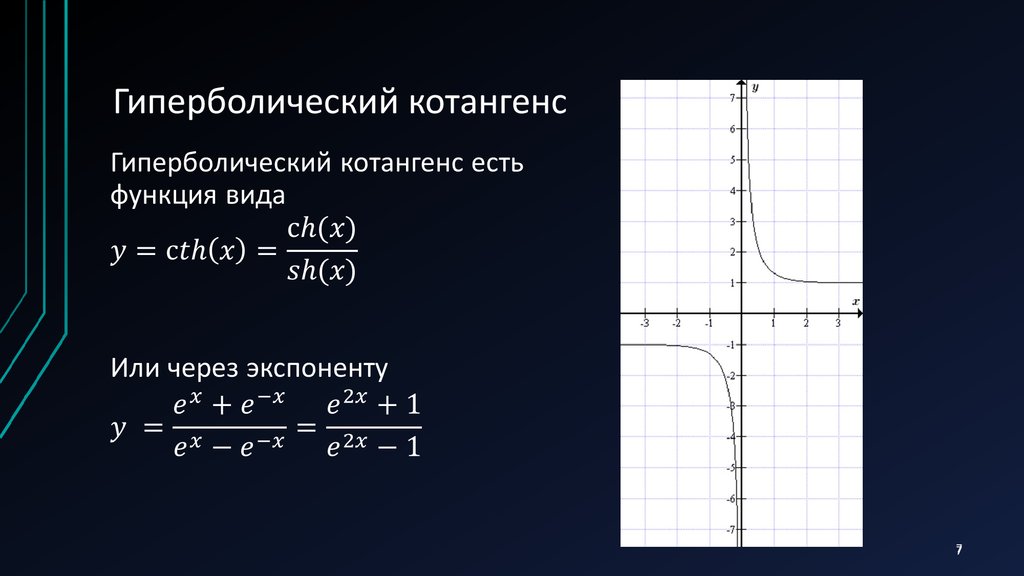 Из-за этого эти специальные функции называются гиперболическими функциями .
Из-за этого эти специальные функции называются гиперболическими функциями .
В этой статье подробно обсуждаются основные гиперболические функции и их свойства, тождества, производные, интегралы, обратные функции и примеры.
- Определение гиперболических функций
- Гиперболические функции: формулы
- Гиперболические функции: графики
- Гиперболические функции: свойства и тождества
- Производные гиперболических функций
- Интегралы гиперболических функций
- Обратные гиперболические функции
- Гиперболические функции: примеры и приложения
Определение гиперболических функций
Что такое гиперболические функции?
гиперболических функций по существу являются тригонометрическими функциями гиперболы. Они расширяют понятие параметрических уравнений для единичной окружности, где , до параметрических уравнений для единичной гиперболы и определяются в терминах естественной экспоненциальной функции (где — число Эйлера), что дает нам следующие две фундаментальные гиперболические формулы:
На основе этих двух определений: гиперболический косинус и гиперболический синус остальные шесть основных гиперболических функций могут быть получены, как показано в таблице ниже.
Гиперболические функции: Формулы
Формулы для гиперболических функций перечислены ниже:
| 6 Основные гиперболические формулы | |||
| Гиперболический SINE: | |||
| Hyperbolic Sine: | 9292|||
| Hyperbolic Sin: | 9017 2|||
| Hyperbolic Sin: | 92|||
| .0169 | |||
| Hyperbolic cosine: | Hyperbolic secant: | ||
| Hyperbolic tangent: | Hyperbolic cotangent: | ||
Whereis pronounced «cinch», is pronounced «cosh», is произносится «танч», произносится «косич», произносится «сич» и произносится «котанч».
Получение экспоненциальных форм
Ключевой характеристикой гиперболических тригонометрических функций является их сходство с тригонометрическими функциями, что видно из Формула Эйлера :
Решение этой формулы для косинуса и синуса дает нам:
Что поразительно похоже на гиперболические функции косинуса и синуса:
часть, которую делает формула Эйлера.
Почему в гиперболических функциях отсутствуют мнимые числа?
Гиперболические функции: графики
Графики двух фундаментальных гиперболических функций: гиперболического синуса и гиперболического косинуса можно начертить с помощью графическое дополнение , как показано ниже.
| График | График | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
График гиперболического синуса с использованием графика Graphysmarter Originals | . График Graphlic Costine Originals | График Graphlic Cosine Originals | График Graphlic Cosine с помощью Graphlicer Cocine. Графики остальных шести основных гиперболических функций показаны ниже.
Обратите внимание, что все эти гиперболические функции имеют горизонтальные (зеленые) и/или вертикальные (розовые) асимптоты. График гиперболического секанса имеет глобальный максимум в точке . Домен и диапазон гиперболических функцийПока мы смотрим на графики гиперболических функций, давайте обратим внимание на их домены и диапазоны!
Hyperbolic Functions: Свойства и тождестваСвойства и тождества гиперболических функций также очень похожи на свойства и тождества их тригонометрических аналогов: Давайте проверим наше понимание этих личностей! Докажите, что (а) и (б) . Решение: (a) Начнем с определения гиперболического косинуса и гиперболического синуса, затем упростим: (b) Начнем с доказательства из части (a): Теперь, если мы разделив обе части на , мы получим: Это упрощает до: Этот пример дал нам некоторое представление о , почему они называются гиперболическими функциями. Давайте погрузимся в это немного глубже! Связь между тригонометрическими и гиперболическими функциями♦ Допустим, у нас есть действительное число, . Тогда точка находится на единичной окружности: , потому что Фактически, действительное число также можно интерпретировать как меру в радианах на изображении ниже. По этой причине тригонометрические функции иногда называют круговыми функциями. Что еще более важно, действительное число представляет собой удвоенную площадь заштрихованного участка круга. График единичной окружности с заштрихованным углом POQ — StudySmarter Originals ♦ Аналогично, если любое действительное число, то точка находится на правой половине единичной гиперболы : потому что 02 куда .В этом случае, однако, не представляет собой меру угла , а вместо этого it представляет удвоенную площадь заштрихованного гиперболического сечения на изображении ниже. График единичной гиперболы с заштрихованным сечением P — StudySmarter Originals Производные гиперболических функцийПроизводные гиперболических функций также аналогичны тригонометрическим функциям. Мы перечисляем эти производные в таблице ниже.
Осторожно! В то время как значений производных те же , что и у тригонометрических функций, знаков для производных гиперболического косинуса и гиперболического секанса равны противоположным их тригонометрическим аналогам. Также важно отметить, что любое из этих правил дифференциации можно комбинировать с помощью Цепного правила. Например, Производные гиперболических функций проще вычислить из-за их использования и простоты их вывода. Например, Интегралы гиперболических функцийКак производные гиперболических функций аналогичны своим тригонометрическим аналогам, так и интегралы гиперболических функций. Перечислим эти интегралы в таблице ниже.
Другие полезные интегралы гиперболических функций перечислены ниже.
Inverse Hyperbolic Functions Based on the graphs of the hyperbolic functions, we can see that (and its reciprocal, ) и (и обратное ему ) являются однозначными функциями , но (и обратное ему ) не являются. Это связано с тем, что Cosine и Secant — даже функций , в то время как SINE , CoseCant , Tangent и Cotangent — WED Функции . Поскольку косинус и секанс являются четными функциями и, следовательно, не являются взаимно однозначными, мы должны ограничить их область определения , чтобы найти их обратные функции. Итак, с областями косинуса и секущей, ограниченными интервалом , все гиперболические функции взаимно однозначны, и мы можем определить обратные гиперболические функции как: Their formulas are:
Обратите внимание, что все обратные гиперболические функции включают логарифмические функции. Давайте посмотрим, как получается обратное значение sinh (также называемое arc sinh). Вывод остальных происходит по аналогичной схеме. Предположим, что: Это означает, что: По определению гиперболического синуса: Переставляя это, мы получаем: Затем, умножая обе части на , мы имеем: Теперь мы решаем это как квадратичную функцию, представляя как , и получаем решение: Так как , единственно возможным решением является положительное: Наконец, возложив обе части на натуральный логарифм, получим: Графики обратных гиперболических функцийГрафики обратных гиперболических функций показаны ниже.
Обратите внимание, что обратные гиперболические косеканс, секанс, тангенс и котангенс имеют горизонтальные (зеленые) и/или вертикальные (розовые) асимптоты. Графики аркгиперболического косинуса и аркгиперболического секанса имеют определенную начальную точку при . Область определения и область значений обратных гиперболических функцийПока мы смотрим на графики обратных гиперболических функций, обратите внимание на области их определения и области значений!
. Производные обратных гиперболических функций перечислены ниже. Производные обратных гиперболических функций перечислены ниже.
Докажем, что . Гиперболические функции: примеры и приложенияНайдите значение if . Решение:
Экспресс и как функция и . Решение:
Существует несколько реальных применений гиперболических функций, например:
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 Статья про обобщенные теоремы…
Статья про обобщенные теоремы…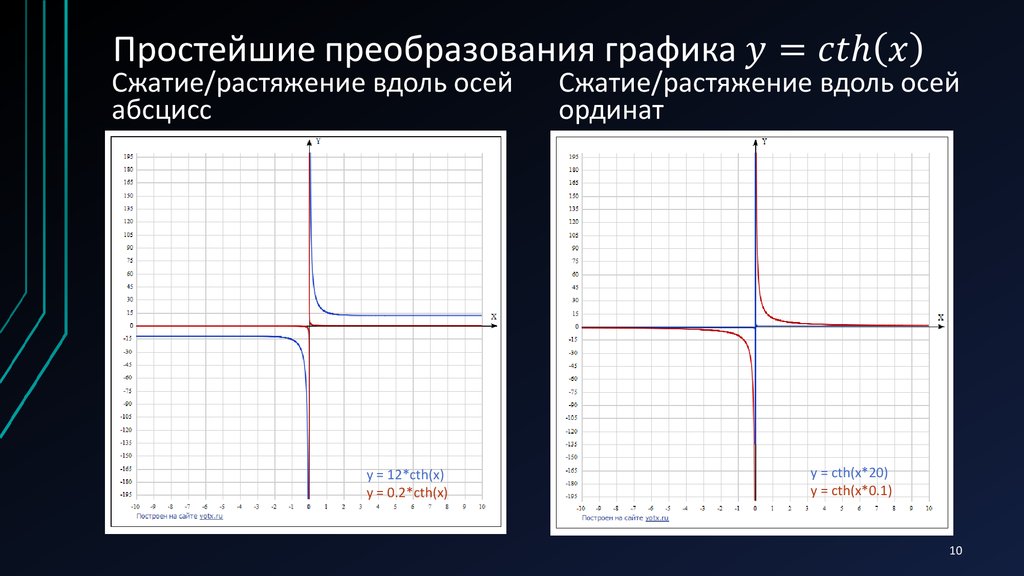


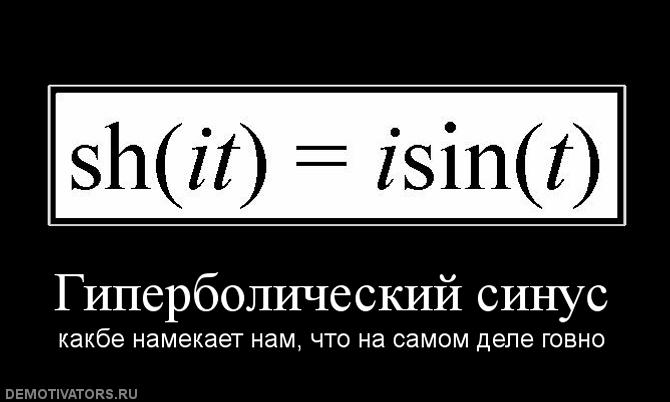
 Это связано с тем, что гиперболические функции включают экспоненциальные функции, а экспоненциальные и логарифмические функции являются обратными друг другу!
Это связано с тем, что гиперболические функции включают экспоненциальные функции, а экспоненциальные и логарифмические функции являются обратными друг другу! Оригиналы
Оригиналы