Math Scene — графики неравенств и таблицы знаков
Math Scene — графики неравенств и таблицы знаков 2008 Расмус Эхф | Печать |
Как можем ли мы решить квадратное неравенство, такое как x 2 − 1 0 ? Если решаем соответствующее квадратное уравнение, получаем два решения.
х 2 — 1 = 0
(х + 1)(х — 1) = 0
Решения: x = 1 и х = −1.
Мы нашли точки, где выражение равно 0, теперь нам нужно найти, где меньше 0. Другими словами, мы должны выяснить, когда выражение отрицательный. Для этого рассмотрим признаки множители (x + 1) и (x − 1) . Другими словами, мы ищем интервалы, в которых они положительны или отрицательны. Для этого делаем таблицу знаков
Начнем с того, что подставим 0 в значения, где каждый из
факторы равны нулю. (x+1) = 0, когда x = −1, и (x − 1) = 0
когда x = 1. Затем мы ставим + или — в зависимости от того, являются ли факторы
положительное или отрицательное. Теперь мы можем использовать
эту информацию для решения неравенства.
Мы знаем, что (x + 1)(x — 1) = x 2 — 1.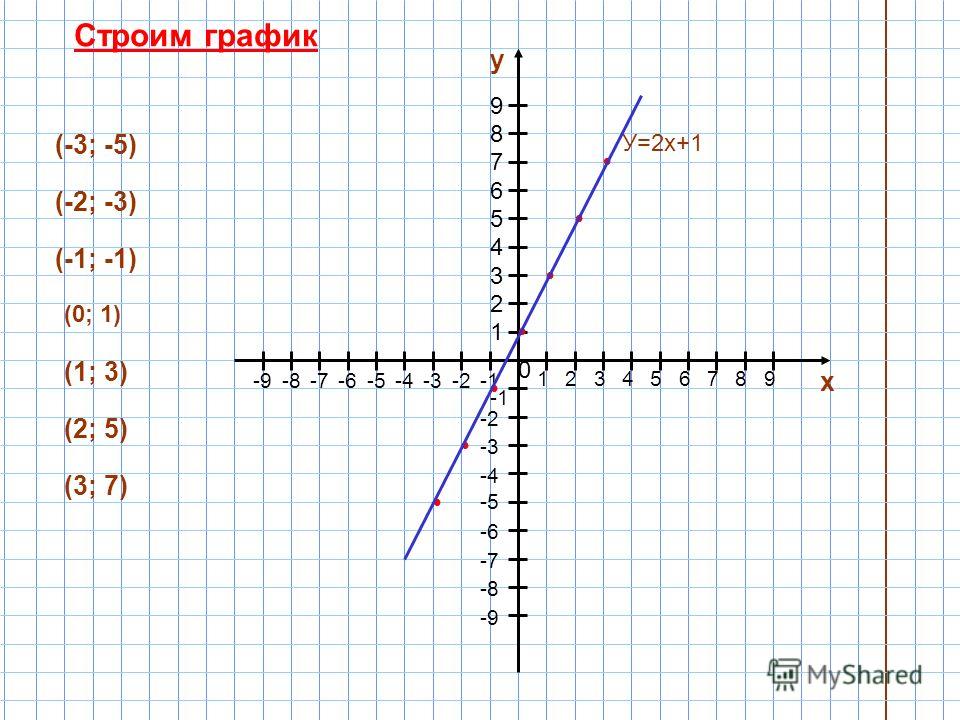
Мы также знаем, что −∙− = + и +∙+ = +. Это означает, что выражение (x + 1)(x − 1) положительна, когда обе скобки имеют одинаковый знак, и отрицательна, когда они имеют противоположные знаки. Теперь мы можем заполнить таблицу. Мы ищем интервал, на котором x 2 − 1 < 0, то есть отрицательно.
Этот интервал удовлетворяет неравенству.
−1 х 1
Мы просто находим корни, решая соответствующие уравнение, а затем подставьте любое значение x между этими корнями. .
Если мы выберем, например, x = 0, мы получим следующее
Если f(x) = x 2 − 1, тогда f(0) = 0 2 — 1 = -1.
Это показывает нам, что f(x) = x 2 − 1 отрицательно на интервале
−1 х 1 .
Если мы попробуем любое значение x, которое меньше -1 og
больше 1 мы получаем положительные значения для функции.
Итак, линия реального числа
будет выглядеть так:
Решение
Мы также можем найти решение, взглянув на график
f(x) = x 2 — 1 . Решение x 2 – 1
0 это интервал, в котором график лежит на оси x или ниже нее.Посмотрите на график ниже.
График лежит на оси x или вокруг нее на интервале −1 х 1 (заштрихованная область графика).
Если мы перевернем знак неравенства, какое решение из
х 2 — 1 0?
Глядя на график, площадь над осью X удовлетворяет этому условию. Если мы посмотрим на таблицу знаков, то там, где выражение положительное.
Решение: x −1 Решение: х 1
Решение неравенства х 2 – 1 0
состоит из двух частей.
х −1 или х 1.
Пример 1
Решить неравенство x 2 − 2x − 3 < x + 1,
Первый
решаем соответствующее уравнение
х
х 2 — 2х — 3 = х + 1
х 2 — 3х — 4 = 0
(х + 1)(х — 4) = 0
Решение: х = -1 и х = 4
Следующий делаем таблицу признаков.
Решение: −1 < х < 4
Если мы нарисуем два графика в одной координате
система
f (х) = х 2 — 2х
− 3 и g(x) = x + 1, то мы ищем область, в которой f(x) (
левая часть выражения ) меньше, чем g(x) (правая часть).
Это заштрихованная область графика, где x принимает значения от -1 до
4.
Пример 2
| Решить неравенство |
Начнем с рассмотрения знаков числителя (x +
1) и знаменатель (x − 1).
Те же правила применяются для деления
что касается умножения. (-/-
= + и -/+ = -). Итак, если числитель и знаменатель совпадают
знак, что результат положительный. Если они имеют противоположные знаки, то результат равен
отрицательный
Решение
Теперь нужно позаботиться о том, чтобы x не мог быть равен
на 1, потому что тогда мы будем делить на 0.
Таким образом, решение равно −1 . х < 1.
Рисуем график, предварительно составив таблицу значений.
Х | f(x) = (x + 1) / (x — 1) | |
| -2 | ≈ 0,3 | |
| -1 | 0 | |
| 0 | -1 | |
| 1 | асимптота | |
1 | 5 | |
| 2 | 3 | |
| 3 | 2 |
График имеет вертикальную асимптоту, когда x = 1 и
лежит под осью x на интервале между −1 и 1 (заштрихованная
область).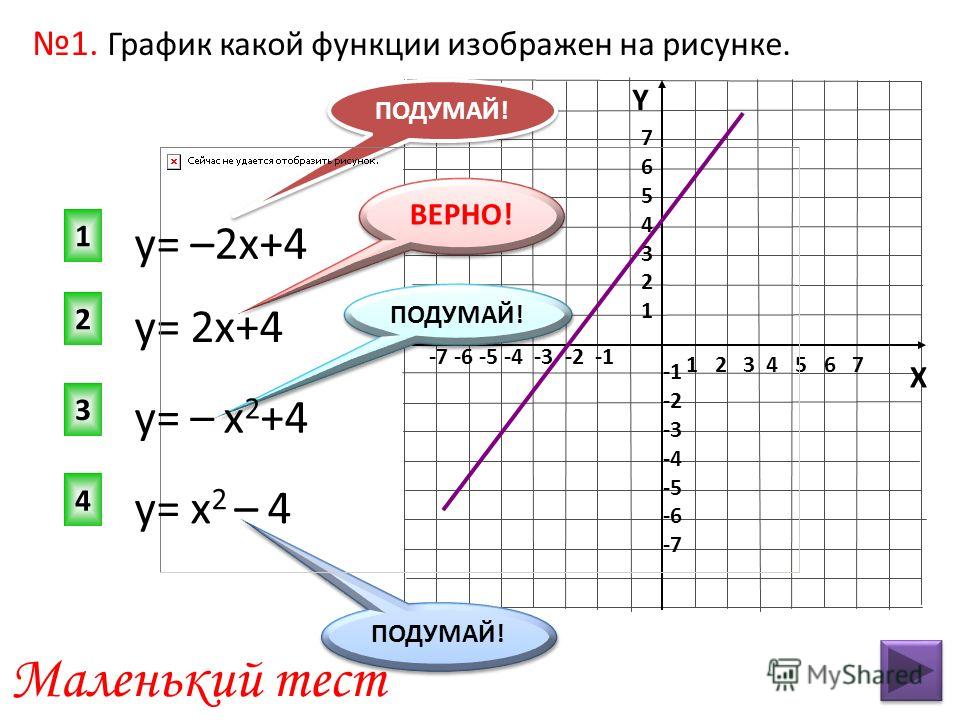
909:25 Пример 3
Решить
Начнем с перемещения 1 к другому часть уравнения, оставив там 0. Мы можем пользоваться таблицей знаков только в том случае, если правая часть равна нулю.
| Мы Найдите общий знаменатель и упростите дробь. |
Решение х < 1
Теперь мы рисуем графики левой части и правая часть неравенства. Левая сторона такая же, как в пример 2. Правая часть g(x) = 1 (горизонтальная линия, на единицу выше x оси).
Мы видим, что график f(x) находится под графиком g(x)
для всех значений x слева от
вертикальная асимптота x = 1 (см. заштрихованную область). х = 1 не
включены в решение, так как это означало бы, что мы делим на ноль.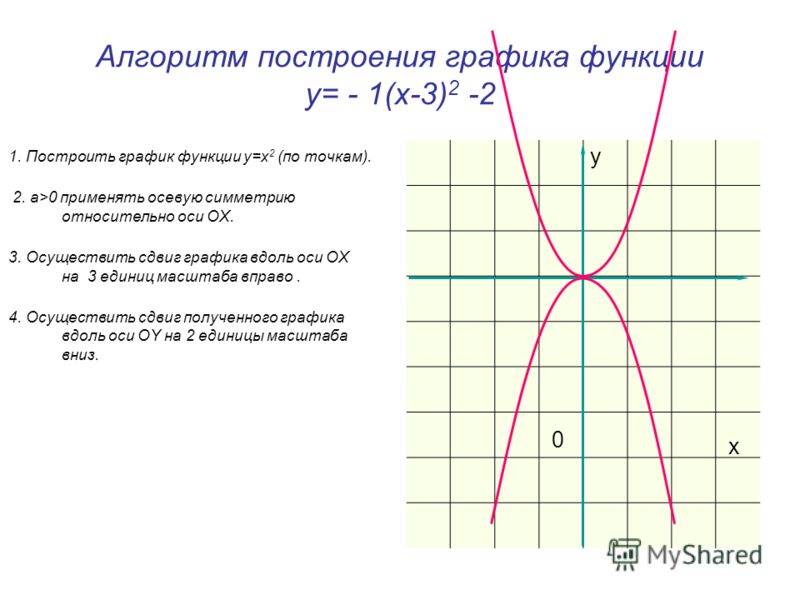
Решить неравенство x 2 < х.
Уравнение x 2 = х имеет решения х = 0 и х = 1.
x 2 < х
х 2 − х < 0 | Упорядочить оба члена в левой части |
Выберите значение x между 0 и 1, например, и введите значение в функцию.
f(x) = x 2 − х
Результат отрицательный, поэтому знак f(x) такой, как показано ниже.
не существует
Решение: 0 < x < 1
Теперь посмотрите на график левой и правой руки. стороны.
График f(x) = x 2 находится ниже графика g(x) = x включено интервал от 0 до 1. (см. заштрихованную область).
Пример 5 Решить неравенство ln x л 1 / х .