library(readxl)
# Прочтем таблицу по экспорту/импорту продукции в регионах России
types = c("text", rep("numeric", 12))
tab = as.data.frame(read_excel("data/ExpImp.xlsx", 1, col_types = types))
str(tab)
## 'data.frame': 96 obs. of 13 variables:
## $ Регион : chr "Российская Федерация" "Центральный федеральный округ" "Белгородская область" "Брянская область" ...
## $ ПродЭкспорт: num 16196.2 4552.9 221.9 28.5 177.9 ...
## $ ПродИмпорт : num 43076 22954 614 650 454 ...
## $ ТЭКЭкспорт : num 371791.8 204331.7 64.7 5 0.9 ...
## $ ТЭКИмпорт : num 3613.6 1660.3 24.1 20.5 16.7 ...
## $ ХимЭкспорт : num 30739.2 8442.7 33.3 24.5 87.7 ...
## $ ХимИмпорт : num 50129.5 34870.4 242.8 71.7 419 ...
## $ ДревЭкспорт: num 10965.8 1101.6 6.2 23.4 57.1 ...
## $ ДревИмпорт : num 6641.5 3942.6 43.3 44.9 9 ...
## $ МетЭкспорт : num 40859.3 9877 2014.1 50.5 29 ...
## $ МетИмпорт : num 22017.4 11763.6 1207.3 68.3 56.6 ...
## $ МашЭкспорт : num 28338.5 12845.9 84.
1 143.2 286.1 ...
## $ МашИмпорт : num 154371 96196 1710 823 469 ...# Выгрузим данные по федеральным округам в отдельную таблицу
filter = grep("федеральный округ", tab$Регион)
okr = tab[filter, ]
# Отсортируем данные по федеральным округам в алфавитном порядке:
okr = okr[order(okr$Регион), ]
# Выгрузим данные по субъектам в отдельную таблицу
filter = grepl("федеральный округ|Федерация|числе",tab$Регион)
sub = tab[!filter, ]5.1 Стандартные графики
Графики (точечные и линейные) – базовый и наиболее часто используемый способ визуализации. Универсальная функция plot() позволяет строить графики по координатам \(X\) и \(Y\), которые передаются, соответственно, в первый и второй аргумент. Если переменные \(X\) и \(Y\) не связаны друг с другом явным образом, то такой график называется диаграммой рассеяния.
5.1.1 Диаграммы рассеяния
Диаграмма рассеяния позволяет установить, есть ли зависимость между переменными, а также понять, как объекты дифференцируются по значениям переменных.
par(mar=c(4,4,3,2))
# Диаграмма рассеяния по экспорту и импорту:
plot(sub$МетЭкспорт,
sub$МетИмпорт,
col="red",
xlab="Экспорт, млн. долл. США",
ylab = "Импорт, млн. долл. США",
main = "Экспорт/импорт металлов и изделий из них по субъектам РФ")В данном случае четко выделяется группа субъектов вблизи начала координат, не отличающихся интенсивным экспортом и импортом продукции металлургии, а также очевидно преобладание экспорта над импортом при больших объемах товарооборота.
При построении диаграмм рассеяния важно сохранить одинаковый масштаб по осям \(X\) и \(Y\). Чтобы обеспечить это условие, необходимо использовать параметр asp = 1:
plot(sub$МетЭкспорт,
sub$МетИмпорт,
col="red",
xlab="Экспорт, млн. долл. США",
ylab = "Импорт, млн. долл. США",
main = "Экспорт/импорт металлов и изделий из них по субъектам РФ",
asp = 1)Попробуйте изменить размер окна на вкладке Plots.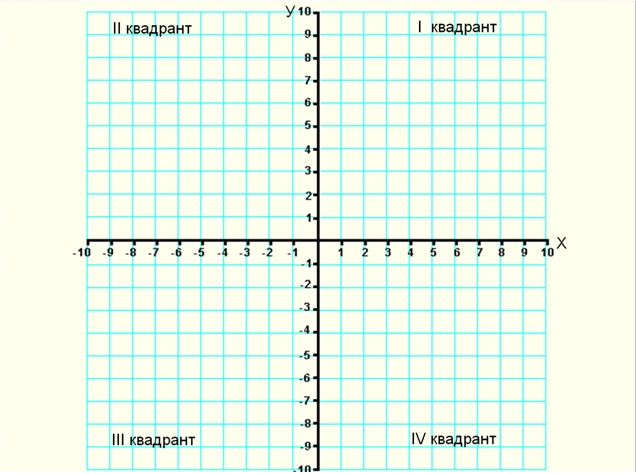 Вы увидите, что масштаб по осям сохраняется пропорциональным.
Вы увидите, что масштаб по осям сохраняется пропорциональным.
Размер и тип значка можно изменить, используя параметры pch = и cex =. Размеры масштабируются параметром cex относительно условной единицы — стандартного размер значка. Сам значок можно выбрать, используя его код в соответствии с нижеприведенным рисунком (на самом деле, вы можете выбирать произвольные символы для визуализации точек):
Типы символов R
plot(sub$МетЭкспорт,
sub$МетИмпорт,
col="red",
xlab="Экспорт, млн. долл. США",
ylab = "Импорт, млн. долл. США",
main = "Экспорт/импорт металлов и изделий из них по субъектам РФ",
asp = 1,
pch = 2,
cex = 0.5) plot(sub$МетЭкспорт,
sub$МетИмпорт,
col="red",
xlab="Экспорт, млн. долл. США",
ylab = "Импорт, млн. долл. США",
main = "Экспорт/импорт металлов и изделий из них по субъектам РФ",
asp = 1,
pch = 20,
cex = 1. 2)
2)5.1.2 Линейные графики
Линейные графики отражают связь между зависимой и независимой переменной. Существует два способа нанесения линий на график: явное рисование линий поверх уже построенного графика с помощью функции lines(), или создание нового линейного графика с помощью функции plot() с дополнительным параметром type =.
Для иллюстрации принципов работы первого способа откроем еще раз данные по объему сброса загрязненных сточных вод по морям России (млрд куб. м):
tab = read.csv2("data/oxr_vod.csv", encoding = 'UTF-8')
plot(tab$Год, tab$Каспийское, pch=20) # для начала нанесем точки
lines(tab$Год, tab$Каспийское) # теперь нанесем линииПо умолчанию функция plot() рисует именно точки. Однако если точки не нужны, а достаточно только линий, или требуется иной подход к построению графиков, можно задать параметр type =, который принимает следующие значения:
-
"p"for points, -
"l"for lines, -
"b"for both, -
"c"for the lines part alone of “b”, -
"o"for both ‘overplotted’, -
"h"for ‘histogram’ like (or ‘high-density’) vertical lines, -
"s"for stair steps, -
"S"for other steps, see ‘Details’ below, -
"n"for no plotting.
Попробуем разные методы визуализации:
plot(tab$Год, tab$Карское,pch=20)
plot(tab$Год, tab$Каспийское, type="p")
plot(tab$Год, tab$Каспийское, type="l")
plot(tab$Год, tab$Каспийское, type="b")
plot(tab$Год, tab$Каспийское, type="c")
plot(tab$Год, tab$Каспийское, type="o")
plot(tab$Год, tab$Каспийское, type="h")
plot(tab$Год, tab$Каспийское, type="s")
Толщину и тип линии можно изменить, используя параметры lwd = и lty = соответственно. Работают они аналогично параметрам pch и cex для точечных символов. Типов линий по умолчанию в стандартной библиотеке R не так много, но в сочетании с цветовым кодированием и толщиной их оказывается вполне достаточно:
Попробуем разные варианты представления линий:
plot(tab$Год, tab$Каспийское, type="l", lwd = 2, lty = 1)
plot(tab$Год, tab$Каспийское, type="l", lwd = 3, lty = 2)
plot(tab$Год, tab$Каспийское, type="l", lwd = 1, lty = 3)
5.
Часто бывает необходимо совместить на одном графике несколько рядов данных. Для этого можно поступить двумя путями:
Нарисовать один ряд данных c помощью функции
plot(), а затем добавить к нему другие ряды с помощью функцийpoints()иlines().Нарисовать пустой график, а затем добавить к нему все ряды данных с помощью функций
points()иlines().
При совмещении нескольких рядов данных на одном графике в первом же вызове функции
plot()необходимо заложить диапазон значений по осям \(X\) и \(Y\), охватывающий все ряды данных. В противном случае будет учтен только разброс значений первого ряда данных, и остальные ряды могут не поместиться в поле графика.
Вариант №1 реализуется следующим образом:
plot(tab$Год,
tab$Каспийское,
pch=20,
type="o",
ylim = c(0,12),
col="red3")
# Добавим теперь на существующий график новый ряд данных, используя функции points() и lines():
points(tab$Год, tab$Карское, pch=20, col="forestgreen")
lines(tab$Год, tab$Карское, pch=20, col="forestgreen") Обратите внимание на то, что если бы мы вызвали еще одну инструкцию
plot()с новым рядом данных, это привело бы к построению нового графика, а не к добавлению его на существующий.
Теперь рассмотрим второй вариант. Заодно устраним недостаток предыдущего кода, в котором диапазон значений по оси \(Y\) указывался вручную.
xrange = range(tab$Год) # вычислим диапазон по оси X
yrange = range(tab$Каспийское, tab$Карское, tab$Азовское) # вычислим диапазон по оси Y
# Построим пустой график, охватывающий полный диапазон данных, и имеющий все необходимые сопроводительные элементы
plot(xrange,
yrange,
main="Объем сброса загрязненных сточных вод",
xlab="Год",
ylab="млрд.куб.м",
type = "n") # n означает, что ряд данных рисоваться не будет
# Теперь добавим на график ряды данных
points(tab$Год, tab$Каспийское, pch=20, col="red3")
lines(tab$Год, tab$Каспийское, pch=20, col="red3")
points(tab$Год, tab$Карское, pch=20, col="forestgreen")
lines(tab$Год, tab$Карское, pch=20, col="forestgreen")
points(tab$Год, tab$Азовское, pch=20, col="steelblue")
lines(tab$Год, tab$Азовское, pch=20, col="steelblue")5.1.4 Функциональные параметры
Графические параметры при построении графиков на самом деле могут быть не константами, а функцией данных.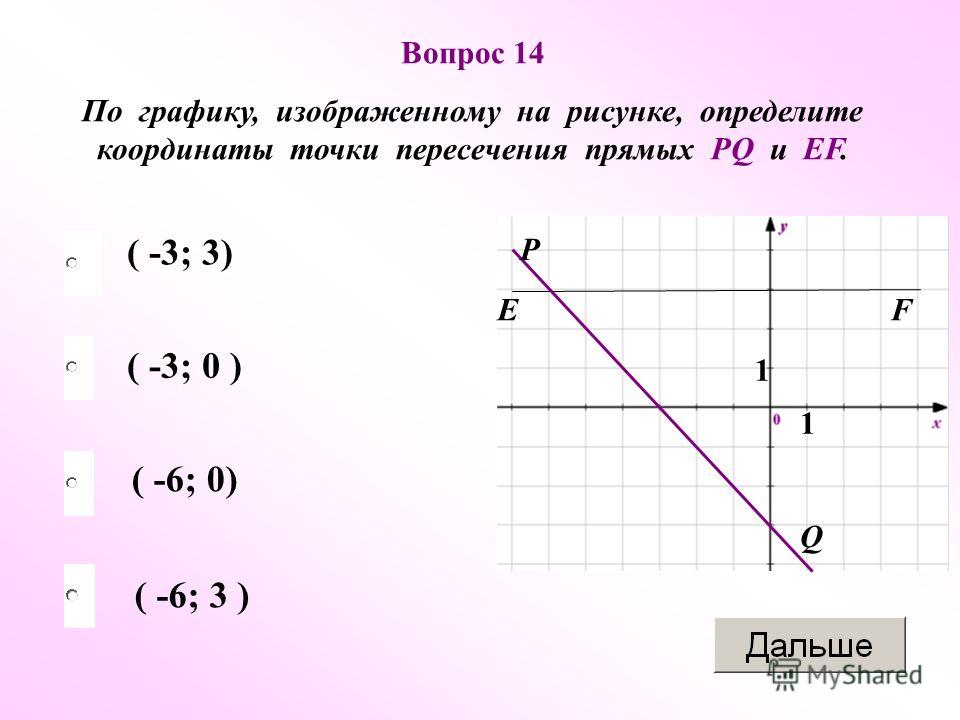 Например, вы можете сказать, что размер точки при построении диаграммы рассеяния должен быть функцией отношения экспорта к импорту, что усилит наглядность отображения:
Например, вы можете сказать, что размер точки при построении диаграммы рассеяния должен быть функцией отношения экспорта к импорту, что усилит наглядность отображения:
plot(okr$МетЭкспорт,
okr$МетИмпорт,
col=rgb(1,0,0,0.5),
xlab="Экспорт, млн. долл. США",
ylab = "Импорт, млн. долл. США",
main = "Экспорт/импорт металлов и изделий из них по ФО РФ (2013 г.)",
asp = 1,
pch = 20,
cex = 2+log(sub$МетИмпорт/sub$МетЭкспорт)) # размер кружка зависит от соотношения импорта и экспорта 5.2 Гистограммы
Гистограммы распределения строятся с помощью функции hist(). Чтобы изменить ширину кармана (столбца) гистограммы, необходимо задать параметр breaks =, а цвет задается в параметре col:
hist(sub$ПродЭкспорт)
# Карманы будут от 0 до 3000 через 100. Заодно добавим цвет: hist(sub$ПродЭкспорт, breaks = seq(0,3000,100), col="olivedrab3")
При построении гистограммы (как и любого другого типа графика) вы можете использовать не весь массив данных, а только его подмножество Например, можно посмотреть гистограмму только для субъектов с объемом экспорта менее 300:
hist(sub$ПродЭкспорт[sub$ПродЭкспорт < 300], col = "olivedrab3", breaks = seq(0, 300, 20))
Наконец, вы можете осуществить преобразование ряда данных перед построением гистограммы.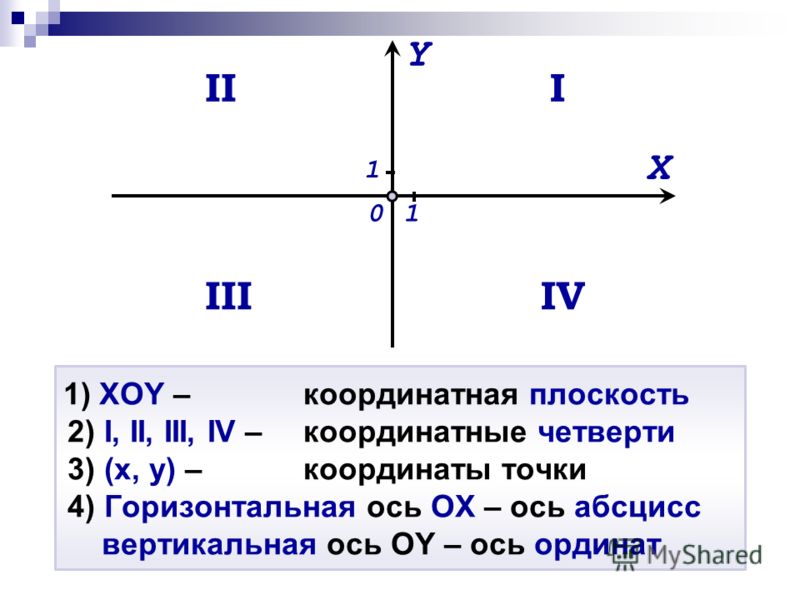 Например, взять логарифм, чтобы проверить,похоже ли распределение на логнормальное:
Например, взять логарифм, чтобы проверить,похоже ли распределение на логнормальное:
hist(log(sub$ПродЭкспорт), col = "olivedrab3")
5.3 Столбчатые графики
Столбчатые графики — barplot — отображают вектор числовых данных в виде столбиков. Это простейший вид графика (наряду с dotchart), который используется для сравнения абсолютных величин. Для построения необходимо вызвать функцию barplot() и передать ей столбец таблицы:
barplot(okr$ХимЭкспорт)
# Или даже просто вектор натуральных чисел от -5 до 5: barplot(-5:5)
# Если у каждого столбика есть название, # нужно передать вектор названий в аргумент names.arg = barplot(okr$ХимЭкспорт, names.arg = okr$Регион)
# при наличии длинных подписей удобнее столбчатую диаграмму разместить горизонтально, используя параметр horiz = TRUE. barplot(okr$ХимЭкспорт, names.arg = okr$Регион, horiz=TRUE)
Чтобы развернуть подписи перпендикулярно столбцам, следует использовать параметр las =.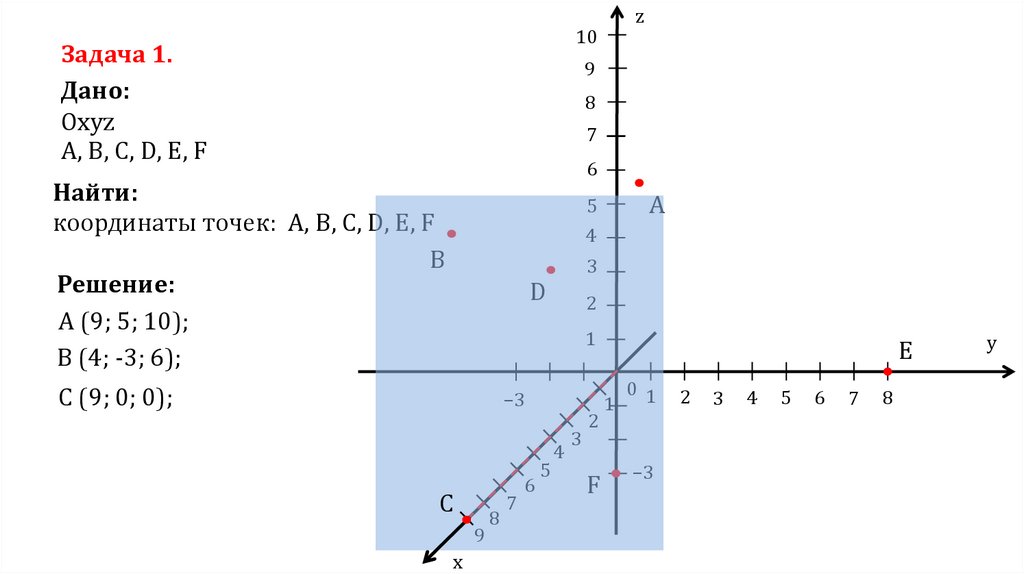 Справка__R__говорит нам о том, что этот параметр дает следующее поведение подписей:
Справка__R__говорит нам о том, что этот параметр дает следующее поведение подписей:
- 0: всегда параллельно осям (по умолчанию),
- 1: всегда горизонтально,
- 2: всегда перпендикулярно осям,
- 3: всегда вертикально.
Выберем вариант, при котором подписи всегда горизонтальны:
barplot(okr$ХимЭкспорт, names.arg = okr$Регион, horiz=TRUE, las = 1)
В данном случае очень массивные названия федеральных не умещаются в пространство графика. Можно было бы вполне убрать словосочетание “федеральный округ”. Для этого используем уже знакомую нам sub().
names = sub("федеральный округ", "", okr$Регион) # "" - означает пустая строка
barplot(okr$ХимЭкспорт, names.arg = names, horiz = TRUE, las = 1)И снова содержимое не поместилось в поле графика. Проблема в том, что вокруг любого графика резервируются поля ограниченного размера для размещения подписей координат и т.д. Автоматически эти поля не пересчитываются, зарезервировать их — ваша задача.
Наберите в консоли ?par. Откроется список всевозможных графических параметров, которые управляют компоновкой и порядком построения графиков. Эти параметры можно установить, вызвав функцию par(). Все дальнейшие вызовы инструкций построения графиков будут учитывать установленные параметры Пролистайте страницу справки вниз и найдите параметр mar = — он отвечает за установку полей в условных единицах. Есть также параметр mai =, который позволяет установить поля графика в дюймах. Обратите внимание на то, что означают параметры этой функции:
# mar=c(bottom, left, top, right) # The default is c(5, 4, 4, 2) + 0.1.
Поскольку в нашем примере проблемы возникают в левым полем, необходимо увеличить второй параметр.
margins.default = par("mar") # запишем текущее значение, чтобы восстановить его потом
par(mar = c(5, 10, 4, 2)) # увеличим поле left до 10 условных единиц
barplot(okr$ХимЭкспорт, names.arg = names, horiz=TRUE, las = 1)Добавим заголовок с помощью параметра main =, а подпись единиц измерения по оси \(X\) — с помощью параметра xlab =.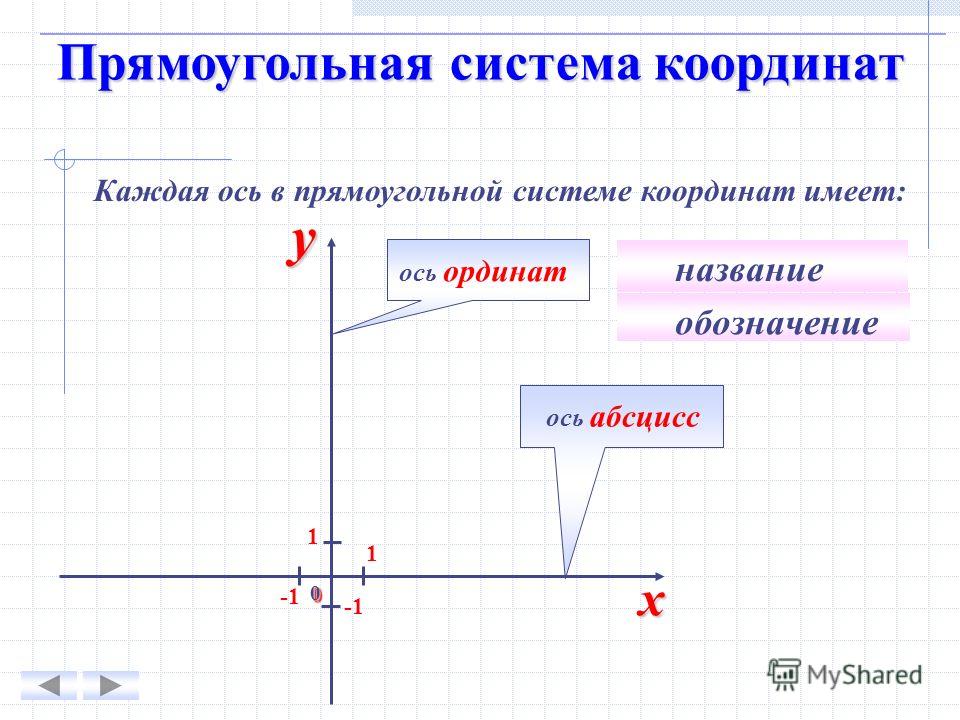 Поскольку количество параметров функции уже достаточно велико, введем каждый из них с новой строчки, чтобы улучшить читаемость кода:
Поскольку количество параметров функции уже достаточно велико, введем каждый из них с новой строчки, чтобы улучшить читаемость кода:
barplot(okr$ХимЭкспорт,
names.arg = names,
main = "Экспорт продукции химической промышленности",
xlab = "млн долл. США",
horiz = TRUE,
las = 1)
# Чтобы увеличить диапазон оси X, можно использовать параметр xlim = c(min, max):
barplot(okr$ХимЭкспорт,
names.arg = names,
main = "Экспорт продукции химической промышленности",
xlab = "млн долл. США",
horiz = TRUE,
las = 1,
xlim = c(0,12000))Работа с цветом на столбчатых диаграммах рассмотрена ниже в отдельном разделе.
5.4 Круговые (секторные) диаграммы
Круговые диаграммы (англ. piechart) строятся с помощью функции pie():
par(mar = c(5, 5, 5, 5)) # установим поля pie(okr$ХимЭкспорт)
# вместо номеров можно использовать подписи секторов, добавив второй параметр: pie(okr$ХимЭкспорт, names)
# в каждую метку можно добавить процент данного округа в общей массе.Для этого его нужно сначала посчитать: percentage = 100 * okr$ХимЭкспорт / sum(okr$ХимЭкспорт) # и округлить до 1 знака после запятой: percentage = round(percentage, digits = 1)
Можно присоединить проценты к названиям округов, добавив обрамляющие скобки. Чтобы функция paste не добавляя пробелы между присоединяемыми строками, необходимо задать параметр sep = , передав ему пустую строку — ““:
names2=paste(names, " (", percentage, "%)", sep = "")
# Используем для аннотирования круговых секторов:
pie(okr$ХимЭкспорт, names2)# Добавить заголовок можно также с помощью параметра main = pie(okr$ХимЭкспорт, names2, main = "Доля федеральных округов в экспорте продукции химической промышленности")
Чтобы перенести часть заголовка на вторую строку, вы можете использовать управляющий символ перевода строки \n, вставив его в требуемое место:
pie(okr$ХимЭкспорт, names2, main = "Доля федеральных округов в экспорте \n продукции химической промышленности")
Управляющие символы играют большое значение в программировании и используются для управления поведением текстового вывода.
Нотация
\nназывается escape-последовательностью. Помимо перевода строки, есть и другие полезные управляющие символы. Кстати, именно из-за того, что escape-последовательности начинаются с обратной косой черты (\), при указании системных путей в функцииsetwd()всегда следует использовать прямую косую черту (/). Например, следующий путь не будет найдет, поскольку он содержит управляющие последовательности\nи\t:C:\data\tables\new.
Наконец, при использовании секторных диаграмм важно уметь менять порядок секторов. По умолчанию сектора откладываются против часовой стрелки начиная с восточного направления. Чтобы сектора откладывались по часовой стрелке с северного направления, следует задать параметр clockwise = TRUE.
pie(okr$ХимЭкспорт,
names2,
main = "Доля федеральных округов в экспорте \n продукции химической промышленности",
clockwise = TRUE)Работа с цветом на круговых диаграммах рассмотрена ниже в отдельном разделе.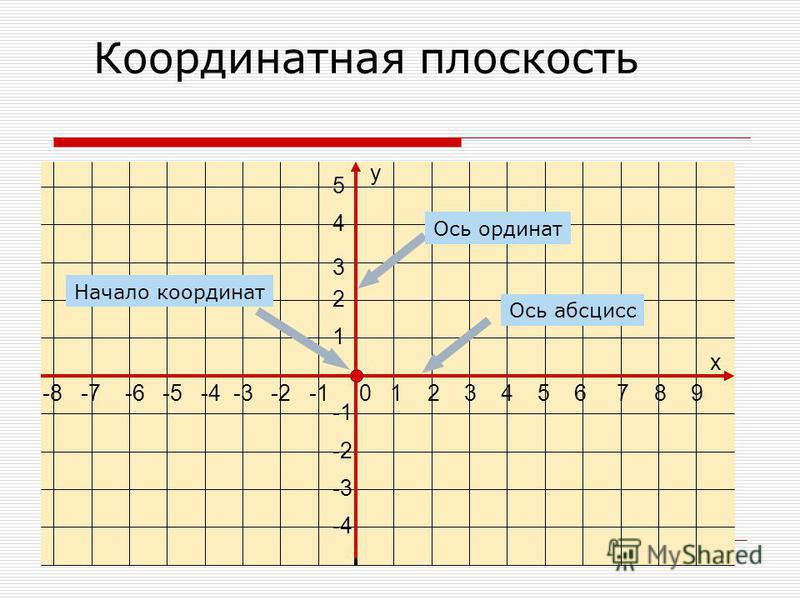
5.5 Цвет и прозрачность
Цвет — одно из основных графических средств, используемых на графиках и диаграммах, поэтому данная тема рассмотрена более подробно в отдельном разделе. Определить цвет можно различными способами. Во-первых, в R есть палитра предопределенных цветов, которые можно выбирать по их названию).
Список названий цветов можно посмотреть, вызвав функцию colors():
head(colors()) ## [1] "white" "aliceblue" "antiquewhite" "antiquewhite1" ## [5] "antiquewhite2" "antiquewhite3"
Основной цвет любого графика или диаграмма задается параметром col =. Это цвет (или цвета) с помощью которых будут отображаться данные. Попробуем изменить цвет графика с серого на пастельно-синий:
par(mar = c(5, 10, 4, 2)) # увеличим поле left до 10 условных единиц
barplot(okr$ХимЭкспорт,
names.arg = names,
main = "Экспорт продукции химической промышленности",
xlab = "млн долл. США",
horiz = TRUE,
las = 1,
xlim = c(0,12000),
col = "steelblue")
США",
horiz = TRUE,
las = 1,
xlim = c(0,12000),
col = "steelblue") Помимо этого вы можете задать цвет с помощью цветовых компонент в различных пространствах. Для этого вы должны быть знакомы с основами теории цвета (посмотрите презентацию UsingColorInR.pdf. Например, фиолетовый цвет в пространстве RGB можно задать с помощью функции rgb(), смешав синюю и красную компоненты:
violet = rgb(0.4, 0, 0.6)
barplot(okr$ХимЭкспорт,
names.arg = names,
main = "Экспорт продукции химической промышленности",
xlab = "млн долл. США",
horiz = TRUE,
las = 1,
xlim = c(0,12000),
col = violet)Чтобы сделать цвет полупрозрачным, есть две возможности:
- При создании нового цвета — передать в функцию
rgb()дополнительный параметрalpha =, который задает долю прозрачности в диапазоне от 0 до 1. - При модификации существующего цвета — вызвать функцию
adjustcolor()с параметромalpha =
Например:
violet.transp = adjustcolor(violet, alpha = 0.5) barplot(okr$ХимЭкспорт, names.arg = names, main = "Экспорт продукции химической промышленности", xlab = "млн долл. США", horiz = TRUE, las = 1, xlim = c(0,12000), col = violet.transp)
green.transp = rgb(0, 1, 0, 0.5) # появился четвертый параметр
barplot(okr$ХимЭкспорт,
names.arg = names,
main = "Экспорт продукции химической промышленности",
xlab = "млн долл. США",
horiz = TRUE,
las = 1,
xlim = c(0,12000),
col = green.transp)Функция
adjustcolor()позволяет модифицировать все компоненты цвета, не только прозрачность.
На графике типа barplot вы имеете фактически несколько переменных, которые представлены столбиками. А это означает что для них можно использовать различные цвета. Вы можете передать в параметр col = вектор из цветов, соответствующих столбикам:
colors = c("red", "green", "blue", "orange", "yellow", "pink", "white","black")
barplot(okr$ХимЭкспорт,
names. arg = names,
main = "Экспорт продукции химической промышленности",
xlab = "млн долл. США",
horiz = TRUE,
las = 1,
xlim = c(0,12000),
col = colors)
arg = names,
main = "Экспорт продукции химической промышленности",
xlab = "млн долл. США",
horiz = TRUE,
las = 1,
xlim = c(0,12000),
col = colors)На самом деле, такой винегрет из цветов на столбчатых диаграммах использовать не принято. Но вы должны понимать, что при необходимости можно поменять цвет отдельно выбранных столбиков. Например, мы можем показать красным цветом Центральный и Приволжский округа, которые являются лидерами по экспорту продукции химической промышленности:
colors = rep("gray", 8) # сделаем 8 серых цветов
colors[2] = "red"
colors[7] = "red"
barplot(okr$ХимЭкспорт,
names.arg = names,
main = "Экспорт продукции химической промышленности",
xlab = "млн долл. США",
horiz = TRUE,
las = 1,
xlim = c(0,12000),
col = colors)Еще одна интересная особенность использования цвета заключается в том, что количество указанных цветом может не совпадать с количеством рядов данных. Вы можете указать 2 или 3 цвета, и они будут циклически повторяться при визуализации данных:
Вы можете указать 2 или 3 цвета, и они будут циклически повторяться при визуализации данных:
colors=c("gray","steelblue")
barplot(okr$ХимЭкспорт,
names.arg = names,
main = "Экспорт продукции химической промышленности",
xlab = "млн долл. США",
horiz =TRUE,
las = 1,
xlim = c(0, 12000),
col = colors)Наконец, вещь, которой совершенно необходимо уметь пользоваться при работе с цветом в R — это цветовые палитры. Палитры чрезвычайно удобны, когда необходимо сгенерировать множество цветов, зная лишь основные оттенки. Для этого нужно создать палитру, используя функцию colorRampPalette():
# задаем 2 опорных цвета: черный белый
palet=colorRampPalette(c("black","white"))
# и автоматически генерируем 8 цветов между ними:
colors=palet(8)
# используем их для отображения:
barplot(okr$ХимЭкспорт,
names.arg = names,
main = "Экспорт продукции химической промышленности",
xlab = "млн долл. США",
horiz = TRUE,
las = 1,
xlim = c(0, 12000),
col= colors)
США",
horiz = TRUE,
las = 1,
xlim = c(0, 12000),
col= colors)
# вы можете включить в палитру произвольное количество цветов:
palet=colorRampPalette(c("steelblue","white","purple4"))
colors=palet(8)
barplot(okr$ХимЭкспорт,
names.arg = names,
main = "Экспорт продукции химической промышленности",
xlab = "млн долл. США",
horiz=TRUE,
las = 1,
xlim = c(0, 12000),
col= colors)В R существует множество стандартных палитр, их список можно найти в справке и документации. Наиболее полезные из них:
colors()gray()rainbow()heat.colors()topo.colors()terrain.colors()
Например, вы можете изменить цвета диаграммы, взяв их из одной из палитр или выбрав случайным образом из полной палитры цветов, используя функцию sample():
pie(okr$ХимЭкспорт, names2, main = "Доля федеральных округов в экспорте \n продукции химической промышленности", col=rainbow(length(names2)))
pie(okr$ХимЭкспорт, names2, main = "Доля федеральных округов в экспорте \n продукции химической промышленности", col=sample(colors(),5))
Более богатый набор палитр можно найти в библиотеке RColorBrewer, которая представляет собой интерпретацию палитр, доступных на сайте colorbrewer2.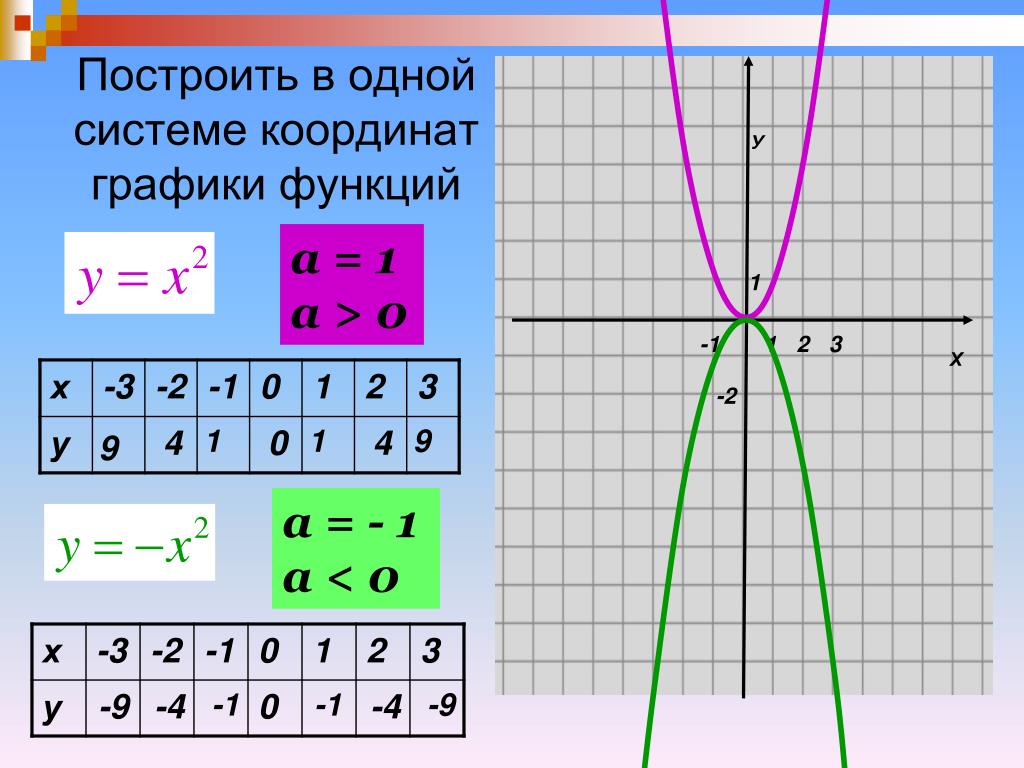 org
org
library(RColorBrewer) # Откроем библиотеку RColorBrewer: display.brewer.all() # Посмотрим, какие в ней имеются палитры
К каждой из этих палитр можно обратиться по названию с помощью функции brewer.pal(). Поскольку нам необходимы цвета для категориальных данных, следует использовать палитры из средней части (Set3 — Accent)
# выберем цвета из палитры Set2 по количеству секторов в круге: colors = brewer.pal(length(names2),"Set1") # И используем их при визуализации par(mar = c(5, 5, 5, 5)) # установим поля pie(okr$ХимЭкспорт, names2, main = "Доля федеральных округов в экспорте \n продукции химической промышленности", col=colors)
# Попробуем палитру Accent: pie(okr$ХимЭкспорт, names2, main = "Доля федеральных округов в экспорте \n продукции химической промышленности", col=brewer.pal(length(names2),"Accent"))
5.6 Настройки отображения
5.6.1 Графические параметры
Изменять размеры элементов графика можно независимо друг от друга, используя следующие параметры:
-
cex— общий масштаб элементов на графике -
cex.— масштаб подписей координат на оси axis
axis -
cex.lab— масштаб подписей названий осей -
cex.main— масштаб заголовка графика -
cex.sub— масштаб подзаголовка графика -
cex.names— масштаб подписей факторов (для некоторых типов диаграмм)
Например:
plot(tab$Год,
tab$Каспийское,
pch=20,
type="o",
ylim = c(0,12),
col="red3",
main="Объем сброса загрязненных сточных вод",
xlab="Год",
ylab="млрд.куб.м",
cex.axis=0.8,
cex.lab=0.7,
cex.main=0.9,
cex = 0.8)
points(tab$Год, tab$Карское, pch=20, col="forestgreen",cex = 0.8)
lines(tab$Год, tab$Карское, pch=20, col="forestgreen")
points(tab$Год, tab$Азовское, pch=20, col="steelblue",cex = 0.8)
lines(tab$Год, tab$Азовское, pch=20, col="steelblue")Аналогично происходит тонкая настройка цвета:
-
colцвет графика -
col.цвет подписей координат axis
axis -
col.labцвет названий осей -
col.mainцвет заголовка -
col.subцвет подзаголовка -
fgцвет элементов переднего плана (оси, рамка и т.д.) -
bgцвет фона графика (background)
plot(tab$Год,
tab$Каспийское,
pch=20,
type="o",
ylim = c(0,12),
col="red3",
main="Объем сброса загрязненных сточных вод",
xlab="Год",
ylab="млрд.куб.м",
cex.axis=0.8,
cex.lab=0.7,
cex.main=0.9,
col.lab = "grey50",
fg = "grey40")
points(tab$Год, tab$Карское, pch=20, col="forestgreen")
lines(tab$Год, tab$Карское, pch=20, col="forestgreen")
points(tab$Год, tab$Азовское, pch=20, col="steelblue")
lines(tab$Год, tab$Азовское, pch=20, col="steelblue")5.6.2 Разметка осей, рамка, сетка координат и произвольные линии
По умолчанию R подбирает оптимальный с точки зрения него шаг разметки осей, в зависимости от разброса значений по осям \(X\) и \(Y\), а также размеров графического устройства, на котором производится рисование. Изменяя размер окна прорисовки, вы получите различную разметку осей.
Изменяя размер окна прорисовки, вы получите различную разметку осей.
В то же время, часто возникает желание (или необходимость) самостоятельно управлять шагом разметки сетки. Для этого необходимо:
- Вызвать функцию
plot(), передав ей дополнительно параметрaxes = FALSE(убирает при рисовании обе оси) или один из параметровxaxt="n"/yaxt="n"(убирают оси \(X\) и \(Y\) соответственно) - Вызвать столько раз функцию
axis(), сколько вы хотите нарисовать осей, передав ей параметры для рисования каждой оси.
Функция axis() принимает следующие параметры:
-
side— сторона графика, на которой будет нарисована ось (1=bottom,2=left,3=top,4=right) -
at— вектор значений, в которых должны быть нарисованы метки оси -
labels— вектор подписей, которые будут нарисованы в местоположениях, указанных в параметреat. Этот параметр можно пропустить, если подписи совпадают с местоположениями меток
Этот параметр можно пропустить, если подписи совпадают с местоположениями меток -
pos— координата, вдоль которой будет нарисована ось -
lty— тип линии -
col— цвет линии и меток -
las— расположение подписей параллельно (\(0\)) или перпендикулярно (\(2\)) оси -
tck— длина метки относительно размера графика. Отрицательные значения дают метки, выходящие за пределы графика. положительные — внутрь графика. \(0\) убирает метки, \(1\) рисует линии сетки.
При ручном построении осей полезно сразу же нарисовать рамку вокруг графика, используя функцию box().
Например:
plot(tab$Год,
tab$Каспийское,
type = "l",
axes = FALSE)
axis(side = 1,
at = seq(min(tab$Год), max(tab$Год), 1),
tck = -0.02,
labels = FALSE) # разметим ось X через 1 год, но рисовать подписи не будем
axis(side = 1,
at = seq(min(tab$Год), max(tab$Год), 3), # а подписи расставим через 3 года
tck = 0) # но рисовать метки не будем
# разметим ось Y через 1 млрд куб. м., округлив предварительно минимальное и максимальное значение до ближайшего целого снизу и сверху соответственно
axis(side = 2,
at = seq(floor(min(tab$Каспийское)), ceiling(max(tab$Каспийское)), 1),
tck = -0.02)
box() # добавим рамку для красоты
м., округлив предварительно минимальное и максимальное значение до ближайшего целого снизу и сверху соответственно
axis(side = 2,
at = seq(floor(min(tab$Каспийское)), ceiling(max(tab$Каспийское)), 1),
tck = -0.02)
box() # добавим рамку для красотыДля размещения сетки координат существует функция grid(nx = NULL, ny = nx, col = "lightgray", lty = "dotted", lwd = par("lwd"), equilogs = TRUE). Как видно из набора ее параметров, сетка определяется количеством линий в горизонтальном и вертикальном направлении. Это не всегда бывает удобно, поскольку как правило мы хотим задать шаг сетки конкретной величины. По умолчанию, однако, линии сетки выбираются автоматически, как и метки:
plot(tab$Год,
tab$Каспийское,
type = "l",
col = "red")
grid()Вы, разумеется, можете поменять их количество, однако R не будет за вас согласовывать шаг сетки и шаг меток осей, поскольку метки генерируются на стадии рисования plot() или axis() и не запоминаются.
plot(tab$Год,
tab$Каспийское,
type = "l",
col = "red")
grid(10, 5)Функция grid() на самом деле является оберткой функции abline(), которая позволяет рисовать произвольные линии на графике. Дана функция предоставляет следующие возможности построения линий и серий линий:
-
a, b— коэффициенты уравнения \(y = ax + b\). Таким образом можно определить только одну линию. -
coef— принимает вектор из двух значений, которые интерпретируются какaиb. То есть, это альтернативная форма записи предыдущего случая. -
h— значение (значения) координат \(y\) для горизонтальной линии (серии горизонтальных линий). То есть, вы можете передать в этот параметр как одиночное значение, так и вектор значений. В зависимости это этого нарисуется одна горизонтальная линия или серия горизонтальных линий. -
v— значение (значения) координат \(x\) для вертикальной линии (серии вертикальных линий). 3\) по оси \(Y\). Для этого выполним следующую последовательность действий:
3\) по оси \(Y\). Для этого выполним следующую последовательность действий:plot(tab$Год, tab$Каспийское, type="n") # режим 'n' позволяет ничего не рисовать, но заложить поле графика в соответствии с данными, указанными в параметрах x и y # Вычисляем линии сетки xlines = seq(min(tab$Год), max(tab$Год), 1) ylines = seq(ceiling(min(tab$Каспийское)), floor(max(tab$Каспийское)), 1) # Рисуем линии сетки abline(h = ylines, v = xlines, col = "lightgray") # Рисуем график lines(tab$Год, tab$Каспийское, col="red3") points(tab$Год, tab$Каспийское, pch = 20, col="red3") # Выделяем значение 10 по оси Y: abline(h = 10, col = "blue", lwd = 2) # Рисуем дополнительно рамку, т.к. сетку координат мы рисовали после графика box()5.6.3 Аннотации данных (текст на графике)
Аннотации данных добавляются на график с помощью функции
text(). В качестве трех обязательных аргументов ей необходимо передать координаты точек размещения текста, и вектор подписей. Также полезным будет указать параметр
Также полезным будет указать параметр pos=, отвечающий за размещение аннотации относительно точки. Значенияpos, равные 1, 2, 3 и 4, соответствуют размещению снизу, слева, сверху и справа от точки:text(tab$Год, tab$Каспийское, labels = tab$Каспийское, cex = 0.75, pos = 3)К сожалению, стандартный механизм размещения аннотаций пакета
graphicsне обладает возможностью устранения конфликтов подписей. Однако это возможно для графиков, построенных с помощью библиотек lattice и ggplot2. Для этого можно воспользоваться пакетом directlabels или ggrepel.5.7 Легенда
Легенда к графику размещается с помощью функции
legend(). Эта функция принимает несколько аргументов, включая: местоположение, заголовок, названия элементов, графические параметры. Местоположение может быть задано координатами \((x,y)\) в системе координат графика, но удобнее пользоваться следующими предопределенными константами:"bottomright","bottom","bottomleft","left","topleft","top","topright","right","center".
Чтобы в легенде появились точки, необходимо задать параметр
pch=. Для линейной легенды, следует задать, соответственно, параметрlty =и/илиlwd =. Каждый из этих параметров должен быть вектором по количеству элементов легенды:par(mar = margins.default) # Найдем ограничивающий прямоугольник вокруг всех рядов данных xrange = range(tab$Год) yrange = range(tab$Каспийское, tab$Карское, tab$Азовское) # Построим пустой график с разметкой осей и всеми заголовками plot(xrange, yrange, type="n", main="Объем сброса загрязненных сточных вод", xlab="Год", ylab="млрд.куб.м", cex.axis=0.8, cex.lab=0.7, cex.main=0.9, col.lab = "grey50", fg = "grey40") # Добавим на график сетку координат grid() # Добавим на график данные points(tab$Год, tab$Каспийское, pch=20, col="red3") lines(tab$Год, tab$Каспийское, pch=20, col="red3") points(tab$Год, tab$Карское, pch=20, col="forestgreen") lines(tab$Год, tab$Карское, pch=20, col="forestgreen") points(tab$Год, tab$Азовское, pch=20, col="steelblue") lines(tab$Год, tab$Азовское, pch=20, col="steelblue") # Определим положение, названия и цвета: main = "Море" location = "topright" labels = c("Каспийское", "Карское", "Азовское") colors = c("red3", "forestgreen", "steelblue") # Если цвет передать в параметр fill, то по умолчанию # нарисуются цветовые плашки: legend(location, labels, title = main, fill=colors)pts = c(20, 20, 20) # каждый элемент показывается точкой типа 20 lns = c(1, 1, 1) # каждый элемент показывается линией толщиной 1 # теперь посмотрим на легенду (она нарисуется поверх старой) legend(location, labels, title = main, col = colors, pch = pts, lwd = lns)
Более подробно с разнообразными опциями размещения легенды на графике вы можете познакомиться, набрав в консоли команду
?legend.
5.8 Краткий обзор
Для просмотра презентации щелкните на ней один раз левой кнопкой мыши и листайте, используя кнопки на клавиатуре:
Презентацию можно открыть в отдельном окне или вкладке браузере. Для этого щелкните по ней правой кнопкой мыши и выберите соответствующую команду.
5.9 Контрольные вопросы и упражнения
5.9.1 Вопросы
- Какая функция базового пакета R отвечает за построение стандартных графиков (диаграмм рассеяния, линейных)?
- Какие функции стандартной библиотеки R позволяют построить: столбчатые диаграммы, круговые секторные диаграммы, гистограммы?
- Как задать интервал или количество интервалов гистограммы?
- Можно ли разместить столбчатую диаграмму горизыонтально? Если да, то как?
- Какая функция отвечает за установку параметров графической подсистемы?
- Как установить поля вокруг графиков?
- Как развернуть подписи на столбчатой диаграмме перпендикулярно оси?
- Как установить запрет на экспоненциальное представление больших чисел при рисовании графиков?
- Какой параметр отвечает за установку цвета в функциях построения графиков стандартной библиотеки R?
- Какие параметры отвечают за установку толщины и типа линии на графиках?
- Какие параметры отвечают за установку размера и типа значка на диаграммах рассеяния?
- Как совместить несколько графиков на одной сетке координат?
- Какая функция рисует рамку вокруг графика?
- Какая функция отвечает за рисование сетки координат?
- Как установить равный масштаб по осям графика?
- Какие параметры позволяют масштабировать текст элементов графика, таких как подписи координат, осей, заголовков и подзаголовков?
- Назовите способы задания цвета в R.

- Как сделать цвет в R полупрозрачным?
- Назовите стандартные цветовые палитры R.
- Как сгенерировать последовательность из нужного количества цветов между заданными опорными цветами?
- Какая функция позволяет разместить легенду на графике?
- Как сделать так, чтобы в легенде показывались точки? Линии? Цветовые плашки?
5.9.2 Упражнения
Постройте для набора данных quakes пакета datasets гистограммы распределения глубин и магнитуд, а также диаграмму рассеяния для двух этих характеристик.
На портале открытых данных Тульской области есть данные о распределении площади лесов и запасов древесины по преобладающим породам и группам возраста. Скачайте эти данные в виде таблицы CSV и постройте по ним круговую и столбчатую диаграмму для категории
Площадь земель, занятых лесными насаждениями (покрытых лесной растительностью), всего. Подберите цвета, попробуйте изменить ориентировку столбцов на горизонтальную, а для круговой диаграммы поменять угол поворота.
Используя данные3 по балансу масс ледника Гарабаши, постройте график с тремя кривыми (аккумуляции, абляции и кумулятивного баланса) за период 1981 по 2017 г. Добавьте на график легенду. Обратите внимание на то, что таблица содержит агрегирующие строки (1982-1997, 1998-2017, 1982-2017), которые вам необходимо предварительно исключить.
Подсказка: Чтобы построить кривую кумулятивного баланса, используйте функцию
cumsum.Таблица storms из пакета dplyr содержит данные трекинга тропических циклонов c 1975 по 2015 год. Извлеките из нее данные по одному выбранному циклону и постройте на их основе график, показывающий трек прохождения циклона в системе координат давление (X) — скорость (Y). Каждое наблюдение циклона визуализируйте в виде кружка, цвет которого зависит от класса циклона (переменная
status), а размер — от диаметра территории, на которой наблюдаются скорости ветра класса тропического шторма и сильнее. Нанесите поверх кружков значение диаметра текстовой подписью. Соедините кружки линиями со стрелкой посередине, чтобы была понятна история жизни циклона.
Нанесите поверх кружков значение диаметра текстовой подписью. Соедините кружки линиями со стрелкой посередине, чтобы была понятна история жизни циклона.В качестве образца используйте рисунок ниже, построенный для урагана Катрина:
Рис. 5.1: Пример выполнения задания №5
Подсказка: Скорость ветра и диаметр в таблице приведены в узлах и милях соответственно. Их необходимо перевести в м/с и км. Для отрисовки стрелок используйте функцию
arrows(). Прочтите справку к ней, чтобы разобраться как она работает. Чтобы стрелка рисовалась посередине отрезка, а не в конце, используйтеdiff()для получения разностей в давлении и скорости между соседними наблюдениями циклона.
Самсонов Т.Е. Визуализация и анализ географических данных на языке R. М.: Географический факультет МГУ, 2022. DOI: 10.5281/zenodo.901911 Введение в R: часть 6
Введение в R: часть 6Pavel Polishchuk, 2014
Содержание
Графические возможности R с пакетом
ggplot2Литература
- Книга от создателя пакета
ggplot2— Wickham, Hadley. ggplot2: Elegant Graphics for Data Analysis. Dordrecht, Heibelberg, London, New York: Springer, 2009.
ggplot2: Elegant Graphics for Data Analysis. Dordrecht, Heibelberg, London, New York: Springer, 2009. - http://docs.ggplot2.org/current/ — подробная авторская документация с примерами
Идеология представления графиков в рамках пакета
ggplot2Пакет
ggplot2предназначен для построения двумерных графиков и диаграмм.График в рамках пакета
ggplot2представляется как конструктор, состоящий из отдельных частей, которые можно соединять произвольным образом, чтобы достичь желаемого эффекта.Основные кирпичики графического конструктора (первые три их них являются обязательными составляющими):
data—data.frame, содержащий данные для представления.aes()— задает связь между данными и их представлением, определяет какие переменные отображаются на осях, какие переменные отвечают за цвет и форму данных, представленных на графике.geom_— группа функций, отвечающих за то что, вы непосредственно видите на графике (точки, гистограммы, линии, текст и т. п.).
п.).scale_— группа функций, соотносящих реальные данные с их графическим представлением. Это может быть цвет, форма, размер, диапазон осей координат и т.п.stat_— группа функций, добавляющих на график различные статистические показатели, например, такие как, среднее значение по группе, линейная или иная аппроксимация данных и т.п.coord_— группа функций, которая задает систему координат для представления данных на плоскости. Это могут быть обычные картезианские координаты, полярные координаты, или географические координаты для представления соответствующих данных.facet_— группа функций, которые позволяют группировать графики по заданному параметру и представлять результаты в виде набора графиков (сетки из графиков).theme— группа функций, позволяющих менять оформление графика, например размер и цвет шрифта координатных осей и делений на них, фон графика и всего рисунка и т. п.
п.
Подготовка данных для визуализации
Возьмем за основу значения растворимости предсказанные ранее различными моделями. Эти данные можно загрузить с сайта, а можно использовать те, которые были получены в ходе самостоятельного моделирования.
cv <- read.table("data/cv_pred.txt", sep="\t", header=TRUE, as.is=TRUE) test <- read.table("data/test_pred.txt", sep="\t", header=TRUE, as.is=TRUE)head(cv)
m.gbm m.knn m.pls m.rf m.svm mean sol_10001 -2.799118 -3.626667 -2.148206 -3.000497 -2.677521 -2.850402 sol_10002 -2.683472 -3.553333 -2.214603 -2.639931 -2.540740 -2.726416 sol_10003 -2.589948 -3.603333 -2.378869 -3.280679 -3.100913 -2.990748 sol_10004 -2.639194 -3.853333 -2.297653 -3.249204 -3.106995 -3.029276 sol_10005 -3.001957 -2.823333 -1.795756 -3.036543 -2.766391 -2.684796 sol_10006 -3.231845 -3.556667 -2.535705 -3.353757 -3.070914 -3.149778 nnls sol_10001 -2.823609 sol_10002 -2. 657990
sol_10003 -2.973854
sol_10004 -2.984015
sol_10005 -2.922233
sol_10006 -3.233097
657990
sol_10003 -2.973854
sol_10004 -2.984015
sol_10005 -2.922233
sol_10006 -3.233097
head(test)
m.gbm m.knn m.pls m.rf m.svm mean sol_10801 -1.1778582 -0.440000 -0.3168113 -0.8795913 -0.6089708 -0.6846463 sol_10802 -1.0579281 -0.440000 -0.2862568 -1.0169123 -1.0142728 -0.7630740 sol_10803 -0.7143699 -0.440000 -0.2963245 -1.1513807 -1.7784464 -0.8761043 sol_10804 -0.8748695 -0.440000 -0.0164618 -1.1532090 -2.2388806 -0.9446842 sol_10805 -0.9348645 -1.346667 -1.4939263 -1.1176407 -0.8709753 -1.1528147 sol_10806 -1.7129724 -1.473333 -1.3859660 -1.2913827 -1.3519756 -1.4431260 nnls sol_10801 -0.8803242 sol_10802 -1.0139525 sol_10803 -1.1994194 sol_10804 -1.4198597 sol_10805 -1.0024755 sol_10806 -1.5129118Округлим результаты для лучшего восприятия данных
cv <- round(cv, 2) test <- round(test, 2)
head(cv)
m.gbm m.knn m.pls m.rf m.svm mean nnls sol_10001 -2.
 80 -3.63 -2.15 -3.00 -2.68 -2.85 -2.82
sol_10002 -2.68 -3.55 -2.21 -2.64 -2.54 -2.73 -2.66
sol_10003 -2.59 -3.60 -2.38 -3.28 -3.10 -2.99 -2.97
sol_10004 -2.64 -3.85 -2.30 -3.25 -3.11 -3.03 -2.98
sol_10005 -3.00 -2.82 -1.80 -3.04 -2.77 -2.68 -2.92
sol_10006 -3.23 -3.56 -2.54 -3.35 -3.07 -3.15 -3.23
80 -3.63 -2.15 -3.00 -2.68 -2.85 -2.82
sol_10002 -2.68 -3.55 -2.21 -2.64 -2.54 -2.73 -2.66
sol_10003 -2.59 -3.60 -2.38 -3.28 -3.10 -2.99 -2.97
sol_10004 -2.64 -3.85 -2.30 -3.25 -3.11 -3.03 -2.98
sol_10005 -3.00 -2.82 -1.80 -3.04 -2.77 -2.68 -2.92
sol_10006 -3.23 -3.56 -2.54 -3.35 -3.07 -3.15 -3.23
head(test)
m.gbm m.knn m.pls m.rf m.svm mean nnls sol_10801 -1.18 -0.44 -0.32 -0.88 -0.61 -0.68 -0.88 sol_10802 -1.06 -0.44 -0.29 -1.02 -1.01 -0.76 -1.01 sol_10803 -0.71 -0.44 -0.30 -1.15 -1.78 -0.88 -1.20 sol_10804 -0.87 -0.44 -0.02 -1.15 -2.24 -0.94 -1.42 sol_10805 -0.93 -1.35 -1.49 -1.12 -0.87 -1.15 -1.00 sol_10806 -1.71 -1.47 -1.39 -1.29 -1.35 -1.44 -1.51
Добавим к этим данным наблюдаемые значения растворимости
y <- local.load("data/sol_y1.RData") y.test <- local.load("data/sol_y2.RData") cv$obs <- y test$obs <- y.testИ добавим колонку в которой укажем, какому набору принадлежат данные кросс-валидации или тестовой выборке.

cv$set <- "cv" test$set <- "test"
head(cv)
m.gbm m.knn m.pls m.rf m.svm mean nnls obs set sol_10001 -2.80 -3.63 -2.15 -3.00 -2.68 -2.85 -2.82 -3.18 cv sol_10002 -2.68 -3.55 -2.21 -2.64 -2.54 -2.73 -2.66 -2.64 cv sol_10003 -2.59 -3.60 -2.38 -3.28 -3.10 -2.99 -2.97 -3.84 cv sol_10004 -2.64 -3.85 -2.30 -3.25 -3.11 -3.03 -2.98 -3.74 cv sol_10005 -3.00 -2.82 -1.80 -3.04 -2.77 -2.68 -2.92 -3.55 cv sol_10006 -3.23 -3.56 -2.54 -3.35 -3.07 -3.15 -3.23 -3.10 cv
head(test)
m.gbm m.knn m.pls m.rf m.svm mean nnls obs set sol_10801 -1.18 -0.44 -0.32 -0.88 -0.61 -0.68 -0.88 -1.11 test sol_10802 -1.06 -0.44 -0.29 -1.02 -1.01 -0.76 -1.01 -0.91 test sol_10803 -0.71 -0.44 -0.30 -1.15 -1.78 -0.88 -1.20 -1.76 test sol_10804 -0.87 -0.44 -0.02 -1.15 -2.24 -0.94 -1.42 -2.36 test sol_10805 -0.93 -1.35 -1.49 -1.12 -0.87 -1.15 -1.00 -0.86 test sol_10806 -1.71 -1.47 -1.39 -1.29 -1.35 -1.44 -1.51 -1.16 test
Объединим эти два набора данных в один.
 Поскольку порядок следования данных в колонках совпадает можно применить функцию объединения по строкам
Поскольку порядок следования данных в колонках совпадает можно применить функцию объединения по строкам rbinddf <- rbind(cv, test)
Все эти манипуляции конечно не обязательны при работе с реальными данными, а служат лишь для того, чтобы продемонстрировать способы работы с данными и подготовки их к дальнейшей отрисовке.
Задание.
Нарисуем графики распределения предсказанных и наблюдаемых значений для каждой из моделей. По мере продвижения к цели будут продемонстрированы некоторые возможности
ggplot2.Пример точечной диаграммы для одной модели
Начнем с самого простого. Нарисуем точечную диаграмму распределения наблюдаемых и предсказанных значений для модели
gbm. Т.е. используем три обязательных компонентаdata,aesиgeom_.require(ggplot2) # single model plot g1 <- ggplot(df, aes(x=obs, y=m.gbm)) + geom_point() g1
В
ggplot2есть альтернативный более простой вариант для создания диаграмм — функцияqplot, которая во многом похожа на обычную функциюplot. Она не обладает большим разнообразием возможностей и подходит для быстрого построения не очень сложных графиков.
Она не обладает большим разнообразием возможностей и подходит для быстрого построения не очень сложных графиков.# shorter version g1.1 <- qplot(x=obs, y=m.gbm, data=df, geom="point") g1.1
# even shorter one g1.2 <- qplot(x=df$obs, y=df$m.gbm, geom="point") g1.2
У нас на графике совместно представлены данные для кросс-валидации и внешнего теста, разделим их по цвету точек.
# add color to distinguish cv and test g2 <- ggplot(df, aes(x=obs, y=m.gbm, color=set)) + geom_point() g2
Добавим дифференциацию точек по форме, задав соответствующее условие.
# add color and shape to distinguish cv and test g3 <- ggplot(df, aes(x=obs, y=m.gbm, color=set, shape=set)) + geom_point() g3
Если мы хотим увеличить размер точек (задать фиксированный размер), то для этого используются параметры функции
geom_point.# change point size g4 <- ggplot(df, aes(x=obs, y=m.
 gbm, color=set, shape=set)) +
geom_point(size=3)
g4
gbm, color=set, shape=set)) +
geom_point(size=3)
g4
Чтобы было лучше видно перекрывающиеся точки, их можно сделать полупрозрачными.
# add transparency to view overlapping points g5 <- ggplot(df, aes(x=obs, y=m.gbm, color=set, shape=set)) + geom_point(size=3, alpha=0.5) g5
Добавим на наш график диагональную линию соответствующую идеальному случаю прогноза.
# add a diagonal line of perfect prediction # since aes in main function relates to all data we set shape and color inside the geom_point function g6 <- ggplot(df, aes(x=obs, y=m.gbm, color=set, shape=set)) + geom_point(size=3, alpha=0.5) + geom_abline(intercept=0, slope=1) g6
Отметим важность очередности следоваания вызова функция для рисования отдельных слоев. Эта очередность определяет последовательность отображения данных на графике.
# order of calls is important it determines to order of layers on the plot g7 <- ggplot(df, aes(x=obs, y=m.
 gbm)) +
geom_abline(intercept=0, slope=1) +
geom_point(aes(color=set, shape=set), size=3, alpha=0.5)
g7
gbm)) +
geom_abline(intercept=0, slope=1) +
geom_point(aes(color=set, shape=set), size=3, alpha=0.5)
g7
Добавляем
stat_Добавим на график элемент
stat_— в нашем случае это будет прямая представляющая собой линейную зависимость предсказанных и наблюдаемых значений. Обратите внимание, что мы к ранее созданному объекту классаggplotможет добавлять новые элементы (режим конструктора!).# add stat to modify previously created plot - it's really like a LEGO! g8 <- g7 + stat_smooth(method="lm") g8
Чтобы аппроксимация строилась для каждой из двух групп точек отдельно укажем это явно в вызываемой функции.
# make stat for each group of point separately g9 <- g7 + stat_smooth(method="lm", aes(group=set)) g9
В дальнейшем мы будем использовать полный вызов функции.
Удалим из аппроксимирующей зависимости отображение диапазона ошибки аппроксимации, отобразим линии на всем диапазоне графика и представим их цветом соответствующем набору данных.

# to be clear further we will use full plot call # remove SE and extend lines to full range and set a color for each line g10 <- ggplot(df, aes(x=obs, y=m.gbm)) + geom_abline(intercept=0, slope=1) + geom_point(aes(color=set, shape=set), size=3, alpha=0.5) + stat_smooth(method="lm", aes(group=set, color=set), fullrange=TRUE, se=FALSE) g10
scale_Применим какую-либо функцию из семейства функций
scale_, например, изменим цветовое представление графика.# use scale for colors (it is possible to scale other aestetics) g11 <- ggplot(df, aes(x=obs, y=m.gbm)) + geom_abline(intercept=0, slope=1) + geom_point(aes(color=set, shape=set), size=3, alpha=0.5) + stat_smooth(method="lm", aes(group=set, color=set), fullrange=TRUE, se=FALSE) + scale_color_grey() g11
Выглядит не очень удачно. Зададим цвета самостоятельно.
# looks bad, lets scale manually to set colors g12 <- ggplot(df, aes(x=obs, y=m.
 gbm)) +
geom_abline(intercept=0, slope=1) +
geom_point(aes(color=set, shape=set), size=3, alpha=0.5) +
stat_smooth(method="lm", aes(group=set, color=set), fullrange=TRUE, se=FALSE) +
scale_color_manual(values=c("red", "blue"))
g12
gbm)) +
geom_abline(intercept=0, slope=1) +
geom_point(aes(color=set, shape=set), size=3, alpha=0.5) +
stat_smooth(method="lm", aes(group=set, color=set), fullrange=TRUE, se=FALSE) +
scale_color_manual(values=c("red", "blue"))
g12
Цвет можно определять также и соответствующим RGB кодом цвета.
# you can use RGB codes for colors g12.1 <- ggplot(df, aes(x=obs, y=m.gbm)) + geom_abline(intercept=0, slope=1) + geom_point(aes(color=set, shape=set), size=3, alpha=0.5) + stat_smooth(method="lm", aes(group=set, color=set), fullrange=TRUE, se=FALSE) + scale_color_manual(values=c("#FF22FF", "#2255FF")) g12.1Соответствующими функциями
scale_можно инвертировать оси координат.# another usage of scale applied for axis g12.2 <- ggplot(df, aes(x=obs, y=m.gbm)) + geom_abline(intercept=0, slope=1) + geom_point(aes(color=set, shape=set), size=3, alpha=0.5) + stat_smooth(method="lm", aes(group=set, color=set), fullrange=TRUE, se=FALSE) + scale_x_reverse() g12.
 2
2
g12.3 <- ggplot(df, aes(x=obs, y=m.gbm)) + geom_abline(intercept=0, slope=1) + geom_point(aes(color=set, shape=set), size=3, alpha=0.5) + stat_smooth(method="lm", aes(group=set, color=set), fullrange=TRUE, se=FALSE) + scale_x_reverse() + scale_y_reverse() g12.3
Изменение координатных осей
Координатные оси можно поменять местами при необходимости
# flip coords to exchange axis g12.4 <- ggplot(df, aes(x=obs, y=m.gbm)) + geom_abline(intercept=0, slope=1) + geom_point(aes(color=set, shape=set), size=3, alpha=0.5) + stat_smooth(method="lm", aes(group=set, color=set), fullrange=TRUE, se=FALSE) + scale_color_manual(values=c("red", "blue")) + coord_flip() g12.4Управление отрисовкой отдельных элементов диаграммы —
themeУправлять отрисовкой отдельных элементов можно использую функции семейства
theme_.# use theme to control graphic output # there are several predifined themes, but you may create your own # to descrease amount of code to copy-paste return to the LEGO mode g13 <- ggplot(df, aes(x=obs, y=m.
 gbm)) +
geom_abline(intercept=0, slope=1) +
geom_point(aes(color=set, shape=set), size=3, alpha=0.5) +
stat_smooth(method="lm", aes(group=set, color=set), fullrange=TRUE, se=FALSE) +
scale_color_manual(values=c("red", "blue"))
g13
gbm)) +
geom_abline(intercept=0, slope=1) +
geom_point(aes(color=set, shape=set), size=3, alpha=0.5) +
stat_smooth(method="lm", aes(group=set, color=set), fullrange=TRUE, se=FALSE) +
scale_color_manual(values=c("red", "blue"))
g13
g13.1 <- g13 + theme_bw() g13.1
g13.2 <- g13 + theme_classic() g13.2
g13.3 <- g13 + theme_minimal() g13.3
В пакете
ggplot2предусмотрен ограниченный набор функцийtheme_. Чтобы самостоятельно управлять отрисовкой отдельных элементов графика следует воспользоваться функциейtheme.Например, изменим цвет, положение, размер шрифта и угол наклона подписей по оси Х.
# change x labels g13.4 <- g13 + theme(axis.text.x = element_text(color="red", size=15, angle=45, hjust=1)) g13.4
Изменим цвет рамки и заливки для области построения диаграммы.
# change plot area background g13.5 <- g13 + theme(axis.
 text.x = element_text(color="red", size=15, angle=45, hjust=1),
panel.background = element_rect(color="pink", fill="lightyellow"))
g13.5
text.x = element_text(color="red", size=15, angle=45, hjust=1),
panel.background = element_rect(color="pink", fill="lightyellow"))
g13.5
Удалим с диаграммы все линии сетки (основные и промежуточные)
# remove all grid lines g13.6 <- g13 + theme(axis.text.x = element_text(color="red", size=15, angle=45, hjust=1), panel.background = element_rect(color="pink", fill="lightyellow"), panel.grid = element_blank()) g13.6facet_Разделим диаграммы для двух наборов данных.
# facet g14 <- ggplot(df, aes(x=obs, y=m.gbm)) + geom_abline(intercept=0, slope=1) + geom_point(aes(color=set, shape=set), size=3, alpha=0.5) + stat_smooth(method="lm", aes(group=set, color=set), fullrange=TRUE, se=FALSE) + scale_color_manual(values=c("red", "blue")) + facet_wrap(~set) g14Пример построения гистограмм
Используем наш набор данных для того, чтобы посмотреть распределение свойства для обучающей и тестовой выборок.
 Ранее мы использовали с этой целью функцию
Ранее мы использовали с этой целью функцию hist.# look at distribution of training and test sets data g15 <- ggplot(df, aes(x=obs)) + geom_histogram() g15
stat_bin: binwidth defaulted to range/30. Use 'binwidth = x' to adjust this.
Зададим ширину каждого столбца в гистограмме
g15.1 <- ggplot(df, aes(x=obs)) + geom_histogram(binwidth=1) g15.1
Раскрасим столбцы в соответствии с выборками
g15.2 <- ggplot(df, aes(x=obs)) + geom_histogram(binwidth=1, aes(fill=set)) g15.2
Добавим для большей привлекательности белые линии в качестве границ
g15.3 <- ggplot(df, aes(x=obs)) + geom_histogram(binwidth=1, aes(fill=set), color="white") g15.3
Разделим гистограмму на две в соответствии с выборками.
g15.4 <- ggplot(df, aes(x=obs)) + geom_histogram(binwidth=1, aes(fill=set), color="white") + facet_wrap(~set) g15.4
Чтобы расположить их друг под другом зададим параметр
ncolg15.
 5 <- ggplot(df, aes(x=obs)) +
geom_histogram(binwidth=1, aes(fill=set), color="white") +
facet_wrap(~set, ncol=1)
g15.5
5 <- ggplot(df, aes(x=obs)) +
geom_histogram(binwidth=1, aes(fill=set), color="white") +
facet_wrap(~set, ncol=1)
g15.5
Можно изменить диапазон значений по каждой или по обеим осям такой диаграммы. Например, зададим, чтобы диаграмммы по оси Y имели независмые шкалы.
g15.6 <- ggplot(df, aes(x=obs)) + geom_histogram(binwidth=1, aes(fill=set), color="white") + facet_wrap(~set, ncol=1, scales="free_y") g15.6
Диаграмма плотности распределения
Вместо гистограмм можно представить распределение данных в виде диаграммы плотности распределения.
g15.7 <- ggplot(df, aes(x=obs)) + geom_density(aes(fill=set), color="white") + facet_wrap(~set, ncol=1) g15.7
Точечные диаграммы для всех моделей и выборок
Отобразим в виде точечных диаграмм наблюдаемые и прогнозируемые значения для каждой модели и для каждого набора данных одновременно.
Но прежде надо преобразовать соответствующим образом имеющиеся данные, чтобы их можно было использовать для создания диаграммы.

# let's plot predictions of all models simultaneously # but first we need to prepare the data df1 <- reshape::melt.data.frame(df, id.vars=c("set","obs")) head(df1)set obs variable value 1 cv -3.18 m.gbm -2.80 2 cv -2.64 m.gbm -2.68 3 cv -3.84 m.gbm -2.59 4 cv -3.74 m.gbm -2.64 5 cv -3.55 m.gbm -3.00 6 cv -3.10 m.gbm -3.23
dim(df1)
[1] 7231 4
colnames(df1)[3:4] <- c("model", "pred") head(df1)set obs model pred 1 cv -3.18 m.gbm -2.80 2 cv -2.64 m.gbm -2.68 3 cv -3.84 m.gbm -2.59 4 cv -3.74 m.gbm -2.64 5 cv -3.55 m.gbm -3.00 6 cv -3.10 m.gbm -3.23
Теперь можно рисовать
# let's draw g16 <- ggplot(df1, aes(x=obs, y=pred)) + geom_point(aes(color=set)) + facet_wrap(~ model) g16
g16.1 <- g16 + theme_classic() g16.1
Пример столбчатой диаграммы
Другой пример — покажем в виде столбчатой диаграммы ошибки моделей (MSE) для кросс-валидации и внешнего теста.
 2_{test} \).
2_{test} \). - Используя файлы этого занятия рассчитать абсолютную ошибку для каждого соединения в каждой модели и построить диаграмму ящик с усами (boxplot) для ошибок моделей, чтобы показать разброс ошибок для разных моделей по соединениям. Сгруппировать данные на одной диаграмме по принадлежности к кросс-валидации и к внешнему тесту.
- чтобы правильно занять свое место в кинотеатре нужно знать две координаты — ряд и место.
- система географических координат (широта ‒ параллели и долгота ‒ меридианы)
- те, кто в детстве играл в морской бой, тоже помнят, что каждая клетка на игровом поле определялась двумя координатами ‒ буквой и цифрой
- с помощью координатной сетки летчики, моряки определяют местоположение объектов
- в биологии ‒ построение схем молекул ДНК, построение диаграмм и графиков, прослеживающих эволюцию развития
- в экономике ‒ разнообразные системы координат применяются для построение графика спроса и предложения, при графическом изображении разных зависимых величин.

- в химии – построение таблицы Менделеева (изменение показателей происходит в горизонтальной и вертикальной плоскости) ‒ взаимное расположение молекул.
Применение прямоугольной системы координат | Обучонок
1.1 История создания прямоугольной системы координат
Впервые прямоугольную систему координат ввел Рене Декарт в своей работе «Рассуждение о методе» в 1637 году. Поэтому прямоугольную систему координат называют также — Декартова система координат.
Координатный метод описания геометрических объектов положил начало аналитической геометрии. Вклад в развитие координатного метода внес также Пьер Ферма, однако его работы были впервые опубликованы уже после его смерти. Декарт и Ферма применяли координатный метод только на плоскости.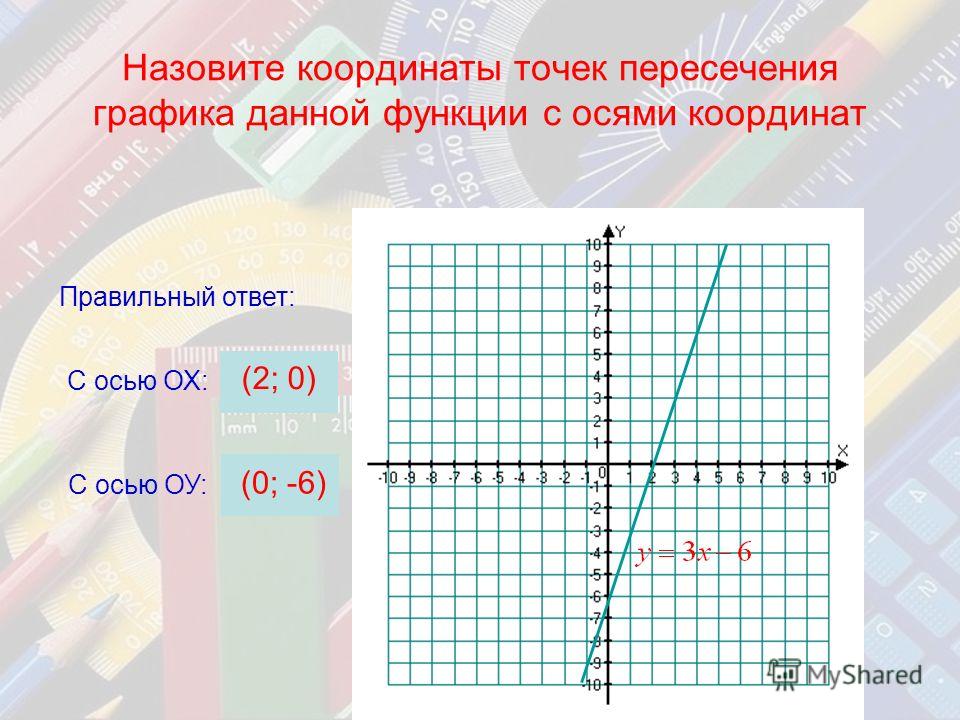
Координатный метод для трёхмерного пространства впервые применил
Леонард Эйлер уже в XVIII веке.
1.2 Координаты вокруг нас
Системы координат пронизывают всю практическую жизнь человека. В нашей речи вы не раз могли слышать такую фразу: «Оставьте мне ваши координаты». Что означает это выражение? Догадались?! Собеседник просит записать свой адрес или номер телефона. У каждого человека бывают ситуации, когда необходимо определить местонахождение: по билету найдите место в зрительном зале или в вагоне поезда. Координаты окружают нас повсюду:
1.3 Прямоугольная система координат на плоскости
Прямоугольная система координат на плоскости образуется двумя взаимно перпендикулярными осями координат Х’Х и Y‘Y. Оси координат пересекаются в точке О, которая называется началом координат, на каждой оси выбрано положительное направление, указанное стрелками, и единица измерения отрезков на осях. Единицы измерения одинаковы для обеих осей.
Положительное направление осей (в правосторонней системе координат) выбирают так, чтобы при повороте оси Х’Х против часовой стрелки на 90° её положительное направление совпало с положительным направлением оси Y‘Y. Четыре угла (I, II, III, IV) образованные осями координат Х’Х и Y‘Y, называются координатными углами (Рис. 2).
Положение точки А на плоскости определяется двумя координатами х и y.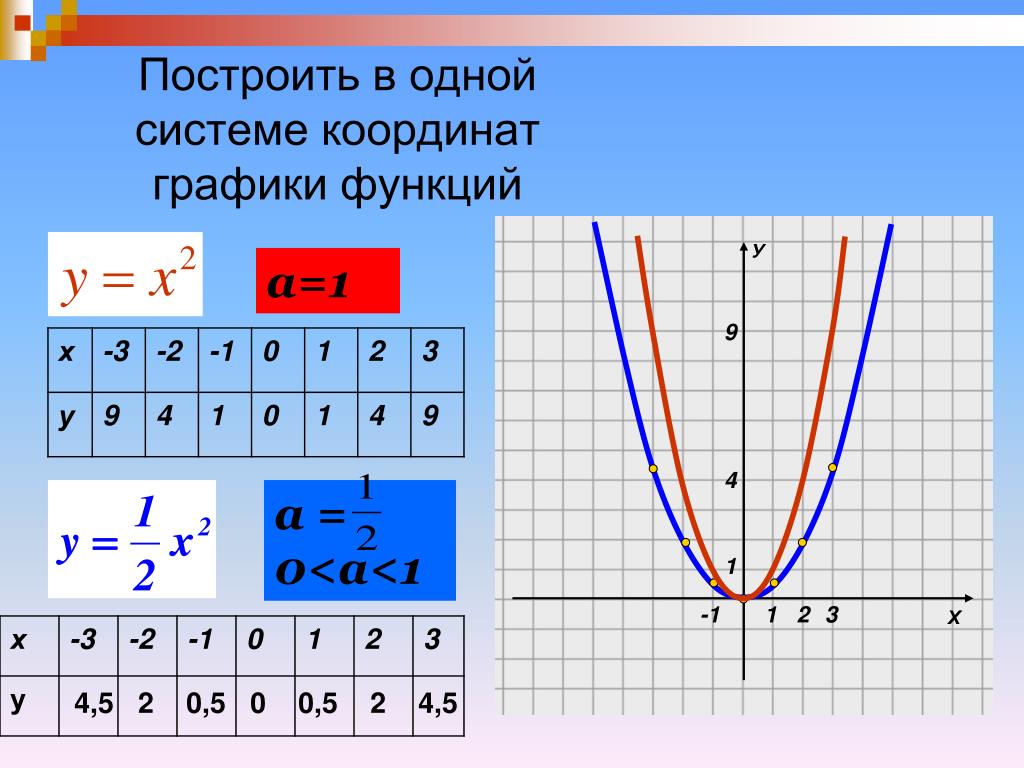 Координата х равна длине отрезка ОВ, координата у -длине отрезка ОС в выбранных единицах измерения. Отрезки ОВ и ОС определяются линиями проведенными из точки А параллельно осям Y’Y и Х‘Х соответственно. Координата х называется абсциссой точки А, координата у ‒ ординатой точки А. Записывают так: А(а.b).
Координата х равна длине отрезка ОВ, координата у -длине отрезка ОС в выбранных единицах измерения. Отрезки ОВ и ОС определяются линиями проведенными из точки А параллельно осям Y’Y и Х‘Х соответственно. Координата х называется абсциссой точки А, координата у ‒ ординатой точки А. Записывают так: А(а.b).
Если точка А лежит в координатном угле I, то точка А имеет положительную абсциссу и ординату. Если точка А лежит в координатном угле II, то точка А имеет отрицательную абсциссу и положительную ординату. Если точка А лежит в координатном угле III, то точка А имеет отрицательную абсциссу и ординату. Если точка А лежит в координатном угле IV, то точка А имеет положительную абсциссу и отрицательную ординату.
Рис. 2 ‒ Координатные углы
1.4 Прямоугольная система координат в пространстве
Прямоугольная система координат в пространстве образуется тремя взаимно перпендикулярными осями координат ОХ, ОY и ОZ. Оси координат пересекаются в точке О, которая называется началом координат, на каждой оси выбрано положительное направление, указанное стрелками, и единица измерения отрезков на осях.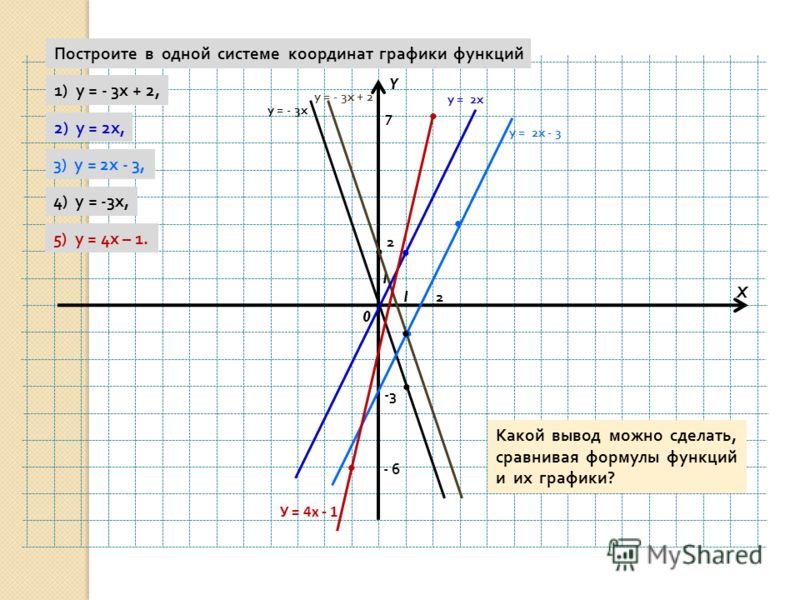 Единицы измерения одинаковы для всех осей.
Единицы измерения одинаковы для всех осей.
OX ‒ ось абсцисс, OY ‒ ось ординат, OZ ‒ ось аппликат. Положительное направление осей выбирают так, чтобы при повороте оси ОХ против часовой стрелки на 90° её положительное направление совпало с положительным направлением оси OY, если этот поворот наблюдать со стороны положительного направления оси ОZ. Такая система координат называется правой.
Если большой палец правой руки принять за направление Х, указательный за направление Y, а средний за направление Z, то образуется правая система координат. Аналогичными пальцами левой руки образуется левая система координат. Правую и левую системы координат невозможно совместить так, чтобы совпали соответствующие оси (Рис. 3).
Положение точки А в пространстве определяется тремя координатами х, у и z. Координата х равна длине отрезка ОВ, координата у ‒ длине отрезка ОС, координата z ‒ длине отрезка OD в выбранных единицах измерения.
Отрезки ОВ, ОС и OD определяются плоскостями , проведенными из точки А параллельно плоскостям YOZ, XOZ и XOY соответственно. Координата х называется абсциссой точки А, координата у ‒ ординатой точки А, координата z ‒ аппликатой точки А. Записывают так: А (а, b, c).
Координата х называется абсциссой точки А, координата у ‒ ординатой точки А, координата z ‒ аппликатой точки А. Записывают так: А (а, b, c).
Рис. 3 ‒ Прямоугольная система координат в пространстве
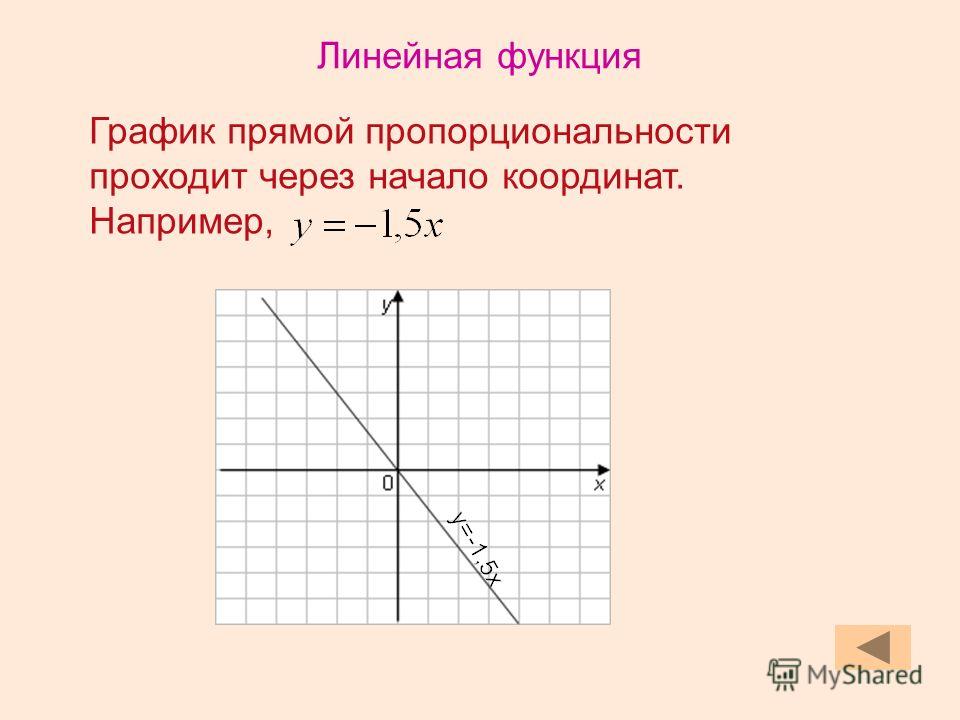
1.5 Построение графиков функций в прямоугольной системе координат
В курсе алгебры изучаются различные функции. Например, линейная функция, квадратичная функция, степенная функция, тригонометрические функции, показательная функция, логарифмическая функция. Для построения графиков данных функций используется табличный способ задания функций, а затем по данным координатам строятся графики функций в прямоугольной системе координат (Рис. 4).
Рис. 4 ‒ Построение графиков функций в прямоугольной системе координат
В прямоугольной системе координат строятся графики функций, которые содержат выражения под знаком модуля.
Задание 1
Постройте график функции: у = (х ‒ 1) ‒ (2 ‒ х) + 2 (Рис.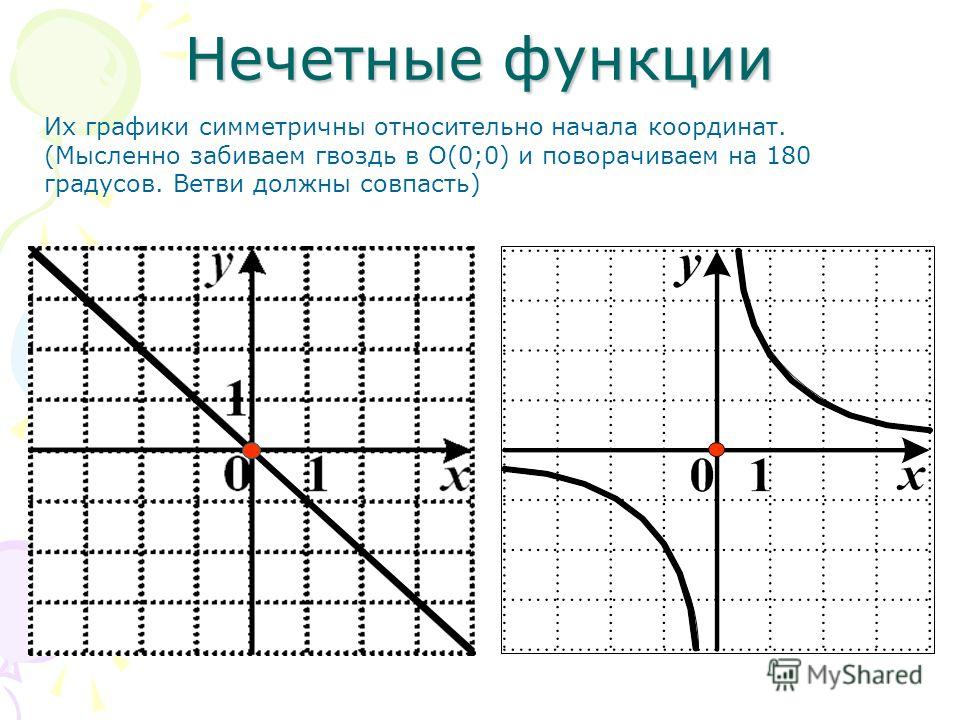 5).
5).
Рис. 5 ‒ график функции: у = (х ‒ 1) ‒ (2 ‒ х) + 2
Решение:
х = 1; х = 2
1) х < 1
у = ‒ х + 1 ‒ 2 + х +2
у = 1
2) 1 < х < 2
у = х ‒ 1 ‒ 2 + х + 2
у = 2х ‒1
х =1; у =1
х = 2; у = 3
3) х > 2
у = х ‒ 1 +2 ‒ х + 2
у = 3
Задание 2
Постройте график функции: у = (х ‒ 1) + (x ‒ 2) + x (Рис. 6).
Рис. 6 ‒ график функции: у = (х ‒ 1) + (x ‒ 2) + x
Решение:
х = 1; х = 2
1) х < 1
у = ‒ х + 1 ‒ х + 2 + х
у = ‒ х + 3
х = 0; у =3
х = ‒ 1; у = 4
2) 1 < х < 2
у = х ‒ 1 ‒ х + 2 + х
у = х + 1
х = 1; у = 2
х = 2; у = 3
3) х > 2
у = х ‒ 1 + х ‒ 2 + х
у = 3х ‒ 3
х = 3; у = 6
х = 4; у = 9
Перейти к главе 2: Графический метод решений
Что означает координатная сетка?
Плоскость — это плоская поверхность. Так же, как пол или стена, это гладкая и плоская поверхность. Однако сетка — это нечто другое. Задумывались ли вы, как городские мегаполисы расположены в соответствии с последовательной и простой в использовании сеткой? Это окончательный пример координатной плоскости.
Однако сетка — это нечто другое. Задумывались ли вы, как городские мегаполисы расположены в соответствии с последовательной и простой в использовании сеткой? Это окончательный пример координатной плоскости.
В таких городах, как Барселона, Нью-Йорк, Онтарио, Саванна и многих других, улицы организованы в определенные кварталы, при этом остается достаточно места для дорог. Это просто пример того, как работают координатные сетки. Чтобы узнать больше о координатной сетке, продолжайте читать разделы ниже, чтобы понять значение координатной плоскости. Но сначала нужно знать, что такое координата.
Что такое координата?Хотя это может показаться немного сложным, координата — это не что иное, как точка на графике.
Граф — это плоскость, на которой есть сетки. Эти сетки помогают найти определенную точку на графике, и эти точки называются координатами.
Координата обычно представляет собой точку на графике, где ось X и ось Y совпадают.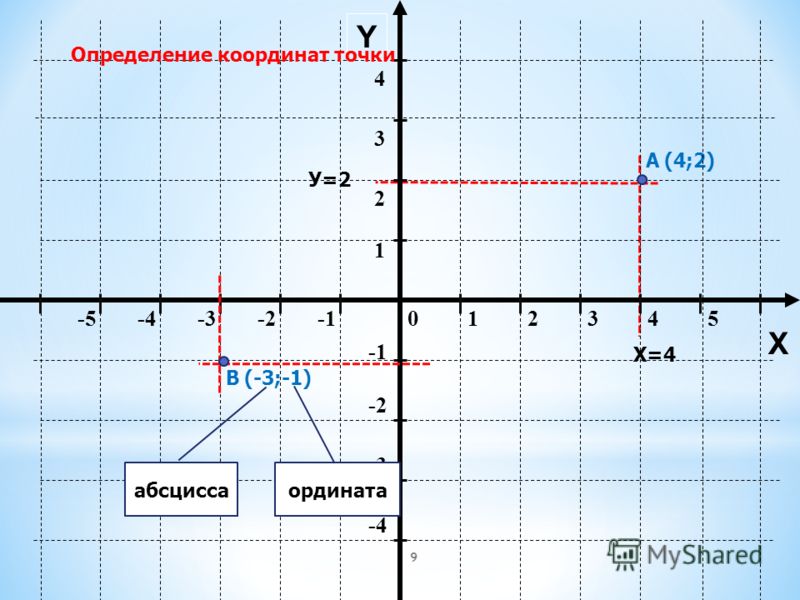 Зная расположение определенных координат на диаграмме, легко предсказать результат результирующей сетки.
Зная расположение определенных координат на диаграмме, легко предсказать результат результирующей сетки.
Сетка — это двумерная поверхность с осью x и осью y. Эти оси являются горизонтальными и вертикальными соответственно.
Что касается этих осей, уклон образуется, когда линии оси x и оси y пересекаются друг с другом. Точка пересечения этих линий называется началом координат.
Важно понимать, что каждая линия оси X перпендикулярна линиям оси Y. Таким образом, делая сечение квадратов в координатной плоскости.
История координатных плоскостейЧтобы лучше понять координатные плоскости, нужно знать их историю.
Плоскость координат — это система, изобретенная в 17 веке французским математиком и философом. Его звали Рене Декарт.
Французский математик изобрел сетку благодаря одному из происшествий в его жизни. Известно, что он лежал в своей постели и заметил у себя на потолке движение мухи.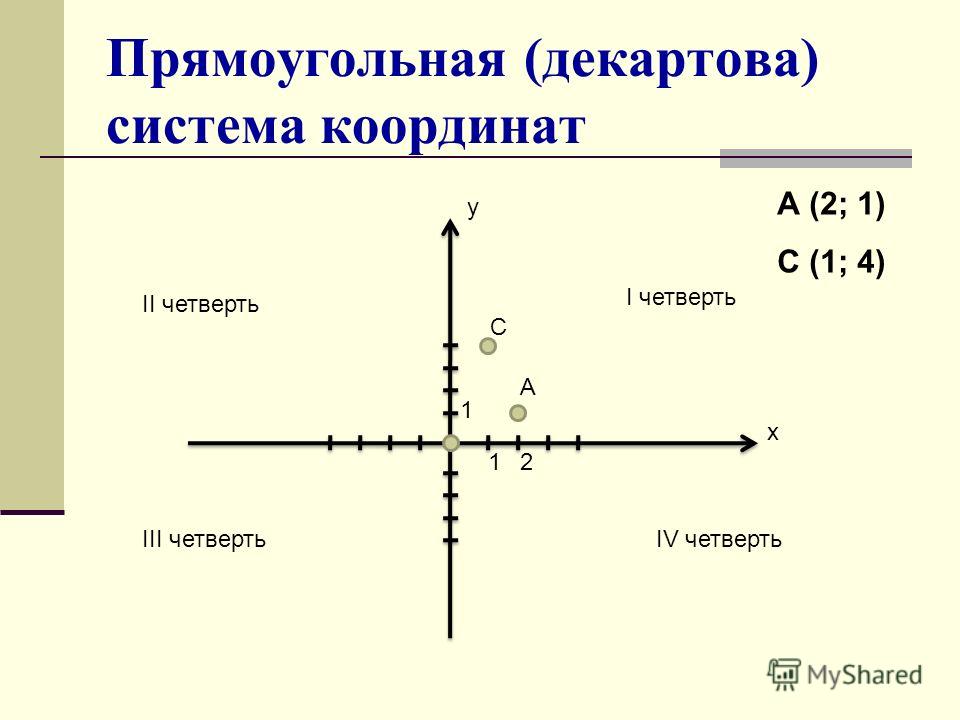 Ему пришло в голову, если бы он мог описать и определить каждое направление, сделанное этой мухой.
Ему пришло в голову, если бы он мог описать и определить каждое направление, сделанное этой мухой.
Следующее, что он делает, это делает один угол потолка в качестве точки отсчета и представляет себе горизонтальные и вертикальные линии, образующие перпендикулярные блоки вдоль потолка, образующие сетку. Это воображение изобрело фундаментальные основы координатной плоскости.
Определение координатной сеткиКто знал, что простое наблюдение математика вдохновит его на создание великого математического инструмента. Его потребность определить местонахождение этой мухи привела к изобретению и применению координатной сетки.
Проще говоря, координатная сетка представляет собой единообразное расположение, в котором горизонтальные линии оси X пересекаются с вертикальными линиями оси Y, образуя однородные блоки. Это блоки, напоминающие рыболовную сеть. Эти блоки объединяются, чтобы создать координатную сетку.
Что вы понимаете в координатной сетке? Координатной сеткой называется прямоугольная плоскость, где пересечение горизонтальных и вертикальных линий образует сетку.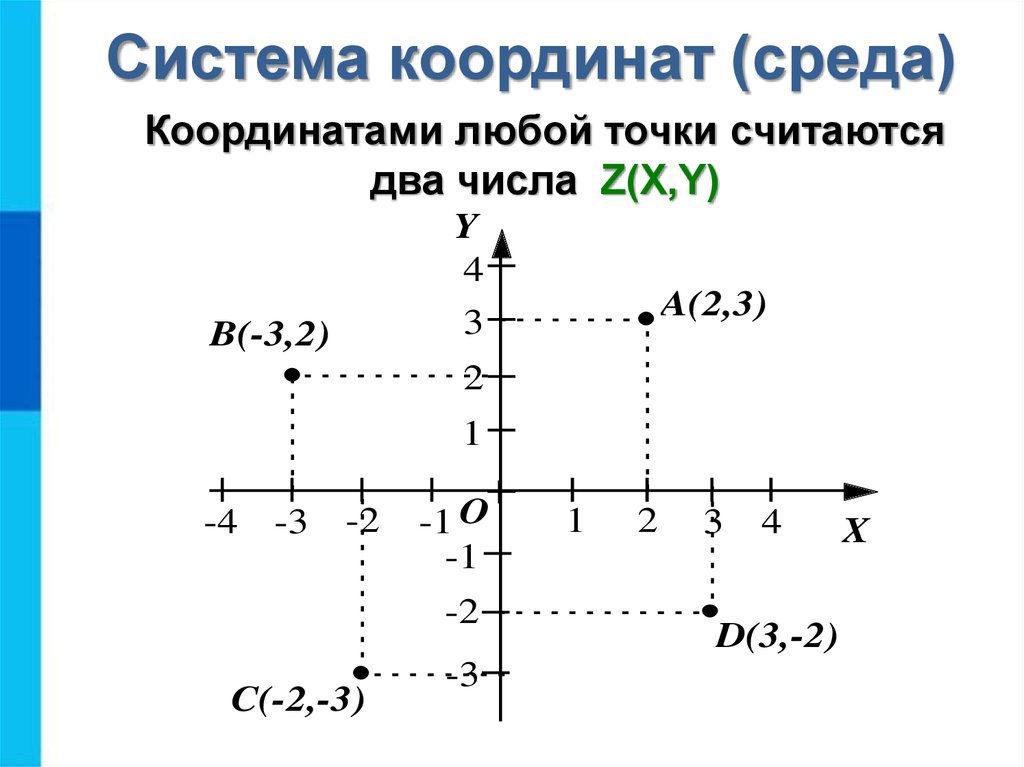 Точка встречи горизонтальной и вертикальной линий под углом, перпендикулярным друг другу.
Точка встречи горизонтальной и вертикальной линий под углом, перпендикулярным друг другу.
Сеть каждой горизонтальной и вертикальной линии образует сетку. Эта сетка действует как карта для указания точного направления от одной точки координат к другой.
Сетка разделена на четыре квадранта, чтобы упростить поиск точки координат в сетке. Каждый квадрант помогает найти конкретную точку на координатной плоскости.
Четыре квадранта координатной плоскости помогают обращаться к различным координатам с помощью графического уравнения. Каждая координатная точка относится к паре координат x и y.
Как найти точку в координатной сетке?Важно знать координаты как по оси X, так и по оси Y, чтобы найти точку в координатной сетке. В случае отсутствия одного из двух невозможно определить точку в координатной сетке.
Думайте об этом как об адресе здания. Если человек хочет определить точное местоположение здания, он должен знать название улицы и номер переулка. Имея эту информацию, будет легко идентифицировать это конкретное здание.
Имея эту информацию, будет легко идентифицировать это конкретное здание.
Теперь, чтобы найти точку на координатной плоскости, нужно знать координатные сетки. Важно знать, что координата оси X записывается первой, а координата оси Y записывается после этого. Например – (x,y)
Кроме того, нужно знать, какая линия горизонтальная (ось x), а какая вертикальная (ось y). Итак, сначала найдите координату оси X вдоль горизонтальной сетки, а затем найдите координату оси Y вдоль вертикальной сетки. Следуя этой процедуре, можно найти точку координат, где встречаются две оси. Это определенная точка в координатной сетке.
Что такое квадрант?Ясно, что каждая горизонтальная и вертикальная линии перпендикулярно пересекают друг друга. Эти линии вместе образуют большую сеть, разделенную на четыре основные области. Эти области известны как квадранты в координатной сетке.
Ось X и ось Y делят координатную плоскость на четыре квадранта, и каждый квадрант обозначается римскими цифрами. Каждый квадрант нумеруется против часовой стрелки.
Каждый квадрант нумеруется против часовой стрелки.
Итак, первый квадрант образует правый верхний угол. Остальные квадранты совершают движение против часовой стрелки вдоль координатной плоскости. Это означает, что верхний левый квадрант является вторым и имеет отрицательные значения по оси X.
Сколько квадрантов в координатной сетке?Каждая координатная сетка имеет четыре квадранта. Каждый квадрант имеет дело с разными значениями оси X и оси значений.
Квадрант I — Верхний правый угол координатной сетки с положительным значением x и положительным значением y
Квадрант II — Верхний левый угол координатной сетки с отрицательным значением x и положительным значением y
Квадрант III — Нижний левый угол координатная сетка с отрицательным значением x и отрицательным значением y
Квадрант IV – Нижний правый угол координатной сетки с положительным значением x и отрицательным значением y
Что такое масштаб в координатной плоскости? И ось X, и ось Y разделены на равные части с помощью чисел, образующих числовую прямую. Эти числа имеют диапазон, который может быть как положительным, так и отрицательным вместе с квадрантами координатной сетки.
Эти числа имеют диапазон, который может быть как положительным, так и отрицательным вместе с квадрантами координатной сетки.
Это означает, что каждая ось (ось X и ось Y) может начинаться от -20 до +20. Таким образом, каждая ось будет охватывать один квадрант координатной плоскости. Шкала представляет диапазон числовой линии каждой оси. Масштаб оси позволяет лучше отображать информацию как на графике, так и в расчетах.
Что вы понимаете под перехватом в координатной сетке?Из приведенной выше информации ясно, что координатная точка состоит из значения по оси X и значения по оси Y. Например: (3,6)
Где 3 — значение по оси X, а 6 — значение по оси Y. Ясно также, что, поскольку обе величины положительны, они лежат где-то в квадранте I. перехват. Итак, если координаты графика равны (0,3), то линия будет проведена только по оси Y. Это будет называться y-перехватом. Аналогично, если координаты (5,0), то линия будет нарисована по оси x. Эта линия будет называться x-перехватом.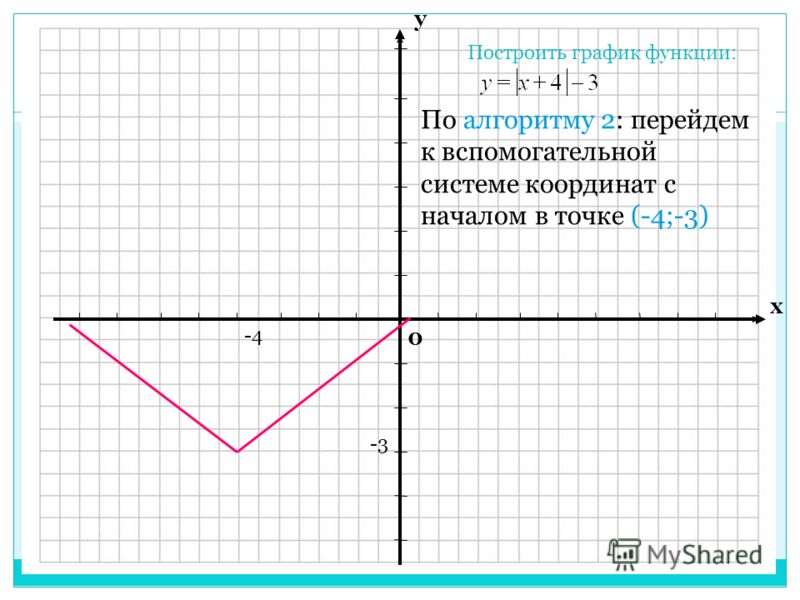
График координатной сетки представляет собой хорошо организованную сеть осей X и Y. Этот график необходим для изучения координатных точек и различных квадрантов координатной плоскости.
С помощью координатной сетки легко наносить координатные точки по осям X и Y. Однако следует помнить о положительных и отрицательных значениях каждой координаты.
Можно легко прочитать карту или найти любую точку на графике с указанной выше информацией на координатной сетке. Мало того, знание особенностей координатной сетки поможет человеку определить местонахождение горизонтальных или вертикальных перемещений относительно математического уравнения.
Краткое описание координатной сетки Вышеприведенная информация о координатных сетках представляет собой тщательно проработанное и подробное объяснение координатных сеток. Тщательно понимая концепцию и особенности координатной плоскости, можно легко идентифицировать и находить числовые линии.
Помимо этого, приведенная выше информация также определяет различные термины и методы, используемые для определения координат на координатной плоскости.
График параллельных координат в Python
Питон > Научные карты > График параллельных координат
Предложить редактирование этой страницыКак сделать графики с параллельными координатами в Python с помощью Plotly.
Впервые в сюжете?
Plotly — бесплатная графическая библиотека с открытым исходным кодом для Python. Мы рекомендуем вам прочитать наше руководство по началу работы, чтобы получить последние инструкции по установке или обновлению, а затем перейти к нашим учебным пособиям по основам Plotly или погрузиться прямо в некоторые учебные пособия по базовым диаграммам.
График с параллельными координатами в Plotly Express¶
Plotly Express — это простой в использовании высокоуровневый интерфейс к Plotly, который работает с различными типами данных и создает простые в стилизации фигуры. На графике параллельных координат с px.parallel_coordinates каждая строка DataFrame представлена ломаной линией, которая пересекает набор параллельных осей, по одной для каждого измерения. Для других представлений многомерных данных см. также параллельные категории, радарные диаграммы и матрицу диаграммы рассеяния (SPLOM).
В [1]:
импортировать plotly.express как px
df = px.data.iris()
рис = px.parallel_coordinates(df, color="species_id", labels={"species_id": "Виды",
"sepal_width": "Ширина чашелистика", "sepal_length": "Длина чашелистика",
"petal_width": "Ширина лепестка", "petal_length": "Длина лепестка", },
color_continuous_scale=px.colors. diverging.Tealrose,
color_continuous_midpoint=2)
рис.шоу()
diverging.Tealrose,
color_continuous_midpoint=2)
рис.шоу()
Параллельные координаты по умолчанию интерактивны. Перетащите линии вдоль осей, чтобы отфильтровать области.
Выберите столбцы, которые будут представлены параметром измерений .
В [2]:
импортируйте plotly.express как px.
df = px.data.iris()
рис = px.parallel_coordinates(df, color="species_id",
размеры = ['sepal_width', 'sepal_length', 'petal_width',
'длина_лепестка'],
color_continuous_scale=px.colors.diverging.Tealrose,
color_continuous_midpoint=2)
рис.шоу()
Карта параллельных координат с go.Parcoords¶
В [3]:
импортировать plotly.graph_objects как есть
рис = идти.Рисунок(данные=
go.Паркоорды(
line_color = 'синий',
размеры = список([
дикт (диапазон = [1,5],
ограничивающий диапазон = [1,2], # измените этот диапазон, перетащив розовую линию
метка = 'A', значения = [1,4]),
dict(диапазон = [1. 5,5],
тиквалы = [1.5,3,4.5],
метка = 'B', значения = [3,1.5]),
дикт (диапазон = [1,5],
тиквалы = [1,2,4,5],
метка = 'C', значения = [2,4],
ticktext = ['текст 1', 'текст 2', 'текст 3', 'текст 4']),
дикт (диапазон = [1,5],
метка = 'D', значения = [4,2])
])
)
)
рис.шоу()
5,5],
тиквалы = [1.5,3,4.5],
метка = 'B', значения = [3,1.5]),
дикт (диапазон = [1,5],
тиквалы = [1,2,4,5],
метка = 'C', значения = [2,4],
ticktext = ['текст 1', 'текст 2', 'текст 3', 'текст 4']),
дикт (диапазон = [1,5],
метка = 'D', значения = [4,2])
])
)
)
рис.шоу()
Параллельные координаты по умолчанию интерактивны. Перетащите линии вдоль осей, чтобы отфильтровать области, и перетащите имена осей по графику, чтобы изменить порядок переменных.
График основных параллельных координат¶
В [4]:
импортировать plotly.graph_objects как есть
импортировать панд как pd
df = pd.read_csv("https://raw.githubusercontent.com/bcdunbar/datasets/master/iris.csv")
рис = идти.Рисунок(данные=
go.Паркоорды(
строка = dict (цвет = df ['species_id'],
цветовая шкала = [[0,'фиолетовый'],[0,5,'светло-зеленый'],[1,'золотой']]),
размеры = список([
дикт (диапазон = [0,8],
диапазон ограничений = [4,8],
label = 'Длина чашелистика', values = df['sepal_length']),
дикт (диапазон = [0,8],
label = 'Ширина чашелистика', values = df['sepal_width']),
дикт (диапазон = [0,8],
label = 'Длина лепестка', values = df['petal_length']),
дикт (диапазон = [0,8],
label = 'Ширина лепестка', values = df['petal_width'])
])
)
)
fig. update_layout(
plot_bgcolor = 'белый',
paper_bgcolor = 'белый'
)
рис.шоу()
update_layout(
plot_bgcolor = 'белый',
paper_bgcolor = 'белый'
)
рис.шоу()
Расширенный график параллельных координат¶
В [5]:
импортировать plotly.graph_objects как есть
импортировать панд как pd
df = pd.read_csv("https://raw.githubusercontent.com/bcdunbar/datasets/master/parcoords_data.csv")
рис = идти.Рисунок(данные=
go.Паркоорды(
строка = dict (цвет = df ['colorVal'],
цветовая шкала = «Электричество»,
Шкала = Верно,
сммин = -4000,
смакс = -100),
размеры = список([
дикт(диапазон = [32000,227900],
диапазон ограничений = [100000,150000],
label = "Высота блока", values = df['blockHeight']),
дикт (диапазон = [0,700000],
label = 'Ширина блока', values = df['Ширина блока']),
dict(tickvals = [0,0.5,1,2,3],
тиктекст = ['A','AB','B','Y','Z'],
label = 'Материал цилиндра', values = df['cycMaterial']),
дикт(диапазон = [-1,4],
тиквалы = [0,1,2,3],
label = 'Материал блока', values = df['blockMaterial']),
дикт(диапазон = [134,3154],
видимый = Истина,
label = 'Общий вес', values = df['totalWeight']),
дикт (диапазон = [9,19984],
label = 'Wt штрафа за сборку', values = df['assemblyPW']),
дикт(диапазон = [49000,568000],
label = 'Высота st Ширина', values = df['HstW'])])
)
)
рис. шоу()
шоу()
Невыбранный цвет и прозрачность линии¶
Новое в версии 5.10
Цвет и непрозрачность невыбранных линий можно установить с помощью unselected . Установив opacity=0 , вы можете скрыть невыбранные линии. Здесь мы устанавливаем цвет светло-серый 9.0145 и непрозрачность 0,5 .
В [6]:
импортировать plotly.graph_objects как есть
рис = идти.Рисунок(данные=
go.Паркоорды(
line_color = 'синий',
размеры = список([
дикт (диапазон = [1,5],
ограничивающий диапазон = [1,2], # измените этот диапазон, перетащив розовую линию
метка = 'A', значения = [1,4]),
dict(диапазон = [1.5,5],
тиквалы = [1.5,3,4.5],
метка = 'B', значения = [3,1.5]),
дикт (диапазон = [1,5],
тиквалы = [1,2,4,5],
метка = 'C', значения = [2,4],
ticktext = ['текст 1', 'текст 2', 'текст 3', 'текст 4']),
дикт (диапазон = [1,5],
метка = 'D', значения = [4,2])
]),
невыбрано = dict (строка = dict (цвет = «зеленый», непрозрачность = 0,5))
)
)
рис. шоу()
шоу()
А как насчет Dash?¶
Dash — это платформа с открытым исходным кодом для создания аналитических приложений, не требующая Javascript и тесно интегрированная с графической библиотекой Plotly.
Узнайте, как установить Dash, по адресу https://dash.plot.ly/installation.
Везде на этой странице, где вы видите fig.show() , вы можете отобразить один и тот же рисунок в приложении Dash, передав его аргументу компонента Graph из встроенного dash_core_components пакет, подобный этому:
import plotly.graph_objects as go # or plotly.express as px
fig = go.Figure() # или любая функция Plotly Express, например. px.bar(...)
# fig.add_trace( ... )
# fig.update_layout( ... )
импортировать тире
импортировать dash_core_components как DCC
импортировать dash_html_components как html
приложение = тире.Dash()
app.layout = html.Div([
dcc.Graph(рисунок=рис)
])
app.run_server(debug=True, use_reloader=False) # Отключить перезагрузку, если внутри Jupyter
График в параллельных координатах — ggparcoord • GGally
Источник: R/ggparcoord. 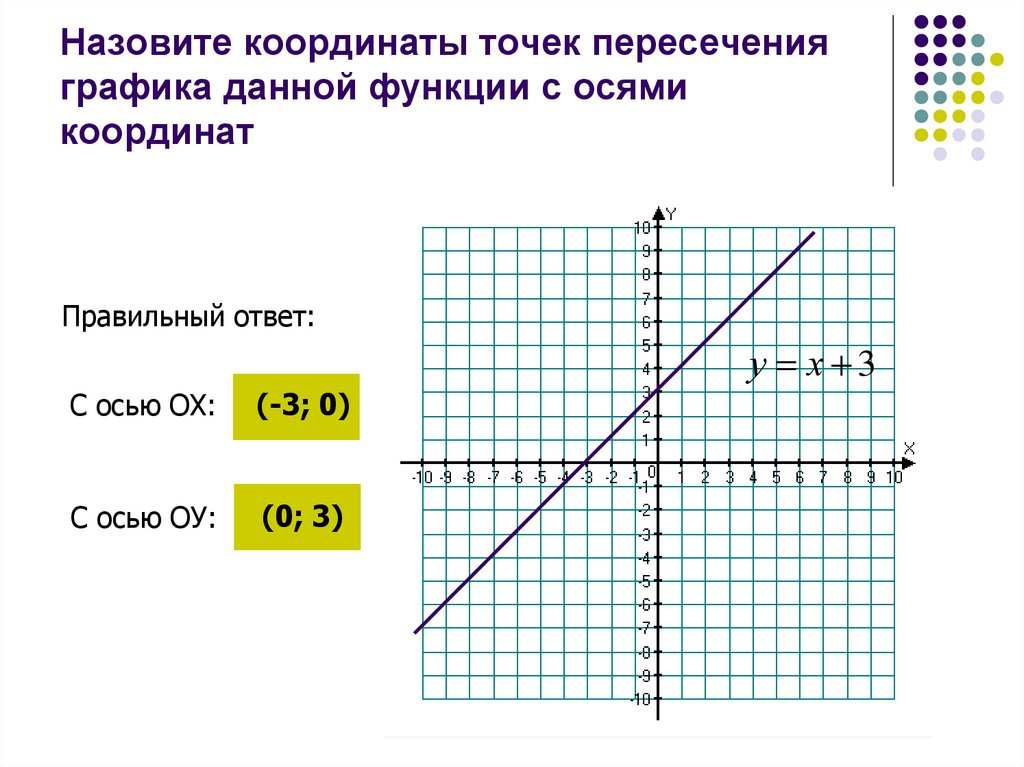 R
R
ggparcoord.Rd
Функция для построения статических графиков в параллельных координатах с использованием
графический пакет ggplot2 .
ggparcoord( данные, столбцы = 1:ncol(данные), групповой столбец = NULL, шкала = "стандарт", масштабСуммари = "среднее", центробсид = 1, отсутствует = "исключить", порядок = столбцы, ШоуПойнтс = ЛОЖЬ, сплайнКоэффициент = ЛОЖЬ, альфа-линии = 1, блочная диаграмма = ЛОЖЬ, шейдбокс = NULL, отображение = NULL, название = "" )
Аргументы
| данные | набор данных для построения |
|---|---|
| столбцы | вектор переменных (имена или индексы), которые будут осями графика |
| groupColumn | одна переменная для группировки (цвет) по |
| шкала | метод, используемый для масштабирования переменных (см. |
| весыСводка | , если масштаб==»центр», сводная статистика в одномерном центрировать каждую переменную по |
| центрОбсID | , если scale==»centerObs», номер строки диаграммы случая должен однозначно центрироваться на |
| отсутствует | метод, используемый для обработки отсутствующих значений (см. Подробности) |
| заказ | способ заказа осей (см. подробности) |
| шоуПоинты | логический оператор, указывающий, следует ли нанесен или нет |
| коэффициент сплайна | логический или числовой оператор, указывающий, следует ли использовать сплайн-интерполяцию. Числовые значения будут умножены на количество столбцов, |
| альфаЛайнс | значение альфа-скейлера для линий графика parcoord или имя столбца данных |
| боксплот | логический оператор, указывающий, должны ли лежит в основе распределения каждой переменной |
| ShadeBox | цвет базовой коробки, которая простирается от минимума до минимума.
max для каждой переменной (коробка не отображается, если |
| отображение | строка aes для передачи объекту ggplot |
| Название | строка символов, обозначающая название сюжета |
Значение
Объект ggplot, который при вызове распечатает
Детали
масштаб — это строка символов, указывающая, как масштабировать переменные.
в параллельном координатном графике. Опции:
станд.: одномерно, вычесть среднее и разделить на стандартное отклонение
надежный: одномерно, вычесть медиану и разделить на абсолютное отклонение медианыuniminmax: одномерно, масштабируйте так, чтобы минимум переменной был равен нулю, а максимум — единицеglobalminmax: масштабирование не выполняется; диапазон графиков определен по глобальному минимуму и глобальному максимумуцентр: используйтеuniminmaxдля стандартизации высоты по вертикали, затем центрировать каждую переменную на значении, заданном параметромscaleSummarycenterObs: используйтеuniminmaxдля стандартизации вертикальной высоты, затем центрировать каждую переменную по значению наблюдения, заданномуcenterObsIDпараметр
отсутствует — это строка символов, указывающая, как обрабатывать отсутствующие
недостающие значения.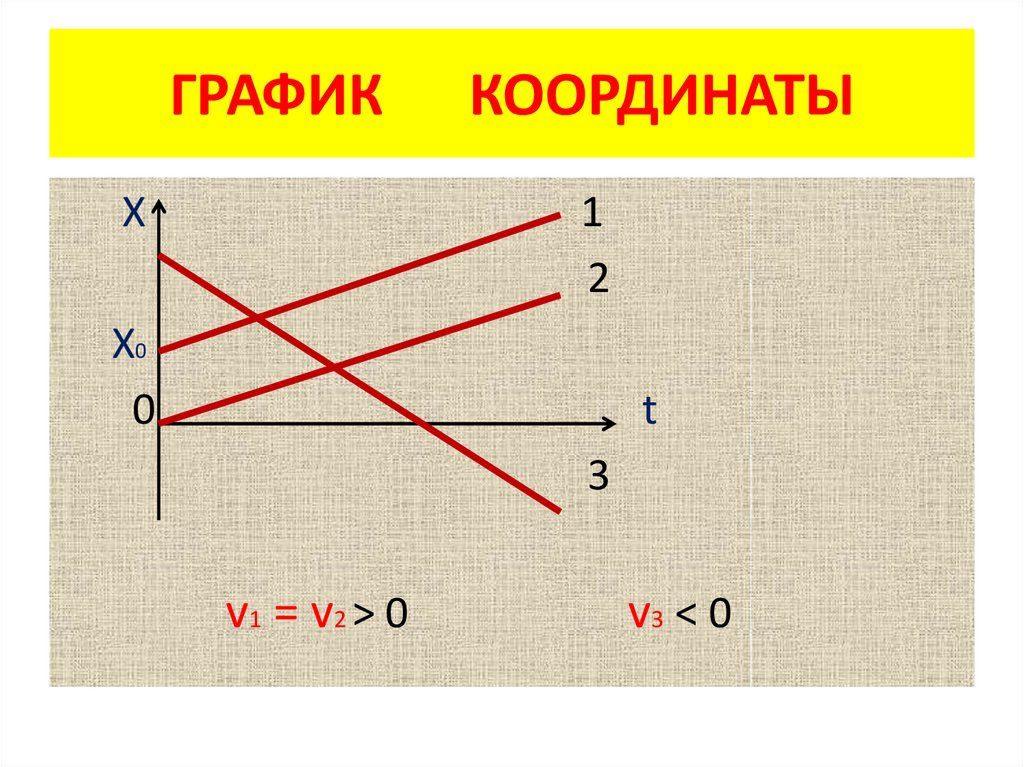 Опции:
Опции:
исключить: удалить все случаи с отсутствующими значениямисреднее значение: установить отсутствующие значения в среднее значение переменноймедиана: установить отсутствующие значения в медиану переменнойmin10: установить отсутствующие значения на 10% ниже минимума переменнойrandom: установить отсутствующие значения в значение случайно выбранного наблюдения для этой переменной
порядок — это либо вектор индексов, либо строка символов, указывающая, как
упорядочить оси (переменные) графика параллельных координат. Опции:
(по умолчанию): порядок по вектору, обозначенномустолбцами(данный вектор): порядок по указанному векторуanyClass: упорядочить переменные по их разделению между любым классом и остальные (в отличие от их общего различия между классами). Это выполнено
путем вычисления F-статистики для каждого класса по сравнению с остальными для каждой переменной оси.
Затем переменные оси упорядочиваются (по убыванию) по их максимуму k F-статистики,
где k — количество классов.
Это выполнено
путем вычисления F-статистики для каждого класса по сравнению с остальными для каждой переменной оси.
Затем переменные оси упорядочиваются (по убыванию) по их максимуму k F-статистики,
где k — количество классов.allClass: упорядочить переменные по их общей статистике F (убыванию) от дисперсионный анализ сgroupColumnв качестве объясняющей переменной (примечание: требуется чтобы указатьgroupColumnс этим методом упорядочения). В принципе, этот метод упорядочивает переменные по их вариации между классами (от большего к меньшему).асимметрия: упорядочить переменные по их выборочной асимметрии (наиболее асимметрично наименее перекошенный)Outlying: порядок по скагностической мере, Outlying, как рассчитано в упаковкеscagnostics. Другие скагностические меры доступны для заказа поПерекошенный,Комковатый,Редкий,Исчерченный,Выпуклый,Тощий,Вязкий, иМонотонный. Примечание. Для использования этих способов заказа необходимо иметь скагностик
Примечание. Для использования этих способов заказа необходимо иметь скагностик
Автор
Джейсон Кроули, Баррет Шлорке, Ди Кук, Хайке Хофманн, Хэдли Уикхэм
Примеры
# небольшая функция для отображения графиков, только если она интерактивная p_ <- GGally::print_if_interactive # использовать образец данных алмазов в иллюстративных целях данные (алмазы, пакет = "ggplot2") бриллианты.samp <- бриллианты [образец (1: тусклый (бриллианты) [1], 100), ] # базовый график с параллельными координатами, с настройками по умолчанию p <- ggparcoord (данные = diamonds.samp, столбцы = c (1, 5:10)) p_(p)
# на этот раз цвет алмазной огранкой p <- ggparcoord(data = diamonds.samp, columns = c(1, 5:10), groupColumn = 2) р_(р)
# Подложка одномерных диаграмм, добавление заголовка, использование масштабирования uniminmax p <- ggparcoord(data = diamonds.samp, columns = c(1, 5:10), groupColumn = 2, масштаб = "uniminmax", boxplot = TRUE, title = "Параллельные координаты.
График данных алмазов") p_(p)
# использовать ggplot2 aes для переключения на более толстые линии p <- ggparcoord(data = diamonds.samp, columns = c(1, 5:10), groupColumn = 2, title ="Параллельные координаты. График данных бриллиантов", mapping = ggplot2::aes(size = 1)) + ggplot2::scale_size_identity() р_(р)
# базовый параллельный график данных msleep с использованием «случайного» вменения и # окрашивание по диете (также можно использовать имена переменных в колонках и groupColumn # аргументы) данные (msleep, пакет = "ggplot2") p <- ggparcoord(data = msleep, columns = 6:11, groupColumn = "vore", отсутствует = "случайный", шкала = "uniminmax") p_(p)
# центрировать каждую переменную по ее медиане, используя обработчик отсутствующих значений по умолчанию, # 'исключать' p <- ggparcoord(data = msleep, columns = 6:11, groupColumn = "vore", scale = "центр", scaleSummary = "медиана") р_(р)
# с данными диафрагмы упорядочить оси по общему разделению классов (видов) с помощью # опция anyClass p <- ggparcoord (данные = радужная оболочка, столбцы = 1:4, groupColumn = 5, порядок = "anyClass") p_(p)
# добавить точки на график, добавить заголовок и использовать альфа-скаляр для построения линий # прозрачный p <- ggparcoord(data = iris, columns = 1:4, groupColumn = 5, order = "anyClass", showPoints = TRUE, title = "Параллельный график координат для данных радужной оболочки", альфа-линии = 0,3) р_(р)
# цвет по колонке ирис2 <- ирис iris2$alphaLevel <- c("setosa" = 0,2, "versicolor" = 0,3, "virginica" = 0)[iris2$Species] p <- ggparcoord(data = iris2, columns = 1:4, groupColumn = 5, order = "anyClass", showPoints = TRUE, title = "Параллельный график координат для данных радужной оболочки", alphaLines = "альфа-уровень") p_(p)
## Использовать сплайны для значений, а не линии (все дают одинаковый результат) столбцы <- c(1, 5:10) p <- ggparcoord(diamonds.


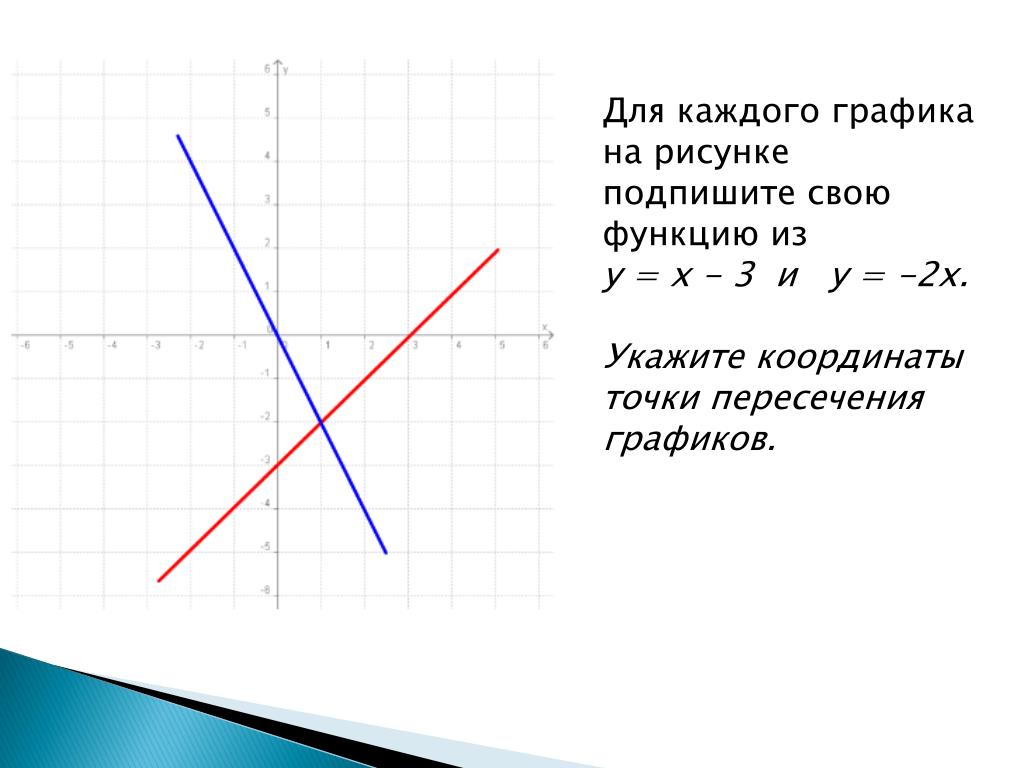 2)
2)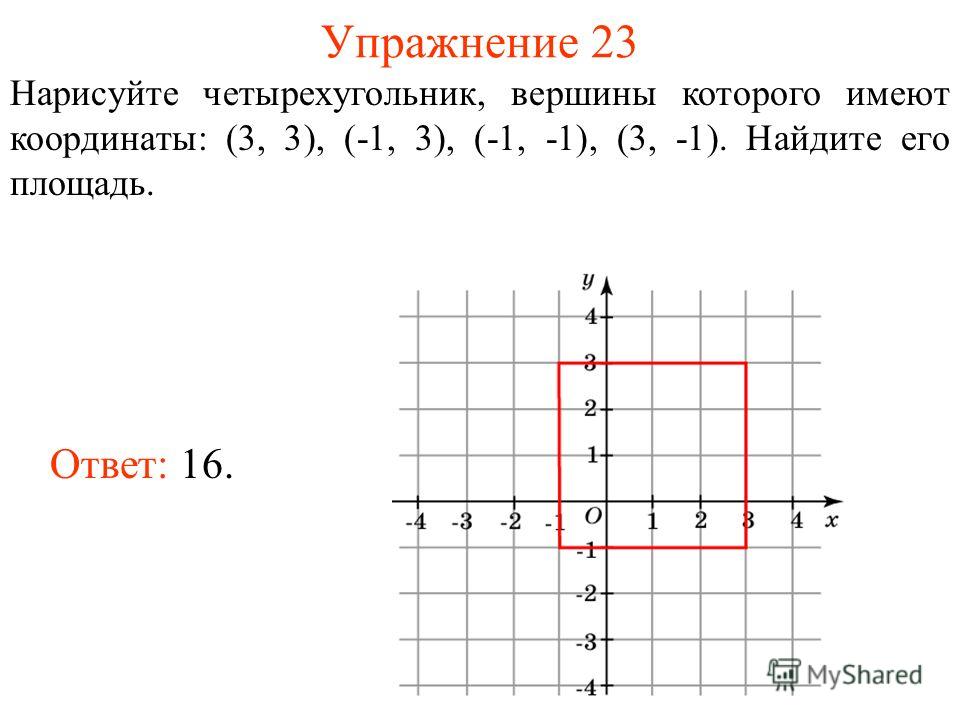
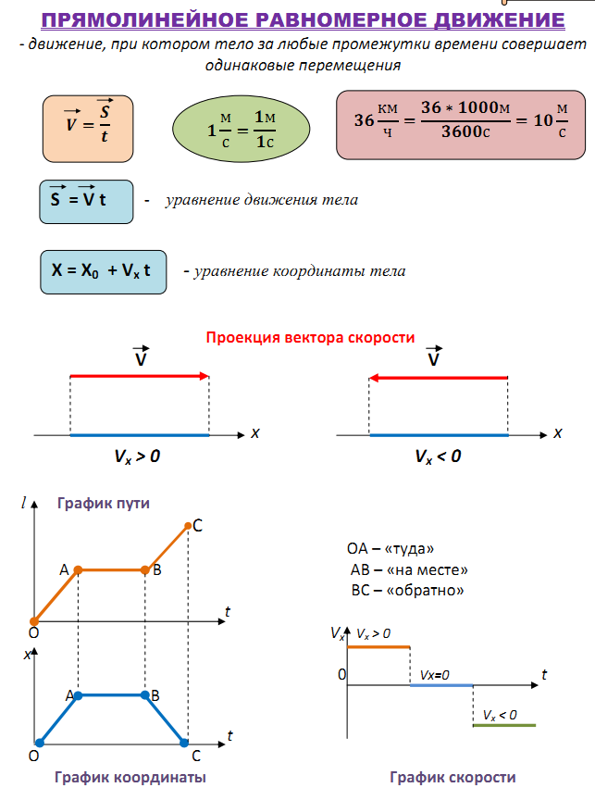
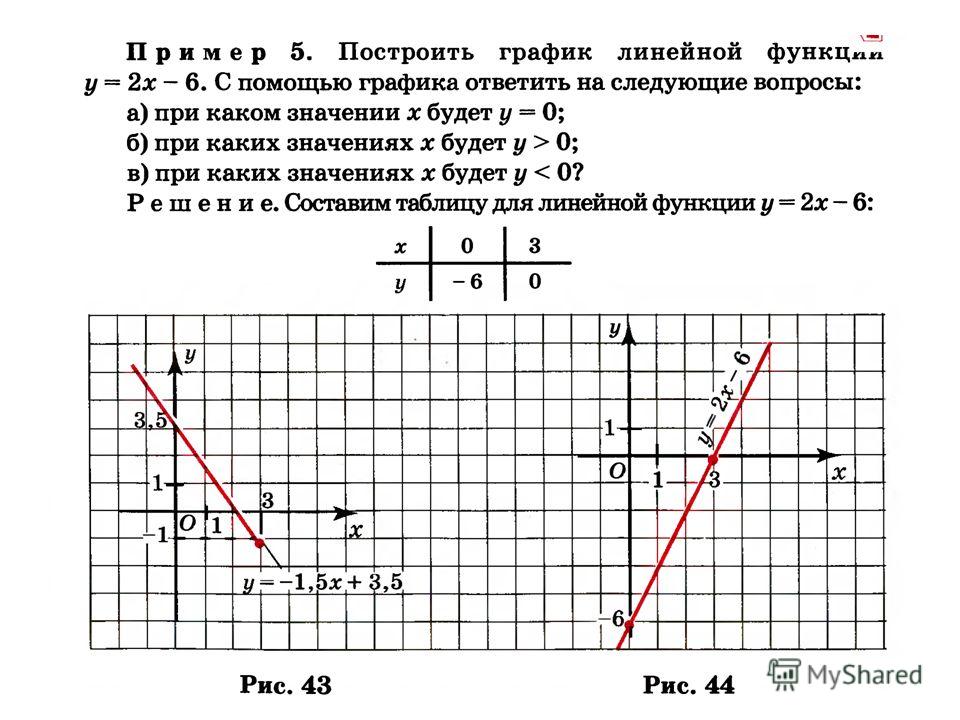 Для этого его нужно сначала посчитать:
percentage = 100 * okr$ХимЭкспорт / sum(okr$ХимЭкспорт)
# и округлить до 1 знака после запятой:
percentage = round(percentage, digits = 1)
Для этого его нужно сначала посчитать:
percentage = 100 * okr$ХимЭкспорт / sum(okr$ХимЭкспорт)
# и округлить до 1 знака после запятой:
percentage = round(percentage, digits = 1) Нотация
Нотация  США",
horiz = TRUE,
las = 1,
xlim = c(0,12000),
col = "steelblue")
США",
horiz = TRUE,
las = 1,
xlim = c(0,12000),
col = "steelblue") transp = adjustcolor(violet, alpha = 0.5)
barplot(okr$ХимЭкспорт,
names.arg = names,
main = "Экспорт продукции химической промышленности",
xlab = "млн долл. США",
horiz = TRUE,
las = 1,
xlim = c(0,12000),
col = violet.transp)
transp = adjustcolor(violet, alpha = 0.5)
barplot(okr$ХимЭкспорт,
names.arg = names,
main = "Экспорт продукции химической промышленности",
xlab = "млн долл. США",
horiz = TRUE,
las = 1,
xlim = c(0,12000),
col = violet.transp) arg = names,
main = "Экспорт продукции химической промышленности",
xlab = "млн долл. США",
horiz = TRUE,
las = 1,
xlim = c(0,12000),
col = colors)
arg = names,
main = "Экспорт продукции химической промышленности",
xlab = "млн долл. США",
horiz = TRUE,
las = 1,
xlim = c(0,12000),
col = colors) США",
horiz = TRUE,
las = 1,
xlim = c(0, 12000),
col= colors)
США",
horiz = TRUE,
las = 1,
xlim = c(0, 12000),
col= colors) axis
axis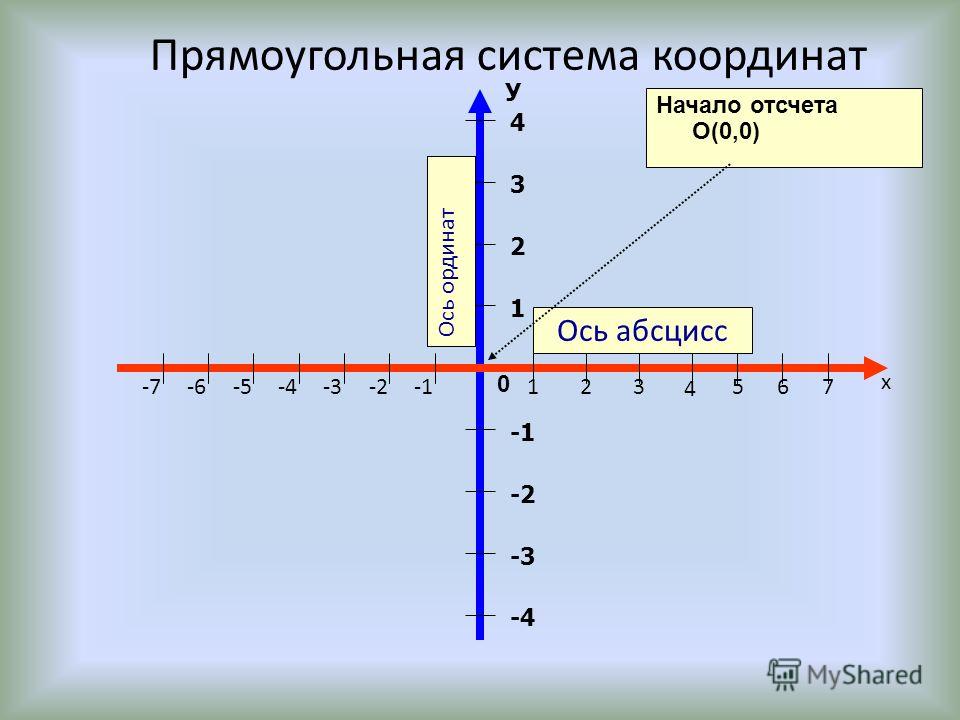 axis
axis Этот параметр можно пропустить, если подписи совпадают с местоположениями меток
Этот параметр можно пропустить, если подписи совпадают с местоположениями меток м., округлив предварительно минимальное и максимальное значение до ближайшего целого снизу и сверху соответственно
axis(side = 2,
at = seq(floor(min(tab$Каспийское)), ceiling(max(tab$Каспийское)), 1),
tck = -0.02)
box() # добавим рамку для красоты
м., округлив предварительно минимальное и максимальное значение до ближайшего целого снизу и сверху соответственно
axis(side = 2,
at = seq(floor(min(tab$Каспийское)), ceiling(max(tab$Каспийское)), 1),
tck = -0.02)
box() # добавим рамку для красоты 3\) по оси \(Y\). Для этого выполним следующую последовательность действий:
3\) по оси \(Y\). Для этого выполним следующую последовательность действий: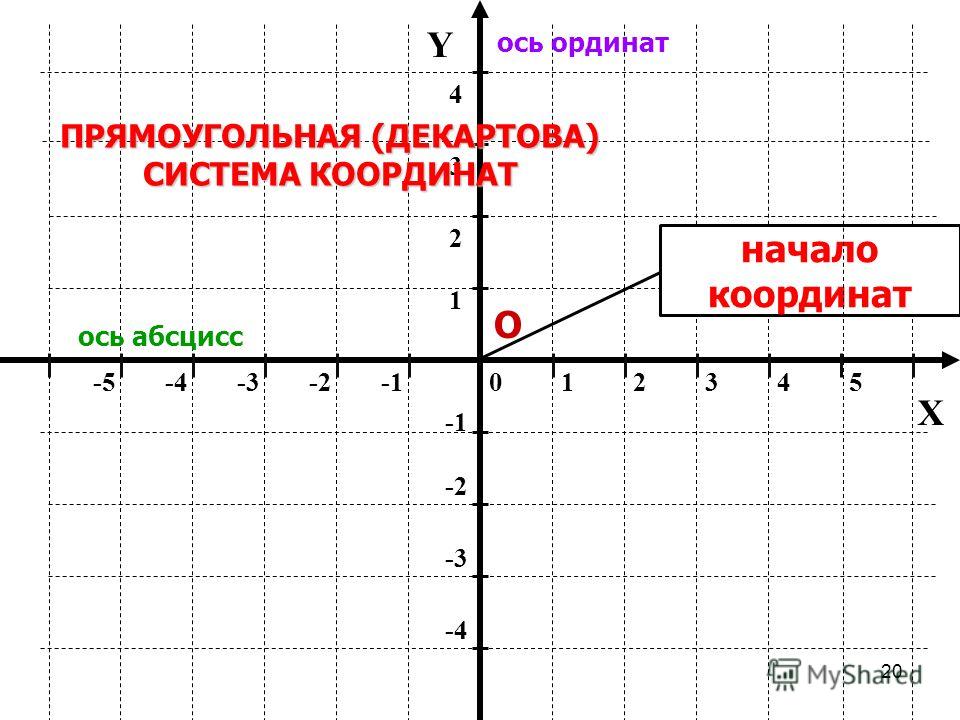 Также полезным будет указать параметр
Также полезным будет указать параметр 
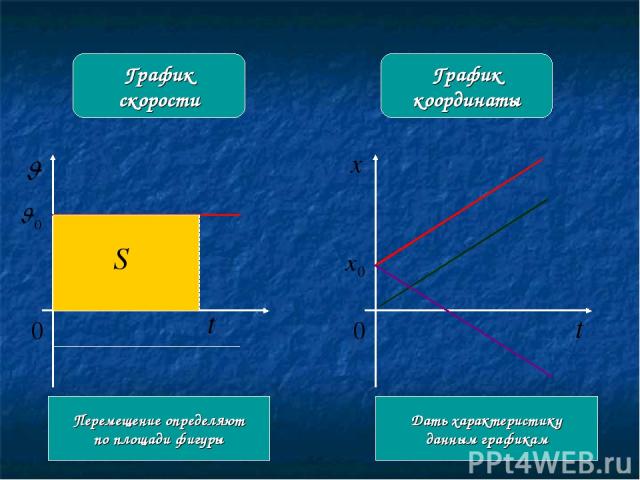

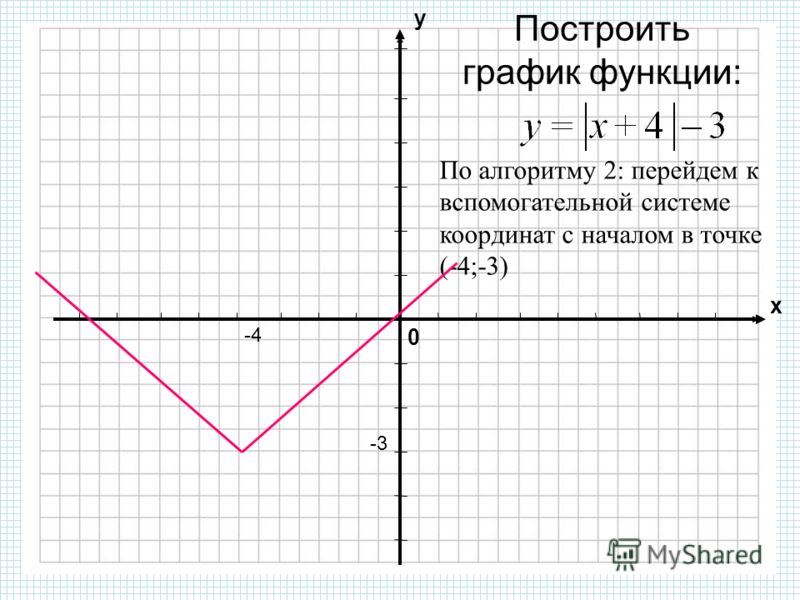 Нанесите поверх кружков значение диаметра текстовой подписью. Соедините кружки линиями со стрелкой посередине, чтобы была понятна история жизни циклона.
Нанесите поверх кружков значение диаметра текстовой подписью. Соедините кружки линиями со стрелкой посередине, чтобы была понятна история жизни циклона. ggplot2: Elegant Graphics for Data Analysis. Dordrecht, Heibelberg, London, New York: Springer, 2009.
ggplot2: Elegant Graphics for Data Analysis. Dordrecht, Heibelberg, London, New York: Springer, 2009.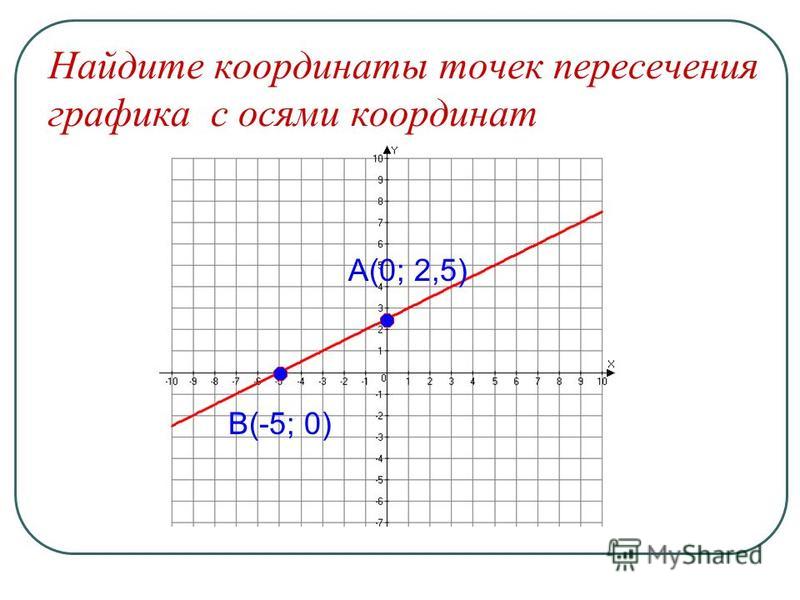 п.).
п.). п.
п. 657990
sol_10003 -2.973854
sol_10004 -2.984015
sol_10005 -2.922233
sol_10006 -3.233097
657990
sol_10003 -2.973854
sol_10004 -2.984015
sol_10005 -2.922233
sol_10006 -3.233097
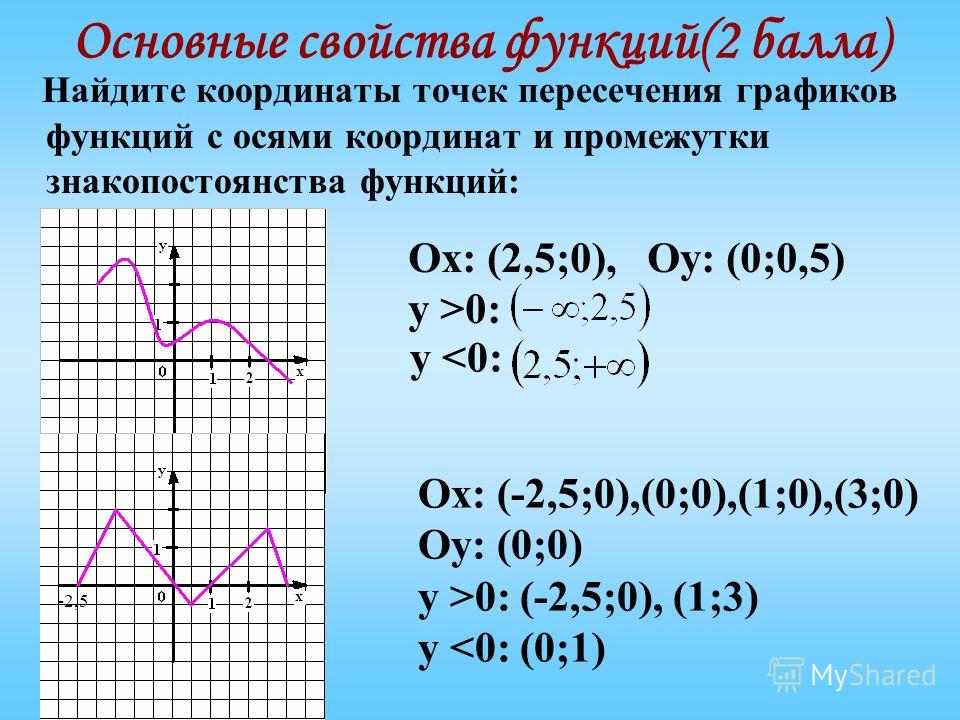 80 -3.63 -2.15 -3.00 -2.68 -2.85 -2.82
sol_10002 -2.68 -3.55 -2.21 -2.64 -2.54 -2.73 -2.66
sol_10003 -2.59 -3.60 -2.38 -3.28 -3.10 -2.99 -2.97
sol_10004 -2.64 -3.85 -2.30 -3.25 -3.11 -3.03 -2.98
sol_10005 -3.00 -2.82 -1.80 -3.04 -2.77 -2.68 -2.92
sol_10006 -3.23 -3.56 -2.54 -3.35 -3.07 -3.15 -3.23
80 -3.63 -2.15 -3.00 -2.68 -2.85 -2.82
sol_10002 -2.68 -3.55 -2.21 -2.64 -2.54 -2.73 -2.66
sol_10003 -2.59 -3.60 -2.38 -3.28 -3.10 -2.99 -2.97
sol_10004 -2.64 -3.85 -2.30 -3.25 -3.11 -3.03 -2.98
sol_10005 -3.00 -2.82 -1.80 -3.04 -2.77 -2.68 -2.92
sol_10006 -3.23 -3.56 -2.54 -3.35 -3.07 -3.15 -3.23

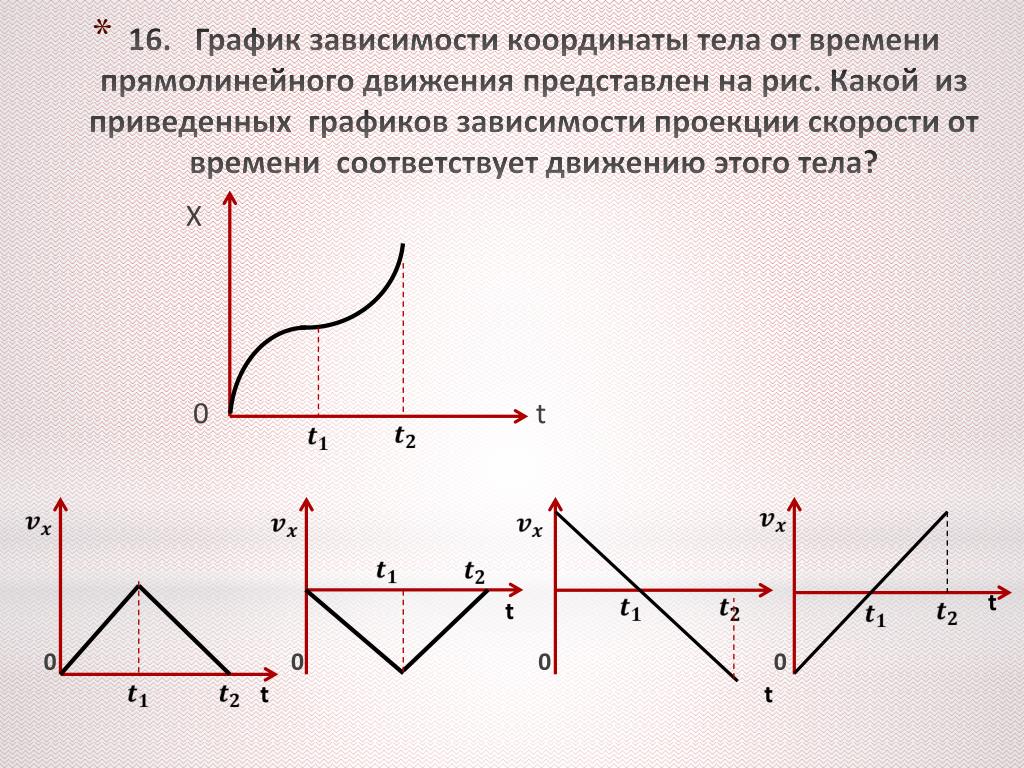 Поскольку порядок следования данных в колонках совпадает можно применить функцию объединения по строкам
Поскольку порядок следования данных в колонках совпадает можно применить функцию объединения по строкам  Она не обладает большим разнообразием возможностей и подходит для быстрого построения не очень сложных графиков.
Она не обладает большим разнообразием возможностей и подходит для быстрого построения не очень сложных графиков. gbm, color=set, shape=set)) +
geom_point(size=3)
g4
gbm, color=set, shape=set)) +
geom_point(size=3)
g4
 gbm)) +
geom_abline(intercept=0, slope=1) +
geom_point(aes(color=set, shape=set), size=3, alpha=0.5)
g7
gbm)) +
geom_abline(intercept=0, slope=1) +
geom_point(aes(color=set, shape=set), size=3, alpha=0.5)
g7
 gbm)) +
geom_abline(intercept=0, slope=1) +
geom_point(aes(color=set, shape=set), size=3, alpha=0.5) +
stat_smooth(method="lm", aes(group=set, color=set), fullrange=TRUE, se=FALSE) +
scale_color_manual(values=c("red", "blue"))
g12
gbm)) +
geom_abline(intercept=0, slope=1) +
geom_point(aes(color=set, shape=set), size=3, alpha=0.5) +
stat_smooth(method="lm", aes(group=set, color=set), fullrange=TRUE, se=FALSE) +
scale_color_manual(values=c("red", "blue"))
g12
 2
2
 gbm)) +
geom_abline(intercept=0, slope=1) +
geom_point(aes(color=set, shape=set), size=3, alpha=0.5) +
stat_smooth(method="lm", aes(group=set, color=set), fullrange=TRUE, se=FALSE) +
scale_color_manual(values=c("red", "blue"))
g13
gbm)) +
geom_abline(intercept=0, slope=1) +
geom_point(aes(color=set, shape=set), size=3, alpha=0.5) +
stat_smooth(method="lm", aes(group=set, color=set), fullrange=TRUE, se=FALSE) +
scale_color_manual(values=c("red", "blue"))
g13
 text.x = element_text(color="red", size=15, angle=45, hjust=1),
panel.background = element_rect(color="pink", fill="lightyellow"))
g13.5
text.x = element_text(color="red", size=15, angle=45, hjust=1),
panel.background = element_rect(color="pink", fill="lightyellow"))
g13.5
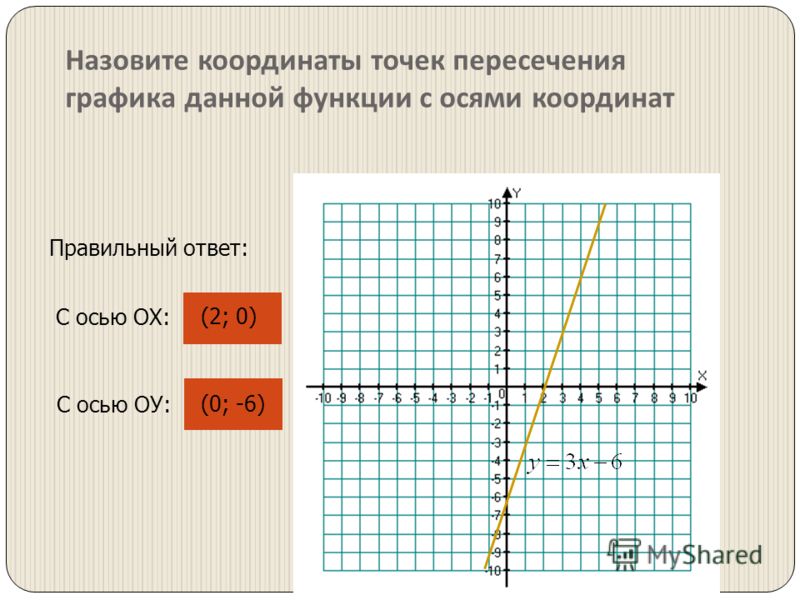 Ранее мы использовали с этой целью функцию
Ранее мы использовали с этой целью функцию  5 <- ggplot(df, aes(x=obs)) +
geom_histogram(binwidth=1, aes(fill=set), color="white") +
facet_wrap(~set, ncol=1)
g15.5
5 <- ggplot(df, aes(x=obs)) +
geom_histogram(binwidth=1, aes(fill=set), color="white") +
facet_wrap(~set, ncol=1)
g15.5

 2_{test} \).
2_{test} \).
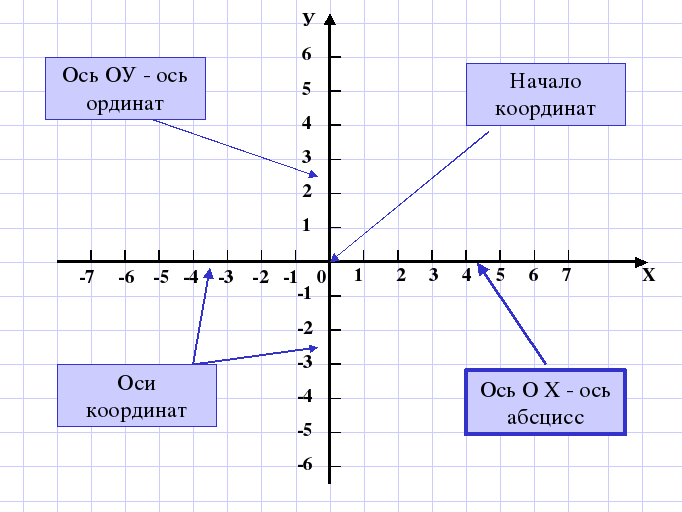 diverging.Tealrose,
color_continuous_midpoint=2)
рис.шоу()
diverging.Tealrose,
color_continuous_midpoint=2)
рис.шоу()
 5,5],
тиквалы = [1.5,3,4.5],
метка = 'B', значения = [3,1.5]),
дикт (диапазон = [1,5],
тиквалы = [1,2,4,5],
метка = 'C', значения = [2,4],
ticktext = ['текст 1', 'текст 2', 'текст 3', 'текст 4']),
дикт (диапазон = [1,5],
метка = 'D', значения = [4,2])
])
)
)
рис.шоу()
5,5],
тиквалы = [1.5,3,4.5],
метка = 'B', значения = [3,1.5]),
дикт (диапазон = [1,5],
тиквалы = [1,2,4,5],
метка = 'C', значения = [2,4],
ticktext = ['текст 1', 'текст 2', 'текст 3', 'текст 4']),
дикт (диапазон = [1,5],
метка = 'D', значения = [4,2])
])
)
)
рис.шоу()
 update_layout(
plot_bgcolor = 'белый',
paper_bgcolor = 'белый'
)
рис.шоу()
update_layout(
plot_bgcolor = 'белый',
paper_bgcolor = 'белый'
)
рис.шоу()
 шоу()
шоу()
 шоу()
шоу()
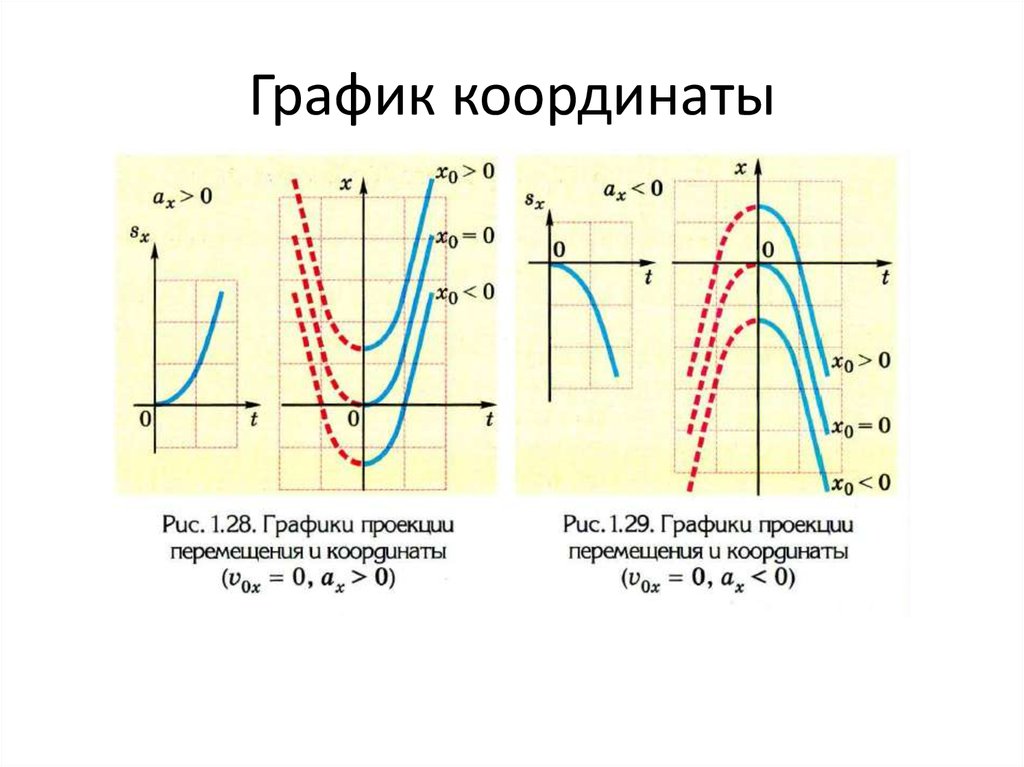 Подробности)
Подробности)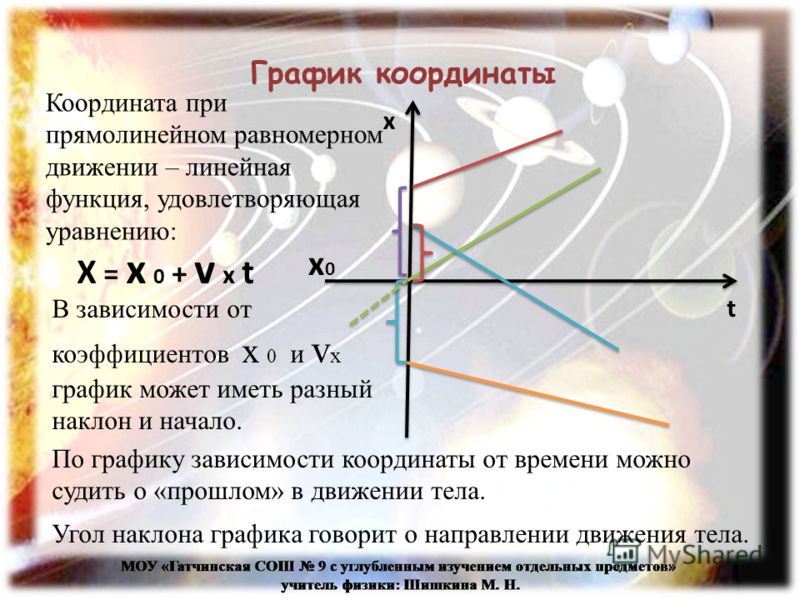

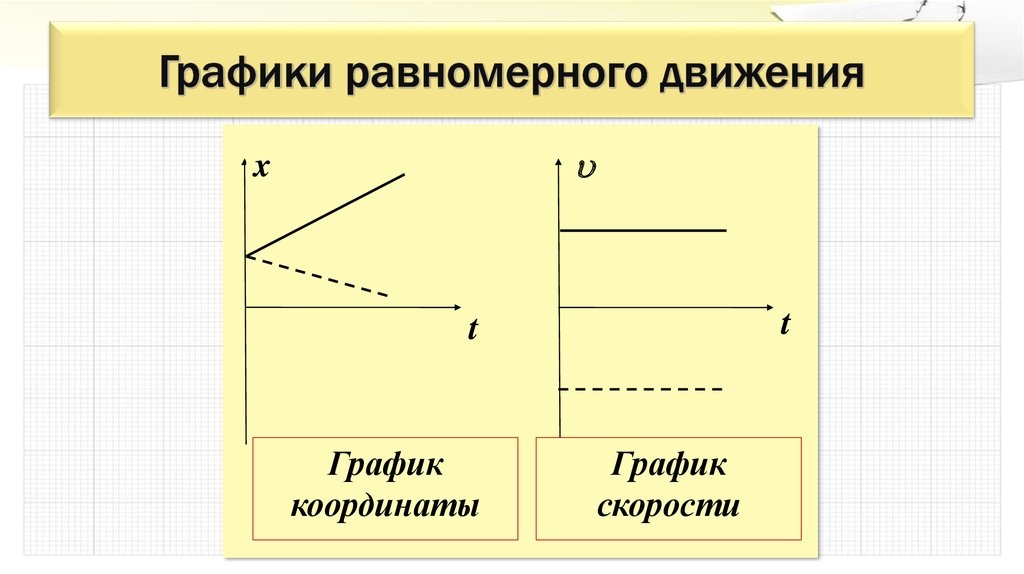 Это выполнено
путем вычисления F-статистики для каждого класса по сравнению с остальными для каждой переменной оси.
Затем переменные оси упорядочиваются (по убыванию) по их максимуму k F-статистики,
где k — количество классов.
Это выполнено
путем вычисления F-статистики для каждого класса по сравнению с остальными для каждой переменной оси.
Затем переменные оси упорядочиваются (по убыванию) по их максимуму k F-статистики,
где k — количество классов.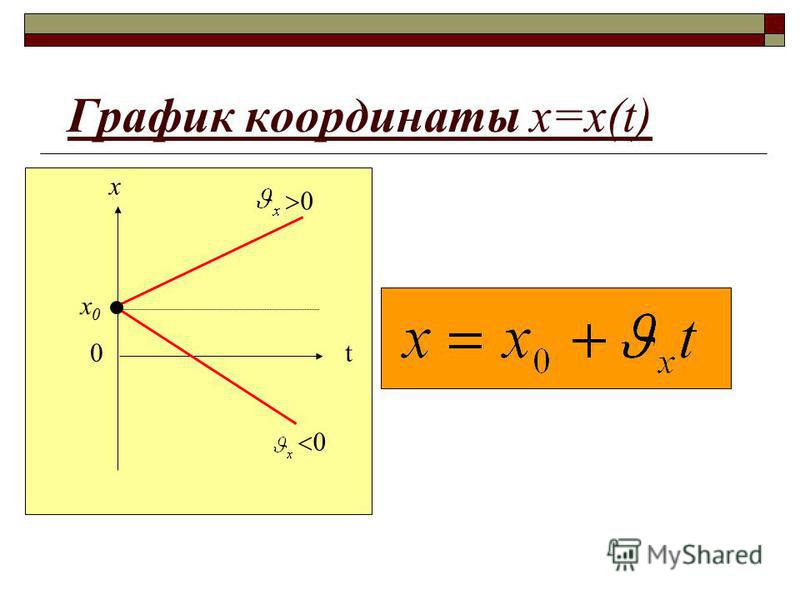 Примечание. Для использования этих способов заказа необходимо иметь скагностик
Примечание. Для использования этих способов заказа необходимо иметь скагностик  График данных алмазов")
p_(p)
График данных алмазов")
p_(p)