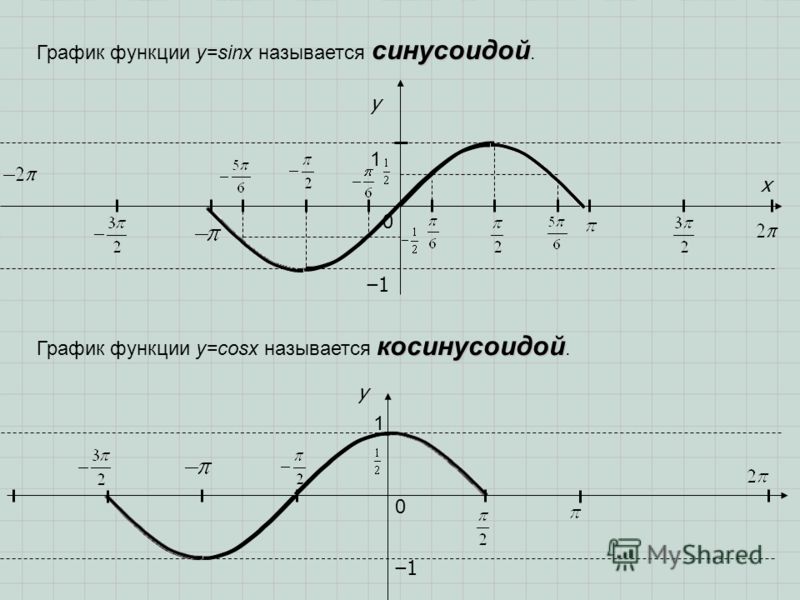
Графики косинуса — презентация онлайн
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
11 класс
Построение и
преобразование
графика функции у = cos x
Выполнила
Бобель Юлия Анатольевна
Фрунзенский район школа №368
содержание
2. Содержание
Построение графика у = cosxСвойства функции у = cosх
Сдвиг вдоль оси абсцисс
Сдвиг вдоль оси ординат
Симметрия относительно оси абсцисс
Сжатие и растяжение к оси ОХ
Сжатие и растяжение к оси ОУ
Построение графика у = ∣cosx∣
содержание
3.
 Построение графика функции у = cosxПостроим график у = cosx на промежутке (-π; π)
Построение графика функции у = cosxПостроим график у = cosx на промежутке (-π; π)У
Х
У
0
1
1,5
1
у=cosx
2
4
2
2
0,5
0
6
3
2
2 3 5
3 4 6
6 4 3 2
-0,5
-1
-1,5
y = cosx – четная функция
Х
3
2
2
3
3
4
5
6
1
2
0
1
2
2
2
3
2
-1
содержание
4. Свойства функции у = cosx
у1,5
1
у = cosx
0,5
2
0
-0,5
2
3
2
2
5
2
х
-1
-1,5
D(y)
R
E(y)
[-1;1]
Период
возрастает
убывает
T=2 π
[π+2πn;2 π+2πn]
[2πn; π+2πn],
n∊Z
четная,
нечетная
у=0
у>0
у<0
уmax
ymin
четная
х=π/2+2 πn, n∊Z
(- π/2+2πn; π/2+2 πn), n∊Z
(π/2+2 πn;3π/2+2 πn), n∊Z
уmax=1, при х=2 πn, n∊Z
уmin= -1, х= π+2 πn, n∊Z
содержание
5. Сдвиг вдоль оси ординат
у=cosx+2у=cosx-2
У
У
3,5
3
2,5
1,5
1
y=cosx+2
0,5
2
0
1,5
-0,5
1
-1
0,5
-1,5
0
-0,5
2
y=cosx
Х
2
Х
-2
-2,5
-1
-3
-1,5
-3,5
Сдвиг вниз
y=cosx
y=cosx-2
Сдвиг вверх
содержание
6.
 Сдвиг вдоль оси абсциссу=cos(x-2).
Сдвиг вдоль оси абсциссу=cos(x-2).у=cos(x+2)
У
У
1,5
1,5
1
y=cosx
y=cos(x-2)
1
0,5
0,5
0
2
Х
0
2
-0,5
-0,5
y=cosx
-1
-1
y=cos(x+2)
-1,5
-1,5
Сдвиг влево
Сдвиг вправо
содержание
Х
7. Задание
№717(1)у = 1 + cosx
Описать свойства.
У
3
Е(1+ cosx) = [0; 2]
2
Нули функции
х = + n, n Z
y=1+cosx
1
0
2
-1
2
3
2
2
y=cosx
Х
Промежутки
возрастания,
убывания
не изменились.
-2
содержание
8. Сжатие и растяжение
y=k∙cosxСжатие и растяжение
у =2cosx
у =1/2cosx
У
У
1,5
2,5
2
1
1,5
1
0,5
0,5
0
2
-0,5
y=cosx
y=cosx
2
-1
3
2
5
2
y=2cosx
-1,5
Х
2
0
-0,5
2
Х
3
2
5
2
y=1/2cosx
-1
-2
-1,5
-2,5
k>1
Растяжение
0<k<1
Сжатие
содержание
9.
 Сжатие и растяжениеy = cos(1/2x)
Сжатие и растяжениеy = cos(1/2x)y = cos(2x)
У
У
2
2
y=cos(2x)
1
1
0
2
0
Х
y=cos(1/2x)
2
-1
-1
y=cosx
y=cosx
-2
-2
k>1
y=cos(kx)
Сжатие
0<k<1
Растяжение
содержание
Х
10. Задание
№715(1) cos2x=1/2 №715(1) cos2x<1/2 на промежутке3
2 ; 2
У
2
cos2x=1/2
2
1
у=0,5
0
2
6
6
х = ±π/6
5
6
7
6
3
2
х =5 π/6;
Х
х = 7π/6
-1
y=cos2x
-2
содержание
11. Симметрия графиков
Уу = — cosx симметрия
графика у = cosx
относительно оси ОХ
2
1
0
2
2
-1
y= — cosx
-2
y=cosx
3
2
Х
y = cosx – четная
функция, поэтому
графики у = cosx и
у = cos(-x) совпадают
содержание
12. Построение графика
y=∣cosx∣У
2
y=∣cosx∣
1
0
2
2
3
2
Х
-1
-2
y = ∣cosx∣ — получается симметрией относительно оси ОХ тех
участков графика у = cosx, которые расположены ниже её.

содержание
13. Задание
№719у = 3-2cos(х-1)
У
6
у = cosх
5
4
у = cos(х-1)
3
у = -2cos(х-1)
2
1
2
0
-1
2
3
2
2
5
2
Х
у = 3-2cos(х-1)
-2
-3
содержание
14. Литература
Ш.А.Алимов, Ю.М.Колягин и др. «Алгебра и началаанализа 10-11»: М. «Просвещение» 2003.
Н.Е.Федорова, М.В. Ткачева «Изучение алгебры и начала
анализа 10-11»: М. «Просвещение» 2004.
English Русский Правила
График косинуса — онлайн справочник для студентов
Косинус-граф имеет вид, как показано на рисунке 1. Кривая, определяющая косинус-граф, называется кривой косинуса.
Рис. 1
График функции \(\
y=\cos x
\) пересекает ось \(\
\mathrm{b} \times \mathrm{E}
\) в точках \(\
x=\frac{\pi}{2}+\pi n
\), \(\
n \in Z
\) . Максимальные значения, равные 1, функция принимает в точках \(\
x=2 \pi n
\), \(\
n \in Z
\) и минимуме, равном \(\
-1
\), \(\
x=\pi+2 \pi n
\), \(\
n \in Z
\) .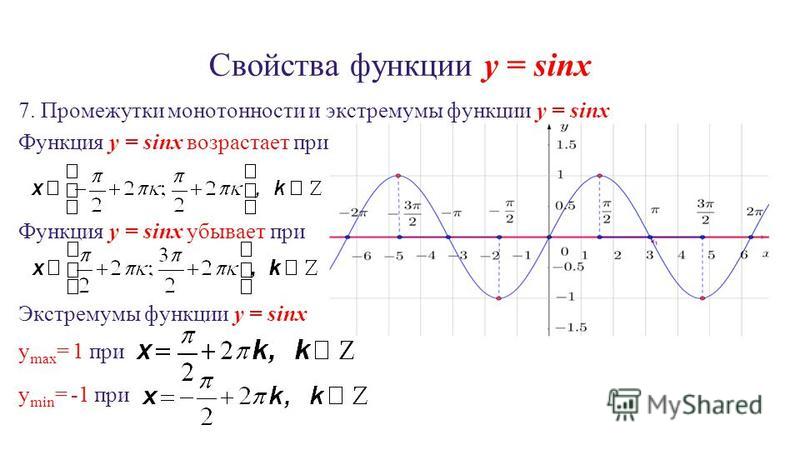 График функции возрастает с \(\
x \in(-\pi+2 \pi n, 2 \pi n)
\), \(\
n \in Z
\) и уменьшается с \(\
x \in(-\pi+2 \pi n, 2 \pi n)
\), \(\
n \in Z
\)
График функции возрастает с \(\
x \in(-\pi+2 \pi n, 2 \pi n)
\), \(\
n \in Z
\) и уменьшается с \(\
x \in(-\pi+2 \pi n, 2 \pi n)
\), \(\
n \in Z
\)
Примеры решения проблем
ПРИМЕР 1
Построить график функции \(\ y=\cos x+1 \)
Желаемый график получается из графика функции \(\ y=\cos x \) в результате параллельного переноса по оси ординат вверх на 1 единицу (рис.2)
Рисунок 2
ПРИМЕР 2
Построить график функции \(\ y=\cos \left(x-\frac{2 \pi}{3}\right) \)
Желаемый график получается из графика функции \(\ y=\cos x \) в результате параллельного переноса по оси абсцисс вправо на \(\ \frac{2 \pi}{3} \) (рис.3).
Рис. 3
ПРИМЕР 3
Построить график функции \(\ y=-3 \cos x \)
Построим данный граф, используя элементарные преобразования графа функции \(\
y=\cos x
\). Во-первых, мы растягиваем график функции \(\
y=\cos x
\) три раза по оси ординат (мы увеличиваем расстояние от каждой точки графа \(\
y=\cos x
\) до оси абсцисс три раза), получаем график функции \(\
y=3 \cos x
\) (рис.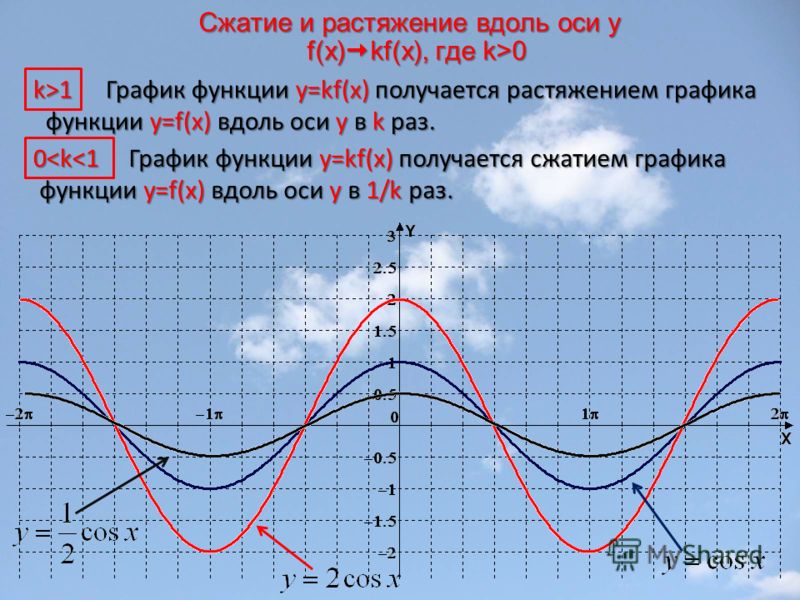 4).
4).
Рис. 4
Затем мы отражаем график функции \(\ y=3 \cos x \) симметрично относительно оси \(\ x \), получаем желаемый график \(\ y=-3 \cos x \) (рис.5).
Рис. 5
Физика
166
Реклама и PR
31
Педагогика
80
Психология
72
Социология
7
Астрономия
9
Биология
30
Культурология
86
Экология
8
Право и юриспруденция
36
Политология
13
Экономика
49
Финансы
9
История
16
Философия
8
Информатика20
Право
35
Информационные технологии
6
Экономическая теория
7
Менеджент
719
Математика
338
Химия
20
Микро- и макроэкономика
1
Медицина
5
Государственное и муниципальное управление
2
География
542
Информационная безопасность
2
Аудит
11
Безопасность жизнедеятельности
3
Архитектура и строительство
1
Банковское дело
1
Рынок ценных бумаг
6
Менеджмент организации
2
Маркетинг
238
Кредит
3
Инвестиции
2
Журналистика
1
Конфликтология
15
Этика
9
Формулы дифференцирования Косинус двойного угла Косинус 60 градусов Косинус 45 градусов Косинус 30 градусов
Узнать цену работы
Узнай цену
своей работы
Имя
Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругое Принимаю Политику конфиденциальностиПодпишись на рассылку, чтобы не пропустить информацию об акциях
графическое представление функции cos(x)
Программное обеспечение для построения графиков онлайн , также известное как графопостроитель ,
это онлайн-график , который позволяет отображать функции в режиме онлайн.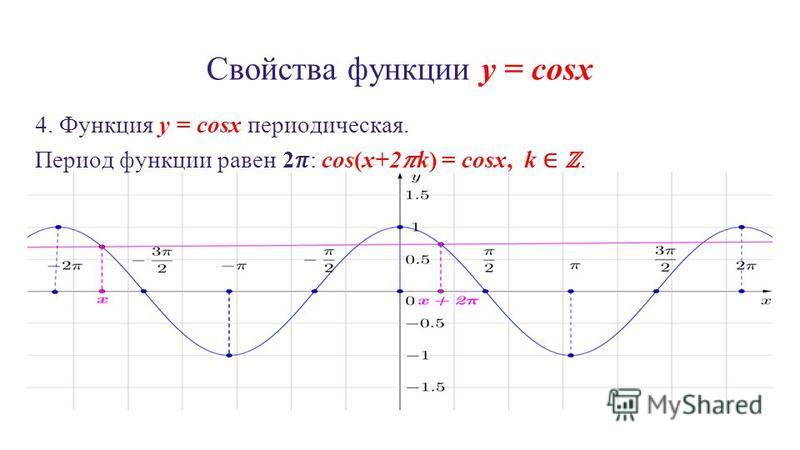 Просто введите выражение в соответствии с x функции, которую нужно построить, используя обычные математические операторы.
Построитель кривых особенно подходит для функционального исследования ,
позволяет получить
Просто введите выражение в соответствии с x функции, которую нужно построить, используя обычные математические операторы.
Построитель кривых особенно подходит для функционального исследования ,
позволяет получить
Онлайн-плоттер также может рисовать параметрические кривые. и рисовать полярные кривые, а для функций достаточно ввести выражение для представления по параметру t.
В графическом калькуляторе для записи математических функций должны использоваться следующие операторы: 9Для питания
Это программное обеспечение для построения кривых позволяет использовать следующие обычных математических функций :
- абс (абсолютное значение), график абсолютного значения
- арккос (арккосинус), арккосинус участка
- арксинус (арксинус), арксинус графика
- арктангенс (арктангенс), арктангенс графика
- ch (гиперболический косинус), построить гиперболический косинус
- cos (косинус), график косинус
- cosec (косеканс), косеканс участка
- котан (котангенс), котангенс участка
- coth (гиперболический котангенс), построить гиперболический котангенс
- cube_root (кубический корень), построить кубический корень
- опыта (экспоненциальный), экспоненциальный график
- ln (напировский логарифм), построить напьеровский логарифм логарифм
- (логарифм), логарифм графика
- сек (секанс), секущая участка
- ш (гиперболический синус), построить гиперболический синус
- sin (синус), график синуса
- sqrt (квадратный корень), участок квадратный корень
- тангенс (тангенс), участок касательной
- -й (гиперболический тангенс), построить гиперболический тангенс
- абс.
 (абсолютное значение),
график абсолютного значения
(абсолютное значение),
график абсолютного значения - арккос (арккосинус), арккосинус участка
- арксинус (арксинус), арксинус графика
- арктангенс (арктангенс), арктангенс графика
- ch (гиперболический косинус), построить гиперболический косинус
- cosec (косеканс), косеканс участка
- котан (котангенс), котангенс участка
- coth (гиперболический котангенс), построить гиперболический котангенс
- cube_root (кубический корень), построить кубический корень
- опыта (экспоненциальный), экспоненциальный график
- ln (напировский логарифм), построить напьеровский логарифм логарифм
- (логарифм), логарифм графика
- сек (секанс), секущая участка
- ш (гиперболический синус), построить гиперболический синус
- sin (синус), график синуса
- sqrt (квадратный корень), участок квадратный корень
- тангенс (тангенс), участок касательной
- -й (гиперболический тангенс), построить гиперболический тангенс
- Графические функции онлайн
Этот онлайн-плоттер позволяет вам рисовать несколько кривых одновременно ,
просто введите выражение функции, которую нужно построить, и нажмите «Добавить», графическое представление функции появляется мгновенно, можно повторить операцию для построения других кривых онлайн .
Переменная, которая будет использоваться для представления функций, — «x».
Координаты точек на кривой можно получить с помощью курсора. Для этого нажмите на кривую, чтобы появился этот курсор, а затем перетащите вдоль кривой, чтобы увидеть ее координаты.
Кривые можно удалить из плоттера:
- Чтобы удалить кривую, выберите кривую, затем нажмите кнопку удаления в меню.
- Чтобы удалить все кривые с графика, нажмите кнопку удалить все в меню.
Можно изменить кривую, представленную на графике, выбрав ее, отредактировав ее выражение и затем щелкнув на кнопку редактирования.
онлайн-плоттер имеет несколько опций, позволяющих настроить график.
Чтобы получить доступ к этим параметрам, нажмите кнопку параметров. Затем можно определить границы графов,
чтобы подтвердить эти изменения, необходимо снова нажать кнопку параметров.
- Проведение касательной функции к точке
- График производной функции
Онлайн-плоттер позволяет провести тангенс функции в точке для этого, вы просто рисуете нужную функцию, затем, как только функция нарисована, нажмите на меню, параметры, а затем кнопку касательной, которая появляется на экране, после чего будет нарисована касательная, можно изменить точку касательной, что приводит к перерисовке касательной. Калькулятор позволяет определить уравнение касательной очень просто, с уравнением кривой.
Онлайн-плоттер позволяет вам построить производную функции для этого,
вы просто рисуете нужную функцию, затем после того, как функция нарисована,
нажмите на меню, на параметры, затем на появившуюся производную кнопку,
затем строится производная функции.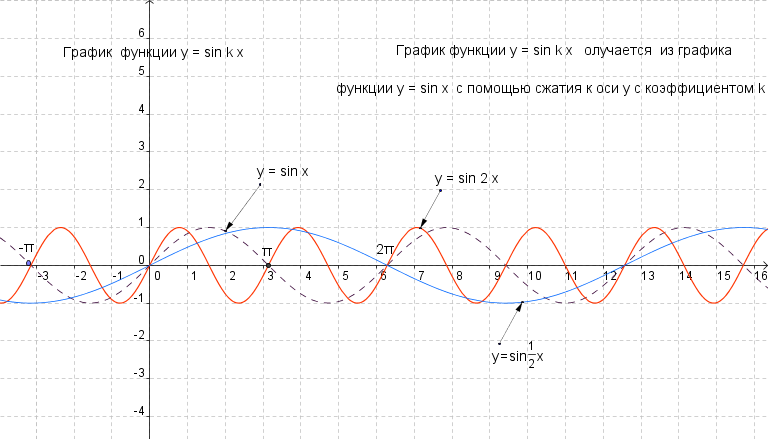
9Построитель кривых 0003 также можно использовать для вычисления производной функции и к участок он для этого, вам нужно нарисовать нужную функцию, затем, как только функция будет нарисована, выберите ее, щелкнув по ней, на кривой появится красный курсор. Затем нажмите на меню, на параметры, затем на производную кнопку «выражение», которая появляется на экране, затем строится и вычисляется производная функции. («Выражение» представляет собой выражение, которое необходимо получить и нанести на график).
Плоттер позволяет рисовать параметрическую кривую , для этого
вам просто нужно ввести абсциссу, ординату как функцию от t,
затем нажмите кнопку «Построить параметрическую кривую»,
кривая автоматически отображается с двумя курсорами для отображения нужных точек.
Построитель кривых можно использовать для построения полярной кривой . Для этого просто введите выражение полярной кривой в зависимости от t, затем нажмите кнопку «Построить полярную кривую», кривая автоматически отобразится с двумя курсорами для отображения нужных точек.
Есть возможность двигаться по кривым и получать координаты точки, на которой находится курсор, Для этого необходимо ввести курсор и перемещать его по графику, координаты X и Y отображаются под графиком.
Можно изменить область графика, для этого необходимо зайти в меню, затем нажать на опции, Затем можно изменить пределы графического дисплея.
Графический калькулятор предлагает возможность масштабировать и перемещать область графика.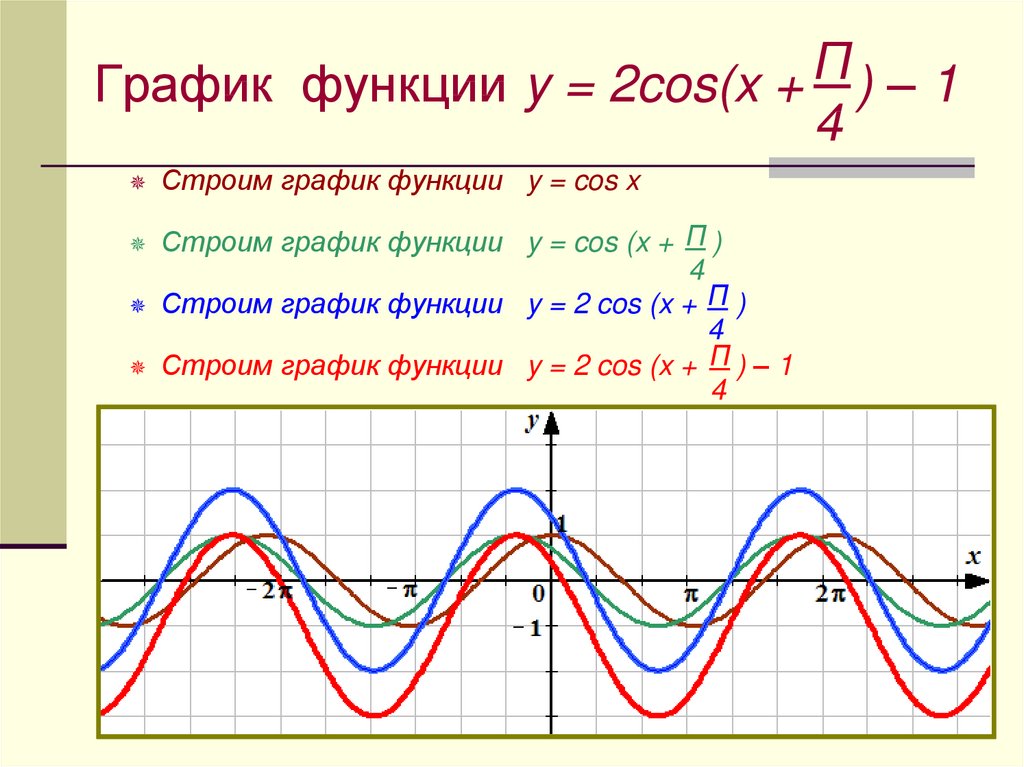 Сделать это,
используйте область в правом нижнем углу графиков.
Сделать это,
используйте область в правом нижнем углу графиков.
- Кнопка + позволяет увеличить масштаб кривых,
- — позволяет уменьшить масштаб кривых,
- Стрелки используются для перемещения кривых,
Можно экспортировать построенные кривые с помощью графического калькулятора , экспорт осуществляется как
изображение в формате PNG. Для этого вам нужно зайти в меню графика, затем в подменю экспорта графиков.
Затем калькулятор отображает построенные кривые в виде изображения, просто щелкните правой кнопкой мыши, чтобы экспортировать изображение,
также возможно скопировать изображение.
Чтобы вернуться к обычному отображению калькулятора, используйте кнопку Выход из режима изображения.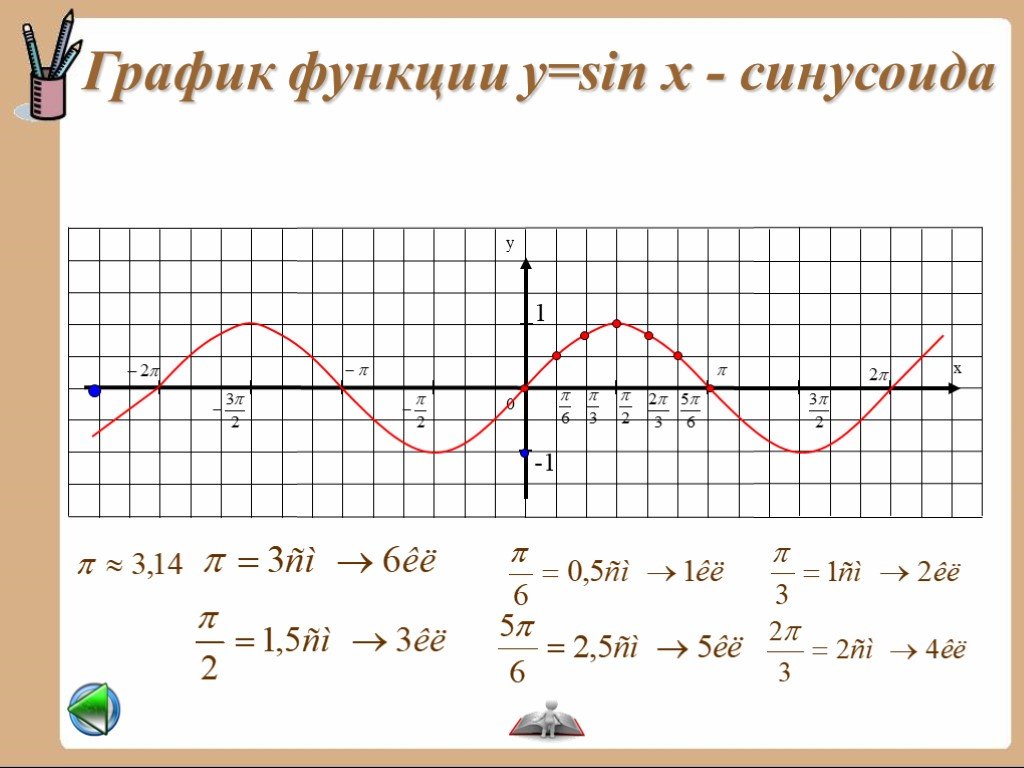
График косинуса, y = cos (x)
График косинуса, y = cos (x) | Pearson+ ChannelsRecent Channels
- Trigonometry
Chemistry
- General Chemistry
- Organic Chemistry
- Analytical Chemistry
- GOB Chemistry
- Biochemistry
Biology
- General Biology
- Microbiology
- Anatomy и физиология
- Генетика
- Cell Biology
Math
- College Algebra
- Trigonometry
- Precalculus
Physics
- Physics
Business
- Microeconomics
- Macroeconomics
- Financial Accounting
Social Sciences
- Психология
Начните печатать, затем используйте стрелки вверх и вниз, чтобы выбрать вариант из списка.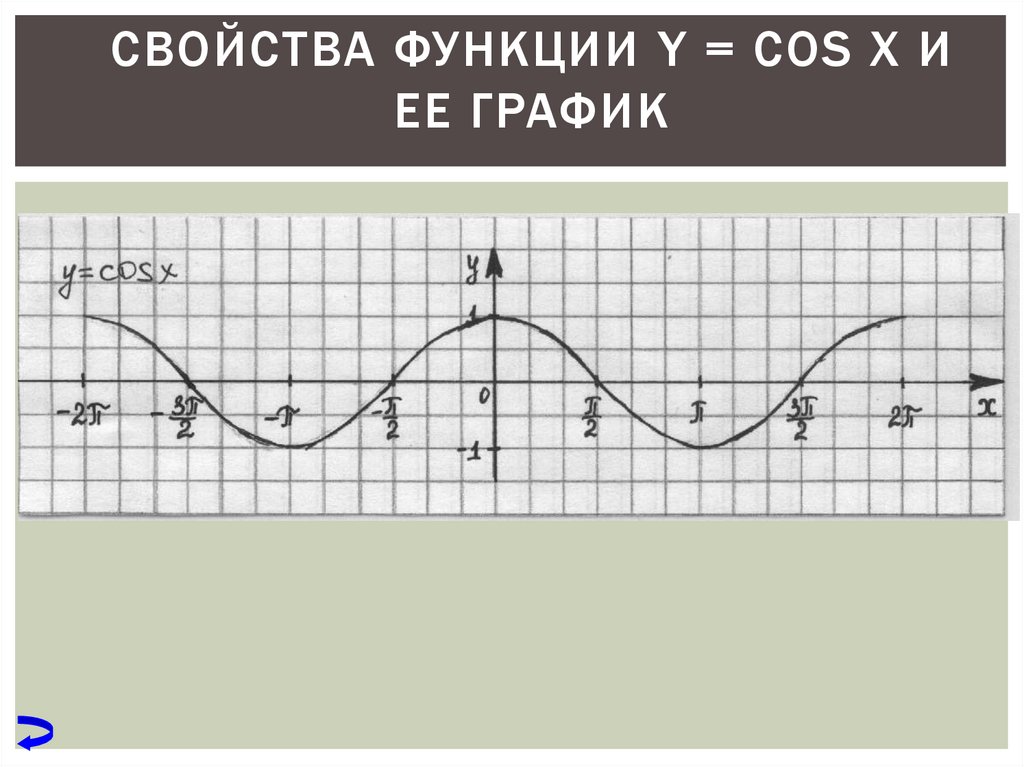
Колледж тригонометрии Графики тригонометрических функций, обратные тригонометрические функции Графики функций синуса и косинуса График изменения y = cos x
patrickJMT
163просмотра
Было ли это полезно?
Related Videos
Graphing Sine and Cosine with Phase (Horizontal) Shifts, Example 2
patrickJMT
67views
Graphing Trigonometric Functions — Graph Transformations
patrickJMT
43views
Graphing a Cosine Function
patrickJMT
56views
Как найти амплитуду графика синуса и косинуса
Brian Mclogan
84Views
Амплитуда и период синуса и косинуса
Mathispower4u
245Views
SINE и косицине функции косинуса
patrickJMT
178views
График косинуса, y = cos (x)
patrickJMT
163views
Графики синусов и косинусов0015
Patrickjmt
47Views
График синуса и косинуса с фазовыми (горизонтальными) сдвигами, пример 1
Patrickjmt
56views
Тригонометрические функции и график: Amplitud, Perier and Horiz -Shiz.

 (абсолютное значение),
график абсолютного значения
(абсолютное значение),
график абсолютного значения