Как решать положительные и отрицательные числа: Сложение Чисел с Разными Знаками

Урок-проект «Мир положительных и отрицательных чисел»

 

 

ТВОРЧЕСКИЙ ПРОЕКТ ПО МАТЕМАТИКЕ

«МИР ПОЛОЖИТЕЛЬНЫХ И ОТРИЦАТЕЛЬНЫХ ЧИСЕЛ»

Класс 6

 

 

 

 

 

 

 

ТВОРЧЕСКИЙ ПРОЕКТ ПО МАТЕМАТИКЕ

«МИР ПОЛОЖИТЕЛЬНЫХ И ОТРИЦАТЕЛЬНЫХ ЧИСЕЛ»

КЛАСС 6

(защита проекта «Положительные и отрицательные числа»

 

Краткая аннотация проекта

 

Проект «Положительные и отрицательные числа», рассчитан на учащихся 6 класса, рассчитан на 3 недели, призван систематизировать и обобщить знания по теме «Положительные и отрицательные числа».

Проект направлен на: формирование представлений о математике как о методе познания действительности, позволяющем описывать и изучать реальные процессы и явления; развитие умений работать с учебным математическим текстом (анализировать, извлекать необходимую информацию),точно и грамотно выражать свои мысли с применением математической терминологии и символики, проводить классификации, логические обоснования, доказательства математических утверждений.

Участвуя в проекте, дети проследят путь развития учения о положительных и отрицательных числах, узнают о применении отрицательных чисел в повседневной жизни; научатся решать задачи по теме «Положительные и отрицательные числа», освоят некоторые сервисы веб.

Итоговым продуктом проекта является памятка правил по теме «Положительные и отрицательные числа, создание  рабочей  тетради, которая поможет оценить   знания учащихся, а также сообщения «Истории возникновения отрицательных чисел»

 

Цели: формирование устойчивого навыка действий с «+» и «-«, создать условия для формирования умений  структурировать и систематизировать информацию;  для самостоятельного получения новых знаний о действиях с числами, способствовать развитию информационной и коммуникативной культуры.

Задачи: формирование навыка действий с положительными и отрицательными числами. Развитие умения использовать способы действий в разных ситуациях.

 

Научить учащихся:

Сотрудничать, приобретать знания самостоятельно, систематизировать полученную информацию , пользоваться приобретенными знаниями для решения конкретных задач, работать в группах, выполняя разные социальные роли, делать выводы и заключения, получить эффективный результат решения проблемы в процессе совместной деятельности.

Подготовка к конференции: ученики заранее делятся на 3 группы: “ Историки”, «Математики»,» Исследователи» “литераторы”, “ ”; все участники собирают материал и пишут рефераты по разделам: ,       “История положительных и отрицательных чисел”, “Математика в литературе”.

 

Ход

  урока

Оборудование: презентация. доклады участников конференции

I  Организационный момент

Эпиграф

 

Лучший способ изучить что-либо — это открыть самому.     (Д. Пойа)

Учитель:

 

Прозвенел звонок,

Начинается урок.

Вы за парты дружно сели,

На меня все посмотрели.

Встало солнышко давно,

Заглянуло к нам в окно,

На урок торопит нас –

Математика сейчас

 

Я рада видеть каждого из вас,

И пусть весна прохладой в окна дышит,

Нам будет здесь уютно, ведь наш класс

Друг друга любит, чувствует и слышит.

 

Давайте, ребята, друг другу улыбнёмся, и начнём урок.

 

А девизом нашего урока пусть будут такие слова:

 

 Думаю! Знаю! Могу!

Интерактивное   упражнение «Стоп-внимание!»)

В течение 20 секунд ученики должны запомнить числа и их цвет в таблице и затем установить их в памяти .

2103201763

II. Мотивация учебной деятельности

Ребята!. Путешествуя интересной, замечательной страной, что зовется Математика, вы ознакомились с новыми правилами , законами, учились логически мыслить, анализировать, делать выводы, помогать друг другу .Сегодня мы подводим итоги вашей деятельности  по изучению  темы: ”Действия с рациональными числами». Окружающий мир настолько сложен и разнообразен, что  натуральных и дробных чисел бывает недостаточно, чтобы измерить некоторые величины, описать многие события. Урок будет проведен в нестандартном виде: урока- конференции,  как итога вашей   исследовательской деятельности.  Сегодня нам предстоит защита проекта «Мир  положительных и отрицательных чисел». 

Тема учебного проекта:
«Мир положительных и отрицательных чисел»

Учебные вопросы:

• Зачем человеку «положительные» и «отрицательные» числа?

•    Используются ли где-нибудь кроме математики понятия «положительный» и «отрицательный»?

•   Когда и где возникли эти числа и всегда ли их так называли?

 

•  Можно ли выполнять действия над числами с разными знаками?

Эпиграф урока.

 

Лучший способ изучить что-либо — это открыть самому. (Д. Пойа)

 

Основная идея проекта:

 

связь математики с решением практических задач, значимость основных понятий математики, расширение кругозора учащихся

Цель: исследовать важность и необходимость

отрицательных  чисел в жизни человека, изучить историю возникновения   отрицательных чисел,

ОСНОВОПОЛАГАЮЩИЙ ВОПРОС

Нужны ли в жизни отрицательные  числа

 

ПРОБЛЕМНЫЕ  ВОПРОСЫ

-Где и кто открыл   отрицательные числа?

-Зачем нужны отрицательные числа?

-Где применяются отрицательные числа?

-Как работать с отрицательными числами?

 

Гипотеза

Отрицательные числа –   «лишние,  ложные» числа

 

«Твой ум без числа ничего не представляет.»
               Н.Кузанский

Высказывание немецкого философа  показывает важность любых чисел в жизни людей, поэтому тема данной работы  актуальна

 

Учебные предметы:

 

Математика, Физика, География, История, Биология, Экономика

Участники проекта-учащиеся 6 класса

 

Группа №1 Историки

-Где и кто открыл   отрицательные числа?

Группа №2  Математики

-Как работать с отрицательными числами ?

Группа №3 Литераторы  

-Сказки

-Поэтические минутки (правила в стихах)

Группа №4  Исследователи

— Зачем нужны отрицательные числа?

—Где применяются отрицательные числа?

—

Да, путь познания не гладок,

Но знаем мы со школьных лет:

Загадок больше, чем отгадок

И поискам предела нет

 

Не беда, что идти нелегко,

И не бойтесь, что путь будет труден.

Никогда не давались легко

Достижения людям

 

Итак, первым предоставляется слово «ИСТОРИКАМ»: они подготовили доклад и  презентацию. после просмотра  которой   нужно ответить на вопросы их викторины.       

Как сказал один из философов: «История пишется для установления строгой истины». А она нам в данный момент очень нужна!

Презентация 1

Мини доклад. (Доклад прилагается)

Ученик: История говорит о том, что люди долго не могли привыкнуть к отрицательным числам. Числа казались непонятными и ими не пользовались, т.к не видели в этом никакого смысла. Впервые отрицательные числа появились в Китае во II веке до н.э. Знаков «+» и «-« тогда не было. Положительные числа записывали красным цветом, отрицательные – черным.

В VII в начали использовать отрицательные числа в Индии. Положительные числа толковались как имущество, а отрицательные как долг.

Индийские математики Брахмагупта и Бхаскары составили свои правила действий для этих чисел

В XII в отрицательные числа появились в Европе и снова как долг.

В XV веке появились термины «положительный» и «отрицательный». Знаки «+» и «-« ввел математик Ян Видман.

В XVII в. французский математик Рене Декарт ввел координатную прямую.

Всеобщее признание отрицательные числа получили в первой половине XVIII.

Отголоском тех времён является то, что в современной  математике  операция вычитания и знак отрицательных чисел обозначаются одним и тем же символом минус —

 

Викторина

Перед вами викторина. Задания на доске и в распечатанном виде и у вас на столах. В течение 3-4 мин постарайтесь ответить на 5 вопросов данной викторины.

                                                Вопрос №1

В какой стране впервые появились отрицательные и положительные числа?
                                                Вопрос №2
В древности ростовщики давая деньги в долг, ставили перед именем должника сумму долга и чёрточку, вроде нашего минуса, а когда должник возвращал деньги, зачёркивали, получался плюс? В какой стране это делали?
                                                Вопрос №3
В каких странах не использовали отрицательные числа?
                                                Вопрос №4
Как в древности называли положительные и отрицательные числа?
                                                Вопрос №5
«Сумма двух имуществ есть имущество», «сумма двух долгов есть долг». Чьи это слова?
                                                Вопрос №6
Когда в Европе начали пользоваться отрицательными и положительными числами?
                                                Вопрос №7 
Как звали математика, который ввёл координатную прямую?
                                                Вопрос№8
Каким знаком обозначал вычитание греческий математик Диофант Александрийский?
                                                Вопрос №9
В каком веке была создана полная теория отрицательных чисел?

Оцените работу команды, а «ИСТОРИКИ» проверяют правильность ответов на викторину 

Слово предоставляется команде « МАТЕМАТИКОВ».

Ух уж эти числа!

Презентация 2

 

Ученик: Я, представитель команды « Математиков»

Числа отрицательные новые для нас.

Лишь совсем недавно изучил наш класс

Сразу прибавилась всем на мороки

Учат, учат правила дети все уроки

Цель нашей работы— обобщить весь учебный материал и решить при этом главную задачу-найти метод изложения правил в форме, которая легко запоминается. Это схемы, наглядный материал, алгоритмы, стихотворная форма.

Мы разбили нашу работу на 4 части: составили   схемы, памятку правил и правила в стихах.

Приступим к рассмотрению 1 части нашей работы:

1. Фишбон
2. Схемы
3. Поэтическая минутка (правила в стихах)

Пляшут числа на стене

Очень интересно мне

Минус-плюс, плюс-минус плюс

    Хороши ль они на вкус?

     Нет, я есть их не хочу

    Я их лучше изучу

(пролистывает свою презентацию)

Ученик: Выучи стихотворенье -веселей пойдет ученье!

(ученик показывает презентацию «памятки» правил) и раздает напечатанные на парту

Мы подготовили памятки для лучшего запоминания правил.(Прилагаются)

Ученик.

Хочется  закончить  свое выступление  словами ученого кораблестроителя А.Н. Крылова: «Без теории нет практики, а без практики нет знаний!».

Поэтому мы и создавали Рабочую тетрадь, которая поможет оценить наши знания

 

Вывод:

В течение всей жизни каждый из нас постоянно пользуется набором всевозможных правил, которые экономят время нам и силы.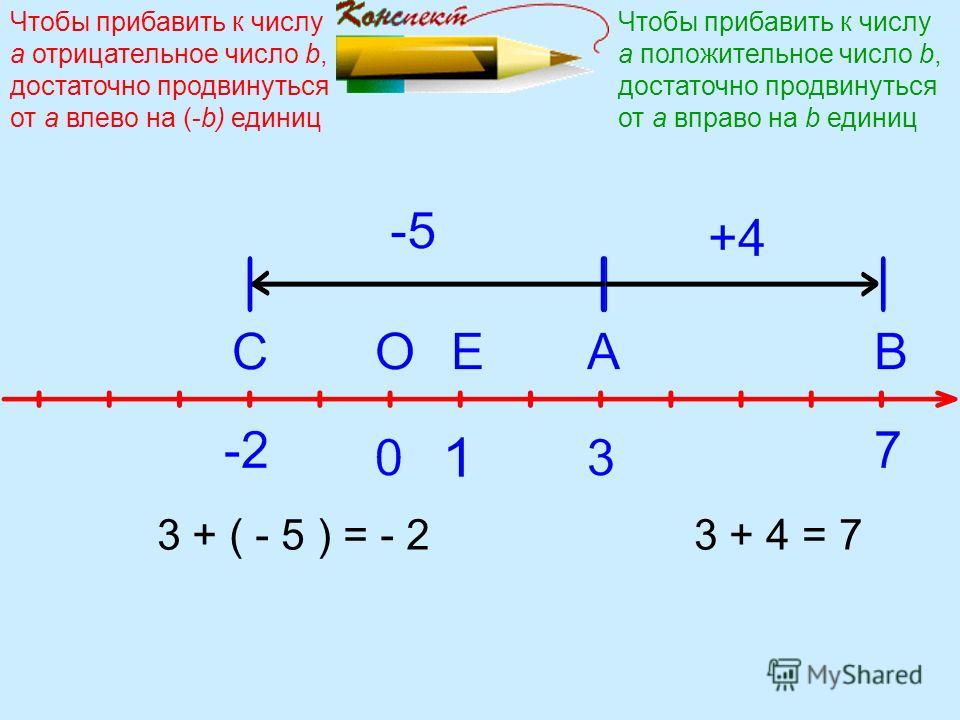 Мы желаем вам, чтобы наши памятки оказали   вам помощь. И не только ученикам, но нашим родителям.

Оцените выступление команды. 

 

 Физкультминутка(офтальмопауза)

А сейчас мы немного отдохнем! А заодно повторим местоположение чисел на координатной прямой. Представьте, что каждый из вас , является точкой отсчета. Если я называю положительное число-поднимите правую руку, если отрицательное число-левую руку. Ноль-руки вместе.

Например: 4- правая рука

                -10- левая рука

                   0-вместе и т.д.

Молодцы! Местоположение чисел на координатной прямой вы знаете.

Следопыты- это люди, которые собирают информацию о чем то.

Слово предоставляется команде « Исследователи»

Презентация 3

Ученик: Немецкий философ сказал: — «Твой ум без числа ничего не представляет». Это говорит о том, что числа имеют большое значение в нашей жизни. Поэтому эта тема очень актуальна и сегодня.

Наша цель изучить и исследовать применение отрицательных чисел на страницах школьных учебников.

Задачи нашего мини проекта:

Изучить литературу по данному вопросу. Понять суть отрицательных чисел. Исследовать применение отрицательных чисел в физике, географии , экономике  биологии. Сделать сообщение учащимся класса.

Чтобы не потерять где и на каких страницах учебника, кроме математики, мы встречались с этими числами, мы составили кластер. Он перед вами.

География: Сейчас мы изучаем и можем сказать глубина — это знак «-», высота знак «+».

В 7 классе на уроках физики увидим замерзание «минус», кипение — «плюс»

Алгебра 7 класс: Координатная плоскость.

В 8 классе химия: Катион – это положительно заряженный ион, анион – отрицательно заряженный ион.

В старших классах на уроках экономики мы изучим подробно, что «долг» — отрицательная величина, а «прибыль» — положительная.

На уроках литературы можно встретить эти знаки, когда характеризуем положительные и отрицательные черты героя.

Но перед нами стояла еще одна задача подготовить вопрос для проверки.

Мы знаем, что в математике свой язык – это язык символов и формул. Напишите в математической символике данный текст, если под «+» понимать друг, а под «-» враг. Задание оценивается в 2 балла.

«Друг моего друга – мой друг»  (интерпретируем, как   «+» × «+» = «+»)

«Враг моего врага – мой друг»  (интерпретируем, как   «-»× «-» = «+»)

«Друг моего врага – мой враг»  (интерпретируем, как      «+»× «-» = «-»)

«Враг моего друга  — мой враг»   (интерпретируем, как    «-»× «+» = «-»)

Кто готов может пойти к доске и написать

 

Презентация 4

Ученик: Хочется начать свое выступление со слов ученого кораблестроителя А.Н. Крылова: «Без теории нет практики, а без практики нет знаний!». А один из философов сказал: «Знание – это сила, чем больше ты имеешь знаний, тем меньше времени потребуется для достижения цели» Поэтому мы и создавали рабочую тетрадь, которая поможет оценить ваши знания

В данную тетрадь вошли задания тренировочного характера по темам: применение отрицательных чисел, координатная прямая и координатная плоскость, сравнение, сложение, вычитание, умножение и деление положительных и отрицательных чисел, решение уравнений. Мы вам предлагаем одно из заданий в игровой форме, так как считаем, что от игры к знаниям — один шаг.

Задание «ЦЕПОЧКА» (см приложение)  Листы с заданием лежат  на столе и на экране. Двигаясь по стрелкам, выполните действия. В результате ответ получается таким, как первое число.

Вывод: Гипотеза опровергнута. Отрицательные числа важны, значимы и необходимы.

Физкультминутка

«Здоровье – это не только отсутствие болезней, это полное физическое, душевное и социальное благополучие». Необходимо помнить всегда, что купить здоровье нельзя, его можно сохранить постоянной заботой о нем. Наша главная задача – беречь своё здоровье.

 

Вспомним:

Интерактивный тренажер

 

Учитель: Ребята, давайте подведем итоги нашей работы, подведите итоги в своих оценочных листах.

Итог урока

— Желаю вам цвести, расти,

Копить, крепить здоровье,

Оно для дальнего пути –

Главнейшее условье.

Пусть каждый день и каждый час

Вам новое добудет,

Пусть добрым будет ум у вас,

А сердце умным будет,

Вам от души желаю я

Друзья, всего хорошего,

А всё хорошее, друзья,

Дается нам недёшево.

С. Маршак

— Здоровья вам и успехов во всём.

Чему вы сегодня научились?  …

Помни всегда

Что без труда

В учебе побед не добиться

Домой.   Составить лото из 9 примеров. Решить их. Нарисовать картинку.

Написать в нужных квадратиках ответы. Разрезать картинку. Все сложить в конверт  .

Спасибо за урок.

Музыка

Рефлексия.

И уходя из класса я прошу вас оценить урок, прикрепив к доске «сердечко» — если урок вам понравился и вам все было понятно, «молнию» — если у вас остались какие-то вопросы и «круг» — если вам ничего не понравилось на уроке

 

— Спасибо всем за урок. Молодцы!

 

правила и примеры. Как образуется Present Perfect. Предложения в Present Perfect.

Понятие настоящего времени в английском языке не всегда совпадает с нашим. Одним из самых ярких примеров такого различия как раз является Present Perfect.

В этой статье мы разберемся, что такое Present Perfect, как оно образуется, в каких случаях употребляется, каким правилам подчиняется и закрепим знания на реальных примерах предложений с переводом.

Что такое Present Perfect Tense?

Present Perfect Tense (Present Perfect) — это настоящее совершенное время в английском языке. Оно обозначает действие, которое завершилось в настоящий момент времени.

В этом и состоит основная сложность времени Present Perfect для изучающих. В русском языке нет времени аналогичного Present Perfect. Для нас если что-то происходит сейчас — это и есть настоящее, а если совершилось — это уже прошлое.

Но не для англичан. Они воспринимают время немного по-другому. По логике носителей языка, действие вполне может закончиться и в настоящем или близко к настоящему моменту. Для выражения такой связи прошлого с настоящим и существует Present Perfect.

Из-за этих особенностей в понимании действий и времени — на русский язык Present Perfect обычно переводится глаголом в прошедшем времени.

I have already done my homework — Я уже сделал домашнее задание

В этом примере используется время Present Perfect (have done), потому что речь идет о том, что действие (работа над домашним заданием) закончилось совсем недавно.

Но на русский язык мы переводим предложение используя прошедшее время (уже сделал).

Как образуется Present Perfect?

Время Present Perfect образуется при помощи вспомогательного глагола have / has и Past Participle (третьей формы смыслового глагола: V3).

Вспомогательный глагол меняется в зависимости от подлежащего:

• I / You / We / They → have (для 1-го, 2-го лица и форм множественного числа)
• She / He / It → has (для 3-го лица единственного числа)

Завершает конструкцию времени Present Perfect смысловой глагол в третьей форме (V3).

Если смысловой глагол правильной формы — то его третья форма (V3) образуется при помощи окончания -ed.

Если смысловой глагол неправильный — то его третью форму (V3) берем из таблицы неправильных глаголов.

Например:

• to try → tried (пытаться) to cook → cooked (готовить) to finish → finished (заканчивать)
• to get → got (получать) to keep → kept (хранить) to see → seen (видеть)

Утверждение:

Утвердительное предложение в Present Perfect образуется при помощи вспомогательного глагола have / has и смыслового глагола с окончанием -ed для правильных глаголов или третьей формы неправильного глагола (V3) по формуле:

• I / You / We / They + have + Ved (V3)
• She / He / It + has + Ved (V3)

I have decided — Я решил

You have played — Ты играл

He has done — Он сделал

It has turned on — Оно включилось

В предложениях и повседневной речи часто можно встретить сокращенную форму вспомогательных глаголов have / has. Она образуется при помощи добавления к подлежащему ‘ve (для have) или ‘s (для has):

• I have = I’ve
• You have = You’ve
• We have = We’ve
• They have = They’ve

• She has = She’s
• He has = He’s
• It has = It’s

I’ve done my tasks — Я выполнил свои задачи

He’s washed the dishes — Он вымыл посуду

Отрицание:

Отрицательные предложения в Present Perfect образуется при помощи добавления частицы not после вспомогательного глагола have / has, но перед основным смысловым глаголом. Формула выглядит следующим образом:

• I / You / We / They + have not + Ved (V3)
• She / He / It + has not + Ved (V3)

I have not done my homework — Я не сделал домашнюю работу

They have not come — Они не пришли

She has not finished her tasks — Она не выполнила свои задачи

It has not turned on — Оно не включилось

В отрицании частицу not можно сократить путем присоединения ее к вспомогательному глаголу have / has:

• Have not = haven’t
• Has not = hasn’t

I haven’t washed my hair — Я не помыл волосы

She hasn’t been to London yet — Она еще не была в Лондоне

Вопрос:

Вопросительное предложение в Present Perfect образуется путем постановки вспомогательного глагола have / has в начало предложения. Формула будет такой:

• Have + I / You / We / They + Ved (V3)
• Has + She / He / It + Ved (V3)

Have I bought all the presents? — Я купил все подарки?

Have you finished the classes? — Ты закончил занятия?

Has she just arrived home? — Она только что приехала домой?

Has it turned on? — Оно включилось?

Специальные вопросы образуются при помощи question words (вопросительных слов). Таких, как when (когда), how (как), what (что), where (где) и других. Далее идет такой же порядок слов, как и в вопросе.

• QW + have + I / You / We / They + Ved (V3)
• QW + has + She / He / It + Ved (V3)

What has he just said? — Что он только что сказал?

How long have you knocked on the door? — Как давно ты стучал в дверь?

Когда употребляется Present Perfect?

А сейчас рассмотрим самые распространенные случаи употребления и использования времени Present Perfect в речи:

• Завершенное действие в настоящем

В таком случае акцент ставится на результат завершенного действия. Другими словами, когда результат действия виден в настоящем.

I have cooked a good dinner — Я приготовил хороший ужин (действие завершилось, результат — хороший ужин)

I know Nina. We have already met — Я знаю Нину. Мы уже встречались (встреча произошла в прошлом, но нас интересует результат в настоящем)

• Незавершенное действие в настоящем

Время Present Perfect используется в случае, когда мы описываем действие, которое началось в прошлом, еще не закончилось в настоящем, но результат очевиден.

I’ve written five pages of the new book this morning — Я написал пять страниц новой книги этим утром (утро еще не закончилось, он может написать еще несколько страниц)

She has finished watching “Harry Potter” this week — Она закончила смотреть «Гарри Поттера» на этой неделе (неделя еще идет, но она уже закончила смотреть фильм)

• Факт действия / личный опыт

Если говорящему важно подчеркнуть факт какого-то свершившегося события без точного указания времени — на помощь также приходит Present Perfect. Часто это время используется, когда мы говорим о своем прошлом опыте или же, спрашиваем об этом своего собеседника.

I have been to Bratislava — Я был (бывал) в Братиславе

В вопросе, когда мы интересуемся фактом из чьей-то жизни — используем также Present Perfect:

Have you ever been to France? — Ты когда-нибудь был (бывал) во Франции?

Маркеры времени Present Perfect

Present Perfect употребляется с неточными выражениями и словами, которые указывают на еще не закончившийся период времени

• never (никогда)
• ever (когда-либо)
• already (уже)
• yet (еще) / not yet (еще нет)
• often (часто)
• lately (в последнее время)
• just (только что)
• once (однажды)
• recently (недавно)
• before (раньше)
• today (сегодня)
• this week (на этой неделе)
• this year (в этом году)
• for an hour (в течение часа)
• for a long time (долгое время)
• since two o’clock – с двух часов
• ince December – с Декабря

Примеры предложений Present Perfect с переводом

Утвердительные:

I’ve studied English since my childhood — Я учил английский язык с детства

She has visited this beauty shop recently — Она недавно заходила в этот магазин косметики

People have walked on the Moon — Люди ходили по Луне.

We’ve just eaten, so we don’t want to go to the cafe — Мы только что поели, так что не хотим идти в кафе

I have just cut my finger — Я только что порезал свой палец

Отрицательные:

He has not returned from school yet — Он еще не вернулся из школы

I haven’t bought the new car. This is my old one — Я не купил новую машину. Это старая

Jane hasn’t been to Asia yet — Джейн еще не была в Азии

I have not been at university this week because of the flu — Я не был на этой неделе в университете из-за гриппа

I haven’t replaced the batteries in the doorbell — Я не заменил батарейки в дверном звонке

Вопросительные:

Have you seen this film about space? — Ты видел этот фильм о космосе?

Has Jimmy bought the tickets yet? — Джимми уже купил билеты?

How many deals has she made at the moment? — Сколько сделок она заключила на текущий момент?

How much coffee have you drunk today? — Сколько кофе ты сегодня выпил?

How long have you known Mary? — Как давно ты знаешь Мэри?

Позитив об отрицательных числах

Выпуск NRICH за январь 2008 г. был посвящен математической теме отрицательных чисел. Я чувствую, что «история», которую мы пытались рассказать, выбирая задачи начального уровня, заслуживает упоминания в этой статье, и, конечно же, я также добавлю несколько задач!

Прежде чем разрабатывать идеи на основе отрицательных чисел в классе, вам может быть полезно прочитать одну из статей, которые были опубликованы вместе с задачами в этом месяце. Он называется просто «Отрицательные числа» и представляет собой очень читаемый отчет о том, как отрицательные числа стали частью «лексикона» математиков. математики, на самом деле только относительно недавно.

Если мы посмотрим на Первичную структуру, то увидим, что отрицательные числа впервые упоминаются в одной из основных целей обучения Year $4$: «использовать положительные и отрицательные числа в контексте и расположить их на числовой прямой». Однако при разработке ресурсов для веб-сайта нам нужно было спросить себя, какими могут быть предварительные идеи. Это привело к серии игр, первые две для Key Stage $1$, которые предназначены для ознакомления детей с понятием счета по обе стороны от центральной точки. Вот первая из этих игр Incy Wincy Spider:

 

До этого момента игра побуждает детей двигаться по дорожке, считая в двух направлениях по обе стороны от начальной точки паука. Далее предлагается:

Далее попробуйте более интересную версию игры. На этот раз используйте два кубика. Когда наступает ваша очередь бросать, вы можете решить, какой номер кубика использовать. В этой игре вы должны приземлиться точно на конец водосточной трубы, чтобы победить.
Может быть, вы придумаете свою версию игры? Пожалуйста, присылайте свои идеи, и другие люди могут их попробовать.
Что делает вашу игру интересной?

Это делает игру более сложной задачей, так как теперь дети должны принимать решения относительно количества мест, которые лучше всего переместить, а не полагаться только на случай.

Игра Tug of War, также опубликованная в январе 2008 г., основана на игре Incey Wincey Spider, в которой вместо числовой дорожки введена числовая линия:

Лучше ли играть в игру, в которой нужно дойти до конца? точно, или где можно перейти через конец? Что вы думаете и почему?

Эта игра также специально связывает идеи сложения и вычитания с числовой линией с использованием словаря «плюс» и «минус». И снова игра предлагает внести некоторые изменения, позволяя детям складывать или вычитать два числа на костях. В этом случае мышление более высокого порядка требуется не только для принятия решений, но и для исследования всех возможности.

Прежде чем играть в третью игру серии с детьми, попробуйте пройти расследование «Бассейн», которое также взято с сайта за январь 2008 года.

Эта задача связана с той же идеей, что и в игре «Перетягивание каната», поскольку она требует, чтобы дети считали в разных направлениях на числовой прямой. Разница лишь в том, что в случае с плавательным бассейном линия вертикальная, а не горизонтальная. Заключительная часть занятия побуждает детей проявлять творческий подход и изобретать собственный способ нумерации ступеней ниже уровня воды. Это, несомненно, предложить несколько интересных моментов для обсуждения всем классом. Вы можете поделиться со всеми некоторыми из их способов, попросив соответствующих детей объяснить, почему, по их мнению, их способ работает хорошо. Могут возникнуть споры о том, какие способы могут работать лучше всего.

На этом этапе можно специально ввести отрицательные числа, если они еще не появились, например, на вертикальной шкале термометра. Было бы здорово иметь термометр под рукой, и тогда вы могли бы вместе посмотреть на отрицательные части шкалы, обсудив, что они означают. Затем вы можете перенести эту шкалу отрицательных чисел в бассейн.

Последняя игра в серии, продолжающая Incey Wincey Spider и Tug of War, называется Tug Harder!. Это хорошо следует из расследования плавательного бассейна, поскольку в нем явно используются отрицательные числа:

В версию, показанную на изображении, играют точно так же, как в перетягивание каната, но на этот раз используется расширенная числовая линия, чтобы дети были более довольны соотношением между положительными и отрицательными числами. Вторая версия снова поднимает игру на более высокий уровень, поскольку на этот раз учеников просят использовать любую операцию для манипулирования числами на костях, чтобы они могли принимать решения как какой расчет выполнять и почему.

Те же самые навыки необходимы в еще одной игре на январском веб-сайте First Connect Three. В этой игре побеждает тот, кто первым завершит ряд из трех по горизонтали, вертикали или диагонали. Игроки по очереди бросают кубики, помещают каждый кубик в один из квадратов и решают, следует ли добавить или вычесть, чтобы получить сумму, показанную на доске. Итого будет покрыто счетчиком.

Эта игра — отличный способ для самих учеников взять на себя ответственность за собственное обучение. Человек может избегать отрицательных чисел, если не уверен, или он может заставить себя вычислить отрицательные ответы. При более полном анализе игры, а не просто игре, идея состоит в том, чтобы дети разработали систему для поиска всех возможных способов составления каждого числа на сетке, чтобы они могли обосновать, что легче всего получить. Затем это приведет к обсуждению того, как это повлияет на то, как вы играете в игру, чтобы выиграть.

Учительница, с которой я работала в Харинги, Лондон, рассказала мне, как она использовала эту игру в своем плохо успеваемом классе $5$. Она начала с того, что играла с собой против компьютера, проговаривая вслух свои мыслительные процессы. Используя числовую линию, которую она имеет в качестве постоянной функции в своем классе (которая простирается назад за ноль), она рассмотрела возможности для каждого броска, считая вперед или назад по строке в зависимости от того, прибавляла она или убавляла. Когда в результате получалось отрицательное число, дети воспринимали это спокойно, так как понимали происходящие процессы. Это означало, что, когда они начали играть друг против друга в парах и начали думать о задействованных стратегиях, расчеты стали простыми, поскольку они тоже использовали число. линия.

К тому времени, когда они переходят в год $6$, Framework предполагает, что дети также должны уметь «находить разницу между… двумя отрицательными целыми числами в контексте». Контекст плавательного бассейна можно легко использовать в качестве основы для изучения этого, как и уровень моря, последний из ресурсов января 2008 г. на первичном уровне. уровень. Используя изображения в этих задачах, сложная концепция становится очень управляемой. Я также призываю вас взглянуть на ресурсы Key Stage $3$, опубликованные в январе 2008 года, которые могут помочь вам увидеть, куда дальше пойдут отрицательные числа!

Я надеюсь, что в какой бы группе вы ни преподавали, вам и вашему классу понравятся эти ресурсы с отрицательными числами. Помните, что вы также можете искать другие актуальные проблемы, используя «Поиск по теме» в правом углу веб-сайта.

Ссылки
DfES (2006) Primary Framework for Literacy and Mathematics

Эта статья впервые была опубликована в журнале Primary Mathematics, издаваемом The Mathematical Association .

 

Положительные и отрицательные числа | МатЧат

Сообщения с тегами ‘Положительные и отрицательные числа’

Ошибка алгебры № 5: Как объединить положительное и отрицательное число без путаницы

Итак, вы могли бы подумать, что комбинирование положительного числа и отрицательного числа будет довольно простой задачей , хм?

К сожалению, многие студенты думают, что это просто. Они думают, что это слишком просто. Они думают, что есть одно простое правило, которое приводит их каждый раз к одному и тому же ответу. И именно здесь они попадают в беду.

Дело в том, что объединение положительного и отрицательного числа — довольно сложная операция, и знак ответа зависит от ряда факторов.

В этом видео показана распространенная ошибка учащихся при решении этих задач. он также показывает правильный подход к этим проблемам, используя аналогию с наличием денег и должником денег, чтобы все имело смысл.

Итак, взгляните и убедитесь, что это объяснение не положит конец путанице раз и навсегда.

И не забывайте: в конце видео есть практические задачи. Сделайте это, чтобы убедиться, что вы поняли концепцию.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Like this:

Like Loading. ..

Category:

Алгебра, Ошибки в алгебре, Порядок действий, Положительные и отрицательные числа, Предварительная алгебра, Без категорий

Ошибка в алгебре № 4: как складывать отрицательные числа без путаницы

Вот распространенная ошибка, и к тому же очень понятная. Студентам нужно объединить два отрицательных числа, и они, конечно же, получат положительный ответ. Почему? Потому что они скажут — указывая на то, что вы сами им это сказали — «Два минуса дают плюс!»

Это видео раскрывает корень этого распространенного заблуждения, помогая учащимся точно понять , когда два отрицательных числа дают положительный результат, а когда они не дают .

 

Обязательно просмотрите видео до конца, так как в конце есть практические задания и ответы на них.

НИЗКА Числа, Правила, Упрощение выражений, Без категорий, Использование историй, чтобы сделать математику понятной

Осмысление неравенства

Хорошо, учителя, родители и воспитатели… поднимите руку, если вы когда-нибудь чувствовали себя некомфортно, когда ученики изображали  этот вопрос о неравенстве?

Этот вопрос звучит так: почему мы переворачиваем символ неравенства, когда умножаем или делим на отрицательное число?

Мне пришлось бы смущенно поднять руку.

Итак, когда на прошлой неделе мне снова задали этот вопрос, я решил разобраться и дать ответ, который помог бы студентам понять этот момент.

Я пришел к выводу, что проще всего объяснить это с помощью комбинации примеров и логики. Во-первых, примеры.

Разобьем ситуацию на три случая. У нас могут быть неравенства, в которых числа на двух сторонах A) оба положительные, B) оба отрицательные, или C) одно число положительное, другое отрицательное.

Начнем со случая А. Предположим, мы начнем с утверждения 2 < 4

Теперь умножим обе части на положительное число (давайте возьмем 3), и мы получим: 6 < 12. Все еще верно, верно?

Но возьмем исходное неравенство и умножим его на отрицательное число (возьмем – 3), и получим: – 6 < – 12. Неправда, да? Но если мы перевернем знак, то получим истинное утверждение: – 6 > – 12

Случай B. Теперь давайте начнем с двух отрицательных чисел в нашем истинном неравенстве: – 4 < – 2 Если мы умножим обе части на положительное число (снова 3), получаем:  – 12 < – 6, что опять верно.

Но если мы умножим это неравенство на отрицательное число (снова – 3), то получим: 12 < 6, что заведомо неверно. Однако если мы еще раз перевернем знак, то получим истинное утверждение: 12 > 6,9.0003

Наконец, случай C. Теперь начнем с неравенства, которое имеет как положительное, так и отрицательное число:  – 2 < 4. Если мы умножим обе части на  положительное 3, мы получим:  – 6 < 12, что по-прежнему верно.

Но если мы снова умножим обе части на – 3, мы получим:  6 < – 12, что снова неверно. И снова нам нужно перевернуть знак, чтобы он стал верным:  6 > – 12.

Пока все хорошо, но этому не хватает логики объяснения. Как мы можем внести немного логики и рассуждений, чтобы помочь учащимся понять, почему все это происходит?

Вот мой — само собой разумеющийся, неофициальный — способ объяснить это. Когда мы умножаем или делим число на положительные числа, мы не меняем его знак; если число было положительным, оно остается положительным, а если оно было отрицательным, оно остается отрицательным. Но когда мы умножаем или делим число на отрицательное число, мы меняем его знак… либо с положительного на отрицательный, либо с отрицательного на положительный.

Итак, причина, по которой мы переворачиваем символ неравенства, должна быть связана с тем, что — умножая или деля обе части неравенства на отрицательное число — мы меняем знаки обоих чисел в неравенстве. Но как именно это работает?

Ответ, как оказалось, коренится в соотношении между абсолютным значением чисел и их относительными размерами. Для положительных чисел есть один способ определить, какое число больше… число с большим абсолютным значением и есть большее число. Например, сравнивая 4 и 12, мы знаем, что 12 больше 4, потому что абсолютное значение 12 больше, чем абсолютное значение 4. Но для отрицательных чисел верно прямо противоположное. Для двух отрицательных чисел число с большим абсолютным значением на самом деле является меньшим числом. Например, сравните – 4 и – 12. Их абсолютные значения равны 4 и 12 соответственно, но число с большим абсолютным значением на самом деле является меньшим, а не большим числом. В этом примере – 12 (с большим абсолютным значением 12) на самом деле меньше, чем – 4 (с меньшим абсолютным значением 4).

Итак, здесь следует помнить, что существуют два разных отношения между абсолютными значениями чисел и относительными размерами чисел. Для положительных чисел чем больше абсолютное значение, тем больше число. Но для отрицательных чисел чем больше абсолютное значение, тем меньше число.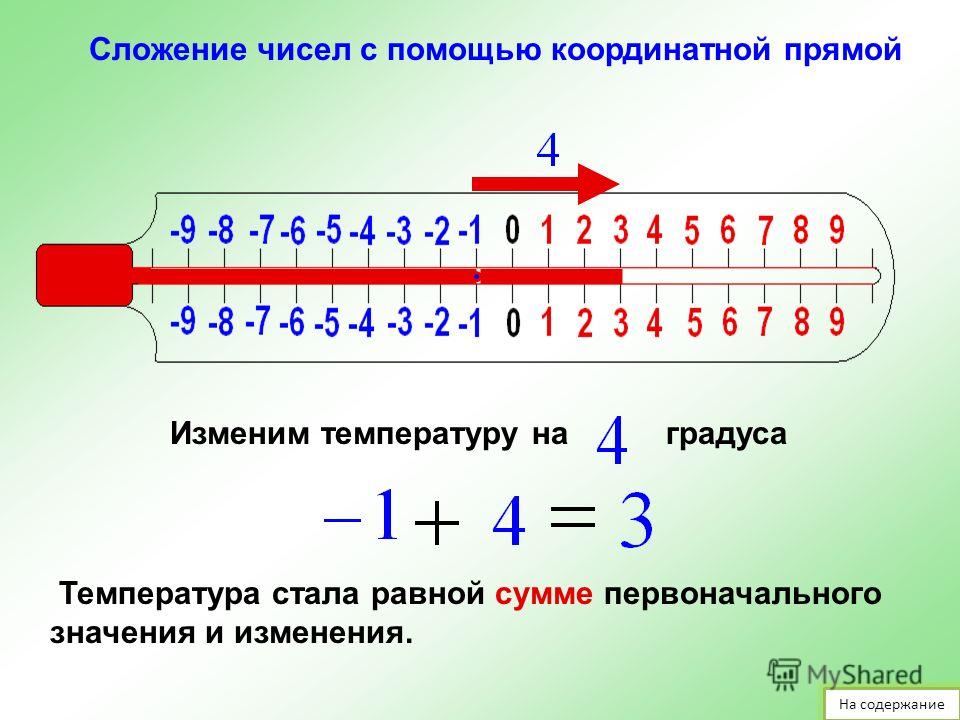

Этот факт влияет на неравенства, в которых мы меняем знаки чисел. До изменения знаков чисел числа в двух частях неравенства имели одно соотношение размера; одно число было больше другого (скажем, число А на данном этапе больше числа Б). Но когда мы умножаем или делим оба этих числа на минус, мы меняем знаки обоих чисел. И, перевернув знаки обоих чисел, мы изменим отношение размера чисел друг к другу. То, что было больше, становится меньше, и наоборот. Таким образом, в нашем абстрактном примере, если число A было больше числа B до изменения их знаков, после изменения обоих знаков число A будет меньше числа B.

Джош Раппапорт является автором пяти книг по математике, в том числе отмеченного наградой Parents Choice «Руководства по выживанию в алгебре». Если вам нравится, как Джош объясняет эти проблемы, вам наверняка понравятся «Руководство по выживанию по алгебре» и сопутствующая рабочая тетрадь, которые доступны на Amazon.com. Просто щелкните ссылки на боковой панели, чтобы получить дополнительную информацию!

Нравится:

Нравится Загрузка. ..

Как быстро и просто совмещать положительные и отрицательные числа

Если вы или кто-то из ваших знакомых затрудняется совмещать числа с противоположными знаками — одно положительное, другое отрицательное — этот пост для вас!

Для ясности, я имею в виду такие проблемы:

 – 2 + 7 [первое число отрицательное, второе число положительное] или

+ 13 – 20  [первое число положительное, второе число отрицательное ]

Чтобы найти ответы, превратите каждую задачу в математическую историю. В таком случае превратите его в историю о перетягивании каната. Вот как.

В первой задаче – 2 + 7 рассмотрите – 2 как означающее, что в «отрицательной» команде 2 человека; аналогично, рассмотрите + 7 как означающее, что в «положительной» команде 7 человек.

В этой математической истории нужно помнить всего три вещи:

1) Каждый «человек», участвующий в перетягивании каната, одинаково силен.

2) Всегда побеждает команда, в которой больше людей; команда с меньшим количеством людей всегда проигрывает.

3)  В рассказе мы выясняем, на сколько человек команда-победитель «превосходит» другую команду. Это просто; это просто означает, насколько больше людей в этой команде, чем в другой команде. Пример: если отрицательная команда состоит из 2 человек, а положительная команда состоит из 7 человек, мы говорим, что положительная команда «численно превосходит» отрицательную команду на 5 человек, поскольку 7 на 5 больше, чем на 2.

Теперь, чтобы упростить такую ​​задачу, просто ответьте на три простых вопроса:

1) Сколько человек в каждой команде?
В нашей первой задаче – 2 + 7 есть 2 человека в отрицательной команде и 7 человек в положительной команде.

2) Какая команда ВЫИГРЫВАЕТ ?
Поскольку в положительной команде больше людей, побеждает положительная команда .

3) На сколько человек выигрывает команда OUTNUMBER проигравшая команда?
Так как у положительных 7, а у отрицательных только 2, положительные числа превосходят отрицательные на 5 .

Теперь проигнорируйте ответ на вводный вопрос, вопрос 1, но сопоставьте свои ответы на вопросы 2 и 3. + 5

В целом это говорит нам о том, что:   – 2 + 7 = + 5

Для тех из вас, кто рвал на себе волосы из-за таких проблем, у меня есть хорошие новости…

… ОНИ ДЕЙСТВИТЕЛЬНО ЭТО ПРОСТО!

Но поверить в это поможет решение еще одной задачи:   + 13 – 20.

Вот, опять же, вопросы здравого смысла и ответы на них.

1) Сколько человек в каждой команде?
В этой задаче + 13 – 20 13 человек входят в положительную команду и 20 человек – в отрицательную.

2) Какая команда ВЫИГРЫВАЕТ ?
Поскольку в этой задаче больше людей в отрицательной команде, отрицательная команда побеждает.

3) На сколько человек выигрывает команда  OUTNUMBER  проигравшая команда?
Поскольку негативов 20, а позитивов только 13, негативов больше, чем позитивов на 7 .

Так же, как и в первой задаче, сложите вместе ответы на вопросы 2 и 3.

ОТВЕТ НА ВОПРОС 2:   —

Ответ на вопрос 3: 7

Ответы вместе: — 7

Всего всего, это говорит нам, что: + 13 — 20 = — 7

для практики:

а) – 3 + 9

б) + 1 – 4

в) – 9 + 23

г) – 37 + 19

д) + 49 – 3

Ответ на практику Задачи:

а) – 3 + 9 = + 6

б) + 1 – 4 = – 3

c) – 9 + 23 = + 14

d) – 37 + 19 = – 18

e) + 49 – 82 = – 33

Джош Раппапорт – автор пяти книг по математике, в том числе Руководство по выживанию по алгебре, удостоенное награды Parents Choice. Если вам нравится, как Джош объясняет эти проблемы, вам, скорее всего, понравятся Руководство по выживанию по алгебре и сопутствующая рабочая тетрадь, которые доступны на Amazon.com. Просто щелкните ссылки на боковой панели, чтобы получить дополнительную информацию!

Вот так:

Нравится Загрузка. ..

Категория:

Руководство по выживанию в алгебре, ЗАБАВНАЯ ПРОБЛЕМА, Премия «Золотое крыльцо», Развлечение по математике, Математические рассказы, Математические теории, Чувство чисел, Теория чисел, Предложение меню опций, Предложение Разнообразие подходов, Порядок операций, Положительные и отрицательные числа, Практические задачи, Предварительная алгебра, Вычитание, Репетиторство, Без категорий

Вычитание целых чисел

Читательница по имени Мишель сказала, что ей понравился мой пост о запоминании таблиц умножения. А потом она спросила, есть ли у меня какие-нибудь советы по обучению студентов ВЫЧИТАТЬ ЦЕЛЫЕ.

Получается, что ответ «да», и есть два места, где я моделирую эту тему.

Первый — это отрывок из моего «Руководства по выживанию в алгебре», отрывок о вычитании целых чисел, с которым вы можете ознакомиться прямо сейчас.

Сначала нажмите на эту ссылку, затем прокрутите вниз, чтобы прочитать страницы 43-46 (вы можете увеличить размер печати, увеличив процентное значение, указанное в верхней строке):

http://www. singingturtle.com/downloads/ASG %20sample%20chapter.pdf

Но это еще не все:

Я написал целую книгу на тему комбинирования целых чисел PreAlgebra Blastoff! Мы создали манипуляторы пены, чтобы передать идею целых чисел. Есть кусок пенопласта с отверстием в центре, НЕГАТон, который означает – 1. Есть кусок, который заполняет отверстие, ПОЗИТон, и этот манипулятор означает + 1. Когда вы помещаете ПОЗИТон внутрь НЕГАТона, вы получаете 0, и это часть называется ZERObi.

Используя эти манипуляторы, вы можете смоделировать и научить учащихся складывать целые числа, а также складывать и вычитать целые числа.

Чтобы узнать больше об этой системе и посмотреть, как работают манипуляторы, перейдите на этот веб-сайт:

http://www.singingturtle.com/pages/ADMINISTRATORS3.html

Дайте мне знать, если у вас есть какие-либо вопросы по этому поводу. тема. Это, безусловно, важный вопрос.

Счастливого обучения!

— Джош

Нравится:

Нравится Загрузка. ..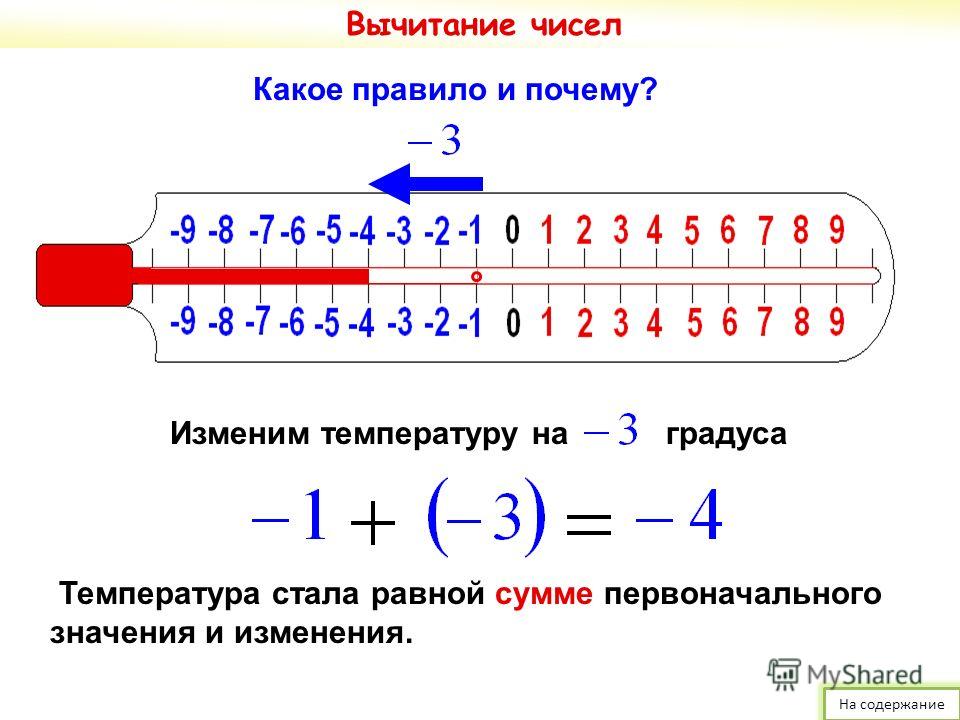

Категория:

Алгебра, целые числа, порядок операций, S-алгебры S-S, положительные и отрицательные0003

Превратите объединение целых чисел в увлекательную рассказ

Кто сказал, что нельзя развлекаться с целыми числами?

В течение нескольких лет я использовал забавную историю, чтобы объяснить концепцию объединения целых чисел с разными знаками. Раньше мне было трудно донести эту концепцию до некоторых детей, но теперь, благодаря этой истории, практически нет никого, кто не мог бы понять эту концепцию, когда ее преподают таким образом.

Я хотел бы поделиться им с вами сейчас, чтобы вы тоже могли им пользоваться.

Впервые идея была представлена ​​на с. 41 моего Руководства по выживанию по алгебре вместе с карикатурной картинкой. Основная идея заключается в том, что вы можете рассматривать такие задачи, как: – 3 + 9, + 6 – 14, – 9 + 4 и т. д., как перетягивание каната.

Ситуация такая — есть две команды, позитивная и негативная. Чтобы увидеть проблему такого рода как созданную двумя командами, вы должны взглянуть на нее определенным образом, способом, который может быть новым для некоторых из вас. Возьмем такую ​​задачу, как – 3 + 9. Вы НЕ рассматриваете это как «минус 3 плюс 9».». Скорее, вы смотрите на него как на две части: часть а – 3 и часть + 9. [Во всяком случае, это всегда имело для меня больше смысла.]

Итак… часть «– 3» говорит нам, что три человека тянут отрицательную команду, в то время как часть «+ 9» говорит нам, что девять человек тянут отрицательную команду. позитивный коллектив.

Во избежание ложных предположений скажите учащимся, что все тянущие люди одинаково сильны. Другими словами, было бы невозможно, например, для 3 из отрицательной команды победить 4 из положительной команды. Та команда, у которой больше людей, должна победить. [Я расскажу о ситуации с равным количеством людей в обеих командах в конце этой записи.]

Затем скажите учащимся, что им нужно задать и ответить всего на два простых вопроса, чтобы найти ответ:

Q#1:  Какая команда победит? [В – 3 + 9 выигрывают положительные игроки, потому что у них больше людей. ]

Вопрос № 2:  На сколько человек команда-победитель превосходит по численности команду проигравших? [В – 3 + 9 количество положительных ответов превышает число отрицательных на 6, поскольку у них 9 тяг по сравнению с отрицательными, у которых всего 3 тяги.]

Когда учащиеся складывают свои ответы вместе, они получают ответ на задачу:  + 6. Удивительно просто, да? Все, что для этого нужно, — это смотреть на вещи по-новому.

Я составил небольшой шаблон, который вы можете воспроизвести и использовать для обучения этому правилу таким образом.

Далее следует пример, который шаг за шагом показывает, как учащиеся будут вводить данные, которые приведут их к правильному ответу.

Сначала мы покажем это для задачи:    – 6 + 2

Пустой шаблон:

Затем учащиеся вводят задачу – 6 + 2 и пишут, сколько человек в каждой команде, например:

 

Следующие учащиеся делают галочки, чтобы показать количество людей, тянущих за каждую команду, 6 баллов на стороне Отрицательной команды; 2 балла за Положительную команду:

 

Следующие учащиеся отвечают на два вопроса прямо в шаблоне.

Наконец, учащиеся записывают ответ, исходя из ответов на вопросы.

 

Вот еще одна модель того, как учащиеся будут использовать шаблон, на этот раз для задачи, ответ на которую положительный:  – 4 + 9

 

 

 

Вот и все. Если вы найдете кого-то, кто не может научиться этому таким образом, дайте мне знать. Я буду поражен.

Я предлагаю использовать шаблон в течение нескольких дней, а затем, как только учащиеся освоятся с идеей, позволить им отказаться от шаблона. Приятно то, что даже после того, как они отойдут от шаблона, если они получат неправильный ответ, на самом деле неправильный ответ, например: – 3 + 5 = – 8, вы можете попросить их обдумать это как перетягивание каната. -война, и они практически всегда будут делать это правильно в этот момент. Круто, да?

В случае, когда в положительной и отрицательной командах одинаковое количество людей, ответ будет нулевым. Пример:  – 4 + 4 = 0.  В терминах перетягивания каната можно сказать, что это ситуация, когда ни одна из команд не побеждает, и это заканчивается ничьей. Таким образом, ничья в реальном мире немного похожа на 0 в математическом мире.

Не стесняйтесь оставлять комментарии в блоге о том, насколько хорошо это работает для вас в вашем обучении.

И, наконец, если у вас еще нет моего «Руководства по выживанию по алгебре», оно наполнено аналогиями и метафорами, такими же, как это. Учителя, родители, домашние школьники пользуются этой книгой и пользуются ею.

СКИДКА 50% Распродажа Руководства по алгебре и рабочей тетради на моем веб-сайте: SingingTurtle.com

 

 

Вы также можете приобрести руководство и рабочую тетрадь на Amazon.com

Вы сможете загрузить пример главы, которая включает в себя концепции, изложенные в этом сообщении, на SingingTurtle.com или Amazon.com

Вы обнаружите, что «Руководство по выживанию в алгебре» имеет 173 отзыва покупателей на Amazon с рейтингом 4,5 звезды!

Счастливого обучения!

-Josh

Например:

, как нагрузка . ..

Категория:

Алгебра, целые числа, математические методы математической инструкции, положительные и отрицательные числа, предварительно-альгебра, необъектива, математика , Использование STORIES

Ошибки в алгебре из-за отрицательных знаков? Используйте ЦВЕТ, чтобы ОБЪЯСНИТЬ.

Вы когда-нибудь замечали, с каким трудом ученики выясняют разницу между этими двумя типами выражений:

Я обнаружил, что ключевым моментом является использование порядка действий для расшифровки значения каждого выражения.

Попросите учащихся подумать, сколько шагов порядка действий содержится в каждом выражении.

Если они на правильном пути, то увидят, что в верхнем выражении всего одна операция: вычисление показателя степени путем двукратного умножения (– 3) на себя. Это выглядит так:

Что касается нижнего выражения, то это сложнее из-за того «свободного» отрицательного знака, отрицательного знака, который не заключен в круглые скобки. Точно так же, как «свободный канон» может быть опасен в армии, «свободный» отрицательный знак может вызвать проблемы на игровом поле алгебры. Студенты будут делать всевозможные странные ошибки, пытаясь понять, что делать с этим маленьким шалопаем.

Но если вы предложите учащимся рассматривать этот «свободный» отрицательный знак как значение (– 1), умноженное на следующее за ним выражение, они могут снова использовать порядок действий, чтобы сначала сделать правильно.

В частности, они замечают, что необходимо выполнить две операции: умножение и возведение в степень, и помнят, что они выполняют операции в степени перед умножением, следуя порядку операций.

После этих шагов упрощение выглядит следующим образом:

И хотя это прекрасно и правильно, обратите внимание, что вы можете «поднять его на ступеньку выше», используя цвет для разделения двух операций. Я использую синий цвет для расшифровки отрицательного знака и его обработки; Я использую красный для термина 3 в квадрате.