Курс высшей математики, Т.1
Курс высшей математики, Т.1
ОглавлениеПРЕДИСЛОВИЕ К ВОСЬМОМУ ИЗДАНИЮГЛАВА I. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ 1. Величина и ее измерение. 2. Число.  3. Величины постоянные и переменные. 4. Промежуток. 5. Понятие о функции. 6. Аналитический способ задания функциональной зависимости. 7. Неявные функции. 8. Табличный способ. 9. Графический способ изображения чисел. 10. Координаты. 11. График и уравнение кривой. 12. Линейная функция. 13. Приращение. Основное свойство линейной функции. 14. График равномерного движения. 15. Эмпирические формулы. 16. Парабола второй степени. 17. Парабола третьей степени. 18. Закон обратной пропорциональности. 19. Степенная функция. 20. Обратные функции. 21. Многозначность функции. 22. Показательная и логарифмическая функции. 23. Тригонометрические функции. 24. Обратные тригонометрические, или круговые, функции. § 2. ТЕОРИЯ ПРЕДЕЛОВ. НЕПРЕРЫВНЫЕ ФУНКЦИИ 25. Упорядоченное переменное. 26. Величины бесконечно малые. 27. Предел переменной величины. 28. Основные теоремы. 29. Величины бесконечно большие.  30. Монотонные переменные. 31. Признак Коши существования предела. 32. Одновременное изменение двух переменных величин, связанных функциональной зависимостью. 33. Примеры. 34. Непрерывность функции. 35. Свойства непрерывных функций. 36. Сравнение бесконечно малых и бесконечно больших величин. 37. Примеры. 38. Число е. 39. Недоказанные предложения. 40. Вещественные числа. 41. Действия над вещественными числами. 42. Точные границы числовых множеств. Признаки существования предела. 43. Свойства непрерывных функций. 44. Непрерывность элементарных функций. ГЛАВА II. ПОНЯТИЕ О ПРОИЗВОДНОЙ И ЕГО ПРИЛОЖЕНИЯ 45. Понятие о производной. 46. Геометрическое значение производной. 47. Производные простейших функций. 48. Производные сложных и обратных функций. 49. Таблица производных и примеры. 50. Понятие о дифференциале. 52. Оценка погрешностей. § 4. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ 53.  Производные высших порядков.54. Механическое значение второй производной. 55. Дифференциалы высших порядков. 56. Разности функций. § 5. ПРИЛОЖЕНИЕ ПОНЯТИЯ О ПРОИЗВОДНОЙ К ИЗУЧЕНИЮ ФУНКЦИЙ 57. Признаки возрастания и убывания функций. 58. Максимумы и минимумы функций. 59. Построение графиков. 60. Наибольшее и наименьшее значения функций. 61. Теорема Ферма. 62. Теорема Ролля. 63. Формула Лагранжа. 64. Формула Коши. 65. Раскрытие неопределенностей. 66. Различные виды неопределенностей. § 6. ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ 68. Частные производные и полный дифференциал функции двух независимых переменных. 69. Производные сложных и неявных функций. § 7. НЕКОТОРЫЕ ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ПОНЯТИЯ О ПРОИЗВОДНЫХ 70. Дифференциал дуги. 71. Выпуклость, вогнутость и кривизна. 72. Асимптоты. 73. Построение графиков. 74. Параметрическое задание кривой. 75. Уравнение Ван-дер-Ваальса. 76. Особые точки кривых. 77.  Элементы кривой.78. Цепная линия. 79. Циклоида. 80. Эпициклоиды и гипоциклоиды. 81. Развертка круга. 82. Кривые в полярных координатах. 83. Спирали. 85. Овалы Кассини и лемниската. ГЛАВА III. ПОНЯТИЕ ОБ ИНТЕГРАЛЕ И ЕГО ПРИЛОЖЕНИЯ 86. Понятие о неопределенном интеграле. 87. Определенный интеграл как предел суммы. 88. Связь определенного и неопределенного интегралов. 89. Свойства неопределенного интеграла. 90. Таблица простейших интегралов. 91. Правило интегрирования по частям. 92. Правило замены переменных. Примеры. 93. Примеры дифференциальных уравнений первого порядка. § 9. СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА 94. Основные свойства определенного интеграла. 96. Существование первообразной функции. 97. Разрыв подынтегральной функции. 98. Бесконечные пределы. 99. Замена переменной под знаком определенного интеграла. 100. Интегрирование по частям. § 10. ПРИЛОЖЕНИЯ ПОНЯТИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ 101.  Вычисление площадей.102. Площадь сектора. 103. Длина дуги. 104. Вычисление объемов тел по их поперечным сечениям. 105. Объем тела вращения. 106. Поверхность тела вращения. 107. Определение центров тяжести. Теоремы Гульдина. 108. Приближенное вычисление определенных интегралов; формулы прямоугольников и трапеций. 109. Формула касательных и формула Понселе. 110. Формула Симпсона. 111. Вычисление определенного интеграла с переменным верхним пределом. 112. Графические способы. 113. Площади быстро колеблющихся кривых. § 11. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ 115. Разбиение промежутка на части и образование различных сумм. 116. Интегрируемые функции. 117. Свойства интегрируемых функций. ГЛАВА IV. РЯДЫ И ИХ ПРИЛОЖЕНИЯ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ 118. Понятие о бесконечном ряде. 119. Основные свойства бесконечных рядов. 120. Ряды с положительными членами. Признаки сходимости. 121. Признаки Коши и Даламбера.  122. Интегральный признак сходимости Коши. 123. Знакопеременные ряды. 124. Абсолютно сходящиеся ряды. 125. Общий признак сходимости. § 13. ФОРМУЛА ТЕЙЛОРА И ЕЕ ПРИЛОЖЕНИЯ 126. Формула Тейлора. 127. Различные виды формулы Тейлора. 128. Ряды Тейлора и Маклорена. 129. Разложение exp(x). 130. Разложение sin x и cos x. 131. Бином Ньютона. 132. Разложение log(1+x). 134. Приближенные формулы. 135. Максимумы, минимумы и точки перегиба. 136. Раскрытие неопределенностей. § 14. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ РЯДОВ 137. Свойства абсолютно сходящихся рядов. 138. Умножение абсолютно сходящихся рядов. 139. Признак Куммера. 140. Признак Гаусса. 141. Гипергеометрический ряд. 142. Двойные ряды. 143. Ряды с переменными членами. Равномерно сходящиеся ряды. 144. Равномерно сходящиеся последовательности функций. 145. Свойства равномерно сходящихся последовательностей. 146. Свойства равномерно сходящихся рядов.  147. Признаки равномерной сходимости. 148. Степенные ряды. Радиус сходимости. 149. Вторая теорема Абеля. 150. Дифференцирование и интегрирование степенного ряда. ГЛАВА V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ § 15. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ФУНКЦИИ 152. О предельном переходе. 153. Частные производные и полный дифференциал первого порядка. 154. Однородные функции. 155. Частные производные высших порядков. 156. Дифференциалы высших порядков. 157. Неявные функции. 158. Пример. 159. Существование неявных функций. 160. Кривые в пространстве и поверхности. § 16. ФОРМУЛА ТЕЙЛОРА. МАКСИМУМЫ И МИНИМУМЫ ФУНКЦИИ ОТ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ 161. Распространение формулы Тейлора на случай функции от нескольких независимых переменных. 162. Необходимые условия максимума и минимума функции. 163. Исследование максимума и минимума функции двух независимых переменных. 164. Примеры. 165. Дополнительные замечания о нахождении максимумов и минимумов функции.  166. Наибольшее и наименьшее значения функции. 168. Дополнительные замечания. 169. Примеры. ГЛАВА VI. КОМПЛЕКСНЫЕ ЧИСЛА, НАЧАЛА ВЫСШЕЙ АЛГЕБРЫ И ИНТЕГРИРОВАНИЕ ФУНКЦИЙ 170. Комплексные числа. 171. Сложение и вычитание комплексных чисел. 172. Умножение комплексных чисел. 173. Деление комплексных чисел. 174. Возвышение в степень. 175. Извлечение корня. 176. Показательная функция. 177. Тригонометрические и гиперболические функции. 178. Цепная линия. 179. Логарифмирование. 180. Синусоидальные величины и векторные диаграммы. 181. Примеры. 182. Кривые в комплексной форме. 183. Представление гармонического колебания в комплексной форме. § 18. ОСНОВНЫЕ СВОЙСТВА ЦЕЛЫХ МНОГОЧЛЕНОВ И ВЫЧИСЛЕНИЕ ИХ КОРНЕЙ 185. Разложение многочлена на множители. 186. Кратные корни. 187. Правило Горнера. 188. Общий наибольший делитель. 189. Вещественные многочлены. 190. Зависимость между корнями уравнения и его коэффициентами.  2 |
Объяснение урока: Графическое построение факторизованных кубических функций
В этом объяснении мы узнаем, как строить графики кубических функций, записанных в факторизованной форме, и определять, где они пересекают оси.
Кубическая функция имеет вид 𝑓(𝑥)=𝑎𝑥+𝑏𝑥+𝑐𝑥+𝑑, где 𝑏, 𝑐 и 𝑑 — действительные числа, а 𝑎 — ненулевое. Чтобы чтобы нарисовать график 𝑦=𝑓(𝑥), мы сначала вспомним, что координаты любой точки на графике эта кривая будет иметь координаты в виде (𝑥,𝑓(𝑥)). Другими словами, 𝑥-координата сообщает нам входное значение функции, а 𝑦-координата сообщает нам соответствующий вывод.
Начертить график кубических функций вообще сложно, так как они могут иметь разную форму. Например, рассмотрим следующие графики 𝑦=𝑥 и 𝑦=−𝑥.
Эти графики имеют подобную форму; однако на первом графике по мере увеличения значений 𝑥 выходы
функция неограниченно возрастает, поэтому кривая продолжает расти вверх.
Описание кривой как неограниченное увеличение (или уменьшение) значений 𝑥 называется конечным поведением графиков. Иногда мы называем это приближением 𝑥 к положительной (или отрицательной) бесконечности. Поэтому, глядя на график 𝑦=𝑥, мы можем сказать, что по мере того, как значения 𝑥 приближаются к бесконечности, выходы также стремятся к бесконечности. Однако, когда значения 𝑥 приближаются к отрицательной бесконечности, выходы также приблизиться к отрицательной бесконечности.
Это не единственное различие, которое мы можем найти в формах различных кубических функций. Рассмотрим следующий график 𝑦=𝑥(𝑥+1)(𝑥+2).
Конечное поведение этого графа такое же, как у 𝑦=𝑥; однако форма другая. Мы видим, что там являются тремя различными 𝑥-перехватами, и кривая поворачивается дважды.
Мы можем найти координаты 𝑥-перехватов, заметив, что 𝑦-координаты этих
точки должны быть равны 0.
Следовательно, функция выводит 0 в этих точках; они являются корнями функции.
В общем случае нахождение 𝑥-пересечений кубического графа означает решение соответствующего уравнения для нахождения корни, что мы еще не рассмотрели. Однако в случае факторизованных кубических уравнений мы можем определить корни факторизованного полинома, заметив, что для того, чтобы произведение было равно 0, один из множителей должен быть равен 0. Например, корнями кубического 𝑥(𝑥+1)(𝑥+2) будут решения уравнения 𝑥(𝑥+1)(𝑥+2)=0.
Мы видим, что либо 𝑥=0, либо 𝑥+1=0, либо 𝑥+2=0. Решение каждого уравнения дает нам 𝑥=−2, −1 или 0. Тогда мы можем видеть, что это 𝑥-перехваты график этой функции.
Свойство: 𝑥-пересечения факторизованного кубического многочлена
𝑥-пересечения графа находятся в 𝑥=𝑏, 𝑥=𝑐 и 𝑥=𝑑.
В общем случае все кубические многочлены имеют не более трех действительных корней, поэтому их графики имеют не более трех 𝑥-перехватов.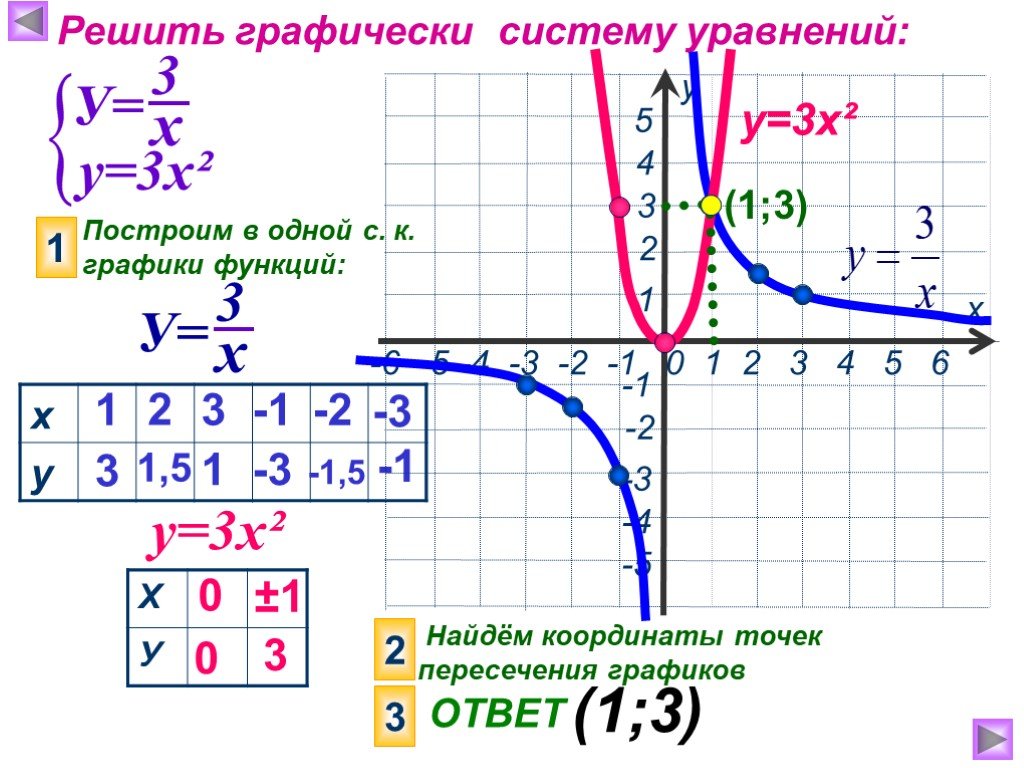
Когда 𝑥 станет очень большим, все множители 𝑥−𝑏, 𝑥−𝑐 и 𝑥−𝑑 будут положительными, поэтому их произведение будет положительным. Следовательно, если 𝑎 тоже положительно, то 𝑦 будет положительным для больших значений 𝑥. С другой стороны, если 𝑎 отрицательно, тогда 𝑦 будет отрицательным для больших значений 𝑥.
Аналогично, если мы рассмотрим большие отрицательные значения 𝑥, мы увидим, что все факторы 𝑥−𝑏, 𝑥−𝑐 и 𝑥−𝑑 будут отрицательными, поэтому их произведение тоже будет отрицательным. Таким образом, если 𝑎 положительно, то 𝑦 будет отрицательным при больших отрицательных значениях 𝑥, и если 𝑎 отрицательно, то 𝑦 будет положительным.
Отметим, что это наблюдение относится и к нефакторизованной форме кубической функции. То есть старший коэффициент (т. 𝑎 в 𝑎𝑥+𝑏𝑥+𝑐𝑥+𝑑) будет определять конечное поведение графа. Эта линия рассуждений приводит нас к следующее свойство.
Свойство: Конечное поведение графиков кубических функций
Конечное поведение графиков кубических функций определяется знаком их старших коэффициентов.
Если старший коэффициент положителен, то при неограниченном увеличении 𝑥 выпуски неограниченно возрастают. Точно так же, когда 𝑥 неограниченно уменьшается, выпуски уменьшаются неограниченно.
Если старший коэффициент отрицательный, то поведение меняется на противоположное; при неограниченном увеличении 𝑥 выпуски неограниченно уменьшаются, а поскольку 𝑥 неограниченно уменьшается, выпуски неограниченно увеличиваются.
Кубические графы с положительными старшими коэффициентами ведут себя так же, как 𝑦=𝑥.
Кубические графы с отрицательными старшими коэффициентами ведут себя так же, как 𝑦=−𝑥.
Последняя часть информации, которую мы можем использовать для наброска графика кубической функции, — это положение 𝑦-перехвата. Напомним, что 𝑦-перехват — это место, где кривая пересекает 𝑦-ось, что происходит, когда
𝑥=0. Для нас это просто вычислить, так как нам просто нужно заменить 𝑥=0
в функцию (что можно сделать независимо от того, находится ли функция в факторизованной форме).
Рисуем график кубического полинома факторингом, находя его 𝑥- и 𝑦-перехваты, а затем проверить знак его старшего коэффициента, чтобы определить конечное поведение.
Теперь рассмотрим пример использования этого метода для построения графика кубической функции.
Пример 1. Определение графика факторизованной кубической функции
Что из следующего является графиком 𝑓(𝑥)=(𝑥−3)(𝑥+1)(𝑥+4)?
Ответ
Самый простой способ ответить на этот вопрос — исключить варианты. Мы можем сделать это, вспомнив, что 𝑥-перехваты происходят, когда функция выводит 0. Это означает, что мы можем найти 𝑥-перехваты решив уравнение 𝑓(𝑥)=0. Это дает нам (𝑥−3)(𝑥+1)(𝑥+4)=0.
Чтобы произведение было равно 0, один из множителей должен быть равен 0. Мы можем установить каждый множитель равным 0 и решить, чтобы определить 𝑥-перехваты. У нас есть 𝑥−3=0, 𝑥=3, 𝑥+1=0, 𝑥=−1, 𝑥+4=0, 𝑥=−4.что дает нам, что дает нам, что дает нам
Следовательно, существует три 𝑥-пересечения кривой в точках 𝑥=- 4, −1 и
3.
Мы видим, что только варианты C и D имеют эти 𝑥-перехваты, поэтому это единственно возможные правильные
графики.
Теперь есть два возможных способа определить правильный график.
Мы можем определить 𝑦-перехват, подставив 𝑥=0 в функцию. Это дает нам 𝑓(0)=(0−3)(0+1)(0+4)=(−3)(1)(4)=−12.
Мы видим, что граф в варианте C имеет положительный 𝑦-перехват, так что это не может быть правильным графом. Этот оставляет график только в варианте D.
В качестве альтернативы мы можем отметить, что старший коэффициент равен 1, и, поскольку он положительный, конечное поведение графика будет быть таким же, как 𝑦=𝑥. Это означает, что график функции должен стремиться к бесконечности как 𝑥 приближается к бесконечности. Мы видим, что граф в варианте C не имеет такого конечного поведения. Значит, ответ должен быть вариантом D.
Стоит отметить, что в приведенном выше примере мы действительно нашли достаточно информации, чтобы самостоятельно набросать график функции.
Для этого мы начнем с отметки трех 𝑥-перехватов и 𝑦-перехватов, как показано.
Затем заметим, что конечное поведение графа такое же, как 𝑦=𝑥, поэтому мы можем соединить точки кубической кривая, которая уходит в бесконечность, когда 𝑥 приближается к бесконечности, чтобы получить следующий график.
В нашем следующем примере мы идентифицируем правильное уравнение кубической функции по ее графику.
Пример 2. Определение факторизованной кубической функции по ее графику
Какое уравнение соответствует графику?
- 𝑓(𝑥)=(𝑥−1)(𝑥+2)(𝑥+3)
- 𝑓(𝑥)=0,25(𝑥−1)(𝑥+2)(𝑥+3)
- 𝑓( 𝑥)=-0,25(𝑥-1)(𝑥+2)(𝑥+3)
- 𝑓(𝑥)=-(𝑥-1)(𝑥+2)(𝑥+3)
- 𝑓(𝑥)= 0,25(𝑥+1)(𝑥−2)(𝑥−3)
Ответ
Прежде всего заметим, что все пять данных вариантов являются факторизованными кубическими функциями. Напомним, что 𝑥-перехваты
происходят, когда функция выводит 0, а для факторизованной функции они возникают, когда каждый фактор равен 0.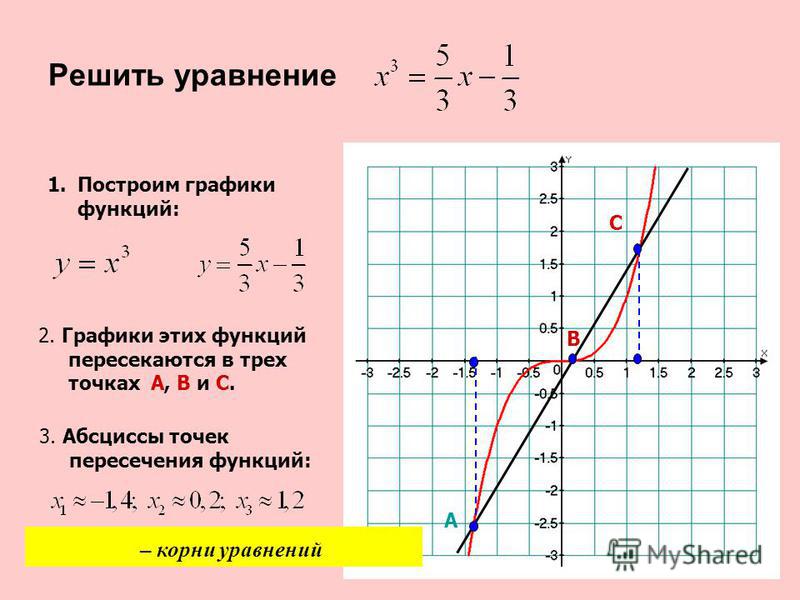
Мы можем отметить, что мы можем
считать 𝑥-перехваты с графа; они находятся на 𝑥=−3, 𝑥=−2 и
𝑥=1.
Мы можем использовать эти значения для определения возможных линейных коэффициентов функции. Поскольку функция выводит 0 при этих значениях а функция является произведением множителей, один из множителей должен быть равен 0 на каждом 𝑥-перехвате. Это означает что у нас есть факторы (𝑥−1), (𝑥+2) и (𝑥+3).
Это говорит нам о том, что наша функция должна иметь вид 𝑓(𝑥)=𝑎(𝑥−1)(𝑥+2)(𝑥+3), где 𝑎 — некоторое действительное значение. Чтобы определить значение 𝑎, мы можем проверить значение 𝑓(𝑥) в ненулевой точке, такой как 𝑦-перехват.
𝑦-отрезок можно прочитать на графике, увидев, где он пересекает 𝑦-ось, т.е. при −1,5. Это означает, что 𝑓(0)=−1,5. Подставив 𝑥=0 в наш выражение для 𝑓(𝑥) дает нам −1,5=𝑎(0−1)(0+2)(0+3)−1,5=−6𝑎.
Деление на −6 дает нам 𝑎=−1,5−6=0,25.
Это дает нам уравнение 𝑓(𝑥)=0,25(𝑥−1)(𝑥+2)(𝑥+3), которое
есть вариант B.
Прежде чем мы перейдем к следующему примеру, нам нужно рассмотреть еще одну возможность, а именно, что происходит, когда у нас есть повторяющиеся корни. Например, представьте, что мы хотим нарисовать график кубической функции 𝑓(𝑥)=(𝑥−2)(𝑥+1).
Мы видим, что у функции всего два корня, поэтому на ее графике всего два 𝑥-перехвата. Это в 𝑥=−1 и 𝑥=2. Мы можем найти его 𝑦-перехват, оценив 𝑓(0). У нас есть 𝑓(0)=(0−2)(0+1)=−2.
Затем мы могли бы нанести точки, чтобы получить представление о форме графика. Если бы мы это сделали, то получили бы следующее.
Мы видим, что есть две точки, в которых график поворачивается, и что конечное поведение графика совпадает с поведением 𝑦=𝑥. Мы также можем заметить, что график касается оси 𝑥 только в точке (−1,0), а не пересекает его, поскольку рядом с этой точкой нет другого пересечения.
В общем, если у нас есть кубическая функция 𝑓(𝑥)=𝑎(𝑥+𝑝)(𝑥+𝑞), где
𝑝≠𝑞, то график будет касаться оси 𝑥 только в точке
(−𝑞, 0).
Есть еще одна последняя возможность: один и тот же корень повторяется три раза. Например, функция 𝑓(𝑥)=(𝑥−2). В этом случае у нас есть только один 𝑥-перехват в точке 𝑥=2, а конечное поведение определяется знаком старшего коэффициента. В случаях с тремя повторными корней, форма кривой аналогична 𝑦=𝑥 (поскольку она также имеет три повторяющихся корня).
Давайте теперь рассмотрим пример использования этого процесса для определения правильного графика кубической функции с повторяющимся множителем.
Пример 3. Идентификация графика факторизованной кубической функции с повторяющимся множителем
Какой из следующих графиков представляет 𝑓(𝑥)=−(𝑥+1)(𝑥−2)?
Ответ
Заметим, что нас просят определить правильный график факторизованного кубического многочлена. Мы можем начать с поиска
𝑥-перехваты и 𝑦-перехваты. Начнем с 𝑥-перехватов. Это происходит
когда выходы функции равны 0. Эта функция является произведением факторов, поэтому один из факторов должен быть равен
0 на 𝑥-перехватах.
У нас есть
𝑥+1=0,𝑥=−1,𝑥−2=0,𝑥=2.что дает нам, что дает нам
Мы можем найти 𝑦-перехват, подставив 𝑥=0 в функцию. Мы рассчитываем 𝑓(0)=−(0+1)(0−2)=−(1)(−2)=−4.
На данный момент мы можем видеть, что только вариант A имеет 𝑦-перехват −4, так что это единственный возможный правильный график функции. Тем не менее, всегда полезно найти всю информацию, чтобы мы могли сделать набросок. наш собственный график функции.
Мы также можем видеть, что функция имеет повторяющийся множитель (𝑥−2). Это означает, что функция коснется только оси 𝑥 в этой точке. Наконец, мы можем заметить, что старший коэффициент отрицательный, поэтому конечное поведение графа будет таким же, как у 𝑦=−𝑥.
Мы можем добавить 𝑥-перехваты и 𝑦-перехваты к графику и отметить конечное поведение.
Начертите кривую кубической формы через эти точки, касаясь только точки (2,0) дает нам следующее.
Мы видим, что этот эскиз соответствует графику в варианте A.
В нашем следующем примере мы найдем значения трех недостающих констант из кубической функции, используя ее график.
Пример 4. Нахождение неизвестных переменных в кубической функции по ее графику
На следующем графике представлена функция 𝑓(𝑥)=𝑘(𝑥−𝑎)(𝑥−𝑏). Найдите значения 𝑘, 𝑎 и 𝑏.
Ответ
Нам дан график кубической функции и просят определить значения трех констант из этой функции. Мы можем сделать это, вспомнив отношения между свойствами графика и структурой функции.
Во-первых, напомним, что 𝑥-пересечение факторизованной кубической функции происходит, когда каждый множитель равен 0. В частности, если (𝑥−𝑝) является фактором, граф будет иметь 𝑥-пересечение в точке 𝑝. На диаграмме видно, что граф имеет два 𝑥-перехвата: −1 и 2. Это означает, что (𝑥−(−1))=(𝑥+1) и (𝑥−2) являются факторами кубической функции.
Чтобы найти, какой множитель повторяется (т. е. имеет квадрат), мы вспоминаем, что повторяющиеся множители приводят к
𝑥-перехват графа, который касается 𝑥-оси только в точке.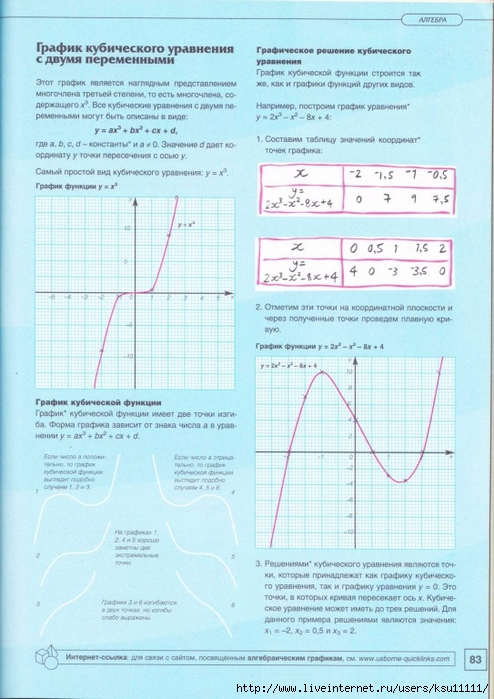
Поскольку это происходит при
𝑥=−1, это означает, что множитель (𝑥+1) должен быть повторяющимся множителем. Этот
дает нам
𝑓(𝑥)=𝑘(𝑥−2)(𝑥+1).
Таким образом, 𝑎=2 и 𝑏=−1.
Чтобы определить значение 𝑘, мы можем использовать 𝑦-перехват графа. Из диаграммы, мы можем видеть, что 𝑦-перехват находится на 4. Это означает, что 𝑓(0)=4. Мы можем подставьте 𝑥=0 в нашу функцию, чтобы получить 𝑓(0)=𝑘(0−2)(0+1)=𝑘(−2)(1)=−2𝑘.
Поскольку 𝑓(0)=4, это говорит нам, что 4=−2𝑘. Таким образом, 𝑘=4−2=−2.
Это дает нам 𝑓(𝑥)=−2(𝑥−2)(𝑥+1).
Следовательно, 𝑘=−2, 𝑎=2 и 𝑏=−1.
В общем, разложить кубический многочлен на множители очень сложно. Факторинг кубиков часто требует продвинутых методов; однако,
есть примеры более простых способов разложения кубиков на множители. Например, если все члены в кубе делят множитель 𝑥,
тогда мы можем убрать этот множитель, оставив нам квадратичный.
Затем мы можем применить наши инструменты для факторизации квадратичных уравнений.
В следующем примере мы факторизуем кубический многочлен, чтобы определить правильный набросок его кривой.
Пример 5. Разложение на множители и идентификация графика кубической функции
- Фактор кубического многочлена 𝑥−𝑥.
- Определите, что из следующего является правильным эскизом кривой 𝑦=𝑥−𝑥.
Ответ
Часть 1
Мы хотим разложить на множители кубический многочлен 𝑥−𝑥. Мы можем сделать это, заметив, что оба термина имеют общий множитель 𝑥. Вычитание общего множителя 𝑥 дает нам 𝑥−𝑥=𝑥𝑥−1.
Тогда мы можем заметить, что 𝑥−1 — это разница между двумя квадратами. Это означает, что мы можем факторизовать это как 𝑥−1=(𝑥−1)(𝑥+1).
Подставив это в функцию, мы получим
Часть 2 равно 0 и
решение для 𝑥. Мы находим, что 𝑥-перехваты находятся в точках 𝑥=0, 𝑥=1,
и 𝑥=−1.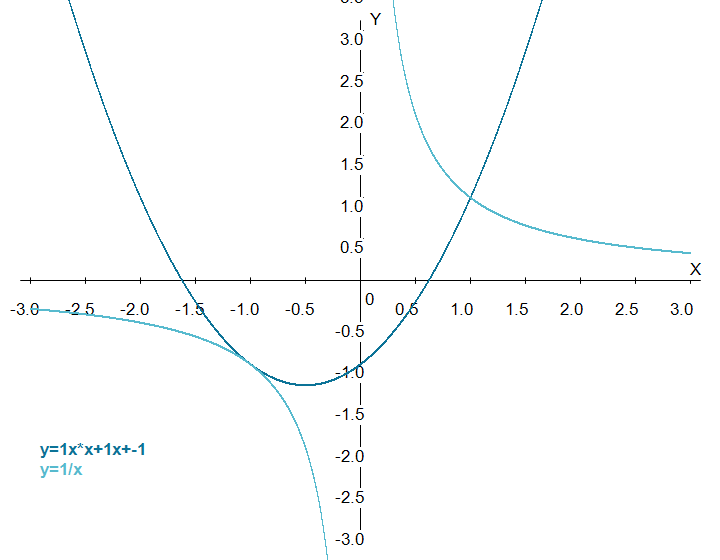
Это означает, что варианты A, B и E не могут быть правильными, поскольку они не имеют этих
𝑥-перехваты.
Мы можем найти 𝑦-пересечение кривой, подставив 𝑥=0 в функцию. Это дает 0(0−1)(0+1)=0.
Итак, 𝑦-перехват находится в 0, что согласуется с тем фактом, что 𝑥=0 является 𝑥-перехват.
Наконец, мы можем определить конечное поведение кривой, заметив, что старший коэффициент полинома положителен. Это означает, что конечное поведение будет таким же, как 𝑦=𝑥. В частности, поскольку значения 𝑥 увеличиваться без ограничений, выходные параметры функции должны увеличиваться без ограничений. Это неверно для варианта C, поэтому правильный ответ должен быть выбором D.
В нашем последнем примере мы факторизуем кубический многочлен, чтобы помочь нам определить набросок графика.
Пример 6. Разложение на множители и идентификация графика кубической функции
- Фактор кубического многочлена 2𝑥+2𝑥−4𝑥.
- Определите, что из следующего является правильным эскизом кривой 𝑦=2𝑥+2𝑥−4𝑥.
Ответ
Часть 1
Мы хотим разложить на множители кубический многочлен 2𝑥+2𝑥−4𝑥. Мы можем сделать это, заметив, что все термины разделить коэффициент 2𝑥. Вычитание общего множителя 𝑥 дает нам 2𝑥+2𝑥−4𝑥=2𝑥𝑥+𝑥−2.
Чтобы разложить квадратное число на множители, нам нужно найти два числа, произведение которых равно -2 и которые в сумме дают 1. Мы можем найти что 2×(−1)=−2 и что 2+(−1)=1. Это позволяет нам учитывать квадратичный следующим образом: 𝑥+𝑥−2=(𝑥+2)(𝑥−1).
Подстановка этого числа в кубический многочлен дает 2𝑥+2𝑥−4𝑥=2𝑥𝑥+𝑥−2=2𝑥(𝑥+2)(𝑥−1).
Часть 2
Заметим, что нас просят определить правильный график факторизованный кубический полином. Мы можем начать с поиска
𝑥-перехваты и 𝑦-перехваты. Начнем с 𝑥-перехватов. Это происходит, когда выход функции равен 0.
Поскольку мы разложили функцию на множители, мы можем найти 𝑥-перехваты
установив по очереди каждый из факторов равным нулю. У нас есть
𝑥=0,𝑥−1=0,𝑥=1,𝑥+2=0,𝑥=−2.что дает нам, что дает нам
Таким образом, наш граф имеет три различных 𝑥-перехвата в точках −2, 0 и 1. Как один из 𝑥-перехват находится в (0,0), это также дает нам 𝑦-перехват графика. Мы видим, что только варианты B и C имеют эти 𝑥-перехваты, поэтому это должен быть один из этих графов.
Наконец, мы можем отметить, что старший коэффициент положительный, поэтому конечное поведение графа будет таким же, как у 𝑦=𝑥.
Мы можем добавить 𝑥-перехваты и 𝑦-перехваты на график и отметить конечное поведение.
Рисование кубической кривой через эти точки с правильным поведением концов дает нам следующее.
Мы видим, что этот набросок соответствует графику, указанному в варианте B.
Давайте закончим повторением некоторых важных моментов из этого объяснения.
Ключевые точки
- 𝑥-пересечения графика 𝑦=𝑎(𝑥−𝑏)(𝑥−𝑐)(𝑥−𝑑) находятся в 𝑥=𝑏, 𝑥=𝑐 и 𝑥=𝑑.
- Все кубические многочлены имеют не более трех действительных корней, поэтому их графики имеют не более трех 𝑥-перехватов.
- Конечное поведение графиков кубических функций определяется знаком их старших коэффициентов. Если ведущий положительный, то кубическая функция ведет себя так же, как 𝑥. Если старший коэффициент отрицательна, то кубическая функция ведет себя так же, как и −𝑥.
- Если есть повторяющийся корень, такой как 𝑦=𝑎(𝑥−𝑝)(𝑥−𝑞), то граф касается только 𝑥-ось в 𝑞.
График кубических функций/кубических уравнений для нулей и корней (-5,0,-20)
The Learning Point > Математика > Графики кубических многочленов, наброски кривых и решения простых кубических уравнений >
Рассмотрим кубическую функцию f(x) = (x+5)(x-0)(x+20) = x 3 + 25x 2 + 100x + 0, Мы проверим график, нули, точки поворота и перегиба в кубической кривой кривой y = f(x). C ubic Полиномы и уравнения Кубический многочлен — это многочлен степени 3. , где a не равно нулю. Уравнение, включающее кубический полином, называется кубическим уравнением и имеет форму f(x) = 0. Существует также решение в замкнутой форме, известное как кубическая формула, которая существует для решений произвольного кубического уравнения. Кубический многочлен представляется функцией вида. А f(x) = 0 — кубическое уравнение. Точки, в которых эта кривая пересекает ось X, являются корнями уравнения. График y = f(x) = (x+5)(x- 0)(x+20) = x 3 + 25x 2 + 100x + 0 Характеристики графика, зарисовки кубических кривых Если задана кубическая функция: f(x) = ax 3 + bx 2 + cx + d Данная нам функция f(x) = (x+5)(x- 0)(x+20) = x 3 + 25x 2 + 100x + 0 И производная для этого равна f'(x) = 3x 2 + 50x + 1 Рассмотрим кубическое уравнение f(x) = (x+5)(x-0)(x+20) = x 3 + 25x 2 + 100x + 0 = 0 Корни этого кубического уравнения находятся в: (х — (-5)) = 0 => х = -5, ИЛИ (x — (0)) = 0 => x = 0, ИЛИ (х — (-20)) = 0 => х =-20 Это кубическое уравнение имеет действительные и уникальные корни в точках -5, 0, -20. Поворотные или неподвижные точки, где f'(x) = 0 => 3x 2 + 50x + 1 = 0 => x = -14,34, x = -2,32 Их также называют «критическими» точками, где производная равна нулю. Переходя к другим геометрическим особенностям этой кривой: точка пересечения этой кривой с осью y находится в точке y=0. Нули многочлена, если они известны, и коэффициенты этого многочлена — это два разных набора чисел, между которыми существуют интересные отношения. Если мы знаем нули, то можем записать алгебраические выражения для коэффициентов. Идти по другому пути гораздо труднее и вообще невозможно. Кубическая функция имеет более разнообразную форму, чем квадратичные многочлены, которые всегда являются параболами. |
