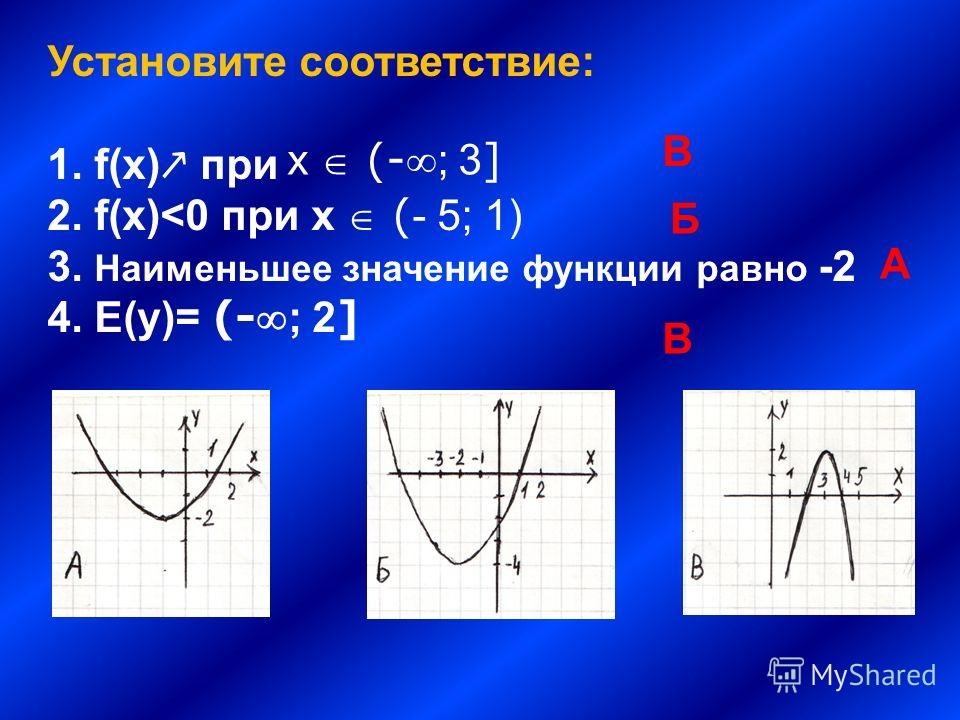
Свойства квадратичной функции
Здесь рассматриваются свойства квадратичной функции вида ,график квадратичной функции и решаются задачи на чтение графиков и задачи с параметром.
Напоминание
Определение. Квадратичной функцией называется функция вида
, где .
График – парабола (см. Рис. 1) с вершиной в точке , где.
Рис. 1. График функции , где
. Функция непрерывна на всей .
Свойства функции
в случае .
Пусть .
Свойства:
1. ;
2. ;
3. убывает при;возрастает при;
4. — не существует;
5. Непрерывна;
6. Выпукла вниз.
Свойства функции
в случае .
Пусть .
Свойства (см. Рис. 2):
Рис. 2. График функции в случае.
1. ;
2. ;
3. возрастает при;убывает при;
4.
5. Непрерывна;
6. Выпукла вверх.
Задача 1 на нахождение пределов изменения конкретной квадратичной функции
Найдите пределы изменения функции, прочитайте график.
а.
Ответ: ;убывает при;возрастает при.
| |
| б. |
Ответ: ;убывает при;возрастает при.
Задача 2 на нахождение пределов изменения конкретной квадратичной функции
Найдите пределы изменения функции, прочитайте график.
| |
| а. |
Ответ: ;возрастает
при;убывает
при.
б.
Ответ: ;возрастает при;убывает при.
Задача 1 с параметром
Найдите число корней уравнения с параметром, где,.
Ответ (см. Рис. 3):
Рис. 3. График функции , рассеченный прямыми, гдеи.
1. Корней нет при ;
2. Уравнение имеет
— один корень при ;
— два корня при .
Задача 2 с параметром
Найдите все значения параметра , при каждом из которых уравнение, где,, имеет хотя бы один корень (см. Рис. 4).
Ответ: .
Задача на построение и чтение графика функции
Постройте и прочитайте график функции
,
Ответ: (см. Рис. 5)
Рис. 5. График функции
1. Возрастает при ;
2. Убывает при .
Задача 3 с параметром
Найдите число корней уравнения , где.
Ответ:
уравнение имеет (см. Рис. 6)
Рис. 6)
Рис. 6. График функции ,
рассеченный прямыми , гдеи.
1. Один корень при ;
2. Два корня при ;
3. Три корня при .
Здесь вспомним свойства степенных функций с целым отрицательным показателем и используем их при решении задач на степенную функцию.
Напоминание: график и свойства функции
Функция
Основные свойства:
1.
2.
3. Функция четная.
4. Две характерные фиксированные точки для всех кривых:
5. Асимптоты: прямые
6. Если тоy возрастает,
Если тоy убывает,
Напоминание: график и свойства функции
Функция
Основные свойства:
1.
2.
3. Функция нечетная.
4. Две фиксированные характерные точки для всех кривых:
5. Асимптоты: прямые
6. Если тоy убывает,
Если тоy убывает,
Решение задач
Рассмотрим типовые задачи:
1. Какая из точек – А или В – принадлежит
графику функции если
Какая из точек – А или В – принадлежит
графику функции если
Решение:
т. А:
т. А принадлежит графику.
т. В:
т. В не принадлежит графику.
Ответ: т. А.
2. Какая из точек А, В, С принадлежит графику функции если
Решение:
т. А:
т. В:
т. С:
Ответ: т. В принадлежит графику.
3. Постройте график функции и прочтите его.
Решение:
Построим график функции (Рис. 5). Его асимптоты – прямыеи.
Чтобы получить график функции необходимо графиксдвинуть на 1 вверх по осиyи на 1 единицу влево по оси x (Рис. 6).
Асимптоты полученного графика – прямые и, характерные точки
Если тоy возрастает,
Если тоy убывает,
4. Найдите все значения параметра m, при каждом из которых уравнение
имеет
хотя бы одно решение.
Решение:
Нам необходимо построить график функции , пересечь его семейством прямых, найти точки пересечения и записать ответ (Рис. 7).
Ответ:
5. Найти все значения параметра m, при каждом из которых уравнение
1. Не имеет решений.
2. Имеет только отрицательные решения.
3. Имеет два корня разных знаков.
Решение:
Ответ:
1.
2.
3.
6. Постройте график функции и прочитайте его.
Решение:
Построим график функции (Рис. 8).
Теперь чтобы получить график функции сдвинем кривуюна 2 вправо вдоль осиx, и на 3 вверх по осиy (Рис. 9).
Прямые иявляются асимптотами.
Характерные точки –
Если тоy убывает,
Если тоy убывает,
7. Найти все значения параметра m, при каждом из которых уравнение
имеет решения
1. На луче
На луче
2. На луче
Решение:
Изобразим график функции и пересечем его семейством прямых(Рис. 10).
Ответ:
1.
2.
8. Решите графически неравенство
Решение:
Построим в одной системе координат график функции и график функции(Рис. 11).
Графики пересекаются в точке
Чтобы выполнялось неравенство криваядолжна располагаться выше прямой
Ответ:
9. Даны две функции, и, где
Докажите, что
Доказательство:
Тождество доказано.
Конспект урока «Квадратичная функция, её график и свойства» (9 класс)
МБОУ «Средняя общеобразовательная школа» с. Дутово
Разработка урока математики
«Функция » в 9 классе
Дутово 2018
Урок математики в 9 классе
Пояснительная записка.
Предмет: алебра
Класс: 9 класс
Тема урока: Функция .
Тип урока: Изучение нового материала.
Цель урока:
научить строить график функции , читать его и использовать приобретенные знания.
Формирование универсальных и специальных предметных учебных действий, формируемых в процессе изучения темы;
активизировать сознательную деятельность учащихся;
Задачи урока:
– образовательные (формирование познавательных УУД, в том числе специально-предметных действий):
научить выделять и формулировать познавательную цель, определять квадратичную функцию; уметь строить и исследовать квадратичную функцию;
– воспитательные (формирование личностных и коммуникативных УУД):
действие смыслообразования (установление связей между целями и мотивами), формирование умений слушать и вступать в диалог, участвовать в коллективном обсуждении проблем, интегрироваться в группу сверстников и строить продуктивное взаимодействие, формировать коммуникативную компетенцию учащихся, воспитывать ответственность и аккуратность;
– развивающие (формирование регулятивных УУД):
постановка учебных задач, формировать умения обрабатывать информацию и систематизировать ее по указанным основаниям; выбирать способы решения задач в зависимости от конкретных условий; рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности.
Планируемые результаты:
предметные:
уметь оперировать понятиями темы «Квадратичная функция и её график»;
уметь строить график функции и исследовать свойства функции;
уметь работать с математическим текстом (анализировать, извлекать необходимую информацию), точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологии и символики, использовать различные языки математики, проводить классификации, логические обоснования, доказательства математических утверждений.
метапредметные:
уметь применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии для решения задач на построение графика квадратичной функции;
уметь самостоятельно ставить цели, выбирать и создавать алгоритмы для построения графика квадратичной функции.
личностные:
уметь ясно, точно, грамотно излагать свои мысли в устной и письменной речи,
понимать смысл поставленной задачи, выстраивать аргументацию,
креативность мышления, инициатива, находчивость, активность при решении математических задач;
уметь контролировать процесс и результат учебной математической деятельности.
Используемые технологии: проблемно – исследовательская технология, групповая технология (обучение в сотрудничестве), технология уровневой дифференциации, здоровьесберегающая технология.
Формы работы учащихся: фронтальная работа, парная и индивидуальная работа, групповая технология.
Необходимое техническое оборудование: компьютер, мультимедийный проектор, доска, экран, планшет: представляет собой файл, в который вставлен лист плотной бумаги с изображением системы координат. На планшете пишут фломастером или маркером, который хорошо стирается губкой.
Изучение предусматривает использование следующего учебно-методического комплекса
1. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебра 8 класс: Учебники. – М. «Вентана Граф», 2017 год
2. Мерзляк А.Г., Полонский В.Б., Рабинович Е.М., Якир М.С. Алгебра 8 класс: Дидактические материалы. – М. «Вентана Граф», 2017 год
«Вентана Граф», 2017 год
ТЕХНОЛОГИЧЕСКАЯ КАРТА УРОКА
Этап урока и его цели | Деятельность учителя | Деятельность ученика | Формируемые УУД | Результат |
I. Вводная часть урока | ||||
1.Организационный этап Цель: приветствие учащихся, организация внимания школьников. Эмоциональный настрой совместной работы. Мотивация учащихся | В алгебре достаточно большой раздел посвящается квадратичной функции. С одним из видов квадратичной функции вы знакомы – это функция . | Многие величины из окружающей нас жизни связаны зависимостью например, площадь квадрата от его стороны. Отражающая поверхность фары в автомобиле имеет параболическую форму. Некоторые законы физики описываются квадратичной функцией. | Познавательные применение квадратичной функции; Коммуникативные точное выражение своих мыслей; Личностные адекватное оценивание себя и других.
| Предметный: Личностный: Вызван интерес к уроку. |
2. Актуализация знаний Цель: актуализация субъективного опыта (опорных знаний и способов действий, ценностных отношений).
| Сколько необходимо знать точек, чтобы построить график функции ? Как с помощью графика функции построить: а) ; б) ; в) ? Постройте эскизы указанных графиков. Сделайте вывод. Быстро определяет правильность построения. | 3 – 4точки: вершину и еще 2 – 3 точки на одной из ветвей параболы.
Строят графики указанных функций на планшете, делает вывод на основании построений.
| Познавательные: анализ информации Регулятивные: самостоятельность Коммуникативные взаимодействие с учителем; участие в диалоге, точное выражение свои мысли | Предметный Обобщение знаний по теме «Функция ». Метапредметный Личностный: |
3. Постановка проблемы Цели: — организация выполнения учащимися пробного учебного действия;
— организация фиксирования учащимися индивидуального затруднения.
| 1. Смогли бы вы построить график функции если коэффициенты и будут заданы? Как вы думаете, какую – нибудь из известных вам кривых напомнит построенный график? Заданы 5 точек на координатной плоскости (задается несколько пятерок). (карточка 1) 2. Посмотрите на изображенные параболы (карточка 2) (1) ; (2) ; (3) . Сосредоточьте свой взгляд, свое внимание на форму на расположение парабол. Запишите на листе все проблемы, которые возникаю при исследовании зависимости между формой, расположением параболы и функцией ее задающей. | Да, если взять достаточно большое количество точек.
Параболу
Работа в парах Попытка построения графика по заданным точкам
Работа в четверках (Записывают вопросы) Отчего зависит расположение вершины параболы? Что может влиять на «ширину» параболы? В каких случаях парабола пересекает ось абсцисс, касается ее или не пересекает? Сколько достаточно знать точек. Чтобы построить график любой квадратичной функции? Любая ли функция вида задает параболу, и как более рационально ее построить (т. | Познавательные: выдвигают гипотезы; планируют свою работу, прогнозируют результат. Регулятивные: регулируют учебную деятельность контролируют и оценивают свои действия Коммуникативные оформляют мысли в устной форме учатся действовать с учетом позиции другого и согласовывать свои действия. | Предметный -Проблемная ситуация: противоречие с опытом. Учащиеся понимают, что ответить они могут лишь наугад т. к. не хватает знаний.
-Среди сформулированных вопросов могут быть и такие, на которые ребята могут знать ответ.
Метапредметные самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных проблем.
личностные: умение работать в парах, группах слушать собеседника и вести диалог, |
4. Цели: Восприятие и осмысление учащимися нового материала Применение исследовательских навыков при решении задач. | Начните исследование функции с частных случаев (например, когда b=0). Рассмотрите функцию
Сравните графики функций и .
Аналогично изучаем функцию . | Работа в четверках Отвечают на следующие вопросы: Какова область допустимых значений аргумента, или область определения функции? Какой знак имеет функция? Выяснить промежутки возрастания и убывания функции Показать, что функция четная. Какая прямая является осью симметрии графика? Чему равно наименьшее значение функции? Для любого значения х значение второй функции на 3 единицы больше соответствующего значения первой. Самостоятельная проверка выводов отвечает на те же вопросы, какие предложены при изучении предыдущей функции. | Познавательные: выделение необходимой информации. Выделение существенных характеристик квадратичной функции. Регулятивные: контроль и коррекция отклонений от собственного понимания. Коммуникативные умение слушать и вступать в диалог. | Предметные уметь работать с математической моделью (графиком), извлекать необходимую информацию (свойства квадратичной функции)
Метапредметные уметь самостоятельно ставить цели для проверки выводов о свойствах квадратичной функции
Личностные уметь ясно, точно, грамотно излагать свои мысли в устной речи,
|
5. Цель: развитие умения выдвигать и проверять гипотезы; формирование основ коммуникативного лидерства. | Рассмотрите следующий частный случай функции второй степени: . Примеры: , ; (1) , . (2)
| Учащиеся выдвигают гипотезы по положению графика на координатной плоскости.
Работа в четверках Построив по точкам графики, учащиеся сравнивают их с графиком функции . Устанавливают, что графики функций (1) и (2) – параболы, полученные переносом параллельно оси абсцисс в случае (1) влево на 3 единицы, в случае (2) вправо на 2 единицы графика функции . Оси параллельны оси ординат и отстоят от нее соответственно на –3 и 2 единицы; вершины лежат в точках (–3; 0), (2; 0). | Познавательные: Нахождение способов решения заданий, выстраивая логическую цепь рассуждений. Коммуникативные коллективное обсуждение проблем | Метапредметные Формирование умения выдвигать гипотезы, которое используется учащимися на уроках: физики, химии и др. |
6. Вывод
Цель: формирование умения делать выводы на основании полученный при исследовании данных | Какой вывод вы смогли сделать?
Предлагает провести исследование, наталкивающее на мысль: выделить полный квадрат двучлена. Рассмотрите функцию , например: . С чего можно начать? Предлагает перейти к упрощенному построению графиков: путем выделения квадрата двучлена найти координаты вершины параболы, построить вершину и ось и по соответствующему шаблону нанести параболу. | График функции можно построить из графика функции , перенося последний параллельно оси абсцисс на m единиц, причем при m > 0 перенос выполняется влево, при m <0 вправо от начала координат.
Выделим полный квадрат: . Сравним эту функцию с функцией .
Обсуждение упрощенного построения графиков.
| Познавательные Выделение полного квадрата двучлена и с его помощью нахождение координаты вершины параболы и ее оси симметрии Регулятивные: оценка осознания усвоенного.
| Предметный Формулирование вывода об упрощенном построение графика квадратичной функции путем выделения квадрата двучлена по результатам исследования
Личностные креативность мышления, инициатива, находчивость, активность при формулировании вывода |
7. Физкультминутка Задача этапа: Смена деятельности. | Меняет деятельность, обеспечивает эмоциональную разгрузку учащихся. Объявляет паузу | Сменили вид деятельности и готовы продолжить работу. Физзорг класса проводит физкультминутку. Учащиеся поднимаются с мест, выполняют упражнения.
| Личностные Регулятивные | Метапредметный: |
8. Цель: содействовать усвоению учащимися изученных знаний, применение их в практических заданиях, установить правильность и осознанность изученного материала; выявить пробелов знаниях учащихся. Провести коррекцию выявленных пробелов в в знаниях учащихся | Организация учащихся на выполнение самостоятельной работы с последующей проверкой. Построить графики функций и исследовать ее свойства: ; ; ; | Самостоятельная работа Индивидуально выполняют задания по вариантам. Учащиеся строят графики на планшетах, записывают свойства функций в тетради, затем обмениваются ими для проверки (взаимная проверка). | Познавательные: самостоятельно применяют полученные знания. Регулятивные: формируют умения контролировать свою работу. Коммуникативные формируют письменную математическую речь | Предметный уметь оперировать понятиями темы «Квадратичная функция и её график»; уметь строить график функции и исследовать свойства функции; личностные: умение работать в парах, слушать собеседника и вести диалог, |
9. Цель: Обеспечение понимания детьми содержания и способов выполнения домашнего задания | Обсуждение домашнего задания Даны функции: 2) +1; 3) ; На оценку «3» — необходимо построить графики трех любых функций и перечислить свойства одной из них; На оценку «4» — необходимо построить графики трех любых функций и перечислить свойства двух из них; На оценку «5» — необходимо построить графики всех функций и перечислить их свойства | Участвуют в обсуждении домашнего задания
Записывают его в дневник | Познавательные:
Личностные: | Предметный — внимательность и умение слушать (правильно записанное домашнее задание) |
10. Рефлексия и подведение итогов урока Цель: Инициировать рефлексию учащихся по поводу своего эмоционального состояния, мотивация своей деятельности и взаимодействия с учителем и одноклассниками дать качественную оценку работы класса и отдельных учащихся. |
— Что вы узнали нового на уроке? — Чему научились? — Что показалось особенно трудным? — Кто считает, что он хорошо разобрался в теме? — Если наш урок был познавательным и интересным, вы много узнали, заботились о своем здоровье, поднимите правую руку. — Если в вашей тетради работа выполнена аккуратно, нет исправлений, поднимите левую руку.
| Обсуждают, что узнали нового на уроке, какие задание вызвали наибольшие затруднения Осуществляют самооценку собственной учебной деятельности, соотносят цель и результаты, степень их соответствия. | Познавательные: учащиеся осознают успешность восприятия и осмысления объекта изучения Регулятивные: понимают причины успеха / неуспеха в учебной деятельности; осуществляют контроль и коррекцию, осознают то, что уже усвоено и что ещё подлежит усвоению, осознают качество и уровня усвоения. Коммуникативные умеют критично относиться к своему мнению |
|
Приложение 1 к уроку
Раздаточный материал
Карточка 1
| Карточка 2 |
Самоанализ урока
Урок математики был проведен в 9 классе по теме «Функция ». В учебном базисном плане отведено 175 часов в год (5 часов в неделю — 35 учебных недель).
В учебном базисном плане отведено 175 часов в год (5 часов в неделю — 35 учебных недель).
Цель урока:
научить строить график функции , читать его и использовать приобретенные знания.
Формирование универсальных и специальных предметных учебных действий, формируемых в процессе изучения темы;
активизировать сознательную деятельность учащихся;
Задачи урока:
– образовательные (формирование познавательных УУД, в том числе специально-предметных действий):
научить выделять и формулировать познавательную цель, определять квадратичную функцию; уметь строить и исследовать квадратичную функцию;
– воспитательные (формирование личностных и коммуникативных УУД):
действие смыслообразования (установление связей между целями и мотивами), формирование умений слушать и вступать в диалог, участвовать в коллективном обсуждении проблем, интегрироваться в группу сверстников и строить продуктивное взаимодействие, формировать коммуникативную компетенцию учащихся, воспитывать ответственность и аккуратность;
– развивающие (формирование регулятивных УУД):
постановка учебных задач, формировать умения обрабатывать информацию и систематизировать ее по указанным основаниям; выбирать способы решения задач в зависимости от конкретных условий; рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности.
Планируемые результаты:
предметные:
уметь оперировать понятиями темы «Квадратичная функция и её график»;
уметь строить график функции и исследовать свойства функции;
уметь работать с математическим текстом (анализировать, извлекать необходимую информацию), точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологии и символики, использовать различные языки математики, проводить классификации, логические обоснования, доказательства математических утверждений.
метапредметные:
уметь применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии для решения задач на построение графика квадратичной функции;
уметь самостоятельно ставить цели, выбирать и создавать алгоритмы для построения графика квадратичной функции.
личностные:
уметь ясно, точно, грамотно излагать свои мысли в устной и письменной речи,
понимать смысл поставленной задачи, выстраивать аргументацию,
креативность мышления, инициатива, находчивость, активность при решении математических задач;
уметь контролировать процесс и результат учебной математической деятельности.
Используемые технологии: проблемно – исследовательская технология, групповая технология (обучение в сотрудничестве), технология уровневой дифференциации, здоровьесберегающая технология.
Формы работы учащихся: фронтальная работа, парная и индивидуальная работа, групповая технология.
Учтены требования, предъявляемые к современному уроку в рамках ФГОС ООО.
По типу урока — это урок открытия нового знания, при использовании проблемно-исследовательской технологии. (Открывают знания сами учащиеся в процессе самостоятельной исследовательской деятельности)
В соответствии с темой урока, целью и задачами были выбраны формы организации учебной работы: фронтальная, парная и групповая. А также использовано оборудование: компьютер, проектор, раздаточный материал.
На уроке были учтены возрастные и психологические особенности учащихся.
Все структурные элементы урока были выдержаны.
Целью первого этапа было быстро включить учащихся в деловой ритм и проверить готовность класса. Для этого учащимся было предложено вспомнить, какие величины их окружающей нас жизни связаны зависимостью .
На втором этапе построение эскизов графиков функций позволил быстрее включиться в деловой ритм урока.
На третьем этапе мною была создана проблемная ситуация и учащиеся убедились, что имеющихся знаний не хватает для построения графика функции . Обучающиеся старались активно включиться в урок, потому что применялся метод обучения с применением различного вида дидактического материала, у ребят возникло желание мыслить. Даже самые пассивные из учащихся включились в урок с желанием. Некоторые задания вызвали затруднения в нахождении результата, таким образом проблемная ситуация мотивировала поиск рационального решения.
На четвертом этапе обучающиеся, проведя исследовательскую работу, убедились в идентичности свойств функций и .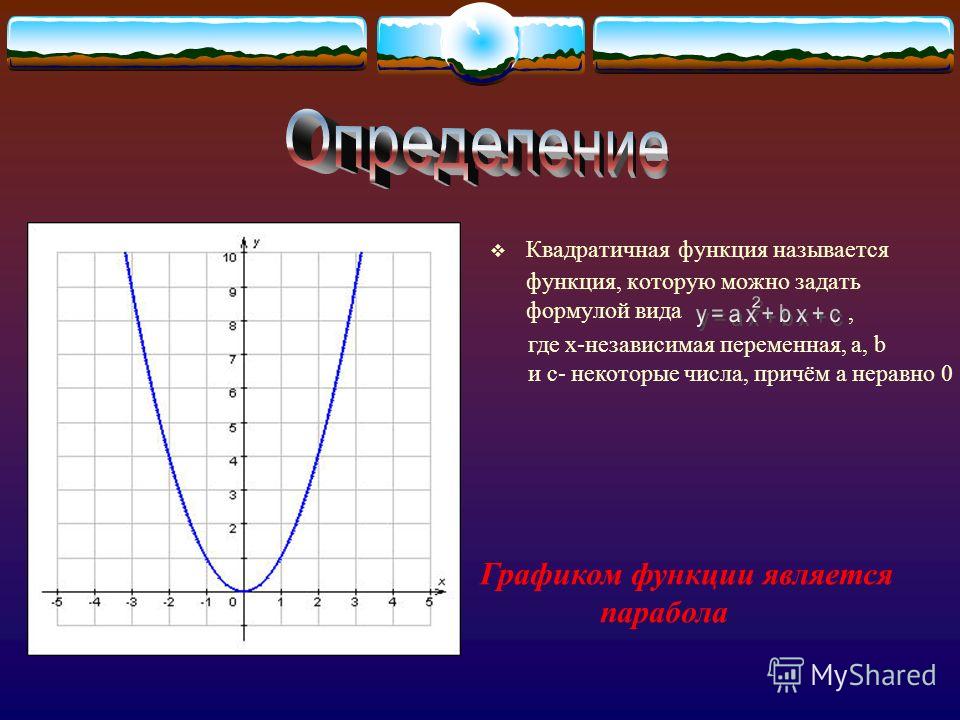
На пятом этапе была выдвинута и проверена гипотеза о положении графика квадратичной функции на координатной плоскости. В процессе урока задачи решались с комментированием. При комментировании шла работа над речевой деятельностью, в которой они выражали суть выполняемых заданий.
На шестом этапе обучающимися был сделан вывод о возможности упрощения построения графика квадратичной функции путем выделения квадрата двучлена в формуле, задающей квадратичную функцию.
На уроке была проведена физическая разминка, как элемент здоровьесберегающих технологий.
Этап самостоятельной работы показал, что каждый ребенок смог себя проверить, осознать: все ли он правильно делал.
Домашнее задание соответствует нормативным требованиям и составлено на основе технологии уровневой дифференциации.
На десятом этапе обучающиеся смогли выразить свое отношение к материалу урока, дать оценку своей работе в ходе него, а также выработали умения применять знания, а также были сформированы УУД. Обучающиеся, которые активно участвовали в работе урока получили соответствующую оценку. И это будет стимулировать их для дальнейшей активной работы на последующих уроках.
Обучающиеся, которые активно участвовали в работе урока получили соответствующую оценку. И это будет стимулировать их для дальнейшей активной работы на последующих уроках.
На всех этапах урока ученики были вовлечены в активную мыслительную и практическую деятельность исследовательского характера, детям надо было не только использовать уже имеющиеся знания по построению графика квадратичной функции, но и найти новый способ с применением выделения квадрата двучлена.
Этапы урока были тесно взаимосвязаны между собой, чередовались различные виды деятельности. Умственные действия по выдвижению гипотез опирались и подкреплялись практическими. Учебный материал на протяжении всего урока работал на организацию посильного поиска и исследования.
Каждый этап урока был нацелен на достижение определённого результата.
Учебное время на уроке использовалось эффективно, запланированный объём урока выполнен. Интенсивность урока была оптимальной с учётом физических и психологических особенностей девятиклассников.
Поставленные задачи были решены и цели достигнуты.
Узнайте о свойствах квадратичных функций
В этом видео мы рассмотрим свойства квадратичных функций. Квадратичные функции записываются в виде
. Самый основной из них. Эти функции являются параболами и имеют U-образную форму. Точка, в которой он останавливается и меняет направление на другое, называется вершиной. Ось симметрии параболы проходит через вершину. После того, как вы закончите этот урок, просмотрите все наши уроки по алгебре 1 и практические задачи.
Графический калькулятор является полезным инструментом, когда дело доходит до работы с квадратичными функциями. После построения графика функции вершину иногда можно увидеть как точку на столе. Ось симметрии имеет уравнение x -координата вершины. В функции
таблица помогла нам определить, что вершина лежит в точке (-2,-6).
Без графического калькулятора мы все равно можем найти эту информацию.
Формула оси симметрии записывается как
В функции . Когда эти значения подставляются в формулу, мы обнаруживаем, что ось симметрии находится в точке x=-2.
Поскольку вершина является точкой на графике, мы можем использовать исходную функцию и значение оси симметрии x для определения точки, в которой находится вершина.
Если мы заменим -2 на x в этой функции, мы получим
, которое упрощается до
и, наконец,
. Это означает, что вершина лежит в точке (-2,-6), что согласуется с тем же точку, которую мы определили с помощью графического калькулятора.
Примеры свойств квадратичных функций
Пример 1
Ось симметрии
, наши значения следующие:
Теперь давайте найдем ось симметрии
Окончательный ответ:
. Подставим значение в уравнение, чтобы получить0005
Подставим значение в уравнение, чтобы получить0005
наши значения следующие:
Теперь давайте найдем ось симметрии
Окончательный ответ
Подставим значение в уравнение, чтобы получить
Таким образом, координаты нашей вершины равны
Стенограмма видеоурока
Давайте пройдемся по свойствам квадратичных функций.
Квадратичные функции имеют следующий вид:
и более основное для:
График имеет вид буквы «U» и симметричен относительно оси
. Он может быть где угодно на графике или вверх ногами.
Если вы посмотрите на линию, она начинается сверху, затем идет вниз и останавливается в точке, а затем снова поднимается.
Точка, в которой он останавливается и поворачивает в другом направлении, называется вершиной.
Кроме того, ось симметрии проходит через вершину.
Что делать, если вершина не находится на определенной отметке?
Мы можем не знать точных цифр.
Но, конечно же, есть способ решить ее алгебраически.
Прежде чем мы приступим к алгебраическому решению, давайте сделаем это сначала на калькуляторе.
У нас есть
Давайте посмотрим на графический калькулятор.
Он опускается, затем останавливается и снова поднимается.
Вот вершина — там, где она идет вверх и вниз по оси симметрии, где она является отражателем другой стороны.
Калькулятор уже определил для нас значения.
По калькулятору вершина
Тогда давайте построим график.
Ось симметрии
Помните, что основной формат для квадратичных функций
.
Итак, учитывая, что наша линия равна
, наши значения следующие:
Теперь давайте найдем ось симметрии
Окончательный ответ:
Теперь, как нам найти вершину?
Вершина — это точка на графике.
Таким образом, мы могли бы использовать функцию, чтобы узнать эту точку.
На данный момент мы знаем, каково значение
. Так как же узнать значение ?
Воспользуемся функцией и подставим значение
.
Итак, координаты нашей вершины
Точно так же, как ответ на калькуляторе ранее.
Свойства квадратичных функций
1. Область определения:
Область определения квадратичной функции f(x) = ax 2 + bx + c — все действительные числа. График квадратичной функции представляет собой параболу.
2. Вершинная форма квадратичной функции равна
f(x) = a(x — h) 2 + k
, где (h, k) — вершина.
3. В f(x) = a(x — h) 2 + k, если a > 0, парабола раскрывается вверх, а если a < o, парабола раскрывается вниз.
4. Диапазон:
В вершинной форме (x) = a(x — h) 2 + k,
(i) если a > 0 (парабола раскрывается), диапазон равен [k, ∞).
(ii) если a < 0 (парабола открывается вниз), диапазон равен (-∞, k].
5. Нули квадратичной функции f(x) = ax 2 + bx + c два значения x, когда f(x) = 0 или ax 2 + bx + c = 0,
6. Нули квадратичной функции f(x) = ax 2 + bx + c – два пересечения параболы по оси x.
7. Количество точек пересечения x квадратичной функции зависит от того, открывается ли график вверх или вниз, а также от того, находится ли вершина выше или ниже оси x.
8. Если график квадратичной функции открывается и вершина находится выше оси x или если график открывается вниз, а вершина находится ниже оси x, тогда не будет х-перехватов.
9. Если вершина касается оси X, то существует одна точка пересечения с x независимо от того, открывается ли график вверх или вниз.
10. Если график квадратичной функции открывается вверх и вершина находится ниже оси x или если график открывается вниз и вершина находится выше оси x, то пересечений x будет два.
11. Существует три метода нахождения двух нулей (х-пересечений) квадратичной функции. Это:
(i) Факторинг
(ii) Квадратичная формула
(iii) Заполнение квадрата
12. Если два нуля квадратичной функции иррациональны, то два нуля (корня) встречаются сопряженными парами. То есть, если (m + √n) — корень, то (m — √n) — другой корень того же уравнения.
13. Сумма нулей квадратичной функции f(x) = ax 2 + bx + c равна -b/a.
14. Произведение нулей квадратичной функции f(x) = ax 2 + bx + c равно c/a.
15. Если один нуль равен другому корню, то их произведение с/а = 1 или с = а.
16. Если один корень равен другому, но противоположен по знаку, то их сумма = 0. То есть, b/a = 0, значит, b = 0.
17. График любой квадратичной функции будет параболой .
18. Нули квадратного уравнения — это координаты x точек, где парабола (график квадратичной функции) пересекает ось x.
19. Если два нуля квадратичной функции мнимые, то график (парабола) никогда не пересечет ось x.

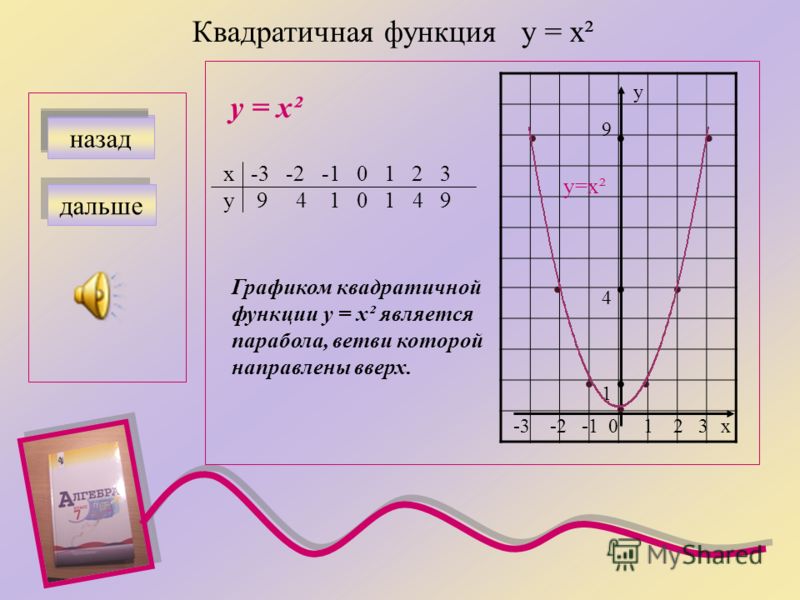 Сегодня мы возвращаемся к рассмотрению квадратичной функции, но заданной в виде . А как вы думаете, почему квадратичной функции нужно уделить особое внимание?
Сегодня мы возвращаемся к рассмотрению квадратичной функции, но заданной в виде . А как вы думаете, почему квадратичной функции нужно уделить особое внимание?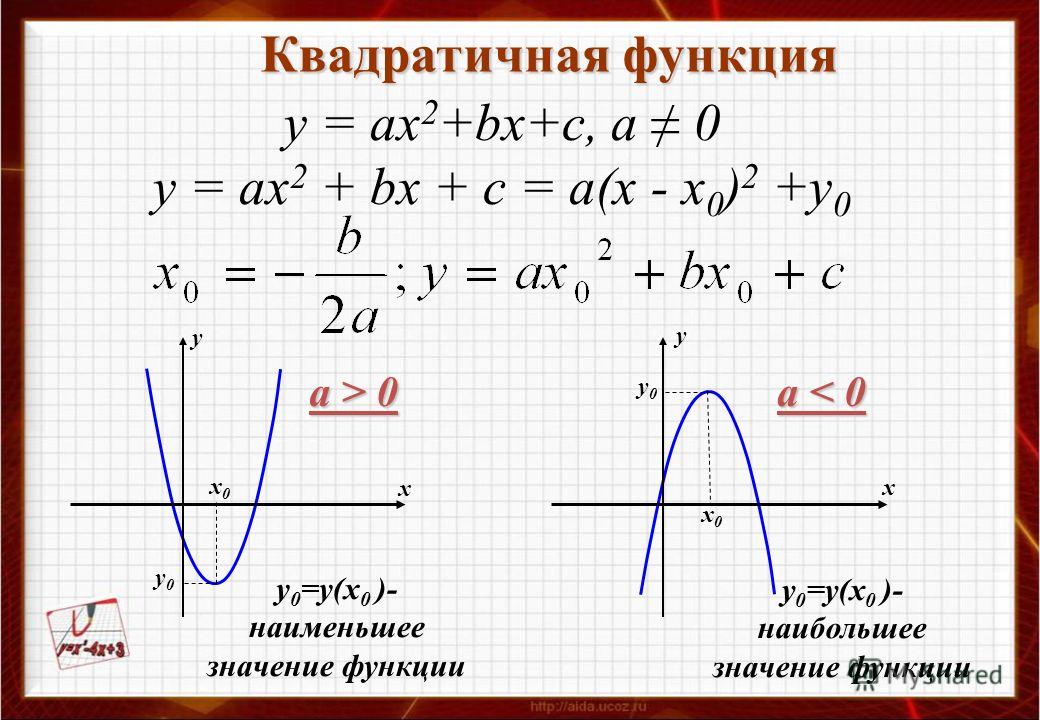

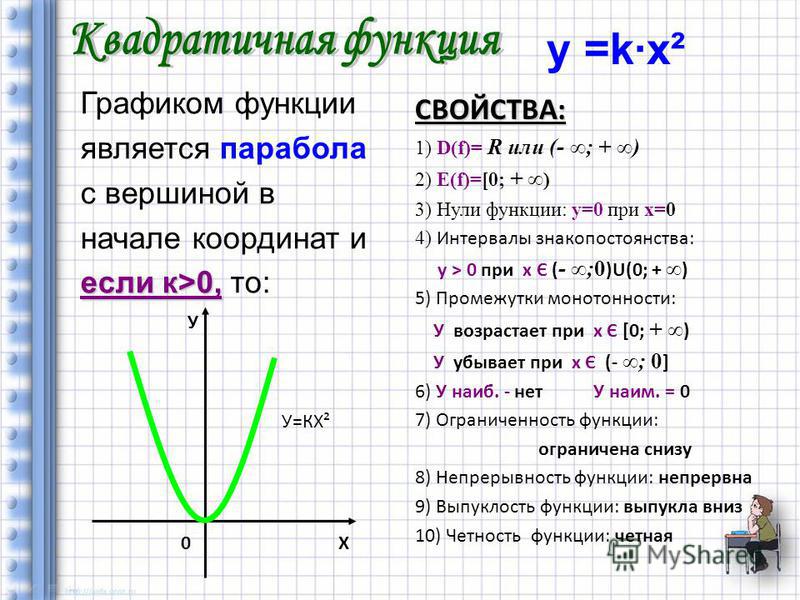
 е. с минимальным количеством точек)?
е. с минимальным количеством точек)? Исследование
Исследование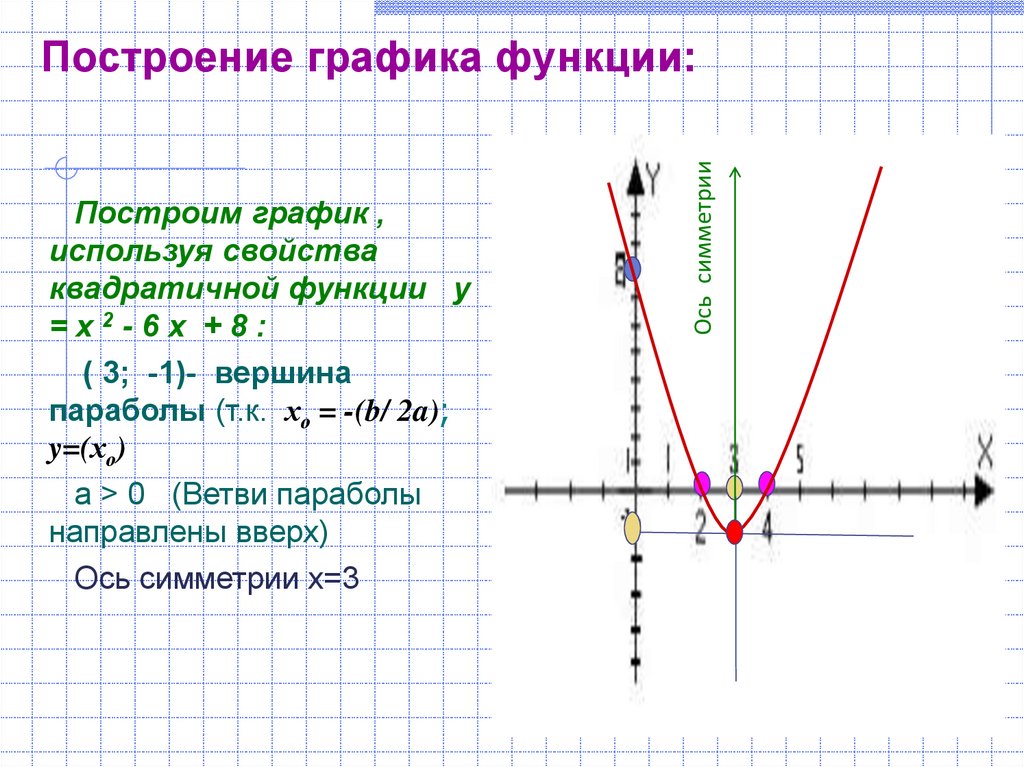 График второй функции есть также парабола полученная переносом первой функции вверх параллельно оси ординат на 3 единицы. Перенос демонстрируют с помощью эскиза на планшете.
График второй функции есть также парабола полученная переносом первой функции вверх параллельно оси ординат на 3 единицы. Перенос демонстрируют с помощью эскиза на планшете.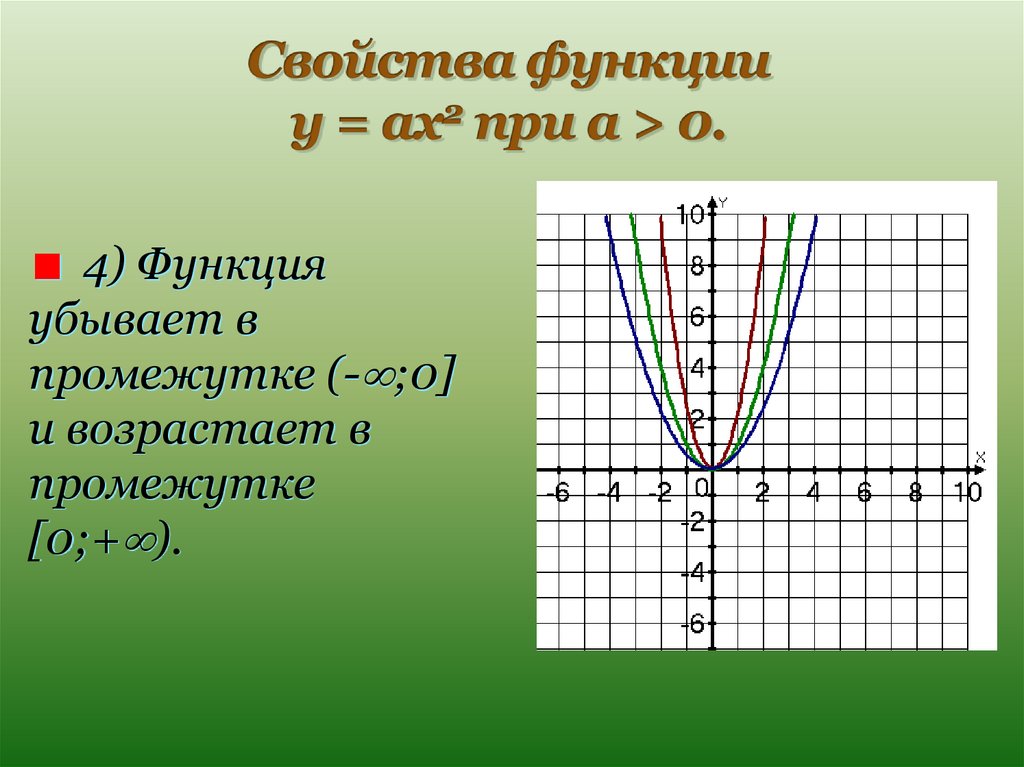 Выдвижение гипотез и проверка их на практике
Выдвижение гипотез и проверка их на практике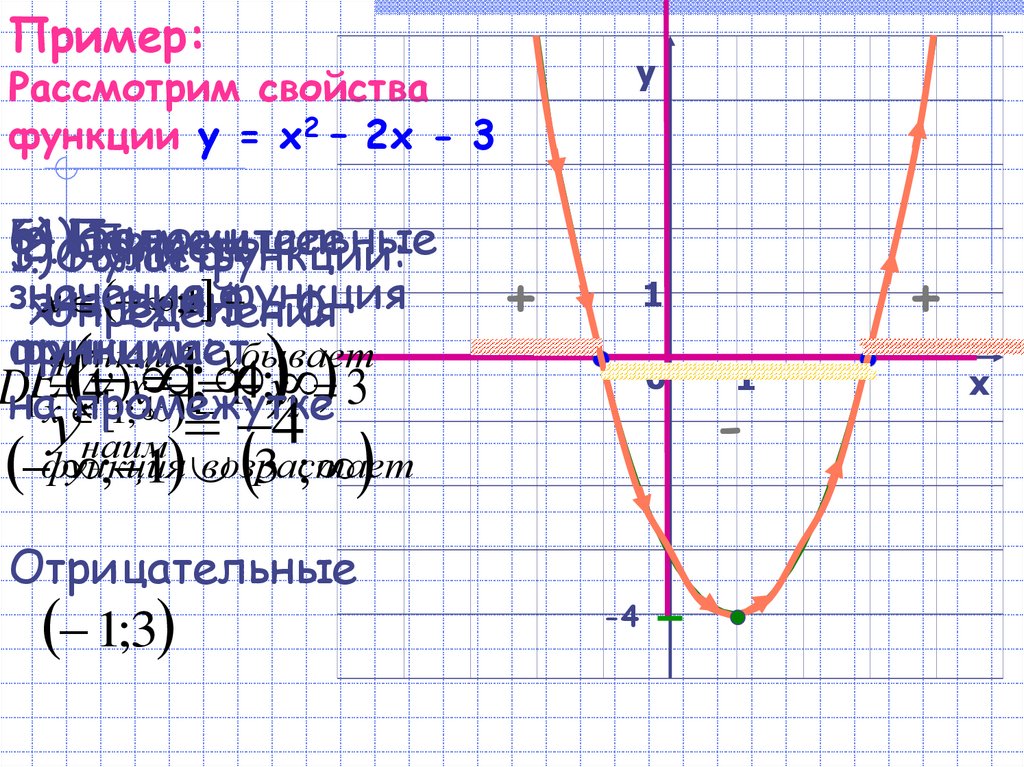
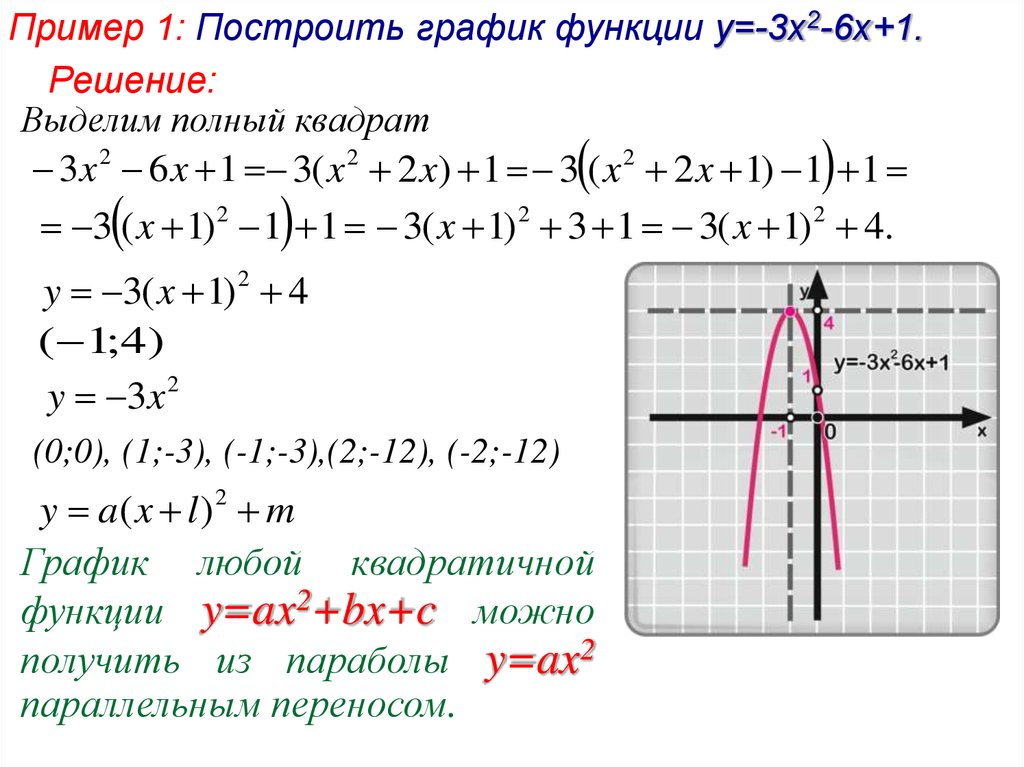

 Первичное применение полученных знаний
Первичное применение полученных знаний Домашнее задание
Домашнее задание