Логарифмическая функция
- Главная
- Справочник
- Исследование функций
- Логарифмическая функция
Основные сведения
Логарифмической функцией называется функция вида y = logax, где a > 0 и a ≠ 1.
График функции имеет следующий вид:
Рассмотрим свойства функции:
- Областью определения функции является множество всех положительных чисел D(y) = (0; +∞).
- Множеством значений функции являются все действительные числа R.
- Наименьшего и наибольшего значений функция не имеет.
- Функция не является ни нечетной, ни четной. Имеет общий вид.
- Функция непереодическая.
- Нули функции: функция пересекает координатную ось Ox в точке (1; 0).
- При a > 1 функция возрастает, при 0 < a < 1 функция убывает.

Примеры решения задач
Задание 1.
В одной координатной плоскости построить графики функций:
- y = log2x
- y = log3x
- y = log5x
- y = log10x
Решение.
Для начала построим график функции y = log2x. Для этого найдем значения функции при x = , , , 1, 2, 4, 8.
| x | 1 | 2 | 4 | 8 | |||
| y(x) | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
Отметим полученные точки на координатной плоскости, соединив их плавной линией.
Большему значению аргумента х соответствует и большее значение функции у. Функция y = log2x возрастает на всей области определения D(y)=R+, так как основание функции 2 > 1.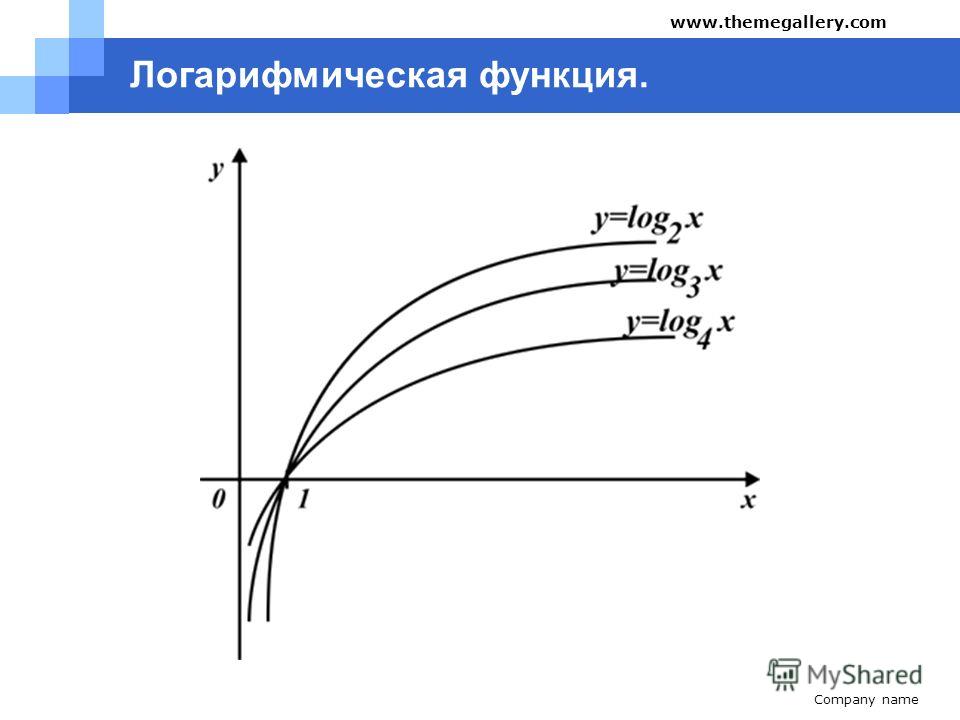
Подобным образом построим графики остальных функций.
Переменная х может принимать только положительные значения (D(y) = R+), при этом значение у может быть любым (E(y) = R).
Графики всех данных функций пересекают ось Оx в точке (0; 1), так как логарифм по любому основанию от единицы равен нулю. C осью Оy графики не пересекаются, так как логарифм по положительному основанию не может быть равен нулю.
Чем больше основание a (если a > 1) логарифмической функции y = logax, тем ближе расположена кривая к оси Оx.
Все данные функции являются возрастающими, так как большему значению аргумента соответствует и большее значение функции.
Задание 2.
В одной координатной плоскости построить графики функций:
Решение.
Для начала построим график функции. Для этого найдем значения функции при x = , , , 1, 2, 4, 8.
| x | 1 | 2 | 4 | 8 | |||
| y(x) | 3 | 2 | 1 | 0 | -1 | -2 | -3 |
Отметим полученные точки на координатной плоскости, соединив их плавной линией.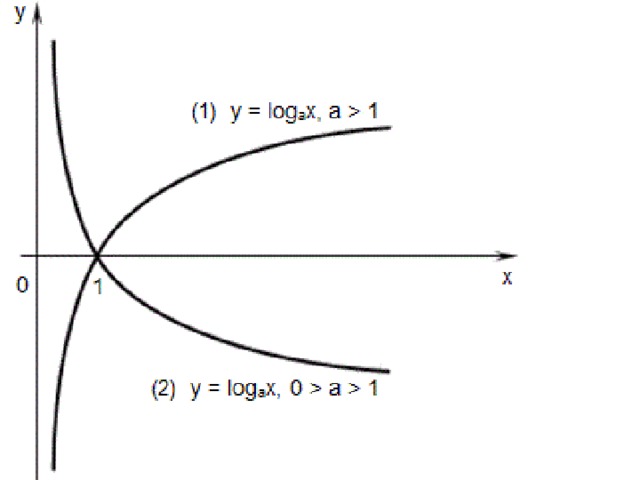
Большему значению аргумента х соответствует меньшее значение функции y. Функция убывает на всей своей области определения: D(y) = R, так как основание функции 0 < < 1.
Подобным образом построим графики остальных функций.
Переменная х может принимать только положительные значения (D(y) = R+), при этом значение у может быть любым (E(y) = R).
Графики всех данных функций пересекают ось Оx в точке (0; 1), так как логарифм по любому основанию от единицы равен нулю. С осью Оy графики не пересекаются, так как логарифм по положительному основанию не может быть равен нулю.
Чем меньше основание a (если 0 < a < 1) логарифмической функции y = logax, тем ближе расположена кривая к оси Оx.
Все данные функции являются убывающими, так как большему значению аргумента соответствует меньшее значение функции.
Задание 3.
Найти обасть определеления функции:
- y = logπ(2x-4)
- y = log2((x-1)(x+5))
Решение
1. y = logπ(2x-4).
y = logπ(2x-4).
Область определения данной функции задается следующим неравенством:
2x-4 > 0
Решим это линейное неравенство:
2x > 4 → x > 2
Ответ: D(y): (2; +∞).
2. y = log2((x-1)(x+5)).
Логарифм определен, если подлогарифмическая функция является положительной, то есть искомая область определения: D(y): (x-1)(x+5) > 0.
Решим полученное уравнение методом интервалов. Для этого найдем нули каждого из сомножителей:
x-1 = 0 → x = 1
x+5 = 0 → x = -5
Наносим их на координатную прямую и определяем знак неравенства на каждом из полученных промежутков.
Поскольку решаем неравенство со знаком «>», то оставляем промежутки со знаком «+», т. е D(y): (-∞; -5)U(1; +∞).
Ответ: D(y): (-∞; -5)U(1; +∞).
- Вперёд >
Y log x по основанию 2. Что такое логарифм
Итак, перед нами степени двойки. Если взять число из нижней строчки, то можно легко найти степень, в которую придется возвести двойку, чтобы получилось это число.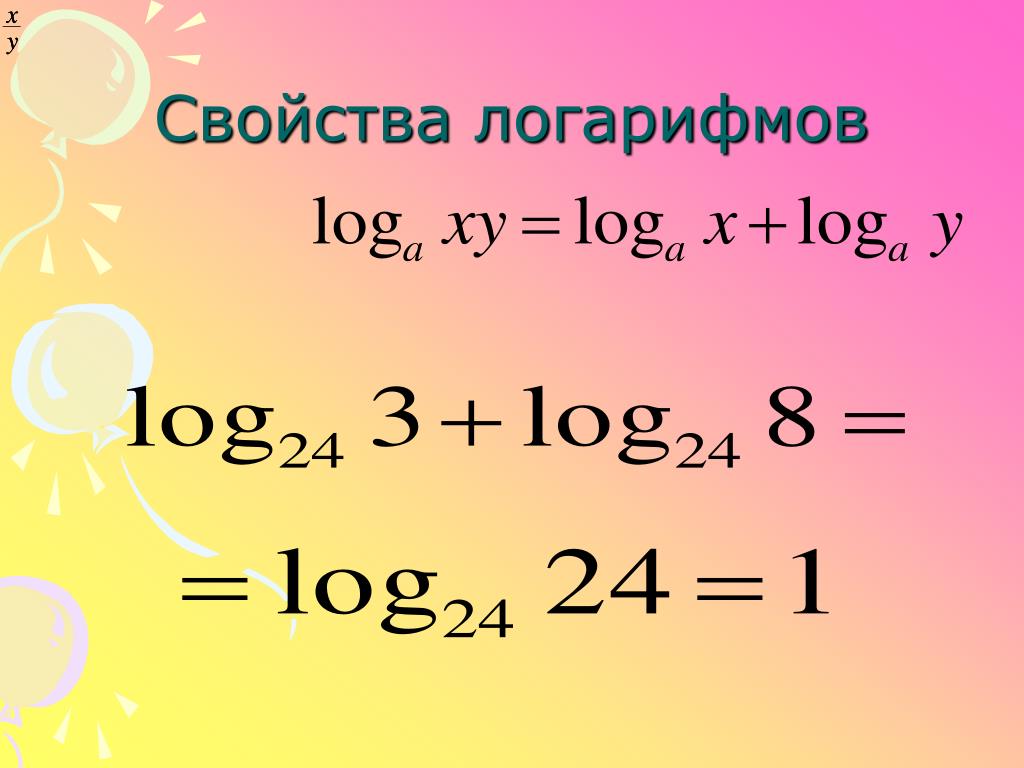 Например, чтобы получить 16, надо два возвести в четвертую степень. А чтобы получить 64, надо два возвести в шестую степень. Это видно из таблицы.
Например, чтобы получить 16, надо два возвести в четвертую степень. А чтобы получить 64, надо два возвести в шестую степень. Это видно из таблицы.
А теперь — собственно, определение логарифма:
Логарифм по основанию a от аргумента x — это степень, в которую надо возвести число a , чтобы получить число x .
Обозначение: log a x = b , где a — основание, x — аргумент, b — собственно, чему равен логарифм.
Например, 2 3 = 8 ⇒ log 2 8 = 3 (логарифм по основанию 2 от числа 8 равен трем, поскольку 2 3 = 8). С тем же успехом log 2 64 = 6 , поскольку 2 6 = 64 .
Операцию нахождения логарифма числа по заданному основанию называют логарифмированием. Итак, дополним нашу таблицу новой строкой:
| 2 1 | 2 2 | 2 3 | 2 4 | 2 5 | 2 6 |
| 2 | 4 | 8 | 16 | 32 | 64 |
| log 2 2 = 1 | log 2 4 = 2 | log 2 8 = 3 | log 2 16 = 4 | log 2 32 = 5 | log 2 64 = 6 |
К сожалению, далеко не все логарифмы считаются так легко.
Такие числа называются иррациональными: цифры после запятой можно писать до бесконечности, и они никогда не повторяются. Если логарифм получается иррациональным, его лучше так и оставить: log 2 5 , log 3 8 , log 5 100 .
Важно понимать, что логарифм — это выражение с двумя переменными (основание и аргумент). Многие на первых порах путают, где находится основание, а где — аргумент. Чтобы избежать досадных недоразумений, просто взгляните на картинку:
Перед нами — не что иное как определение логарифма. Вспомните: логарифм — это степень , в которую надо возвести основание, чтобы получить аргумент. Именно основание возводится в степень — на картинке оно выделено красным. Получается, что основание всегда находится внизу! Это замечательное правило я рассказываю своим ученикам на первом же занятии — и никакой путаницы не возникает.
С определением разобрались — осталось научиться считать логарифмы, т.е. избавляться от знака «log». Для начала отметим, что из определения следует два важных факта:
- Аргумент и основание всегда должны быть больше нуля. Это следует из определения степени рациональным показателем, к которому сводится определение логарифма.
- Основание должно быть отличным от единицы, поскольку единица в любой степени все равно остается единицей. Из-за этого вопрос «в какую степень надо возвести единицу, чтобы получить двойку» лишен смысла. Нет такой степени!
Такие ограничения называются областью допустимых значений (ОДЗ). Получается, что ОДЗ логарифма выглядит так: log a x = b ⇒ x > 0 , a > 0 , a ≠ 1 .
Заметьте, что никаких ограничений на число b (значение логарифма) не накладывается. Например, логарифм вполне может быть отрицательным: log 2 0,5 = −1 , т.к. 0,5 = 2 −1 .
Впрочем, сейчас мы рассматриваем лишь числовые выражения, где знать ОДЗ логарифма не требуется. Все ограничения уже учтены составителями задач. Но когда пойдут логарифмические уравнения и неравенства, требования ОДЗ станут обязательными. Ведь в основании и аргументе могут стоять весьма неслабые конструкции, которые совсем необязательно соответствуют приведенным выше ограничениям.
Все ограничения уже учтены составителями задач. Но когда пойдут логарифмические уравнения и неравенства, требования ОДЗ станут обязательными. Ведь в основании и аргументе могут стоять весьма неслабые конструкции, которые совсем необязательно соответствуют приведенным выше ограничениям.
Теперь рассмотрим общую схему вычисления логарифмов. Она состоит из трех шагов:
- Представить основание a и аргумент x в виде степени с минимально возможным основанием, большим единицы. Попутно лучше избавиться от десятичных дробей;
- Решить относительно переменной b уравнение: x = a b ;
- Полученное число b будет ответом.
Вот и все! Если логарифм окажется иррациональным, это будет видно уже на первом шаге. Требование, чтобы основание было больше единицы, весьма актуально: это снижает вероятность ошибки и значительно упрощает выкладки. Аналогично с десятичными дробями: если сразу перевести их в обычные, ошибок будет в разы меньше.
Посмотрим, как работает эта схема на конкретных примерах:
Задача.
Вычислите логарифм: log 5 25
- Представим основание и аргумент как степень пятерки: 5 = 5 1 ; 25 = 5 2 ;
- Получили ответ: 2.
Составим и решим уравнение:
log 5 25 = b
⇒ (5 1) b
= 5 2 ⇒ 5 b
= 5 2 ⇒ b
= 2 ;
Задача. Вычислите логарифм:
Задача. Вычислите логарифм: log 4 64
- Представим основание и аргумент как степень двойки: 4 = 2 2 ; 64 = 2 6 ;
- Составим и решим уравнение:
- Получили ответ: 3.
Задача. Вычислите логарифм: log 16 1
- Представим основание и аргумент как степень двойки: 16 = 2 4 ; 1 = 2 0 ;
- Составим и решим уравнение:
log 16 1 = b ⇒ (2 4) b = 2 0 ⇒ 2 4b = 2 0 ⇒ 4b = 0 ⇒ b = 0 ; - Получили ответ: 0.
Задача. Вычислите логарифм: log 7 14
- Представим основание и аргумент как степень семерки: 7 = 7 1 ; 14 в виде степени семерки не представляется, поскольку 7 1
- Из предыдущего пункта следует, что логарифм не считается;
- Ответ — без изменений: log 7 14.

Небольшое замечание к последнему примеру. Как убедиться, что число не является точной степенью другого числа? Очень просто — достаточно разложить его на простые множители. Если в разложении есть хотя бы два различных множителя, число не является точной степенью.
Задача. Выясните, являются ли точными степенями числа: 8; 48; 81; 35; 14 .
8 = 2 · 2 · 2 = 2 3 — точная степень, т.к. множитель всего один;
48 = 6 · 8 = 3 · 2 · 2 · 2 · 2 = 3 · 2 4 — не является точной степенью, поскольку есть два множителя: 3 и 2;
81 = 9 · 9 = 3 · 3 · 3 · 3 = 3 4 — точная степень;
35 = 7 · 5 — снова не является точной степенью;
14 = 7 · 2 — опять не точная степень;
Заметим также, что сами простые числа всегда являются точными степенями самих себя.
Десятичный логарифм
Некоторые логарифмы встречаются настолько часто, что имеют специальное название и обозначение.
Десятичный логарифм от аргумента x — это логарифм по основанию 10, т.
е. степень, в которую надо возвести число 10, чтобы получить число x . Обозначение: lg x .
Например, lg 10 = 1; lg 100 = 2; lg 1000 = 3 — и т.д.
Отныне, когда в учебнике встречается фраза типа «Найдите lg 0,01», знайте: это не опечатка. Это десятичный логарифм. Впрочем, если вам непривычно такое обозначение, его всегда можно переписать:
lg x
= log 10 x
Все, что верно для обычных логарифмов, верно и для десятичных.
Натуральный логарифм
Существует еще один логарифм, который имеет собственное обозначение. В некотором смысле, он даже более важен, чем десятичный. Речь идет о натуральном логарифме.
Натуральный логарифм от аргумента x — это логарифм по основанию e , т.е. степень, в которую надо возвести число e , чтобы получить число x . Обозначение: ln x .
Многие спросят: что еще за число e
? Это иррациональное число, его точное значение найти и записать невозможно. Приведу лишь первые его цифры:
e
= 2,718281828459.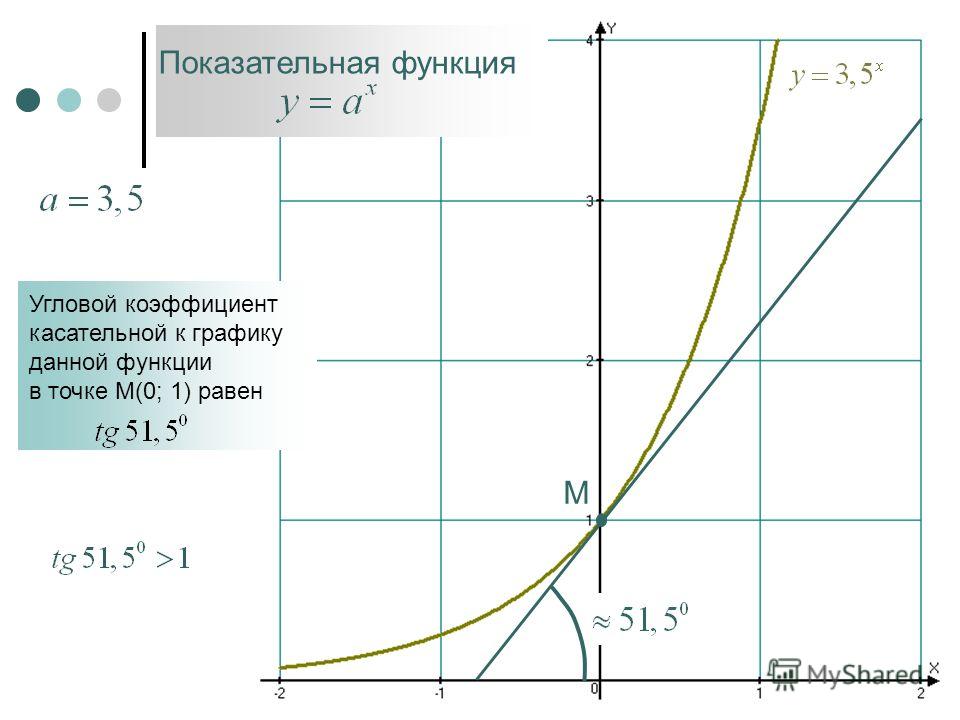 {-5}=\)\(\frac{1}{32}\)
{-5}=\)\(\frac{1}{32}\)
Аргумент и основание логарифма
Любой логарифм имеет следующую «анатомию»:
Аргумент логарифма обычно пишется на его уровне, а основание — подстрочным шрифтом ближе к знаку логарифма. А читается эта запись так: «логарифм двадцати пяти по основанию пять».
Как вычислить логарифм?
Чтобы вычислить логарифм — нужно ответить на вопрос: в какую степень следует возвести основание, чтобы получить аргумент?
Например , вычислите логарифм: а) \(\log_{4}{16}\) б) \(\log_{3}\)\(\frac{1}{3}\) в) \(\log_{\sqrt{5}}{1}\) г) \(\log_{\sqrt{7}}{\sqrt{7}}\) д) \(\log_{3}{\sqrt{3}}\)
а) В какую степень надо возвести \(4\), чтобы получить \(16\)? Очевидно во вторую. Поэтому:
\(\log_{4}{16}=2\)
\(\log_{3}\)\(\frac{1}{3}\) \(=-1\)
в) В какую степень надо возвести \(\sqrt{5}\), чтобы получить \(1\)? А какая степень делает любое число единицей? Ноль, конечно!
\(\log_{\sqrt{5}}{1}=0\)
г) В какую степень надо возвести \(\sqrt{7}\), чтобы получить \(\sqrt{7}\)? В первую – любое число в первой степени равно самому себе. {b}=c\) \(\Leftrightarrow\) \(\log_{a}{c}=b\)
{b}=c\) \(\Leftrightarrow\) \(\log_{a}{c}=b\)
\(\log_{4}{10}=5x-4\)
Зеркально перевернем уравнение, чтобы икс был слева
\(5x-4=\log_{4}{10}\)
Перед нами . Перенесем \(4\) вправо.
И не пугайтесь логарифма, относитесь к нему как к обычному числу.
\(5x=\log_{4}{10}+4\)
Поделим уравнение на 5
\(x=\)\(\frac{\log_{4}{10}+4}{5}\)
Вот наш корень. Да, выглядит непривычно, но ответ не выбирают.
Ответ : \(\frac{\log_{4}{10}+4}{5}\)
Десятичный и натуральный логарифмы
Как указано в определении логарифма, его основанием может быть любое положительное число, кроме единицы \((a>0, a\neq1)\). И среди всех возможных оснований есть два встречающихся настолько часто, что для логарифмов с ними придумали особую короткую запись:
Натуральный логарифм: логарифм, у которого основание — число Эйлера \(e\) (равное примерно \(2,7182818…\)), и записывается такой логарифм как \(\ln{a}\).
 {\log_{6}{5}}\)
{\log_{6}{5}}\)Решение :
Ответ : \(25\)
Как число записать в виде логарифма?
Как уже было сказано выше – любой логарифм это просто число. Верно и обратное: любое число может быть записано как логарифм. Например, мы знаем, что \(\log_{2}{4}\) равен двум. Тогда можно вместо двойки писать \(\log_{2}{4}\).
Но \(\log_{3}{9}\) тоже равен \(2\), значит, также можно записать \(2=\log_{3}{9}\) . Аналогично и с \(\log_{5}{25}\), и с \(\log_{9}{81}\), и т.д. То есть, получается
\(2=\log_{2}{4}=\log_{3}{9}=\log_{4}{16}=\log_{5}{25}=\log_{6}{36}=\log_{7}{49}…\)
Таким образом, если нам нужно, мы можем где угодно (хоть в уравнении, хоть в выражении, хоть в неравенстве) записывать двойку как логарифм с любым основанием – просто в качестве аргумента пишем основание в квадрате.
Точно также и с тройкой – ее можно записать как \(\log_{2}{8}\), или как \(\log_{3}{27}\), или как \(\log_{4}{64}\)… Здесь мы как аргумент пишем основание в кубе:
\(3=\log_{2}{8}=\log_{3}{27}=\log_{4}{64}=\log_{5}{125}=\log_{6}{216}=\log_{7}{343}.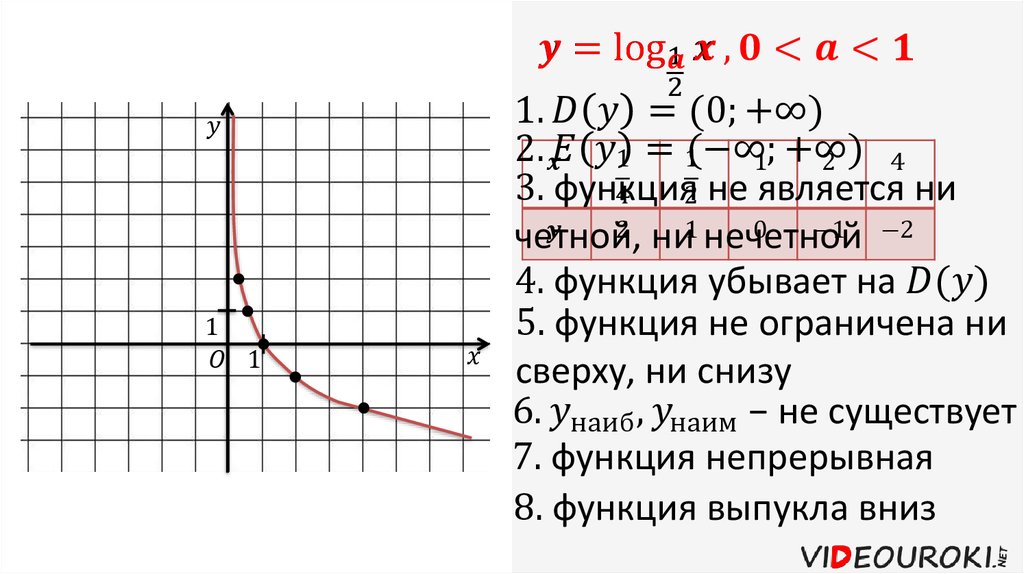 {a}}\)
{a}}\)
Пример : Найдите значение выражения \(\frac{\log_{2}{14}}{1+\log_{2}{7}}\)
Решение :
Ответ : \(1\)
логарифм по основанию 10
—
Тематики
EN
- logarithm to base 10
- logarithm to the base 10
2 logarithm to the base 10
- логарифм по основанию 10
логарифм по основанию 10
—
[Л.Г.Суменко. Англо-русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.]
Тематики
- информационные технологии в целом
EN
- logarithm to base 10
- logarithm to the base 10
3 base 2 logarithmic representation
- логарифм по основанию 2
логарифм по основанию 2
—
[Л.Г.Суменко. Англо-русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.]
Тематики
- информационные технологии в целом
EN
- base 2 logarithmic representation
4 logarithm of a to base b
5 logarithm of a to base b
логарифм числа a по основанию b
См.
 также в других словарях:
также в других словарях:логарифм по основанию 10 — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN logarithm to base 10logarithm to the base 10 …
логарифм по основанию 2 — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN base 2 logarithmic representation … Справочник технического переводчика
ЛОГАРИФМ — ЛОГАРИФМ, вспомогательный прием (формула) для произведения вычислений, выведенный в 1614 г. Джоном НЕПЕРОМ и разработанный впоследствии английским математиком Генри Бриггсом (1561 1631). Логарифмом числа () является показатель степени (х), в… … Научно-технический энциклопедический словарь
ЛОГАРИФМ — (logarithm) Степень, в которую надо возвести какое либо служащее основанием число, большее 1, чтобы получить какое либо определенное положительное число. Если х является логарифмом с основанием у от z, то z=уx. Логарифмы имеют такое свойство, что … Экономический словарь
Если х является логарифмом с основанием у от z, то z=уx. Логарифмы имеют такое свойство, что … Экономический словарь
ЛОГАРИФМ Современная энциклопедия
Логарифм — (от греческого logos отношение и arithmos число) числа N по основанию a (O … Иллюстрированный энциклопедический словарь
Логарифм — График двоичного логарифма Логарифм числа … Википедия
ЛОГАРИФМ — число, применение которого позволяет упростить многие сложные операции арифметики. Использование в вычислениях вместо чисел их логарифмов позволяет заменить умножение более простой операцией сложения, деление вычитанием, возведение в степень… … Энциклопедия Кольера
Логарифм — числа N по основанию а, показатель степени m, в которую следует возвести число а (основание Л.), чтобы получить N; обозначается logaN. Итак, m = logaN, если ам = N. Например, log10 100 = 2; log2 1/32 = 5; loga 1 = 0, т. к. 100 = 102, 1/32 … Большая советская энциклопедия
ЛОГАРИФМ — числа Nпо основанию а показатель степени т, в к рую следует возвести число (основание Л. ), чтобы получить N;обозначается logaN, т. е. m=logaN, если am=N. Каждому положительному числу соответствует при данном основании единственный действительный… … Математическая энциклопедия
), чтобы получить N;обозначается logaN, т. е. m=logaN, если am=N. Каждому положительному числу соответствует при данном основании единственный действительный… … Математическая энциклопедия
ЛОГАРИФМ — [от греч. logos слово, здесь (соотношение и arithmos число] числа N по основанию а показатель степени т, в к рую следует возвести а, чтобы получить N; обозначается logаN. Т. о., т = logaN, если ат = N (предполагается, что а > 0, а не равно 1).… … Большой энциклопедический политехнический словарь
Свойства логарифмов — формулы. Что такое логарифм. Как посчитать логарифм. Свойства логарифмов. Примеры решения логарифмов
Содержание
- Условия определения логарифма.
- Графики логарифма
- Основные методы решения
- Логарифм как обратная функция к показательной
- Особенности логарифмов.
- Что такое логарифм и как его посчитать
- Примеры решения
- Вторая задача
- Третий пример
- Замечание по поводу области определения
- Область определения, множество значений, возрастание, убывание
- Когда нужная степень не подбирается
- Типичные ошибки при решении
- Метод группировки
- Обратный логарифм
- Частные значения
- Логарифмы со специальным обозначением
- Десятичный логарифм
- Натуральный логарифм
- Таблица свойств логарифмов
- Основные формулы логарифмов
- Виды логарифмов
- Логарифмы
Условия определения логарифма.

Стоит отдельно рассмотреть условия a > 0, a ≠ 1, b > 0.при которых дается определение логарифма. Рассмотрим, почему взяты эти ограничения. В это нам поможет равенство вида x = logαb , называемое основным логарифмическим тождеством, которое напрямую следует из данного выше определения логарифма.
Возьмем условие a≠1. Поскольку единица в любой степени равна единице, то равенство x=logαb может существовать лишь при b=1, но при этом log1 1 будет любым действительным числом. Для исключения этой неоднозначности и берется a≠1.
Докажем необходимость условия a>0. При a=0 по формулировке логарифма может существовать только при b=0. И соответственно тогда log00 может быть любым отличным от нуля действительным числом, так как нуль в любой отличной от нуля степени есть нуль. Исключить эту неоднозначность дает условие a≠0. А при a<0 нам бы пришлось отвергнуть разбор рациональных и иррациональных значений логарифма, поскольку степень с рациональным и иррациональным показателем определена лишь для неотрицательных оснований. Именно по этой причине и оговорено условие a>0.
Именно по этой причине и оговорено условие a>0.
И последнее условие b>0 вытекает из неравенства a>0, поскольку x=logαb, а значение степени с положительным основанием a всегда положительно.
Графики логарифма
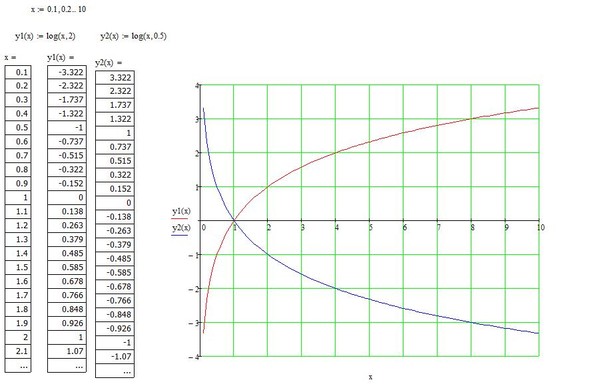
Графики логарифма y = loga x при различных значениях основания a.График логарифма получается из графика показательной функции зеркальным отражением относительно прямой y = x. Слева изображены графики функции y = loga x для четырех значений основания логарифма: a = 2, a = 8, a = 1/2 и a = 1/8. На графике видно, что при a > 1 логарифм монотонно возрастает. С увеличением x рост существенно замедляется. При 0 < a < 1 логарифм монотонно убывает.
Основные методы решения
Существует множество способов решения таких конструкций. Например, большинство учителей в школе предлагают такой способ: Сразу выразить функцию f (x) по формуле f (x) = ab. Т. е.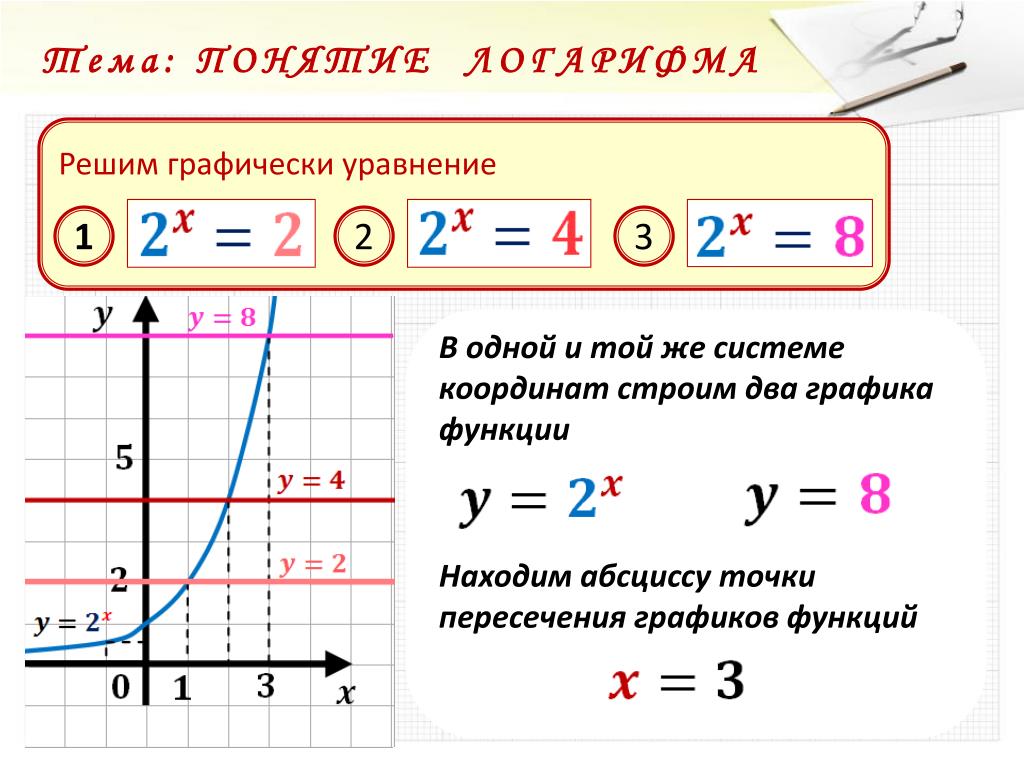 когда вы встречаете простейшую конструкцию, сразу без дополнительных действий и построений можете перейти к решению.
когда вы встречаете простейшую конструкцию, сразу без дополнительных действий и построений можете перейти к решению.
Да, безусловно, решение получится правильным. Однако проблема этой формулы состоит в том, что большинство учеников не понимают, откуда она берется и почему именно букву а мы возводим в букву b.
В результате я часто наблюдаю очень обидные ошибки, когда, например, эти буквы меняются местами. Данную формулу нужно либо понять, либо зубрить, причем второй способ приводит к ошибкам в самые неподходящие и самые ответственные моменты: на экзаменах, контрольных и т. д.
Именно поэтому всем своим ученикам я предлагаю отказаться от стандартной школьной формулы и использовать для решения логарифмических уравнений второй подход, который, как вы уже наверняка догадались из названия, называется канонической формой.
Идея канонической формы проста. Давайте еще раз посмотрим на нашу задачу: слева у нас есть loga, при этом под буквой a имеется в виду именно число, а ни в коем случае не функция, содержащая переменную х. Следовательно, на эту букву распространяются все ограничения, которые накладываются на основание логарифма. а именно:
Следовательно, на эту букву распространяются все ограничения, которые накладываются на основание логарифма. а именно:
1 ≠ a > 0
С другой стороны, из того же самого уравнения мы видим, что логарифм должен быть равен числу b, и вот на эту букву никаких ограничений не накладывается, потому что он может принимать любые значения — как положительные, так и отрицательные. Все зависит от того, какие значения принимает функция f (x).
И вот тут мы вспоминаем наше замечательное правило, что любое число b может быть представлено в виде логарифма по основанию а от а в степени b:
b = loga ab
Как запомнить эту формулу? Да очень просто. Давайте запишем следующую конструкцию:
b = b · 1 = b · loga a
Разумеется, что при этом возникают все ограничения, которые мы записали вначале. А теперь давайте воспользуемся основным свойством логарифма, и внесем множитель b в качестве степени а. Получим:
b = b · 1 = b · loga a = loga ab
В результате исходное уравнение перепишется в следующем виде:
loga f (x) = loga ab → f (x) = ab
Вот и все. Новая функция уже не содержит логарифма и решается стандартными алгебраическими приемами.
Новая функция уже не содержит логарифма и решается стандартными алгебраическими приемами.
Конечно, кто-то сейчас возразит: а зачем вообще было придумывать какую-то каноническую формулу, зачем выполнять два дополнительных ненужных шага, если можно было сразу перейти от исходной конструкции к итоговой формуле? Да уже хотя бы затем, что большинство учеников не понимают, откуда берется эта формула и, как следствие, регулярно допускают ошибки при ее применении.
А вот такая последовательность действий, состоящая из трех шагов, позволяет вам решить исходное логарифмическое уравнение, даже если вы не понимаете, откуда берется та самая итоговая формула. Кстати, канонической формулой называется именно эта запись:
loga f (x) = loga ab
Удобство канонической формы состоит еще и в том, что ее можно применять для решения очень широкого класса логарифмических уравнений, а не только простейших, которые мы рассматриваем сегодня.
Логарифм как обратная функция к показательной
Логарифмическая функция y = logb(x) является обратной функцией к показательной x=b y.
Так что, если мы вычислим показательную функцию логарифма х (х > 0), получится:
f (f -1(x)) = blogb(x) = x
Или если мы вычислим логарифм показательной функции х:
f -1(f (x)) = logb(bx) = x
Особенности логарифмов.
Логарифмы характеризуются отличительными особенностями, которые обусловили их повсеместное употребление для значительного облегчения кропотливых расчетов. При переходе «в мир логарифмов» умножение трансформируется на значительно более легкое сложение, деление — на вычитание, а возведение в степень и извлечение корня трансформируются соответствующе в умножение и деление на показатель степени.
Формулировку логарифмов и таблицу их значений (для тригонометрических функций) впервые издал в 1614 году шотландский математик Джон Непер.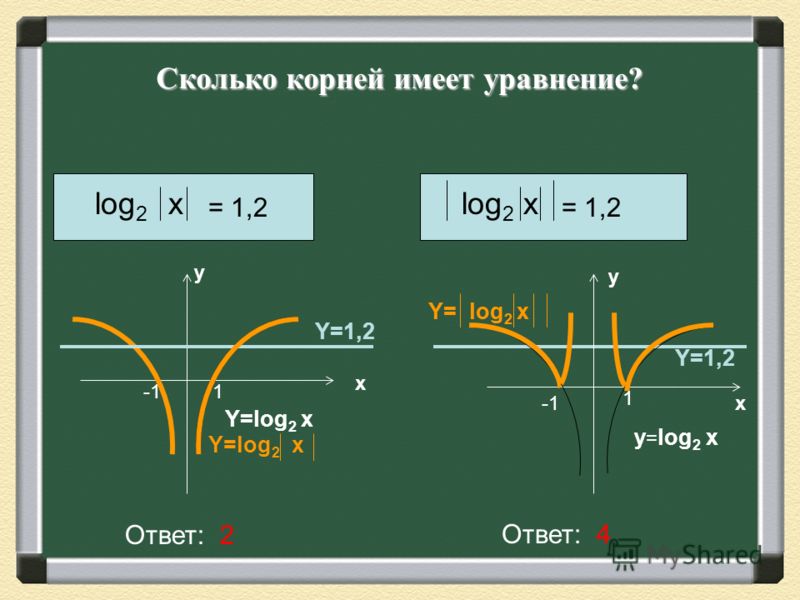 Логарифмические таблицы, увеличенные и детализированные прочими учеными, широко использовались при выполнении научных и инженерных вычислений, и оставались актуальными пока не стали применяться электронные калькуляторы и компьютеры.
Логарифмические таблицы, увеличенные и детализированные прочими учеными, широко использовались при выполнении научных и инженерных вычислений, и оставались актуальными пока не стали применяться электронные калькуляторы и компьютеры.
Что такое логарифм и как его посчитать
Логарифм имеет следующий вид:
где a – это основание логарифма,
b – это аргумент логарифма
Чтобы узнать значение логарифма приравняем его к X.и преобразовываем ви преобразовываем вЗапомните, что именно основание (оно выделено красным) возводится в степень.
Чтобы было легче, можно запоминать так – основание всегда остается внизу (и в первом, и во втором выражении a внизу)!
Приведем пример:
Чтобы вычислить данный логарифм, необходимо приравнять его к X и воспользоваться правилом, описанным выше:А в какую степень нужно возвести 2, чтобы получилось 8? Конечно же в третью степень, таким образом:
Еще раз обращаю ваше внимание, что основание (в нашем случае это – 2) всегда находится внизу и именно оно возводится в степень.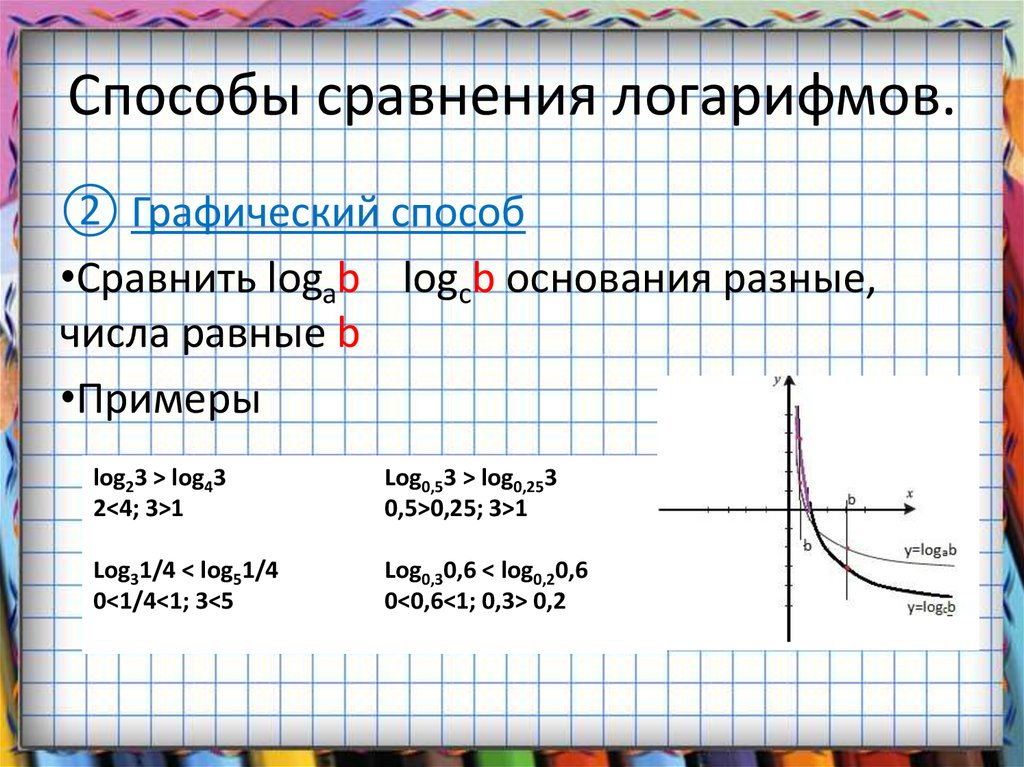
Еще примеры:
Примеры решения
А теперь давайте рассмотрим реальные примеры. Итак, решаем:
log0,5 (3x − 1) = −3
Давайте перепишем его следующим образом:
log0,5 (3x − 1) = log0,5 0,5−3
Многие ученики торопятся и пытаются сразу возвести число 0,5 в степень, которая пришла к нам из исходной задачи. И действительно, когда вы уже хорошо натренируетесь в решении подобных задач, вы можете сразу выполнять этот шаг.
Однако если сейчас вы только приступаете к изучению этой темы, лучше никуда не торопиться, чтобы не допускать обидных ошибок. Итак, перед нами каноническая форма. Имеем:
3x − 1 = 0,5−3
Это уже не логарифмическое уравнение, а линейное относительно переменной х. Чтобы решить его, давайте для начала разберемся с числом 0,5 в степени −3. Заметим, что 0,5 — это 1/2.
(1/2) −3 = (2/1)3 = 8
Все десятичные дроби переводите в обычные, когда вы решаете логарифмическое уравнение.
Переписываем и получаем:
3x − 1 = 8
3x = 9
x = 3
Все, мы получили ответ. Первая задача решена.
Вторая задача
Переходим ко второй задаче:
Как видим, это уравнение уже не является простейшим. Уже хотя бы потому, что слева стоит разность, а не один-единственный логарифм по одному основанию.
Следовательно, нужно каким-то образом избавиться от этой разности. В данном случае все очень просто. Давайте внимательно посмотрим на основания: слева стоит число под корнем:
Общая рекомендация: во всех логарифмических уравнениях старайтесь избавиться от радикалов, т. е. от записей с корнями и переходить к степенным функциям, просто потому что показатели этих степеней легко выносятся за знак логарифма и в конечном счета такая запись существенно упрощает и ускоряет вычисления. Вот давайте так и запишем:
Теперь вспоминаем замечательное свойство логарифма: из аргумента, а также из основания можно выносить степени.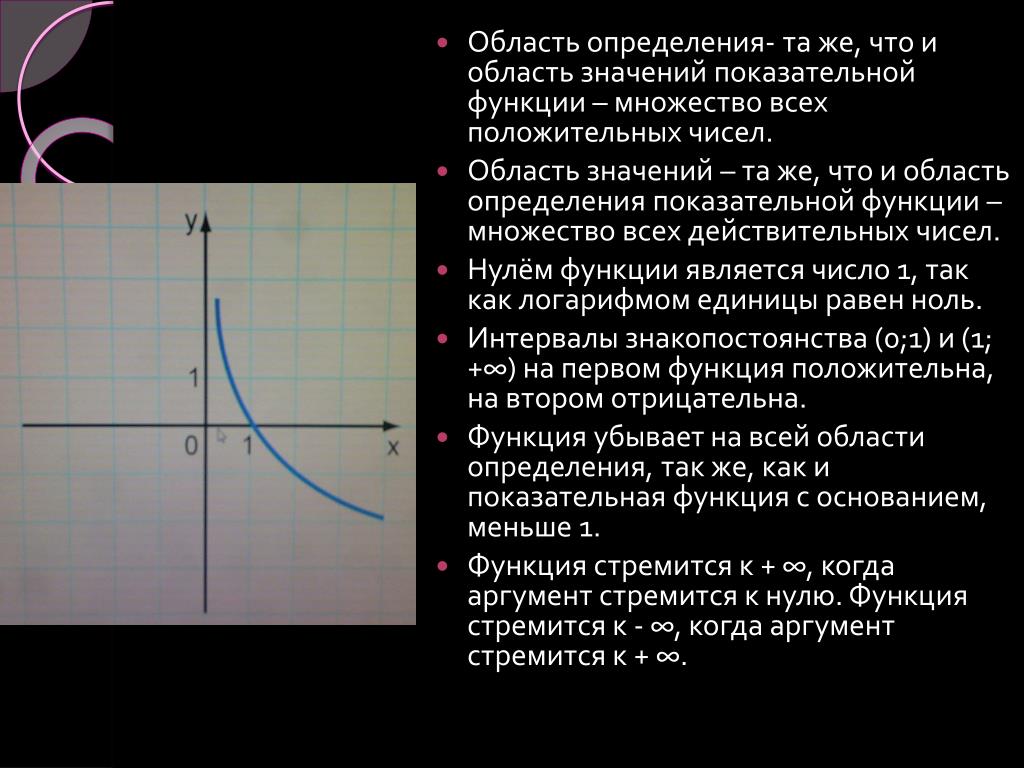 В случае с основаниями происходит следующее:
В случае с основаниями происходит следующее:
logak b = 1/k loga b
Другими словами, число, которое стояло в степени основания, выносится вперед и при этом переворачивается, т. е. становится обратным числом. В нашем случае стояла степень основания с показателем 1/2. Следовательно, мы можем вынести ее как 2/1. Получим:
5 · 2 log5 x − log5 x = 18
10 log5 x − log5 x = 18
Обратите внимание: ни в коем случае нельзя избавляться от логарифмов на этом шаге. Вспомните математику 4—5 класса и порядок действий: сначала выполняется умножение, а лишь затем — сложение и вычитание. В данном случае мы из 10 элементов вычитаем один такой же:
9 log5 x = 18
log5 x= 2
Теперь наше уравнение выглядит как надо. Это простейшая конструкция, и мы решаем его с помощью канонической формы:
log5 x = log5 52
x = 52
x = 25
Вот и все. Вторая задача решена.
Вторая задача решена.
Третий пример
Переходим к третьей задаче:
lg (x + 3) = 3 + 2 lg 5
Напомню следующую формулу:
lg b = log10 b
Если вас по каким-либо причинам смущает запись lg b, то при выполнении всех вычислений вы можете записать просто log10 b. С десятичными логарифмами можно работать так же, как и с другими: выносить степени, складывать и представлять любые числа в виде lg 10.
Вот именно этими свойствами мы сейчас и воспользуемся для решения задачи, поскольку она не является простейшей, которую мы записали в самом начале нашего урока.
Для начала заметим, что множитель 2, стоящий перед lg 5, может быть внесен и станет степенью основания 5. Кроме того, свободное слагаемое 3 также представимо в виде логарифма — это очень легко наблюдать из нашей записи.
Судите сами: любое число можно представить в виде log по основанию 10:
3 = log10 103 = lg 103
Перепишем исходную задачу с учетом полученных изменений:
lg (x − 3) = lg 1000 + lg 25
lg (x − 3) = lg 1000 · 25
lg (x − 3) = lg 25 000
Перед нами снова каноническая форма, причем мы получили ее, минуя стадию преобразований, т. е. простейшее логарифмическое уравнение у нас нигде не всплывало.
е. простейшее логарифмическое уравнение у нас нигде не всплывало.
Именно об этом я и говорил в самом начале урока. Каноническая форма позволяет решать более широкий класс задач, нежели стандартная школьная формула, которую дают большинство школьных учителей.
Ну и все, избавляемся от знака десятичного логарифма, и получаем простую линейную конструкцию:
x + 3 = 25 000
x = 24 997
Все! Задача решена.
Замечание по поводу области определения
Тут бы хотелось привести важное замечание по поводу области определения. Наверняка сейчас найдутся ученики и учителя, которые скажут: «Когда мы решаем выражения с логарифмами, необходимо обязательно помнить, что аргумент f (x) должен быть больше нуля!» В связи с этим возникает логичный вопрос: почему ни в одной из рассмотренных задач мы не требовали, чтобы это неравенство выполнялось?
Не переживайте. Никаких лишних корней в этих случаях не возникнет. И это еще одна замечательная хитрость, которая позволяет ускорить решение. Просто знайте, что если в задаче переменная х встречается лишь в одном месте (а точнее — в одном-единственном аргументе одного-единственного логарифма), и больше нигде в нашем случае нет переменной х, то записывать область определения не нужно, потому что она будет выполняться автоматически.
Просто знайте, что если в задаче переменная х встречается лишь в одном месте (а точнее — в одном-единственном аргументе одного-единственного логарифма), и больше нигде в нашем случае нет переменной х, то записывать область определения не нужно, потому что она будет выполняться автоматически.
Судите сами: в первом уравнении мы получили, что 3х − 1, т. е. аргумент должен быть равен 8. Это автоматически означает, что 3х − 1 будет больше нуля.
С тем же успехом мы можем записать, что во втором случае х должен быть равен 52, т. е. он заведомо больше нуля. А в третьем случае, где х + 3 = 25 000, т. е. опять же заведомо больше нуля. Другими словами, область определения выполняется автоматически, но только при условии, что х встречается лишь в аргументе лишь одного логарифма.
Вот и все, что нужно знать для решения простейших задач. Уже одно это правило вместе с правилами преобразования позволит вам решать очень широкий класс задач.
Но давайте будем честными: для того, чтобы окончательно разобраться с этим приемом, чтобы научиться применять каноническую форму логарифмического уравнения, недостаточно просто посмотреть один видеоурок. Поэтому прямо сейчас скачайте варианты для самостоятельного решения, которые прилагаются к данному видеоуроку и начните решать хотя бы одну из этих двух самостоятельных работ.
Поэтому прямо сейчас скачайте варианты для самостоятельного решения, которые прилагаются к данному видеоуроку и начните решать хотя бы одну из этих двух самостоятельных работ.
Времени у вас уйдет буквально несколько минут. А вот эффект от такого обучения будет намного выше по сравнению с тем, если бы вы просто просмотрели данный видеоурок.
Надеюсь, этот урок поможет разобраться вам с логарифмическими уравнениями. Применяйте каноническую форму, упрощайте выражения с помощью правил работы с логарифмами — и никакие задачи вам будут не страшны. А у меня на сегодня все.
Область определения, множество значений, возрастание, убывание
Логарифм является монотонной функцией, поэтому экстремумов не имеет. Основные свойства логарифма представлены в таблице.
| 1″ class=”MathJax_SVG sprite”> | ||
| Область определения | 0 < x < + ∞ | 0 < x < + ∞ |
| Область значений | – ∞ < y < + ∞ | – ∞ < y < + ∞ |
| Монотонность | монотонно возрастает | монотонно убывает |
| Нули, y = 0 | x = 1 | x = 1 |
| Точки пересечения с осью ординат, x = 0 | нет | нет |
| + ∞ | – ∞ | |
| – ∞ | + ∞ |
Когда нужная степень не подбирается
Как я уже говорил, далеко не всегда удается подобрать такую степень. Но это не значит, что такого числа не существует, просто его можно вычислить только на калькуляторе.
Но это не значит, что такого числа не существует, просто его можно вычислить только на калькуляторе.
Например, . Видим, что это число расположено между и , и это понятно: ведь это значит, чтобы получить , нужно возводить в степень больше , но меньше .
На ЕГЭ пользоваться калькулятором нельзя, но даже если бы было можно, нельзя записывать приближенные вычисления. Поэтому, если перед нами задача первой части, ответ обязательно должен получиться «хороший», и его можно посчитать в уме. В письменной части могут попасться и «плохие» числа; в этом случае пугаться не нужно, в ответе можно просто написать логарифм. Например, ответ вполне может выглядеть так: , или даже так: .
Но увлекаться и халтурить тоже не стоит – если в ответе оставить , высший балл за задачу не поставят. То есть, если ответ возможно упростить и представить в виде рационального числа, это обязательно нужно будет сделать. Потренируйся на следующих простых примерах:
Типичные ошибки при решении
Сегодня мы разберем два типичных логарифмических уравнения, на которых спотыкаются многие ученики. На примере этих уравнения мы увидим, какие ошибки чаще всего допускаются в процессе решения и преобразования исходных выражений.
На примере этих уравнения мы увидим, какие ошибки чаще всего допускаются в процессе решения и преобразования исходных выражений.
Метод группировки
Сегодня мы разберем два логарифмических уравнения, одно из которых не решается «напролом» и требует специальных преобразований, а второе… впрочем, не буду рассказывать все сразу. Смотрите видео, скачивайте самостоятельную работу — и учитесь решать сложные задачи.Итак, группировка и вынесение общих множителей за скобку. Дополнительно я расскажу вам, какие подводные камни несет область определения логарифмов, и как небольшие замечания по области определений могут существенно менять как корни, так и все решение.
Начнем из группировки. Нам нужно решить следующее логарифмическое уравнение:
log2 x · log2 (x − 3) + 1 = log2 (x2 − 3x)
В первую очередь отметим, что x2 − 3x можно разложить на множители:
log2 x(x− 3)
Затем вспоминаем замечательную формулу:
loga fg = loga f + loga g
Сразу же небольшое замечание: данная формула прекрасно работает, когда а, f и g— обычные числа. Но когда вместо них стоят функции, данные выражения перестают быть равноправными. Представьте себе такую гипотетическую ситуацию:
Но когда вместо них стоят функции, данные выражения перестают быть равноправными. Представьте себе такую гипотетическую ситуацию:
f < 0; g < 0
В этом случае произведение fg будет положительным, следовательно, loga (fg) будет существовать, а вот loga f и loga g отдельно существовать не будут, и выполнить такое преобразование мы не сможем.
Игнорирование данного факта приведет к сужению области определения и, как следствие, к потере корней. Поэтому прежде чем выполнять такое преобразование, нужно обязательно заранее убедиться, что функции f и g положительные.
В нашем случае все просто. Поскольку в исходном уравнении есть функция log2 x, то x > 0 (ведь переменная x стоит в аргументе). Также имеется log2 (x − 3), поэтому x − 3 > 0.
Следовательно, в функции log2 x(x − 3) каждый множитель будет больше нуля. Поэтому можно смело раскладывать произведение на сумму:
log2 x log2 (x − 3) + 1 = log2 x + log2 (x − 3)
log2 x log2 (x − 3) + 1 − log2 x− log2 (x − 3) = 0
На первый взгляд может показаться, что легче не стало. Напротив: количество слагаемых лишь увеличились! Чтобы понять, как действовать дальше, введем новые переменные:
Напротив: количество слагаемых лишь увеличились! Чтобы понять, как действовать дальше, введем новые переменные:
log2 x = а
log2 (x − 3) = b
Получим:
a· b + 1 − a − b = 0
А теперь сгруппируем третье слагаемое с первым:
(a · b − a) + (1 − b) = 0
a(1 · b − 1) + (1 − b) = 0
Заметим, что и в первой, и во второй скобке стоит b− 1 (во втором случае придется вынести «минус» за скобку). Разложим нашу конструкцию на множители:
a (1 · b − 1) − (b − 1) = 0
(b − 1)(а · 1 − 1) = 0
А теперь вспоминаем наше замечательно правило: произведение равно нулю, когда хотя бы один из множителей равен нулю:
b − 1 = 0 ⇒ b = 1;
a − 1 = 0 ⇒ a = 1.
Вспоминаем, что такое b и а. Получим два простейших логарифмических уравнения, в которых останется лишь избавиться от знаков logи приравнять аргументы:
log2 x = 1 ⇒ log2 x = log2 2 ⇒ x1 =2;
log2 (x − 3) = 1 ⇒ log2 (x − 3) = log2 2 ⇒ x2 = 5
Мы получили два корня, но это не решение исходного логарифмического уравнения, а лишь кандидаты в ответ. Теперь проверим область определения. Для первого аргумента:
Теперь проверим область определения. Для первого аргумента:
x > 0
Оба корня удовлетворяют первому требованию. Переходим ко второму аргументу:
x − 3 > 0 ⇒ x > 3
А вот здесь уже x = 2 нас не удовлетворяет, зато x = 5 вполне нас устраивает. Следовательно, единственным ответом будет x = 5.
Переходим ко второму логарифмическому равнению. На первый взгляд, оно существенно проще. Однако в процессе его решения мы рассмотрим тонкие моменты, связанные с областью определения, незнание которых существенно усложняет жизнь начинающим ученикам.
log0,7 (x2 − 6x + 2) = log0,7 (7 − 2x)
Перед нами каноническая форма логарифмического уравнения. Ничего преобразовывать не нужно — даже основания одинаковые. Поэтому просто приравниваем аргументы:
x2 − 6x + 2 = 7 − 2x
x2 − 6x + 2 − 7 + 2x = 0
x2 − 4x − 5 = 0
Перед нами приведенное квадратное уравнение, оно легко решается по формулам Виета:
(x − 5) (x + 1) = 0;
x − 5 = 0 ⇒ x = 5;
x + 1 = 0 ⇒ x = −1.
Но эти корни еще не являются окончательными ответами. Нужно найти область определения, поскольку в исходном уравнении присутствуют два логарифма, т.е. учет области определения строго обязателен.
Итак, выпишем область определения. С одной стороны, аргумент первого логарифма должен быть больше нуля:
x2 − 6x + 2 > 0
7 − 2x > 0
Эти требования должны выполняться одновременно. И вот тут начинается самое интересное. Безусловно, мы можем решить каждое из этих неравенств, затем пересечь их и найти область определения всего уравнения. Но зачем так усложнять себе жизнь?
Давайте заметим одну тонкость. Избавляясь от знаков log, мы приравниваем аргументы. Отсюда следует, что требования x2 − 6x + 2 > 0 и 7 − 2x > 0 равносильны. Как следствие, любое из двух неравенств можно вычеркнуть. Давайте вычеркнем самое сложное, а себе оставим обычное линейное неравенство:
−2x > −7
x < 3,5
Поскольку мы делили обе части на отрицательное число, знак неравенства поменялся.
Итак, мы нашли ОДЗ без всяких квадратных неравенств, дискриминантов и пересечений. Теперь осталось просто выбрать корни, которые лежат на данном интервале. Очевидно, что нас устроит лишь x = −1, потому что x = 5 > 3,5.
Можно записать ответ: x = 1 является единственным решением исходного логарифмического уравнения.
Выводы из данного логарифмического уравнения следующие:
- Не бойтесь раскладывать логарифмы на множители, а потом множители раскладывать на сумму логарифмов. Однако помните, что разбивая произведение на сумму двух логарифмов, вы тем самым сужаете область определения. Поэтому прежде чем выполнять такое преобразование, обязательно проверьте, каковы требования области определения. Чаще всего никаких проблем не возникает, однако лишний раз перестраховаться не помешает.
- Избавляясь от канонической формы, старайтесь оптимизировать вычисления. В частности, если от нас требуется, чтобы f > 0 и g > 0, но в самом уравнении f = g, то смело вычеркиваем одно из неравенств, оставляя себе лишь самое простое.
 Область определения и ответы при этом никак не пострадают, а вот объем вычислений существенно сократится.
Область определения и ответы при этом никак не пострадают, а вот объем вычислений существенно сократится.
Обратный логарифм
Обратный логарифм (или антилогарифм) числа n – это число, логарифм которого по основанию a равен числу n.
ant logan = an
Частные значения
Логарифм по основанию 10 называется десятичным логарифмом и обозначается так:
Логарифм по основанию e называется натуральным логарифмом:
Логарифмы со специальным обозначением
Для некоторых логарифмов в математике введены специальные обозначения. Это связано с тем, что такие логарифмы встречаются особенно часто. К таким логарифмам относятся десятичный логарифм и натуральный логарифм. Для этих логарифмов справедливы все правила, что и для обычных логарифмов.
Десятичный логарифм
Десятичный логарифм обозначается lg и имеет основание 10, т.е.
Чтобы вычислить десятичный логарифм, нужно 10 возвести в степень X.
Например, вычислим lg100
Натуральный логарифм
Натуральный логарифм обозначается ln и имеет основание e, то есть
Чтобы вычислить данный логарифм нужно число е возвести в степень x. Некоторые из вас спросят, что это за число такое е? Число е – это иррациональное число, т.е. точное его значение вычислить невозможно. е = 2,718281…
Сейчас не будем подробно разбирать, зачем это число нужно, просто запомним, что
И вычислить его можно таким образом:
Таблица свойств логарифмов
Ниже представлены основные свойства логарифмов в табличном виде.
 png" width="130" height="308" data-full="https://exceltut.ru/wp-content/uploads/2020/06/logarifm-exc-10.png"><meta itemprop="width" content="130"><meta itemprop="height" content="308"></td><td class="htLeft htMiddle" data-order=» itemprop=»url image» src=»https://exceltut.ru/wp-content/uploads/2020/06/logarifm-exc-11.png» size-full=»» data-full=»https://exceltut.ru/wp-content/uploads/2020/06/logarifm-exc-11.png»/>‘ data-original-value=’‘ data-cell-type=”text” data-db-index=”6″ data-y=”6″ data-x=”2″ data-cell-id=”C6″>
png" width="130" height="308" data-full="https://exceltut.ru/wp-content/uploads/2020/06/logarifm-exc-10.png"><meta itemprop="width" content="130"><meta itemprop="height" content="308"></td><td class="htLeft htMiddle" data-order=» itemprop=»url image» src=»https://exceltut.ru/wp-content/uploads/2020/06/logarifm-exc-11.png» size-full=»» data-full=»https://exceltut.ru/wp-content/uploads/2020/06/logarifm-exc-11.png»/>‘ data-original-value=’‘ data-cell-type=”text” data-db-index=”6″ data-y=”6″ data-x=”2″ data-cell-id=”C6″> png"><meta itemprop="width" content="130"><meta itemprop="height" content="280"></td><td class="htLeft htMiddle" data-order=» itemprop=»url image» src=»https://exceltut.ru/wp-content/uploads/2020/06/logarifm-exc-5.png» size-full=»» data-full=»https://exceltut.ru/wp-content/uploads/2020/06/logarifm-exc-5.png»/>‘ data-original-value=’‘ data-cell-type=”text” data-db-index=”7″ data-y=”7″ data-x=”2″ data-cell-id=”C7″>
png"><meta itemprop="width" content="130"><meta itemprop="height" content="280"></td><td class="htLeft htMiddle" data-order=» itemprop=»url image» src=»https://exceltut.ru/wp-content/uploads/2020/06/logarifm-exc-5.png» size-full=»» data-full=»https://exceltut.ru/wp-content/uploads/2020/06/logarifm-exc-5.png»/>‘ data-original-value=’‘ data-cell-type=”text” data-db-index=”7″ data-y=”7″ data-x=”2″ data-cell-id=”C7″>
Основные формулы логарифмов
Свойства логарифма, вытекающие из определения обратной функции:
Виды логарифмов
loga b – логарифм числа b по основанию a (a > 0, a ≠ 1, b > 0)
lg b – десятичный логарифм (логарифм по основанию 10, a = 10).

ln b – натуральный логарифм (логарифм по основанию e, a = e).
Логарифмы
Источники
- https://www.calc.ru/Ponyatiye-Logarifma.html
- https://1cov-edu.ru/mat_analiz/funktsii/logarifm/
- https://www.berdov.com/docs/logarithm/logarifmicheskie-uravneniya/
- https://MicroExcel.ru/logarifmy/
- https://yourrepetitor.ru/chto-takoe-logarifm-kak-poschitat-logarifm-svojstva-logarifmov-primery-resheniya-logarifmov/
- https://youclever.org/book/logarifmy-1
- https://www.berdov.com/docs/logarithm/kvadratnie-logarifmicheskie-uravneniya/
- https://ru.onlinemschool.com/math/formula/logarithm_formula/
алгоритм — Почему для вычисления сложности алгоритмов используется log N вместо lb N?
Вопрос задан
Изменён 1 год 8 месяцев назад
Просмотрен 5k раз
Во всех источниках сложность алгоритмов обозначается как log N (без указания основания). При этом имеется в виду логарифм по основанию 2.
При этом имеется в виду логарифм по основанию 2.
Но для такого логарифма есть свое обозначение lb. Причем это обозначение стандартизировано ISO 31-11 и наверное было бы логичнее и правильнее пользоваться именно им, но этого по какой-то причине не просходит, почему?
UPD: у меня нет никакого математического образования и все, что я знаю о логарифмах, что это действие обратное возведению в степень.
Возьмем конкретный пример — бинарный поиск. Везде описывают его сложность как log N. При этом под log N, как мне кажется, все таки подразумевается логарифм N по основанию именно 2, т.к. количество операций составляет именно логарифм N по основанию 2, т.е. в какую степень надо возвести именно 2 (а не 10 и не 100), чтобы получить N. Поэтому, если честно, я не понимаю ответов типа «потому что постоянные коэффициенты в обозначении O(n) не имеют значения» или «так как запись с большим O на константы не реагирует — неважно, какой именно логарифм использовать.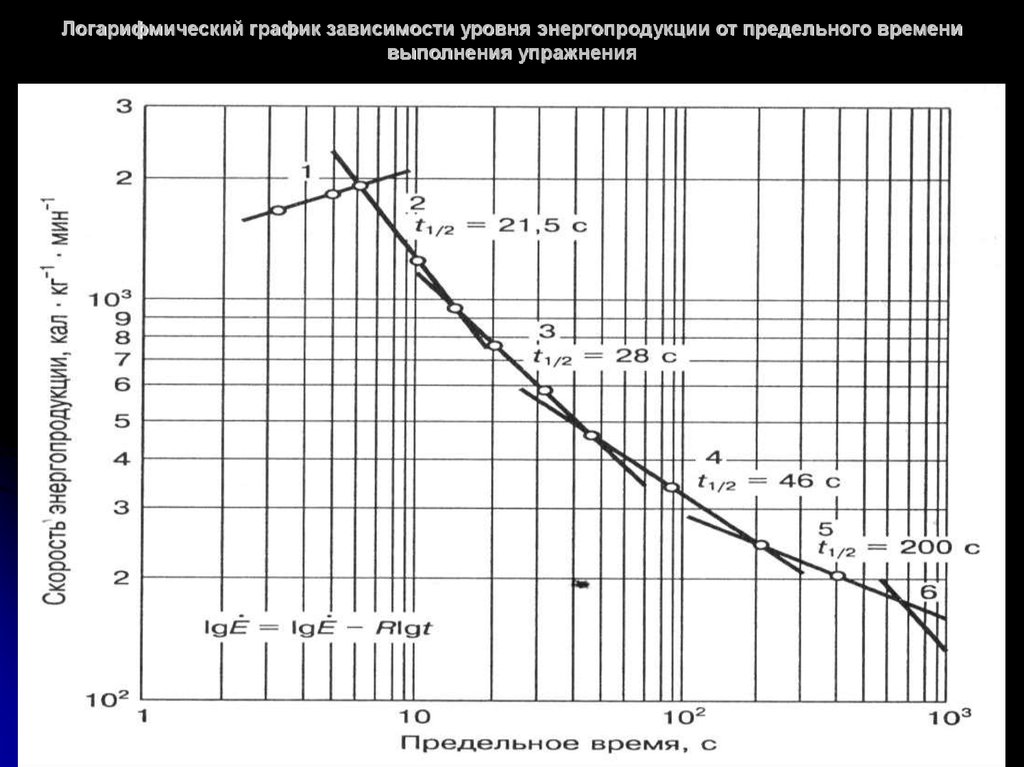 ..» и буду признателен за более развернутый ответ, написанный не для математиков. Разве правило, что «константы в О-большом не имеют значения», относится к основанию логарифма? Разве для бинарного поиска не имеет никакой разницы как записать его сложность — логарифмом по основанию 2 или по основанию 100?
..» и буду признателен за более развернутый ответ, написанный не для математиков. Разве правило, что «константы в О-большом не имеют значения», относится к основанию логарифма? Разве для бинарного поиска не имеет никакой разницы как записать его сложность — логарифмом по основанию 2 или по основанию 100?
Если под log N для бинарного поиска подразумевается именно логарифм по основанию 2, то почему бы его не записать как lb N, раз уж для двоичного логарифма есть свое обозначение, вместо того, чтобы записывать вообще без указания основания?
UPD 2: я понимаю что «O(N) — это ни в коем случае не количество сравнений, это оценка времени работы алгоритма, максимально отвязанная от деталей реализации и машины.»
Но вот этого: «А так как запись с большим O на константы не реагирует — неважно, какой именно логарифм использовать…» я не понимаю. Почему не важно какой логарифм использовать? Вот графики трех логарифмов — двоичного, натурального и по основанию 0,5:
Возьмем все тот же бинарный поиск.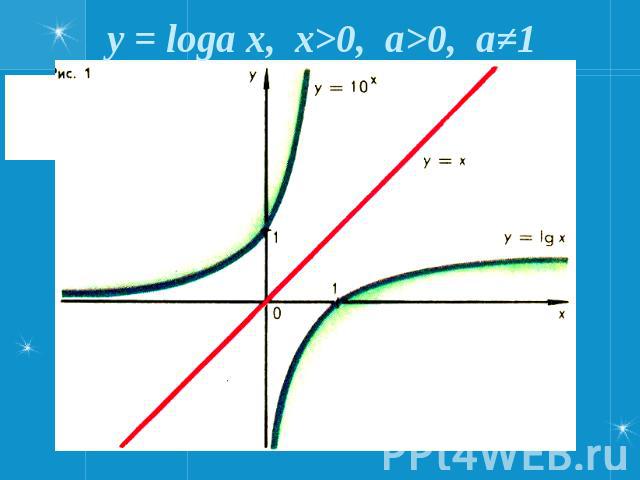 Разве мы можем заменить в его сложности основание у логарифма с два на десять? А с два на 0,5? Мне кажется, не можем. Т.е. мы не можем подставить в выражении log N произвольное основание потому что зависимость будет совершенно другая — это хорошо видно на графике. Т.о. какой именно логарифм использовать важно. Или я не прав?
Разве мы можем заменить в его сложности основание у логарифма с два на десять? А с два на 0,5? Мне кажется, не можем. Т.е. мы не можем подставить в выражении log N произвольное основание потому что зависимость будет совершенно другая — это хорошо видно на графике. Т.о. какой именно логарифм использовать важно. Или я не прав?
- алгоритм
- математика
- сложность
1
Поскольку все логарифмы одинаковы с точностью до константы 🙂
А так как запись с большим O на константы не реагирует — неважно, какой именно логарифм использовать…
Update на ваше обновление вопроса.
Смысл не в конкретном количестве сравнений, а в том, как растет это количество (а значит, и время работы) с ростом N. Это ни в коем случае не конкретное количество тех или иных операций! То, что некоторый алгоритм имеет сложность O(g(N)) всего лишь означает, что если мы путем экспериментов будем строить некую функцию зависимости времени работы алгоритма от N и получим некую f(N), то сможем найти некоторые такие константные c и N0, что для всех N>=N0 будет выполняться неравенство 0 <= f(N) <= cg(N).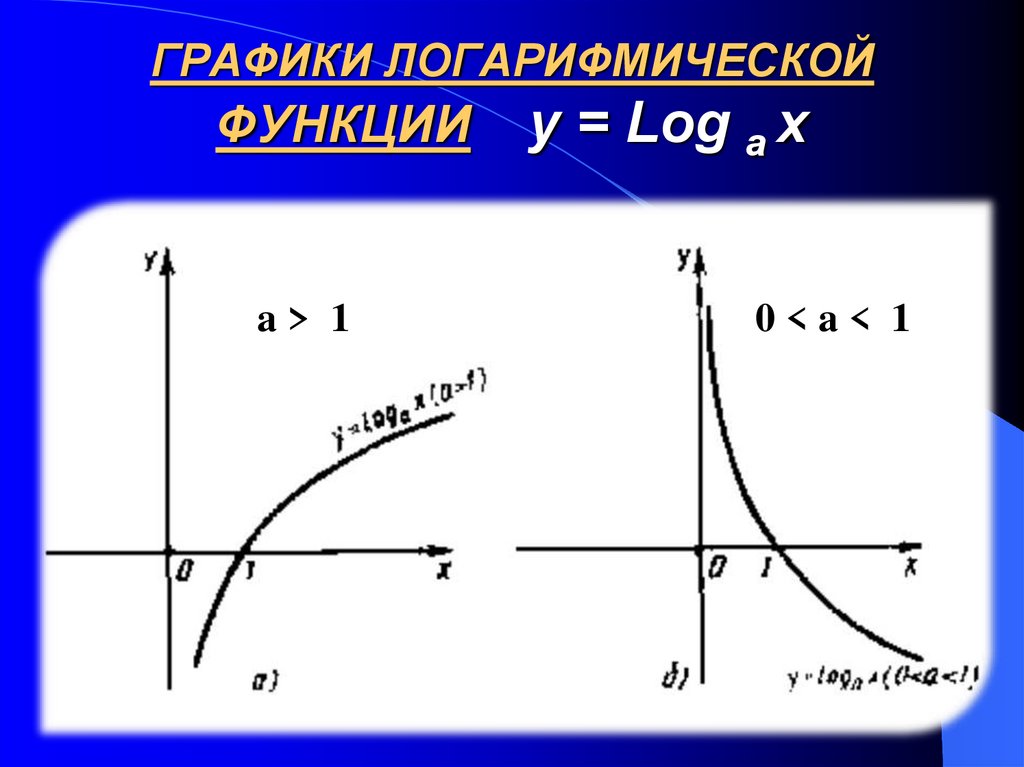 Это — определение записи с большим О.
Это — определение записи с большим О.
Еще раз — O(N) — это ни в коем случае не количество сравнений, это оценка времени работы алгоритма, максимально отвязанная от деталей реализации и машины.
Update 2
Я реализую алгоритм бинарного поиска и при этом ужасно туплю, так что вместо одного сравнения я делаю их 20. Вы делаете их ровно столько, сколько нужно. Но и ваша, и моя реализации будут работать время O(log N) — пусть моя и будет работать в 100 раз медленнее вашей. Потому что и моя, и ваша реализации при возрастании N в 100 раз будут работать дольше на некоторое время — пусть и у каждого свое, скажем, у вас на минуту, у меня — на час. Главное, что вид зависимости будет одинаков — при увеличении в сколько-то раз рост будет на сколько-то.
И, кстати, у вас зависимости log2x и ln x как раз одинаковы — стоит только немного изменить масштаб по оси y. Что до логарифма по основанию, меньшему 1 — ну, как говорится, не стоит утрировать.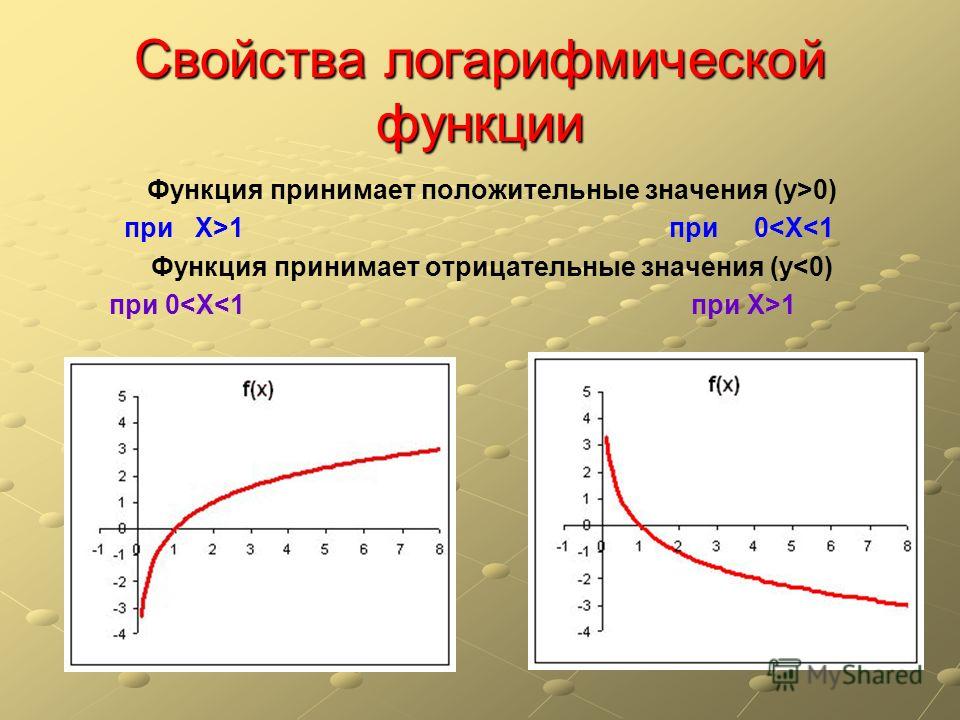 Но и тут — достаточно взять его по модулю или отрицательную константу 🙂
Но и тут — достаточно взять его по модулю или отрицательную константу 🙂
Кстати, посмотрите несколько ссылок здесь.
7
Мне кажется, я нашел ответ на свой изначальный вопрос:
«Во всех источниках сложность алгоритмов обозначается как log N (без указания основания). При этом имеется в виду логарифм по основанию 2. Но для такого логарифма есть свое обозначение lb. Причем это обозначение стандартизировано ISO 31-11 и наверное было бы логичнее и правильнее пользоваться именно им, но этого по какой-то причине не просходит, почему?»
вот здесь: https://en.wikipedia.org/wiki/Logarithm#Particular_bases
т.е. например, в информатике log N используется вместо lb N или log N по конкретному основанию, потому что основание логарифма понятно из контекста.
Возможно, основание логарифма вообще значения не имеет, когда речь идет об О-большое, как ответил @Harry.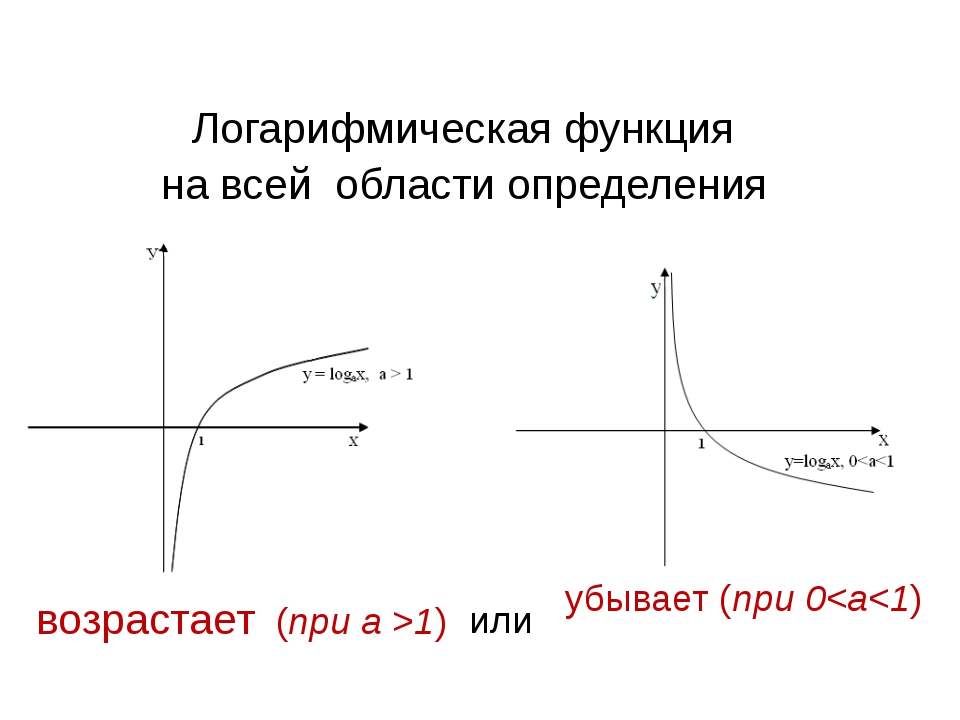 Но, если честно, моих математических знаний на данный момент не хватает, чтобы дать этому утверждению оценку. Поэтому я предпочту пока более общую формулировку про то, что «основание определено контекстом»
Но, если честно, моих математических знаний на данный момент не хватает, чтобы дать этому утверждению оценку. Поэтому я предпочту пока более общую формулировку про то, что «основание определено контекстом»
UPD: Набрел в одной книг по алгоритмам (как раз в разделе бинарного поиска) на фразу: «Is it log base 2, log base 10, or the natural log? In the above example, log base 2 applies. However, since Big O notation only concerns itself with the shape of the performance the actual base doesn’t matter.» Так что, да, похоже основание логарифма не важно )
1
Ваш ответ
Зарегистрируйтесь или войдите
Регистрация через Google
Регистрация через Facebook
Регистрация через почту
Отправить без регистрации
Почта
Необходима, но никому не показывается
Отправить без регистрации
Почта
Необходима, но никому не показывается
Нажимая на кнопку «Отправить ответ», вы соглашаетесь с нашими пользовательским соглашением, политикой конфиденциальности и политикой о куки
страница 1 |
|||||||||||||||||||||||||||||||||||||||||||||
|
Похожие работы
|
«Логарифмы, логарифмическая функция, её свойства и график» — страница №1/1 Урок алгебры в 10 классе Тема: «Логарифмы, логарифмическая функция, её свойства и график» Цели:
Тип урока: Комбинированный Методы обучения: Частично-поисковый, диалоговый. Оборудование: Раздаточный материал, копировальная бумага, миллиметровая бумага, учебник Ш.А. Алимов, Алгебра и начала анализа 10 – 11 класс, сборник задач для подготовки к ЕГЭ. Ход урока: Вводная часть урока: Целевая установка. Логарифмы — это всё! Музыка и звуки И без них никак нельзя Обойтись науке! Вступительное слово учителя: Более трёхсот лет прошло с того дня, как в 1614 году были опубликованы первые логарифмические таблицы. Значение логарифмов трудно переоценить. Они нужны инженеру и астроному, штурману и артиллеристу, всем, кому приходится вести громоздкие вычисления. Совершенно прав великий французский математик и астроном Лаплас, который сказал: «Изобретение логарифмов, сокращая вычисления нескольких месяцев в труд нескольких дней, словно удваивает жизнь астрономов». Сегодня вам предстоит открыть новые знания и на этом пути нам предстоит пройти несколько этапов:
Учащимся предлагаются устные упражнения с использованием определения логарифма, его свойств, формул перехода к новому основанию, решения простейших логарифмических и показательных уравнений, примеров на нахождение области допустимых значений подлогарифмических выражений. (Приложение 2) Устные упражнения 2)Для контроля усвоения материала предлагается тест с кодированными ответами. В результате правильного выполнения, которого получается фамилия шотландского математика Непера. (Приложение 3)
НЕПЕР При правильном решении, при верном выборе ответа, должен получиться НЕПЕР – фамилия шотландского математика, который впервые предложил использовать запятую, как математический знак и в 1614 изобретал логарифм. 2)Основная часть:
Подводятся итоги урока: Рефлексия в форме диалога: «На уроке я работал активно / пассивно» «Совей работой на уроке я доволен / не доволен» «Урок мне показался коротким / длинным» «Я не достиг хорошего результата потому, что …» «Материал урока мне был понятен / не понятен» «Моё настроение стало лучше / хуже». Схема социально – педагогического проекта урока по теме: «Логарифмы, логарифмическая функция, её свойства и график» Этот урок завершающий в теме «Логарифмы» и вводный в теме «Логарифмическая функция, её свойства и график». Он связывает понятие логарифма и его свойств с решением показательного уравнения, корень которого выражается через логарифм некоторого числа и алгоритмом нахождения функции, обратной данной. Урок также ориентирован на перспективу, хорошо подготавливая учащихся к восприятию таких тем как логарифмические уравнения и неравенства, решение которых основывается на свойствах логарифмической функции. В результате урока использовались поисковые и эвристические методы обучения, урок проходил в форме диалога. Очевидной целью урока является выделение задачи, организация действий и диалога таким образом, чтобы задача была увидена и сформулирована, что и оказывается впоследствии логическим завершением урока. На каждом этапе урока ставилась определённая цель:
Данный урок способствовал вовлечению всех учащихся в творческий познавательный процесс, преодолению посильных трудностей, развитию познавательной активности учащихся и их общему развитию. Побуждал учеников к самоконтролю и самоанализу своей деятельности. Наряду с учением и воспитанием урок способствует психологическому и социально-нравственному развитию личности, это выражается в следующем: На этапе введения в новую тему и при её завершении использовались задания на формирование таких мыслительных операций, как анализ и синтез, обобщение и конкретизация. С помощью фактов из истории, теста с кодированными ответами, подбора устных упражнений, поддерживалось внимание, развивалась память и мышление учащихся. На уроке создавались ситуации выбора, успеха, сотрудничества друг с другом, учебной самостоятельности. Для учащихся с различными каналами восприятия были использованы разнообразные задания и иллюстративный материал. Методическое обоснование урока Для завершения предыдущей темы и введения новой необходимо было восстановить имеющиеся знания учащихся о понятиях логарифма , функции и их свойств. Для этого использовалась серия устных упражнений с заведомо нерешаемыми заданиями, которые развивают внимательность, сосредоточенность и точность в определении понятий. Задания комментируются учащимися, в форме диалога выявляются необходимые знания, что обеспечивает хороший уровень повторения. При подведении микроитога у некоторых учащихся возникают затруднения, которые тут же разрешаются. Введение нового материала проходит на практической основе. Решая уравнение, из которого надо выразить одно неизвестное через другое, учащиеся самостоятельно выходят на то, что полученное выражение есть функция и называется она логарифмической. Анализируя полученные функции с определёнными основаниями, учащийся обобщают знания и дают определение логарифмической функции. Выполняя задание на построение графика логарифмической функции и определение её свойств. Учащиеся анализируют пройденный материал по теме «Степенная функция», повторяют определение логарифма при заполнении таблицы значений неизвестных, устанавливают связи между аналитической формой записи функции и её графической интерпретацией. С помощью небольшой самостоятельно работы по тестам ЕГЭ учащиеся осознают значимость данной темы в курсе. Данная работа проводится под копирку, что позволяет мгновенно выявить степень усвоения новой темы и своевременно устранить пробелы. Задание на дом предполагает выбор и творческий подход. |
Основание логарифма 2
Логарифмическая функция — это функция, обратная экспоненциальной функции.

Цель логарифма — рассказать нам о показателе степени.
Логарифмические функции используются для изучения свойств экспоненциальных функций и используются для решения различных экспоненциальных уравнений.
Логарифмическая база 2 — это обратное представление степени числа 2. Например, здесь n = bx, n — действительное положительное число. И х — это показатель степени. Тогда базовый формат журнала для этого будет Logb n = x. 9x} = b\]
Что такое логарифмическая база 2 или двоичный логарифм?
Логарифм по основанию 2 также известен как двоичный логарифм.
Обозначается как (log2n).
Логарифм по основанию 2 или двоичный логарифм — это логарифм по основанию 2.

Это функция, обратная степени двух функций.
Двоичный логарифм — это степень, в которую нужно возвести число 2, чтобы получить значение n. 9{\mathbf{x}}} = {\text{ }}{\mathbf{n}}\]
График для логарифмической базы 2
Свойства логарифмической базы 2
Есть несколько свойств логарифмические функции с основанием 2. Они перечислены в таблице ниже.
Поскольку мы обсуждаем логарифм с основанием 2, мы будем считать, что здесь основание равно 2.
Основные правила регистрации
Правило произведения –
наоборот.
\[lo{g_b}\left( {x{\text{}} \times {\text{}}y} \right){\text{}} = {\text{}}lo{g_b}x {\text{ }} + {\text{ }}lo{g_b}y\]
Правило частных –
Если логарифм дан как отношение двух величин, то его можно записать как разность логарифмов каждого из числительных.

\[lo{g_b}\left( {\frac{x}{y}} \right)\; = {\text{}}lo{g_b}x{\text{}} — {\text{}}lo{g_b}y\]
Степенное правило — 9k}) = k{\text{}}lo{g_b}x\]
Правило нуля –
Если b больше 0, но не равно 1. Логарифм x = 1 может быть записывается как 0.
\[lo{g_b}\left( 1 \right){\text{ }} = {\text{ }}0\]
тогда основание b и аргумент логарифма (в скобках) равны,
\[lo{g_b}\left( b \right){\text{}} = {\text{}}1\]
Вот несколько примеров, которые показывают, как работают приведенные выше основные правила записывается как
Log (20 × 2)
правило побочных продуктов ?
logb(b) = 1, по правилу идентификации
Следовательно, log4(4) = 1,
Формула изменения основания
Логарифм может быть в форме логарифма по основанию e или логарифма по основанию 10 или любого другого основания.
 Вот общая формула для изменения основания —
Вот общая формула для изменения основания —\[{\mathbf{Lo}}{{\mathbf{g}}_{\mathbf{b}}}\;{\mathbf{x}}{\text{ }} = {\ text {}} \ frac {{{\ mathbf {Lo}} {{\ mathbf {g}} _ {\ mathbf {a}}} \; {\ mathbf {x}}}} {{ {\mathbf{Lo}}{{\mathbf{g}}_{\mathbf{a}}}\;{\mathbf{b}}}}\;\]
Чтобы найти значение логарифмической базы 2, сначала нам нужно преобразовать его в логарифм по основанию 10, который также известен как десятичный логарифм.
\[Log{\text{}}base{\text{}}2{\text{}}of{\text{}}x = \frac{{ln\left( x \right)}}{{ ln\left( 2 \right)}}\]
Теперь вам может быть интересно, что такое десятичная логарифмическая функция?
Логарифмическая функция или десятичный логарифм — это логарифм с основанием, равным 10.
Он также известен как десятичный логарифм из-за его основания.

Десятичный логарифм x обозначается как log x.
909{y} = x\]Suppose we have a question, log216 = x
Using the log rule,
2x= 16
We know that 16 in powers of 2 можно записать как (2×2×2×2 =16), 2x=24
Следовательно, x равно 4.
Вопросы, которые необходимо решить –
Вопрос 1) Вычислить значение логарифма по основанию 2 из 64.
Решение) Здесь
X= 64
Используя формулу,
\[Log{\text{ }}base{\text{ }}2{\text{ }}of{\text{ }}X = \frac{{ln\left( {64 } \right)}}{{ln\left( 2 \right)}} = 6\].

Логарифмическая база 2 из 64 =\[\frac{{ln\left( {64} \right)}}{{ln\left( 2 \right)}} = 6\].
Следовательно, логарифмическая база 2 из 64 = 6
Вопрос 2) Найдите значение log2(2).
Решение) Чтобы найти значение log2(2), воспользуемся основным правилом тождества:
\[lo{g_b}\left( b \right){\text{ }} = {\text{ }}1 ,\].
Следовательно, log2(2) = 1.
Вопрос 3) Каково значение log 2 по основанию 10?
Решение) Значение log 2 по основанию 10 можно вычислить по правилу
\[Lo{g_a}\left( b \right){\text{}} = \frac{{\log b}}{ {\log а}}\].
\[Lo{g_{10}}\left( 2 \right){\text{}} = \frac{{\log 2}}{{\log 10}}\; = {\text{}}0,3010\].
Следовательно, значение log 2 по основанию 10 = 0,3010.
Вопрос 4) Каково значение log 10 по основанию 2?
Решение) Значение log 10 по основанию 2 можно вычислить по правилу
\[Lo{g_b}\left( a \right){\text{}} = \frac{{\log b}}{ {\log а}}\].

\[Lo{g_2}\left( {10} \right){\text{}} = \frac{{\log 10}}{{\log 2}}\; = {\text{3}}{\text{.3 = 2}}\].
Следовательно, значение log 10 по основанию 2 = 3,32.
Использование логарифмов в повседневной жизни
Землетрясения регистрируются с помощью сейсмографов, а амплитуда регистрируется по шкале Ритчера. Логарифмические значения используются для понимания этих значений
Он также используется для определения значения pH любого вещества.
Логарифмы используются для измерения интенсивности звука. Как правило, интенсивность звука измеряется громкостью, которая, в свою очередь, измеряется с помощью логарифмов
. Они также используются для измерения комплексных величин.

Как повысить баллы в логарифме Глава
Логарифм — это прямо противоположное выражение числа в степени цифры. Многие студенты сталкиваются с трудностями при изучении этого предмета, так как им приходится думать и решать задачи в обратном порядке. Вот несколько советов, как улучшить свои результаты в логарифмах:
Поймите, что логарифм — это обратное выражение степеней или показателей. Все, что вам нужно сделать, это решить их в обратном порядке
Наизусть выучить все законы логарифмирования и знать, какой будет конечный результат для конкретной задачи, если решить ее с помощью формулы
Понимание конца результат может быть достигнут путем понимания формулы, которую вы применяете для решения проблемы. Когда вы применяете формулу, у которой есть ответ, вы узнаете конечный результат
Решите как можно больше задач с различными логарифмическими значениями
Обратитесь к вопросам предыдущего года, чтобы узнать шаблон экзамена, типы вопросов, задаваемых на экзамене, и оценить глубину вопросов, заданных экзаменатором.

Любые сомнения можно уточнить у учителя-предметника или на веб-сайте онлайн-обучения, таком как Vedantu.
Диаграмма, которая не может начинаться с нуля
Часть 2. Диаграмма, которая не может начинаться с нуля
Лиза Шарлотта Мут
Это вторая часть серии статей, посвященных логарифмическим шкалам. Посетите часть 1 и часть 3.
На прошлой неделе мы открыли кондитерский бизнес, чтобы узнать о логарифмических шкалах и о том, как они показывают нам не абсолютные числа, а темпы роста. На этой неделе мы съедим больше конфет и рассмотрим еще один аспект логарифмических шкал: экспоненциальный рост и число величин. И мы узнаем о законе Мура :
Закон Мура был идеей соучредителя Intel Гордона Мура в 1965. По его словам, количество транзисторов [1] на микропроцессорах удваивается каждые 18-24 месяца . Это не естественный закон: многие заявляют, что конец этому закону близок, хотя до сих пор он хорошо работал как самосбывающееся пророчество для производителей процессоров, таких как Apple или Intel.

Чтобы поэкспериментировать с этой диаграммой или бесплатно встроить ее в свои собственные статьи, наведите на нее курсор и нажмите «Редактировать эту диаграмму» в правом верхнем углу.
Давайте попробуем немного лучше понять логарифмические шкалы, прежде чем интерпретировать эту диаграмму с помощью наших новых знаний:
Логарифмические шкалы показывают нам величины
Как мы видели на прошлой неделе, логарифмические шкалы — это странные шкалы, в которых расстояние между 0,1 и 1 такое же большое, как расстояние между 1 и 10, 100 000 и 1 000 000.
Эти отметки — 0,1, 1, 10, 100 и т. д. — показывают нам порядок величин ; также называется степенями десяти, коэффициентом десяти или декадами. Порядок величины 1000 равен 3, поэтому его можно записать как 10 3 . (В вашем старом школьном калькуляторе и в программировании это будет 1e3.) Вы можете легко запомнить величины: просто посчитайте нули в числе. 1000 имеет три нуля, поэтому мы можем записать это как 10 3 .
 1 не имеет нулей, так что это 10 0 . А 0,0001 имеет четыре нуля и является отрицательным, поэтому это 10 -4 . Таким образом, логарифмическая шкала не показывает числа на линейной шкале, но показывает величины в линейной форме: 0, 1, 2, 3 и т. д.
1 не имеет нулей, так что это 10 0 . А 0,0001 имеет четыре нуля и является отрицательным, поэтому это 10 -4 . Таким образом, логарифмическая шкала не показывает числа на линейной шкале, но показывает величины в линейной форме: 0, 1, 2, 3 и т. д.Примечание: логарифмические шкалы не могут начинаться с нуля
Причина, по которой логарифмические шкалы показывают нам величины, является причиной, по которой мы никогда не сможем расширить диаграмму с логарифмической шкалой до нуля: расстояние между 0,000001 и 0,0000001 равно расстоянию между 100 и 1000. Или расстояние между 00000000000,1 и 000000000000,1 . =Ноль скрылся из виду. Логарифмическая шкала никогда не испытает радости от ее достижения:
Порядок величин = показатели степени
«Экспоненциальный рост» — это то, что мы знаем о росте клеток, распространении вирусов, финансовых пирамидах, экономическом росте и старых историях, в которые попадают любители математики.
 богатый зернами пшеницы и шахматной доской: мы все слышали слово «экспоненциальный» раньше. Давайте вспомним, что это значит.
богатый зернами пшеницы и шахматной доской: мы все слышали слово «экспоненциальный» раньше. Давайте вспомним, что это значит.Экспоненциальный рост означает, что что-то удваивается, утраивается, учетверяется и т. д. каждую минуту/день/год и т. д. Помните, как на прошлой неделе ваш кондитерский бизнес рос на 100 % каждый год? Каждый год вы съедаете в два раза больше конфет, чем в прошлом году. Это экспоненциальный рост. Каждый год вы съедаете в два раза больше конфет, поэтому так называемое основание равно 2. «Показатель степени» (крохотное выпуклое число рядом с 2) эквивалентно количеству лет:
Итак. у нас есть экспоненциальный рост каждый раз, когда экспонента растет линейно. Вы говорите, это выглядит знакомо? Да: порядки в нашей логарифмической шкале тоже являются показателями! Вот где все это сходится. Если мы заменим основание 2 на основание 10, оно будет выглядеть точно так же, как порядок величин, если немного прокрутить вверх: 10 0 , 10 1 , 10 2 и т.
 д. Та же сделка. Логарифмическая шкала «растет экспоненциально», если ее показатели степени (= порядок величин) «растут линейно».
д. Та же сделка. Логарифмическая шкала «растет экспоненциально», если ее показатели степени (= порядок величин) «растут линейно». Достижение следующей величины
Если вы показываете экспоненциальный рост в экспоненциальной шкале — то есть в нашей логарифмической шкале — экспоненциальный эффект выравнивается. Получаем прямую. Это означает: Если вы видите прямую линию на диаграмме в логарифмическом масштабе, что-то растет экспоненциально . Каждую минуту/день/год количество чего-либо будет удваиваться (или уменьшаться вдвое).
И если что-то удваивается каждые x лет/дней/минут, оно будет достигать следующей величины через постоянные промежутки времени. Что меня ошеломляет. Но это складывается, если мы делаем математику, например. для нашего кондитерского бизнеса:
В первый год мы съедаем 1 конфету.
Через 3,3 года вы съедите 10 1 = 10 конфет.
Через 6,6 лет вы едите 10 2 = 100 конфет.
Примерно через десять лет 10 3 = 1000 конфет.
Примерно через двадцать лет 10 6 = 1 000 000 конфет.Таким образом, мы можем подсчитать, что через сорок лет величина снова удвоится, и вы съедите 10 12 конфет.
Как читать график по закону Мура
Что же тогда мы можем прочитать на нашем графике?
Сначала проверяем, логарифмическая ли это шкала. Это! Ось Y имеет логарифмический масштаб. Затем смотрим на график. Если бы мы провели линию через эти транзисторы, это была бы довольно прямая линия. Мы можем сделать вывод, что количество транзисторов растет экспоненциально : оно удваивается каждые x лет.
Через сколько лет? Это то, что мы не можем узнать без математики — поэтому это написано в заголовке. Что мы можем сказать, просто взглянув на эту диаграмму, так это то, что количество транзисторов увеличивается на две величины каждые пятнадцать лет .
 Это означает, что потребовалось 15 лет, чтобы перейти от 1000 транзисторов к 100 000 транзисторов, и потребовалось 15 лет, чтобы перейти от 100 миллионов транзисторов к 10 миллиардам.
Это означает, что потребовалось 15 лет, чтобы перейти от 1000 транзисторов к 100 000 транзисторов, и потребовалось 15 лет, чтобы перейти от 100 миллионов транзисторов к 10 миллиардам.Это было очень важно! На следующей неделе мы снова рассмотрим логарифмические шкалы, но в статье, которая будет немного более компактной. Посетите часть 3 этой серии здесь.
Транзисторы являются основой всех вычислений. Они крошечные и выполняют крошечные задачи, которые в сумме дают вам возможность играть в World of Warcraft. Чем больше транзисторов помещается в процессор, тем быстрее работает ваш компьютер или тем меньше он может быть. Думайте о смартфонах, а затем об умных часах.↩︎
Лиза Шарлотта Мут
(@lisacmuth, ранее Лиза Шарлотта Рост) отвечает за общение в Datawrapper, особенно за блог. Она писала о Data vis в течение многих лет и рада учиться и учить.
Понравилась статья? Возможно, ваши друзья тоже:
Формула смены базы | Purplemath
Основные правилаExpandingCondensingTrick Q’s
Purplemath
Есть еще одно «правило» журнала, но это скорее формула, чем правило.

Возможно, вы заметили, что ваш калькулятор имеет ключи только для вычисления значений для обычного (то есть по основанию 10) журнала и естественного (то есть по основанию и ) журнала. Для других баз ключей нет. Некоторые студенты пытаются обойти это, «оценивая» что-то вроде «журнал 3 (6)» с помощью следующих нажатий клавиш:
[ LOG ] [ 3 ] [ ( ] [ 6 ] [ 6 ] [ ) ]
Конечно, тогда они получают неправильный ответ, потому что приведенное выше фактически (обычно) вычисляет значение «log 10 (3) × 6». Это не то, что было задумано.
Содержание продолжается ниже. :
На практике это правило говорит о том, что вы можете оценить журнал нестандартной базы, преобразовав его в дробь формы «(стандартная база аргумента), разделенная на (такая же стандартная база лог нестандартной базы)».
 Я поддерживаю это прямо, глядя на положение вещей. В исходном журнале аргумент находится «над» базой (поскольку база индексирована), поэтому я оставлю все так, когда разделю их:
Я поддерживаю это прямо, глядя на положение вещей. В исходном журнале аргумент находится «над» базой (поскольку база индексирована), поэтому я оставлю все так, когда разделю их:Вот простой пример применения этой формулы:
Аргумент равен 6, а основание равно 3. Я подставлю их в формулу изменения базы, используя натуральный журнал в качестве журнала новой базы:
Тогда ответ, округленный до трех знаков после запятой, будет :
log 3 (6) = 1,631
Я получил бы тот же окончательный ответ, если бы использовал обыкновенный логарифм вместо натурального логарифма, хотя числитель и знаменатель промежуточной дроби отличались бы от то, что я показал выше:
Как видите, не имеет значения, какой журнал стандартной базы вы используете, если вы используете одну и ту же базу как для числителя, так и для знаменателя.
Хотя я показал значения числителя и знаменателя в приведенных выше расчетах, на самом деле лучше всего выполнять расчеты полностью в вашем калькуляторе.
 Вам не нужно утруждать себя записью этого промежуточного шага.
Вам не нужно утруждать себя записью этого промежуточного шага.На самом деле, чтобы свести к минимуму ошибки округления, лучше попытаться выполнить все шаги по делению и вычислению в калькуляторе за один раз. В приведенном выше вычислении вместо того, чтобы записывать первые восемь или около того знаков после запятой в значениях ln(6) и ln(3) и затем делить, вы просто сделали бы «ln(6) ÷ ln(3)» в своем калькулятор.
Вы можете получить несколько простых (но довольно бесполезных) упражнений на эту тему. Не завидуйте им; это простые пункты, пока вы держите формулу смены основания прямо в голове. Например:
Я не могу придумать какой-либо конкретной причины, по которой журнал с основанием 5 может быть полезен, поэтому я думаю, что единственная цель этих проблем — дать вам возможность попрактиковаться в использовании изменения основания. Отлично; Я включу и запущу:
С какой стати мне это делать (в «реальной жизни»), если я уже могу оценить натуральный логарифм в своем калькуляторе? я бы не стал; это упражнение предназначено только для практики (и простых моментов).

Я подключу и пыхтит к формуле изменения основания:
Поскольку получение фактического десятичного значения не является целью в упражнениях такого рода (преобразование с использованием изменения основания точку), просто оставьте ответ в виде логарифмической дроби.
Хотя приведенные выше упражнения были довольно бессмысленными, использование формулы изменения базы может быть очень удобно для поиска точек графика при построении графиков нестандартных журналов, особенно когда предполагается использование графического калькулятора.
Если бы я работал вручную, я бы использовал определение бревен, чтобы отметить, что:
- , поскольку 2 -2 = ¼, то логарифм 2 (¼) = -2
- , так как 2 –1 = ½, тогда log 2 (½) = –1
- , так как 2 0 = 1, тогда log 2 (1) = 0
- , так как 2 1 = 2, тогда log 2 (2) = 1
- , так как 2 2 = 4, тогда log 2 (4) = 2
- , так как 2 3 = 8, тогда log 2 (8) = 3
- , так как 2 4 = 16, тогда log 2 (16) = 4
А потом я рисовал свой график от руки.

(Почему я выбрал именно эти значения x ? Потому что любое меньшее значение было бы слишком крошечным для построения графика вручную, а любое большее привело бы к смехотворно широкому графику. Я выбрал значения, которые соответствовали моим потребностям.)
Но в данном случае я должен построить график с помощью своего графического калькулятора. Как я могу это сделать? (Или что, если я просто хочу использовать функцию «ТАБЛИЦА» моего графического калькулятора, чтобы найти несколько хороших аккуратных сюжетных точек?) У меня нет кнопки «логарифм с основанием два». Однако я могу ввести заданную функцию в свой калькулятор, используя формулу изменения базы, чтобы преобразовать исходную функцию в нечто, указанное в терминах базы, которую может понять мой калькулятор. Подбрасывая монету, я выбираю натуральное бревно:
(Я мог бы также использовать общий журнал. В этом случае функция была бы « y 1 = log( x )/log(2)».)
В моем графическом калькуляторе , после настройки окна просмотра на отображение полезных частей плоскости, график будет выглядеть примерно так:
Кстати, можно проверить, что график содержит ожидаемые «аккуратные» точки (т.
 е. точки I рассчитал бы вручную, как показано выше), чтобы убедиться, что на картинке отображается правильный график:
е. точки I рассчитал бы вручную, как показано выше), чтобы убедиться, что на картинке отображается правильный график:URL: https://www.purplemath.com/modules/logrules5.htm
Страница 1 Страница 2 Страница 3 Страница 4
3 простых способа создать GGPlot с логарифмической шкалой
Главная ggplot2 Преобразование логарифмической шкалы GGPlot
13 ноя
Преобразование логарифмической шкалы GGPlot
В этой статье описывается, как создать ggplot с логарифмической шкалой . Это можно легко сделать с помощью функций ggplot2 scale_x_continuous () и scale_y_continuous (), которые позволяют установить масштаб оси log2 или log10. Другой возможностью является функция scale_x_log10 () и scale_y_log10 (), которые преобразуют, соответственно, шкалы по осям x и y в логарифмическую шкалу : основание 10 .
Обратите внимание, что функции масштабирования преобразуют данные.
 Если вы подгоните что-нибудь к данным, это, вероятно, изменит подходящие значения.
Если вы подгоните что-нибудь к данным, это, вероятно, изменит подходящие значения.Альтернативой является использование функции coord_trans () для преобразованной декартовой системы координат. coord_trans () отличается от преобразования масштаба тем, что происходит после статистического преобразования и влияет только на внешний вид геометрии.
В этом учебном пособии по R-графике вы узнаете, как:
- Логарифмическое преобразование осей x и y в масштаб log2 или log10
- Показать экспоненту после логарифмических изменений путем форматирования меток делений оси.
- Отображение делений шкалы журнала . Функция R: annotation_logticks ()
Содержимое:
- Ключ ggplot2 Функции R
- Установить ось в масштабе log2
- Установить ось в масштабе log10
- Отметка делений шкалы журнала отображения
- Заключение
Ключевые функции ggplot2 R
Начните с создания точечной диаграммы с использованием набора данных
cars: библиотека(ggplot2) p <- ggplot(cars, aes(x = скорость, y = расстояние)) + геометрическая_точка() стр.

Функции R для установки логарифмической оси:
- p + scale_x_log10(), p + scale_y_log10() : график x и y в масштабе log 10 соответственно.
- p + coord_trans(x = «log2», y = «log2»): Преобразованная декартова система координат. Возможные значения для x и y: «log2», «log10», «sqrt», …
- p + scale_x_continuous (trans = «log2»), p + scale_y_continuous (trans = «log2»). Допустимое значение для аргумента trans, включая также «log10».
- p + scale_y_log10() + annotation_logticks(): отображение тиков шкалы журнала. 9.x)))
Установить ось в масштабе log10
Следующий код R изменяет масштаб оси Y в масштабе log10 с помощью функции
scale_y_log10():p + scale_y_log10()
9, альтернативно вы можете использовать функцию
scale_y_continuous(), которая позволяет преобразовывать разрывы и формат меток.p + scale_y_continuous(trans = "log10")
Отображение отметок делений логарифмической шкалы
Обратите внимание, что отметки логарифмической шкалы имеют смысл только для логарифмической шкалы с основанием 10.
 .x))) +
тема_bw()
часть 2
.x))) +
тема_bw()
часть 2 - Отображение делений шкалы журнала:
p2 + annotation_logticks()
Обратите внимание, что отметки журнала по умолчанию находятся внизу и слева. Чтобы указать стороны тиков журнала:
# Такты журнала слева и справа p2 + annotation_logticks(sides="lr") # Все стороны p2+annotation_logticks(sides="trbl")
Допустимые значения для аргумента
стороныявляются комбинацией «t» (сверху), «r» (справа), «b» (снизу), «l» (слева) ).Заключение
Мы расскажем, как создать ggplot с логарифмическим масштабом. Вкратце шаги следующие:
- Создайте пример ggplot:
библиотека (ggplot2) p <- ggplot(cars, aes(x = скорость, y = расстояние)) + geom_point()
- Логарифмическое преобразование масштаба оси:
# логарифмическая база 2 масштаб p + scale_x_continuous (транс = 'log2') + scale_y_continuous (транс = 'log2') # Шкала логарифма по основанию 10 + деления логарифма (слева и снизу) p + scale_x_continuous (транс = 'log10') + scale_y_continuous (транс = 'log10') + annotation_logticks(стороны="lb")
Версия: Французский
Порядки величины, логарифмические шкалы и децибелы
Абсолютная электроника: практическое проектирование и анализ схем
≡ Оглавление
«
1.
Алгебраические приближения 1
1»
1.3
Комплексные числаУдобная работа с числовыми величинами, которые варьируются во много порядков. 10 минут чтения
Электротехника в большей степени, чем многие другие области техники, характеризуется сосуществующими взаимодействующими величинами на многие порядки величины. Оба 1 Ом резистор и 1 МОм = 106 Ом резисторы являются обычным явлением, и нередко можно найти печатную плату, на которой есть хотя бы один из них.
Определение сопротивления конкретного резистора: 100 Ом, 1 кОм, 10 кОм или 100 кОм гораздо важнее, чем должно ли оно быть 1 кОм или 2,2 кОм .
Логарифмы сжимают значения от многих порядков до меньшего размера. Некоторые из основных правил, касающихся логарифмов, которые следует помнить, включают: 9.0909
logb(bx)=xblogbx=xlogb1=0logbb=1logb(x⋅y)=logbx+logbylogb(xy)=logbx−logbylogb(xy)=y⋅logbxlogyx=logbxlogbyдля любого b>1
(Уравнение log216= 4 читается вслух как: «Лог-основание-два из шестнадцати равно четырем».
 )
)Если основание не указано явно, контекст обычно определяет предполагаемое основание. База б=10 обычно используется в технике и обычно записывается как log(x) . В математике натуральное основание b=e=2,71828… обычно используется и записывается как ln (x) . В информатике основание b=2 обычно используется и записывается как lg(x) . Если это когда-либо не указано и неясно, спросите.
Логарифмирование сжимает мультипликативные различия в аддитивные различия. Например, если у нас есть две функции x(t) и y(t)=25⋅x(t) , то логарифмы (по любому основанию) этих двух функций будут отличаться только на константу:
logby(t)=logb(25⋅x(t))=logb25+logbx(t)
Это полезный способ думать о множестве электронных систем, таких как усилители и фильтры, которые обычно применяют мультипликативные преобразования к входному сигналу. С логарифмами мы можем думать об этом мультипликативном преобразовании как о простом сдвиге значения вверх или вниз по оси Y.
Разница в децибелах между двумя мультипликативно связанными сигналами напряжения или тока определяется как:
A=20logVoutVin
где A в дБ.
 В этом контексте логарифм определяется по основанию 10.
В этом контексте логарифм определяется по основанию 10.Откуда берется множитель 20? Ответ заключается в том, что это было определено таким образом, что 10-кратное мультипликативное увеличение мощности будет эквивалентно добавлению +10 дБ.
Поскольку мощность пропорциональна квадрату напряжения (что мы обсудим более подробно в разделе «Мощность»), 10-кратный увеличение на напряжение через усилитель дает 102=100X увеличение мощности или +20дБ.
Так как PoutPin=(VoutVin)2 , затем:
A=20log√PoutPin=20⋅12logPoutPin=10logPoutPin
(Чтобы не усложнять обсуждение децибелов на этом раннем этапе, мы не будем говорить здесь об эталонном импедансе. Поскольку логарифмы отрицательных чисел не Если они не существуют, мы также обычно говорим о огибающей или амплитуде сигнала, а не о самой форме сигнала.)
Вот несколько общих значений децибел и намеков на то, откуда они от:
Decibelsv или I Multiplierp Multiplier Multiplier+40 DB10010000104+30 DB√10001000103+20 DB10102+10 DB√1010101+6 DB2410010606… 3 DB10606… 3 DB10606… 3 3 DB241010606… 3 DB1010102+10 DB√1010101+6 DB2410010606… 3 DB10101102+10 DB ?1010101+6 DB241001060610010201020102 √22100.
 30103… 0 DB11100–3 DB√121210 - 0,30103… −6 DB121410 - 0,60206… -10 DB√110110101121410111010110110 гг. см. значения децибел за пределами этих границ: +80 дБ представляет собой множитель мощности 108
и множитель напряжения 104
. В общем, мы можем просто инвертировать приведенные выше уравнения для A дБ:
30103… 0 DB11100–3 DB√121210 - 0,30103… −6 DB121410 - 0,60206… -10 DB√110110101121410111010110110 гг. см. значения децибел за пределами этих границ: +80 дБ представляет собой множитель мощности 108
и множитель напряжения 104
. В общем, мы можем просто инвертировать приведенные выше уравнения для A дБ:VoutVin=10(A/20)PoutPin=10(A/10)
Значения ±3 дБ и ±6 дБ не являются точными, но являются общими приближениями, потому что:
20log102=6,0206…≈620log10√2=3,0103…≈3
Эти точные значения в децибелах для умножения на 2 и √2 обычно усекаются. Вот почему инженеры в просторечии говорят о +3 дБ или +6 дБ, имея в виду коэффициент усиления по мощности, равный 2, или коэффициент усиления по напряжению, равный 2, соответственно.
Если мы последовательно соединим два усилителя, каждый из которых будет иметь 10-кратное усиление по напряжению, то каждый из них даст усиление +20 дБ. Мы можем сложить значения в децибелах, чтобы получить общий коэффициент усиления по напряжению +40 дБ — коэффициент 102.
 по напряжению и коэффициентом 104
в силе.
по напряжению и коэффициентом 104
в силе.Любая единица измерения, указанная только как «дБ», относится только к относительному коэффициенту между сигналами.
Однако часто бывает удобно определить знаменатель как конкретную единичную величину подшипника.
Например, «дБм» означает «децибелы относительно 1 милливатт». Таким образом, +20 дБм соответствует «+20 дБ относительно 1 мВт». Поскольку ватты — это единица мощности, а +20 дБ — это 100-кратное умножение мощности, то «+20 дБм» — это просто сокращение от «100 милливатт».
В другом примере «дБВ» означает «децибелы относительно 1 Вольта». Следовательно, -60 дБв представляет собой «-60 дБ относительно 1 вольта». Поскольку -60 дБ по напряжению соответствует коэффициенту напряжения 10−3. , то «-60 дБВ» — это просто сокращение от «1 милливольт».
Внимательно следите за тем, является ли единица измерения децибел относительной или абсолютной, и представляет ли абсолютная ссылка уровень мощности или напряжения.

В следующих разделах, когда мы будем говорить о частотных характеристиках усилителей и фильтров, мы иногда будем рассматривать такие числа, как «-20 дБ/декада» или «-6 дБ/октава».
Декадой называется увеличение частоты в 10 раз, например, со 100 Гц до 1000 Гц. Выражение «минус 20 дБ за декаду» может означать, что выходной сигнал на частоте 1000 Гц составляет всего 110 такая же большая по амплитуде напряжения, как и сигнал на частоте 100 Гц.
Октава — это двукратное увеличение частоты, как и в музыке. Например, 100 Гц и 200 Гц разделены одной октавой. Выражение «минус 6 дБ на октаву» может означать, что выходной сигнал на частоте 200 Гц составляет всего 12 такая же большая по амплитуде напряжения, как и сигнал на частоте 100 Гц.
Оказывается, эти два примера на самом деле относятся к одному и тому же:
−20 дБ/декада≈−6 дБ/октава
Давайте докажем это. Сколько октав в декаде?
k=log210=log10log2≈3,322
Если начать с частоты f и удвоить его три раза (т.
 е. подняться на три октавы вверх), мы получим 23⋅f=8⋅f
- почти достаточно, чтобы достичь 10⋅f
, но не совсем. Если мы удвоим f
четыре раза (т.е. подняться на четыре октавы вверх), мы получим 24⋅f=16⋅f
– более десяти лет; мы зашли слишком далеко. Реальное количество октав, необходимое для завершения декады, составляет от трех до четырех и отображается как k.
выше.
е. подняться на три октавы вверх), мы получим 23⋅f=8⋅f
- почти достаточно, чтобы достичь 10⋅f
, но не совсем. Если мы удвоим f
четыре раза (т.е. подняться на четыре октавы вверх), мы получим 24⋅f=16⋅f
– более десяти лет; мы зашли слишком далеко. Реальное количество октав, необходимое для завершения декады, составляет от трех до четырех и отображается как k.
выше.Если наш сигнал уменьшится на -6 дБ/октава, а частота поднимется на 3,322 октавы, общее уменьшение составит: действительно точно -20дБ если принять во внимание тот факт, что -6 дБ является только округленным приближением для 20log102≈6,0206 .
На полулогарифмическом графике ось Y отображается в логарифмическом масштабе, а ось X остается линейной. Это превращает экспоненциально изменяющиеся (с любым основанием) функции в прямые. Например, рассмотрим стоимость сберегательного счета с начальной стоимостью 1000, увеличивающуюся на 5% в год со временем t годами. Стоимость счета:
m(t)=1000⋅1,05t
Если взять логарифм,
logm(t)=log(1000⋅1,05t)logm(t)=log1000+log1,05tlogm(t)=log1000+t ⋅log1,05logm(t)≈3+0,02119⋅t
Логарифм превратил экспоненту (с основанием 1,05) в прямую.

В аналогичном примере график стоимости акции или взаимного фонда должен быть построен на полулогарифмическом графике. (Его также следует построить с реинвестированными дивидендами, чтобы показать общую прибыль, хотя это отдельный вопрос, который мы не можем здесь рассматривать.) Почему логарифмический? Потому что, если мы построим график с линейной шкалой, похоже, что весь рост произошел только за последние несколько лет. Если построить график в логарифмическом масштабе, то окажется, что на самом деле инвестор примерно в любой момент примерно удвоил свою инвестиционную стоимость примерно за десятилетие. Это отражает идею о том, что в целом в любой конкретный год прибыль компании (будь то нераспределенная прибыль или распределенная в виде дивидендов) будет составлять примерно несколько процентов от ее текущей стоимости.
Чтобы убедиться в этом, загрузите эти данные, нажмите «Макс», чтобы установить максимальную временную шкалу с 1970 года. Линейный график выглядит совсем крошечным для первой половины набора данных.
 Теперь нажмите «Редактировать график», нажмите «Формат» и установите флажок «Масштаб журнала»; если горизонтальная шкала сбрасывается, вам, возможно, придется снова нажать «Макс». Теперь, хотя это не является гладким, последовательным или безрисковым, вы увидите, что на самом деле общая тенденция роста (в %/годовом смысле роста) присутствовала в течение многих десятилетий.
Теперь нажмите «Редактировать график», нажмите «Формат» и установите флажок «Масштаб журнала»; если горизонтальная шкала сбрасывается, вам, возможно, придется снова нажать «Макс». Теперь, хотя это не является гладким, последовательным или безрисковым, вы увидите, что на самом деле общая тенденция роста (в %/годовом смысле роста) присутствовала в течение многих десятилетий.Если построение графика с логарифмической шкалой по оси Y является эффективным, то построение графика с логарифмической шкалой как по оси X, так и по оси Y действительно эффективно.
Рассмотрим нашу функцию y(x)=11+x которые мы использовали для вычисления различных приближений в разделе «Алгебраические приближения». Взяв логарифм обеих сторон:
y(x)=11+xlogy(x)=log(11+x)logy(x)=-log(1+x)
Это само по себе не выглядит очень простым. понятно, но давайте опять применим различные приближения в разных предельных асимптотах для x :
логика(х)=-log(1+x)≈-log(1)=0для |x|≪1логика(x)=-log(1+x)≈-log(x)для x≫1
Теперь определим p=logx и q = логика .
 Они представляют собой логарифмически преобразованный x
и ты
оси для черчения.
Они представляют собой логарифмически преобразованный x
и ты
оси для черчения.q≈0для |x|≪1q≈−pдля x≫1
Теперь у нас есть два очень простых уравнения для прямых, которые являются хорошим приближением для q в разных режимах: первый участок имеет уклон 0 (горизонтальная линия), а второй участок имеет уклон -1. Линия аппроксимации плохо работает вблизи «колена», где встречаются два приближения, но хорошо работает во всех остальных местах. 9q(p)=min(0,−p)
Это просто компактное представление двух приведенных выше сегментов, но, что важно, это представление, которое программное обеспечение вычисления математических выражений внутри CircuitLab умеет обрабатывать непосредственно с помощью MIN( а, б) нотация — см. документацию по выражениям для получения дополнительной информации.
Мы покажем, насколько хорош логарифмический график, рассмотрев значение p от 10−5 до 10+5 – коэффициент 10 миллиардов снизу вверх!
Логарифмические приближения построения графика 9д (р) неплохо для p≤−1 и р≥+1 , что соответствует x≤0,1 и х≥10 .
 В середине ни одно из приближений не является превосходным, но теперь, когда мы знаем, что ошибка существует, ее можно определить количественно.
В середине ни одно из приближений не является превосходным, но теперь, когда мы знаем, что ошибка существует, ее можно определить количественно.Мы взяли сложную на вид дробь и превратили ее в набор отрезков прямых с помощью двух инструментов: логарифмических графиков и асимптотических приближений. В этом сила логарифмического построения: оно превращает рациональные многочлены (дроби с xn в числителе или знаменателе) в прямолинейные приближения, которые работают на многие порядки.
Обратите внимание, что второй отрезок имеет наклон -1, соответствующий x−1 . Если исходная дробь имела x−2 , наклон будет -2.
Графики в логарифмическом масштабе и концепция линейной аппроксимации снова всплывут, когда мы рассмотрим фильтры, усилители и частотную характеристику. Log-log отлично подходит для этого, потому что независимая переменная (частота) варьируется на много порядков, как и зависимая переменная (усиление величины).
И, как мы увидим, АЧХ обычных фильтров можно описать рациональными полиномами, так что и здесь мы получим аппроксимации отрезков прямых при использовании тех же инструментов.
 Например, простой RC фильтр нижних частот будет иметь 1/f
амплитудная характеристика для частот выше его угловой частоты, точно отображая пример, который мы только что проиллюстрировали.
Например, простой RC фильтр нижних частот будет иметь 1/f
амплитудная характеристика для частот выше его угловой частоты, точно отображая пример, который мы только что проиллюстрировали.Если концепции асимптотических приближений, полулогарифмических и логарифмических графиков все еще незнакомы, рекомендуется освежить и изучить эти концепции на бумаге и/или в моделировании, поскольку они будут возникать снова и снова по мере мы идем.
Поскольку электронные величины охватывают много порядков, в электронике принято использовать префиксы единиц, которые помогают обозначать порядки величины при различных степенях 103. . Это упрощает удобочитаемые числа.
ValuePrefixAbbreviationExample1012teraT3 THz=3×1012 Hz109гигаГц2,4 ГГц=2,4×109 Гц106мегаМ10 МОм=107 Ом103 килоок2,2 кОм=2200 Ом100−−5 В10−3 миллим5,3 мВ=0,0053 В10−6микроμ22 мкФ=0,000022 F10−9нанон200 нВp2p2p2 picopV10 =12×10−12 F10−15femtof200fs=2×10−14 с
, строчная греческая буква мю. Однако, поскольку это трудно ввести в компьютер, часто пишут только строчной буквой u: 22 мкФ = 22 мкФ.
 , но произносится вслух как «двадцать два микрофарад» в любом случае.
, но произносится вслух как «двадцать два микрофарад» в любом случае.Большинство программ для электроники, включая программу моделирования CircuitLab, распознает эти префиксы, если префикс идет сразу после цифр номера (без пробела между ними). Например, вы можете ввести «2,2 кОм» в поле значения для резистора, чтобы получить сопротивление 2200 Ом. Один сбивающий с толку случай заключается в том, что мега представлено заглавной буквой «М», а милли — строчной «м»; современное программное обеспечение, такое как CircuitLab, будет правильно интерпретировать эти два слова, как они написаны, но некоторые более старые схемные программы на основе SPICE датируются 19 веком.70-х и не может понять разницу между прописными и строчными буквами! Эти старые программы вместо этого используют «MEG» для обозначения мега. Будьте осторожны, чтобы компьютер правильно интерпретировал ваше значение.
В следующем разделе «Комплексные числа» мы поговорим о действительных и мнимых числах и их связи с окружностями, тригонометрией и синусоидами.


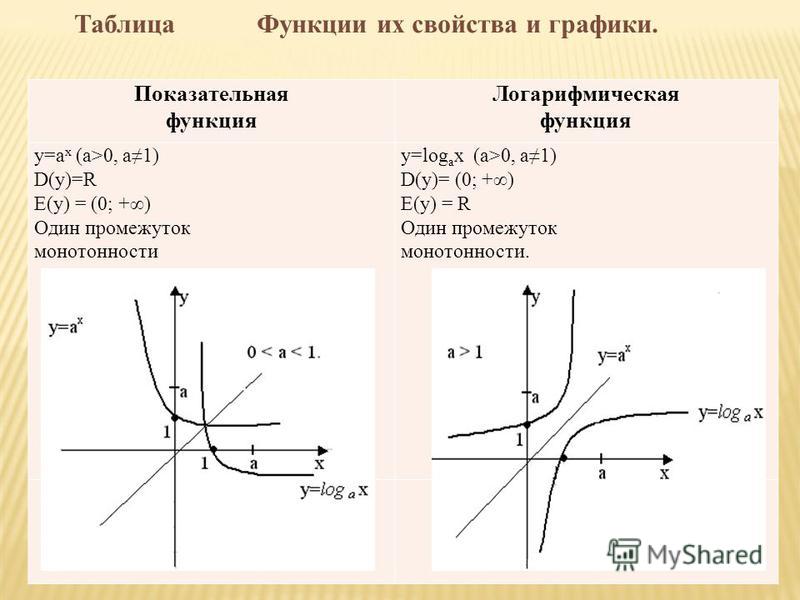 Вычислите логарифм: log 5 25
Вычислите логарифм: log 5 25
 е. степень, в которую надо возвести число 10, чтобы получить число x
. Обозначение: lg x
.
е. степень, в которую надо возвести число 10, чтобы получить число x
. Обозначение: lg x
.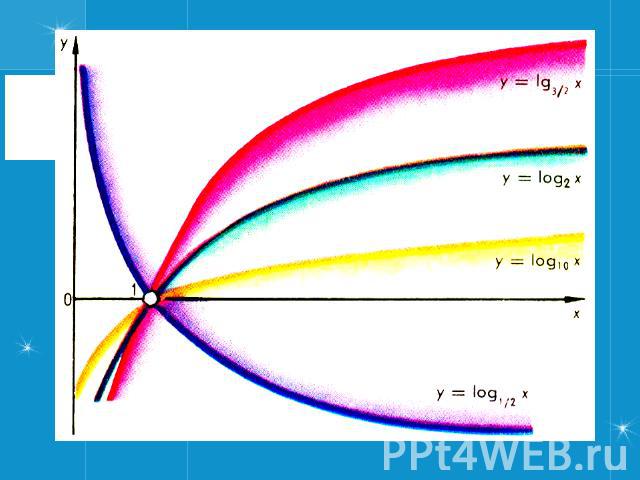
 Область определения и ответы при этом никак не пострадают, а вот объем вычислений существенно сократится.
Область определения и ответы при этом никак не пострадают, а вот объем вычислений существенно сократится.
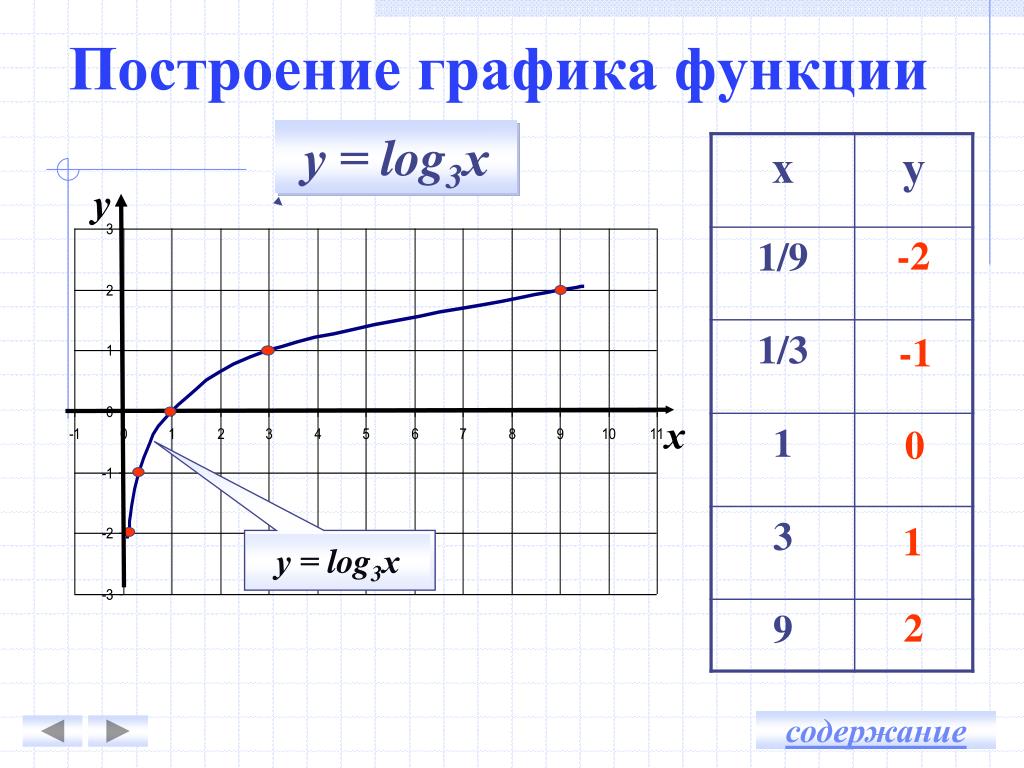 ..
..
 4kb.
4kb.
 98kb.
98kb.
 Формировать навыки общения, диалога, умение работать в коллективе.
Формировать навыки общения, диалога, умение работать в коллективе. 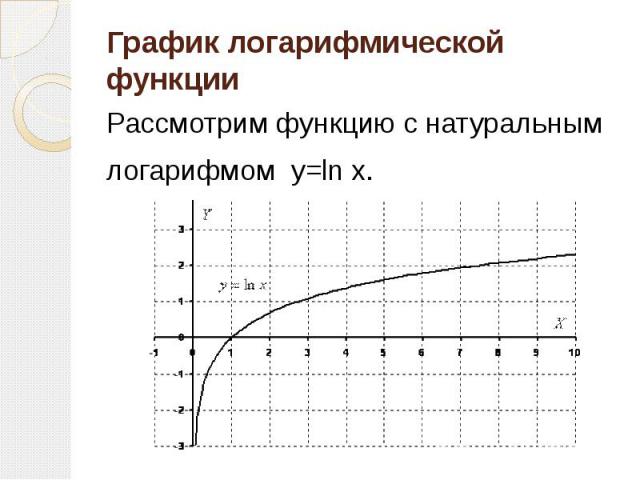 В подтверждение разберём три примера (Приложение 1) Примеры на вычисление логарифма
В подтверждение разберём три примера (Приложение 1) Примеры на вычисление логарифма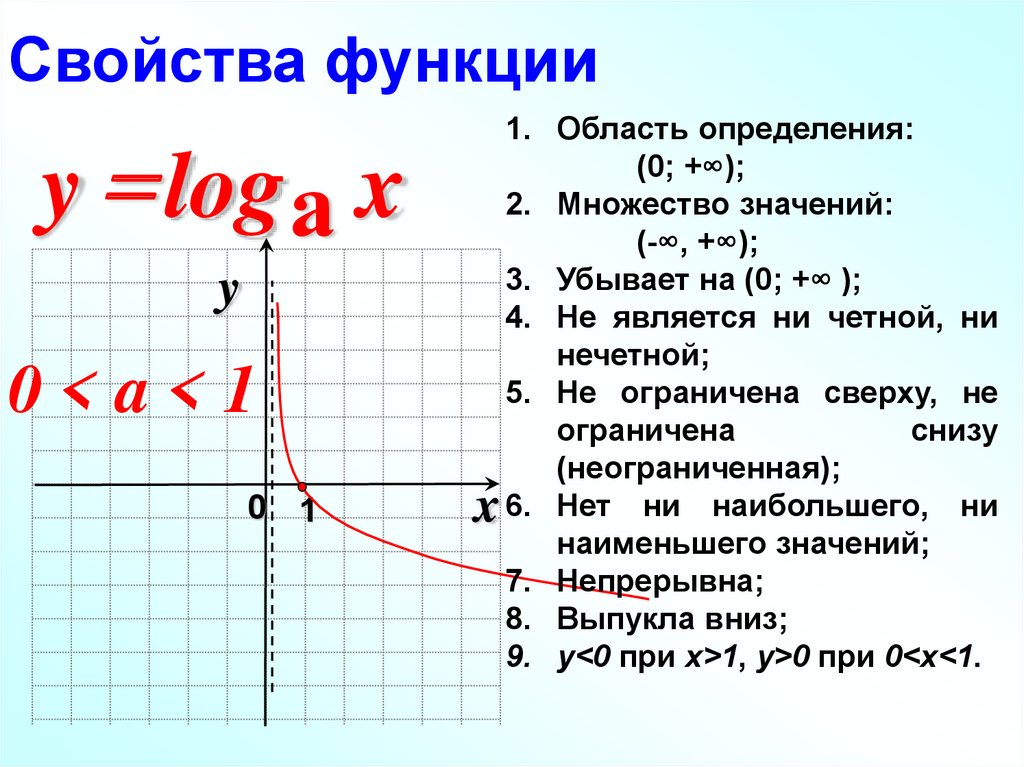
 На вопрос учителя: «Как бы вы назвали эту функции?» учащиеся говорят, что она логарифмическая, так как переменная стоит под знаком логарифма: . На вопрос: «Находит ли эта функция применение в окружающем нас мире?», ответит с помощью своего сообщения о логарифмической спирали учащаяся (Приложение 4).
На вопрос учителя: «Как бы вы назвали эту функции?» учащиеся говорят, что она логарифмическая, так как переменная стоит под знаком логарифма: . На вопрос: «Находит ли эта функция применение в окружающем нас мире?», ответит с помощью своего сообщения о логарифмической спирали учащаяся (Приложение 4). 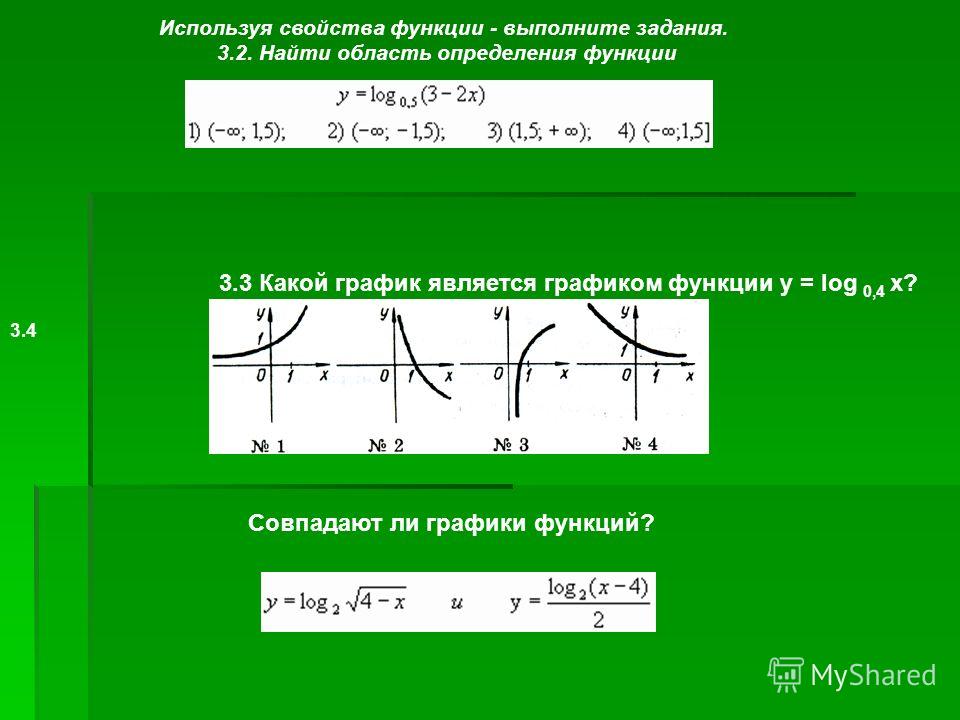

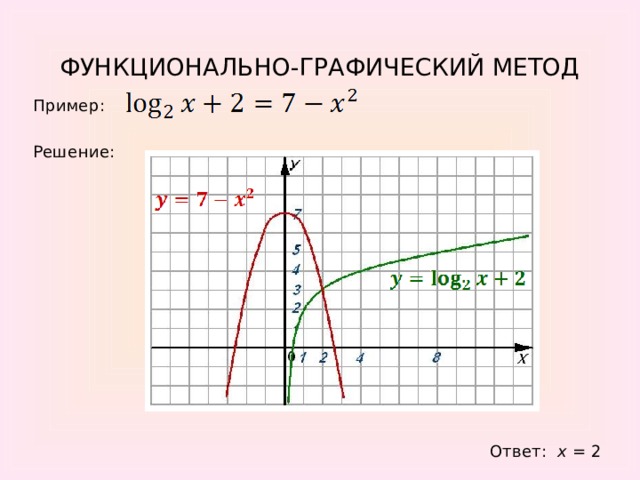


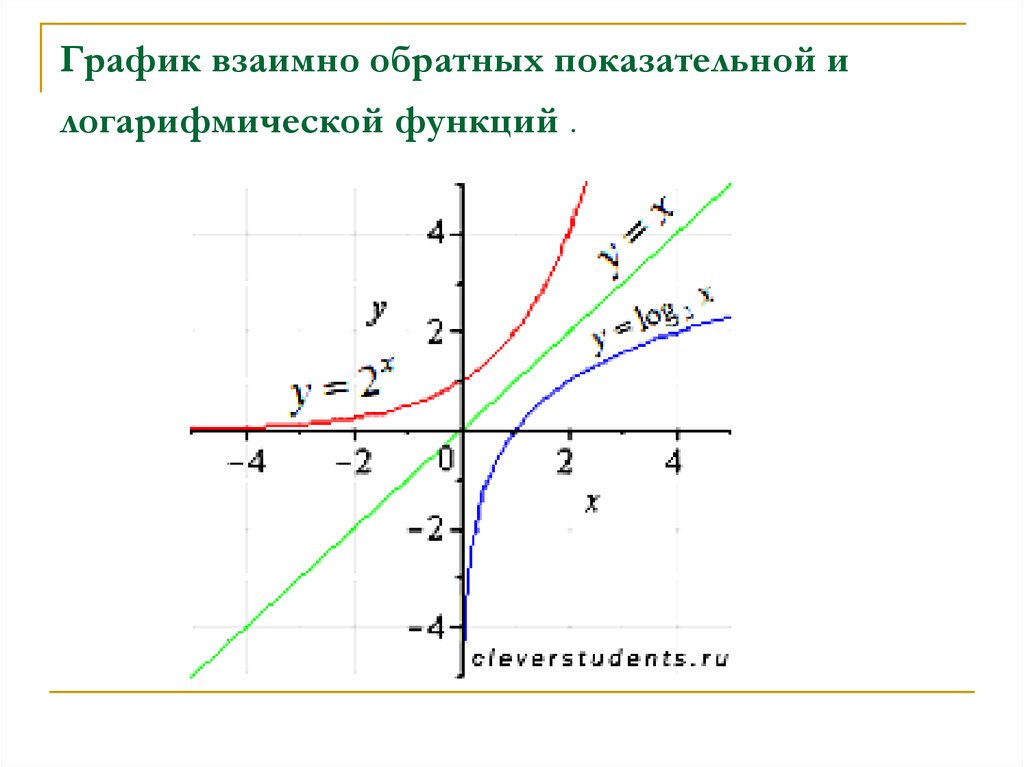 Подводя итоги урока, выясняется, что было известно учащимся, что нового узнали и чему научились на этом уроке.
Подводя итоги урока, выясняется, что было известно учащимся, что нового узнали и чему научились на этом уроке. 


 Вот общая формула для изменения основания —
Вот общая формула для изменения основания —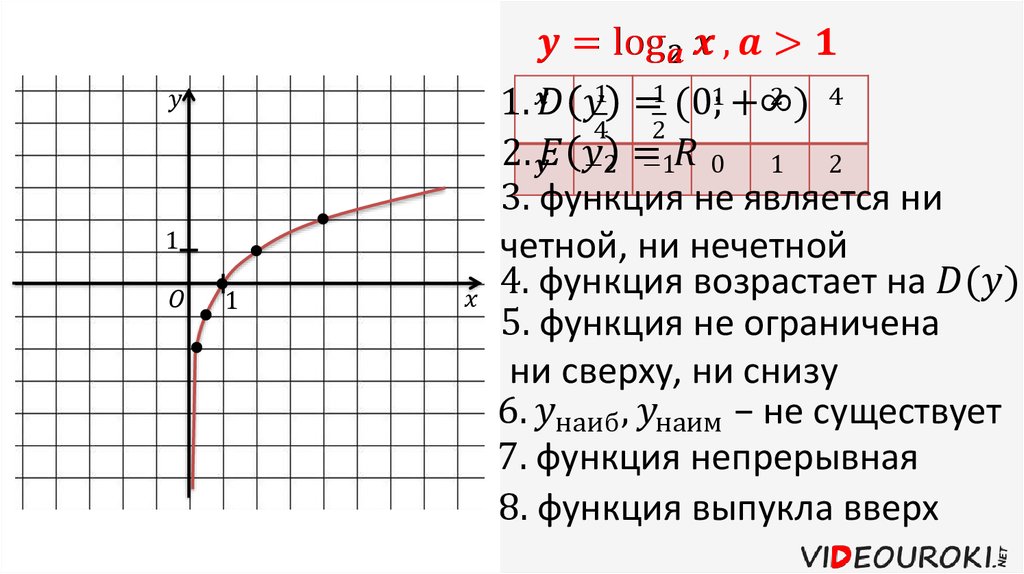


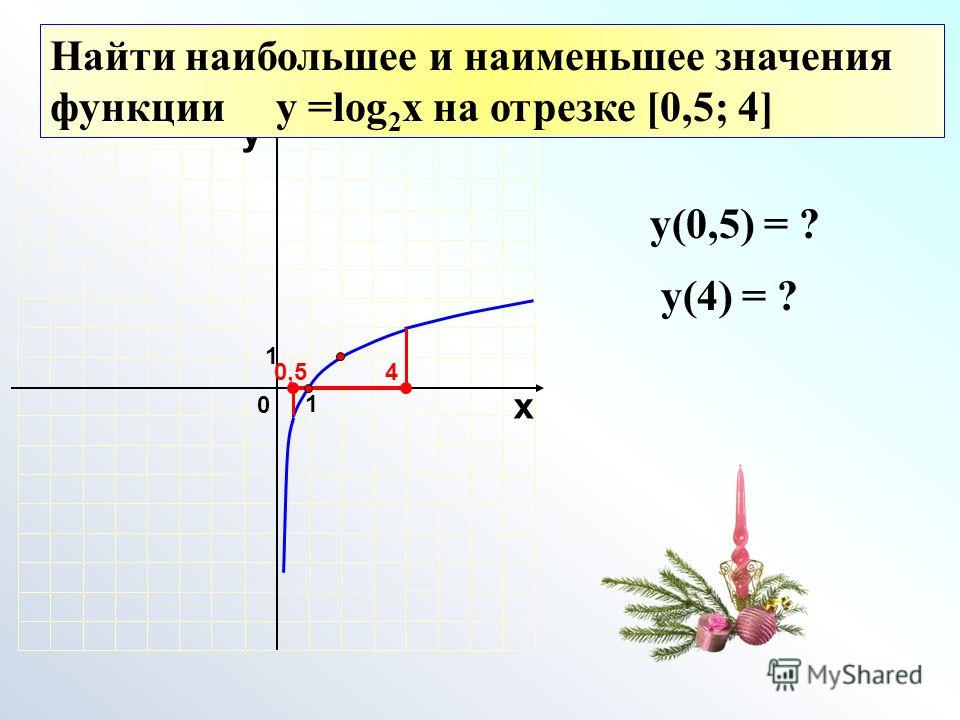
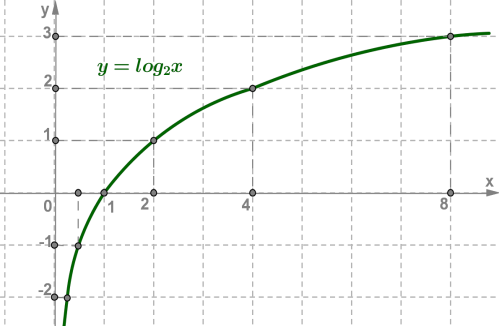
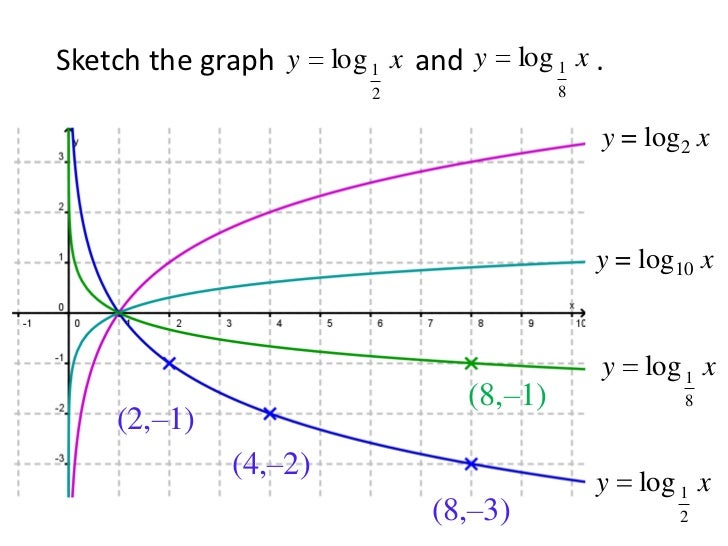
 1 не имеет нулей, так что это 10 0 . А 0,0001 имеет четыре нуля и является отрицательным, поэтому это 10 -4 . Таким образом, логарифмическая шкала не показывает числа на линейной шкале, но показывает величины в линейной форме: 0, 1, 2, 3 и т. д.
1 не имеет нулей, так что это 10 0 . А 0,0001 имеет четыре нуля и является отрицательным, поэтому это 10 -4 . Таким образом, логарифмическая шкала не показывает числа на линейной шкале, но показывает величины в линейной форме: 0, 1, 2, 3 и т. д. богатый зернами пшеницы и шахматной доской: мы все слышали слово «экспоненциальный» раньше. Давайте вспомним, что это значит.
богатый зернами пшеницы и шахматной доской: мы все слышали слово «экспоненциальный» раньше. Давайте вспомним, что это значит.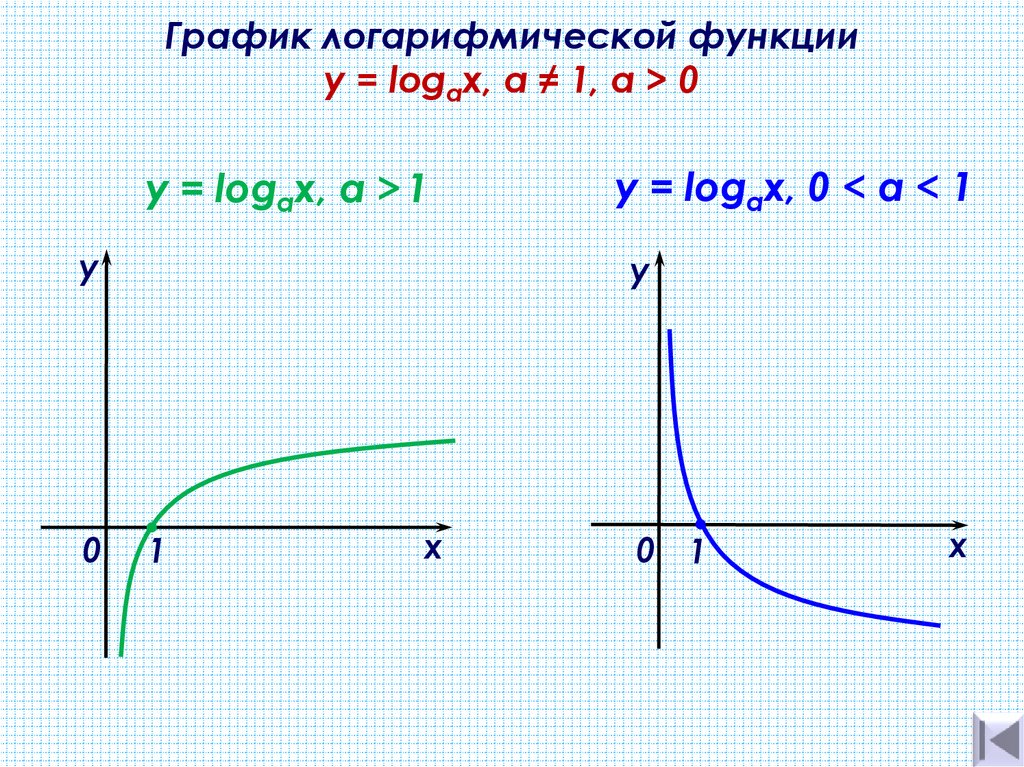 д. Та же сделка. Логарифмическая шкала «растет экспоненциально», если ее показатели степени (= порядок величин) «растут линейно».
д. Та же сделка. Логарифмическая шкала «растет экспоненциально», если ее показатели степени (= порядок величин) «растут линейно». 
 Это означает, что потребовалось 15 лет, чтобы перейти от 1000 транзисторов к 100 000 транзисторов, и потребовалось 15 лет, чтобы перейти от 100 миллионов транзисторов к 10 миллиардам.
Это означает, что потребовалось 15 лет, чтобы перейти от 1000 транзисторов к 100 000 транзисторов, и потребовалось 15 лет, чтобы перейти от 100 миллионов транзисторов к 10 миллиардам.
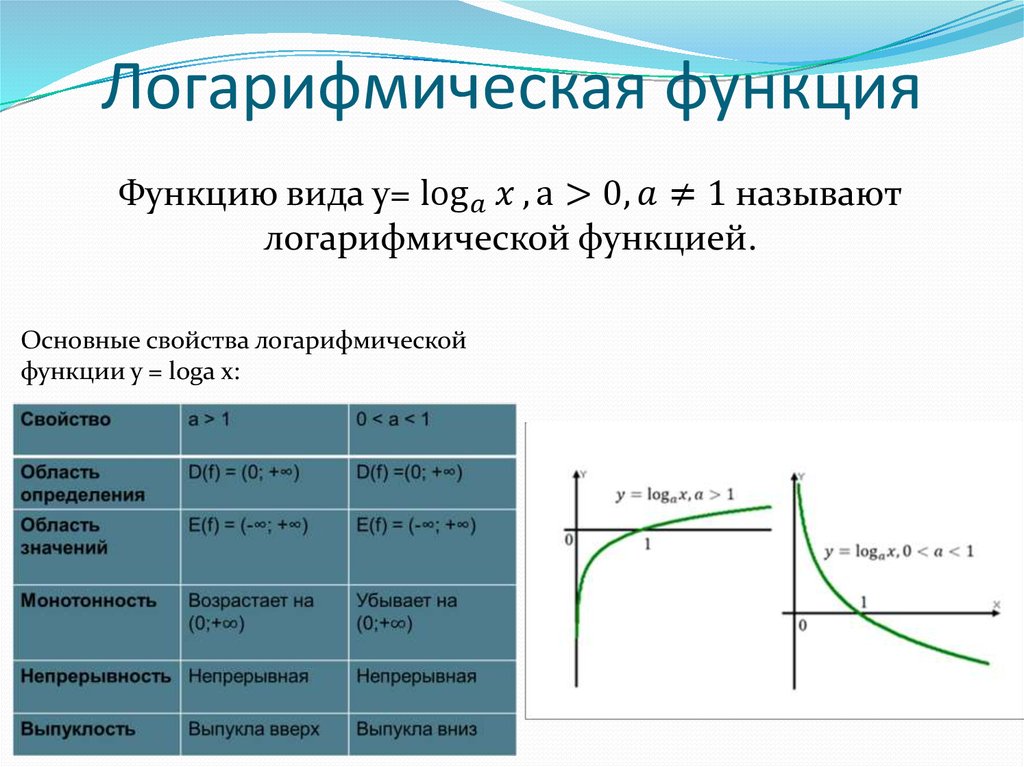 Я поддерживаю это прямо, глядя на положение вещей. В исходном журнале аргумент находится «над» базой (поскольку база индексирована), поэтому я оставлю все так, когда разделю их:
Я поддерживаю это прямо, глядя на положение вещей. В исходном журнале аргумент находится «над» базой (поскольку база индексирована), поэтому я оставлю все так, когда разделю их: Вам не нужно утруждать себя записью этого промежуточного шага.
Вам не нужно утруждать себя записью этого промежуточного шага.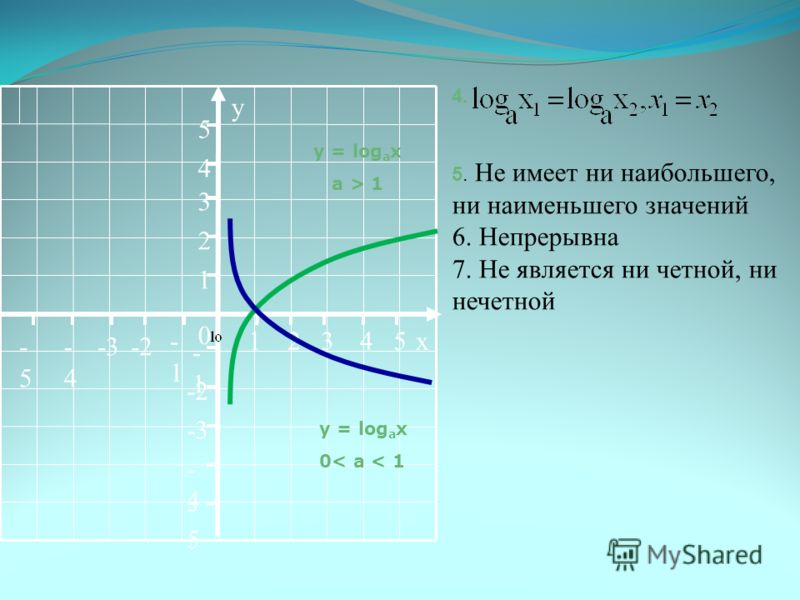

 е. точки I рассчитал бы вручную, как показано выше), чтобы убедиться, что на картинке отображается правильный график:
е. точки I рассчитал бы вручную, как показано выше), чтобы убедиться, что на картинке отображается правильный график: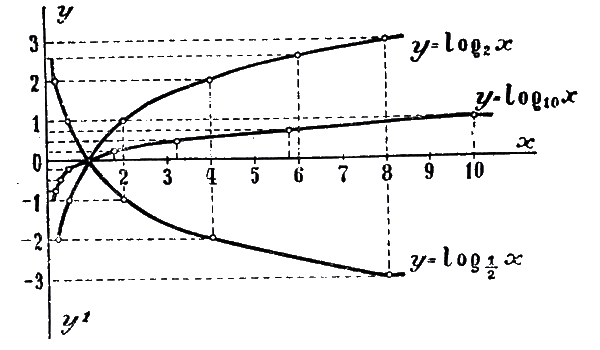 Если вы подгоните что-нибудь к данным, это, вероятно, изменит подходящие значения.
Если вы подгоните что-нибудь к данным, это, вероятно, изменит подходящие значения.
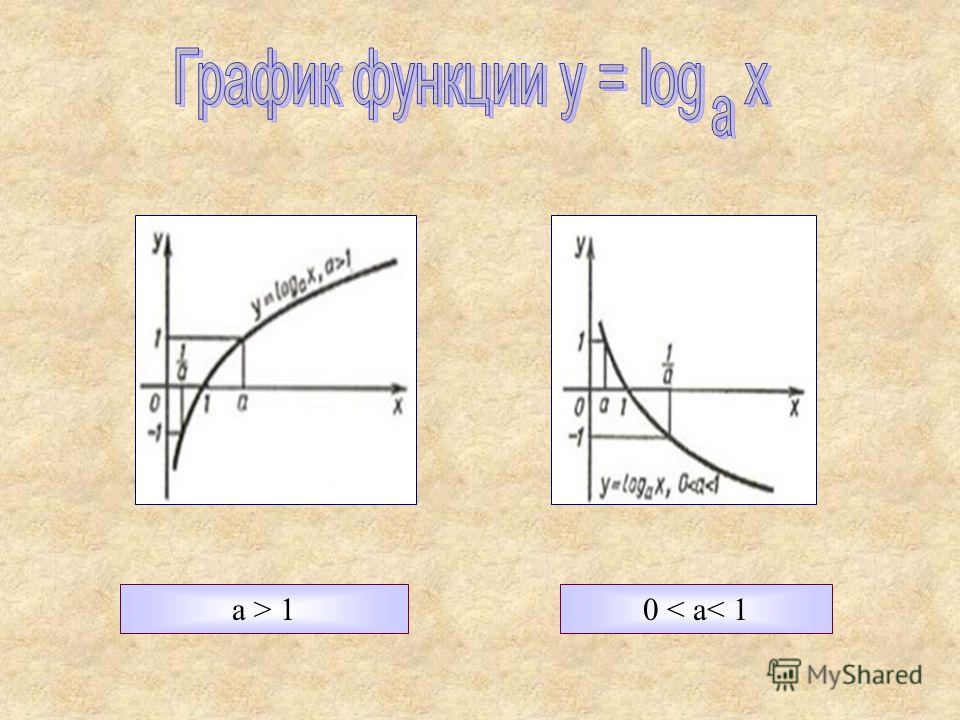 .x))) +
тема_bw()
часть 2
.x))) +
тема_bw()
часть 2 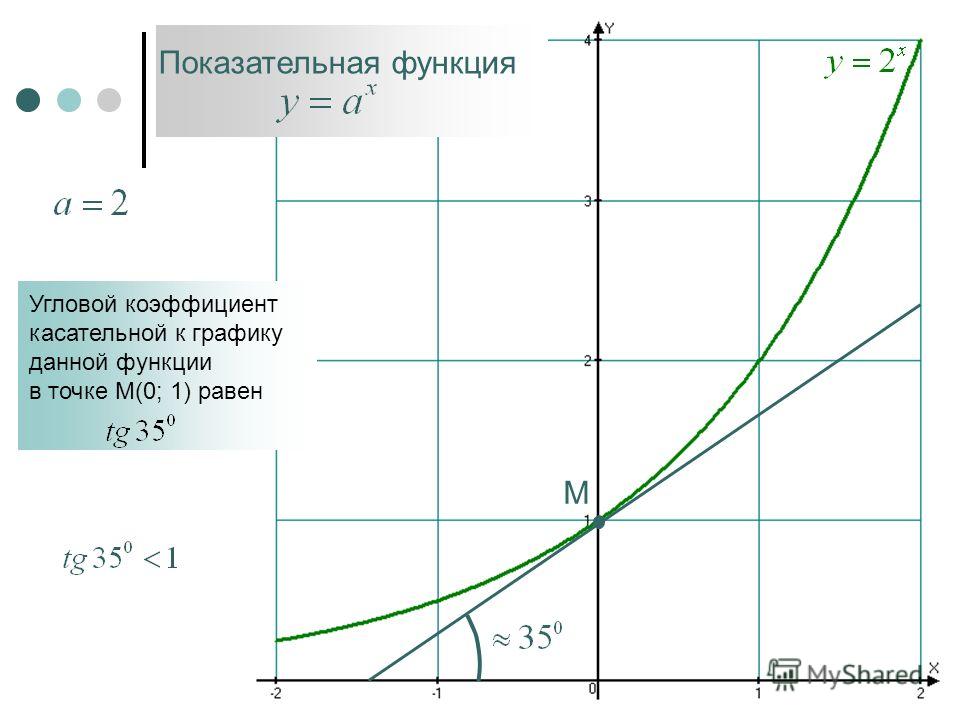 1
1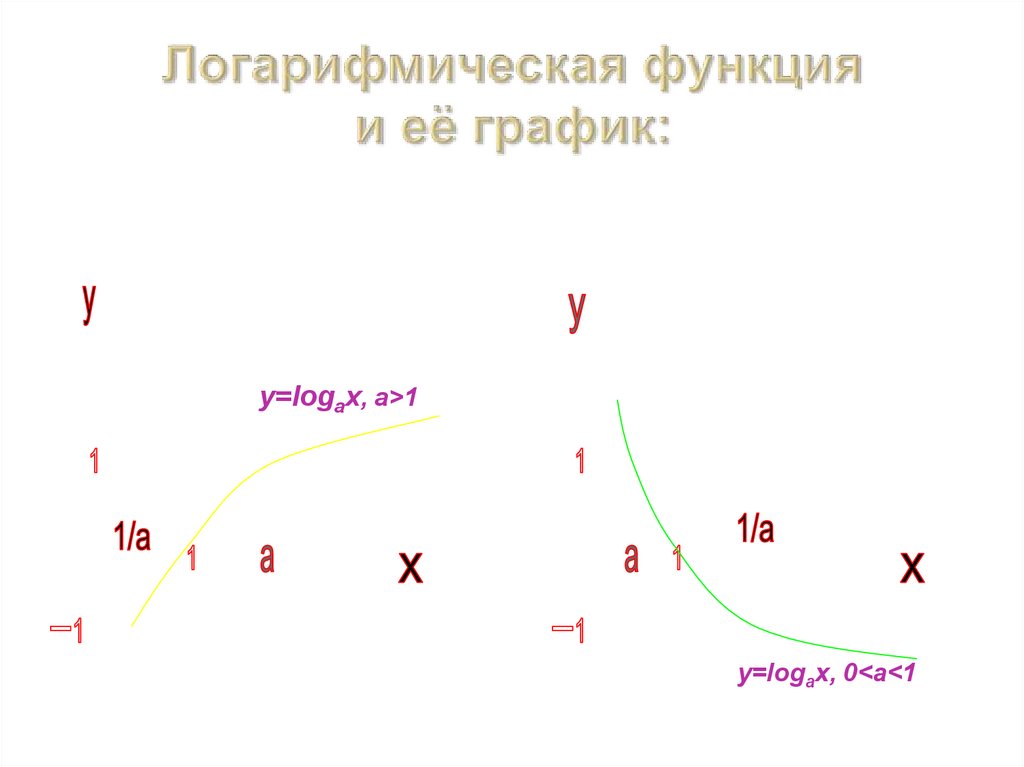 )
)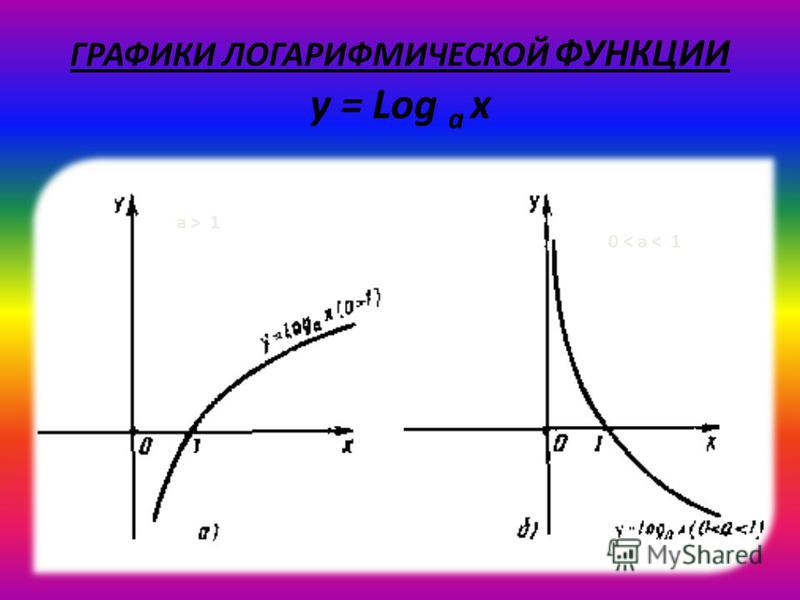 В этом контексте логарифм определяется по основанию 10.
В этом контексте логарифм определяется по основанию 10.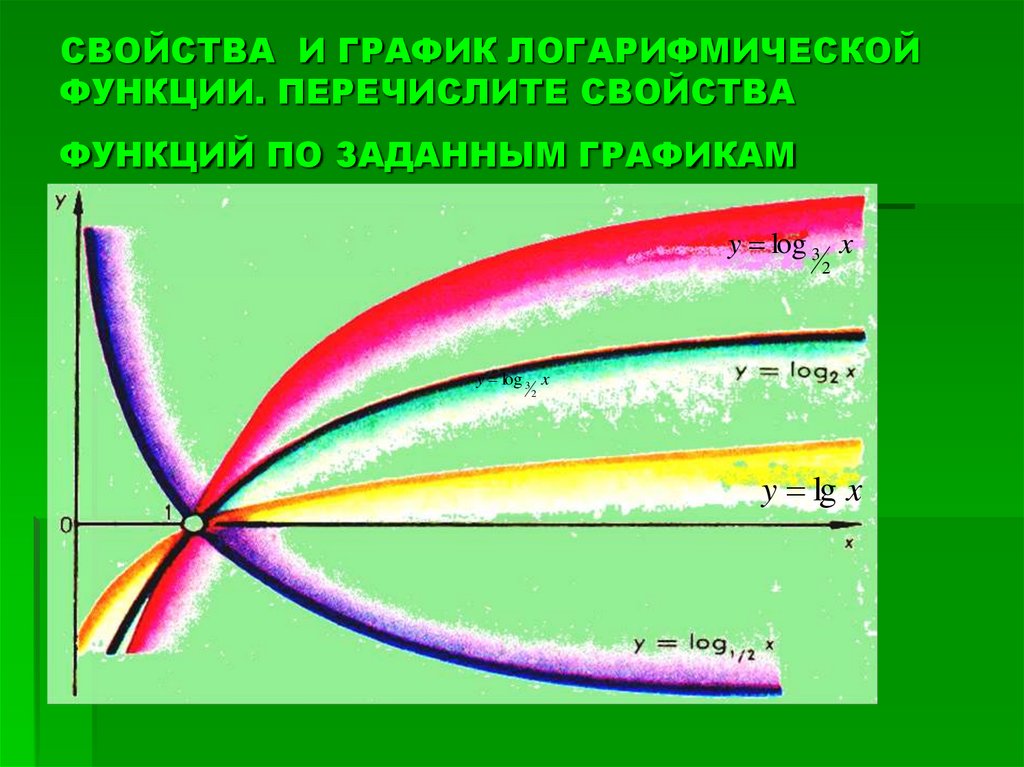 30103… 0 DB11100–3 DB√121210 - 0,30103… −6 DB121410 - 0,60206… -10 DB√110110101121410111010110110 гг. см. значения децибел за пределами этих границ: +80 дБ представляет собой множитель мощности 108
и множитель напряжения 104
. В общем, мы можем просто инвертировать приведенные выше уравнения для A дБ:
30103… 0 DB11100–3 DB√121210 - 0,30103… −6 DB121410 - 0,60206… -10 DB√110110101121410111010110110 гг. см. значения децибел за пределами этих границ: +80 дБ представляет собой множитель мощности 108
и множитель напряжения 104
. В общем, мы можем просто инвертировать приведенные выше уравнения для A дБ: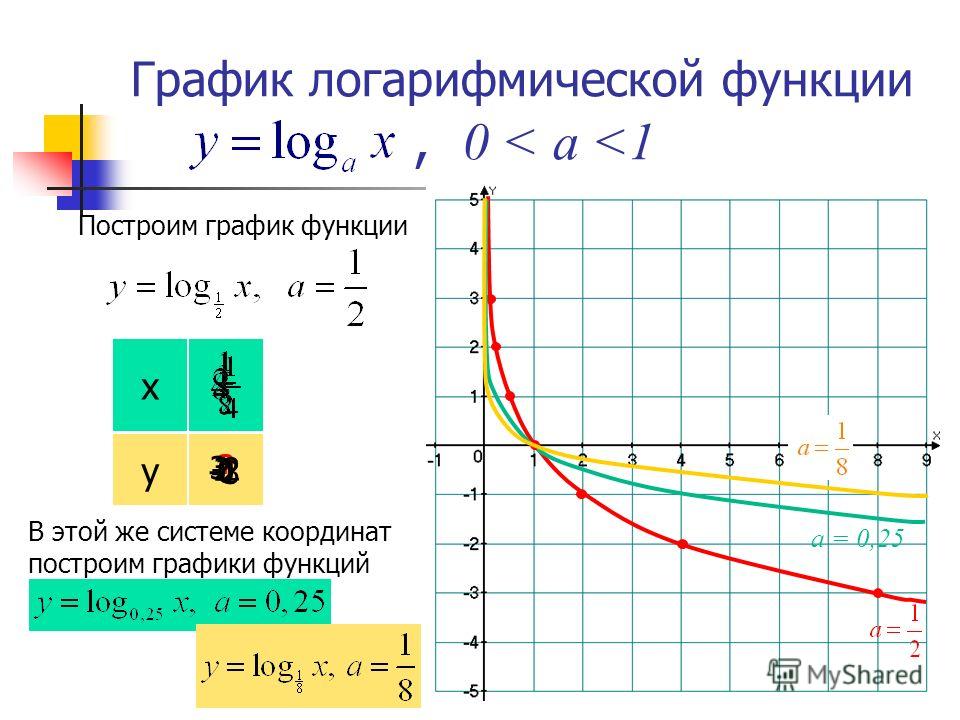 по напряжению и коэффициентом 104
в силе.
по напряжению и коэффициентом 104
в силе.
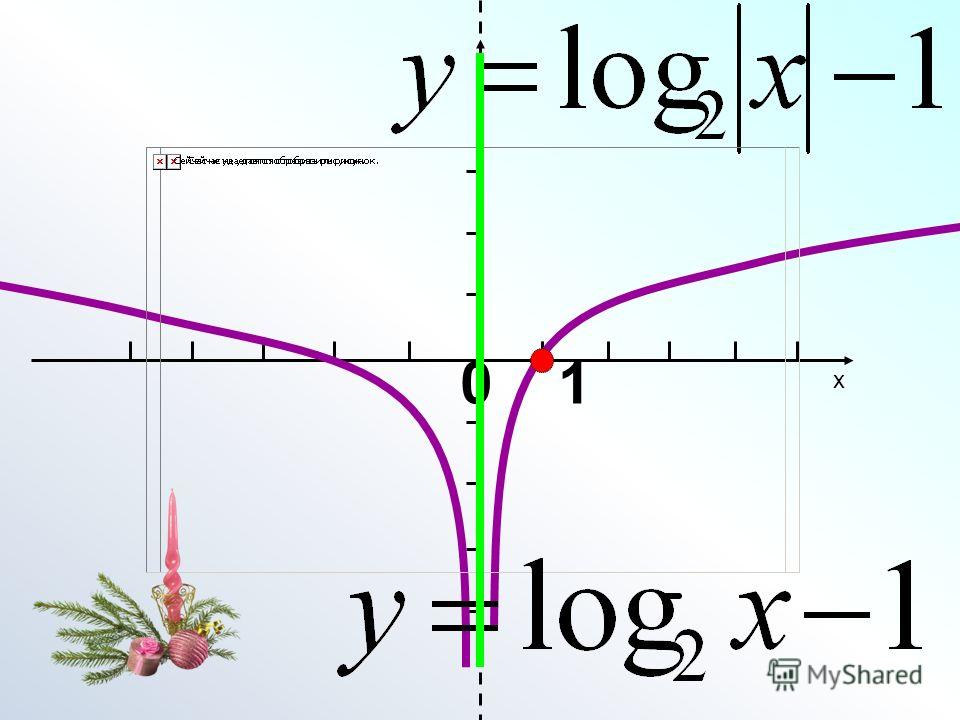 е. подняться на три октавы вверх), мы получим 23⋅f=8⋅f
- почти достаточно, чтобы достичь 10⋅f
, но не совсем. Если мы удвоим f
четыре раза (т.е. подняться на четыре октавы вверх), мы получим 24⋅f=16⋅f
– более десяти лет; мы зашли слишком далеко. Реальное количество октав, необходимое для завершения декады, составляет от трех до четырех и отображается как k.
выше.
е. подняться на три октавы вверх), мы получим 23⋅f=8⋅f
- почти достаточно, чтобы достичь 10⋅f
, но не совсем. Если мы удвоим f
четыре раза (т.е. подняться на четыре октавы вверх), мы получим 24⋅f=16⋅f
– более десяти лет; мы зашли слишком далеко. Реальное количество октав, необходимое для завершения декады, составляет от трех до четырех и отображается как k.
выше.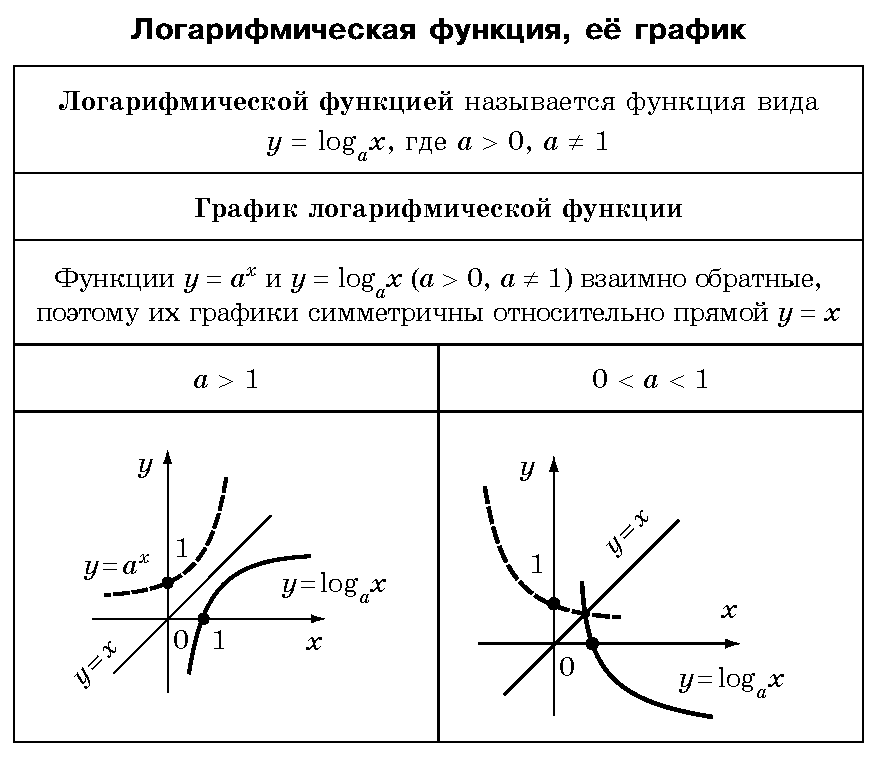
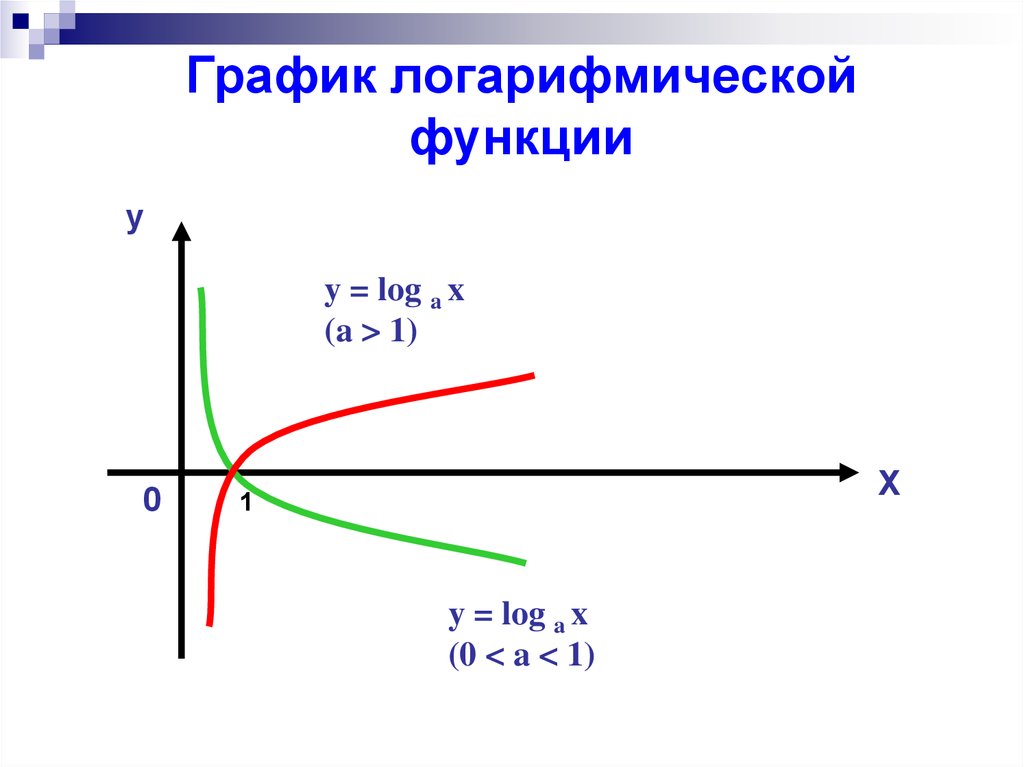 Теперь нажмите «Редактировать график», нажмите «Формат» и установите флажок «Масштаб журнала»; если горизонтальная шкала сбрасывается, вам, возможно, придется снова нажать «Макс». Теперь, хотя это не является гладким, последовательным или безрисковым, вы увидите, что на самом деле общая тенденция роста (в %/годовом смысле роста) присутствовала в течение многих десятилетий.
Теперь нажмите «Редактировать график», нажмите «Формат» и установите флажок «Масштаб журнала»; если горизонтальная шкала сбрасывается, вам, возможно, придется снова нажать «Макс». Теперь, хотя это не является гладким, последовательным или безрисковым, вы увидите, что на самом деле общая тенденция роста (в %/годовом смысле роста) присутствовала в течение многих десятилетий.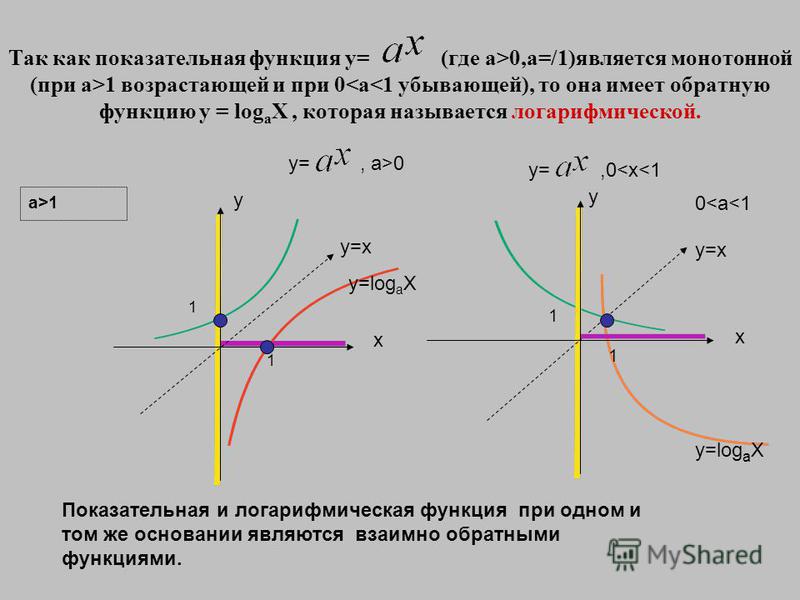 Они представляют собой логарифмически преобразованный x
и ты
оси для черчения.
Они представляют собой логарифмически преобразованный x
и ты
оси для черчения.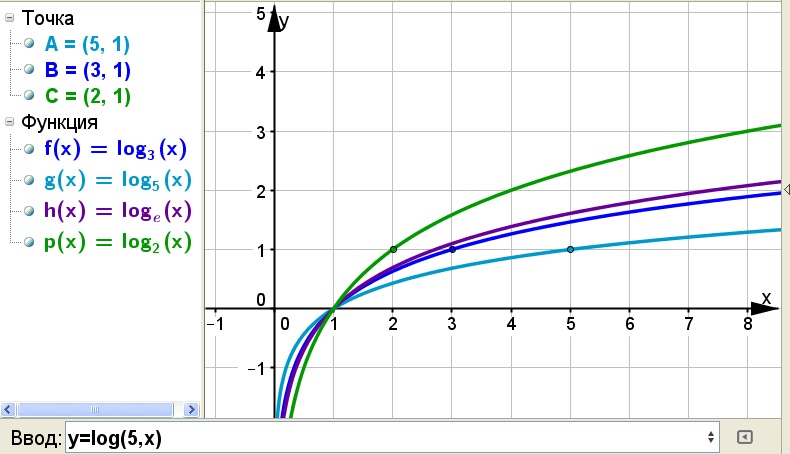 В середине ни одно из приближений не является превосходным, но теперь, когда мы знаем, что ошибка существует, ее можно определить количественно.
В середине ни одно из приближений не является превосходным, но теперь, когда мы знаем, что ошибка существует, ее можно определить количественно. Например, простой RC фильтр нижних частот будет иметь 1/f
амплитудная характеристика для частот выше его угловой частоты, точно отображая пример, который мы только что проиллюстрировали.
Например, простой RC фильтр нижних частот будет иметь 1/f
амплитудная характеристика для частот выше его угловой частоты, точно отображая пример, который мы только что проиллюстрировали.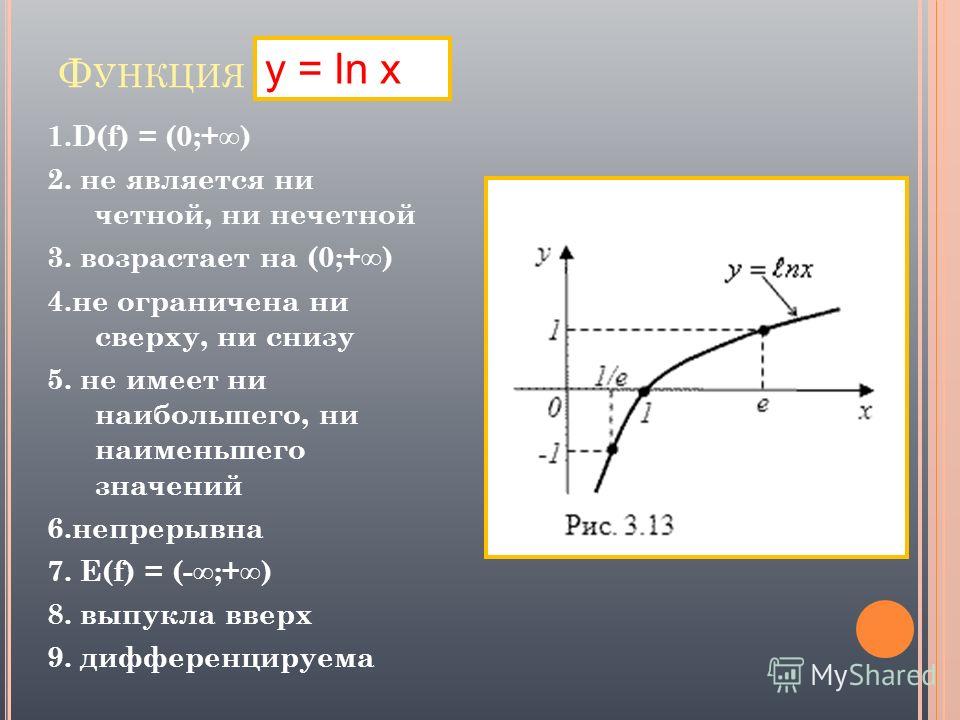 , но произносится вслух как «двадцать два микрофарад» в любом случае.
, но произносится вслух как «двадцать два микрофарад» в любом случае.