Текстовые задачи. Задачи на проценты с решениями
Математика
перейти к содержанию курса текстовых задач
- Учитель зарабатывает на 25% меньше, чем профессор. На сколько процентов больше, чем учитель, зарабатывает профессор? Решение
- Найти число, если известно, что 25% его равны 45% от 640 000. Решение
- После двух последовательных повышений зарплата возросла в раза. На сколько процентов повысилась зарплата в первый раз, если второе повышение было в процентном отношении вдвое больше первого? Решение
- Для офиса решили купить 4 телефона и 3 факса на сумму 1470 долларов. Удалось снизить цену на телефон на 20%, и в результате за ту же покупку уплатили 1326 долларов. Найдите цену факса. Решение
- За первый квартал автозавод выполнил 25% годового плана выпуска машин. Количество машин, выпущенных за второй, третий и четвертый кварталы, оказалось пропорциональным числам 15, 16 и 18.

- Рабочий день сократился с 8 ч до 7 ч. На сколько процентов нужны повысить производительность труда, чтобы при тех же расценках заработная плата возросла бы на n % процентов? Решение
- Банк выделил определенную сумму денег на кредиты трем организациям сроком на год. Организация A получила кредит в размере 40% от выделенной суммы под 30% годовых, организация B — 40% от оставшейся суммы под 15% годовых. Последнюю часть выделенной суммы получила организация C. Через год, когда кредиты были погашены, оказалось, что банк получил прибыль в размере 21%. Под какие проценты был выдан кредит организации C? Решение
- В результате реконструкции цеха число высвободившихся рабочих заключено в пределах от 1,7 до 2,3 % от общего числа рабочих цеха. Найдите минимальное число рабочих, которое могло быть занято в цехе до реконструкции.
 Решение
Решение - Объем вещества А составляет половину суммы объемов веществ В и С, а объем вещества В составляет 20% суммы объемов веществ А и С. Найдите отношение объема вещества С к сумме объемов веществ А и В. Решение
- Банк начисляет ежегодно р % от суммы вклада. Через сколько лет внесенная сумма увеличится в 5 раз? Решение
- Предприятие работало три года. Выработка продукции за второй год работы предприятия возросла на р %, а на следующий год прирост был на 10% больше, чем в предыдущий. Определите, на сколько процентов увеличилась выработка за второй год, если известно, что за два года она увеличилась в общей сложности на 48,59%. Решение
- В конце года вкладчику на его сбережения сбербанк начислил проценты, что составило 6 долларов. Добавив 44 доллара, вкладчик оставил деньги еще на год. После истечения года вновь были начислены проценты, и теперь вклад вместе с процентами составил 257 долларов 50 центов. Какая сумма первоначально была положена в сбербанк? Решение
- Сухие грибы по массе содержат 12% воды, а свежие — 90%.
 Сколько получится сухих грибов из 22 кг свежих грибов? Решение
Сколько получится сухих грибов из 22 кг свежих грибов? Решение - Число 51,2 трижды увеличивали на одно и то же количество процентов, а затем трижды уменьшали на то же самое количество процентов. В результате получили 21,6. На сколько процентов увеличивали, а затем уменьшали данное число? Решение
Задачи для самостоятельного решения
- В двух мешках вместе находится 140 кг муки. Если из первого мешка переложить во второй 12,5 % муки, находящейся в первом мешке, то в обоих мешках будет одинаковое количество муки. Сколько килограммов муки в каждом мешке? Ответ: 80 кг и 60 кг
- В январе завод выполнил 105% месячного плана, а в феврале дал продукции на 4% больше, чем в январе. На сколько процентов завод перевыполнил двухмесячный план? Ответ: на 7,1 %
- Количество студентов в университете, увеличиваясь на одно и то же число процентов ежегодно, возросло за три года с 5000 до 6655 человек. На сколько процентов увеличивалось число студентов ежегодно? Ответ: на 10%
Вкладчик на свои сбережения через год получил 150 р.
 процентных денег. Добавив 850 р., он оставил деньги еще на один год. По истечении года вклад вместе с процентами составил 4200 р. Какая сумма была положена первоначально и какие годовые проценты дает банк? Ответ: 3000 р, 5%
процентных денег. Добавив 850 р., он оставил деньги еще на один год. По истечении года вклад вместе с процентами составил 4200 р. Какая сумма была положена первоначально и какие годовые проценты дает банк? Ответ: 3000 р, 5%Зарплата продавца составляет 3% выручки. Он реализовал товар стоимостью 6000 р. по цене на 5% выше его себестоимости. На сколько повысилась зарплата продавца? Ответ: на 9 р.
Одна сторона прямоугольника в 2,5 раза меньше другой. Как и на сколько процентов изменятся его периметр и площадь, если большую сторону уменьшить на 25%, а меньшую увеличить на 80%? Ответ: +5%, +35%
- Два брата купили акции одного достоинства на сумму 3640 долларов. Когда цена на эти акции возросла, они продали часть акций на сумму 3927 долларов. Первый брат продал 75% своих акций, а второй — 80% своих. При этом сумма, полученная от продажи акций вторым братом, превышает сумму от продажи акций первым братом на 140%. На сколько процентов возросла цена акции? Ответ: на 37,5%
В начале года вкладчик положил своих денег в один банк, а остальные — в другой.
 К концу года сумма на этих вкладах выросла до 1340 р., а к концу следующего года — до 1498 р. Было подсчитано, что если бы с самого начала денег вкладчик положил во второй банк, а остальные — в первый, то по итогам первого года сумма на этих вкладах составила бы 1420 р. Определить величину вклада по истечении двух лет, предполагая, что вкладчик положил все деньги в первый банк. Ответ: 1452 р.
К концу года сумма на этих вкладах выросла до 1340 р., а к концу следующего года — до 1498 р. Было подсчитано, что если бы с самого начала денег вкладчик положил во второй банк, а остальные — в первый, то по итогам первого года сумма на этих вкладах составила бы 1420 р. Определить величину вклада по истечении двух лет, предполагая, что вкладчик положил все деньги в первый банк. Ответ: 1452 р.
Метки проценты, текстовые задачи. Смотреть запись.
Сложные задачи на проценты — Шевкин.Ru
Задачи этого раздела являются необязательными для всех учащихся, среди них есть действительно сложные задачи, но есть и такие, в которых всем учащимся разобраться полезно. Это задачи на так называемые сложные проценты — проценты начисляемые на процентные деньги. Первая задача этого раздела была дана на олимпиаде Малого мехмата МГУ для семиклассников в 1991 году. Шутливое отражение в ней политических страстей того времени не должно отвлечь учащихся от важного вопроса: что получится, если число сначала увеличить, а потом уменьшить на 50 % (на одно и то же число процентов). Полученный здесь опыт поможет решить и другие олимпиадные задачи.
Полученный здесь опыт поможет решить и другие олимпиадные задачи.
Ошибочное решение задачи 345 нетрудно предвидеть: учащиеся сложат проценты от разных величин.
345.* 1) Число увеличили на 10 %, потом еще на 10 %. На сколько процентов увеличили число за два раза?
2) Число увеличили на 10 %, результат уменьшили на 10 %. Какое получилось число — большее или меньшее первоначального? На сколько процентов?
346. * Вася прочитал в газете, что за последние 3 месяца цены на продукты питания росли в среднем на 10 % за каждый месяц. На сколько процентов выросли цены за 3 месяца?
* Вася прочитал в газете, что за последние 3 месяца цены на продукты питания росли в среднем на 10 % за каждый месяц. На сколько процентов выросли цены за 3 месяца?
347.* Женя за весну похудел на 20 %, потом поправился за лето на 30 %, за осень опять похудел на 20 % и за зиму прибавил в весе 10 %. Остался ли за этот год его вес прежним?
Если Женя весил x кг, то после уменьшения веса на 20 % он стал весить 0,8x кг, а после увеличения веса на 30 % – 0,8x·1,3 кг и т. д., в итоге Женя весил 0,8x·1,3·0,8·1,1 или 0,9152x кг, что меньше x кг. Значит, Женя похудел.
348.* Две противоположные стороны прямоугольника увеличили на 10 %. На сколько процентов увеличилась его площадь? Зависит ли результат от того, какую пару сторон увеличили на 10
349.* Все стороны прямоугольника увеличили на 10 %. На сколько процентов увеличилась его площадь?
На сколько процентов увеличилась его площадь?
350.* Каждую сторону квадрата увеличили на 20 %. На сколько процентов увеличилась его площадь?
351.* Две противоположные стороны прямоугольника увеличили на 20 %, две другие — уменьшили на 20 %. Как изменилась площадь прямоугольника?
352.* Две противоположные стороны прямоугольника увеличили на 20 %, две другие — уменьшили на 10 %. На сколько процентов увеличилась площадь прямоугольника?
353.* Длину прямоугольника уменьшили на 20 %. На сколько процентов надо увеличить ширину прямоугольника, чтобы его площадь не изменилась?
354
.* Магазин продал на прошлой неделе некоторый товар. На этой неделе запланировано продать того же товара на 10 % меньше, но по цене на 10 % больше. Большую или меньшую сумму выручит магазин от продажи товара на этой неделе и на сколько процентов?355. * На некотором участке пути машинист уменьшил скорость поезда на 25 %. На сколько процентов увеличится время движения на этом участке?
* На некотором участке пути машинист уменьшил скорость поезда на 25 %. На сколько процентов увеличится время движения на этом участке?
356.* Арбуз массой 20 кг содержал 99 % воды. Когда он немного усох, содержание воды в нем уменьшилось до 98 %. Какова теперь масса арбуза?
На первый взгляд кажется, что масса арбуза мало изменилась, но это на первый взгляд! Масса «сухого вещества» арбуза составляла 100 – 99 = 1 (%). Это 20·0,01 = 0,2 кг. После усушки его масса составляла уже 100 – 98 = 2 (
Интересная переформулировка этой известной задачи встретилась недавно на олимпиаде.
357.* Некий леспромхоз решил вырубить сосновый лес, но экологи запротестовали. Тогда директор леспромхоза всех успокоил, сказав: «В нашем лесу 99% сосны. После рубки сосна будет составлять 98% всех деревьев». Какую часть леса может вырубить леспромхоз?
После рубки сосна будет составлять 98% всех деревьев». Какую часть леса может вырубить леспромхоз?
Если бы экологи хорошо знали проценты, то они смогли бы возразить предприимчивому директору леспромхоза, планирующему вырубить как минимум половину леса – это при условии, что вырубать будут только сосны. Если же топор коснется и других деревьев, то от соснового леса можно оставить меньше половины. Ведь удовлетворить условию задачи можно, оставив в лесу 50 деревьев: 49 сосен и 1 березу.
358.* а) Яблоки, содержащие 70 % воды, потеряли при сушке 60 % своей массы. Сколько процентов воды содержат сушеные яблоки?
б) Груши, содержащие 65 % воды, потеряли при сушке 50 % своей массы. Сколько процентов воды содержат сушеные груши?
Объясняя решение задачи 358 (а), воспользуемся следующей иллюстрацией.
Вода составляла 70 % массы яблок, 60 из них испарилось, а 10 осталось. Теперь 10 частей воды приходится на 30 частей «сухого вещества» яблок или на 40 частей массы сушеных яблок. Масса воды составляет 10:40 = 0,25, или 25 % массы сушеных яблок?
Теперь 10 частей воды приходится на 30 частей «сухого вещества» яблок или на 40 частей массы сушеных яблок. Масса воды составляет 10:40 = 0,25, или 25 % массы сушеных яблок?
359.* а) Сколько граммов воды нужно добавить к 600 г раствора, содержащего 15 % соли, чтобы получить 10%-й раствор соли?
б) Сколько граммов воды нужно добавить к 120 г раствора, содержащего 30 % сахара, чтобы получить раствор, содержащий 20 % сахара?
360.* На коробке вермишели написано: «Масса нетто 500 г при влажности 13 %». Какова масса вермишели, если она хранится при влажности 25 %?
361.* Для получения томат-пасты протертую массу томатов выпаривают в специальных машинах. Сколько томат-пасты, содержащей 30 % воды, получится из 28 т протертой массы томатов, содержащей 95 % воды?
362. * Из 40 т руды выплавили 20 т металла, содержащего 6 % примесей. Сколько процентов примесей в руде?
* Из 40 т руды выплавили 20 т металла, содержащего 6 % примесей. Сколько процентов примесей в руде?
363.* Свежие фрукты содержат 72 % воды, а сухие — 20 %. Сколько сухих фруктов получится из
40 кг свежих?
364.* До сушки влажность зерна составляла 23 %, а после сушки составила 12 %. Сколько процентов массы теряет зерно при сушке?
365.* В драмкружке число мальчиков составляет 80 % от числа девочек. Сколько процентов составляет число девочек от числа мальчиков в этом кружке?
I способ. Число мальчиков составляют 80 % от числа девочек (100 %). Определим, сколько процентовсоставляют 100 % от 80 % :
100/80 = 100×100/80 % = 125 %.
II способ. Число мальчиков (m) составляют 80 % от числа девочек (d), значит, m = 0,8d. Отсюда d = 1,25m, то есть число девочек составляет 125 % от числа мальчиков.
Число мальчиков (m) составляют 80 % от числа девочек (d), значит, m = 0,8d. Отсюда d = 1,25m, то есть число девочек составляет 125 % от числа мальчиков.
III способ. На 10 девочек приходится 8 мальчиков, число девочек составляет 10/8 или 125 % от числа мальчиков.
366. С 1 октября 1993 г. за хранение денег на срочном депозите в течение года Сбербанк выплачивал доход из расчета 150% от вложенной суммы; в течение полугода — 130% годовых, в течение трех месяцев — 120 % годовых. Каким образом за год на условиях Сбербанка можно было получитьнаибольший доход на 100 000 р.? Каков этот наибольший доход?
На первый взгляд самое выгодное вложение денег на год — под 150 % годовых (через год сумма обратится в 100·2,5 = 250 тыс. р.). Но это только на первый взгляд! Давайте для сравнения положим деньги на полгода, а через полгода получим их обратно с доходом 130:2 =
= 65 (%) от вложенной суммы. Затем все полученные деньги положим еще на полгода. Таким образом через год мы получим:
Затем все полученные деньги положим еще на полгода. Таким образом через год мы получим:
100·1,65·1,65 = 272,25 (тыс. р.).
Это несколько больше полученной ранее суммы. Попросите учащихся провести расчеты для третьего случая. Пусть они убедятся, что знание процентов может быть полезным при выборе более выгодного способа вложения денег.
367.* Компания X выплачивает доход по своим акциям ежегодно из расчета 140 % годовых. Компания Y выплачивает доход по акциям 1 раз в полгода из того же расчета. В акции какой компании выгоднее вложить деньги на 1 год?
368.* Производительность труда повысили на 25 %. На сколько процентов уменьшится время выполнения задания.
369.* Если при повышении производительности труда рабочего на 10 % повысить его зарплату на 6,7 %, то это позволит снизить расход на оплату труда в расчете на единицу продукции на 3 %. Проверьте это.
Проверьте это.
370.* Рабочий повысил производительность труда на 15 %, а его зарплата увеличилась на 10,4 %. На сколько процентов уменьшился расход на оплату труда в расчете на единицу продукции?
371.* Купили конфеты и печенье. За 1 кг конфет заплатили на 50 % больше, чем за 1 кг печенья, но их купили на 50 % меньше, чем печенья. За что заплатили больше?
372.* Кусок сплава весом 700 г, содержащий 80 % олова, сплавили с куском олова весом 300 г. Определите процентное содержание олова в полученном сплаве.
373.* Имеется 500 г 40 %-го раствора кислоты. Сколько воды требуется добавить, чтобы получить 25 %-й раствор кислоты?
374.* В первый день рабочий перевыполнил дневное задание на 2 %, во второй день он перевыполнил дневное задание на 4 %. На сколько процентов рабочий перевыполнил задание двух дней?
На сколько процентов рабочий перевыполнил задание двух дней?
375.* В автоинспекции города N подсчитали, что число легковых автомобилей увеличивалось в последние годы на 15 % ежегодно. Во сколько раз увеличится число легковых автомобилей за пять лет, если эта тенденция сохранится?
376.* Деньги, вложенные в акции известной фирмы, приносят ежегодно 20 % дохода. За сколько летвложенная сумма удвоится?
377.* В спортивной секции девочки составляют 60 % числа мальчиков. Сколько процентов числа всех участников секции составляют девочки?
Если число мальчиков принять за 100 %, то число девочек от него составляет 60 %, а число всех участников секции 160 % от числа мальчиков. 60 % от 160 % составляет 60×100/160 = 37,5 (%).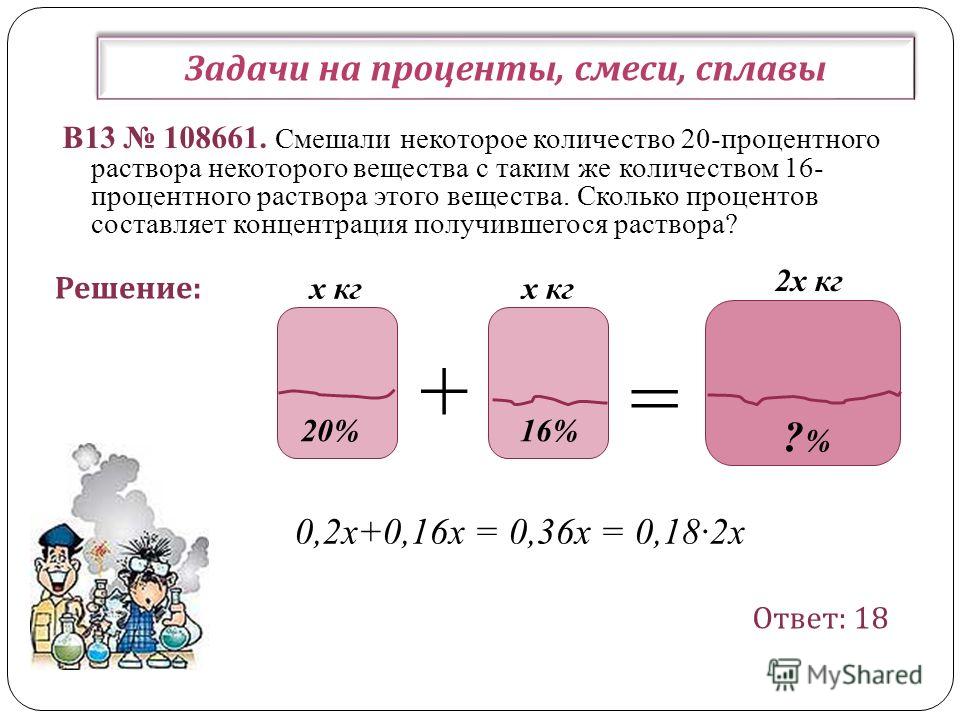 Но понять это решение из-за нагромождения процентов нелегко. Если же число мальчиков обозначитьбуквой x, то те же самые действия легче объяснить и понять. Итак, число девочек равно 0,6x, а число всех участников секции x + 0,6x = 1,6x. Определим, сколько процентов от 1,6х составляет число 0,6х:
Но понять это решение из-за нагромождения процентов нелегко. Если же число мальчиков обозначитьбуквой x, то те же самые действия легче объяснить и понять. Итак, число девочек равно 0,6x, а число всех участников секции x + 0,6x = 1,6x. Определим, сколько процентов от 1,6х составляет число 0,6х:
0,6x×100/1,6x = 37,5 (%).
- В некотором царстве, в некотором государстве пятиклассники стали изучать математику не 6, а 5 уроков в неделю. Кроме того, урок у них стал длиться не 45, а 40 минут. Сколько процентов учебного времени потеряли пятиклассники? Ответ округлите до десятых.
Эту задачу могли бы решить учителя математики всего несколько лет назад, чтобы объяснить себе катастрофическую нехватку времени, которая стала ощущаться в связи с указанными в условии задачи нововведениями.
Учебное время теперь составляет 5/6×40/45 = 20/27 от прежнего. Потеря составила 1 – 20/27 =
Потеря составила 1 – 20/27 =
= 7/27 = 0,2592…, или примерно 25,9 %.
379.* а) Торговец продал книгу со скидкой 5 % от назначенной цены и получил 14 % прибыли. Сколько процентов прибыли планировал получить торговец при продаже книги?
б) Торговец продал товар, имевший небольшой дефект, уступив покупателю 30 % от назначенной цены. При этом он имел 16 % убытка. Какой процент прибыли планировал получить торговец при продаже товара?
Рассмотрим решение первой задачи. Пусть торговец планировал продать книгу за a р., тогда он продал ее за (1 – 0,05)a = 0,95a р. Эта сумма составила 100 + 14 = 114 (%) цены, по которой торговец сам купил книгу и которая составляла 0,95а/1,14 = 5/6 а р. Подсчитаем доход, который планировал получить торговец (в процентах):
a: 5/6 a ·100 = 120 (%).
Торговец планировал получить 120 – 100 = 20 % дохода.
Сложные задачи на проценты — Сайт учителя математики Кобец Анны Викторовны
СЛОЖНЫЕ ЗАДАЧИ НА ПРОЦЕНТЫ
1.* В начале года винтики, шпунтики и гаечки продавались по одинаковой цене 1 р. за 1 кг. 30 февраля Верховный Совет СССР принял закон о повышении цен на винтики на 50 % и снижению цен на шпунтики на 50 %. 31 февраля Верховный Совет РСФСР принял закон о снижении цен на винтики на 50 % и повышению цен на шпунтики на 50 %. Какой товар будет самым дорогим и какой самым дешевым в марте?
2.* 1) Число увеличили на 10 %, потом еще на 10 %. На сколько процентов увеличили число за два раза?
2) Число увеличили на 10 %, результат уменьшили на 10 %. Какое получилось число — большее или меньшее первоначального? На сколько процентов?
3. * Вася прочитал в газете, что за последние 3 месяца цены на продукты питания росли в среднем на 10 % за каждый месяц. На сколько процентов выросли цены за 3 месяца?
* Вася прочитал в газете, что за последние 3 месяца цены на продукты питания росли в среднем на 10 % за каждый месяц. На сколько процентов выросли цены за 3 месяца?
4.* Женя за весну похудел на 20 %, потом поправился за лето на 30 %, за осень опять похудел на 20 % и за зиму прибавил в весе 10 %. Остался ли за этот год его вес прежним?
5.* Две противоположные стороны прямоугольника увеличили на 10 %. На сколько процентов увеличилась его площадь? Зависит ли результат от того, какую пару сторон увеличили на 10 %?
6.* Все стороны прямоугольника увеличили на 10 %. На сколько процентов увеличилась его площадь?
7.* Каждую сторону квадрата увеличили на 20 %. На сколько процентов увеличилась его площадь?
8.* Две противоположные стороны прямоугольника увеличили на 20 %, две другие — уменьшили на 20 %. Как изменилась площадь прямоугольника?
Как изменилась площадь прямоугольника?
9.* Две противоположные стороны прямоугольника увеличили на 20 %, две другие — уменьшили на 10 %. На сколько процентов увеличилась площадь прямоугольника?
10.* Длину прямоугольника уменьшили на 20 %. На сколько процентов надо увеличить ширину прямоугольника, чтобы его площадь не изменилась?
11.* Магазин продал на прошлой неделе некоторый товар. На этой неделе запланировано продать того же товара на 10 % меньше, но по цене на 10 % больше. Большую или меньшую сумму выручит магазин от продажи товара на этой неделе и на сколько процентов?
12.* На некотором участке пути машинист уменьшил скорость поезда на 25 %. На сколько процентов увеличится время движения на этом участке?
13.* Арбуз массой 20 кг содержал 99 % воды. Когда он немного усох, содержание воды в нем уменьшилось до 98 %. Какова теперь масса арбуза?
Какова теперь масса арбуза?
14.* Некий леспромхоз решил вырубить сосновый лес, но экологи запротестовали. Тогда директор леспромхоза всех успокоил, сказав: «В нашем лесу 99% сосны. После рубки сосна будет составлять 98% всех деревьев». Какую часть леса может вырубить леспромхоз?
15.* а) Яблоки, содержащие 70 % воды, потеряли при сушке 60 % своей массы. Сколько процентов воды содержат сушеные яблоки?
б) Груши, содержащие 65 % воды, потеряли при сушке 50 % своей массы. Сколько процентов воды содержат сушеные груши?
16.* а) Сколько граммов воды нужно добавить к 600 г раствора, содержащего 15 % соли, чтобы получить 10%-й раствор соли?
б) Сколько граммов воды нужно добавить к 120 г раствора, содержащего 30 % сахара, чтобы получить раствор, содержащий 20 % сахара?
17.* На коробке вермишели написано: «Масса нетто 500 г при влажности 13 %». Какова масса вермишели, если она хранится при влажности 25 %?
Какова масса вермишели, если она хранится при влажности 25 %?
18.* Для получения томат-пасты протертую массу томатов выпаривают в специальных машинах. Сколько томат-пасты, содержащей 30 % воды, получится из 28 т протертой массы томатов, содержащей 95 % воды?
19.* Из 40 т руды выплавили 20 т металла, содержащего 6 % примесей. Сколько процентов примесей в руде?
20.* Свежие фрукты содержат 72 % воды, а сухие — 20 %. Сколько сухих фруктов получится из
40 кг свежих?
21.* До сушки влажность зерна составляла 23 %, а после сушки составила 12 %. Сколько процентов массы теряет зерно при сушке?
22.* В драмкружке число мальчиков составляет 80 % от числа девочек. Сколько процентов составляет число девочек от числа мальчиков в этом кружке?
23. С 1 октября 1993 г. за хранение денег на срочном депозите в течение года Сбербанк выплачивал доход из расчета 150 % от вложенной суммы; в течение полугода — 130 % годовых, в течение трех месяцев — 120 % годовых. Каким образом за год на условиях Сбербанка можно было получить наибольший доход на 100 000 р.? Каков этот наибольший доход?
С 1 октября 1993 г. за хранение денег на срочном депозите в течение года Сбербанк выплачивал доход из расчета 150 % от вложенной суммы; в течение полугода — 130 % годовых, в течение трех месяцев — 120 % годовых. Каким образом за год на условиях Сбербанка можно было получить наибольший доход на 100 000 р.? Каков этот наибольший доход?
24.* Компания X выплачивает доход по своим акциям ежегодно из расчета 140 % годовых. Компания Y выплачивает доход по акциям 1 раз в полгода из того же расчета. В акции какой компании выгоднее вложить деньги на 1 год?
25.* Производительность труда повысили на 25 %. На сколько процентов уменьшится время выполнения задания.
26.* Если при повышении производительности труда рабочего на 10 % повысить его зарплату на 6,7 %, то это позволит снизить расход на оплату труда в расчете на единицу продукции на 3 %. Проверьте это.
Проверьте это.
27.* Рабочий повысил производительность труда на 15 %, а его зарплата увеличилась на 10,4 %. На сколько процентов уменьшился расход на оплату труда в расчете на единицу продукции?
28.* Купили конфеты и печенье. За 1 кг конфет заплатили на 50 % больше, чем за 1 кг печенья, но их купили на 50 % меньше, чем печенья. За что заплатили больше?
29.* Кусок сплава весом 700 г, содержащий 80 % олова, сплавили с куском олова весом 300 г. Определите процентное содержание олова в полученном сплаве.
30.* Имеется 500 г 40 %-го раствора кислоты. Сколько воды требуется добавить, чтобы получить 25 %-й раствор кислоты?
31.* В первый день рабочий перевыполнил дневное задание на 2 %, во второй день он перевыполнил дневное задание на 4 %. На сколько процентов рабочий перевыполнил задание двух дней?
На сколько процентов рабочий перевыполнил задание двух дней?
32.* В автоинспекции города N подсчитали, что число легковых автомобилей увеличивалось в последние годы на 15 % ежегодно. Во сколько раз увеличится число легковых автомобилей за пять лет, если эта тенденция сохранится?
33.* Деньги, вложенные в акции известной фирмы, приносят ежегодно 20 % дохода. За сколько лет вложенная сумма удвоится?
34.* В спортивной секции девочки составляют 60 % числа мальчиков. Сколько процентов числа всех участников секции составляют девочки?
35. В некотором царстве, в некотором государстве пятиклассники стали изучать математику не 6, а 5 уроков в неделю. Кроме того, урок у них стал длиться не 45, а 40 минут. Сколько процентов учебного времени потеряли пятиклассники? Ответ округлите до десятых.
36.* а) Торговец продал книгу со скидкой 5 % от назначенной цены и получил 14 % прибыли. Сколько процентов прибыли планировал получить торговец при продаже книги?
Сколько процентов прибыли планировал получить торговец при продаже книги?
б) Торговец продал товар, имевший небольшой дефект, уступив покупателю 30 % от назначенной цены. При этом он имел 16 % убытка. Какой процент прибыли планировал получить торговец при продаже товара?
Литература: Шевкин А.В. Текстовые задачи по математике в 5-6 классах
Иллюстративная математика
Иллюстративная математикаКласс 7
7 класс
- Восхождение по ступеням Эль-Кастильо
- буровая установка
- Дуэли Кандидатов
- Идеальная фиолетовая краска II
- Распродажа!
- Обмен акциями, Вариант 2
- Обмен акциями, Вариант 3
- Изменение температуры
- Гром и молния
- Отслеживание практики
- Сидр против сока — Вариант 1
- Сидр против сока — вариант 2
- Готовим из всей чашки
- Бег Молли
- Бег Молли, вариант оценки
- Отслеживание практики
- Художественный класс, вариант оценки
- Художественный класс, Вариант 1
- Художественный класс, Вариант 2
- Покупка бананов, ознакомительная версия
- Покупка кофе
- Музыкальные компании, Вариант 1
- Гонки роботов
- Гонки роботов, вариант оценки
- Масштабирование углов и полигонов
- Боль в горле, Вариант 1
- Прогулка 2
- Сидр против сока — вариант 2
- Планы членства в тренажерном зале
- Сидр против сока — Вариант 1
- Сидр против сока — вариант 2
- Планы членства в тренажерном зале
- Соразмерность
- Пока нет задач, иллюстрирующих этот стандарт.
- Анна в округе Колумбия
- Покупка протеиновых батончиков и журналов
- Шахматный клуб
- Сравнение лет
- Двойные скидки
- Нахождение увеличения на 10%
- Встреча друзей на велосипедах
- Такси Готэм-сити
- Насколько быстр Усэйн Болт?
- Математическая задача Линкольна
- Измерение площади круга
- Музыкальные компании, Вариант 2
- Песок под качелями
- Продажа компьютеров
- Налог и чаевые
- Цена хлеба
- Танец для двух школ
7.РП. 7 класс — Соотношения и пропорциональные отношения
7.РП.А. Анализируйте пропорциональные отношения и используйте их для решения реальных и математических задач.
7.
 РП.А.1. Вычислить удельные ставки, связанные с отношениями фракций, включая отношения длин, площадей и других величин, измеренных в одинаковых или разных единицах. Например, если человек проходит $1/2$ мили за каждые $1/4$ часа, рассчитайте удельную норму как комплексную дробь $\frac{1/2}{1/4}$ миль в час, что эквивалентно $2$ миль. в час.
РП.А.1. Вычислить удельные ставки, связанные с отношениями фракций, включая отношения длин, площадей и других величин, измеренных в одинаковых или разных единицах. Например, если человек проходит $1/2$ мили за каждые $1/4$ часа, рассчитайте удельную норму как комплексную дробь $\frac{1/2}{1/4}$ миль в час, что эквивалентно $2$ миль. в час.7.РП.А.2. Распознавать и представлять пропорциональные отношения между величинами.
7.
 РП.А.2.а. Определите, находятся ли две величины в пропорциональном соотношении, например, проверив эквивалентные отношения в таблице или нарисовав график на координатной плоскости и наблюдая, является ли график прямой линией, проходящей через начало координат.
РП.А.2.а. Определите, находятся ли две величины в пропорциональном соотношении, например, проверив эквивалентные отношения в таблице или нарисовав график на координатной плоскости и наблюдая, является ли график прямой линией, проходящей через начало координат.7.РП.А.2.б. Определите константу пропорциональности (единичную норму) в таблицах, графиках, уравнениях, схемах и словесных описаниях пропорциональных отношений.
7.RP.A.2.c. Представьте пропорциональные отношения уравнениями. Например, если общая стоимость $t$ пропорциональна количеству $n$ товаров, купленных по постоянной цене $p$, соотношение между общей стоимостью и количеством товаров может быть выражено как $t = pn$.
7.
 РП.А.2.д. Объясните, что означает точка $(x, y)$ на графике пропорциональной зависимости с точки зрения ситуации, обратив особое внимание на точки $(0, 0)$ и $(1, r)$, где $r$ является единичной ставкой.
РП.А.2.д. Объясните, что означает точка $(x, y)$ на графике пропорциональной зависимости с точки зрения ситуации, обратив особое внимание на точки $(0, 0)$ и $(1, r)$, где $r$ является единичной ставкой.7.РП.А.3. Используйте пропорциональные отношения для решения многошаговых задач соотношения и процентов. Примеры: простые проценты, налоги, надбавки и уценки, чаевые и комиссионные, сборы, процентное увеличение и уменьшение, процентная ошибка.
- Аккаунт книжного магазина
- Сравнение точек замерзания
- Различия и расстояния
- Различия целых чисел
- Расстояния между домами
- Расстояния по числовой прямой 2
- Операции над числовой прямой
- Округление и вычитание
- Пока нет задач, иллюстрирующих этот стандарт.

- Различия целых чисел
- Различия целых чисел
- буровая установка
- Почему отрицательное время всегда отрицательное?
- Распределительное свойство умножения
- Почему отрицательное время всегда отрицательное?
- Изменение температуры
- Десятичные разложения дробей
- Эквивалентные дроби приближаются к неповторяющимся десятичным дробям
- Повторяющееся десятичное число как приближение
- Повторение или прекращение?
- буровая установка
- Разделение призовых денег
7.
 НС. 7 класс — Система счисления
НС. 7 класс — Система счисления7.Н.С.А. Применяйте и расширяйте прежнее понимание операций с дробями, чтобы складывать, вычитать, умножать и делить рациональные числа.
7.НС.А.1. Применять и расширять прежнее понимание сложения и вычитания, чтобы складывать и вычитать рациональные числа; представляют сложение и вычитание на горизонтальной или вертикальной диаграмме с числовыми линиями.
7.НС.А.1.а. Опишите ситуации, в которых противоположные величины объединяются, чтобы получить 0. Например, атом водорода имеет нулевой заряд, потому что две его составляющие заряжены противоположно.
7.НС.А.1.б. Под $p + q$ понимается число, расположенное на расстоянии $|q|$ от $p$ в положительном или отрицательном направлении, в зависимости от того, является ли число $q$ положительным или отрицательным. Покажите, что число и его противоположность имеют сумму 0 (аддитивные инверсии). Интерпретируйте суммы рациональных чисел, описывая контексты реального мира.
7.NS.A.1.c. Поймите вычитание рациональных чисел как добавление аддитивной обратной, $p — q = p + (-q)$. Покажите, что расстояние между двумя рациональными числами на числовой прямой равно абсолютному значению их разности, и примените этот принцип в контексте реального мира.
7.НС.А.2. Применяйте и расширяйте прежнее понимание умножения и деления, а также дробей, чтобы умножать и делить рациональные числа.
7.
 НС.А.2.а. Поймите, что умножение распространяется с дробей на рациональные числа, требуя, чтобы операции продолжали удовлетворять свойствам операций, в частности свойству распределения, что приводит к таким продуктам, как $(-1)(-1) = 1$ и правилам умножения со знаком числа. Интерпретируйте произведения рациональных чисел, описывая контексты реального мира.
НС.А.2.а. Поймите, что умножение распространяется с дробей на рациональные числа, требуя, чтобы операции продолжали удовлетворять свойствам операций, в частности свойству распределения, что приводит к таким продуктам, как $(-1)(-1) = 1$ и правилам умножения со знаком числа. Интерпретируйте произведения рациональных чисел, описывая контексты реального мира.7.НС.А.2.б. Поймите, что целые числа можно делить при условии, что делитель не равен нулю, и каждое частное целых чисел (с ненулевым делителем) является рациональным числом. Если $p$ и $q$ — целые числа, то $-(p/q) = (-p)/q = p/(-q)$. Интерпретируйте частные рациональных чисел, описывая контексты реального мира.
7.NS.A.2.d. Преобразование рационального числа в десятичное с использованием длинного деления; известно, что десятичная форма рационального числа оканчивается на 0 или со временем повторяется.

7.НС.А.3. Решайте реальные и математические задачи, включающие четыре операции с рациональными числами. Вычисления с рациональными числами расширяют правила обращения с дробями до сложных дробей.
- Эквивалентные выражения?
- Мили в Километры
- Написание выражений
- Билет на поезд
- Угадай мой номер
- Анна в округе Колумбия
- Книги со скидкой
- Такси Готэм-сити
- Уменьшение
- Витражи
- Кто лучше тесто?
- Аккаунт книжного магазина
- буровая установка
- Рыболовные приключения 2
- Такси Готэм-сити
- Пока нет задач, иллюстрирующих этот стандарт.
- Комплект спортивного инвентаря
7.EE. 7 класс — Выражения и уравнения
7.Э.Э.А. Используйте свойства операций для создания эквивалентных выражений.
7.EE.A.1. Применяйте свойства операций как стратегии для сложения, вычитания, факторизации и расширения линейных выражений с рациональными коэффициентами.
7.
 EE.A.2. Поймите, что переписывание выражения в разных формах в контексте задачи может пролить свет на проблему и на то, как связаны в ней величины. Например, $a + 0,05a = 1,05a$ означает, что «увеличение на $5\%$» равносильно «умножению на $1,05$».
EE.A.2. Поймите, что переписывание выражения в разных формах в контексте задачи может пролить свет на проблему и на то, как связаны в ней величины. Например, $a + 0,05a = 1,05a$ означает, что «увеличение на $5\%$» равносильно «умножению на $1,05$».7.Э.Э.Б. Решайте реальные и математические задачи, используя числовые и алгебраические выражения и уравнения.
7.EE.B.3. Решайте многоэтапные задачи из реальной жизни и математические задачи с положительными и отрицательными рациональными числами в любой форме (целые числа, дроби и десятичные дроби), стратегически используя инструменты. Применять свойства операций для вычисления с числами в любой форме; конвертировать между формами по мере необходимости; и оценить обоснованность ответов, используя умственные вычисления и стратегии оценки. Например: если женщина, зарабатывающая $\$25$ в час, получает прибавку в размере $10\%$, она будет дополнительно зарабатывать $\frac{1}{10}$ своей зарплаты в час, или $\$2,50$, за новая зарплата $\$27.
 50$. Если вы хотите разместить полотенцесушитель $9\frac34$ дюймов в центре двери шириной $27 \frac12$ дюймов, вам нужно будет разместить планку на расстоянии около $9$ дюймов от каждого края; эту оценку можно использовать в качестве проверки точного вычисления.
50$. Если вы хотите разместить полотенцесушитель $9\frac34$ дюймов в центре двери шириной $27 \frac12$ дюймов, вам нужно будет разместить планку на расстоянии около $9$ дюймов от каждого края; эту оценку можно использовать в качестве проверки точного вычисления.7.EE.B.4. Используйте переменные для представления величин в реальной или математической задаче и создавайте простые уравнения и неравенства для решения задач, рассуждая о величинах.
7.EE.B.4.а. Решите текстовые задачи, ведущие к уравнениям вида $px + q = r$ и $p(x + q) = r$, где $p$, $q$ и $r$ — конкретные рациональные числа. Решите уравнения этих форм бегло. Сравните алгебраическое решение с арифметическим, указав последовательность операций, используемых в каждом подходе.
 Например, периметр прямоугольника равен $54$ см. Его длина $6$ см. Какова его ширина?
Например, периметр прямоугольника равен $54$ см. Его длина $6$ см. Какова его ширина?7.EE.B.4.b. Решайте текстовые задачи, приводящие к неравенствам вида $px + q > r$ или $px + q
< r$, где $p$, $q$ и $r$ — конкретные рациональные числа. Нарисуйте график множества решений неравенства и интерпретируйте его в контексте проблемы. Например: как продавец, вам платят 50 долларов в неделю плюс 3 доллара за продажу. На этой неделе вы хотите, чтобы ваша зарплата была не менее $100. Напишите неравенство для количества продаж, которое вам нужно сделать, и опишите решения.- Приблизительно площадь круга
- Окружность круга
- Поэтажный план
- Расстояние карты
- Изменение масштаба Вашингтонского парка
- Масштабирование углов и полигонов
- Задача, связанная со стандартом 7.G.A.2
- Кубические ниндзя!
- Пить озеро
- Окружность круга и площадь области, которую он заключает
- Приблизительно площадь круга
- Окружность круга
- Дизайн
- Восемь кругов
- Измерение площади круга
- Витражи
- Клинья круга
- Пока нет задач, иллюстрирующих этот стандарт.
- Песок под качелями
7.Г. 7 класс — Геометрия
7.Г.А. Рисовать, строить и описывать геометрические фигуры и описывать отношения между ними.
7.Г.А.1. Решайте задачи, связанные с чертежами геометрических фигур в масштабе, включая вычисление фактических длин и площадей на основе чертежа в масштабе и воспроизведение чертежа в масштабе в другом масштабе.

7.Г.А.2. Рисовать (от руки, с линейкой и транспортиром и с техникой) геометрические фигуры с заданными условиями. Сосредоточьтесь на построении треугольников по трем мерам углов или сторон, отмечая, когда условия определяют уникальный треугольник, более одного треугольника или отсутствие треугольника.
7.Г.А.3. Опишите двумерные фигуры, которые получаются в результате разрезания трехмерных фигур, например, в плоских сечениях прямоугольных призм и прямоугольных пирамид.
7.Г.Б. Решайте реальные и математические задачи, связанные с измерением угла, площади, площади поверхности и объема.

7.G.B.4. Знать формулы площади и длины окружности и использовать их для решения задач; дать неформальный вывод отношения между длиной окружности и площадью круга.
7.GB.5. Используйте факты о дополнительных, дополнительных, вертикальных и смежных углах в многоэтапной задаче, чтобы написать и решить простые уравнения для неизвестного угла в фигуре.
7.GB.6. Решайте реальные и математические задачи, связанные с площадью, объемом и площадью поверхности двух- и трехмерных объектов, состоящих из треугольников, четырехугольников, многоугольников, кубов и прямых призм.

- Предвыборный опрос, Вариант 1
- Предвыборный опрос, Вариант 2
- Предвыборный опрос, Вариант 3
- Оценка средней площади состояния
- Класс мистера Бриггса любит математику
- Валентина Марблс
- Спортсмены колледжа
- Линейные игроки нападения
- Спортсмены колледжа
- Линейные игроки нападения
- Остаться или поменяться?
- Пока нет задач, иллюстрирующих этот стандарт.
- Орел или решка
- Игра в кости
- Бросающие цилиндры
- Игра в кости
- Сколько кнопок?
- Пока нет задач, иллюстрирующих этот стандарт.
- Красный, зеленый или синий?
- Роллинг дважды
- Время ожидания
- Сидя друг напротив друга
- Тетраэдрические кости
- Сидя друг напротив друга
- Тетраэдрические кости
- Пока нет задач, иллюстрирующих этот стандарт.
7.СП. 7 класс — Статистика и вероятность
7.СП.А. Используйте случайную выборку, чтобы сделать выводы о совокупности.
7.СП.А.1. Понимать, что статистику можно использовать для получения информации о населении путем изучения выборки населения; обобщения о совокупности из выборки действительны только в том случае, если выборка репрезентативна для этой совокупности. Поймите, что случайная выборка, как правило, дает репрезентативные выборки и поддерживает достоверные выводы.
7.СП.А.2. Используйте данные из случайной выборки, чтобы сделать выводы о совокупности с неизвестной интересующей характеристикой. Создайте несколько выборок (или смоделированных выборок) одинакового размера, чтобы оценить различия в оценках или прогнозах.
 Например, оцените среднюю длину слова в книге путем случайной выборки слов из книги; предсказать победителя школьных выборов на основе случайно выбранных данных опроса. Оцените, насколько далеко может быть оценка или прогноз.
Например, оцените среднюю длину слова в книге путем случайной выборки слов из книги; предсказать победителя школьных выборов на основе случайно выбранных данных опроса. Оцените, насколько далеко может быть оценка или прогноз.7.СП.Б. Сделайте неформальные сравнительные выводы о двух популяциях.
7.СП.Б.3. Неформально оцените степень визуального перекрытия двух распределений числовых данных с похожими вариациями, измеряя разницу между центрами, выражая ее как кратную меру вариабельности. Например, средний рост игроков баскетбольной команды на 10 см больше, чем средний рост игроков футбольной команды, что примерно вдвое превышает вариабельность (среднее абсолютное отклонение) в любой из команд; на точечном графике заметно разделение между двумя распределениями высот.
7.СП.Б.4. Используйте меры центра и меры изменчивости для числовых данных из случайных выборок, чтобы сделать неформальные сравнительные выводы о двух популяциях.
 Например, решите, длиннее ли слова в главе учебника по естествознанию для седьмого класса, чем слова в главе из учебника по естествознанию для четвертого класса.
Например, решите, длиннее ли слова в главе учебника по естествознанию для седьмого класса, чем слова в главе из учебника по естествознанию для четвертого класса.7.С.П. Исследуйте случайные процессы и разрабатывайте, используйте и оценивайте вероятностные модели.
7.СП.С.5. Поймите, что вероятность случайного события — это число от 0 до 1, которое выражает вероятность наступления события. Большие числа указывают на большую вероятность. Вероятность, близкая к 0, указывает на маловероятное событие, вероятность около 1/2 указывает на событие, которое не является ни маловероятным, ни вероятным, а вероятность, близкая к 1, указывает на вероятное событие.
7.СП.С.6. Аппроксимируйте вероятность случайного события, собирая данные о случайном процессе, который его производит, и наблюдая его долгосрочную относительную частоту, и предскажите приблизительную относительную частоту с учетом вероятности.
 Например, подбрасывая числовой куб 600 раз, предскажите, что число 3 или 6 выпадет примерно 200 раз, но, вероятно, не ровно 200 раз.
Например, подбрасывая числовой куб 600 раз, предскажите, что число 3 или 6 выпадет примерно 200 раз, но, вероятно, не ровно 200 раз.7.СП.С.7. Разработайте вероятностную модель и используйте ее для определения вероятностей событий. Сравните вероятности из модели с наблюдаемыми частотами; если согласие неудовлетворительное, объясните возможные источники несоответствия.
7.SP.C.7.а. Разработайте единую вероятностную модель, назначив всем исходам равную вероятность, и используйте эту модель для определения вероятностей событий. Например, если из класса случайным образом выбран ученик, найдите вероятность того, что будет выбрана Джейн, и вероятность того, что будет выбрана девочка.
7.SP.C.7.b. Разработайте вероятностную модель (которая может быть неоднородной), наблюдая частоты в данных, полученных в результате случайного процесса.
 Например, найдите приблизительную вероятность того, что крутящийся пенни упадет решкой вверх или что брошенный бумажный стаканчик упадет открытым концом вниз. Судя по наблюдаемым частотам, результаты для крутящегося пенни кажутся равновероятными?
Например, найдите приблизительную вероятность того, что крутящийся пенни упадет решкой вверх или что брошенный бумажный стаканчик упадет открытым концом вниз. Судя по наблюдаемым частотам, результаты для крутящегося пенни кажутся равновероятными?7.SP.C.8. Найдите вероятности составных событий, используя упорядоченные списки, таблицы, древовидные диаграммы и моделирование.
7.SP.C.8.а. Поймите, что, как и в случае с простыми событиями, вероятность составного события представляет собой долю исходов в выборочном пространстве, для которого происходит составное событие.
7.SP.C.8.b. Представляйте примеры пространств для составных событий, используя такие методы, как организованные списки, таблицы и древовидные диаграммы.
 Для события, описанного повседневным языком (например, «выпадение двойных шестерок»), определите исходы в выборочном пространстве, составляющие событие.
Для события, описанного повседневным языком (например, «выпадение двойных шестерок»), определите исходы в выборочном пространстве, составляющие событие.7.SP.C.8.c. Разработайте и используйте симуляцию для генерации частот для составных событий. Например, используйте случайные числа в качестве инструмента моделирования для аппроксимации ответа на вопрос: если 40% доноров имеют кровь группы А, какова вероятность того, что потребуется не менее 4 доноров, чтобы найти одного с кровью группы А?
Урок 1 | процент и масштабирование | Математика 7-го класса
Цель
Определение процентов и преобразование между дробями, десятичными знаками и процентами. Решайте процентные задачи в уме с эталонными процентами.
Общие базовые стандарты
Основные стандарты
Основные стандарты, рассмотренные в этом уроке
A628D5C3-5B97-4E03-B1EC-5AD5C66D89507.
 РП.А.3
— Используйте пропорциональные отношения для решения многошаговых задач на соотношение и проценты. Примеры: простые проценты, налоги, надбавки и скидки, чаевые и комиссионные, сборы, процентное увеличение и уменьшение, процентная ошибка.
РП.А.3
— Используйте пропорциональные отношения для решения многошаговых задач на соотношение и проценты. Примеры: простые проценты, налоги, надбавки и скидки, чаевые и комиссионные, сборы, процентное увеличение и уменьшение, процентная ошибка.
Основополагающие стандарты
Основные стандарты, рассмотренные в этом уроке
A628D5C3-5B97-4E03-B1EC-5AD5C66D89506.РП.А.3.С
Критерии успеха
Основные концепции, которые учащиеся должны продемонстрировать или понять для достижения цели урока
Советы учителям
Рекомендации для учителей по проведению этого урока
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950 Этот урок приближается к 7. RP.3 и рассматривает понятия процента в шестом классе, которые являются основополагающими для этого модуля. Это хорошая возможность вернуться к 7.NS.3 и включить задачи, связанные с операциями с рациональными числами.
RP.3 и рассматривает понятия процента в шестом классе, которые являются основополагающими для этого модуля. Это хорошая возможность вернуться к 7.NS.3 и включить задачи, связанные с операциями с рациональными числами.
Fishtank Plus
Разблокируйте функции, чтобы оптимизировать время подготовки, планировать увлекательные уроки и следить за успеваемостью учащихся.
Проблемы с якорем
Задачи, предназначенные для изучения ключевых моментов урока, и наводящие вопросы, помогающие ученикам понять
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950Проблема 1
Заштрихуйте сетки для обозначения следующих дробей:
| a. $${30\более 100}$$ | б. $${3\over100}$$ | с. $${{1\over3}\более 100}$$ |
Наводящие вопросы
Создайте бесплатную учетную запись или войдите, чтобы получить доступ к наводящим вопросам для этой основной проблемы.
Каталожные номера
EngageNY Mathematics Grade 7 Mathematics > Модуль 4 > Тема A > Урок 1 — Вступительное упражнение 2
Математика для 7 класса > Модуль 4 > Тема A > Урок 1 общеобразовательной программы штата Нью-Йорк по математике от EngageNY и Great Minds. © 2015 Великие умы. Лицензировано EngageNY Департамента образования штата Нью-Йорк в соответствии с лицензией США CC BY-NC-SA 3.0. По состоянию на 2 декабря 2016 г., 17:15.
Проблема 2
Заполните таблицу ниже, чтобы представить эквивалентные дроби, десятичные числа и проценты.
| Дробь | Десятичный | Проценты |
| $$\frac{1}{4}$$ | ||
| 0,5 | ||
| 20% | ||
| $$\frac{1}{3}$$ | ||
| 0,05 | ||
| $$\frac{3}{8}$$ | ||
| 1,3 | ||
| $$\frac{1}{2}$$% |
Наводящие вопросы
Создайте бесплатную учетную запись или войдите, чтобы получить доступ к наводящим вопросам для этой основной проблемы.
Проблема 3
Ответьте на приведенные ниже вопросы с помощью вычислений в уме.
а. Что такое 50% от 20?
Сколько будет 25% от 48?
Что такое 10% от 125?
Что такое 5% от 50?
б. 6 составляет 50% от какого числа?
10 составляет 25% от какого числа?
9 составляет 10% от какого числа?
в. 21 это сколько процентов от 210?
450 сколько процентов от 900?
20 сколько процентов от 80?
30 сколько процентов от 20?
Наводящие вопросы
Создайте бесплатную учетную запись или войдите, чтобы получить доступ к наводящим вопросам для этой основной проблемы.
Набор проблем
Набор предлагаемых ресурсов или типов задач, которые учителя могут преобразовать в набор задач
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950 Следующие ресурсы включают проблемы и действия, связанные с целью
урок, который можно использовать для создания собственного набора задач.
- EngageNY Mathematics Grade 7 Mathematics > Модуль 4 > Тема A > Урок 1 — Примеры и набор задач; в конце этого урока также есть спринт «Дроби, десятичные числа и проценты».
- Открытые ресурсы 6 класс, раздел 3, урок 13 — Практические задачи №1-4
- Kuta Software Бесплатные предварительные алгебраические рабочие листы Преобразование между процентами, дробями и десятичными знаками
Целевая задача
Задание, которое представляет собой пик мышления урока — мастерство покажет, была ли достигнута цель
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950Выполните следующее:
a. Что такое 5% в виде десятичной и дробной части?
б. Что такое 5% от 200?
в. Объясните, как можно найти 5% от любого числа, используя ментальную арифметику.
Ответ учащегося
Создайте бесплатную учетную запись или войдите, чтобы просмотреть ответ учащегося
icon/стрелка/вправо/большойУрок 2
Calvin’s Clearance | 3 Act Math Task
Работа с процентами для оценки и расчета скидок
В следующем учебном материале представлены Реальные математические задачи , которые были созданы с учетом учебной программы по математике для 6 класса Онтарио.
Учителя из школ Онтарио, а также школ по всему миру могут использовать этот урок и серию видео/фотографий в своих классах, чтобы познакомить своих учеников с реальным приложением, чтобы укрепить навыки оценки и вычисления процентов, а также применять их понимание скидок в процентах. На протяжении всего урока учащихся просят оценить стоимость каждого предмета одежды после применения скидки, поощряя при этом использование понятных чисел и их понимание процента как части (процента) целого (из 100). Затем учащиеся смогут взять свою оценку и выполнить расчет с помощью калькулятора, чтобы сравнить свою оценку с фактическим результатом.
Цели обучения:
После нашего Урока математики в процентах реального мира я буду в состоянии:
- оценивать количества, используя эталоны 10%, 25%, 50%, 75% и 100%;
- рассчитать количество в процентах; и,
- применить процентные скидки, чтобы найти цену продажи предмета.

Покажите учащимся видео акта 1.
Затем спросите учащихся:
Что вы заметили? Что вам интересно?
Дайте учащимся время записать некоторые из своих замечаний и вопросов на листе бумаги или на доске/парте с помощью неперманентного маркера. Обычно я даю студентам минуту времени на то, чтобы они «быстро записали» эти идеи.
Затем я предлагаю учащимся поделиться своими наблюдениями и сомнениями, в то время как я обычно перечисляю их в виде точек на доске или в заметке на моем компьютере, чтобы все видели. Присвоение названий этим идеям может быть хорошим способом повысить ответственность и поощрить обмен мнениями.
Так как цена в видео явно заблокирована, я надеюсь, что кому-то будет интересно узнать цену или цену со скидкой на пиджак с такими идеями:
Сколько стоит до скидки?
Сколько сэкономит вам скидка?
Какова будет продажная цена, которую вы должны заплатить?
И многое другое…
Хотя вопросы, которые я ловлю, не всегда выходят, это нормально. Обсуждение имеет ключевое значение для того, чтобы зацепить моих студентов, и их любопытство может быть легко сформировано после того, как они поделились таким количеством интересных идей. Мы часто тратим некоторое время, пытаясь ответить на другие их вопросы, чтобы убедиться, что студенты знают, что их голос ценится.
Затем я прошу учащихся сделать прогноз.
Я попрошу учащихся поделиться этими прогнозами, записать свои имена и попытаться устроить в классе небольшое дружеское соревнование, чтобы вызвать студенческую беседу в нашей безопасной классной среде.
Акт 2 – Дайте некоторую информацию
Затем мы попросим учащихся просмотреть видео акта 2, сцены 1, чтобы узнать первоначальную розничную цену.
Затем учитель может попросить учащихся провести обсуждение в своих группах за столом, чтобы определить, как они могут оценить цену продажи после скидки. Несколько наводящих вопросов:
- Какие дружественные проценты мы можем использовать, чтобы получить близкое приближение?
- Поможет ли здесь округление розничной цены до удобного числа?
- и так далее…
После обсуждения учащиеся могут поделиться своими идеями через Apple TV или использовать диаграммную бумагу в классе, чтобы смоделировать как можно больше творческих решений. Затем учащиеся могут проверить свои оценки с помощью калькулятора и, возможно, побудить их попытаться найти более эффективную стратегию по мере выполнения оставшихся заданий.
Акт 2, Сцена 2
Учащиеся будут смотреть видео акта 2, сцены 2.
Затем учащиеся могут использовать стратегии оценки, чтобы найти скидку и цену продажи товара.
Акт 2, сцена 3
Учащиеся посмотрят видео акта 2, сцены 3.
Затем учащиеся могут использовать стратегии оценки, чтобы найти скидку и цену продажи товара.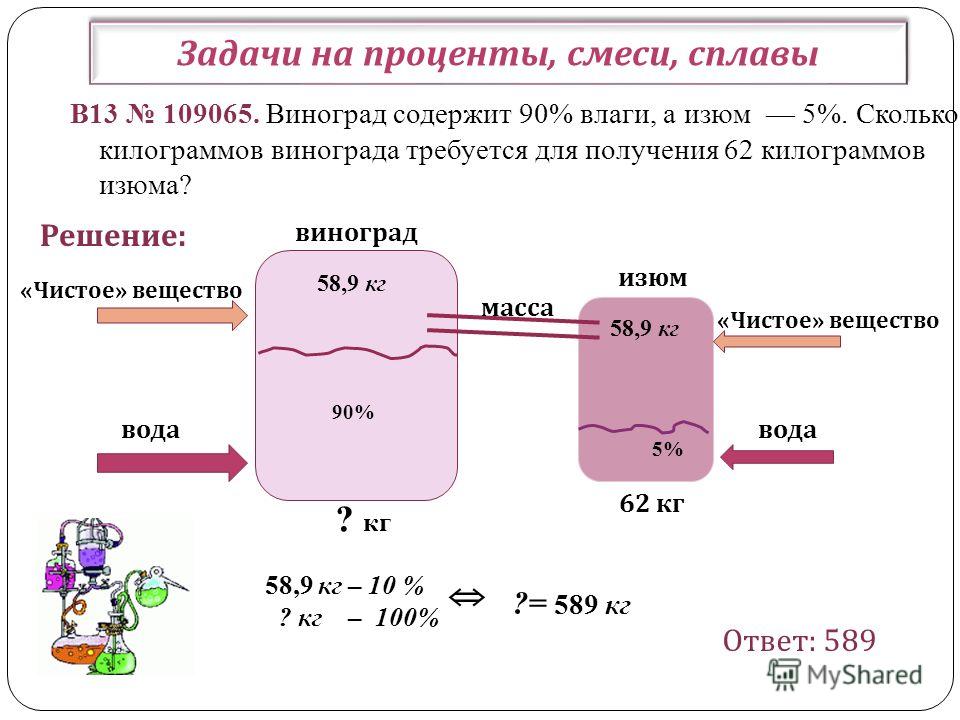
Акт 2, сцена 4
Учащиеся посмотрят видео акта 2, сцены 4.
Затем учащиеся могут использовать стратегии оценки, чтобы найти скидку и цену продажи товара.
Акт 2, Сцена 5
Теперь учащимся предлагается подсчитать промежуточную сумму и определить общий счет, который мы должны ожидать при покупке всех четырех предметов.
Действие 3 – Покажите счет
Затем вы можете показать, как будет выглядеть счет, чтобы учащиеся подтвердили свое мнение. Поскольку я живу в Онтарио, я показал здесь счет с использованием Гармонизированного налога с продаж (HST) в размере 13%:
Что-то еще, что я обычно делаю со своими студентами, это чтобы они вычислили, сколько будет счет в Мичигане, так как мы так близко к границе, и многие семьи едут в Детройт и его окрестности, чтобы делать покупки:
Вот изображение с окончательным счетом из Берч-Ран, Мичиган:
Дополнительные фотографии со скидкой для использования в классе:
- Скидки на одежду моей дочери
- Куртка для моей дочери
- Обычная цена на куртку моей дочери
- Прайс-лист со скидкой
- Покупки в Calvin Klein
- Распродажа костюмов Calvin Klein
- Пиджак Calvin Klein по обычной цене
- Обычная цена на брюки Calvin Klein Suit
- Обычная цена ремня Calvin Klein
- Кельвин Кляйн Шорты
- Обычная цена на шорты Calvin Klein
Подходит для следующих учебных курсов по математике в Онтарио:
- Математика для 6 класса
- Математика 7 класс
- Математика 8 класс
- Математика 9 класс
- MAT1L – Местная математика, 9
- MFM1P – Основы математики, 9
- MPM1D – Основы математики, 9
{БЕСПЛАТНО} Задания по анализу процентных ошибок 7-8 классы
Хорошо ли ваши ученики средней школы понимают 9?0658 процентов ? Помогите им углубить понимание, отрабатывая основные навыки, используя этот БЕСПЛАТНЫЙ набор из задач анализа процентных ошибок .
Использование процентов и решение задач, связанных с процентами, является одним из самых важных математических понятий, которые изучают наши дети. Мы используем и процентов в нашей повседневной жизни все время. И хотя мы можем определенно использовать калькулятор (и должны!), если вы на самом деле недостаточно хорошо понимаете проценты правильно пользоваться калькулятором, он вам абсолютно не поможет . Поэтому, если вы изучаете процентов , процентов доли , процентов изменений , налогов , советов и т. д. со своими учениками, возьмите этот бесплатный набор задач по анализу ошибок, чтобы помочь им обсудить проблемы и сделать конечно понимают!
Что такое задача анализа ошибок? Анализ ошибок означает анализ ошибки . Это означает рассмотрение шагов, использованных или математических рассуждений, примененных к проблеме, обнаружение ошибки или неправильного представления и объяснение того, что пошло не так .
Другими словами, это больше, чем просто исправление ошибки . Конечно, дети могут решить задачу и сказать вам, какой ответ правильный, но могут ли они четко сформулировать , почему другой ответ неверен ?
Объясняя, что пошло не так, студенты вынуждены противостоять собственному пониманию . Действительно ли они понимают, как решить эту математическую задачу, или они просто следуют случайному набору шагов или запутанному алгоритму?
Если они не могут объяснить ошибку другу, они не смогут найти и исправить свои собственные ошибки.
А если не могут найти и объяснить ошибку, у них очень поверхностное понимание предмета.
С другой стороны, находя и объясняя (и исправляя) распространенные ошибки, они будут углубить собственное понимание и получить лучшее представление о типичных ошибках, чтобы они могли искать их в своей работе в будущем.
Хотя я часто призываю учащихся находить и исправлять свои собственные ошибки , иногда проще и менее пугающе смотреть на ошибку «третьего лица». Они не чувствуют сопричастности к проблеме и не принимают ее на свой счет, потому что это не их работа.
Также позволяет обсудите распространенные заблуждения со всем классом, потому что вы можете просмотреть и проанализировать одни и те же шаги и ошибки.
Процентные математические навыки:Эта загрузка включает 6 различных задач анализа ошибок , охватывающих различные математические задачи процентного типа. Вы найдете следующие навыки:
- Использование процентной пропорции
- Использование уравнения процентов
- Преобразование дробей, десятичных знаков и процентов
- Использование формулы простых процентов
- Процент изменения
- Налог с продаж
Анализ задачи на проценты — отличный способ разогреть детей перед началом урока . Это не должно занимать много времени: вы можете спроецировать слайд перед аудиторией и попросить учащихся писать в журнале или на доске, или вы можете распечатать страницы на половину листа и дать каждому учащемуся по одному листу при входе. учебный класс.
Это не должно занимать много времени: вы можете спроецировать слайд перед аудиторией и попросить учащихся писать в журнале или на доске, или вы можете распечатать страницы на половину листа и дать каждому учащемуся по одному листу при входе. учебный класс.
Дайте учащимся около 5 минут , чтобы просмотреть проблему, проанализировать шаги и окончательное решение и сформировать свое мнение.
В данном случае задания называются «Правда?»
Причина этого состоит в том, чтобы побудить учащихся действительно рассмотреть проблему, ситуацию и окончательный ответ, , а не просто знать или предполагать, что работа и ответ неверны .
Иногда работа и решение ДЕЙСТВИТЕЛЬНО верны. Но иногда это не так, и ученикам приходится объясните почему и исправьте .
Другая идея состоит в том, чтобы использовать их в конце урока в качестве выходного билета на для оценки понимания .
Задачи включают различные задачи на проценты, поэтому вы можете напечатать задачу, которая непосредственно относится к сегодняшнему уроку , и позволить учащимся решить ее самостоятельно в конце урока. Затем они могут передать их вам на выходе , чтобы вы могли увидеть, что они понимают и насколько хорошо они могут обосновать свои рассуждения.
Включено в загрузку:Когда вы зайдете в мой магазин и возьмете pdf-файл, вы найдете следующее. Надеюсь, это поможет вам использовать это, ищете ли вы цифровую задачу или задачу для печати.
- Советы по обучению и доступ к цифровой версии, предназначенной для Google Slides
- Указания по совместному использованию слайдов в классе Google
- Версия для печати всех задач анализа 6-процентных ошибок
- Ключи ответов на все 6 задач
Как бы вы ни решили использовать эти задачи, я надеюсь, что они обеспечат содержательное изучение математики для ваших учеников и вызовут захватывающую математическую беседу в ваших классах!
Готовы забрать свой набор? Воспользуйтесь ссылкой ниже, чтобы получить эту халяву в моем магазине.
- {БЕСПЛАТНО} Вы бы предпочли…? Соотношение и процентные задачи | ЦИФРОВОЙ
- Практические проценты: уроки, игры и НЕ ТОЛЬКО
- Преобразование дробей в десятичные и проценты: БЕСПЛАТНЫЕ головоломки
Никогда не иссякайте веселые математические идеи
Если вам понравился этот пост, вам понравится быть частью сообщества Math Geek Mama! Каждую неделю я отправляю электронное письмо с забавными и увлекательными математическими идеями, бесплатными ресурсами и специальными предложениями. Присоединяйтесь к более чем 163 000 читателей, поскольку мы помогаем каждому ребенку добиться успеха и преуспеть в математике! ПЛЮС, получи мою БЕСПЛАТНУЮ электронную книгу, 5 математических игр, в которые можно играть СЕГОДНЯ , в подарок вам !
процентов — Введение | SkillsYouNeed
Термин «процент» означает «из ста». В математике проценты используются так же, как дроби и десятичные дроби, как способы описания частей целого. Когда вы используете проценты, считается, что целое состоит из ста равных частей. Символ % используется, чтобы показать, что число представляет собой процент, и реже может использоваться аббревиатура «процент».
В математике проценты используются так же, как дроби и десятичные дроби, как способы описания частей целого. Когда вы используете проценты, считается, что целое состоит из ста равных частей. Символ % используется, чтобы показать, что число представляет собой процент, и реже может использоваться аббревиатура «процент».
Вы увидите проценты почти везде: в магазинах, в Интернете, в рекламе и в СМИ. Способность понимать, что означают проценты, является ключевым навыком, который потенциально сэкономит вам время и деньги, а также сделает вас более востребованным.
Значение процентов
Процент — это латинский термин, означающий «из ста».
Следовательно, каждое «целое» можно рассматривать как разделенное на 100 равных частей, каждая из которых составляет один процент.
В поле ниже показано это для простой сетки, но это работает одинаково для всего: детей в классе, цен, гальки на пляже и так далее.
Визуализация процентов
В сетке ниже 100 ячеек.
- Каждая ячейка равна 1% от целого (красная ячейка равна 1%).
- Две ячейки равны 2% (зеленые ячейки).
- Пять ячеек равны 5% (синие ячейки).
- Двадцать пять ячеек (фиолетовые ячейки) равны 25% от целого или одной четверти (¼).
- Пятьдесят ячеек (желтые ячейки) равны 50% целого или половины (½).
Сколько имеется незаштрихованных (белых) клеток? Каков процент незаштрихованных ячеек?
Ответ: Есть два способа решить эту проблему.
- Подсчитайте лейкоциты. Их 17. Таким образом, из 100 клеток 17% белые.
- Сложите количество других ячеек и вычтите их из 100. Есть одна красная ячейка, две зеленые, пять синих, 25 фиолетовых и 50 желтых. В сумме это 83. 100−83 = 17. Опять же, из 100 клеток 17 белых, или 17%.
Легко вычислить процентное соотношение, когда есть 100 отдельных «вещей», составляющих целое, как в сетке выше. А если их больше или меньше?
А если их больше или меньше?
Ответ заключается в том, что вы преобразуете отдельные элементы, составляющие целое, в проценты. Например, если бы в сетке было 200 ячеек, каждый процент (1%) был бы равен двум ячейкам, а каждая ячейка — половине процента.
Мы используем проценты, чтобы упростить расчеты. С частями числа 100 работать намного проще, чем с третей, двенадцатой и так далее, тем более, что довольно много дробей не имеют точного (неповторяющегося) десятичного эквивалента. Важно отметить, что это также значительно упрощает сравнение процентов (которые фактически имеют общий знаменатель 100), чем между дробями с разными знаменателями. Отчасти поэтому так много стран используют метрическую систему измерения и десятичную валюту.
Нахождение процента
Общее правило для нахождения данного процента от заданного целого:
Определите значение 1%, затем умножьте его на процент, который вам нужно найти.
Это проще всего понять на примере. Предположим, вы хотите купить новый портативный компьютер. Вы проверили местных поставщиков, и одна компания предложила вам скидку 20% от прейскурантной цены в 500 фунтов стерлингов. Сколько будет стоить ноутбук от этого поставщика?
Предположим, вы хотите купить новый портативный компьютер. Вы проверили местных поставщиков, и одна компания предложила вам скидку 20% от прейскурантной цены в 500 фунтов стерлингов. Сколько будет стоить ноутбук от этого поставщика?
В этом примере вся сумма составляет 500 фунтов стерлингов или стоимость ноутбука до применения скидки. Процент, который вам нужно найти, составляет 20%, или скидка, предлагаемая поставщиком. Затем вы вычтите это из полной цены, чтобы узнать, сколько вам будет стоить ноутбук.
Начните с определения значения 1%
Один процент от 500 фунтов стерлингов равен 500 ÷ 100 = 5 фунтов стерлингов.
Умножьте на процент, который вы ищете
После того, как вы вычислили значение 1%, вы просто умножаете его на искомый процент, в данном случае на 20%.
5 фунтов стерлингов × 20 = 100 фунтов стерлингов.
Теперь вы знаете, что скидка составляет 100 фунтов стерлингов.

Завершите вычисление, прибавив или вычтя необходимое.
Цена ноутбука, включая скидку, составляет 500–20%, или 500–100 фунтов = 90 658 400 фунтов стерлингов.
Простой способ вычислить 1% любого числа
1% — это целое (каким бы оно ни было), деленное на 100.
вправо (или переместите запятую на два знака влево).
Вы можете узнать больше о числах и разрядах на нашей странице Числа , но вот краткое резюме:
500 фунтов стерлингов состоят из 5 сотен, ноль десятков и ноль единиц. 500 фунтов стерлингов также имеют ноль пенсов (центов, если вы работаете в долларах), поэтому их можно записать как 500 фунтов стерлингов с нулевыми десятыми или сотыми долями.
| Сотни | Десятки | Единиц | Точка | Десятки | Сотые |
| 5 | 0 | 0 | . | 0 | 0 |
Когда мы делим на 100, мы сдвигаем наш номер на два столбца вправо. 500 разделить на 100 = 005, или 5. Начальные нули (нули «снаружи слева» числа, например, в 005, 02, 00014) не имеют значения, поэтому их не нужно записывать.
500 разделить на 100 = 005, или 5. Начальные нули (нули «снаружи слева» числа, например, в 005, 02, 00014) не имеют значения, поэтому их не нужно записывать.
Вы также можете думать об этом как о перемещении десятичной точки на два знака влево.
| Сотни | Десятки | Единиц | Точка | Десятки | Сотые |
| 0 | 0 | 5 | . | 0 | 0 |
Это правило применяется ко всем числам, поэтому 327 фунтов стерлингов, разделенные на 100, составляют 3,27 фунта стерлингов. Это то же самое, что сказать, что 3,27 фунта стерлингов составляют 1% от 327 фунтов стерлингов. 1 фунт стерлингов, деленный на 100 = 0,01 фунта стерлингов или один пенс. В фунте сто пенсов (и в долларе сто центов). Таким образом, 1 пенс составляет 1% от 1 фунта стерлингов.
После того, как вы подсчитали 1% от целого, вы можете затем умножить свой ответ на процент, который вы ищете (см. нашу страницу на умножение для справки).
нашу страницу на умножение для справки).
Математика в уме
По мере развития ваших математических навыков вы сможете увидеть другие способы получения того же ответа. Приведенный выше пример ноутбука довольно прост, и с практикой вы можете использовать свои математические способности в уме, чтобы думать об этой проблеме по-другому, чтобы упростить ее. В этом случае вы пытаетесь найти 20 %, поэтому вместо того, чтобы найти 1 % и затем умножить его на 20, вы можете найти 10 % и затем просто удвоить его. Мы знаем, что 10% — это то же самое, что 1/10, и мы можем разделить число на 10, переместив запятую на один разряд влево (удалив ноль из 500). Следовательно, 10% от 500 фунтов стерлингов составляют 50 фунтов стерлингов, а 20% составляют 100 фунтов стерлингов.
Полезным математическим приемом в уме является то, что проценты обратимы, поэтому 16% от 25 равно 25% от 16. Несомненно, одно из этих значений будет гораздо легче вычислить в уме… попробуйте!
Воспользуйтесь нашими калькуляторами процентов , чтобы быстро решить свои процентные задачи.
Работа с процентами
Мы рассчитали 20% скидку в приведенном выше примере, а затем вычли ее из общей суммы, чтобы узнать, сколько будет стоить новый ноутбук.
Мы можем не только отнять процент, но и добавить процент к числу. Это работает точно так же, но на последнем шаге вы просто добавляете вместо вычитания.
Например: Джордж получил повышение и зарплату повысили на 5%. В настоящее время Джордж зарабатывает 24 000 фунтов стерлингов в год, так сколько же он будет зарабатывать после того, как его зарплата повысится?
Выработать 1% от всего
Все в этом примере представляет собой текущую зарплату Джорджа, 24 000 фунтов стерлингов. 1% от 24 000 фунтов стерлингов равен 24 000 ÷ 100 = 240 фунтов стерлингов.
Умножьте это на процент, который вы ищете
Джордж получает повышение зарплаты на 5%, поэтому нам нужно знать значение 5%, или 5 умножить на 1%.

240 фунтов стерлингов × 5 = 1200 фунтов стерлингов.
Завершите расчет, добавив к исходной сумме
Повышение заработной платы Джорджа составляет 1200 фунтов стерлингов в год. Таким образом, его новая зарплата составит 24 000 фунтов стерлингов + 1 200 фунтов стерлингов = 25 200 фунтов стерлингов.
Проценты выше 100%
Проценты могут превышать 100%. Этот пример один: новая зарплата Джорджа на самом деле составляет 105% от его старой.
Однако его старая зарплата не равна 100% новой. Вместо этого он составляет чуть более 95%.
Когда вы вычисляете проценты, важно убедиться, что вы работаете с правильным целым числом. В данном случае «все» — это старая зарплата Джорджа.
Проценты в виде десятичных дробей и дробей
Один процент равен одной сотой части целого. Поэтому его можно записать как десятичную, так и дробную часть.
Чтобы записать процент в виде десятичного числа, просто разделите его на 100.
Например, 50% становится 0,5, 20% становится 0,2, 1% становится 0,01 и так далее.
Используя это знание, мы можем рассчитывать проценты. 50% — это половина, поэтому 50% от 10 — это 5, потому что пять — это половина от 10 (10 ÷ 2). Десятичная часть 50% равна 0,5. Таким образом, еще один способ найти 50% от 10 — это, скажем, 10 × 0,5, или 10 половин.
20% от 50 — это то же самое, что сказать 50 × 0,2, что равно 10.
17,5% от 380 = 380 × 0,175, что равно 66,5.
Повышение зарплаты Джорджа выше составило 5% от 24 000 фунтов стерлингов. 24 000 фунтов стерлингов × 0,05 = 1 200 фунтов стерлингов.
Преобразование десятичной дроби в проценты осуществляется в обратном порядке: умножьте десятичную дробь на 100.
0,5 = 50 %
0,875 = 87,5 %
из 100, и разделите его на наименьшую возможную форму.
50% = 50/100 = 5/10 = ½
20% = 20/100 = 2/10 = 1/5
30% = 30/100 = 3/10
ВНИМАНИЕ!
Можно преобразовать дроби в проценты путем преобразования знаменателя (нижнего числа дроби) в 100. (неповторяющийся) десятичный или процентный.
(неповторяющийся) десятичный или процентный.
Если знаменатель вашей дроби целое число раз не делится на 100, то простого преобразования не будет. Например, 1/3, 1/6 и 1/9.не составляют «чистых» процентов (они составляют 33,33333%, 16,66666% и 11,11111%).
Расчет процентов от целого
До сих пор мы рассмотрели основы работы с процентами и способы прибавления или вычитания процента от целого.
Иногда бывает полезно вычислить проценты от целого, когда вам известны соответствующие числа.
Например, предположим, что в организации работает 9 менеджеров, 12 администраторов, 5 бухгалтеров, 3 специалиста по персоналу, 7 уборщиц и 4 работника общественного питания. Какой процент каждого типа персонала он использует?
Начните с проработки целого.
В этом случае вы не знаете «всего» или общей численности персонала в организации. Таким образом, первым шагом является объединение различных типов персонала.

9 менеджеров + 12 администраторов + 5 бухгалтеров + 3 специалиста по кадрам + 7 уборщиков + 4 работника общественного питания = 40 сотрудников.
Рассчитайте долю (или долю) персонала в каждой категории.
Нам известно количество сотрудников в каждой категории, но нам нужно преобразовать его в долю от целого, выраженную в виде десятичной дроби. Расчет, который нам нужно сделать, это:
Персонал в категории ÷ Всего (См. нашу страницу отдела для помощи с суммами деления или используйте калькулятор)
В качестве примера мы можем использовать менеджеров:
9 менеджеров ÷ 40 = 0,225
В этом случае может быть полезно, если вместо того, чтобы думать о символе деления «÷» как о значении «делится на», мы можем заменить слова «из». Мы часто используем это в контексте результатов тестов, например, 8/10 или «8 из 10» правильных ответов. Таким образом, мы вычисляем «количество менеджеров из всего штата».
 Когда мы используем слова для описания расчета, это может сделать его более понятным.
Когда мы используем слова для описания расчета, это может сделать его более понятным.Преобразование доли целого в проценты
0,225 — доля сотрудников, занимающих руководящие должности, выраженная в виде десятичной дроби. Чтобы преобразовать это число в проценты, нам нужно умножить его на 100. Умножение на 100 аналогично делению на сто, за исключением того, что вы перемещаете числа в другую сторону по шкале разрядов. Таким образом, 0,225 становится 22,5.
Другими словами, 22,5% сотрудников организации являются менеджерами.
Затем мы делаем те же два расчета для каждой другой категории.
- 12 администраторов ÷ 40 = 0,3. 0,3 × 100 = 30%.
- 5 бухгалтеров ÷ 40 = 0,125. 0,125 × 100 = 12,5%.
- 3 специалиста по кадрам ÷ 40 = 0,075. 0,075 × 100 = 7,5%.
- 7 уборщиков ÷ 40 = 0,175. 0,175 × 100 = 17,5%.
- 4 обслуживающего персонала ÷ 40 = 0,1.
 0,1 × 100 = 10%.
0,1 × 100 = 10%.
СОВЕТ! Проверьте, что у вас есть в общей сложности 100%
Когда вы закончите вычислять проценты, рекомендуется сложить их вместе, чтобы убедиться, что они равны 100%. Если нет, то проверьте свои расчеты.
Подводя итог, можно сказать, что организация состоит из:
| Ролей | Численность персонала | % персонала |
| Менеджеры | 9 | 22,5% |
| Администраторы | 12 | 30% |
| Бухгалтеры | 5 | 12,5% |
| Специалисты по кадрам | 3 | 7,5% |
| Очистители | 7 | 17,5% |
| Персонал общественного питания | 4 | 10% |
| Итого | 40 | 100% |
Может быть полезно отображать процентные данные, представляющие целое на круговой диаграмме. Вы можете быстро увидеть пропорции категорий персонала на примере.
Вы можете быстро увидеть пропорции категорий персонала на примере.
Дополнительную информацию о круговых диаграммах и других типах графиков и диаграмм см. на нашей странице: Графики и диаграммы .
Что нужно помнить
- Проценты — это способ описания частей целого.
- Они чем-то похожи на десятичные, за исключением того, что целое всегда делится на 100, а не на десятые, сотые, тысячные и т. д. единицы.
- Проценты предназначены для упрощения вычислений.
Дальнейшее чтение из раздела «Навыки, которые вам нужны»
Пропорция
Часть руководства по необходимым навыкам счета
В этой электронной книге рассматриваются пропорции, рассматривающие числа как части других чисел, как части большего целого или по отношению к другим числам.
В книге рассматриваются дроби и десятичные дроби, отношения и проценты с рабочими примерами, чтобы вы могли попробовать и развить свои навыки.
Если вы хотите освежить свои знания или помочь своим детям в обучении, эта книга для вас.
Интерактивные математические навыки в седьмом классе
Ссылки проверены 23.08.2018
1. Преобразование дроби в проценты. Щелкните изображение, чтобы увеличить его
Потренируйтесь переводить дроби в проценты. Включает урок с практическими задачами.  ПОДРОБНЕЕ
2. Преобразование процентов в десятичные числа. г. Щелкните изображение, чтобы увеличить его
Потренируйтесь переводить проценты в десятичные дроби. Включает урок с практическими задачами.  ПОДРОБНЕЕ
3. Применение процентов. Щелкните изображение, чтобы увеличить его
Тест по главе с самопроверкой из двенадцати вопросов.  ПОДРОБНЕЕ
4. Применение процентов II. Щелкните изображение, чтобы увеличить его
Самопроверка главы из четырнадцати вопросов.  ПОДРОБНЕЕ
5. Преобразование десятичной дроби в проценты. Щелкните изображение, чтобы увеличить его
Потренируйтесь переводить десятичные дроби в проценты; Включает урок с практическими задачами.  ПОДРОБНЕЕ
6. Преобразование процентов в дроби. Щелкните изображение, чтобы увеличить его
Потренируйтесь переводить проценты в дроби. Включает урок с практическими задачами.  ПОДРОБНЕЕ
7. Определите процентное значение. Щелкните изображение, чтобы увеличить его
Сколько процентов составляет первое число второго? Определите ответ до ближайшего целого числа.  ПОДРОБНЕЕ
8. Оценка в процентах. Щелкните изображение, чтобы увеличить его
Проверьте свои знания о процентах с помощью этих тестов для самопроверки из 5 вопросов:  ПОДРОБНЕЕ
9. Нахождение процента от количества. Щелкните изображение, чтобы увеличить его
Проверьте свои знания о процентах с помощью этих тестов для самопроверки из 5 вопросов.  ПОДРОБНЕЕ
10. Нахождение процента от числа. Щелкните изображение, чтобы увеличить его
Урок с практическими задачами.  ПОДРОБНЕЕ
11. Дроби и проценты. Щелкните изображение, чтобы увеличить его
Проверьте свои знания о процентах с помощью этих тестов для самопроверки из 5 вопросов:  ПОДРОБНЕЕ
12. Дроби, десятичные дроби и проценты. Щелкните изображение, чтобы увеличить его
Проверьте свои знания о процентах с помощью этих тестов для самопроверки из 5 вопросов.  ПОДРОБНЕЕ
13. Математика в торговом центре.
Щелкните изображение, чтобы увеличить его
Попрактикуйтесь в процентах и найдите лучшее предложение во время покупок в виртуальном торговом центре. Найдите процентную скидку и цену продажи, рассчитайте проценты, полученные в банке, сравните абонементы для здоровья в тренажерном зале и выясните, сколько чаевых давать официанту.  ПОДРОБНЕЕ
14. Онлайн-калькулятор процентов. Щелкните изображение, чтобы увеличить его
Этот онлайн-калькулятор процентов показывает, как процент представляется в виде доли числа.  ПОДРОБНЕЕ
15. Игра «Пингвин-официант». Щелкните изображение, чтобы увеличить его
FunBrain покажет вам ваш счет за ужин и чаевые в процентах, которые вы должны оставить. Вы должны рассчитать правильные чаевые, чтобы оставить пингвина официанту. Четыре уровня: легкий, средний, сложный и супермозг.  ПОДРОБНЕЕ
16. Процент и оценка. Щелкните изображение, чтобы увеличить его
Проверьте свои знания о процентах с помощью этого теста для самопроверки из 5 вопросов. ПОДРОБНЕЕ
17. Проценты и дроби. Щелкните изображение, чтобы увеличить его
Проверьте свои знания о процентах с помощью этого теста для самопроверки из 5 вопросов.  ПОДРОБНЕЕ
18. Проценты и целые числа. Щелкните изображение, чтобы увеличить его
Проверьте свои знания о процентах с помощью этих тестов для самопроверки из 5 вопросов:  ПОДРОБНЕЕ
19. Проценты от числа (2).
Щелкните изображение, чтобы увеличить его
Проверьте свои знания о процентах с помощью этого теста для самопроверки из 5 вопросов.  ПОДРОБНЕЕ
20. Процент от числа. Щелкните изображение, чтобы увеличить его
Проверьте свои знания о процентах с помощью этого теста для самопроверки из 5 вопросов.  ПОДРОБНЕЕ
21. Процент изменения. Щелкните изображение, чтобы увеличить его
Проверьте свои знания о процентах с помощью этого теста для самопроверки из 5 вопросов.  ПОДРОБНЕЕ
22. Процент проблем. Щелкните изображение, чтобы увеличить его
Игра для одного или двух игроков от Quia. Ответьте на вопросы правильно, чтобы набрать очки.  ПОДРОБНЕЕ
23. Проценты с калькулятором. Щелкните изображение, чтобы увеличить его
Урок и практические задачи, которые нужно решить, но не водите мышью по цветным блокам, пока не придумаете ответ.  ПОДРОБНЕЕ
24. Процент — Уроки. Щелкните изображение, чтобы увеличить его
Указатель страниц, на которых обучают навыкам работы с процентами и соотношениями, изучаемыми в математических курсах K8. На каждой странице есть инструкция и обзор, практика и тест.  ПОДРОБНЕЕ
25. Проценты и пропорции. Щелкните изображение, чтобы увеличить его
Проверьте свои знания о процентах с помощью этого теста для самопроверки из 5 вопросов.  ПОДРОБНЕЕ
26. Проценты и десятичные дроби (2). Щелкните изображение, чтобы увеличить его
Проверьте свои знания о процентах с помощью этого теста для самопроверки из 5 вопросов.  ПОДРОБНЕЕ
27. Проценты и десятичные дроби. Щелкните изображение, чтобы увеличить его
Проверьте свои знания о процентах с помощью этого теста для самопроверки из 5 вопросов. ПОДРОБНЕЕ
28. Проценты больше 100% и проценты меньше 1%. Щелкните изображение, чтобы увеличить его
Проверьте свои знания о процентах с помощью этого теста для самопроверки из 5 вопросов.  ПОДРОБНЕЕ
29. Круговая диаграмма. Щелкните изображение, чтобы увеличить его
Создатель интерактивной круговой диаграммы. (Параметры: количество секторов, размер сектора в процентах) Связанные ресурсы на вкладке ученика.  ПОДРОБНЕЕ
30. Практика решения процентных задач. Щелкните изображение, чтобы увеличить его
Пятнадцать вопросов с доступными ответами.  ПОДРОБНЕЕ
31. Покупки в Troy’s Toys. Щелкните изображение, чтобы увеличить его
Решите 5 задач на каждом уровне. [Уровень 1: Найдите цену продажи, когда известны первоначальная цена и скидка в процентах. Уровень 2: Найдите скидку в процентах, когда известны первоначальная цена и цена продажи.]  ПОДРОБНЕЕ
32. Решение задач на проценты с помощью пирамидальной сетки. Щелкните изображение, чтобы увеличить его
Интерактивное учебное задание с примерами задач. Учащиеся используют метод пирамиды для решения задач на проценты. Пирамидальная сетка обеспечивает визуальный способ настройки уравнения.  ПОДРОБНЕЕ
33. Spy Guys Interactive – Процент. Щелкните изображение, чтобы увеличить его
Смотрите видео и отвечайте в разных местах. Это видео включает в себя разделы, в которых учащимся предлагается ввести ответы.  ПОДРОБНЕЕ
34.


 Решение
Решение Сколько получится сухих грибов из 22 кг свежих грибов? Решение
Сколько получится сухих грибов из 22 кг свежих грибов? Решение процентных денег. Добавив 850 р., он оставил деньги еще на один год. По истечении года вклад вместе с процентами составил 4200 р. Какая сумма была положена первоначально и какие годовые проценты дает банк? Ответ: 3000 р, 5%
процентных денег. Добавив 850 р., он оставил деньги еще на один год. По истечении года вклад вместе с процентами составил 4200 р. Какая сумма была положена первоначально и какие годовые проценты дает банк? Ответ: 3000 р, 5% К концу года сумма на этих вкладах выросла до 1340 р., а к концу следующего года — до 1498 р. Было подсчитано, что если бы с самого начала денег вкладчик положил во второй банк, а остальные — в первый, то по итогам первого года сумма на этих вкладах составила бы 1420 р. Определить величину вклада по истечении двух лет, предполагая, что вкладчик положил все деньги в первый банк. Ответ: 1452 р.
К концу года сумма на этих вкладах выросла до 1340 р., а к концу следующего года — до 1498 р. Было подсчитано, что если бы с самого начала денег вкладчик положил во второй банк, а остальные — в первый, то по итогам первого года сумма на этих вкладах составила бы 1420 р. Определить величину вклада по истечении двух лет, предполагая, что вкладчик положил все деньги в первый банк. Ответ: 1452 р.
 РП.А.3
— Используйте пропорциональные отношения для решения многошаговых задач на соотношение и проценты. Примеры: простые проценты, налоги, надбавки и скидки, чаевые и комиссионные, сборы, процентное увеличение и уменьшение, процентная ошибка.
РП.А.3
— Используйте пропорциональные отношения для решения многошаговых задач на соотношение и проценты. Примеры: простые проценты, налоги, надбавки и скидки, чаевые и комиссионные, сборы, процентное увеличение и уменьшение, процентная ошибка. 




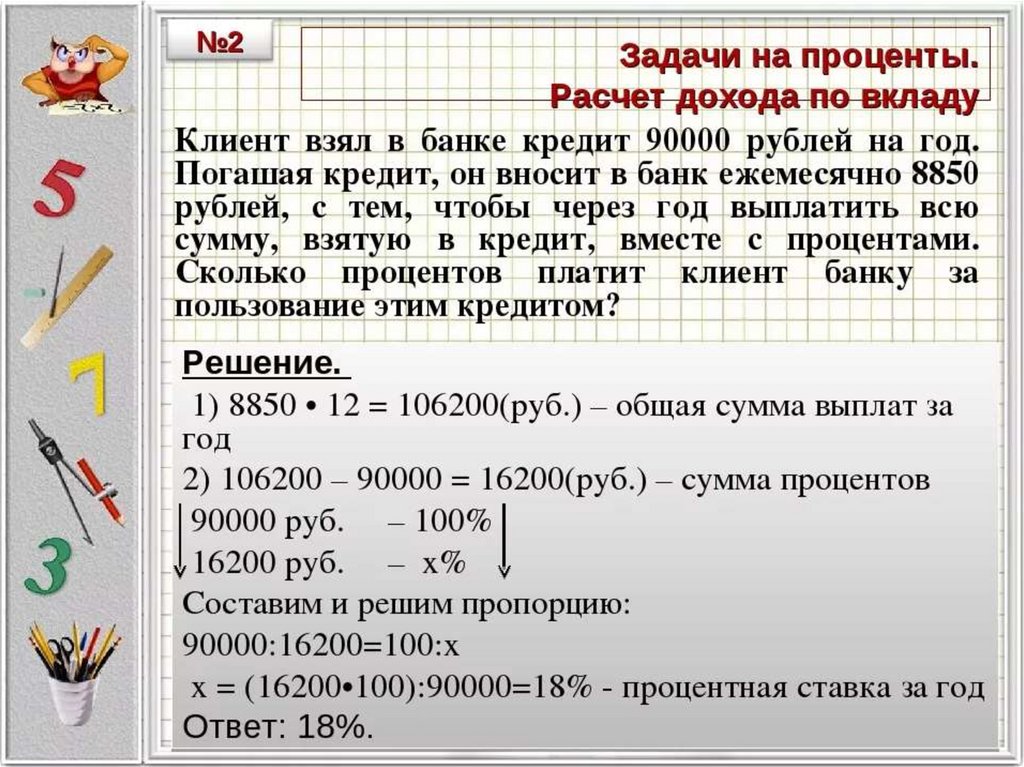 Когда мы используем слова для описания расчета, это может сделать его более понятным.
Когда мы используем слова для описания расчета, это может сделать его более понятным. 0,1 × 100 = 10%.
0,1 × 100 = 10%.
 Включает урок с практическими задачами.
 ПОДРОБНЕЕ
Включает урок с практическими задачами.
 ПОДРОБНЕЕ 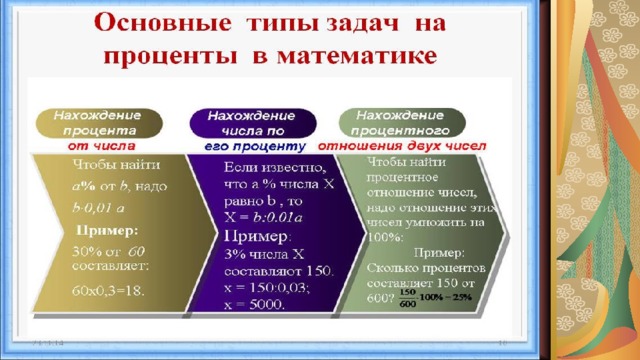  ПОДРОБНЕЕ
 ПОДРОБНЕЕ  Математика в торговом центре.
Математика в торговом центре. Вы должны рассчитать правильные чаевые, чтобы оставить пингвина официанту. Четыре уровня: легкий, средний, сложный и супермозг.
 ПОДРОБНЕЕ
Вы должны рассчитать правильные чаевые, чтобы оставить пингвина официанту. Четыре уровня: легкий, средний, сложный и супермозг.
 ПОДРОБНЕЕ  Проценты от числа (2).
Проценты от числа (2). Ответьте на вопросы правильно, чтобы набрать очки.
 ПОДРОБНЕЕ
Ответьте на вопросы правильно, чтобы набрать очки.
 ПОДРОБНЕЕ   ПОДРОБНЕЕ
 ПОДРОБНЕЕ   ПОДРОБНЕЕ
 ПОДРОБНЕЕ  Уровень 2: Найдите скидку в процентах, когда известны первоначальная цена и цена продажи.]
 ПОДРОБНЕЕ
Уровень 2: Найдите скидку в процентах, когда известны первоначальная цена и цена продажи.]
 ПОДРОБНЕЕ 