График минус корень из минус икс: y=минус корень из x . Как выглядит график? и какие там точки соединения?

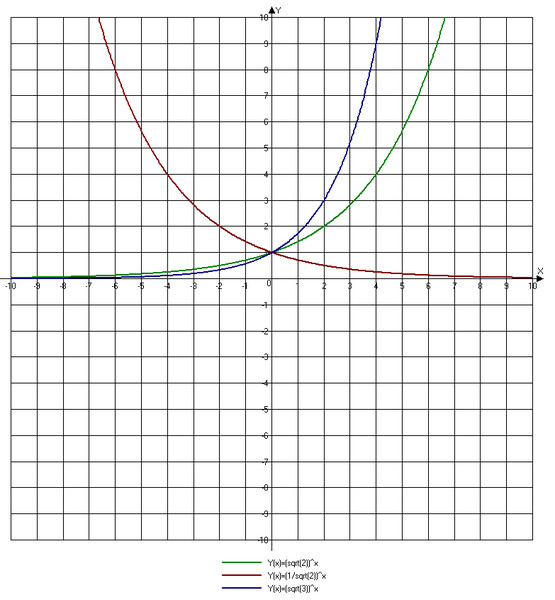
Видео с вопросами: определение точечного отражения графика радикальной функции

Стенограмма видео

Графики 𝐴 и 𝐵 на диаграмме представляют собой графики функций квадратного корня. Они симметричны относительно начала координат. Уравнение графика 𝐴: 𝑦 равно корню в одну треть 𝑥 плюс два плюс один. Зная, что точечное отражение относительно начала координат эквивалентно отражению по оси 𝑥, за которым следует отражение по оси 𝑦, найдите уравнение графика 𝐵.

В этом вопросе нам говорят, что граф 𝐴 отображается на граф 𝐵 посредством вращения вокруг начала координат и что это эквивалентно отражению по оси 𝑥, за которым следует отражение по оси 𝑦. Итак, давайте напомним себе об алгебраических манипуляциях, которые мы можем применить к нашей функции, которая достигает этих результатов. Предположим, у нас есть функция 𝑦, равная 𝑓 от 𝑥. Функция 𝑦 равна отрицательному 𝑓 из 𝑥 является отражением этой исходной функции на оси 𝑥. Точно так же график 𝑦 равен 𝑓 отрицательного 𝑥 является отражением 𝑦 равно 𝑓 из 𝑥 на оси 𝑦. Итак, мы видим, что возьмем уравнение нашего исходного графика и применим оба этих преобразования.

Мы определим 𝑦 равным 𝑓 из 𝑥 таким образом, что 𝑓 из 𝑥 является третьим корнем 𝑥 плюс два плюс один. Это будет отображено на отрицательное 𝑓 из 𝑥 отражением по оси 𝑥. Итак, чтобы добиться этого отражения по оси 𝑥, давайте оценим отрицательное 𝑓 из 𝑥. Это находится просто путем умножения всего выражения на отрицательное. Таким образом, мы получаем отрицательный корень третьей степени 𝑥 плюс два плюс один. Распределив отрицательную единицу по скобкам, мы обнаружим, что отрицательное 𝑓 из 𝑥 равно отрицательному корню в одну треть 𝑥 плюс два минус один. Итак, мы добились нашего отражения по оси 𝑥. Итак, наш график 𝑦 равно отрицательному 𝑓 из 𝑥 будет выглядеть примерно так.

Теперь мы действительно видим, что нам нужно выполнить отражение по оси 𝑦, чтобы отобразить это на графе 𝐵. Поскольку мы отображаем отрицательное 𝑓 из 𝑥 на эту функцию, теперь нам нужно найти отрицательное 𝑓 отрицательного 𝑥.

Это даст нам отражение графика 𝑦 равно отрицательному 𝑓 из 𝑥 на оси 𝑦. И все, что нам нужно сделать здесь, это заменить 𝑥 отрицательным 𝑥, так что мы получим отрицательный корень одной трети отрицательного 𝑥 плюс два минус один. Итак, у нас есть уравнение графика 𝐵. Теперь мы заменим отрицательное 𝑓 отрицательного 𝑥 на 𝑦, и мы получим 𝑦 равно отрицательному корню в одну треть отрицательному 𝑥 плюс два минус один.

Часто имеет смысл проверить наш ответ там, где это возможно. Здесь мы можем выбрать пару точек, лежащих на кривой 𝐵, и проверить, удовлетворяют ли они нашему уравнению. Поскольку четыре маленьких квадрата представляют две единицы, два маленьких квадрата представляют одну единицу. Итак, мы видим, что наш график проходит через точку два, отрицательную. Другими словами, когда 𝑥 равно двум, 𝑦 должно быть равно отрицательной единице. Подстановка 𝑥 равняется двум в наше уравнение, и мы получаем 𝑦 равно отрицательной одной трети, умноженной на квадратный корень из отрицательных двух плюс два минус один, что равно отрицательной единице.

Итак, эта точка действительно удовлетворяет нашему уравнению.

Проверим еще одну координату. Мы видим, что он проходит примерно через ноль, минус 1,5. Итак, мы подставляем 𝑥 равно нулю в наше уравнение, и мы получаем отрицательную одну треть, умноженную на квадратный корень из отрицательного нуля плюс два минус один, что с точностью до двух знаков после запятой равно отрицательному значению 1,47. Итак, поскольку наш график проходит немного выше минус 1,5 по оси 𝑦, мы можем сделать вывод, что это, вероятно, также верно.

1. Как влияет k в f(x)=x√+k на графике функции квадратного корня, x√, и почему? *Значение k сдвигает график вправо, если оно положительное или слева, если отрицательный, потому что он меняет значение того, что квадратный корень, в результате чего значения функция f иметь те же высоты, но на другие значения x, чем x√. *Значение k сдвигает график влево, если оно положительное или правильно, если отрицательное, потому что это меняет значение того, что квадратный корень, в результате чего значения функция f иметь те же высоты, но на другие значения x, чем x√.

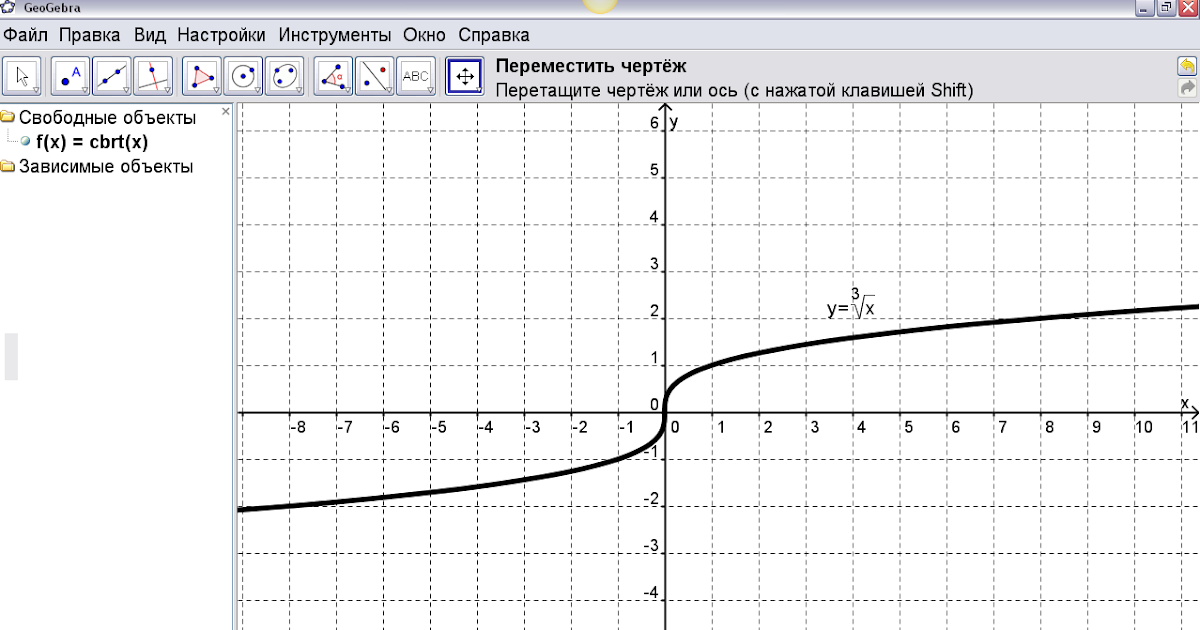*Значение k сдвигает график вниз, если оно положительное или вверх, если отрицательный, потому что он добавляется после вычисления x√, поэтому значение k изменяет высоту каждая точка на графике x√. *Значение k сдвигает график вверх, если оно положительное или вниз, если отрицательный, потому что он добавляется после вычисления x√, поэтому значение k изменяет высоту каждая точка на графике x√. Как график f(x)=3x√ связан с график функции квадратного корня, x√? Число 3 заставляет график сжиматься по вертикали в 9 раз.поскольку x теперь должен быть в 9 раз меньше, чтобы достичь ту же высоту в функции f, что и в обычная функция квадратного корня. Число 3 растягивает функцию квадратного корня по вертикали на коэффициент 3, так как он умножает высоты каждой точки вдоль график функции квадратного корня на 3. 3 перемещает точку пересечения по оси Y квадратного корня функция вертикально вверх на 3 из-за умножения. 3 заставляет весь график сместиться вверх на 3 единицы, так как каждая точка на графике функции квадратного корня будет иметь его высота умножается на 3. Опишите эффект от умножая x√ на −1 как в f(x)=−x√. (1 балл) Функция f(x) становится неопределенной, так как квадрат корень никогда не может быть отрицательным. График x√ отражается относительно ось Y. График x√ отражается относительно ось х. Ничего не происходит, потому что умножение на число, абсолютное значение 1 не приводит к вертикальному растяжению или сжатию. График y=f(x)=x√−9вытянут по горизонтали от оси yy в 3 раза, чтобы создать новый функция. Каково уравнение для этой новой функции? (1 балл) г(х)=х√−6 г(х)=13х—√-3 г(х)=х√−24 г(х)=13х—√-9 Какой эффект дает k в f(x)=x+k−−−−−√ имеют на график функции квадратного корня x√ и почему?(1 точка) Значение k сдвигает график вверх, если положительный или вниз, если отрицательный, потому что он добавляется после вычисление x√, поэтому значение k равно изменение высоты каждой точки на графике x√. Значение k сдвигает график влево, если положительный или правильный, если отрицательный, потому что он меняет значение из чего извлекается квадратный корень, что приводит к значениям функция f иметь те же высоты, но на другие значения x, чем x√. Значение k сдвигает график вправо, если положительный или оставленный, если отрицательный, потому что он меняет значение из чего извлекается квадратный корень, что приводит к значениям функция f иметь те же высоты, но на другие значения x, чем x√. Значение k сдвигает график вниз, если положительный или вверх, если отрицательный, потому что он добавляется после вычисление x√, поэтому значение k равно изменение высоты каждой точки на графике x√.

Вопрос

Пошаговый ответ

AI Рекомендуемый ответ:

Чтобы найти x в уравнении f(x)=x+k?????, нам сначала нужно найти значение k. Это делается путем решения уравнения f(x) = x+k относительно k. Если k отрицательно, то уравнение принимает вид f(x) = x?k. В этом случае график f(x) смещается влево, потому что ?k сдвигает график влево. Если k положительно, то уравнение принимает вид f(x) = x+k. В этом случае график f(x) смещается вправо, потому что +k сдвигает график вправо. Поскольку k не влияет на график x?, мы можем спокойно игнорировать его при поиске x.

93 0 ≤t≤36 (A) Когда скорость роста, Н'(т), увеличивается и уменьшается? Чтобы определить, когда Н'(т) увеличивается и уменьшается, найти N′′(т), производная от Н'(т). Сначала определите Н'(т). Н(т) знак равно 1600+54t2−t3 Н'(т) знак равно 108т−3т2 Теперь найдите N′′(т). Н'(т) знак равно 108т−3т2 Н»(т) знак равно 108−6т Далее установите Н»(т) равным нулю, чтобы найти номера разделов для N′′(т). Н»(т) знак равно 0 108−6т знак равно 0 т знак равно 18 Темпы роста увеличиваются для N′′(t)>0 и уменьшается для N′′(t)<0. Составьте таблицу знаков, чтобы определить, когда Н'(т) увеличивается и уменьшается. 0 +++ --- (0,18) (18,36) 18 Таким образом, скорость роста увеличивается на (0,18) и уменьшается на (18,36). (B) Найдите точки перегиба для графика N. Напомним, что возможные точки перегиба возникают там, где N′′(t)=0 или где Н''(т) не существует. Точка перегиба возникает там, где Н''(т) меняет знак. Заметить, что Н''(т) меняет знак на т=18. Следовательно, точка перегиба N находится в т=18. (C) Нарисуйте графики N и Н’ в той же системе координат. Сначала определите y-пересечение N. Подставьте 0 вместо t в N(t). Н(т) знак равно 1600+54t2−t3 Н(0) знак равно 1600+54(0)2−(0)3 знак равно 1600 Таким образом, y-пересечение N находится в у=1600. Затем найдите значение y точки перегиба. Заменять т=18 в N(t). Н(т) знак равно 1600+54t2−t3 Н(18) знак равно 1600+54(18)2−(18)3 знак равно 13 264 Следовательно, точка перегиба находится в (18,13264). Теперь найдите значение y в конечной точке интервала. Заменять т=36 в N(t). Н(т) знак равно 1600+54t2−t3 Н(36) знак равно 1600+54(36)2−(36)3 знак равно 24,928 Следовательно, N(t) имеет конечную точку (36,24928) Сюжет (0,1600), (18,13264), и (36,24928) на графике. На графике показаны три точки правильно. 036025,000xy Система координат имеет горизонтальную ось X, отмеченную от 0 до 36 дюймов. с шагом 4 и вертикальная ось Y, отмеченная от 0 до 25000 в с шагом 2500. Наносятся следующие точки: (0, 1600), (18, 13264), (36, 24928). Чтобы нарисовать график Н'(т), сначала найдите y-перехват. Подставьте 0 вместо t в Н'(т). Н'(т) знак равно 108т−3т2 Н'(0) знак равно 108(0)−3(0)2 знак равно 0 Таким образом, Н'(т) имеет точки пересечения x и y в точках (0,0). Затем найдите значение y, где Н'(т) имеет максимум. С Н'(т) имеет максимум в т=18, Заменять 18 в для т в Н'(т). Н'(т) знак равно 108т−3т2 Н'(18) знак равно 108(18)−3(18)2 знак равно 972 Следовательно, Н'(т) имеет максимум в (18 972). Наконец, определите y-значение Н'(т) в конечной точке интервала. Н'(т) знак равно 108т−3т2 Н'(36) знак равно 108(36)−3(36)2 знак равно 0 Следовательно, Н'(т) имеет конечную точку (36,0). Участок (0,0), (18 972), и (36,0) в той же системе координат, что и N(t). Все шесть точек показано на графике справа. 036025,000xy Н Н’ Система координат имеет горизонтальную ось X, отмеченную от 0 до 36 дюймов. с шагом 4 и вертикальная ось Y, отмеченная от 0 до 25000 в с шагом 2500. Следующие точки нанесены на график и обозначены N: (0, 1600), (18, 13264), (36, 249)28). Следующие пункты нанесено и помечено N штрихом: (0, 0), (18, 972), (36, 0).