График онлайн построение: Построение графика функции онлайн

Построение графиков онлайн на миллиметровке. Строим график функций онлайн

К сожалению, не все студенты и школьники знают и любят алгебру, но готовить домашние задания, решать контрольные и сдавать экзамены приходится каждому. Особенно трудно многим даются задачи на построение графиков функций: если где-то что-то не понял, не доучил, упустил — ошибки неизбежны. Но кому же хочется получать плохие оценки?

Не желаете пополнить когорту хвостистов и двоечников? Для этого у вас есть 2 пути: засесть за учебники и восполнить пробелы знаний либо воспользоваться виртуальным помощником — сервисом автоматического построения графиков функций по заданным условиям. С решением или без. Сегодня мы познакомим вас с несколькими из них.

Лучшее, что есть в Desmos.com, это гибко настраиваемый интерфейс, интерактивность, возможность разносить результаты по таблицам и бесплатно хранить свои работы в базе ресурса без ограничений по времени. А недостаток — в том, что сервис не полностью переведен на русский язык.

Grafikus.ru

Grafikus.ru — еще один достойный внимания русскоязычный калькулятор для построения графиков. Причем он строит их не только в двухмерном, но и в трехмерном пространстве.

Вот неполный перечень заданий, с которыми этот сервис успешно справляется:

• Черчение 2D-графиков простых функций: прямых, парабол, гипербол, тригонометрических, логарифмических и т. д.
• Черчение 2D-графиков параметрических функций: окружностей, спиралей, фигур Лиссажу и прочих.
• Черчение 2D-графиков в полярных координатах.
• Построение 3D-поверхностей простых функций.
• Построение 3D-поверхностей параметрических функций.

Готовый результат открывается в отдельном окне. Пользователю доступны опции скачивания, печати и копирования ссылки на него. Для последнего придется авторизоваться на сервисе через кнопки соцсетей.

Координатная плоскость Grafikus.ru поддерживает изменение границ осей, подписей к ним, шага сетки, а также — ширины и высоты самой плоскости и размера шрифта.

Самая сильная сторона Grafikus.ru — возможность построения 3D-графиков. В остальном он работает не хуже и не лучше, чем ресурсы-аналоги.

Выберем на плоскости прямоугольную систему координат и будем откладывать на оси абсцисс значения аргумента х , а на оси ординат — значения функции у = f (х) .

Графиком функции y = f(x) называется множество всех точек, у которых абсциссы принадлежат области определения функции, а ординаты равны соответствующим значениям функции.

Другими словами, график функции y = f (х) — это множество всех точек плоскости, координаты х, у которых удовлетворяют соотношению y = f(x) .

На рис. 45 и 46 приведены графики функций у = 2х + 1 и у = х 2 — 2х .

Строго говоря, следует различать график функции (точное математическое определение которого было дано выше) и начерченную кривую, которая всегда дает лишь более или менее точный эскиз графика (да и то, как правило, не всего графика, а лишь его части, расположенного в конечной части плоскости).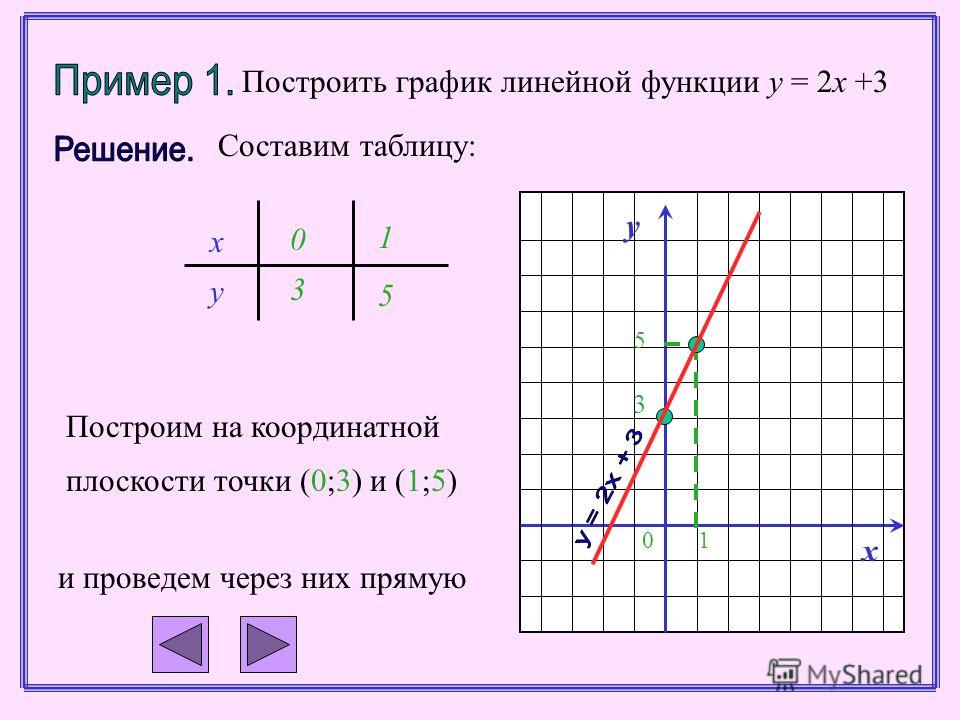

В дальнейшем, однако, мы обычно будем говорить «график», а не «эскиз графика».

С помощью графика можно находить значение функции в точке. Именно, если точка х = а принадлежит области определения функции y = f(x) , то для нахождения числа f(а) (т. е. значения функции в точке х = а ) следует поступить так. Нужно через точку с абсциссой х = а провести прямую, параллельную оси ординат; эта прямая пересечет график функции y = f(x) в одной точке; ордината этой точки и будет, в силу определения графика, равна f(а) (рис. 47).

Например, для функции f(х) = х 2 — 2x с помощью графика (рис. 46) находим f(-1) = 3, f(0) = 0, f(1) = -l, f(2) = 0 и т. д.

График функции наглядно иллюстрирует поведение и свойства функции. Например, из рассмотрения рис. 46 ясно, что функция у = х 2 — 2х принимает положительные значения при х и при х > 2 , отрицательные — при 0 наименьшее значение функция у = х 2 — 2х принимает при х = 1 .

Для построения графика функции f(x) нужно найти все точки плоскости, координаты х , у которых удовлетворяют уравнению y = f(x) . В большинстве случаев это сделать невозможно, так как таких точек бесконечно много. Поэтому график функции изображают приблизительно — с большей или меньшей точностью. Самым простым является метод построения графика по нескольким точкам. Он состоит в том, что аргументу х придают конечное число значений — скажем, х 1 , х 2 , x 3 ,…, х k и составляют таблицу, в которую входят выбранные значения функции.

Таблица выглядит следующим образом:

Составив такую таблицу, мы можем наметить несколько точек графика функции y = f(x) . Затем, соединяя эти точки плавной линией, мы и получаем приблизительный вид графика функции y = f(x).

Следует, однако, заметить, что метод построения графика по нескольким точкам очень ненадежен. В самом деле поведение графика между намеченными точками и поведение его вне отрезка между крайними из взятых точек остается неизвестным.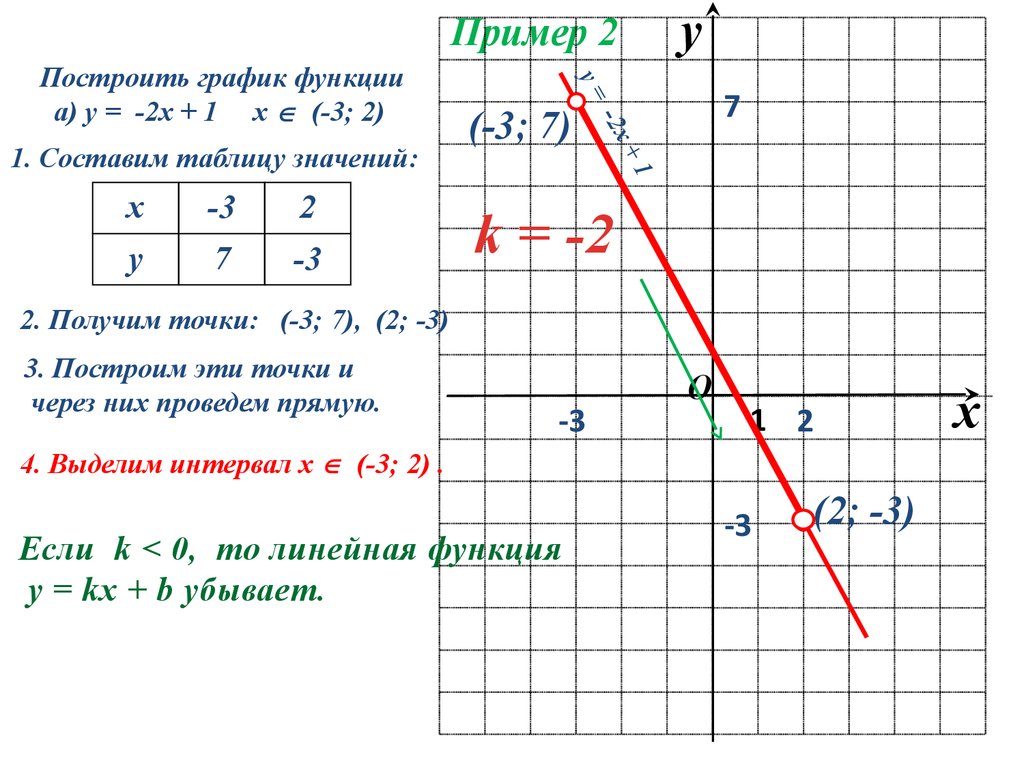

Пример 1 . Для построения графика функции y = f(x) некто составил таблицу значений аргумента и функции:

Соответствующие пять точек показаны на рис. 48.

На основании расположения этих точек он сделал вывод, что график функции представляет собой прямую (показанную на рис. 48 пунктиром). Можно ли считать этот вывод надежным? Если нет дополнительных соображений, подтверждающих этот вывод, его вряд ли можно считать надежным. надежным.

Для обоснования своего утверждения рассмотрим функцию

.

Вычисления показывают, что значения этой функции в точках -2, -1, 0, 1, 2 как раз описываются приведенной выше таблицей. Однако график этой функции вовсе не является прямой линией (он показан на рис. 49). Другим примером может служить функция y = x + l + sinπx; ее значения тоже описываются приведенной выше таблицей.

Эти примеры показывают, что в «чистом» виде метод построения графика по нескольким точкам ненадежен. Поэтому для построения графика заданной функции,как правило, поступают следующим образом.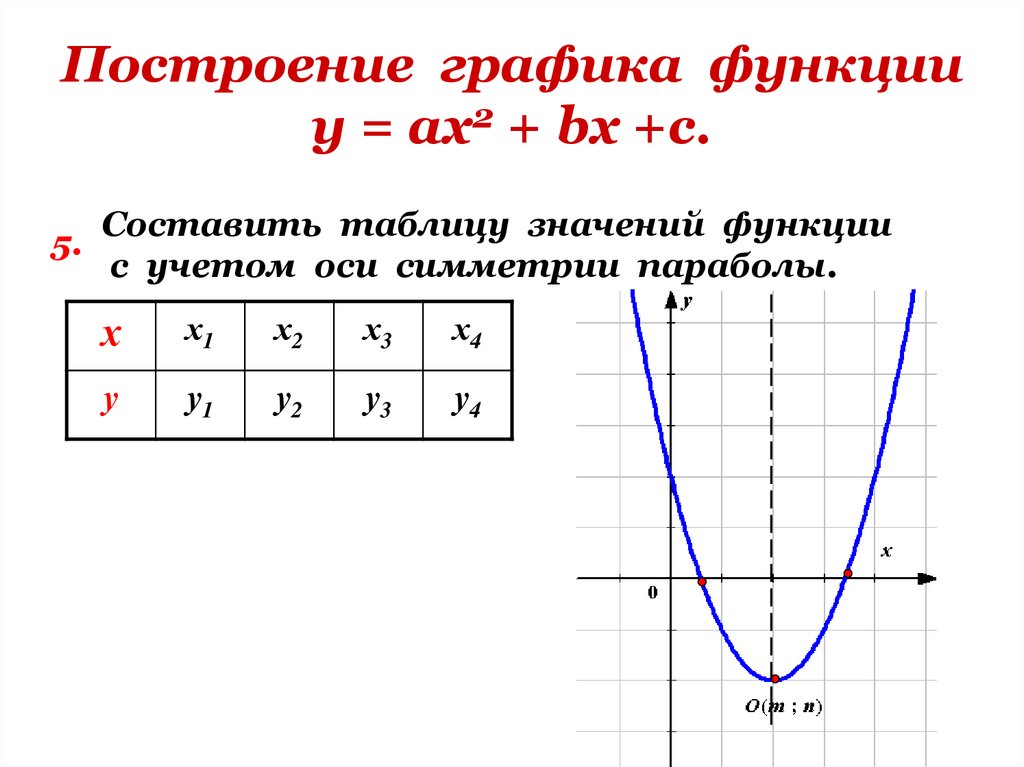 Сначала изучают свойства данной функции, с помощью которых можно построить эскиз графика. Затем, вычисляя значения функции в нескольких точках (выбор которых зависит от установленных свойств функции), находят соответствующие точки графика. И, наконец, через построенные точки проводят кривую, используя свойства данной функции.

Некоторые (наиболее простые и часто используемые) свойства функций, применяемые для нахождения эскиза графика, мы рассмотрим позже, а сейчас разберем некоторые часто применяемые способы построения графиков.

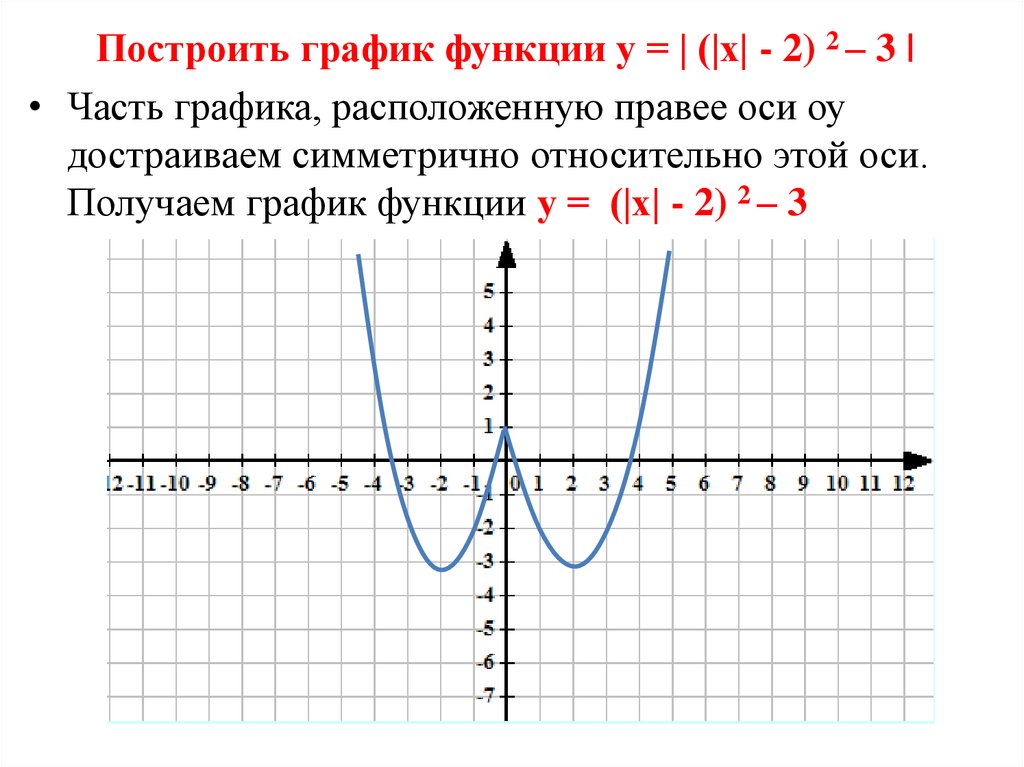
График функции у = |f(x)|.

Нередко приходится строить график функции y = |f(x) |, где f(х) — заданная функция. Напомним, как это делается. По определению абсолютной величины числа можно написать

Это значит, что график функции y =|f(x)| можно получить из графика, функции y = f(x) следующим образом: все точки графика функции у = f(х) , у которых ординаты неотрицательны, следует оставить без изменения; далее, вместо точек графика функции y = f(x) , имеющих отрицательные координаты, следует построить соответствующие точки графика функции

у = -f(x) (т.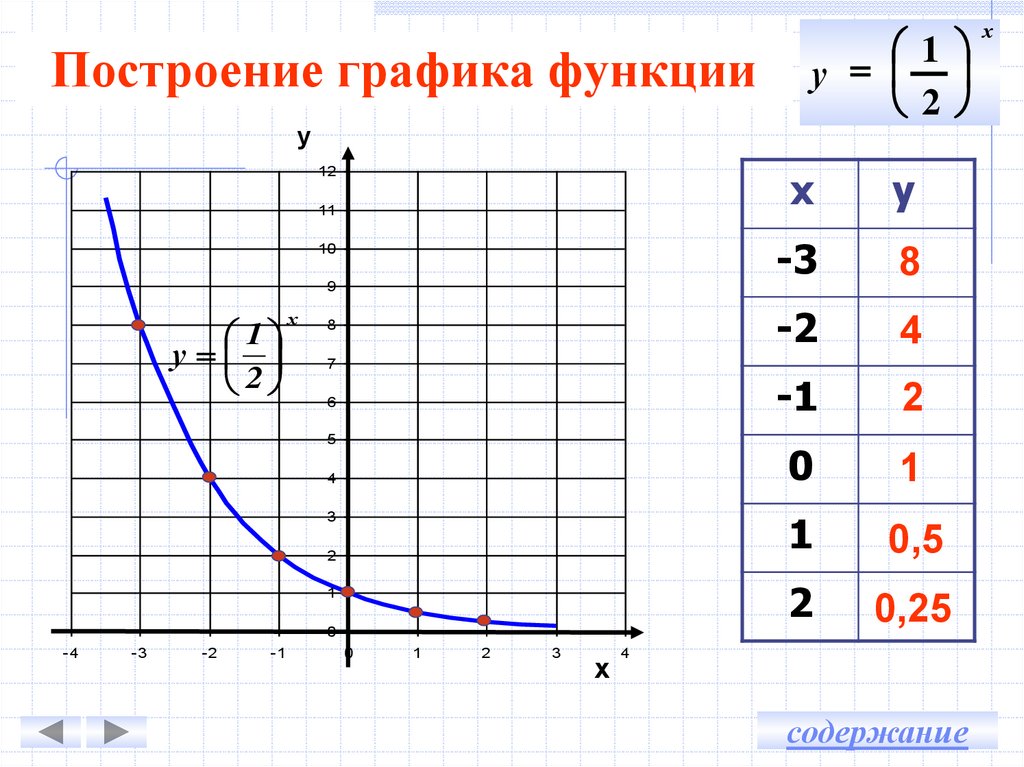 е. часть графика функции
y = f(x) , которая лежит ниже оси х, следует симметрично отразить относительно оси х ).

Пример 2. Построить график функции у = |х|.

Берем график функции у = х (рис. 50, а) и часть этого графика при х (лежащую под осью х ) симметрично отражаем относительно оси х . В результате мы и получаем график функции у = |х| (рис. 50, б).

Пример 3 . Построить график функции y = |x 2 — 2x|.

Сначала построим график функции y = x 2 — 2x. График этой функции — парабола, ветви которой направлены вверх, вершина параболы имеет координаты (1; -1), ее график пересекает ось абсцисс в точках 0 и 2. На промежутке (0; 2) фукция принимает отрицательные значения, поэтому именно эту часть графика симметрично отразим относительно оси абсцисс. На рисунке 51 построен график функции

у = |х 2 -2х| , исходя из графика функции у = х 2 — 2x

График функции y = f(x) + g(x)

Рассмотрим задачу построения графика функции y = f(x) + g(x).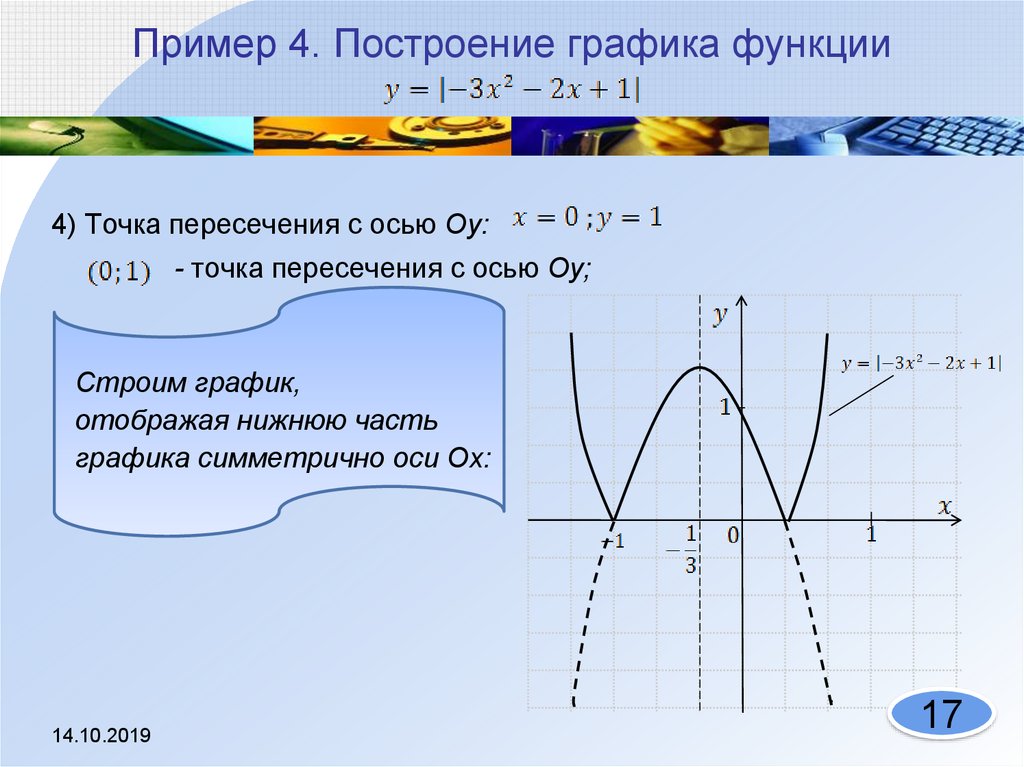 если заданы графики функций y = f(x) и y = g(x) .

Заметим, что областью определения функции y = |f(x) + g(х)| является множество всех тех значений х, для которых определены обе функции y = f{x) и у = g(х), т. е. эта область определения представляет собой пересечение областей определения, функций f{x) и g{x).

Пусть точки (х 0 , y 1 ) и (х 0 , у 2 ) соответственно принадлежат графикам функций y = f{x) и y = g(х) , т. е. y 1 = f(x 0), y 2 = g(х 0). Тогда точка (x0;. y1 + y2) принадлежит графику функции

у = f(х) + g(х) (ибо f(х 0) + g(x 0 ) = y1 +y2 ),. причем любая точка графика функции y = f(x) + g(x) может быть получена таким образом. Следовательно, график функции у = f(х) + g(x) можно получить из графиков функций y = f(x) . и y = g(х) заменой каждой точки (х n , у 1) графика функции y = f(x) точкой (х n , y 1 + y 2), где у 2 = g(x n ), т. е. сдвигом каждой точки (х n , у 1 ) графика функции y = f(x) вдоль оси у на величину y 1 = g(х n ). При этом рассматриваются только такие точки х n для которых определены обе функции y = f(x) и y = g(x) .

Такой метод построения графика функции y = f(x) + g(х ) называется сложением графиков функций y = f(x) и y = g(x)

Пример 4 . На рисунке методом сложения графиков построен график функции

y = x + sinx .

При построении графика функции y = x + sinx мы полагали, что f(x) = x, а g(x) = sinx. Для построения графика функции выберем точки с aбциссами -1,5π, -, -0,5, 0, 0,5,, 1,5, 2. Значения f(x) = x, g(x) = sinx, y = x + sinx вычислим в выбранных точках и результаты поместим в таблице.

Построение графиков функций, содержащих модули, обычно вызывает немалые затруднения у школьников. Однако, все не так плохо. Достаточно запомнить несколько алгоритмов решения таких задач, и вы сможете без труда построить график даже самой на вид сложной функции. Давайте разберемся, что же это за алгоритмы.

1. Построение графика функции y = |f(x)|

Заметим, что множество значений функций y = |f(x)| : y ≥ 0. Таким образом, графики таких функций всегда расположены полностью в верхней полуплоскости.

Построение графика функции y = |f(x)| состоит из следующих простых четырех этапов.

1) Построить аккуратно и внимательно график функции y = f(x).

2) Оставить без изменения все точки графика, которые находятся выше оси 0x или на ней.

3) Часть графика, которая лежит ниже оси 0x, отобразить симметрично относительно оси 0x.

Пример 1. Изобразить график функции y = |x 2 – 4x + 3|

1) Строим график функции y = x 2 – 4x + 3. Очевидно, что график данной функции – парабола. Найдем координаты всех точек пересечения параболы с осями координат и координаты вершины параболы.

x 2 – 4x + 3 = 0.

x 1 = 3, x 2 = 1.

Следовательно, парабола пересекает ось 0x в точках (3, 0) и (1, 0).

y = 0 2 – 4 · 0 + 3 = 3.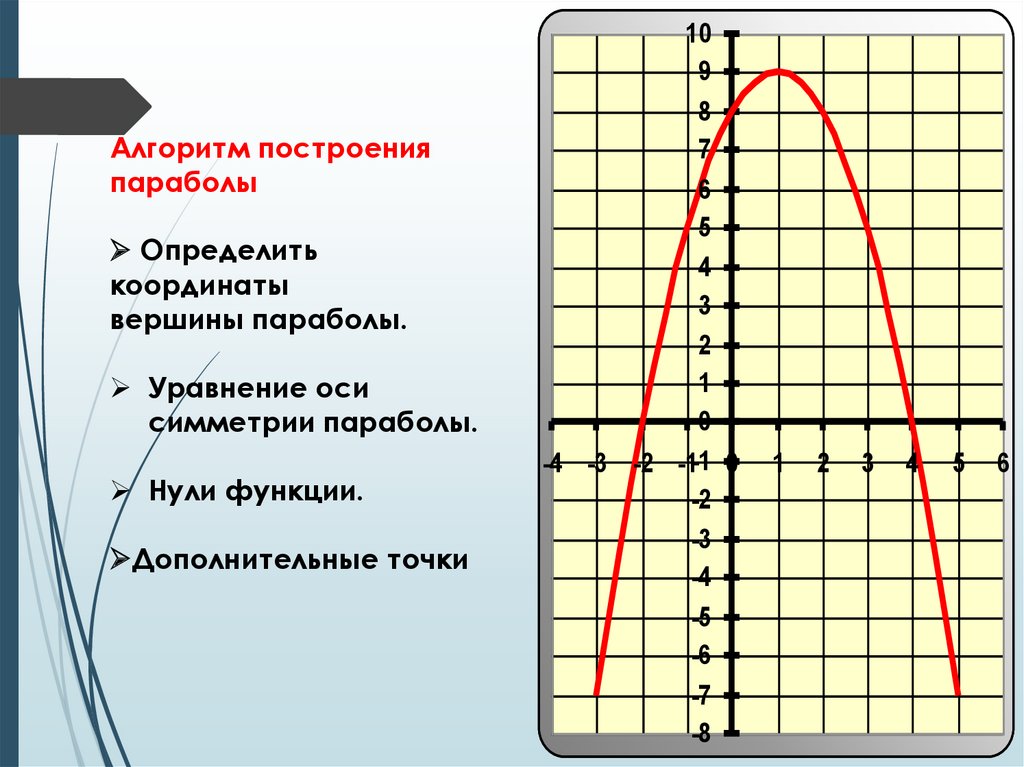

Следовательно, парабола пересекает ось 0y в точке (0, 3).

Координаты вершины параболы:

x в = -(-4/2) = 2, y в = 2 2 – 4 · 2 + 3 = -1.

Следовательно, точка (2, -1) является вершиной данной параболы.

Рисуем параболу, используя полученные данные (рис. 1)

2) Часть графика, лежащую ниже оси 0x, отображаем симметрично относительно оси 0x.

3) Получаем график исходной функции (рис. 2 , изображен пунктиром).

2. Построение графика функции y = f(|x|)

Заметим, что функции вида y = f(|x|) являются четными:

y(-x) = f(|-x|) = f(|x|) = y(x). Значит, графики таких функций симметричны относительно оси 0y.

Построение графика функции y = f(|x|) состоит из следующей несложной цепочки действий.

1) Построить график функции y = f(x).

2) Оставить ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.

3) Отобразить указанную в пункте (2) часть графика симметрично оси 0y.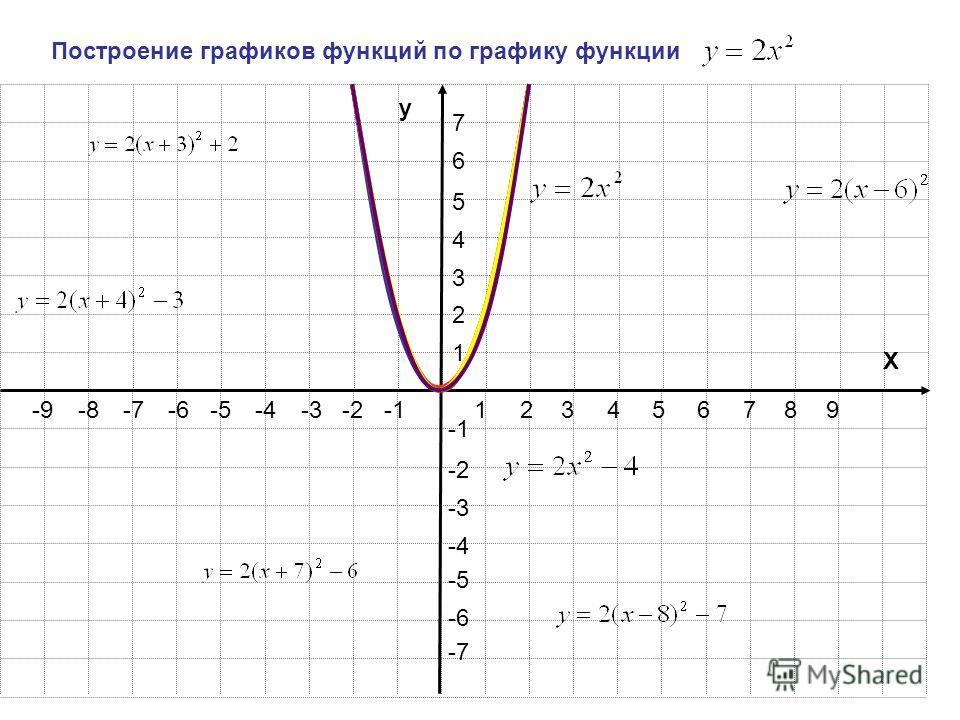

4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).

Пример 2. Изобразить график функции y = x 2 – 4 · |x| + 3

Так как x 2 = |x| 2 , то исходную функцию можно переписать в следующем виде: y = |x| 2 – 4 · |x| + 3. А теперь можем применять предложенный выше алгоритм.

1) Строим аккуратно и внимательно график функции y = x 2 – 4 · x + 3 (см. также рис. 1 ).

2) Оставляем ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.

3) Отображаем правую часть графика симметрично оси 0y.

(рис. 3) .

Пример 3. Изобразить график функции y = log 2 |x|

Применяем схему, данную выше.

1) Строим график функции y = log 2 x (рис. 4) .

3. Построение графика функции y = |f(|x|)|

Заметим, что функции вида y = |f(|x|)| тоже являются четными. Действительно, y(-x) = y = |f(|-x|)| = y = |f(|x|)| = y(x), и поэтому, их графики симметричны относительно оси 0y.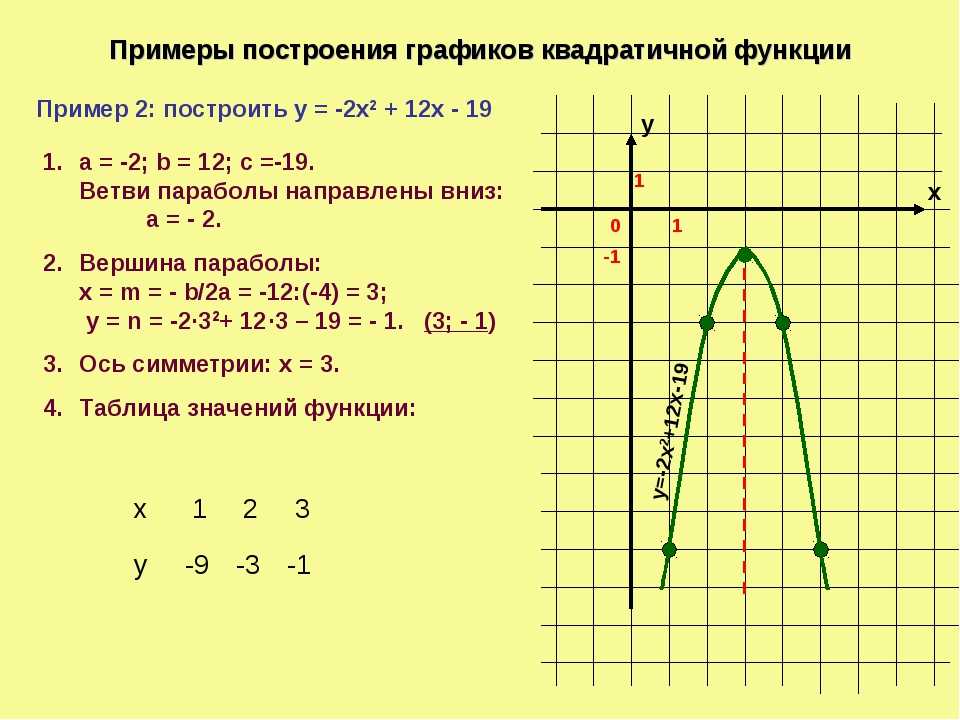 Множество значений таких функций: y ≥ 0. Значит, графики таких функций расположены полностью в верхней полуплоскости.

Чтобы построить график функции y = |f(|x|)|, необходимо:

1) Построить аккуратно график функции y = f(|x|).

2) Оставить без изменений ту часть графика, которая находится выше оси 0x или на ней.

3) Часть графика, расположенную ниже оси 0x, отобразить симметрично относительно оси 0x.

4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).

Пример 4. Изобразить график функции y = |-x 2 + 2|x| – 1|.

1) Заметим, что x 2 = |x| 2 . Значит, вместо исходной функции y = -x 2 + 2|x| – 1

можно использовать функцию y = -|x| 2 + 2|x| – 1, так как их графики совпадают.

Строим график y = -|x| 2 + 2|x| – 1. Для этого применяем алгоритм 2.

a) Строим график функции y = -x 2 + 2x – 1 (рис. 6) .

b) Оставляем ту часть графика, которая расположена в правой полуплоскости.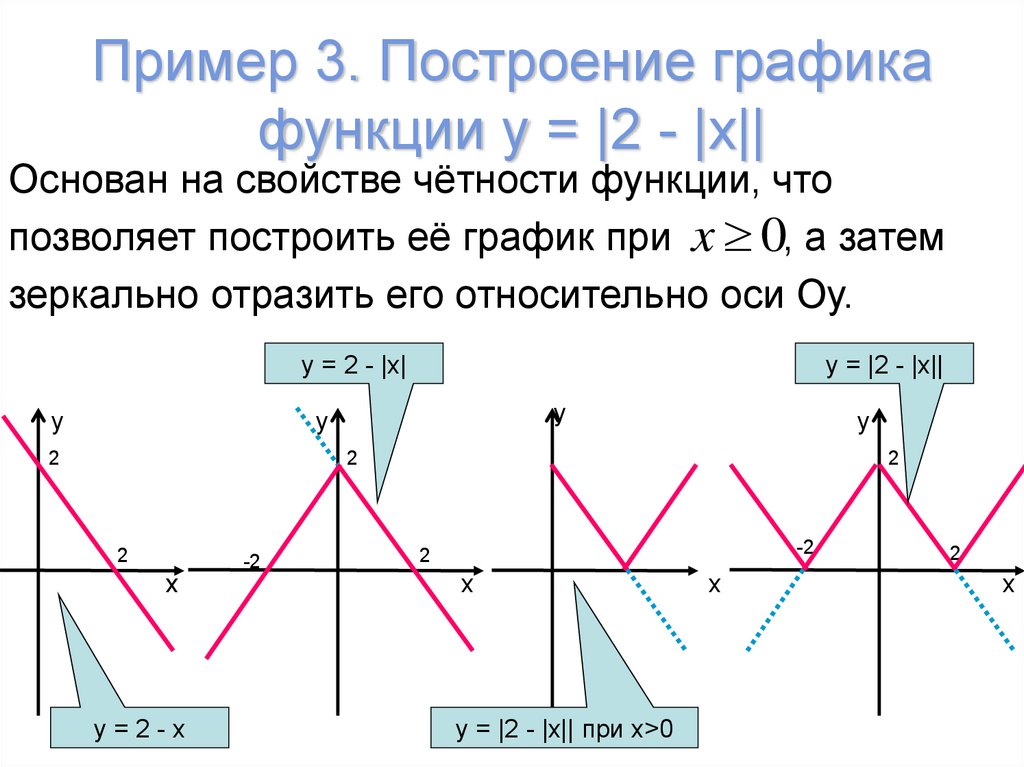

c) Отображаем полученную часть графика симметрично оси 0y.

d) Полученный график изображен на рисунке пунктиром (рис. 7) .

2) Выше оси 0х точек нет, точки на оси 0х оставляем без изменения.

3) Часть графика, расположенную ниже оси 0x, отображаем симметрично относительно 0x.

4) Полученный график изображен на рисунке пунктиром (рис. 8) .

Пример 5. Построить график функции y = |(2|x| – 4) / (|x| + 3)|

1) Сначала необходимо построить график функции y = (2|x| – 4) / (|x| + 3). Для этого возвращаемся к алгоритму 2.

a) Аккуратно строим график функции y = (2x – 4) / (x + 3) (рис. 9) .

Заметим, что данная функция является дробно-линейной и ее график есть гипербола. Для построения кривой сначала необходимо найти асимптоты графика. Горизонтальная – y = 2/1 (отношение коэффициентов при x в числителе и знаменателе дроби), вертикальная – x = -3.

2) Ту часть графика, которая находится выше оси 0x или на ней, оставим без изменений.

3) Часть графика, расположенную ниже оси 0x, отобразим симметрично относительно 0x.

4) Окончательный график изображен на рисунке (рис. 11) .

сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

В золотой век информационных технологий мало кто будет покупать миллиметровку и тратить часы для рисования функции или произвольного набора данных, да и зачем заниматься столь муторной работой, когда можно построить график функции онлайн. Кроме того, подсчитать миллионы значений выражения для правильного отображения практически нереально и сложно, да и несмотря на все усилия получится ломаная линия, а не кривая. Потому компьютер в данном случае – незаменимый помощник.

Что такое график функций

Функция – это правило, по которому каждому элементу одного множества ставится в соответствие некоторый элемент другого множества, например, выражение y = 2x + 1 устанавливает связь между множествами всех значений x и всех значений y, следовательно, это функция.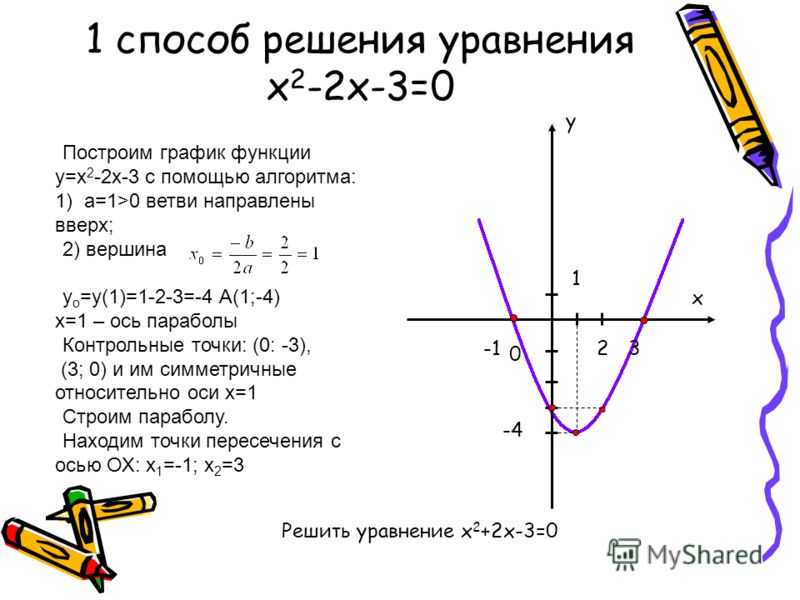 Соответственно, графиком функции будет называться множество точек, координаты которых удовлетворяют заданному выражению.

На рисунке мы видим график функции y = x . Это прямая и у каждой ее точки есть свои координаты на оси X и на оси Y . Исходя из определения, если мы подставим координату X некоторой точки в данное уравнение, то получим координату этой точки на оси Y .

Сервисы для построения графиков функций онлайн

Рассмотрим несколько популярных и лучших по сервисов, позволяющих быстро начертить график функции.

Открывает список самый обычный сервис, позволяющий построить график функции по уравнению онлайн. Umath содержит только необходимые инструменты, такие как масштабирование, передвижение по координатной плоскости и просмотр координаты точки на которую указывает мышь.

Инструкция:

1. Введите ваше уравнение в поле после знака «=».
2. Нажмите кнопку «Построить график» .

Как видите все предельно просто и доступно, синтаксис написания сложных математических функций: с модулем, тригонометрических, показательных — приведен прямо под графиком. Также при необходимости можно задать уравнение параметрическим методом или строить графики в полярной системе координат.

В Yotx есть все функции предыдущего сервиса, но при этом он содержит такие интересные нововведения как создание интервала отображения функции, возможность строить график по табличным данным, а также выводить таблицу с целыми решениями.

Инструкция:

1. Выберите необходимый способ задания графика.
2. Введите уравнение.
3. Задайте интервал.
4. Нажмите кнопку «Построить» .

Для тех, кому лень разбираться, как записать те или иные функции, на этой позиции представлен сервис с возможностью выбирать из списка нужную одним кликом мыши.

Инструкция:

1. Найдите в списке необходимую вам функцию.
2. Щелкните на нее левой кнопкой мыши
3. При необходимости введите коэффициенты в поле «Функция:» .
4. Нажмите кнопку «Построить» .

В плане визуализации есть возможность менять цвет графика, а также скрывать его или вовсе удалять.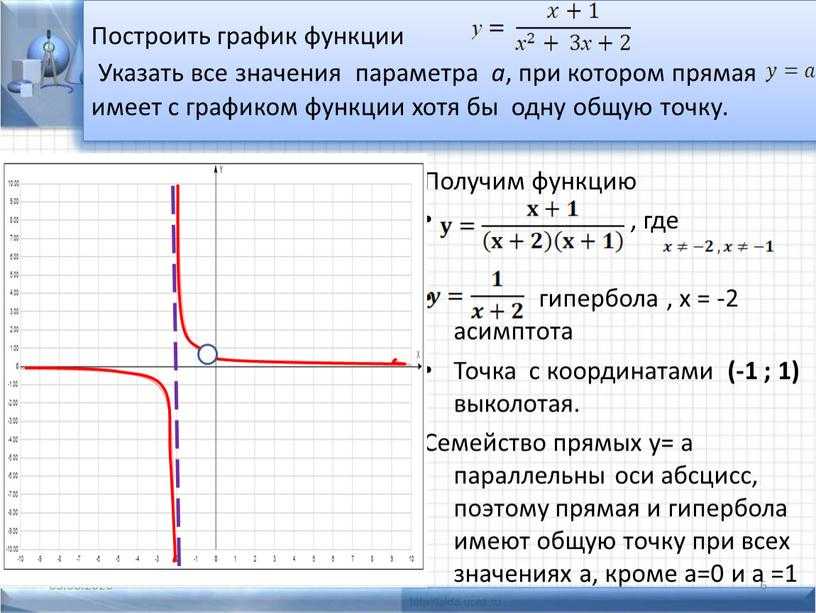

Desmos безусловно – самый навороченный сервис для построения уравнений онлайн. Передвигая курсор с зажатой левой клавишей мыши по графику можно подробно посмотреть все решения уравнения с точностью до 0,001. Встроенная клавиатура позволяет быстро писать степени и дроби. Самым важным плюсом является возможность записывать уравнение в любом состоянии, не приводя к виду: y = f(x).

Инструкция:

1. В левом столбце кликните правой кнопкой мыши по свободной строке.
2. В нижнем левом углу нажмите на значок клавиатуры.
3. На появившейся панели наберите нужное уравнение (для написания названий функций перейдите в раздел «A B C»).
4. График строится в реальном времени.

Визуализация просто идеальная, адаптивная, видно, что над приложением работали дизайнеры. Из плюсов можно отметить огромное обилие возможностей, для освоения которых можно посмотреть примеры в меню в верхнем левом углу.

Сайтов для построения графиков функций великое множество, однако каждый волен выбирать для себя исходя из требуемого функционала и личных предпочтений. Список лучших был сформирован так, чтобы удовлетворить требования любого математика от мала до велика. Успехов вам в постижении «царицы наук»!

Y 4 x 4 xy график. Построение графиков онлайн. Построение графика линейной функции

«Натуральный логарифм» — 0,1. Натуральные логарифмы. 4. «Логарифмический дартс». 0,04. 7. 121.

«Степенная функция 9 класс» — У. Кубическая парабола. У = х3. 9 класс учитель Ладошкина И.А. У = х2. Гипербола. 0. У = хn, у = х-n где n – заданное натуральное число. Х. Показатель – четное натуральное число (2n).

«Квадратичная функция» — 1 Определение квадратичной функции 2 Свойства функции 3 Графики функции 4 Квадратичные неравенства 5 Вывод. Свойства: Неравенства: Подготовил ученик 8А класса Герлиц Андрей. План: График: -Промежутки монотонности при а > 0 при а

«Квадратичная функция и её график» — Решение.у=4x А(0,5:1) 1=1 А-принадлежит. При а=1 формула у=аx принимает вид.

«8 класс квадратичная функция» — 1) Построить вершину параболы.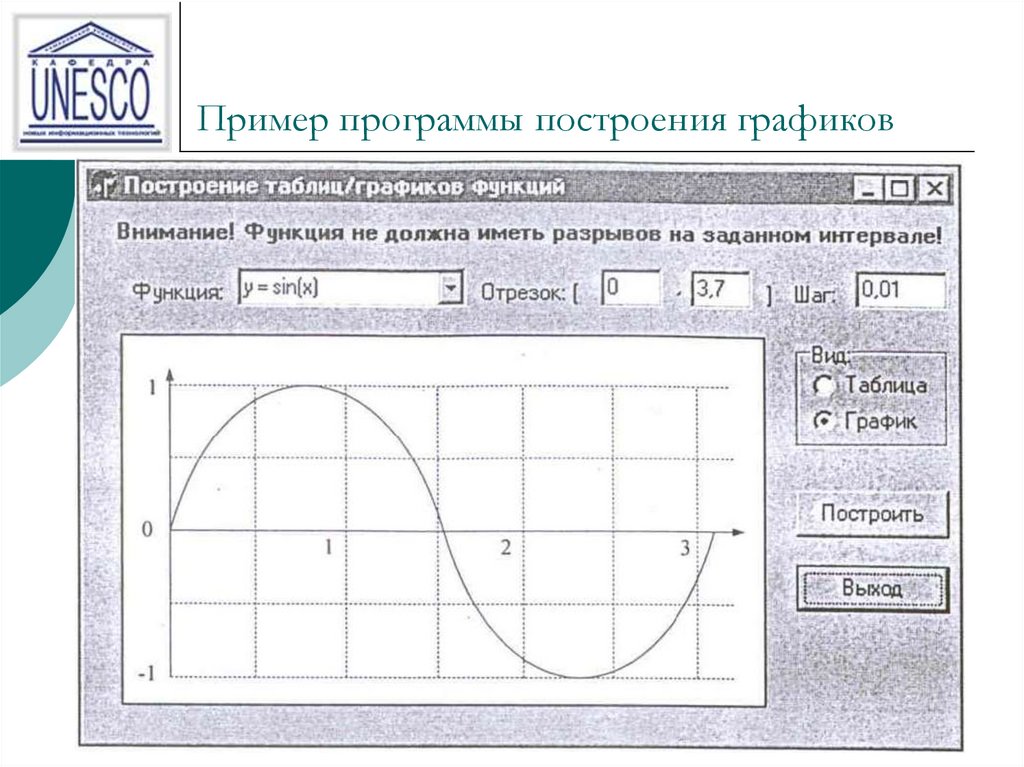 Построение графика квадратичной функции. x. -7. Построить график функции. Алгебра 8 класс Учитель 496 школы Бовина Т. В. -1. План построения. 2) Построить ось симметрии x=-1. y.

Построение графиков функций — одна из возможностей Excel. В этой статье мы рассмотрим процесс построение графиков некоторых математических функций: линейной, квадратичной и обратной пропорциональности.

Функция, это множество точек (x, y), удовлетворяющее выражению y=f(x). Поэтому, нам необходимо заполнить массив таких точек, а Excel построит нам на их основе график функции.

1) Рассмотрим пример построения графика линейной функции: y=5x-2

Графиком линейной функции является прямая, которую можно построить по двум точкам. Создадим табличку

В нашем случае y=5x-2. В ячейку с первым значением y введем формулу: =5*D4-2 . В другую ячейку формулу можно ввести аналогично (изменив D4 на D5 ) или использовать маркер автозаполнения.

В итоге мы получим табличку:

Теперь можно приступать к созданию графика.

Выбираем: ВСТАВКА — > ТОЧЕЧНАЯ -> ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ И МАРКЕРАМИ (рекомендую использовать именно этот тип диаграммы)

Появиться пустая область диаграмм. Нажимаем кнопку ВЫБРАТЬ ДАННЫЕ

Выберем данные: диапазон ячеек оси абсцисс (х) и оси ординат (у). В качестве имени ряда можем ввести саму функцию в кавычках «y=5x-2» или что-то другое. Вот что получилось:

Нажимаем ОК. Перед нами график линейной функции.

2) Рассмотрим процесс построения графика квадратичной функции — параболы y=2x 2 -2

Параболу по двум точкам уже не построить, в отличии от прямой.

Зададим интервал на оси x , на котором будет строиться наша парабола. Выберу [-5; 5].

Задам шаг. Чем меньше шаг, тем точнее будет построенный график. Выберу 0,2 .

Заполняю столбец со значениями х , используя маркер автозаполнения до значения х=5 .

Столбец значений у рассчитывается по формуле: =2*B4^2-2.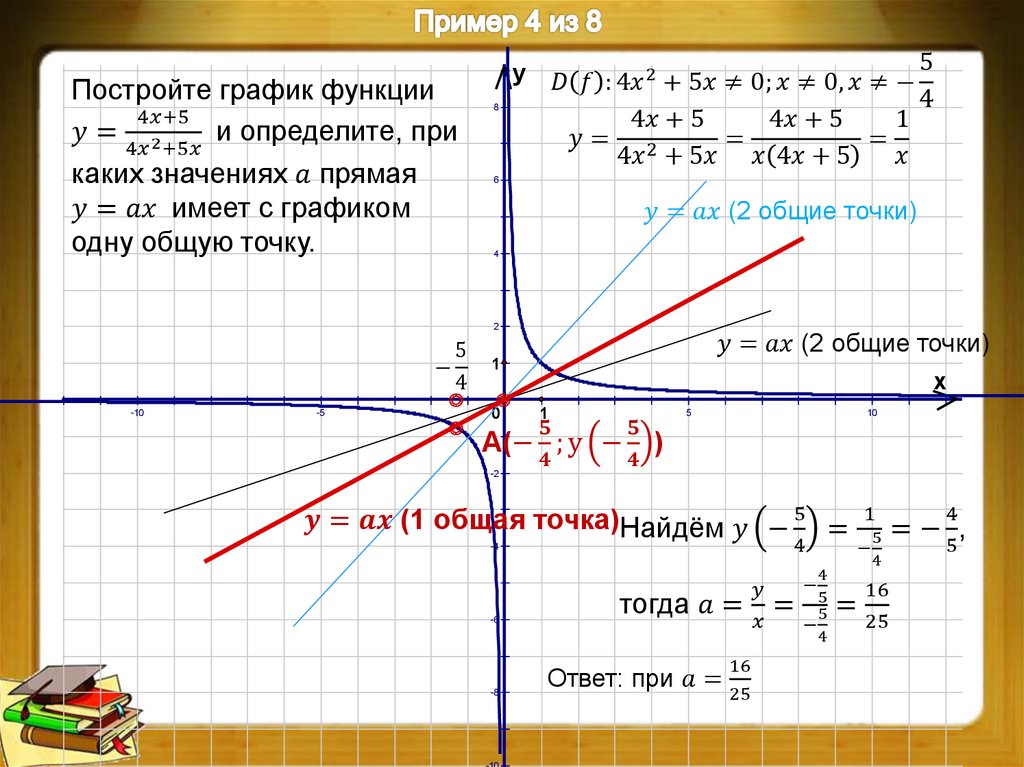 Используя маркер автозаполнения, рассчитываем значения у для остальных х .

Выбираем: ВСТАВКА — > ТОЧЕЧНАЯ -> ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ И МАРКЕРАМИ и действуем аналогично построению графика линейной функции.

Чтобы не было точек на графике, поменяйте тип диаграммы на ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ.

Любые другие графики непрерывных функций строятся аналогично.

3) Если функция кусочная, то необходимо каждый «кусочек» графика объединить в одной области диаграмм.

Рассмотрим это на примере функции у=1/х .

Функция определена на интервалах (- беск;0) и (0; +беск)

Создадим график функции на интервалах: [-4;0) и (0; 4].

Подготовим две таблички, где х изменяется с шагом 0,2 :

Находим значения функции от каждого аргумента х аналогично примерам выше.

На диаграмму вы должны добавить два ряда — для первой и второй таблички соответственно

Получаем график функции y=1/x

В дополнение привожу видео — где показан порядок действий, описанный выше.

В следующей статье расскажу как создать 3-мерные графики в Excel.

Спасибо за внимание!

Выберем на плоскости прямоугольную систему координат и будем откладывать на оси абсцисс значения аргумента х , а на оси ординат — значения функции у = f (х) .

Графиком функции y = f(x) называется множество всех точек, у которых абсциссы принадлежат области определения функции, а ординаты равны соответствующим значениям функции.

Другими словами, график функции y = f (х) — это множество всех точек плоскости, координаты х, у которых удовлетворяют соотношению y = f(x) .

На рис. 45 и 46 приведены графики функций у = 2х + 1 и у = х 2 — 2х .

Строго говоря, следует различать график функции (точное математическое определение которого было дано выше) и начерченную кривую, которая всегда дает лишь более или менее точный эскиз графика (да и то, как правило, не всего графика, а лишь его части, расположенного в конечной части плоскости).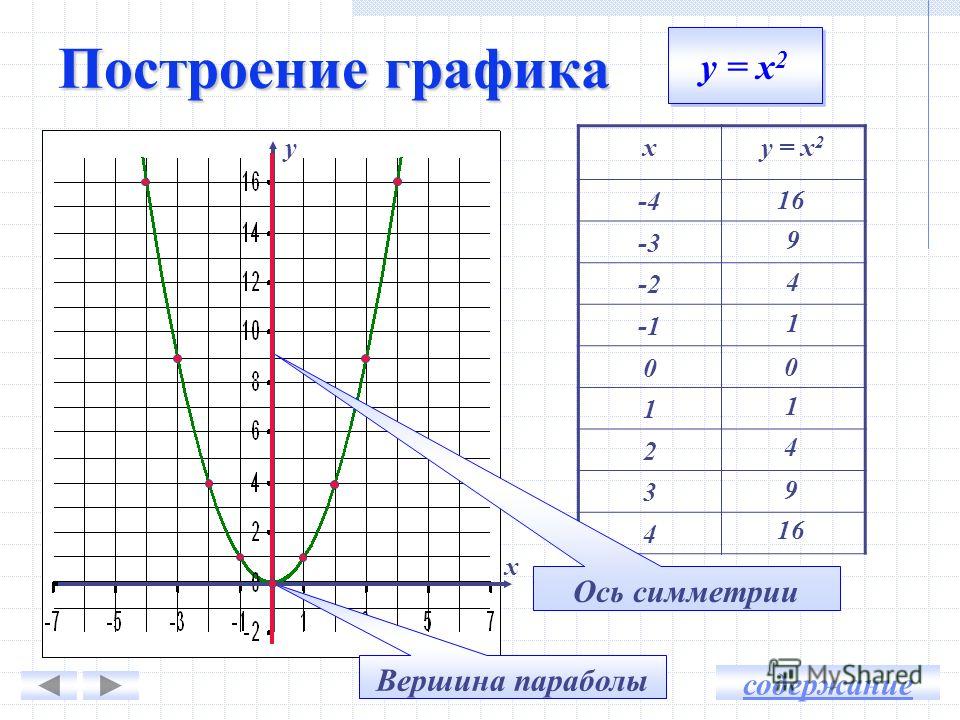 В дальнейшем, однако, мы обычно будем говорить «график», а не «эскиз графика».

С помощью графика можно находить значение функции в точке. Именно, если точка х = а принадлежит области определения функции y = f(x) , то для нахождения числа f(а) (т. е. значения функции в точке х = а ) следует поступить так. Нужно через точку с абсциссой х = а провести прямую, параллельную оси ординат; эта прямая пересечет график функции y = f(x) в одной точке; ордината этой точки и будет, в силу определения графика, равна f(а) (рис. 47).

Например, для функции f(х) = х 2 — 2x с помощью графика (рис. 46) находим f(-1) = 3, f(0) = 0, f(1) = -l, f(2) = 0 и т. д.

График функции наглядно иллюстрирует поведение и свойства функции. Например, из рассмотрения рис. 46 ясно, что функция у = х 2 — 2х принимает положительные значения при х и при х > 2 , отрицательные — при 0 наименьшее значение функция у = х 2 — 2х принимает при х = 1 .

Для построения графика функции f(x) нужно найти все точки плоскости, координаты х , у которых удовлетворяют уравнению y = f(x) . В большинстве случаев это сделать невозможно, так как таких точек бесконечно много. Поэтому график функции изображают приблизительно — с большей или меньшей точностью. Самым простым является метод построения графика по нескольким точкам. Он состоит в том, что аргументу х придают конечное число значений — скажем, х 1 , х 2 , x 3 ,…, х k и составляют таблицу, в которую входят выбранные значения функции.

Таблица выглядит следующим образом:

Составив такую таблицу, мы можем наметить несколько точек графика функции y = f(x) . Затем, соединяя эти точки плавной линией, мы и получаем приблизительный вид графика функции y = f(x).

Следует, однако, заметить, что метод построения графика по нескольким точкам очень ненадежен. В самом деле поведение графика между намеченными точками и поведение его вне отрезка между крайними из взятых точек остается неизвестным.

Пример 1 . Для построения графика функции y = f(x) некто составил таблицу значений аргумента и функции:

Соответствующие пять точек показаны на рис. 48.

На основании расположения этих точек он сделал вывод, что график функции представляет собой прямую (показанную на рис. 48 пунктиром). Можно ли считать этот вывод надежным? Если нет дополнительных соображений, подтверждающих этот вывод, его вряд ли можно считать надежным. надежным.

Для обоснования своего утверждения рассмотрим функцию

.

Вычисления показывают, что значения этой функции в точках -2, -1, 0, 1, 2 как раз описываются приведенной выше таблицей. Однако график этой функции вовсе не является прямой линией (он показан на рис. 49). Другим примером может служить функция y = x + l + sinπx; ее значения тоже описываются приведенной выше таблицей.

Эти примеры показывают, что в «чистом» виде метод построения графика по нескольким точкам ненадежен. Поэтому для построения графика заданной функции,как правило, поступают следующим образом.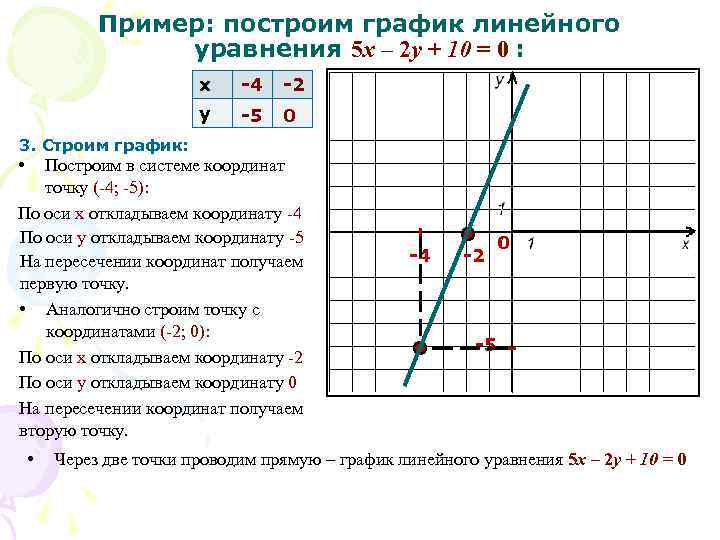 Сначала изучают свойства данной функции, с помощью которых можно построить эскиз графика. Затем, вычисляя значения функции в нескольких точках (выбор которых зависит от установленных свойств функции), находят соответствующие точки графика. И, наконец, через построенные точки проводят кривую, используя свойства данной функции.

Некоторые (наиболее простые и часто используемые) свойства функций, применяемые для нахождения эскиза графика, мы рассмотрим позже, а сейчас разберем некоторые часто применяемые способы построения графиков.

График функции у = |f(x)|.

Нередко приходится строить график функции y = |f(x) |, где f(х) — заданная функция. Напомним, как это делается. По определению абсолютной величины числа можно написать

Это значит, что график функции y =|f(x)| можно получить из графика, функции y = f(x) следующим образом: все точки графика функции у = f(х) , у которых ординаты неотрицательны, следует оставить без изменения; далее, вместо точек графика функции y = f(x) , имеющих отрицательные координаты, следует построить соответствующие точки графика функции у = -f(x) (т. е. часть графика функции
y = f(x) , которая лежит ниже оси х, следует симметрично отразить относительно оси х ).

Пример 2. Построить график функции у = |х|.

Берем график функции у = х (рис. 50, а) и часть этого графика при х (лежащую под осью х ) симметрично отражаем относительно оси х . В результате мы и получаем график функции у = |х| (рис. 50, б).

Пример 3 . Построить график функции y = |x 2 — 2x|.

Сначала построим график функции y = x 2 — 2x. График этой функции — парабола, ветви которой направлены вверх, вершина параболы имеет координаты (1; -1), ее график пересекает ось абсцисс в точках 0 и 2. На промежутке (0; 2) фукция принимает отрицательные значения, поэтому именно эту часть графика симметрично отразим относительно оси абсцисс. На рисунке 51 построен график функции у = |х 2 -2х| , исходя из графика функции у = х 2 — 2x

График функции y = f(x) + g(x)

Рассмотрим задачу построения графика функции y = f(x) + g(x).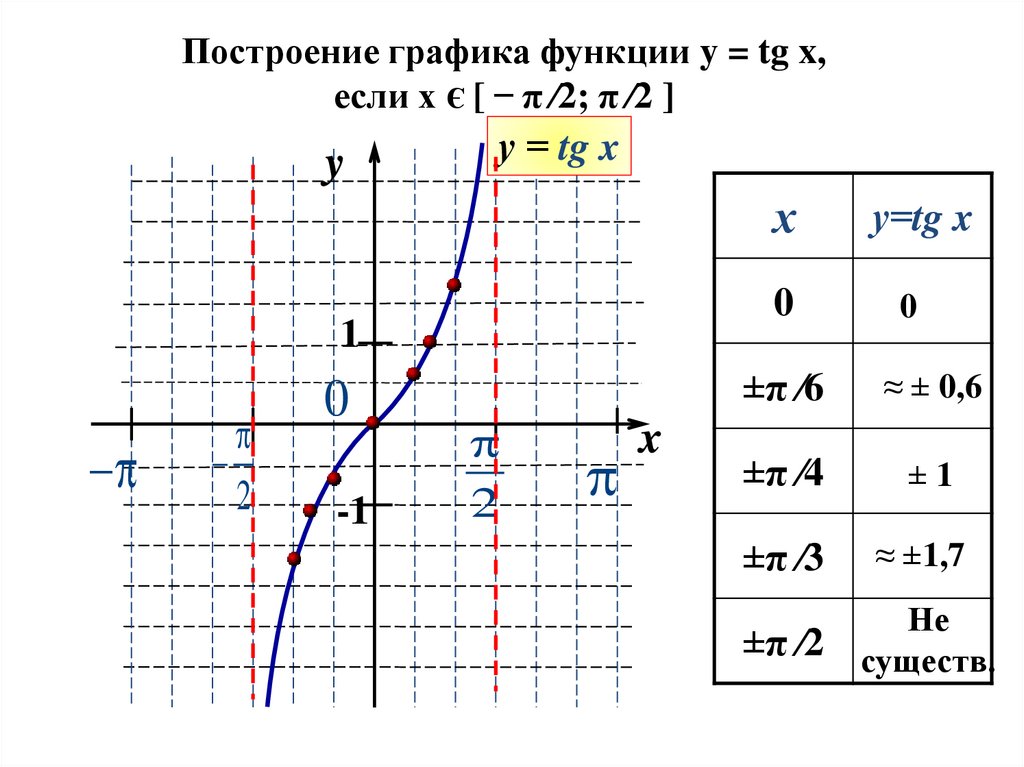 если заданы графики функций y = f(x) и y = g(x) .

Заметим, что областью определения функции y = |f(x) + g(х)| является множество всех тех значений х, для которых определены обе функции y = f{x) и у = g(х), т. е. эта область определения представляет собой пересечение областей определения, функций f{x) и g{x).

Пусть точки (х 0 , y 1 ) и (х 0 , у 2 ) соответственно принадлежат графикам функций y = f{x) и y = g(х) , т. е. y 1 = f(x 0), y 2 = g(х 0). Тогда точка (x0;. y1 + y2) принадлежит графику функции у = f(х) + g(х) (ибо f(х 0) + g(x 0 ) = y1 +y2 ),. причем любая точка графика функции y = f(x) + g(x) может быть получена таким образом. Следовательно, график функции у = f(х) + g(x) можно получить из графиков функций y = f(x) . и y = g(х) заменой каждой точки (х n , у 1) графика функции y = f(x) точкой (х n , y 1 + y 2), где у 2 = g(x n ), т. е. сдвигом каждой точки (х n , у 1 ) графика функции y = f(x) вдоль оси у на величину y 1 = g(х n ). При этом рассматриваются только такие точки х n для которых определены обе функции y = f(x) и y = g(x) .

Такой метод построения графика функции y = f(x) + g(х ) называется сложением графиков функций y = f(x) и y = g(x)

Пример 4 . На рисунке методом сложения графиков построен график функции
y = x + sinx .

При построении графика функции y = x + sinx мы полагали, что f(x) = x, а g(x) = sinx. Для построения графика функции выберем точки с aбциссами -1,5π, -, -0,5, 0, 0,5,, 1,5, 2. Значения f(x) = x, g(x) = sinx, y = x + sinx вычислим в выбранных точках и результаты поместим в таблице.

В золотой век информационных технологий мало кто будет покупать миллиметровку и тратить часы для рисования функции или произвольного набора данных, да и зачем заниматься столь муторной работой, когда можно построить график функции онлайн. Кроме того, подсчитать миллионы значений выражения для правильного отображения практически нереально и сложно, да и несмотря на все усилия получится ломаная линия, а не кривая. Потому компьютер в данном случае – незаменимый помощник.

Что такое график функций

Функция – это правило, по которому каждому элементу одного множества ставится в соответствие некоторый элемент другого множества, например, выражение y = 2x + 1 устанавливает связь между множествами всех значений x и всех значений y, следовательно, это функция. Соответственно, графиком функции будет называться множество точек, координаты которых удовлетворяют заданному выражению.

На рисунке мы видим график функции y = x . Это прямая и у каждой ее точки есть свои координаты на оси X и на оси Y . Исходя из определения, если мы подставим координату X некоторой точки в данное уравнение, то получим координату этой точки на оси Y .

Сервисы для построения графиков функций онлайн

Рассмотрим несколько популярных и лучших по сервисов, позволяющих быстро начертить график функции.

Открывает список самый обычный сервис, позволяющий построить график функции по уравнению онлайн. Umath содержит только необходимые инструменты, такие как масштабирование, передвижение по координатной плоскости и просмотр координаты точки на которую указывает мышь.

Инструкция:

1. Введите ваше уравнение в поле после знака «=».
2. Нажмите кнопку «Построить график» .

Как видите все предельно просто и доступно, синтаксис написания сложных математических функций: с модулем, тригонометрических, показательных — приведен прямо под графиком. Также при необходимости можно задать уравнение параметрическим методом или строить графики в полярной системе координат.

В Yotx есть все функции предыдущего сервиса, но при этом он содержит такие интересные нововведения как создание интервала отображения функции, возможность строить график по табличным данным, а также выводить таблицу с целыми решениями.

Инструкция:

1. Выберите необходимый способ задания графика.
2. Введите уравнение.
3. Задайте интервал.
4. Нажмите кнопку «Построить» .

Для тех, кому лень разбираться, как записать те или иные функции, на этой позиции представлен сервис с возможностью выбирать из списка нужную одним кликом мыши.

Инструкция:

1. Найдите в списке необходимую вам функцию.
2. Щелкните на нее левой кнопкой мыши
3. При необходимости введите коэффициенты в поле «Функция:» .
4. Нажмите кнопку «Построить» .

В плане визуализации есть возможность менять цвет графика, а также скрывать его или вовсе удалять.

Desmos безусловно – самый навороченный сервис для построения уравнений онлайн. Передвигая курсор с зажатой левой клавишей мыши по графику можно подробно посмотреть все решения уравнения с точностью до 0,001. Встроенная клавиатура позволяет быстро писать степени и дроби. Самым важным плюсом является возможность записывать уравнение в любом состоянии, не приводя к виду: y = f(x).

Инструкция:

1. В левом столбце кликните правой кнопкой мыши по свободной строке.
2. В нижнем левом углу нажмите на значок клавиатуры.
3. На появившейся панели наберите нужное уравнение (для написания названий функций перейдите в раздел «A B C»).
4. График строится в реальном времени.

Визуализация просто идеальная, адаптивная, видно, что над приложением работали дизайнеры. Из плюсов можно отметить огромное обилие возможностей, для освоения которых можно посмотреть примеры в меню в верхнем левом углу.

Сайтов для построения графиков функций великое множество, однако каждый волен выбирать для себя исходя из требуемого функционала и личных предпочтений. Список лучших был сформирован так, чтобы удовлетворить требования любого математика от мала до велика. Успехов вам в постижении «царицы наук»!

Бесплатный онлайн-конструктор графиков | Доверяют 11 млн пользователей

Перейти к содержимому

Создайте график бесплатно, не имея опыта проектирования. Piktochart, которому доверяют 11 миллионов пользователей, прост и быстр. Используйте готовый шаблон для создания графиков и диаграмм онлайн без опыта проектирования.

11 миллионов человек во всем мире используют Piktochart

Создайте график и подключите его к Google Sheets

Из необработанных данных вы можете построить график онлайн с помощью Piktochart и сэкономить время. Свяжите свой файл Excel или электронную таблицу Google, чтобы легко создавать диаграммы, которые автоматически обновляются вместе с вашими данными. Объедините различные диаграммы на одной странице, чтобы создать профессионально выглядящую интерактивную информационную панель, готовую к совместному использованию с вашими заинтересованными сторонами.

Выберите один из нескольких форматов, типов диаграмм и бесплатных шаблонов, которые превратят человека, не являющегося дизайнером, в профессионала.

Создайте бесплатную учетную запись

Держите свои графики в соответствии с брендом

Загрузите, затем перетащите свой логотип или снимок экрана вашего веб-сайта, чтобы автоматически извлечь цвета вашего бренда.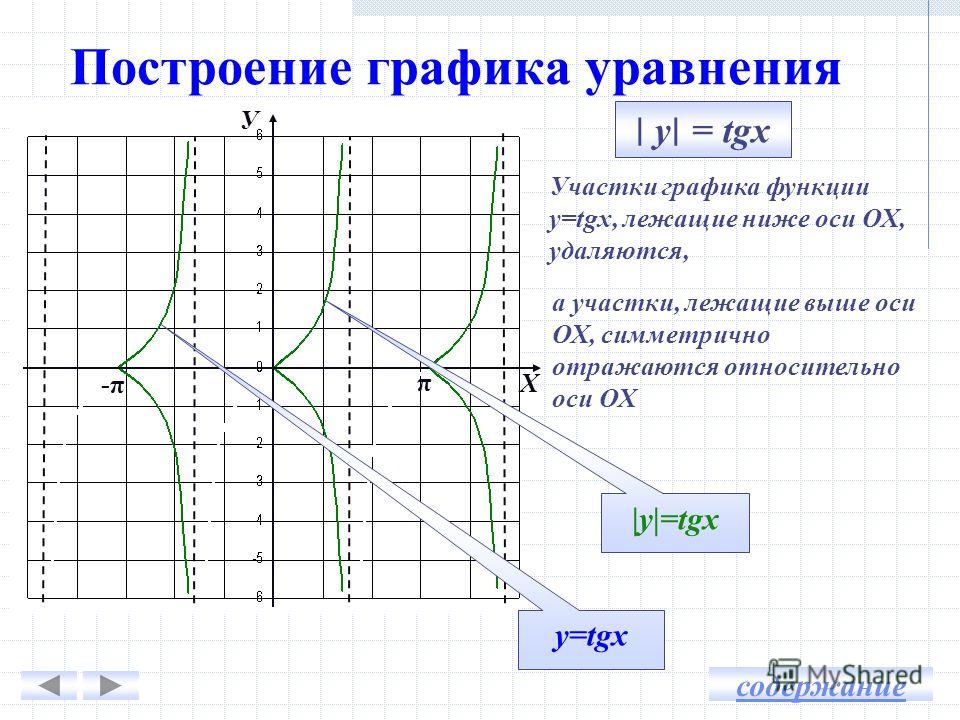 Хотите использовать фирменные шрифты? Без проблем. Ваша пользовательская цветовая палитра и загруженные шрифты всегда будут доступны в редакторе.

Все типы графиков имеют множество параметров настройки, чтобы ваши графики выглядели так, как вы хотите. гистограммы, круговые диаграммы, диаграммы — в галерее есть профессионально разработанные шаблоны для красивой визуализации данных.

Изучите Piktochart прямо сейчас

Диаграммы, графики и диаграммы

Простое переключение между различными типами диаграмм

Нужны ли вам диаграммы, линейные диаграммы, гистограммы, круговые диаграммы или диаграммы любого другого типа, в галерее Piktochart есть предварительные настройки. сделал шаблоны для любого формата. Введите свой ряд данных один раз и посмотрите, как выглядит визуализация данных с использованием различных диаграмм. Если вы вернетесь и решите, что хотите использовать другой тип диаграммы, вы можете использовать наш конструктор диаграмм, чтобы изменить его снова.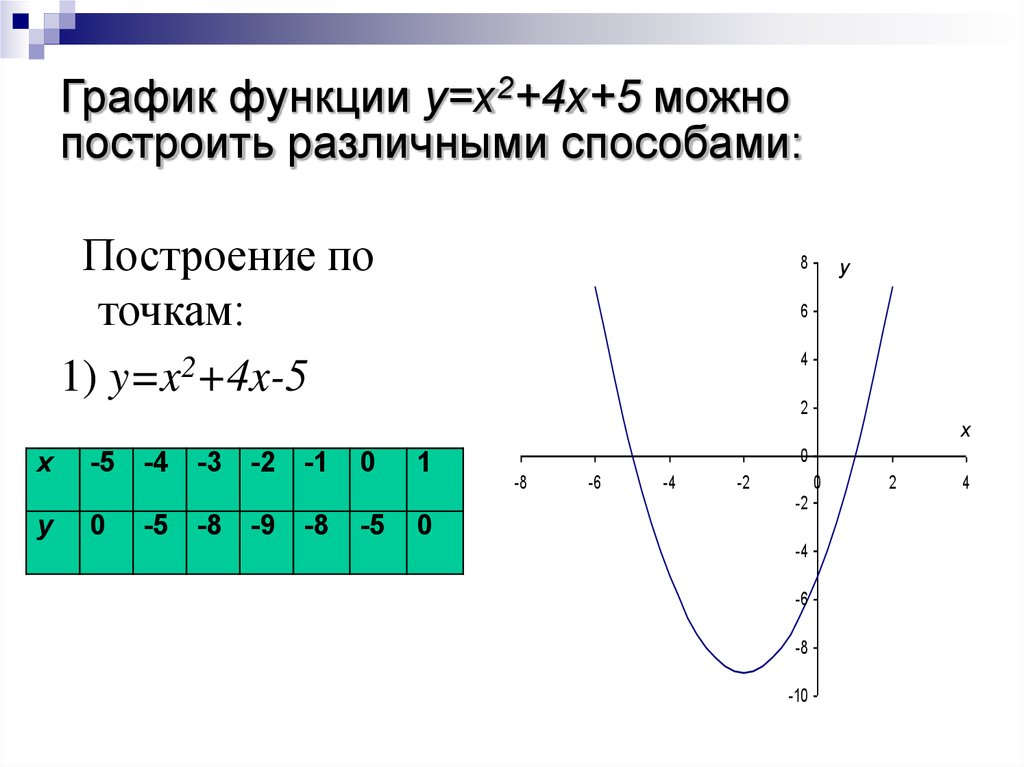

Зарегистрируйтесь бесплатно

Создание контента с помощью бесплатных шаблонов

Добавьте свою диаграмму в любой формат

С помощью нашего онлайн-конструктора диаграмм вы можете легко создавать отчеты, презентации, инфографику (и многое другое), которые произведут впечатление на ваших коллег. Piktochart настолько прост, что им можно сразу пользоваться без обучения. Отредактируйте шаблон диаграммы, разработанный экспертами, или создайте графику с нуля.

Создавайте дизайн с помощью бесплатной библиотеки графики, значков, шрифтов и шаблонов диаграмм, загружайте собственные изображения и создавайте визуальные эффекты без особых усилий. Вы можете просто добавить к своим слайдам круговую диаграмму, столбчатую диаграмму или график другого типа.

Попробуйте прямо сейчас

Создайте один раз, используйте навсегда

С групповой учетной записью нет необходимости тратить часы на повторное создание одного и того же отчета или диаграммы каждую неделю или месяц. Организуйте свои шаблоны и прошлые проекты в папках. Предоставьте любому члену вашей команды возможность перепрофилировать контент на лету, что в конечном итоге сэкономит их время.

Создать сейчас

Добавьте свои собственные графики в любой шаблон

Годовая информационная панель

Панель управления наймом

Маркетинговый прогресс

Ежемесячный маркетинговый отчет

Квартальная панель продаж

Вебинар

Отзывы

Эрика Барто

Специалист по отбору, тестированию и оценке, Valero Energy Corporation

«Piktochart — это мой инструмент, когда я ищу способ обобщить данные, которые нашему высшему руководству будет легко просмотреть. Piktochart предоставляет мне инструменты для творческого и визуально привлекательного отображения данных».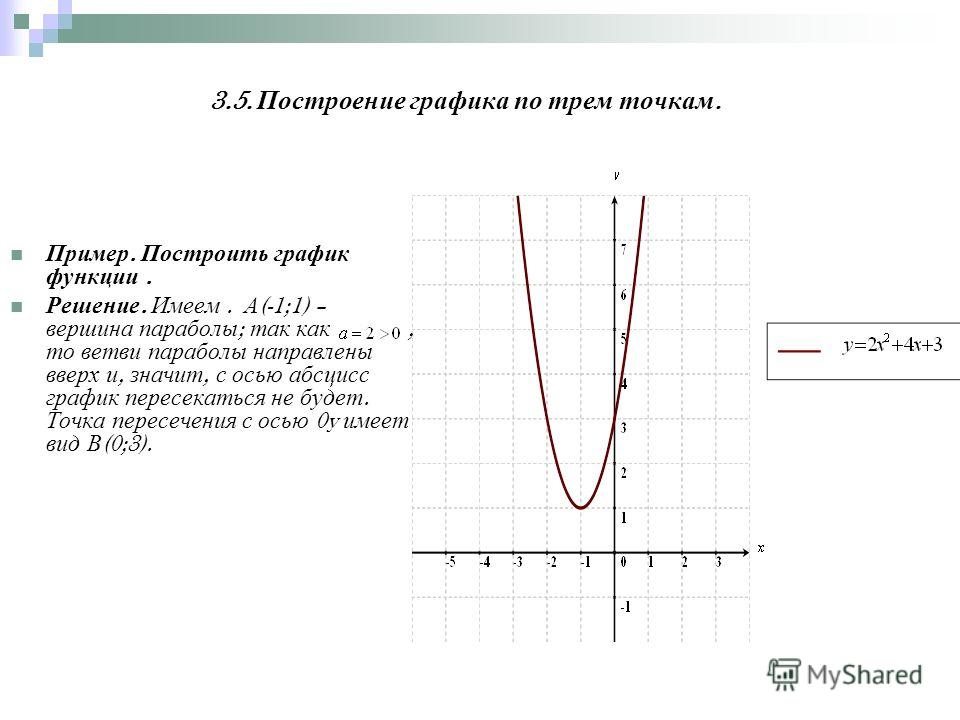

Клаудия Байод Боррего

Руководитель отдела внутренних коммуникаций, Arval BNP Paribas Group

«Piktochart позволил мне изменить стиль общения в моей компании. Кампании стали более наглядными, современными и привлекательными благодаря шаблонам, которые всегда служат источником вдохновения. Теперь им пользуются даже мои коллеги! Piktochart помог мне привлечь внимание к мероприятиям, увеличить количество участников, повысить ценность внутренних кампаний и укрепить культуру и коммуникативный поток моего бизнеса».

Присцила Алдана

Управление талантами, Boston Scientific

«Как ассистент отдела кадров я должен находить новые и творческие способы привлечения наших сотрудников и эффективного общения в крупной организации. Piktochart очень помог мне в этом».

Шарон Йенг

Бухгалтер, SIA Engineering Ltd.

«Piktochart помогает мне переводить часто сухие финансовые политики и стандарты бухгалтерского учета в понятные и краткие одностраничные изображения для руководства».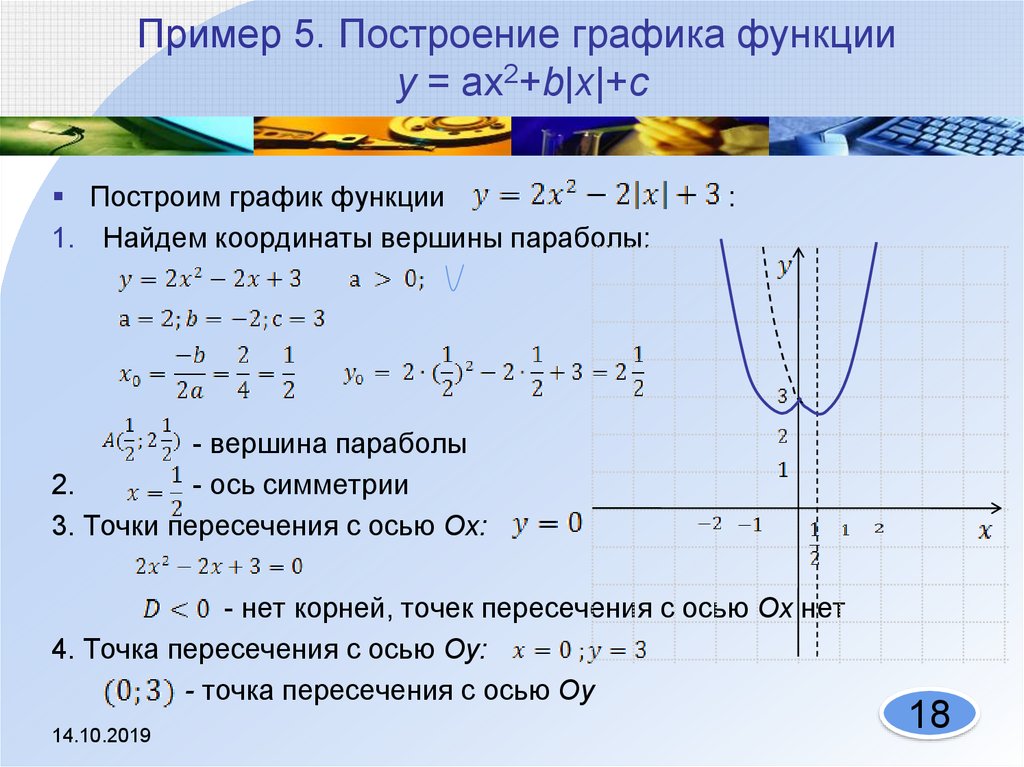

Как сделать график онлайн

1. Войдите в систему

Подпишитесь на бесплатный план или войдите в свою учетную запись Piktochart.

2. Выберите бесплатный шаблон

Выберите шаблон графика, созданный дизайнерами, или начните с нуля.

3. Откройте средство создания диаграмм

Перейдите в раздел «Инструменты» и откройте средство создания диаграмм Piktochart. Вы сможете построить график онлайн.

4. Введите свой набор данных

Скопируйте и вставьте точки необработанных данных в наш редактор графиков или загрузите файл Excel или CSV. Вы можете связать Google Sheet, чтобы данные на графике обновлялись автоматически.

5. Настройка

Отредактируйте один из шаблонов (выберите из различных типов графиков или диаграмм) и настройте метки данных, ось X, ось Y, заголовок графика, цвет фона и многое другое.

6. Загрузите пользовательскую диаграмму или поделитесь

Загрузите графику в формате jpg, png или pdf. Кроме того, поделитесь своей диаграммой в Интернете.

Исследуйте другие шаблоны

SWOT-матрица

Панель управления вербовкой

Ежеквартальный отчет по социальным сетям

Визуализация данных с помощью различных типов графиков

Line Graph Maker

Создавайте линейные графики для иллюстрации информации, которая меняется с течением времени. С помощью графического редактора Piktochart вы можете визуализировать данные за считанные секунды. Выберите из галереи шаблоны, значки, шрифты и изображения для настройки.

Создатель кольцевых диаграмм

Свяжите свой файл Excel или Google Sheet для создания кольцевых диаграмм, которые автоматически обновляются в Piktochart. Используйте разные диаграммы в одной презентации с помощью нашего онлайн-конструктора диаграмм.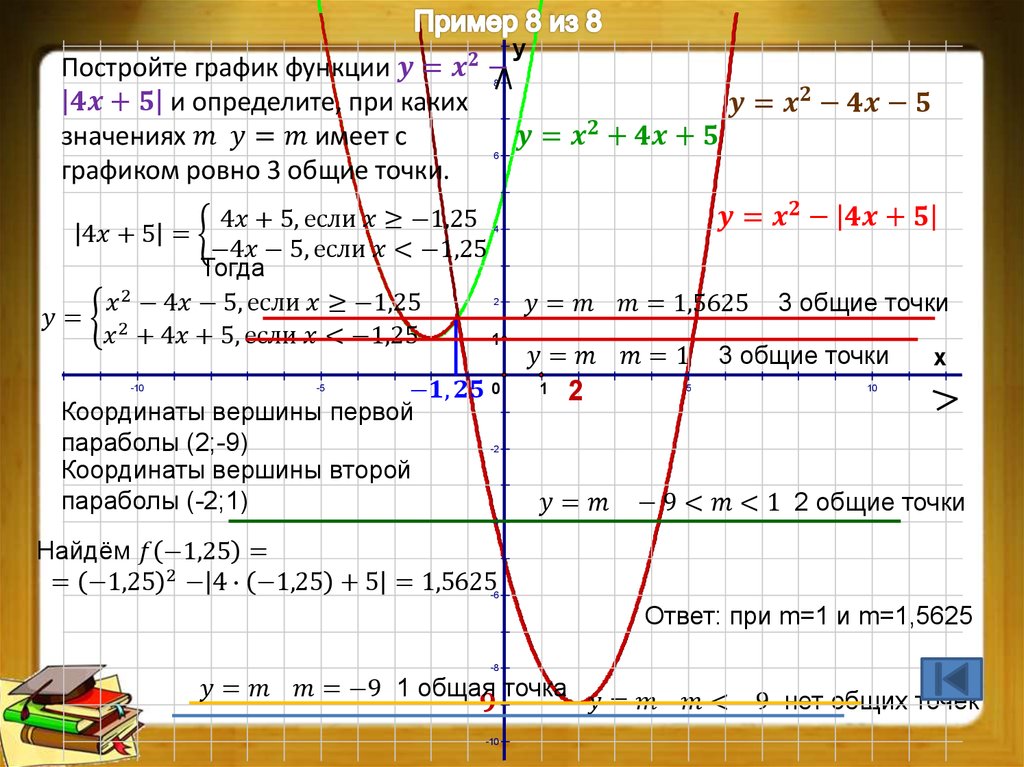

Средство создания точечных диаграмм

Включите точечную диаграмму на панель инструментов, чтобы преобразовать набор данных в наглядную историю, которая привлечет внимание вашей аудитории. Добавляйте значки и изображения в шаблоны диаграмм для создания профессиональной графики и загружайте свою работу, когда она будет готова.

Средство создания круговых диаграмм

Создайте профессиональную интерактивную информационную панель, которой можно поделиться с заинтересованными сторонами, и добавьте круговую диаграмму в цветах вашего бренда. Вы можете получить доступ к бесплатным шаблонам графиков и диаграмм, которые сделают все ваши визуальные эффекты и круговые диаграммы красивыми.

Средство создания гистограмм

С помощью Piktochart вы можете создавать впечатляющие отчеты, презентации и инфографику. Используйте средство создания диаграмм, чтобы представить данные в этих визуальных элементах без каких-либо усилий.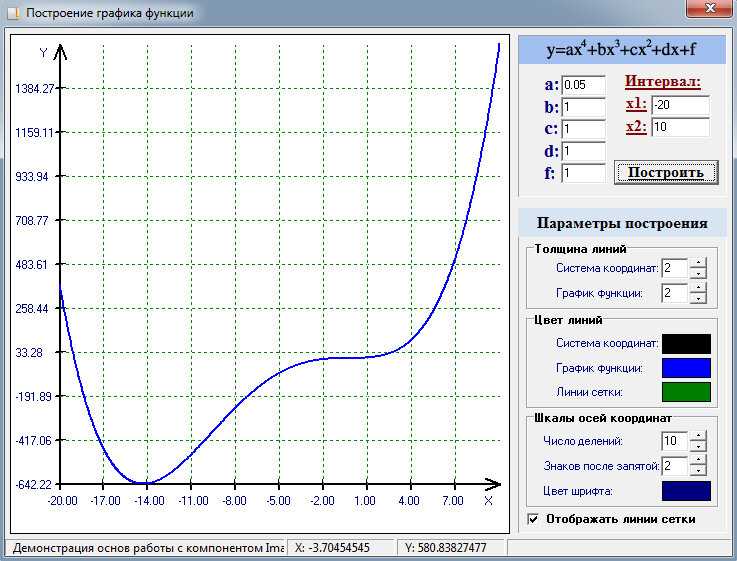

Средство создания сравнительных диаграмм

Сравните два продукта или выделите плюсы и минусы той или иной темы с помощью сравнительной таблицы в Piktochart. Выберите цвета, которые вы предпочитаете, и быстро создайте визуальный образ. С помощью нашего редактора перетаскивания вы создадите график за считанные минуты.

Готовы создавать графики за считанные минуты?

Присоединяйтесь к более чем 11 миллионам людей, которые уже используют бесплатный конструктор графиков Piktochart.

Создайте бесплатную учетную запись

Часто задаваемые вопросы

Да, средство для создания графиков Piktochart можно использовать бесплатно. План предлагает доступ ко многим функциям инструмента, включая загрузки. Кроме того, бесплатный план не требует использования нашего водяного знака; визуальные эффекты, которые вы создаете, принадлежат вам. Дополнительные преимущества могут быть доступны с платными планами.

Нет, вам не нужен опыт проектирования, чтобы использовать средство для создания графиков. Пока вы используете онлайн-инструмент, предназначенный для недизайнеров, например Piktochart или Canva. Выберите бесплатный шаблон из галереи Piktochart, отредактируйте и настройте его в соответствии с вашим брендом, чтобы создать профессиональный визуальный элемент. После завершения просто загрузите график в нужном вам формате. Онлайн-платформа также позволяет импортировать данные из Excel или Google Sheets.

С помощью средства создания диаграмм вы можете создавать широкий спектр диаграмм и графиков, в том числе:

• Гистограммы
• Диаграммы рассеяния
• Сравнительные диаграммы
• Линейные графики
• Пиктограммы

Да, вы можете использовать средство создания диаграмм для создания диаграмм и графиков для презентаций или отчеты, если вы используете для этого специальный инструмент. Онлайн-конструкторы диаграмм, такие как Piktochart и Canva, позволяют пользователям добавлять несколько диаграмм в один и тот же отчет и настраивать дизайн своих шаблонов.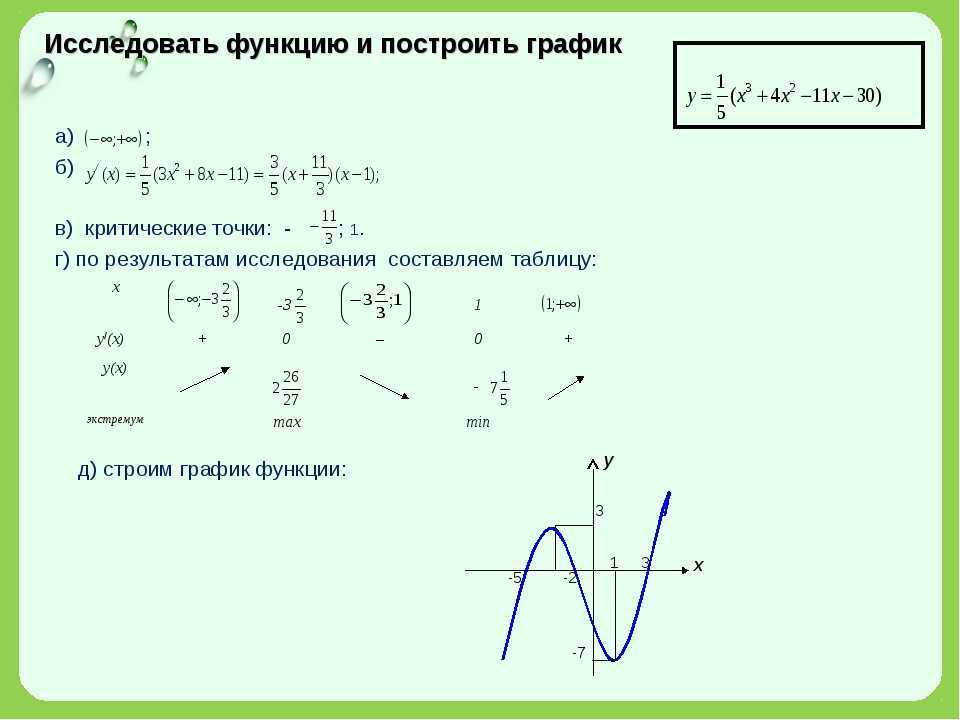

При выборе графического редактора необходимо учитывать:

• Предлагаемые функции. Чем он сложнее, тем больше гибкости вам потребуется для построения графика.
• Свобода тестирования инструмента путем создания пользовательских диаграмм с пробным или бесплатным планом.
• Ресурсы для изучения инструмента и простоты использования.
• Соотношение цены и качества. Что вы получаете за платный план. Создатели графиков, такие как Piktochart, предлагают хранение, загрузку и доступ ко многим функциям. Кроме того, он не накладывает водяной знак на визуальные эффекты, создаваемые пользователями.

Это зависит от выбранного вами графического редактора. Piktochart позволяет импортировать данные из файлов Excel и Google Таблиц. Когда вы обновляете эти документы, данные в ваших графиках Piktochart обновляются автоматически.

Бесплатный онлайн-конструктор графиков для всей вашей команды

Превратите необработанные данные в истории с помощью нашего онлайн-конструктора графиков. Настроить наши более 100 шаблонов диаграмм, которые подойдут вашему бренду и аудитории.
Тогда мгновенно поделиться и экспортировать.

Создайте мой график сейчас Кредитная карта не требуется

Используется 2 000 000  человек по всему миру

Сделайте цифры красивыми с помощью нашего бесплатного онлайн-конструктора диаграмм

Любой член вашей команды может визуализировать данные и создавать диаграммы в всего несколько минут.

Работайте где угодно Создайте график онлайн, сотрудничайте с вашей командой в реальном времени и сохраните свою работу в облаке.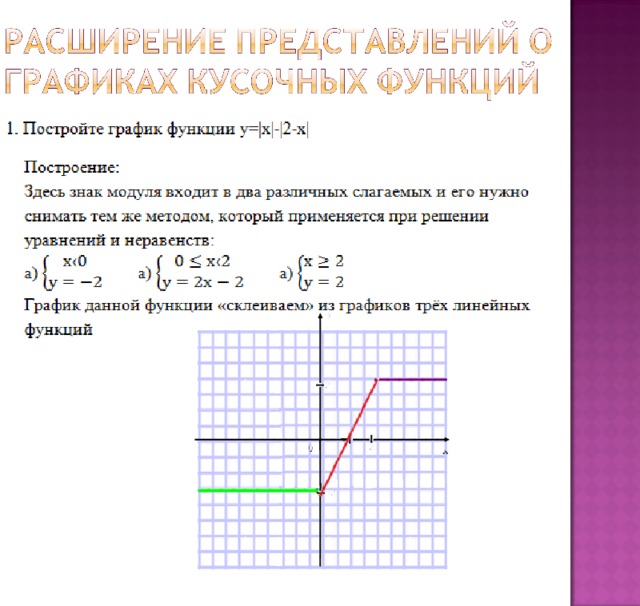

Быстрая настройка Выберите шаблон, соответствующий вашим потребностям. Тогда используйте наш простой график генератор для добавления данных, цветов и брендинга.

Делитесь мгновенно Представляйте свою команду, делитесь ссылками в Интернете, добавляйте на информационные панели, размещать в социальных сетях и экспортировать.

Создайте свой график за 4 простых шага

Вот как это работает

1

Выберите шаблон

Выбирайте из более чем 100 профессионально разработанных шаблонов и типы диаграмм. Не нужно начинать с нуля — хотя вы можете перетаскивать сделать это тоже!

2

Добавьте свой набор данных

Введите данные в нашу полностью редактируемую таблицу или вставьте информацию непосредственно из CSV.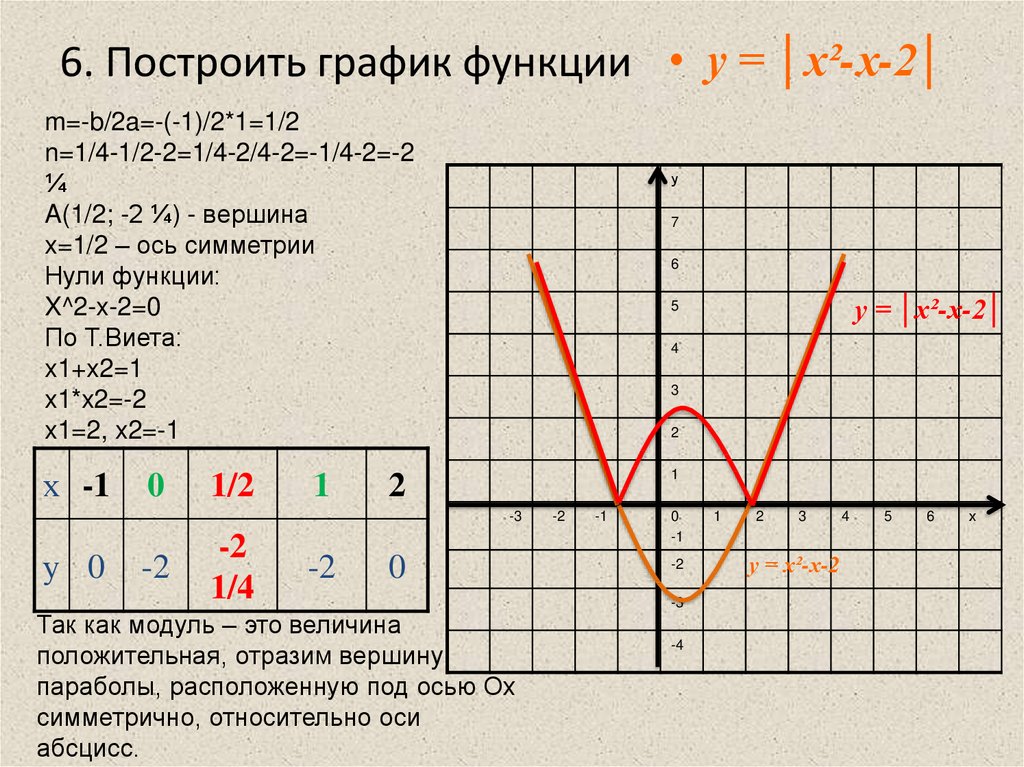

3

Персонализация и стиль

Настройте свой график в соответствии с вашим брендом и аудиторией, добавив легенды или сетки, выбор цветов и шрифтов, настройка прокладка и многое другое.

4

Делиться и экспортировать

Представляйте и сотрудничайте в режиме реального времени, получайте обратную связь прямо на страницу, пригласить и поделиться в частном порядке, добавить на панель инструментов, и экспортировать в PNG или PDF.

Создать мою пользовательскую диаграмму сейчас Кредитная карта не требуется

Найдите правильную диаграмму и график для ваших данных

Гистограмма Создайте гистограмму для отслеживания изменений с течением времени, определите лучших к худшим исполнителям или ранжировать значения от наибольшего к худшему.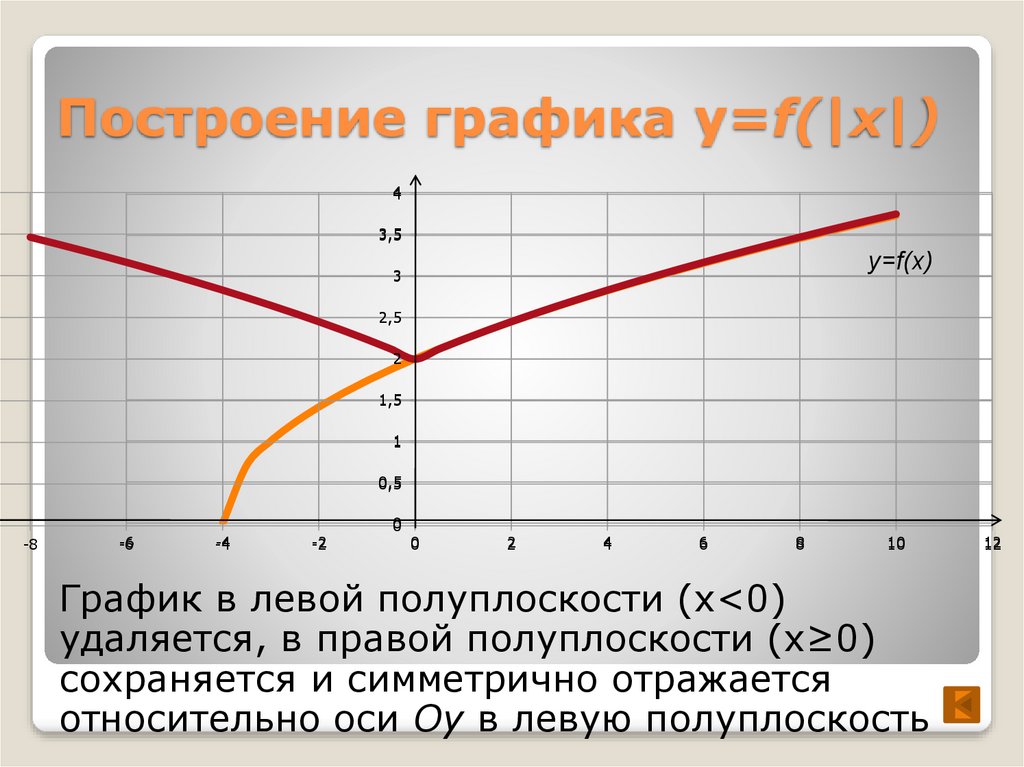 самый маленький.

Столбчатая диаграмма Сделайте столбчатую диаграмму, чтобы отобразить все виды бизнеса, финансовые и логистические данные и представляют собой отрицательные ценности более эффективно.

Линейный график Используйте линейный график, чтобы визуализировать прогресс во времени или на расстоянии соединяя непрерывные точки данных с сегментами линии.

Гистограмма с накоплением Создайте столбчатую диаграмму с накоплением, чтобы создать слои внутри ваших столбцов, и показать, как подгруппы вносят вклад в каждую категорию общий.

Столбчатая диаграмма с накоплением Используйте столбчатую диаграмму с накоплением для отображения возрастающих значений – такие как даты или группы доходов, а также включая подгруппы внутри ваших колонок.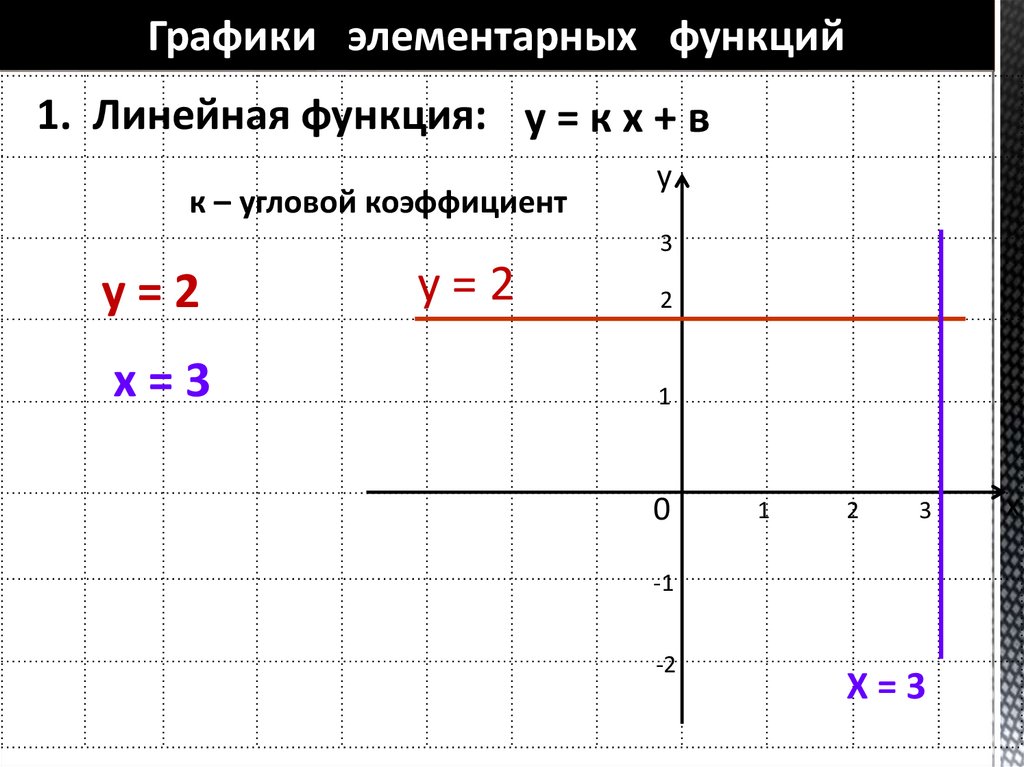

Диаграмма областей Создайте диаграмму с областями для сравнения связанных групп внутри категорию и представлять отношения части к целому по мере их изменение с течением времени.

Диаграмма с областями с накоплением Создайте диаграмму с областями с накоплением, чтобы отслеживать части целого по время, а также для анализа тенденций, таких как посещения страниц по источнику или доходы против расходов.

Круговая диаграмма и кольцевая диаграмма Используйте круговую или кольцевую диаграмму, чтобы показать категории в виде срезов и проценты — и сделать отношения части к целому легко понять.

Воронкообразная диаграмма Составьте воронкообразную диаграмму для анализа прогрессивных стадий процесс или процедура для выявления проблем и устранения узкие места.

И экспериментируйте свободно Одним щелчком мыши вы можете исследовать множество красивых визуализаций данных. чтобы найти только правильный для вашей аудитории и информации!

Идите дальше с Moqups

Максимизируйте влияние ваших данных, добавляя диаграммы и графики в информационные панели, каркасы, прототипы, доски и диаграммы — все в одном приложении!

Творческое сотрудничество

Работайте над идеями, решайте проблемы и быстро приходите к консенсусу. Ваша команда может обмениваться информацией, общаться и координировать свои действия в любое время. уровень — с помощью нашего визуального инструмента для совместной работы.

Редактирование в реальном времени

Визуальные комментарии

Живой чат

Командные роли

Обмен

Наши клиенты

Как владелец продукта и генеральный директор с 75 сотрудниками, я использую Moqups в первую очередь для дизайна продукта. Но мы также использовали его для всего, от организационных диаграмм до планировки нашего офиса космос. Это невероятно интуитивно понятно, быстро и доступно повсюду. Это буквально мой любимый инструмент.

Люк Фрейлер, Генеральный директор Centercode

С Moqups я могу создавать блок-схемы, каркасы и карты сайта. все в одном проекте, который отлично подходит для управления.

Дэйв Теккерей, Контент-стратег в Word and Mouth

Ключевым моментом является создание интерактивных каркасов для сложных проектов. к нашему успеху в разработке отмеченных наградами приложений для наших клиенты. Функции совместной работы Moqups помогают нам общаться четко на каждом этапе развития – от зарождения до выполнение.