График параболы: Построение графика квадратичной функции — урок. Алгебра, 8 класс.

2-4x+2$$

Содержание

Построение графика параболы в MS EXCEL

history 8 января 2023 г.

Диаграммы и графики

file_download Файл примера

Построим параболу, используя стандартную диаграмму MS EXCEL. C помощью элементов управления построим удобную форму для смещения вершины параболы вверх/низ, отражения ее относительно осей координат.

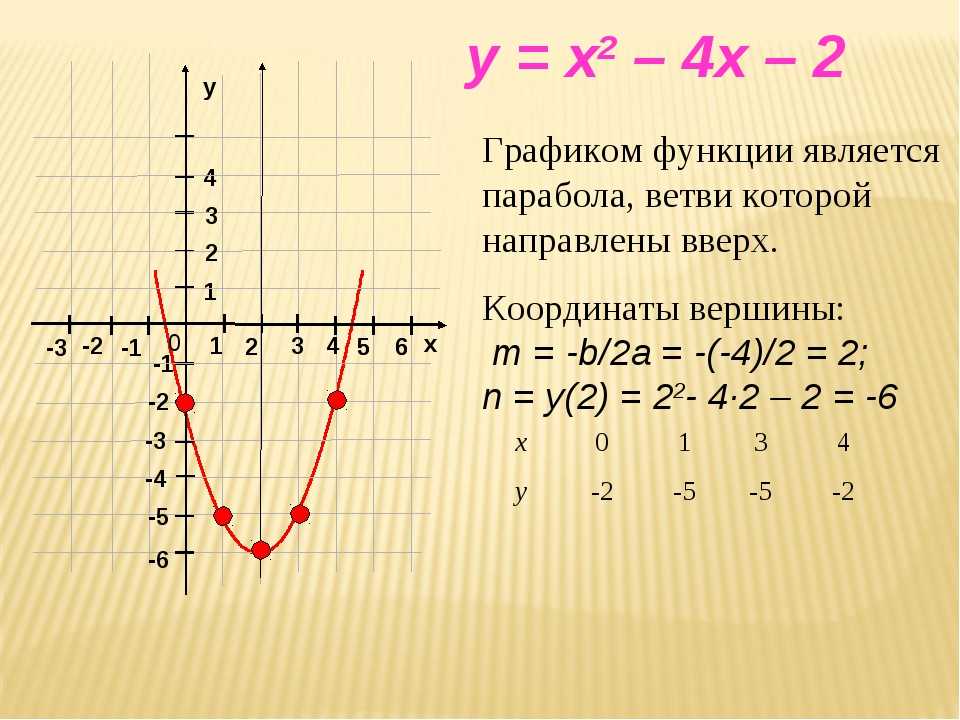
Построим Параболу имеющую уравнение y=x².
Отметим на диаграмме ее особые точки: пересечения с осями (осью) и вершину.
Создадим на листе кнопки для смещения вершины параболы в произвольном направлении
Выберем такой шаг по оси Х и диапазон изменения переменной Х, чтобы после смещения параболы на диаграмме обе ее ветви отображались одинаковой длины и присутствовали все особые точки
Вычислим новые значения параметров параболы y=ax² + bx + с

С помощью точечной диаграммы построим Параболу имеющую уравнение y=x², назовем ее исходной параболой.

Для этого на листе в файле примера подготовлена таблица исходных значений по Х и Y.

Особенностью этого набора данных является то, что значения Х отсчитываются от координат вершины параболы с определенным шагом.

Для определения вершины параболы можно использовать различные формулы, например через производную или по формуле х0=-b/2a. Для этого в файле примера делаются соответствующие вычисления (при изменении местоположения параболы эти вычисления производятся автоматически).

Для определения масштаба изменения переменной Х, вычисляются точки пересечения, а затем вычисляется такой шаг по Х, чтобы все эти точки пересечения гарантированно были отражены на диаграмме.

Чтобы шаг по Х не был равен значениям с длинной десятичной частью, используется округление до первой значащей цифры.

Смещение вершины параболы будем производить с помощью Полосы прокрутки и Элемента управления Счетчик.

Смещение по оси Х будем обозначать m, а по Y обозначим n.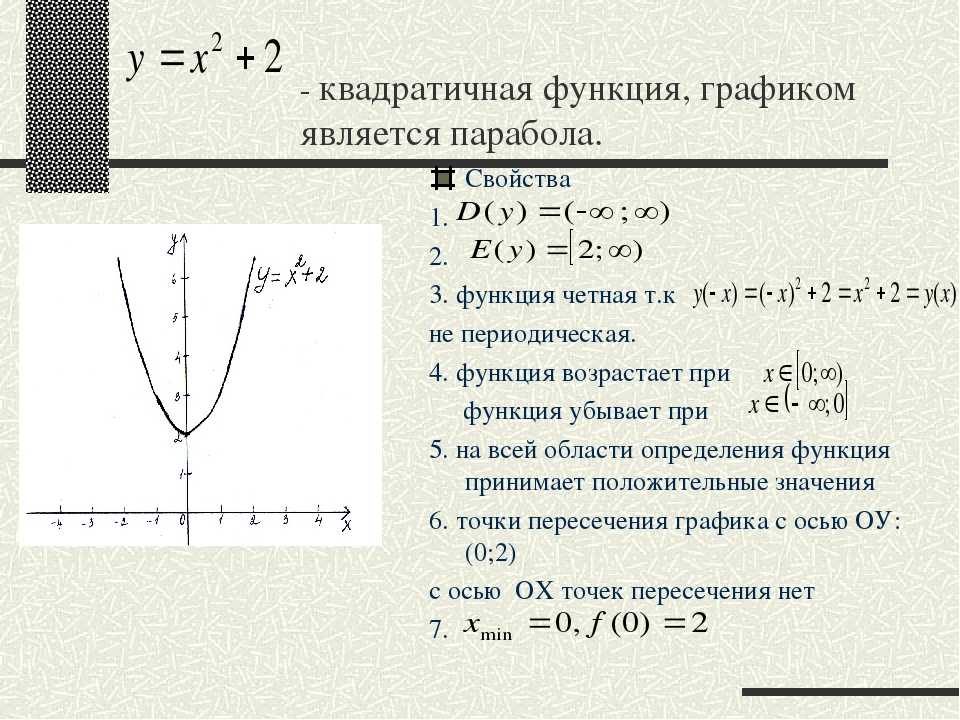 Значения m и n являются новыми координатами вершины смещенной параболы.

Изменив, например, с помощью Счетчика значение n на 2, автоматически пересчитаются значения параметров параболы в строке 10: y=ax² + bx + с, а следовательно и координаты вершины вместе со всеми значениями исходной таблицы — парабола сместится на величину 2 по Y.

Примечание: альтернативная запись параболы через координаты вершины: y=a(x-m)²+n

Параметр а отвечает за масштаб параболы. Например, парабола с уравнением y=2x² будет вытянута по оси Х в 2 раза по отношению к y=x².

В файле примера изменение масштаба параболы реализовано с помощью элемента Счетчик, аналогичным образом, как и смещение.

Смещенную параболу можно отразить относительно оси Х, относительно оси Y и относительно прямой параллельной Ох и проходящей через вершину параболы. Все эти манипуляции реализованы с помощью формул и элементов управления Переключатель.

Выбирая нужный тип отражения параболы, диаграмма отобразит нужный график.

Построить параболу не сложно, сложнее вычислить значения параболы (a, b, с), которая была смещена, у которой также был изменен масштаб и, наконец, она была отражена.

Все эти вычисления приведены в формулах строки 10 в файле примера. На листе «произвольная» расчеты параметров сделаны относительно исходной параболы с произвольными значениями параметров. Формулы получаются в этом случае достаточно громоздкими, т.к. параметры смещенной параболы зависят как от параметров исходной параболы, так и от значений m, n и масштаба.

Parabolic Graphs

Интерактивная математика для 9 класса — второе издание

Параболические графики

Отношение является квадратичным функция , если наибольшая степень местоимения в отношении равна два. Графики y = ax , a > 0 Пример 1 Решение:

Когда мы нанесем эти точки и соединим их плавной кривой, мы получим квадратичный граф , показанный выше. Кривая называется параболой . Он имеет множество приложений в наука и техника. Например, траектория полета снаряда и форма отражатель в автомобильных фарах или прожекторах. Глядя на график и форму кривой, можно представить, что зеркало расположено вдоль оси и : слева и справа от кривые являются зеркальным отображением друг друга. Это свойство называется симметрией . Мы говорим, что граф симметрична относительно оси y , а ось y называется осью симметрии . Итак ось симметрии имеет уравнение x = 0 в примере. Парабола направлена вверх. Минимальное значение y равно нулю и это происходит, когда x = 0. Точка (0, 0) называется точка поворота или вершина парабола. Вообще: В приведенном выше примере a = 1. Пример 2 Решение:

Когда мы наносим эти точки и соединяем их плавной кривой, мы получаем график, показанный выше. Примечание: График представляет собой параболу, направленную вверх. Минимальное значение y равно 0, а встречается, когда x = 0. Точка (0, 0) называется вершиной парабола. График симметричен около x = 0, т.е. ось y-. Графики y = ax , a < 0 Пример 3 Решение:

Когда мы наносим эти точки и соединяем их плавной кривой, мы получаем график, показанный выше. Примечание: График представляет собой параболу, направленную вниз. Ясно, что график симметричен относительно оси y . Следовательно, уравнение ось симметрии x = 0, Максимальное значение y равно 0, и это происходит, когда x = 0, Вершиной параболы является точка (0, 0). Вообще: В приведенном выше примере a = 1. Пример 4 Решение:

Когда мы наносим эти точки и соединяем их плавной кривой, мы получаем график, показанный выше. Ключевые термины квадратичная функция, квадратичный график, парабола, ось симметрии, симметрия, точка поворота, вершина

Инструкции по авторскому праву для образовательных учреждений

Пожалуйста, ознакомьтесь с Условиями использования этого Веб-сайт и наша политика конфиденциальности и другие политики.

Если у Вас возникли трудности при использовании данного Сайта, сообщите нам через форму обратной связи или позвонив по контактному телефону.

Уравнение окружности и параболы Пошаговое решение математических задач

7.5 Уравнение окружности 92

Из этого последнего уравнения мы узнаем, что его график представляет собой окружность с центром (3/4,-1) и радиусом 7/4.

Давайте посмотрим, как наш генератор графов решает эту и подобные задачи и генерирует графики. Нажмите кнопку «Решить подобное», чтобы увидеть больше примеров.

Решите похожую задачуВведите свою задачу

7. 6 Некоторые параболы и их уравнения

Во многих ситуациях появляется кривая определенного типа, называемая параболой. Например, путь, прочерченный брошенным в воздух камнем (не вертикально), является частью параболы. Дуга воды из шланга является частью параболы. Отражающее зеркало автомобильной фары имеет форму параболической тарелки, как и зеркала хорошего телескопа-рефлектора. 92

, где a – ненулевое действительное число. Если а положительно, то парабола направлена вверх. в то время как если a отрицательно, он открывается вниз. Чтобы нарисовать

РИСУНОК 8.

-3

-2

-1

1 92.

Это парабола с вершиной в начале координат и осью Y в качестве оси симметрии. Поскольку коэффициент -1/2 отрицательный, парабола открывается вниз.

92.

Это парабола с вершиной в точке (-1,3), которая раскрывается. Его осью симметрии является линия x=-1.

х	г
-4	-8
-3	-9/2
-2	-2
-1	-1/2

График полученного уравнения представляет собой параболу с вершиной в точке (-3/4,-17/8) и осью симметрии на линии x=-3/4

х	г
-4	6
-3	13/3
-2	3/10
-1	3
0	3/10

х	г
-2	1
-3	8
1	4
2	13

Аналогично уравнения вида 92

График этого уравнения представляет собой параболу с вершиной в (1,2), она выходит на

вправо, а ее осью симметрии является прямая y=2.

Построение графика параболы в MS EXCEL

history 8 января 2023 г.

Parabolic Graphs

Пример 1

Решение:

Решение:

Пример 3

Решение:

Решение:

Уравнение окружности и параболы Пошаговое решение математических задач

Добавить комментарий Отменить ответ