Задача с параметром. Полуокружность
Необходимо найти значение параметра, такое, чтобы уравнение имело единственное решение. Знакомимся с видом уравнения, задающего полуокружность.
Задача. Чему равно значение параметра , если уравнение
имеет единственное решение?
Перепишем немного иначе:
Поработаем с правой частью:
Теперь займемся левой частью.
В левой части имеем уравнение полуокружности с центром в точке . Как это понять? Возведем в квадрат:
Получили уравнение окружности радиуса 24 с центром в точке . Но наличие корня «отрежет» все ординаты, меньшие нуля, вот и останется только верхняя половинка окружности.
А что в правой? Похоже, что прямая, только есть зависимость ее уравнения от параметра, поэтому необходимо понять, что с этой прямой происходит с изменением параметра. Заметим, что при любом точка с абсциссой 11 и ординатой 0 принадлежит прямой. То есть точка – центр вращения нашей прямой, у которой может меняться как коэффициент наклона , так и коэффициент . Нас, очевидно, интересует случай касания прямой и полуокружности. Причем найти надо коэффициент наклона прямой, то есть тангенс угла .
Рассмотрим чертеж.
Полуокружность и касающаяся ее прямая
Треугольник – прямоугольный с прямым углом , его катет , а гипотенуза , поэтому второй его катет равен 7 (по теореме Пифагора).
Треугольники и подобны (оба прямоугольные и угол равен углу как углы со взаимно перпендикулярными сторонами). Поэтому для этих треугольников можно записать отношение сходственных сторон:
А искомый коэффициент наклона прямой равен:
Тогда и
Других вариантов решения у этой задачи нет, так как только при касании прямая будет иметь одну общую точку с полуокружностью, во всех остальных случаях – либо две, либо ни одной.
Ответ: .
easy-physic.ru
Задача с параметром. Задание С5
Решим задачу из Задания С5 для подготовки к ЕГЭ по математике:
Найдите все значения параметра ,при каждом из которых уравнение имеет единственное решение.
Будем решать задачу графическим способом. Оставим корень слева, а все остальное перенесем вправо. Представим наше уравнение в виде системы
Построим график каждой функции и найдем, при каком значении параметра графики имеют единственную точку пересечения.
Первая функция:
Вынесем за скобку:
График этой функции представляет из себя семейство прямых, которые имеют различный коэффициент наклона и общую точку с координатами (2;3):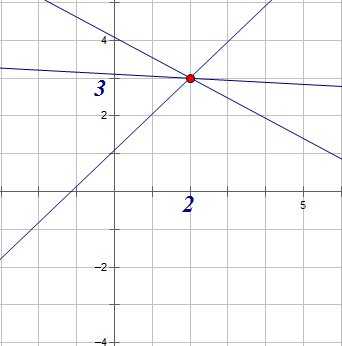
Вторая функция:
Преобразуем выражение под корнем — выделим полный квадрат:
График функции представляет из себя полуокружность с центром в точке (-4;0) и радиусом 3.
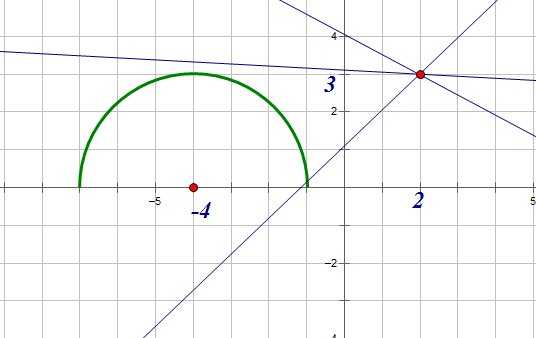
Определим, при каком коэффициенте наклона прямая имеет с полуокружностью одну точку пересечения: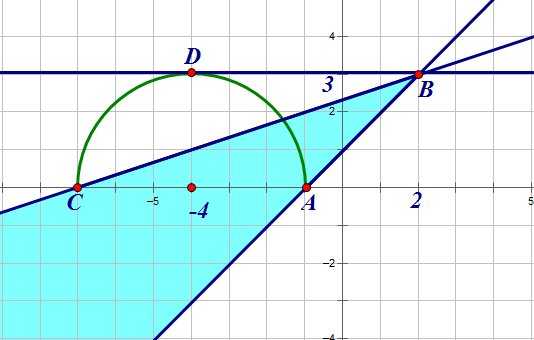
Мы видим, что прямые, заключенные между прямыми и имеют с полуокружностью одну общую точку. Прямая имеет одну общую точку, а прямая — две. Прямая также имеет с полуокружностью одну общую точку.
Найдем коэффициенты наклона этих прямых. Для этого мы рассмотрим соответствующие прямоугольные треугольники: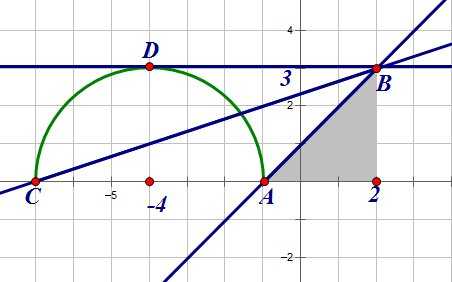
Коэффициент наклона прямой равен 1.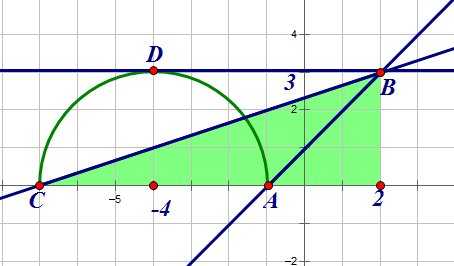
Коэффициент наклона прямой равен 3/9=1/3.
Коэффициент наклона прямой равен нулю.
Итак, прямая и полуокружность имеют одну общую точку, если и .
Умножим первое неравенство на -1 и получим
Ответ:
И.В. Фельдман, репетитор по математике.
ege-ok.ru
Задача с параметром про окружности
2014-03-03 | Автор: Анна
Здравствуйте, дорогие читатели! Сегодня мне попалась красивая задача с параметром, и хотелось бы поделиться с вами решением.
Задача такая: найти положительное значение параметра a, такое, чтобы система имела единственное решение.
Сразу можно заметить, что оба уравнения – это уравнения окружностей. У первой радиус равен трем, у второй – a. Интересно, что в уравнении первой окружности присутствует модуль х. То есть на самом-то деле это не одна, а две окружности, симметрично расположенные относительно оси у и имеющие центры в точках (5, 4) и (-5, 4) и радиус три. В этом и есть маленькая хитрость этой задачи, поскольку, если честно, задача-то совсем простая. Осталось догадаться, что вторая окружность радиуса
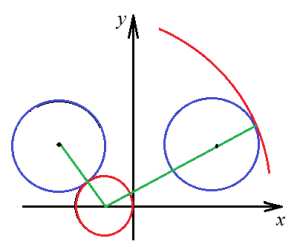
Видим, что решений два: либо красная окружность касается левой синей “внутри”, либо красная окружность имеет такой радиус, чтобы касаться правой синей “снаружи”. Любая другая точка касания не будет единственной: в других случаях красная окружность обязательно заденет или пересечет обе синие окружности, а это не соответствует условию задачи.
Найдем радиусы красных окружностей, в этом нам поможет теорема Пифагора (зеленые треугольники). Тогда расстояние между центрами малой красной окружности и синей (левой):
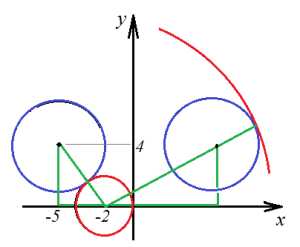
Чтобы найти искомый радиус, надо вычесть из данного расстояния 3:
Рассмотрим теперь второй треугольник и найдем расстояние между центрами большей красной окружности и синей (правой):
Не забудем, что к этому расстоянию надо добавить радиус синей окружности:
Итак, ответ:
easy-physic.ru
Помогите решить / разобраться (М)
Задача: Графиком функции служит полуокружность с центром в начале координат и радиусом, равным , расположенная в верхней координатной полуплоскости. Существует ли для этой функции обратная?Решение:
Уравнение окружности: .
,
,
,
По условиям задачи: . Следовательно, функция полуокружности в верхней полуплоскости имеет запись: .
Для нахождения обратной функции:
— выразим через :
;
;
;
— поменяем местами и : .
Получается, что при преобразовании указанной выше функции полуокружности в обратную каждому обратной функции соответствует 2 значения обратной функции , что не является собственно функциональной зависимостью, а, следовательно, вышеуказанная функция полуокружности в верхней полуплоскости необратима.
Необратимость данной функции также очевидна, если ее преобразовать с помощью правила: Чтобы получить график функции , надо график функции преобразовать симметрично относительно прямой .
При таком преобразовании получается изображение полуокружности в правой полуплоскости, которое функцией не является.
Однако, почему-то в ответах в конце учебника на вопрос о существовании обратной функции для данной дается положительный ответ: «Да».
В то же время, в ответах в данном учебнике часто допускаются ошибки, и, возможно, здесь также допущена ошибка, однако, для меня это не очевидно.
В интернете решение данной задачи не нашел.
dxdy.ru
Окружность. Уравнение окружности
Аналитическая геометрия дает единообразные приемы решения геометрических задач. Для этого все заданные и искомые точки и линии относят к одной системе координат.
В системе координат можно каждую точку охарактеризовать ее координатами, а каждую линию – уравнением с двумя неизвестными, графиком которого эта линия является. Таким образом геометрическая задача сводится к алгебраической, где хорошо отработаны все приемы вычислений.
Окружность есть геометрическое место точек с одним определенным свойством (каждая точка окружности равноудалена от одной точки, называется центром). Уравнение окружности должно отражать это свойство, удовлетворять этому условию.
Геометрическая интерпретация уравнения окружности – это линия окружности.
Если поместить окружность в систему координат, то все точки окружности удовлетворяют одному условию – расстояние от них до центра окружности должно быть одинаковым и равным окружности.
Окружность с центром в точке А и радиусом R поместим в координатную плоскость.
Если координаты центра (а;b), а координаты любой точки окружности (х; у), то уравнение окружности имеет вид:
Если квадрат радиуса окружности равен сумме квадратов разностей соответствующих координат любой точки окружности и ее центра, то это уравнение является уравнением окружности в плоской системе координат.
Если центр окружности совпадает с точкой начала координат, то квадрат радиуса окружности равен сумме квадратов координат любой точки окружности. В этом случае уравнение окружности принимает вид:
Следовательно, любая геометрическая фигура как геометрическое место точек определяется уравнением, связывающим координаты ее точек. И наоборот, уравнение, связывающее координаты х и у, определяют линию как геометрическое место точек плоскости, координаты которых удовлетворяют данному уравнению.
Примеры решения задач про уравнение окружности
Задача. Составить уравнение заданной окружности
Составьте уравнение окружности с центром в точке O (2;-3) и радиусом 4.Решение.
Обратимся к формуле уравнения окружности:
R2 = (x-a)
Подставим значения в формулу.
Радиус окружности R = 4
Координаты центра окружности (в соответствии с условием)
a = 2
b = -3
Получаем:
(x — 2)2 + (y — (-3))2 = 42
или
(x — 2)2 + (y + 3)2 = 16.
Задача. Принадлежит ли точка уравнению окружности
Проверить, принадлежит ли точка A(2;3) уравнению окружности (x — 2)2 + (y + 3)2 = 16.Решение.
Если точка принадлежит окружности, то ее координаты удовлетворяют уравнению окружности.
Чтобы проверить, принадлежит ли окружности точка с заданными координатами, подставим координаты точки в уравнение заданной окружности.
В уравнение (x — 2)2 + (y + 3)2 = 16
подставим, согласно условию, координаты точки А(2;3), то есть
x = 2
y = 3
Проверим истинность полученного равенства
(2 — 2)2 + (3 + 3)2 = 16
0 + 36 = 16 равенство неверно
Таким образом, заданная точка не принадлежит заданному уравнению окружности.
Содержание главы:Площадь геометрической фигуры | Описание курса | Задачи про окружность
profmeter.com.ua
График зависимости скорости тела от времени имеет вид полуокружности
Условие задачи:
График зависимости скорости тела от времени имеет вид полуокружности. Максимальная скорость тела \(\upsilon_0\), время движения \(t_0\). Определить путь, пройденный телом. Рисунок, приведенный в условии задачи, изображен справа.
Задача №1.1.4 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\upsilon_0\), \(t_0\), \(S-?\)
Решение задачи:
Также, как и во втором способе решения этой задачи, используем тот факт, что путь, пройденный телом, возможно определить как площадь фигуры под графиком зависимости скорости тела от времени (на рисунке к решению заштриховано). Так как график имеет вид полуокружности, то и его площадь находится как половина площади круга:
\[S = \frac{1}{2}\pi {r^2}\]
Запишем формулу в такой форме:
\[S = \frac{1}{2}\pi r \cdot r\]
Это необходимо для того, чтобы человек, решающий эту задачу не подставил вместо \(r\) либо только \(\upsilon_0\), либо только \(\frac{t_0}{2}\), поскольку в таком случае ответ не будет подходить по размерности с размерностью пути. Поэтому, вместо первого \(r\) подставим \(\upsilon_0\), а вместо второго — \(\frac{t_0}{2}\). Только в этом случае мы сможем получить верный ответ:
\[S = \frac{1}{2}\pi {\upsilon _0} \cdot \frac{{{t_0}}}{2} = 0,25\pi {\upsilon _0}{t_0}\]
Ответ: \(0,25\pi {\upsilon _0}{t_0}\).
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Если Вам понравилась задача и ее решение, то Вы можете поделиться ею с друзьями с помощью этих кнопок.
easyfizika.ru
Формула Пика
Как определить площадь сложной фигуры? Если она нарисована на клетчатой бумаге, и невырождена -площадь ее ненулевая, все вершины имеют целые координаты, а стороны не пересекают друг друга – то удобно воспользоваться формулой Пика.
Если обозначить: В – количество целочисленных точек внутри этой фигуры, Г – количество целочисленных точек на ее границе, S – площадь фигуры, то
S=В+Г/2-1
Рассмотрим следующую фигуру:
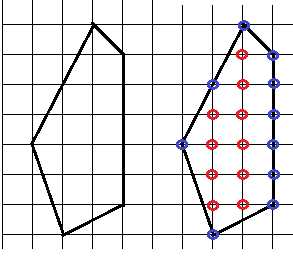
Формула Пика – определение числа узлов внутри и на границе фигуры.
Обозначим все внутренние целочисленные точки красными кружками, а те, что на границах – синими. Целочисленные – это те, что лежат на пересечениях сетки (в ее узлах). Считаем те и другие: В=12, Г=4. Определим теперь площадь по формуле: S=В+Г/2-1=12+2-1=13.
Давайте проверим правильность наших расчетов, тем более, что здесь это просто: рассчитаем площадь квадрата, обведенного красным, и вычтем площади цветных треугольников:
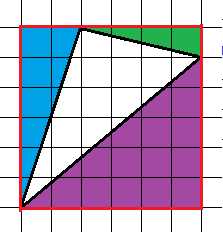
Вычисление площади при помощи отрезания “лишнего”
Тогда площадь квадрата Sкв=36, площадь голубого треугольника 6, площадь зеленого – 2, площадь фиолетового 15.
Площадь белого треугольника тогда: S=36-6-15-2=13.
Рассмотрим такую фигуру:
Еще один пример определения площади сложной фигуры с помощью формулы Пика
Для нее S=В+Г/2-1=4+3-1=6.
Проверим:
Отрежем лишнее
Тогда площадь прямоугольника Sпр=20, площадь голубого треугольника 5, площадь зеленого – 4, площадь фиолетового 5.
Площадь искомой фигуры тогда: S=20-5-4-5=6.
Третья фигура:
Еще один пример работы с формулой Пика
Для нее S=В+Г/2-1=4+4-1=7.
Проверим: площадь треугольников, составляющих нашу фигуру: голубого – 4, зеленого – 1, оранжевого – 2. Сумма их площадей S=4+1+2=7.
Расчет площади с помощью разрезания фигуры
Еще две фигуры:
Узлы решетки внутри и на границе фигуры
Площадь первой: S=10+2-1=11,
Узлы решетки внутри и на границе
второй – S=10+5-1=14.
Проверить правильность расчета их площадей вы можете самостоятельно.
easy-physic.ru
