Программное обеспечение — Все для студента
Algebrator — это лидирующее алгебраическое программное обеспечение, которое только доступно на сегодняшний день студентам, преподавателям, работающим специалистам и учебным заведениям. Algebrator — это один из наиболее мощных алгебраических пакетов, которые когда-либо разрабатывались. Он пытается решить сложнейшие алгебраические задачи, которые вы на него возлагаете. А также может…
- №1
- 4,80 МБ
- дата добавления неизвестна
- изменен
Универсальная программа по математике: решение уравнений, различные вычисления и многое другое.
- №2
- 241,72 КБ
- дата добавления неизвестна
- изменен
Прикладная программа «Approximator-Mini» максимально облегчает представление экспериментальных кривых в виде формулы. Данная прикладная программа разработана для применения в среде Microsoft Office Excel. В настоящее время аппроксимация кривых проводится самыми разными способами, включая кривые Безье и другие экзотические формулы. В то же время в технических задачах для…
- №3
- 45,56 КБ
- добавлен
- изменен
ОС: WinALL Язык: Английский (English) Cabri 3D представляет собой приложение, которое было разработано для помощи в построении 3d моделей и фигур, содержит все преимущества интерактивной геометрии. Используя Cabri 3D v2, вы быстро научитесь строить, просматривать и управлять всеми видами объектов в трех измерениях: линии, плоскости, конусы, сферы, многогранники. Вы можете…
- №4
- 39,53 МБ
- дата добавления неизвестна
- изменен
www.twirpx.com
РАЗРАБОТКИ | В категории разработок: 71 Фильтр по целевой аудитории — Целевая аудитория -для 1 классадля 2 классадля 3 классадля 4 классадля 5 классадля 6 классадля 7 классадля 8 классадля 9 классадля 10 классадля 11 классадля учителядля классного руководителядля дошкольниковдля директорадля завучейдля логопедадля психологадля соц.педагогадля воспитателя Данная программа создает примеры с обыкновенными дробями. Можно выбирать диапазон чисел в числителе и знаменателе, а также тип примеров по знаку действия. Доступна случайная генерация примеров. Ведется подсчет верно решенных примеров, неверно решенных и пропущенных примеров. Для пропуска примера достаточно кликнуть по примеру мышкой. Для работы программы требуется установленная на компьютере JRE версии не ниже 1.4.0. Обновлено: Добавлена версия 2.0. В этой версии, на данный момент, увеличен шрифт в области вывода примеров, заменен знак деления (слеш на двоеточие), произведена оптимизация кода и другие небольшие изменения. Обновлено: Добавлена версия 3.0. В этой версии исправлена ошибка с вычислением целой части. Целевая аудитория: для 5 класса Просто надо было автоматизировать выполнение рутинной работы. Можно было использовать Excel, но вдруг пришла идея создать простую Тестировал примерами из пособия Е. Данко, А. Г . Попов, Т. Я. Кожевникова «Высшая математика в упражнениях и задачах».
Целевая аудитория: для учителя В новой версии приложения добавлена возможность демонстрировать простые числа. По указанному пользователем числу n выводится n-е по порядку простое число. Кроме того, есть возможность демонстрировать первые n простых чисел, идущих после указанного числа m и простые числа, меньшие числа m. Для этого надо выбрать одну из трех кнопок. Приложение имеет две вкладки. Вкладка <Делители, простые делители, вид и разложение> — для информации о делителях указанного пользователем числа (эта часть существенно переделана в новой версии). Вкладка <Простые числа> — для демонстрации простых чисел. Если надо получить первые n натуральных чисел, то следует указать значение для m 0 или 1. Целевая аудитория: для 6 класса Программа составлена для учащихся 6 класса. Программа генерирует случайные числа и предлагает выполнить действия сложения, умножения и деления с обыкновенными дробями, на экране показывает правильный ответ и ответ обучаемого. Программа работает только в операционной системе Windows. Компьютерная программка –тренажёр «действия с обыкновенными дробями» может быть использована для отработки навыков счёта в форме индивидуальной самостоятельной работы во время урока и внеурочное время.
Целевая аудитория: для 6 класса Программа создана для учащихся 5 и 6 класса. Программа генерирует случайные числа и предлагает выполнить действия сложения, умножения и деления с десятичными дробями, на экране показывает правильный ответ и ответ обучаемого. Разделителем между целой и дробной частью служит точка вместо запятой. Программа работает только в операционной системе Windows. Если кнопки не умещаются на экране, следует установить разрешение экрана 1024 на 768 или выше. Компьютерная программка «5 и 6 кл. действия с десятичными дробями может быть использована для отработки навыков счёта с десятичными дробями в форме индивидуальной самостоятельной работы во время урока и внеурочное время, а также для изготовления карточек.
Целевая аудитория: для 5 класса В текстовые поля вводятся обыкновенные дроби. Программка подсчитывает сумму, произведение и частное двух и трёх дробей. дроби могут быть как положительные, так и отрицательные. Программку можно использовать для самоконтроля при выполнении самостоятельной работы.
Целевая аудитория: для 6 класса Программа для отработки вычислительных навыков по темам «выделение целой части» и «сокращение дробей». Работает только в операционной системе Windows. Целевая аудитория: для 6 класса Trigonom — приложение, которое составлено из ранее составленных и выставленных на портал приложений по отдельным вопросам тригонометрии. Произведены некоторые улучшения, добавлена возможность «выполнять» преобразования графиков тригонометрических функций, свойства тригонометрических функций не только демонстрируются на графике, но и указываются, тоже касается базовых уравнений и неравенств.Основные понятия не только показаны визуально, есть возможность прочитать числовые значения. Думаю, что приложение будут использовать учителя математики.
Целевая аудитория: для учителя Программа генерирует примеры и уравнения по 14-ти разным схемам. Программа позволяет вести запись результатов, а также выставляет оценки по пятибалльной системе. Программа требует наличия на компьютере пользователя виртуальной машины Java и в случае ее отсутствия поможет ее установить. Добавлена новая версия 2.0: В этой версии повышена стабильность приложения, и исправлены некоторые ошибки. Удалены всплывающие сообщения за их ненадобностью. Добавлена новая версия 3.0: В новой версии полностью переписан интерфейс приложения. Большинство элементов перемещено в меню. Исправлены некоторые ошибки. Добавлена новая версия 4.0: В этой версии в формулах примеров и уравнений знак деления (/) заменен на двоеточие. Переписана логика регистрации в файле истории.
Целевая аудитория: для 7 класса Программа «Соответствие» — реализация тренажера по решению задач. Но ее можно использовать и для определения уровня учебных достижений. В каждом задании (их всего 20) требуется установить функциональное, инъективное соответствие между элементами двух списков. Задания взяты из разных разделов математики. В архиве inject имеется файл read_me, в котором находятся все, что требуется для работы с приложением и его использовании.
Целевая аудитория: для 11 класса | Конкурсы Диплом и справка о публикации каждому участнику! |
www.uchportal.ru
Программы математических расчётов (МatLab ) — курсовая работа
ФГОУ ВПО «КУБАНСКИЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ УНИВЕРСИТЕТ»
Кафедра системного анализа и обработки информации
КУРСОВАЯ РАБОТА
по дисциплине информатика
на тему: Программы математических расчётов (МatLab )
выполнил студент группы ФК-1104 Самарина Э.А.
Допущен к защите
Руководитель проекта Скворцова Н.М.
Нормоконтролер________________
Защищен____________________
Члены комиссии______________________
______________________________
______________________________
______________________________
Краснодар – 2012
ФГОУ ВПО «КУБАНСКИЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ УНИВЕРСИТЕТ»
Кафедра системного анализа и обработки информации
УТВЕРЖДАЮ:
Зав. Кафедрой____________________
ЗАДАНИЕ
на курсовую работу
Студенту: Самариной Элине Андреевне группы 1104курса 2
Факультета специальности Финансы и кредит
Тема проекта: Программы математических расчётов (МatLab)
Содержание задания:___________
______________________________
Объем работы:
а) пояснительная записка к
б) графическая часть_____________
Рекомендуемая литература:___________________
______________________________
Срок выполнения проекта: с «1» октября по «20» декабря 2011г.
Срок защиты:
Дата выдачи задания: «1» октября 2012 г.
Дата сдачи проекта
на кафедру:
Руководитель проекта__________
Задание принял студент_______________________
Краснодар – 2011
Реферат
Ключевые слова: ПРОГРАММЫ МАТЕМАТИЧЕСКИХ РАСЧЁТОВ, СУПЕРКАЛЬКУЛЯТОРЫ, СРЕДА MATLAB, ФУНКЦИЯ, ОПЕРАТОР.
Цель работы – исследование функциональных возможностей программ математического расчёта на примере MatLab.
Объект исследования – программа математических расчётов MatLab.
Предмет исследования – функциональные возможности системы MatLab.
Система MATLAB является интерактивной системой для выполнения инженерных и научных расчетов, которая ориентирована на работу с массивами данных.
MATLAB состоит из пяти основных частей.
1) Язык MATLAB — это язык матриц и массивов высокого уровня с управлением потоками, функциями, структурами данных, вводом-выводом и особенностями объектно-ориентированного программирования.
2) Среда MATLAB — это набор инструментов и приспособлений, с которыми работает пользователь или программист MATLAB. Она включает в себя средства для управления переменными в рабочем пространстве MATLAB, вводом и выводом данных, а также создания, контроля и отладки М-файлов и приложений MATLAB.
3) Управляемая графика — это графическая система MATLAB, которая включает в себя команды высокого уровня для визуализации двух- и трехмерных данных, обработки изображений, анимации и иллюстрированной графики. Она также включает в себя команды низкого уровня, позволяющие полностью редактировать внешний вид графики.
4) Библиотека математических функций- это обширная коллекция вычислительных алгоритмов от элементарных функций.
5) Программный интерфейс- это библиотека, которая позволяет писать программы на Си и Фортране, которые взаимодействуют с MATLAB.
Результат работы: использование Math Lab для автоматизации математических расчётов.
MATLAB – это интерактивная
система, основным объектом
В курсовой работе реализован
алгоритм решения финансово-
СОДЕРЖАНИЕ
ВВЕДЕНИЕ
Развитие научно-технического прогресса привело к тому, что на сегодняшний день ни одна серьезная разработка в любой отрасли науки и производства не обходится без трудоемких математических расчетов. С одной стороны это способствует существенному расширению содержания обучения математическим дисциплинам, особенно в сфере прикладной математики, что нацелено на формирование специалистов, способных на высоком профессиональном уровне владеть требуемыми подходами к решению сложнейших математических задач, возникающих на практике. С другой стороны, усложнение и расширение математических расчетов, и существенный всплеск развития современных информационных технологий влекут за собой массовую разработку и профессиональное использование специализированных компьютерных систем автоматизации различных математических операций. Очевидно, что два перечисленных динамично развивающихся процесса влекут за собой и следствие, связанное с необходимостью внедрения компьютерных средств автоматизации расчетов в систему подготовки специалистов в рамках высшего профессионального образования. Данная задача требует отдельного детального рассмотрения возможных компьютерных математических пакетов и подходов к их классификации с точки зрения специфики их функционирования и использования для достижения образовательных целей.
ГЛАВА 1. СИСТЕМЫ МАТЕМАТИЧЕСКИХ РАСЧЁТОВ
1.1 Основные сведения
о системах математических расчётов
Для автоматизации математических расчетов используются компьютерные программы узкого специального назначения или универсальные программные средства, составленные с использованием конструкций языков высокого уровня (таких как Фортран, Pascal, Cи и других). Однако разработка таких программных средств, имеющих современный графический интерфейс, требует как соответствующей подготовки в практике программирования, так и достаточно большого времени, которые могут отсутствовать у инженеров или исследователей.
Широкую известность и заслуженную популярность еще в середине восьмидесятых годов прошлого века приобрели так называемые интегрированные системы для автоматизации математических расчетов. В качестве примера подобной системы можно отметить достаточно распространенное и популярное программное обеспечение семейства MathCаd, разрабатываемое американской фирмой MathSoft. Существенным достоинством подобного программного обеспечения является то, что в нем описание решения математических задач дается с помощью привычных для человека математических формул и знаков. Такой же вид имеют и результаты вычислений. Более того, в последних версиях MathCаd пользователям предоставлена возможность составлять «собственные» программы-функции и использовать принципы модульного программирования для реализации оригинальных вычислительных алгоритмов.
Спектр подобных компьютерных
средств автоматизации
Определенный интерес с точки зрения преподавания прикладной математики вызывает и система MatLab, являющаяся одной из старейших, тщательно проработанных и проверенных временем систем автоматизации математических расчетов, построенная на расширенном представлении и применении матричных операций. Это нашло отражение в названии системы – MATrix LABoratory – матричная лаборатория. Подобная система, очевидно, должна найти широчайшее применение не только в процессе обучения алгебре, геометрии, математическому моделированию, решению уравнений состояния динамических объектов и другим темам и дисциплинам математической подготовки, но и должна являться одним из базовых инструментов, которым должен владеть выпускник по окончании обучения.
MatLab обладает достаточно богатыми дидактическими возможностями в связи с тем, что синтаксис языка программирования данной системы продуман настолько тщательно, что ориентация на работу со столь сложными и громоздкими объектами, каковыми являются матрицы, почти не ощущается теми пользователями, которых не интересуют непосредственно матричные вычисления. В обширном и постоянно пополняемом комплексе команд, функций и прикладных программ (пакетов расширения и пакетов инструментов) системы содержатся специальные средства для электротехнических и радиотехнических расчетов (операции с комплексными числами, матрицами, векторами и полиномами, обработка данных, анализ сигналов и цифровая фильтрация), обработки изображений, реализации нейронных сетей, а также средства, относящиеся к другим новым направлениям науки и техники. Они иллюстрируются множеством примеров, полезных с точки зрения практики и учебного процесса.
Важными достоинствами системы являются открытость и расширяемость. Большинство ее команд и функций реализованы в виде текстовых файлов и файлов на языке Си, причем все файлы доступны для модификации. Пользователю дана возможность создавать не только отдельные файлы, но и библиотеки файлов для реализации специфических задач. Поразительная легкость модификации системы и возможность ее адаптации к решению специфических задач науки и техники привели к созданию десятков пакетов прикладных программ, намного расширивших сферы применения системы. Некоторые из них, например Notebook (интеграция с текстовым процессором Word и подготовка «живых» электронных книг), Symbolic Math, Extended Symbolic Math (символьные вычисления с применением ядра системы Maple) и Simulink (моделирование динамических систем и устройств, заданных в виде системы блоков), настолько органично интегрировались с системой MatLab, что стали ее составными частями.
Слово «интегрированный» в названии большинства математических пакетов указывает на то, что в подобных системах объединены удобная оболочка, редактор выражений и текстовых комментариев, вычислитель и графический программный процессор, что является достаточно привлекательным с точки зрения практики обучения. В этом случае педагогу и студентам не приходится использовать различные инструменты, ориентируясь на различные подходы к оперированию и вычислениям. В новой версии средств автоматизации математических расчетов и, в частности, в MatLab, используются такие мощные типы данных, как многомерные массивы, массивы ячеек, массивы структур, массивы Java и разреженные матрицы, что открывает возможности применения подобных систем при создании и отладке новых алгоритмов матричных и основанных на них параллельных вычислений и крупных баз данных.
В целом MаtLab – это достаточно богатый комплекс реализаций современных численных методов компьютерной математики, созданных за последние три десятка лет. Данная интегрированная система, используемая в обучении, вобрала в себя опыт, правила и методы математических вычислений, накопленные за тысячи лет развития математики. Это сочетается с мощными средствами графической визуализации и даже анимационной графики. Систему с прилагаемой к ней обширной документацией вполне можно рассматривать как фундаментальный многотомный электронный справочник по математическому обеспечению массовых персональных компьютеров, что должно быть учтено в процессе формирования и развития систем обучения основам оперирования с информационными технологиями и дисциплинам прикладной математической подготовки.
1.2. Классификация пакетов математических программ. Суперкалькуляторы.
Частично пакеты математических программ классифицированы в публикациях Т.Э. Кренкеля, А.Г. Когана и А.М. Тараторина . Ими выделены три категории программ,
имеющие отношение к автоматизации математических расчетов:
- библиотеки программ для математических расчетов, включающие в себя набор подпрограмм численного анализа;
- специализированные пакеты для решения конкретных математических задач: специализированные системы для статистического анализа, решения дифференциальных уравнений и др.;
- декларативные языки и системы для математических вычислений: специализированные языки программирования и диалоговые системы, позволяющие формулировать и решать расчетные задачи максимально естественным образом.
Компьютерные системы автоматизации математических расчетов следует отнести к классу прикладных программных средств. В свою очередь, все системы автоматизации расчетов можно разделить на так называемые суперкалькуляторы и еще более сложные системы аналитических вычислений (пример – система Reduce). Возможна и более глубокая градация описываемых средств автоматизации вычислений. В частности, все суперкалькуляторы можно разделить на виды в зависимости от их функционального назначения. В этом случае можно выделить в обособленные подвиды пакеты прикладных программ для работы с табличной информацией (табличные процессоры, такие как SuperCalc, Excel, Lotus) и специализированные пакеты прикладных программ для математических расчетов (такие как Derive и MathCad).
Согласно определения Г. Берга, суперкалькулятором называется программа, которая умеет «не просто вычислять и вычерчивать графики простых функций – в нем должно быть предусмотрено использование встроенных переменных и то, что может быть названо «программированностью».
На современном этапе развития программного обеспечения достаточно сложно провести четкую грань между различными классами систем автоматизации расчетов. Происходит очевидное слияние суперкалькуляторов и систем аналитических вычислений, что особенно четко просматривается в функциональных возможностях таких достаточно новых систем как Derive, Математика, Maple, MathCad Plus 5.0. Все они позволяют проводить как числовые, так и аналитические расчеты.
Кроме вышеназванных подходов к классификации и описанию суперкалькуляторов, можно выделить и критерии, согласно которых все суперкалькуляторы можно разделить на программы «ограниченного действия» (Eureka, PC-MatLab), ориентированные на высокоэффективное решение математических задач ограниченного круга и универсальные программы (MathCad), оперирующие с достаточно общими аналитическими объектами, обладающие широким набором алгоритмов и развитым интерфейсом.
student.zoomru.ru
Python для математических вычислений / Habr
 Экосистема языка python стремительно развивается. Это уже не просто язык общего назначения. С его помощью можно успешно разрабатывать веб-приложения, системные утилиты и много другое. В этой заметке мы сконцентрируемся все же на другом приложении, а именно на научных вычислениях.
Экосистема языка python стремительно развивается. Это уже не просто язык общего назначения. С его помощью можно успешно разрабатывать веб-приложения, системные утилиты и много другое. В этой заметке мы сконцентрируемся все же на другом приложении, а именно на научных вычислениях.
Мы попытаемся найти в языке функции, которые обычно требуем от математических пакетов. Рассмотрим сильные и слабые стороны идеи использования python вместо MATLAB, Maple, Mathcad, Mathematica.
Среда разработки
Код на python может быть помещен в файл с расширением .py и отправлен интерпретатору для выполнения. то классический подход, который обычно разбавляется использованием среды разработки, например pyCharm. Однако, для python (и не только) существует другой способ взаимодействия с интерпретатором — интерактивные блокноты jupyter, сохраняющие промежуточное состояние программы между выполнением различных блоков кода, которые могут быть выполнены в произвольном порядке. Этот способ взаимодействия позаимствован у блокнотов Mathematica, позже аналог появился и в MATLAB (Live script).
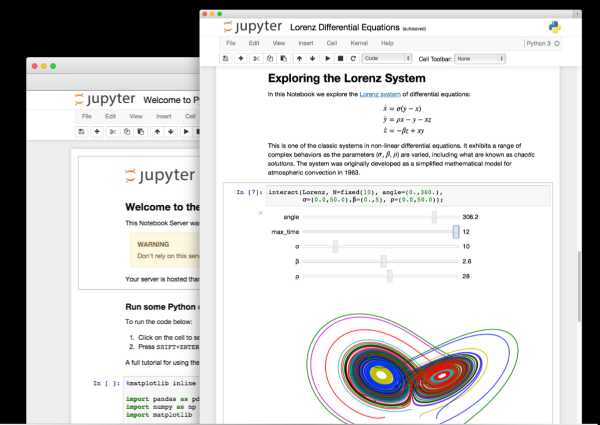
Таким образом вся работа с python-кодом переносится в браузер. Получившейся блокнот можно открыть с помощью nbviewer.jupyter.org, github (и gist) умеют самостоятельно показывать содержимое таких файлов (преобразовывать).
Из браузерной природы jupyter следуют его недостатки: отсутствие отладчика и проблемы с печатью большого количества информации (зависание окна браузера). Последняя проблема решается расширением, которое ограничивает максимальное количество символов, которое можно вывести в результате выполнения одной ячейки.
Визуализация данных
Для визуализации данных обычно используется библиотека matplotlib, команды которой очень похожи на MATLABовские. В Stanford’е была разработана библиотека, расширяющая возможности matplotlib — seaborn (необычные графики для статистики).
Рассмотрим пример построения гистограммы для сгенерированной выборки данных.
import numpy as np
import matplotlib.mlab as mlab
import matplotlib.pyplot as plt
# example data
mu = 100 # mean of distribution
sigma = 15 # standard deviation of distribution
x = mu + sigma * np.random.randn(10000)
num_bins = 50
# the histogram of the data
n, bins, patches = plt.hist(x, num_bins, normed=1, facecolor='green', alpha=0.5)
# add a 'best fit' line
y = mlab.normpdf(bins, mu, sigma)
plt.plot(bins, y, 'r--')
plt.xlabel('Smarts')
plt.ylabel('Probability')
plt.title(r'Histogram of IQ: $\mu=100$, $\sigma=15$')
# Tweak spacing to prevent clipping of ylabel
plt.subplots_adjust(left=0.15)
plt.show()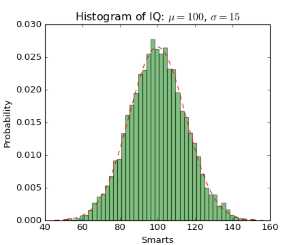
Мы видим, что синтаксис matplotlib очень похож на синтаксис MATLAB. Стоит так же заметить, что в заголовке графика используется latex.
Вычислительные математика
Для линейной алгебры в python принято использовать numpy, вектора и матрицы которого типизированы, в отличии от встроенный в язык списков. Для научных вычислений используется библиотека scipy.
Специально для пользователей MATLAB написан гайд по переходу с MATLAB на numpy.
import scipy.integrate as integrate
import scipy.special as special
result = integrate.quad(lambda x: special.jv(2.5,x), 0, 4.5)В данном примере численно вычисляется значение определенного интеграла функции Бесселя на отрезке [0,0.45] с помощью библиотеки QUADPACK (Fortran).
Символьные вычисления
Для использования символьных вычислений можно использовать библиотеку sympy. Однако, код, написанный с помощью sympy, уступает в красоте коду, написанному на Mathematica, которая специализирована на символьных вычислениях.
# python
from sympy import Symbol, solve
x = Symbol("x")
solve(x**2 - 1)По функциональности Sympy уступает Mathematica, однако, с учетом ваших потребностей, может оказаться, что для вас их возможности приблизительно равны. Более подробное сравнение можно найти в wiki репозитория sympy.
Ускоряем код
Для ускорения вашего кода за счет преобразования в C++ может быть реализовано по средствам библиотеки theano. Платой за такое ускорение становится синтаксис, теперь вам требуется писать theano-ориентированные функции и указывать типы всех переменных.
import theano
import theano.tensor as T
x = T.dmatrix('x')
s = 1 / (1 + T.exp(-x))
logistic = theano.function([x], s)
logistic([[0, 1], [-1, -2]])Некоторые библиотеки для сверточных нейронных сетей, такие как Lasagne и Keras, используют theano для своих вычислений. Стоит так же добавить, что theano поддерживает ускорение за счет вычислений на GPU.
Машинное обучение
Самой популярной библиотекой машинного обучения для python является scikit-learn, которая содержит все основные алгоритмы машинного обучения, а так же метрики качества, инструменты для валидации алгоритмов, инструменты для пред-обработки данных.

from sklearn import svm
from sklearn import datasets
clf = svm.SVC()
iris = datasets.load_iris()
X, y = iris.data, iris.target
clf.fit(X, y)
clf.predict(X)Для работы загрузки данных из табличных форматов данных (excel, csv) обычно используется pandas. Загруженные данные представляются в памяти в виде DataFrame’ов, к которым можно применять различные операции: как строчные (построчная обработка), так и групповые (фильтры, группировки). Обзор основных функций pandas можно найти в презентации «Pandas: обзор основных функций» (Автор: Александр Дьяконов, профессор МГУ).
Не все так гладко…
Однако, не все так гладко в python. Например, сейчас уживается две версии языка 2. и 3., обе они развиваются параллельно, однако синтаксис 2ой версии не совместим полностью с синтаксисом 3ей версии.
Еще одна проблема может возникнуть у вас, если вы не обладатель linux, в этом случае при установке ряда библиотек у вас могут возникнуть трудности, некоторые библиотеки будут полностью не совместимы, например tensorflow.
Библиотеки, о которых шла речь
- Jupyter (онлайн блокноты)
- Matplotlib (графики)
- Seaborn (графики)
- Numpy (линейная алгебра)
- Scipy (научные вычисления)
- Sympy (символьные вычисления)
- Theano (преобразование в C++, вычисления на GPU)
- Scikit-learn (машинное обучение)
- Pandas (загрузка данных и простые операции над ними)
P.S: все библиотеки для python, о которых говорилось данной статье, имеют открытый исходный код и распространяются бесплатно. Для их загрузки можно воспользоваться командой pip или просто скачать сборку Anaconda, которая содержит все основные библиотеки.
habr.com