Как выглядит график функции корень из х. График функции квадратного корня, преобразования графиков
Основные цели:
1) сформировать представление о целесообразности обобщённого исследования зависимостей реальных величин на примере величин, связанных отношением у=
2) формировать способность к построению графика у= и его свойства;
3) повторить и закрепить приёмы устных и письменных вычислений, возведение в квадрат, извлечение квадратного корня.
Оборудование, демонстрационный материал: раздаточный материал.
1. Алгоритм:
2. Образец для выполнения задания в группах:
3. Образец для самопроверки самостоятельной работы:
4. Карточка для этапа рефлексии:
1) Я понял, как построить график функции у=.
2) Я могу по графику перечислить его свойства.
3) Я не допустил ошибок в самостоятельной работе.
4) Я допустил ошибки в самостоятельной работе (перечислить эти ошибки и указать их причину).
Ход урока
1. Самоопределение к учебной деятельности
Самоопределение к учебной деятельности
Цель этапа:
1) включить учащихся в учебную деятельность;
2) определить содержательные рамки урока: продолжаем работать с действительными числами.
Организация учебного процесса на этапе 1:
– Что мы изучали на прошлом уроке? (Мы изучали множество действительных чисел, действия с ними, построили алгоритм для описания свойств функции, повторяли функции изученные в 7 классе).
– Сегодня мы продолжим работать с множеством действительных чисел, функцией.
2. Актуализация знаний и фиксация затруднений в деятельности
Цель этапа:
1) актуализировать учебное содержание, необходимое и достаточное для восприятия нового материала: функция, независимая переменная, зависимая переменна, графики
y = kx + m, y = kx, y =c, y =x 2 , y = — x 2 ,
2) актуализировать мыслительные операции, необходимые и достаточные для восприятия нового материала: сравнение, анализ, обобщение;
3) зафиксировать все повторяемые понятия и алгоритмы в виде схем и символов;
4) зафиксировать индивидуальное затруднение в
деятельности, демонстрирующее на личностно
значимом уровне недостаточность имеющихся
знаний.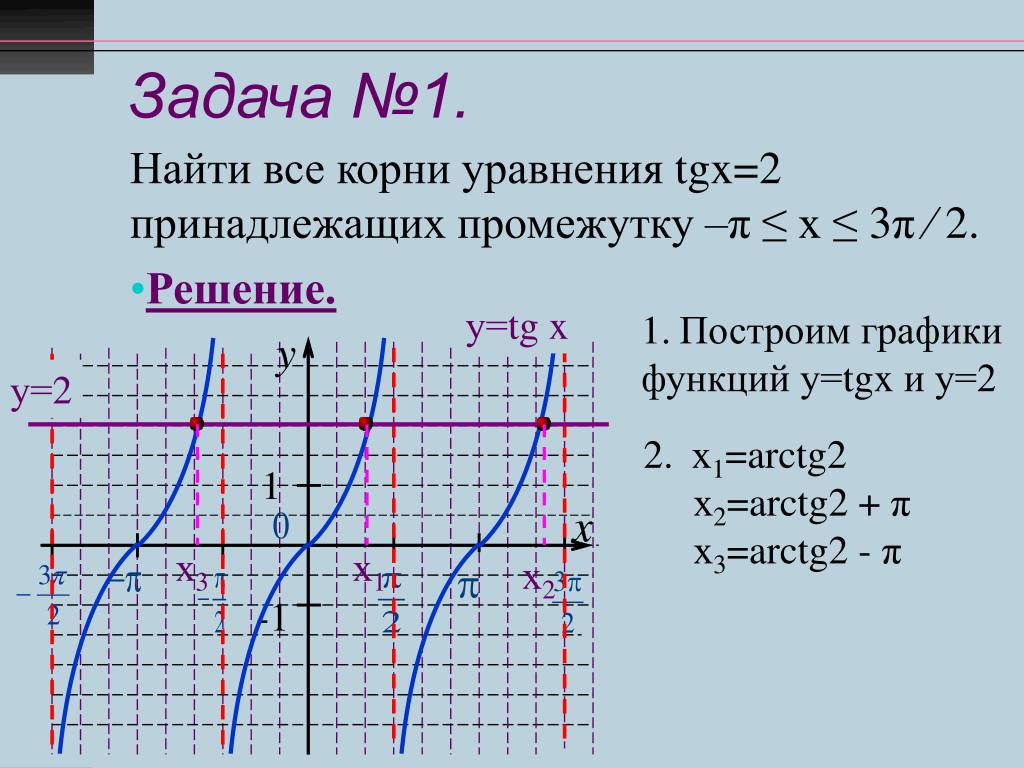
Организация учебного процесса на этапе 2:
1. Давайте вспомним как можно задать зависимости между величинами? (С помощью текста, формулы, таблицы, графика)
2. Что называется функцией? (Зависимость между двумя величинами, где каждому значению одной переменной соответствует единственное значение другой переменной y = f(x)).
Как называется х? (Независимая переменная — аргумент)
Как называется у? (Зависимая переменная).
3. В 7- м классе мы изучили функции? (y = kx + m, y = kx, y =c, y =x 2 , y = — x 2 , ).
Индивидуальное задание:
Что является графиком функций y = kx + m, y =x 2 , y = ?
3. Выявление причин затруднений и постановка цели деятельности
Цель этапа:
1) организовать коммуникативное взаимодействие, в ходе которого выявляется и фиксируется отличительное свойство задания, вызвавшего затруднение в учебной деятельности;
2) согласовать цель и тему урока.
Организация учебного процесса на этапе 3:
– Что особенного в этом задании? (Зависимость
задана формулой y = с которой мы еще не встречались).
– Какая цель урока? (Познакомиться с функцией y = , ее свойствами и графиком. Функцией в таблице определять вид зависимости, строить формулу и график.)
– Можно сформулировать тему урока? (Функция у=, ее свойства и график).
– Запишите тему в тетради.
4. Построение проекта выхода из затруднения
Цель этапа:
1) организовать коммуникативное взаимодействие для построения нового способа действия, устраняющего причину выявленного затруднения;
2) зафиксировать новый способ действия в знаковой, вербальной форме и с помощью эталона.
Организация учебного процесса на этапе 4:
Работу на этапе можно организовать по группам, предложив группам построить график y = , затем проанализировать получившиеся результаты. Также группам можно предложить по алгоритму описать свойства данной функции.
5. Первичное закрепление во внешней речи
Цель этапа: зафиксировать изученное учебное содержание во внешней речи.
Организация учебного процесса на этапе 5:
Постройте график у= — и опишите его свойства.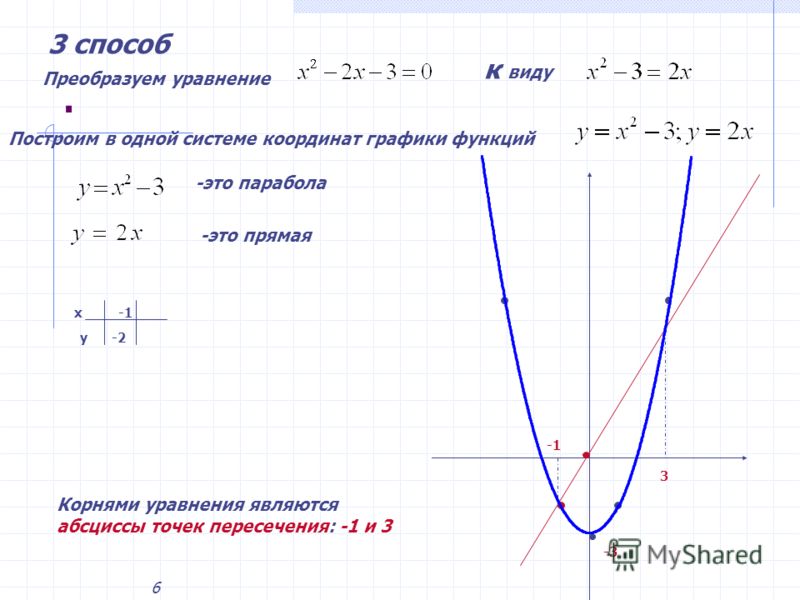
Свойства у= — .
1.Область определения функции.
2.Область значений функции.
3. y = 0, y> 0, y
y =0, если x = 0.
y
4.Возрастания, убывания функции.
Функция убывает при х .
Построим график у=.
Выделим его часть на отрезке . Заметим, что у наим. = 1 при х = 1, а у наиб. =3 при х = 9.
Ответ: у наим. = 1, у наиб. =3
6. Самостоятельная работа с самопроверкой по эталону
Цель этапа: проверить своё умение применять новое учебное содержание в типовых условиях на основе сопоставления своего решения с эталоном для самопроверки.
Организация учебного процесса на этапе 6:
Учащиеся выполняют задание самостоятельно, проводят самопроверку по эталону, анализируют, исправляют ошибки.
Построим график у=.
С помощью графика найдите наименьшее и наибольшее значения функции на отрезке .
7. Включение в систему знаний и повторение
Цель этапа: тренировать навыки
использования нового содержания совместно с
ранее изученным: 2) повторить учебное содержание,
которое потребуется на следующих уроках.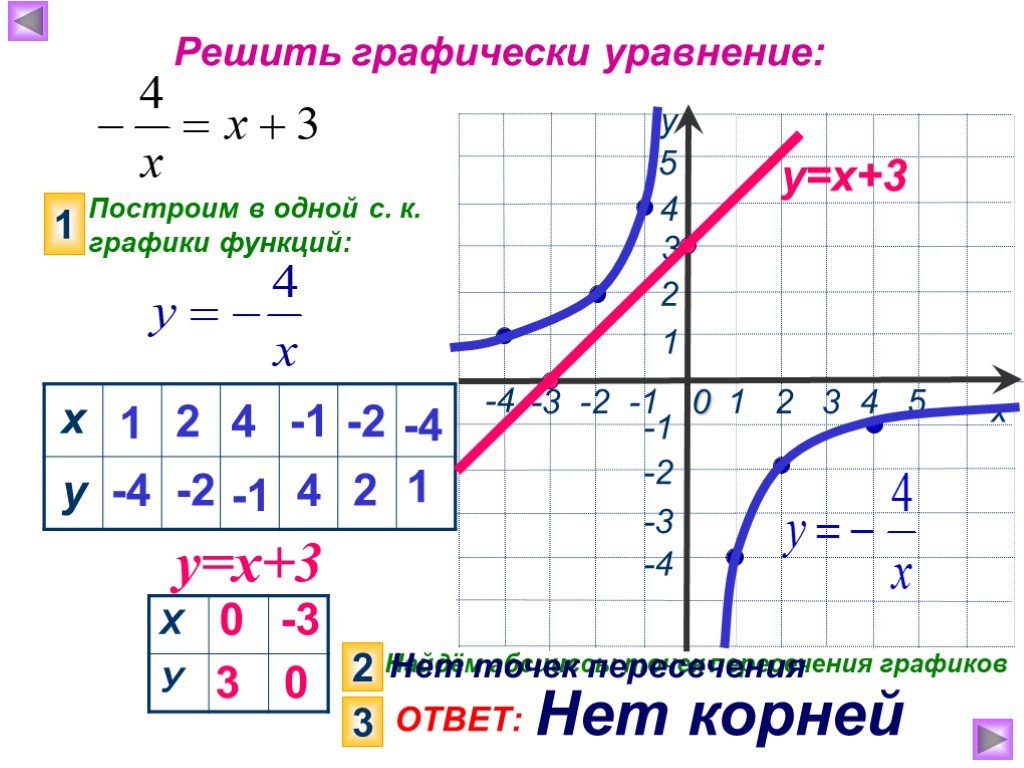
Организация учебного процесса на этапе 7:
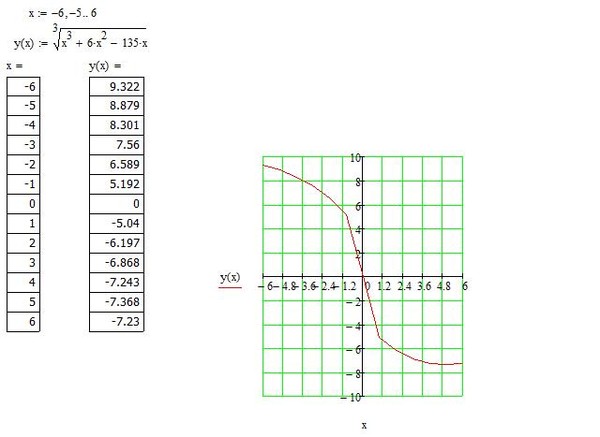
Решите графически уравнение: = х – 6.
Один ученик у доски остальные в тетрадях.
8. Рефлексия деятельности
Цель этапа:
1) зафиксировать новое содержание, изученное на уроке;
2) оценить собственную деятельность на уроке;
3) поблагодарить одноклассников, которые помогли получить результат урока;
4) зафиксировать неразрешённые затруднения как направления будущей учебной деятельности;
5) обсудить и записать домашнее задание.
Организация учебного процесса на этапе 8:
– Ребята, какая цель стояла сегодня перед нами? (Изучить функцию у=, ее свойства и график).
– Какие знания нам помогли в достижении цели? (Умение искать закономерности, умение читать графики.)
– Проанализируйте свою деятельность на уроке. (Карточки с рефлексией)
Домашнее задание
п. 13 (до примера 2) № 13.3, 13.4
Решите графически уравнение.
Основные цели:
1) сформировать представление о целесообразности обобщённого исследования зависимостей реальных величин на примере величин, связанных отношением у=
2) формировать способность к построению графика у= и его свойства;
3) повторить и закрепить приёмы устных и
письменных вычислений, возведение в квадрат,
извлечение квадратного корня.
Оборудование, демонстрационный материал: раздаточный материал.
1. Алгоритм:
2. Образец для выполнения задания в группах:
3. Образец для самопроверки самостоятельной работы:
4. Карточка для этапа рефлексии:
1) Я понял, как построить график функции у=.
2) Я могу по графику перечислить его свойства.
3) Я не допустил ошибок в самостоятельной работе.
4) Я допустил ошибки в самостоятельной работе (перечислить эти ошибки и указать их причину).
Ход урока
1. Самоопределение к учебной деятельности
Цель этапа:
1) включить учащихся в учебную деятельность;
2) определить содержательные рамки урока: продолжаем работать с действительными числами.
Организация учебного процесса на этапе 1:
– Что мы изучали на прошлом уроке? (Мы изучали множество действительных чисел, действия с ними, построили алгоритм для описания свойств функции, повторяли функции изученные в 7 классе).
– Сегодня мы продолжим работать с множеством
действительных чисел, функцией.
2. Актуализация знаний и фиксация затруднений в деятельности
Цель этапа:
1) актуализировать учебное содержание, необходимое и достаточное для восприятия нового материала: функция, независимая переменная, зависимая переменна, графики
y = kx + m, y = kx, y =c, y =x 2 , y = — x 2 ,
2) актуализировать мыслительные операции, необходимые и достаточные для восприятия нового материала: сравнение, анализ, обобщение;
3) зафиксировать все повторяемые понятия и алгоритмы в виде схем и символов;
4) зафиксировать индивидуальное затруднение в деятельности, демонстрирующее на личностно значимом уровне недостаточность имеющихся знаний.
Организация учебного процесса на этапе 2:
1. Давайте вспомним как можно задать зависимости между величинами? (С помощью текста, формулы, таблицы, графика)
2. Что называется функцией? (Зависимость между
двумя величинами, где каждому значению одной
переменной соответствует единственное значение
другой переменной y = f(x)).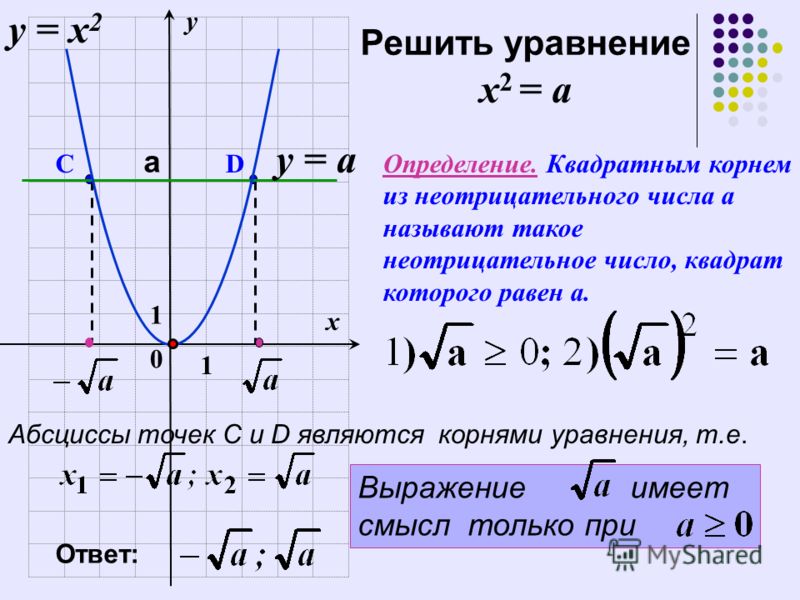
Как называется х? (Независимая переменная — аргумент)
Как называется у? (Зависимая переменная).
3. В 7- м классе мы изучили функции? (y = kx + m, y = kx, y =c, y =x 2 , y = — x 2 , ).
Индивидуальное задание:
Что является графиком функций y = kx + m, y =x 2 , y = ?
3. Выявление причин затруднений и постановка цели деятельности
Цель этапа:
1) организовать коммуникативное взаимодействие, в ходе которого выявляется и фиксируется отличительное свойство задания, вызвавшего затруднение в учебной деятельности;
2) согласовать цель и тему урока.
Организация учебного процесса на этапе 3:
– Что особенного в этом задании? (Зависимость задана формулой y = с которой мы еще не встречались).
– Какая цель урока? (Познакомиться с функцией y = , ее свойствами и графиком. Функцией в таблице определять вид зависимости, строить формулу и график.)
– Можно сформулировать тему урока? (Функция у=, ее свойства и
график).
– Запишите тему в тетради.
4. Построение проекта выхода из затруднения
Цель этапа:
1) организовать коммуникативное взаимодействие для построения нового способа действия, устраняющего причину выявленного затруднения;
2) зафиксировать новый способ действия в знаковой, вербальной форме и с помощью эталона.
Организация учебного процесса на этапе 4:
Работу на этапе можно организовать по группам, предложив группам построить график y = , затем проанализировать получившиеся результаты. Также группам можно предложить по алгоритму описать свойства данной функции.
5. Первичное закрепление во внешней речи
Цель этапа: зафиксировать изученное учебное содержание во внешней речи.
Организация учебного процесса на этапе 5:
Постройте график у= — и опишите его свойства.
Свойства у= — .
1.Область определения функции.
2.Область значений функции.
3. y = 0, y> 0, y
y =0, если x = 0.
y
4.Возрастания, убывания функции.
Функция убывает при х .
Построим график у=.
Выделим его часть на отрезке . Заметим, что у наим. = 1 при х = 1, а у наиб. =3 при х = 9.
Ответ: у наим. = 1, у наиб. =3
6. Самостоятельная работа с самопроверкой по эталону
Цель этапа: проверить своё умение применять новое учебное содержание в типовых условиях на основе сопоставления своего решения с эталоном для самопроверки.
Организация учебного процесса на этапе 6:
Учащиеся выполняют задание самостоятельно, проводят самопроверку по эталону, анализируют, исправляют ошибки.
Построим график у=.
С помощью графика найдите наименьшее и наибольшее значения функции на отрезке .
7. Включение в систему знаний и повторение
Цель этапа: тренировать навыки использования нового содержания совместно с ранее изученным: 2) повторить учебное содержание, которое потребуется на следующих уроках.
Организация учебного процесса на этапе 7:
Решите графически уравнение: = х – 6.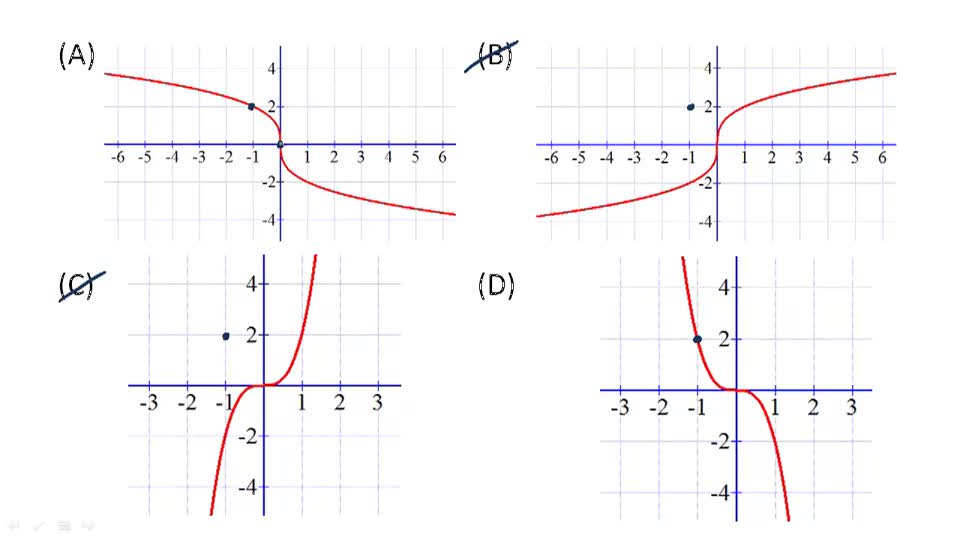
Один ученик у доски остальные в тетрадях.
8. Рефлексия деятельности
Цель этапа:
1) зафиксировать новое содержание, изученное на уроке;
2) оценить собственную деятельность на уроке;
3) поблагодарить одноклассников, которые помогли получить результат урока;
4) зафиксировать неразрешённые затруднения как направления будущей учебной деятельности;
5) обсудить и записать домашнее задание.
Организация учебного процесса на этапе 8:
– Ребята, какая цель стояла сегодня перед нами? (Изучить функцию у=, ее свойства и график).
– Какие знания нам помогли в достижении цели? (Умение искать закономерности, умение читать графики.)
– Проанализируйте свою деятельность на уроке. (Карточки с рефлексией)
Домашнее задание
п. 13 (до примера 2) № 13.3, 13.4
Решите графически уравнение.
Урок и презентация на тему: «Степенные функции. Корень кубический. Свойства корня кубического»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой. 3}=\frac{a}{b}$.
3}=\frac{a}{b}$.
Получили, что число $\sqrt{\frac{a}{b}}$ в кубе равно $\frac{a}{b}$ и тогда равно $\sqrt{\frac{a}{b}}$, что и требовалось доказать.
Ребята, давайте построим график нашей функции.
1) Область определения множество действительных чисел.
2) Функция нечетная, так как $\sqrt{(-x)}$=-$\sqrt{x}$. Далее рассмотрим нашу функцию при $х≥0$, после отразим график относительно начала координат.
3) Функция возрастает при $х≥0$. Для нашей функции, большему значению аргумента соответствует большее значение функции, что и означает возрастание.
4) Функция не ограничена сверху. На самом деле из сколь угодно большого числа можно вычислить корень третьей степени, и мы можем двигаться до бесконечности вверх, находя все большие значения аргумента.
5) При $х≥0$ наименьшее значение равно 0. Это свойство очевидно.
Построим график функции по точкам при х≥0.
Построим наш график функции на всей области определения. Помним, что наша функция нечетная.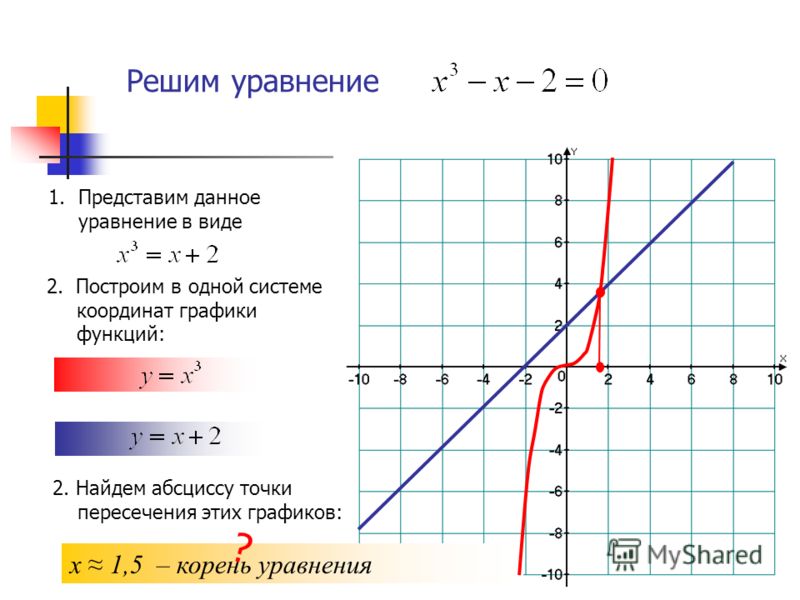
Свойства функции:
1) D(y)=(-∞;+∞).
2) Нечетная функция.
3) Возрастает на (-∞;+∞).
4) Неограниченна.
5) Наименьшего и наибольшего значения нет.
7) Е(у)= (-∞;+∞).
8) Выпукла вниз на (-∞;0), выпукла вверх на (0;+∞).
Примеры решения степенных функций
Примеры
1. Решить уравнение $\sqrt{x}=x$.
Решение. Построим два графика на одной координатной плоскости $y=\sqrt{x}$ и $y=x$.
Как видим наши графики пересекаются в трех точках.
Ответ: (-1;-1), (0;0), (1;1).
2. Построить график функции. $y=\sqrt{(x-2)}-3$.
Решение. График нашей получается из графика функции $y=\sqrt{x}$, параллельным переносом на две единицы вправо и три единицы вниз.
3. Построить график функции и прочитать его.
$\begin{cases}y=\sqrt{x}, x≥-1\\y=-x-2, x≤-1 \end{cases}$.
Решение. Построим два графика функций на одной координатной плоскости с учетом наших условий. При $х≥-1$ строим график корня кубического, при $х≤-1$ график линейной функции.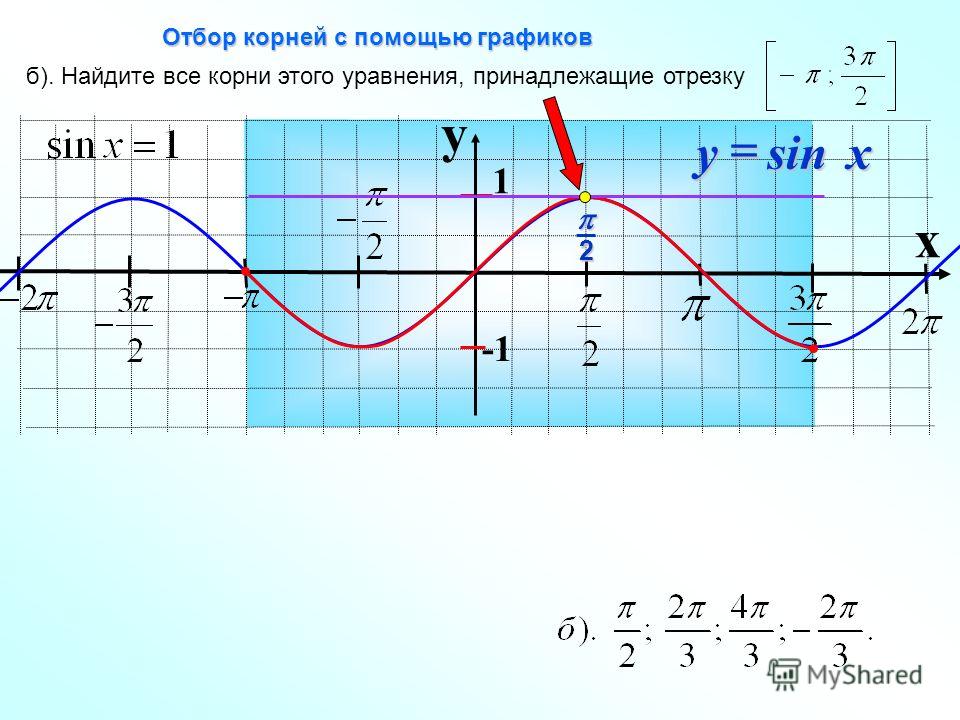 2+1, x≤1 \end{cases}$.
2+1, x≤1 \end{cases}$.
Урок и презентация на тему: «График функции квадратного корня. Область определения и построение графика»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.
Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 8 класса
Электронное учебное пособие к учебнику Мордковича А.Г.
Электронная рабочая тетрадь по алгебре для 8 класса
График функции квадратного корня
Ребята, с построением графиков функций мы с вами уже встречались, и не раз. Мы строили множества линейных функций и парабол . В общем виде любую функцию удобно записать, как $y=f(x)$. Это уравнение с двумя переменными — для каждого значения x мы получаем y. Выполнив некоторую заданную операцию f, мы отображаем множество всех возможных x на множество y. В качестве функции f мы можем записывать практически любую математическую операцию. 2$ удобно использовать следующую таблицу:
Отметим полученные точки на декартовой системе координат и аккуратно соединим их гладкой кривой. Наша функция не ограничена. Только этими точками мы можем подставить совершенно любое значение х из заданной области определения, то есть тех х, при которых выражение имеет смысл.
2$ удобно использовать следующую таблицу:
Отметим полученные точки на декартовой системе координат и аккуратно соединим их гладкой кривой. Наша функция не ограничена. Только этими точками мы можем подставить совершенно любое значение х из заданной области определения, то есть тех х, при которых выражение имеет смысл.
На одном из прошлых уроков мы изучили новую операцию извлечения корня квадратного . Возникает вопрос, а можем ли мы, используя эту операцию, задать какую-нибудь функцию и построить ее график? Воспользуемся общим видом функции $y=f(x)$. y и х оставим на своем месте, а вместо f введем операцию корня квадратного: $y=\sqrt{x}$.
Зная математическую операцию, мы смогли задать функцию.
Построение графика функции квадратного корня
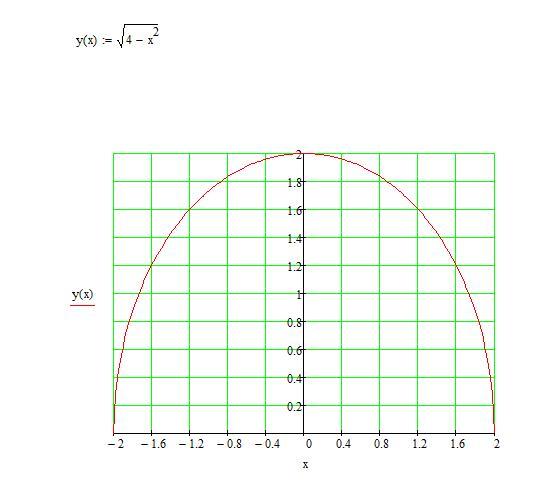
Давайте построим график этой функции. Исходя из определения корня квадратного, мы можем вычислять его только из неотрицательных чисел, то есть $x≥0$.
Составим таблицу:
Отметим наши точки на координатной плоскости.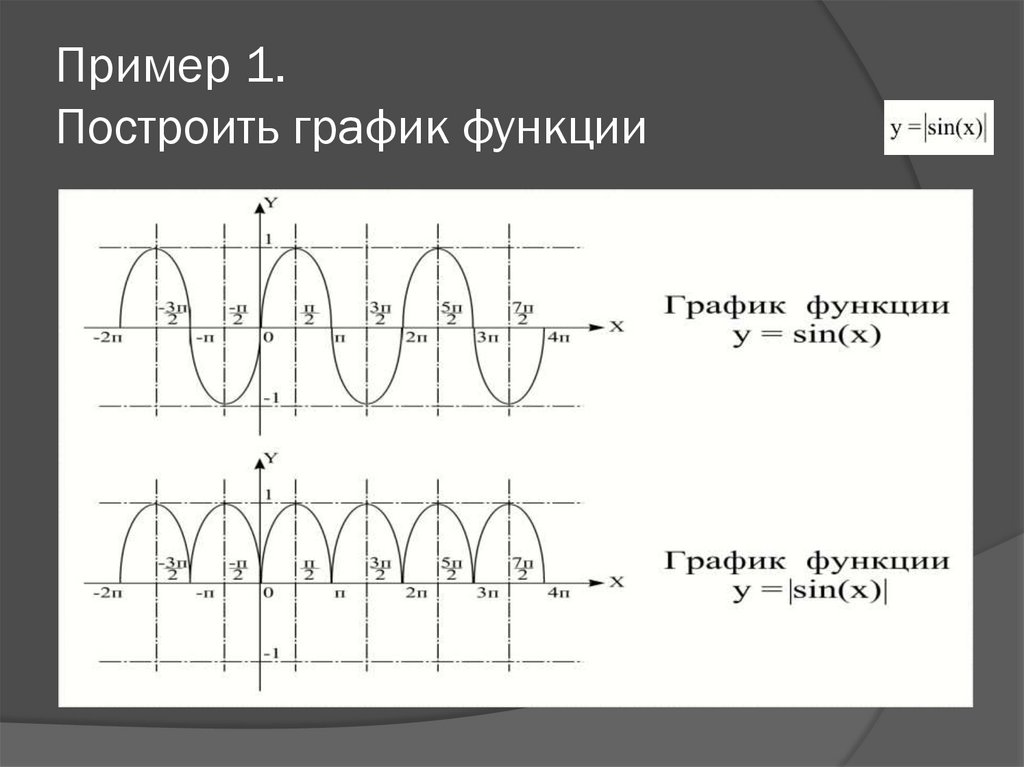
Нам осталось аккуратно соединить полученные точки.
Ребята, обратите внимание: если график нашей функции повернуть на бок, то получится левая ветка параболы. На самом деле, если строчки в таблице значений поменять местами (верхнюю строчку с нижней), то у нас получаться значения, как раз для параболы.
Область определения функции $y=\sqrt{x}$
Используя график функции, свойства описать довольно таки просто.
1. Область определения: $$.
б) $$.
Решение.
Мы можем решить наш пример двумя способами. В каждой букве опишем разные способы.
А) Вернемся к графику функции, построенному выше, и отметим требуемые точки отрезка. Хорошо видно, что при $х=9$ функция больше всех остальных значений. Значит и наибольшее значение она достигает в этой точке. При $х=4$ значение функции ниже всех остальных точек, а значит, тут и есть наименьшее значение.
$y_{наиб}=\sqrt{9}=3$, $y_{наим}=\sqrt{4}=2$.
Б) Мы знаем, что наша функция возрастающая. Значит, каждому большему значению аргумента соответствует большее значение функции. Наибольшее и наименьшее значение достигаются на концах отрезка:
Значит, каждому большему значению аргумента соответствует большее значение функции. Наибольшее и наименьшее значение достигаются на концах отрезка:
$y_{наиб}=\sqrt{11}$, $y_{наим}=\sqrt{2}$.
Пример 2.
Решить уравнение:
$\sqrt{x}=12-x$.
Решение.
Проще всего построить два графика функции и найти их точку пересечения.
На графике хорошо видна точка пересечения с координатами $(9;3)$. А значит, $х=9$ — решение нашего уравнения.
Ответ: $х=9$.
Ребята, а можем ли мы быть уверены, что больше решений у этого примера нет? Одна из функций возрастает, другая — убывает. В общем случае, они либо не имеют общих точек, либо пересекаются только в одной.
Пример 3.
Построить и прочитать график функции:
$\begin {cases} -x, x 9. \end {cases}$
Нам нужно построить три частных графика функции, каждый на своем промежутке.
Опишем свойства нашей функции:
1. Область определения: $(-∞;+∞)$.
2. $y=0$ при $х=0$ и $х=12$; $у>0$ при $хϵ(-∞;12)$; $y
3. Функция убывает на отрезках $(-∞;0)U(9;+∞)$. Функция возрастает на отрезке $(0;9)$.
4. Функция непрерывна на всей области определения.
5. Наибольшего и наименьшего значения нет.
6. Область значений: $(-∞;+∞)$.
Задачи для самостоятельного решения
1. Найти наибольшее и наименьшее значение функции корня квадратного на отрезке:
а) $$;
б) $$.
2. Решить уравнение: $\sqrt{x}=30-x$.
3. Построить и прочитать график функции: $\begin {cases} 2-x, x 4. \end {cases}$
4. Построить и прочитать график функции: $y=\sqrt{-x}$.
Квадратный корень как элементарная функция.
Квадратный корень — это элементарная функция и частный случай степенной функции при . Арифметический квадратный корень является гладким при , а нуле он непрерывен справа, но не дифференцируется.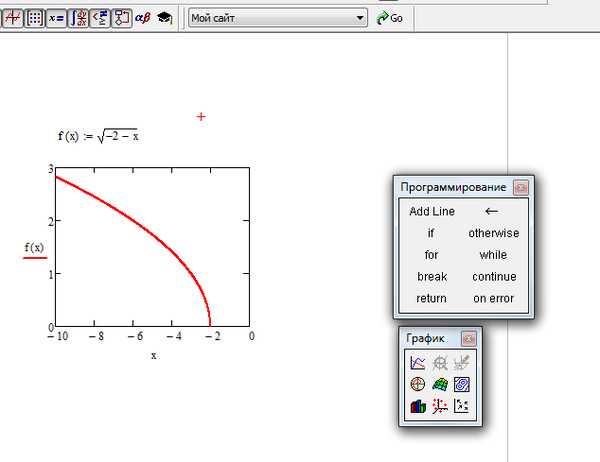
Как функция комплексный переменный корень — двузначная функция, у которой листы сходятся в нуле.
Построение графика функции квадратного корня.
- Заполняем таблицу данных:
2. Наносим точки, которые мы получили на координатную плоскость.
3. Соединяем эти точки и получаем график функции квадратного корня:
Преобразования графика функции квадратного корня.
Определим, какие преобразования функции необходимо сделать для того, чтобы построить графики функций. Определим виды преобразований.
Вид преобразования | Преобразование | |
Перенос функции по оси OY на 4 ед. вверх. | ||
внутреннее | Перенос функции по оси OX на 1 ед. вправо. | |
внутреннее | График приближается к оси OY в 3 раза и сжимается по оси OХ . | |
График отдаляется от оси OX OY . | ||
внутреннее | График отдаляется от оси OY в 2 раза и растягивается по оси OХ . |
Зачастую преобразования функций оказываются комбинированными.
Например , нужно построить график функции . Это график квадратного корня , который нужно перенести на одну единицу вниз по оси OY и на единицу вправо по оси ОХ и одновременно растянув в 3 раза его по оси OY .
Бывает непосредственно перед построением графика функции, нужны предварительные тождественные преобразования либо упрощения функций.
Функция корень n — степени из x, свойства и график
Функция корень n — степени из x, свойства и график
Вопросы занятия:
· рассмотреть свойства функции корень n-ой степени из x;
· рассмотреть график функции корень n-ой степени из x;
· рассмотреть примеры на построение и нахождение свойств функций этого вида.
Материал урока
Прежде чем перейти к изучению нового материала, давайте повторим основные понятия, с которыми мы познакомились на предыдущих уроках.
Корнем n-ой степени из неотрицательного числа a называют такое неотрицательное число, при возведении которого в степень n получается число а.
Корнем нечётной степени n-ой из отрицательного числа а называют такое отрицательное число, при возведении которого в степень n получается а.
Обозначают:
Число а – это подкоренное число, число n – показатель корня.
Обобщая эти понятия, можно сказать, что из любого неотрицательного числа можно извлечь корень любой степени (второй, третьей, четвертой и так далее), а из отрицательного числа можно извлечь только корень нечётной степени.
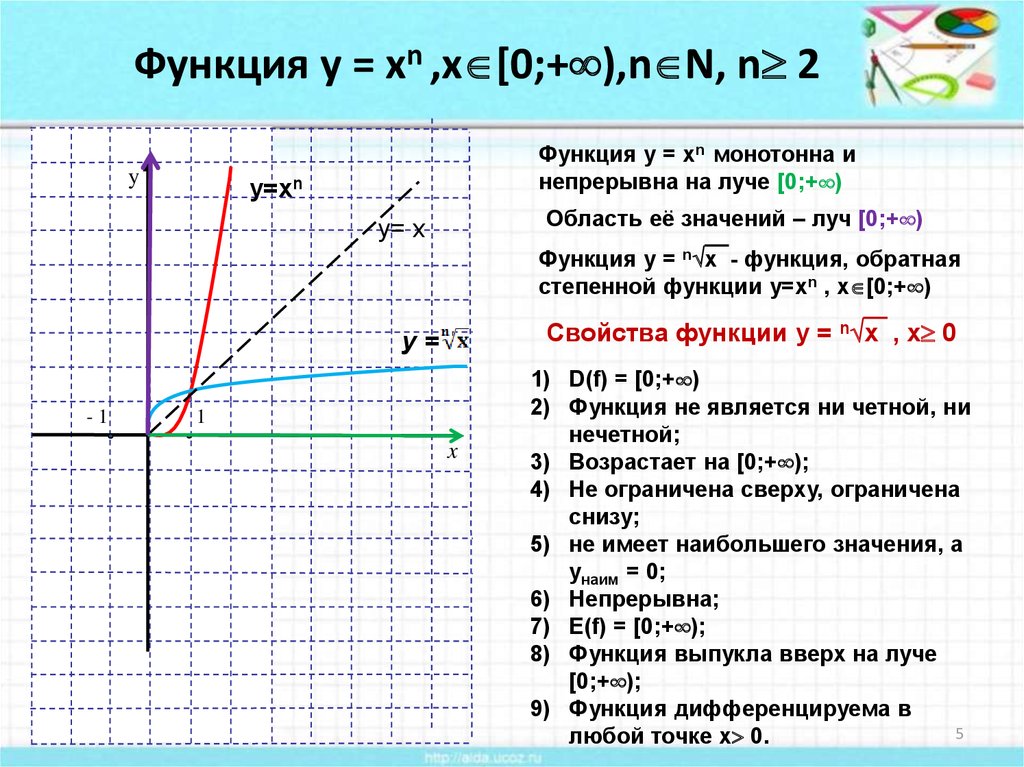
То есть на [0; +∞) каждому числу x можно поставить в соответствие единственное число корень n-ой степени из x при любом значении n.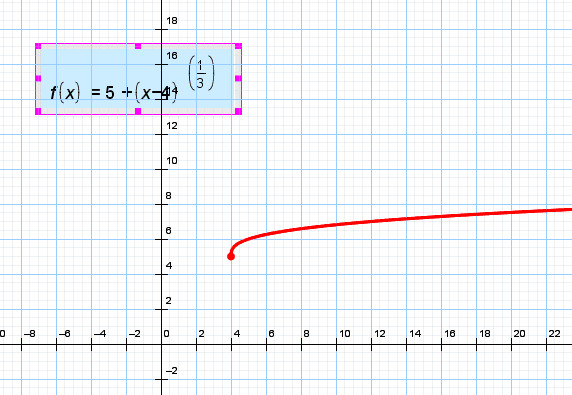
Другими словами, на множестве [0; +∞) можно говорить о функции:
Давайте попробуем найти свойства этой функции и построить её график.
Основные свойства:
Областью определения будет являться промежуток [0; +∞).
Поскольку корнем n-ой степени из неотрицательного числа является неотрицательное число, то областью значений функции будет промежуток [0; +∞).
Поскольку область определения функции не является симметричным множеством, то функция не является ни чётной, ни нечётной.
Операцию извлечения корня мы вводили как операцию обратную возведению в соответствующую степень.
Тогда можно сказать, что:
Зная это, нетрудно построить график функции.
Используя построенный график, мы можем записать оставшиеся свойства функции.
Функция возрастает на промежутке [0; +∞).
Функция не ограничена сверху, но ограничена снизу, например, прямой y = -0,5.
Наименьшим значением функции будет 0, наибольшего значения функция не имеет.
Функция непрерывна на всей области определения.
Функция выпукла вверх на всей области определения.
При изучении темы дифференцирование функций, мы говорили, что если функция дифференцируема в каждой точке некоторого промежутка, то она непрерывна на данном промежутке. Из курса базовой школы мы знаем:
Тогда:
Эта производная существует в любой точке промежутка [0; +∞) за исключением точки 0.
Таким образом, функция имеет производную в любой точке промежутка (0; +∞), то есть функция дифференцируема на промежутке (0; +∞).
Рассмотрим несколько примеров.
Пример.
Пример.
Мы с вами говорили о функции y равно корень n-ой степени из x только для неотрицательных значений аргумента.
Но если эн нечётное число, то выражение корень n-ой степени из x имеет смысл и для отрицательных x.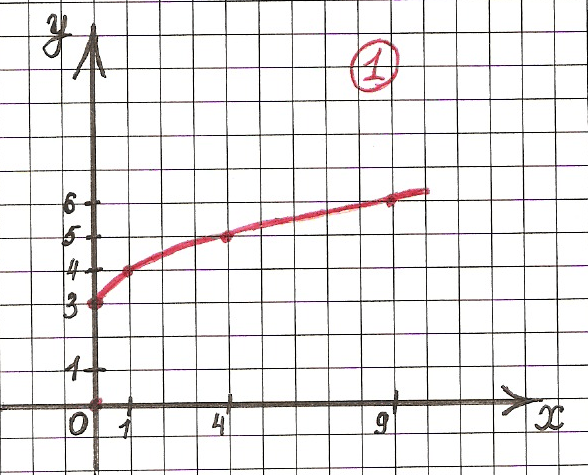 Значит, можно говорить о функции:
Значит, можно говорить о функции:
Теперь давайте запишем свойства этой функции.
Областью определения будет промежуток (– ∞; + ∞).
Областью значений будет промежуток (– ∞; + ∞).
Поскольку область определения является симметричным множеством, то можно исследовать данную функцию на чётность:
Получаем, что функция при нечётном n будет нечётной.
Давайте построим график функции.
Воспользуемся свойством нечётности функции и добавим к этой ветви ветвь, симметричную ей относительно начала координат.
По графику легко записать оставшиеся свойства функции.
Функция возрастает на всей области определения.
Функция не ограничена ни сверху ни снизу.
Функция не имеет ни наименьшего, ни наибольшего значений.
Функция непрерывна на всей области определения.
Функция выпукла вниз на промежутке (– ∞; 0) и выпукла вверх на промежутке (0; + ∞).
Функция дифференцируема на всей области определения за исключением точки 0.
Рассмотрим несколько примеров.
Пример.
Пример.
Пример.
Build Lifecycle
Ранее мы говорили, что ядром Gradle является язык программирования на основе зависимостей. В терминах Gradle это означает, что вы можете определять задачи и зависимости между задачами. Gradle гарантирует, что эти задачи выполняются в порядке их зависимостей и что каждая задача выполняется только один раз. Эти задачи образуют направленный ациклический граф. Существуют инструменты сборки, которые строят такой граф зависимостей по мере выполнения своих задач. Gradle строит полный граф зависимостей до выполняется любая задача. Это лежит в основе Gradle и делает возможным многое, что иначе было бы невозможно.
Сценарии сборки настраивают этот граф зависимостей. Поэтому они строго говоря скрипты конфигурации сборки .
Сборка Gradle состоит из трех отдельных этапов.
- Инициализация
Gradle поддерживает одно- и многопроектные сборки. На этапе инициализации Gradle определяет, какие проекты будут участвовать в сборке, и создает экземпляр Project для каждого из этих проектов.
- Конфигурация
На этом этапе настраиваются объекты проекта. Скрипты сборки выполняются для всех проектов , входящих в состав сборки.
- Исполнение
Gradle определяет подмножество задач, созданных и настроенных на этапе настройки, которые необходимо выполнить. Подмножество определяется аргументами имени задачи, переданными команде
gradle, и текущим каталогом. Затем Gradle выполняет каждую из выбранных задач.
Помимо файлов сценария сборки, Gradle определяет файл настроек. Файл настроек определяется Gradle по соглашению об именах. Имя по умолчанию для этого файла — settings.gradle . Позже в этой главе мы объясним, как Gradle ищет файл настроек.
Файл настроек выполняется на этапе инициализации. Многопроектная сборка должна иметь файл settings.gradle в корневом проекте многопроектной иерархии. Это необходимо, поскольку файл настроек определяет, какие проекты участвуют в многопроектной сборке (см. Создание многопроектных сборок). Для однопроектной сборки файл настроек необязателен. Помимо определения включенных проектов, вам может понадобиться добавить библиотеки в путь к классам сценария сборки (см. Организация проектов Gradle). Давайте сначала проанализируем одну сборку проекта:
Пример 1. Сборка одного проекта
settings.gradle
rootProject.name = 'basic' println 'Это выполняется на этапе инициализации.'
build.gradle
println «Выполняется на этапе настройки».
tasks.register('настроен') {
println 'Это также выполняется на этапе настройки, потому что :configured используется в сборке.'
}
tasks.register('тест') {
сделатьпоследний {
println 'Это выполняется на этапе выполнения. '
}
}
tasks.register('testBoth') {
сделатьпервый {
println 'Это выполняется первым на этапе выполнения.'
}
сделатьпоследний {
println 'Это выполняется последним на этапе выполнения.'
}
println 'Это также выполняется на этапе настройки, потому что :testBoth используется в сборке.'
}
'
}
}
tasks.register('testBoth') {
сделатьпервый {
println 'Это выполняется первым на этапе выполнения.'
}
сделатьпоследний {
println 'Это выполняется последним на этапе выполнения.'
}
println 'Это также выполняется на этапе настройки, потому что :testBoth используется в сборке.'
} settings.gradle.kts
rootProject.name = "базовый"
println("Это выполняется на этапе инициализации") build.gradle.kts
println("Это выполняется на этапе настройки")
tasks.register("настроено") {
println("Это также выполняется на этапе настройки, потому что в сборке используется :configured.")
}
tasks.register("тест") {
сделатьпоследний {
println("Это выполняется на этапе выполнения."
}
}
tasks.register("testBoth") {
сделатьпервый {
println("Это выполняется первым на этапе выполнения.")
}
сделатьпоследний {
println("Это выполняется последним на этапе выполнения.")
}
println("Это также выполняется на этапе настройки, потому что в сборке используется :testBoth. ")
}
")
} Вывод
gradle test testBoth > gradle test testBoth Это выполняется на этапе инициализации. > Настроить проект: Это выполняется на этапе настройки. Это также выполняется на этапе настройки, поскольку в сборке используется :testBoth. > Задача: тест Это выполняется на этапе выполнения. > Задача: testBoth Это выполняется первым на этапе выполнения. Это выполняется последним на этапе выполнения. ПОСТРОИТЬ УСПЕШНО в 0s 2 действенные задачи: 2 выполнено
> тестовый тест GradleОба Это выполняется на этапе инициализации. > Настроить проект: Это выполняется на этапе настройки. Это также выполняется на этапе настройки, поскольку в сборке используется :testBoth. > Задача: тест Это выполняется на этапе выполнения. > Задача: testBoth Это выполняется первым на этапе выполнения. Это выполняется последним на этапе выполнения. ПОСТРОИТЬ УСПЕШНО в 0s 2 действенные задачи: 2 выполнено
Для скрипта сборки доступ к свойствам и вызовы методов делегируются объекту проекта. Точно так же доступ к свойствам и вызовы методов в файле настроек делегируются объекту настроек. Дополнительные сведения см. в классе Settings в документации по API.
Точно так же доступ к свойствам и вызовы методов в файле настроек делегируются объекту настроек. Дополнительные сведения см. в классе Settings в документации по API.
Как Gradle узнает, следует ли выполнять сборку с одним или несколькими проектами?
Если вы запускаете многопроектную сборку из каталога с файлом settings.gradle , Gradle использует его для настройки сборки.
Gradle также позволяет выполнять сборку из любого подпроекта, участвующего в сборке. [1] Если вы запускаете Gradle из проекта без файла settings.gradle , Gradle ищет файл settings.gradle следующим образом:
Ищет
settings.gradleв родительских каталогах.Если не найдено, сборка выполняется как сборка одного проекта.
Если найден файл
settings.gradle, Gradle проверяет, является ли текущий проект частью многопроектной иерархии, определенной в найденномфайл settings.. Если нет, сборка выполняется как сборка одного проекта. В противном случае выполняется многопроектная сборка. gradle
gradle
Какова цель такого поведения? Gradle необходимо определить, является ли проект, в котором вы находитесь, подпроектом многопроектной сборки или нет.
Конечно, если это подпроект, создаются только подпроект и его зависимые проекты, но Gradle необходимо создать конфигурацию сборки для всей многопроектной сборки (см. Конфигурация и выполнение).
Если текущий проект содержит settings.gradle сборка всегда выполняется как:
сборка одного проекта, если файл
settings.gradleне определяет иерархию нескольких проектовмногопроектная сборка, если файл
settings.gradleопределяет многопроектную иерархию.
Автоматический поиск файла settings.gradle работает только для многопроектных сборок с макетом проекта по умолчанию, где пути к проектам соответствуют физическому макету подпроекта на диске. Gradle поддерживает произвольные физические макеты для многопроектной сборки, но для таких произвольных макетов нужно выполнять сборку из каталога, где находится файл настроек.
Сведения о том, как запускать частичные сборки из корня, см. в разделе Выполнение задач по их полному имени.
Gradle поддерживает произвольные физические макеты для многопроектной сборки, но для таких произвольных макетов нужно выполнять сборку из каталога, где находится файл настроек.
Сведения о том, как запускать частичные сборки из корня, см. в разделе Выполнение задач по их полному имени.
Gradle создает объект Project для каждого проекта, участвующего в сборке. Для многопроектной сборки это проекты, указанные в объекте Settings (плюс корневой проект). Каждый объект проекта по умолчанию имеет имя, равное имени его каталога верхнего уровня, и каждый проект, кроме корневого проекта, имеет родительский проект. Любой проект может иметь дочерние проекты.
Для сборки одного проекта рабочий процесс после инициализации фаз довольно прост. Сценарий сборки выполняется для объекта проекта, который был создан на этапе инициализации. Затем Gradle ищет задачи с именами, равными переданным в качестве аргументов командной строки. Если эти имена задач существуют, они выполняются как отдельная сборка в том порядке, в котором вы их передали.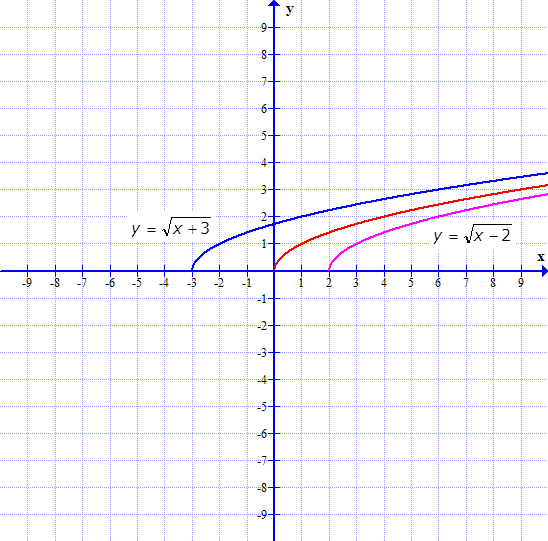 Конфигурация и выполнение многопроектных сборок обсуждаются в разделе Конфигурация и выполнение.
Конфигурация и выполнение многопроектных сборок обсуждаются в разделе Конфигурация и выполнение.
Сценарий сборки может получать уведомления по мере прохождения сборки через свой жизненный цикл. Эти уведомления обычно принимают две формы: вы можете либо реализовать конкретный интерфейс прослушивателя, либо предоставить замыкание, которое будет выполняться при запуске уведомления. В приведенных ниже примерах используются замыкания. Для получения подробной информации о том, как использовать интерфейсы прослушивателя, обратитесь к документации по API.
Оценка проекта
Вы можете получать уведомления непосредственно перед и после оценки проекта. Это можно использовать для выполнения таких действий, как выполнение дополнительной настройки после применения всех определений в сценарии сборки, или для некоторого пользовательского ведения журнала или профилирования.
Ниже приведен пример добавления задачи test к каждому проекту, у которого свойство hasTests имеет значение true.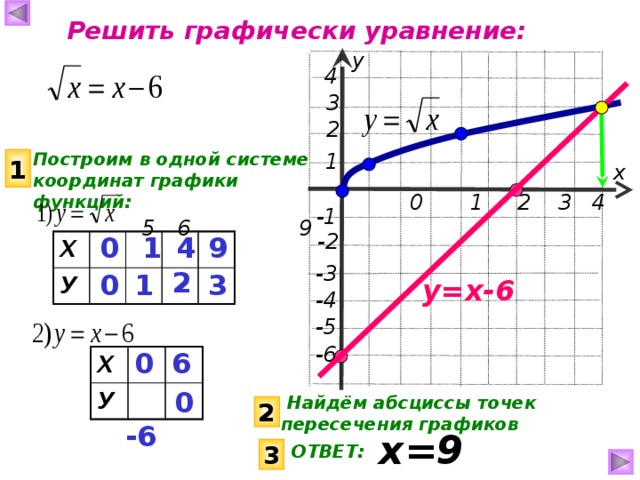
Пример 2. Добавление тестового задания в каждый проект с определенным набором свойств
build.gradle
allprojects {
после оценки { проект ->
если (проект.hasTests) {
println "Добавление тестовой задачи в $project"
проект.задача('тест') {
сделатьпоследний {
println "Выполнение тестов для $project"
}
}
}
}
} проект-a.gradle
hasTests = true
build.gradle.kts
allprojects {
// Установить значение по умолчанию
экстра["hasTests"] = ложь
послеоценить {
if (extra["hasTests"] как Boolean) {
println("Добавление тестовой задачи в $project")
tasks.register("тест") {
сделатьпоследний {
println("Выполнение тестов для $project")
}
}
}
}
} проект-a. gradle.kts
gradle.kts
экстра["hasTests"] = true
Вывод gradle -q test
> gradle -q test Добавление тестового задания в проект ':project-a' Выполнение тестов для проекта ':project-a'
В этом примере используется метод Project.afterEvaluate() для добавления закрытия, которое выполняется после оценки проекта.
Также можно получать уведомления при оценке любого проекта. В этом примере выполняется некоторая пользовательская регистрация оценки проекта. Обратите внимание, что уведомление afterProject получено независимо от того, успешно ли оценивается проект или нет с исключением.
Пример 3. Уведомления
build.gradle
gradle.afterProject { проект ->
если (проект.состояние.сбой) {
println "Оценка $project FAILED"
} еще {
println "Оценка $project выполнена успешно"
}
} build.gradle.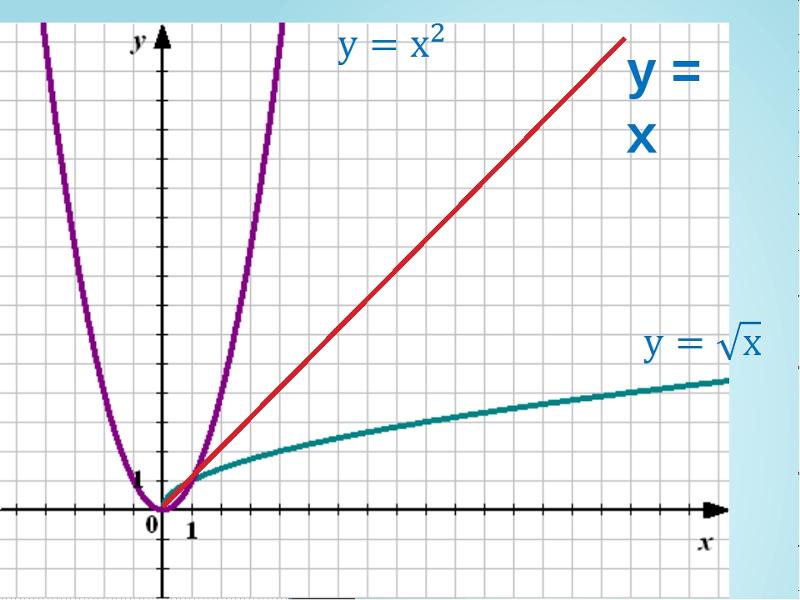 kts
kts
gradle.afterProject {
если (state.failure != ноль) {
println("Оценка $project FAILED")
} еще {
println("Оценка $project выполнена успешно")
}
} Вывод
тест gradle -q > тест gradle -q Оценка корневого проекта 'build-project-evaluate-events' выполнена успешно Оценка проекта ':project-a' выполнена успешно Оценка проекта ':project-b' FAILED ОШИБКА: сборка не удалась с исключением. * Где: Строка файла сборки '/home/user/gradle/samples/project-b.gradle': 1 * Что пошло не так: Возникла проблема при оценке проекта ':project-b'. > сломанный * Пытаться: > Запустите с параметром --stacktrace, чтобы получить трассировку стека. > Запустите с опцией --info или --debug, чтобы получить больше выходных данных журнала. > Запустите с параметром --scan, чтобы получить полную информацию. * Получите дополнительную помощь на https://help.gradle.org СБОЙ ПОСТРОЙКИ через 0 с
> тест градиента -q Оценка корневого проекта 'build-project-evaluate-events' выполнена успешно Оценка проекта ':project-a' выполнена успешно Оценка проекта ':project-b' FAILED ОШИБКА: сборка не удалась с исключением.* Где: Строка файла сборки '/home/user/gradle/samples/project-b.gradle.kts': 1 * Что пошло не так: сломанный * Пытаться: > Запустите с параметром --stacktrace, чтобы получить трассировку стека. > Запустите с опцией --info или --debug, чтобы получить больше выходных данных журнала. > Запустите с параметром --scan, чтобы получить полную информацию. * Получите дополнительную помощь на https://help.gradle.org СБОЙ ПОСТРОЙКИ через 0 с
Вы также можете добавить ProjectEvaluationListener в Gradle для получения этих событий.
Создание задачи
Вы можете получить уведомление сразу после добавления задачи в проект. Это можно использовать для установки некоторых значений по умолчанию или добавления поведения до того, как задача станет доступной в файле сборки.
В следующем примере задается свойство srcDir каждой задачи по мере ее создания.
Пример 4. Установка определенного свойства для всех задач
build.gradle
tasks.whenTaskAdded { задача -> task.ext.srcDir = 'src/main/java' } tasks.register('a') println "исходный каталог $a.srcDir"
build.gradle.kts
tasks.whenTaskAdded {
экстра["srcDir"] = "источник/основной/java"
}
val a по задачам.регистрация
println("исходный каталог ${a.get().extra["srcDir"]}") Вывод gradle -q a
> gradle -q a исходный каталог: src/main/java
Вы также можете добавить действие в TaskContainer для получения этих событий.
График выполнения задачи готов
Вы можете получить уведомление сразу после заполнения графика выполнения задачи.
Вы также можете добавить TaskExecutionGraphListener в TaskExecutionGraph для получения этих событий.
Выполнение задачи
Вы можете получать уведомления непосредственно до и после выполнения любой задачи.
В следующем примере регистрируются начало и конец выполнения каждой задачи. Обратите внимание, что уведомление
Обратите внимание, что уведомление afterTask получено независимо от того, завершается ли задача успешно или завершается с ошибкой с исключением.
Пример 5. Регистрация начала и окончания выполнения каждой задачи
build.gradle
tasks.register('ok')
tasks.register('сломан') {
зависит от ок
сделатьпоследний {
бросить новое исключение RuntimeException («сломан»)
}
}
gradle.taskGraph.beforeTask { Задача задачи ->
println "выполняется $task..."
}
gradle.taskGraph.afterTask { Задача задачи, состояние TaskState ->
если (состояние.сбой) {
println "ОШИБКА"
}
еще {
println "сделано"
}
} build.gradle.kts
tasks.register("ok")
tasks.register ("сломан") {
зависит от ("хорошо")
сделатьпоследний {
бросить RuntimeException("сломан")
}
}
gradle.taskGraph.beforeTask {
println("выполнение $this...")
}
gradle.taskGraph.afterTask {
если (state. failure != ноль) {
println("ОШИБКА")
} еще {
println("сделано")
}
}
failure != ноль) {
println("ОШИБКА")
} еще {
println("сделано")
}
} Вывод
gradle -q не работает > gradle -q не работает выполнение задачи ':ok'... Выполнено выполнение задачи ':broken'... НЕ УДАЛОСЬ ОШИБКА: сборка не удалась с исключением. * Где: Строка файла сборки '/home/user/gradle/samples/build.gradle': 6 * Что пошло не так: Не удалось выполнить задачу ':broken'. > сломанный * Пытаться: > Запустите с параметром --stacktrace, чтобы получить трассировку стека. > Запустите с опцией --info или --debug, чтобы получить больше выходных данных журнала. > Запустите с параметром --scan, чтобы получить полную информацию. * Получите дополнительную помощь на https://help.gradle.org СБОЙ ПОСТРОЙКИ через 0 с
> gradle -q не работает выполнение задачи ':ok'... Выполнено выполнение задачи ':broken'... НЕ УДАЛОСЬ ОШИБКА: сборка не удалась с исключением. * Что пошло не так: Не удалось выполнить задачу ':broken'.> сломанный * Пытаться: > Запустите с параметром --stacktrace, чтобы получить трассировку стека. > Запустите с опцией --info или --debug, чтобы получить больше выходных данных журнала. > Запустите с параметром --scan, чтобы получить полную информацию. * Получите дополнительную помощь на https://help.gradle.org BUILD FAILED in 0s
Вы также можете использовать TaskExecutionListener для TaskExecutionGraph для получения этих событий.
1. Gradle поддерживает частичные многопроектные сборки (см. Выполнение многопроектных сборок).
Обзор Microsoft Graph — Microsoft Graph
Обратная связь Редактировать
Твиттер LinkedIn Фейсбук Эл. адрес
- Статья
- 6 минут на чтение
Microsoft Graph — это шлюз к данным и аналитике в Microsoft 365. Он предоставляет унифицированную модель программирования, которую можно использовать для доступа к огромному объему данных в Microsoft 365, Windows и Enterprise Mobility + Security. Используйте множество данных в Microsoft Graph для создания приложений для организаций и потребителей, которые взаимодействуют с миллионами пользователей.
Данные и службы, лежащие в основе платформы Microsoft 365
В платформе Microsoft 365 три основных компонента облегчают доступ и поток данных:
- API Microsoft Graph предлагает единую конечную точку,
https:// graph.microsoft.com, чтобы обеспечить доступ к богатым, ориентированным на людей данным и аналитическим данным в облаке Microsoft, включая Microsoft 365, Windows и Enterprise Mobility + Security. Вы можете использовать API-интерфейсы REST или пакеты SDK для доступа к конечной точке и создания приложений, поддерживающих сценарии Microsoft 365, охватывающих производительность, совместную работу, образование, аналитику людей и рабочих мест и многое другое. Microsoft Graph также включает в себя мощный набор служб, которые управляют идентификацией пользователей и устройств, доступом, соответствием требованиям и безопасностью и помогают защитить организации от утечки или потери данных.
Microsoft Graph также включает в себя мощный набор служб, которые управляют идентификацией пользователей и устройств, доступом, соответствием требованиям и безопасностью и помогают защитить организации от утечки или потери данных. - Соединители Microsoft Graph работают во входящем направлении, доставляя данные, внешние по отношению к облаку Microsoft, в службы и приложения Microsoft Graph для улучшения возможностей Microsoft 365, таких как Microsoft Search. Коннекторы существуют для многих часто используемых источников данных, таких как Box, Google Drive, Jira и Salesforce.
- Microsoft Graph Data Connect предоставляет набор инструментов для оптимизации безопасной и масштабируемой доставки данных Microsoft Graph в популярные хранилища данных Azure. Кэшированные данные служат источниками данных для инструментов разработки Azure, которые можно использовать для создания интеллектуальных приложений.
Вместе API Microsoft Graph, соединители и Data Connect обеспечивают платформу Microsoft 365. Имея возможность доступа к данным Microsoft Graph и другим наборам данных, вы можете получать ценные сведения и аналитику, расширять возможности Microsoft 365 и создавать уникальные интеллектуальные приложения.
Имея возможность доступа к данным Microsoft Graph и другим наборам данных, вы можете получать ценные сведения и аналитику, расширять возможности Microsoft 365 и создавать уникальные интеллектуальные приложения.
Что есть в Microsoft Graph?
Microsoft Graph предоставляет REST API и клиентские библиотеки для доступа к данным в следующих облачных службах Microsoft:
- Основные службы Microsoft 365: Bookings, Calendar, Delve, Excel, соответствие требованиям Microsoft 365 eDiscovery, поиск Microsoft, OneDrive, OneNote, Outlook/Exchange, люди (контакты Outlook), Planner, SharePoint, Teams, To Do, Viva Insights
- Службы Enterprise Mobility + Security: Advanced Threat Analytics, Advanced Threat Protection, Azure Active Directory, Identity Manager и Intune
- Службы Windows: действия, устройства, уведомления, Universal Print
- Службы Dynamics 365 Business Central
Дополнительные сведения см. в разделе Основные службы и функции Microsoft Graph.
в разделе Основные службы и функции Microsoft Graph.
Что можно делать с Microsoft Graph?
Используйте Microsoft Graph для создания возможностей на основе уникального контекста пользователя, чтобы повысить его продуктивность. Представьте себе приложение, которое…
- Просматривает вашу следующую встречу и помогает вам подготовиться к ней, предоставляя профильную информацию об участниках, включая их должности и менеджеров, а также информацию о последних документах, над которыми они работают, и люди, с которыми они сотрудничают.
- Сканирует ваш календарь и предлагает лучшее время для следующей встречи команды.
- Извлекает последнюю диаграмму прогноза продаж из файла Excel в вашем OneDrive и позволяет обновлять прогноз в режиме реального времени с вашего телефона.
- Подписывается на изменения в вашем календаре, отправляет вам оповещение, когда вы проводите слишком много времени на собраниях, и дает рекомендации для тех, кого вы можете пропустить или делегировать, в зависимости от того, насколько важны для вас участники.

- Помогает разобраться в личной и рабочей информации на телефоне; например, путем классификации изображений, которые должны отправляться в ваш личный OneDrive, и бизнес-квитанций, которые должны отправляться в OneDrive для бизнеса.
- Анализирует масштабные данные Microsoft 365, чтобы лица, принимающие решения, могли получить ценную информацию о распределении времени и схемах совместной работы, которые повышают производительность бизнеса.
- Переносит пользовательские бизнес-данные в Microsoft Graph, индексируя их, чтобы сделать их доступными для поиска вместе с данными из служб Microsoft 365.
В качестве примера выберите первый сценарий исследования участников собрания. С помощью API Microsoft Graph вы можете:
- Получить адреса электронной почты участников собрания.
- Ищите их по отдельности как пользователя в Azure Active Directory, чтобы получить информацию об их профилях.
Затем вы можете перейти к другим ресурсам, используя отношения:
- Подключиться к своему менеджеру через отношения менеджера.

- Получайте ценную информацию и сведения, в том числе о популярных файлах пользователей.
- Получите наиболее релевантных людей вокруг пользователя.
- Расширьте сценарий, чтобы получить доступ к группам пользователей через отношение memberOf.
- Доберитесь до других участников в каждой группе.
- Воспользуйтесь другими сценариями, доступными для групп, такими как обучение и командная работа.
Microsoft Graph продолжает открывать платформу Microsoft 365 для разработчиков и всегда только с соответствующими разрешениями.
Примечание
Используя API Microsoft Graph, вы соглашаетесь с Условиями использования API Microsoft и Заявлением о конфиденциальности Microsoft.
Популярные запросы API
Ознакомьтесь с некоторыми из этих распространенных сценариев работы с Microsoft Graph API. Ссылки ведут к обозревателю графов.
| Операция | URL-адрес |
|---|---|
| ПОЛУЧИТЬ мой профиль | https://graph. |
| ПОЛУЧИТЬ мои файлы | https://graph.microsoft.com/v1.0/me/drive/root/children |
| ПОЛУЧИТЕ мою фотографию | https://graph.microsoft.com/v1.0/me/photo/$value |
| ПОЛУЧИТЬ мою почту | https://graph.microsoft.com/v1.0/me/messages |
| ПОЛУЧИТЬ мою важную электронную почту | https://graph.microsoft.com/v1.0/me/messages?$filter=importance%20eq%20'high' |
| ПОЛУЧИТЬ события моего календаря | https://graph.microsoft.com/v1.0/me/events |
| ПОЛУЧИТЕ моему менеджеру | https://graph.microsoft.com/v1.0/me/manager |
| ПОЛУЧИТЬ последнего пользователя, изменившего файл foo.txt | https://graph.microsoft.com/v1.0/me/drive/root/children/foo.txt/lastModifiedByUser |
| ПОЛУЧИТЬ группы Microsoft 365 Я являюсь участником | https://graph. |
| Пользователи GET в моей организации | https://graph.microsoft.com/v1.0/users |
| Группы GET в моей организации | https://graph.microsoft.com/v1.0/groups |
| ПОЛУЧИТЕ людей, связанных со мной | https://graph.microsoft.com/v1.0/me/people |
| ПОЛУЧИТЬ предметы, которые меня интересуют | https://graph.microsoft.com/beta/me/insights/trending |
| ПОЛУЧИТЬ мои заметки | https://graph.microsoft.com/v1.0/me/onenote/notebooks |
Перенос данных из внешнего источника контента в Microsoft Graph
Используйте соединители Microsoft Graph для переноса данных, которые являются внешними по отношению к облаку Microsoft, в Microsoft Graph. Примерами таких данных могут быть база данных кадровой службы организации или каталог продуктов, размещенные локально или в общедоступных или частных облаках.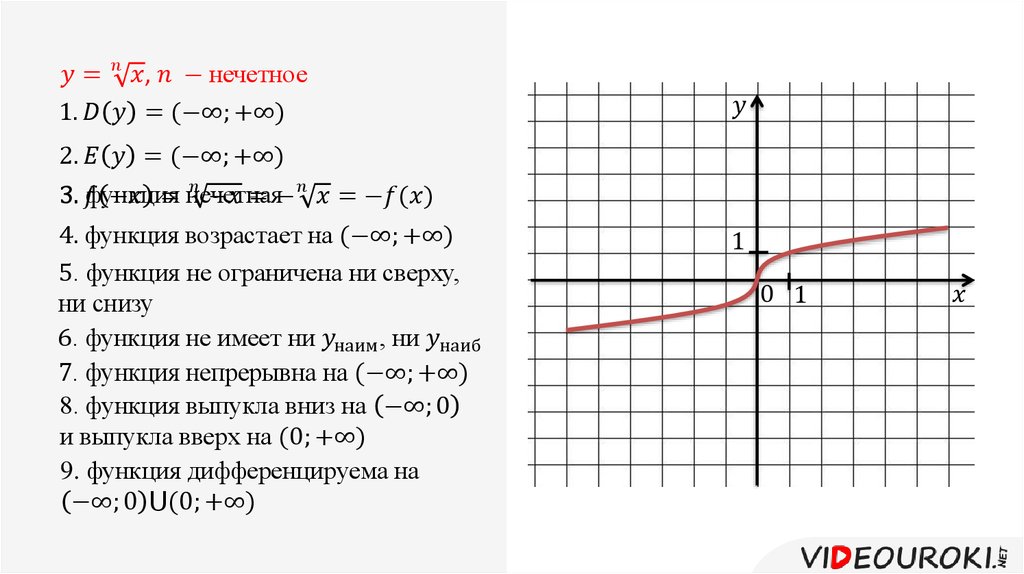
Соединители Microsoft Graph создают подключения к внешним источникам данных, индексируют данные и сохраняют их в виде внешних настраиваемых элементов и файлов. После индексации эти элементы могут отображаться в Microsoft Search и в приложениях, использующих Microsoft Search API.
Доступ к данным Microsoft Graph в масштабе
Используйте Microsoft Graph Data Connect для доступа к данным в Microsoft Graph в масштабе, предоставляя администраторам детальное согласие и полный контроль над своими данными Microsoft Graph. Data Connect оптимизирует доставку этих данных в Microsoft Azure.
С помощью инструментов Azure вы сможете создавать интеллектуальные приложения, которые:
- Найдите ближайшего эксперта по теме в вашей организации.
- Автоматизировать создание базы знаний.
- Проанализируйте приглашения на собрания, чтобы получить представление об использовании конференц-залов.
- Обнаружение мошенничества с помощью данных о производительности и связи.

Когда следует использовать Microsoft Graph API или Data Connect?
Microsoft Graph Data Connect предоставляет новый способ взаимодействия с данными, доступными через API Microsoft Graph. Data Connect предоставляет уникальный набор инструментов, упрощающих создание интеллектуальных приложений в облаке Microsoft.
| Особенность | API Microsoft Graph | Подключение к данным Microsoft Graph |
|---|---|---|
| Область доступа | Один пользователь или весь арендатор | Много пользователей или групп |
| Шаблон доступа | В реальном времени | Периодическое расписание |
| Операции с данными | Работает с мастером данных | Работает с кэшем данных |
| Защита данных | Данные защищены в Microsoft 365 | Защита данных распространяется на кеш данных в вашей подписке Azure |
| Согласие пользователя | Сам Типы ресурсов | Нет |
| Согласие администратора | Вся организация Типы ресурсов | Выберите группы пользователей Типы и свойства ресурсов За исключением пользователей |
| Инструменты доступа | RESTful веб-запросы | Фабрика данных Azure |
Следующие шаги
- Ознакомьтесь с некоторыми решениями партнеров.


 '
}
}
tasks.register('testBoth') {
сделатьпервый {
println 'Это выполняется первым на этапе выполнения.'
}
сделатьпоследний {
println 'Это выполняется последним на этапе выполнения.'
}
println 'Это также выполняется на этапе настройки, потому что :testBoth используется в сборке.'
}
'
}
}
tasks.register('testBoth') {
сделатьпервый {
println 'Это выполняется первым на этапе выполнения.'
}
сделатьпоследний {
println 'Это выполняется последним на этапе выполнения.'
}
println 'Это также выполняется на этапе настройки, потому что :testBoth используется в сборке.'
}  ")
}
")
}  gradle
gradle 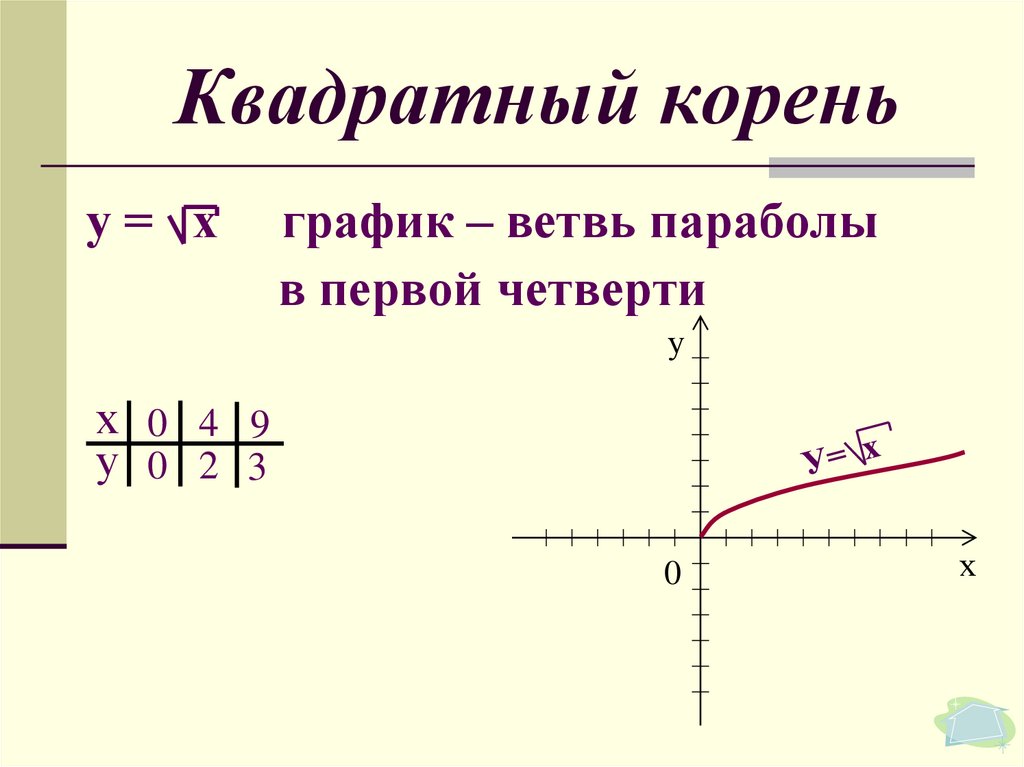 * Где:
Строка файла сборки '/home/user/gradle/samples/project-b.gradle.kts': 1
* Что пошло не так:
сломанный
* Пытаться:
> Запустите с параметром --stacktrace, чтобы получить трассировку стека.
> Запустите с опцией --info или --debug, чтобы получить больше выходных данных журнала.
> Запустите с параметром --scan, чтобы получить полную информацию.
* Получите дополнительную помощь на https://help.gradle.org
СБОЙ ПОСТРОЙКИ через 0 с
* Где:
Строка файла сборки '/home/user/gradle/samples/project-b.gradle.kts': 1
* Что пошло не так:
сломанный
* Пытаться:
> Запустите с параметром --stacktrace, чтобы получить трассировку стека.
> Запустите с опцией --info или --debug, чтобы получить больше выходных данных журнала.
> Запустите с параметром --scan, чтобы получить полную информацию.
* Получите дополнительную помощь на https://help.gradle.org
СБОЙ ПОСТРОЙКИ через 0 с 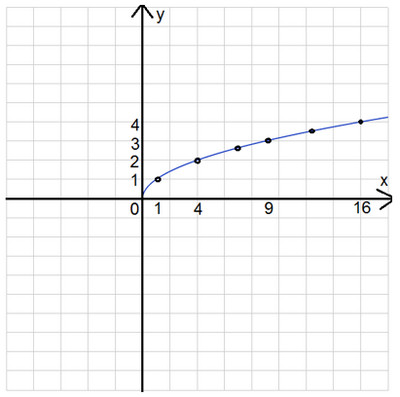 whenTaskAdded { задача ->
task.ext.srcDir = 'src/main/java'
}
tasks.register('a')
println "исходный каталог $a.srcDir"
whenTaskAdded { задача ->
task.ext.srcDir = 'src/main/java'
}
tasks.register('a')
println "исходный каталог $a.srcDir"  failure != ноль) {
println("ОШИБКА")
} еще {
println("сделано")
}
}
failure != ноль) {
println("ОШИБКА")
} еще {
println("сделано")
}
}  > сломанный
* Пытаться:
> Запустите с параметром --stacktrace, чтобы получить трассировку стека.
> Запустите с опцией --info или --debug, чтобы получить больше выходных данных журнала.
> Запустите с параметром --scan, чтобы получить полную информацию.
* Получите дополнительную помощь на https://help.gradle.org
BUILD FAILED in 0s
> сломанный
* Пытаться:
> Запустите с параметром --stacktrace, чтобы получить трассировку стека.
> Запустите с опцией --info или --debug, чтобы получить больше выходных данных журнала.
> Запустите с параметром --scan, чтобы получить полную информацию.
* Получите дополнительную помощь на https://help.gradle.org
BUILD FAILED in 0s  Microsoft Graph также включает в себя мощный набор служб, которые управляют идентификацией пользователей и устройств, доступом, соответствием требованиям и безопасностью и помогают защитить организации от утечки или потери данных.
Microsoft Graph также включает в себя мощный набор служб, которые управляют идентификацией пользователей и устройств, доступом, соответствием требованиям и безопасностью и помогают защитить организации от утечки или потери данных.
 microsoft.com/v1.0/me
microsoft.com/v1.0/me 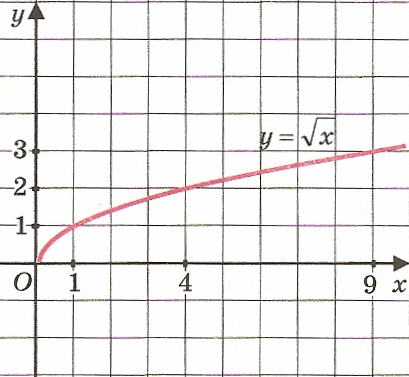 microsoft.com/v1.0/me/memberOf/$/microsoft.graph.group?$filter=groupTypes/any(a:a%20eq%20'unified')
microsoft.com/v1.0/me/memberOf/$/microsoft.graph.group?$filter=groupTypes/any(a:a%20eq%20'unified')