| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | ||
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град.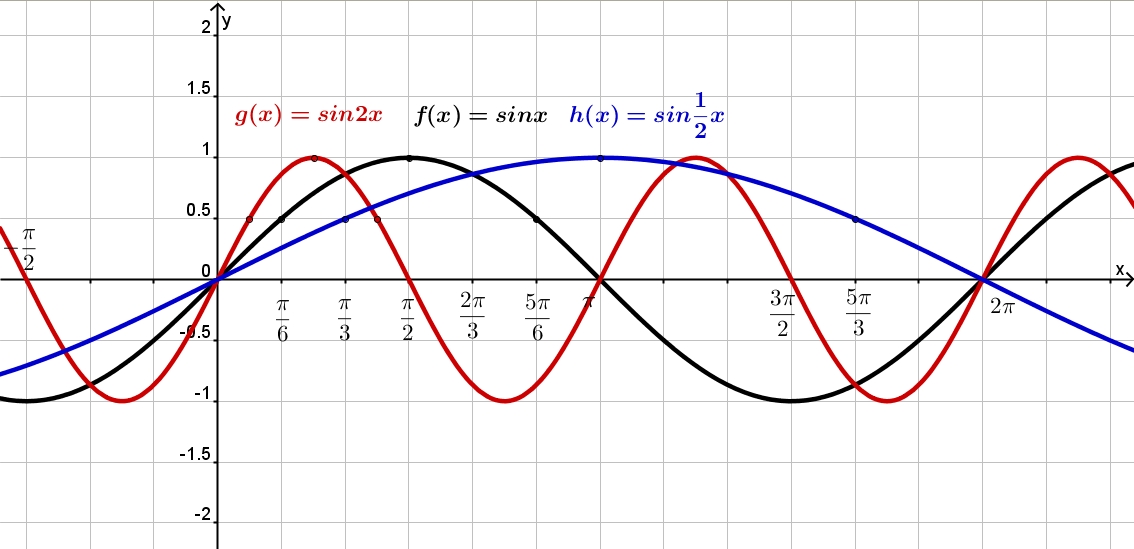 ) ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град.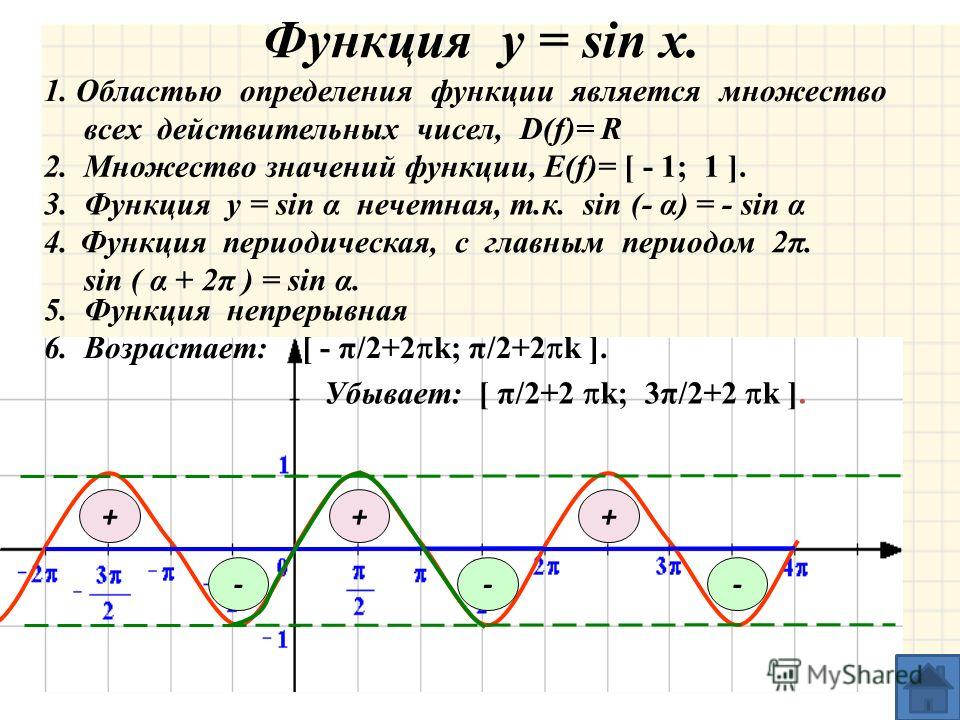 ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град.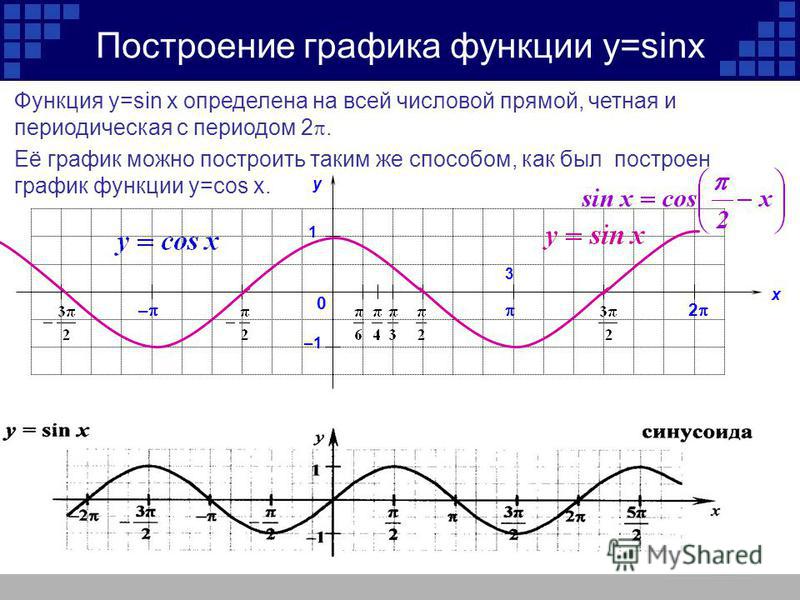 ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град.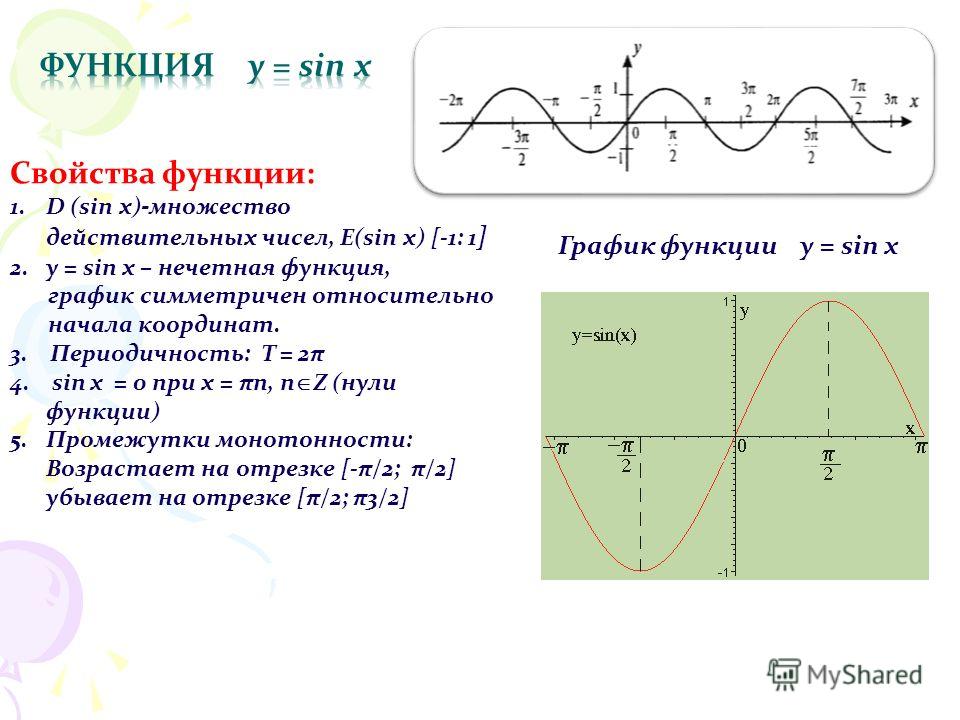 ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град.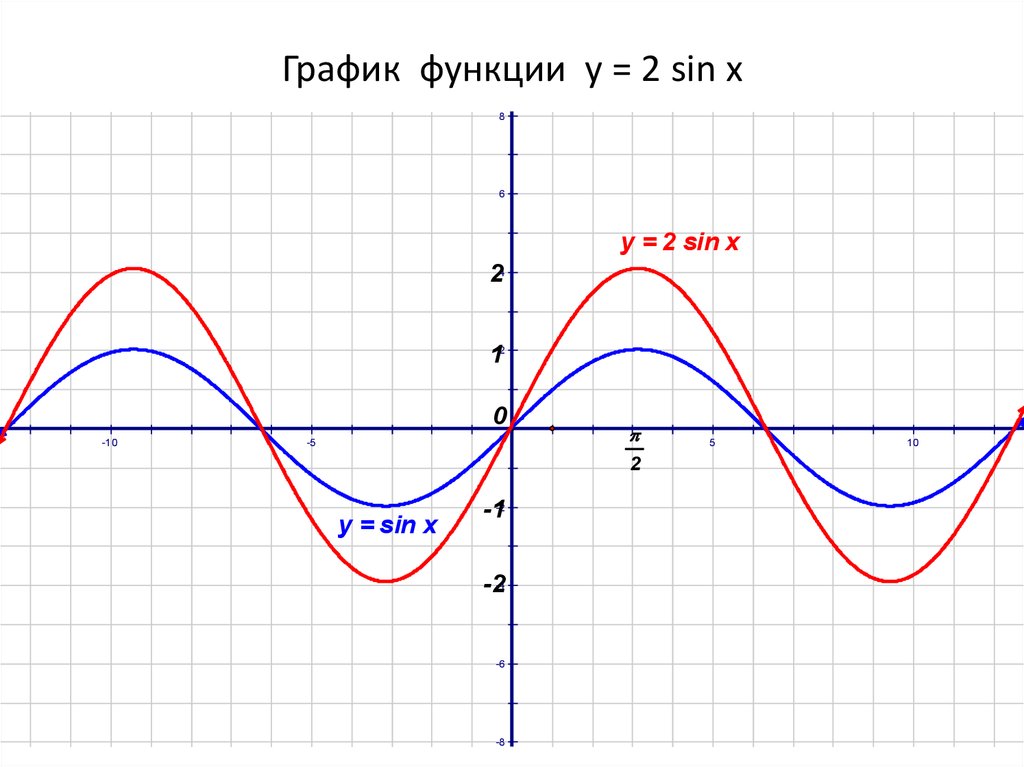 ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град.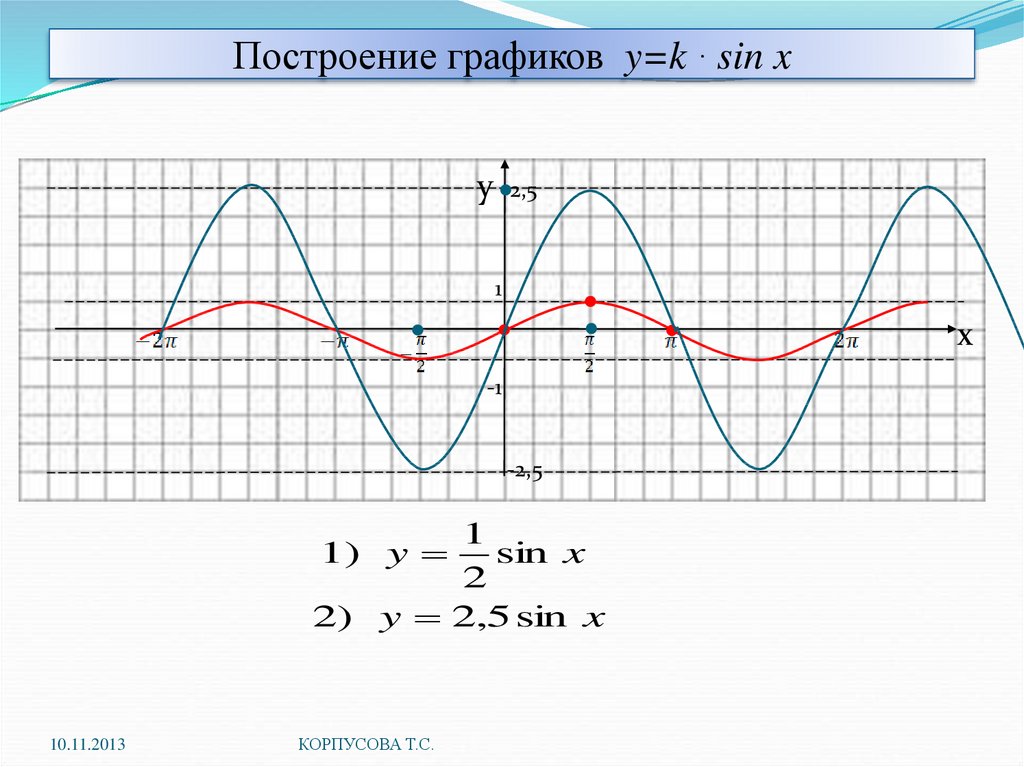 ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
| 1 | Trovare la Derivata — d/dx | натуральный логарифм x | |
| 2 | Вычислим интеграл | интеграл натурального логарифма x по x | |
| 3 | Trovare la Derivata — d/dx | e^x | |
| 4 | Вычислим интеграл | интеграл e^(2x) по x | |
| 5 | Trovare la Derivata — d/dx | 1/x | |
| 6 | Trovare la Derivata — d/dx | x^2 | |
| 7 | Trovare la Derivata — d/dx | 1/(x^2) | |
| 8 | Trovare la Derivata — d/dx | sin(x)^2 | |
| 9 | Trovare la Derivata — d/dx | sec(x) | |
| 10 | Вычислим интеграл | интеграл e^x по x | |
| 11 | Вычислим интеграл | интеграл x^2 по x | |
| 12 | Вычислим интеграл | интеграл квадратного корня из x по x | |
| 13 | Trovare la Derivata — d/dx | cos(x)^2 | |
| 14 | Вычислим интеграл | интеграл 1/x по x | |
| 15 | Вычислим интеграл | интеграл sin(x)^2 по x | |
| 16 | Trovare la Derivata — d/dx | x^3 | |
| 17 | Trovare la Derivata — d/dx | sec(x)^2 | |
| 18 | Вычислим интеграл | интеграл cos(x)^2 по x | |
| 19 | Вычислим интеграл | интеграл sec(x)^2 по x | |
| 20 | Trovare la Derivata — d/dx | e^(x^2) | |
| 21 | Вычислим интеграл | интеграл в пределах от 0 до 1 кубический корень из 1+7x по x | |
| 22 | Trovare la Derivata — d/dx | sin(2x) | |
| 23 | Trovare la Derivata — d/dx | tan(x)^2 | |
| 24 | Вычислим интеграл | интеграл 1/(x^2) по x | |
| 25 | Trovare la Derivata — d/dx | 2^x | |
| 26 | График | натуральный логарифм a | |
| 27 | Trovare la Derivata — d/dx | cos(2x) | |
| 28 | Trovare la Derivata — d/dx | xe^x | |
| 29 | Вычислим интеграл | интеграл 2x по x | |
| 30 | Trovare la Derivata — d/dx | ( натуральный логарифм от x)^2 | |
| 31 | Trovare la Derivata — d/dx | натуральный логарифм (x)^2 | |
| 32 | Trovare la Derivata — d/dx | 3x^2 | |
| 33 | Вычислим интеграл | интеграл xe^(2x) по x | |
| 34 | Trovare la Derivata — d/dx | 2e^x | |
| 35 | Trovare la Derivata — d/dx | натуральный логарифм 2x | |
| 36 | Trovare la Derivata — d/dx | -sin(x) | |
| 37 | Trovare la Derivata — d/dx | 4x^2-x+5 | |
| 38 | Trovare la Derivata — d/dx | y=16 корень четвертой степени из 4x^4+4 | |
| 39 | Trovare la Derivata — d/dx | 2x^2 | |
| 40 | Вычислим интеграл | интеграл e^(3x) по x | |
| 41 | Вычислим интеграл | интеграл cos(2x) по x | |
| 42 | Trovare la Derivata — d/dx | 1/( квадратный корень из x) | |
| 43 | Вычислим интеграл | интеграл e^(x^2) по x | |
| 44 | Вычислить | e^infinity | |
| 45 | Trovare la Derivata — d/dx | x/2 | |
| 46 | Trovare la Derivata — d/dx | -cos(x) | |
| 47 | Trovare la Derivata — d/dx | sin(3x) | |
| 48 | Trovare la Derivata — d/dx | 1/(x^3) | |
| 49 | Вычислим интеграл | интеграл tan(x)^2 по x | |
| 50 | Вычислим интеграл | интеграл 1 по x | |
| 51 | Trovare la Derivata — d/dx | x^x | |
| 52 | Trovare la Derivata — d/dx | x натуральный логарифм от x | |
| 53 | Trovare la Derivata — d/dx | x^4 | |
| 54 | Оценить предел | предел (3x-5)/(x-3), если x стремится к 3 | |
| 55 | Вычислим интеграл | интеграл x^2 натуральный логарифм x по x | |
| 56 | Trovare la Derivata — d/dx | f(x) = square root of x | |
| 57 | Trovare la Derivata — d/dx | x^2sin(x) | |
| 58 | Вычислим интеграл | интеграл sin(2x) по x | |
| 59 | Trovare la Derivata — d/dx | 3e^x | |
| 60 | Вычислим интеграл | интеграл xe^x по x | |
| 61 | Trovare la Derivata — d/dx | y=x^2 | |
| 62 | Trovare la Derivata — d/dx | квадратный корень из x^2+1 | |
| 63 | Trovare la Derivata — d/dx | sin(x^2) | |
| 64 | Вычислим интеграл | интеграл e^(-2x) по x | |
| 65 | Вычислим интеграл | интеграл натурального логарифма квадратного корня из x по x | |
| 66 | Trovare la Derivata — d/dx | e^2 | |
| 67 | Trovare la Derivata — d/dx | x^2+1 | |
| 68 | Вычислим интеграл | интеграл sin(x) по x | |
| 69 | Trovare la Derivata — d/dx | arcsin(x) | |
| 70 | Оценить предел | предел (sin(x))/x, если x стремится к 0 | |
| 71 | Вычислим интеграл | интеграл e^(-x) по x | |
| 72 | Trovare la Derivata — d/dx | x^5 | |
| 73 | Trovare la Derivata — d/dx | 2/x | |
| 74 | Trovare la Derivata — d/dx | натуральный логарифм 3x | |
| 75 | Trovare la Derivata — d/dx | x^(1/2) | |
| 76 | Trovare la Derivata — d/d@VAR | f(x) = square root of x | |
| 77 | Trovare la Derivata — d/dx | cos(x^2) | |
| 78 | Trovare la Derivata — d/dx | 1/(x^5) | |
| 79 | Trovare la Derivata — d/dx | кубический корень из x^2 | |
| 80 | Вычислим интеграл | интеграл cos(x) по x | |
| 81 | Вычислим интеграл | интеграл e^(-x^2) по x | |
| 82 | Trovare la Derivata — d/d@VAR | f(x)=x^3 | |
| 83 | Вычислим интеграл | интеграл 4x^2+7 в пределах от 0 до 10 по x | |
| 84 | Вычислим интеграл | интеграл ( натуральный логарифм x)^2 по x | |
| 85 | Trovare la Derivata — d/dx | логарифм x | |
| 86 | Trovare la Derivata — d/dx | arctan(x) | |
| 87 | Trovare la Derivata — d/dx | натуральный логарифм 5x | |
| 88 | Trovare la Derivata — d/dx | 5e^x | |
| 89 | Trovare la Derivata — d/dx | cos(3x) | |
| 90 | Вычислим интеграл | интеграл x^3 по x | |
| 91 | Вычислим интеграл | интеграл x^2e^x по x | |
| 92 | Trovare la Derivata — d/dx | 16 корень четвертой степени из 4x^4+4 | |
| 93 | Trovare la Derivata — d/dx | x/(e^x) | |
| 94 | Оценить предел | предел arctan(e^x), если x стремится к 3 | |
| 95 | Вычислим интеграл | интеграл (e^x-e^(-x))/(e^x+e^(-x)) по x | |
| 96 | Trovare la Derivata — d/dx | 3^x | |
| 97 | Вычислим интеграл | интеграл xe^(x^2) по x | |
| 98 | Trovare la Derivata — d/dx | 2sin(x) | |
| 99 | Вычислить | sec(0)^2 | |
| 100 | Trovare la Derivata — d/dx | натуральный логарифм x^2 |
Функция y=sin x и её свойства и график с примерами решений
Содержание:
Рассматривая произвольное действительное число
Таким образом, мы установим соответствие между множеством действительных чисел и множеством значений синусов углов. Каждому действительному числу соответствует единственное значение синуса. Такое соответствие определяет тригонометрическую функцию
Каждому действительному числу соответствует единственное значение синуса. Такое соответствие определяет тригонометрическую функцию
Определение:
Зависимость, при которой каждому действительному числу соответствует значение называется функцией
Рассмотрим свойства функции и построим ее график:
Область определения функции y=sin x
Областью определения функции является множество всех действительных чисел, так как для любого существует
Графически это означает, что для любой абсциссы найдется точка графика функции
Множеством значений функции y=sin x
Множеством значений функции является промежуток так как ординаты точек единичной окружности (значения синусов чисел) изменяются от -1 до 1.
Графически это означает, что график функции расположен в полосе между прямыми (рис. 74).
Периодичность функции y=sin x
Периодичность функции Точки единичной окружности совпадают для любого (рис.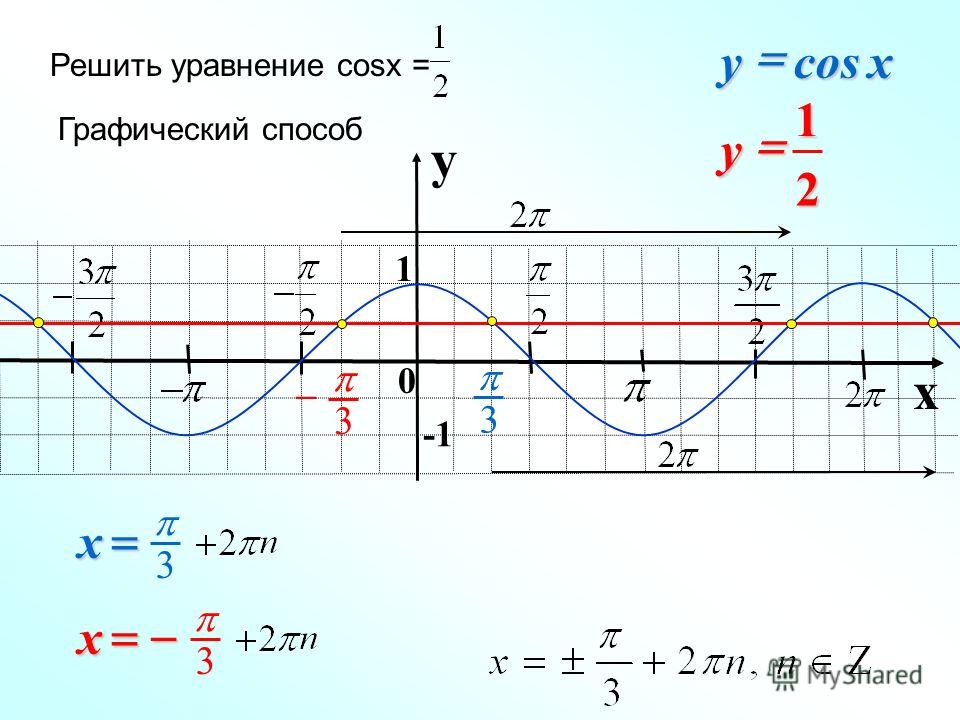 75), значит, значения синусов этих углов также совпадают, т. е.
75), значит, значения синусов этих углов также совпадают, т. е.
Говорят, что число является периодом функции
Определение:
Функция называется периодической функцией с периодом если для любого значения из области определения функции числа также принадлежат области определения и при этом верно равенство
Чтобы определить, является ли функция периодической с периодом необходимо проверить:
- принадлежат ли области определения функции числа если принадлежит области определения функции;
- выполняется ли равенство
Определим, верно ли, что число является периодом функции
- Числа принадлежат области определения функции, так как
- Проверим, выполняется ли равенство для всех
Пусть
Значит, число не является периодом функции
Периодом функции являются числа вида Число является наименьшим положительным периодом функции
Функция является периодической с наименьшим положительным периодом (рис.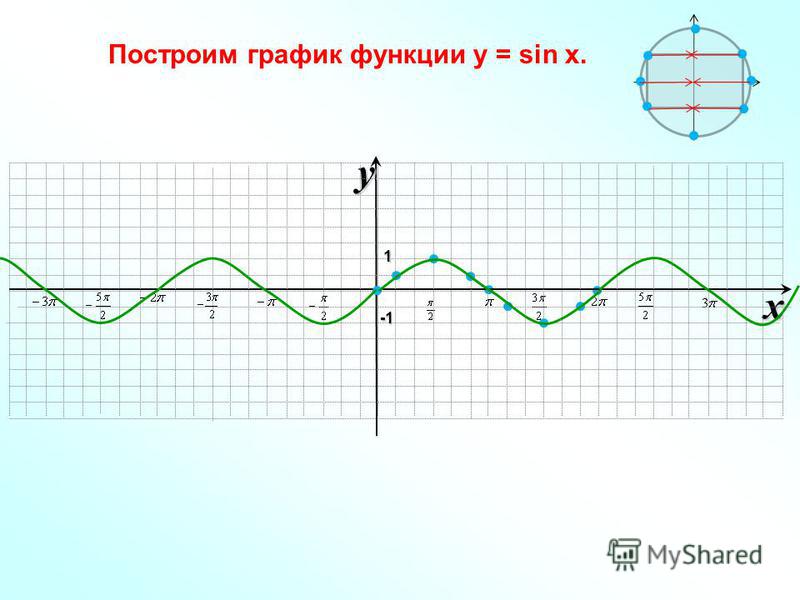 76). Это означает, что ее график состоит из повторяющихся частей, поэтому достаточно его построить на отрезке длиной (например, а затем повторить построение на каждом следующем отрезке длиной
76). Это означает, что ее график состоит из повторяющихся частей, поэтому достаточно его построить на отрезке длиной (например, а затем повторить построение на каждом следующем отрезке длиной
Четность (нечетность) функции y=sin x
Четность (нечетность) функции y=sin x — симметрична относительно нуля. Так как точки единичной окружности симметричны относительно оси абсцисс для любого то ординаты этих точек противоположны, т. е. (рис. 77). Значит, функция нечетная.
Для построения ее графика достаточно построить его часть для неотрицательных значений аргумента и отобразить эту часть симметрично относительно начала координат.
Нули функции y=sin x
Нули функции. Ординаты точек и равны нулю. Значит, в точка (рис. 78), т. е. график функции пересекает ось абсцисс в точках с абсциссами
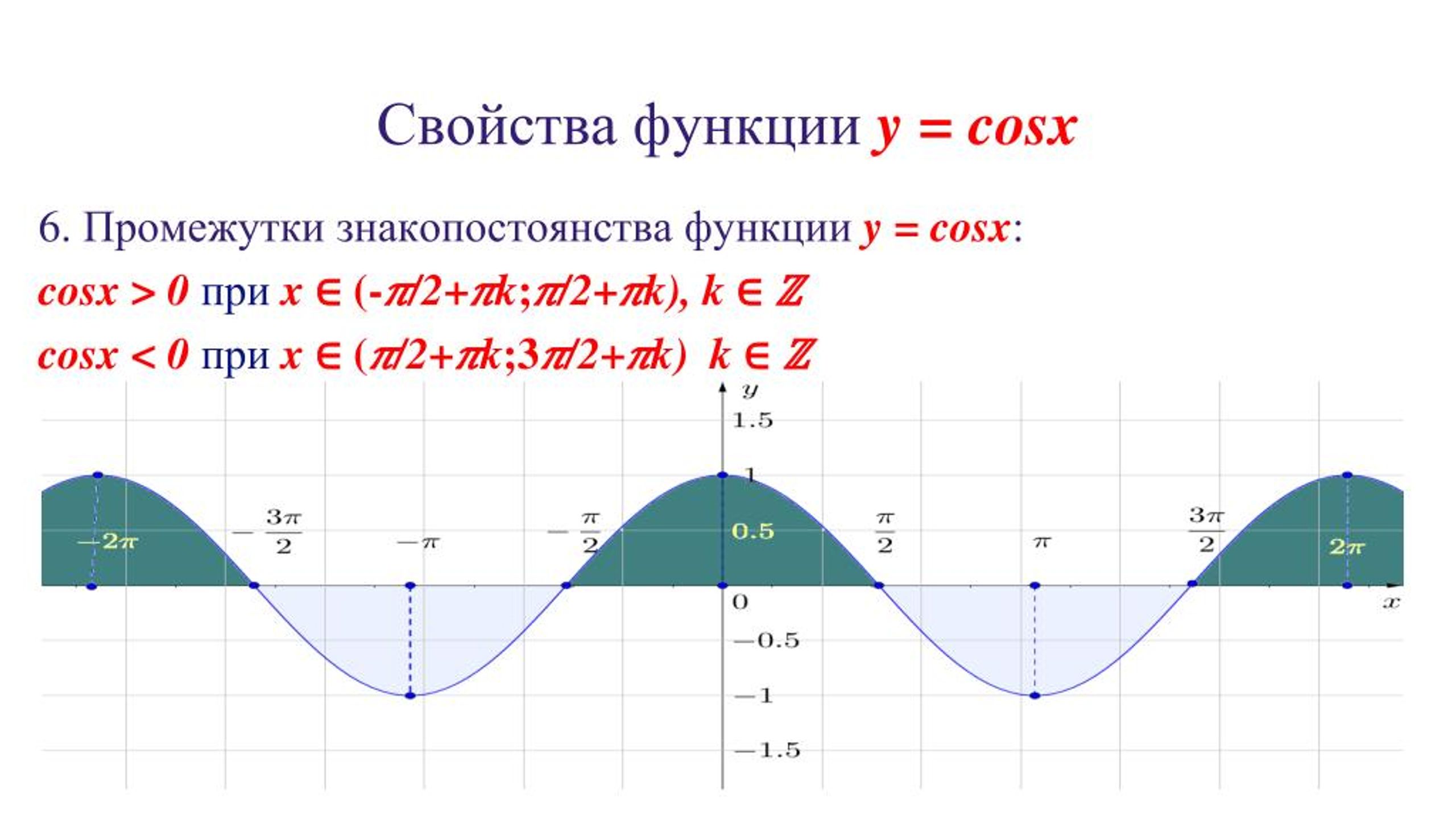
Промежутки знакопостоянства функции y=sin x
На промежутках функция принимает положительные значения, так как ординаты точек единичной окружности положительны в первой и во второй четвертях (рис.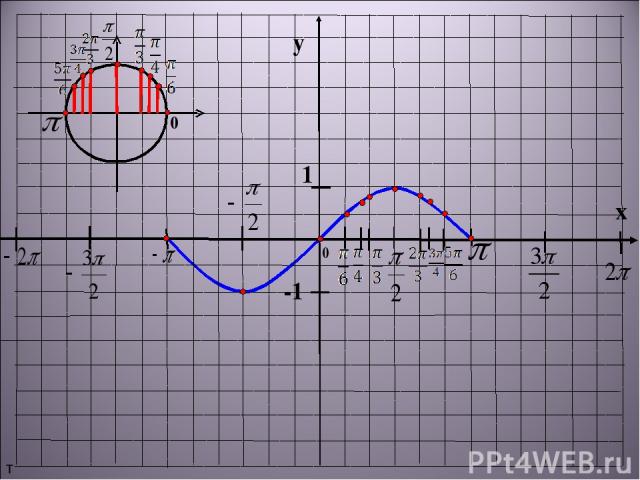 79, а).
79, а).
На промежутках функция принимает отрицательные значения, так как ординаты точек единичной окружности отрицательны в третьей и четвертой четвертях (рис. 79, б).
Монотонность функции y=sin x
Монотонность функции. Так как ординаты точек единичной окружности увеличиваются от -1 до 1 при изменении угла от (рис. 80, а) и уменьшаются от 1 до -1 при изменении угла от (рис. 80, б), то с учетом периодичности определим промежутки возрастания функции и промежутки убывания функции
Функции возрастает на промежутках и убывает на промежутках
Наибольшее значение функции равно 1 и достигается в точках
Наименьшее значение функции равно и достигается в точках
На основании проведенного исследования построим график функции на отрезке от длина которого равна т. е. длине периода функции
На этом периоде функция
- равна нулю в точках
- достигает значений, равных 1 и -1, соответственно в точках
- принимает положительные значения при значениях аргумента от 0 до а отрицательные — при значениях аргумента от до 0;
- возрастает от и убывает от
На рисунке 81 изображена часть графика функции на промежутке от
Перенесем эту часть на другие периоды и получим график функции (рис.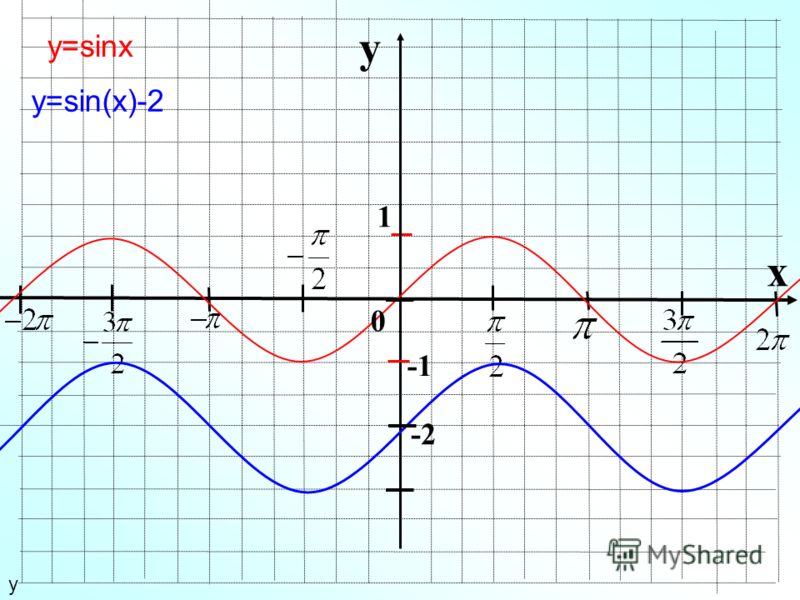 82). График функции называется синусоидой.
82). График функции называется синусоидой.
Примеры заданий и их решения
Пример №1Определите, принадлежит ли графику функции точка:
Решение:
а) Подставим в формулу значение аргумента найдем соответствующее значение функции
Полученное значение функции равно ординате точки значит, точка принадлежит графику функции
б) При получим Точка не принадлежит графику функции
в) При получим Точка принадлежит графику функции
г) При получим Точка не принадлежит графику функции
Пример №2Найдите область определения и множество значений функции:
Решение:
а) Так как область определения функции все действительные числа, т.е значит, Таким образом,
Множеством значений функции является отрезок значит, Тогда по свойству неравенств Таким образом,
б) Поскольку то по свойству неравенств
т.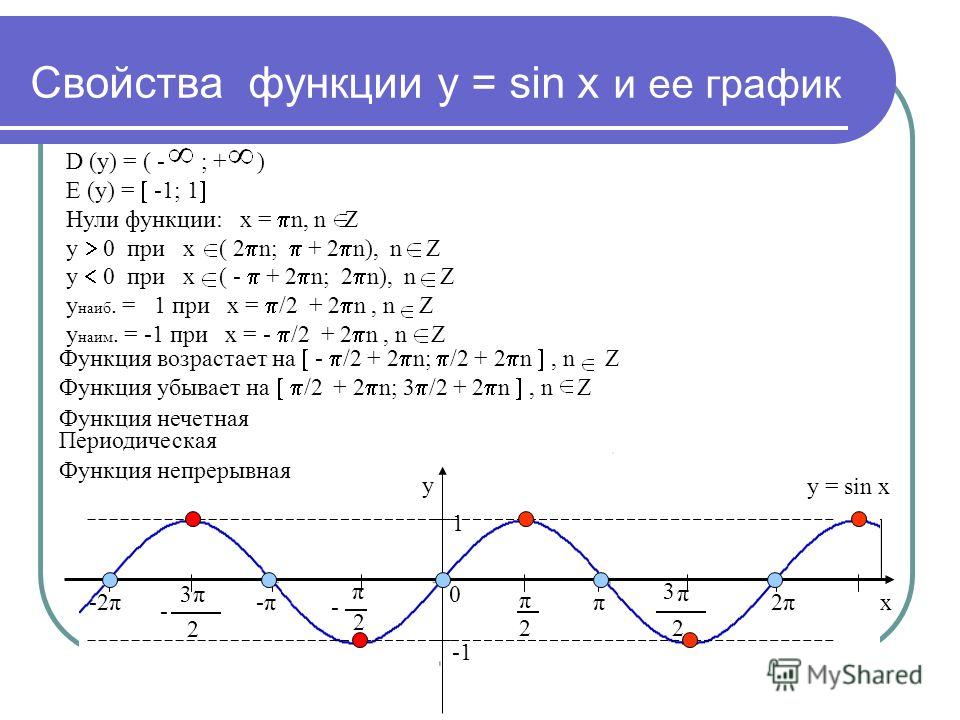 е.
е.
Найдите наибольшее значение функции
Решение:
Так как значит, тогда Таким образом, имеем: Наибольшее значение функции равно 7.
- Заказать решение задач по высшей математике
Найдите значение выражения, используя свойство периодичности функции
Решение:
Так как число является наименьшим положительным периодом функции Тогда:
Пример №5Найдите значение выражения, используя свойство нечетности функции
Решение:
Так как функция нечетная, то
Тогда:
Пример №6Исследуйте функцию на четность (нечетность):
Решение:
a) — область определения симметрична относительно нуля;
значит, функция является нечетной.
область определения симметрична относительно нуля;
значит, функция является четной.
Найдите нули функции:
Решение:
а) Пусть Нулями функции являются числа Тогда значит, Таким тобразом, числа являются нулями функции
б) Пусть Нулями функции являются числа Тогда значит,
Таким образом, числа являются нулями функции
Пример №8Определите знак произведения
Решение:
Так как то т. е. угол 4 радиана принадлежит промежутку на котором функция принимает отрицательные значения, значит,
Углы 2 радиана и 1 радиан принадлежат промежутку на котором функция принимает положительные значения, т. е. Значит,
Пример №9Что больше: или
Решение. Так как функция возрастает на промежутке то из того, что следует, что
Пример №10Постройте график функции:
Решение:
а) График функции получаем из графика функции сдвигом его вдоль оси абсцисс на влево (рис.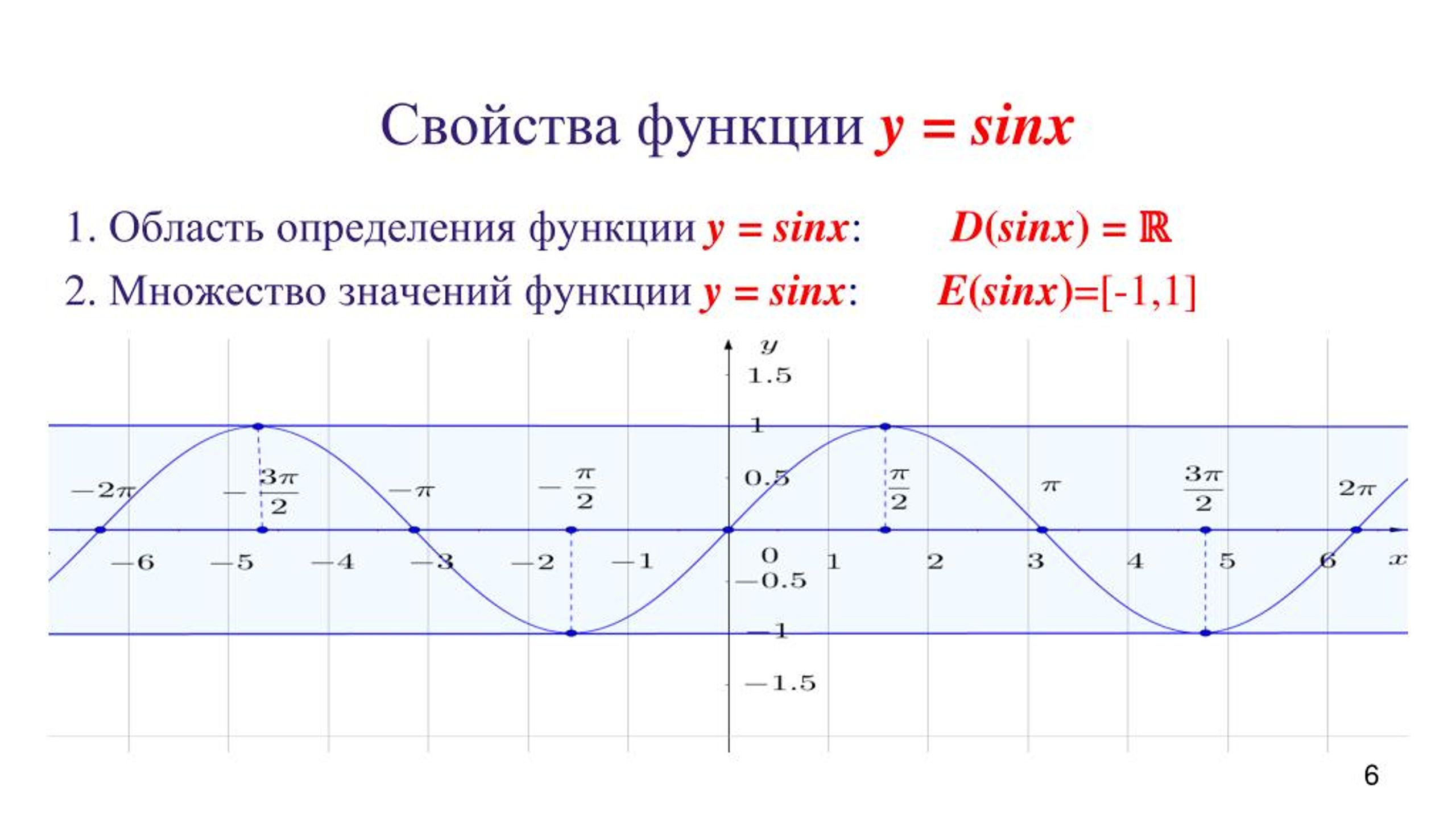 84).
84).
б) График функции получаем из графика функции сдвигом его вдоль оси ординат на 2 единицы вверх (рис. 85).
Свойства и график функции у = sin x презентация, доклад
Тема урока:
Свойства и график функции y = sin x.
Учитель математики МБОУ СОШ № 25 г. Крымска Е.В. Малая
10.11.2013
Определение:
Исследуем свойства функций по плану:
Область значения функции
Периодичность
Четность, нечетность
Промежутки знакопостоянства
Промежутки монотонности
Наибольшее (наименьшее) значение функции
Нули функции
Область определения функции
Функции у = sin x, y = cos x, y = tg x, y = ctg x называются тригонометрическими функциями.
х
у
0
0
2π
1
-1
D(у) = (- ∞ ; + ∞ )
Е(у)= [-1; 1]
Область определения. Область значений функции.
Область значений функции.
Область определения
функции синус ̶ любое
действительное число, т. е.
2) Область значений функции синус ̶ отрезок
от -1 до 1, т. е.
IV. sin (− х) = − sin х, т. е.
f (− х)= − f (х) функция нечетная
f (х +Т) = f (х –Т) = f (х) Функция периодическая,
T = 2π – наименьший положительный период
Периодичность
III. sin (x +2πn) = sin х, n ϵ Z
Чётность, нечётность
x
y
0
0
M
y
2π
π
-y
x
-x
Наибольшее и наименьшее значение функции
y > 0 при 0
y > 0 при х ϵ (2πn; π+2πn), n ϵ Z
y
y
у
— π/2
3π/2
2π
х
0
-π
0
π
π/2
при х =
при х = —
1
-1
унаиб. = 1
= 1
+ 2πn, n ϵ Z
унаим.= -1
+ 2πn, n ϵ Z
у = 0
πn, n ϵ Z
0
+
Промежутки знакопостоянства
Нули функции
Промежутки монотонности
у
2
π
х
0
0
π
-π
—
2
π
π
2
3
у 1
у 2
М 1
М 2
Функция возрастает на [ — π/2 + 2πn; π/2 + 2πn ] , n
Функция убывает на [ π/2 + 2πn; 3π/2 + 2πn ] , n Z
Z
х1
х2
I. х 1
IV х 1
sin х 1
II. х 1
sin х1 > sin х 2
III. х 1 sin х 1 > sin х 2
sin х 1
Свойства функции у = sin х и ее график
y
x
0
2
π
2
π
—
—
-π
π
2π
-2π
1
-1
D (у) = ( — ; + )
Е (у) = [ -1; 1]
Нули функции: х = πn, n Z
у > 0 при х ( 2πn; π + 2πn), n Z
у унаиб.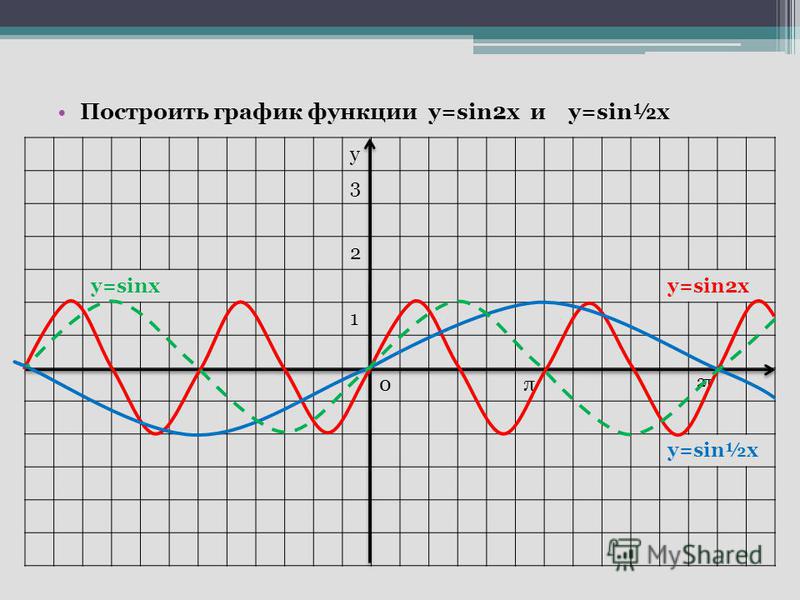 = 1 при х = π/2 + 2πn , n Z
= 1 при х = π/2 + 2πn , n Z
унаим. = -1 при х = — π/2 + 2πn , n Z
y = sin x
Функция непрерывная
Периодическая
Функция нечетная
Функция возрастает на [ — π/2 + 2πn; π/2 + 2πn ] , n Z
Функция убывает на [ π/2 + 2πn; 3π/2 + 2πn ] , n Z
Построение графика функции y = sin x.
Построение графика функции y = sin x.
Построение графика функции y = sin x.
I I I I I I
O
x
y
-1
1
1/2
Найти все корни уравнения sin x = 1/2
принадлежащих промежутку –π ≤ х ≤ 3π ∕ 2.
y = sin x.
Ответ: х = π/6; х = 5π/6
Пример №1
I I I I I I
O
x
y
-1
1
1/2
Найти все решения неравенства sin x ≥ 1/2
принадлежащих промежутку –3π/2 ≤ х ≤ π .
y = sin x.
Ответ:
Пример №2
Скачать презентацию
Функция y = sin x, её свойства и график. 10-й класс
Тип урока: урок введения нового знания.
Педагогическая технология: проблемное обучение.
Формируемые результаты:
- Предметные: формировать умение строить график функции у = sin x, читать график и применять свойства при решении задач.
- Личностные: умение применять решение, применять независимость суждений.

- Метапредметные: формировать умение соотносить свои действия с планируемыми результатами.
Планируемые результаты: обучающиеся научатся применять свойства функции у = sin x и читать график.
Основные понятия: синусоида, свойства функции у = sin x.
Оборудование: ПК, проектор, Microsoft PowerPoint, презентация «Функция y = sin x, её свойства и график», таблица «Тригонометр».
Ход урока
1. Организационный момент2. Целеполагание— «Много из математики не остается в памяти, но когда поймешь ее, тогда легко при случае вспомнить забытое.», писал Михаил Васильевич Остроградский (1801-1862, российский математик, механик). Как вы понимаете эти слова? (Слайд 1)
— Перед вами 4 графика. (Слайд 2)
— Как можно одним словом объединить эти графики? (функции)
— Опишите свойства графиков, представленных на слайде?
— Какие из предложенных графиков функций вам известны?
— Сформулируйте тему урока.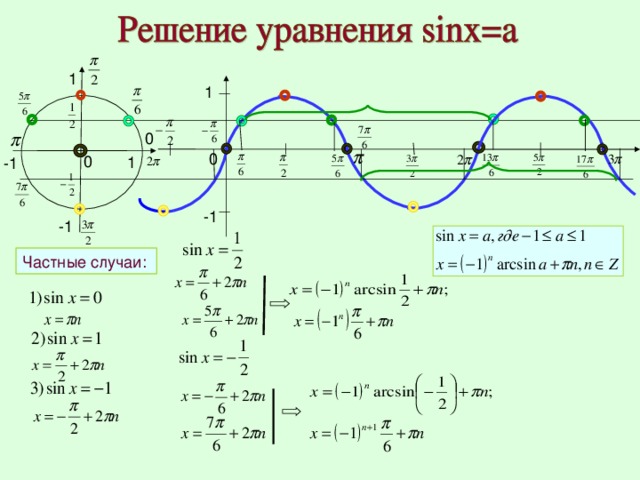
Тема урока: «Функция y = sin x, её свойства и график» (Слайд 3)
— Давайте попробуем определить цели нашего сегодняшнего урока, что мы уже знаем, и чему должны или можем научиться? (учитель вместе с обучающимися формирует цели, записывает их на доске).
— Познакомимся с историей возникновения слова синус (Слайд 4)
Синус (история имени)
Синус (sin) — название тригонометрической функции, появившееся благодаря удивительной цепочке искажений во время переводов математических трактатов. Древние индийские математики называли функцию «полу-тетивой», а затем просто «тетивой» — «джива», так как при геометрическом построении изображение напоминало лук. Арабские математики при знакомстве с трудами индийских коллег не стали переводить слово «джива» на арабский, а просто записали его по буквам. В процессе адаптации, устного использования и пр. оно превратилось в арабское выражение «джайб», которое можно перевести как пазуха, складка, карман, впадина.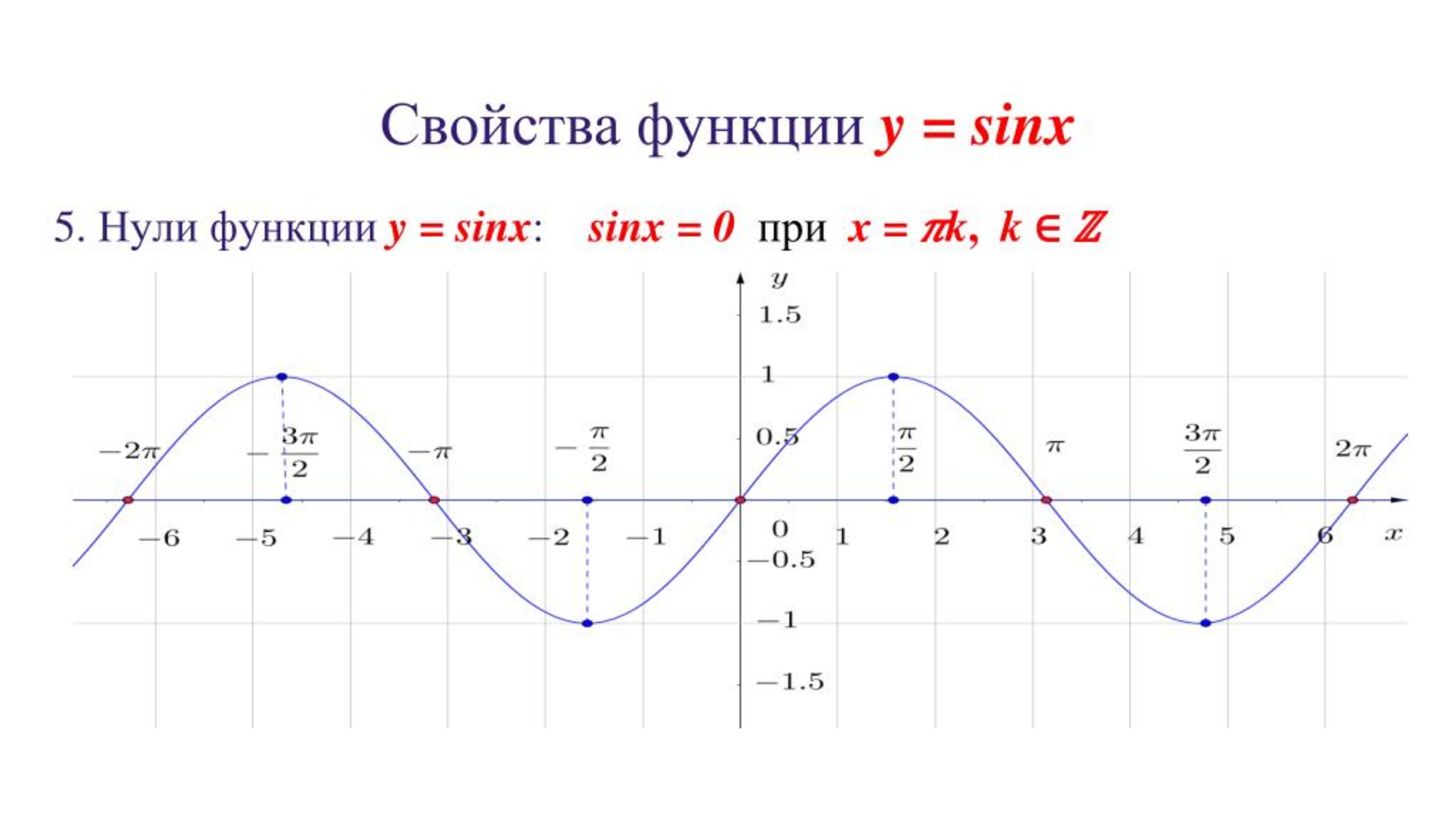 Когда, в свою очередь, арабские математические трактаты попали к европейским математикам, те перевели джайб на латинский, благо под рукой как раз было изящное слово, обозначающее складку или пазуху на римской тоге — слово sinus. Родственную функцию назвали complementi sinus, дополнительный синус. Позже утвердилось современное сокращение: sin и cos.
Когда, в свою очередь, арабские математические трактаты попали к европейским математикам, те перевели джайб на латинский, благо под рукой как раз было изящное слово, обозначающее складку или пазуху на римской тоге — слово sinus. Родственную функцию назвали complementi sinus, дополнительный синус. Позже утвердилось современное сокращение: sin и cos.
— Составим план работы (перечень свойств, которые будут исследоваться).
Обучающиеся записывают план исследования синуса в тетрадях.
План
- Область определения
- Область значения
- Нули функции
- Промежутки возрастания, убывания функции
- Промежутки знакопостоянства
- Четность функции
- Монотонность функции
- Наименьшее и наибольшее значение функции
— Какую функцию называют периодической?
— Что такое период?
— Какое число является главным периодом функции у = sin x?
4. Восприятие, осмысление, первичное закрепление
Восприятие, осмысление, первичное закрепление— Что происходит с ординатой точки при ее движении по первой четверти? (ордината увеличивается). Что происходит с ординатой точки при ее движении по второй четверти? (ордината постепенно уменьшается). Как это связано с монотонностью функции? (функция у = sin t возрастает на отрезке и убывает на отрезке ).
— Запишем функцию у = sin t в привычном для нас виде у = sin x (строить будем в привычной системе координат хОу) и составим таблицу значений этой функции.
0 | |||||||
у | 0 | 1 | 0 |
Изучение нового материала (презентация, слайды 5-6).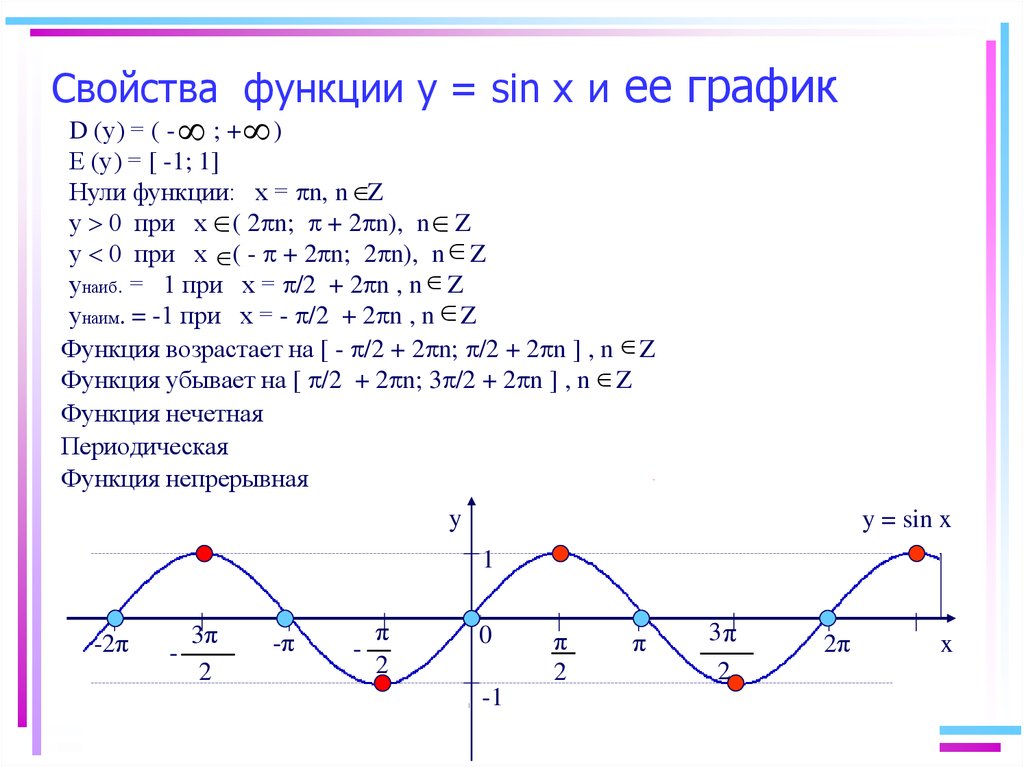
Построение графика функции у = sin x и запись свойств функции в тетради. (Слайды 7–10)
1) D(y) =
2) E (y) =
3) функция ограничена и сверху, и снизу
4) унаиб = 1, унаим = -1
5) непрерывная функция
6) нечетная функция
7) возрастает на ; убывает на
— Стихотворение (отрывок)
5. Применение знаний и способов при решении задачИ линия эта волною качается,
И синусом график ее называется,
И через период она повторяется,
В периоде трижды она обнуляется,
Она полпериода вверх поднимается,
Придет в единицу и вниз опускается,
И так вдоль абсциссы все время болтается.
В системе, которую создал Декарт.
— Постройте график функции (самостоятельно с проверкой, слайды 11-14):
а) у = sin x + 2
б) у = sin x — 1
в) у = sin
г) у = sin
— Решите графически уравнение sin x = (проверка слайд 15).
№ 21.5 (1), 21.9 (1)
7. Рефлексия— Предлагаю оценить факт достижения цели урока: на все ли вопросы найдены ответы?
— Оцените свою работу на уроке. Закончите предложение. (Слайд 17)
Урок –
- заставил задуматься…
- навёл меня на размышления…
- Что нового вы узнали на уроке?
- Что вы считаете нужным запомнить?
- Над чем ещё надо поработать?
- п. 21 (учить свойства функции у = sin x)
- учебник № 21.6 (1)
- Построить график функции у = sin (x — )
— Спасибо за урок
Использованные материалы и ресурсы- Мерзляк А.Г., и др. Алгебра и начала математического анализа (углублённый уровень) 10 кл. – М.: «Вентана-Граф», 2017.
- Мерзляк А.Г., и др.
 Дидактические материалы к учебнику Алгебра и начала математического анализа (углублённый уровень) – М.: «Вентана-Граф», 2017.
Дидактические материалы к учебнику Алгебра и начала математического анализа (углублённый уровень) – М.: «Вентана-Граф», 2017. - http://matematikam.ru/calculate-online/grafik.php
Построить график функции у=sin2x и у=sin. График функции y=sin x Задачи на синус для самостоятельного решения
Как построить график функции y=sin x? Для начала рассмотрим график синуса на промежутке .
Единичный отрезок берём длиной 2 клеточки тетради. На оси Oy отмечаем единицу.
Для удобства число π/2 округляем до 1,5 (а не до 1,6, как требуется по правилам округления). В этом случае отрезку длиной π/2 соответствуют 3 клеточки.
На оси Ox отмечаем не единичные отрезки, а отрезки длиной π/2 (через каждые 3 клеточки). Соответственно, отрезку длиной π соответствует 6 клеточек, отрезку длиной π/6 — 1 клеточка.
При таком выборе единичного отрезка график, изображённый на листе тетради в клеточку, максимально соответствует графику функции y=sin x.
Составим таблицу значений синуса на промежутке :
Полученные точки отметим на координатной плоскости:
Так как y=sin x — нечётная функция, график синуса симметричен относительно начала отсчёта — точки O(0;0).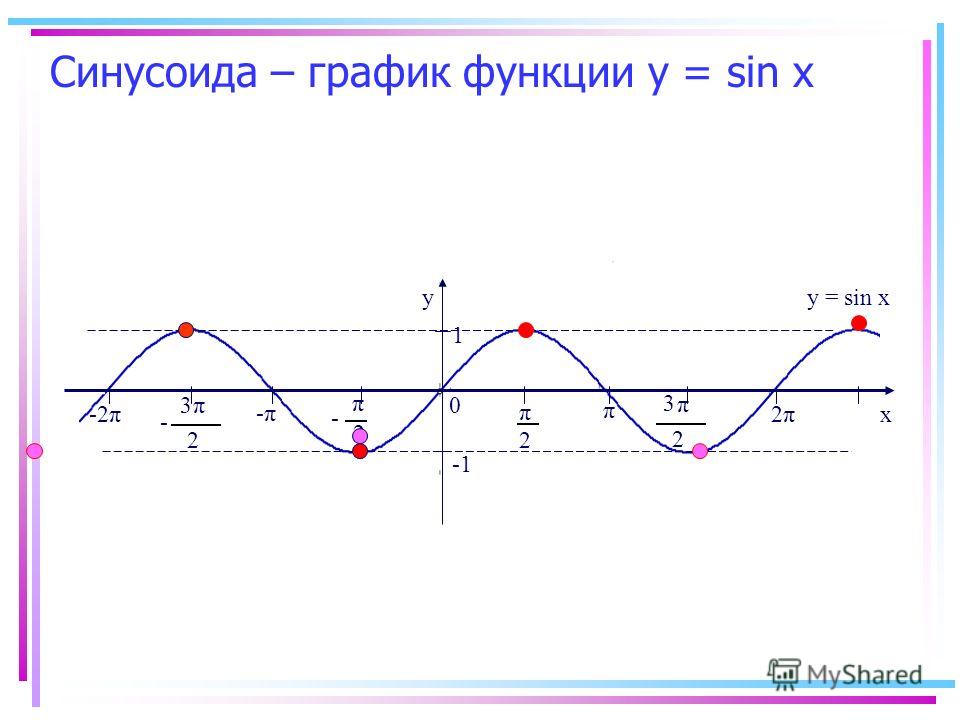 С учётом этого факта продолжим построение графика влево, то точки -π:
С учётом этого факта продолжим построение графика влево, то точки -π:
Функция y=sin x — периодическая с периодом T=2π. Поэтому график функции, взятый на на промежутке [-π;π], повторяется бесконечное число раз вправо и влево.
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Пособия и тренажеры в интернет-магазине «Интеграл» для 10 класса от 1С
Решаем задачи по геометрии. Интерактивные задания на построение для 7-10 классов
Программная среда «1С: Математический конструктор 6.1»
Что будем изучать:
- Свойства функции Y=sin(X).
- График функции.
- Как строить график и его масштаб.
- Примеры.
Свойства синуса. Y=sin(X)
Ребята, мы уже познакомились с тригонометрическими функциями числового аргумента. Вы помните их?
Давайте познакомимся поближе с функцией Y=sin(X)
Запишем некоторые свойства этой функции:
1) Область определения – множество действительных чисел.
2) Функция нечетная. Давайте вспомним определение нечетной функции. Функция называется нечетной если
выполняется равенство: y(-x)=-y(x). Как мы помним из формул привидения: sin(-x)=-sin(x). Определение выполнилось, значит Y=sin(X) – нечетная функция.
3) Функция Y=sin(X) возрастает на отрезке и убывает на отрезке [π/2; π]. Когда мы движемся по первой четверти (против часовой стрелки), ордината увеличивается, а при движении по второй четверти она уменьшается.
4) Функция Y=sin(X) ограничена снизу и сверху. Данное свойство следует из того, что
-1 ≤ sin(X) ≤ 1
5) Наименьшее значение функции равно -1 (при х = — π/2+ πk). Наибольшее значение функции равно 1 (при х = π/2+ πk).
Давайте, воспользовавшись свойствами 1-5, построим график функции Y=sin(X). Будем строить наш график последовательно, применяя наши свойства. Начнем строить график на отрезке .
Особое внимание стоит обратить на масштаб. На оси ординат удобнее принять единичный отрезок равный 2 клеточкам, а на оси абсцисс — единичный отрезок (две клеточки) принять равным π/3 (смотрите рисунок).
Построение графика функции синус х, y=sin(x)
Посчитаем значения функции на нашем отрезке:
Построим график по нашим точкам, с учетом третьего свойства.
Таблица преобразований для формул привидения
Воспользуемся вторым свойством, которое говорит, что наша функция нечетная, а это значит, что ее можно отразить симметрично относительно начало координат:
Мы знаем, что sin(x+ 2π) = sin(x). Это значит, что на отрезке [- π; π] график выглядит так же, как на отрезке [π; 3π] или или [-3π; — π] и так далее. Нам остается аккуратно перерисовать график на предыдущем рисунке на всю ось абсцисс.
График функции Y=sin(X) называют — синусоидой.
Напишем еще несколько свойств согласно построенному графику:
6) Функция Y=sin(X) возрастает на любом отрезке вида: [- π/2+ 2πk; π/2+ 2πk], k – целое число и убывает на любом отрезке вида: [π/2+ 2πk; 3π/2+ 2πk], k – целое число.
7) Функция Y=sin(X) – непрерывная функция. Посмотрим на график функции и убедимся что у нашей функции нет разрывов, это и означает непрерывность.
8) Область значений: отрезок [- 1; 1]. Это также хорошо видно из графика функции.
9) Функция Y=sin(X) — периодическая функция. Посмотрим опять на график и увидим, что функция принимает одни и те же значения, через некоторые промежутки.
Примеры задач с синусом
1. Решить уравнение sin(x)= x-π
Решение: Построим 2 графика функции: y=sin(x) и y=x-π (см. рисунок).
Наши графики пересекаются в одной точке А(π;0), это и есть ответ: x = π
2. Построить график функции y=sin(π/6+x)-1
Решение: Искомый график получится путем переноса графика функции y=sin(x) на π/6 единиц влево и 1 единицу вниз.
Решение: Построим график функции и рассмотрим наш отрезок [π/2; 5π/4].
На графике функции видно, что наибольшие и наименьшие значения достигаются на концах отрезка, в точках π/2 и 5π/4 соответственно.
Ответ: sin(π/2) = 1 – наибольшее значение, sin(5π/4) = наименьшее значение.
Задачи на синус для самостоятельного решения
- Решите уравнение: sin(x)= x+3π, sin(x)= x-5π
- Построить график функции y=sin(π/3+x)-2
- Построить график функции y=sin(-2π/3+x)+1
- Найти наибольшее и наименьшее значение функции y=sin(x) на отрезке
- Найти наибольшее и наименьшее значение функции y=sin(x) на отрезке [- π/3; 5π/6]
Построить функцию
Мы предлагаем вашему вниманию сервис по потроению графиков функций онлайн, все права на который принадлежат компании Desmos . 2/16=1)
2/16=1)
С нами легко в режиме онлайн строить графики различной сложности. Построение производится мгновенно. Сервис востребован для нахождения точек пересечения функций, для изображения графиков для дальнейшего их перемещения в Word документ в качестве иллюстраций при решении задач, для анализа поведенческих особенностей графиков функций. Оптимальным браузером для работы с графиками на данной странице сайта является Google Chrome. При использовании других браузеров корректность работы не гарантируется.
«Построение графика функции с модулем» — Y = lnx. Закрепили знания на ранее изученных функциях. Построение графиков функций. Вопрос классу. Y = x2 – 2x – 3. Проектная деятельность. Урок обобщения и систематизации знаний. График функции. Актуализация знаний о графиках функций. Обобщение. Попробуйте самостоятельно построить графики. Y = f(x).
Построение графиков функций. Вопрос классу. Y = x2 – 2x – 3. Проектная деятельность. Урок обобщения и систематизации знаний. График функции. Актуализация знаний о графиках функций. Обобщение. Попробуйте самостоятельно построить графики. Y = f(x).
««Графики функций» 9 класс» — Цели урока. Большему значению аргумента соответствует большее значение функции. Нули функции. Определение. Заполните пропуски. Установите соответствие между функцией и вершиной. Тренажер. Выберите уравнение, с помощью которого задана линейная функция. Установите соответствие. Выберите уравнение. Обратная пропорциональность.
«Графики функций с модулями» — Найдём вершину функции. Кубическая функция. Отрицательная сторона. Графики функций. Квадратичная функция. Сложная функция. Функция с модулем. Графики функций надо обязательно уметь строить. Подготовка к ЕГЭ. Графики функций с модулями. Парабола. График функции.
«Уравнение касательной к графику функции» — Производная в точке. Правила дифференцирования. График функции. Алгоритм нахождения уравнения. Ответьте на вопросы. Геометрический смысл производной. Номера из учебника. Уравнение касательной к графику функции. Определение. Касательная к графику функции. Основные формулы дифференцирования. Провести касательную.
График функции. Алгоритм нахождения уравнения. Ответьте на вопросы. Геометрический смысл производной. Номера из учебника. Уравнение касательной к графику функции. Определение. Касательная к графику функции. Основные формулы дифференцирования. Провести касательную.
«Построение графиков функций» — Построение графика функции y = sinx. Линия тангенсов. Алгебра. Тема: Построение графиков функций. График функции y = sinx. Выполнила: Филиппова Наталья Васильевна учитель математики Белоярская средняя общеобразовательная школа №1. Построить график функции y=sin(x) +cos(x).
«График обратной пропорциональности» — Применение гиперболы. Гипербола. Монотонность функции. Чётность, нечётность. Функция «Обратная пропорциональность». График. Построение графика обратной пропорциональности. Гипербола и космические спутники. Однополостной гиперболоид. Асимптота. Применение гиперболоидов. Определение обратной пропорциональности.
Всего в теме 25 презентаций
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
6.
 1 Графики функций синуса и косинуса — предварительный расчет 2e
1 Графики функций синуса и косинуса — предварительный расчет 2eЦели обучения
В этом разделе вы:
- График вариантов y=sin(x)y=sin(x) и y=cos(x)y=cos(x) .
- Использовать фазовые сдвиги синусоидальных и косинусоидальных кривых.
Рисунок 1 Свет можно разделить на цвета из-за его волнообразных свойств. (кредит: «wonderferret»/Flickr)
Белый свет, такой как свет солнца, на самом деле вовсе не белый. Вместо этого это композиция всех цветов радуги в виде волн. Отдельные цвета можно увидеть, только когда белый свет проходит через оптическую призму, которая разделяет волны в соответствии с их длинами волн, образуя радугу.
Световые волны графически могут быть представлены синусоидальной функцией. В главе о тригонометрических функциях мы рассмотрели тригонометрические функции, такие как функция синуса. В этом разделе мы будем интерпретировать и создавать графики функций синуса и косинуса.
График функций синуса и косинуса
Напомним, что функции синуса и косинуса связывают действительные числовые значения с координатами x и y точки на единичной окружности. Так как же они выглядят на графике в координатной плоскости? Начнем с функции синуса. Мы можем создать таблицу значений и использовать их для построения графика. В таблице 1 перечислены некоторые значения функции синуса на единичном круге.
| хх | 00 | π6π6 | π4π4 | π3π3 | π2π2 | 2π32π3 | 3π43π4 | 5π65π6 | ππ |
| грех (х) грех (х) | 00 | 1212 | 2222 | 3232 | 11 | 3232 | 2222 | 1212 | 00 |
Стол 1
Нанесение точек из таблицы и продолжение вдоль оси x дает форму функции синуса. См. рис. 2.
См. рис. 2.
Рис. 2 Функция синуса
Обратите внимание, что значения синуса положительны между 0 и π, π, которые соответствуют значениям функции синуса в квадрантах I и II на единичной окружности, а значения синуса отрицательны между ππ и 2π, 2π , которые соответствуют значениям функции синуса в квадрантах III и IV на единичной окружности. См. рис. 3.
Рисунок 3 График значений функции синуса
Теперь давайте аналогично посмотрим на функцию косинуса. Опять же, мы можем создать таблицу значений и использовать их для построения графика. В таблице 2 перечислены некоторые значения функции косинуса на единичном круге.
| хх | 00 | π6π6 | π4π4 | π3π3 | π2π2 | 2π32π3 | 3π43π4 | 5π65π6 | № |
| cos(x)cos(x) | 11 | 3232 | 2222 | 1212 | 00 | −12−12 | −22−22 | −32−32 | −1−1 |
Стол 2
Как и в случае функции синуса, мы можем нанести точки на график функции косинуса, как показано на рис. 4.
4.
Рисунок 4 Функция косинуса
Поскольку мы можем вычислить синус и косинус любого действительного числа, обе эти функции определены для всех действительных чисел. Думая о значениях синуса и косинуса как о координатах точек на единичной окружности, становится ясно, что диапазон обеих функций должен быть интервалом [−1,1].[−1,1].
На обоих графиках форма графика повторяется через 2π,2π, что означает периодичность функций с периодом 2π,2π. Периодическая функция — это функция, для которой определенное горизонтальное смещение, P , приводит к функции, равной исходной функции: f(x+P)=f(x)f(x+P)=f(x) для все значения xx в области определения ф.ф. Когда это происходит, мы называем наименьшее такое горизонтальное смещение с P>0P>0 периодом функции. На рис. 5 показаны несколько периодов функций синуса и косинуса.
Рисунок 5
Повторный взгляд на функции синуса и косинуса в области с центром на оси y помогает обнаружить симметрию. Как мы видим на рисунке 6, синусоидальная функция симметрична относительно начала координат. Вспомним из «Других тригонометрических функций», что мы определили по единичному кругу, что синусоидальная функция является нечетной функцией, потому что sin(-x)=-sinx.sin(-x)=-sinx.
Теперь мы можем ясно увидеть это свойство на графике.
Как мы видим на рисунке 6, синусоидальная функция симметрична относительно начала координат. Вспомним из «Других тригонометрических функций», что мы определили по единичному кругу, что синусоидальная функция является нечетной функцией, потому что sin(-x)=-sinx.sin(-x)=-sinx.
Теперь мы можем ясно увидеть это свойство на графике.
Рисунок 6 Нечетная симметрия синуса
На рис. 7 показано, что функция косинуса симметрична относительно оси y . Опять же, мы определили, что функция косинуса является четной функцией. Теперь из графика видно, что cos(−x)=cosx.cos(−x)=cosx.
Рисунок 7 Четная симметрия функции косинуса
Характеристики функций синуса и косинуса
Функции синуса и косинуса имеют несколько различных характеристик:
- Это периодические функции с периодом 2π,2π.
- Область определения каждой функции — (−∞,∞)(−∞,∞), а диапазон — [−1,1].
 [−1,1].
[−1,1]. - График y=sinxy=sinx симметричен относительно начала координат, потому что это нечетная функция.
- График y=cosxy=cosx симметричен относительно оси yy, потому что это четная функция.
Исследование синусоидальных функций
Как мы видим, функции синуса и косинуса имеют правильный период и диапазон. Если мы понаблюдаем за океанскими волнами или рябью на пруду, мы увидим, что они напоминают функции синуса или косинуса. Однако они не обязательно идентичны. Некоторые выше или длиннее других. Функция, которая имеет ту же общую форму, что и функция синуса или косинуса, известна как синусоидальная функция. Общие формы синусоидальных функций
y=Asin(Bx-C)+Dandy=Acos(Bx-C)+Dy=Asin(Bx-C)+Dandy=Acos(Bx-C)+D
Определение периода синусоидальных функций
Глядя на формы синусоидальных функций, мы можем видеть, что они являются преобразованиями функций синуса и косинуса. Мы можем использовать то, что мы знаем о преобразованиях, для определения периода.
В общей формуле BB связано с периодом соотношением P=2π|B|.P=2π|B|. Если |B|>1,|B|>1, то период меньше 2π2π и функция испытывает горизонтальное сжатие, а если |B|<1,|B|<1, то период больше 2π2π и функция подвергается горизонтальному растяжению. Например, f(x)=sin(x),f(x)=sin(x),B=1,B=1, поэтому период равен 2π,2π, что мы знали. Если f(x)=sin(2x),f(x)=sin(2x), то B=2,B=2, поэтому период равен ππ и график сжимается. Если f(x)=sin(x2),f(x)=sin(x2), то B=12,B=12, поэтому период равен 4π4π и график растянут. Обратите внимание на рис. 8, как период косвенно связан с |B|.|B|.
Рисунок 8
Период синусоидальных функций
Если положить C=0C=0 и D=0D=0 в общий вид уравнений функций синуса и косинуса, то получим формы
y=Asin(Bx)y=Asin(Bx)
y= Acos(Bx)y=Acos(Bx)
Период равен 2π|B|.2π|B|.
Пример 1
Определение периода функции синуса или косинуса
Определение периода функции f(x)=sin(π6x). f(x)=sin(π6x).
f(x)=sin(π6x).
Решение
Начнем со сравнения уравнения с общей формой y=Asin(Bx).y=Asin(Bx).
В данном уравнении B=π6,B=π6, поэтому период будет
P=2π|B|=2ππ6=2π⋅6π=12P=2π|B|=2ππ6=2π⋅6π=12
Попытайся #1
Определить период функции g(x)=cos(x3).g(x)=cos(x3).
Определение амплитуды
Возвращаясь к общей формуле для синусоидальной функции, мы проанализировали, как переменная BB связана с периодом. Теперь давайте обратимся к переменной AA, чтобы мы могли проанализировать, как она связана с 9.0934 амплитуда или наибольшее расстояние от покоя. AA представляет собой коэффициент вертикального растяжения, а его абсолютное значение |A||A| это амплитуда. Локальные максимумы будут на расстоянии |A||A| над горизонтальной средней линией графика, которая представляет собой линию y=D;y=D; поскольку в этом случае D=0D=0, средней линией является ось x . Локальные минимумы будут на таком же расстоянии ниже средней линии. Если |A|>1,|A|>1, функция растягивается. Например, амплитуда f(x)=4sinxf(x)=4sinx вдвое больше амплитуды f(x)=2sinx.f(x)=2sinx. Если |A|<1,|A|<1, функция сжимается. Рисунок 9сравнивает несколько синусоидальных функций с разными амплитудами.
Локальные минимумы будут на таком же расстоянии ниже средней линии. Если |A|>1,|A|>1, функция растягивается. Например, амплитуда f(x)=4sinxf(x)=4sinx вдвое больше амплитуды f(x)=2sinx.f(x)=2sinx. Если |A|<1,|A|<1, функция сжимается. Рисунок 9сравнивает несколько синусоидальных функций с разными амплитудами.
Рисунок 9
Амплитуда синусоидальных функций
Если мы допустим C=0C=0 и D=0D=0 в общей форме уравнений синуса и косинуса, мы получим формы
y=Asin(Bx) и y=Acos(Bx)y=Asin (Bx) и y=Acos(Bx)
Амплитуда равна |A|,|A|, то есть высоте по вертикали от средней линии. Кроме того, обратите внимание, что в примере
|A| = амплитуда = 12|максимум – минимум||A| = амплитуда = 12|максимум – минимум|
Пример 2
Определение амплитуды функции синуса или косинуса
Какова амплитуда синусоидальной функции f(x)=−4sin(x)?f(x)=−4sin(x)? Растянута или сжата функция по вертикали?
Решение
Начнем со сравнения функции с упрощенной формой y=Asin(Bx). y=Asin(Bx).
y=Asin(Bx).
В заданной функции A=−4,A=−4, поэтому амплитуда равна |A|=|−4|=4.|A|=|−4|=4. Функция растянута.
Анализ
Отрицательное значение AA приводит к отражению по оси x синусоидальной функции, как показано на рисунке 10.
Рисунок 10
Попытайся #2
Какова амплитуда синусоидальной функции f(x)=12sin(x)?f(x)=12sin(x)? Растянута или сжата функция по вертикали?
Анализ графиков вариаций
y = sin x и y = cos xпеременные CC и D.D. Напомним общий вид:
y=Asin(Bx−C)+D и y=Acos(Bx−C)+Dory=Asin(B(x−CB))+D и y=Acos(B(x−CB))+Dy=Asin (Bx−C)+D и y=Acos(Bx−C)+Dory=Asin(B(x−CB))+D и y=Acos(B(x−CB))+D
Значение CBCB для синусоидальной функции называется фазовым сдвигом или горизонтальным смещением основной функции синуса или косинуса. Если C>0,C>0, график сдвигается вправо. Если C<0,C<0, то график сдвигается влево. Чем больше значение |C|,|C|, тем сильнее сдвигается график. На рис. 11 видно, что график f(x)=sin(x−π)f(x)=sin(x−π) смещается вправо на ππ единиц, что больше, чем мы видим на графике f(x )=sin(x−π4),f(x)=sin(x−π4), что сдвигается вправо на π4π4 единиц.
Если C>0,C>0, график сдвигается вправо. Если C<0,C<0, то график сдвигается влево. Чем больше значение |C|,|C|, тем сильнее сдвигается график. На рис. 11 видно, что график f(x)=sin(x−π)f(x)=sin(x−π) смещается вправо на ππ единиц, что больше, чем мы видим на графике f(x )=sin(x−π4),f(x)=sin(x−π4), что сдвигается вправо на π4π4 единиц.
Рисунок 11
В то время как CC относится к сдвигу по горизонтали, DD указывает сдвиг по вертикали от средней линии в общей формуле для синусоидальной функции. См. рисунок 12. Функция y=cos(x)+Dy=cos(x)+D имеет среднюю линию в точке y=D.y=D.
Рисунок 12
Любое значение DD, отличное от нуля, сдвигает график вверх или вниз. На рис. 13 сравнивается f(x)=sin(x)f(x)=sin(x) с f(x)=sin(x)+2,f(x)=sin(x)+2, сдвинутым на 2 единицы вверх на графике.
Рисунок 13
Вариации функций синуса и косинуса
Для заданного уравнения в форме f(x)=Asin(Bx−C)+Df(x)=Asin(Bx−C)+D или f(x)=Acos(Bx−C)+D,f( x)=Acos(Bx-C)+D,CBCB — фазовый сдвиг, DD — вертикальный сдвиг.
Пример 3
Определение фазового сдвига функции
Определите направление и величину фазового сдвига для f(x)=sin(x+π6)−2.f(x)=sin(x+π6)−2.
Решение
Начнем с сравнения уравнения с общей формой y=Asin(Bx−C)+D.y=Asin(Bx−C)+D.
Обратите внимание, что в данном уравнении B=1B=1 и C=−π6.C=−π6. Таким образом, фазовый сдвиг составляет
CB=−π61=−π6CB=−π61=−π6
или π6π6 единиц влево.
Анализ
Мы должны обратить внимание на знак в уравнении для общего вида синусоидальной функции. Уравнение показывает знак минус перед C.C. Следовательно, f(x)=sin(x+π6)−2f(x)=sin(x+π6)−2 можно переписать как f(x)=sin(x−(−π6))−2.f(x )=sin(x−(−π6))−2. Если значение CC отрицательно, сдвиг происходит влево.
Попытайся #3
Определите направление и величину фазового сдвига для f(x)=3cos(x−π2). f(x)=3cos(x−π2).
f(x)=3cos(x−π2).
Пример 4
Определение вертикального сдвига функции
Определите направление и величину вертикального сдвига для f(x)=cos(x)−3.f(x)=cos(x)−3.
Решение
Начнем с сравнения уравнения с общей формой y=Acos(Bx−C)+D.y=Acos(Bx−C)+D.
В приведенном уравнении D=−3D=−3, поэтому сдвиг равен 3 единицам вниз.
Попытайся #4
Определите направление и величину вертикального смещения для f(x)=3sin(x)+2.f(x)=3sin(x)+2.
Как
Дана синусоидальная функция в виде f(x)=Asin(Bx−C)+D,f(x)=Asin(Bx−C)+D, определить срединную линию, амплитуду, период и фазу сдвиг.
- Определите амплитуду как |A|.|A|.
- Определите период как P=2π|B|.P=2π|B|.
- Определить фазовый сдвиг как CB.
 CB.
CB. - Определите среднюю линию как y=D.y=D.
Пример 5
Идентификация вариаций синусоидальной функции из уравнения
Определите среднюю линию, амплитуду, период и фазовый сдвиг функции y=3sin(2x)+1.y=3sin(2x)+1.
Решение
Начнем с сравнения уравнения с общей формой y=Asin(Bx−C)+D.y=Asin(Bx−C)+D.
A=3,A=3, поэтому амплитуда |A|=3.|A|=3.
Далее, B=2,B=2, поэтому период равен P=2π|B|=2π2=π.P=2π|B|=2π2=π.
В скобках нет добавленной константы, поэтому C=0C=0, а фазовый сдвиг равен CB=02=0.CB=02=0.
Наконец, D=1,D=1, поэтому средняя линия y=1.y=1.
Анализ
Изучая график, мы можем определить, что период равен π, π, средняя линия равна y=1, y=1, а амплитуда равна 3. См. рисунок 14.
Рисунок 14
Попытайся #5
Определите среднюю линию, амплитуду, период и фазовый сдвиг функции y=12cos(x3−π3). y=12cos(x3−π3).
y=12cos(x3−π3).
Пример 6
Определение уравнения для синусоидальной функции на графике
Определите формулу для функции косинуса на рисунке 15.
Рисунок 15
Решение
Чтобы определить уравнение, нам нужно идентифицировать каждое значение в общем виде синусоидальной функции.
y=Asin(Bx-C)+Dy=Acos(Bx-C)+Dy=Asin(Bx-C)+Dy=Acos(Bx-C)+D
График может представлять синус или функция косинуса, которая сдвигается и/или отражается. Когда x=0,x=0, график имеет крайнюю точку (0,0).(0,0). Поскольку функция косинуса имеет крайнюю точку при x=0,x=0, запишем наше уравнение в терминах функции косинуса.
Начнем со средней линии. Мы видим, что график поднимается и опускается на одинаковое расстояние выше и ниже y=0,5.y=0,5. Это значение, которое является средней линией, является DD в уравнении, поэтому D=0,5.D=0,5.
Наибольшее расстояние выше и ниже средней линии — это амплитуда. Максимумы на 0,5 единицы выше средней линии, а минимумы на 0,5 единицы ниже средней линии. Таким образом, |A|=0,5.|A|=0,5. Другой способ определить амплитуду — это признать, что разница между высотой локальных максимумов и минимумов равна 1, поэтому |A|=12=0,5.|A|=12=0,5. Также на графике отражено около x -ось, так что A=-0,5.A=-0,5.
Максимумы на 0,5 единицы выше средней линии, а минимумы на 0,5 единицы ниже средней линии. Таким образом, |A|=0,5.|A|=0,5. Другой способ определить амплитуду — это признать, что разница между высотой локальных максимумов и минимумов равна 1, поэтому |A|=12=0,5.|A|=12=0,5. Также на графике отражено около x -ось, так что A=-0,5.A=-0,5.
График не растягивается и не сжимается по горизонтали, поэтому B=1;B=1; и график не смещен по горизонтали, поэтому C=0.C=0.
Собираем все это вместе,
g(x)=-0,5cos(x)+0,5g(x)=-0,5cos(x)+0,5
Попытайся #6
Определите формулу синуса на рисунке 16.
Рисунок 16
Пример 7
Определение уравнения синусоидальной функции по графику
Определите уравнение для синусоидальной функции на рисунке 17.
Рисунок 17
Решение
При наибольшем значении 1 и наименьшем значении −5,−5 средняя линия будет находиться посередине между значениями −2,−2. Итак, D=−2.D=−2.
Итак, D=−2.D=−2.
Расстояние от средней линии до самого высокого или самого низкого значения дает амплитуду |A|=3.|A|=3.
Период графика равен 6, который можно измерить от пика при x=1x=1 до следующего пика при x=7,x=7 или от расстояния между самыми низкими точками. Следовательно, P=2π|B|=6.P=2π|B|=6. Используя положительное значение для B, B, мы находим, что
B=2πP=2π6=π3B=2πP=2π6=π3
На данный момент наше уравнение имеет вид либо y=3sin(π3x−C)−2y=3sin(π3x−C)−2, либо y=3cos(π3x− С)−2.y=3cos(π3x−C)−2. Для формы и сдвига у нас есть более одного варианта. Мы могли бы записать это как любое из следующего:
- косинус сдвинулся вправо
- отрицательный косинус сдвинут влево
- синус смещен влево
- отрицательный синус смещен вправо
Хотя любое из этих значений было бы правильным, в данном случае с косинусными сдвигами работать легче, чем с синусоидальными, поскольку они включают целые числа. Итак, наша функция становится
y=3cos(π3x−π3)−2 или y=−3cos(π3x+2π3)−2y=3cos(π3x−π3)−2 или y=−3cos(π3x+2π3)−2
Опять же, эти функции эквивалентны, поэтому обе дают один и тот же график.
Попытайся #7
Напишите формулу функции, изображенной на рисунке 18.
Рисунок 18
Графические вариации
y = sin x и y = cos xВ этом разделе мы узнали о типах вариаций функций синуса и косинуса и использовали эту информацию для написания уравнений из графиков. Теперь мы можем использовать ту же информацию для создания графиков из уравнений.
Вместо того, чтобы сосредоточиться на уравнениях общей формы
y=Asin(Bx−C)+D и y=Acos(Bx−C)+D,y=Asin(Bx−C)+D и y=Acos(Bx−C)+D,
мы примем C=0C=0 и D=0D=0 и будем работать с упрощенной формой уравнений в следующих примерах.
Как
Для заданной функции y=Asin(Bx),y=Asin(Bx) нарисуйте ее график.
- Определите амплитуду |A|.
 |A|.
|A|. - Определите период, P=2π|B|.P=2π|B|.
- Начните с исходной точки, при этом функция увеличивается вправо, если значение AA положительное, или уменьшается, если значение AA отрицательное.
- При x=π2|B|x=π2|B| существует локальный максимум для A>0A>0 или минимум для A<0,A<0, при y=A.y=A.
- Кривая возвращается к оси x в точке x=π|B|.x=π|B|.
- Существует локальный минимум для A>0A>0 (максимум для A<0A<0 ) при x=3π2|B|x=3π2|B| с y=–A.y=–A.
- Кривая снова возвращается к оси x в точке x=2π|B|.x=2π|B|.
Пример 8
График функции и определение амплитуды и периода
Нарисуйте график функции f(x)=−2sin(πx2).f(x)=−2sin(πx2).
Решение
Начнем со сравнения уравнения с формой y=Asin(Bx).y=Asin(Bx).
Четверть очков включает минимум при x=1x=1 и максимум при x=3. x=3. Локальный минимум будет на 2 единицы ниже средней линии при x=1,x=1, а локальный максимум будет на 2 единицы выше средней линии при x=3.x=3. На рис. 19 показан график функции .
x=3. Локальный минимум будет на 2 единицы ниже средней линии при x=1,x=1, а локальный максимум будет на 2 единицы выше средней линии при x=3.x=3. На рис. 19 показан график функции .
Рисунок 19
Попытайся #8
Нарисуйте график зависимости g(x)=−0,8cos(2x).g(x)=−0,8cos(2x). Определите среднюю линию, амплитуду, период и фазовый сдвиг.
Как
Дана синусоидальная функция со сдвигом по фазе и по вертикали, нарисуйте ее график.
- Выразите функцию в общем виде y=Asin(Bx−C)+D или y=Acos(Bx−C)+D.y=Asin(Bx−C)+D или y=Acos(Bx−C) + Д.
- Определите амплитуду |A|.|A|.
- Определите период, P=2π|B|.P=2π|B|.
- Определите фазовый сдвиг, CB.CB.
- Нарисуйте график функции f(x)=Asin(Bx)f(x)=Asin(Bx), сдвинутой вправо или влево на CBCB и вверх или вниз на D.D.
Пример 9
Построение преобразованной синусоиды
Нарисуйте график функции f(x)=3sin(π4x−π4). f(x)=3sin(π4x−π4).
f(x)=3sin(π4x−π4).
Решение
- Шаг 1. Функция уже записана в общем виде: f(x)=3sin(π4x−π4).f(x)=3sin(π4x−π4). Этот график будет иметь форму синусоидальной функции, начиная со средней линии и увеличиваясь вправо.
- Шаг 2. |А|=|3|=3.|А|=|3|=3. Амплитуда 3.
- Шаг 3. Поскольку |B|=|π4|=π4,|B|=|π4|=π4, период определяется следующим образом.
P=2π|B|=2ππ4=2π⋅4π=8P=2π|B|=2ππ4=2π⋅4π=8
Период равен 8.
- Шаг 4. Поскольку C=π4,C=π4, фазовый сдвиг равен
CB=π4π4=1.CB=π4π4=1.
Фазовый сдвиг составляет 1 единицу.
- Шаг 5. На рис. 20 показан график функции.

Рисунок 20 Горизонтально сжатая, вертикально растянутая и сдвинутая по горизонтали синусоида
Попытайся #9
Нарисуйте график зависимости g(x)=−2cos(π3x+π6).g(x)=−2cos(π3x+π6). Определите среднюю линию, амплитуду, период и фазовый сдвиг.
Пример 10
Определение свойств синусоидальной функции
Учитывая y=−2cos(π2x+π)+3,y=−2cos(π2x+π)+3, определить амплитуду, период, фазовый сдвиг и вертикальный сдвиг. Затем постройте график функции.
Решение
Начните со сравнения уравнения с общей формой и выполните шаги, описанные в примере 9. уже написано в общем виде.
 P=2π|B|=2ππ2=2π⋅2π= 4. Период 4.
P=2π|B|=2ππ2=2π⋅2π= 4. Период 4.Поскольку AA отрицательное значение, график функции косинуса отражается относительно оси x .
На рис. 21 показан один цикл графика функции.
Рисунок 21
Использование преобразования функций синуса и косинуса
Мы можем использовать преобразования функций синуса и косинуса во многих приложениях. Как упоминалось в начале главы, круговое движение можно моделировать с помощью функции синуса или косинуса.
Пример 11
Нахождение вертикальной составляющей кругового движения
Точка вращается вокруг окружности радиусом 3 с центром в начале координат. Нарисуйте график y -координата точки как функция угла поворота.
Нарисуйте график y -координата точки как функция угла поворота.
Решение
Напомним, что для точки на окружности радиусом r y -координата точки равна y=rsin(x),y=rsin(x), поэтому в этом случае мы получаем уравнение y(x)=3sin(x).y(x)=3sin(x). Константа 3 вызывает вертикальное растяжение y -значений функции в 3 раза, что мы можем видеть на графике на рисунке 22.
Рисунок 22
Анализ
Обратите внимание, что период функции по-прежнему равен 2π;2π; по мере движения по окружности мы возвращаемся в точку (3,0)(3,0) для x=2π,4π,6π,…x=2π,4π,6π,… Поскольку выходы график теперь будет колебаться между –3–3 и 3,3, амплитуда синусоиды равна 3,3.
Попытайся #10
Какова амплитуда функции f(x)=7cos(x)?f(x)=7cos(x)? Нарисуйте график этой функции.
Пример 12
Нахождение вертикальной составляющей кругового движения
Круг радиусом 3 фута установлен так, что его центр находится на расстоянии 4 фута от земли. Ближайшая к земле точка обозначена P , как показано на рис. 23. Нарисуйте график высоты над землей точки PP при вращении круга; затем найдите функцию, которая дает высоту через угол поворота.
Рисунок 23
Решение
Зарисовывая высоту, мы отмечаем, что она начинается с 1 фута над землей, затем увеличивается до 7 футов над землей и продолжает колебаться на 3 фута выше и ниже центрального значения в 4 фута, как показано на рисунке 24.
Рисунок 24
Хотя мы могли бы использовать преобразование функции синуса или косинуса, мы начнем с поиска характеристик, которые облегчили бы использование одной функции по сравнению с другой. Давайте использовать функцию косинуса, потому что она начинается с самого высокого или самого низкого значения, а функция синуса начинается со среднего значения. Стандартный косинус начинается с самого высокого значения, а этот график начинается с самого низкого значения, поэтому нам нужно включить вертикальное отражение.
Стандартный косинус начинается с самого высокого значения, а этот график начинается с самого низкого значения, поэтому нам нужно включить вертикальное отражение.
Во-вторых, мы видим, что график колеблется на 3 выше и ниже центра, в то время как основной косинус имеет амплитуду 1, поэтому этот график был растянут по вертикали на 3, как в последнем примере.
Наконец, чтобы переместить центр круга на высоту 4, график был сдвинут вверх на 4 по вертикали. Объединив эти преобразования, мы находим, что
y=−3cos(x)+4y=−3cos (х)+4
Попытайся #11
Груз прикреплен к пружине, которую затем подвешивают к доске, как показано на рис. 25. Когда пружина колеблется вверх и вниз, положение yy груза относительно доски колеблется в пределах –1–1 дюйм ( в момент времени x=0)x=0) до –7–7 дюймов (в момент времени x=π)x=π) ниже доски. Предположим, что положение yy задано как синусоидальная функция x.x. Нарисуйте график функции, а затем найдите функцию косинуса, которая дает позицию yy через x. x.
x.
Рисунок 25
Пример 13
Определение роста всадника на колесе обозрения
Лондонский глаз — это огромное колесо обозрения диаметром 135 метров (443 фута). Он совершает один оборот каждые 30 минут. Всадники садятся с платформы на высоте 2 метра над землей. Выразите высоту всадника над землей как функцию времени в минутах.
Решение
При диаметре 135 м колесо имеет радиус 67,5 м. Высота будет колебаться с амплитудой 67,5 м выше и ниже центра.
Посадка пассажиров на высоте 2 м над уровнем земли, поэтому центр колеса должен располагаться на высоте 67,5+2=69,567,5+2=69,5 м над уровнем земли. Средняя линия колебаний будет на высоте 69,5 м.
Колесу требуется 30 минут, чтобы совершить 1 оборот, поэтому высота будет колебаться с периодом 30 минут.
Наконец, поскольку райдер садится в самую нижнюю точку, высота начинается с наименьшего значения и увеличивается в соответствии с формой вертикально отраженной косинусоидальной кривой.
- Амплитуда: 67,5,67,5, поэтому A=67,5A=67,5
- Средняя линия: 69,5,69,5, поэтому D=69,5D=69,5
- Период: 30,30, поэтому B=2π30=π15B=2π30=π15
- Форма: −cos(t)−cos(t)
Уравнение для роста всадника будет следующим:
y=-67,5cos(π15t)+69,5y=-67,5cos(π15t)+69,5
, где tt выражается в минутах, а yy измеряется в метрах.
6.1 Секционные упражнения
Устный
1.
Почему функции синуса и косинуса называются периодическими функциями?
2.
Как выглядит график y=sinxy=sinx сравните с графиком y=cosx?y=cosx? Объясните, как можно горизонтально перевести график y=sinxy=sinx. чтобы получить y=cosx.y=cosx.
3.
Для уравнения Acos(Bx+C)+D,Acos(Bx+C)+D, какие константы влияют на диапазон функции и как они влияют на диапазон?
4.
Как диапазон переведенной синусоидальной функции соотносится с уравнением y=Asin(Bx+C)+D?y=Asin(Bx+C)+D?
5.
Как можно использовать единичный круг для построения графика функции f(t)=sint?f(t)=sint?
Графический
Для следующих упражнений нарисуйте два полных периода каждой функции и укажите амплитуду, период и среднюю линию. Укажите максимальное и минимальное значения y и соответствующие им значения x за один период для x>0.x>0. При необходимости округлить ответы до двух знаков после запятой.
6.
f(x)=2sinxf(x)=2sinx
7.
f(x)=23cosxf(x)=23cosx
8.
f(x)=−3sinxf(x)=−3sinx
9.
f(x)=4sinxf(x)=4sinx
10.
f(x)=2cosxf(x)=2cosx
11.
f(x)=cos(2x)f(x)=cos(2x)
12.
f(x)=2sin(12x)f(x)=2sin(12x)
13.
f(x)=4cos(πx)f(x)=4cos(πx)
14.
f(x)=3cos(65x)f(x)=3cos(65x)
15.
у=3sin(8(x+4))+5y=3sin(8(x+4))+5
16.
у=2sin(3x−21)+4y=2sin(3x−21)+4
17.
у=5sin(5x+20)−2y=5sin(5x+20)−2
Для следующих упражнений нарисуйте один полный период каждой функции, начиная с x=0.x=0. Для каждой функции укажите амплитуду, период и среднюю линию. Укажите максимальное и минимальное значения y и соответствующие им значения x за один период для x>0.x>0. Укажите фазовый сдвиг и вертикальное смещение, если применимо. При необходимости округлить ответы до двух знаков после запятой.
При необходимости округлить ответы до двух знаков после запятой.
18.
f(t)=2sin(t−5π6)f(t)=2sin(t−5π6)
19.
f(t)=−cos(t+π3)+1f(t)=−cos(t+π3)+1
20.
f(t)=4cos(2(t+π4))−3f(t)=4cos(2(t+π4))−3
21.
f(t)=−sin(12t+5π3)f(t)=−sin(12t+5π3)
22.
f(x)=4sin(π2(x−3))+7f(x)=4sin(π2(x−3))+7
23.
Определите амплитуду, среднюю линию, период и уравнение, включающее функцию синуса, для графика, показанного на рис. 26.
Рисунок 26
24.
Определите амплитуду, период, среднюю линию и уравнение с косинусом для графика, показанного на рисунке 27.
Рисунок 27
25.
Определите амплитуду, период, среднюю линию и уравнение с косинусом для графика, показанного на рисунке 28.
Рисунок 28
26.
Определите амплитуду, период, среднюю линию и уравнение, включающее синус, для графика, показанного на рис. 29..
Рисунок 29
27.
Определите амплитуду, период, среднюю линию и уравнение с косинусом для графика, показанного на рисунке 30.
Рисунок 30
28.
Определите амплитуду, период, среднюю линию и уравнение, включающее синус, для графика, показанного на рисунке 31.
Рисунок 31
29.
Определите амплитуду, период, среднюю линию и уравнение с косинусом для графика, показанного на рис. 32.
Рисунок 32
30.
Определите амплитуду, период, среднюю линию и уравнение с синусоидой для графика, показанного на рисунке 33.
Рисунок 33
Алгебраический
Для следующих упражнений пусть f(x)=sinx. f(x)=sinx.
f(x)=sinx.
31.
На [0,2π),[0,2π) решить f(x)=0.f(x)=0.
32.
На [0,2π),[0,2π) решить f(x)=12.f(x)=12.
33.
Вычислить f(π2).f(π2).
34.
О [0,2π),f(x)=22.[0,2π),f(x)=22. Найдите все значения x.x.
35.
На [0,2π),[0,2π) максимальное значение(я) функции возникает(я) при каком x -значении?
36.
На [0,2π),[0,2π) минимальное значение(я) функции встречается(ются) при каком x -значении?
37.
Покажите, что f(−x)=−f(x).f(−x)=−f(x). Это означает, что f(x)=sinxf(x)=sinx является нечетной функцией и обладает симметрией относительно ________________.
Для следующих упражнений пусть f(x)=cosx. f(x)=cosx.
f(x)=cosx.
38.
На [0,2π),[0,2π) решить уравнение f(x)=cosx=0.f(x)=cosx=0.
39.
На [0,2π),[0,2π) решить f(x)=12.f(x)=12.
40.
На [0,2π),[0,2π) найти x -пересечений f(x)=cosx.f(x)=cosx.
41.
На [0,2π),[0,2π) найти x значений, при которых функция имеет максимальное или минимальное значение.
42.
На [0,2π),[0,2π) решить уравнение f(x)=32.f(x)=32.
Технология
43.
График h(x)=x+sinxh(x)=x+sinx на [0,2π].[0,2π]. Объясните, почему график выглядит именно так.
44.
График h(x)=x+sinxh(x)=x+sinx на [−100,100].[−100,100]. Получился ли график таким, как предсказано в предыдущем упражнении?
45.
Постройте график f(x)=xsinxf(x)=xsinx на [0,2π][0,2π] и объясните, как график отличается от графика f(x)=sinx.f(x)=sinx.
46.
Постройте график f(x)=xsinxf(x)=xsinx в окне [−10,10][−10,10] и объясните, что показывает график.
47.
Постройте график f(x)=sinxxf(x)=sinxx в окне [−5π,5π][−5π,5π] и объясните, что показывает график.
Реальные приложения
48.
Колесо обозрения имеет диаметр 25 метров и садится на платформу, которая находится на высоте 1 метр над землей. Шесть часов на колесе обозрения находятся на одном уровне с грузовой платформой. Колесо совершает 1 полный оборот за 10 минут. Функция h(t)h(t) дает рост человека в метрах над землей t минут после начала вращения колеса.
- ⓐ Найдите амплитуду, среднюю линию и период h(t).h(t).
- ⓑ Найдите формулу для функции высоты h(t).
 h(t).
h(t). - ⓒ На какой высоте находится человек над землей через 5 минут?
Обратный синус — формула, область и диапазон, график, свойства
Обратный синус — одна из обратных тригонометрических функций, записывается как sin -1 x и читается как « sin inverse x «. Он также записывается как arcsin(x) (читается как ‘арксинус x’). Обратите внимание, что sin -1 x (sin, обратный x) – это не то же самое, что (sin x) -1 ( обратная величина sin x, которая равна csc x. У нас есть 6 обратных тригонометрических функций, таких как:
- arcsin x = sin -1 x = обратная функция sin x
- arccos x = cos -1 x = инверсия cos x
- arctan x = тангенс -1 x = обратный тангенсу x
- arccsc х = csc -1 x = инверсия csc x
- угловых секунд x = -1 x = обратное значение секунды x
- arccot x = кроватка -1 x = инверсия кроватки x
Здесь мы подробно изучим функцию обратного синуса (sin inverse), а также ее график, область определения, диапазон и свойства. Кроме того, мы изучим формулы, производные и интеграл от греха, обратного х, а также несколько решенных примеров для лучшего понимания концепции.
Кроме того, мы изучим формулы, производные и интеграл от греха, обратного х, а также несколько решенных примеров для лучшего понимания концепции.
| 1. | Что такое обратный синус? |
| 2. | Инверсия греха x Формула |
| 3. | Домен и диапазон обратного синуса |
| 4. | Грех, обратный график |
| 5. | шага, чтобы найти инверсию греха x |
| 6. | Свойства обратного синуса |
| 7. | Производная обратного синуса |
| 8. | Интеграл обратного синуса |
| 9. | Часто задаваемые вопросы об обратном синусе |
Что такое арксинус?
Функция обратного синуса является обратной функцией синуса и, таким образом, является одной из обратных тригонометрических функций. Она также известна как функция арксинуса, которая произносится как «арксинус». Математически это записывается как «asin x» (или) «sin -1 x» или «arcsin x». Мы читаем «sin -1 x» как «sin, обратный x». Мы знаем, что если две функции f и f -1 являются обратными друг другу, то f(x) = y ⇒ x = f -1 (y).Таким образом, sin x = y ⇒ x = sin -1 (y) , т. е. когда «sin» перемещается с одной стороны на другую На стороне уравнения получается sin -1 . Давайте рассмотрим несколько примеров, чтобы увидеть, как работает функция обратного синуса:
Она также известна как функция арксинуса, которая произносится как «арксинус». Математически это записывается как «asin x» (или) «sin -1 x» или «arcsin x». Мы читаем «sin -1 x» как «sin, обратный x». Мы знаем, что если две функции f и f -1 являются обратными друг другу, то f(x) = y ⇒ x = f -1 (y).Таким образом, sin x = y ⇒ x = sin -1 (y) , т. е. когда «sin» перемещается с одной стороны на другую На стороне уравнения получается sin -1 . Давайте рассмотрим несколько примеров, чтобы увидеть, как работает функция обратного синуса:
Примеры обратного синуса
- sin 0 = 0 ⇒ 0 = sin -1 (0)
- грех π/2 = 1 ⇒ π/2 = грех -1 (1)
- sin π/6 = 0,5 ⇒ π/6 = sin -1 (0,5)
Инверсия греха x Формула
В прямоугольном треугольнике синус угла (θ) равен отношению его противолежащего катета к гипотенузе. т. е. sin θ = (противоположная сторона) / (гипотенуза). Тогда по определению арксинуса θ = sin -1 [(противоположная сторона)/(гипотенуза)] . Как показано на изображении ниже, чтобы найти меру угла θ, мы используем формулу sin, обратную x, которая определяется как θ = arcsin[(противоположная сторона)/(гипотенуза)]. Обратный синус дает меру угла для соответствующего значения функции синуса, так что угол лежит в диапазоне обратного синуса (мы обсудим область и диапазон обратного синуса в следующем разделе).
т. е. sin θ = (противоположная сторона) / (гипотенуза). Тогда по определению арксинуса θ = sin -1 [(противоположная сторона)/(гипотенуза)] . Как показано на изображении ниже, чтобы найти меру угла θ, мы используем формулу sin, обратную x, которая определяется как θ = arcsin[(противоположная сторона)/(гипотенуза)]. Обратный синус дает меру угла для соответствующего значения функции синуса, так что угол лежит в диапазоне обратного синуса (мы обсудим область и диапазон обратного синуса в следующем разделе).
Таким образом, функция обратного синуса используется для нахождения угла в прямоугольном треугольнике, когда известны противолежащая сторона и гипотенуза. Кроме того, его можно использовать для нахождения неизвестных углов в любом треугольнике с помощью закона синусов. В треугольнике ABC, если AB = c, BC = a и CA = b, то по закону синусов
(sin A) / a = (sin B) / b
Отсюда
sin A = (a sin B) / b
A = sin -1 [ (a sin B) / b ]
Точно так же мы можем найти другие углы треугольника.
Домен и диапазон обратного синуса
В этом разделе давайте посмотрим, как мы можем найти область определения и диапазон функции обратного синуса. Мы знаем, что функция синуса является функцией из R → [-1, 1]. Но функция синуса НЕ является взаимно однозначной в области R, и, следовательно, ее обратная функция не существует. Чтобы синусоидальная функция была взаимно однозначной, ее область определения можно ограничить одним из интервалов [-3π/2, -π/2], [-π/2, π/2], [π/2, 3π/ 2] и т. д. Каждому из этих интервалов соответствует ветвь обратного синуса. Но область определения синусоидальной функции обычно ограничивается [-π/2, π/2], чтобы сделать ее однозначной. Ветвь обратной функции синуса, когда область определения функции синуса равна [-π/2, π/2], называется ветвью главного значения.
Мы знаем, что обратная функция существует тогда и только тогда, когда она биективна, а область определения и область значений функции меняются местами, чтобы быть областью значений и областью определения ее обратной функции соответственно. Следовательно,
Следовательно,
- область sin, обратная x, равна [-1, 1]
- диапазон sin, обратный x, равен [-π/2, π/2] .
т. е. arcsin x (или) sin -1 x : [-1, 1] → [-π/2, π/2]
Грех, обратный график
г.График функции обратного синуса с диапазоном значений главной ветви [-π/2, π/2] можно построить с помощью следующей таблицы. Здесь мы выбрали случайные значения для x в области sin, обратного x, что равно [-1, 1]. Мы знаем значения функции синуса, используя тригонометрическую таблицу и используя функционирование обратной функции синуса, мы имеем следующую таблицу.
| х | у = sin -1 х |
|---|---|
| -1 | sin -1 (-1) = -sin -1 (1) = -π/2 |
| -0,5 | sin -1 (-0,5) = -sin -1 (0,5) = -π/6 |
| 0 | грех -1 (0) = 0 |
| 0,5 | sin -1 (0,5) = π/6 |
| 1 | грех -1 (1) = π/2 |
Нанеся эти точки на график, мы получим график обратного синуса.
шагов, чтобы найти инверсию греха x
Вот шаги, чтобы найти sin, обратный x.
- Поскольку диапазон sin, обратный x, равен [-π/2, π/2], ответ должен лежать в этом интервале.
- Предположим, что y = sin -1 x. Тогда по определению обратного синуса sin y = x.
- Подумайте, какое значение y в интервале [-π/2, π/2] удовлетворяет уравнению sin y = x, и это ответ.
Вот несколько примеров для понимания этих шагов.
Примеры нахождения sin, обратного x
Обратите внимание, что sin -1 x всегда должен давать некоторый угол, лежащий в интервале [-π/2, π/2].
- sin -1 (1) = π/2, поскольку sin π/2 = 1
- sin -1 (-1) = -π/2 как sin (-π/2) = -1
- sin -1 (-0,5) = -π/6 как sin (-π/6) = -0,5
Свойства функции обратного синуса
г. Вот некоторые свойства/формулы обратного синуса. Они очень полезны при решении задач, связанных с обратным грехом в тригонометрии.
Они очень полезны при решении задач, связанных с обратным грехом в тригонометрии.
- sin(sin -1 x) = x только тогда, когда x ∈ [-1, 1]
([Когда x ∉ [-1, 1], sin(sin -1 x) НЕ определен) - sin -1 (sin x) = x, только когда x ∈ [-π/2, π/2]. Чтобы узнать, как вычислить sin -1 (sin x), когда x ∉ [-π/2, π/2], нажмите здесь.
- грех -1 (-x) = -sin -1 x, когда x ∈ [-1, 1]
- sin -1 (1/x) = csc -1 x, когда |x| ≥ 1
- sin -1 x + cos -1 x = π/2, когда x ∈ [-1, 1]
- sin -1 (2x √1 — x²) = 2 sin -1 x, когда -1/√2 ≤ x ≤ 1/√2 и
sin -1 (2x √1 — x²) = 2 cos -1 x, когда 1/√2 ≤ x ≤ 1
Производная обратного синуса
Найдем производную от y = sin -1 x. По определению обратного синуса y = sin -1 x можно записать как sin y = x. Дифференцируя это с обеих сторон по x с помощью цепного правила,
Дифференцируя это с обеих сторон по x с помощью цепного правила,
cos y (dy/dx) = 1
dy/dx = 1/cos y … (1)
Теперь у нас есть sin 2 y + cos 2 y = 1 ⇒ cos 2 y = 1 — sin 2 y ⇒ cos y = √1 — sin²y = √1 — x²
Подставляя это в (1), 90
Таким образом, производная обратного синуса (или) производная от синуса, обратная х, равна 1/√1 — x².
Интеграл обратного синуса
Найдем ∫ sin -1 x dx с помощью интегрирования по частям. Для этого запишем приведенный выше интеграл в виде
∫ sin -1 x · 1 dx
. Используя LIATE, f(x) = sin -1 x и g(x) = 1.
Интегрируя по части,
∫f(x) . g(x) dx = f(x) ∫g(x) dx − ∫(f′(x) ∫g(x) dx) dx + C
∫ sin -1 x · 1 dx = sin -1 x ∫1 dx — ∫ [d/dx(sin -1 x) ∫x dx] + C
∫ sin -1 x dx = sin -1 x (x) — ∫ [1/√1 — x²] x dx + C
Вычислим интеграл в правой части методом u-подстановки. Для этого предположим, что 1 — х 2 = и. Отсюда -2x dx = du (или) x dx = -1/2 du.
Для этого предположим, что 1 — х 2 = и. Отсюда -2x dx = du (или) x dx = -1/2 du.
∫ sin -1 x dx = x sin -1 x — ∫(1/√u) (-1/2) du + C
= x sin -1 x + 1/2 ∫u -1/2 du + C
= x sin -1 x + (1/2) (u 1/2 /(1/2)) + C
= x sin -1 x + √u + C
= x sin -1 x + √(1 — x²) + C
Следовательно, ∫ sin -1 x dx = x sin — 1 x + √1 — x² + C.
Важные примечания по Sin Inverse:
- Обратный синус можно записать как sin -1 (или) arcsin (или) asin, и это функция с доменом [-1, 1] и диапазон [-π/2, π/2].
- Обратный sin НЕ совпадает с (sin x) -1 как (sin x) -1 = 1/(sin x) = csc x.
- sin(sin -1 x) НЕ всегда x. sin(sin -1 x) = x только тогда, когда x ∈ [-1, 1].
- sin -1 (sin x) НЕ всегда x.
 sin -1 (sin x) = x только тогда, когда x ∈ [-π/2, π/2].
sin -1 (sin x) = x только тогда, когда x ∈ [-π/2, π/2].
☛ Похожие темы:
- Закон синусов
- грех кост загар
- Тригонометрическая таблица
- Калькулятор обратного синуса
- Тригонометрические функции
Часто задаваемые вопросы об обратном синусе
Что такое Sin, обратный x в тригонометрии?
Синус, обратный x, является обратной функцией синуса. т. е. если y = sin x, то x = sin -1 (y). Здесь sin -1 является обратной функцией синуса.
Как найти арксинус x?
Чтобы найти арксинус любого числа, просто посмотрите, какой угол синуса дает это число. Например, грех -1 (1/√2) = π/4, поскольку sin π/4 = 1/√2. Но убедитесь, что угол лежит в интервале [-π/2, π/2], так как диапазон обратного греха равен [-π/2, π/2].
Какой Sin обратный 1?
Мы знаем, что sin π/2 = 1. Тогда по определению обратного синуса sin -1 (1) = π/2. т. е. значение обратного синуса 1 равно π/2.
т. е. значение обратного синуса 1 равно π/2.
Что такое обратное значение домена и диапазона греха?
Мы знаем, что функция имеет обратную, если она биективна, но функция синуса не является однозначно-единичной, если ее область определения равна R. Итак, мы ограничиваем ее область определения до [–π/2, π/2], чтобы сделать ее однозначной. один, а его диапазон равен [–1, 1]. Область определения и область значений функции меняются местами, чтобы быть областью значений и областью определения ее обратной функции соответственно. Следовательно,
- область определения sin, обратная x, равна [-1, 1]
- диапазон sin, обратный x, равен [-π/2, π/2].
Инверсия синуса Csc?
Нет, инверсия синуса не косесек. На самом деле, функция, обратная синусу, это sin -1 (или) функция arcsin. Но обратите внимание, что (sin x) -1 = 1/(sin x) = csc x является обратной величиной синуса, но не обратной синусоидальной функцией.
Как написать обратный синус?
Обратный синус x записывается одним из следующих способов:
- арксинус (х)
- асин (х)
- грех -1 х
Что такое арксинус числа 1/2?
Мы знаем, что sin (π/6) = 1/2, и, используя определение sin, обратное x, мы имеем sin -1 (1/2) = π/6, которое лежит в интервале [-π/2, π/2].
Почему мы используем функцию обратного синуса?
Функция обратного синуса используется для нахождения углов в прямоугольном треугольнике, когда известны его противоположная сторона и гипотенуза. т. е. угол = sin -1 (сторона, противоположная углу/гипотенузе).
Что такое производная от Sin, обратная x?
Производная sin -1 x равна 1/√1 — x². Математически это записывается как d/dx(sin -1 x) = 1/√1 — x² (или) (sin -1 x)’ = 1/√1 — x².
Что такое интеграл обратного синуса?
Интеграл sin -1 x is x sin -1 x + √1 — x² + C. Математически он записывается как ∫ sin -1 x dx = x sin -1 9{−1}}\) и определить их графики.
Напомним, что функция — это правило, которое назначает один объект y из одного набора (диапазон ) каждому объекту x из другого набора (домен ). Мы можем записать это правило как y = f ( x ), где f — функция (см. рис. 1). Существует простое вертикальное правило для определения того, является ли правило y = f ( x ) является функцией: f является функцией тогда и только тогда, когда каждая вертикальная линия пересекает график y = f ( x ) в координатной плоскости xy в чаще всего один раз (см. рис. 2).
Мы можем записать это правило как y = f ( x ), где f — функция (см. рис. 1). Существует простое вертикальное правило для определения того, является ли правило y = f ( x ) является функцией: f является функцией тогда и только тогда, когда каждая вертикальная линия пересекает график y = f ( x ) в координатной плоскости xy в чаще всего один раз (см. рис. 2).
Напомним, что функция f равна взаимно однозначному (часто записывается как 1−1), если она присваивает различные значения y различным значениям x . Другими словами, если x 1 \(\ne\) x 2 , затем f ( x 1 ) \(\ne\) f ( x 2 ). Эквивалентно, F -это один-один, если F ( x 1 ) = F ( x 2 ). Существует простое горизонтальное правило для определения того, является ли функция y = f ( x ) однозначной: f взаимно однозначно тогда и только тогда, когда каждая горизонтальная линия пересекает график y = f ( x ) в координатной плоскости xy не более одного раза (см. рис. 3).
Существует простое горизонтальное правило для определения того, является ли функция y = f ( x ) однозначной: f взаимно однозначно тогда и только тогда, когда каждая горизонтальная линия пересекает график y = f ( x ) в координатной плоскости xy не более одного раза (см. рис. 3).
Если функция f взаимно однозначна в своей области определения, то f имеет обратную функцию , обозначаемую f −1 , такую, что ) тогда и только тогда, когда f −1 ( y ) = х . Домен f −1 представляет собой диапазон f .
Основная идея состоит в том, что f −1 «отменяет» то, что делает f, и наоборот. Другими словами, f −1 ( f ( x )) = x для всех x в области f , и f ( f −1 ( y )) = y для всех y в диапазоне f .
Из их графиков мы знаем, что ни одна из тригонометрических функций не является взаимно однозначной во всей своей области определения. Однако мы можем ограничить эти функции 92 473 подмножествами 90 926 их доменов, где они 92 473 являются 90 926 взаимно однозначными. Например, y = sin x взаимно однозначно на интервале \(\left[−\frac{π}{2}, \frac{π}{2} \right]\), как на графике ниже:
{-1} x) = x \text{ for } −1 ≤ x ≤ 1 \; \; \; \; (2)$$
Пример 1
Найти sin −1 \(\left(sin \frac{π}{4}\right)\).
Решение : Поскольку \(−\frac{π}{2} ≤ \frac{π}{4} ≤ \frac{π}{2}\), мы знаем, что sin −1 \(\ left(sin \frac{π}{4}\right)\) = \(\boxed{\frac{π}{4}}\), по формуле (1).
Пример 2
Найти sin −1 \(\left(sin \frac{5π}{4}\right)\).
Решение 909:35 : Поскольку \(\frac{5π}{4} > \frac{π}{2}\), мы не можем использовать формулу (1). Но мы знаем, что sin \(\frac{5π}{4} = −\frac{1}{\sqrt{2}}\). Таким образом, sin −1 sin \(\left(sin \frac{5π}{4}\right)\) = sin −1 \(\left(\frac{1}{\sqrt{2}} \right)\) по определению представляет собой угол y такой, что \(−\frac{π}{2} ≤ y ≤ \frac{π}{2}\) и sin y = −\( \frac{1}{\sqrt{2}}\). Этот угол равен y = \(−\frac{π}{4}\), поскольку
Но мы знаем, что sin \(\frac{5π}{4} = −\frac{1}{\sqrt{2}}\). Таким образом, sin −1 sin \(\left(sin \frac{5π}{4}\right)\) = sin −1 \(\left(\frac{1}{\sqrt{2}} \right)\) по определению представляет собой угол y такой, что \(−\frac{π}{2} ≤ y ≤ \frac{π}{2}\) и sin y = −\( \frac{1}{\sqrt{2}}\). Этот угол равен y = \(−\frac{π}{4}\), поскольку
$$sin \left(−\frac{π}{2}\right) = −sin \left(\frac {π}{2}\right) = \frac{1}{\sqrt{2}}$$ 9{−1}}\) на калькуляторе. Вместо угла от 0º до 360º (т.е. от 0 до 2π радиан) мы получили угол от −90º до 90º (т.е. от \(−\frac{π}{2}\) до \(\frac{π}{2} \) радианы).
В общем случае график обратной функции f −1 является отражением графика f вокруг линии y = x . График y = sin −1 x показан на рисунке 5. Обратите внимание на симметрию относительно линии y = x с графиком y = sin x .
Функция арккосинуса y = cos −1 x (иногда называемая арккосинусом и обозначаемая как y = arccos
Таким образом, y = cos −1 9{-1} x) = x \text{ for } −1 ≤ x ≤ 1 \; \; \; \; (4)$$
График y = cos −1 x показан ниже на рисунке 9. Обратите внимание на симметрию относительно линии y = x с графиком y = потому что х .
Пример 3
Найдите cos −1 \(\left(cos \frac{π}{3}\right)\).
Решение : Поскольку 0 ≤ \(\frac{π}{3}\) ≤ π , мы знаем, что cos −1 \(\left(cos \frac{π}{3}\right)\) = \(\boxed{\frac{π}{3}}\), по формуле (3).
Пример 4
Найдите cos −1 \(\left(cos \frac{4π}{3}\right)\).
Решение : Поскольку \(\frac{4π}{3}\) > π , мы не можем использовать формулу (3). Но мы знаем, что cos \(\frac{4π}{3}\) = −\(\frac{1}{2}\). Таким образом, cos −1 \(\left(cos \frac{4π}{3}\right)\) = cos −1 \(\left(−cos \frac{1}{2}\right) \) есть, по определению, угол y такое, что 0 ≤ y ≤ π и cos y = −\(\frac{1}{2}\). Этот угол равен y = \(\frac{2π}{3}\) (т.е. 120º). Таким образом, \(\left(cos \frac{4π}{3}\right)\) = \(\frac{2π}{3}\)
общее правило для обратных функций: f −1 ( f ( x )) = x для всех x в области f . Но это правило применяется только тогда, когда функция f один к одному по всему домену . Нам пришлось ограничить функции синуса и косинуса очень маленькими подмножествами всех их областей, чтобы эти функции были тождественными. Таким образом, это общее правило справедливо только для x в этих небольших подмножествах в случае арксинуса и арккосинуса.
Таким образом, это общее правило справедливо только для x в этих небольших подмножествах в случае арксинуса и арккосинуса.
Функция арктангенса y = tan −1 x (иногда называется арктангенсом и обозначается цифрой y = arctg x ) можно определить аналогично. Функция y = tan x взаимно однозначна на интервале \(\left(−\frac{π}{2}, \frac{π}{2} \right)\), так как мы см. на рис. 8:
График y = tan −1 x показан ниже на рис. = тангенс −1 x . Обратите также внимание на симметрию относительно линии 9{-1} x) = x \text{ for } \text{all real }x \; \; \; \; (6)$$
Пример 5
Найдите тангенс −1 \(\left(tan \frac{π}{4}\right)\).
Решение : Поскольку \(−\frac{π}{2} ≤ \frac{π}{4} ≤ \frac{π}{2}\), мы знаем, что tan −1 \(\ left(tan \frac{π}{4}\right)\) = \(\frac{π}{4}\), по формуле (5). 2}\). Таким образом, загар 92}}\) для −1 < x < 1,
2}\). Таким образом, загар 92}}\) для −1 < x < 1,
Обратные функции для котангенса, косеканса и секанса можно определить, посмотрев на их графики. Например, функция y = cot x является взаимно однозначной в интервале (0, π ), где ее диапазон равен множеству всех действительных чисел. Таким образом, арккотангенс y = cot −1 x является функцией, областью определения которой является множество всех действительных чисел, а областью значений является интервал (0, 9{-1} x) = x \text{ for } \text{all real }x \; \; \; \; (8)$$
График y = cot −1 x показан ниже на рисунке 11. 1 x — это функция, область определения которой | х | ≥ 1 и чей диапазон равен \(−\frac{π}{2} ≤ y ≤ \frac{π}{2}\), y \(\ne\) 0. Аналогично, арсеканс y = sec − 1 x — это функция, область определения которой | 9{-1} x) = x \text{ for } |x| ≥ 1 \; \; \; \; (12) $$
также часто называют COT −1 x , CSC -1 x и SEC −1 x и 3 4. , и арксеканс , соответственно, x . Графики y = csc -1 x и y = sec -1 x показаны на рисунке 12:
, и арксеканс , соответственно, x . Графики y = csc -1 x и y = sec -1 x показаны на рисунке 12:
Пример 9{-1}x) = x $$
по формуле (8). Так как tan (tan −1 x ) = x для всех x , это означает, что tan (tan −1 x ) = tan \(\left(\frac{π}{ 2}−θ\справа)\). Таким образом, tan (tan −1 x ) = tan (\(\frac{π}{2}\) −cot −1 x ). Теперь мы знаем, что 0 < кроватка −1 x < π , поэтому −\(\frac{π}{2}\) < \(\frac{π}{2}\) − кроватка −1 x < \(\frac{π}{2}\), то есть \(\frac{π}{2}\) −cot −1 x находится в ограниченном подмножестве, на котором функция тангенса взаимно однозначна. Следовательно, tan (tan −1 x ) = tan (\(\frac{π}{2}\) −cot −1 x ) подразумевает, что tan −1 x = \ (\frac{π}{2}\) −cot −1 x , что доказывает тождество.
Пример 10 Является ли tan −1 a + tan −1 b = tan −1 \(\left(\frac{a + b}{1−ab}\right)\) тождеством? 909{-1}\left(\frac{a + b}{1 — ab} \right)$$
по определению арктангенса. Однако напомним, что −\(\frac{π}{2}\) < tan −1 x < \(\frac{π}{2}\) для всех действительных чисел x . Так, в частности, мы должны иметь −\(\frac{π}{2}\) < tan −1 \(\left(\frac{a + b}{1−ab}\right)\) < \ (\ гидроразрыва {π} {2} \). Но возможно, что tan −1 a + tan −1 b равен , а не в интервале ¡ \(\left(−\frac{π}{2}, \frac{π} {2}\справа)\). Например, 9{-1}2 = 1,8 > \frac{π}{2} ≈ 1,570796 .$$
И мы видим, что \(\left(\frac{1 + 2}{1−(1)(2)}\ справа)\) = tan −1 (−3) = −1,249045 \(\ne\) tan −1 1 + tan −1 2. Таким образом, формула верна только тогда, когда −\(\frac{ π}{2}\) < tan −1 a + tan −1 b < \(\ frac{π}{2}\).
6.6 Тригонометрические функции | Функции
6.6 Тригонометрические функции (EMA52)
В этом разделе описываются графики тригонометрических функций.
Синусоидальная функция (EMA53)
Функции вида \(y=\sin\theta\) (EMA54)
Рабочий пример 16: Построение графика синусоиды
\(y=f(\theta) = \sin\theta \quad \left[0° \le \theta \le 360°\right]\)
С помощью калькулятора заполните следующую таблицу.
Выберите подходящий масштаб и нанесите значения \(\theta\) на ось \(x\) и \(\sin\theta\) на \(y\)-ось. Округлите ответы до \(\text{2}\) знаков после запятой.
\(\тета\) | \(0°\) | \(30°\) | \(60°\) | \(90°\) | \(120°\) | \(150°\) | \(180°\) | \(210°\) | \(240°\) | \(270°\) | \(300°\) | \(330°\) | \(360°\) |
\(\sin\тета\) |
Замените значения для \(\theta\)
\(\тета\) | \(0°\) | \(30°\) | \(60°\) | \(90°\) | \(120°\) | \(150°\) | \(180°\) | \(210°\) | \(240°\) | \(270°\) | \(300°\) | \(330°\) | \(360°\) |
\(\sin\тета\) | \(\текст{0}\) | \(\текст{0,5}\) | \(\текст{0,87}\) | \(\текст{1}\) | \(\текст{0,87}\) | \(\текст{0,5}\) | \(\текст{0}\) | \(-\текст{0,5}\) | \(-\текст{0,87}\) | \(-\текст{1}\) | \(-\текст{0,87}\) | \(-\текст{0,5}\) | \(\текст{0}\) |
Нанесите точки и соедините их плавной кривой
Обратите внимание на волнообразную форму графика. Для завершения каждой полной волны требуется \(360°\). Это называется
период. Высота волны выше и ниже оси \(x\) называется амплитудой графика. Максимум
значение \(y=\sin\theta\) равно \(\text{1}\), а минимальное значение равно \(-\text{1}\).
Для завершения каждой полной волны требуется \(360°\). Это называется
период. Высота волны выше и ниже оси \(x\) называется амплитудой графика. Максимум
значение \(y=\sin\theta\) равно \(\text{1}\), а минимальное значение равно \(-\text{1}\).
Домен: \(\left[0°;360°\right]\)
Диапазон: \(\left[-1;1\right]\)
\(x\)-отрезки: \(( 0°;0)\), \((180°;0)\), \((360°;0)\)
\(y\)-отрезок: \((0°;0)\)
Максимальная точка поворота: \((90°;1)\)
Минимальная точка поворота: \((270°;-1)\)
Функции вида \(y=a\sin\theta +q\) (EMA55)
Влияние \(a\) и \(q\) на синусоидальный график
В уравнении \(y=a\sin\theta +q\), \(a\) и \(q\) являются константами и по-разному влияют на график. На том же наборе осей постройте следующие графики для \(0°\le \theta \le 360°\):
\({у}_{1} = \sin\тета -2\)
\({у}_{2} = \sin\тета -1\)
\({у}_{3} = \sin\тета\)
\({у}_{4} = \sin\тета +1\)
\({у}_{5} = \sin\тета +2\)
Используйте полученные результаты, чтобы вывести эффект \(q\).
На том же наборе осей постройте следующие графики для \(0° \le \theta \le 360°\):
\({у}_{6}=-2\sin\тета\)
\({y}_{7}=-\sin\theta\)
\({у}_{8}=\грех\тета\)
\({у}_{9}=2\sin\тета\)
Используйте полученные результаты, чтобы вывести эффект \(a\).
Эффект \(q\)
Эффект \(q\) называется вертикальным сдвигом, потому что весь график синусоиды смещается вверх или вниз на \(q\) единиц.
При \(q>0\) график смещается вертикально вверх на \(q\) единиц.
Для \(q<0\) график смещается вертикально вниз на \(q\) единиц.
Эффект \(а\)
Значение \(a\) влияет на амплитуду графика; высота пиков и глубина впадин.
Для \(a>1\) имеет место вертикальное растяжение и увеличение амплитуды.
Для \(0
Для \(a<0\) имеется отражение относительно оси \(x\).
Для \(-1
При \(a<-1\) происходит отражение относительно оси \(x\) и амплитуда увеличивается.
Обратите внимание, что амплитуда всегда положительна.
Влияние \(а\) | |
\(a>1\): вертикальное растяжение, амплитуда увеличивается | |
\(a=1\): основной график синуса | |
\(0 | |
\(-1 | |
\(a<-1\): отражение относительно \(x\) оси \(a>1\) |
Влияние \(а\) на синусоидальный график.
Влияние \(q\) | |
\(q>0\): вертикальное смещение вверх на \(q\) единиц | |
\(q=0\): основной график синуса | |
\(q<0\): вертикальное смещение вниз на \(q\) единиц |
Влияние \(q\) на синусоидальный график.
Изучение характеристик (EMA56)
Домен и диапазон
Для \(f(\theta) = a\sin\theta +q\) домен равен \(\left[0°;360°\right]\)
Диапазон \(f(\theta) = a\sin\theta +q\) зависит от значений \(a\) и \(q\).
Для \(а>0\):
\начать{выравнивать*} -1& \le \sin \theta \le 1 \\ -a& \le a\sin\theta \le a \\ -a+q& \le a\sin\theta +q \le a+q \\ -a+q& \le f(\theta) \le a+q \конец{выравнивание*} Для всех значений \(\theta\), \(f(\theta)\) всегда находится между \(-a+q\) и \(a+q\).
Следовательно, для \(a>0\) диапазон \(f(\theta) = a\sin\theta +q\) равен \(\left\{f(\theta):f(\theta)\ в \влево[-a+q, a+q\вправо]\вправо\}\)
Аналогично, для \(a<0\) диапазон \(f(\theta)=a \sin\theta +q\) равен \(\left\{f(\theta):f(\theta) \в \влево[a+q, -a+q\вправо]\вправо\}\)
Период
Период \(y=a\sin\theta +q\) равен \(360°\). Это означает, что одна синусоида завершается за \(360°\).
Перехваты
\(y\)-отрезок \(f(\theta)=a\sin\theta +q\) является просто значением \(f(\theta)\) в \(\theta = 0°\)
\начать{выравнивать*} у& = f(0°) \\ & = а\sin 0° + q \\ & = а (0) + q \\ & = д \конец{выравнивание*}Это дает точку \((0;q)\)
Важно: при построении тригонометрических графиков всегда начинайте с основного графика, а затем
рассмотрим эффекты \(a\) и \(q\).
Рабочий пример 17: Эскиз графика синусоиды
Нарисуйте график \(f(\theta)=2\sin\theta +3\) для \(\theta \in \left[0°;360°\right]\).
Изучите стандартную форму уравнения
Из уравнения видно, что \(a>1\), поэтому график вытянут по вертикали. Мы также видим, что \(q>0\), поэтому график смещается вертикально вверх на \(\text{3}\) единиц.
Заменить значения для \(\theta\)
\(\тета\) | \(0°\) | \(30°\) | \(60°\) | \(90°\) | \(120°\) | \(150°\) | \(180°\) | \(210°\) | \(240°\) | \(270°\) | \(300°\) | \(330°\) | \(360°\) |
\(f(\тета)\) | \(\текст{3}\) | \(\текст{4}\) | \(\текст{4,73}\) | \(\текст{5}\) | \(\текст{4,73}\) | \(\текст{4}\) | \(\текст{3}\) | \(\текст{2}\) | \(\текст{1,27}\) | \(\текст{1}\) | \(\текст{1,27}\) | \(\текст{2}\) | \(\текст{3}\) |
Нанесите точки и соедините их плавной кривой
Домен: \(\left[0°;360°\right]\)
Диапазон: \(\left[1;5\right]\)
\( x\)-точки пересечения: нет
\(y\)-точки: \((0°;3)\)
Максимальная точка поворота: \((90°;5)\)
Минимальная точка поворота: \ ((270°;1)\)
временный текстФункция косинуса (EMA57)
Функции вида \(y=\cos\theta\) (EMA58)
Рабочий пример 18: Построение графика косинуса
\(y=f(\theta)=\cos\theta \quad \left[0°\le \theta \le 360°\right]\)
С помощью калькулятора заполните следующую таблицу.
Выберите подходящий масштаб и отобразите значения \(\theta\) по оси \(x\) и \(\cos\theta\) по оси \(y\)-ось. Округлите свои ответы до \(\text{2}\) знаков после запятой.
\(\тета\) | \(0°\) | \(30°\) | \(60°\) | \(90°\) | \(120°\) | \(150°\) | \(180°\) | \(210°\) | \(240°\) | \(270°\) | \(300°\) | \(330°\) | \(360°\) |
\(\cos\тета\) |
Замените значения для \(\theta\)
\(\тета\) | \(0°\) | \(30°\) | \(60°\) | \(90°\) | \(120°\) | \(150°\) | \(180°\) | \(210°\) | \(240°\) | \(270°\) | \(300°\) | \(330°\) | \(360°\) |
\(\cos\тета\) | \(\текст{1}\) | \(\текст{0,87}\) | \(\текст{0,5}\) | \(\текст{0}\) | \(-\текст{0,5}\) | \(-\текст{0,87}\) | \(-\текст{1}\) | \(-\текст{0,87}\) | \(-\текст{0,5}\) | \(\текст{0}\) | \(\текст{0,5}\) | \(\текст{0,87}\) | \(\текст{1}\) |
Нанесите точки и соедините их плавной кривой.

Обратите внимание на схожую волновую форму графика. Период также \(360°\) и амплитуда \(\текст 1}\). Максимальное значение \(y=\cos\theta\) равно \(\text{1}\), а минимальное значение равно \(-\text{1}\).
Домен: \(\left[0°;360°\right]\)
Диапазон: \(\left[-1;1\right]\)
\(x\)-отрезки: \(( 90°;0)\), \((270°;0)\)
\(y\): \((0°;1)\)
Максимальное количество точек поворота: \((0°;1) \), \((360°;1)\)
Минимальная точка поворота: \((180°;-1)\)
Функции вида \(y=a\cos\theta +q\) (EMA59)
Влияние \(a\) и \(q\) на косинусоидальный график
В уравнении \(y=a\cos\theta +q\), \(a\) и \(q\) являются константами и по-разному влияют на график.
На том же наборе осей постройте следующие графики для \(0° \le \theta \le 360°\):
\({y}_{1}=\cos\theta -2\)
\({y}_{2}=\cos\theta -1\)
\({y}_{3}=\cos\theta\)
\({y}_{4}=\cos\тета +1\)
\({y}_{5}=\cos\theta +2\)
Используйте полученные результаты, чтобы вывести эффект \(q\).
На том же наборе осей постройте следующие графики для \(0° \le \theta \le 360°\):
\({y}_{6}=-2\cos\theta\)
\({y}_{7}=-\cos\theta\)
\({y}_{8}=\cos\theta\)
\({y}_{9}=2\cos\theta\)
Используйте полученные результаты, чтобы вывести эффект \(a\).
Эффект \(q\)
Эффект \(q\) называется вертикальным сдвигом, потому что весь график косинуса сдвигается вверх или вниз на \(q\) единиц.
При \(q>0\) график смещается вертикально вверх на \(q\) единиц.
Для \(q<0\) график смещается вертикально вниз на \(q\) единиц.
Эффект \(а\)
Значение \(a\) влияет на амплитуду графика; высота пиков и глубина впадин.
Для \(a>0\) имеет место вертикальное растяжение и увеличение амплитуды.
Для \(0
Для \(a<0\) имеется отражение относительно оси \(x\).
Для \(-1
При \(a<-1\) происходит отражение относительно оси \(x\) и амплитуда увеличивается.
Обратите внимание, что амплитуда всегда положительна.
Влияние \(а\) | |
\(a>1\): вертикальное растяжение, амплитуда увеличивается | |
\(a=1\): базовый график косинуса | |
\(0 | |
\(-1 | |
\(a<-1\): отражение относительно оси \(x\), амплитуда увеличивается |
Влияние \(a\) на косинусоидальный график.
Влияние \(q\) | |
\(q>0\): вертикальное смещение вверх на \(q\) единиц | |
\(q=0\): базовый график косинуса | |
\(q<0\): вертикальное смещение вниз на \(q\) единиц |
Влияние \(q\) на косинусоидальный график.
Изучение характеристик (EMA5B)
Домен и диапазон
Для \(f(\theta)=a\cos\theta +q\) областью является \(\left[0°;360°\right]\)
Легко видеть, что диапазон \(f(\theta)\) будет таким же, как диапазон \(a\sin\theta +q\). Этот
потому что максимальное и минимальное значения \(a\cos \theta + q\) будут такими же, как максимальное и минимальное
значения \(a\sin\theta +q\).
Для \(a>0\) диапазон \(f(\theta)=a\cos\theta +q\) равен \(\left\{f(\theta):f(\theta)\in \влево[-a+q;a+q\вправо]\вправо\}\)
Для \(a<0\) диапазон \(f(\theta)=a \cos\theta +q\) равен \(\left\{f(\theta):f(\theta)\in \влево[а+д;-а+д\вправо]\вправо\}\)
Период
Период \(y=a\cos\theta +q\) равен \(360°\). Это означает, что одна волна косинуса завершается за \(360°\).
Перехваты
\(y\)-отрезок \(f(\theta)=a\cos\theta +q\) вычисляется так же, как и для синуса.
\начать{выравнивать*} у& = f(0°) \\ & = а\cos 0°+q \\ & = а(1)+q \\ & = а + д \конец{выравнивание*}Это дает точку \((0°;a+q)\).
Рабочий пример 19: Эскиз графика косинуса
Нарисуйте график \(f(\theta)=2\cos\theta +3\) для \(\theta \in \left[0°;360°\right]\).
Изучите стандартную форму уравнения
Из уравнения видно, что \(a>1\), поэтому график вытянут по вертикали. Мы также видим, что
\(q>0\), поэтому график смещается вертикально вверх на \(\text{3}\) единиц.
Мы также видим, что
\(q>0\), поэтому график смещается вертикально вверх на \(\text{3}\) единиц.
Замените значения для \(\theta\)
\(\тета\) | \(0°\) | \(30°\) | \(60°\) | \(90°\) | \(120°\) | \(150°\) | \(180°\) | \(210°\) | \(240°\) | \(270°\) | \(300°\) | \(330°\) | \(360°\) |
\(f(\тета)\) | \(\текст{5}\) | \(\текст{4,73}\) | \(\текст{4}\) | \(\текст{3}\) | \(\текст{2}\) | \(\текст{1,27}\) | \(\текст{1}\) | \(\текст{1,27}\) | \(\текст{2}\) | \(\текст{3}\) | \(\текст{4}\) | \(\текст{4,73}\) | \(\текст{5}\) |
Нанесите точки и соедините их плавной кривой
Домен: \(\left[0°;360°\right]\)
Диапазон: \(\left[1;5\right]\)
\( x\)-точки пересечения: нет
\(y\)-точка: \((0°;5)\)
Максимальные точки поворота: \((0°;5)\), \((360°; 5)\)
Минимальная точка поворота: \((180°;1)\)
temp textСравнение графиков \(y=\sin\theta\) и \(y=\cos\theta\) (EMA5C)
Обратите внимание, что два графика очень похожи. Обе волны движутся вверх и вниз вдоль оси \(x\). Расстояния
между пиками для каждого графика одинакова. Высота пиков и глубины впадин также являются
такой же.
Обе волны движутся вверх и вниз вдоль оси \(x\). Расстояния
между пиками для каждого графика одинакова. Высота пиков и глубины впадин также являются
такой же.
Если вы сдвинете всю косинусную диаграмму вправо на \(90°\), она полностью перекроется с синусоидальной диаграммой. Если вы сдвинете синусоидальный график \(90°\) влево, он будет полностью перекрываться с косинусным графиком. Этот означает, что:
\[\begin{массив}{ccl} \sin \theta & = \cos \left(\theta -90°\right) & \left(\text{сдвиг графика косинуса к верно-верно) \\ \cos \theta & =\sin \left(\theta +90°\right) & \left(\text{сдвиг графика синуса влево}\right) \конец{массив}\]Касательная функция (EMA5D)
Функции вида \(y=\tan\theta\) (EMA5F)
Рабочий пример 20: Построение касательной
\(y=f(\theta)=\tan\theta \quad \left[0°\le \theta \le 360°\right]\)
С помощью калькулятора заполните следующую таблицу.
Выберите подходящий масштаб и нанесите значения с \(\theta\) на оси \(x\) и \(\tan\theta\) на оси \(y\)-ось. Округлите свои ответы до \(\text{2}\) знаков после запятой.
\(\тета\) | \(0°\) | \(30°\) | \(45°\) | \(60°\) | \(90°\) | \(120°\) | \(135°\) | \(150°\) | \(180°\) |
\(\загар\тета\) | |||||||||
\(\тета\) | \(210°\) | \(235°\) | \(240°\) | \(270°\) | \(300°\) | \(315°\) | \(330°\) | \(360°\) | |
\(\загар\тета\) |
Замените значения для \(\theta\)
\(\тета\) | \(0°\) | \(30°\) | \(45°\) | \(60°\) | \(90°\) | \(120°\) | \(135°\) | \(150°\) | \(180°\) |
\(\загар\тета\) | \(\текст{0}\) | \(\текст{0,58}\) | \(\текст{1}\) | \(\текст{1,73}\) | неопределенный | \(-\текст{1,73}\) | \(-\текст{1}\) | \(-\текст{0,58}\) | \(\текст{0}\) |
\(\тета\) | \(210°\) | \(235°\) | \(240°\) | \(270°\) | \(300°\) | \(315°\) | \(330°\) | \(360°\) | |
\(\загар\тета\) | \(\текст{0,58}\) | \(\текст{1}\) | \(\текст{1,73}\) | неопределенный | \(-\текст{1,73}\) | \(-\текст{1}\) | \(-\текст{0,58}\) | \(\текст{0}\) |
Нанесите точки и соедините их плавной кривой
Существует простой способ визуализировать касательную диаграмму. Рассмотрим наши определения \(\sin\theta\) и
\(\cos\theta\) для прямоугольных треугольников:
Рассмотрим наши определения \(\sin\theta\) и
\(\cos\theta\) для прямоугольных треугольников:
\начать{выравнивать*} \ гидроразрыва {\ греха \ тета} {\ соз \ тета} & = \frac{\left(\frac{\text{напротив}}{\text{гипотенуза}}\right)}{\left(\frac{\text{смежный}}{\text{гипотенуза}}\right)} \\ & = \frac{\text{напротив}}{\text{гипотенуза}} \times \frac{\text{гипотенуза}}{\text{смежно}} \\ & = \ frac{\ text {напротив}} {\ text {смежно}} \\ & = \загар\тета \конец{выравнивание*}
Итак, для любого значения \(\theta\):
\ (\ загар {\ тета} = \ dfrac {\ грех \ тета} {\ соз \ тета} \)
Итак, мы знаем, что для значений \(\theta\), для которых \(\sin\theta = 0\), мы также должны иметь \(\tan\theta =0\).
Также, если \(\cos\theta =0\), значение \(\tan\theta\) не определено, так как мы не можем разделить на \(\text{0}\). пунктирные вертикальные линии соответствуют значениям \(\theta\), где \(\tan\theta\) не определено и называется
асимптоты.
пунктирные вертикальные линии соответствуют значениям \(\theta\), где \(\tan\theta\) не определено и называется
асимптоты.
Асимптоты: линии \(\theta =90°\) и \(\theta =270°\)
Период: \(180°\)
Домен: \(\left\{\theta :0° \le \theta \le 360°, \theta \ne 90°; 270°\right\}\)
Диапазон: \(\left\{f\left(\theta \right):f\left(\theta \right)\in \mathbb{R}\ вправо\}\)
\(x\)-отрезки: \(\влево(0°;0\вправо)\), \(\влево(180°;0\вправо)\), \(\влево( 360°;0\вправо)\)
\(y\)-перехват: \(\left(0°;0\right)\)
Функции вида \(y=a\tan\theta + q\) (EMA5G)
Эффекты \(a\) и \(q\) на касательном графе
На том же наборе осей постройте следующие графики для \(0° \le \theta \le 360°\):
\({у}_{1}=\загар\тета -2\)
\({у}_{2}=\загар\тета -1\)
\({у}_{3}=\загар\тета\)
\({у}_{4}=\загар\тета +1\)
\({у}_{5}=\загар\тета +2\)
Используйте полученные результаты, чтобы вывести эффект \(q\).
На том же наборе осей постройте следующие графики для \(0° \le \theta \le 360°\):
\({y}_{6}=-2\tan\theta\)
\({у}_{7}=-\загар\тета\)
\({у}_{8}=\загар\тета\)
\({у}_{9}=2\тангенс\тета\)
Используйте полученные результаты, чтобы вывести эффект \(a\).
Эффект \(q\)
Эффект \(q\) называется вертикальным сдвигом, потому что весь график касательной смещается вверх или вниз на \(q\) единицы.
При \(q>0\) график смещается вертикально вверх на \(q\) единиц.
Для \(q<0\) график смещается вертикально вниз на \(q\) единиц.
Эффект \(а\)
Значение \(a\) влияет на крутизну каждой из ветвей графика. Чем больше значение \(a\),
тем быстрее ветви графика приближаются к асимптотам.
Чем больше значение \(a\),
тем быстрее ветви графика приближаются к асимптотам.
\(а<0\) | \(а>0\) | |
\(д>0\) | ||
\(д=0\) | ||
\(д<0\) |
Таблица 6.4: Влияние \(a\) и \(q\) на касательной граф.
Изучение характеристик (EMA5H)
Домен и диапазон
Из графика видно, что \(\tan\theta\) не определено в точках \(\theta =90°\) и \(\theta =270°\).
Следовательно, домен равен \(\left\{\theta :0°\le \theta \le 360°, \theta \ne 90°;
270°\вправо\}\).
Диапазон равен \(\left\{f(\theta):f(\theta)\in \mathbb{R}\right\}\).
Период
Период \(y=a\tan\theta +q\) равен \(180°\). Это означает, что один касательный цикл завершается за \(180°\).
Перехваты
\(y\)-отрезок \(f(\theta)=a\tan\theta +q\) является просто значением \(f(\theta)\) в \(\theta =0°\).
\начать{выравнивать*} у& = f(0°) \\ & = а\тангенс 0°+q \\ & = а(0)+q \\ & = д \конец{выравнивание*}Это дает точку \((0°;q)\).
Асимптоты
График имеет асимптоты в точках \(\theta = 90°\) и \(\theta =270°\).
Рабочий пример 21: набросок касательной
Нарисуйте график \(y=2\tan\theta +1\) для \(\theta \in \left[0°;360°\right]\).
Изучите стандартную форму уравнения
Мы видим, что \(a>1\), поэтому ветви кривой будут более крутыми. Мы также видим, что \(q>0\), поэтому
график сдвинут вертикально вверх на \(\text{1}\) единицу.
Мы также видим, что \(q>0\), поэтому
график сдвинут вертикально вверх на \(\text{1}\) единицу.
Замените значения для \(\theta\)
\(\тета\) | \(0°\) | \(30°\) | \(60°\) | \(90°\) | \(120°\) | \(150°\) | \(180°\) | \(210°\) | \(240°\) | \(270°\) | \(300°\) | \(330°\) | \(360°\) |
\(у\) | \(\текст{1}\) | \(\текст{2,15}\) | \(\текст{4,46}\) | – | \(-\текст{2,46}\) | \(-\текст{0,15}\) | \(\текст{1}\) | \(\текст{2,15}\) | \(\текст{4,46}\) | – | \(-\текст{2,46}\) | \(-\текст{0,15}\) | \(\текст{1}\) |
Нанесите точки и соедините их плавной кривой
Домен: \(\left\{\theta :0°\le \theta \le 360°,\theta \ne 90°;270°\right\}\)
Диапазон: \(\left\{f(\theta):f(\theta)\in \mathbb{R}\right\}\)
temp text Учебник Упражнение 6. 6
9{\circ};0)\). Для этого графика мы видим, что эта точка была
сдвигается вверх на \(\text{1,5}\) или \(\frac{3}{2}\) пробелов. Поэтому \(q = \frac{3}{2}\).
6
9{\circ};0)\). Для этого графика мы видим, что эта точка была
сдвигается вверх на \(\text{1,5}\) или \(\frac{3}{2}\) пробелов. Поэтому \(q = \frac{3}{2}\).
Чтобы найти \(a\), заметим, что значение \(y\) в середине (точка \(A\)) равно \(\text{1,5}\), а \(y\)-значение наверху (точка \(B\)) равно 3. Мы можем найти амплитуду, вычислив расстояние от вершины графика к середине графика: \(3 — \text{1,5} = \text{1,5}\). Поэтому \(а = \фракция{3}{2}\). 9{\circ};\text{2})\), определите значения \(a\) и \(q\).
Чтобы найти \(a\), заметим, что значение \(y\) внизу (точка \(A\)) равно \(-\text{6}\), а
\(y\)-значение наверху (точка \(B\)) равно 2. Мы можем найти амплитуду, вычислив расстояние от
верхней части графика к нижней части графика, а затем разделить это на 2, так как это расстояние равно
удвоенная амплитуда: \(\frac{2 — (-6)}{2} = 4\). Поэтому \(а = 4\). {\circ};-\text{1,5})\), и
9{\circ};-\text{0,5})\). Вычислите значения \(a\) (амплитуда
график) и \(q\) (вертикальный сдвиг графика).
{\circ};-\text{1,5})\), и
9{\circ};-\text{0,5})\). Вычислите значения \(a\) (амплитуда
график) и \(q\) (вертикальный сдвиг графика).
Чтобы найти \(a\), заметим, что значение \(y\) внизу (точка \(A\)) равно \(-\text{1,5}\), а \(y\)-значение вверху (точка \(B\)) равно \(-\text{0,5}\). Мы можем найти амплитуду, вычислив расстояние от верхней части графика до нижней части графика, а затем разделить его на 2, так как это расстояние в два раза больше амплитуды: \(\frac{-\text{0,5} — (-\text{1,5})}{2} = \frac{1}{2}\). Следовательно \(а = \фракция{1}{2}\). 9{\circ};\text{0,5})\). Для этого графика мы видим, что эта точка сместилась вниз на \(\text{1}\) пробел. Поэтому \(q = 1\).
Полное уравнение для графика, показанного в этом вопросе, имеет вид \(y = \frac{1}{2}\cos \theta — 1\).
Следовательно, \(a = \frac{1}{2}, \text{ и } q= -1\).
На приведенном ниже графике показано тригонометрическое уравнение следующего вида: \(y = a \cos{\theta} + q\). Два точки показаны на графике: Точка А 909{\circ};-\text{0,5})\). Вычислите значения \(a\) (амплитуда графика) и \(q\) (вертикальный сдвиг графика).
Чтобы найти \(a\), заметим, что значение \(y\) внизу (точка \(B\)) равно \(-\text{0,5}\), а \(y\)-значение в середине (точка \(A\)) равно \(\text{0}\). Мы можем найти амплитуду, вычислив расстояние от вершины графика до середины графика: \(\text{0} — (-\text{0,5}) = \фракция{1}{2}\). Поэтому \(a = \frac{1}{2}\). 9{\circ}} + \frac{1}{3} \\ \frac{10}{3} & = a(1) + \frac{1}{3} \\ \frac{10}{3} — \frac{1}{3} & = a \\ 3 & = а \конец{выравнивание*}
Полное уравнение: \(y = 3 \tan{\theta} + \frac{1}{3}\).
Следовательно, \(a = 3 \text{ и } q = \frac{1}{3}\).
На приведенном ниже графике показана касательная кривая с уравнением вида \(y = a \tan{\theta} + q\). Два точки отмечены на кривой: 9{\circ}} \\ 1 & = а(1) \\ 1 & = а \конец{выравнивание*}
Полное уравнение: \(y = \tan{\theta}\).
Следовательно \(a = 1 \text{ и } q = 0\).
\(y = \sin{\theta}\)
\(h(x)\)
\(y = \frac{1}{2}\sin{\theta}\)
\( k(x)\)
\(y = 3\sin{\theta}\)
\(f(x)\)
\(y = 2\sin{\theta}\)
\( g(x)\)
На приведенном ниже графике показаны функции \(f(x)\) и \(g(x)\) 9{\ круг} \\ \hline \tan{\theta} & 0 & 1 & \text{undefined} & -1 & 0 & 1 & \text{undefined} &-1 & 0 \\ \hline 3\tan{\theta} & 0 & 3 & \text{undefined} & -3 & 0 & 3 & \text{undefined} &-3&0\ \hline \frac{1}{2}\tan{\theta} & 0 & \frac{1}{2} & \text{undefined} & -\frac{1}{2} & 0 & \frac{1}{2} & \text{undefined} & -\frac{1}{2} & 0 \\ \hline \конец{массив}\] 9{\ круг} \\ \hline \cos{\theta} — 2 & -1 & -2 & -3 & -2 & -1 \\ \hline \cos{\тета} + 4 и 5 и 4 и 2 и 4 и 5 \\ \hline \cos{\тета} + 2 & 3 & 2 & 1 & 2 & 3 \\ \hline \конец{массив}\]
Нам дана таблица со значениями, поэтому мы наносим каждую из этих точек и соединяем их плавной линией. изгиб. 9{\circ};1) \text{ , диапазон } y \in \mathbb{R} \text{и домен} 0 \le \theta \le 360, x \neq
90, x\neq 270\)
изгиб. 9{\circ};1) \text{ , диапазон } y \in \mathbb{R} \text{и домен} 0 \le \theta \le 360, x \neq
90, x\neq 270\)
\(y=2\sin\theta\)
В этом случае \(q = 0\) и, следовательно, основной график синуса не сдвигается вверх или вниз. Мы также отмечаем что \(a = 2\) и поэтому график растянут на 2 единицы. Максимальное значение будет 2, а минимальное значение будет \(-\text{2}\).
\(y=-4\cos\theta\)
В этом случае \(q = 0\) основной косинусоидальный график не сдвигается вверх или вниз. Мы также отмечаем что \(a = -4\) и поэтому график растягивается на \(-\text{4}\) единиц. Максимальное значение будет 4 а минимальное значение будет \(-\text{4}\).
\(y=-2\cos\theta + 1\)
В этом случае \(q = 1\) и, следовательно, основной график косинуса сдвинут вверх на 1 единицу. Мы также отмечаем
что \(a = -2\) и поэтому график растягивается на \(-\text{2}\) единиц. Максимальное значение будет 3
а минимальное значение будет \(-\text{1}\).
Максимальное значение будет 3
а минимальное значение будет \(-\text{1}\).
\(y=\sin\theta — 3\)
В этом случае \(q = -3\) и, следовательно, график основного синуса сдвинут вниз на 3 единицы. Мы также отмечаем что \(a = 1\) и поэтому граф не растянут. Максимальное значение будет \(-\text{2}\), а минимальное значение будет \(-\text{4}\). 9\circ\), \(y = -2\).
\(y=2\cos\theta — 1\)
В этом случае \(q = -1\) и поэтому основной график косинуса сдвинут вниз на 1 единицу. Мы также отмечаем что \(a = 2\) и поэтому график растянут на 2 единицы. Максимальное значение будет \(\text{1}\) и минимальное значение будет \(-\text{3}\).
Общая форма косинусного графика: \(y = a \cos \theta + q\). Отметим, что в этом случае график не сдвинут. Также отметим, что график растянут на \(-\text{2}\) единиц. 9{\circ}) &= -3 — (-2)\\ &=-1 \конец{выравнивание*}
Математическая сцена — Тригонометрические функции
Математическая сцена — Тригонометрические функции — Графики тригонометрических функций урок 3 2008 Расмус Эф | Печать |
Урок 3 Графики триггерных функций
Теперь посмотрим на графики триггерных функций
начиная с функции f(v)
= sin v. Угол v равен
измеряется от оси x, и мы смотрим, что происходит, когда угол v становится
больше.
Угол v равен
измеряется от оси x, и мы смотрим, что происходит, когда угол v становится
больше.
Составляем таблицу значений:
Мы уже вычислили sin 30 и sin 60, используя тот факт, что в треугольниках с углами 30, 60 и 90, сбоку против угла 30 градусов половина длины гипотенузы. Это означает, что мы можем легко найти значения sin v на 30 интервалах. Мы также можем использовать sin x функцию в калькуляторе или электронной таблице.
v | f(v) = sin v | |
| 0 | 0 | 0 |
| 30 | 1 / 2 | 0,5 |
| 60 | / 2 | 0,866 |
| 90 | 1 | 1 |
| 120 | / 2 | 0,866 |
| 150 | 1 / 2 | 0,5 |
| 180 | 0 | 0 |
| 210 | — 1 / 2 | -0,5 |
| 240 | —/ 2 | -0,866 |
| 270 | -1 | -1 |
| 300 | —/ 2 | -0,866 |
| 330 | — 1 / 2 | -0,5 |
| 360 | 0 | 0 |
Теперь рисуем график по этим значениям, отмечая
углы v по оси x и sin v по оси y.
Результатом является синусоида, хорошо известная явления в физике и естественных науках. Проблема в том, что синусоидальные волны в природа — это функции времени и длины, а не степени, как мы здесь использовали.
Для решения этой проблемы новый способ измерения используются углы. Эта единица измерения угла называется радианом и находится путем измерения длины дуги единичного круга между радиусом, который образует одну сторону угла и ось x.
Один радиан равен углу, который заметает дугу длиной в одну единицу на единичной окружности (см. схему).
Представьте себе провод такой же длины, как радиуса, в точке на оси x, где x = 1. Теперь согните проволоку вокруг окружность круга. Угол в центре окружности, которая охватывает эта дуга составляет один радиан. Единицу иногда называют рад. Вы видите из диаграмме, что 1 рад чуть меньше 60?.
Но как найти точную связь между градусы и радианы? Как мы можем измениться между градусами и радианами?
Мы делаем это, отмечая, что длина окружности
окружность равна 2∙r∙ или 2 в данном случае, где r = 1.
Другими словами, единичный круг, охватывающий угол 360, длина окружности 2.
Это приводит к следующему результату:
2 эквивалентно 360, то есть эквивалентно 180 |
Чтобы перейти от радианов к градусам, мы умножаем на 180 /. |
Чтобы перейти от градусов к радианам, мы умножаем на /180 . |
Пример 1
Теперь посмотрим на синусоиду в нашей обычной системе координат x y.
Кому для этого нам нужно изменить углы с градусов на радианы, умножив на /180 и отменив как можно больше.
Теперь вставляем углы радианы как значения по оси x. Хорошо оставьте степени для сравнение.
Пример 2
Подсчитать количество
градусов в одном радиане.
Для этого мы должны умножить на 180 /, используя значение на калькуляторе ≈ 3,14
1∙180 / ≈ 57,3
Пример 3
Изменить 5/ 4 радиан на градусы.
Мы снова можем умножить на 180/ или использовать тот факт, что p радиан такое же, как 180. Таким образом, мы можем просто заменить на 180.
5/4 = 5∙180/4 = 225.
Его очень легко рисовать графики триггерных функций, если используется графический калькулятор.
Ниже описано, как сделать это с помощью калькулятора CASIO. Первое, что нужно сделать, это решить, в чем единиц измеряемый угол. Калькулятор предлагает три возможности. Градусы, радианы и грады.
Грады аналогичны градусам но с 400 градами по кругу, а не с 360.
Единицы изменены выбрав график в меню, а затем нажав
Смена и настройка.
Окно, которое открывает предложения
различные возможности, но на данный момент нас интересует только угол
измерение. Используйте стрелки на калькуляторе и перейдите на
Используйте стрелки на калькуляторе и перейдите на
Угол.
Следующие три варианта можно сделать:
Градус, Рад, Гра
Нажав F1, F2 или F3.
Мы выбираем либо градусы (градусы) или Rad (радианы) и нажмите exe.
Далее выбираем шкалу на оси x, нажав
Shift og View Окно (F3) и выбор триггера (F2)
Теперь мы готовы нарисовать график.
Например, график y = sin x
Теперь мы можем нарисовать график, нажав F6.
Пример 4
Теперь мы увидим, как Excel
можно использовать для рисования триггерных графиков. Сначала мы нарисуем график f(x) = cos
х, для х на интервале от –90 до 450
и найти значения cos x через 30 интервалов. Начнем с ввода −90 в
столбец для углов (B3), затем −60 и
скоро. (Лучше всего сделать это, скопировав)
Начнем с ввода −90 в
столбец для углов (B3), затем −60 и
скоро. (Лучше всего сделать это, скопировав)
Excel использует радианы, поэтому мы используем столбец C для значений углов в радианах. Это делается путем умножения на /180. Формула в C3 будет выглядеть так: =B3*Pi()/180. Затем формула копируется вниз по столбцу C.
Подставляем формулу для функция косинуса в столбце D. Формула в D3 будет =cos(C3) . Опять же может быть скопировано вниз по столбцу.
График построен по блокируя столбцы B и D, выбирая инструмент построения графика, а затем XY (разброс). внешний вид графика можно изменить, щелкнув правой кнопкой мыши. Электронная таблица Excel будет выглядеть следующим образом:
График y = cos x выглядит так:
Мы видим, что график косинуса точно такой же, как и график
синусоидальный график, если он перемещается на /2
(90) вправо.
Посмотрите, что произойдет, если мы вычтите /2 из значений в столбце C и найдите косинус новых значений. (см. столбцы F G), затем нарисуйте график y = cos(x − /2).
Таким образом мы перевели график косинуса
на/2 (90) вправо и в
Результатом является график функции синуса.
Это показывает, что выполняется следующее правило:
sin x = cos(x − /2)
Верно следующее общее правило:
Графики триггерных функций можно перевести вправо, вычитая постоянное значение из переменной x.
Графики y = sin(x − a) и y = cos(x
− а) такие же, как графики y = sin x и |
Если a отрицательное, мы получаем два отрицательных значения и
поэтому добавление к значению x. Это эквивалентно переводу на
оставил. Можно также сказать, что граф
y = cos(x + b) совпадает с графиком y = cos x, переведенным b единиц в
оставил.
Это эквивалентно переводу на
оставил. Можно также сказать, что граф
y = cos(x + b) совпадает с графиком y = cos x, переведенным b единиц в
оставил.
Пример 5
Теперь мы будем использовать Excel, чтобы увидеть эффект, который умножение синусоидальной функции на постоянное число оказывает на график.
Ну посмотрите на графики из y = sin x, y = 2∙sin x и 92 182 у = ∙sin х
Графики следующие:
Как и следовало ожидать амплитуда волны удваивается, когда мы умножаем 2. Амплитуда — это максимальная высота волны над линией симметрии (в этом случае x ось). Если мы умножим на число меньше единицы, амплитуда будет меньше этой исходной синусоиды.
Если умножить на минус число волна отражается по оси x (переворачивается вверх ногами).
Пример 6
Теперь давайте посмотрим, какой эффект
умножение x на постоянное число имеет на графиках. Ну сравните графики
из y = sin x, y = sin 2x и y = sin x / 2 .
Ну сравните графики
из y = sin x, y = sin 2x и y = sin x / 2 .
Мы видим, что умножение x на константа влияет на то, как часто волна повторяется. Другими словами, это влияет на период или длину волны графика.
Основная функция синуса имеет период или длина волны 2, или 360. Это означает, что он повторяется через 2 интервала. Это длина по оси x от начала одной волны к началу следующего.
Период функции f(x) = sin 2x — половина периода исходной функции, т. е. . Или мы можем сказать количество волн на заданном интервале по оси x удвоился.
Период функции f(x) = sin x/2 в два раза больше периода исходной функции, то есть равен 4. На этот раз количество волн на заданном интервале уменьшилось вдвое.
В общем случае мы можем показать, что если x умножить на константу b, то период волны будет 2/b.
Вот краткое изложение
результаты, найденные в приведенных выше примерах.
Учитывая функцию f(x) = c∙sin b∙(x − a) + e а — перенос волны вправо, если а положительно, влево если а отрицательно. Период или длина волны 2/b. c – амплитуда волна. e — вертикальный перенос волны. Вверх, если e > 0, вниз, если e < 0. |
Пример 7
Посмотрите на функцию f(x) = 3∙sin 2(x − /4) + 3 и сравните с базовой функцией f(x) = sin x.
a = p/4, что означает, что волна сместилась на /4 (45) вправо.
e = 3, поэтому волна была переведены на 3 единицы вертикально вверх.
b = 2, поэтому период равен 2/ 2 = .
c = 3, поэтому амплитуда волна равна 3.
Теперь используйте эту информацию для построения графика.
Пример 8
Нарисуйте график f(x) = tan Икс.
Мы знаем, что tan x = sin x/cos x, поэтому он не существует, когда cos x = 0.

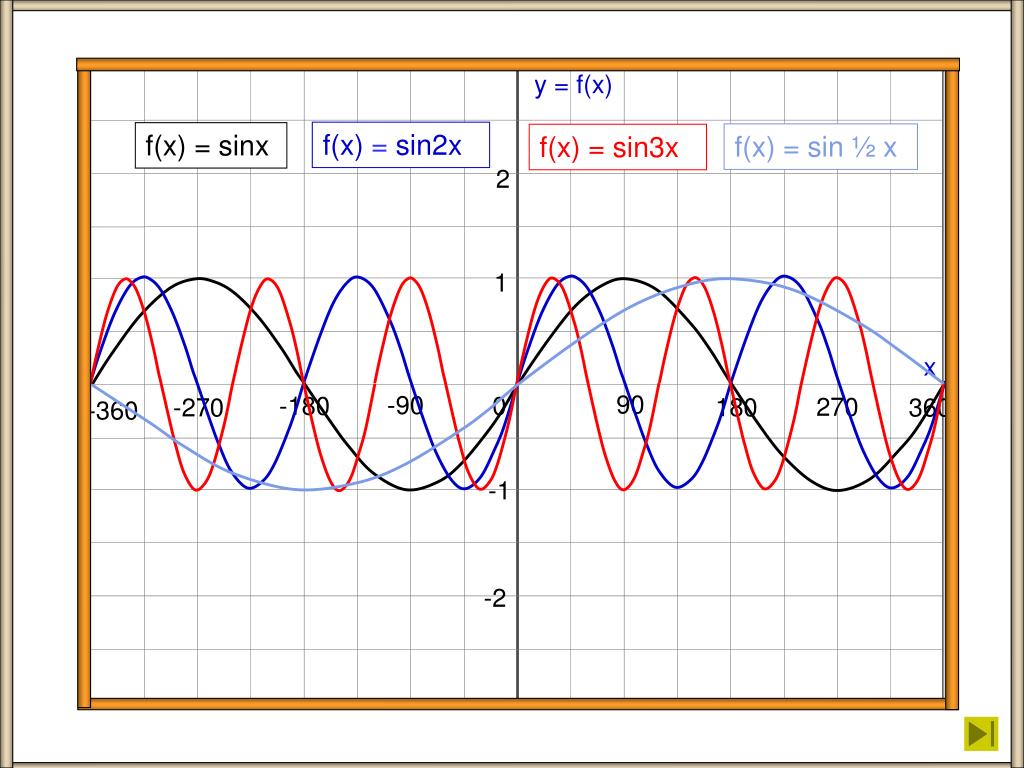 Дидактические материалы к учебнику Алгебра и начала математического анализа (углублённый уровень) – М.: «Вентана-Граф», 2017.
Дидактические материалы к учебнику Алгебра и начала математического анализа (углублённый уровень) – М.: «Вентана-Граф», 2017.