График у x 4. Как построить график функции в Microsoft Excel. Сервисы для построения графиков функций онлайн
Выберем на плоскости прямоугольную систему координат и будем откладывать на оси абсцисс значения аргумента х , а на оси ординат — значения функции у = f (х) .
Графиком функции y = f(x) называется множество всех точек, у которых абсциссы принадлежат области определения функции, а ординаты равны соответствующим значениям функции.
Другими словами, график функции y = f (х) — это множество всех точек плоскости, координаты х, у которых удовлетворяют соотношению y = f(x) .
На рис. 45 и 46 приведены графики функций у = 2х + 1 и у = х 2 — 2х .
Строго говоря, следует различать график функции (точное математическое определение которого было дано выше) и начерченную кривую, которая всегда дает лишь более или менее точный эскиз графика (да и то, как правило, не всего графика, а лишь его части, расположенного в конечной части плоскости).
С помощью графика можно находить значение функции в точке. Именно, если точка х = а принадлежит области определения функции y = f(x) , то для нахождения числа f(а) (т. е. значения функции в точке х = а ) следует поступить так. Нужно через точку с абсциссой х = а провести прямую, параллельную оси ординат; эта прямая пересечет график функции y = f(x) в одной точке; ордината этой точки и будет, в силу определения графика, равна f(а) (рис. 47).
Например, для функции f(х) = х 2 — 2x с помощью графика (рис. 46) находим f(-1) = 3, f(0) = 0, f(1) = -l, f(2) = 0 и т. д.
График функции наглядно иллюстрирует поведение и свойства функции. Например, из рассмотрения рис. 46 ясно, что функция у = х 2 — 2х принимает положительные значения при х и при х > 2 , отрицательные — при 0 наименьшее значение функция у = х 2 — 2х принимает при х = 1 .
Для построения графика функции f(x) нужно найти все точки плоскости, координаты х , у которых удовлетворяют уравнению y = f(x) . В большинстве случаев это сделать невозможно, так как таких точек бесконечно много. Поэтому график функции изображают приблизительно — с большей или меньшей точностью. Самым простым является метод построения графика по нескольким точкам. Он состоит в том, что аргументу х придают конечное число значений — скажем, х 1 , х 2 , x 3 ,…, х k и составляют таблицу, в которую входят выбранные значения функции.
Таблица выглядит следующим образом:
Составив такую таблицу, мы можем наметить несколько точек графика функции y = f(x) . Затем, соединяя эти точки плавной линией, мы и получаем приблизительный вид графика функции y = f(x).
Следует, однако, заметить, что метод построения графика по нескольким точкам очень ненадежен. В самом деле поведение графика между намеченными точками и поведение его вне отрезка между крайними из взятых точек остается неизвестным.
Пример 1 . Для построения графика функции y = f(x) некто составил таблицу значений аргумента и функции:
Соответствующие пять точек показаны на рис. 48.
На основании расположения этих точек он сделал вывод, что график функции представляет собой прямую (показанную на рис. 48 пунктиром). Можно ли считать этот вывод надежным? Если нет дополнительных соображений, подтверждающих этот вывод, его вряд ли можно считать надежным. надежным.
Для обоснования своего утверждения рассмотрим функцию
.
Вычисления показывают, что значения этой функции в точках -2, -1, 0, 1, 2 как раз описываются приведенной выше таблицей. Однако график этой функции вовсе не является прямой линией (он показан на рис. 49). Другим примером может служить функция y = x + l + sinπx; ее значения тоже описываются приведенной выше таблицей.
Эти примеры показывают, что в «чистом» виде метод построения графика по нескольким точкам ненадежен. Поэтому для построения графика заданной функции,как правило, поступают следующим образом.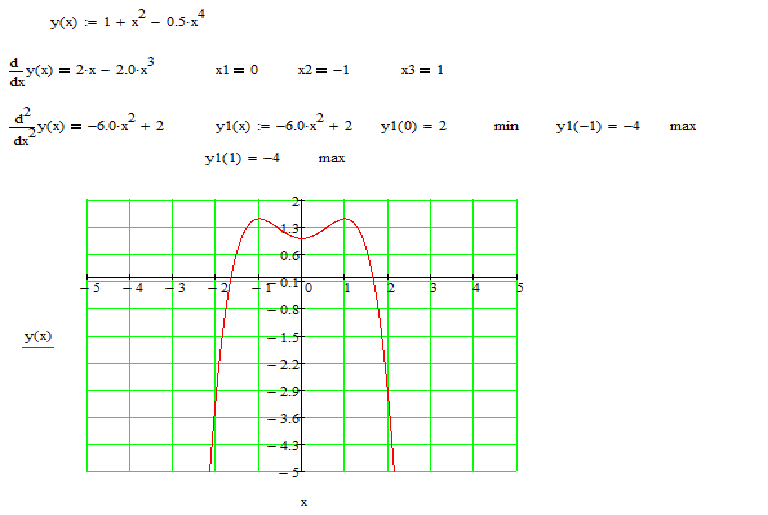 Сначала изучают свойства данной функции, с помощью которых можно построить эскиз графика. Затем, вычисляя значения функции в нескольких точках (выбор которых зависит от установленных свойств функции), находят соответствующие точки графика. И, наконец, через построенные точки проводят кривую, используя свойства данной функции.
Сначала изучают свойства данной функции, с помощью которых можно построить эскиз графика. Затем, вычисляя значения функции в нескольких точках (выбор которых зависит от установленных свойств функции), находят соответствующие точки графика. И, наконец, через построенные точки проводят кривую, используя свойства данной функции.
Некоторые (наиболее простые и часто используемые) свойства функций, применяемые для нахождения эскиза графика, мы рассмотрим позже, а сейчас разберем некоторые часто применяемые способы построения графиков.
График функции у = |f(x)|.
Нередко приходится строить график функции y = |f(x) |, где f(х) — заданная функция. Напомним, как это делается. По определению абсолютной величины числа можно написать
Это значит, что график функции y =|f(x)| можно получить из графика, функции y = f(x) следующим образом: все точки графика функции у = f(х) , у которых ординаты неотрицательны, следует оставить без изменения; далее, вместо точек графика функции y = f(x) , имеющих отрицательные координаты, следует построить соответствующие точки графика функции у = -f(x) (т.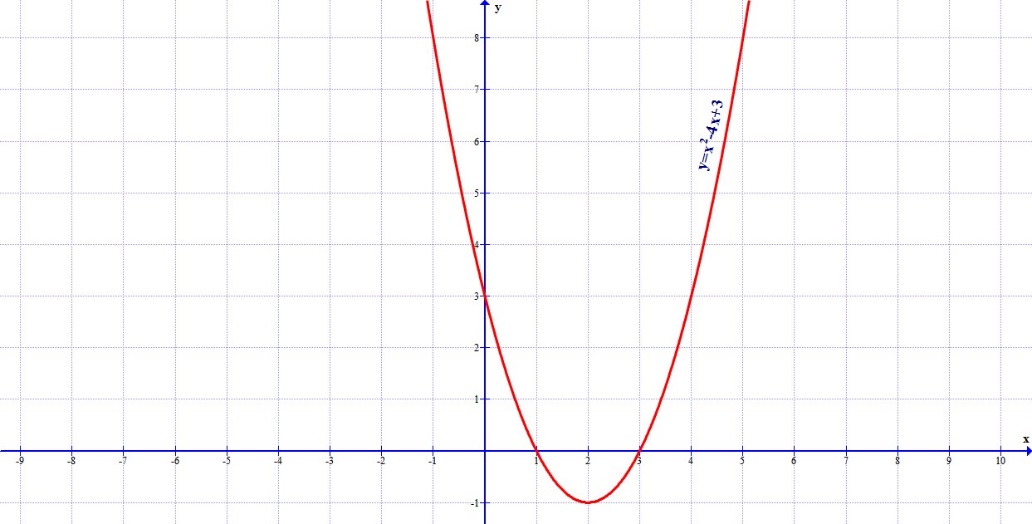 е. часть графика функции
е. часть графика функции
y = f(x) , которая лежит ниже оси х, следует симметрично отразить относительно оси х ).
Пример 2. Построить график функции у = |х|.
Берем график функции у = х (рис. 50, а) и часть этого графика при х (лежащую под осью х ) симметрично отражаем относительно оси х . В результате мы и получаем график функции у = |х| (рис. 50, б).
Пример 3 . Построить график функции y = |x 2 — 2x|.
Сначала построим график функции y = x 2 — 2x. График этой функции — парабола, ветви которой направлены вверх, вершина параболы имеет координаты (1; -1), ее график пересекает ось абсцисс в точках 0 и 2. На промежутке (0; 2) фукция принимает отрицательные значения, поэтому именно эту часть графика симметрично отразим относительно оси абсцисс. На рисунке 51 построен график функции у = |х 2 -2х| , исходя из графика функции у = х 2 — 2x
График функции y = f(x) + g(x)
Рассмотрим задачу построения графика функции y = f(x) + g(x).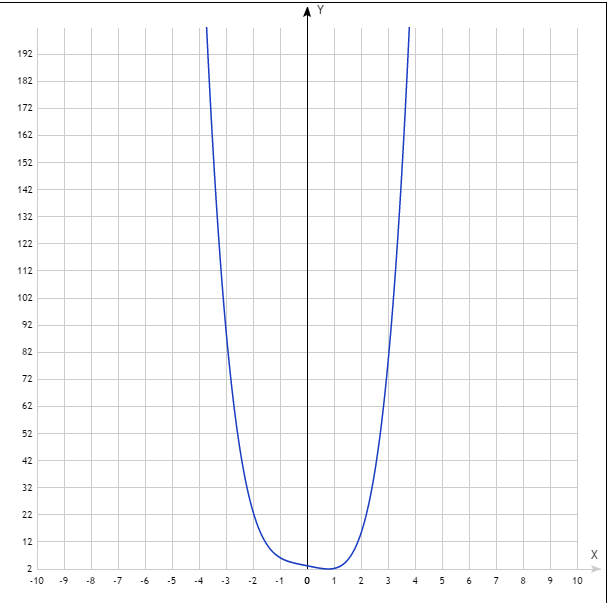
Заметим, что областью определения функции y = |f(x) + g(х)| является множество всех тех значений х, для которых определены обе функции y = f{x) и у = g(х), т. е. эта область определения представляет собой пересечение областей определения, функций f{x) и g{x).
Пусть точки (х 0 , y 1 ) и (х 0 , у 2 ) соответственно принадлежат графикам функций y = f{x) и y = g(х) , т. е. y 1 = f(x 0), y 2 = g(х 0). Тогда точка (x0;. y1 + y2) принадлежит графику функции у = f(х) + g(х) (ибо f(х 0) + g(x 0 ) = y1 +y2 ),. причем любая точка графика функции y = f(x) + g(x) может быть получена таким образом. Следовательно, график функции у = f(х) + g(x) можно получить из графиков функций y = f(x) . и y = g(х) заменой каждой точки (х n , у 1) графика функции y = f(x) точкой (х n , y 1 + y 2),
где у 2 = g(x n ), т.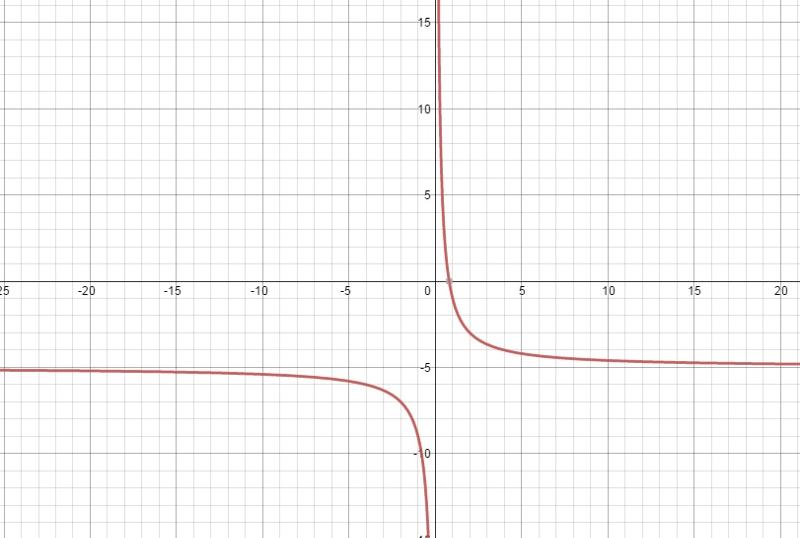 3$.
3$.2. Найдем точку А, координата x, которой равна 1,5. Мы видим, что координата функции находится между значениями 3 и 4 (см. рис. 2). Значит надо заказать 4 куба.
К сожалению, не все студенты и школьники знают и любят алгебру, но готовить домашние задания, решать контрольные и сдавать экзамены приходится каждому. Особенно трудно многим даются задачи на построение графиков функций: если где-то что-то не понял, не доучил, упустил — ошибки неизбежны. Но кому же хочется получать плохие оценки?
Не желаете пополнить когорту хвостистов и двоечников? Для этого у вас есть 2 пути: засесть за учебники и восполнить пробелы знаний либо воспользоваться виртуальным помощником — сервисом автоматического построения графиков функций по заданным условиям. С решением или без. Сегодня мы познакомим вас с несколькими из них.
Лучшее, что есть в Desmos.com, это гибко настраиваемый интерфейс, интерактивность, возможность разносить результаты по таблицам и бесплатно хранить свои работы в базе ресурса без ограничений по времени.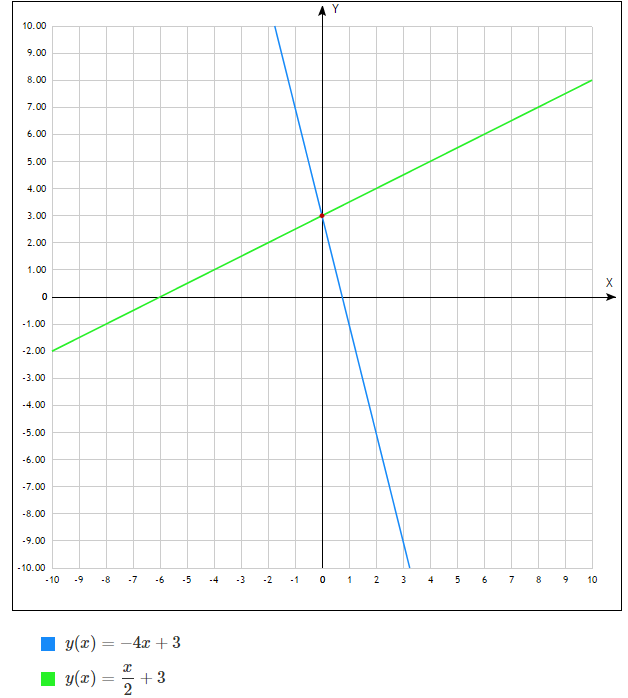 А недостаток — в том, что сервис не полностью переведен на русский язык.
А недостаток — в том, что сервис не полностью переведен на русский язык.
Grafikus.ru
Grafikus.ru — еще один достойный внимания русскоязычный калькулятор для построения графиков. Причем он строит их не только в двухмерном, но и в трехмерном пространстве.
Вот неполный перечень заданий, с которыми этот сервис успешно справляется:
- Черчение 2D-графиков простых функций: прямых, парабол, гипербол, тригонометрических, логарифмических и т. д.
- Черчение 2D-графиков параметрических функций: окружностей, спиралей, фигур Лиссажу и прочих.
- Черчение 2D-графиков в полярных координатах.
- Построение 3D-поверхностей простых функций.
- Построение 3D-поверхностей параметрических функций.
Готовый результат открывается в отдельном окне. Пользователю доступны опции скачивания, печати и копирования ссылки на него. Для последнего придется авторизоваться на сервисе через кнопки соцсетей.
Координатная плоскость Grafikus.ru поддерживает изменение границ осей, подписей к ним, шага сетки, а также — ширины и высоты самой плоскости и размера шрифта.
Самая сильная сторона Grafikus.ru — возможность построения 3D-графиков. В остальном он работает не хуже и не лучше, чем ресурсы-аналоги.
Onlinecharts.ru
Онлайн-помощник Onlinecharts.ru строит не графики, а диаграммы практически всех существующих видов. В том числе:
- Линейные.
- Столбчатые.
- Круговые.
- С областями.
- Радиальные.
- XY-графики.
- Пузырьковые.
- Точечные.
- Полярные бульки.
- Пирамиды.
- Спидометры.
- Столбчато-линейные.
Пользоваться ресурсом очень просто. Внешний вид диаграммы (цвет фона, сетки, линий, указателей, форма углов, шрифты, прозрачность, спецэффекты и т. д.) полностью определяется пользователем. Данные для построения можно ввести как вручную, так и импортировать из таблицы CSV-файла, хранимого на компьютере. Готовый результат доступен для скачивания на ПК в виде картинки, PDF-, CSV- или SVG-файлов, а также для сохранения онлайн на фотохостинге ImageShack. Us или в личном кабинете Onlinecharts.ru. Первый вариант могут использовать все, второй — только зарегистрированные.
Us или в личном кабинете Onlinecharts.ru. Первый вариант могут использовать все, второй — только зарегистрированные.
Построение графиков онлайн весьма полезный способ графически отобразить то, что не в силах передать словами.
Информация – это будущее электронного маркетинга, при этом правильно преподнесенные зрительные образы являются мощным инструментом для привлечения целевой аудитории.
Тут на помощь приходит инфографика, позволяющая в простой и выразительной форме преподносить различного рода информацию.
Однако построение инфографических изображений требует определенного аналитического мышления и богатства фантазии.
Спешим вас обрадовать – в интернете достаточно ресурсов, предоставляющих построение графиков онлайн.
Yotx.ru
Замечательный русскоязычный сервис, осуществляющий построение графиков онлайн по точкам (по значениям) и графиков функций (обычных и параметрических).
Этот сайт обладает интуитивно понятным интерфейсом и легок в использовании. Не требует регистрации, что существенно экономит время пользователя.
Не требует регистрации, что существенно экономит время пользователя.
Позволяет быстро сохранять готовые графики на компьютере, а также генерирует код для размещения на блоге или сайте.
На Yotx.ru есть учебник и примеры графиков, которые были созданы пользователями.
Возможно, для людей, углубленно изучающих математику или физику, этого сервиса будет мало (например, нельзя построить график в полярных координатах, так как на сервисе нет логарифмической шкалы), но для выполнения самых простых лабораторных работ вполне достаточно.
Преимуществом сервиса является то, что он не заставляет как многие другие программы, искать полученный результат по всей двумерной плоскости.
Размер графика и интервалы по осям координат автоматически генерируются так, чтобы график оказался удобным для просматривания.
Одновременно на одной плоскости есть возможность построить несколько графиков.
Дополнительно на сайте можно использовать калькулятор матриц, с помощью которого легко производить различные действия и преобразования.
ChartGo
Англоязычный сервис для разработки многофункциональных и разноцветных гистограмм, линейных графиков, круговых диаграмм.
Для обучения пользователям представляется подробное руководство и деморолики.
ChartGo будет полезен для тех, кто нуждается в регулярно. Среди подобных ресурсов отличается простотой «Create a graph online quickly».
Построение графиков онлайн осуществляется по таблице.
В начале работы необходимо выбрать одну из разновидностей диаграмм.
Приложение обеспечивает пользователям ряд простых вариантов настройки построения графиков различных функций в двумерных и трехмерных координатах.
Можно выбрать одну из разновидностей диаграмм и переключаться между 2D и 3D.
Настройки размера обеспечивают максимальный контроль между вертикальной и горизонтальной ориентацией.
Пользователи могут настраивать свои диаграммы с уникальным названием, а также присваивать названия для X и Y элементов.
Для построения графиков онлайн xyz в разделе «Example» доступно множество макетов, которые можно изменять на свое усмотрение.
Обратите внимание! В ChartGo в одной прямоугольной системе может быть построено множество графиков. При этом каждый график составлен с помощью точек и линий. Функции действительного переменного (аналитические) задаются пользователем в параметрическом виде.
Разработан и дополнительный функционал, который включает мониторинг и вывод координат на плоскости или в трехмерной системе, импорт и экспорт числовых данных в определенных форматах.
Программа имеет гибко настраиваемый интерфейс.
После создания диаграммы, пользователь может воспользоваться функцией печати результата и сохранения графика в виде статичного рисунка.
OnlineCharts.ru
Еще одно отличное приложение для эффектного представления информации вы можете найти на сайте OnlineCharts.ru, где можно построить график функции онлайн бесплатно.
Сервис способен работать с множеством видов диаграмм, включая линейные, пузырьковые, круговые, столбчатые и радиальные.
Система обладает очень простым и наглядным интерфейсом. Все доступные функции разделены вкладками в виде горизонтального меню.
Все доступные функции разделены вкладками в виде горизонтального меню.
Чтобы начать работу необходимо выбрать тип диаграммы, которую вы хотите построить.
После этого можно настроить некоторые дополнительные параметры внешнего вида, в зависимости от выбранного типа графика.
Во вкладке «Добавить данные» пользователю предлагается задать количество строк и если необходимо количество групп.
Также можно определить цвет.
Обратите внимание! Вкладка «Подписи и шрифты» предлагает задать свойства подписей (нужно ли их выводить вообще, если да, то каким цветом и размером шрифта). Также предоставляется возможность выбора типа шрифта и его размера для основного текста диаграммы.
Все предельно просто.
Aiportal.ru
Самый простой и наименее функциональный из всех, представленных здесь онлайн-сервисов. Создать трехмерный график онлайн на этом сайте не удастся.
Он предназначен для построения графиков сложных функций в системе координат на определенном интервале значений.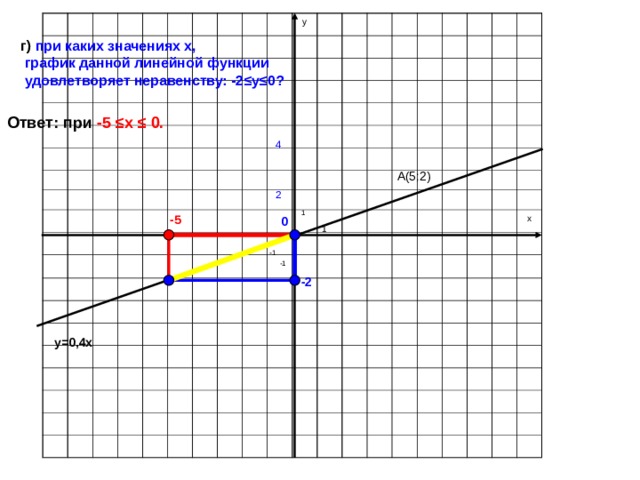
Для удобства пользователей сервис предоставляет справочные данные по синтаксису различных математических операций , а также по перечню поддерживаемых функций и константных значений.
Все необходимые для составления графика данные вводятся в окно «Функции». Одновременно на одной плоскости пользователь может построить несколько графиков.
Поэтому разрешается вносить подряд несколько функций, но после каждой функции необходимо вставлять точку с запятой. Также задается и область построения.
Предусмотрена возможность построения графиков онлайн по таблице или без нее. Поддерживается цветовая легенда.
Несмотря на небогатый функционал, все же это онлайн-сервис, поэтому вам не придется долго искать, скачивать и устанавливать какое-либо программное обеспечение.
Для построения графика достаточно лишь иметь с любого имеющегося устройства: ПК, ноутбука, планшета или смартфона.
Построение графика функции онлайн
ТОП-4 лучших сервиса для построения графиков онлайн
Постройте график функции y x4 13×2 36 x 3 x 2
Обновлено: 12. — 13\right) = 0$$
— 13\right) = 0$$
Решаем это уравнение
Корни этого ур-ния
$$x_ = — \frac>$$
$$x_ = \frac>$$
Интервалы выпуклости и вогнутости:
Найдём интервалы, где функция выпуклая или вогнутая, для этого посмотрим, как ведет себя функция в точках перегибов:
Вогнутая на промежутках
Выделим полные квадраты:
Источник: ГИА-2013. Математика. Тренировочная работа № 2.(1 вар)
Постройте график функции Определите, при каких значениях m прямая имеет с графиком ровно три общие точки.
Раскроем модуль. При имеем:
Графиком данной функции является парабола, ветви которой направлены вверх. Абсцисса вершины: ордината вершины Точка пересечения графика с осью ординат: Точки пересечения с осью абсцисс найдем из уравнения получим: Дополнительная точка:
Графиком данной функции является парабола, ветви которой направлены вверх. Абсцисса вершины: ордината вершины Точка пересечения графика с осью ординат: Точки пересечения с осью абсцисс найдем из уравнения получим: Дополнительная точка:
График функции изображен на рисунке.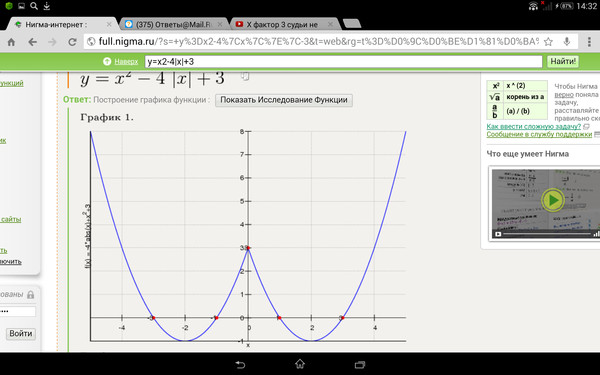
Прямая имеет с построенным графиком ровно три общие точки при и
Приведём другой способ построения графика.
Выделим полные квадраты:
Постройте график функции Определите, при каких значениях прямая имеет с графиком ровно две общие точки.
Раскроем модуль. При имеем:
Графиком данной функции является парабола, ветви которой направлены вверх. Абсцисса вершины: ордината вершины Точка пересечения графика с осью ординат: Точки пересечения с осью абсцисс найдем из уравнения получим: Дополнительная точка:
Графиком данной функции является парабола, ветви которой направлены вниз. Абсцисса вершины: ордината вершины Точка пересечения графика с осью ординат: Точки пересечения с осью абсцисс найдем из уравнения получим: Дополнительная точка:
График функции изображен на рисунке.
Прямая имеет с построенным графиком ровно две общие точки при и
Приведём другой способ построения графика.
Выделим полные квадраты:
Следовательно, график функции получается из графика функции сдвигом на а график функции получается из графика функции сдвигом на
Разложим числитель дроби на множители.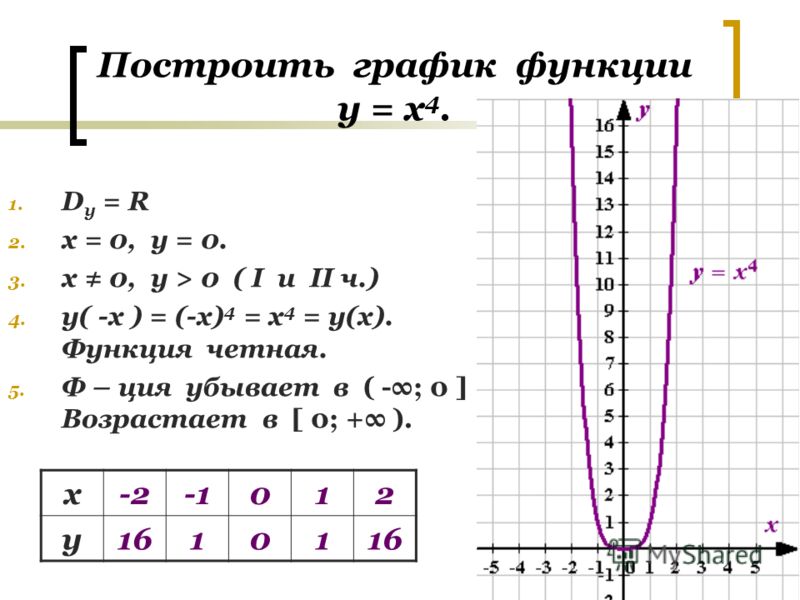 Для этого приравняем его к 0 и решим биквадратное уравнение через теорему Виета.
Для этого приравняем его к 0 и решим биквадратное уравнение через теорему Виета.
Подставляем полученное разложение в дробь и сокращаем ее.
Графиком нашей функции будет парабола, направленная вверх, причем она имеет выколотые точки при x = 3 и х = -2 (т.к. знаменатель исходной дроби при этих значениях обращается в ноль).
Найдем вершину параболы О(m; n):
Чертим координатную плоскость и на ней отмечаем точку О(-0,5; -6,25). Чертим стандартную параболу со смещенным центром.
**Что значит стандартная парабола? Она не суженная и не расширенная. Эта та парабола, которую мы все рисуем в самом начале изучения парабол по формуле y=x 2 . Обычно все точки, которые нужны для построения к 9 классу все знают наизусть: (0;0) — начало координат, (1; 1), (2; 4), (3; 9) плюс симметричные. В нашем случае за начало координат берется точка О и точки ставятся аналогично. В любом случае, всегда можно нарисовать таблицу значений, если возникнут трудности. Содержание Формулы сокращенного умножения включают в себя следующие группы формул: Группа формул «Сумма нечетных степеней» приведена в Таблице 3. Таблица 3. – Сумма нечетных степеней Сумма кубов x3 + y3 = Сумма пятых степеней x5 + y5 = Сумма седьмых степеней x7 + y7 = Сумма степеней порядка 2n + 1 Если в формулах из Таблицы 3 заменить y на – y , то мы получим группу формул «Разность нечетных степеней» (Таблица 4. Таблица 4. – Разность нечетных степеней Разность седьмых Разность кубов x3– y3 = Разность пятых степеней x5– y5 = Разность седьмых x7– y7 = Разность степеней порядка 2n + 1 Группа формул «Разность четных степеней» приведена в Таблице 5. Таблица 5. – Разность четных степеней Разность квадратов x2– y2 = (x + y) (x – y) Разность четвертых степеней Разность шестых степеней Разность восьмых степеней Разность степеней порядка 2n * * * Замечание. x2n– y2n , приведенные в последней строке Таблицы 5, можно продолжить и далее, по аналогии с тем, как это сделано в других строках таблицы. Другие формулы сокращенного умножения можно посмотреть в разделе «Формулы сокращенного умножения: степень суммы, степень разности» нашего справочника. На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике. Предлагаю идею сайта-аукциона по выполнению домашних заданий. Он будет включать: Основное отличие от большинства сайтов, предлагающих выполнение работ на заказ – сайт рассчитан на две категории пользователей: заказчиков и решающих задания. Основой для идеи послужили несколько работающих систем, объединение которых позволит сделать сервис для решения задач на заказ. Эти системы: Для удобства и проведения аналогий с реальной жизнью назовем заказчиков студентами, а решающих задания – репетиторами. Итак, студенту необходимо решить несколько задач. Он заходит на сайт, выбирает раздел с соответствующей дисциплиной и создает новую тему (аналогия с форумом). Но при создании темы он также указывает стартовую (максимальную) цену, которую он готов заплатить за решение задач и крайний срок исполнения задания. Можно будет назначить и нулевую цену – если студенту нужно только бесплатное решение. Как только тема создана, все пожелавшие подписаться на раздел репетиторы получают уведомление. Причем, условие получения уведомлений можно настроить. Например, уведомлять только о заказах со стартовой ценой более 500 р. и сроком решения не менее недели. Заинтересовавшиеся репетиторы делают ставки. Причем студент (автор темы) видит ставки и может посмотреть информацию по каждому репетитору (его решения, рейтинг, дату начала участия в проекте). Когда студент посчитает нужным, он может остановить аукцион и назначить задание одному из репетиторов, сделавшему ставку (не обязательно самую низкую, т. Деньги блокируются на счете студента, и репетитор начинает решать задание. Он должен представить его к сроку, заданному изначально. Выполненное решение публикуется в свободном доступе и его может оценить как заказчик, так и другие репетиторы. На этих оценках и строится рейтинг. Если к решению нет претензий – деньги окончательно переводятся со счета студента на счет репетитора. Первое – положительная обратная связь. Чем больше условий задач и решений будет опубликовано на сайте, тем чаще его будут находить пользователи через поисковики, будет больше ссылок на готовые решения. Именно поэтому важно размещать решенные задачи в свободном доступе. Знаю это по опыту своего сайта exir.ru (ex irodov.nm.ru) – большая ссылочная база получена исключительно за счет благодарных пользователей. Второе – удобный сервис для заказчиков и для желающих заработать на решениях. Студентам и школьникам не нужно перебирать десятки сайтов для сравнения цен, а потом надеяться, что после оплаты они получат качественное решение (и, вообще, все не закончится перечислением денег). Заказчики создают аукцион на понижение цены и могут смотреть на рейтинги желающих решить задачи и ранее выполненные ими решения. Кроме того, деньги окончательно перечисляются исполнителю только после полного решения. Не нужно создавать и продвигать свой сайт, размещать множество объявлений во всех доступных источниках информации. Заказчики сами придут к вам. Не нужно решать все присланные задания с целью поддержания репутации – можно выбирать те, которые будут интересны по уровню сложности, цене и срокам решения. Если вы не понимаете, какую выгоду получит делающий вам какое-нибудь предложение – будьте осторожны! 🙂 У меня уже есть большой опыт работы с сайтом, предоставляющим бесплатные решения по физике. В будущем возможен вариант и с получением некоторого небольшого процента от оплаты заказов. Но процент этот должен быть минимален и на начальном этапе он взиматься точно не будет. Поэтому я собираю предварительные заявки от посетителей, готовых заниматься решениями. Не нужно подписания никаких договоров о намерениях. Просто сообщите, на какие темы вы готовы решать задания, какой у вас опыт подобной работы (e-mail: [email protected]). Когда сервис заработает – я пришлю приглашение на регистрацию. В прошлой статье мы рассмотрели задания на определение точек максимума (минимума) степенной функции. Здесь представлено 7 примеров со степенной функцией. Требуется определить наибольшее (или наименьшее) значение функции на интервале. На блоге уже рассматривались подобные примеры функций с числом е, логарифмические, тригонометрические, рациональные. Стандартный алгоритм решения таких заданий предполагает после нахождения нулей функции, определение знаков производной на интервалах. Затем вычисление значений в найденных точках максимума (или минимума) и на границе интервала, в зависимости от того какой вопрос стоит в условии. Советую поступать немного по-другому. Почему? Писал об этом здесь. Предлагаю решать такие задания следующим образом: 1. Находим производную. В ходе решения представленных примеров подробно не рассмотрено решение квадратных уравнений, это вы должны уметь делать. Так же должны знать производные элементарных функций. Рассмотрим примеры: 77422. Найдите наибольшее значение функции у=х3–3х+4 на отрезке [–2;0]. Найдём производную заданной функции: Найдем нули производной: Указанному в условии интервалу принадлежит точка х = –1. Вычисляем значения функции в точках –2, –1 и 0: Наибольшее значение функции равно 6. Ответ: 6 77425. Найдите наименьшее значение функции у = х3 – 3х2 + 2 на отрезке [1;4]. Найдём производную заданной функции: Найдем нули производной: Указанному в условии интервалу принадлежит точка х = 2. Вычисляем значения функции в точках 1, 2 и 4: Наименьшее значение функции равно –2. Ответ: –2 77426. Найдите наибольшее значение функции у = х3 – 6х2 на отрезке [–3;3]. Найдём производную заданной функции: Найдем нули производной: Указанному в условии интервалу принадлежит точка х = 0. Вычисляем значения функции в точках –3, 0 и 3: Наименьшее значение функции равно 0. Ответ: 0 77429. Найдите наименьшее значение функции у = х3 – 2х2 + х +3 на отрезке [1;4] . Найдём производную заданной функции: Найдем нули производной, решаем квадратное уравнение: 3х2 – 4х + 1 = 0 Получим корни: х1 = 1 х1 = 1/3. Указанному в условии интервалу принадлежит только х = 1. Найдём значения функции в точках 1 и 4: Получили, что наименьшее значение функции равно 3. Ответ: 3 77430. Найдите наибольшее значение функции у = х3 + 2х2 + х + 3 на отрезке [– 4; –1]. Найдём производную заданной функции: Найдем нули производной, решаем квадратное уравнение: 3х2 + 4х + 1 = 0 Получим корни: Указанному в условии интервалу принадлежит корень х = –1. Находим значения функции в точках –4, –1, –1/3 и 1: Получили, что наибольшее значение функции равно 3. Ответ: 3 77433. Найдите наименьшее значение функции у = х3 – х2 – 40х +3 на отрезке [0;4]. Найдём производную заданной функции: Найдем нули производной, решаем квадратное уравнение: 3х2 – 2х – 40 = 0 Получим корни: Указанному в условии интервалу принадлежит корень х = 4. Находим значения функции в точках 0 и 4: Получили, что наименьшее значение функции равно –109. Ответ: –109 Рассмотрим способ определения наибольшего и наименьшего значения функций без производной. 77437. Найдите наименьшее значение функции у=7+12х–х3 на отрезке [–2;2]. Подставляем точки от –2 до 2: у(–2)=7+12 (–2) – (–2)3 = – 9 у(–1)=7+12 (–1) – (–1)3 = – 6 у(0)=7+12∙0 – 03 = 7 у(1)=7+12∙1 – 13 = 18 у(2)=7+12∙2 – 23 = 23 Наименьшее значение равно –9. Ответ: –9 77441. Найдите наименьшее значение функции у=9х2–х3 на отрезке [–2;2]. Подставляем точки от –2 до 2: у(–2)=9 (–2)2 – (–2)3 = 44 у(–1)=9 (–1)2 – (–1)3 = 10 у(0)=9∙02 – 03 = 0 у(1)=9∙12 – 13 = 8 у(2)=9∙22 – 23 = 28 Наименьшее значение равно 0. Ответ: 0 77442. Найдите наибольшее значение функции у=9х2–х3 на отрезке [2;10]. Подставляем точки от 2 до 10. В данном примере интервал большой и вычислений будет больше, но способ вполне применим. Ответ: 108 *Чем меньше интервал, тем быстрее решите задачу. 77421. Найдите наименьшее значение функции у=х3 –27х на отрезке [0;4]. Посмотреть решение 77434. Найдите наибольшее значение функции у=х3 + 2х2 – 4х + 4 на отрезке [–2;0]. Посмотреть решение На этом всё. Успеха вам! С уважением, Александр Крутицких. P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях. 2 «. Еще 2 аналогичные замены. 2.1 Найдите корни (нули): F (x) = x 4 -x 3 -7x 2 + x + 6 Rational Roots Test является одним из вышеупомянутых инструментов. Теорема рационального корня утверждает, что если полином обнуляется для рационального числа P / Q, то P является множителем конечной константы и Q является фактором ведущего коэффициента В этом случае ведущий коэффициент равен 1, а конечная константа — 6. Факторы: ведущего коэффициента: 1 Проверим…. Теорема о факторах утверждает, что если P / Q является корнем многочлена, то этот многочлен можно разделить на q * xp. Обратите внимание, что q и p происходят из уменьшенного P / Q. до самых низких значений В нашем случае это означает, что 2.2 Полиномиальное деление в длину 900 — Quo x 3 + 2x 2 -x-2 Остаток: 0 2. См. Теорию в шаге 2.1 Фактор (ы): ведущего коэффициента: 1 Давайте проверим …. Факторная теорема утверждает, что если P / Q является корнем многочлена, то этот многочлен можно разделить на q * xp. В нашем случае это означает, что 2,4 Полином Long Division 74 Коэффициент: x 2 + 3x + 2 Остаток: 0 2. Первый член x 2 , его коэффициент равен 1. Шаг 1: Умножьте коэффициент первого члена на константу 1 • 2 = 2 Шаг 2: Найдите два множителя 2, сумма которых равна коэффициенту среднего члена, который равен 3. Шаг 3: Перепишите полином, разделяющий средний член, используя два фактора, найденные на шаге 2 выше: 1 и 2 Шаг 4: сложите первые 2 члена, вычитая одинаковые множители: 3. Если произведение двух или более членов равно нулю, то хотя бы одно из членов должно быть равно нулю. Теперь мы решим каждый член = 0 отдельно Другими словами, мы собираемся решить столько уравнений, сколько членов есть в продукте Любое решение для члена = 0 также решает продукт = 0. 3.2 Решение: x + 2 = 0 Вычтите 2 из обеих частей уравнения: 3.3 Решите: x + 1 = 0 Вычтите 1 из обеих частей уравнения: 3.4 Решите: x-1 = 0 Добавьте 1 к обеим сторонам уравнения: 3.5 Решите: x-3 = 0 Добавьте 3 к обеим сторонам уравнения: Ранее мы разложили этот многочлен на множители, разделив средний член. 4.1. Найдите вершину y = x 2 + 3x + 2 Параболы имеют наибольшее или наименьшее значение. точка называется Вершиной. Наша парабола открывается и, соответственно, имеет самую низкую точку (также известную как абсолютный минимум). Мы знаем это даже до того, как нанесли «y», потому что коэффициент первого члена, 1, положительный (больше нуля). Каждая парабола имеет вертикальную линию симметрии, проходящую через ее вершину.Из-за этой симметрии линия симметрии, например, будет проходить через середину двух x-точек пересечения (корней или решений) параболы. То есть, если парабола действительно имеет два реальных решения. Параболы могут моделировать множество реальных жизненных ситуаций, например высоту над землей объекта, брошенного вверх через некоторый промежуток времени. Вершина параболы может предоставить нам информацию, например, максимальную высоту, которую может достичь объект, брошенный вверх. Для любой параболы Ax 2 + Bx + C координата x вершины задается как -B / (2A). В нашем случае координата x равна -1,5000 Подставив в формулу параболы -1,5000 для x, мы можем вычислить координату y: Корневой график для: y = x 2 + 3x + 2 4.2 Решение x 2 + 3x + 2 = 0 путем завершения квадрата. Вычтем 2 из обеих частей уравнения: Теперь умный бит: возьмите коэффициент при x, равный 3, разделите его на два, получив 3/2 и, наконец, возведите в квадрат. Добавьте 9/4 к обеим частям уравнения: При сложении 9/4 левая часть завершилась в виде полного квадрата: Мы будем называть это уравнение уравнением. # 4.2.1 Принцип квадратного корня гласит, что когда две вещи равны, их квадратные корни равны. Обратите внимание, что квадратный корень из Теперь, применяя принцип квадратного корня к уравнению. Вычтем 3/2 с обеих сторон, чтобы получить: Поскольку квадратный корень имеет два значения, одно положительное, а другое отрицательное Обратите внимание, что √ 1/4 можно записать как 4.3 Решение x 2 + 3x + 2 = 0 по квадратичной формуле. Согласно квадратичной формуле, x, решение для Ax 2 + Bx + C = 0, где A, B и C — числа, часто называемые коэффициентами, определяется по формуле: В нашем случае A = 1 Соответственно B 2 — 4AC = Применяя квадратную формулу: -3 ± √ 1 Итак, теперь мы смотрим на: Два Реальные решения: x = (- 3 + √1) / 2 = -1. 3.1 Факторы вытягивания: x 4 — x 3 — 2x 2 = x 2 • (x 2 — x — 2) 3.2 Факторинг x 2 — x — 2 Первый член, x 2 , его коэффициент равен 1. Шаг-1: Умножьте коэффициент первого члена на константу 1 • -2 = -2 Шаг-2: Найдите два множителя -2, сумма которых равен коэффициенту среднего члена, который равен -1. Шаг 3: Перепишите полиномиальное разбиение среднего члена, используя два фактора, найденные в шаг 2 выше, -2 и 1 Шаг 4: сложите первые 2 члена, извлекая аналогичные множители: 4. Если произведение двух или более членов равно нулю, то хотя бы одно из членов должно быть равно нулю. Теперь мы решим каждый член = 0 отдельно Другими словами, мы собираемся решить столько уравнений, сколько членов есть в продукте Любое решение для члена = 0 также решает продукт = 0. 4.2 Решение: x 2 = 0 Решение: x 2 = 0 4.3 Решите: x + 1 = 0 Вычтите 1 из обеих частей уравнения: 4.4 Решите: x-2 = 0 Добавьте 2 к обоим Стороны уравнения: Ранее мы разложили этот многочлен на множители, разделив средний член.давайте теперь решим уравнение, заполнив квадрат и используя квадратичную формулу 5. Параболы имеют наивысший или a самая низкая точка называется Вершиной. Наша парабола открывается и, соответственно, имеет самую низкую точку (также известную как абсолютный минимум). Мы знаем это даже до того, как нанесли «y», потому что коэффициент первого члена, 1, положительный (больше нуля). Каждая парабола имеет вертикальную линию симметрии, проходящую через ее вершину.Из-за этой симметрии линия симметрии, например, будет проходить через середину двух x-точек пересечения (корней или решений) параболы. То есть, если парабола действительно имеет два реальных решения. Параболы могут моделировать множество реальных жизненных ситуаций, например высоту над землей объекта, брошенного вверх через некоторый промежуток времени. Вершина параболы может предоставить нам информацию, например, максимальную высоту, которую может достичь объект, брошенный вверх. По этой причине мы хотим иметь возможность найти координаты вершины. Для любой параболы Ax 2 + Bx + C координата x вершины задается как -B / (2A). Подставив в формулу параболы 0,5000 для x, мы можем вычислить координату y: Корневой график для: y = x 2 -x-2 5.2 Решение x 2 -x-2 = 0 путем завершения квадрата. Добавьте 2 к обеим частям уравнения: Теперь умный бит: возьмите коэффициент при x, равный 1, разделите его на два, получив 1/2, и возведите его в квадрат. давая 1/4 Добавьте 1/4 к обеим частям уравнения: Сложение 1/4 превратила левую часть в полный квадрат: Мы будем называть это уравнение уравнением. # 5.2.1 Принцип квадратного корня гласит, что когда две вещи равны, их квадратные корни равны. Обратите внимание, что квадратный корень из Теперь, применяя принцип квадратного корня к уравнению.# 5.2.1 получаем: Добавьте 1/2 к обеим сторонам, чтобы получить: Поскольку квадратный корень имеет два значения, одно положительное, а другое отрицательное Обратите внимание, что √ 9/4 можно записать как 5. Согласно квадратичной формуле, x, решение для Ax 2 + Bx + C = 0, где A, B и C — числа, часто называемые коэффициентами, определяется по формуле: В нашем случае A = 1 Соответственно B 2 — 4AC = Применение квадратичной формулы: 1 ± √ 9 Можно ли упростить √ 9? Да! Разложение 9 на простые множители равно √ 9 = √ 3 • 3 = Итак, теперь мы смотрим на: Два реальных решения: x = ( 1 + √9) / 2 = (1 + 3) / 2 = 2.000 или: x = (1-√9) / 2 = (1-3) / 2 = -1.000 % PDF-1. Mac OS X 10. application / pdfproof: pdfuuid: ebdf3f67-4485-e74e-8a6b-bdbe7ddb6335uuid: b69b2c3d-aaf4-914a-9635-55cbdcbd6ea3
конечный поток
эндобдж
9 0 объект
>
эндобдж
1 0 объект
> / Ресурсы> / Шрифт> / ProcSet [/ PDF / Text] / Свойства >>> / TrimBox [0. Нужна помощь в ответах на эти вопросы по математике 1.Запишите следующий набор в форме записи конструктора {7,12,17,22,27,32,37,42,47,52} 2. Перечислить элементы данного набора в записи реестра {x | 7 –x = 9; x, целое число} 3. Перечислите все подмножества наборов {8, 1, 3} 4. Найдите наименьший возможный набор (то есть набор с наименьшим количеством элементов), который содержит данный набор как подмножества. Из-за формы полиномиальной функции мы можем видеть бесконечное разнообразие в количестве членов и степени переменной. Рисунок 6 Мы часто переставляем многочлены так, чтобы их степени были убывающими. Когда многочлен записывается таким образом, мы говорим, что он имеет общий вид. Укажите степень, старший член и старший коэффициент следующих полиномиальных функций.{6} + 2x — 6 \\ [/ латекс]. Решение Знание степени полиномиальной функции помогает нам предсказать ее конечное поведение. Чтобы определить его конечное поведение, посмотрите на главный член полиномиальной функции. Поскольку степень ведущего члена самая высокая, этот член будет расти значительно быстрее, чем другие члены, поскольку x становится очень большим или очень маленьким, поэтому его поведение будет доминировать на графике.{3} \\ [/ латекс] Опишите поведение конца и определите возможную степень полиномиальной функции на рисунке 7. Рисунок 7 Поскольку входные значения x становятся очень большими, выходные значения [latex] f \ left (x \ right) \\ [/ latex] неограниченно увеличиваются. Поскольку входные значения x становятся очень маленькими, выходные значения [latex] f \ left (x \ right) \\ [/ latex] неограниченно уменьшаются.Мы можем символически описать конечное поведение, написав [латекс] \ begin {case} \ text {as} x \ to — \ infty, f \ left (x \ right) \ to — \ infty \\ \ text {as} x \ to \ infty, f \ left (x \ right) \ to \ infty \ end {case} \\ [/ latex] На словах можно сказать, что, когда значения x приближаются к бесконечности, значения функций приближаются к бесконечности, а когда значения x приближаются к отрицательной бесконечности, значения функций приближаются к отрицательной бесконечности. Мы можем сказать, что этот график имеет форму степенной функции нечетной степени, которая не была отражена, поэтому степень полинома, создающего этот график, должна быть нечетной, а старший коэффициент должен быть положительным. . [латекс] \ begin {case} \ text {as} x \ to — \ infty, f \ left (x \ right) \ to — \ infty \\ \ text {as} x \ to \ infty, f \ left (x \ right) \ to — \ infty \ end {case} \\ [/ latex] Дана функция [латекс] f \ left (x \ right) = 0,2 \ left (x — 2 \ right) \ left (x + 1 \ right) \ left (x — 5 \ right) \\ [/ latex] , выразить функцию как полином в общем виде и определить главный член, степень и конечное поведение функции. Решение Помимо конечного поведения полиномиальных функций, нас также интересует, что происходит в «середине» функции. В частности, нас интересуют места, где меняется поведение графа. Поворотная точка — это точка, в которой значения функции изменяются от увеличения к уменьшению или от уменьшения к увеличению. Рисунок 10 Нас также интересуют перехваты.Как и во всех функциях, точка пересечения y- — это точка, в которой график пересекает вертикальную ось. Точка соответствует паре координат, в которой входное значение равно нулю. Поскольку многочлен является функцией, каждому входному значению соответствует только одно выходное значение, поэтому может быть только один перехват y- [latex] \ left (0, {a} _ {0} \ right) \\ [/ latex ]. Перехваты x- происходят при входных значениях, которые соответствуют нулевому выходному значению. Возможно иметь более одной точки пересечения x-. Точка поворота графика — это точка, в которой график меняет направление с увеличения на уменьшение или от уменьшения к увеличению. Перехват y- — это точка, в которой функция имеет нулевое входное значение. Дана полиномиальная функция [латекс] f \ left (x \ right) = \ left (x — 2 \ right) \ left (x + 1 \ right) \ left (x — 4 \ right) \\ [/ latex] , записанный в факторизованной форме для вашего удобства, определите интервалы перехвата y и x . Перехват y- происходит, когда входной сигнал равен нулю, поэтому замените 0 на x . [латекс] \ begin {case} f \ left (0 \ right) = \ left (0-2 \ right) \ left (0 + 1 \ right) \ left (0-4 \ right) \ hfill \\ \ текст {} = \ left (-2 \ right) \ left (1 \ right) \ left (-4 \ right) \ hfill \\ \ text {} = 8 \ hfill \ end {case} \\ [/ latex] Перехватчик y- равен (0, 8). Перехват x происходит, когда выходной сигнал равен нулю. [латекс] \ begin {case} \ text {} 0 = \ left (x — 2 \ right) \ left (x + 1 \ right) \ left (x — 4 \ right) \ hfill \\ x — 2 = 0 \ hfill & \ hfill & \ text {или} \ hfill & \ hfill & x + 1 = 0 \ hfill & \ hfill & \ text {или} \ hfill & \ hfill & x — 4 = 0 \ hfill \\ \ text {} x = 2 \ hfill & \ hfill & \ text {или} \ hfill & \ hfill & \ text {} x = -1 \ hfill & \ hfill & \ text {или} \ hfill & \ hfill & x = 4 \ end {case} [/ latex] Преобразования x : [latex] \ left (2,0 \ right), \ left (-1,0 \ right) \\ [/ latex] и [latex] \ left (4,0 \ right) )\\[/латекс]. {2} -20x \\ [/ latex], определите y — и x — перехватывает. Решение Степень полиномиальной функции помогает нам определить количество точек пересечения x и количество точек поворота. Непрерывная функция не имеет разрывов в графике: график можно нарисовать, не отрывая перо от бумаги. Плавная кривая — это график без острых углов. Поворотные точки гладкого графика всегда должны приходиться на закругленные кривые. Графики полиномиальных функций бывают как непрерывными, так и гладкими. Многочлен степени n будет иметь не более n x -перехваченных точек и n — 1 точек поворота. Решение Какой мы можем сделать вывод о полиноме, представленном графиком, показанным на графике на рисунке 13, на основе его пересечений и точек поворота? Рисунок 13 Рисунок 14 Конечное поведение графа говорит нам, что это граф полинома четной степени. График имеет 2 точки пересечения x , что соответствует степени 2 или больше, и 3 точки поворота, что соответствует степени 4 или больше.Исходя из этого, было бы разумно сделать вывод, что степень ровная и не менее 4. Что мы можем сделать о полиноме, представленном на рис. 15, на основании его пересечений и точек поворота? Рисунок 15 Решение Учитывая функцию [латекс] f \ left (x \ right) = — 4x \ left (x + 3 \ right) \ left (x — 4 \ right) \\ [/ latex], определите локальное поведение. Перехват y находится путем вычисления [latex] f \ left (0 \ right) \\ [/ latex]. [латекс] \ begin {case} f \ left (0 \ right) = — 4 \ left (0 \ right) \ left (0 + 3 \ right) \ left (0-4 \ right) \ hfill \ hfill \ \ \ text {} = 0 \ hfill \ end {case} \\ [/ latex] Прерывание y — [латекс] \ left (0,0 \ right) \\ [/ latex]. Перехваты x находятся путем определения нулей функции. [латекс] \ begin {case} 0 = -4x \ left (x + 3 \ right) \ left (x — 4 \ right) \\ x = 0 \ hfill & \ hfill & \ text {или} \ hfill & \ hfill & x + 3 = 0 \ hfill & \ hfill & \ text {или} \ hfill & \ hfill & x — 4 = 0 \ hfill \\ x = 0 \ hfill & \ hfill & \ text {или} \ hfill & \ hfill & \ text {} x = -3 \ hfill & \ hfill & \ text {или} \ hfill & \ hfill & \ text {} x = 4 \ end {case} \\ [/ latex] Преобразования x : [latex] \ left (0,0 \ right), \ left (-3,0 \ right) \\ [/ latex] и [latex] \ left (4,0 \ right) )\\[/латекс]. Степень равна 3, поэтому график имеет не более 2 поворотных точек. Дана функция [латекс] f \ left (x \ right) = 0,2 \ left (x — 2 \ right) \ left (x + 1 \ right) \ left (x — 5 \ right) \\ [/ latex] , определить местное поведение. Решение BMW Llevaba Tiempo Expoendonos Sus todocaminos Medios Más Deportivos, unos BMW X3 y X4 M , который завершается после того, как вы хотите, чтобы его показывали, когда вы производите исправление ошибок, когда вы находитесь в процессе депортации и по оборудованию с двумя автомобилями; de hecho, para ambos estará disponible una version Competition para los más exigentes. BMWCar и водитель Los dos nuevos integration de la división M presumen de un kit de carrocería específico , con paragolpes más agresivos y entradas de aire de mayor tamaño, retrovisores aerodinámicos, faldones laterales, equantas-de-20, unci. BMWCar и водитель Pero el secreto mejor guardado de BMW hasta la fecha, es el que encontramos bajo el capó. Un nuevo motor de seis cilindros en línea con tecnología M TwinPower Turbo, который содержит анимацию в амбушюрной модели и se trata de un propulsor de 3.0 litros con 480 caballos de потенции y 600 Nm de par máximo.En el caso de los Competition estas cifras se elevan hasta los 510 CV. Ambos SUV получил автоматическую трансмиссию M Steptronic и систему общей трансмиссии M xDrive que estrenó el último M5. BMWCar и водитель Respecto al interior, se añaden elements como los asientos deportivos M Sport, la tapicería de cuero Merino, металические вставки для умбралей-де-лас-пуэртас и эмблема M junto al nombre del modelo en la consola central. Las opciones para las versiones Competition, también una tapicería especial en Alcantara. Por último, la compañía no quiso pronunciarse acerca de cuándo se lanzarán los modelos, pero el президент de BMW M, Frank van Meel, dijo: «Con sus características específicas de rendimiento M, el BMW X4 M establecerán puntos de referencia en términos de dinámica en sus respectivos segmentos de vehículos ». BMWCar и водитель Лос-Анджелес BMW X3 M и BMW X4 M от 0 до 100 км / ч в 4,2 секунды, 4,1 в соревнованиях. BMWCar и водитель Tras su de debut internacional en Ginebra, los BMW X3 y X4 M llegarán a los Concesionarios españoles antes del verano y estarán disponibles en los colores Red metalice y Donington Grey, con un Precio que, aunque todavía no ha sido revelado 80.000 евро. Этот контент создается и поддерживается третьей стороной и импортируется на эту страницу, чтобы помочь пользователям указать свои адреса электронной почты.Вы можете найти больше информации об этом и подобном контенте на сайте piano.io. . Отрывок из книги: Гурский Юрий Анатольевич, Гурская Ирина Владимирована, Жвалевский Андрей Валентинович Издательский дом Питер Объемная бутылка Одной из основных особенностей Adobe Illustrator является возможность работы с трехмерной графикой. Причем речь идет не о средствах имитации объема, которые есть, скажем, в Photoshop, а о встроенном, вполне полноценном редакторе трехмерной графики. Именно поэтому многие приемы, применяющиеся в профессиональном трехмерном моделировании, актуальны и для Illustrator. В этом примере мы продемонстрируем технику создания тел вращения — будем рисовать бутылку вина. Прежде всего нужно нарисовать контур правой половины бутылки. Теперь нужно нарисовать пробку. Это делается тем же самым инструментом Pen (Перо). При этом можно ориентироваться на рис. 002. Зальем бутылку желтым цветом, а пробку — коричневым и сгруппируем их (удобнее всего это сделать с помощью сочетания клавиш Ctrl+G, предварительно выделив оба объекта). После этого можно перейти к самому главному — приданию работе объема. Запустите эффект Revolve (Вращение в пространстве): Effect3DRevolve (Эффект3DВращение в пространстве). Использованные настройки показаны на рис. 003 Бутылка почти готова. Но не спешите закрывать окно эффекта Revolve (Вращение в пространстве). Мы добавим на нее этикетку. Для этого нажмите кнопку Map Art (Текстура). Откроется окно редактора, позволяющего добавлять на поверхности объемной фигуры объекты, помещенные в символы (это могут быть любые растровые картинки, фотографии или текст). Выберите в меню Symbol (Символ) изображение заготовки для надписи. Затем переключайте значение параметра Surface (Поверхность) до тех пор, пока нужная нам внешняя сторона бутылки не подсветится красными линиями. Расположите заготовку так, как показано на рис. 004. На этом пример выполнен. В итоговом изображении показана созданная бутылка под разными углами просмотра (рис.005). Свиток пергамента Встроенные эффекты редактирования трехмерной графики в Illustrator дают пользователям самые широкие возможности. Однако не стоит забывать о том, что для полноценной работы с ними вам потребуется действительно мощный компьютер. Даже этот относительно простой пример может поставить ваш компьютер в тупик. Мы будем рисовать свиток пергамента. Сначала с помощью инструмента Line (Линия) создайте линию, имеющую небольшой наклон вправо. Затем, запустив инструмент Twirl (Скручивание) и выбрав достаточно крупную кисть, создайте завитки по краям свитка (рис. Если результат вполне похож на контур свитка, можно переходить ко второму этапу нашей работы. Запустите инструмент Type (Текст) и что-нибудь напишите. Условие одно: шрифт должен напоминать готический, а надписи должны быть достаточно крупными. Авторский вариант показан на рис 007. Теперь необходимо превратить текст в символ. Для этого достаточно просто перетянуть его на палитру Symbols (Символы) (рис. 008). Пришло время придать свитку объемный вид. Запустим эффект Extrude & Bevel (Объем и скос): Effect3DExtrude & Bevel (Эффект3DОбъем и скос). Использованные авторами настройки показаны на рис. 009. Осталось добавить на свиток текст. Для этого в диалоговом окне Extrude & Bevel (Объем и скос) нажмем кнопку Map Art (Текстура). Затем в поле Symbol (Символ) выберем созданный нами текст и, переключая значение параметра Surface (Поверхность), наложим его на свиток (рис. 010). Теперь пример выполнен. Итоговый результат показан на рис. Голова сыра Этот простой пример продемонстрирует интересную возможность создания фигур неполного вращения. Мы будем рисовать голову сыра. Выберите инструмент Rounded Rectangle (Закруглен-ный прямоугольник) и нарисуйте фигуру, напоминающую голову сыра в разрезе. Затем с помощью инструмента Scissors (Ножницы) обрежьте левую сторону фигуры, чтобы она стала подобна изображенной на рис. 012. Задайте обводку (Stroke) сыра толщиной 3 пункта коричневого цвета, а заливку (Fill) — «сырного» желтого (см. рис. 012). Если все получилось нормально, можно переходить к приданию сыру объема. Запустите эффект Revolve (Вращение в пространстве): Effect3DRevolve (Эф-фекты3DВращение в пространстве). Использованные при этом настройки показаны на рис.013. Осталось нарисовать отрезанный кусок сыра. Для это-го скопируйте (Ctrl+C) и вставьте (Ctrl+V) созданную только что голову. Поместите копию немного в стороне и примените настройки, показанные на рис. На этом пример готов. Результат нашей работы, занявшей всего несколько минут, — вполне симпатичный сыр (рис. 015). Рисуем флаг В главе, посвященной трюкам в CorelDRAW, мы уже говорили о том, как рисовать псевдо-объемный флаг. Тогда для этого был использован градиент (кстати, по точно такой же технологии можно работать и в Illustrator). В данном примере мы применим более совершенный инструментарий, поэтому и результат получится реалистичнее. Запустите инструмент Pen (Перо) и повторите кривую, показанную на рис. 016. Ее толщина должна составлять 1 пункт, заливки быть не должно. После того как кривая будет готова, о ней можно на время забыть. Отодвиньте ее в сторону — нам нужно нарисовать то, что ляжет на объемное полотнище, а именно изображение флага. Авторы предпочли имитировать флаг Швейцарии. Нарисовать флаг этой страны очень просто — запустите инструмент Rectangle (Прямоугольник) и создайте квадрат красного цвета. Затем выделите все три элемента и сгруппируйте их (Ctrl+G). Получившийся флаг перетяните на палитру Symbols (Символы). Это позволит сразу добавить его к списку символов в активной группе, что понадобится нам при моделировании флага. Вернитесь к созданной в начале примера кривой. Пришло время превратить ее в настоящий флаг. Запустим эффект Extrude & Bevel (Объем и скос): Effect3DExtrude & Bevel (Эф-фект3DОбъем и скос). Использованные авторами настройки показаны на рис. 018. В результате задания этих настроек мы получим уже нечто достаточно похожее на флаг, но черного цвета. Нужно наложить на лицевую поверхность созданный ранее рисунок швейцарского флага. Для этого в окне Extrude & Bevel (Объем и скос) нажмите кнопку Map Art (Текстура) и повторите то, что показано на рис. Итог — полностью готовое полотнище (рис. 020). Теперь пришло время заняться древком. Мы можем смоделировать его с помощью эффекта Extrude & Bevel (Объем и скос). Для этого нарисуйте маленький кружок, диаметром соответствующий диаметру древка, с обводкой коричневого цвета и повторите настройки, показанные на рис. 021. Если древко подходит, нужно совместить его с полотнищем. Вряд ли это получится с ходу — скорее всего, придется изменить несколько значений в настройках объема. Эта возможность всегда доступна с помощью палитры Appearance (Внешний вид). После того как удалось совместить древко и полотнище флага, остался последний шаг — создать острие. С помощью инструмента Pen (Перо) повторите контур, показанный на рис. 022. Запустим эффект Revolve (Вращение в пространстве): Effect3DRevolve (Эффект3DВра-щение в пространстве) — и применим его с настройками, показанными на рис. 023. Осталось совместить все части флага, и он полностью готов (рис. «Хищный» текст В этом примере мы продемонстрируем, как можно сочетать в работе эффекты и готовые стили для получения интересного результата. Для начала напишем текст. Гарнитуру можно выбрать практически любую, а вот размер символов должен быть большим — в нашем случае 150 пунктов (рис. 025). Затем получим эффект переплетающихся нитей: Effect Stylize Scribble (Эффект Стилизация Каракули). Авторские настройки этого полезнейшего инструмента показаны на рис. 026. Теперь применим готовый стиль, который позволит повторить пятнистость, характерную для многих хищников. Откройте палитру Swatches (Образцы) и используйте вариант Jaguar. Пришло время добавить надписи свечение: Effect Stylize Outer Glow (Эффект Стилизация Внешнее свечение) (рис. 027). После этого шага никаких видимых изменений с изображением не произойдет, но он необходим для получения итогового результата. На этом все почти готово. Эффект создан полностью. Однако помните: прежде чем передавать такую работу в печать, лучше перевести ее в растр, иначе могут быть проблемы. Итоговый вариант показан на рис. 029. Надпись углем Этот пример достаточно точно отражает идеологию создания большинства эффектов в Illustrator — использование дополнительных обводок и заливок. Мы будем рисовать текст, написанный штрихами уголька. Создайте любую надпись достаточно крупного размера (примерно 200 пунктов). Наш вариант показан на рис. 030. Теперь необходимо создать новую обводку. Это делается с помощью меню палитры Appearance (Внешний вид) (рис. 031). Оставьте эту палитру активной — в процессе выполнения примера она нам еще понадобится. На палитре Stroke (Обводка) изменим толщину только что созданного элемента до 3 пунктов. Первая часть примера закончена. Мы больше не будем работать с новой обводкой и вернемся к надписи. Для этого на палитре Appearance (Внешний вид) нужно выделить строку Characters (Символы). Применим эффект Drop Shadow (Отбросить тень): Effect Stylize Drop Shadow (Эффект Стилизация Отбросить тень) — с настройками, показанными на рис. 033. Остался последний шаг. Применим к надписи эффект Sprayed Strokes (Аэрограф): Effect Brush Strokes Sprayed Strokes (Эффект Штрихи кисти Аэрограф). Использованные настройки показаны на рис. 034. Теперь пример выполнен полностью. Причем, обратите внимание, текст остался текстом — вы можете дописать или убрать что-то из надписи, а стиль останется неизменным. Очень удобно! Итоговое изображение показано на рис. 035. Неоновая надпись В этом примере мы средствами Adobe Illustrator будем реализовывать один из классических трюков компьютерной графики — неоновый текст. Создайте любую надпись любой гарнитурой достаточно крупного кегля (около 100 пунктов). Мы остановились на варианте, показанном на рис. 036. Используя команду Add New Stroke (Добавить новую обводку) меню палитры Appearance (Внешний вид), создайте новую обводку. Переключив палитру Color (Цвет) с помощью ее меню в режим HSB, задайте для новой обводки цвет, значения которого показаны на рис. 037. Добавьте еще одну новую обводку и задайте для нее точно такой же цвет, только сдвинув значение S — Saturate (Насыщенность) — на 10 %, до 90. Повторите этот шаг еще восемь раз, пока значение Saturate (Насыщенность) не дойдет до 0 %. Затем увеличьте толщину некоторых обводок с помощью палитры Stroke (Обводка), как показано на рис. 038. На этом большая часть эффекта выполнена, и он уже напоминает неоновые вывески. Однако впереди у нас еще два шага. Сначала добавим надписи немного свечения с помощью эффекта Outer Glow (Внешнее свечение): Effect Stylize Outer Glow (Эффект Стилизация Внешнее свечение). Неоновая надпись готова, но грубые формы выбранной гарнитуры портят общее впечатление от работы. Это можно исправить с помощью эффекта Round Corners (Закругление углов): Effect Stylize Round Corners (Эффект Стилизация Закругление углов) (рис. 040). Работа выполнена. Итоговое изображение показано на рис. 041. Рассмотрим, как получить не просто анимированное изображение, а картинку, которая плавно изменяется. Например, создадим перетекание слова «вода» в «суша» и обратно. Создадим документ нужного размера, например 300 Ч 180 пикселов (рис. 042). Теперь напишем слова «вода» и «суша», подгоним их по расположению и окрасим (рис. 043). Следует перевести их в кривые командой Type Create Outlines (Текст Преобразовать в кривые) и построить между ними пошаговый переход. Последняя операция выполняется с помощью команды Object Blend Make (Объект Переход Создать). Если результат вас не устроит, попробуйте изменить количество промежуточных шагов, воспользовавшись командой Object Blend Blend Options (Объект Переход Настройки перехода) (рис. 045). Так мы получили заготовку для перетекания первого слова во второе. Теперь нужно подготовить обратное перетекание, от «воды» к «суше». Для этого достаточно скопировать переход (например, нажав сначала Ctrl+C, а затем Ctrl+V) и применить к копии команду Object Blend Reverse Front to Back (Объект Переход Поменять планы). На экране получится «каша», но пока это неважно. Выделите оба перехода и примените к ним команду Object Blend Expand (Объект Переход Преобразовать). В результате все промежуточные шаги переходов превратятся в обычные объекты. Правда, они сгруппированы, что будет нам мешать. Поэтому выделим все (Ctrl+A) и выполним команду Object Ungroup (Объект Разгруппировать). Теперь нужно выровнять объекты друг относительно друга. и . Осталось самое интересное — превратить набор разноцветных фигур в анимированное изображение формата Flash. Для этого обратимся к палитре Layers (Слои). Выберите в меню этой палитры пункт Release to Layers (Sequence) (Разбить по слоям (последовательно)), и каждый объект будет переброшен на индивидуальный уровень. Теперь можно перейти к формированию SWF-файла. Выполните команду File Save for Web & Devices (Файл Сохранить для веб и устройств). Появится окно (рис.046), хорошо знакомое пользователям Photoshop. В правой части окна во втором сверху списке выберите пункт SWF, а в списке ниже — Layers to SWF Frames (Слои в кадры SWF). Это позволит превратить содержимое каждого слоя в кадр анимации. Установка флажка Loop (Повторять) сделает мультфильм непрерывным. Параметр Frame Rate (Частота кадров) управляет скоростью анимации — чем меньше значение, тем плавнее изменение изображения. Проконтролировать результат можно, нажав кнопку вызова браузера в нижней части окна. Если вид баннера вас устроил, закрывайте браузер и нажимайте кнопку Save (Сохранить). Появится окно (рис. 047), в списке Тип файла которого лучше всего выбрать пункт HTML and Images (HTML и изображения). В этом случае будет сохранен не только SWF-файл, но и до-кумент HTML с фрагментом кода. Этот фрагмент нужно вставить в код вашей странички, чтобы баннер на ней отображался. Как видите, никаких специальных знаний и даже самой программы Flash не требуется. В заключение — несколько слов о добавлении к баннеру «кликабельности», то есть возможности перейти по определенному веб-адресу. Для этого перед сохранением выделите все объекты, разгруппируйте их и вызовите палитру Attributes (Атрибуты) (рис. 048). В списке Image Map (Карта изображения) выберите Rectangle (Прямоугольник), а в поле под ним впишите нужный адрес. Если теперь сохранить SWF-файл, то все объекты в нем будут содержать гиперссылки. Это в теории. На самом деле попасть по такой ссылке довольно сложно, особенно при высокой частоте смены кадров. Для создания нормально работающей гиперссылки все-таки придется осваивать Flash. Однако минимальную задачу — нарисовать небольшое анимированное изображение — как видите, можно решить и силами Illustrator. И размер такого файла вполне приемлемый — менее 30 Кбайт. Вращающийся баннер Попробуем создать еще один вид интересного анимированного баннера — объект, вращающийся вокруг некоторой оси. Для простоты рассмотрим вращение симметричной фигуры (Атрибуты) относительно вертикальной оси. Идея довольно проста: нужно создать в документе несколько слоев, на каждый из них поместить объект, повернутый на разные углы эффектом 3DRotate (3DВращение), а затем экспортировать результат в формат SWF. Но прежде чем начать работу, прибегнем к маленькой хитрости, которая позволит сэкономить массу времени при создании баннера с другим вращающимся изображением. Хитрость заключается в том, что эффект мы будем применять не к объекту, а к слою, на котором этот объект расположен. Начнем с того, что прикинем, сколько кадров нужно использовать, чтобы вращение было достаточно плавным, процесс — не слишком трудоемким, а результат — небольшим по раз-меру. По опыту можем сказать, что 10 кадров вполне достаточно для имитации вращения на 180°, то есть копия на каждом последующем слое должна быть повернута относительно предыдущей на 18°. Создадим документ нужного размера и нарисуем объект (рис. 049). По умолчанию он находится на слое Layer 1. Откроем палитру Layers (Слои) и скопируем Layer 1. Для этого достаточно перетащить его на значок в нижней части палитры. Теперь внимание! Справа от имени слоя есть кружок — по умолчанию полый. Выделив его, можно применять эффекты ко всему слою в целом (то есть к каждому объекту, который находится на данном слое, будет создан или перемещен на него). Щелкните на этом маркере возле имени скопированного слоя (Layer 1 copy), и вокруг кружка появится еще один. Поскольку мы решили имитировать вращение вокруг вертикальной оси с шагом 18°, введем в поля и значение 0°, а в поле — 18°. Нажимаем OK. Снова копируем слой и повторяем операцию. Правда, на сей раз не применяем эффект заново, а обращаемся к палитре Appearance (Внешний вид). Когда выделены все объекты слоя, к которому применен эффект, палитра принимает примерно такой вид, как на рис. 7.51. Выделите слой Layer 1 copy 2 и щелкните на палитре Appearance (Внешний вид) на строке в поле следует ввести 36°. Повторите копирование слоя и изменение параметров эффекта еще семь раз, пока не достигнете в поле значения 180°. СОВЕТ На пятом шаге, когда нужно вводить 90°, лучше немного «ошибиться» и указать 89° или 91°. Дело в том, что при точном значении фигура нулевой толщины поворачивается к зрителю ребром, то есть кадр будет пустым. Если вы не ошиблись в расчетах, то должно получиться 11 слоев — исходный плюс десять копий. Осталось последнее действие — вызвать окно Save for Web & Devices (Сохранить для веб и устройств) и сохранить баннер в SWF-формате. Обратите внимание, что размер файла составит всего около 3 Кбайт. Как видите, работа несложная, но довольно кропотливая. Чтобы не проделывать ее каждый раз, когда вы хотите создать вращающееся Flash-изображение, используйте только что созданный вами документ. Во избежание случайно-при выделении всех объектов го удаления полезной информации сохраните его в виде слоя, к которому применен шаблона командой File Save as Template (Файл Сохранить эффект как шаблон), а при необходимости открывайте командой FileNew from Template (Файл Новый из шаблона). После открытия шаблонного документа удалите все объекты, а затем заполните слои копия-ми одного и того же изображения. Все эффекты вращения автоматически перенесутся на новые объекты. Можно использовать даже растровую картинку, правда, в этом случае баннер может получиться не таким компактным. Мы рассмотрели самый простой случай вращающегося анимированного изображения. Поэкспериментируйте с настройками, и вы сможете заставить фигуры вращаться более причудливо и реалистично. Можем подсказать несколько идей. — Если вы хотите, чтобы на вашей веб-странице рядом вращалось несколько объектов, причем каждый — вокруг собственной оси, создайте несколько SWF-файлов по количеству объектов и расположите их рядом. Изменяя значение параметра Frame Rate (Частота кадров) в окне Save for Web & Devices (Сохранить для веб и устройств), можно заставить каждую фигуру вращаться с индивидуальной скоростью. — Варьируя параметры , и окна эффекта Rotate (Вращение), вы можете придать объекту вращение во всех плоскостях одновременно. Правда, в этом случае, скорее всего, понадобится большее количество кадров. — Если объект не обладает осевой симметрией, то количество кадров следует удвоить, так как цикл составляет не 180, а 360°. Дополнительные слои можно не создавать, а дублировать уже имеющиеся. — Дополнительной реалистичности можно добиться, используя параметры освещенности. Они становятся доступными в окне эффекта при нажатии кнопки More Options (Дополнительные параметры). При этом также рекомендуется увеличить количество кадров. Точно так же каков наклон X 4? x=4 означает, что для всех значений y x=4. Таким образом, линия x=4 вертикальна оси x. Поэтому наклон tan90= не определено. Таким образом, вы можете ответить на него как «наклон не определен. Является ли х 4 прямой линией? Поскольку х=4 это вертикальная линия, точка пересечения по оси Y отсутствует, а наклон не определен. Каков домен X 4? Примеры алгебры Домен выражения все действительные числа, за исключением случаев, когда выражение не определено. В этом случае нет действительного числа, которое делает выражение неопределенным. Во-вторых, как построить линию x 4? Вы можете нарисовать график, точки построения первый. В этом случае x всегда равно 4, независимо от значения y. Возможные баллы могут быть (4;-5), (4;-2), (4;0), (4;7) и т. д. Нанесение точек даст вам вертикальную линию, проходящую через ось x в точке 4. тогда x 4 горизонтальный или вертикальный? Уравнение x=4 представляет собой вертикальный линия, пересекающая ось x в точке (4,0) . Каждая упорядоченная пара с 4 в качестве первой координаты является решением. (Уравнение означает «x равно 4, а y может быть любым».) — горизонтальная линия, пересекающая ось y в точке (0,−3) . Что такое градиентная линия? Градиент линии насколько крута прямая линия. X — алгебраическая переменная, которая не имеет определенного значения. X — это своего рода вселенская переменная, используемая в большинстве уравнений. Что такое диапазон X4? BMW X4 — это 5-местный роскошный автомобиль, доступный в ценовом диапазоне от Rs. 62.40 — 71.50 лакха*. Как найти домен? Как вы делаете домен и диапазон? Другой способ определить домен и диапазон функций — это используя графики. Поскольку домен относится к набору возможных входных значений, домен графика состоит из всех входных значений, показанных на оси x. Диапазон — это набор возможных выходных значений, которые отображаются на оси ординат. Уравнение x=4 представляет вертикальная линия который пересекает ось x в точке (4,0) . Каждая упорядоченная пара с 4 в качестве первой координаты является решением. (Уравнение означает «x равно 4, а y может быть любым».) — горизонтальная линия, пересекающая ось y в точке (0,−3) . Является ли уравнение y 4 функцией? Ответ был бы Да так как он проходит тест вертикальной линии. Тест вертикальной линии говорит нам, что если мы проводим вертикальную линию через любую точку графика и она проходит только через одну точку на каждой линии, то это функция. Если он проходит более чем через одну точку, он не проходит. Наклон горизонтальной линии равен нулю. Как найти склон? Используя две точки на линии, вы можете найти наклон линии по формуле найти взлет и бег. Вертикальное изменение между двумя точками называется подъемом, а горизонтальное изменение называется бегом. Уклон равен подъему, разделенному на пробег: уклон = подъемный участок, уклон = подъемный участок. Каков наклон 0? Наклон линии можно рассматривать как «подъем над бегом». Когда «подъем» равен нулю, тогда линия горизонтальна или плоская, а наклон линии равен нулю. Проще говоря, нулевой наклон идеально ровный в горизонтальном направлении. Линия с нулевым наклоном горизонтальный. X 0 горизонтальный или вертикальный? Уравнение горизонтальной линии имеет коэффициент y, равный 0. вертикальный линия имеет коэффициент х, равный 0. Какой тип линии имеет нулевой наклон? Горизонтальная линия имеет нулевой наклон, поскольку не поднимается вертикально (т.е. y1 — у2 = 0), в то время как вертикальная линия имеет неопределенный наклон, поскольку она не проходит горизонтально (т. Е. X1 — х2 = 0). Что такое нулевой градиент? Линия, которая проходит прямо через (Горизонтально) имеет нулевой градиент. Чтобы вычислить градиент прямой линии, мы выбираем две точки на самой линии. Как рассчитать градиент? Градиент функции f(x, y) в двух измерениях определяется как: gradf(x, y) = Vf(x, y) = ∂f ∂xi + ∂f ∂yj. Градиент функции представляет собой векторное поле. Его получают применение векторного оператора V к скалярной функции f(x, y). Gel-Pak усовершенствовал химический состав своих эластомеров, чтобы обеспечить широкий диапазон уровней липкости (удерживания) от крайне низкого гелевого эластомера или эластомера Vertec для удержания небольшой полированной оптики до высокого липкий гель или эластомер Vertec для крепления больших керамических подложек. Этикетка Уровень удерживания XT Описание Гель со сверхнизкой липкостью Продукты Этикетка Уровень удержания XL Описание Гель с низкой липкостью Продукты Этикетка Уровень удержания X0 Описание Гель с низкой липкостью Продукты Этикетка Уровень удержания X4 Описание Гель средней фиксации Продукты Этикетка Уровень удержания X5 Описание Гель средней фиксации Продукты Этикетка Уровень удержания X6 Описание Гель High Tack Продукты Этикетка Уровень удержания X8 Описание Гель High Tack Продукты Этикетка Уровень удержания ER0 Описание Гель для электростатических разрядов с низкой липкостью Продукты Этикетка Уровень удержания ER4 Описание Гель для защиты от электростатических разрядов средней липкости Продукты Этикетка Уровень удержания ER6 Описание Гель для защиты от электростатических разрядов средней липкости Продукты Этикетка Уровень удержания ER8 Описание High Tack ESD Товары Мы используем файлы cookie, чтобы оптимизировать ваш опыт, анализировать трафик и персонализировать контент. Store
|
Ступица 1638 1903 15074 Сравнить с другими… 3 исследовать функцию, построить график — ЭкоДом: Дом своими руками
3 исследовать функцию, построить график — ЭкоДом: Дом своими рукамиПодготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра — Формулы сокращенного умножения
Сумма нечетных степеней
Название формулы Формула Сумма кубов x3 + y3 = (x + y) (x2 – xy + y2) Сумма пятых
степенейx5 + y5 = (x + y) (x4 – x3y + x2y2 – xy3 + y4) Сумма седьмых
степенейx7 + y7 = (x + y) (x6 – x5y + x4y2 – x3y3 + x2y4 – xy5 + y6) … … Сумма степеней
порядка 2n + 1 x2n + 1 + y2n + 1 = (x + y) (x2n – x2n – 1y + x2n – 2 y2 – …– xy2n – 1 + y2n)
= (x + y) (x2 – xy + y2)
= (x + y) (x4 – x3y +
+ x2y2 – xy3 + y4)
= (x + y) (x6 – x5y +
+ x4y2 – x3y3 +
+ x2y4 – xy5 + y6)… x2n + 1 + y2n + 1 =
= (x + y) (x2n –
– x2n – 1y +
+ x2n – 2 y2 –
– …– xy2n – 1 + y2n)Разность нечетных степеней
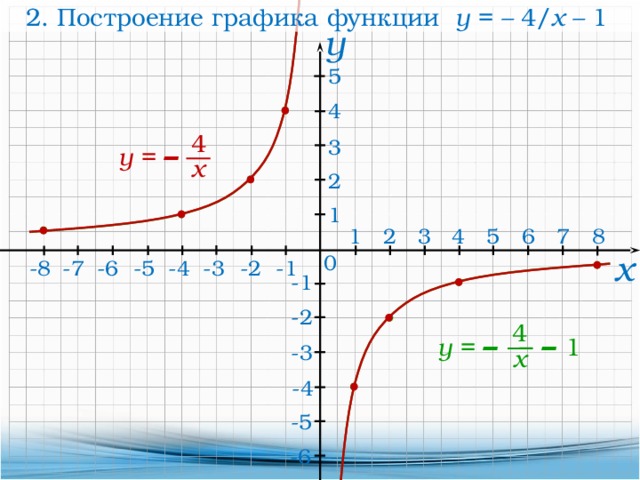 ):
):Название формулы Формула Разность кубов x3– y3 = (x – y) (x2 + xy + y2) Разность пятых
степенейx5– y5 = (x – y) (x4 + x3y + x2y2 + xy3 + y4)
степенейx7– y7 = (x – y) (x6 + x5y + x4y2 + x3y3 + x2y4 + xy5 + y6) … … Разность степеней
порядка 2n + 1x2n + 1– y2n + 1 = (x – y) (x2n + x2n – 1y + x2n – 2 y2 + …+ xy2n – 1 + y2n)
= (x – y) (x2 + xy + y2)
= (x – y) (x4 + x3y +
+ x2y2 + xy3 + y4)
степеней
= (x – y) (x6 + x5y +
+ x4y2 + x3y3 +
+ x2y4 + xy5 + y6)… x2n + 1– y2n + 1 =
= (x – y) (x2n +
+ x2n – 1y +
+ x2n – 2 y2 +
+ …+ xy2n – 1 + y2n)Разность четных степеней
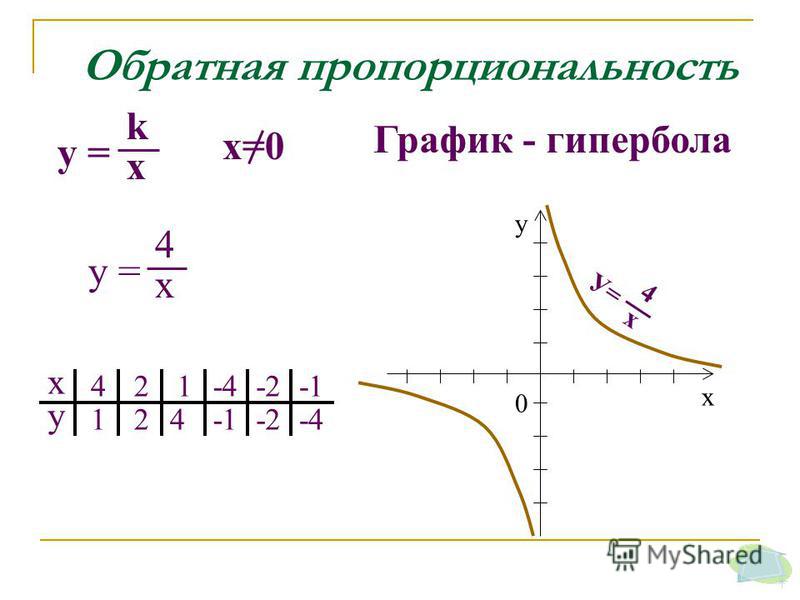
Название формулы Формула Разность квадратов x2– y2 = (x + y) (x – y) Разность четвертых
степенейx4– y4 =
= (x + y) (x3 – x2y + xy2 –y3) =
= (x + y) (x – y) (x2 + y2)Разность шестых
степенейx6– y6 =
= (x + y) (x5 – x4y + x3y2 – x2y3 + xy4 –y5) =
= (x + y) (x – y) (x2 – xy + y2) (x2 + xy + y2)Разность восьмых
степенейx8– y8 =
= (x + y) (x7 – x6y + x5y2 – x4y3 + x3y4 – x2y5 + xy6 –y7) =
= (x + y) (x – y) (x2 + y2) (x4 + y4)… … Разность степеней
порядка 2nx2n– y2n = (x + y) (x2n – 1 – x2n – 2 y + x2n – 3 y2 – …+ xy2n – 2 – y2n – 1) ,
x2n– y2n = (x – y) (x2n – 1 + x2n – 2 y + x2n – 3 y2 + …+ xy2n – 2 + y2n – 1)x4– y4 =
= (x + y) (x3 – x2y +
+ xy2 –y3) =
= (x + y) (x – y) (x2 +
+ y2)x6– y6 =
= (x + y) (x5 – x4y +
+ x3y2 –
– x2y3 +
+ xy4 –y5) =
= (x + y) (x – y) (x2 –
– xy + y2) (x2 +
+ xy + y2)x8– y8 =
= (x + y) (x7 – x6y +
+ x5y2 – x4y3 +
+ x3y4 –
– x2y5 + xy6 –y7) =
= (x + y) (x – y) (x2 +
+ y2) (x4 + y4)… x2n– y2n =
= (x + y) (x2n – 1 –
– x2n – 2 y +
+ x2n – 3 y2 –
– …+ xy2n – 2 –
– y2n – 1)x2n– y2n =
= (x – y) (x2n – 1 +
+ x2n – 2 y +
+ x2n – 3 y2 +
+ …+ xy2n – 2 +
+ y2n – 1) Оба разложения на множители двучлена:
Оба разложения на множители двучлена:заказ решений на аукционе за минимальную цену с максимальным качеством
 Причем, по желанию (чтобы заработать, увеличить свой рейтинг, получить решение сложной задачи) пользователи могут играть любую из этих ролей.
Причем, по желанию (чтобы заработать, увеличить свой рейтинг, получить решение сложной задачи) пользователи могут играть любую из этих ролей.Объединение сервисов в одну систему
Принцип работы
 к. можно учитывать и другие факторы – см. выше).
к. можно учитывать и другие факторы – см. выше).За счет чего будет развиваться сервис
Преимущества для заказчиков
Преимущества для решающих задания
Преимущества для владельца сервиса
 И вариант с получением прибыли от размещения рекламы подходит и для нового сервиса. Кроме того, мне нравится помогать людям и довольно тяжело смотреть, как множество вопросов по задачам остаются на форуме без ответа. Предложенный аукцион решений сможет значительно сократить число вопросов без ответов.
И вариант с получением прибыли от размещения рекламы подходит и для нового сервиса. Кроме того, мне нравится помогать людям и довольно тяжело смотреть, как множество вопросов по задачам остаются на форуме без ответа. Предложенный аукцион решений сможет значительно сократить число вопросов без ответов.Что необходимо для создания сервиса

Найдите наибольшее значение функции
2. Находим нули производной.
3. Определяем какие из них принадлежат данному интервалу.
4. Вычисляем значения функции на границах интервала и точках п.3.
5. Делаем вывод (отвечаем на поставленный вопрос).
 Этот подход можно использовать, если с определением производной у вас большие проблемы. Принцип простой – в функцию подставляем все целые значения из интервала (дело в том, что во всех подобных прототипах ответом является целое число).
Этот подход можно использовать, если с определением производной у вас большие проблемы. Принцип простой – в функцию подставляем все целые значения из интервала (дело в том, что во всех подобных прототипах ответом является целое число).
Пошаговое решение:
Шаг 1:
Уравнение в конце шага 1:
((((x 4 ) - (x 3 )) - 7x 2 ) + x) +6 = 0
Шаг 2:
Калькулятор полиномиальных корней:
Калькулятор полиномиальных корней представляет собой набор методов, направленных на поиск значений x, для которых F (x) = 0 Он может найти только рациональные корни, то есть числа x, которые можно выразить как частное двух целых чисел
Он может найти только рациональные корни, то есть числа x, которые можно выразить как частное двух целых чисел
конечной постоянной: 1, 2, 3, 6 P Q P / Q F (P / Q) Делитель -1 1 -1,00 0,00 x + 1 -2 1 -2.00 0,00 x + 2 -3 1 -3,00 48,00 -6 1 -6,00 1260,00 1 1 1.  00
00 0,00 x-1 2 1 2,00 -12,00 3 1 3,00 0,00 x-3 6 1 6.00 840,00
x 4 -x 3 -7x 2 + x + 6
можно разделить на 4 различных полинома, в том числе на x-3 Полиномиальное деление в длину :
Деление: x 4 -x 3 -7x 2 + x + 6
(«Дивиденд»)
По: x-3 («Делитель») делимое x 4 — x 3 — 7x 2 + x + 6 — делитель * x 3 x 4 — 3x 3 остаток 2x 3 — 7x 2 + x + 6 — делитель * 2x 2 2x 3 — 6x 2 остаток x 2 + x + 6 — делитель * -x 1 — x 2 + 3x остаток — 2x + 6 — делитель * — 2x 0 900 75 — 2x + 6 остаток 0 Калькулятор полиномиальных корней:
 3 Найдите корни (нули): F (x) = x 3 + 2x 2 -x-2
3 Найдите корни (нули): F (x) = x 3 + 2x 2 -x-2
В этом случае ведущий коэффициент равен 1, а конечная константа -2 .
конечной постоянной: 1, 2 P Q P / Q F (P / Q) Делитель -1 1 -1.00 0,00 x + 1 -2 1 -2,00 0,00 x + 2 1 1 1,00 0,00 x-1 2 1 2.00 12.00  Обратите внимание, что q и p происходят из уменьшенного P / Q. до самых низких значений
Обратите внимание, что q и p происходят из уменьшенного P / Q. до самых низких значений
x 3 + 2x 2 -x-2
можно разделить на 3 разных полинома, в том числе на x-1 Полиномиальное деление в длину:
Деление: x 3 + 2x 2 -x-2
(«Дивиденд»)
По: x-1 («Делитель») дивиденд x 3 + 2x 2 — x — 2 — делитель * x 2 x 3 — x 2 остаток 3x 2 — x — 2 — делитель * 3x 1 3x 2 — 3x остаток 2x — 2 — делитель * 2x 0 2x — 2 остаток 9 0075 0 Попытка разложить на множители путем разделения среднего члена
 5 Факторинг x 2 + 3x + 2
5 Факторинг x 2 + 3x + 2
Средний член + 3x, его коэффициент равен 3.
Последний член, «константа», равен +2-2 + -1 = -3 -1 + -2 = -3 1 + 2 = 3 Вот и все
x 2 + 1x + 2x + 2
x • (x + 1)
Складываем последние 2 члена, вычитая общие множители :
2 • (x + 1)
Шаг 5: сложите четыре члена из шага 4:
(x + 2) • (x + 1)
Какая желаемая факторизация Уравнение в конце шага 2:
(x + 2) • (x + 1) • (x - 1) • (x - 3) = 0
Шаг 3:
Теория — Истоки продукта:
 1 Произведение нескольких членов равно нулю.
1 Произведение нескольких членов равно нулю. Решение уравнения с одной переменной:
x = -2 Решение уравнения с одной переменной:
x = -1 Решение уравнения с одной переменной:
x = 1 Решение уравнения с одной переменной:
x = 3 Дополнение: Решение квадратного уравнения Непосредственно
Решение x 2 + 3x + 2 = 0 напрямую
 давайте теперь решим уравнение, заполнив квадрат и используя квадратичную формулу
давайте теперь решим уравнение, заполнив квадрат и используя квадратичную формулу Парабола, найдя вершину:
 По этой причине мы хотим иметь возможность найти координаты вершины.
По этой причине мы хотим иметь возможность найти координаты вершины.
y = 1,0 * -1,50 * -1,50 + 3,0 * -1,50 + 2,0
или y = — 0,250 Парабола, графическая вершина и пересечения по оси X:
Ось симметрии (пунктирная линия) {x} = {- 1,50}
Вершина в точке {x, y } = {-1.50, -0,25}
x -Перехваты (корни):
корень 1 при {x, y} = {-2,00, 0,00}
корень 2 при {x, y} = {-1,00, 0,00} Решите квадратное уравнение путем заполнения квадрата
x 2 + 3x = -2 это дает 9/4
это дает 9/4
В правой части мы имеем:
-2 + 9/4 или, (-2/1) + (9/4)
. общий знаменатель этих двух дробей равен 4. Сложение (-8/4) + (9/4) дает 1/4
Таким образом, сложив обе части, мы, наконец, получаем:
x 2 + 3x + (9/4) = 1 / 4
x 2 + 3x + (9/4) =
(x + (3/2)) • (x + (3/2)) =
(x + (3/2)) 2
Вещи, которые равны одному и тому же, также равны друг другу.Поскольку
x 2 + 3x + (9/4) = 1/4 и
x 2 + 3x + (9/4) = (x + (3/2)) 2
, то по закону транзитивность,
(x + (3/2)) 2 = 1/4
(x + (3/2)) 2 равен
(x + (3/2)) 2/2 =
(x + (3/2)) 1 =
x + (3/2) # 4.2.1 получаем:
# 4.2.1 получаем:
x + (3/2) = √ 1/4
x = -3/2 + √ 1/4
x 2 + 3x + 2 = 0
имеет два решения:
x = -3/2 + √ 1/4
или
x = -3/2 — √ 1 / 4
√ 1 / √ 4, что равно 1/2 Решите квадратное уравнение, используя квадратичную формулу
— B ± √ B 2 -4AC
x = ————————
2A
B = 3
C = 2
9 — 8 =
1
x = —————
2
x = (-3 ± 1) / 2 2 «. Еще 2 аналогичные замены.
2 «. Еще 2 аналогичные замены. Пошаговое решение:
Шаг 1:
Уравнение в конце шага 1:
((x 4 ) - (x 3 ) ) - 2x 2 = 0
Шаг 2:
Шаг 3:
Вытягивание как термины:
Попытка разложить на множители путем разделения среднего члена
Средний член, -x, его коэффициент -1.
Последний член, «константа», равен -2-2 + 1 = -1 Вот и все
x 2 — 2x + 1x — 2
x • (x-2)
сложите последнее 2 члена, извлекая общие множители:
1 • (x-2)
Шаг 5: сложите четыре члена шага 4:
(x + 1) • (x-2)
Какое будет желаемое факторизация Уравнение в конце шага 3:
x 2 • (x + 1) • (x - 2) = 0
Шаг 4:
Теория — Истоки продукта:
 1 Произведение нескольких членов равно нулю.
1 Произведение нескольких членов равно нулю. Решение уравнения с одной переменной:
Решение уравнения с одной переменной:
x = -1 Решение уравнения с одной переменной:
x = 2 Приложение: Непосредственное решение квадратного уравнения
Непосредственное решение x 2 -x-2 = 0
Парабола, найдя вершину:
 1 Найдите вершину y = x 2 -x-2
1 Найдите вершину y = x 2 -x-2 В нашем случае координата x равна 0,5000
В нашем случае координата x равна 0,5000
y = 1,0 * 0,50 * 0,50 — 1,0 * 0,50 — 2,0
или y = -2,250 Парабола, Графическое изображение вершины и пересечения с осью X:
Ось симметрии (пунктирная линия) {x} = {0,50}
Вершина в точке {x, y} = {0.50, -2,25}
x -перехваты (корни):
корень 1 при {x, y} = {-1,00, 0,00}
корень 2 при {x, y} = {2,00, 0,00} Решите квадратное уравнение с помощью Завершение квадрата
x 2 -x = 2
В правой части мы имеем:
2 + 1/4 или, (2/1) + (1/4)
Общий знаменатель две дроби равны 4. Сложение (8/4) + (1/4) дает 9/4
Сложение (8/4) + (1/4) дает 9/4
Таким образом, сложив обе стороны, мы, наконец, получаем:
x 2 -x + (1/4) = 9/4
x 2 -x + (1/4) =
(x- (1/2)) • (x- (1/2)) =
( x- (1/2)) 2
Вещи, которые равны одному и тому же, также равны друг другу.Так как
x 2 -x + (1/4) = 9/4 и
x 2 -x + (1/4) = (x- (1/2)) 2
то по закону транзитивности,
(x- (1/2)) 2 = 9/4
(x- (1/2)) 2 равен
(x- (1/2)) 2/2 =
(x- (1/2)) 1 =
x- (1/2)
x- (1/2) = √ 9/4
x = 1/2 + √ 9/4
x 2 — x — 2 = 0
имеет два решения:
x = 1/2 + √ 9/4
или
x = 1/2 — √ 9/4
√ 9 / √ 4, что равно 3/2 Решите квадратное уравнение с помощью квадратичной формулы
 3 Решение x 2 -x-2 = 0 по квадратичной формуле.
3 Решение x 2 -x-2 = 0 по квадратичной формуле.
— B ± √ B 2 -4AC
x = ————————
2A
B = -1
C = -2
1 — (-8) =
9
x = ————
2
3 • 3
Чтобы можно было удалить что-либо из-под корня, должно быть 2 экземпляра этого (потому что мы берем квадрат i.е. второй корень).
± 3 • √ 1 =
± 3
x = (1 ± 3) / 2 Были найдены три решения :
 5
%
14 0 объект
>
эндобдж
24 0 объект
> поток
2005-07-19T22: 10: 08-06: 002019-07-24T21: 05: 36-07: 002019-07-24T21: 05: 36-07: 00
5
%
14 0 объект
>
эндобдж
24 0 объект
> поток
2005-07-19T22: 10: 08-06: 002019-07-24T21: 05: 36-07: 002019-07-24T21: 05: 36-07: 00 4.2 Кварц PDFContext1FalseFalse750.000000824.000000 Очки
4.2 Кварц PDFContext1FalseFalse750.000000824.000000 Очки 0 0.0 750.0 824.0] / Тип / Страница >>
эндобдж
67 0 объект
> поток
HWKeG
_qg \ / 6eX !! B3H} 3Z]> ~ | _? |}}] 9OG =
z; K) ㍤;) m {o`? \ X «pF9 ~ _zŧ
, d | {10? + v} = β:> ~ w? 6 Нет
O S] Wb @ + (ID? Ǯ
8 었 ro [~ FE | up = $ ԂԂ փփ FH; SZ-yy & L ~ O ‘}’}, չ? UII_I_% s. / -oi ~ K {wiHG? ϴ 3iLg? ϴ 3_iJW ڿ ~ L_f _ * cU +++ Tr.Tϵ
x Dų; lśm1 = gɵ = (a-
Q @ 1 ~
М +
* $ @@ (
0 0.0 750.0 824.0] / Тип / Страница >>
эндобдж
67 0 объект
> поток
HWKeG
_qg \ / 6eX !! B3H} 3Z]> ~ | _? |}}] 9OG =
z; K) ㍤;) m {o`? \ X «pF9 ~ _zŧ
, d | {10? + v} = β:> ~ w? 6 Нет
O S] Wb @ + (ID? Ǯ
8 었 ro [~ FE | up = $ ԂԂ փփ FH; SZ-yy & L ~ O ‘}’}, չ? UII_I_% s. / -oi ~ K {wiHG? ϴ 3iLg? ϴ 3_iJW ڿ ~ L_f _ * cU +++ Tr.Tϵ
x Dų; lśm1 = gɵ = (a-
Q @ 1 ~
М +
* $ @@ ( y = x3 y = x4 y = x5
7.2 Графики полиномиальных функций y = x2
у = х4
у = х3
у = х5
1
• Если функция равна ___________, а ведущий коэффициент равен _____________, то график поднимается с обеих сторон.• Если функция ___________, а старший коэффициент _____________, то график падает с обеих сторон.
• Если функция ___________ и ведущий коэффициент _____________, то график падает слева и поднимается справа.
• Если функция ___________ и ведущий коэффициент _____________, то график падает справа и поднимается слева.
2
Относительные экстремумы
Многочлен n степени может иметь до ___________ относительных экстремумов.
 у = х5
у = х5 5x3 + 4x
у = х5 + 8x4 + 18x3 27x
3
У многочлена будет ноль, который является действительным числом в каждой точке, в которой он пересекает x
ось.Это означает, что мы можем построить график, найдя ______________ функции.
Мы можем сделать это ...
1) Факторинг (несколько способов)
2) Квадратичная формула
3) Синтетический дивизион
4
Пример 1: График f (x) = x5 5x3 + 4x
5
Множественность корней
Если (xr) - множитель, граф «плавно» проходит через корень.
Если n нечетно и больше 1, график будет пересекать ось x в точке x = r и выравниваться по мере прохождения через эту точку.
Если n четно, график будет касаться оси x в точке x = r и не будет пересекать ось x в этой точке.6
Пример 2 График f (x) = x5 8x4 + 18x3 27x
7
Пример 3: График f (x) = (x3) (x + 2) (x1). yintercept = 6
Пример 4: График f (x) = x4 x2
8
Пример 5: Определите уравнение для полинома для показанного графика.
9
При использовании графического калькулятора важно анализировать функцию. 1. Вам нужно следить за ошибками при вводе.
у = х5
у = х5 5x3 + 4x
у = х5 + 8x4 + 18x3 27x
3
У многочлена будет ноль, который является действительным числом в каждой точке, в которой он пересекает x
ось.Это означает, что мы можем построить график, найдя ______________ функции.
Мы можем сделать это ...
1) Факторинг (несколько способов)
2) Квадратичная формула
3) Синтетический дивизион
4
Пример 1: График f (x) = x5 5x3 + 4x
5
Множественность корней
Если (xr) - множитель, граф «плавно» проходит через корень.
Если n нечетно и больше 1, график будет пересекать ось x в точке x = r и выравниваться по мере прохождения через эту точку.
Если n четно, график будет касаться оси x в точке x = r и не будет пересекать ось x в этой точке.6
Пример 2 График f (x) = x5 8x4 + 18x3 27x
7
Пример 3: График f (x) = (x3) (x + 2) (x1). yintercept = 6
Пример 4: График f (x) = x4 x2
8
Пример 5: Определите уравнение для полинома для показанного графика.
9
При использовании графического калькулятора важно анализировать функцию. 1. Вам нужно следить за ошибками при вводе. Если вы знаете основную форму графика, это поможет вам заметить, если график неправильный. 2. Стандартный прямоугольник просмотра может не отображать четко поведение функции и, возможно, его необходимо изменить.Вы смотрите на 3 вещи:
1. Общая форма графика
2. Нули функции
3. Относительные экстремумы функции
10
Пример 6: Используя графический калькулятор, график f (x) = x4 + 3x3 4x. Определите каждый действительный ноль и количество относительных экстремумов. Затем выразите функцию как произведение линейных факторов. 11
Если вы знаете основную форму графика, это поможет вам заметить, если график неправильный. 2. Стандартный прямоугольник просмотра может не отображать четко поведение функции и, возможно, его необходимо изменить.Вы смотрите на 3 вещи:
1. Общая форма графика
2. Нули функции
3. Относительные экстремумы функции
10
Пример 6: Используя графический калькулятор, график f (x) = x4 + 3x3 4x. Определите каждый действительный ноль и количество относительных экстремумов. Затем выразите функцию как произведение линейных факторов. 11
РЕШЕНИЕ: Упростить: (x4 / x3) 3, (3x2y-2) 3 / (9xy3) 3 и (2x-3y4) 3 (x3 + y) 0 / (4xy-2) 3
 {6, 1, 3}, {a, e} 5. Найдите наименьший возможный набор (то есть набор с наименьшим количеством элементов), который содержит данный набор как подмножества. {Volkswagen, GM, Nissan}, {Porche, Volvo, Chrysler} 6.c n C8. Определите, не пересекается ли данная пара множеств. {2,3,4,5} {4,5,6,7} 9. Пусть A = {2,4,6,8} и B = {2,3,5,7,9}. Вычислить n (A). 10. В ходе опроса 122 потребителей, проведенного в торговом центре, 82 потребителя указали, что они покупают бренд A определенного продукта, 71 покупают бренд B и 46 покупают оба бренда. Сколько потребителей, участвовавших в опросе, покупают только бренд А? 11. В ходе опроса, проведенного среди 180 активных инвесторов, было обнаружено, что 100 используют дисконтных брокеров, 122 используют брокеров с полным спектром услуг и 54 используют как дисконтных брокеров, так и брокеров с полным спектром услуг.в) .16. Опрос 900 подписчиков на Los Angeles Times показал, что 700 человек подписываются на ежедневное утреннее издание и 400 подписчиков как на ежедневное, так и на воскресное издание.
{6, 1, 3}, {a, e} 5. Найдите наименьший возможный набор (то есть набор с наименьшим количеством элементов), который содержит данный набор как подмножества. {Volkswagen, GM, Nissan}, {Porche, Volvo, Chrysler} 6.c n C8. Определите, не пересекается ли данная пара множеств. {2,3,4,5} {4,5,6,7} 9. Пусть A = {2,4,6,8} и B = {2,3,5,7,9}. Вычислить n (A). 10. В ходе опроса 122 потребителей, проведенного в торговом центре, 82 потребителя указали, что они покупают бренд A определенного продукта, 71 покупают бренд B и 46 покупают оба бренда. Сколько потребителей, участвовавших в опросе, покупают только бренд А? 11. В ходе опроса, проведенного среди 180 активных инвесторов, было обнаружено, что 100 используют дисконтных брокеров, 122 используют брокеров с полным спектром услуг и 54 используют как дисконтных брокеров, так и брокеров с полным спектром услуг.в) .16. Опрос 900 подписчиков на Los Angeles Times показал, что 700 человек подписываются на ежедневное утреннее издание и 400 подписчиков как на ежедневное, так и на воскресное издание. Сколько подписчиков на воскресное издание? 17. Три различных типа месячных проездных билетов предлагаются местными транспортными властями города для трех разных групп пассажиров. Сколько разных видов пассов должно быть возможно? 18. В карточной игре комбинация из двух карт, состоящая из туза и либо лицевой карты бубна, либо 10, называется «выигрышем».Если используется стандартная колода из 52 карт, определите, сколько выигрышных рук может быть сдано («лицевая карта» — это валет, дама или король). 19. Среди телезрителей кабельного телевидения будет проведен опрос. Будут заданы четыре вопроса с несколькими вариантами ответов, каждый с тремя вариантами ответа. Сколько разных способов может заполнить опрос зритель, если на каждый вопрос дан ровно один ответ? Идентификационный номер гарантии для определенного продукта состоит из буквы алфавита, за которой следует четырехзначное число.Сколько существует возможных идентификационных номеров, если первая цифра четырехзначного числа должна быть ненулевой? 21.
Сколько подписчиков на воскресное издание? 17. Три различных типа месячных проездных билетов предлагаются местными транспортными властями города для трех разных групп пассажиров. Сколько разных видов пассов должно быть возможно? 18. В карточной игре комбинация из двух карт, состоящая из туза и либо лицевой карты бубна, либо 10, называется «выигрышем».Если используется стандартная колода из 52 карт, определите, сколько выигрышных рук может быть сдано («лицевая карта» — это валет, дама или король). 19. Среди телезрителей кабельного телевидения будет проведен опрос. Будут заданы четыре вопроса с несколькими вариантами ответов, каждый с тремя вариантами ответа. Сколько разных способов может заполнить опрос зритель, если на каждый вопрос дан ровно один ответ? Идентификационный номер гарантии для определенного продукта состоит из буквы алфавита, за которой следует четырехзначное число.Сколько существует возможных идентификационных номеров, если первая цифра четырехзначного числа должна быть ненулевой? 21. Экзамен состоит из шести вопросов типа «правда или ложь». Предполагая, что на каждый вопрос дан ответ, сколькими способами студент может сдать экзамен? Какими способами можно сдать экзамен, если за каждый неправильный ответ налагается штраф, чтобы учащийся мог оставить некоторые вопросы без ответа? 22. Номер социального страхования состоит из семи цифр. Сколько номеров социального страхования возможно? 23.В опросе, проведенном профсоюзом, членов попросили оценить важность следующих вопросов: (1) гарантия занятости, (2) увеличение дополнительных льгот и (3) улучшение условий труда. На каждый вопрос было разрешено шесть разных ответов. Сколько было возможных ответов на этот опрос среди заполненных опросов? 24. BMW 335i Coupe 2010 предлагается с выбором из 9 цветов кузова (7 цветов «металлик» и 2 стандартных), 5 цветов интерьера и 4 вариантов отделки салона. Сколько комбинаций цвета и отделки доступно для данной модели? 25.Сколько международных номеров прямого набора возможно, если каждый номер состоит из четырехзначного кода зоны (первая цифра должна быть отличной от нуля) и восьмизначного телефонного номера (первая цифра должна быть отличной от нуля)?
Экзамен состоит из шести вопросов типа «правда или ложь». Предполагая, что на каждый вопрос дан ответ, сколькими способами студент может сдать экзамен? Какими способами можно сдать экзамен, если за каждый неправильный ответ налагается штраф, чтобы учащийся мог оставить некоторые вопросы без ответа? 22. Номер социального страхования состоит из семи цифр. Сколько номеров социального страхования возможно? 23.В опросе, проведенном профсоюзом, членов попросили оценить важность следующих вопросов: (1) гарантия занятости, (2) увеличение дополнительных льгот и (3) улучшение условий труда. На каждый вопрос было разрешено шесть разных ответов. Сколько было возможных ответов на этот опрос среди заполненных опросов? 24. BMW 335i Coupe 2010 предлагается с выбором из 9 цветов кузова (7 цветов «металлик» и 2 стандартных), 5 цветов интерьера и 4 вариантов отделки салона. Сколько комбинаций цвета и отделки доступно для данной модели? 25.Сколько международных номеров прямого набора возможно, если каждый номер состоит из четырехзначного кода зоны (первая цифра должна быть отличной от нуля) и восьмизначного телефонного номера (первая цифра должна быть отличной от нуля)? Определить степень и старший коэффициент полиномиальных функций
 Хотя порядок членов в полиномиальной функции не важен для выполнения операций, мы обычно располагаем члены в порядке убывания степени или в общем виде. степени полинома — это наивысшая степень переменной, которая встречается в полиноме; это мощность первой переменной, если функция имеет общий вид. Главный член — это член, содержащий наивысшую степень переменной или член с наивысшей степенью. Старший коэффициент — это старший член.
Хотя порядок членов в полиномиальной функции не важен для выполнения операций, мы обычно располагаем члены в порядке убывания степени или в общем виде. степени полинома — это наивысшая степень переменной, которая встречается в полиноме; это мощность первой переменной, если функция имеет общий вид. Главный член — это член, содержащий наивысшую степень переменной или член с наивысшей степенью. Старший коэффициент — это старший член. Общее примечание: терминология полиномиальных функций
Как сделать: для заданной полиномиальной функции определите степень и старший коэффициент.
, чтобы определить градусную функцию.
, чтобы найти главный член.
Пример 5: Определение степени и ведущего коэффициента полиномиальной функции
Определение конечного поведения полиномиальных функций
Пример 6: Определение конечного поведения и степени полиномиальной функции

Решение
 {4} \\ [/ латекс]; следовательно, степень полинома равна 4. Степень четная (4), а старший коэффициент отрицательный (–3), поэтому конечное поведение равно
{4} \\ [/ латекс]; следовательно, степень полинома равна 4. Степень четная (4), а старший коэффициент отрицательный (–3), поэтому конечное поведение равно Попробуй 5
Определение локального поведения полиномиальных функций

Общее примечание: точки пересечения и поворотные точки полиномиальных функций
 Перехваты x — это точки, в которых выходное значение равно нулю.
Перехваты x — это точки, в которых выходное значение равно нулю. Как: по заданной полиномиальной функции определить точки пересечения.
Пример 8: Определение точек пересечения полиномиальной функции
Решение

Сравнение гладких и непрерывных графиков
 Полиномиальная функция n -й степени является произведением n факторов, поэтому она будет иметь не более n корней или нулей, или x -перехватывание. График полиномиальной функции степени n должен иметь не более n — 1 поворотных точек.Это означает, что у графика самое большее на одну точку поворота меньше, чем степень многочлена, или на одну меньше, чем количество факторов.
Полиномиальная функция n -й степени является произведением n факторов, поэтому она будет иметь не более n корней или нулей, или x -перехватывание. График полиномиальной функции степени n должен иметь не более n — 1 поворотных точек.Это означает, что у графика самое большее на одну точку поворота меньше, чем степень многочлена, или на одну меньше, чем количество факторов. Общее примечание: точки пересечения и поворотные точки многочленов
 {3} \\ [/ латекс]
{3} \\ [/ латекс] Пример 11: Выводы о полиномиальной функции из графика
Решение
Попробуй 8
Пример 12: Выводы о полиномиальной функции из множителей

Решение

Попробуй 9
Лос-внедорожник более
 de frenos de alto rendimiento, Alerones posteriores y las ya tradicionales cuatro salidas de escape. Un inédito paquete opcional M Carbon , включая декоративные элементы фибра-де-карбоно, en las tomas de aire delanteras, las frontales del paragolseas, el diffusor de los retrovisores.En el caso de los Competition, también alalerón trasero.
de frenos de alto rendimiento, Alerones posteriores y las ya tradicionales cuatro salidas de escape. Un inédito paquete opcional M Carbon , включая декоративные элементы фибра-де-карбоно, en las tomas de aire delanteras, las frontales del paragolseas, el diffusor de los retrovisores.En el caso de los Competition, también alalerón trasero. BMW asegura que «Гарантия максимальной скорости передачи и распределения по мощности двигателя для автомобилей с экстремальными динамическими характеристиками» . La guinda al pastel tecnológico la pone un Diferencial Activo M en el eje trasero, que reduce las pérdidas de tracción al minimo y que permite que los los BMW X3 M y BMW X4 M aceleren de 0 a 100 km / h en 4,2 segundos , 4,1 en el caso de los Competition.Это необходимо для потребления средней плотности 10,5 литров / 100 километров с выбросами 239 г / км.
BMW asegura que «Гарантия максимальной скорости передачи и распределения по мощности двигателя для автомобилей с экстремальными динамическими характеристиками» . La guinda al pastel tecnológico la pone un Diferencial Activo M en el eje trasero, que reduce las pérdidas de tracción al minimo y que permite que los los BMW X3 M y BMW X4 M aceleren de 0 a 100 km / h en 4,2 segundos , 4,1 en el caso de los Competition.Это необходимо для потребления средней плотности 10,5 литров / 100 километров с выбросами 239 г / км. Veremos que nos ofrece BMW.
Veremos que nos ofrece BMW.
Photoshop CS4, CorelDRAW X4, Illustrator CS4. Трюки и эффекты. Глава 7. Трюки и эффекты в Illustrator CS4
«Компьютерная графика: Photoshop CS4, CorelDRAW X4, Illustrator CS4. Трюки и эффекты»7.1. Эффекты объема
 Чтобы было легче это сделать, включите отображение сетки: View Show Grid (Вид Показать сетку). Затем запустите инструмент Pen (Перо) и повторите контур, показанный на рис. 001
Чтобы было легче это сделать, включите отображение сетки: View Show Grid (Вид Показать сетку). Затем запустите инструмент Pen (Перо) и повторите контур, показанный на рис. 001
 006).
006). 011.
011. 014.
014. Затем этим же инструментом нарисуйте белую полосу, соответствующую по габаритам будущему кресту. Дублируйте ее, поверните на 90°и поместите все полученные элементы по центру относительно друг друга (рис. 017).
Затем этим же инструментом нарисуйте белую полосу, соответствующую по габаритам будущему кресту. Дублируйте ее, поверните на 90°и поместите все полученные элементы по центру относительно друг друга (рис. 017). 019.
019. 024).
024).7.2. Текстовые эффекты
 Для большей контрастности добавим тень: Effect Stylize Drop Shadow (Эффект Стилизация Отбросить тень) — с настройками, показанными на рис. 028.
Для большей контрастности добавим тень: Effect Stylize Drop Shadow (Эффект Стилизация Отбросить тень) — с настройками, показанными на рис. 028. Затем применим к обводке эффект Roughen (Огрубление): EffectDistort & Transform Roughen (Эффект Искажение и трансформирование Огрубление). Авторские настройки показаны на рис. 032.
Затем применим к обводке эффект Roughen (Огрубление): EffectDistort & Transform Roughen (Эффект Искажение и трансформирование Огрубление). Авторские настройки показаны на рис. 032.
 Цвет при этом также нужно выбрать фиолетовый, остальные настройки показаны на рис. 039.
Цвет при этом также нужно выбрать фиолетовый, остальные настройки показаны на рис. 039.7.3. Flash в Illustrator Анимированный баннер с деформацией
 Должно получиться примерно следующее (рис. 044).
Должно получиться примерно следующее (рис. 044). Это можно выполнить с помощью палитры Align (Выравнивание), нажав кнопки
Это можно выполнить с помощью палитры Align (Выравнивание), нажав кнопки


 Затем вызовите окно эффекта Effect3DRotate (Эффект3DВращение) (рис. 050).
Затем вызовите окно эффекта Effect3DRotate (Эффект3DВращение) (рис. 050).


What is the graph of x 4? – Reviews Wiki
 y=4 — прямая линия, перпендикулярная оси y в точке (0,4) , что означает, что диапазон представляет собой набор из одного значения {4} .
y=4 — прямая линия, перпендикулярная оси y в точке (0,4) , что означает, что диапазон представляет собой набор из одного значения {4} .Как построить график наклона 4?
 В общем уравнении прямой линии y = mx + c градиент обозначается буквой m. … При расчете обменного курса двух валют мы можем рассчитать градиент линии, чтобы найти скорость изменения между ними.
В общем уравнении прямой линии y = mx + c градиент обозначается буквой m. … При расчете обменного курса двух валют мы можем рассчитать градиент линии, чтобы найти скорость изменения между ними.Каково значение X?

х 4 это вертикальная или горизонтальная линия?

Какое отношение имеет нулевой наклон?
Как найти градиент?
 Разница в высоте (координаты y) ÷ Разница в ширине (координаты x). Если ответ отрицательный, то линия направлена вниз.
Разница в высоте (координаты y) ÷ Разница в ширине (координаты x). Если ответ отрицательный, то линия направлена вниз. Gel-Pak | Разработка уникальных материалов для работы с устройствами Таблица удерживающих этикеток Gel-Pak
| Разработка уникальных материалов для обработки устройств | Хейворд, Калифорния Gel-Pak Уровень липкости (удержания) Таблица 
Этикетка Уровень хранения Описание Продукты н.э. БД компакт-диск ВР ПФ ВФ ДГЛ ХТ Гель со сверхнизкой липкостью XL Гель с низкой липкостью Х0 Гель с низкой липкостью Х4 Гель средней фиксации Х5 Гель средней фиксации Х6 Гель с высокой липкостью Х8 Гель с высокой липкостью ER0 Антистатический гель с низкой липкостью ER4 Гель для защиты от электростатического разряда средней липкости ER6 Гель для защиты от электростатического разряда средней липкости ФП64 Vertec с низкой липкостью ФМ71 Средняя липкость Vertec ФЭ70 Средняя липкость ESD Vertec EH02 Низкая липкость ESD Vertec EH07 Высокая липкость ESD Vertec ФК79 Высокая липкость Vertec EH06 Электростатический разрядник Vertec 
 Чтобы узнать больше, посетите нашу Политику конфиденциальности. Используя наш сайт без отключения файлов cookie, вы даете согласие на их использование. Настройки файлов cookieRejectACCEPT
Чтобы узнать больше, посетите нашу Политику конфиденциальности. Используя наш сайт без отключения файлов cookie, вы даете согласие на их использование. Настройки файлов cookieRejectACCEPT X4: Foundations — Steam Charts
игра
24-часовой пик
рекордный пик Месяц Ср. Игроки Усиление % Коэффициент усиления Пик игроков Последние 30 дней 1476.46 +18,2 +1,24% 2502 август 2022 г. 1458.30 -380,56 -20,70% 2502 июль 2022 г. 1838,86 288,36 +18,60% 3062 июнь 2022 г. 1550.50 -676,66 -30,38% 2780 май 2022 г. 
2227.16 -1047.48 -31,99% 4280 апрель 2022 г. 3274,64 177,94 +5,75% 6181 март 2022 г. 3096,71 1085.48 +53,97% 7525 февраль 2022 г. 2011.23 -208,56 -9,40% 3632 январь 2022 г. 2219,78 305,71 +15,97% 3725 декабрь 2021 г. 1914.07 535.03 +38,80% 3154 ноябрь 2021 г. 1379.04 48,84 +3,67% 2977 октябрь 2021 г. 1330.19 -96.03 -6,73% 2250 сентябрь 2021 г. 1426.22 157,86 +12,45% 2569 август 2021 г. 1268,37 -91,83 -6,75% 2529 июль 2021 г. 
1360.20 -136,09 -9,10% 2382 июнь 2021 г. 1496.29 -998,99 -40,04% 2739 май 2021 г. 2495.28 -827,84 -24,91% 4713 апрель 2021 г. 3323.12 145,99 +4,59% 6205 март 2021 г. 3177.13 1911.62 +151,06% 9136 февраль 2021 г. 1265,51 -178,71 -12,37% 2095 январь 2021 г. 1444.22 206.05 +16,64% 2378 декабрь 2020 г. 1238.17 117,36 +10,47% 2082 ноябрь 2020 г. 1120.81 146,92 +15,09% 2015 Октябрь 2020 г. 973,89 -141.  01
01 -12,65% 1640 сентябрь 2020 г. 1114.90 155,50 +16,21% 2039 август 2020 г. 959,40 -163.04 -14,53% 2181 июль 2020 г. 1122.44 -240,57 -17,65% 2035 июнь 2020 г. 1363.01 -653,97 -32,42% 2590 май 2020 г. 2016.98 -1306.33 -39,31% 4145 апрель 2020 г. 3323,31 2685,72 +421,23% 5882 март 2020 г. 637,59 14.03 +2,25% 3257 февраль 2020 г. 623,56 -134,09 -17,70% 1196 январь 2020 г. 757,65 -5,02 -0,66% 1431 декабрь 2019 г. 
762,67 95,20 +14,26% 1408 ноябрь 2019 г. 667,47 150,45 +29,10% 1290 Октябрь 2019 517.02 45,16 +9,57% 1066 сентябрь 2019 г. 471,87 6,54 +1,41% 844 август 2019 г. 465,33 -28,32 -5,74% 838 июль 2019 г. 493,65 -41.18 -7,70% 906 июнь 2019 г. 534,82 -8,35 -1,54% 929 май 2019 г. 543,17 -156,82 -22,40% 988 апрель 2019 г. 699,99 -428,68 -37,98% 1350 март 2019 г. 1128,67 91.13 +8,78% 2239 февраль 2019 1037,54 -983,17 -48,65% 2059 январь 2019 г. 
2020.72 -4226.33 -67,65% 5021 декабрь 2018 г. 6247.04 6246.48 +1110485,66% 15074 март 2018 г. 0,56 -0,18 -23,90% 5 февраль 2018 0,74 0,20 +36,48% 5 январь 2018 г. 0,54 0,17 +46,60% 5 декабрь 2017 г. 0,37 -0,01 -1,48% 5 ноябрь 2017 г. 0,38 0,07 +24,55% 4 Октябрь 2017 г. 0,30 -0,52 -63,26% 4 сентябрь 2017 г. 0,82 — — 6
Твиты от @steamcharts
Все данные основаны на Steam. Никак не связан с Valve. Все товарные знаки являются собственностью соответствующих владельцев в США и других странах. Наша цель — предоставить уникальное представление об игровых тенденциях. © steamcharts.com
Все товарные знаки являются собственностью соответствующих владельцев в США и других странах. Наша цель — предоставить уникальное представление об игровых тенденциях. © steamcharts.com
Велообувь для гравия — Terra Powerstrap X4
Вероятно, в вашем браузере отключен JavaScript. Для наилучшего взаимодействия с нашим сайтом обязательно включите Javascript в своем браузере.
Бесплатная доставка свыше 100$ | Матч в конце лета: скидка 20% на ленту для седла и руля
Читать отзывы
Велотуфли для гравия с нашей системой застежек Powerstrap Velcro для обволакивающей посадки и подошвой X4, обеспечивающей заданную жесткость и резиновый протектор для смешанных поверхностей.
В наличии
| ДЛИНА (мм) | 230 | 237 | 240 | 243,5 | 247 | 250 | 253,5 | 257 | 260 | 263,5 | 267 | 270 | 273,5 | 277 | 280 | 283,5 | 287 | 290 | 293,5 | 297 | 300 | 303,5 | 310 |
| США | 4 ¼ | 5 ¼ | 5 ½ | 6 | 6 ¼ | 6 ¾ | 7 | 7 ½ | 8 | 8 ¼ | 8 ¾ | 9 | 9 ½ | 9 ¾ | 10 ¼ | 10 ¾ | 11 | 11 ½ | 11 ¾ | 12 ¼ | 12 ½ | 13 | 13 ¾ |
| ЕС | 36 | 37 | 37,5 | 38 | 38,5 | 39 | 39,5 | 40 | 40,5 | 41 | 41,5 | 42 | 42,5 | 43 | 43,5 | 44 | 44,5 | 45 | 45,5 | 46 | 46,5 | 47 | 48 |
| Великобритания | 3 ¼ | 4 ¼ | 4 ½ | 5 | 5 ¼ | 5 ¾ | 6 | 6 ½ | 7 | 7 ¼ | 7 ¾ | 8 | 8 ½ | 8 ¾ | 9 ¼ | 9 ¾ | 10 | 10 ½ | 10 ¾ | 11 ¼ | 11 ½ | 12 | 12 ¾ |
РАСПЕЧАТАТЬ РУКОВОДСТВО ПО РАЗМЕРАМ ОБУВИ
| 230 | 4 ¼ | 36 | 3 ¼ |
| 237 | 5 ¼ | 37 | 4 ¼ |
| 240 | 5 ½ | 37,5 | 4 ½ |
| 243,5 | 6 | 38 | 5 |
| 247 | 6 ¼ | 38,5 | 5 ¼ |
| 250 | 6 ¾ | 39 | 5 ¾ |
| 253,5 | 7 | 39,5 | 6 |
| 257 | 7 ½ | 40 | 6 ½ |
| 260 | 8 | 40,5 | 7 |
| 263,5 | 8 ¼ | 41 | 7 ¼ |
| 267 | 8 ¾ | 41,5 | 7 ¾ |
| 270 | 9 | 42 | 8 |
| 273,5 | 9 ½ | 42,5 | 8 ½ |
| 277 | 9 ¾ | 43 | 8 ¾ |
| 280 | 10 ¼ | 43,5 | 9 ¼ |
| 283,5 | 10 ¾ | 44 | 9 ¾ |
| 287 | 11 | 44,5 | 10 |
| 290 | 11 ½ | 45 | 10 ½ |
| 293,5 | 11 ¾ | 45,5 | 10 ¾ |
| 297 | 12 ¼ | 46 | 11 ¼ |
| 300 | 12 ½ | 46,5 | 11 ½ |
| 303,5 | 13 | 47 | 12 |
| 310 | 13 ¾ | 48 | 12 ¾ |
Terra Powerstrap X4
От
159. 99$
99$
Читать отзывы
Перейти в конец галереи изображений
Перейти к началу галереи изображений
ОБРАТНАЯ СВЯЗЬ
10.02.2022
Обувь качественная и удобная, немного большемерит
Проверенный покупатель | Код заказа: 109574913
03.
 02.2022
02.2022Отлично подошли на узкую ногу, как у меня.
Проверенный покупатель | Код заказа: 108530729
21.01.2022
Оттимо rapporto qualità prezzo, il prodotto rispecchia le caratteristiche укажите в описании
Проверенный покупатель | Код заказа: 107741090
15.01.2022
Моя вторая пара обуви Fizik, и они ФАНТАСТИЧЕСКИЕ! Подходит к моей ноге как перчатка. 10/10
Проверенный покупатель | Код заказа: 107273384
06.01.2022
Наконец-то действительно удобная обувь для гравия!
Проверенный покупатель | Код заказа: 103332567
20.11.2021
У меня есть туфли уже полгода, и они потрясающие.
 Тем более, что у меня ступня более широкая, а обувь идеально ей подходит. У меня 40-й размер (моя повседневная невелосипедная обувь 39-го).
Тем более, что у меня ступня более широкая, а обувь идеально ей подходит. У меня 40-й размер (моя повседневная невелосипедная обувь 39-го).Проверенный покупатель | Код заказа : 95624496
18.11.2021
Так удобно! Определенно хочу получить еще и черный
Проверенный покупатель | Код заказа: 102704838
18.11.2021
Ремни потрясающие, но форма подошвы и общий объем не соответствуют моим ногам. Возможно, мне нужно было больше сосредоточиться на более широкой посадке бренда, чтобы сделать лучший выбор.
Проверенный покупатель | Код заказа: 101986887
12.11.2021
В них удобно ходить без велосипеда, хороший вместительный носок и в целом очень красивая обувь.

Проверенный покупатель | Код заказа: 101681074
01.11.2021
ВНЕДОРОЖНИК — Разработан и спроектирован для работы в условиях бездорожья, от одноколейных до гравийных дорог и всего, что между ними
Сравнение продуктов — фургон Wonderfold
Общие характеристики Общие характеристики Общие характеристики Общие характеристики Вместимость сиденья Съемные высокие сиденья Съемная ткань Съемная корзина Регулируемый навес Руль из веганской кожи Вместимость сиденья Съемные высокие сиденья Съемная ткань Съемная корзина Регулируемый навес Руль из веганской кожи Вместимость сиденья Съемные высокие сиденья Съемная ткань Съемная корзина Регулируемый навес Руль из веганской кожи Функциональные особенности Функциональные особенности Функциональные особенности Функциональные особенности Тяни и толкай Пружинная рукоятка Регулируемая ручка для толкания Установленные подшипники Установленная подвеска Сиденье с пространством для ног Дверца на молнии Вентиляционная боковая сетка Регулируемые штанги навеса Сиденья с откидной спинкой Боковые сетчатые панели на молнии Вездеходные колеса XL Дополнительное хранилище Магнитные ремни безопасности Одноместный водитель Манеж-трансформер Тяни и толкай Пружинная рукоятка Регулируемая ручка для толкания Установленные подшипники Установленная подвеска Сиденье с пространством для ног Дверца на молнии Боковая сетка для вентиляции Регулируемые штанги навеса Сиденья с откидной спинкой Боковые сетчатые панели на молнии Вездеходные колеса XL Дополнительное хранилище Магнитные ремни безопасности Опция для одного водителя Манеж-трансформер Тяни и толкай Пружинная рукоятка Регулируемая ручка для толкания Установленные подшипники Установленная подвеска Сиденье с пространством для ног Дверца на молнии Вентиляционная боковая сетка Регулируемые штанги навеса Сиденья с откидной спинкой Боковые сетчатые панели на молнии Вездеходные колеса XL Дополнительное хранилище Магнитные ремни безопасности Одноместный водитель Манеж-трансформер Средства безопасности Средства безопасности Средства безопасности Средства безопасности Замок безопасности в сложенном состоянии 5-точечный ремень Ножной тормоз
Замок безопасности в сложенном состоянии 5-точечный ремень Ножной тормоз Замок безопасности в сложенном состоянии 5-точечный ремень Ножной тормоз Технические характеристики Технические характеристики Технические характеристики Характеристики Материал шины с протектором: Полиуретан Грузоподъемность: 300 фунтов Грузоподъемность сиденья/скамьи: 99 фунтов Размер переднего колеса: 10 дюймов Размер заднего колеса: 12 дюймов Вес продукта: 58 фунтов Материал шины с протектором: Полиуретан Грузоподъемность: 300 фунтов Грузоподъемность сиденья/скамьи: 99 фунтов Размер переднего колеса: 10 дюймов Размер заднего колеса: 12 дюймов Вес продукта: 58 фунтов Материал протектора шины: ПУ Грузоподъемность: 300 фунтов Грузоподъемность сиденья/скамьи: 99 фунтов Размер переднего колеса: 10 дюймов Размер заднего колеса: 12 дюймов Вес продукта: 58 фунтов Таблица размеров | The Original Muck Boot Company™
Таблица размеров для мужчин
США Великобритания евро МЕТРИЧЕСКАЯ 3 2 34 210 3 1/2 2,5 35 215 4 3 35,5 220 4 1/2 3,5 36 225 5 4 37 230 5 1/2 4,5 37,5 235 6 5 38 240 6 1/2 5,5 39 245 7 6 39,5 250 7 1/2 6,5 40 255 8 7 41 260 8 1/2 7,5 41,5 265 9 8 42 270 9 1/2 8,5 42,5 275 10 9 43 280 10 1/2 9,5 44 285 11 10 44,5 290 11 1/2 10,5 45 295 12 11 46 300 12 1/2 11,5 46,5 305 13 12 47 310 14 13 49 320 15 14 50 330 16 15 51 340 17 16 52 350 Таблица размеров для женщин
США Великобритания евро МЕТРИЧЕСКАЯ ДЮЙМОВ 4 2 35 210 8,27 4 1/2 2,5 35,5 215 8,46 5 3 36 220 8,66 5 1/2 3,5 36,5 225 8,86 6 4 37 230 9.  06
066 1/2 4,5 38 235 9,25 7 5 38,5 240 9,45 7 1/2 5,5 39 245 9,65 8 6 40 250 9,84 8 1/2 6,5 40,5 255 10.04 9 7 41 260 10,24 9 1/2 7,5 41,5 265 10,43 10 8 42 270 10,63 10 1/2 8,5 43 275 10,83 11 9 43,5 280 11.02 11 1/2 9,5 44 285 11.  22
2212 10 45 290 11.42 12 1/2 10,5 45,5 295 11,61 13 11 46 300 11,81 Таблица размеров для детей
Размер возраст США в см малыши
1-5 летРебенок 4 4,6 11,7 Ребенок 5 5 12,6 Ребенок 6 5,3 13,4 Ребенок 7 5,6 14,3 Ребенок 8 6 15,1 Ребенок 9 6,3 16 Ребенок 10 6,6 16,8 Ребенок 11 7 17,7 Ребенок 12 7,3 18,5 Ребенок 13 7,6 19,4 ДЕТСКИЙ
6+ летМолодежь 1 8 20,2 Молодежь 2 8,3 21 Молодежь 3 8,6 21,9 Молодежь5 9 22,7 Молодежь 5 9,3 23,6 Молодежь 6 9,6 24,4 Молодежь 7 10 25,3 Таблица преобразования размера обуви в размер носков
Размер носка Fit Youth
Размер обувиFit Ladies
Размер обувиПодходит для мужчин
Размер обувиПодходит для Великобритании
Размер обувиПодходит для ЕС
Размер обувиИС 4-7 Малыш г.  м.
м.7-10 Малышей ЮЛ 10-2 3-5 10-3 28-31 YX 1-5 4-7 3-5 1/2 32-38 СМ/МС 1-5 4-7 3-5 1/2 32-38 МД 6-10 5-9 1/2 5-8 37-42 ЛГ 10-13 9-12 8-11 1/2 43-47 XL 12-15 12-14 47-50 2 л 15-17 15+ 51+ Мы рекомендуем носить защитную обувь на размер больше.
Для наиболее точного определения размера Подошва обуви/сапога должна быть измерена.Размер мужской обуви Fit Подходит для женской обуви, размер Размер стельки XS 3-5,5 5-6,5 10,3″x4″ С 6-7,5 7-8,5 11 дюймов x 4,3 дюйма М 8-8,5 9-10,5 11,8 x 4,4 дюйма Л 9-10,5 11-12,5 12,4″x4,5″ XL 11,5-13 — 12,8 x 4,6 дюйма XXL 13,5-15 — 13,5 x 4,8 дюйма XXXL 15,5-17 — 14 x 5 дюймов Мы рекомендуем носить защитную обувь на размер больше.

Для наиболее точного определения размера Подошва обуви/сапога должна быть измерена.Подходящая мужская обувь, размер Подходит для женской обуви, размер Размер стельки XS 3-4,5 4-5,5 10,3″x4″ С 5-6,5 6-8 11 дюймов x 4,3 дюйма М 7-8,5 8,5-10 11,8 x 4,4 дюйма Л 9-10,5 10,5-12 12,4 x 4,5 дюйма XL 11-12,5 — 12,8 x 4,6 дюйма XXL 13-14,5 — 13,5 x 4,8 дюйма XXXL 15-16,5 — 14 x 5 дюймов БАТКАДДИ — Иди как профессионал!
ОСТАВАЙТЕСЬ В ФОРМЕ – ЭКОНОМЬТЕ ДЕНЬГИ – СНИЖАЙТЕ ВАШ ИНФОРМАЦИЯ
Иди как профессионал!
купить новые бэткадди магазин демо и трейд-ин
Обменяйте свою старую тележку на новый Batcaddy уже сегодня!
КЭШ5КАДДИС!
Принимаем тележки без привода и с электроприводом всех марок!
Детали обмена
В наличии
Быстрый просмотр
BATCADDY X8R
от 1099,95 долларов США
Титан Серебро Призрачный черный Арктический белый
В наличии
Быстрый просмотр
BATCADDY X4R
от $899,95
Титан Серебро Призрачный черный Арктический белый
В наличии
Быстрый просмотр
BATCADDY X3R
от $699,95
Титан Серебро Призрачный черный Арктический белый
БАТКАДДИ — это революция! Экономьте деньги, чувствуйте себя лучше, играйте лучше! Больше людей играет в гольф, и больше игроков в гольф ходят пешком, чем когда-либо прежде.
 BATCADDY лидирует в индустрии электрических толкателей в США с 2004 года и по сей день остается лидером в этой области. 6 моделей и до 3 вариантов аккумуляторов для каждой — Batcaddy для каждого игрока в гольф и бюджета. Присоединяйтесь к семье BATCADDY и узнайте, каково это Walk Like a Pro сегодня!
BATCADDY лидирует в индустрии электрических толкателей в США с 2004 года и по сей день остается лидером в этой области. 6 моделей и до 3 вариантов аккумуляторов для каждой — Batcaddy для каждого игрока в гольф и бюджета. Присоединяйтесь к семье BATCADDY и узнайте, каково это Walk Like a Pro сегодня!Магазин Batcaddys
Кэдди с дистанционным управлением Неудаленные Кэдди Демонстрации и подержанные Аксессуары для бэткадди Батареи Пользовательские цвета!Сердцем каждой тележки для гольфа с электроприводом является аккумулятор. BATCADDY предлагает самую разнообразную линейку аккумуляторов в отрасли. И мы являемся единственным брендом, который позволяет вам комбинировать каждую из наших батарей с любой из наших моделей Batcaddy. Нажмите здесь, чтобы просмотреть нашу сравнительную таблицу аккумуляторов и определить, какой аккумулятор подходит именно вам!
Сравнить батареи
youtube.com/embed/6T8jm9ag5Es?rel=0&showinfo=0&vq=720″ frameborder=»0″ allowfullscreen=»»>★ ★ ★ ★ ★
Все еще люблю свой Bat-Caddy и не вижу снижения заряда батареи! Я почти обратил друга, чтобы он присоединился к семье Bat-Caddy… В прошлое воскресенье он попросил поменяться со мной, когда мы поднимались на холм. Я толкнул его Sun Mountain, а он последовал за моей Bat-Caddy, на вершине холма он был серьезно настроен получить ее … Еще раз спасибо за отличный продукт!
Деннис С.Cisco, TX
★★★★★
Мне очень нравится мой Bat Caddy X4R! Очень легко собирается, легкий и простой в использовании. Очень отзывчивая, обычная рабочая лошадка, с обтекаемой внешностью! Все, кто видел, были впечатлены! Зачем кому-то еще какая-то электрическая тележка для сумок? Возможно, скоро закажем еще один для жены.
Рип Р.Йорба Линда, Калифорния
★★★★★
Я пользуюсь своей тележкой X4R уже пять месяцев, и она мне очень нравится.
Джим Г. Я изучил множество электрических тележек, прежде чем принять решение о покупке X4R. На рынке есть много электрических тележек, и большинство из них очень дорогие, очень уродливые или и то, и другое. X4R имеет такой простой и элегантный дизайн и всегда привлекает внимание. Я ценю его легкий вес, отличный дизайн и конструкцию по разумной цене. Ваше обслуживание клиентов было таким же образцовым, как дизайн и стоимость этой тележки.
Я изучил множество электрических тележек, прежде чем принять решение о покупке X4R. На рынке есть много электрических тележек, и большинство из них очень дорогие, очень уродливые или и то, и другое. X4R имеет такой простой и элегантный дизайн и всегда привлекает внимание. Я ценю его легкий вес, отличный дизайн и конструкцию по разумной цене. Ваше обслуживание клиентов было таким же образцовым, как дизайн и стоимость этой тележки.Сан-Матео, Калифорния
★★★★★
Мой новый Bat-Caddy так же хорош, как и в других отзывах. Теперь я просто гуляю в парке, когда играю в гольф. Раньше мне нравилось ходить с тележкой или нести сумку. Но вы знаете, как он идет по холмистой трассе к середине задней девятки. Я устал, как и все. Теперь это другая история. Я говорю своей жене после каждого раунда, как я ценю ее подарок ко Дню отца, который она мне подарила месяцем ранее в мае.
Терри Х.Бельфонтен, Огайо
★★★★★
С нетерпением жду большого будущего гольфа с моим Bat-Caddy.
Том В. К вашему сведению, три других члена нашего клуба приобрели Bat-Caddy X3R в прошлом месяце. Один джентльмен провел все исследования и обнаружил, что Bat-Caddy имеет наилучшее соотношение цены и качества (качество, функциональность и стоимость). Около 65% наших членов посещают наши два частных курса, и я ожидаю, что после того, как они увидят, как ходить станет немного легче. с Bat-Caddy больше людей могут выбрать тележки с дистанционным управлением.
К вашему сведению, три других члена нашего клуба приобрели Bat-Caddy X3R в прошлом месяце. Один джентльмен провел все исследования и обнаружил, что Bat-Caddy имеет наилучшее соотношение цены и качества (качество, функциональность и стоимость). Около 65% наших членов посещают наши два частных курса, и я ожидаю, что после того, как они увидят, как ходить станет немного легче. с Bat-Caddy больше людей могут выбрать тележки с дистанционным управлением.Уоллес, Северная Каролина
★★★★★
Я бы даже не стал рассматривать Kangaroo, Bag Boy или PowaKaddy из-за стиля. Я думаю, что Bat-Caddy очень хорошо сочетает в себе производительность/цену и стиль. Что это позволяет мне делать, так это ходить по полю для гольфа прямо, а не наклоняться вперед, когда я толкаю свою Sun Mountain.
Гордон С.Сан-Рафаэль, Калифорния
★★★★★
Мне нравится мой новый Bat-Caddy X3R! Я сыграл 2 раунда, и это фантастика.
Том З. Он очень легко настраивается прямо из коробки. Я надеялся протестировать его в местном парке, но в итоге я получил раннее время игры на следующий день после доставки, и я могу честно сказать, что им очень легко пользоваться. Я люблю ходить по газонам и не забирать свою старую тележку. Это действительно держит вас в потоке вашей игры. Пульт дистанционного управления достаточно мал, чтобы поместиться в любой карман. Это была отличная инвестиция в мое здоровье и игру в гольф. Спасибо за предложение отличного продукта!
Он очень легко настраивается прямо из коробки. Я надеялся протестировать его в местном парке, но в итоге я получил раннее время игры на следующий день после доставки, и я могу честно сказать, что им очень легко пользоваться. Я люблю ходить по газонам и не забирать свою старую тележку. Это действительно держит вас в потоке вашей игры. Пульт дистанционного управления достаточно мал, чтобы поместиться в любой карман. Это была отличная инвестиция в мое здоровье и игру в гольф. Спасибо за предложение отличного продукта!Итонтаун, Нью-Джерси
★★★★★
Просто короткая записка, чтобы поблагодарить вас. Как вы знаете, моя Bat Caddy пошла плавать… Ваше предложение поработать с Роном в вашем сервисном центре не могло не радовать. Рон обеспечил лучшее обслуживание клиентов, которое я когда-либо испытывал за последние пять лет. Он был очень профессиональным, вежливым и искренне хотел помочь… Я благодарю его за его усилия. Его действия очень положительно отражаются на вашей компании! Я бы рекомендовал и буду рекомендовать ваш продукт и, что более важно, вашу службу поддержки всем.
Хью С. У вас есть клиент на всю жизнь, и я желаю вам всяческих успехов.
У вас есть клиент на всю жизнь, и я желаю вам всяческих успехов.Карлайл, Пенсильвания
★★★★★
На прошлой неделе я заказал и быстро получил новый Bat-Caddy X4R. После трех раундов я очень доволен его выступлением! Перед заказом единственной оговоркой, которую я имел, было то, что я не мог найти отзывы о ваших продуктах, кроме как на вашем веб-сайте. Я смог поговорить напрямую с пользователем Bat-Caddy, который был очень доволен. Я сделал прыжок веры и не мог быть более счастливым. X4R был подарком на мой 51-й день рождения. Я всегда ходил и носил свою сумку. Благодаря вашему продукту я надеюсь идти по этому пути еще 25 лет.
Билл Г.Цинциннати, Огайо
BATCADDY — Лидер никогда не следует
Добро пожаловать в ведущую североамериканскую марку электрических тележек для гольфа!
Batcaddy — Electric Golf Caddy предлагает проверенную, хорошо спроектированную, высококачественную и недорогую серию электрических моторизованных толкающих тележек для каждого игрока в гольф, условий поля и бюджета, подкрепленную лучшим обслуживанием клиентов и долгосрочной стабильностью бизнеса в промышленность.

Самая удобная велосипедная обувь, которая у меня была. Очень хорошо работают с педалями Look.
Проверенный покупатель | Код заказа: 125827776
11.08.2022
Noch keine Langzeit-Testung, nach den ersten Radeinheiten bin ich aber total zufrieden. Wie gewünscht der richtige Schuh für meine neuen Gravel-Erlebnisse. Sitzt gut am Fuß, nicht zu eng (habe in Sportschuhen immer eine Schuhgröße mehr -> 38 statt 37; so auch in diesen Schuhen). Angenehme Weiteneinstellung mittels der zwei Klettverschlüsse. Im Fersenbereich finden sich außerdem Gummiapplikationen, um ein Rutschen zu vermeiden. Gehen ist etwas bequemer als in Rennradschuhen, aber natürlich trotzdem kein Vergleich zu normalen Straßenschuhen. Und optisch finde ich den Schuh großartig.
Und optisch finde ich den Schuh großartig.
Проверенный покупатель | Код заказа: 123860937
28.07.2022
Отличные туфли, простые и хорошо сидят на моей стопе. Ремешки на липучке — это легко и без суеты, как горжетки и причудливые вещи!
Проверенный покупатель | Код заказа: 124662177
28.07.2022
Дизайн и комфорт в нелла кальцата. Оттимо материал!
Проверенный покупатель | Код заказа: 123285415
21.07.2022
Я очень доволен этими гравийными ботинками уже 2 года. Я решила купить еще одну пару со скидкой, только другого цвета.
Проверенный покупатель | Код заказа: 123841359
19.07.2022
La chaussure est très belle et très bien faite. Mais l’intérieur ne me fournit pas suffisamment de soutien au milieu de la voute plantaire, je devrait très Certainement change la semelle intérieure.
Mais l’intérieur ne me fournit pas suffisamment de soutien au milieu de la voute plantaire, je devrait très Certainement change la semelle intérieure.
Проверенный покупатель | Код заказа: 123055850
15.07.2022
Простой дизайн, такой как обувь для шоссейного велосипеда для педалей mtb, которые отлично подходят для катания на велосипеде и вне его. Таким образом, они не перегружены, как большинство кроссовок для горных велосипедов, для пересеченной местности. Хотелось бы, чтобы он поставлялся с циферблатом Boa для регулировки или обувью для шоссейного велосипеда, разработанной для педалей mtb с учетом практичности.
Проверенный покупатель | Код заказа: 123524749
15.07.2022
Очень удобно и легко для новичков надевать обувь без клипс. Проблем при дальних поездках не встречал. Двойная липучка обеспечивает достаточную регулировку. Исходя из плоских педалей с туфлями MTB, я определенно могу заметить большую мощность с этими туфлями и педалями spd.
Двойная липучка обеспечивает достаточную регулировку. Исходя из плоских педалей с туфлями MTB, я определенно могу заметить большую мощность с этими туфлями и педалями spd.
Проверенный покупатель | Код заказа: 123554925
15.07.2022
Las cintas не се aflojan así дие не те паше apretándolas я дие эль ajuste ан марша не эс комо кон Боа. Poca ventilación, Ideales para invierno. Más flexibles y cómodas al caminar Que las X5 pero peor agarre que estas (carecen de taqueado). Estilo más enfocado a carretera у pistas fáciles Que las X5. Buenos materiales y acabados.
Проверенный покупатель | Код заказа: 122537387
11.07.2022
Прекрасно подходят и женские ноги. Отлично подходит для гравия с хорошим сцеплением. Супер быстрая бесплатная доставка до двери вашего дома.
Проверенный покупатель | Код заказа: 122848558
07. 07.2022
07.2022
Размер соответствует таблице размеров. У меня узкая стопа и мне подошли. Ремешок очень надежный. Остается посмотреть на долговечность липучки, но пока все хорошо, и мне очень нравится обувь.
Проверенный покупатель | Код заказа: 121779412
05.07.2022
Для красавицы и комода. Точный и пунктуальный сервис
Проверенный покупатель | Код заказа: 121695340
02.07.2022
Качественная и очень удобная обувь.
Проверенный покупатель | Код заказа: 122283742
01.07.2022
Люблю эти туфли до сих пор! Они подходят в размер. Они у меня всего пару недель, поэтому я не могу говорить об их долговечности, но мне нравится их качество сборки, и они должны прослужить долго. Я видел несколько отзывов, в которых ставилась под сомнение воздухопроницаемость, но до сих пор для меня это не было проблемой. Я с нетерпением жду еще много поездок впереди!
Я видел несколько отзывов, в которых ставилась под сомнение воздухопроницаемость, но до сих пор для меня это не было проблемой. Я с нетерпением жду еще много поездок впереди!
Проверенный покупатель | Код заказа: 122359173
01.07.2022
Хорошее качество сборки, удобная, хорошо работающая липучка. Короткие сроки доставки!
Проверенный покупатель | Код заказа: 122071133
29.06.2022
Очень удобная обувь. Его можно идеально отрегулировать благодаря ремням, а передача мощности на педаль действительно хороша. Достаточно места и для пальцев ног.
Проверенный покупатель | Код заказа: 121566809
26.06.2022
Sono belle dal vivo e comode, siccome farò un uso piuttosto invernale invece della mia taglia 39, ho deciso di prendere mezza taglia in più per l’uso con le calze invernali.
Проверенный покупатель | Код заказа: 121809513
25.06.2022
Удивительные туфли. Легкий вес. Наконец, башмак шипа с 2 болтами, который выглядит как дорожный башмак. Липучка работает отлично! Я подал в суд на Terra, которые более громоздки и больше подходят для горных велосипедов. Езжу по дорогам и гравию. Но больше дороги. Теперь у меня есть идеальная обувь. Эта обувь отлично подойдет для туров и тренировок у дверей. Я надеюсь, что Fizik продолжит выпускать такие туфли. Ни одна другая компания не производит такую обувь. ВЕЛИКОЛЕПНОСТЬ!!!
Проверенный покупатель | Код заказа: 120719004
25.06.2022
Veramente comode электронной функциональности. Суола твердая для ип ottimo trasferimento di potenza. Кальзано приходит в себя. Si Cammina agevolmente.
Проверенный покупатель | Код заказа: 121429082
21. 06.2022
06.2022
Отличная посадка и красивая обувь.
Проверенный покупатель | Код заказа: 121138356
17.06.2022
Пока мне это нравится. Но хотелось бы, чтобы лямки были длиннее.
Проверенный покупатель | Код заказа: 119942497
10.06.2022
Быстрая, топовая обувь, топовый дизайн……..
Проверенный покупатель | Код заказа: 120715195
11.06.2022
Я взял размер в 1,5 раза больше, чем моя обычная обувь.
Проверенный покупатель | Код заказа: 119719191
31.05.2022
У меня плоскостопие очень широкое, я как пингвин, это мои первые велосипедные туфли, две недели я думал о размере, который я покупаю 43, это мой размер во всех туфлях, он подходит как перчатка, его размер соответствует размеру, рекомендованному мне руководством по размерам 41, 5, но я купил свой истинный размер, они совсем не узкие для моего окончательного плоскостопия, 5 поездок до сих пор без боли, я вообще не чувствую их впервые в велосипедной обуви и. Они меняют мой опыт катания на удивительных туфлях
Они меняют мой опыт катания на удивительных туфлях
Проверенный покупатель | Код заказа: 119519667
29.05.2022
Выглядеть и чувствовать себя невероятно. Снимал их всего несколько раз, но у меня нет никаких нареканий.
Проверенный покупатель | Код заказа: 119515456
28.05.2022
Scarpe di ottima fattura, comode gia dal primo utilizzo e esteticamente molto belle.
Проверенный покупатель | Код заказа: 118315665
16.05.2022
Я еще не катался в этих ботинках, но с нетерпением жду, когда наконец надену их на велосипед. Они выглядят потрясающе. Поддержка свода стопы выше, чем я привык, но в остальном посадка замечательная. Много места в области носка — гораздо больше, чем у других итальянских брендов!
Проверенный покупатель | Код заказа: 116
12. 05.2022
05.2022
Ich brauche normalerweise die Grosse 39 aber brauchte für die Schuhe 39,5 und bin ehrlich gesagt sehr zufrieden mit den Schuhen und meiner Entscheidung.
Проверенный покупатель | Код заказа: 117166256
12.05.2022
Отлично все вокруг с производительностью, и, конечно, они выглядят потрясающе. Я использую их для эндуро и гравия
Проверенный покупатель | Код заказа: 1166
04.05.2022
Очень удобно, мне нравится система лямок, они мне идеально подходят.
Проверенный покупатель | Код заказа: 115056631
23.04.2022
Удобная обувь до сих пор, и хорошо сделана.
Проверенный покупатель | Код заказа: 115141731
18.04.2022
Обувь была именно такой, какой я хотел. Дорога выглядит с атмосферой MTB.
Проверенный покупатель | Код заказа: 115137842
17.04.2022
Супер Шух. Leider habe ich falsche Größe bestellt.
Проверенный покупатель | Код заказа: 114440103
17.04.2022
Быстрая доставка всего 2 дня. Обувь идеально сидит
Проверенный покупатель | Код заказа: 114139425
13.04.2022
Это моя первая пара кроссовок для велоспорта, и они просто фантастические. Удобно на велосипеде и достаточно легко ходить пешком на короткие расстояния. Они выглядят точно так же, как на фотографиях и соответствуют размеру.
Они выглядят точно так же, как на фотографиях и соответствуют размеру.
Проверенный покупатель | Код заказа: 111
07.03.2022
владею ими недостаточно долго, чтобы дать полный обзор. Все идет нормально.
Проверенный покупатель | Код заказа: 111026013
02.03.2022
Обувь прекрасно себя чувствует во время поездок. Чувствую себя сильным и прочным. Очень удобно при ходьбе и очень стильно
Проверенный покупатель | Код заказа: 111553165
01.03.2022
Это хорошо сделанная обувь и легкий вес. Однако они не предназначены для женщин и несколько громоздки. Посадка немного шире в области носка, чем мне хотелось бы, что оказывает большее давление на верхний свод стопы.
Проверенный покупатель | Код заказа: 110989288
01.03.2022
Отличный товар, соответствует размеру, цвету. Ранее имел неудачный опыт с другими обувными брендами, изображающими другой цвет, чем тот, который показан на их сайте. Кроме того, очень быстрая доставка, хотя этот товар был отправлен из Италии в США
Проверенный покупатель | Код заказа: 111027930
24.02.2022
Super Schuh und toller Service. War begeistert
Проверенный покупатель | Код заказа: 111025897
23.02.2022
Отличная и удобная обувь. Очень хорошее обслуживание клиентов.
Проверенный покупатель | Код заказа : 1094
