Вычисление пределов примеры: Предел функции. Примеры решения

Содержание

Предел функции. Примеры решения

Продолжаем разбирать ответы к пределам функций и последовательностей. Примеров накопилось настолько много, что можно написать отдельную книгу — методичку по их вычислению.
В каждой публикации разжевываем методику вычислений до элементарных мелочей, при таких объяснениях каждый студент может без проблем решить подобные примеры.
Однако дальше от студентов поступают новые заказы с просьбой найти предел.
Порой нужно помочь с простыми функциями, что составляет впечатление что студенты имеют худшую подготовку, чем ученики в 11 классе, которые изучают эту тему.

Пример 11. Вычислить предел последовательности:

Решение: Подстановка большого номера в последовательность дает особенность вида бесконечность разделить на бесконечность. Для ее раскрытия в числителе и знаменателе дроби выделяем слагаемое, что вносит наибольший вклад. В скобках останутся константы + слагаемые, которые стремятся к нулю.

На общий множитель упрощаем, а константы дают значение предела последовательности.

Пример 12. Найти предел последовательности:

Решение: В предельном переходе имеем неопределенность вида бесконечность минус бесконечность. Функция представлена разницей корней. Чтобы избавиться от неопределенности, умножим и поделим разницу на сумму корней (сопряженное выражение). В результате придем к неопределенности бесконечность разделить на бесконечность. Чтобы ее раскрыть выносим множитель, что вносит наибольший вклад из числителя и знаменателя и сокращаем на него. Все что останется и будет пределом последовательности

Пример 13. Найти предел функции

Решение: При переменной стремящейся к нулю имеем неопределенность {0/0}. Для ее раскрытия разницу корней умножим и разделим на сопряженное выражение, чтобы в числителе образовать разность квадратов. В знаменателе имеем полином, который содержит особенность, поэтому разложим его на простые множители. После упрощений получим зависимость, предел которой легко находим методом подстановки

Пример 14. Вычислить предел

Решение: Переменная стремится к нулю, а функция задана долей синуса и тангенса в квадрате. В таких случаях нужно преобразовать выражение, чтобы в нем можно было легко выделить первый замечательный предел и его следствие. Для компенсации изменений в числитель и знаменатель записываем соответствующие константы. Далее переходим к произведению известных границ, вклад от каждой из которых равен единице.

Пример 15. Определить предел функции

Решение: При переменной стремящейся к нулю получим неопределенность вида единица в степени бесконечность. Для ее раскрытия выразим в степени множитель, который обратно пропорционален sin(4x).
Таким образом получим второй замечательный предел – экспоненту, а все что останется в показателе, даст степень экспоненты. Но здесь имеем долю sin(4x)/tan(3x), поэтому переходим к лимиту в показателе, а сам показатель сводим к первому замечательному пределу его следствии.

Из последнего «лимита» можно вывести простую формулу, которая может быть рассмотрена как следствие первого замечательного предела. Лимит доли тангенса к синусу (или наоборот) ровен доле их аргументов.

Пример 16. Найти предел последовательности:

Решение: Для раскрытия особенности вида бесконечность разделить на бесконечность необходимо три раза применить правило Лопиталя. Другая схема заключается в вынесении из числителя и знаменателя наибольшего множителя, и сокращении на него. В результате останутся константы и бесконечно малые функции. Последние стремятся к нулю, поэтому лимит последовательности равен

Пример 17. Вычислить предел последовательности:

Решение: Таких лимитов в предыдущих публикациях вычислено немало и суть раскрытия подобных неопределенностей заключается в умножении на сопряженное выражение – сумму корней. На это же выражение следует разделить функцию, чтобы не изменить значение лимита. В результате в числителе дроби получим разность квадратов и таким образом избавляемся от иррациональности, а предел выражения получим через оценку максимальных множителей.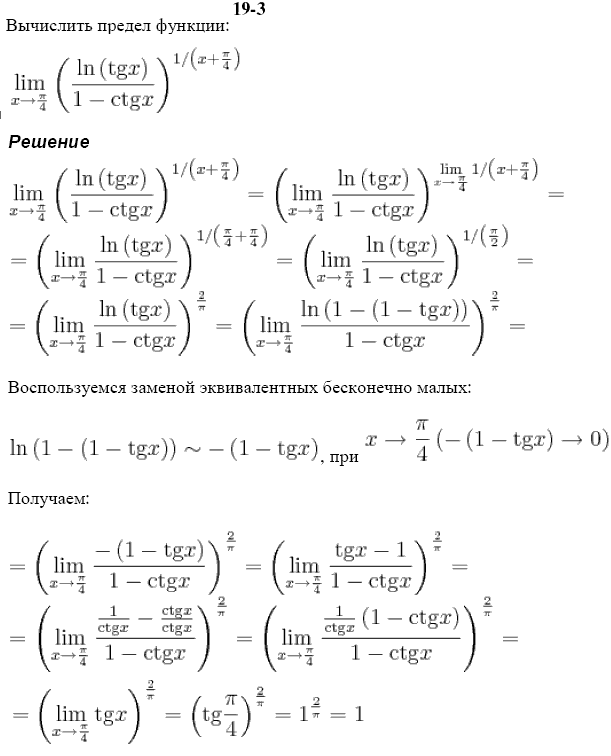

Пример 18. Определить лимит функции

Решение: Когда переменная стремится к 3 имеем неопределенность вида {0/0}. Для раскрытия неопределенности в знаменателе дроби избавляемся от иррациональности умножением на сопряженное выражение, а в числителе полином раскладываем на простые множители. В результате и тат и там получаем выражение (х-3), на которое упрощаем.

Лимит функции, что осталась, вычисляем методом подстановки.

Пример 19. Найти предел функции

Решение: Предел функции в нуле дает особенность {0/0}. Ее не так просто раскрывать, как предыдущие.
Здесь следует свести выражение к первому и второму замечательному пределу и их следствиям.
Ln(1+x)/x в предельном переходе даст единицу, так же как и tan(x)/x и sin(x)/x.
Число 4/25 и будет лимитом функции.

Пример 20. Найти лимит

Решение: Предел функции в точке имеет неопределенность вида единица в степени бесконечность. Для ее раскрытия нужно преобразовать функцию под второй замечательный предел. Для этого и в скобках, и в показателе выделяем множитель, что вносит особенность (x-3) и делаем замену переменных t=x-3.
Далее переходим к экспоненте, и определяем лимит показательной функции.

Как Вы могли убедиться, задания на пределы не самые сложные в высшей математике.
Нужно знать не так много правил, чтобы без труда находить правильный ответ.

как понять, вычислить, подробное объяснение с решением

Теория пределов – раздел математического анализа. Наряду с системами линейных уравнений и диффурами пределы доставляют всем студентам, изучающим математику, немало хлопот. Чтобы решить предел, порой приходится применять массу хитростей и выбирать из множества способов решения именно тот, который подойдет для конкретного примера.

В этой статье мы не поможем вам понять пределы своих возможностей или постичь пределы контроля, но постараемся ответить на вопрос: как понять пределы в высшей математике? Понимание приходит с опытом, поэтому заодно приведем несколько подробных примеров решения пределов с пояснениями.

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Понятие предела в математике

Первый вопрос: что это вообще за предел и предел чего? Можно говорить о пределах числовых последовательностей и функций. Нас интересует понятие предела функции , так как именно с ними чаще всего сталкиваются студенты. Но сначала — самое общее определение предела:

Допустим, есть некоторая переменная величина. Если эта величина в процессе изменения неограниченно приближается к определенному числу a, то a – предел этой величины.
Для определенной в некотором интервале функции f(x)=y пределом называется такое число A, к которому стремится функция при х, стремящемся к определенной точке а. Точка а принадлежит интервалу, на котором определена функция.

Звучит громоздко, но записывается очень просто:

Lim — от английского limit — предел.

Существует также геометрическое объяснение определения предела, но здесь мы не будем лезть в теорию, так как нас больше интересует практическая, нежели теоретическая сторона вопроса. Когда мы говорим, что х стремится к какому-то значению, это значит, что переменная не принимает значение числа, но бесконечно близко к нему приближается.

Приведем конкретный пример. Задача — найти предел.

Чтобы решить такой пример, подставим значение x=3 в функцию. Получим:

Кстати, если Вас интересуют базовые операции над матрицами, читайте отдельную статью на эту тему.

В примерах х может стремиться к любому значению. Это может быть любое число или бесконечность. Вот пример, когда х стремится к бесконечности:

Интуитивно понятно, что чем больше число в знаменателе, тем меньшее значение будет принимать функция.

Так, при неограниченном росте х значение 1/х будет уменьшаться и приближаться к нулю.

Как видим, чтобы решить предел, нужно просто подставить в функцию значение, к которому стремиться х. Однако это самый простой случай. Часто нахождение предела не так очевидно. В пределах встречаются неопределенности типа 0/0 или бесконечность/бесконечность. Что делать в таких случаях? Прибегать к хитростям!

Неопределенности в пределах

Неопределенность вида бесконечность/бесконечность

Пусть есть предел:

Если мы попробуем в функцию подставить бесконечность, то получим бесконечность как в числителе, так и в знаменателе. Вообще стоит сказать, что в разрешении таких неопределенностей есть определенный элемент искусства: нужно заметить, как можно преобразовать функцию таким образом, чтобы неопределенность ушла. В нашем случае разделим числитель и знаменатель на х в старшей степени. Что получится?

Из уже рассмотренного выше примера мы знаем, что члены, содержащие в знаменателе х, будут стремиться к нулю. Тогда решение предела:

Для раскрытия неопределенностей типа бесконечность/бесконечность делим числитель и знаменатель на х в высшей степени.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Еще один вид неопределенностей: 0/0

В таких случаях рекомендуется раскладывать числитель и знаменатель на множители. Но давайте посмотрим на конкретный пример. Нужно вычислить предел:

Как всегда, подстановка в функцию значения х=-1 дает 0 в числителе и знаменателе. Посмотрите чуть внимательнее и Вы заметите, что в числителе у нас квадратное уравнение. Найдем корни и запишем:

Сократим и получим:

Итак, если Вы сталкиваетесь с неопределенностью типа 0/0 – раскладывайте числитель и знаменатель на множители.

Чтобы Вам было проще решать примеры, приведем таблицу с пределами некоторых функций:

Правило Лопиталя в пределах

Еще один мощный способ, позволяющий устранить неопределенности обоих типов. В чем суть метода?

Если в пределе есть неопределенность, берем производную от числителя и знаменателя до тех пор, пока неопределенность не исчезнет.

Наглядно правило Лопиталя выглядит так:

Важный момент: предел, в котором вместо числителя и знаменателя стоят производные от числителя и знаменателя, должен существовать.

А теперь – реальный пример:

Налицо типичная неопределенность 0/0. Возьмем производные от числителя и знаменателя:

Вуаля, неопределенность устранена быстро и элегантно.

Надеемся, что Вы сможете с пользой применить эту информацию на практике и найти ответ на вопрос «как решать пределы в высшей математике». Если нужно вычислить предел последовательности или предел функции в точке, а времени на эту работу нет от слова «совсем», обратитесь в профессиональный студенческий сервис за быстрым и подробным решением.

Что такое предел функции как его найти

Общее понятие предела
Предел функции
Основные теоремы о пределах
Найти предел самостоятельно, а затем посмотреть решение
Решение пределов через раскрытие неопределённостей
Раскрыть неопределённости самостоятельно, а затем посмотреть решения

Решение пределов онлайн калькулятор

При каком условии Вам будут совсем не страшны любые задачи, где требуется найти предел функции? Условие следующее: у Вас есть базовый навык деления одних чисел на другие, на очень-очень маленькие числа и на очень-очень большие числа. Успех придет в процессе решения.

А теперь посмотрим, что о пределе функции гласит теория. Впрочем, можно зайти чуть-чуть вперед и сразу перейти к задачам, а потом вернуться к теории. Как удобнее.

Обобщённое понятие предела: число a есть предел некоторой переменной величины, если в процессе своего изменения эта переменная величина неограниченно приближается к a.

Поясним это на примере, который также проиллюстрируем. А после примера приведём общий алгоритм решения пределов.

В нижнюю часть равнобедренного треугольника вписана окружность. Диаметр этой окружности обозначим как . На рисунке диаметр проведён синим цветом. К окружности параллельно основанию первоначального треугольника проведена касательная (она на рисунке серого цвета). В результате получен треугольник, подобный первоначальному. В этот треугольник точно так же вписана окружность. Её диаметр — (диаметры на рисунке ограничены касательными). Аналогичные построения продолжаются, пока позволяет высота треугольника. Получена последовательность уменьшающихся окружностей и соответствующая им последовательность длин их диаметров: . Эта последовательность длин диаметров даёт пример переменной величины , которая с возрастанием номера окружности x неограниченно приближается к нулю. Предел этой последовательности равен нулю: .

Запишем приведённый пример на языке формул. Итак, номер окружности возрастает и стремится к бесконечности, то есть . Допустим, существует такой равнобедренный треугольник, что длина диаметра каждой вписанной в него окружности расчитывается по формуле

Величина, которую нам требуется найти, будет записана так:

Lim это и есть предел, а под ним указывается переменная, которая стремится к определённому значению – нулю, любому другому числу, бесконечности.

Теперь вычислим предел, присвоив переменной x значение бесконечность (в более строгом определении это называется «доопределить функцию», с этим определением вы можете ознакомиться в последующих частях главы «Предел»). Примем, что конечная величина, поделенная на бесконечность, равна нулю:

С рассмотренной последовательностью окружностей свяжем другую переменную величину — последовательность сумм их диаметров:

Рассмотрев рисунок снова, обнаружим, что предел последовательности равен h – высоте равнобедренного треугольника. Вообще, предел может быть равен нулю, любому другому числу или бесконечности.

Теперь более строгие определения предела функции, которые Вас могут спросить на экзамене, и для понимания которых потребуется чуть больше внимания.

Предел функции при

Пусть функция f(x) определена на некотором множестве X и пусть дана точка . Возьмём из X последовательность точек, отличных от :

(1)

сходящуюся к . Значения функции в точках этой последовательности также образуют числовую последовательность

(2)

и можно ставить вопрос о существовании её предела.

Определение 1. Число A называется пределом функции f(x) в точке (или при ), если для любой сходящейся к последовательности (1) значений аргумента x, отличных от , соответствующая последовательность (2) сходится к числу A.

Символически это записывается так:

Это означает: чтобы найти предел функции, нужно в функцию вместо x подставить то значение, к которому стремится x.

Пример 1. Найти предел функции при .

Решение. Подставляем вместо x значение 0. Получаем:

Итак, предел данной функции при равен 1.

Кроме того, решённые в этом уроке примеры и любые другие задачи на пределы, можно на проверить на

калькуляторе пределов онлайн.

Предел функции при , при и при

Кроме рассмотренного понятия предела функции при существует также понятие предела функции при стремлении аргумента к бесконечности.

Определение 2. Число A называется пределом функции f(x) при , если для любой бесконечно большой последовательности (1) значений аргумента соответствующая последовательность (2) значений функции сходится к A.

Символически это записывается так: .

Определение 3. Число A называется пределом функции f(x) при (), если для любой бесконечно большой последовательности значений аргумента, элементы которой положительны (отрицательны), соответствующая последовательность (2) значений функции сходится к

Символически это записывается так: ().

Это, как и в случае определения 1, означает: чтобы найти предел функции, нужно в функцию вместо x подставить бесконечность, плюс бесконечность или минус бесконечность.

Пример 2. Найти предел функции при .

Решение. Подставляем вместо x бесконечность. Получаем, что последовательность значений функции является бесконечно малой величиной и поэтому имеет предел, равный нулю:

Для наглядности и убедительности, решая данный пример в черновике, можете подставить вместо x супербольшое число. При делении получите супермалое число.

А проверить решение задачи на пределы можно на калькуляторе пределов онлайн.

Теорема 1. (о единственности предела функции). Функция не может иметь более одного предела.

Следствие. Если две функции f(x) и g(x) равны в некоторой окрестности точки , за исключением, может быть, самой точки , то либо они имеют один и тот же предел при , либо обе не имеют предела в этой точке.

Теорема 2. Если функции f(x) и g(x) имеют пределы в точке , то:

1) предел алгебраической суммы функций равен алгебраической сумме пределов слагаемых, т.е.

(3)

2) предел произведения функций равен произведению пределов сомножителей, т.е.

(4)

3)предел частного двух функций равен частному от деления предела делимого на предел делителя, если предел делителя не равен нулю, т.

е.

(5)

Замечание. Формулы (3) и (4) справедливы для любого конечного числа функций.

Следствие 1. Предел постоянной равен самой постоянной, т.е.

Следствие 2. Постоянный множитель можно выносить за знак предела, т.е.

Пример 3. Найти предел:

Решение.

А проверить решение задачи на пределы можно на калькуляторе пределов онлайн.

Пример 4. Найти предел:

Решение. Предварительно убедимся, что предел делителя не равен нулю:

Таким образом, формула (5) применима и, значит,

А проверить решение задачи на пределы можно на калькуляторе пределов онлайн.

Теорема 3 (о пределе сложной функции). Если существует конечный предел

а функция f(u) непрерывна в точке , то

Другими словами, для непрерывных функций символы предела и функции можно поменять местами.

Непосредственное применение теорем о пределах, однако, не всегда приводит к цели. Например, нельзя применить теорему о пределе частного, если предел делителя равен нулю. В таких случаях необходимо предварительно тождественно преобразовать функцию, чтобы иметь возможность применить следствие из теоремы 1.

Пример 5. Найти предел:

Решение. Теорема о пределе частного здесь неприменима, так как

Преобразуем заданную дробь, разложив числитель и знаменатель на множители. В числителе получим

где

корни квадратного трёхчлена (если Вы забыли, как решать квадратные уравнения, то Вам сюда). Теперь сократим дробь и, используя следствие из теоремы 1, вычислим предел данной функции:

Пример 6. Найти предел:

Правильное решение и ответ.

Пример 7. Найти предел:

Правильное решение и ответ.

Пример 8. Найти предел:

Правильное решение и ответ.

Пример 9. Найти предел:

Правильное решение и ответ.

Пример 10. Найти предел:

Правильное решение и ответ.

Пример 11. Найти пределы:

Правильное решение и ответ.

Нет времени вникать в решение? Можно заказать работу!

К началу страницы

Пройти тест по теме Предел

При решении примеров 5 и 8 нам уже встретилась неопределённость вида . Эта неопределённость и неопределённость вида — самые распространённые неопределённости, которые требуется раскрывать при решении пределов.

БОльшая часть задач на пределы, попадающихся студентам, как раз несут в себе такие неопределённости. Для их раскрытия или, точнее, ухода от неопределённостей существует несколько искусственных приёмов преобразования вида выражения под знаком предела. Эти приёмы следующие: почленное деление числителя и знаменателя на старшую степень переменной, домножение на сопряжённое выражение и разложение на множители для последующего сокращения с использованием решений квадратных уравнений и формул сокращённого умножения.

Освоим эти приёмы на примерах.

Для преобразования выражений потребуются пособия Действия со степенями и корнями и Действия с дробями.

Неопределённость вида

Пример 12. Раскрыть неопределённость и найти предел .

Решение. Здесь старшая степень переменной n равна 2. Поэтому почленно делим числитель и знаменатель на :

Комментарий к правой части выражения. Стрелками и цифрами обозначено, к чему стремятся дроби после подстановки вместо n значения бесконечность. Здесь, как и в примере 2, степень n в знаменателя больше, чем в числителе, в результате чего вся дробь стремится к бесконечно малой величине или «супермалому числу».

Получаем ответ: предел данной функции при переменной, стремящейся к бесконечности, равен .

Проверить решение задачи на пределы можно на калькуляторе пределов онлайн.

Пример 13. Раскрыть неопределённость и найти предел .

Решение. Здесь старшая степень переменной x равна 1. Поэтому почленно делим числитель и знаменатель на x:

Комментарий к ходу решения. В числителе загоняем «икс» под корень третьей степени, а чтобы его первоначальная степень (1) оставалась неизменной, присваиваем ему ту же степень, что и у корня, то есть 3. Стрелок и дополнительных чисел в этой записи уже нет, так что попробуйте мысленно, но по аналогии с предыдущим примером определить, к чему стремятся выражения в числителе и знаменателе после подстановки бесконечности вместо «икса».

Получили ответ: предел данной функции при переменной, стремящейся к бесконечности, равен нулю.

Проверить решение задачи на пределы можно на калькуляторе пределов онлайн.

Неопределённость вида

Пример 14. Раскрыть неопределённость и найти предел .

Решение. В числителе — разность кубов. Разложим её на множители, применяя формулу сокращённого умножения из курса школьной математики:

В знаменателе — квадратный трёхчлен, который разложим на множители, решив квадратное уравнение (ещё раз ссылка на решение квадратных уравнений):

Запишем выражение, полученное в результате преобразований и найдём предел функции:

Проверить решение задачи на пределы можно на калькуляторе пределов онлайн.

Пример 15. Раскрыть неопределённость и найти предел

Решение. Теорема о пределе частного здесь неприменима, поскольку

Поэтому тождественно преобразуем дробь: умножив числитель и знаменатель на двучлен, сопряжённый знаменателю, и сократим на x +1. Согласно следствию из теоремы 1, получим выражение, решая которое, находим искомый предел:

Пример 16. Раскрыть неопределённость и найти предел

Решение. Непосредственная подстановка значения x = 0 в заданную функцию приводит к неопределённости вида 0/0. Чтобы раскрыть её, выполним тождественные преобразования и получим в итоге искомый предел:

Пример 17. Раскрыть неопределённость и найти предел

Правильное решение и ответ.

Пример 18. Раскрыть неопределённость и найти предел

Правильное решение и ответ.

Пример 19. Раскрыть неопределённость и найти предел

Правильное решение и ответ.

Назад

Листать

Вперёд>>>

Нет времени вникать в решение? Можно заказать работу!

К началу страницы

Пройти тест по теме Предел

Продолжение темы «Предел»

Первый замечательный предел

Второй замечательный предел

Бесконечно малые

Поделиться с друзьями

Вычисление простейших пределов, 11 класс (теория+практика).

Предел функции (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке.
Записывается предел следующим образом .

Вычислим предел:
Подставляем вместо х – 3.
Заметим, что предел числа равен самому числу.

Примеры: вычислите пределы

Если в некоторой точке области определения функции существует предел и этот предел равен значению функции в данной точке, то функция называется непрерывной (в данной точке).

Вычислим значение функции в точке x₀ = 3 и значение его предела в этой точке.

Значение предела и значение функции в этой точке совпадает, следовательно, функция непрерывна в точке x₀ = 3.

Но при вычислении пределов зачастую появляются выражения, значение которых не определено. Такие выражения называют неопределённостями.

Основные виды неопределенностей:

Раскрытие неопределенностей

Для раскрытия неопределенностей используют следующее:

упрощают выражение функции: раскладывают на множители, преобразовывают функцию с помощью формул сокращенного умножения, тригонометрических формул, домножают на сопряженное, что позволяет в дальнейшем сократить и т.д., и т.п.;
если предел при раскрытии неопределенностей существует, то говорят, что функция сходится к указанному значению, если такого предела не существует, то говорят, что функция расходится.

Пример: вычислим предел.
Разложим числитель на множители

3. Вычисление пределов функции

Пример 1. Вычислите предел функции:

При прямой подстановке, получается неопределенность:

Разложим на множители числитель и знаменатель и вычислим предел.

Пример 2. Вычислите предел функции:

При прямой подстановке, получается неопределенность.

Помножим и числитель, и знаменатель на .

Учтем, что если число разделить на бесконечно большое число получится ноль. То есть предел Аналогично

Пример 3. Вычислите предел функции:

При прямой подстановке, получается неопределенность.

Помножим и числитель, и знаменатель на .

Мы учли, что

4. Самостоятельные упражнения

Вычислите пределы:

6. Домашнее задание

Домашнее задание раздается на карточках каждому ученику.

Свойства пределов функции

Предел постоянной величины равен самой постоянной величине:
Предел суммы двух функций равен сумме пределов этих функций: Аналогично предел разности двух функций равен разности пределов этих функций.
Постоянный коэффициент можно выносить за знак предела:
Предел произведения двух функций равен произведению пределов этих функций:
Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю:

Замечание. Принято считать, что Следующие пределы считают неопределенностью: . Если в примере встретилась неопределенность, то надо найти пути для ее устранения. Общие правила:

1) если в числителе и знаменателе находятся многочлены, и имеется неопределенности вида или , то для решения нужно разложить числитель и знаменатель на множители или разделить на максимальную степень числителя (или знаменателя) и числитель и знаменатель;2) если же в числителе или в знаменателе находятся иррациональные выражения и имеется неопределенности вида или , то для решения надо избавляться от иррациональности, помножив и числитель, и знаменатель на сопряженное выражение;3) если же в числителе или в знаменателе находятся тригонометрические выражения и имеется неопределенности вида или , то для решения используют формулу замечательного предела

Вычисление пределов функции

Пример 1.Найти предел функции:

Пример 2.Найти предел функции:

Пример 3. Найти предел функции:

Пример 4.Найти предел функции:

Пример 5.Найти предел функции:

Пример 6.Найти предел функции:

Пример 7.Найти предел функции:

Пример 8.Найти предел функции:

Пример 9.Найти предел функции:

Пример 10.Найти предел функции: Непрерывность функции Мы интуитивно понимаем, что если функция непрерывна, то мы можем ее нарисовать, не отрывая карандаша от листа бумаги.Функция у = f (x) называется непрерывной, если она непрерывна в каждой точке своей области определения.Чтобы понять, что такое непрерывность функции в целом, сначала надо разобраться, что такое непрерывность функции в точке.Функция у = f (x) называется непрерывной в точке х = с, если предел функции в точке х = с равен значению функции в этой точке: Т.е. должны выполняться одновременно три условия:

1) функция определена и в самой точке х = с и в некоторой окрестности этой точки, причем U(с) ϵ D(f);2) существует ;3) A = f(c).

Заметим, что в случае непрерывной функции в точке x = c, на графике данная точка выколотой быть не может.Для иллюстрации, как работает данное определение, рассмотрим три функции (см. табл.). Все три условия определения выполняются только у первой функции у = х + 1. У второй — не выполняется третье условие, а у третьей функции — первое.

Непрерывная функция	Разрывная в т. х = 1	Разрывная в т. х = 1

Пример 11.Найти точку разрыва функции

Решение

Найдем область определения функции: 5x + 7 ≠ 0, x ≠ -1,4.Ответ: -1,4.

Пример 12.Найти сумму значений точек разрыва функции

РешениеНайдем область определения функции: х² + 2х — 3 ≠ 0. По теореме, обратной к теореме Виета: х₁ ≠ 1, x₂ ≠ -3.Далее находим сумму значений 1 + (-3) = -2.Ответ: -2.

Пример 13.Указать точку разрыва функции:

РешениеПостроим график данной функции на указанных промежутках. Видим, что целостность функции нарушается при х = 2.Ответ: 2.

Примеры решения пределов с корнями с ответами

Основные свойства пределов с корнями

Теорема

Для нахождения предела функции необходимо подставить в предел вместо Х то значение переменной, к которому стремится Х.

Нужна помощь в написании работы?

Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.

Заказать работу

Примеры решений пределов с корнями

Пример №1

Задание

Найти предел

Решение

Мы имеем неопределенность вида

Первый шаг – разделить числитель и знаменатель на ”х” в высшей степени. Старшая степень для числителя в данном случае равна двум.
Со знаменателем немного сложнее. Так как у нас корень, обращаем внимание только на самое ”старшее” слагаемое –

Число (4) – это константа, его тоже отбрасываем. Находим корень

Так как числитель и знаменатель оказываются одного порядка роста, предел равен конечному числу, отличному от нуля.

Видим, что функции эквивалентны на бесконечности.

Оформляем решение:

Ответ: 1

Пример № 2

Задание

Найти предел с корнем

Решение

Подставляем

в подпредельную функцию:

Получаем неопределенность

Домножаем числитель и знаменатель на выражение, сопряженное к нему –

так как он содержит корень.
Далее, пользуясь формулой разности квадратов

и раскрывая скобки, упрощаем предел. Последний шаг – сокращение функции на

Ответ: -8

Пример №3

Задание

Решить предел с корнем

Решение

Подставляем

в предел и получаем неопределённость вида

Как и в предыдущих примерах, находим старшую степень для числителя и знаменателя, и выносим её за скобки.

И опять подставляем

в предел и решаем:

Ответ:

Пример №4

Задание

Вычислить предел корня:

Решение

Аналогично предыдущим примерам, подставляем

в предел и видим:

Находим сопряженное, в данном случае это

Как и в примере №2, пользуясь формулой разности квадратов

и раскрывая скобки, упрощаем предел:

Раскрываем скобки и упрощаем. Затем выносим х за скобки и сокращаем:

Как и в начале, подставляем в предел, получаем:

Ответ:

Пример №5

Задание

Вычислить предел функции

Решение

Если подставить х=1, видно, что и числитель, и знаменатель обращаются в ноль. Получаем неопределенность вида

Как и в предыдущих примерах, первым шагом находим сопряжённое –

и домножаем на него числитель и знаменатель.

Применяем правило разности квадратов

и преобразовываем предел:

Сокращаем числитель и знаменатель на (x-1) и приходим к конечному ответу:

Ответ: 6

Пример № 6

Задание

Вычислить предел:

Решение:

Первый шаг – подставить в предел выражение

и убедиться, что выходит неопределённость вида

Шаг второй – раскрываем нашу неопределенность путём умножения числителя и знаменателя на сопряжённое выражение, в данном случае –

Далее, пользуясь формулой разности квадратов раскладываем числитель:

Подставляем х=3 в предел и вычисляем:

Ответ:

Пример №7

Задание

Вычислить предел

Решение

Как и в предыдущих заданиях, подставляем

и убеждаемся, что имеем дело с неопределённостью вида

Порядок действий стандартный. Избавляемся от иррациональности в знаменателе с помощью домножения числителя и знаменателя на сопряженное выражение. В данном примере сопряжённое выражение имеет вид –

Перемножаем знаменатель и сокращаем в числителе и знаменателе

Подставляем, как и ранее, х=3 и находим ответ:

Ответ: 17,8

Пример №8

Задание

Определить предел функции

Решение

Смотрим на функцию, подставляем

мы имеем дело с неопределённостью вида:

Начинаем работать с функциями, содержащими корень. Умножаем числитель и знаменатель на сопряжённое выражение и упрощаем предел:

После преобразований получаем ответ:

Ответ: -2

Пример №9

Задание

Решить предел

Решение:

Подставляя

в выражение лимита, подтверждаем догадки, что перед нами неопределённость вида

Как и раньше, первый шаг – избавиться от иррациональности с помощью домножения числителя и знаменателя на соответствующее сопряженное выражение.

Раскрываем скобки и сокращаем выражения на

Неопределённости

больше нет и ничего нам не мешает вычислить пример:

Ответ:

Пример №10

Задание

Вычислить предел

Решение

Оба лимита числителя и знаменателя равны нулю, значит опять неопределённость вида

Находим сопряжённое к числителю и знаменателю число:

Домножаем на полученное выражение числитель и знаменатель, раскрываем скобки и упрощаем:

Раскладываем числитель и знаменатель:

Вычисляем предел:

Ответ:

Средняя оценка 4 / 5. Количество оценок: 4

Поставьте вашу оценку

Сожалеем, что вы поставили низкую оценку!

Позвольте нам стать лучше!

Расскажите, как нам стать лучше?

18626

Закажите помощь с работой

Не отобразилась форма расчета стоимости? Переходи по ссылке

Подготовка школьников к ЕГЭ (Справочник по математике — Элементы математического анализа

Справочник по математике

Элементы математического анализа

Функции

Предел функции

Свойства пределов функций

Раскрытие неопределенностей типа

Первый замечательный предел

Раскрытие неопределенностей типа .

Второй замечательный предел

Предел функции

В ряде разделов нашего справочника, где требуется применение понятия предела функции, встречаются несколько ситуаций в зависимости от того, куда стремится аргумент функции x , и того, куда при этом стремится значение функции. Определения предела функции для этих случаев удобно представить в форме таблицы. Однако таблица, описывающая все возможные случаи, должна содержать 24 строки и является слишком громоздкой. Для удобства читателей мы привели в таблице только те определения предела функции, которые использованы в нашем справочнике.

Название

Обозначение

Определение

Предел функции f (x) при x, стремящемся к числу a, равен числу A

Число A называют пределом функции f (x) при x, стремящемся к числу a, если для любого положительного числа ε найдется такое положительное число δ , что при всех , удовлетворяющих неравенству

| x – a | < δ ,

будет выполняться неравенство

| f (x) – A | < ε .

f (x) → A

при x → a

Предел функции f (x) при x, стремящемся к , равен числу A

Число A называют пределом функции f (x) при x , стремящемся к, если для любого положительного числа ε найдется такое положительное число С, что при всех x, удовлетворяющих неравенству

x > C ,

будет выполняться неравенство

| f (x) – A | < ε .

f (x) → A

при

Предел функции f (x) при x, стремящемся к , равен числу A

Число A называют пределом функции f (x) при x , стремящемся к, если для любого положительного числа ε найдется такое отрицательное число С, что при всех x, удовлетворяющих неравенству

x < C ,

будет выполняться неравенство

| f (x) – A | < ε .

f (x) → A

при

Предел функции f (x) при x, стремящемся к , равен числу A

| x | > C ,

будет выполняться неравенство

| f (x) – A | < ε .

f (x) → A

при x →

Предел функции f (x) при x, стремящемся к , равен

Функция f (x) стремится к при x, стремящемся к , если для любого положительного числа D найдется такое положительное число С, что при всех x, удовлетворяющих неравенству

| x | > C ,

будет выполняться неравенство

| f (x)| > D .

f (x) →

при x →

Предел функции f (x) при x, стремящемся к , равен

x > C ,

будет выполняться неравенство

| f (x)| > D .

f (x) →

при

Предел функции f (x) при x, стремящемся к , равен

Функция f (x) стремится к при x, стремящемся к , если для любого положительного числа D найдется такое отрицательное число С, что при всех x, удовлетворяющих неравенству

x < C ,

будет выполняться неравенство

| f (x)| > D .

f (x) →

при

Предел функции f (x) при x, стремящемся к числу a слева, равен

Замечание. Когда говорят, что x стремится к a слева, то это означает, что при определении предела функции рассматриваются только те значения x , которые меньше a .

Функция f (x) стремится к , при x, стремящемся к числу a слева, если для любого положительного числа С найдется такое положительное число δ что при всех x, удовлетворяющих неравенству

a – δ < x < a ,

будет выполняться неравенство

| f (x)| > C .

f (x) →

при x → a – 0

Предел функции f (x) при x, стремящемся к числу a справа, равен

Замечание. Когда говорят, что x стремится к a справа, то это означает, что при определении предела функции рассматриваются только те значения x , которые больше a .

Функция f (x) стремится к , при x , стремящемся к числу a справа, если для любого положительного числа С, найдется такое положительное число δ что при всех x, удовлетворяющих неравенству

a < x < a + δ ,

будет выполняться неравенство

| f (x)| > C .

f (x) →

при x → a + 0

Название:

Предел функции f (x) при x, стремящемся к числу a, равен числу A

Обозначения:

или

f (x) → A при x → a

Определение:

| x – a | < δ ,

будет выполняться неравенство

| f (x) – A | < ε .

Название:

Предел функции f (x) при x, стремящемся к , равен числу A

Обозначения:

или

f (x) → A при

Определение:

Число A называют пределом функции f (x) при x , стремящемся к , если для любого положительного числа ε найдется такое положительное число С, что при всех x, удовлетворяющих неравенству

x > C ,

будет выполняться неравенство

| f (x) – A | < ε .

Название:

Предел функции f (x) при x, стремящемся к , равен числу A

Обозначения:

или

f (x) → A при

Определение:

Число A называют пределом функции f (x) при x , стремящемся к , если для любого положительного числа ε найдется такое отрицательное число С, что при всех x, удовлетворяющих неравенству

x < C ,

будет выполняться неравенство

| f (x) – A | < ε .

Название:

Предел функции f (x) при x, стремящемся к , равен числу A

Обозначения:

или

f (x) → A при x →

Определение:

| x | > C ,

будет выполняться неравенство

| f (x) – A | < ε .

Название:

Предел функции f (x) при x, стремящемся к , равен

Обозначения:

или

f (x) → при x →

Определение:

| x | > C ,

будет выполняться неравенство

| f (x)| > D .

Название:

Предел функции f (x) при x, стремящемся к , равен

Обозначения:

или

f (x) → при

Определение:

x > C ,

будет выполняться неравенство

| f (x)| > D .

Название:

Предел функции f (x) при x, стремящемся к , равен

Обозначения:

или

f (x) → при

Определение:

x < C ,

будет выполняться неравенство

| f (x)| > D .

Название:

Предел функции f (x) при x, стремящемся к числу a слева, равен

Обозначения:

или

f (x) → при x → a – 0 .

Определение:

a – δ < x < a ,

будет выполняться неравенство

| f (x)| > C .

Название:

Предел функции f (x) при x, стремящемся к числу a справа, равен

Обозначения:

или

f (x) → при x → a + 0 .

Определение:

a < x < a + δ ,

будет выполняться неравенство

| f (x)| > C .

Свойства пределов функций

Если у функций f (x) и g (x) при x , стремящемся к a , существуют пределы

и ,

где A и B – некоторые числа, то при x , стремящемся к a , существуют также и пределы суммы, разности и произведения этих функций, причем

* * *

Если, кроме того, выполнено условие

то при x , стремящемся к a , существует предел дроби

причем

Для любой непрерывной функции F (x) справедливо равенство

Раскрытие неопределенностей типа

Определение 1 . Если при нахождении предела дроби выясняется, что и числитель дроби, и знаменатель дроби стремятся к стремятся к, то вычисление такого предела называют раскрытием неопределенности типа .

Часто неопределенность типа удается раскрыть, если и в числителе дроби, и в знаменателе дроби вынести за скобки «самое большое» слагаемое. Например, в случае, когда в числителе и в знаменале дроби стоят многочлены, «самым большим» слагаемым будет член с наивысшей степенью.

Пример 1. Найти предел функции предел функции

Решение. Вынесем за скобки «самое большое» слагаемое в каждой из скобок числителя и знаменателя дроби и, используя свойства пределов функций, получим

Ответ.

Пример 2. Найти предел функции предел функции

Решение. Преобразуем выражение, стоящее под знаком предела, к более удобному виду:

Далее, используя свойства пределов функций, находим

Ответ. 3 .

Раскрытие неопределенностей типа

Определение 2 . Если при нахождении предела дроби выясняется, что пределы числителя и знаменателя дроби равны 0 , то вычисление такого предела называют раскрытием неопределенности .

В алгебраических дробях неопределенность при x → a раскрывается при помощи разложения на множители числителя и знаменателя дроби с последующим сокращением на соответствующую степень множителя (x – a) .

Пример 3. Найти предел функции

Решение. Поскольку и числитель, и знаменатель дроби стремятся к 0 при x → – 2 , то для того, чтобы раскрыть неопределенность типа , разложим числитель и знаменатель дроби на множители. С этой целью в числителе применим формулу сокращенного умножения «сумма кубов», а в знаменателе – разложение квадратного трехчлена на множители, а затем сократим дробь на (x + 2) :

Теперь предел знаменателя дроби равен – 11 , и, воспользовавшись свойствами пределов функций, получаем

Ответ.

Пример 4. Найти предел функции

Решение. В этом примере также возникает неопределенность типа .

Поскольку знаменатель дроби является разностью двух квадратных корней, каждый из которых стремится к одному и тому же числу 5 при x → 5 , то домножим и числитель, и знаменатель дроби на сумму этих квадратных корней и применим формулу сокращенного уножения «разность квадратов»:

Разложим теперь квадратный трехчлен 4x² – 9x – 55 на множители, а затем сократим числитель и знаменатель на (x – 5) :

Воспользовавшись свойствами пределов функций, получаем

К сожалению, из-за большого размера формул для расчета подробные вычисления на Вашем мобильном устройстве не видны. Их можно посмотреть только на устройствах с разрешением экрана по ширине не менее 768 пикселей (например, на стационарных компьютерах, ноутбуках и некоторых планшетах).

Указания к решению примера. Поскольку знаменатель дроби является разностью двух квадратных корней, каждый из которых стремится к одному и тому же числу 5 при x → 5 , то сначала необходимо домножить и числитель, и знаменатель дроби на сумму этих квадратных корней и применить формулу сокращенного уножения «разность квадратов». Затем, разложив квадратный трехчлен 4x² – 9x – 55 на множители, сократить числитель и знаменатель на (x – 5) .

После этого, воспользовавшись свойствами пределов функций, получить ответ.

На Вашем мобильном устройстве отображается только результат описанных операций.

Ответ.

Первый замечательный предел

В пределах, содержащих тригонометрические функции, неопределенность раскрывается с помощью первого замечательного предела

Пример 5. Найти предел функции

Решение. Числитель и знаменатель дроби стремятся к 0 при x → 0 , поэтому для того, чтобы раскрыть неопределенность типа , разложим числитель и знаменатель дроби на множители. С этой целью в числителе вынесем за скобки x², а в знаменателе воспользуемся формулой «разность косинусов»:

Теперь, воспользовавшись первым замечательным пределом и свойствами пределов функций, получаем

Ответ.

Пример 6. Найти предел функции

Решение. Чтобы вычислить данный предел, перейдем от переменной x к новой переменной z по формуле

Поскольку

то предел можно преобразовать к виду

Применяя формулы приведения и формулу для косинуса двойного угла, получаем

Теперь, воспользовавшись первым замечательным пределом и свойствами пределов функций, получаем

Ответ.

Раскрытие неопределенности типа . Второй замечательный предел

Определение 3. Если при нахождении предела степени некоторого выражения выясняется, что предел основания степени равен 1, а предел показателя степени равен , то вычисление такого предела называют раскрытием неопределенности .

Неопределенность раскрывается с помощью второго замечательного предела:

(1)

Если взять натуральный логарифм от обеих частей формулы (1), то второй замечательный предел примет вид:

(2)

Пример 7. Найти предел функции предел функции

Решение. Рассмотрим функцию

и, взяв от нее натуральный логарифм, найдем сначала предел функции y = ln f (x) при x →. Применяя свойства логарифмов, получаем

Преобразуем выражение, стоящее под знаком логарифма к виду, удобному для применения второго замечательного предела,

и заметим, что

Поэтому, воспользовавшись вторым замечательным пределом в виде (2) и свойствами пределов функций, находим

Поэтому функцию y = ln f (x) удобно представить в сдедующем виде

Воспользовавшись вторым замечательным пределом в виде (2), находим

В пределе

и числитель, и знаменатель дроби стремятся к стремятся к, поэтому для раскрытия неопределенности вынесем за скобки «самое большое» слагаемое в числителе дроби и «самое большое» слагаемое в знаменателе дроби и, используя свойства пределов функций, получим

Следовательно,

Следовательно, воспользовавшись свойствами пределов функций, получаем

Таким образом,

Ответ.

Пример 8. Найти предел функции

Решение. Рассмотрим функцию

и, взяв от нее натуральный логарифм, найдем сначала предел функции y = ln f (x) при x → – 6 . Применяя свойства логарифмов, получаем

Чтобы вычислить предел функции y = ln f (x) при x → – 6 , перейдем от переменной x к новой переменной z по формуле

x = – 6 + z .

Поскольку

то предел (3) можно преобразовать к виду, с помощью формулы (3), получаем

Воспользовавшись вторым замечательным пределом в виде (2) и свойствами пределов функций, получаем

Следовательно,

Ответ.

На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.

Пределы — Оценка

Сначала вы должны прочитать Ограничения (Введение)

Краткое описание ограничений

Иногда мы не можем что-то решить напрямую… но мы можем увидеть, что должно быть, по мере того, как мы подходим все ближе и ближе!

Пример:

(х ² − 1) (х — 1)

Рассчитаем для x=1:

(1 ² − 1) (1 − 1) знак равно (1 − 1) (1 − 1) знак равно 0 0

Теперь 0/0 — это сложность! На самом деле мы не знаем значения 0/0 (оно «неопределенно»), поэтому нам нужен другой способ ответить на этот вопрос.

Итак, вместо того, чтобы пытаться решить это для x = 1, давайте попробуем приближаться к все ближе и ближе:

Продолжение примера:

x		(х ² − 1) (х — 1)
0,5		1,50000
0,9		1.
0,99		1,99000
0,999		1,99900
0,9999		1,99990
0,99999		1,99999
…		…

Теперь мы видим, что когда x приближается к 1, тогда (х ² −1) (х-1) получает близко к 2

Теперь мы столкнулись с интересной ситуацией:

Когда x=1 мы не знаем ответа (это неопределенное )
Но мы видим, что будет 2

Мы хотим дать ответ «2», но не можем, поэтому вместо этого математики точно говорят, что происходит, используя специальное слово «предел»

предел из (х ² −1) (х-1) по мере приближения x к 1 равно 2

И записывается символами как:

lim x→1 x ² −1 x−1 = 2

Так что это особый способ сказать, «не обращая внимания на то, что происходит, когда мы туда добираемся, но по мере того, как мы подходим все ближе и ближе, ответ становится все ближе и ближе к 2»

На графике это выглядит так:

Так что, по правде говоря, мы не можем сказать, каково значение при x=1.

Но мы можем говорят, что когда мы приближаемся к 1, , предел равен 2.

Оценка пределов

«Оценка» означает нахождение значения ( думаю e-» значение» -ating )

В приведенном выше примере мы сказали, что ограничение равно 2, потому что выглядело так, будто должно было быть . Но этого на самом деле недостаточно!

На самом деле существует много способов , чтобы получить точный ответ. Давайте посмотрим на некоторые:

1. Просто введите значение

Первое, что нужно попробовать, это просто ввести значение ограничения и посмотреть, работает ли оно (другими словами, подстановка).

Пример:

lim x→10 x 2

10 2 = 5

Легко!

Пример:

lim x→1 x ² −1 x−1

(1−1) (1−1) = 0 0

Не повезло. Нужно попробовать что-то другое.

2. Факторы

Можем попробовать факторинг.

Пример:

lim x→1 x ² −1 x−1

lim x→1 x ² −1 x−1 = lim x→1 (x−1) (x−18) 0 (90 90−1)(x01) 0 (90 90−1)(x01) 1

= lim x→1 (x+1)

Теперь мы можем просто подставить x=1, чтобы получить предел:

lim х→1 (х+1) = 1+1 = 2

3. Конъюгат

Для некоторых дробей может помочь умножение верхнего и нижнего числа на сопряженное число.

В сопряжении мы меняем
знак в середине двух терминов, например:

Вот пример, где это поможет нам найти предел:

lim x→4 2−√x 4-х

Оценка этого при x=4 дает 0/0, что не является хорошим ответом!

Итак, давайте попробуем переставить:

Умножить верх и низ на сопряжение верха:		2−√x 4−x × 2+√x 2+√x

Упростить верх, используя (a+b)(a−b) = a ² − b ² :		2 ² − (√x) ² (4−x)(2+√x)

Упростить верх дальше:		4−x (4−x)(2+√x)

Отмена (4-x) сверху и снизу:		1 2+√x

Итак, теперь у нас есть:

LIM x → 4 2 — √x 4 -X = LIM x → 4 1 2+√x = 1 2+a 1 4

Готово!

4.

Бесконечные пределы и рациональные функции
Рациональная функция представляет собой отношение двух многочленов:
f(x) = P(x) Q(x)

Например, здесь P(x) = x ³ + 2x — 1 и Q(x) = 6x ² :
x ³ + 2x − 1 6x ²
Найдя общую степень функции, мы можем узнать, равен ли предел функции 0, бесконечности, -бесконечности или легко вычисляется из коэффициентов.
Подробнее читайте на странице Пределы бесконечности.

5. Правило Лопиталя
Правило Лопиталя может помочь нам оценить пределы, которые на первый взгляд кажутся «неопределенными», такие как 0 0 и ∞ ∞ .
Узнайте больше на сайте L’Hôpital’s Rule.

6. Формальный метод
Формальный метод доказывает, что мы можем максимально приблизить к ответу , приблизив «x» к «a».
Подробнее читайте в разделе «Пределы (формальное определение)»

Ограничения (формальное определение)
Сначала прочтите Введение в ограничения
Приближается…
Иногда мы не можем что-то решить напрямую… но мы можем увидеть, что должно быть, по мере того, как мы подходим все ближе и ближе!
Пример:
(x ² − 1) (x − 1)
Рассчитаем для x=1:
(1 ² − 1) (1 − 1) = (1 − 1) (1 − 1) = 0 0
Теперь 0/0 — это сложность! На самом деле мы не знаем значения 0/0 (оно «неопределенно»), поэтому нам нужен другой способ ответить на этот вопрос.
Итак, вместо того, чтобы пытаться решить это для x = 1, давайте попробуем приближаться к все ближе и ближе:
Продолжение примера:
x (х ² − 1) (х − 1)
0,5 1,50000
0,9 1.
0,99 1,99000
0,999 1,99900
0,9999 1,99990
0,99999 1,99999
… …
Теперь мы видим, что когда x приближается к 1, тогда (x ² −1) (x−1) получает близко к 2
Теперь мы столкнулись с интересной ситуацией:
Когда x=1 мы не знаем ответа (это неопределенное )
Но мы видим, что будет 2
Мы хотим дать ответ «2», но не можем, поэтому вместо этого математики точно говорят, что происходит, используя специальное слово «предел»
предел из (x ² −1) (x−1) при приближении x к 1 равно 2
И записывается символами как:
lim x→1 x ² −1 x−1 = 2
Так что это особый способ сказать, «не обращая внимания на то, что происходит, когда мы туда добираемся, но по мере того, как мы подходим все ближе и ближе, ответ становится все ближе и ближе к 2»
На графике это выглядит так:
Так что, по правде говоря, мы не можем сказать, каково значение при x=1.
Но мы можем сказать, что по мере приближения к 1, предел равен 2.

Более формальный
Но вместо того, чтобы говорить, что предел равен некоторому значению, потому что он выглядел так, как будто он приближается к , мы можем дать более формальное определение.
Итак, начнем с общей идеи.
От английского к математике
Скажем сначала по-английски:
«f(x) приближается к некоторому пределу , когда x приближается к некоторому значению»
Когда мы называем Предел «L», а значение, при котором x приближается к «a», мы можем сказать
«f(x) приближается к L, когда x приближается к a»
Расчет «Закрыть»
Итак, как математически можно сказать «близко»… можем ли мы вычесть одно значение из другого?
Пример 1: 4,01 − 4 = 0,01 (выглядит хорошо)
Пример 2: 3,8 − 4 = −0,2 ( отрицательно близко?)
Так что же нам делать с негативами? Нас не волнует положительное или отрицательное, мы просто хотим знать, как далеко. .. что является абсолютным значением.
«Насколько близко» = |a−b|
Пример 1: |4.01−4| = 0,01
Пример 2: |3,8−4| = 0,2
И когда |a−b| мал, мы знаем, что мы близки, поэтому пишем:
«|f(x)−L| мало, когда |x−a| мало»
А эта анимация показывает, что происходит с функцией
f(x) = (x ² −1) (x−1)
изображения/limit-lines.js
f(x) приближается к L=2, когда x приближается к a=1,
поэтому |f(x)−2| мало, когда |x−1| маленький.
Дельта и Эпсилон
Но «маленький» по-прежнему английский, а не «математический».
Выберем два значения должен быть меньше :
δ что |x−a| должен быть меньше
ε что |f(x)−L| должен быть меньше
Примечание: эти две греческие буквы (δ — это «дельта» и ε — это «эпсилон») — это
, поэтому они часто используются, поэтому мы получаем фразу « дельта-эпсилон 9». 0010 »
А у нас есть:
|f(x)−L|<ε при |x−a|<δ
Это действительно так! Итак, если вы понимаете, что понимаете ограничения…
… но чтобы было абсолютно точным , нам нужно добавить следующие условия:
верно для любого ε>0
δ существует и >0
x — это , не равное a, что означает 0<|x−a|
И вот что мы получаем:
Для любого ε>0 существует δ>0, такое что |f(x)−L|<ε при 0<|x−a|<δ
Это формальное определение. На самом деле это выглядит довольно страшно, не так ли?
Но по сути там написано что-то простое:
f(x) приближается к L , когда x приближается к
Как использовать в пруфе
Чтобы использовать это определение в доказательстве, мы хотим пройти
От кого: Кому:
0<|x−a|<δ |f(x)−L|<ε
Обычно это означает поиск работающей формулы для δ (в терминах ε).
Как найти такую формулу?
Угадай и проверь!
Верно, мы можем:
Поэкспериментируйте, пока не найдете формулу, которая может работать
Протестируйте , чтобы увидеть, работает ли эта формула
Пример: Попробуем показать, что
lim х→3 2х+4 = 10
Используя буквы, о которых мы говорили выше:
Значение, к которому x приближается, «a», равно 3
Предел «L» равен 10
Итак, мы хотим знать, как нам перейти от:
0<|x−3|<δ от
до
|(2x+4)−10|<ε
Шаг 1: Поэкспериментируйте, пока не найдете формулу, по которой
может работать
Начните с: |(2x+4)−10| < ε
Упрощение: |2x−6| < ε
Шаг 2 снаружи ||: 2|х−3| < ε
Разделите обе части на 2: |х−3| < е/2
Теперь мы можем предположить, что δ=ε/2 может работать
Шаг 2:
Проверьте , чтобы увидеть, работает ли эта формула.
Итак, можем ли мы получить из 0<|x−3|<δ от до |(2x+4)−10|<ε … ?
Посмотрим…
Начните с: 0 < |х-3| < δ
Замените δ на ε/2: 0 < |х-3| < ε/2
Умножить все на 2: 0 < 2|х−3| < ε
Переместите 2 внутрь ||: 0 < |2x−6| < ε
Заменить «−6» на «+4−10»: 0 < |(2x+4)−10| < ε
Да! Мы можем перейти от 0<|x−3|<δ к |(2x+4)−10|<ε , выбрав δ=ε/2
ГОТОВО!
Итак, мы видели, что по заданному ε можно найти δ, поэтому верно, что:
Для любого ε существует такое δ, что |f(x)−L|<ε при 0<|x−a|<δ
И мы доказали, что
lim х→3 2х+4 = 10
Заключение
Это было довольно простое доказательство, но, надеюсь, оно объясняет странную формулировку «есть …» и показывает хороший подход к такого рода доказательствам.

Пределы — формула, значение, примеры
Пределы в математике определяются как значения, к которым функция приближается к выходным данным для заданных входных значений. Пределы играют жизненно важную роль в вычислениях и математическом анализе и используются для определения интегралов, производных и непрерывности. Он используется в процессе анализа и всегда касается поведения функции в конкретной точке. Предел последовательности далее обобщается в понятии предела топологической сети и связан с пределом и прямым пределом в категории теории. Обычно интегралы делятся на два типа, а именно: определенные и неопределенные интегралы. Для определенных интегралов правильно определены верхний и нижний пределы. Тогда как неопределенные интегралы выражаются без ограничений, и при интегрировании функции он будет иметь произвольную константу. Давайте подробно обсудим определение и представление пределов функции со свойствами и примерами.
1. Что такое ограничения?
2. Ограничения и функции
3. Свойства пределов
4. Предел функции двух переменных
5. Пределы сложных функций
6. Пределы экспоненциальных функций
9. Часто задаваемые вопросы о лимитах
Что такое ограничения?
Пределы в математике — это уникальные действительные числа. Рассмотрим вещественную функцию «f» и действительное число «c», предел обычно определяется как $\lim _{x \rightarrow c} f(x)=L$. Это читается как «предел f для x, когда x приближается к c, равному L». «lim» показывает предел, а тот факт, что функция f(x) приближается к пределу L, когда x приближается к c, показан правой стрелкой. 9{+}} \mathrm{f}(\mathrm{x})=\mathrm{L}\)
Примечание: Предел функции существует между любыми двумя последовательными целыми числами.
Свойства пределов
Вот некоторые свойства пределов функции: Если пределы $ \lim _{x \rightarrow a}$ f(x) и $\lim _{x \rightarrow a}\ ) g(x) существует, а n является целым числом, тогда
Закон сложения: \(\lim _{x \rightarrow a}[f(x)+g(x)]=\lim _{x \rightarrow a} f(x)+\lim _{x \rightarrow a} g(x)$
Закон вычитания: $ \lim _{x \rightarrow a}[f(x)-g(x)]=\lim _{x \rightarrow a} f(x)-\lim _{x \rightarrow a } г(х)$
Закон умножения: $\lim _{x \rightarrow a}[f(x) \cdot g(x)]=\lim _{x \rightarrow a} f(x) \cdot \lim _{x \ стрелка вправо a} g(x)$
Закон деления: $ \lim _{x \rightarrow a}\left[\frac{f(x)}{g(x)}\right]=\frac{\lim _{x \rightarrow a} f (x)}{\lim _{x \rightarrow a} g(x)}, \text { где } \lim _{x \rightarrow a} g(x) \neq 0$ 9{2}}\) < ∆ . Он определяется как $\lim _{(x, y) \rightarrow(a, b)}$ f(x,y) = C.
Пределы функций и непрерывность
Пределы функции и непрерывность функции тесно связаны друг с другом. Функции могут быть непрерывными и прерывистыми. Чтобы функция была непрерывной, если есть небольшие изменения на входе функции, то должны быть небольшие изменения и на выходе.
В элементарном исчислении условие f(X) →λ при x → a означает, что число f(x) может лежать сколь угодно близко к числу λ, пока мы берем число, не равное числу а, но достаточно близко к а. Что показывает, что f(a) может быть очень далеко от λ и нет необходимости даже определять f(a). Очень важный результат, который мы используем для вывода функции, таков: f'(a) данной функции f при числе a можно рассматривать как
f'(a) =$\lim _{x \rightarrow a} \frac{f(x)-f(a)}{x-a}$
Пределы сложных функций
Чтобы дифференцировать функции сложной переменной, следуйте следующей формуле:
Функция $f(z)$ называется дифференцируемой в $z=z_{0}$, если
$\lim _{\Delta z \rightarrow 0} \frac{f\left(z_{0}+\Delta z\right)-f\left(z_{0}\right)}{\Delta z}\ ) существуют. Здесь \(\Delta \mathrm{z}=\Delta \mathrm{x}+\mathrm{i} \Delta \mathrm{y}$
9{х}=\infty\)
☛ Также проверьте:
Исчисление
Формула ограничения
Интеграция
Производная формула
Формулы интегрирования
Часто задаваемые вопросы о лимитах
Что такое предельная формула?
Формула пределов: Пусть y = f(x) как функция x. Если в точке х = а функция f(x) принимает неопределенный вид, то можно рассматривать значения функции, очень близкой к а. Если эти значения стремятся к некоторому определенному уникальному числу, когда x стремится к a, то полученное уникальное число называется пределом f(x) при x = a.
Что такое ограничения в вычислениях?
Предел сообщает нам значение, к которому приближается функция по мере того, как входные данные этой функции становятся все ближе и ближе (приближаются) к некоторому числу. Идея предела лежит в основе всех дифференциалов и интегралов в исчислении.
Когда предел не может существовать?
Обычная ситуация, когда предел функции не существует, — это когда односторонние пределы существуют и не равны: функция «прыгает» в точке. Предела при x→0 не существует.
Почему мы используем ограничения в математике?
Предел, математическое понятие, основанное на идее близости, используется главным образом для присвоения значений определенным функциям в точках, где значения не определены, таким образом, чтобы они соответствовали ближайшим значениям.
Как узнать, является ли ограничение односторонним?
Односторонний предел — это значение, к которому функция приближается, когда значения x приближаются к пределу *только с одной стороны*. Например, f(x)=|x|/x возвращает -1 для отрицательных чисел, 1 для положительных чисел и не определено для 0. Односторонний *правый* предел f при x=0 равен 1, и односторонний *левый* предел при x=0 равен -1.
Как пределы вычислений используются в реальной жизни?
Пределы также используются в качестве реального приближения к расчету производных. Таким образом, для выполнения расчетов инженеры будут аппроксимировать функцию, используя небольшие различия в функции, а затем пытаться вычислить производную функции, используя все меньшие и меньшие интервалы в интервалах выборки функции.
Каков предел функции синуса?
Поскольку sin(x) всегда где-то в диапазоне от -1 до 1, мы можем установить g(x) равным -1/x и h(x) равным 1/x. Мы знаем, что предел как -1/x, так и 1/x при приближении x к положительной или отрицательной бесконечности равен нулю, поэтому предел sin(x)/x при приближении x к положительной или отрицательной бесконечности равен нулю.
Как найти предел функции алгебраически
Если вам нужно найти предел функции алгебраически, у вас есть четыре метода на выбор: подстановка значения x , разложение на множители, рационализация числителя и нахождение наименьшего общий знаменатель.
Лучше всего начать с первой техники. Вы можете использовать этот метод только в том случае, если функция непрерывна при значении x , при котором вы берете предел. Если функция не определена в этом x , вы должны перейти к другим методам, чтобы упростить вашу функцию, чтобы вы могли подставить приближенное значение для x.
Найдите предел, подставив значение
x Первый метод алгебраического решения для предела состоит в том, чтобы подставить число, к которому приближается x , в функцию. Если вы получаете неопределенное значение (0 в знаменателе), вы должны перейти к другому методу. Но если ваша функция непрерывна в этом x , вы получите значение, и все готово; Вы нашли свой предел! Например, с помощью этого метода вы можете найти этот предел:
Предел равен 3, потому что f (5) = 3, и эта функция непрерывна при x = 5.
Найдите предел, разложив на множители
Факторинг — это метод, который стоит попробовать, когда подключение не удается, особенно когда какая-либо часть данной функции является полиномиальным выражением.
Скажем, вас попросили найти этот предел:
Сначала вы пытаетесь подставить 4 в функцию, и вы получаете 0 в числителе и знаменатель, который говорит вам перейти к следующей технике. Квадратное выражение в числителе требует, чтобы вы попытались его разложить на множители. Обратите внимание, что числитель предыдущей функции равен ( x – 4)( x – 2). x – 4 сокращения сверху и снизу дроби. На этом шаге у вас останется f ( x ) = x – 2. Вы можете подставить 4 в эту непрерывную функцию, чтобы получить 2.
Если построить график этой функции, она будет выглядеть как прямая линия 9.0015 f ( x ) = x – 2, но у него есть дыра, когда x = 4, потому что исходная функция все еще не определена (потому что она создает 0 в знаменателе). Рисунок иллюстрирует это.
Если после того, как вы разложили на множители верхнюю и нижнюю часть дроби, член в знаменателе не сократился и искомое значение не определено, предел функции при этом значении составляет x не существует (что можно записать как DNE ).
Например, эта функция действует следующим образом:
( x – 7) вверху и внизу отменяется. Поэтому, если вас попросят найти предел функции, поскольку x приближается к 7, вы можете подставить 7 в отмененную версию и получить 11/8. Но если вы пытаетесь найти
предела DNE, потому что вы получите 0 в знаменателе. Таким образом, эта функция имеет предел везде, кроме случаев, когда x приближается к –1.
Найдите предел, рационализируя числитель
Третий метод, который вам нужно знать, чтобы найти пределы алгебраически, требует, чтобы вы рационализировали числитель. Функции, требующие этого метода, имеют квадратный корень в числителе и полиномиальное выражение в знаменателе. Например, вас попросили найти предел этой функции, поскольку x приближается к 13:
Подстановка чисел завершается ошибкой, когда вы получаете 0 в знаменателе дроби. Факторинг терпит неудачу, потому что уравнение не имеет многочлена к фактору. В этой ситуации, если вы умножите числитель и знаменатель на сопряженное с числителем, член в знаменателе, который был проблемой, сократится, и вы сможете найти предел:
Умножьте верхнюю и нижнюю часть дроби на сопряженную.
Сопряженный числитель равен
.
Умножив, вы получите такую настройку:
Умножьте члены, используя первый, внешний, внутренний, последний (FOIL) метод в числителе, чтобы получить
, что упрощается до x – 13 (два средних члена отменяются, и вы комбинируете аналогичные термины из ФОЛЬГИ).
Факторы отмены.
Отмена дает вам это выражение:
Условия ( x – 13) отменяются, оставляя вам следующий результат:
Рассчитать пределы.
Когда вы подставляете 13 в функцию, вы получаете 1/6, что является пределом.
Найдите предел, найдя наименьший общий знаменатель
Когда вам дана сложная рациональная функция, вы используете четвертый и последний алгебраический метод нахождения предела. Техника вставки не работает, потому что вы получаете 0 в одном из знаменателей. Функция неразложима, и у вас нет квадратных корней, которые можно было бы рационализировать. Поэтому вы знаете, чтобы перейти к последней технике. С помощью этого метода вы объединяете функции, находя наименьший общий знаменатель (LCD). Условия отменяются, и в этот момент вы можете найти предел.
Например, выполните следующие действия, чтобы найти предел:
Найдите ЖК-дисплей фракций вверху.
Распределите числители сверху.
Сложите или вычтите числители, а затем сократите члены.
Вычитание числителей дает
, который затем упрощается до
.
Используйте правила дробей для дальнейшего упрощения.
Подставьте предельное значение в эту функцию и упростите.
Вы хотите найти предел, поскольку x приближается к 0, поэтому предел здесь равен –1/36.
Об этой статье
Эта статья взята из книги:
Предварительное исчисление для чайников,
Об авторе книги:
Мэри Джейн Стерлинг, изучающая алгебру, деловое исчисление, геометрию и конечную математику в Университете Брэдли в Пеории, штат Иллинойс, более 30 лет. Она является автором нескольких книг For Dummies, , в том числе Рабочая тетрадь по алгебре для чайников, Алгебра II для чайников, и Рабочая тетрадь по алгебре II для чайников.
Эту статью можно найти в категории:
Предварительное исчисление,
Формула пределов – определение, свойства, формулы и примеры
Примеры пределов – одно из самых сложных понятий в математике, по мнению многих студентов. Однако благодаря более легкому пониманию и постоянной практике учащиеся могут тщательно изучить концепции пределов в математике, пример предела функции, определение пределов и свойства пределов. Предельная математика — одно из самых важных понятий в исчислении. Исчисление — это раздел математики, который занимается вычислениями, связанными с постоянно меняющимися величинами. Формула математического предела может быть определена как значение, которое функция возвращает в качестве вывода для заданных входных значений.
Что такое пределы и формула пределов в математике?
Пределы Математика очень важна в вычислениях. Это одна из основных предпосылок для понимания других концепций исчисления, таких как непрерывность, дифференцирование, формула предела интегрирования и т. Д. В большинстве случаев математические формулы предела представляют собой представление поведения функции в определенной точке. Следовательно, понятие пределов используется для анализа функции. Математическое понятие предела топологической сети обобщает предел последовательности и, следовательно, связывает математику пределов с категорией теории. Интегралы в общем подразделяются на определенные и неопределенные интегралы. Верхний и нижний пределы указываются в случае определенной формулы предела интегрирования. Однако формулы неопределенного предела интегрирования определяются без указанных пределов и, следовательно, имеют произвольную константу после интегрирования. В последующих разделах представлен краткий обзор различных концепций, необходимых для лучшего понимания формул математических пределов.
Формула пределов: Пусть y = f(x) как функция x. Если в точке х = а функция f(x) принимает неопределенный вид, то можно рассматривать значения функции, очень близкой к а. Если эти значения стремятся к некоторому определенному уникальному числу, когда x стремится к a, то полученное уникальное число называется пределом f(x) при x = a.
Пределы Математика
Предел действительнозначной функции ‘f’ относительно переменной ‘x’ может быть определен как:
\[\lim_{x\rightarrow p}f(x)=L\]
В приведенном выше уравнении слово «lim» относится к пределу.
Он обычно описывает, что функция f(x) с действительным знаком стремится достичь предела «L», когда «x» стремится к «p», и обозначается стрелкой вправо.
Мы можем прочитать это как: «предел любой заданной функции ‘f’ от ‘x’, когда ‘x’ приближается к ‘p’, равен ‘L’».
Каковы свойства или законы пределов?
Свойства пределов следующие:
Обозначение предела
Предел функции обозначается как f (x) → L как x → p или в обозначении предела как:
\[\lim_{x\rightarrow p}f(x)=L\]
Предположим, что существует \[\lim_{x\rightarrow p}f(x)\], \[\lim_{x\rightarrow p}g(x)\], \[\lim_{x\rightarrow p }f_1(x)\]……. .\[\lim_{x\стрелка вправо p}f_n(x)\]. Это предположение сделано для объяснения других свойств пределов.
Правило сумм
Правило сумм утверждает, что сумма индивидуальных пределов любых двух функций равна пределу суммы этих функций.
\[\lim_{x\стрелка вправо p}f(x)\] + \[\lim_{x\стрелка вправо p}g(x)\] =\[\lim_{x\стрелка вправо p}\mid f( x)+g(x)\mid \]
Расширенное правило сумм
Расширенное правило сумм совпадает с правилом сумм. Однако он определен для пределов более чем двух функций.
\[\lim_{x\стрелка вправо p}f_1(x)\] + \[\lim_{x\стрелка вправо p}f_2(x)\] +……..\[\lim_{x \rightarrow p}f_n(x)\] =\[\lim_{x\rightarrow p}\mid f_1(x)+f_2(x)+…….f_n(x)\mid \]
Правило постоянной функции
Правило постоянной функции утверждает, что предел постоянной функции равен константе.
Множественное правило констант
Предел функции, умноженный на постоянное значение, равен константе, умноженной на предел функции.
\[\lim_{x\rightarrow p}kf(x)\] = k \[\lim_{x\rightarrow p}f(x)\]
Правило произведения
Правило произведения гласит, что произведение пределов двух отдельных функций равно пределу произведения функций.
\[\lim_{x\rightarrow p}f(x)\ast \lim_{x\rightarrow p}g(x)=\lim_{x\rightarrow p}\mid f(x)\ast g(x )\mid \]
Расширенное правило продукта
Расширенное правило продукта совпадает с правилом продукта. Однако учитываются более двух функций.
\[\lim_{x\стрелка вправо p}f_1(x)\ast \lim_{x\стрелка вправо p}f_2(x)\ast . …..\lim_{x\стрелка вправо p}f_n(x) =\lim_{x\стрелка вправо p}\mid \lim_{x\стрелка вправо p}f_1(x)\ast \lim_{x\стрелка вправо p}f_2(x)\ast ……\lim_{x\ стрелка вправо p}f_n(x)\mid \]
Правило частного
Частное частных пределов двух функций, когда предел знаменателя не равен нулю, равен пределу частного двух функций, где функция знаменателя не равна нуль.
\[\ frac {\ displaystyle \ lim \ limit_ {x \ rightarrow p} f (x)} {\ displaystyle \ lim \ limits_ {x \ rightarrow p} g (x)} = \ lim_ {x \ rightarrow p }\frac{f(x)}{g(x)}\]
Степенное правило
9n}\]
, где ‘n’ — любое целое число
Аналогично, когда степени представляют собой дроби, правило степеней можно сформулировать следующим образом:
\[\lim_{x\rightarrow p}\sqrt{\ mid f(x)\mid }=\sqrt{\lim_{x\стрелка вправо p}f(x)}\]
Список формул важных пределов в пределах
Список формул математических пределов
1
\[\lim_{x\стрелка вправо 0}\]\[sinx=0\]
2 9n\]
Выше приведен список формул ограничения.
Если пределы функции заданы в форме частного, как я могу ее оценить?
Если предел функции задан в виде частного, можно вычислить выражение методом факторизации. Шаги для того же:
Полностью сведите числитель и знаменатель к его множителям.
Теперь упростим выражение, разделив числитель и знаменатель на любой общий для них множитель.
Теперь вы можете оценить полученный лимит, не забывая о правильном домене.
Как я могу оценить пределы частного?
Вы можете очень легко оценить предел частного, предсказав LCD рассматриваемого выражения. Шаги, которые вы можете предпринять для такой оценки:
Предсказать LCD двух членов в числителе для знаменателя.
Преобразуйте обе дроби в числителе так, чтобы они имели LCD в знаменателе.
Умножьте знаменатель и числитель с помощью ЖК-дисплея.
Теперь применим распределительное свойство пределов.
Упростите полученное выражение и разложите числитель.
Отменить одинаковые дроби, присутствующие в результирующем выражении.
Вычислите выражение, сохраняя пределы x в формуле.
Как оценить предел функции, содержащей корень?
Очень легко вычислить предел функции, содержащей корень, используя сопряженный метод. Вы можете применить этот метод, просто выполнив шаги, указанные ниже:
Непосредственно вычислить частное, если оно не дано в неопределенной форме, то есть (0/0).
Вы также можете использовать метод наименьшего общего знаменателя (LCD), чтобы преобразовать два рассматриваемых частных в одно частное, взяв их сумму или разность.
Если рассматриваемый числитель также содержит корень, то рационализируйте числитель, а затем умножьте числитель и знаменатель на сопряженное число числителя.
Теперь упростим полученное выражение и оценим полученный предел.
Как я могу оценить пределы, если частное с абсолютными значениями дано?
Вы можете легко оценить пределы выражения, содержащего частное с абсолютными значениями. Следуйте инструкциям ниже, чтобы решить проблемы такого рода:
Найдите наименьший общий знаменатель (НОД) рассматриваемой дроби.
Если вы не можете найти предел, выберите различные значения, близкие к неопределенной функции по обе стороны от входа.
Теперь вы можете использовать числовые данные для анализа ограничений с обеих сторон.
Пределы функции — краткий обзор
Различные свойства пределов используются для выполнения операций с пределами функции, а не с самой функцией.
Вы можете предсказать предел полиномиальной функции, вычислив сумму отдельных членов.
Предел функции, возведенной в степень, равен степени предела функции, широко известный как метод прямой подстановки.
Корень предела функции равен пределу корня функции.
Запись частного в факторизованной форме с последующим упрощением может помочь найти предел функции, выраженной в виде частного.
Можно найти предел сложной функции, найдя ее ЖК-дисплей.
Метод сопряжения можно использовать для нахождения предела функции, содержащей корень.
Метод факторинга также можно использовать для нахождения предела некоторых функций
Численное свидетельство или кусочная установка могут помочь в оценке предела частного, содержащего абсолютные значения.
Ограничения Примеры и решения
Вычислить \[\lim_{x\стрелка вправо 2}\](1×3 — 3×2 + 6x -3)
Ответ:
\[\lim_{x\стрелка вправо 2}\](1×3 — 3×2 + 6x -3)
= \[\lim_{x\стрелка вправо 2}\](1×3) — \[\lim_{x\стрелка вправо 2}\](3×2) + \[\lim_{x\стрелка вправо 2} \](6x) — \[\lim_{x\стрелка вправо 2}\](3)
= 1\[\lim_{x\стрелка вправо 2}\](x3) — 3\[\lim_{x\стрелка вправо 2}\](x2) + 6\[\lim_{x\стрелка вправо 2}\](x) — (3)
= 1(2)3 — 3(2)2 +6(2) -3
= 1 х 8 — 3 х 4 + 12 — 3
= 8 — 12 + 9
= 17-12
= 5
0 Разделить на 0: решение предельных задач в математическом анализе, часть 1
ограничений, но у вас могут возникнуть проблемы с решением проблем с ограничениями в домашнем задании, особенно когда вы сначала найдете «0, деленное на 0». В этом посте мы покажем вам методы, которые вы должны знать для решения подобных проблем.
I. Идея пределов и
Замена (очень просто, когда работает)
Вам, наверное, уже говорили что-то вроде
$\displaystyle{\lim_{x \to a}f(x)} = L$ означает, что x все ближе и ближе к a ,
функция f приближается к L (даже если она никогда не равняется L ).
Вы уже на пути к пониманию пределов, если это утверждение имеет для вас смысл, и вы можете посмотреть на рисунок, подобный приведенному ниже, и сразу увидеть, что
$$\lim_{x \to 2}f(x) = 4 $$
потому что независимо от того, движемся ли мы к $x=2$ слева или справа, мы приближаемся к высоте $y = 4$.
В этом случае пределом является просто значение функции при x = 2: $\displaystyle{\lim_{x \to 2}f(x)} = f(2) = 4$.
А в некоторых домашних заданиях и тестовых вопросах (если ваш учитель чувствует себя хорошо), чтобы найти предел, вы просто подставляете значение x в функцию и находите значение в этом месте. Мы назовем этот подход Тактика №1: Замена .
Пример 1 .
Найдите $\displaystyle{\lim_{x \to 2}x+2}$.
Решение .
Давайте попробуем просто подставить $x=2$ в выражение:
$$\lim_{x \to 2}x+2 = 2 + 2 = 4 \quad \cmark$$
Это тот же предел, что показан на графике выше: на графике изображена функция $f(x) = x+2$, поэтому, приближаясь к $x =2$ слева или справа, мы приближаемся к фактическому значению функции в $x=2$, то есть $y = f(2) = 4$.
В этом случае простая подстановка значения x = 2 в функцию работает: вы получаете число ($f(2) =4$), и все готово. Достаточно было простой техники «Подстановки».
[Конец примера 1.]
Пример 2 .
Найдите $\displaystyle{\lim_{x \to \pi/2}\sin x}$.
Решение .
Давайте снова попробуем Подстановку и установим $x = \dfrac{\pi}{2}$:
$$\lim_{x \to \dfrac{\pi}{2}}\sin x = \sin \dfrac{ \pi}{2} = 1 \quad \cmark$$

График показывает $y = \sin x$. Когда вы приближаетесь к $x = \dfrac{\pi}{2}$ слева или справа, вы приближаетесь к высоте y = 1, которая является значением функции на $x = \dfrac {\pi}{2}$. Следовательно, предел как $x \to \dfrac{\pi}{2}$ sin x равен 1.
В этом случае снова работает подстановка: вы подставляете значение $x = \dfrac{\pi} {2}$, и вы получите число $\left(f\left(\dfrac{\pi}{2}\right) =1 \right)$. Вы закончили; легкий. 92-4}{x-2} = \frac{4-4}{2-2} = \frac{0}{0}$$
О-о: $\dfrac{0}{0}$ .
Это проблема. Давайте на мгновение остановим этот пример. . .

Почти во всех ваших домашних заданиях и тестовых вопросах, когда вы пытаетесь заменить, вы получите 0, деленное на 0. Затем вам понадобится другая тактика, чтобы найти предел.
Морщина : Нам не понадобилось бы понятие предела, если бы вы всегда могли просто подставить число и найти там значение функции. Вместо этого, правда в том, что когда вы попробуете заменить почти все свои домашние задания и контрольные вопросы, вы получите $\dfrac{0}{0}$, «ноль, деленный на ноль». Этот результат известен как неопределенный предел , что является причудливым способом сказать «еще не известно». Он говорит вам, что на самом деле ответ может быть любым — вы просто еще не знаете — и поэтому у вас есть еще над чем поработать.
В частности, результат $\dfrac{0}{0}$ указывает на необходимость использования другого метода для нахождения предела. К счастью, три простые тактики позволят вам решить большинство проблем. Давайте посмотрим на каждый.
II. Когда вы получите 0, деленное на 0, сначала попробуйте
разложить на множители
. Если вы попытаетесь заменить и получите $\dfrac{0}{0}$, вашим следующим шагом будет попытка 92-4}{x-2}}$ $=$ $\displaystyle{\lim_{x \to 2}\frac{(x+2)(x-2)}{x -2}}$ Ах, теперь мы можем отменить проблемный член: $=$ $\displaystyle{\lim_{x \to 2} (x+2)\cancel{(x-2)}}{\cancel{x-2}}}$ $=$ $\displaystyle{\lim_{x \to 2} \,(x+2)}$ А теперь простая замена для завершения: 92-4}{x-2}} = \lim_{x \to 2}(x+2) = 4$.
[Конец примера 3.]
Если вы учитесь на уроках исчисления, мы гарантируем, что вы столкнетесь со многими задачами, требующими факторизации функции для нахождения предела. Действительно, на каждом экзамене по математическому анализу, который мы видели, была по крайней мере одна проблема, когда вы изначально получаете $\dfrac{0}{0}$ и должны учитывать, чтобы получить окончательный ответ. Откройте следующее поле, чтобы увидеть больше примеров.
Откройте, чтобы увидеть больше примеров факторинга для нахождения предела. 92 -3x+2} &&= \lim_{x \to 1}\frac{(x+2)(x-1)}{(x-2)(x-1)} &&= \lim_{x \to 1}\frac{x+2}{x-2} &&= \frac{1+2}{1-2} = -3 \quad \cmark
\end{align*}
[collapse]
Эти Проблемы становятся простыми, как только вы научитесь их распознавать и умеете учитывать.
Если можно, фактор.
Результат : если подстановка дает результат в виде $\dfrac{0}{0}$, первое, что вы должны попробовать, – это факторинг. Если вы можете факторизовать числитель и/или знаменатель, проблемный член в знаменателе отменяется. Гарантировано.
ДОПОЛНИТЕЛЬНЫЕ МАТЕРИАЛЫ
Оценка пределов: проблемы и полные решения
III. Тактика № 3. Используйте
сопряженных чисел
Если функция содержит квадратный корень и подстановка дает $\dfrac{0}{0}$, 0 делится на 0, затем умножьте числитель и знаменатель на
$$1 = \frac{\text{сопряжение члена (числителя или знаменателя) с корнем}}{\text{сопряжение члена (числителя или знаменателя) с корнем}}$$
Как и в случае факторинга, этот подход, вероятно, приведет к возможности отмены срока. Пример 4 иллюстрирует.
Пример 4 .
Найдите $\displaystyle{\lim_{x \to 0}\dfrac{\sqrt{x+5} – \sqrt{5}}{x}}$.
Решение .
Сначала попробуем замену:
$$\lim_{x \to 0}\frac{\sqrt{x+5} – \sqrt{5}}{x} = \frac{\sqrt{0+5}-\ sqrt{5}}{0} = \frac{0}{0}$$
Поскольку предел представлен в виде $\dfrac{0}{0}$ , он не определен – мы еще не знаем, что такое Это. Нам нужно проделать некоторую работу, чтобы привести его в форму, в которой мы сможем определить предел.
Итак, давайте избавимся от квадратных корней, используя сопряжение, как вы тренировались в алгебре: умножьте и числитель, и знаменатель на сопряжение числителя, $\sqrt{x+5} + \sqrt{5}$.
\begin{align*}
\lim_{x \to 0}\dfrac{\sqrt{x+5} – \sqrt{5}}{x} &= \lim_{x \to 0}\dfrac{\ sqrt{x+5} – \sqrt{5}}{x} \cdot \dfrac{\sqrt{x+5} + \sqrt{5}}{\sqrt{x+5} + \sqrt{5}} \\ \\
&= \lim_{x \to 0}\dfrac{\sqrt{x+5}\sqrt{x+5} + \sqrt{x+5}\sqrt{5} — \sqrt{5 }\sqrt{x+5} -\sqrt{5}\sqrt{5}}{x[\sqrt{x+5} + \sqrt{5}]} \\ \\
&= \lim_{x \to 0}\dfrac{(x+5) – 5}{x[\sqrt{x+5} + \sqrt{5}]} \\ \\
&= \lim_{ x \to 0}\dfrac{x}{x[\sqrt{x+5} + \sqrt{5}]} \\ \\
&= \lim_{x \to 0}\dfrac{\cancel{x }}{\cancel{x}[\sqrt{x+5} + \sqrt{5}]} \\ \\
&= \lim_{x \to 0}\dfrac{1}{\sqrt{x+ 5} + \sqrt{5}} \\ \\
&=\dfrac{1}{\sqrt{0+5} + \sqrt{5}} = \dfrac{1}{2\sqrt{5}} \quad \cmark
\end{align*}
Функция, с которой мы начали, $\dfrac{\sqrt{x+5} – \sqrt{5}}{x}$, , и та, которой мы закончили (после умножение на сопряженное), $\dfrac{1}{\sqrt{x+5} + \sqrt{5}}$, одинаковы, за исключением того, что первая функция не определена в точке х = 0 (поскольку его знаменатель там равен нулю), а второй нет. Мы показали это на параллельных графиках ниже. Следовательно, их пределы такие же, как $x \to 0$, и поэтому $\displaystyle{\lim_{x \to 0}\dfrac{\sqrt{x+5} – \sqrt{5}}{x} = \ lim_{x \to 0}\dfrac{1}{\sqrt{x+5} + \sqrt{5}} = \dfrac{1}{2\sqrt{5}} }$.

[Конец примера 4.]
Как показано в примере 4, если подстановка дает вам $\dfrac{0}{0}$ и функция имеет квадратные корни, тактика умножения числителя и знаменателя на сопряженное части квадратного корня даст вам новую функцию, в которой работает подстановка. Всегда.
Откройте, чтобы увидеть другой пример с квадратными корнями.
Пример 5 .
Найдите $\displaystyle{\lim_{x \to 9}\dfrac{9-x}{3-\sqrt{x}}}$.
Решение .
Сначала попробуем замену:
$$\lim_{x \to 9}\frac{9-x}{3-\sqrt{x}} = \frac{9-9}{3-\sqrt{9}} = \frac{0}{0} $$
Поскольку предел представлен в виде $\dfrac{0}{0}$ , он не определен – мы пока не знаем, что это такое. Итак, давайте умножим числитель и знаменатель на сопряженное значение знаменателя, $3+\sqrt{x}$:
\begin{align*}
\lim_{x \to 9}\frac{9-x}{3-\sqrt{x}} &= \lim_{x \to 9}\frac{9-x}{ 3-\sqrt{x}} \cdot \frac{3+\sqrt{x}}{3+\sqrt{x}} \\[8px] &= \lim_{x \to 9}\frac{(9-x)\left(3+\sqrt{x} \right)}{9 +3 \sqrt{x} -3 \sqrt{x} -x } \\[8px] &= \lim_{x \to 9}\frac{(9-x)\left(3+\sqrt{x} \right)}{9 -x} \\[8px] &= \lim_{x \to 9}\frac{\cancel{(9-x)}\left(3+\sqrt{x} \right)}{\cancel{9-x}} \\[8px] &= \lim_{x \to 9}3+\sqrt{x} \\[8px] &= 3+ \sqrt{9} = 3+3 = 6 \quad \cmark
\end{align*}
[collapse]
Результат: Если у вас есть квадратные корни, умножьте числитель и знаменатель на сопряженную часть квадратного корня.
Мы рассмотрим больше ключевых тактик для работы с 0, разделенным на 0, в нашей следующей статье «Как решать задачи с ограничениями в исчислении — часть 2». Мы также представим несколько других ограничений, которые вы должны просто научиться распознавать.
No related posts.