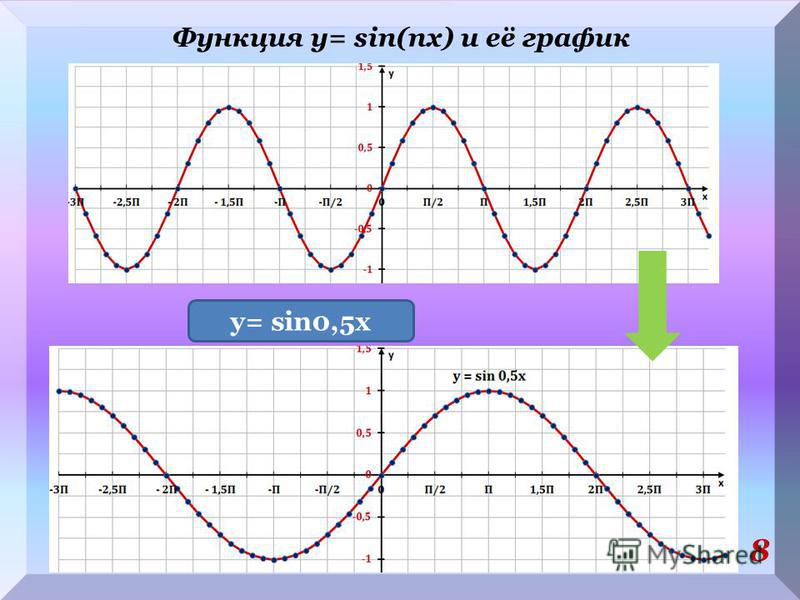
Функция y = sinx её свойства и график
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
Функция
y = sinx
её свойства и график
Цель:
Изучить функцию y = sinx
Задачи:
1. Изучить свойства функции у = sin x.
2. Уметь применять свойства функции у = sin x и
читать график.
3. Формировать практические навыки построения
графика функции у = sin x на основе изученного
теоретического материала.
заданий.
Функция y = sin x определена на всей числовой прямой, и
множеством её значений является отрезок [−1;1].
Следовательно, график этой функции расположен в полосе
между прямыми y= −1 и y=1.
Так как функция y = sin x периодическая с периодом 2π, то
достаточно построить её график на каком-нибудь
промежутке длиной 2π, например, на отрезке 0≤x≤2π,
тогда на промежутках, получаемых сдвигами выбранного
отрезка на 2πn, n∈Z, график будет таким же.
Функция y = sin x является нечётной. Поэтому её график
симметричен относительно начала координат.
Для построения графика на отрезке 0≤x≤2π достаточно
построить его для 0≤x≤π, а затем симметрично отразить его
относительно начала координат
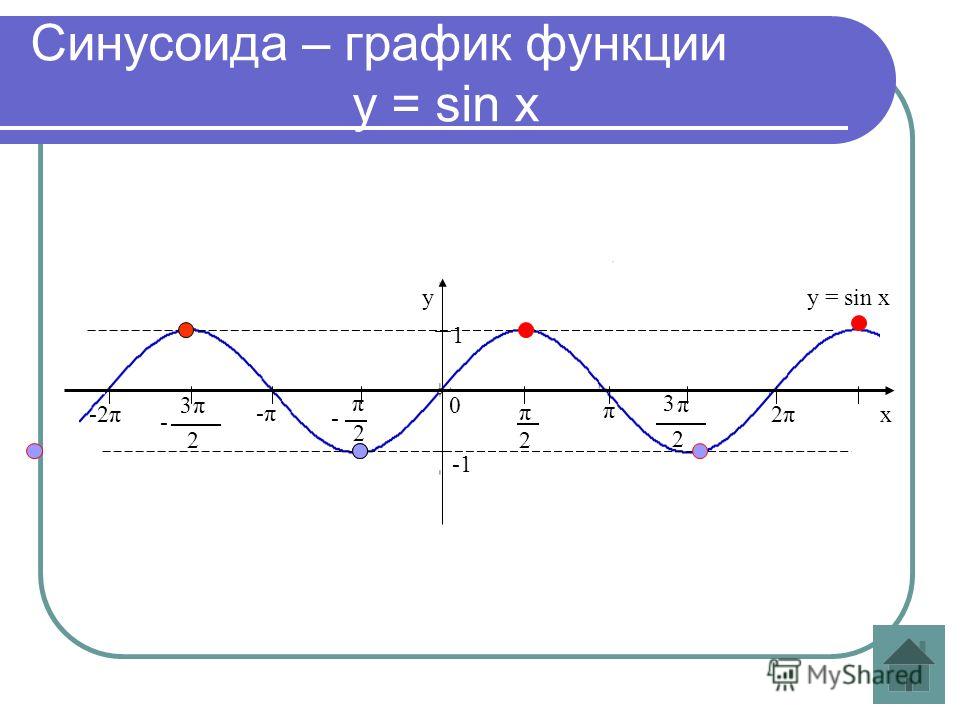
График функции y = sin x
Кривая, являющаяся графиком функции y=sinx,
называется синусоидой.
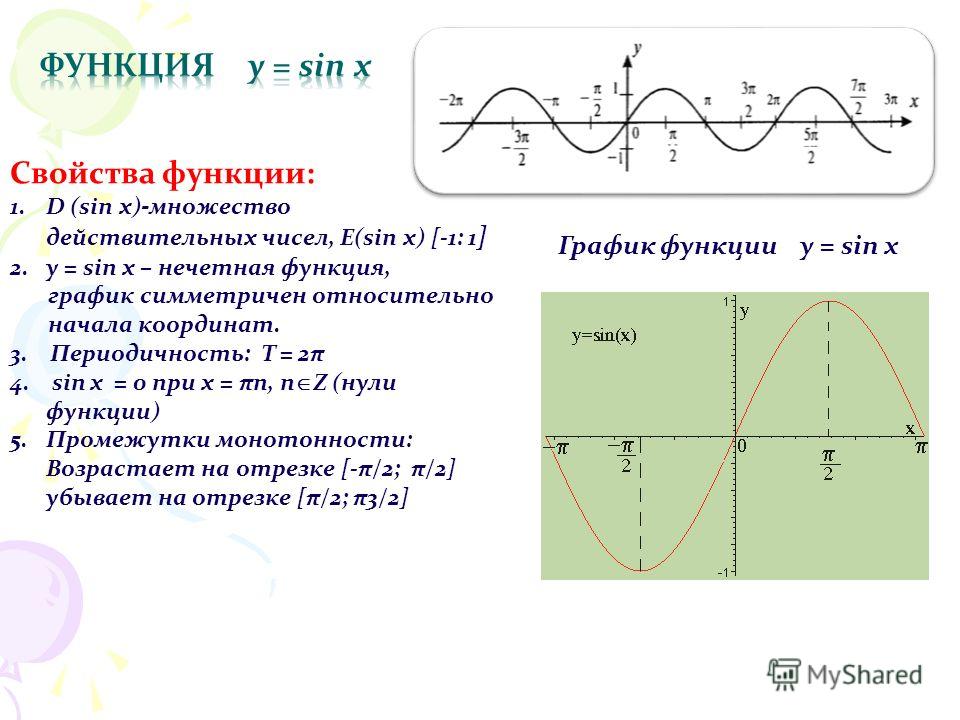
Свойства функции y = sin x
1. Область определения — множество R всех действительных
чисел. D(y) = (-∞; + ∞)
2.
Множество значений Е(у) = [−1;1]3. Функция периодическая с периодом T= 2π.
4. Функция нечётная sin(-x) = -sin x
(график симметричен относительно начала координат).
5. Функция ограничена и сверху, и снизу.
6. Функция y=sinx принимает:
— значение, равное 0, при x=πn, n∈Z;
— наибольшее значение, равное 1, при x=π/2+2πn, n∈Z;
— наименьшее значение, равное −1, при x=−π/2+2πn, n∈Z;
7. Промежутки, на которых функция принимает
положительные значения при
x ∈ (2πn; π+2πn), n ∈ Z
Промежутки, на которых функция принимает отрицательные
значения при
x ∈ (-π+2πn; 2πn), n ∈ Z
8. Функция возрастает на x ∈ [−π/2 + 2 πn; π/2+ 2 πn], n ∈ Z
функция убывает на x ∈ [π/2 + 2 πn; 3π/2+ 2 πn], n ∈ Z
Решение задач
Задача 1.
Найти наибольшее и наименьшее значение функции
y=sin t на отрезке [- /6; /2]
Решение
Функция монотонно возрастает на указанном промежутке,
отрезка у( /2)=1, а наименьшее значение принимает на его
левом конце у( /6) = -1/2
Задача 2.
Найти наибольшее и наименьшее значение функции
y=sin t на отрезке [- /4; — /6]
Решение
Функция монотонно возрастает на указанном промежутке,
значит, наибольшее значение принимает на правом конце
отрезка у(- /6) = -1/2, а наименьшее значение принимает на его
левом конце у(- /4) = — 2/2
Задача 3.
Найти наибольшее и наименьшее значение функции
y=sin t на отрезке [- /6; 2 /3]
Решение
На заданном промежутке функция немонотонна. На
графике видим, что функция меняется в пределах [-1/2; 1]
Наименьшее y(- /6) = — 1/2, наибольшее у( /2) = 1
Задача 4.
Построить график функции
y sin t
6
Решение
Построим график функции y = sin t. В силу периодичности
достаточно будет рассмотреть график на участке [0;2 ]. Для
получения искомого графика кривую y = sin t необходимо
сдвинуть на /6 вправо по оси х
Задача 5.
Найти наибольшее и наименьшее значение функции
на отрезке [0; /2]
y sin t
yнаиб
6
Решение
3
sin
2
3
yнаим
1
sin
2
6
Задача 6.
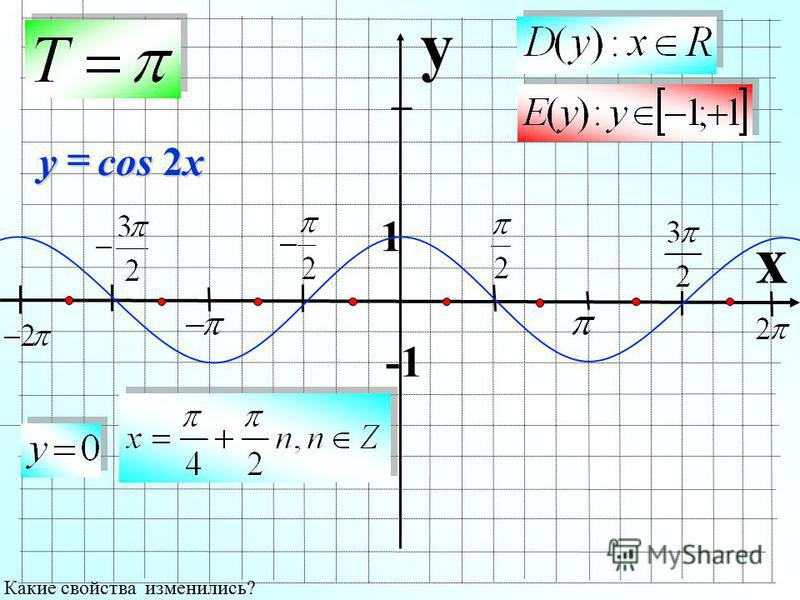
Построить график функции y = — sin x +1 на [0; 2 ]
Решение
Для этого необходимо построить график функции y = sin x,
отобразить его симметрично относительно оси ОХ и сдвинуть
на 1 вверх по оси ОУ
х
Задача 7.
sin х
2
2
Найти число решений уравнения
Решение
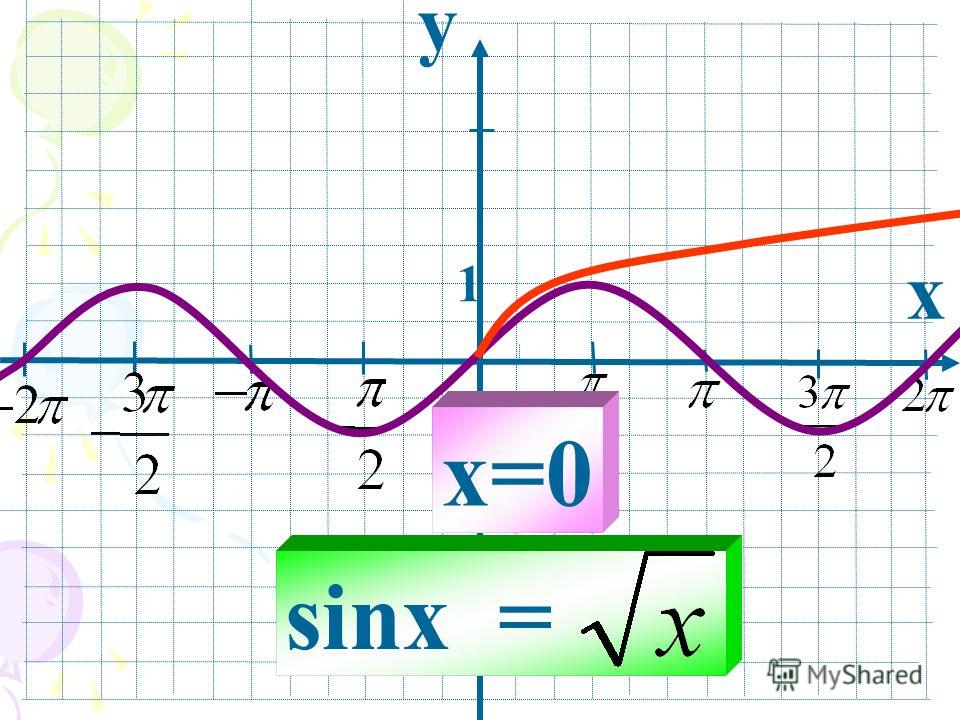
Построим в одних координатных осях графики функций
2
y sin x
и
y x
2
Видно, что графики
функций
пересекаются в двух
точках. Значит всего
уравнение имеет два
решения.
Задача 8.
sin x x 1
2
2
Решение
Построим в одних координатных осях графики функций
y sin x
и
2
у x 1
2
На рисунке
видно, что
построенные
графики
функций имеют
только одну
общую точку с
абсциссой
2
Задания для самостоятельного
решения
Постройте графики функций
1) у = sinx + 1;
2) у = sinx – 1;
3) у = sin (x + π/2)
4) у = sin (x – π/3)
5) Найти наибольшее и наименьшее значение
функции y=sin (x) на отрезке [0; 4π/3]
Заключение.
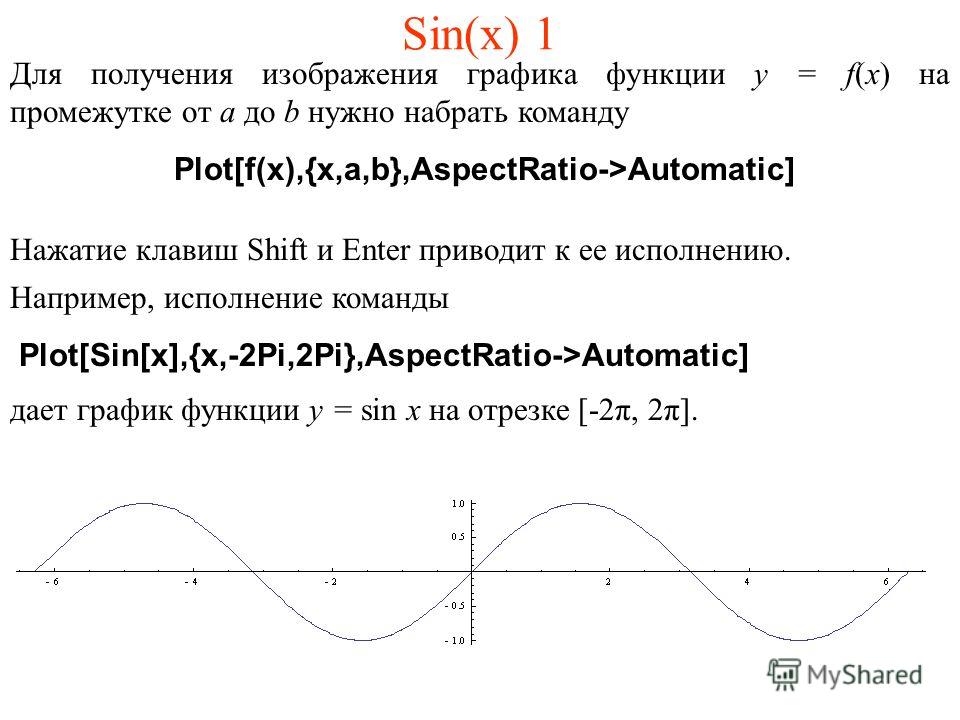
Мы рассмотрели график функции
y = sin x ,
изучили особенности ее поведения,
использовали их и свойства функции при
решении задач, в том числе и задач с
параметром
English Русский Правила
Презентация к уроку «Функция y=sin x, ее свойства и график»
Цели урока:
- Сформировать у учащихся умение изображать график функции y=sinx, по графику читать ее свойства. Создать условия контроля усвоения знаний и умений.
- Развивающие – способствовать формированию умений применять приемы: сравнения, обобщения, выявления главного, переноса знаний в новую ситуацию, развитию математического кругозора, мышления и речи, внимания и памяти.
- Воспитательные – содействовать воспитанию интереса к математике и ее приложениям, активности, мобильности, умения общаться, общей культуры.
Методы обучения: частично-поисковый.
Проверка уровня знаний, работа по обобщающей схеме, решение познавательных обобщающих задач, системные обобщения, самопроверка, восприятие нового материала, взаимопроверка.
Формы организации урока: индивидуальная, фронтальная, работа в парах.
Оборудование и источники информации:
План урока:
- Оргмомент.
- Повторение изученного материала.
- Проверочная работа по контролю знаний тема: «Формулы приведения».
- Систематизация теоретического материала по построению графика функции y=sinx и по ее свойствам.
- Объяснение нового материала.
- Закрепление нового материала.
- Подведение итогов урока.
- Домашнее задание.
(Слайд 2)
Французский писатель Анатоль Франс (1844–1924) однажды заметил: «Учиться можно только весело… Чтобы переваривать знания, надо поглощать их с аппетитом». Так вот, давайте сегодня на уроке будем следовать этому совету писателя, будем активны, внимательны, будем поглощать знания с большим желанием, ведь они пригодятся вам в вашей дальнейшей жизни.*(МОУ СОШ №256 г. Фокино).
Сегодня у нас первый урок по теме тригонометрические функции. Мы рассмотрим их графики и свойства. А начнем изучение с темы: «Функция y=sinx, ее свойства и график». Перед нами стоит задача – применить свои знания и умения при построении графиков функций.
II. Повторение изученного материала.(Слайд 3)
Тема: «Формулы приведения»
Цель: Повторить правило применения формул приведения.
Акцентировать внимание на модели правила: четверть, знак, функция.
1. Рассмотреть примеры: , , , , .
III. Проверочная работа.(Слайд 4)
Тема: «Формулы приведения»
Цель: Контроль знаний и приведение в систему знаний по формулам приведения.
Работа проводится в двух вариантах, задания проецируются на экран. Два ученика выполняют тоже задание за досками по карточкам.
| Вариант 1 | Вариант 2 |
|
|
|
Работа окончена, ученики меняются тетрадями для взаимопроверки, на экране два ученика отмечают свои ответы, класс комментирует правильность выполнения заданий.
Учащиеся контролируют правильность выполнения проверочной работы и выставляют соседу оценку. «5» – 5 выполненных заданий, «4» – 4 задания, «3» – 3 задания. Собираются тетради с проверочной работой и выполненной домашней работой. Оценка будет озвучена на следующем уроке с учетом полноты выполненной домашней работы.
(Слайд 5)
Тема: «Свойства графиков функций»
Цель: Повторение описания свойств функции по готовому графику.
Учащимся предлагается прочитать готовый график. Записать свойства, которыми обладает график показанный на слайде
- область определения;
- нули функции;
- промежутки знакопостоянства;
- возрастание, убывание функции;
- ограниченность;
- четность, нечетность;
- область значений;
- найти наибольшее и наименьшее значение функции на отрезке [1; 4].
(Слайд 6-8)
Цель: рассмотреть график функции; сформулировать свойства функции.
Ученики в тетрадях изображают координатную единичную окружность и систему координат, для параллельного рассмотрения на единичной окружности значений синуса и нанесения точек в заготовленную систему координат. После того, как ученики осознают принцип построения кривой учитель комментирует эту работу через «клеточки». Точки строятся по схеме через :
«на оси», «уголок клетки», «почти единица», «единица», затем движение происходит в обратном порядке: «почти единица», «уголок клетки», «на оси».
Учитель говорит, что данная кривая получила название синусоида.
(Слайд 9.)
После построения графика ученики аналогично проделанной работе с предыдущей функцией записывают свойства функции.
| Свойства функции |
| нули функции: x=πk, |
| >0 на (2πk, π+ 2πk), |
| <0 на (-π+ 2πk, 2πk), |
| — возрастает на , |
| — убывает на , |
| , , |
| , , |
| функция нечетная |
Закрепление пройденного материала.(Слайд 10)
Цель: Применение полученных знаний: нахождение значений функции.
- Для функции y=f(x), где f(x)= sinx, найти f(), f(-). Для этого находим значение функции аналитически и графически для данных значений.
- Найдите значение функции y=-sin(x+) при x=-.
- По графику функции найдите наименьшее и наибольшее значение функции y=sinx на отрезке . Для нахождения наибольшего и наименьшего значения функции выделим «кусок» графика соответствующее отрезку , определяем значение самой высокой точки и самой низкой.
- Для работы в классе предлагаются №10.1-10.6 (в), самостоятельно решают №10.1-10.6 (г). Учитель берет на проверку 3 тетради, просматривает правильность решения на перемене.
(Слайд 11)
Учебник п.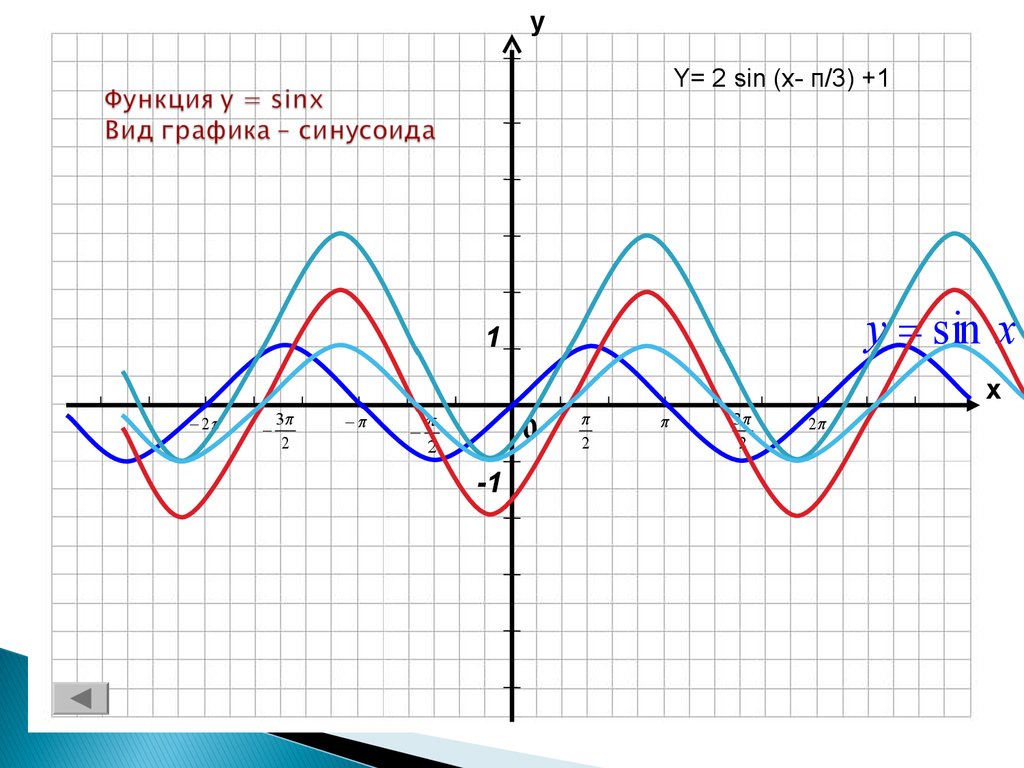
10, задачник № 10.1 (а, б) – 10.6 (а,б) стр. 26 – «Алгебра и начала анализа – 10-11» А.Ю. Макарычев. (2009 г.)
1. Ответы для заданий на повторение:
= -, =-sint , =tgt, =-sint, =-cost
2. Ответы для заданий проверочной работы:
| Вариант 1 | Вариант 2 |
| 1) = cost | 1) = cost |
| 2) = -sint | 2) = -cost |
| 3) = -ctgt | 3) = tgt |
| 4) = -cost | 4) = -sint |
| 5) = | 5) = |
3.
Ответы для задания на прочтение графика:
- область определения; D(f)=(-6;8]
- нули функции; у=0, при х=-3, х=-1
- промежутки знакопостоянства; >0, при х(-6, -3)(-1;8], <0, при х(-3;-1)
- возрастание, убывание функции; возрастает, при х[-2;3] и [5;8]; убывает при х (-6;-2] и [3;5]
- ограниченность; функция ограниченная , при х=3; , при х=-2;
- четность, нечетность; функция обычного вида, четностью или нечетностью не обладает;
- область значений E(f)=[-1;4]
- найти наибольшее и наименьшее значение функции на отрезке [1; 4] =4, =2
| Вариант 1 | Вариант 2 |
|
|
|
Сдвиг синусоидальной функции на графике
Игра с амплитудой и периодом синусоидальной кривой может привести к некоторым интересным изменениям базовой кривой на графике.
Тем не менее, эта кривая все еще узнаваема. Вы можете видеть катящуюся плавную кривую, пересекающую среднюю линию вперед и назад.
В дополнение к этим изменениям у вас есть два других варианта изменения синусоиды — смещение кривой вверх или вниз или в сторону. Эти сдвиги называются переводами кривой.
Перемещение функции вверх или вниз по графику
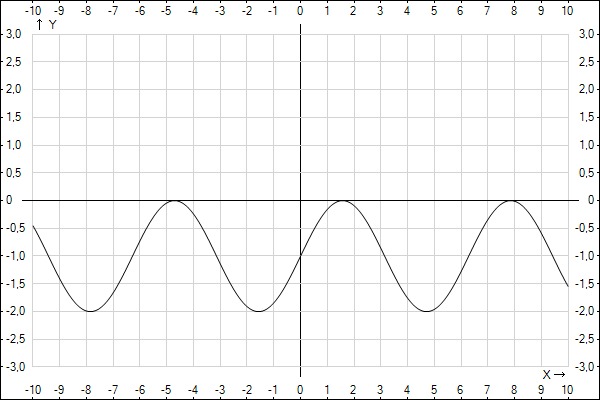
Вы можете перемещать синусоиду вверх или вниз, просто добавляя или вычитая число из уравнения кривой. Например, график y = sin x + 4 перемещает всю кривую вверх на 4 единицы, при этом кривая синусоиды пересекает линию y = 4 вперед и назад. С другой стороны, график y = sin x – 1 сдвигает все вниз на 1 единицу. На следующем рисунке показано, как выглядят эти два графика.
Графики y = sin x + 4 и y = sin x – 1.
Как видите, основная форма синусоиды по-прежнему узнаваема — кривые просто сдвинуты вверх или вниз по координатной плоскости.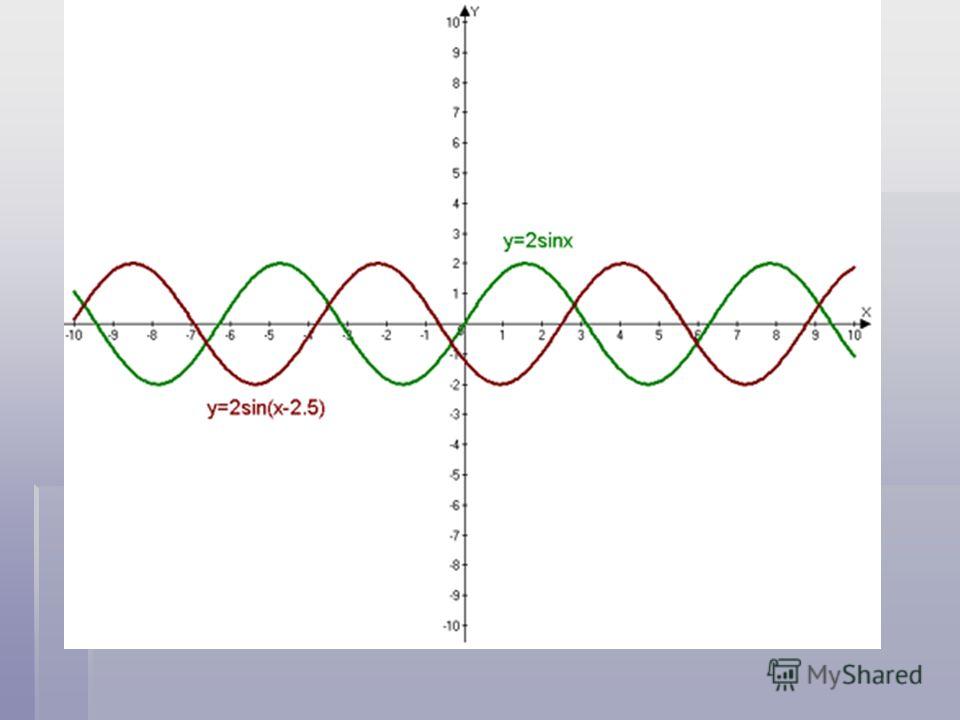
Перемещение функции влево или вправо на графике
Добавляя или вычитая число из угла (переменной) в уравнении синуса, вы можете перемещать кривую влево или вправо от ее обычного положения. Сдвиг или перевод 90 градусов может изменить кривую синусоиды на кривую косинуса. Но перевод самого синуса важен: сдвиг кривой влево или вправо может изменить места, где кривая пересекает ось x или какую-либо другую горизонтальную линию.
Например, график y = sin ( x + 1) приводит к тому, что обычная синусоида сдвинется на 1 единицу влево, а график y = sin ( x – 3) сдвинет ее 3 единицы вправо. На рисунке ниже показаны графики исходного уравнения синуса и этих двух сдвинутых уравнений.
Сравнение графиков y = sin x , y = sin ( x + 1) и y = sin ( x – 3).
Взгляните на точки, отмеченные на каждом графике на рисунке выше. Эта точка показывает, как точка пересечения (где кривая пересекает ось) смещается на графике, когда вы добавляете или вычитаете число из переменной угла.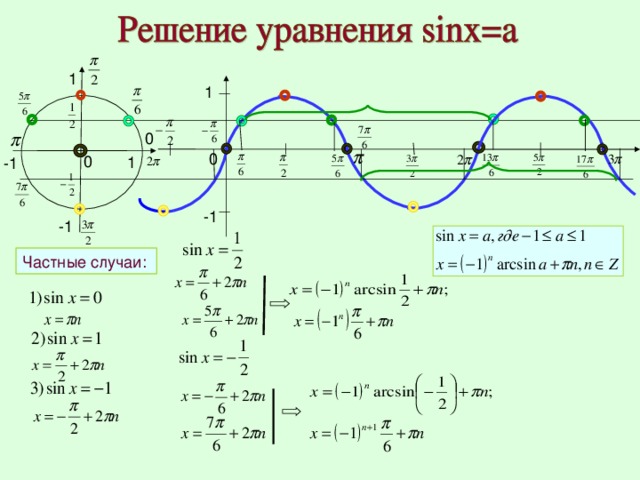
Обратите внимание на разницу между добавлением или вычитанием числа к функции и добавлением или вычитанием числа из меры угла. Эти операции по-разному влияют на кривую, как вы можете видеть, сравнивая предыдущие рисунки.
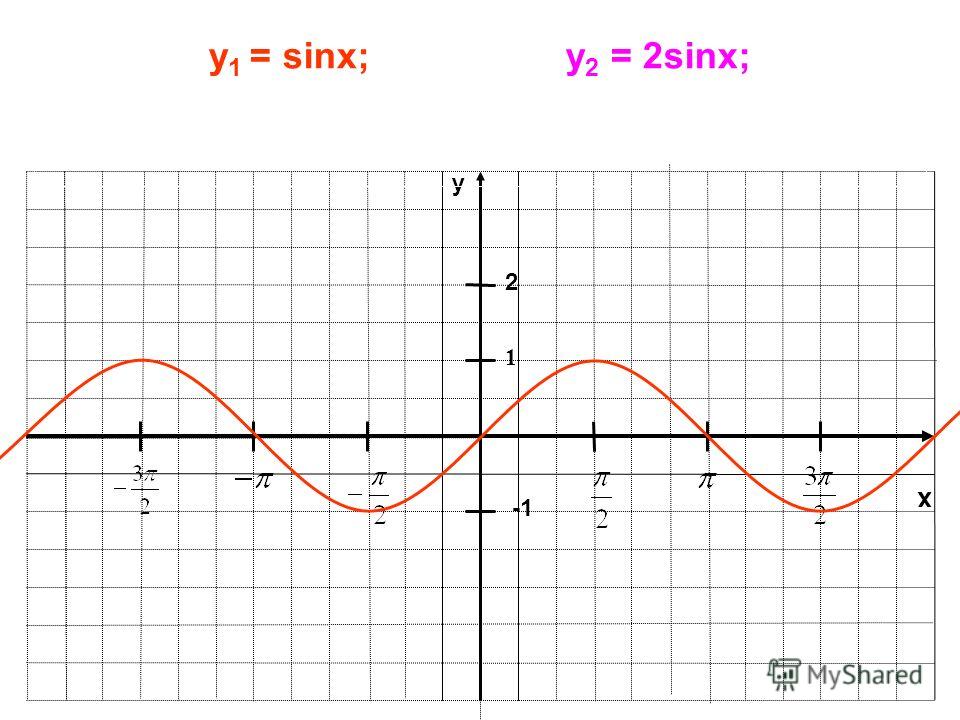
y = sin x + 2: Добавление 2 к функции поднимает кривую на 2 единицы.
y = sin ( x + 2): Добавление 2 к переменной угла сдвигает кривую на 2 единицы влево.
Об этой статье
Эту статью можно найти в категории:
- Тригонометрия ,
Трансляция и фазовые сдвиги синусоидальных и косинусоидальных графиков. Как уравнение связано с графиком. Иллюстрированные демонстрации и примеры
Перевод — это изометрический тип преобразования (изометрический означает, что форма никоим образом не искажается).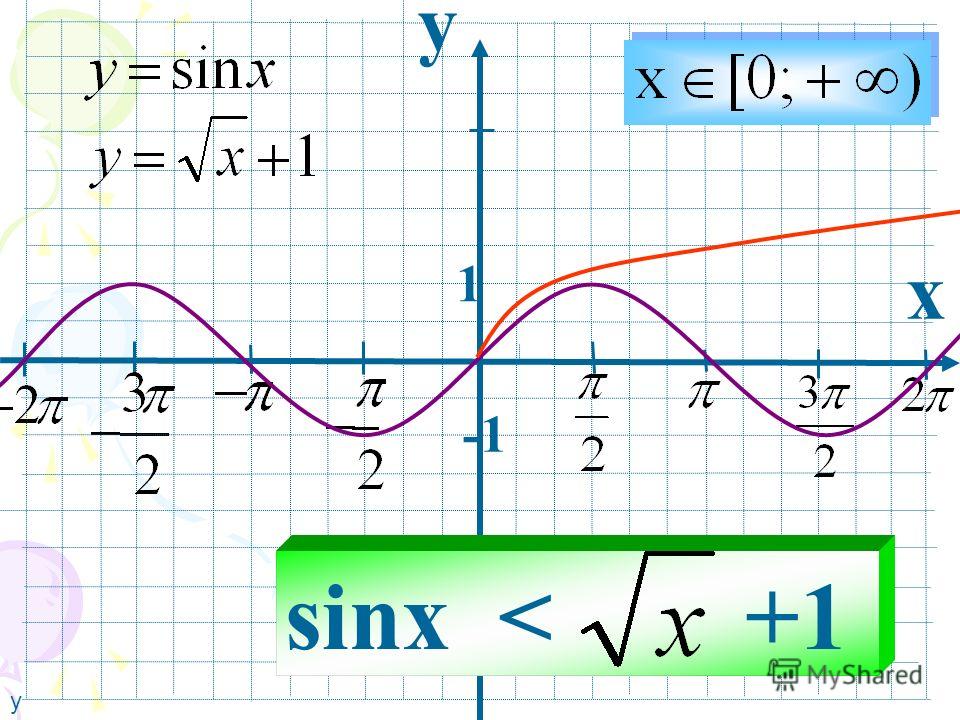
Перевод графика, будь то его синус, косинус или что-то еще, можно рассматривать как «слайд». Чтобы перевести график, все, что вам нужно сделать, это сдвинуть или сдвинуть весь график в другое место.
Вертикальные переводы синусоидальных и косинусоидальных графиков
Пример
Если вы находитесь на этой веб-странице, вы должны быть хорошо знакомы с графиком y =sin(x), как показано ниже $$ 0 \le x \le 2 \pi $$. Пример первого типа перевода, который мы рассмотрим, это y = sin(x) + 1.
Ниже вы можете увидеть как исходный график y = sin(x), так и график перевода y = sin(x) + 1.
Проблема 1
На основе приведенного выше примера вы можете понять, как будет выглядеть график следующего перевода y = sin(x) − 1.
Этот перевод выражает вертикальный сдвиг вниз на 1.
Проблема 2
Как будет выглядеть график следующего уравнения:
$$
\frac{1}{2} sin(2x) — \frac{1}{2}
$$
?
(Обратите внимание, что этот вопрос предполагает, что вы изучили амплитуду синусоидальных уравнений, а также период синусоидальных и косинусных графиков).
Проблема 3
Каким будет график функции $$g(x)=\sin (-x)$$ по сравнению с графиком функции $$f(x)=\sin (x)$$?
График f(x) = sin(-x) является отражением графика f(x) = sin(x) относительно оси x.
Каждая пара соответствующих точек на графиках имеет одинаковое расстояние от оси x.
Например, точки A и B — это две соответствующие точки на графиках, находящиеся на одинаковом расстоянии от оси x. То есть АМ = БМ.
Проблема 4
Каким будет график функции $$g(x)=\sin \left(x+\frac{5\pi}{4} \right)$$ по сравнению с графиком $$f(x)=\sin \left(x+\frac{\pi}{4} \right)$$?
Разница между переменными двух функций:
$$\left(x+\frac{5\pi}{4} \right)-\left(x+\frac{\pi}{4} \right)$$
= $$x+\frac{5\pi}{4} -x-\frac{\pi}{4}$$
= $$\frac{5\pi}{4} -\frac{\pi}{4}$$
= $$\frac{4\pi}{4}$$
= $$\пи$$
Таким образом, график функции f(x) переносится на $$\pi $$ единиц влево для создания графика функции g(x).
Проблема 5
Как график функции $$f(x)=\sin\left(3x-\frac{\pi}{3} \right)$$ переносится на график $$g(x)=\sin\left( 3x+\frac{\pi}{3} \right)$$?
Разница между переменными двух функций:
$$\left(3x+\frac{\pi}{3} \right)-\left(3x-\frac{\pi}{3} \right)$$
= $$3x+\frac{\pi}{3} -3x+\frac{\pi}{3}$$
= $$\frac{\pi}{3} +\frac{\pi}{3}$$
= $$\frac{2\pi}{3}$$
Таким образом, график функции f(x) переносится на $$\frac{2\pi}{3} $$ единиц влево для построения графика функции g (x)
Проблема 6
Каким будет график функции $$g(x)=\sin (-x)-3$$ по сравнению с графиком функции $$f(x)=\sin (-x)$$?
Разница между значениями f(x) и g(x) составляет -3.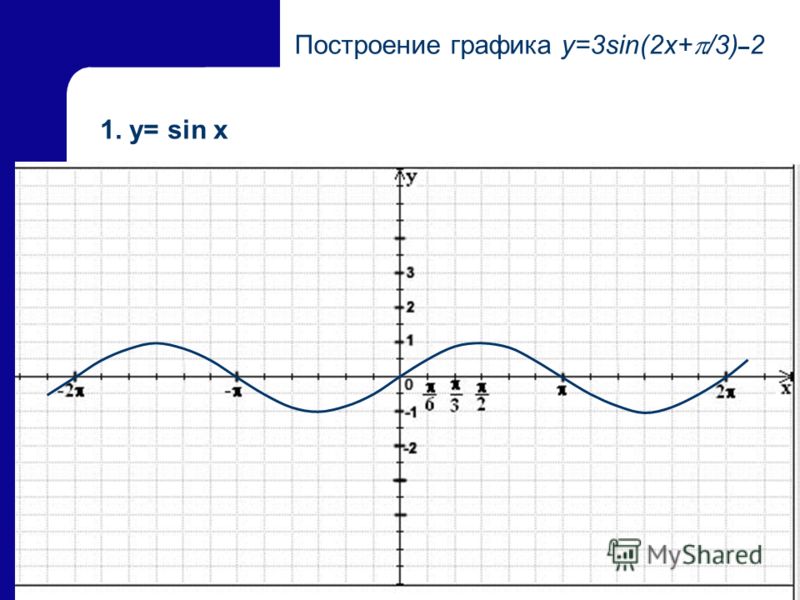
Следовательно, g(x) получается путем перемещения f(x) на 2 единицы вниз.
Проблема 7
Как график функции $$f(x)=\sin (x)$$ перевести на график $$g(x)=\sin (x+2)+2$$?
Первый график $$f(x)=\sin (x)$$ переносится на график $$h(x)=\sin (x+2)$$ путем перемещения на 2 единицы влево, как показано на график ниже.
Затем график g(x) получается путем перемещения графика h(x) вверх на 2 единицы.
Проблема 8
Каким будет график функции $$f(x)=\cos (-x)$$ по сравнению с графиком функции $$g(x)=-\cos (x)$$?
График cos (-x) точно такой же, как график cos (x).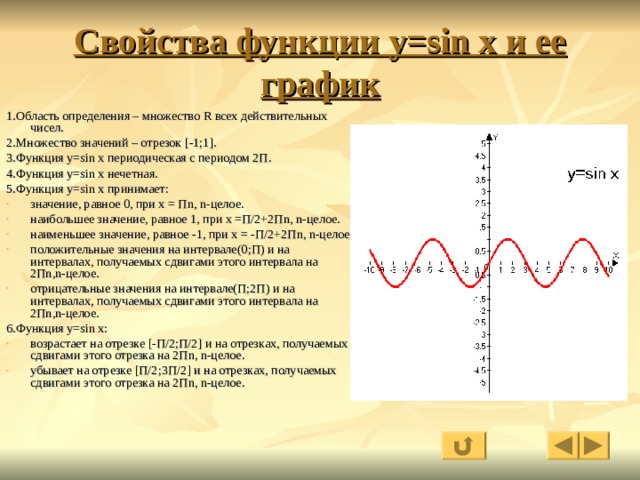
Итак, g(x) — это точное отражение f(x) относительно оси x.
Проблема 9
Как график функции $$f(x)=\cos \left(x-\frac{5\pi}{3} \right)$$ переносится на график $$g(x)=\cos \left(x-\frac{5\pi}{3} \right)-\frac{5\pi}{3} $$?
$$g(x)-f(x)=\left[\cos \left(x-\frac{5\pi}{3} \right)-\frac{5\pi}{3} \right] — \cos\left(x-\frac{5\pi}{3} \right)$$
= $$\cos \left(x-\frac{5\pi}{3} \right)-\frac{5\pi}{3} -\cos \left(x-\frac{5\pi}{ 3} \справа)$$
= $$-\frac{5\pi}{3} $$
Таким образом, график функции f(x) сдвигается на $$\frac{5\pi}{3} $$ единиц вниз, чтобы получить график функции g(x).
Проблема 10
Каким будет график функции $$g(x)=-\cos \left(x-\pi \right)$$ по сравнению с графиком $$f(x)=\cos \left(\pi — х\справа)$$?
$$f(x)=\cos \left(\pi -x\right)$$ совпадает с $$f(x)=\cos \left(x-\pi \right)$$. Таким образом, $$g(x)=-\cos \left(x-\pi \right)$$ является отражением f(x) относительно оси x.
Проблема 11
Каким образом график функции $$f(x)=\cos \left(x-\frac{\pi}{3} \right)$$ переносится на график $$g(x)=\cos \left(\frac{\pi}{3} \, \, -\, \, x\right)\, \, -\, \, \frac{\pi}{3} $$?
$$g(x)=\cos\left(\frac{\pi}{3} \, \, -\, \, x\right)\, \, -\, \, \frac{\pi}{ 3} $$ совпадает с $$g(x)=\cos \left(x-\frac{\pi}{3} \, \, \right)\, \, -\, \, \frac{ \pi}{3} $$.