Вывод:
Надеюсь, из кода всё понятно, но немного поясню.
Поскольку |y| может быть только больше нуля, нам нужно выделить значения функции, которые >= 0 и нарисовать в основной части графика только их. Для этого мы делаем булевую маску для всех значений f(x) (в моём коде это значение обозначено как y, но мой y это не y из вашей формулы).
ind = y >= 0
Более понятно можно записать так:
ind = (y >= 0)
В ind у нас теперь булева маска, содержащая True на тех позициях, где y >= 0 и False, где y < 0.
Далее, мы отбираем по этой маске значения из наших массивов y:
x1 = x[ind]
y1 = y[ind]
А также мы отбираем остальные значения x и y, для чего инвертируем маску с помощью булевой операции инверсии ~ (где было True станет False и наоборот:
x2 = x[~ind]
y2 = y[~ind]
После этого мы рисуем основной график, причём два раза — один раз используя f(x), а другой раз -f(x) (по формуле |y| = f(x) получается, что у нас есть два графика: y = f(x) и y = -f(x)).
И затем рисуем псевдо-график там, где функция f(x) могла бы продолжаться, но из-за условия равенства модулю |y| она в этом месте прерывается.
2.Квадратичная функция y=x² — Функции и их графики
В уравнении квадратичной функции:
a – старший коэффициент
b – второй коэффициент
с — свободный член.
Графиком квадратичной функции является квадратичная парабола, которая для функции имеет вид:
Точки, обозначенные зелеными кружками – это, так называемые «базовые точки». Чтобы найти координаты этих точек для функции , составим таблицу:
Внимание! Если в уравнении квадратичной функции старший коэффициент , то график квадратичной функции имеет ровно такую же форму, как график функции при любых значениях остальных коэффициентов.
График функции имеет вид:
Для нахождения координат базовых точек составим таблицу:
Обратите внимание, что график функции симметричен графику функции относительно оси ОХ.
Итак, мы заметили:
Если старший коэффициент a>0, то ветви параболы напрaвлены вверх.
Если старший коэффициент a<0, то ветви параболы напрaвлены вниз.
Второй параметр для построения графика функции – значения х, в которых функция равна нулю, или нули функции. На графике нули функции — это точки пересечения графика функции с осью ОХ.
Поскольку ордината (у) любой точки, лежащей на оси ОХ равна нулю, чтобы найти координаты точек пересечения графика функции с осью ОХ, нужно решить уравнение .
В случае квадратичной функции нужно решить квадратное уравнение .
В процессе решения квадратного уравнения находим дискриминант: , который определяет число корней квадратного уравнения.
И здесь возможны три случая:
1. Если ,то уравнение не имеет решений, и, следовательно, квадратичная парабола не имеет точек пересечения с осью ОХ. Если ,то график функции выглядит как-то так:
2.
3. Если ,то уравнение имеет два решения, и, следовательно, квадратичная парабола имеет две точки пересечения с осью ОХ:
,
Если ,то график функции выглядит примерно так:
Следующий важный параметр графика квадратичной функции – координаты вершины параболы:
Прямая, прохдящая через вершину параболы параллельно оси OY является осью симметрии паработы.
И еще один параметр, полезный при построении графика функции – точка пересечения параболы с осью OY.
Поскольку абсцисса любой точки, лежащей на оси OY равна нулю, чтобы найти точку пересечения параболы с осью OY, нужно в уравнение параболы вместо х подставить ноль: .
То есть точка пересечения параболы с осью OY имеет координаты (0;c).
Итак, основные параметры графика квадратичной функции показаны на рисунке:
Построить график функции у=-x²+2x+8 (парабола) – решение и ответ
Формулировка задания: Построить график функции у = -x² + 2x + 8.
Решение:
Для построения графика параболы нужно построить таблицу значений x и y.
Для удобства начнем с точек, находящихся на осях Ox и Oy. Если точка лежит на оси Oy (x = 0), тогда:
x = 0 ⇒
y = -0² + 2 ⋅ 0 + 8 = 8
Если точка лежит на оси Ox (y = 0), нужно решить квадратное уравнение:
y = 0 ⇒
-x² + 2x + 8 = 0
a = -1, b = 2, c = 8
D = 2² – 4 ⋅ (-1) ⋅ 8 = 36
x1 = (-2 + 6) / (-2) = -2
x2 = (-2 – 6) / (-2) = 4
Таким образом, мы получили 3 точки пересечения с осями. Заполняем ими таблицу:
Возьмем еще пару точек, которые будет просто посчитать, например, x = 1 и x = -1:
x = 1 ⇒
y = -1² + 2 ⋅ 1 + 8 = 9
x = -1
y = -(-1)² + 2 ⋅ (-1) + 8 = 5
Таблица значений теперь выглядит следующим образом:
Отметим полученные точки на координатной плоскости:
Координату x вершины параболы можно определить по любым 2 точкам параболы, у которых равно значение y: она лежит точно между ними.
2 называется квадратичной функцией. Графиком квадратичной функции является парабола. Общий вид параболы представлен на рисунке ниже.
Квадратичная функция
Рис 1. Общий вид параболы
Как видно из графика, он симметричен относительно оси Оу. Ось Оу называется осью симметрии параболы. Это значит, что если провести на графике прямую параллельную оси Ох выше это оси. То она пересечет параболу в двух точках. Расстояние от этих точек до оси Оу будет одинаковым.
Ось симметрии разделяет график параболы как бы на две части. Эти части называются ветвями параболы. А точка параболы которая лежит на оси симметрии называется вершиной параболы. То есть ось симметрии проходит через вершину параболы. Координаты этой точки (0;0).
Основные свойства квадратичной функции
1. При х =0, у=0, и у>0 при х0
2. Минимальное значение квадратичная функция достигает в своей вершине. Ymin при x=0; Следует также заметить, что максимального значения у функции не существует.
3 называется кубической функцией. Графиком кубической функции называется кубическая парабола. Общий вид параболы представлен на рисунке ниже.
Если график квадратичной функции был симметричен оси Оу, то график кубической параболы симметричен относительно начала координат, то есть точки (0;0).
Свойства кубической функции
Перечислим основные свойства кубической функции
- При х =0, у=0. у>0 при х>0 и y
- У кубической функции не существует не максимального ни минимального значения.
- Кубическая функция возрастает на всей числовой оси (-∞;+∞).
- Противоположным значениям х, соответствуют противоположные значения y.
Нужна помощь в учебе?
Предыдущая тема: Умножение одночленов и возведение одночлена в степень + примеры
Следующая тема:   Абсолютная погрешность: понятие, как вычислить + примеры
Сдвиги графиков функций
☰
Изменение значения k влияет на вид графика (степень крутизны в случае параболы), расположение ветвей в координатных четвертях и др.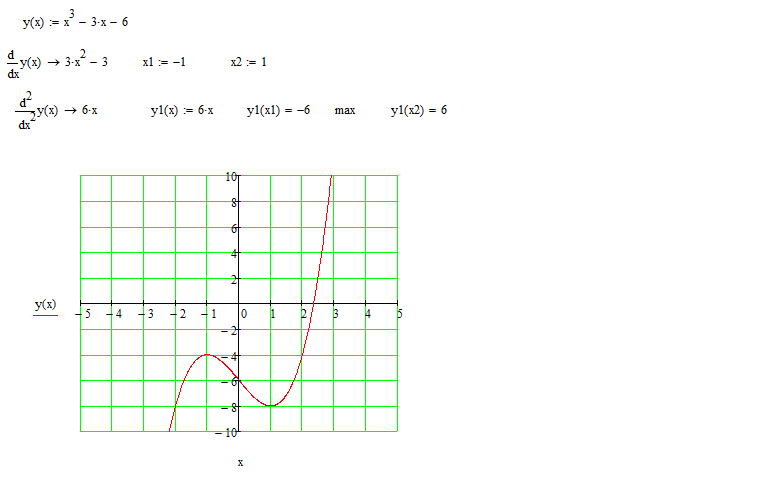
Однако точкой, через которую можно провести ось симметрии графиков, является точка O с координатами (0; 0).
Если же рассматривать функций, подобные перечисленным выше, у которых к переменной x или ко всей исходной функции прибавляется (или вычитается) какое-либо число, то графики этих функций остаются такими же как у исходных, однако смещаются относительно точки (0; 0).
Если обозначить исходные функции как y = f(x), то прибавление к x числа дает функции вида y = f(x+l), а прибавление ко всей исходной функции значения дает вид y = f(x) + m.
Например, если исходная функция y = 2x2, то примером первого типа будет функция y = 2(x+5)2, а второго — y = 2x2 + 5.
Для функций вида y = f(x+l) график смещается влево на l единиц, если l прибавляется. Если же l вычитается, то график смещается вправо. Действительно, представим параболу функции y = x2 и сравним ее с функцией y = (x+1)2. Когда x = 1, то для первой функции y = 1, а для второй — y = 4.
То есть график второй функции касается оси x в точке (–1; 0). Это значит, что график смещен влево по сравнению с исходным на 1.
Для функций вида y = f(x) + m график соответствующей функции y = f(x) смещается на m единиц, но уже по вертикальной оси (ось y). Здесь если m прибавляется, то график сдвигается вверх. Если m вычитается, то график сдвигается вниз.
Рассмотрим ту же параболу y = x2 и функцию y = x2 + 1. Когда x = 0, первая принимает значение 0, а у второй y = 1. Получить у второй функции значение y, которое равно 0, вообще невозможно. Это значит, что парабола имеет точку симметрии с координатами (0; 1), т. е. сдвинута от исходной вверх на 1.
«Смешанные» функции вида y = f(x + l) + m сдвигаются вдоль оси x и y. Вдоль оси x они сдвигаются на l, а вдоль y — на значение m.
График x 2 2x 3.
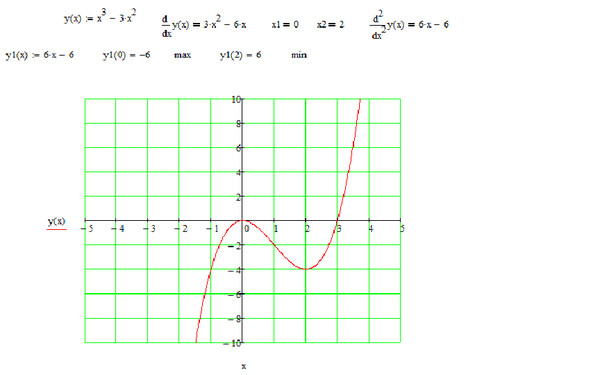
Как построить график функции. Преимущества построения графиков онлайнКак построить параболу? Существует несколько способов построения графика квадратичной функции. Каждый из них имеет свои плюсы и минусы. Рассмотрим два способа.
Начнём с построения графика квадратичной функции вида y=x²+bx+c и y= -x²+bx+c.
Пример.
Построить график функции y=x²+2x-3.
Решение:
y=x²+2x-3 — квадратичная функция. График — парабола ветвями вверх. Координаты вершины параболы
От вершины (-1;-4) строим график параболы y=x²(как от начала координат. Вместо (0;0) — вершина (-1;-4). От (-1;-4) идём вправо на 1 единицу и вверх на 1 единицу, затем влево на 1 и вверх на 1; далее: 2 — вправо, 4 — вверх, 2- влево, 4 — вверх; 3 — вправо, 9 — вверх, 3 — влево, 9 — вверх. Если этих 7 точек недостаточно, далее — 4 вправо, 16 — вверх и т. д.).
График квадратичной функции y= -x²+bx+c — парабола, ветви которой направлены вниз.
Для построения графика ищем координаты вершины и от неё строим параболу y= -x².
Пример.
Построить график функции y= -x²+2x+8.
Решение:
y= -x²+2x+8 — квадратичная функция. График — парабола ветвями вниз. Координаты вершины параболы
От вершины строим параболу y= -x² (1 — вправо, 1- вниз; 1 — влево, 1 — вниз; 2 — вправо, 4 — вниз; 2 — влево, 4 — вниз и т. д.):
Этот способ позволяет построить параболу быстро и не вызывает затруднений, если вы умеете строить графики функций y=x² и y= -x². Недостаток: если координаты вершины — дробные числа, строить график не очень удобно. Если требуется знать точные значения точек пересечения графика с осью Ох, придется дополнительно решить уравнение x²+bx+c=0 (или —x²+bx+c=0), даже если эти точки непосредственно можно определить по рисунку.
Другой способ построения параболы — по точкам, то есть можно найти несколько точек графика и через них провести параболу (с учетом того, что прямая x=хₒ является её осью симметрии).
Обычно для этого берут вершину параболы, точки пересечения графика с осями координат и 1-2 дополнительные точки.
Построить график функции y=x²+5x+4.
Решение:
y=x²+5x+4 — квадратичная функция. График — парабола ветвями вверх. Координаты вершины параболы
то есть вершина параболы — точка (-2,5; -2,25).
Ищем . В точке пересечения с осью Ох y=0: x²+5x+4=0. Корни квадратного уравнения х1=-1, х2=-4, то есть получили две точки графике (-1; 0) и (-4; 0).
В точке пересечения графика с осью Оy х=0: y=0²+5∙0+4=4. Получили точку (0; 4).
Для уточнения графика можно найти дополнительную точку. Возьмем х=1, тогда y=1²+5∙1+4=10, то есть еще одна точка графика — (1; 10). Отмечаем эти точки на координатной плоскости. С учетом симметрии параболы относительно прямой, проходящей через её вершину, отметим еще две точки: (-5; 6) и (-6; 10) и проведем через них параболу:
Построить график функции y= -x²-3x.
Решение:
y= -x²-3x — квадратичная функция.
График — парабола ветвями вниз. Координаты вершины параболы
Вершина (-1,5; 2,25) — первая точка параболы.
В точках пересечения графика с осью абсцисс y=0, то есть решаем уравнение -x²-3x=0. Его корни — х=0 и х=-3, то есть (0;0) и (-3; 0) — еще две точки графика. Точка (о; 0) является также точкой пересечения параболы с осью ординат.
При х=1 y=-1²-3∙1=-4, то есть (1; -4) — дополнительная точка для построения графика.
Построение параболы по точкам — более трудоёмкий, по сравнению с первым, способ. Если парабола не пересекает ось Oх, дополнительных точек потребуется больше.
Прежде чем продолжить построение графиков квадратичных функций вида y=ax²+bx+c, рассмотрим построение графиков функций с помощью геометрических преобразований. Графики функций вида y=x²+c также удобнее всего строить, используя одно из таких преобразований — параллельный перенос.
Рубрика: |«Преобразование функций» — Качелями. Сдвиг по оси y вверх. Включи полную громкость – увеличишь a (амплитуду) колебаний воздуха.
Сдвиг по оси x влево. Задачи урока. 3 балла. Музыкой. Постройте график функции и определите D(f), E(f) и T: Сжатие по оси x. Сдвиг по оси y вниз. Добавь красного цвета в палитру – уменьшишь k (частоту) электромагнитных колебаний.
«Функции нескольких переменных» — Производные высших порядков. Функцию двух переменных можно изобразить графически. Дифференциальное и интегральное исчисления. Внутренние и граничные точки. Определение предела функции 2-х переменных. Курс математического анализа. Берман. Предел функции 2-х переменных. График функции. Теорема. Ограниченная область.
«Понятие функции» — Способы построение графиков квадратичной функции. Изучение разных способов задания функции – важный методический прием. Особенности изучения квадратичной функции. Генетическая трактовка понятия «функция». Функции и графики в школьном курсе математики. Представление о линейной функции выделяется при построении графика некоторой линейной функции.
«Тема Функция» — Анализ. Нужно выяснить не то, что ученик не знает, а то, что он знает.
Заложение основ для успешной сдачи ЕГЭ и поступление в ВУЗы. Синтез. Если ученики работают по-разному, то и учитель должен с ними работать по-разному. Аналогия. Обобщение. Распределение заданий ЕГЭ по основным блокам содержания школьного курса математики.
«Преобразование графиков функций» — Повторить виды преобразований графиков. Сопоставить каждому графику функцию. Симметрия. Цель урока: Построение графиков сложных функций. Рассмотрим примеры преобразований, объясним каждый вид преобразования. Преобразование графиков функций. Растяжение. Закрепить построение графиков функций с использованием преобразований графиков элементарных функций.
«Графики функций» — Функция вида. Область значений функции – все значения зависимой переменной у. Графиком функции является парабола. Графиком функции является кубическая парабола. Графиком функции является гипербола. Область определения и область значений функции. Каждую прямую соотнесите с её уравнением: Область определения функции – все значения независимой переменной х.
2 называется квадратичной функцией. Графиком квадратичной функции является парабола. Общий вид параболы представлен на рисунке ниже.
Квадратичная функция
Рис 1. Общий вид параболы
Как видно из графика, он симметричен относительно оси Оу. Ось Оу называется осью симметрии параболы. Это значит, что если провести на графике прямую параллельную оси Ох выше это оси. То она пересечет параболу в двух точках. Расстояние от этих точек до оси Оу будет одинаковым.
Ось симметрии разделяет график параболы как бы на две части. Эти части называются ветвями параболы. А точка параболы которая лежит на оси симметрии называется вершиной параболы. То есть ось симметрии проходит через вершину параболы. Координаты этой точки (0;0).
Основные свойства квадратичной функции
1. При х =0, у=0, и у>0 при х0
2. Минимальное значение квадратичная функция достигает в своей вершине. Ymin при x=0; Следует также заметить, что максимального значения у функции не существует.
3. Функция убывает на промежутке (-∞;0] и возрастает на промежутке ; график f(х) = х + 2 – это прямая, параллельная прямой f(х) = х, но сдвинутая на две единицы вверх и поэтому проходящая через точку с координатами (0,2) (потому что постоянная равна 2).
Построение графика сложной функции
Найдите нули функции. Нули функции – это значения переменной «х», при которых у = 0, то есть это точки пересечения графика с осью Х. Имейте в виду, что нули имеют не все функции, но это первый шаг процесса построения графика любой функции. Чтобы найти нули функции, приравняйте ее к нулю. Например:
Найдите и отметьте горизонтальные асимптоты. Асимптота – это прямая, к которой график функции приближается, но никогда не пересекает ее (то есть в этой области функция не определена, например, при делении на 0). Асимптоту отметьте пунктирной линией. Если переменная «х» находится в знаменателе дроби (например, y = 1 4 − x 2 {\displaystyle y={\frac {1}{4-x^{2}}}}
), приравняйте знаменатель к нулю и найдите «х».
В полученных значения переменной «х» функция не определена (в нашем примере проведите пунктирные линии через х = 2 и х = -2), потому что на 0 делить нельзя. Но асимптоты существуют не только в случаях, когда функция содержит дробное выражение. Поэтому рекомендуется пользоваться здравым смыслом:
План построения квадратичной функции.
1. Область определения функции (D (y )).
2. Графиком данной функции является парабола, ветви которой направлены вверх (вниз), т.к. а = __ > 0 (а = __
3. Координаты вершины параболы.
4. Уравнение оси симметрии.
5. Точка пересечения графика с осью OY .
6. Нули функции.
7. Таблица значений функции.
8. График.
Пример построения графика функции y = x 2 – 4 x + 3
1. D (y ) = (- ∞; + ∞).
2. Графиком данной функции является парабола, ветви которой направлены вверх, т. к. а = 1 > 0.
3. Координаты вершины параболы:
x 0 = — , y 0 = 2 2 — 4·2 + 3 = 4 – 8 + 3 = — 1.
4. Уравнение оси симметрии x = 2.
5. Точка пересечения с осью OY (0; 3).
6. Нули функции:
x 2 – 4 x + 3 = 0 D = (- 4) 2 – 4 ·1·3 = 16 -12 = 4 = 2 2
x 1 = = 1 x 2 = = 3
7. Составим таблицу значений функции:
0
1
2
3
3
0
— 1
0
8. Построим график
Свойства функции:
1. Множество значений функции (E (y )).
2. Промежутки знакопостоянства функции (y >0, y
3. Промежутки монотонности функции (возрастает, убывает).
4. Точки максимума и минимума функции.
Свойства функции y = x 2 – 4 x + 3.
1. E (y ) = [-1; + ∞).
2.
y x (1; 3).
|
КВАДРАТИЧНАЯ ФУНКЦИЯ
y = ax2 + bx + c, где a 0. График квадратичной функции — парабола.
Свойства функции и вид её графика определяются, в основном, значениями коэффициента a
|
Например, если уравнение ax2 + bx + c = 0 имеет два корня, удобно использовать координаты вершины параболы и координаты двух точек пересечения параболы с осью х.
ПОСТРОЕНИЕ ГРАФИКА КВАДРАТИЧНОЙ ФУНКЦИИ ПО НАПРАВЛЕНИЮ ВЕТВЕЙ, ХАРАКТЕРНЫМ ТОЧКАМ И ОСИ СИММЕТРИИ ПАРАБОЛЫ
Примеры:
Растяжение графика функции y = x 2 вдоль оси y в 2 разаy = x2-2x-3 и как вы это изобразите?
Содержание:
Шаг 1: Поиск вершины
Шаг 2: Поиск двух точек слева от оси симметрии
Шаг 3: Отражение двух точек для получения точек справа от оси симметрии
Шаг 4: Построение точек (с таблицей)
Шаг 5: Построение параболы
Чтобы построить график, мы можем выполнить следующие шаги:
Шаг 1) Найдите вершину (вершина — это самая высокая или самая низкая точка на графике).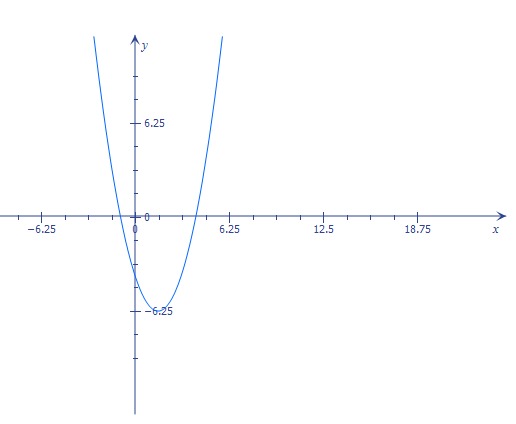
Также вершина находится на оси симметрии параболы (т.е. делит ее пополам).
Шаг 2) Когда у вас есть вершина, найдите две точки слева от оси симметрии (линия, которая вертикально проходит через вершину).
Шаг 3) Отразите эти две точки над осью симметрии, чтобы получить еще две точки справа от оси симметрии.
Шаг 4) Постройте все найденные точки (включая вершину).
Шаг 5) Проведите кривую через все точки, чтобы построить параболу.
Давайте подробно рассмотрим эти шаги
Перейти к началу страницы
Шаг 1)
Нахождение вершины:
Чтобы найти вершину, нам сначала нужно найти x-координату вершины.
Чтобы найти координату x вершины, используйте эту формулу:.
Начните с данной формулы.
Из, мы видим, что, и.
Подключите и.
Отменить получить.
Умножаем 2 и получаем.
Разделить.
Итак, координата x вершины. Примечание: это означает, что ось симметрии тоже.
Теперь, когда мы знаем координату x вершины, мы можем использовать ее, чтобы найти координату y вершины.
Начните с данного уравнения.
Подключите.
Квадратпр.
Умножаем и получаем.
Умножаем и получаем.
Объедините похожие термины.
Итак, y-координата вершины.
Так вершина есть.
———————————————— ———————
Перейти к началу страницы
Шаг 2)
Найдите две точки слева от оси симметрии:
Давайте найдем значение y, когда
Начнем с данного уравнения.
Подключите.
Квадратпр.
Умножаем и получаем.
Умножаем и получаем.
Объедините похожие термины.
Итак, первая точка слева от оси симметрии (-1,0)
———————
Давайте найдем значение y, когда
Начнем с данного уравнения.
Подключите.
Квадратпр.
Умножаем и получаем.
Умножаем и получаем.
Объедините похожие термины.
Итак, вторая точка слева от оси симметрии (0, -3)
———————————————— ———————
Перейти к началу страницы
Шаг 3)
Отражение двух точек по оси симметрии:
Теперь запомните, парабола симметрична относительно оси симметрии (которая есть)
Это означает, что значение y для (которое находится на расстоянии одной единицы от оси симметрии) равно значению y (которое также находится на расстоянии одной единицы от оси симметрии).Итак, когда, что дает нам точку (2, -3). Таким образом, мы по существу отразили точку (0, -3) на (2, -3).
Кроме того, значение y для (которое находится в двух единицах от оси симметрии) равно значению y (которое также находится на расстоянии двух единиц от оси симметрии). Итак, когда, что дает нам точку (3,0). Таким образом, мы по существу отразили точку (-1,0) на (3,0).
———————————————— ———————
Перейти к началу страницы
Шаг 4)
Нанесение точек:
Теперь давайте составим таблицу вычисленных нами значений:
график y = (x-7) (x + 3) — Mathskey.
2 + k , где (h, k) = вершина и ось симметрии x = h .Уравнение y = (x — 7) (x + 3).
Записываем уравнение в виде y = x 2 — 4x — 21.
Вышеприведенное уравнение представляет собой параболу.
Запишите уравнение в стандартной форме уравнения параболы.
Чтобы преобразовать выражение [x 2 — 4x — 21] в трехчлен полного квадрата , сложите и вычтите (половина коэффициента x ) ²
Здесь x коэффициент = — 4.2 + k , где (h, k) = вершина и ось симметрии x = h .
Вершина (h, k) = (2, — 25) и ось симметрии x = 2.
Составьте таблицу значений, чтобы найти упорядоченные пары, удовлетворяющие уравнению.
Выберите значения для x и найдите соответствующие значения для y .
х | у = (х — 2) 2 -25 | (х, у) |
| — 4 | y = (- 4-2) 2 -25 = (- 6) 2 -25 = 36-25 = 11 | (- 4, 11) |
— 3 | y = (- 3 — 2) 2 — 25 = (- 5) 2 — 25 = 25 — 25 = 0 | (- 3, 0) |
— 2 | y = (- 2 — 2) 2 — 25 = (- 4) 2 — 25 = 16 — 25 = — 9 | (- 2, — 9) |
— 1 | y = (- 1-2) 2 -25 = (- 3) 2 -25 = 9-25 = — 16 | (- 1, — 16) |
0 | y = (0 — 2) 2 — 25 = (- 2) 2 — 25 = 4 — 25 = — 21 | (0, — 21) |
2 | y = (2 — 2) 2 — 25 = (0) 2 — 25 = — 25 | (2, — 25) |
| 4 | y = (4-2) 2 -25 = (2) 2 -25 = 4-25 = — 21 | (4, — 21) |
| 6 | y = (6-2) 2 -25 = (4) 2 -25 = 16-25 = — 9 | (6, — 9) |
| 8 | y = (8-2) 2 -25 = (6) 2 -25 = 36-25 = 11 | (8, 11) |
Как построить график Y X 2 2x 3 Socratic — Cute 766
Как вы изобразите линию X Y 2 Socratic
Пояснение: из данного уравнения x2 y2 2x −3 = 0.
2 к; (h, k) является вершиной, здесь h = 0,25, k = 3,125, a = 2, поэтому вершина находится в точке (0,25, 3,125), поскольку a положительно, парабола. Установите y = 0, потому что ось x пересекает ось y в точке y = 0. 0 = 2 (x 1) 2 3. вычтите 3 с обеих сторон. −3 = 2 (х 1) 2. разделите обе части на 2. — 3 2 = (x 1) 2. квадратный корень с обеих сторон. √− 3 2 = x 1. поскольку мы извлекаем отрицательное значение из квадрата, это означает, что кривая не пересекает ось x и не касается ее. См. Пояснение: минимальное количество точек, необходимое для построения графика с прямой линией, равно 2.однако 3 лучше, так как один из них составляет чек. они все должны выстроиться в линию. если нет, то что-то не так. График: y = 3 2x 3. вам нужны две точки, чтобы построить прямую линию. пересечения по осям x и y найти легче всего, особенно когда уравнение имеет стандартную форму. преобразовать в стандартную форму, ax by = c, вычитая 3 2x с обеих сторон. — 3 2x y = 3. x intercept: значение x, когда y = 0. подставляем 0 вместо y и решаем относительно x.
График каждой функции Y 2 X 2
Все уравнения вида a x 2 b x c = 0 можно решить, используя формулу корней квадратного уравнения: 2 a — b ± b 2 — 4 a c.{2} bx c = 0. замените 1 на a, 2 на b. Шаги по решению линейного уравнения. y = 2x 3. y = — 2 x — 3. Поменяйте местами стороны так, чтобы все переменные члены находились слева. поменяйте местами стороны так, чтобы все переменные термины находились слева. 2х 3 = у. — 2 х — 3 = у. прибавьте 3 с обеих сторон. прибавьте 3 с обеих сторон. График y = 3 2x 2. Перепишем в форме пересечения наклона. нажмите, чтобы увидеть больше шагов, форма пересечения наклона: где — наклон, а — точка пересечения по оси y. напишите в форме.
Как построить график Y X 3, пример