Графики косинуса и синуса: Свойства функции синуса, косинуса, тангенса, котангенса, арксинуса, арккосинуса. Графики. Тест

Свойства функции синуса, косинуса, тангенса, котангенса, арксинуса, арккосинуса. Графики. Тест

Математика->Тригонометрия->тригонометрические функции->

Тестирование онлайн

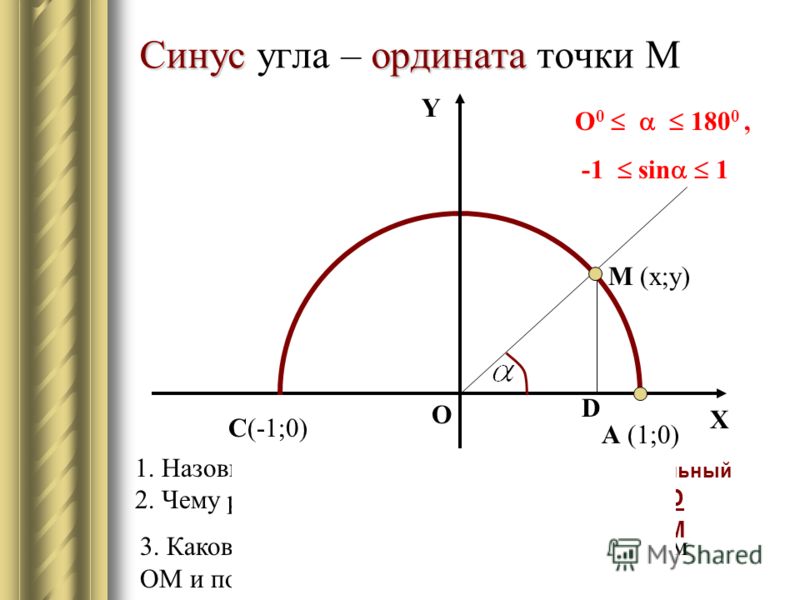
• Функция синуса, косинуса

• Функция тангенса, котангенса

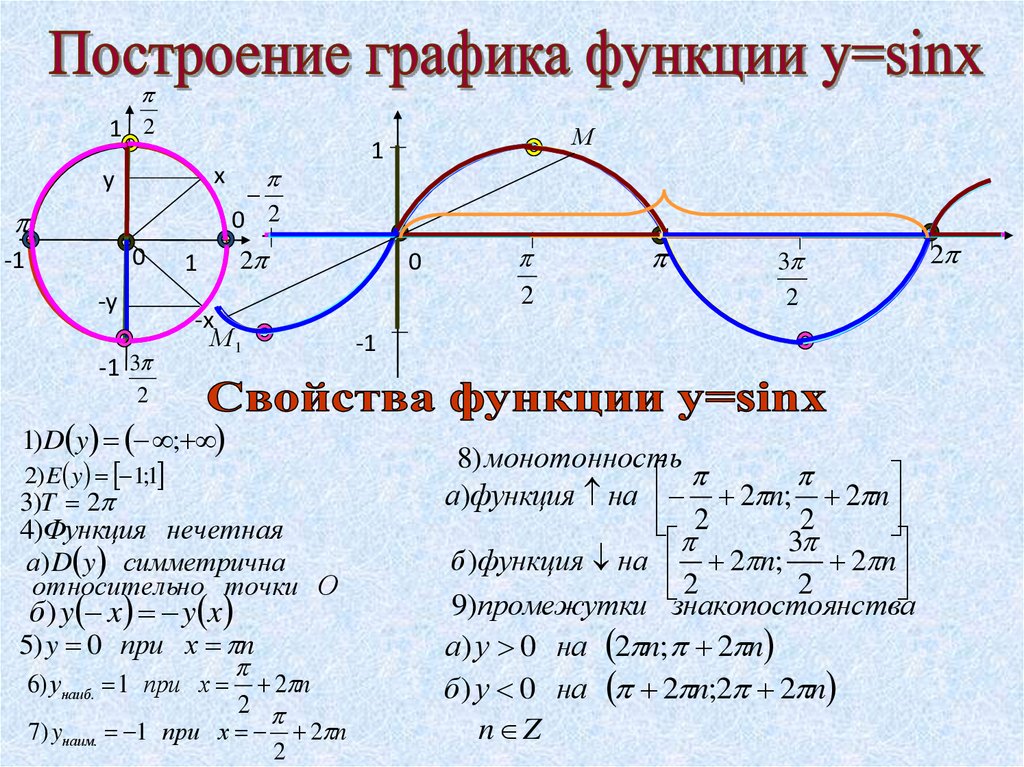
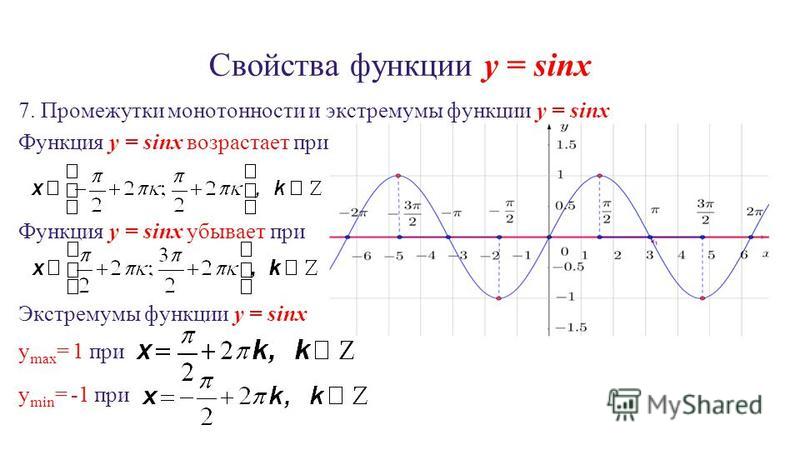
Функция синуса

На рисунке показано построение графика синуса на отрезе .

Рассмотрим основные свойства функции y=sinx:

1) Область определения функции — множество всех действительных чисел

2) Множеством значений функции является промежуток

3) Функция является нечетной, график симметричен относительно начала координат (0;0).

4) Функция периодическая. Наименьший положительный период равен

5) График функции пересекает ось Ох (нули функции) в точках

6) График функции пересекает ось Оy в точке (0; 0).

7) Функция принимает положительные значения на промежутках

8) Функция принимает отрицательные значения на промежутках

9) Функция возрастает на промежутках

10) Функция убывает на промежутках

11) Точки минимума:

12) Точки максимума:

13) Графиком функции является синусоида

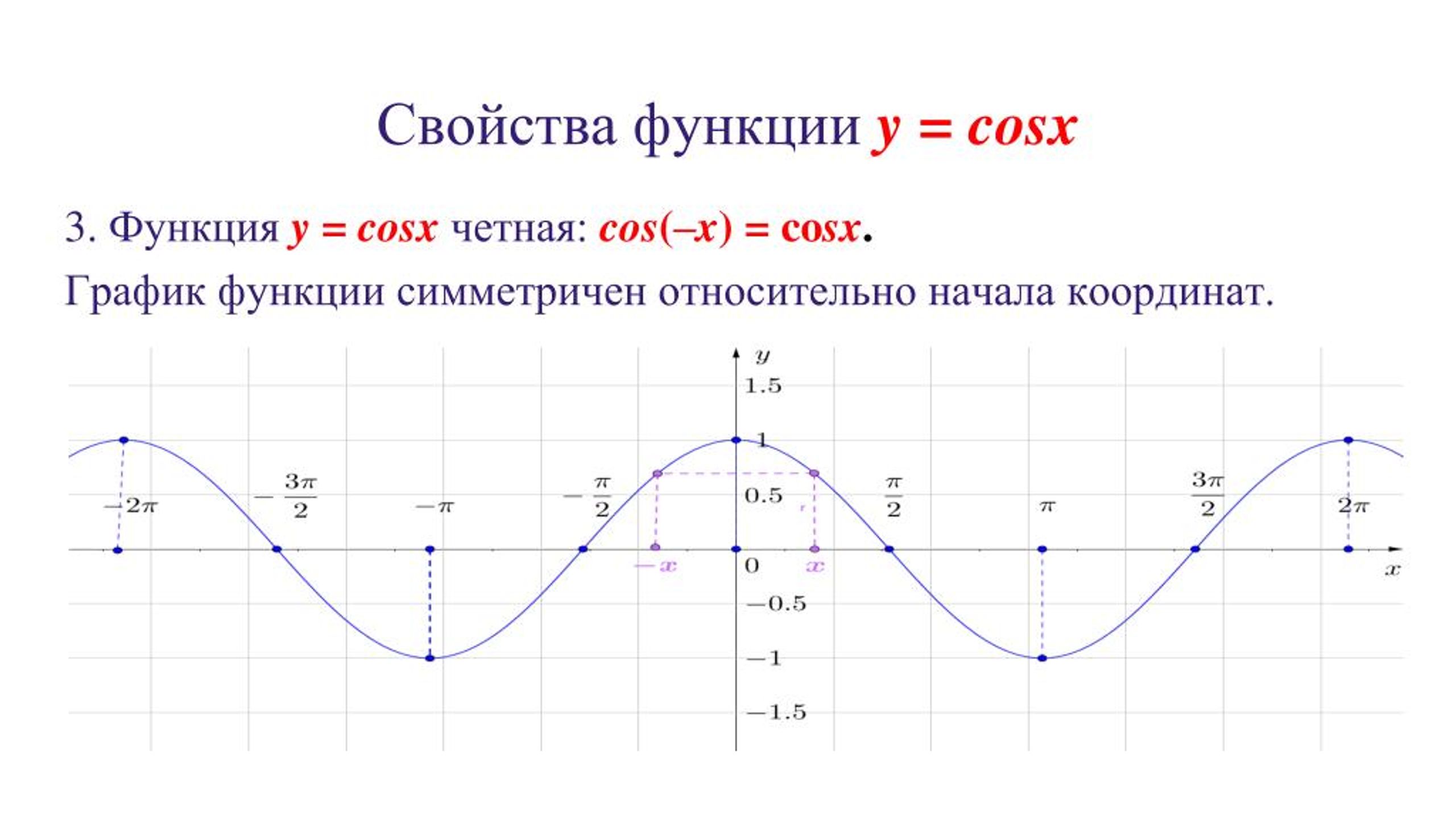
Функция косинуса

График косинуса получается из графика синуса с помощью параллельного переноса на расстояние влево.

Основные свойства функции y=cosx:

1) Область определения функции — множество всех действительных чисел

2) Множеством значений функции является промежуток

3) Функция является четной, график симметричен относительно оси Оу.

4) Функция периодическая. Наименьший положительный период равен

5) График функции пересекает ось Ох (нули функции) в точках

6) График функции пересекает ось Оy в точке (0; 1).

7) Функция принимает положительные значения на промежутках

8) Функция принимает отрицательные значения на промежутках

9) Функция возрастает на промежутках

10) Функция убывает на промежутках

11) Точки минимума:

12) Точки максимума:

13) Графиком функции является косинусоида

Функция тангенса

Основные свойства функции y=tgx:

1) Область определения функции:

2) Множеством значений функции:

3) Функция является нечетной, график симметричен относительно начала координат (0;0).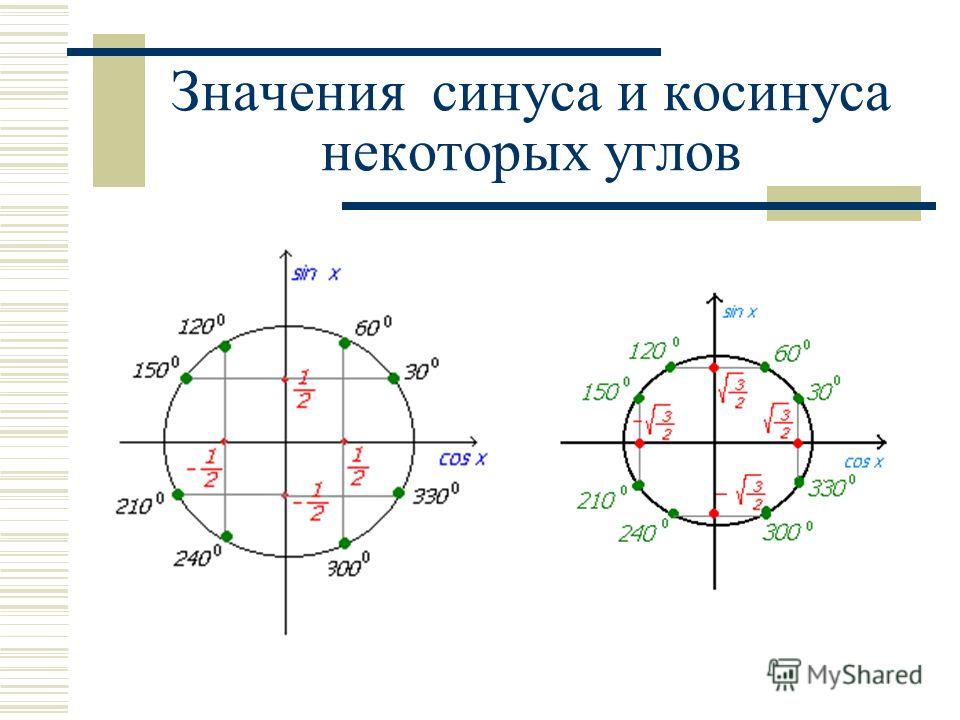

4) Функция периодическая. Наименьший положительный период равен

5) График функции пересекает ось Ох (нули функции) в точках

6) График функции пересекает ось Оy в точке (0; 0).

7) Функция принимает положительные значения на промежутках

8) Функция принимает отрицательные значения на промежутках

9) Функция возрастает на промежутках

10) Промежутки убывания отсутствуют.

11) Точек минимума нет.

12) Точек максимума нет.

13) Графиком функции является тангенсоида:

Функция котангенса

Основные свойства функции y=сtgx:

1) Область определения функции:

2) Множеством значений функции:

3) Функция является нечетной, график симметричен относительно начала координат (0;0).

4) Функция периодическая. Наименьший положительный период равен

5) График функции пересекает ось Ох (нули функции) в точках

6) Функции не пересекает ось Оy.

7) Функция принимает положительные значения на промежутках

8) Функция принимает отрицательные значения на промежутках

9) Функция не имеет промежутков возрастания.

10) Промежутки убывания:

11) Точек минимума нет.

12) Точек максимума нет.

13) Графиком функции является котангенсоида:

Период функции

1) Если T — основной период функции y=f(x), то число является основным периодом функции y=f(ax), где a — любое положительное число.

2) Если периодические функции y=f(x) и y=g(x) имеют один и тот же период T, то их сумма, разность и произведение тоже будет иметь период T.

3) Если периодические функции y=f(x) и y=g(x) имеют соизмеримые периоды T₁ и T₂, то они имеют общий период.

4) Период сложной функции y=g(f(x)) совпадает с периодом функции y=f(x).

Графики функций синуса и косинуса

Похожие презентации:

Построение графиков тригонометрических функций

Построение графиков тригонометрических функций

Синус и косинус

Синус, косинус, тангенс, котангенс

Синус и косинус

Синус, косинус и тангенс угла

Логарифмическая функция, ее свойства и график

Синус, косинус и тангенс угла

Синус, косинус и тангенс угла

Определение синуса и косинуса угла

1.

Графики функций синуса и косинусаy
2
y = sin x
2
3 3
4
2
5
6
3
4
1
6
0
0
7
6
5
4 4
3
3
2
11
7 6
5 4
-1
3
-2
6 4 3
2
2 3 5
3 4 6
х
y = sin x
2
3 3
4
2
5
6
3
4
6
7
6
0
5
4 4
3
11
6
7
3
2
5 4
3
7 5 4
6 4 3
3
2
5 7 11 2
3 4 6
х
y
3
2
y = sin x
1
-3
2
5 -2 — — —
7
6 3 2 3 6
6
0
6 3
-1
-2
-3
2 5 7
2
3 6
6
3
2
х
y
3
2
y = соs x
-3
2
1
5 -2 — — —
7
6 3 2 3 6
6
0
6 3
-1
-2
-3
2 5 7
2
3 6
6
3
2
х
y
3
2
y = соs x
-3
2
y = sin x
1
5 -2 — — —
7
6 3 2 3 6
6
0
6 3
-1
-2
-3
2 5 7
2
3 6
6
3
2
х
№ 16. 27 (а)
y = sin x
y = sin(x )
3
y
3
2
1
х
-3
2
5 -2 — — —
7
6 3 2 3 6
6
0
6 3
-1
-2
-3
2 5 7
2
3 6
6
3
2
№ 16.27 (б)
y = sin x
y = sin(x + )
4
y
3
2
1
х
-3
2
5 -2 — — —
7
6 3 2 3 6
6
0
6 3
-1
-2
-3
2 5 7
2
3 6
6
3
2
№ 16.28 (а)
y = sin x
y = sin x 2
y
3
2
1
х
-3
2
5 -2 — — —
7
6 3 2 3 6
6
0
6 3
-1
-2
-3
2 5 7
2
3 6
6
3
2
№ 16.28 (б)
y = sin x
y = sin x + 1
y
3
2
1
х
-3
2
5 -2 — — —
7
6 3 2 3 6
6
0
6 3
-1
-2
-3
2 5 7
2
3 6
6
3
2
№ 16.29 (а)
y
y = sin x
y = sin(x – )
4
y = sin(x – ) + 1
4
3
2
1
х
-3
2
5 -2 — — —
7
6 3 2 3 6
6
0
6 3
-1
-2
-3
2 5 7
2
3 6
6
3
2
№ 16. 30 (а)
y
3
y = sin x
y = – sin x
y = – sin(x + 6 )
2
1
х
-3
2
5 -2 — — —
7
6 3 2 3 6
6
0
6 3
-1
-2
-3
2 5 7
2
3 6
6
3
2
y
3
y = 3sin x
2
1
х
-3
2
5 -2 — — —
7
6 3 2 3 6
6
y = sinx
0
6 3
-1
-2
-3
2 5 7
2
3 6
6
3
2
y
3
y = sin x
y = sin 2x
y = sin 0,5x
2
1
х
-3
2
5 -2 — — —
7
6 3 2 3 6
6
0
6 3
-1
-2
-3
2 5 7
2
3 6
6
3
2
y
3
y = соs x
y = соs 3x
y = соs 3x/2
2
1
х
-3
2
5 -2 — — —
7
6 3 2 3 6
6
0
6 3
-1
-2
-3
2 5 7
2
3 6
6
3
2

16. Самостоятельное решение:

Из сборника задач решать:
№ 16.31(б)
№ 16.34 (в)
№ 16.50 (а,б)
№ 16.57 (а)

English     Русский Правила

Графики функций синуса и косинуса — Понятие

Синус и косинус являются периодическими функциями, что означает, что графики синуса и косинуса повторяются в шаблонах. Вы можете построить графики функций синуса и косинуса, зная их период и амплитуду. Графики синуса и косинуса

связаны с графиком функции тангенса, хотя графики выглядят совсем иначе.

периодические функции период амплитуда

Я хочу поговорить о построении графиков функций синуса и косинуса. Но сначала мне нужно рассмотреть свойство, которым обладают функции синуса и косинуса, а также эти три функции. Вот у меня вопрос, что общего у этих функций? У меня есть три функции очень разной формы, но все они имеют нечто общее: они периодически повторяются. Эта треугольная форма повторяется на графике y=t(x). Этот шаблон чередующихся интервалов повторяется в y=r(x). И этот волновой паттерн повторяется в y=s(x). Как бы мы описали это свойство математически?
Это свойство называется периодичностью, а эти функции называются периодическими функциями. Определение немного сложное, но давайте посмотрим, сможем ли мы пройтись по нему и понять, что оно означает.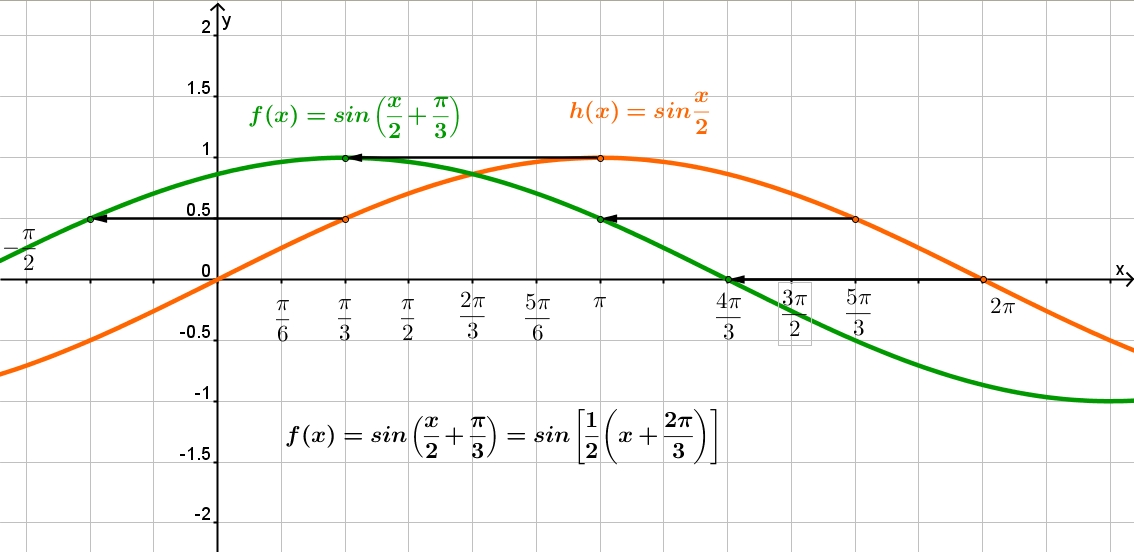

В нем говорится, что если существует число P такое, что f(x)+P=f(x) для всех x в области определения f, то f является периодической функцией. Что это значит, f(x+P)=f(x)? Это означает, что если я найду правильное значение P, я всегда могу добавить это значение к x, к входным данным и получить то же самое на выходе.
Давайте посмотрим на функции. Предположим, я начинаю со значения x, равного 2. Что я могу добавить к 2 и получить точно такой же вывод, как здесь, то есть 0? Я мог бы добавить два, и это дало бы мне 0. Если я прибавлю два к 2, я получу х, равный 0, что имеет выход 0. А если я добавлю два к 0, я получу 2, и это даст 0 , Если я снова добавлю два, я получу 4, и на выходе получится 0,9.0009 Итак, я нашел нужное значение P? Ответ — нет, потому что это значение P не будет работать для всех входных данных. Позвольте мне привести вам пример, 3. Если я добавлю два к 3, я получу 1. И выход 1 равен 1, это не 1, поэтому у меня разные выходы. Опять же, если я начну с 1 и добавлю 2, я получу 1. Выход в единице равен +1, а выход 1 равен 1, разные выходы.
Так что я должен найти другое значение P, которое будет работать для всех x. И получается, что значение этой разницы равно 4. Я могу перейти от одного максимума к другому, прибавив 4: 3+4=1. Итак, четыре — это число, которое сработает. И я бы сказал, что t(x)+4=t(x).
Давайте посмотрим на y=r(x). Теперь здесь, если я начну с красивого числа, такого как 2, и добавлю 2, я получу тот же результат. Здесь на выходе 0, а здесь на выходе 0. И если я снова добавлю два, на выходе все равно будет 0. Но сейчас я настроен немного скептически; Я хочу попробовать это для других входов. Итак, позвольте мне попробовать что-то вроде 1.5. А для 1,5 на выходе 1. Если я прибавлю к этому два, то получу 0,5, а там на выходе 1. А если прибавлю к этому два, то получу 2,5, а там на выходе 1.

Тригонометрические графики с Octave — Мысли Томаса Дерфлингера

Octave — это бесплатная научная вычислительная платформа с открытым исходным кодом.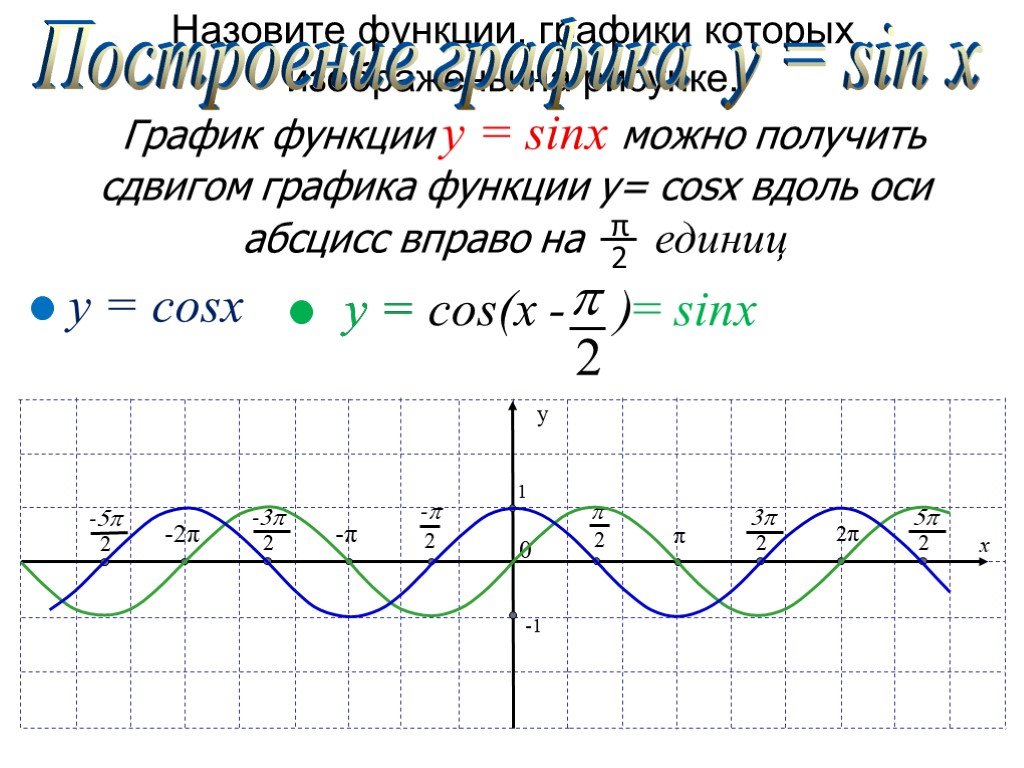 Он особенно подходит для математических операции и имеет простой механизм для построения данных. Визуализация тригонометрии особенно эффективна с Octave. Эта статья о том, как построить визуализацию тригонометрии с помощью Octave.

О Octave

Разработка Octave началась в 1992 году Джоном У. Итоном. Он в основном написан на C++ и содержит интерпретатор языка сценариев высокого уровня Octave. Язык Octave в основном совместим с Matlab. Его синтаксис на основе матриц и поддерживает различные структуры данных и даже позволяет объектно-ориентированное программирование (ООП). Octave можно запустить из командной строки, но он также имеет графический интерфейс пользователя (GUI).

Тригонометрические функции в Octave

Octave охватывает множество тригонометрических функций. Большинство работ с радианами. Но ряд функций тоже работает прямо со степенями. Если вы хотите перевести градусы в радианы, вы можете умножить градусы на пи/180.

Таким образом:

 радиан = градус * пи/180 

Список всех доступных тригонометрических функций доступен по адресу сайте Октавы.

Построение синуса

Чтобы сделать его более интересным, этот простой скрипт отображает как sin(x), так и sin(x*3) на одном графике.

Чтобы отличить одно от другого, я использую черный цвет для sin(x) и красный для sin(x*3).

Вот сценарий Octave, который вы можете ввести в редакторе или запустить в командной строке Octave:

sine.m

 x = -10:0.1:10;
plot (x, sin(x), 'k', x, sin(x*3), 'r') 

X определяет диапазон значений графика, от -10 до 10.

На графике видно, что sin(x*3) имеет три умножить на частоту sin(x). Он плотнее упакован.

Построение синуса и косинуса

Мы также можем объединить функции синуса и косинуса в один график. Таким образом, вы сможете увидеть разницу между две функции четко.

косинус.м

 х = -10:0,1:10;
plot (x, sin(x), 'k', x, cos(x), 'b') 

В этом случае функция синуса черная, а косинус функция окрашена в синий цвет.

Построение тангенса

Еще одна интересная функция для построения графика — это тангенс функция. Тангенс — это отношение между синусом и косинусом.

Единственная проблема с этой функцией, когда косинус становится нулем, потому что на ноль делить нельзя. Таким образом, всякий раз, когда косинус становится равным нулю, это обозначается асимптоты.

Октава также позволяет нам добавлять название и описания для осей x и y. Они добавлены в сценарий ниже:

tan-1.m

 x = -10:0.1:10;
график (х, тангенс (х), '--')
заголовок('Касательная')
xметка('х')
ylabel('tan(x)') 

График для касательной заштрихован, что связано с третий параметр функции графика (‘- -‘).

Будьте осторожны, не называйте имя файла сценария одинаково как функцию Octave, потому что тогда вы получите ошибку.

Заключение

Написание этих маленьких скриптов Octave для построения тригонометрических графиков функции не сложны. Я надеюсь вы вдохновились этой статьей и начали изучать чудеса математики самостоятельно.

Ссылки

Octave: https://www.