Средняя линия трапеции
Четырёхугольник, у которого две противоположные стороны параллельны, а другие две — не параллельны, называется трапецией.
На чертеже 252 у четырёхугольника АВDС АВ || СD, AC ||BD. АВDС — трапеция.
Параллельные стороны трапеции называются её основаниями; АВ и СD — основания трапеции. Остальные две стороны называются боковыми сторонами трапеции; АС и ВD — боковые стороны трапеции.
Если боковые стороны равны, то трапеция называется равнобедренной.
Трапеция АВОМ равнобедренная, так как АМ=ВО (рис. 253).
Трапеция, у которой одна из боковых сторон перпендикулярна к основанию, называется прямоугольной (рис. 254).
Средней линией трапеции называется отрезок, соединяющий середины боковых сторон трапеции.
Теорема. Средняя линия трапеции параллельна каждому из ее оснований и равна их полусумме.
Дано: ОС — средняя линия трапеции АВDК, т. е. ОК = ОА и ВС = СD (рис. 255).
255).
Надо доказать:
1) ОС || КD и ОС || АВ;
2) OC = \(\frac{KD + AB}{2}\)
Доказательство. Через точки А и С проведём прямую, пересекающую продолжение основания КD в некоторой точке Е.
В треугольниках АBС и DСЕ:
ВС = СD — по условию;
∠1 = ∠2, как вертикальные,
∠4 = ∠3, как внутренние накрест лежащие при параллельных АВ и KЕ и секущей ВD. Следовательно, \(\Delta\)АBС = \(\Delta\)DСЕ.
Отсюда АС = СЕ, т.е. ОС является средней линией треугольника КАЕ. Следовательно:
1) ОС || КЕ и, значит, ОС || КD и ОС || AВ;
2) OC = \(\frac{KE}{2} = \frac{KD + DE}{2}\), но DЕ = АВ (из равенства треугольников АBС и DСЕ), поэтому отрезок DЕ можно заменить равным ему отрезком АВ. Тогда получим:
OC = \(\frac{KD + AB}{2}\)
Теорема доказана.
Свойства трапеции, которые часто используются при решении задач:
- Диагонали трапеции разбивают её начетыре треугольника с общей вершиной.
 Площади треугольников, прилежащие к боковым сторонам, равны.
Площади треугольников, прилежащие к боковым сторонам, равны.
- В любой трапеции середины оснований, точка пересечения диагоналей и точка пересечения прямых, на которой лежат боковые стороны, лежат на одной прямой (точки М, N, О и К).
- В равнобокой трапеции углы при основании равны.
- В равнобокой трапеции прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии этой трапеции
- В равнобокой трапеции диагонали равны.
- В равнобокой трапеции высота, опущенная на большее основание из конца меньшего основания, делит его на два отрезка, один из которых равен полуразности оснований, а другой — их полусумме.
- Во всякой трапеции серединам боковых сторон и середины диагоналей лежат на одной прямой.
- Во всякой трапеции отрезок, соединяющий середины диагоналей, параллелен основаниям и равен полуразности оснований.

- Во всякой трапеции сумма квадратов диагоналей равна сумме квадратов боковых сторон и удвоенного произведения оснований.
- Трапецию можно вписать в окружность тогда и только тогда, когда она равнобокая.
- Трапецию можно описать около окружности тогда и только тогда, когда сумма оснований равна сумме боковых сторон.
3.1 Теорема о средней линии трапеции. Мысленный эксперимент в структуре геометрического доказательства
Мысленный эксперимент в структуре геометрического доказательства
дипломная работа
Рассмотрим теорему о средней линии трапеции. Эта теорема по-разному представлена в школьных учебниках геометрии под авторством Погорелова А.В. и Атанасяна Л.С. В учебнике Атанасяна Л.С. [3,стр. 200 — 201] теорема доказывается через понятие вектора, а точнее через правило построения суммы нескольких векторов, называемое правилом многоугольника. Рассмотрим доказательством этой теоремы, приведенной в учебнике А.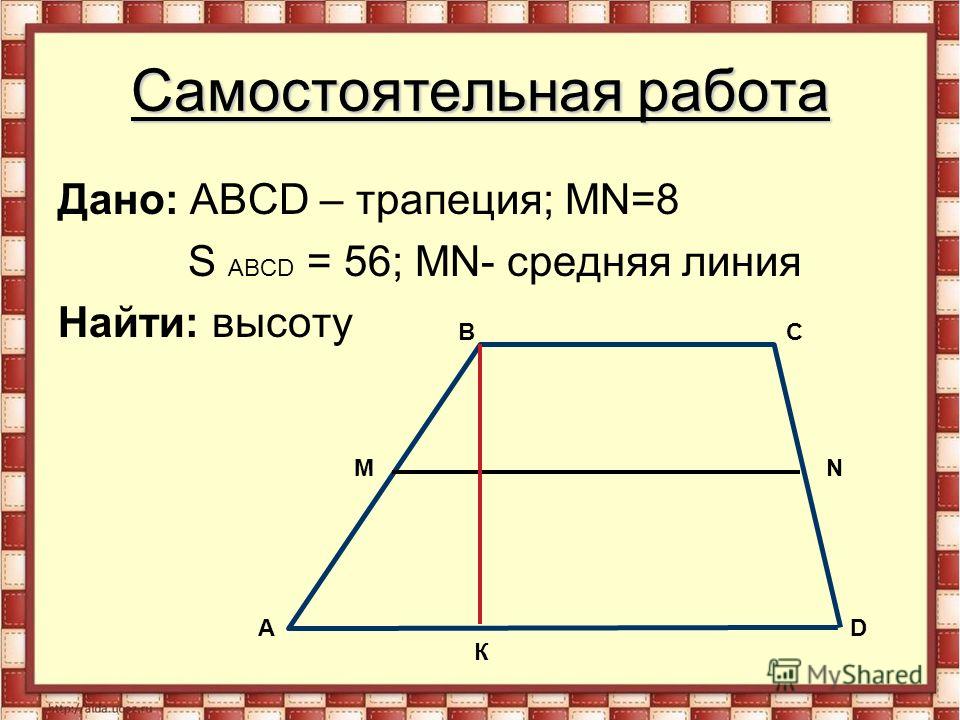 В. Погорелова [14, стр. 92], поскольку она доказывается с помощью дополнительного построения, и в этом смысле более «просто» и схоже с евклидовым. Приведем его дословно:
В. Погорелова [14, стр. 92], поскольку она доказывается с помощью дополнительного построения, и в этом смысле более «просто» и схоже с евклидовым. Приведем его дословно:
«Теорема. Средняя линия трапеции параллельна основаниям и равна их полусумме.
Определение трапеции: трапеция — это четырехугольник, у которого только две противолежащие стороны параллельны.
Доказательство. Пусть ABCD — данная трапеция. Проведем через вершину В и середину Р боковой стороны CD прямую. Она пересекает прямую AD в некоторой точке Е.
Треугольники PBC и PED равны по второму признаку равенства треугольников. У них CP=DP по построению, углы при вершине Р равны как вертикальные, а углы РСВ и PDE равны как внутренние накрест лежащие при параллельных прямых ВС и АD и секущей СD.
Из равенства треугольников следует равенство сторон: РВ=РЕ, ВС=ЕD. Значит, средняя линия PQ трапеции является средней линией треугольника АВЕ. По свойству средней линии треугольника PQ || AE и отрезок PQ=12AE=12*(AD+BC).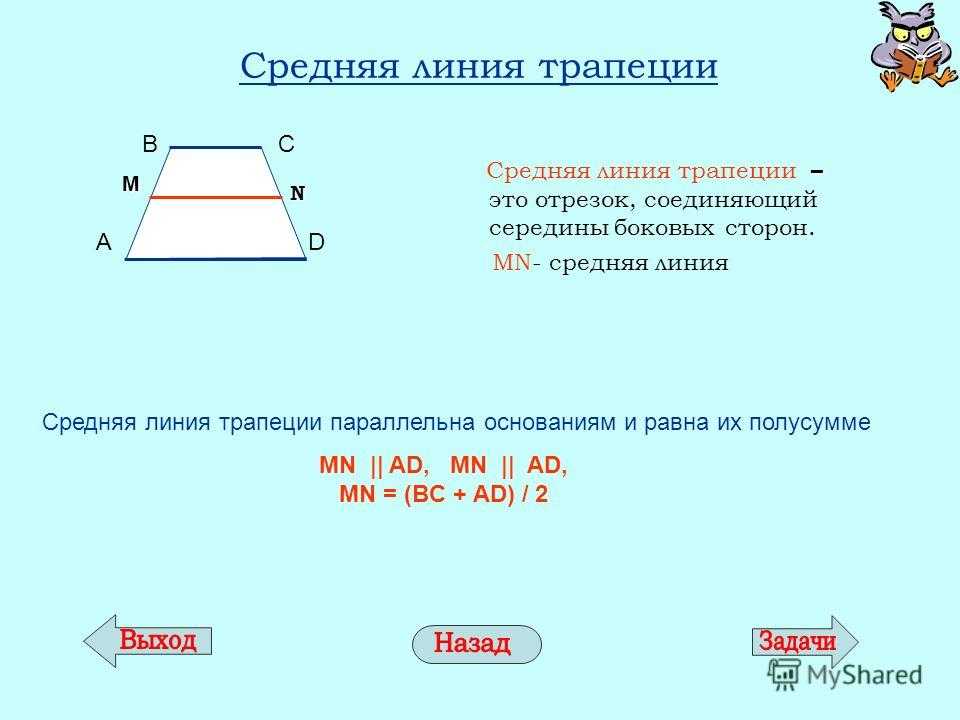 Теорема доказана».
Теорема доказана».
Такое доказательство не позволяет «понять», откуда берется идея построения линии ВЕ. Тогда как именно в проведение этой линии и свернут акт мысленного эксперимента. Ведь после такого «дополнительного построения» остается лишь доказать равенство нужных треугольников. Наша задача состоит в «реконструкции» мысленного эксперимента как важного компонента доказательства.
Доказательство теоремы с использованием мысленного эксперимента.
Итак, предмет мысли нашего мысленного эксперимента — отрезок, соединяющий середины боковых сторон трапеции с ее основаниями, т.е. средняя линия трапеции (рис.1.). Но мы не сможем что-либо узнать об этом отрезке, пока он находится в условиях трапеции. Мы должны поместить его мысленно в такие условия, в которых его сущность может раскрыться с особой определенностью (1этап).
Такими условиями является наделение одной из боковых сторон трапеции следующими идеальными свойствами:
— боковая сторона трапеции способна сжиматься и растягиваться, сохраняя при этом прямизну линии;
— точки боковой стороны, соприкасающиеся с основаниями, способны скользить по прямым линиям, содержащим основания трапеции. При этом точка, являющаяся серединой боковой стороны не должна менять своего расположения (т.е быть центром скольжения).
При этом точка, являющаяся серединой боковой стороны не должна менять своего расположения (т.е быть центром скольжения).
Такие сконструированные условия позволяют нам раскрыть сущность средней линии трапеции с особой определенностью (1 этап) — быть параллельной ее основаниям.
В самом деле: проводя последующие мысленные трансформации (2 этап) путем «вращения» идеализированной боковой стороны, мы будем получать различные варианты четырехугольника, с двумя параллельными сторонами, стремящегося в предельном случаи (совмещении двух вершин) к треугольнику (рис.3), где средняя линия трапеции сохраняет свойство быть средней линией получаемых фигур. Трансформация средней линии трапеции заключается в том, что она перестает быть средней линией трапеции, становясь средней линией другого геометрического объекта — треугольника.
Производя обозначение вершин трапеции, треугольника, средней линии (рис.4), мы тем самым мысленно формируем ту среду, ту систему связей, в которую помещаем наш предмет мысли (3 этап).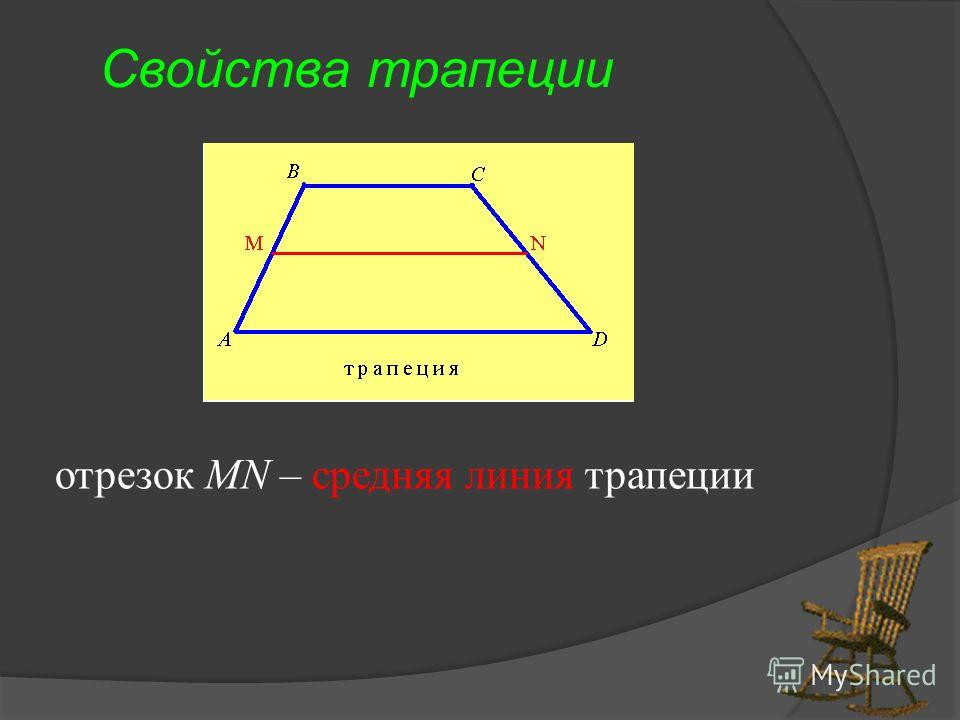
Так как мы наложили условие сохранения прямизны, то, очевидно, что точки C и D боковой стороны CD, скользя по прямым AE и BC проходят одинаковые расстояния (длины). То есть CC1=DD1. Получается — происходит одинаковое растягивание отрезков CP и DP. Очевидно, что при таком скольжении их длины всегда равны (C1P = D1P и BP = EP). Значит отрезок QP — всегда средняя линия получаемого четырехугольника. Который, «при скольжении», стремится к совмещению двух своих вершин (точек С и В) и «превращению» в треугольник АВЕ.
QP — средняя линия треугольника АВЕ, а значит она параллельна стороне АЕ. Из этого вытекает параллельность сторонам AD и BC. Пройденные длины CB и DE — равны. Значит длина АЕ равна сумме длин AD и BC. Получается, что средняя линия QP трапеции ABCD параллельна основаниям BC и AD и равна их полусумме.
Делись добром 😉
Взаимосвязь физического воспитания с другими сторонами воспитания
2.2.1 Линии умственного воспитания
В аспекте задач умственного воспитания в процессе физического воспитания предусматривается:
обогащение специальными знаниями, относящимися к сфере физической культуры, спорта; систематическое расширение и углубление их. ..
..
Взаимосвязь физического воспитания с другими сторонами воспитания
2.2.2 Линии эстетического воспитания
Занятия физическими упражнениями создают благоприятные условия для эстетического воспитания. В процессе занятий формируется красивая осанка, осуществляется гармоничное развитие форм телосложения…
Застосування похідної для доведення рівностей та нерівностей в курсі математики середньої школи
2.2.1 Теорема Ролля
ТЕОРЕМА 1 (Ролля). Нехай функція задовільняє наступним умовам: 1) функція неперервна на проміжку 2) функція диференційована на інтервалі 3) тоді існує точка . Доведення Нехай ,. По теоремі Вейерштраса числа які існують і існують точки й :…
Застосування похідної для доведення рівностей та нерівностей в курсі математики середньої школи
2.2.2 Теорема Лагранжа
ТЕОРЕМА 2 (Лагранжа про середнє значення, або про кінцевий приріст). Якщо функція неперервна на проміжку й диференційована у всіх внутрішніх точках цього проміжка, то усередині проміжка найдеться точка така. ..
..
Застосування похідної для доведення рівностей та нерівностей в курсі математики середньої школи
2.2.3 Теорема Коші
ТЕОРЕМА 3 (Коші). Якщо кожна із двох функцій і неперервна на проміжку й диференційована у всіх внутрішніх точках цього проміжка і якщо, крім того похідна відмінна від нуля всюди усередині проміжка…
Методика обучения решению задач с параметрами на уроках алгебры основной школы
Глава ||. Содержание «линии задач с параметрами» в программе математики средней школы (7-9 классы) на примере учебников А.Г. Мордковича
Несмотря на то, что программа по математике средней общеобразовательной школы не упоминает в явном виде о задачах с параметрами, было бы ошибкой утверждать…
Методика формирования у учащихся средней школы обобщенных умений и навыков при изучении определенного интеграла в процессе решения задач
4.3 Задача о площади криволинейной трапеции
Пусть в плоскости, снабженной декартовой системой координат, задана фигура , ограниченная отрезком оси , прямыми и , кривой , где — однозначная, непрерывная неотрицательная на отрезке функция. ..
..
Мысленный эксперимент в структуре геометрического доказательства
3.2 Теорема о соотношении между сторонами и углами треугольника
Эта теорема сформулирована и доказана в учебнике Атанасяна Л.С. [3,с. 68-69], в учебнике Погорелова А.В. такой теоремы нет. Видимо, связанно это с тем, что неравенство треугольника у Атанасяна Л.С. доказывается с использованием выше указанной теоремы…
Мысленный эксперимент в структуре геометрического доказательства
3.3 Теорема о сумме углов треугольника
Эта теорема сформулирована и в учебнике Атанасяна Л.С. [3,с.66], и в учебнике Погорелова А.В. [14,с.54-55]. Доказательства этой теоремы в этих учебниках существенно не отличаются, а поэтому приведем ее доказательство, например, из учебника Погорелова А.В…
Понятие площади и измерение площадей в школьном курсе математики
2.8 Площадь криволинейной трапеции
Криволинейной называется трапеция, одна из боковых сторон которой — отрезок кривой.
Нахождение площади криволинейной трапеции рассматривается в школе как одно из применений интеграла.
Проектирование уроков по теме «Площади плоских фигур»
5.2 Площади параллелограмма, треугольника и трапеции
Назначение параграфа — опираясь на основные свойства площадей и теорему о площади прямоугольника, вывести формулы для вычисления площадей параллелограмма, треугольника и трапеции. Кроме того…
Решение треугольников в 9 классе
4.3 Теорема синусов
В начале данного урока рекомендуется провести математический диктант, обучающего характера, на 10 минут (см. Приложение). Проверку данного математического диктанта рекомендуется провести в классе, ошибки…
Решение треугольников в 9 классе
4.4 Теорема косинусов
Для доказательства теоремы косинусов необходимо повторить формулы для вычисления координат точки и формулу для вычисления координат точки и формулу для вычисления расстояния между двумя точками: d2= (x1 — x2)2+ (y1 — y2)2…
Элективный курс по математике для классов спортивно-оборонного профиля
Теорема: выбор без учета порядка
Общее количество выборок в схеме выбора k элементов из n без возвращения и без учета порядка определяется формулой
и называется числом сочетаний из n элементов по k элементов.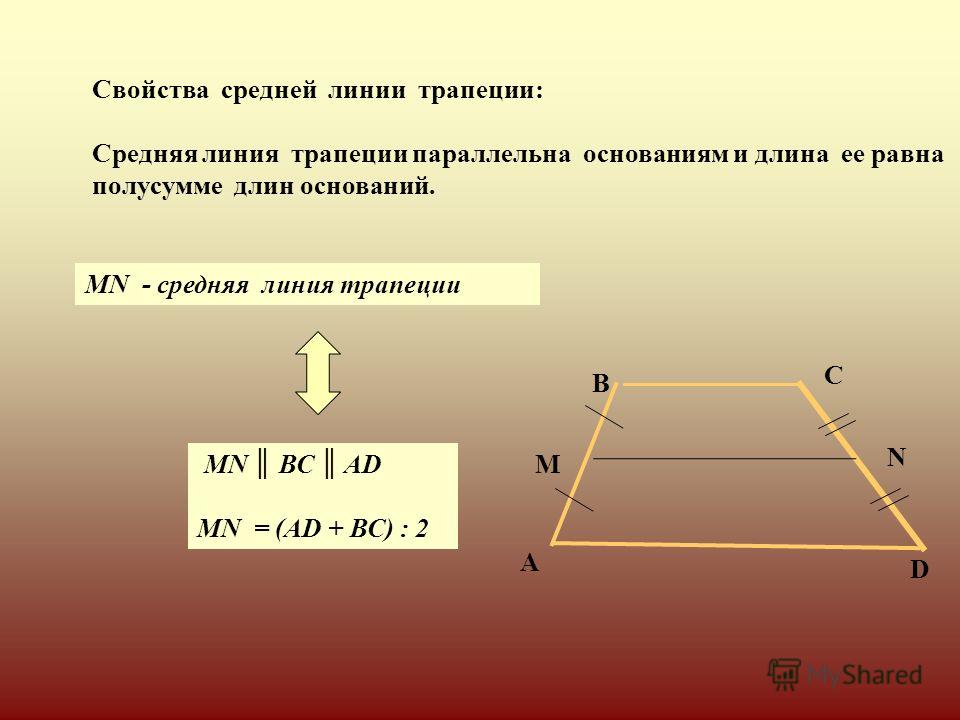 ..
..
Элементы интегрального исчисления в курсе средней школы
3. Методическая схема изучения теоремы о площади криволинейной трапеции
Центральное место в изучении этой темы является теорема о площади криволинейной трапеции: «Пусть f — непрерывная и неотрицательная на отрезке [a, b] функция, S — площадь соответствующей криволинейной трапеции…
Теорема о среднем сегменте трапеции | Помощь по геометрии
Главная » Четырехугольники » Трапеции » Теорема о середине трапеции
Последнее обновление: Идо Сариг · Этот веб-сайт зарабатывает на рекламе и использует файлы cookie · Условия использования · Политика конфиденциальности теорема о середине треугольника.
Теорема о средней линии треугольника утверждает, что прямая, соединяющая середины двух сторон треугольника, называемая средней линией, параллельна третьей стороне, а ее длина равна половине длины третьей стороны.
Аналогичная теорема существует и для трапеций: прямая, соединяющая середины двух катетов трапеции, параллельна основаниям, а ее длина равна половине суммы длин оснований.
Задача
ABCD трапеция, AB || CD . EF — линия, соединяющая середины ветвей AD и BC , AE = ED и BF = FC . Докажите, что EF || DC и что EF =½( AB + DC )
Стратегия
Поскольку мы имеем дело с серединами сегментов, мы будем использовать то, что мы уже доказали для середины сегментов треугольника. Давайте создадим такие треугольники, проведя линию из вершины A через середину F, пока она не пересечет продолжение основания DC в точке G:
Мы можем легко показать, что ΔABF и ΔGCF конгруэнтны, используя угол-сторона -Угловой постулат. Отсюда мы можем показать, что EF — средняя линия треугольника ΔADG. Таким образом, согласно теореме о середине треугольника, он параллелен DG и равен половине DG .
, но DG — DC + CG , а ΔABF и ΔGCF — конгруэнтные, CG = AB , SO EF равен половине DC + .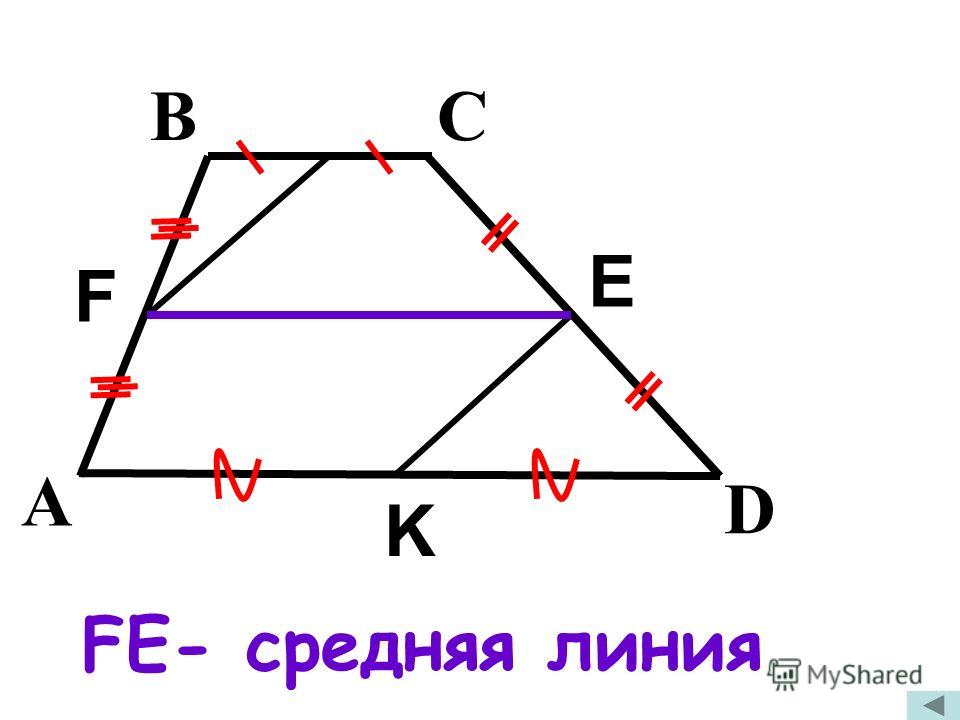 Другими словами, длина EF есть среднее арифметическое (среднее) длин оснований.
Другими словами, длина EF есть среднее арифметическое (среднее) длин оснований.
Доказательство
Вот как доказать теорему о середине трапеции:
(1) AB||DG //Дано, ABCD — трапеция
(2) ∠BAF ≅ ∠CGF // Теорема о чередующихся внутренних углах
(3)∠AED ≅ ∠CEF // Вертикальные углы
(4) BF=FC //Дано
(5)ΔABF ≅ ΔGCF // (2), (3), (4), Угол-Сторона-Угол
(6) AF=FG / /(5), соответствующие стороны конгруэнтных треугольников
(7) EF является средней линией //(6), определение средней линии
(8) EF||DG //(7), теорема о средней линии треугольника
(9)EF=½DG //(7), теорема о середине треугольника
(10) DG = DC + CG
(11) CG = AB //(5), соответствующие стороны конгруэнтных треугольников
(12)EF=1/2 DC CG ) //(9), (10) , Транзитивность равенства
(13) EF=½ (DC + AB ) //(11), (12) , Транзитивность равенства
Верно и обратное утверждение этой теоремы: прямая, параллельная одному из оснований трапеции и пересекающая середину одного катета, пересекает и середину другого катета, а ее длина равна половине суммы длин оснований.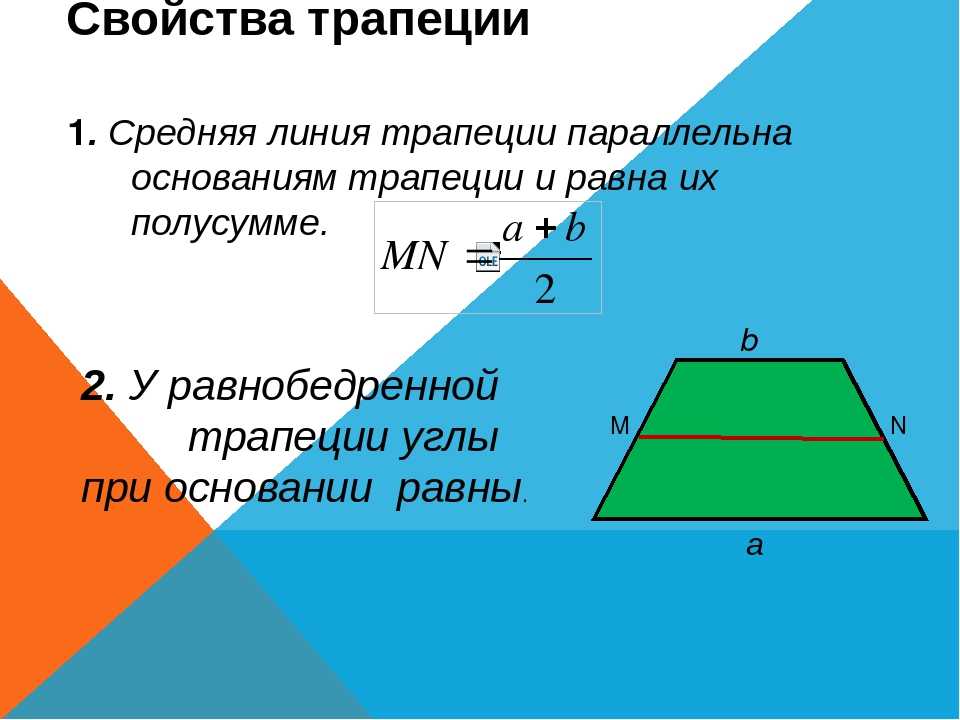
Об авторе
Идо Сариг — руководитель отдела высоких технологий со степенью бакалавра вычислительной техники. Его цель — помочь вам разработать лучший подход к решению геометрических задач. Вы можете связаться с ним по телефону [email protected]
геометрия — Докажите, что периметр и средняя линия трапеции, описанной около окружности, соизмеримы.
$\begingroup$
Трапеция ABCD, описывающая окружность O http://www.hicksvillepublicschools.org/cms/lib2/NY01001760/Centricity/Domain/1129/trapezoidcircle2.bmp
Определение: Два отрезка называются соизмеримыми, если они имеют общую меру
Определение: Общая мера двух отрезков есть третий отрезок такой, что в каждом из первых двух содержится целое число раз без остатка
Итак, у меня есть трапеция ABCD, которая описывает окружность O. Я провел среднюю линию трапеции EF. Я также построил перпендикуляры из точек B и C вниз к отрезку AD.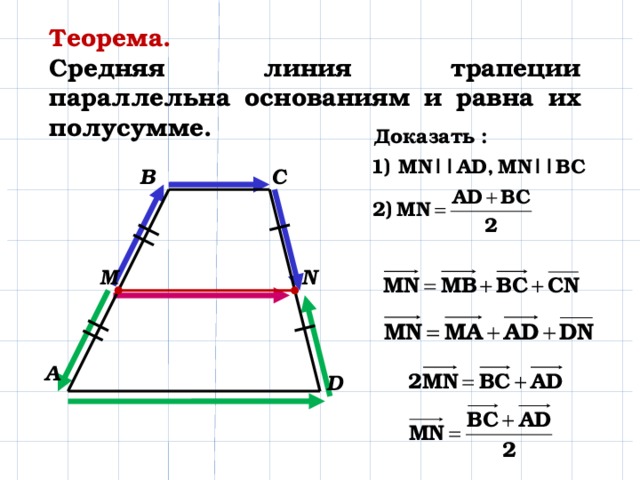
Теперь я знаю, что EI составляет половину AG, так как это средняя линия треугольника ABG. Аналогичный аргумент для FJ и HD. И IJ конгруэнтно OH.
BC конгруэнтно IJ, так как BCJI является параллелограммом (легко доказывается)
AG + GH + HD + DC + BC + BA = периметр EI + IJ + JF = средняя линия
2EI + IJ + 2JF + DC + IJ + BA = периметр
2EI + 2IJ + 2JF + DC + BA = периметр
2*средняя линия + DC + BA = периметр.
И тут я застреваю. Я даже не уверен, правильно ли я подхожу к этому вопросу.
- геометрия
- евклидова геометрия
$\endgroup$
1
$\begingroup$
Подсказка: поскольку ваша трапеция описана в окружности, расстояние от вершины до двух точек касания сторон, которые встречаются в этой вершине, одинаково. Отсюда следует, что $AB+CD=AD+CB$.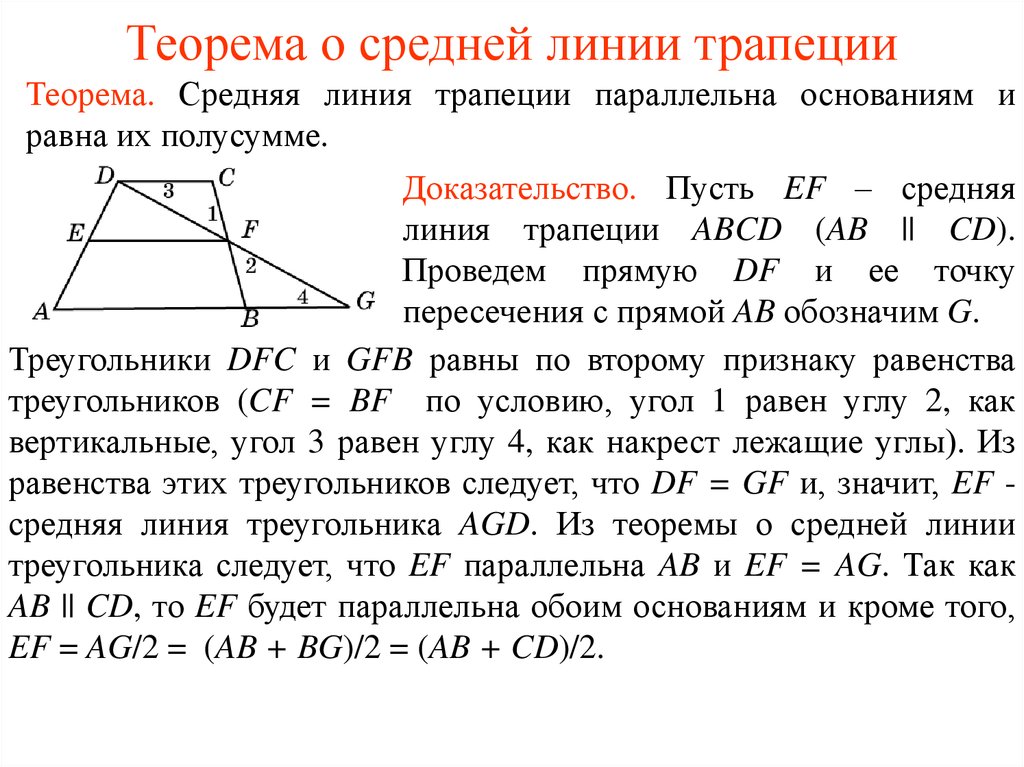

 Площади треугольников, прилежащие к боковым сторонам, равны.
Площади треугольников, прилежащие к боковым сторонам, равны.
