Графики важнейших функций и их преобразования — Математика — Теория, тесты, формулы и задачи
- Главная —
- Формулы и прочее —
- Математика: Графики функций
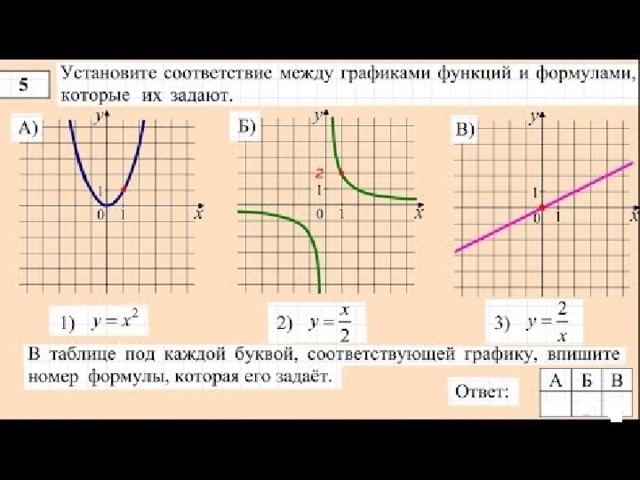
На этой странице представлены графики важнейших функций, изучаемых в школьном курсе математики. Также представлены примеры преобразования этих графиков в различных типичных ситуациях (рассмотрены случаи когда графики смешаются вдоль осей, симметрично отражаются относительно различных осей). Представлен также вид некоторых графиков функций с модулями.
Знание того, как выглядят графики основных математических функций, а также того, как они преобразовываются в различных ситуациях, может очень помочь при решении различных сложных задач на экзаменах.
Изучать графики основных функций и их преобразования онлайн:
- Назад
- Вперёд
Как успешно подготовиться к ЦТ по физике и математике?
Для того чтобы успешно подготовиться к ЦТ по физике и математике, среди прочего, необходимо выполнить три важнейших условия:
- Изучить все темы и выполнить все тесты и задания приведенные в учебных материалах на этом сайте. Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен, где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности.
Последнему научиться можно только решив тысячи задач. - Выучить все формулы и законы в физике, и формулы и методы в математике. На самом деле, выполнить это тоже очень просто, необходимых формул по физике всего около 200 штук, а по математике даже чуть меньше. В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами.
- Посетить все три этапа репетиционного тестирования по физике и математике. Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию.
Последнему научиться можно только решив тысячи задач.
Успешное, старательное и ответственное выполнение этих трех пунктов, а также ответственная проработка итоговых тренировочных тестов, позволит Вам показать на ЦТ отличный результат, максимальный из того, на что Вы способны.
Нашли ошибку?
Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на электронную почту (адрес электронной почты здесь). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.
3.5. Математические основы векторной графики
В основе векторной
графики лежат математические представления
о свойствах геометрических фигур.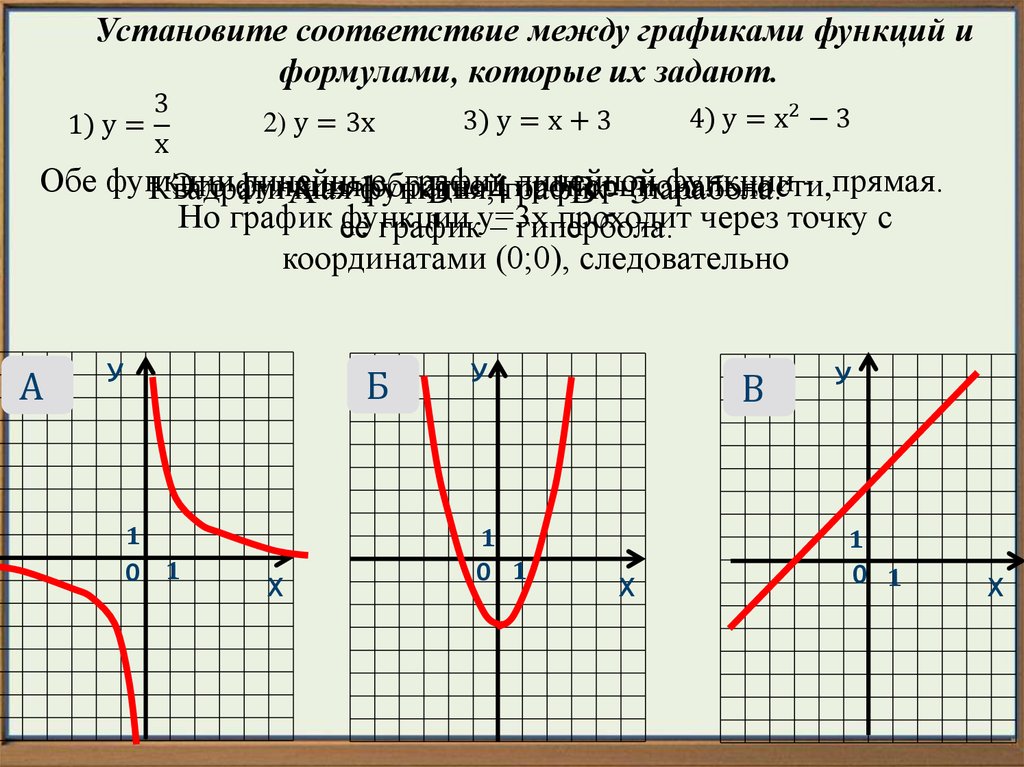
Точка
Точка на плоскости задается двумя числами (х, у),определяющими ее положение относительно начала координат.
Прямая линия
Из курса алгебры известно, что для задания прямой линии достаточно двух параметров. Обычно график прямой линии описывается уравнением y = kx + b.Зная параметрыkиb,всегда можно нарисовать бесконечную прямую линию в известной системе координат.
Отрезок прямой
Для задания отрезка
прямой надо знать еще пару параметров,
например координаты х
Кривая второго порядка
К кривым второго
порядка относятся параболы, гиперболы,
эллипсы, окружности и другие линии,
уравнения которых не содержат степеней
выше второй.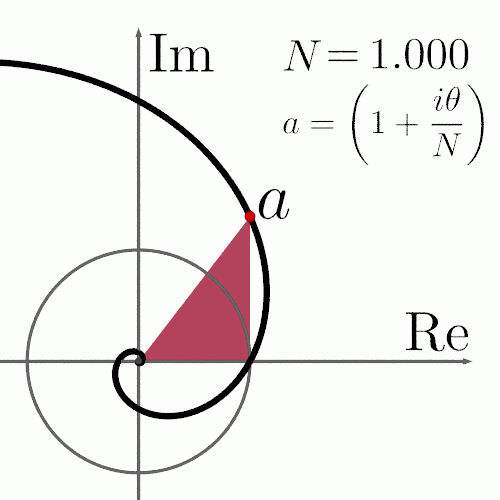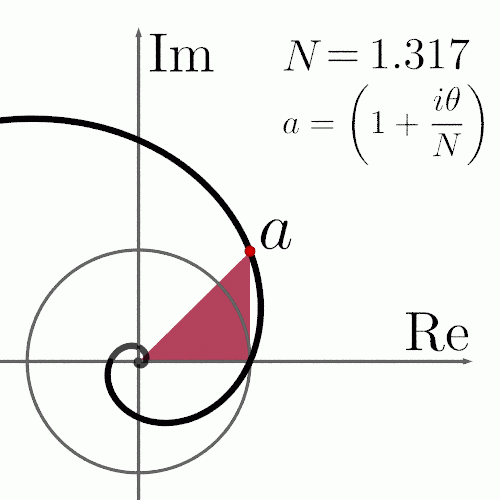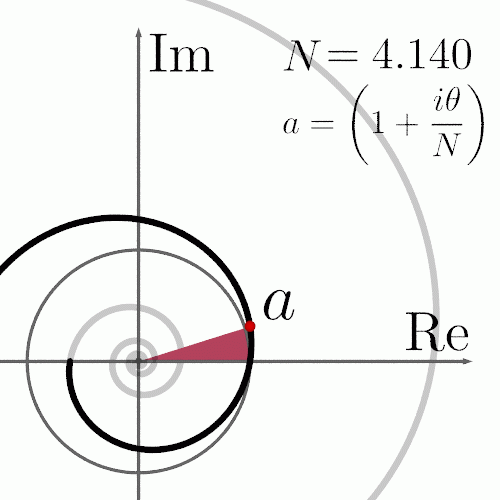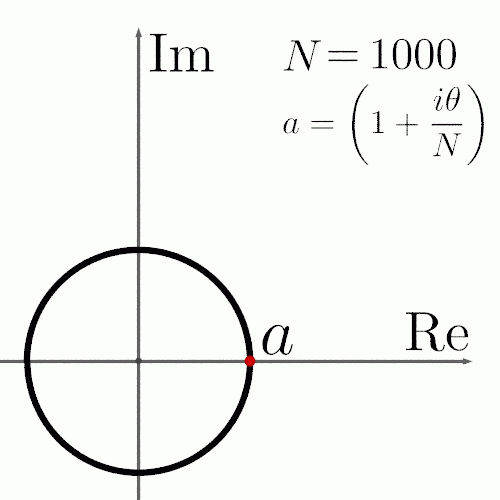
Прямые линии — это частный
случай кривых второго порядка. Отличаются
кривые второго порядка тем, что не имеют точек перегиба.Самая общая формула
кривой второго порядка может выглядеть,
например, так:
x2 + a1y2 + a2xy + a3x + a4y + a5 = 0
Как видите, пяти параметров вполне достаточно для описания бесконечной кривой второго порядка. Для записи отрезка кривой второго порядка необходимо на два параметра больше.
Точка на координатной плоскости
Прямая
Парабола
Кривая третьего порядка
Отличительная
особенность этих более сложных кривых
состоит в том, что они могут иметь точку
перегиба. Если вы знакомы с графиком
функции y=х3, то
конечно видели тот перегиб, который
происходит в начале координат. Кривые
третьего порядка хорошо соответствуют
тем линиям, которые мы наблюдаем в живой
природе, например линиям изгиба
человеческого тела, поэтому в качестве
основных объектов векторной графики
используют именно такие линии.
Все
прямые и кривые второго порядка (например,
окружности или эллипсы) являются частными
случаями кривых третьего порядка.
В общем случае уравнение кривой третьего порядка можно записать так:
x3 + a1y3 + a2x2
Видно, что для записи кривой третьего порядка достаточно девяти параметров. Для задания отрезка кривой третьего порядка надо иметь на два параметра больше.
Кривые Безье
Рисовать кривую
третьего порядка по заданным коэффициентам
ее уравнения — занятие не слишком
интересное. Для упрощения этой утомительной
процедуры в векторных редакторах
применяют не любые кривые третьего
порядка, а их особый вид, называемый кривыми Безье.Отрезки кривых Безье
— это частный случай отрезков кривых
третьего порядка. Они описываются не
одиннадцатью параметрами, как произвольные
отрезки кривых третьего порядка, а лишь
восемью, и потому работать с ними удобнее.
Метод построения кривой Безье основан на использовании пары касательных, проведенных к линии в точках ее концов. На практике эти касательные выполняют роль «рычагов», с помощью которых линию изгибают так, как это необходимо. На форму линии влияет не только угол наклона касательной, но и длина ее отрезка. Управление касательной (а вместе с ней и формой линии) производят перетаскиванием маркера с помощью мыши.
Большинство векторных редакторов для изображения и хранения кривых линий используют именно кривые Безье.
График функции y = x3
Кривая Безье
Что такое график в математике? Определение, примеры решений, факты
Что такое график?
В математике график может быть определен как графическое представление или диаграмма, которая представляет данные или значения в организованном порядке.
Точки на графике часто представляют отношения между двумя или более вещами.
Здесь, например, мы можем представить приведенные ниже данные, тип и количество школьных принадлежностей, используемых учащимися в классе, на графике. Мы начинаем с подсчета каждой поставки и представления данных определенными цветами в систематическом порядке в таблице.
Мы также можем представить данные в виде гистограммы. Количество каждого из расходных материалов представлено столбиками. Чем выше высота столбца, тем больше количество используемого припаса или предметов.
Типы графиков:
Пиктограмма
Представление информации посредством изображений называется пиктограммой. Каждое изображение представляет определенное количество предметов. Например, вы можете использовать изображение биты для крикета, чтобы показать, сколько бит для крикета продается в магазине в течение определенной недели.
На этой пиктограмме 1 изображение биты для крикета соответствует 4 битам для крикета. Итак, судя по графику, во вторник было продано 12 ракеток (4+4+4).
Гистограмма
Гистограмма — это представление числовых данных в виде прямоугольников (или столбцов) одинаковой ширины и различной высоты. Зазор между одним стержнем и другим равномерен на всем протяжении. Гистограммы могут быть как горизонтальными, так и вертикальными. Высота или длина каждого столбца напрямую связана с его значением.
Линейный график:
На линейном графике точки, соединенные линиями, показывают изменения за определенный период времени.
Круговая диаграмма:
Круговая диаграмма также известна как круговая диаграмма. Он показывает, как целое делится на разные части. Круговая диаграмма показывает относительный размер каждого набора данных по отношению ко всему набору данных. Проценты используются, чтобы показать, сколько всего занимает каждая категория.
Решенные Примеры:
Пример 1: Укажите, верны или нет данные утверждения.
- В гистограмме ширина столбцов может быть разной.
- На гистограмме столбцы одинаковой ширины могут отображаться как по вертикали, так и по горизонтали.
- На гистограмме расстояние между двумя последовательными столбцами может быть разным.
- На гистограмме каждый столбец представляет только одно числовое значение.
Решение:
- Ложь. На гистограмме полосы имеют одинаковую ширину.
- Правда
- Ложь. На гистограмме промежуток между двумя последовательными столбцами должен быть одинаковым.
- Правда
Пример 2: Назовите тип каждого из данных графиков.
______________________________
______________________________
______________________________
______________________________
Solution:
(a) Bar graph
(b) Pie chart
(c) Pictograph
(d) Линейный график
Пример 3: Обратитесь к данной пиктограмме и ответьте на вопросы.
- Какой аромат был самым популярным?
- 60 рожков какого вкуса продано?
- Сколько ванильных рожков было продано?
- Сколько всего конусов было продано?
Решение:
- Мятно-шоколадная стружка
- Клубника
- 50 конусов
- 340 конусов
Пример 4: Прочтите гистограмму и ответьте на вопросы.
(a) Сколько отжиманий было сделано в четверг?
(б) В какой день не отжимались?
(c) В какой день было сделано максимальное количество отжиманий?
(d) Целью Сэма было отжиматься не менее 140 раз в неделю. Проверьте, не смог ли Сэм достичь своей цели.
Решение:
(a) 25
(b) Среда
(c) Воскресенье
(d) Всего отжиманий за неделю = 15 + 20 + 0 + 25 + 20 + 30 + 35 = 145 отжиманий
Таким образом, чтобы достичь цели в 150, нужно было сделать еще 5 отжиманий.
Практические задачи
1
Круговой график, в котором каждый сектор представляет определенную величину, называется a:
Линейный график
Пиктограмма
Круговая диаграмма
Гистограмма
Правильный ответ: Круговая диаграмма Круговая диаграмма
граф, делящий окружность на разные сектора. Каждый сектор создается пропорционально для представления определенного количества.
2
Какой тип графика отображает данные, которые непрерывно изменяются в течение определенного периода времени?
Линейный график
Пиктограмма
Круговая диаграмма
Гистограмма
Правильный ответ: Линейный график
На линейном графике точки, соединенные линиями, показывают изменения за определенный период времени.
3
Какой тип графика представляет данные в виде прямоугольников одинаковой ширины?
Линейный график
Пиктограмма
Круговая диаграмма
Гистограмма
Правильный ответ: Гистограмма
Гистограммы используют прямоугольники или узкие столбцы для представления данных.
4
Пиктограмма использует следующие два изображения. Используйте приведенную ниже информацию, чтобы найти неизвестное значение:
10
50
100
200
Правильный ответ: 50
100 ÷ 2 = 50.
Часто задаваемый вопрос
Что такое данные?
Данные — это совокупность фактов, собранных для получения значимой информации.
Что отличает данные от информации?
Данные представляют собой набор числовых фактов в необработанной и неорганизованной форме. Информация – это обработанные данные, организованные в организованном и структурированном виде.
Зачем нам нужно изучать представление данных?
Представление данных в визуальной форме или в виде графиков дает четкое представление о том, что означает информация, и облегчает понимание и выявление тенденций и закономерностей.
Графики (математика): определение, примеры и типы
Графики — это визуальное представление уравнений, которые могут помочь нам понять взаимосвязь между двумя переменными.
Использование графиков для алгебраических взаимосвязей
Вы можете использовать координатную плоскость , которую вы видите ниже, для графического построения любых алгебраических взаимосвязей. Координатная плоскость состоит из горизонтальной линии (ось x) и вертикальной линии (ось y) и разделена на четыре квадранта , обозначенных римскими цифрами (I, II, III и IV).
Различные точки на графике имеют координат , записанных как упорядоченных пар (пары чисел в скобках, разделенных запятой). Первое число в упорядоченной паре (x, y) представляет значение x, а второе представляет значение y для данной точки. Например, средняя точка, где пересекаются оси x и y, называется началом координат , а ее координаты равны (0, 0).
Графики помогают нам анализировать поведение переменных и могут использоваться, чтобы делать выводы о них и облегчать интерпретацию данных.
Координатная плоскость
Графики и эскизы
При построении графиков вы можете либо рисовать, либо делать эскизы. Для построения графика вы обычно используете миллиметровую бумагу и составляете таблицу значений координат x и y и наносите их как можно точнее.
Если у вас есть уравнение y = x, вы можете построить его график следующим образом:0298
6 2
. Вам нужно нарисовать оси x и y и набросать общую форму кривой, включая точки, где она пересекает оси x и y. В случае линейного графика вам нужно всего несколько точек, чтобы провести линию, пересекающую эти две точки. Когда вы рисуете линейный график для y = x, вам нужна только еще одна точка, так как вы знаете, что линия пересекает начало координат (0, 0).
Набросок графика
Какие существуют типы графиков?
В зависимости от типа функции, которую вы изображаете, вы получите различные характерные формы для их кривой. Ниже описаны основные типы графиков.
Линейные графики
Линейные графики представляют собой прямую линию . Они представляют собой график функций, в уравнении которого наивысший показатель степени равен 1.
В линейных графиках наклон — скорость изменения линии в вертикальном направлении. Уклон может быть пологим или крутым, в зависимости от его величины. Чем больше значение наклона, тем круче будет линия, а чем меньше значение наклона, тем пологее будет линия. Также вам нужно будет помнить, что наклон горизонтальной линии равен нулю, а наклон вертикальной линии не определен.
Любое линейное уравнение может быть представлено в форме точки пересечения, например:
y = м x + b
x = независимая переменная
y = зависимая переменная
m = уклон (насколько крута линия) пересекает ось y)
Уклон можно рассчитать по формуле:
м =
м = =
, где и — любые две точки на прямой.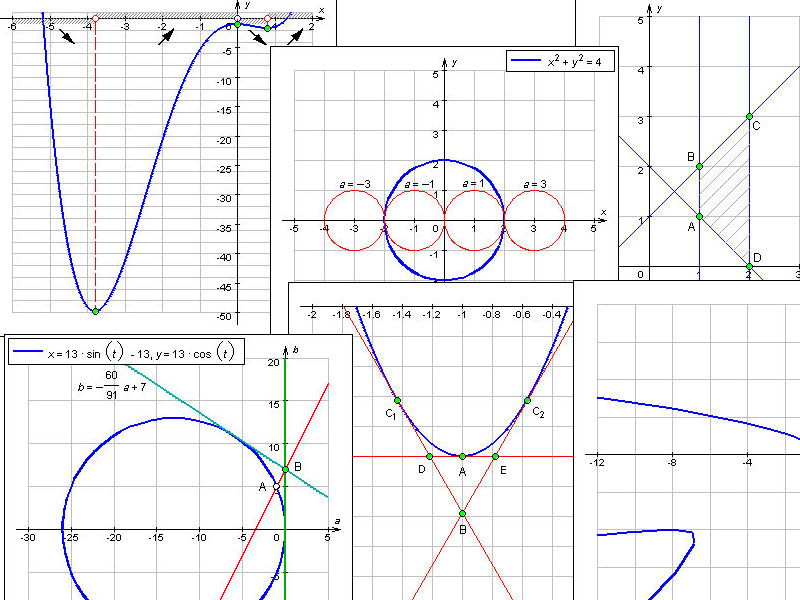
Если у вас нет уравнения линейного графика, но вы можете определить две точки на линии A = (2, 2) и B = (5, 5).
Расчет уклона
Тогда вы можете рассчитать уклон следующим образом:
м = 1
одинаковый.
Если у вас есть линейное уравнение y = mx + b, вам не нужно вычислять наклон. Вы можете определить в уравнении значение m, которое будет наклоном линии. Точно так же значение b будет точкой пересечения с осью y.
Для уравнения y = 2x + 3, m = 2 и b = 3.
Чтение прямых графиков расширит ваши знания по этой теме.
Квадратичные графики
Если функция, которую мы хотим построить, представляет собой квадратичную , в общем представленную как , то форма y = f (x) будет параболой .
Если коэффициент при ( ) положительный, то парабола будет направлена вверх.
Квадратичный график с положительным коэффициентом
Если коэффициент при ( ) отрицателен, то парабола будет перевернута.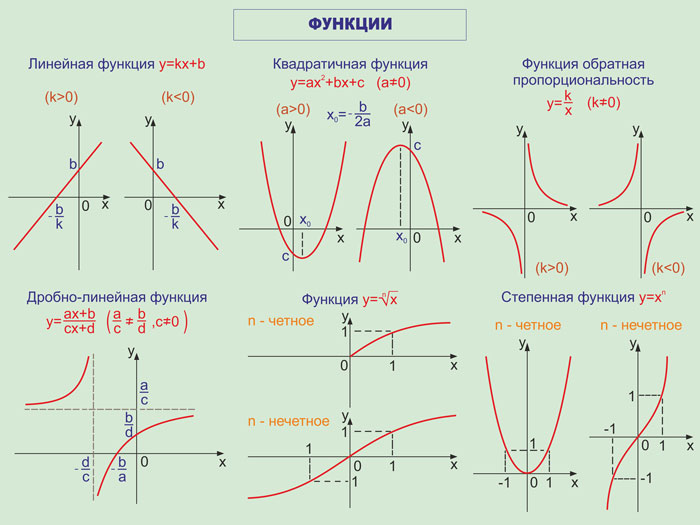
Квадратичный график с отрицательным коэффициентом
Помимо определения того, будет ли парабола направлена вверх или вниз, для построения квадратичного графика необходимо действовать следующим образом:
Подставить x = 0 в функцию , чтобы получить координата y, где парабола пересекает ось y, равная c.
Приравняем функцию к нулю и найдем корни функции f(x). Корни будут координатами x, где парабола пересекает ось x. Вы можете найти корни, разложив на множители, дополнив квадрат или используя формулу квадрата.
Найдите точку поворота параболы (минимальную или максимальную), либо заполнив квадрат, либо используя симметрию.
Если вы завершите квадрат, то точка поворота будет (-p, q), если .
Если вы используете симметрию, x-координата точки поворота будет находиться в середине двух корней, найденных на предыдущем шаге (сложите их вместе, а затем разделите на 2). После этого нужно подставить полученное значение x в исходную функцию, чтобы найти координату y точки поворота.
Нарисуйте график.
Нарисуйте график и найдите координаты его поворотной точки.
- Коэффициент при ( ) положительный, поэтому парабола будет направлена вверх и будет иметь точку минимума.
- При x = 0, y = 2 парабола пересекает ось y в точке (0, 2)
- Найдите корни функции, разложив на множители
Корни составляют и
- с использованием симметрии, чтобы найти поворотный точ
Набросок квадратичного графика
Кубические графики
Если функция, которую вы рисуете, представляет собой кубическую , в общем представленную как , то форма y = f (x) показана ниже, если коэффициент ( ) положительный.
Кубический график с положительным коэффициентом
Если коэффициент при ( ) отрицательный, то форма будет такой:
Кубический график с отрицательным коэффициентом
корни функции.
Нарисуйте кривую, показывающую точки пересечения осей координат.
- Когда y = 0,
Корни равны , , и
Следовательно, кривая пересекает ось x в точках (-1, 0), (-2, 0) и (-3, 0) )
- Когда x = 0,
Кривая пересекает ось Y в точке (0, 6) представляют собой квартику , в общем представленную как , то форма y = f (x) может иметь разные формы в зависимости от ее корней. Одна из возможных форм, если коэффициент при ( ) положительный, показан ниже.
Квартальный граф с положительным коэффициентом
Если коэффициент при ( ) отрицателен, его кривая может принять следующий вид:
График четвертой степени с отрицательным коэффициентом
Опять же, чтобы начертить график функции четвертой степени, необходимо найти корни функции.
Нарисуйте кривую, показывающую точки пересечения осей координат.
- Когда y = 0,
Корни x = 0, x = 1, x = -3 и x = 2
Следовательно, кривая пересекает ось x в точке (0, 0), (1, 0), (-3, 0) и (2, 0)
- При x = 0, y = 0
Кривая пересекает ось Y в точке (0, 0)
- Набросок графика:
Набросок графика четвертой степени
Пожалуйста, обратитесь к статье Полином Графики для более подробной информации и примеров о квадратичных, кубических и квартических графах.
Графики функции модуля
Функция модуля , также известная как функция абсолютного значения, представлена в общем виде. Модуль числа x будет тем же числом, но положительным. Типичная форма модульной функции показана ниже.
График функции модуля
Если у вас есть выражение внутри функции модуля, вычислите значение внутри, а затем найдите положительную версию результата.
Если у вас есть функция find
Чтобы начертить график функции модуля, вам нужно начертить и отразить часть линии, которая идет ниже оси x, в ось x.
Нарисуйте график, показывающий точки пересечения осей координат.
Не обращая внимания на модуль, нужно начертить график
- Когда y = 0, x = 1
Линия пересекает ось x в точке (1, 0)
- Когда x = 0, y = -1
Линия пересекает ось y в точке (1, 0) (0, -1)
- Нарисуйте график для:
Нарисуйте график функции модуля
- Для отрицательных значений y отразите по оси x. В этом случае (0, -1) становится (0, 1)
Набросок графика модульной функции
Прочтите о функции модуля, чтобы узнать больше об этом типе графика.
Взаимные графики
Взаимные функции обычно представляются как , и . Чтобы набросать этот тип графика, необходимо рассмотреть его асимптоты. Асимптота — это линия, к которой кривая подходит очень близко, но никогда ее не касается. График обратных функций имеет асимптоты при x = 0 и y = 0. Форма обратной функции, где , , показана ниже.
График обратной связи с положительным коэффициентом
Форма обратной функции где , , следующая.
График обратной зависимости в квадрате
Эскиз графика для
Набросок графика обратной зависимости
Для получения дополнительной информации и примеров об этом типе графика см. раздел Графики обратной зависимости.
Круговые диаграммы
Другим важным типом диаграмм, которые вы найдете в Координатной геометрии, являются круговые диаграммы.
Окружность — это набор точек, находящихся на одинаковом расстоянии от фиксированной точки, называемой центром. Уравнение окружности с центром (0, 0) и радиусом r равно . Если центр находится в (a, b), то уравнение меняется на .График круга
Запишите уравнение круга с центром (6, 5) и радиусом 3, затем нарисуйте его график.
Набросок круговой диаграммы
Узнайте больше о Круговой математике.
Графики — ключевые выводы
Графики — это визуальное представление уравнений, которые могут помочь нам понять взаимосвязь между двумя переменными.
При наброске вам не нужно быть таким точным, как при черчении; вам нужно нарисовать оси x и y и набросать общую форму кривой, включая точки, где она пересекает оси x и y.
Наклон линии и точка пересечения с осью y могут использоваться для построения графика линейного уравнения.
Для построения квадратных, кубических и квадратных уравнений необходимо определить корни функции, а также точку пересечения кривой с осью y.
В этом случае (0, -1) становится (0, 1)
Окружность — это набор точек, находящихся на одинаковом расстоянии от фиксированной точки, называемой центром. Уравнение окружности с центром (0, 0) и радиусом r равно . Если центр находится в (a, b), то уравнение меняется на .