Графы онлайн: Инструмент для работы с графами онлайн

Инструмент для работы с графами онлайн

Задайте матрицу смежности. Используйте запятую «,» в качестве разделителя

Для мультиграфа матрица содержит значения минимальных дуг между вершинами.

Мартрица имеет неправильный формат. Используйте запятую «,» в качестве разделителя. Матрица должна иметь одинаковое количество столбцов и строк.

Задайте матрицу инцидентности. Используйте запятую «,» в качестве разделителя

Мартрица имеет неправильный формат. Используйте запятую «,» в качестве разделителя.

Ваш алгоритм отправлен на модерацию и в случае успеха он будет добавлен на сайт.

Ошибка создания графа. Матрица смежности имеет неправильный формат. Нажимте кнопку «исправить матрицу» чтобы исправить матрицу или кнопку «справка» чтобы открыть справку о формате матрицы

Ошибка создания графа. Матрица инцидентности имеет неправильный формат. Нажимте кнопку «исправить матрицу» чтобы исправить матрицу или кнопку «справка» чтобы открыть справку о формате матрицы

Выделите и перемещайте объекты или перемещайте рабочую область.

Перемещайте курсор для перемещения объекта

Выделите и перемещайте объекты или перемещайте рабочую область.

Перемещайте курсор для перемещения объекта

Кликните на рабочую область, чтобы добавить вершину. Нумерация вершин

Выделите первую вершину для создания дуги

Выделите вторую вершину, которую хотите соединить

Выделите вершину, из которой хотите найти кратчайших путь

Выделите конечную вершину кратчайшего пути

Расстояние между вершинами %d

Пути не существует

Кликните по объекту, который хотите удалить

Добавить ребро

Ориентированную

Неориентированную

Матрица смежности

Сохранить

Отмена

Мин. расстояние =

Матрица инцидентности

Сохранение графа

закрыть

Число компонентов связности графа равно

Число слабо связных компонентов равно

Что вы думаете о сайте?

Имя (email для ответа)

Написать

Отправить

Напишите нам

исправить матрицу

справка

Матрица имеет неправильный формат

Сохранение изображения графа

Полный отчёт

Краткий отчёт

Граф не содержит Эйлеров цикл

Граф содержит Эйлеров цикл

Обработка…

Добавить вершину

Переименовать вершину

Переименовать

ru

Изменить вес

ненагруженный

Групповое переименование

Опрос

Рекомендовать алгоритмы

Граф не содержит Эйлерову цепь

Граф содержит Эйлерову цепь

Граф минимальных расстояний.

Нажмите для сохранения

Показать матрицу расстояний

Матрица расстояний

Выделите исток максимального потока

Выделите сток максимального потока

Максимальный поток из %2 в %3 равен %1

Поток из %1 в %2 не существует

Исток

Сток

Граф не содержит Гамильтонов цикл

Граф содержит Гамильтонов цикл

Граф не содержит Гамильтонову цепь

Граф содержит Гамильтонову цепь

Выбирете начальную вершину обхода

Порядок обхода:

Изгиб дуги

Отменить

Сохранить граф

По умолчанию

Стиль отрисовки вершины

Стиль отрисовки дуги

Цвет фона

Мультиграф не поддерживает все алгоритмы

ненагруженный

Выделите несколько объектов используя Cmd⌘.

Выделите несколько объектов используя Ctrl.

Перемещайте группу.

Копировать

Удалить

Поиск в ширину

Раскраска графа

Найти компоненты связности

Поиск в глубину

Найти Эйлеров цикл

Найти Эйлерову цепь

Алгоритм Флойда — Уоршелла

Упорядочить граф

Найти Гамильтонов цикл

Найти Гамильтонову цепь

Поиск максимального потока

Поиск минимального остовного дерева

Визуализация на основе весов

Поиск радиуса и диаметра графа

Поиск кратчайший путь алгоритмом Дейкстры

Рассчитать степень вершин

Создание графа онлайн

Для сформированного графа можно выполнить следующее действия:

Здесь будет показано решение

В этом разделе собраны примеры, иллюстрирующие возможности редактора графов.

Граф состояний кредитной карты

KП PSCashBack

Здесь объектом анализа выступает такой банковский продукт как кредитная карта K. На графе состояний операций по кредитной карте отмечены следующие события: начисления процентов на остаток счета (P — петля), покупка П на сумму S, возврат CashBack в виде бонусных баллов на счет карты.

Сетевой график получения кредитной истории

1 2 3 4 5 6

1 — устройство на работу с трудовой книжкой; 2,3 — получение кредитной карты с минимальным кредитным лимитом. Некоторые банки выдают кредиты уже после 3-х месячного трудового стажа, другие банки устанавливают этот срок от 1 года; 4,5 — продвинутый уровень, получение кредитных карт с большим cashback-ом; 6 — хорошая кредитная история, полученная с выгодой от использования кредитных карт.

Схема транспортной сети

3 8 10 B 159 км 134 км 190 км 67 км 81 км

На схеме показаны взаимное расположение пунктов, длинны звеньев, потребность грузов в развозочной системе.

Задача календарного планирования с заданной технологией

НачалоКонец 14,B14,A 14,C14,D 10,A10,B

Здесь показан пример ориентированного графа

Схема канала распределения

ФирмаОптовая продажа Розничная продажаПотребитель

Товар после изготовления поступает в оптовую продажу, далее доходит либо до потребителя, либо следует в розничную продажу, а затем уже к потребителю. По данной схеме работают и продуктовые рынки.

Еще один пример построения схемы классификации аннуитетных платежей можно посмотреть здесь.

Видеоинструкция

Для добавления вершины на графическое полотно необходимо использовать соответствующую фигуре кнопку Добавить. Если название вершины не задано, будет показан ее номер. По умолчанию, нумерация начинается с номера 1. Чтобы нумерация начиналась с 0, необходимо снять отметку с пункта Нумерация вершин с №1. Название вершины может содержать символьную строку (перенос строк осуществляется через символ |).
Чтобы соединить вершины, их необходимо предварительно выбрать (один клик мыши по объекту), а затем нажать на кнопку Соединить. Если выбрана одна вершина, то будет создана петля. У выбранных элементов (вершин или дуг) можно изменить свойства или удалить их.

Ребра графа – линии, соединяющие вершины. Чтобы соединить вершины, необходимо выбрать одну или две из них. Каждое ребро графа имеет собственные свойства:

цвет и толщина линии, значение (отображается поверх ребра).

Ребро графа называется неориентированным, если порядок расположения его концов (направление стрелок) в графе не принимается во внимание. Ребро графа называется ориентированным, если этот порядок существенен. Ориентированное ребро называют также дугой графа. Две вершины, соединённые дугой или ребром называются смежными. Для задания дуги необходимо при соединении вершин отметить пункт концевой маркер →. Для изменения типа дуги необходимо выделить ее левой кнопки мыши и нажать на кнопку Свойства.

С каждым ребром можно связать число или символ — вес ребра. Для задачи коммивояжера это может быть расстояние между городами, а для транспортной сети — стоимость проезда. Такой граф называется взвешенным.

Для каждого графа G(Х)

существует обратный граф G^-1(Х), полученный изменением ориентации каждого из ребер графа G(Х) на противоположную.

Петлей называется ребро g(xi,xi), у которого начальная и конечная вершины совпадают. Петля обычно считается неориентированной. Для создания петли необходимо выделить только одну вершину и нажать на кнопку Соединить.

Ребра ориентированного графа с одинаковыми весами могут быть представлены в разном виде. Для настройки отображения используйте пункт Дуги с одинаковыми весами.

В неизменном виде: отображается каждая дуга с весом.
12345372032724184120181

Представить как неориентированные: отображается неориентированная дуга с общим весом.
12345372420181

Соединять в одну: две ориентированные дуги с общим весом соединяются в одну.

12345372420181

Сеть это граф, в котором вершины связаны между собой по принципу «многие ко многим».

Примером ориентированного графа являются блок-схемы алгоритмов.

Новости сервиса Граф Онлайн

Ниже представлены последнии обновления нашего сервиса

Изгиб дуг

Добавили возможность изгибать дуги. Выделите дугу и нажимайте на кнопку + или -.

Админ 15.02.2019

Завершение сбора стредств

Благодаря неравнодушным пользователям нашего сервиса мы завершили сбор средств для разработки новых алгоритмов для сайта. Мы уже добавили алгоритм поиска диаметра и радиуса графа, далее будет поиск максимального потока и раскраска графа.

Админ 07.04.2018

Алгоритм Флойда — Уоршелла

Добавили алгоритм Флойда — Уоршелла. Теперь вы можете получить матрицу расстояний графа.

Админ 10.12.2017

Опрос

Мы завершили опрос о функциях, которые вы хотели бы видеть на graphonline.ru. Результаты распределились следующим образом:

• Больше алгоритмов — 53%
• Улучшение визуализации — 24%
• Личный кабинет — 13%
• Улучшение поддержки больших графов — 8%

По результатам опроса мы скоро запустим краудфандинговую программу по сбору средсв для разработки новых алгоритмов.

Админ 13.09.2017

Завершение сбора стредств

Мы рады сообщить, что сбор на хостинг завершён. Благодаря 20 неравнодушным пользователям нам удалось собрать 1500р, для продления хостинга на год. Теперь мы можем не боясть блокировки до 2019 года.

Админ 02.07.2017

Обновления

По постоянно работаем над улучшением сайта, за последние несколько месяцев было сделано следующее: обновлены ролики у на нашем канале на Youtube https://www.youtube.com/channel/UCrUEnaF7yz6sclCZi1-7XMA, добавлены примеры графов, добавлен алгоритм поиска минимального остовного дерева, улучшена мобильная версия сайта и другие мелкие правки.

Админ 10.03.2017

Произвольный текст для вершин

Добавили возможноть задавать произвольный текст для вершин.

Админ 04.07.2016

Размещение графа на плоскости

Добавлен алгоритм для красивого размещения графа на плоскости. Мы будем улучшать этот алгоритм.

Админ 12.06.2016

Масштабирование

Добавлена функциональность для управления масштабом рабочей области.

Админ 11.06.2016

Анимация

Мы добавили анимацию для алгоритмов поиска кратчайшего пути и Эйлерового цикла. Также улучшили отчёт.

Админ 23.01.2016

Эйлеров цикл

Добавили алгоритм поиска Эйлеровго цикла. Также немного улучшили интерфейс главной страницы.

Админ 09.01.2016

Построить граф по матрице

Построить ненаправленный граф по матрице

Заданная матрица смежности ненаправленного графа

Полученный граф, построенный по матрице

Первая работа по теории графов, принадлежащая известному швейцарскому математику Л. Эйлеру, появилась в 1736 г.

Вначале теория графов казалась довольно незначительным разделом математики, так как она имела дело в основном с математическими развлечениями и головоломками.

Однако дальнейшее развитие математики и особенно ее приложений дало сильный толчок развитию теории графов.

Уже в XIX столетии графы использовались при построении схем электрических цепей и молекулярных схем.

Граф — это  одно из представлений  связей, между объектами / событиями.

В настоящее время теория графов находит многочисленные применения в разнообразных практических вопросах: при установлении разного рода соответствий, при решении транспортных задач, задач о потоках в сеги нефтепроводов и вообще в так называемом «программировании». Теория графов теперь применяется и в таких областях, как экономика, психология и биология. 

В виде графов преобразовываются электрические схемы,  производственные цепочки на предприятии, план мероприятий, оптимальная логистическая доставка, связи между родственниками, друзьями  и многое другое.

Графы делятся на ненаправленные, направленные, с весовыми коэффицикентами(взвешенные) и без коэффициентов.

Каждый граф имеет определенные характеристики. Основные из них это остов графа, матрица смежности, матрица инцидентности.

Остов графа — это подграф данного графа, содержащий все его вершины и являющийся деревом.

Матрица смежности графа — это квадратная матрица ( по числу вершин графа) где, каждый элемент матрицы (на пересечении i- столбца и j-ряда) есть состояния связи  между вершинами i и j.

Элемент матрицы равен 1 если i-вершина графа, соединена с j-вершиной графа.

Во всех других случаях, в том числе когда i=j, значение элемента матрицы равно 0.

Это условие применимно только для ненаправленных графов и только для связей которые не начинаются и заканчиваются на одной и той же вершине ( петля)

Ненаправленный граф — граф, где не указаны направления движения связей между любыми  вершинами.

Невзвешенный граф — граф, где связям между любыми вершинами не присвоено никакое значение, а показывает только лишь сам факт связи этих двух вершин

На этой странице  бот строит ненаправленный граф, если  для него задана  матрица смежности.

Если мы не можете в уме построить матрицу смежности, то для этого есть ресурс Теория графов. Матрица смежности онлайн где можно построить такую матрицу. 

Интересные особенности

В матрице смежности неориентированного графа (взвешенного или невзвешенного) не важно, есть одна очень важная особенность

Значения матрицы  относительно главной диагонали — одинаковы.

Таким образом в принципе достаточно в качестве исходных данных вводить только верхнюю(диагональную) часть матрицы, но для удобства восприятия, ввод данных был сделан для полной матрицы.

Второй вывод который следует из вышесказанного следующий( и в примерах он прослеживается): Бот не проверяет  симметричность-соответствие  данных  в позициях матрицы относительно главной диагонали. 

Примеры:

Задана матрица смежности такого вида

 

В запросе пишем  0 0 1 0 1 0 1 0 0 0 1 1 0 1 0 0

и получаем ответ

Заданная матрица смежности ненаправленного графа

Полученный граф, построенный по матрице

---

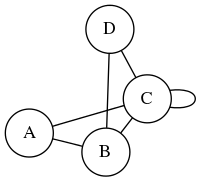Матрица задана таким видом

Пишем в запросе 

0 0 1 0 1 0 1 0 0 0 1 1 0 1 0 0 0 0 0 0 1 0 0 0  0 1 0  0 0 1 0 1 0 0 1 0 1 0 1 0 0 0 0 0  1 0 0 0 0 1 0 0 0 1 0 0

получем ответ

Заданная матрица смежности ненаправленного графа

Полученный граф, построенный по матрице

 

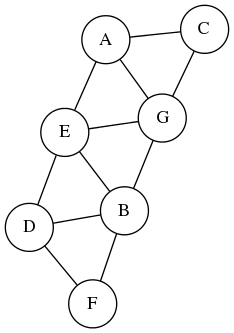Удачи в расчетах!!

 

• Построить график функции c помощью GeoGebra >>