Разработка уроков по теме: «Квадратные уравнения»
Цель: Познакомить учащихся с квадратными уравнениями, дискриминантом, теоремой Виета.
Показать учащимся, как решаются квадратные уравнения различных видов.
Развивать внимание и логическое мышление учащихся.
Воспитывать аккуратность и четкость в записях учащихся.
Оборудование:
Ход урока:
- Оргмомент.
- Составление конспекта лекции.
Определение. Уравнение вида ax2+bx+c=0, где а, b и c – некоторые числа, причем а 0, а х – переменная, называется квадратным.
Примеры: 2х2+2х+1=0;
-3х2+4х=0; 9х2-25=0. В каждом из уравнений назвать,
чему равны коэффициенты.
Определение. Если в уравнении вида ax2+bx+c=0 хотя бы один из коэффициентов b или с равен 0, то уравнение называют неполным квадратным.
1. Если с=0, то уравнение имеет вид ax2+bx=0. Оно решается разложением на множители. Уравнение данного вида всегда имеет два корня, всегда один из них равен нулю.
Пример: 4х2+16х=0 Решить самостоятельно:
4х (х+4) = 0 3х2-6х=0
4х=0 или х+4=0
х=0 х= -4
Ответ: х=0, х= -4.
2. Если b=0, то уравнение имеет вид ax2+c=0. Оно решается только тогда, когда у коэффициентов а и с разные знаки. При решении уравнений применяет формулу разности квадратов.
Пример: 1) 1-4y2=0 2) 6х2+12=0(1-2y) (1+2y) =0 Решений нет, так как это сумма квадратов, а не разность.
1-2y=0 или 1+2y=0 3) Решить самостоятельно -х2+3=0 2y=1 2y= -1 (3-х)(3+х)=0 y=0,5 y= -0,5 3-х=0 или 3+х=0 Ответ: y=0,5; y= -0,5 х= 3 х=-3 3. Если b=0 и с=0, то уравнение имеет вид ах2=0. Уравнение имеет единственный корень х=0.
Решение полных квадратных уравнений
Определение. Выражение вида D=b2-4ac называют дискриминантом квадратного уравнения.
Примеры. Вычислите дискриминант
2х
5х2-2х-1=0, a=5, b=-2, c=-1 D=(-2)2-4* 5* (-1)= 24
Самостоятельно: вычислите дискриминант -2х2-2х+5=0, 3х2+7х-3=0.
Для нахождения корней квадратного уравнения ax2+bx+c=0 пользуются формулами:
Если второй коэффициент является четным числом, формулу корней удобно записать в другом виде: ax2+2kx+c=0; D= k2-2ac,
Вывод:
1. Если D>0, то уравнение имеет два
разных корня.
Если D>0, то уравнение имеет два
разных корня.
2. Если D=0, то уравнение имеет два равных корня.
3. Если D<0, то уравнение не имеет решений.
Примеры:
1) 3х2+5х-8=0
Решение:
a=3, b=5, c=-8, D=32-4E 5* (-8)= 121>0
Ответ:
2) х2+5х+10=0
Решение:
a=1, b=5, c=10, D=52-4E 1* 10= -15<0
Ответ: корней нет.
3) Решить самостоятельно
х2-6х+9=0 a=1, b=-6, c=9
| I способ (х-3)2=0 | II способ D=(-6)2-4* 1* 9= 0 |
| х=6/2 | |
| х=3 | |
Ответ: х=3. |
Решение задач с помощью квадратных уравнений.
Задача1. Сумма двух чисел равна 13, их произведение равно 40. Найдите эти числа
Решение: I+II=13, I * II=40
Пусть х – первое число, тогда (13-х) – второе число. Зная, что их произведение равно 40, составляем уравнение:
х (13-х)=40,
-х2+13х-40=0,
х2-13х+40=0,
D=(-13)2-4 * 1 * 40= 9
х1=8, х2=5.
Если первое число 8, тогда второе 5; если первое число 5, тогда второе 8.
Ответ: 8 и 5.
Теорема Виета.
Определение. Квадратное уравнение с
первым коэффициентом, равным единице, называется
приведенным x2+bx+c=0. Любое квадратное уравнение можно
сделать приведенным.
5х2-2х+3=0. Разделим обе части уравнения на 5.
– приведенное квадратное уравнение.
Теорема Виета. Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.
Пример. Проверить теорему Виета для уравнения.
1) х2-9х+20=0.
х1+х2=9 х1=4 D=(-9)2-4* 20= 1
х1E х2=20 х2=5 , х1=4, х2=5
Ответ: х1=4, х2=5.
2) самостоятельно х2+16х+63=0
Обратная теорема. Если два числа в
сумме равны b, а в
произведении равны с, то эти числа являются
корнями квадратного уравнения x2-bx+c=0.
Если два числа в
сумме равны b, а в
произведении равны с, то эти числа являются
корнями квадратного уравнения x2-bx+c=0.
Пример: 1) Составить квадратное уравнение, чтобы корни его были 2 и 3.
Решение. х1+х2=2+3=5, значит, b=-5
х1* х2=6, значит, с=6
Ответ: х2
-5х+6=0.2) самостоятельно х1=4, х2=6. Составить квадратное уравнение.
Определение. Уравнение вида ax4+bx2+c=0, называется биквадратным.
Биквадратное уравнение решается с помощью замены вида x2=t
Пример 1) x4-15x2-96=0
Решение
Пусть x2=t, тогда t2-15t-96=0
t1+t2=15, t1=16
t1* t2=-16, t2=-1
x2=16 x2=-1
х=G 4 корней нет
Ответ: х1=4, х2=-4.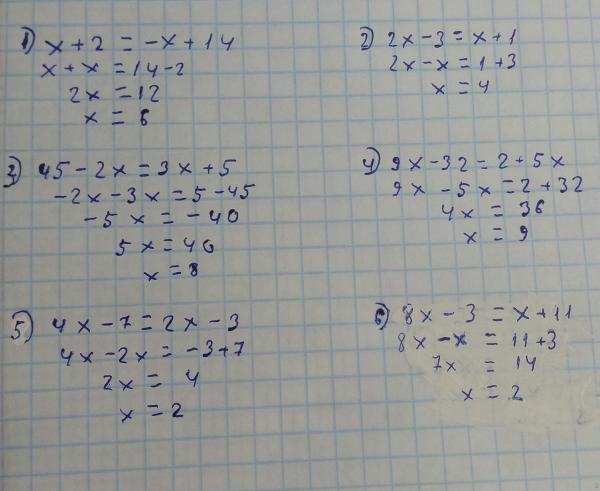
2) самостоятельно x4-11x2-12=0.
Итог урока.
Домашнее задание. Выучить конспект, п 19-23, ответить на вопросы 1-5 после п. 23
Урок решения типовых задач.
Тема: Решение уравнений и задач с помощью составления уравнений.
Цели: Вырабатывать у учащихся умения и навыки по решению уравнения и задач, применяя теорему Виета и формулы корней квадратного уравнения.
Развивать логическое мышление и внимание учащихся.
Проверить усвоение теоретического материала по теме “Квадратные уравнения”.
Оборудование; таблицы, кодоскоп, листочки для математического диктанта.
Ход урока:
- оргмомент.
- индивидуальная работа одного ученика у доски по карточке:
- В) Устно по кодоскопу со всем классом.
- Г) Математический диктант на листочках.
- Работа с классом.
- Оргмомент.
- Устно по кодоскопу:
- Работа учащихся у доски.
- Вопросы:
1. Запишите в общем виде квадратное
уравнение.
2. Формула дискриминанта.
3. Формулы корней квадратного уравнения.
4. Теорема Виета.
1. Назовите коэффициенты в уравнениях
3х2-5х=0 -5х2+3х+6=0 х2-2х-2=0 4х2+7=0 3х2=9
2. Найдите корни уравнения
х2-2х-35=0 b2-10b+24=0
1. Запишите квадратное уравнение, у которого первый коэффициент 3 (-5), второй –5 (3), свободный член равен 0.
2. Запишите приведенное квадратное уравнение, у которого второй коэффициент и свободный член равны –2 (-3).
3. Запишите неполное квадратное
уравнение, у которого первый коэффициент равен
–5 (-3), свободный член равен 7 (5) и решите его.
Запишите неполное квадратное
уравнение, у которого первый коэффициент равен
–5 (-3), свободный член равен 7 (5) и решите его.
4. Запишите неполное квадратное уравнение, у которого первый коэффициент равен 3 (5), второй коэффициент равен 5(7) и решите его.
Решите уравнения.
| 1. 2х2+7х-9=0 | 2. 3х2=18х |
| Решение: | Решение: |
| а=2, b=7, с=-9 | 3х2-18х=0 |
| D=b2-4ac, D=49-4* 2* (-9), D=121, D>0 2 корня | 3x(x-6)=0 |
| 3x=0 или x-6=0 | |
| x=0 или х=6 | |
| Ответ: x1=1, x2=-4,5. | Ответ: 0; 6. |
| 3. 100х2-16=0, | 4. х2-2х-35=0 |
| Решение: | Решение: |
| (10x+4)(10x-4)=0 | х1+х2=2 х1=7 |
| 10x+4=0 или | 10x-4=0 х1х2=-35 х2=-5 |
| х=-0,4 х=0,4 | |
| Ответ: х 1=0,4 х 2=-0,4 | Ответ: х1=7; х2=-5 |
Решите задачи
1. Периметр прямоугольника равен 20 см.
Найдите его стороны, если известно, что площадь
прямоугольника равна 24 см2.
Периметр прямоугольника равен 20 см.
Найдите его стороны, если известно, что площадь
прямоугольника равна 24 см2.
Решение: Пусть х см длина прямоугольника, тогда y см – ширина. Зная, что Р=20 см и S=24 см2составляем систему уравнений:
2(x+y)=20,
xy=24;
x+y=10, x=6 или х=4
xy=24 у=4 у=6
Ответ: 6 см и 4 см.
2. В уравнении x2+px-18=0 один из корней равен –9. Найдите другой корень и коэффициент р.
Решение: х1+х2=-p, -9+ х2= -р,
х1 * х2=-18; -9 * х2=-18 х2=2, тогда р=7.
Ответ: х2=2, р=7.
Итог урока.
Домашнее задание.
“3”: Решите уравнения: 3х2+13х-10=0, 2х2-3х=0, 16х2=49, х2-16х+63=0.
“4” и “5”: Решите задачи: 1. Периметр прямоугольника равен 30 см, а площадь 56 см2. Найдите его стороны. 2. В уравнении x2+11x+q=0 х1=-7. Найдите другой корень и коэффициент q.
Урок-зачет по теме “Квадратные уравнения”.
Цели: Проверить знания учащихся, полученные на уроках по заданной теме.
Систематизировать знания, умения и навыки учащихся по решению квадратных уравнений.
Развивать логическое мышление учащихся.
Работать над четкостью и аккуратностью записей учащихся.
Оборудование: Зачетные карточки,
рис. 1, рис.2, кодоскоп.
1, рис.2, кодоскоп.
Ход урока:
1. Укажите в квадратном уравнении его коэффициенты:
х2+4х+5=0, 3х2-2х-11=0, 12х2-4х=0, х2-3=0.
2. Решите уравнение: 4х2-9=0, 1- 4y2=0, 5u2-u=0.
1. Решить уравнения 3х2-7х=0, х2-5=0.
2. Записать коэффициенты и вычислить D: -2х2+3х+7=0, 3х2-х+2=0.
3. Решить уравнение х2-х-12=0.
4. Составить уравнение по его корням:
5. Решить уравнения выделением
квадрата: х2+8х-1=0, х2+10х+25=0.
6. Решить биквадратное уравнение: x4-13x2+36=0.
- Какое уравнение называется квадратным?
- Какое уравнение называется неполным квадратным?
- Виды неполного квадратного уравнения и способы их решения.
- Какое уравнение называется приведенным квадратным?
- Способы решения приведенного квадратного уравнения.
- Какое выражение называется дискриминантом?
- Сколько корней может иметь квадратное уравнение?
- Формулы корней квадратного уравнения.
- Как читается теорема Виета?
Дополнительно, на “4” и “5”:
- Вывести формулу корней квадратного уравнения.
- Доказать теорему Виета и ей обратную.
- Какое уравнение называется биквадратным? Как оно решается?
- Составьте квадратное уравнение, чтобы оно имело корни: 0 и 7/3, 1 и 10.
Практическая часть зачета (в 4
вариантах, задания аналогичные).
1) Решить уравнения: 16х2-625=0, 100х2-10х=0, 3х2-5х-2=0, х2-6х-7=0.
2) Найдите два последовательных целых числа, сумма квадратов которых равна 221.
Итог урока.
Домашнее задание по [1] (на две недели):
“3”: № 510 (а,д), 507 (б,г), 526 (а), 534 (а,б), 556.
“4”: № 512 (а), 515, 526 (в), 536 (д,е), 551 (б), 559, 557.
“5”: № 514 (б,д), 517, 525 (г), 540 (е,ж), 551 (а), 564, 567.
Обобщающий урок “Оцени себя” по теме “Квадратные уравнения”.
Цели:
Обобщить, систематизировать и расширить знания учащихся по теме “Квадратные уравнения”.

Развивать логическое мышление и элементы творческой деятельности учащихся.
Воспитывать стремление к непрерывному совершенствованию своих знаний, формировать дружеские отношения и умение контролировать свои действия.
Оборудование: телефоны (2 шт.), кодоскоп, табло “Секундная стрелка”, три подсказки (50х50, звонок другу, помощь зала), задания игрокам.
Ход урока:
- Оргмомент.
- Учащиеся разбиты на три группы.
Ведущая: учитель математики
Помощники: два ученика из класса.
Диктор: ученик класса.
I отборочный тур (на ответ 10 секунд). Расположите в порядке изучения нами тем.
1. Квадратные уравнения.
2. Квадратные корни.
3. Рациональные дроби.
Рациональные дроби.
Ответ: 3, 2, 1.
Победитель отборочного тура отвечает на 9 вопросов. Ответы: A, B, C, D. Оценка ставится в зависимости от числа правильных ответов: за три первых вопроса – оценка “3”, за три следующих вопроса – оценка “4”, за три последних – оценка “5”. В случаях, когда количество ответов находится в промежутке между 3 и 6 или 6 и 9, оценка ставится по нижней границе интервала ответов. Участник может воспользоваться тремя подсказками.
Вопросы:
1. Квадратным уравнением называется уравнение вида …
a) ax2+bx+c=0; b) bx+c=0,; c) ax2+c=0,; d) ax2=0, где х- переменная и а0.
2. В каком из квадратных уравнений правильно указаны его коэффициенты?
a) 5х2-9х+4=0, a=5, b=9, c=4; b) х2+3х-10=0, a=1, b=3, c=-10;
c) -х2-8х+1=0, a=1, b=-8, c=1; d)
6х2-30=0, a=3, b=-30, c=0.
3. Решите уравнение 2х2=0. a) 2; b) -1; c) 1; d) 0 .
4. Какое из выражений называют дискриминантом?
a) d=b2-4ac; b) d=-(-b)2-4ac; c) d=b2+4ac; d) d=b-4ac.
5. Чему равен дискриминант квадратного уравнения 2х2+3х+1=0?
a) 0; b) 2; c) -1; d) 1.
6. При каком условии дискриминанта уравнение не имеет корней?
a) d>0; b) d>1; c) d<0; d) d=0.
7. Какой теоремой можно пользоваться при решении приведенного квадратного уравнения?
a) Пифагора; b) Виета; c) о сумме углов; d) нет такой теоремы.
8. Найдите значение корня † 2809. a) 35; b) 33; c) 53; d) 43 .
9. Решите уравнение х2-7х+10=0. a) 5 и 2; b) –5 и 2; c) –5 и -2; d) 5 и -2 .
Итог I тура. Рекламная пауза. Сообщение “Квадратные
уравнения в Древнем Вавилоне”. [2]
Рекламная пауза. Сообщение “Квадратные
уравнения в Древнем Вавилоне”. [2]
II отборочный тур. В какой последовательность был нами изучен материал по теме “Квадратные уравнения”:
1. Решение задач с помощью квадратных уравнений.
2. Определение квадратного уравнения.
3. Решение квадратных уравнений по формуле.
Вопросы.
1. Как правильно пишется слово d?
a) дискриминант; b) дескриминант; c) дискреминант; d) дискрименант .
2. Сколько корней имеет квадратное уравнение, если d=25?
a) нет корней; b) 1; c) 2; d) 5 .
3. Какой формулой пользуемся при решении квадратного уравнения?
a) b) c) d)
4. Назовите, чему равна сумма и
произведение корней квадратного уравнения х2-37х+27=0.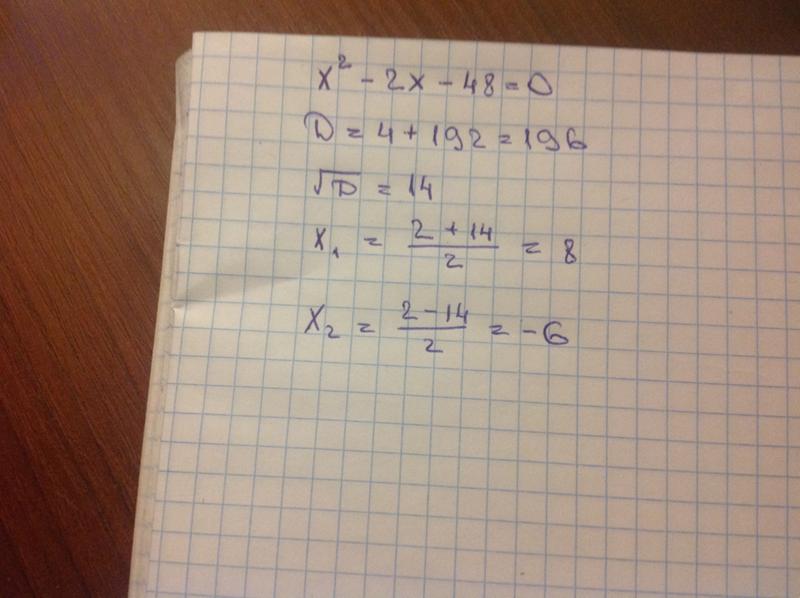
a) 37, 27; b) –37, 27; c) –37, -27; d) 37, -27 .
5. Найдите корни уравнения х2-6=0. a) 6; b) -6; c) +/- 6; d) 6.
6. Найдите подбором корни уравнения х2-9х+20=0.
a) –5 и -4; b) 9 и 11; c) 5 и 4; d) –5 и 4 .
7. В уравнении х2+pх-35=0 один из корней равен 5. Найдите другой корень.
a) -7; b) 7; c) 30; d) 35 .
8. Если в уравнении левая и правая части являются рациональными выражениями, то такие уравнения называются…
a) квадратными; b) неполными; c) целыми; d) рациональными.
9.Вычислите 552.
a) 3025; b) 2525; c) 2025; d) 110.
Итог II тура. Рекламная пауза. Сообщение “Как составлял и решал квадратные уравнения Диофант” [2].
III отборочный тур. При решении дробных уравнений целесообразно поступать следующим образом…
1. Исключить из его корней те, которые
обращают в нуль общий знаменатель.
Исключить из его корней те, которые
обращают в нуль общий знаменатель.
2. Решить получившееся целое уравнение.
3. Умножить обе части уравнения на общий знаменатель.
4. Найти общий знаменатель дробей, входящих в уравнение.
Вопросы.
1. Выберите биквадратное уравнение
a) k4-3k2+2=0; b) k3+3k2+k=0; c) k2+3=0; d) 4k2-k=0 .
2. При каком условии d уравнение имеет один корень? a) d=0; b) d<0; c) d>0; d) d=1.
3. Найди корни уравнения х2=-16. a) решений нет; b) 4, -4; c) 4; d) -4 .
4. Реши уравнение х2-8х+7=0. a) –7 и -1; b) –7 и 1; c) 7 и -1; d) 7 и 1 .
5. Автор учебника, где рассматривается тема “Квадратные уравнения”?
a) Виленкин; b) Погорелов; c)
Пифагор; d) Макарычев.
6. Реши уравнение 2х2+3х=0. a) 0 и 1,5; b) 0 и –1,5; c) 0; d) 1,5 .
7. При каких значениях х верно равенство (3х+1)2=3х+1?
a) 0; b) -1; c) 1; d) нет таких значений .
8. Как устроен данный числовой “угол”? Как будет выглядеть следующая строка?
1
2 6
3 9 27
a) 4, 12, 36, 108; b) 4, 8, 16, 32; c) 4, 9, 13, 18; d) 4, 15, 26, 37 .
9. Вычисли 196+ 7396. a) 10; b) 14; c) 86; d) 100 .
Итог III тура. Рекламная пауза. Сценка на уроке алгебры в 8 классе – тема “Квадратный корень” (связь с биологией тема “Корень”).
Итог урока. Выставление оценок учащимся.
Список литературы
1. Алгебра. Учебник для 8 класса общеобразовательных учреждений.
Под ред. С. А. Теляковского. – М.: Просвещение, 2000.
2. Глейзер Г. И. История математики в школе. VII-VIII классы. – М.: Просвещение, 1982.
Развертка машинная к/х 12,0 h22 Р18 — РИНКОМ
Развертка машинная к/х 12,0 h22 Р18 — РИНКОМГлавная
Инструменты
Развертки
Развертка машинная
Код товара: 108622
Поделиться
Описание инструмента
Как купить?
Доставка и оплата
Статьи по теме
Машинная развертка – это металлорежущий инструмент, который применяется для окончательной обработки отверстий в деталях из конструкционных сталей и чугунов после их предварительного зенкерования, сверления и растачивания. Главной целью развертывания, как процесса, является достижение повышенной точности и чистоты в работе при обрабатывании поверхностей деталей. В процессе работы развертка, помимо основного вращательного движения вокруг своей оси, выполняет так называемое движение подачи, т. е. одновременно передвигается по оси отверстий.
е. одновременно передвигается по оси отверстий.
Развертка машинная цельная с коническим хвостовиком (к/х) изготовляется из быстрорежущей стали марки «Р6М5» по ГОСТу 1672-80. Собственно назначением конического хвостовика является закрепление самой развертки на станке, поэтому данный вид разверток используют для машинного развертывания на координатно-расточных, револьверных, сверлильных, токарных и других видах станков. Развертки машинные к/х производятся диаметром от 5,5 до 50мм, с полями допусков G6, Н6, Js6, К6, G7, Н7, Js7, К7, М7, N7, Р7, Е8, U8, F8, Н8, D9, Е9, F9, Н9, Н10, Н11 и припуском под доводку — N 1, 2, 3, 4, 5, 6.
Нашли ошибку? Сообщите нам!
Для того чтобы заказать и купить выбранный вами товар, найдите его в каталоге инструмента, укажите его количество и щелкните на кнопку «Добавить в корзину»
Перейти в пункт меню «Ваша корзина» и заполнить небольшую форму заказа.
На вашу электронную почту придет письмо, о том что ваша заявка принята. Статусы заказа можете отслеживать в личном кабинете.
Доставка инструмента Развертка машинная к/х 12,0 h22 Р18
Заказанный в нашей компании инструмент доставляется практически в любой город России с помощью транспортных компаний. Подробнее о доставке.
Оплата возможна через:
Оплата картой
Оплата по счету
Оплата по QR-коду
Лучшие отвертки для домашнего и производственного использования
Тельферы и тали: различия и ассортимент
Автомобильная резьба: разновидности и способы определения
Разновидности и специфика использования штангенциркулей
Методы измерения резьбы на производстве и в домашних условиях
Как пользоваться развертками
Испытания абразивных инструментов
Как разобрать сверлильный патрон
Похожие товары
Не нашли нужной позиции в каталоге?
Мы готовы изготовить и поставить уникальные виды инструмента специально под ваш заказ!
Заказать
Каталог
Корзина СравнитьВход
Мы используем файлы cookie. Они помогают улучшить ваше взаимодействие с сайтом.
Они помогают улучшить ваше взаимодействие с сайтом.
Принимаю
?>
2 «.Шаг за пошаговым решением:
Шаг 1:
Пытаясь учитывать, разделяя средний термин
1.1 Факторинг x 2 -x -12
Первый термин -x 2 его коэффициент равен 1.
Средний член равен -x, его коэффициент равен -1.
Последний член, «константа», равен -12
Шаг 1: Умножьте коэффициент первого члена на константу 1 • -12 = -12
Шаг 2. Найдите два множителя -12 , сумма которых равна коэффициенту среднего члена, который равен -1 .
| -12 | + | 1 | = | -11 | ||
| -6 | + | 2 | = | -4 | ||
| -4 | + | 3 | = | -1 | Это это |
Шаг -3: Повторный полиномиальный раздел, разделяющий средний срок, используя два фактора. и 3
и 3
x 2 — 4x+3x — 12
Шаг -4: Сложите первые 2 термина, вытягивая, как факторы:
x • (x -4)
Складывают последние 2 термина, вытягивая общие факторы:
3 • (x-4)
Шаг-5: Сложите четыре члена шага 4:
(x+3) • (x-4)
, что является желаемой факторизацией
Уравнение в конце шага 1:
(х + 3) • (х - 4) = 0
Шаг 2 :
Теория – корни произведения:
2.1 Произведение нескольких членов равно нулю.
Если произведение двух или более слагаемых равно нулю, то хотя бы одно из слагаемых должно быть равно нулю.
Теперь мы будем решать каждый термин = 0 отдельно
Другими словами, мы собираемся решить столько уравнений, сколько членов в произведении
Любое решение термина = 0 также решает произведение = 0.
Решение уравнения с одной переменной:
2,2 Решение: x+3 = 0
Вычитание 3 с обеих сторон уравнения:
x = -3
Решение единого переменного уравнения:
2,3 Решай: x -4 = 0
Добавить 4 to to to to to to to to to to to to to to to to to to to to to to to обе стороны уравнения :
x = 4
Дополнение : Решение квадратного уравнения напрямую
Решение x 2 -x-12 = 0 Этот многочлен напрямую был разделен на множители
9000.давайте теперь решим уравнение, заполнив квадрат и используя квадратную формулу
Парабола, нахождение вершины :
3.1 Найдите вершину y = x 2 -x-12
Параболы имеют самую высокую или самую низкую точку, называемую вершиной. Наша парабола раскрывается и, соответственно, имеет низшую точку (абсолютный минимум). Мы знаем это еще до того, как начертили "у", потому что коэффициент первого члена, 1 , положителен (больше нуля).
Каждая парабола имеет вертикальную линию симметрии, проходящую через ее вершину. Из-за этой симметрии линия симметрии, например, будет проходить через середину двух точек пересечения x (корней или решений) параболы. То есть, если парабола действительно имеет два действительных решения.
Параболы могут моделировать многие реальные жизненные ситуации, такие как высота над землей объекта, брошенного вверх через некоторый период времени. Вершина параболы может предоставить нам такую информацию, как максимальная высота, на которую может подняться объект, брошенный вверх.
По этой причине мы хотим иметь возможность найти координаты вершины.
Для любой параболы, Ax 2 +Bx+C, x-координата вершины определяется как -B/(2A) . В нашем случае координата x равна 0,5000
Подключение к формуле параболы 0,5000 для x Мы можем рассчитать y -координату:
y = 1,0 * 0,50 * 0,50 -1,0 * 0,50 -12,0
или y = -12,250Parabola, график вертекс и X -Intercess:
.
Корневой график для: y = x 2 -x-12
Ось симметрии (штриховая) {x}={ 0,50}
Вершина в {x,y} = {0,50,-12,25}
x -Перехваты (корни ) :
Корень 1 в точке {x,y} = {-3,00, 0,00}
Корень 2 в точке {x,y} = {4,00, 0,00}Решить квадратное уравнение, заполнив квадрат
3.2 Решение x 2 -x-12 = 0, заполнив квадрат .
Прибавьте 12 к обеим частям уравнения:
x 2 -x = 12Теперь немного хитрости: возьмите коэффициент при x , равный 1, разделите на два, получив 1/2, и, наконец, возведите его в квадрат.
что дает 1/4
Добавьте 1/4 к обеим частям уравнения:
В правой части мы имеем:
12 + 1/4 или, (12/1)+(1/4)
Общим знаменателем двух дробей является 4 Сложение (48/4)+(1/4) дает 49/4
Таким образом, складывая обе части, мы окончательно получаем :
x 2 -x+(1/4) = 49 /4Добавление 1/4 завершило левую часть в полный квадрат:
x 2 -x+(1/4) =
(x-(1/2)) • (x-(1/2) )) =
(x-(1/2)) 2
Вещи, равные одной и той же вещи, также равны друг другу. Поскольку
x 2 -x+(1/4) = 49/4 и
x 2 -x+(1/4) = (x-(1/2)) 2
тогда по закону транзитивности
(x-(1/2)) 2 = 49 /4Мы будем называть это уравнение уравнением. #3.2.1
Принцип квадратного корня гласит, что когда две вещи равны, их квадратные корни равны.
Обратите внимание, что квадратный корень из
(x-(1/2)) 2 равен
(x-(1/2)) 2/2 =
(x-(1/2)) 1 =
x-(1/2)Теперь, применяя принцип квадратного корня к уравнению #3.
2.1 получаем:
x-(1/2) = √ 49/4Добавьте 1/2 к обеим частям, чтобы получить:
x = 1/2 + √ 49/4другое отрицательное число
x 2 - x - 12 = 0
имеет два решения:
x = 1/2 + √ 49/4
или
x = 1/2 - √ 49/4Обратите внимание, что можно записать как
√ 49 / √ 4 что равно 7/2Решить квадратное уравнение с помощью формулы квадратного уравнения
3.3 Решение x 2 -x-12 = 0 по квадратичной формуле.
Согласно квадратичной формуле, x, решение для AX 2 +BX +C = 0, где A, B и C-числа, часто называемые коэффициентами, определяются как:
-B ± √ B 2 -4AC
x = ————————
2AВ нашем случае A = 1
B = -1
C = -12Соответственно, B 2 -4AC =
1-(-48) =
49Применение квадратичной формулы:
1 ± √ 49
x = ————
2можно упрощенный?
Да! Первичная факторизация числа 49 это
7•7
Чтобы иметь возможность удалить что-то из-под корня, его должно быть 2 вхождения (потому что мы берем квадрат, т.е. второй корень).
√ 49 = √ 7 • 7 =
± 7 • √ 1 =
± 7, так что теперь мы рассмотрим:
x = (1 ± 7)/2Два реальных решения:
x = ( 1+√49)/2=(1+7)/2= 4,000
или:
x =(1-√49)/2=(1-7)/2= -3,000
Было найдено два решения :
- x = 4
- x = -3
алгебра, глава 10.1, многочлены, классифицирующие многочлены, ключ ответа
AlleBilderVideosBücherMapsNewsShopping
suchoptionen
[PDF] Алгебра
amhdar.weebly.com › загрузки › poly_worksheet_wed_2-12
Алгебра. ГЛАВА 10.1. ПОЛИНОМЫ.・Ср 2-12. Имя. Период. Дата. Классифицирующие полиномы. Многочлены можно классифицировать (называть) по количеству членов.
[PDF] Алгебра - SharpSchool
cdn5-ss2.sharpschool.com › Серверы › Файл › Рабочий лист Cody
Алгебра. ПОЛИНОМЫ. Имя. Ключ. Период. Дата. Классифицирующие полиномы. Многочлены можно классифицировать (называть) по количеству членов.
Полиномиальный.
[PDF] Классифицирующие полиномы
www.djuhsd.org › cms › lib › Centricity › Domain › 10.1_A Classifyi...
Алгебра. ГЛАВА 10.1. ПОЛИНОМЫ. Имя. Период ______ Дата. Классифицирующие полиномы. Многочлены можно классифицировать (называть) по количеству членов.
[PDF] Алгебра - Классифицирующие полиномы
www.kent.k12.md.us › Downloads › Алгебра 1
Алгебра. ГЛАВА 10.1. ПОЛИНОМЫ ... Многочлены также можно классифицировать по степени (наибольшему показателю степени ... Ответ запишите в стандартной форме.
[PDF] 3.1 Классифицирующие полиномы (рабочий лист, 3A) v1 20131017
2.files.edl.io › ...
Запишите в стандартной форме. Затем назовите каждый многочлен по степени и количеству членов. 9) −10p2. 10) 7м2 - м + 8м4 + 6м3.
Классифицирующие полиномы.pdf - Имя алгебры _ ГЛАВА 10.1...
www.coursehero.com › файл › Классифицирующая полиномия... Название алгебры _ ГЛАВА 10.
1 ПОЛИНОМЫ Период _ Дата _ Классификация ...
Bilder
Alle anzeigen
Alle anzeigen
Ch 10 1 Classifying Polynomials - Course Hero
www.coursehero.com › file › Ch-10-1-Classifying-P...
AlgebraClassifying PolynomialsName___________________Chapter . .. PolynomialDegreeName–240 градусов (без степени x) 82 x 1-я степень (x до ... i HW KEY.pdf.
10.1 - A Классифицирующие полиномы - E - Предпочтительный PDF - Scribd
www.scribd.com › документ › 10-1-A-Классификация-...
10.1_A Классифицирующие полиномы_E_Предпочитаемые - Копировать.pdf - Скачать бесплатно в формате PDF ... Глава 4 Полиномы ... Ultimate Algebra Worksheets eBook Preview No TOC.
Классификация полиномов и стандартная форма - YouTube
www.youtube.com › смотреть
28.11.2020 · Линейные, кубические, пятерные, трехчленные, биномиальные, ПОЛИНОМНЫЕ. Узнайте, как классифицировать многочлены...
Dauer: 5:31
Прислан: 28.


 Под ред.
С. А. Теляковского. – М.: Просвещение, 2000.
Под ред.
С. А. Теляковского. – М.: Просвещение, 2000. давайте теперь решим уравнение, заполнив квадрат и используя квадратную формулу
давайте теперь решим уравнение, заполнив квадрат и используя квадратную формулу По этой причине мы хотим иметь возможность найти координаты вершины.
По этой причине мы хотим иметь возможность найти координаты вершины. что дает 1/4
что дает 1/4  2.1 получаем:
2.1 получаем:  е. второй корень).
е. второй корень). Полиномиальный.
Полиномиальный. 1 ПОЛИНОМЫ Период _ Дата _ Классификация ...
1 ПОЛИНОМЫ Период _ Дата _ Классификация ...