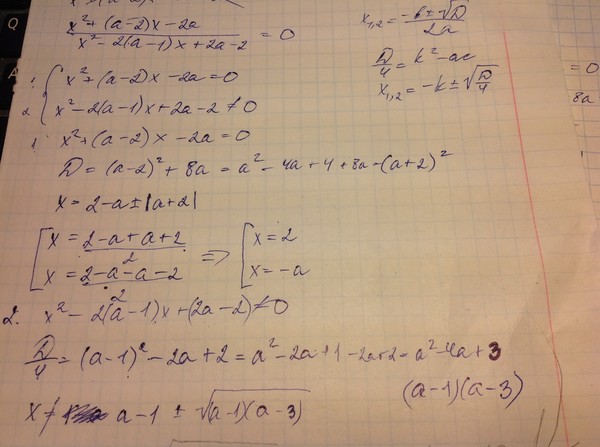|
Задачи с параметрами — одна из самых трудных тем в математике. Неизвестные величины принято обозначать последними буквами латинского алфавита икс, игрек, зэт и так далее, параметры – первыми буквами а, бэ, цэ, и так далее. |
Текст. Тема «Уравнения с параметрами»
Неизвестные величины принято обозначать последними буквами латинского алфавита(х, у, z,…), параметры – первыми буквами (а,b,c,…) |
|
Определение первое. Уравнением с параметром а называют уравнение вида эф от икс а равно нулю, которое надо решить относительно икс и в котором буквой а обозначено произвольное действительное число. |
Текст. Определение1. Уравнением с параметром а 
|
|
Определение второе. Решить уравнение с параметром – значит для каждого значения параметра найти множество всех корней данного уравнения или доказать, что корней нет. |
Текст. Определение2. Решить уравнение с параметром – значит для каждого значения параметра найти множество всех корней данного уравнения, а может их не быть. |
|
Задачи с параметрами решаются теми же приемами, что и аналогичные задачи без параметров. При решении используются аналитические и графические методы. Рассмотрим примеры, которые дадут вам некоторое представление о том, как рассуждают при решении уравнений и неравенств с параметрами. Решим простейшие линейные неравенства. |
Текст. Задачи с параметрами решаются теми же приемами, что и аналогичные задачи без параметров. |
|
Задание 1 Решить уравнение а икс равно одному. Решение Рассмотрим два случая. Первый случай, если а не равно нулю, то уравнение имеет единственное решение: икс равен один деленное на а; Второй случай, если a равно нулю, уравнение примет вид ноль умноженное на икс равно единице и, следовательно, оно не имеет решений. Ответ: если а не равно нулю, то икс равен |
Пример 1. Решить уравнение ax = 1. Решение. Рассмотрим два случая. 1)если a ≠ 0 уравнение имеет единственное решение, x = 1/a; 2)если a = 0 уравнение примет вид 0·x = 1 и, следовательно, оно не имеет решений. Ответ: если a ≠0,то x = 1/a; если a = 0, то уравнение не имеет решений. |
|
Задание 2 Решить уравнение а квадрат икс минус один равно икс плюс a. Решение Перенесем икс в левую часть уравнения и вынесем его за скобки. Получим: икс умноженное на разность а квадрат и один равно a плюс один.Рассмотрим три случая: Первый случай, если а квадрат плюс один не равно единице, то есть a не равно плюс минус одному, то икс равен дроби, числитель которой — один, а знаменатель — а минус один. Второй случай, если a равно единице, то уравнение примет вид: ноль умноженное на икс равно двум и, следовательно, не имеет решений. Третий случай, если a равно минус единице, то уравнение примет вид: ноль умноженное на икс равно нулю, и, следовательно, любое действительное число является решением этого уравнения. Ответ: если a не равно плюс минус единице, то икс равен дроби, числитель которой один, а знаменатель — а минус один. Если a равно единице, то уравнение не имеет решений; если a равно минус единице, то любое действительное число является решением этого уравнения. |
Пример2. Решить уравнение a2x — 1 = x + a; Решение. Получим: a2x — 1 = x + a ; a2x — x = a + 1; x(a2 — 1) = a + 1. Рассмотрим три случая: 1) если a2-1 ≠ 0, то есть a ≠ ±1, то есть a не равно плюс минус одному, то икс равен дроби, числитель которой — один, а знаменатель — а минус один.
2) если a = 1, то уравнение примет вид 0·x = 2 и, следовательно, не имеет решений; 3) если a = -1, то уравнение примет вид 0·x = 0, и, следовательно, любое действительное число является решением этого уравнения. Ответ: если a ≠ ±1,то икс равен дроби, числитель которой один, если a = 1, то уравнение не имеет решений; если a = -1, то любое действительное число является решением этого уравнения. |
|
Задание 3 Решить уравнение: дробь, числитель которой — икс минус два а, знаменатель – икс минус четыре равно нулю. Решение Находим ОДЗ уравнения — икс неравен четырем. Решаем уравнение икс минус два а равно нулю; Икс равен два а, если икс неравен четырем, то есть два а не равно четырем, а не равно двум. Итак, если а не равно двум, то уравнение имеет единственное решение — икс равно два а. Если a равно двум, то уравнение не имеет решений. Ответ: если не равно двум, то уравнение имеет единственное решение — икс равно два а. Если a равно двум, то уравнение не имеет решений. |
Текст. Пример 3. Решить уравнение. дробь, числитель которой — икс минус два а, знаменатель – икс минус четыре равно нулю. Решение. Находим ОДЗ уравнения х-4≠0. х≠4. Решаем уравнение х-2а=0; х=2а, если х≠4, то есть 2а≠4, а≠2.Итак, если а≠2, то уравнение имеет единственное решение x = 2a, если a = 2, то уравнение не имеет решений. Ответ: если а≠2, то уравнение имеет единственное решение x = 2a; если a = 2, то уравнение не имеет решений. |
|
Задание 4 Решить уравнение модуль выражения икс минус а равно двум. Решение По определению модуля имеем: модуль икс минус а равно двум равно совокупности двух уравнений икс равен а плюс два и икс равен а минус два. Таким образом, для любого действительного a уравнение имеет два различных решения, икс первое равно а плюс два и икс второе равно а минус два. Ответ: для любого действительного a уравнение имеет два различных решения: икс первое равно а плюс два и икс второе равно а минус два. |
Текст. Пример 4. Решить уравнение |x — a| = 2 Решение. По определению модуля имеем: |x — a| = 2Û х-а=2 , Û х=а+2, х-а=-2; х= а-2. Таким образом, для любого действительного a уравнение имеет два различных решения, x1 = a + 2 и x2 = a — 2.Ответ: для любого действительного a уравнение имеет два различных решения, x1 = a + 2 и x2 = a — 2 |
|
Задание 5 Решить уравнение модуль икс плюс модуль выражения икс минус а равно нулю. Решение Левая часть уравнения принимает неотрицательные значения(как сумма двух неотрицательных слагаемых), а правая часть равна нулю. Таким образом, если a равно нулю, то система (а, следовательно, и уравнение) имеет единственное решение икс равно нулю, а если a не равно нулю, то система (и исходное уравнение) решений не имеет. Ответ: если a равно нулю, то икс равно нулю; если a не равно нулю, то уравнение корней не имеет. |
Текст. Пример 5. Решить уравнение |x| + |x — a| = 0 Решение. Имеем, х=0 , х- a =0;
х=0, х= a . Таким образом, если a = 0, то система (а, следовательно, и уравнение) имеет единственное решение x = 0, а если a ≠ 0, то система (и исходное уравнение) решений не имеет. Ответ: если a = 0, то x = 0; если a ≠ 0, то уравнение корней не имеет. |
|
Рассмотрим более сложные примеры. Задание 6 При всех значениях параметра а определим число корней кубического уравнения икс куб минус три икс плюс два минус а равно нулю. Решение Выразим а из этого уравнения, имеем: а равно икс куб минус три икс плюс два. Построим график функции а от икс. График пересекается с осью Ох в точках: икс первое равно минус два и икс второе равно одному. Вычислим производную а штрих от икс равно три икс квадрат минус три. Критические точки функции: икс равно плюс минус один. В точке икс равное минус единице функция имеет максимум, равный четырем и в точке икс равное единице — минимум, равный нулю.
|
Текст. Рассмотрим более сложные примеры. Пример 6. При всех значениях параметра а определим число корней кубического уравнения х3-3х+2-а =0 Решение. Выразим а из этого уравнения, имеем: а = х3-3х+2. Построим график функции а(х). График пересекается с осью Ох в точках: х1=-2; х2=1. Вычислим производную а /(х) =3х2-3. Критические точки функции х=±1. В точке х=-1 функция имеет максимум аmax=4 и в точке х=1- минимум аmin= 0. Картинка. |
|
При а меньшем нуля и а большем четырех графики пересекаются в одной точке (данное уравнение имеет один корень), если а равно нулю и а равно четырем графики пересекаются в двух точках (два корня), если а меньше нуля и больше четырех – в трех точках (три корня). Ответ: если а меньше нуля и а больше четырех, то данное уравнение имеет один корень; если а равно нулю и а равно четырем — два корня; если а больше нуля и меньше четырех — три корня. |
Текст. При а0 и а>4 графики пересекаются в одной точке (данное уравнение имеет один корень), при а=0 и а=4 графики пересекаются в двух точках (два корня), при 0 а4 – в трех точках(три корня) Ответ: если а0 и а>4, то данное уравнение имеет один корень один корень; если а=0 и а=4- два корня; если 0 а4 -три корня. |
|
Задание 7 Решить уравнение эм икс квадрат плюс три эм икс минус сумма эм и двух равно нулю. Решение ОДЗ этого уравнения — все действительные числа и имеет смысл при любых действительных значениях параметра эм. Рассмотрим два случая. Первый, если эм равно нулю, то уравнение примет вид: ноль икс квадрат плюс ноль икс минус два равно нулю — неверное равенство, уравнение корней не имеет. Второй случай, если эм не равно нулю, то уравнение является квадратным. Находим дискриминант, дэ равно эм умноженное на сумму тринадцати эм и восьми. Если дэ больше либо равно нулю, то эм принадлежит объединению числового луча от минус бесконечности до минус восьми тринадцатых и открытого числового луча от нуля до плюс бесконечности. Уравнение имеет два корня: икс первое, второе равно один деленное на два эм умноженное на минус три эм плюс-минус квадратный корень из произведения эм и суммы тринадцати эм и восьми. Ответ: если эм равно нулю, то уравнение не имеет корней; если эм не равно нулю, то уравнение имеет два корня: икс первое, второе равно один деленное на два эм умноженное на минус три эм плюс минус квадратный корень из произведения эм и суммы тринадцати эм и восьми. |
Текст. Пример7. Решить уравнение mх2+3 mх-(m+2)=0. Решение. ОДЗ этого уравнения все действительные числа и имеет смысл при любых действительных значениях параметра m. Рассмотрим два случая. 1)Если m=0, то уравнение примет вид 0х2+0х-2=0- неверное равенство, уравнение корней не имеет. 2) Если m≠0, то уравнение является квадратным. Находим D=m(13m+8). Если D=m(13m+8).≥0, mÎ(-∞;-8/13]È(0;+∞), то уравнение имеет два корня икс первое, второе равно один деленное на два эм умноженное на минус три эм плюс-минус квадратный корень из произведения эм и суммы тринадцати эм и восьми. Ответ: если эм равно нулю, то уравнение не имеет корней; если эм не равно нулю, то уравнение имеет два корня: икс первое, второе равно один деленное на два эм умноженное на минус три эм плюс минус квадратный корень из произведения эм и суммы тринадцати эм и восьми. |
|
Задание 8 При каких значениях параметра а уравнение минус два синус квадрат икс равно произведению суммы а в квадрате, пять а и два на синус икс имеет ровно четыре корня на отрезке от нуля до двух пи? Решение Построим график функции игрек равно синус икс на отрезке от нуля до двух пи.
|
Текст. Пример8. При каких значениях параметра а уравнение -2sin2х=( а 2+5 а+2) sinх имеет ровно четыре корня на отрезке [0;2π]? Решение. Построим график функции у = sinх на отрезке [0;2π] Картинка.
|
|
Выполним преобразования: перенесем все члены уравнения в правую часть, разложим на множители, получим: ноль равен синус икс умноженное на сумму синус икс и а квадрат плюс пять а плюс два деленное на два. Это уравнение равносильно совокупности двух уравнений синус икс равно нулю и синус икс равен минус выражение а квадрат плюс пять а плюс два деленное на два. Уравнение синус икс равно нулю имеет три корня на отрезке от нуля до двух пи. Значит, второе уравнение на этом отрезке должно иметь один корень, а это возможно тогда, когда минус выражение а квадрат плюс пять а плюс два деленное на два будет равно плюс минус одному. Получаем совокупность двух уравнений, которая имеет четыре решения: а равно минус единице, а равно минус четырем, а равно нулю, а равно минус пяти. Ответ: а равно минус единице, а равно минус четырем, а равно нулю, а равно минус пяти.
|
Текст. Получим: 0= sinх(sinх+( а 2+5 а+2)/2). Это уравнение равносильно совокупности двух уравнений sinх=0, sinх= -( а 2+5 а+2)/2. Уравнение sinх=0 имеет три корня на отрезке [0;2π]. Значит, второе уравнение на этом отрезке должно иметь один корень, а это возможно тогда, когда -( а 2+5 а+2)/2 будет равно ±1. Получаем совокупность уравнений совокупность двух уравнений, которая имеет четыре решения: а равно минус единице, а равно минус четырем, а равно нулю, а равно минус пяти которая имеет четыре решения : а=-1, а=-4, а=0, а=-5. Ответ: а=-1, а=-4, а=0, а=-5. |
Квадратное уравнение и его корни 8 класс онлайн-подготовка на Ростелеком Лицей
122. Квадратное уравнение и его корни
Квадратным уравнением называют уравнение вида ах2+bx+c = 0, где х –переменная, a, b, c – некоторые числа,
причем а≠0.
Приведем примеры квадратных уравнений:
7х2-5х+3 = 0, в этом уравнении а = 7, b = -5, с = 3;
-0,5х2+4 = 0, здесь a = -0,5; b = 0; c = 4;
3х2-6х = 0, здесь а = 3, b = -6, с = 0.
Числа а, b, с называют коэффициентами квадратного уравнения; а – первый коэффициент, b – второй коэффициент, с – свободный член.
Если а – коэффициент при х2 равен 1, то такое уравнение называется приведенным. Например, х2+4х+3 = 0.
Например, х2+4х+3 = 0.
Если второй коэффициент и/или свободный член равны 0, то такое квадратное уравнение называется неполным.
Неполные квадратные уравнения бывают трех видов:
ах2+с = 0, с≠0
ах2+bx = 0, b≠0
aх2 = 0
Рассмотрим решение каждого из этих видов:
-
ах2+с = 0, с≠0
ax2 = -c
x2 = -c:a
x=±-ca
-
ах2+bx = 0, b≠0
х(ах+b) = 0
x1 = 0, x2 = -b:a
-
aх2 = 0
x=0
Разберем решения на конкретных примерах.
-
5х2-125 = 0, здесь а = 5, b = 0, с = -125
5х2 = 125
х2 = 125:5 = 25
х1 = 25 = 5
х2 = -25 = -5
-
6х2+7х = 0
x(6х+7) = 0
x1 = 0
6х+7 = 0
6х = -7
x2 = -76
-
23х2 = 0
x2 = 0:23 = 0
x = 0
Теперь рассмотрим решение квадратного уравнения, у которого все коэффициенты отличны от нуля.
Основной метод, который используется для выведения формул корней квадратных уравнений, – метод выделения полного квадрата. Рассмотрим несколько конкретных примеров квадратных уравнений, которые мы решим с помощью использования этого метода.
Пример 1. Решить квадратное уравнение х2-2х-3 = 0
Коэффициенты данного квадратного уравнения: а = 1, b = -2, c = -3.
Для применения метода выделения полного квадрата воспользуемся следующей формулой:
(x-t)2 = x2-2xt+t2
Метод выделения полного квадрата для данного примера состоит в том, чтобы подобрать число t так, чтобы -2xt = -2x. Значит, t=1.
Получаем:
x2-2x-3 = x2-2·x·1+12-12-3 = (x-1)2-4 = 0
Данное уравнение можно решать двумя способами.
Способ 1
(x-1)2 = 4
x-1 = ±2
Отсюда x = 3 или x = -1.
Ответ: -1; 3.
Способ 2
(x-1)2-4 = 0
(x-1)2-22 = 0
(x-1-2)(x-1+2) = 0
(x-3)(x+1) = 0
Произведение равно 0 тогда и только тогда, когда хотя бы один из его множителей равен 0. Поэтому данное уравнение эквивалентно двум: x-3 = 0, x = 3 и x+1 = 0, x = -1.
Поэтому данное уравнение эквивалентно двум: x-3 = 0, x = 3 и x+1 = 0, x = -1.
Ответ: -1; 3.
Мы рассмотрели метод выделения полного квадрата на частном примере. Рассмотрим еще один, чуть более сложный пример, в котором старший коэффициент не будет равняться 1.
Пример 2. Решить квадратное уравнение: 2x2-5x+2 = 0.
Коэффициенты данного квадратного уравнения: a = 2, b = -5, c = 2.
Прежде чем выделять полный квадрат, вынесем 2 за скобки в первых двух слагаемых:
2×2-52x+2=0
Теперь в скобках выделим полный квадрат. Опять же, необходимо подобрать t так, чтобы выполнялось -2tx=-52x. Значит, t=54.
Получаем следующее уравнение:
2×2-52x+2=2×2-2∙54∙x+542-542+2=2x-542-542+2=2x-542-258+2=2x-542-98=0
Отсюда:
2x-542=98
x-542=916
x-54=±34
Отсюда x=2 или x=12.
Ответ: 12; 2.
Разобрав конкретные примеры, можем перейти к получению общей формулы корней квадратного уравнения.
Итак, рассмотрим уравнение ax2+bx+c=0.
Вынесем старший коэффициент за скобки в первых двух слагаемых
ax2+bax+c=0.
Теперь выделим в скобочках полный квадрат
ax2+2∙b2a∙x+b2a2-b2a2+c=0
ax+b2a2-b24a2+c=0
ax+b2a2-b24a+c=0
ax+b2a2=b24a-c
ax+b2a2=b2-4ac4a
Теперь поделим обе части уравнения на a, так как знаем, что в квадратном уравнении a≠0
x+b2a2=b2-4ac4a2
Выражение D=b2-4ac называется дискриминантом квадратного уравнения и обозначается буквой D.
Пока мы будем считать, что в нашем уравнении D≥0, то есть из него можно извлечь корень.
Тогда получаем:
x+b2a2=D4a2
x+b2a=±D2a
x=-b±D2a
То есть x1=-b-D2a; x2=-b+D2a
Это и есть формула для корней квадратного уравнения в общем виде.
Если теперь мы вернемся к нашим примерам, то в уравнении x2-2x-3 = 0 дискриминант равен
D = (-2)2-4·1·(-3) = 4+12 = 16.
Тогда:
x1=-(-2)-42=-1;
x2=-(-2)+42=3.
Если дискриминант меньше нуля, то уравнение действительных корней не имеет.
3-8

 При решении используются аналитические и графические методы.
При решении используются аналитические и графические методы.
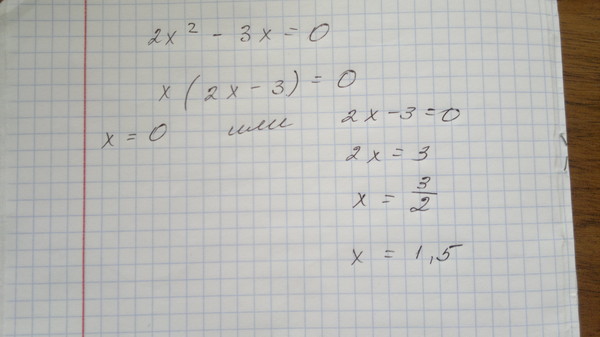




 Имеем, систему из двух уравнений икс равно нулю и икс минус а равно нулю или система из двух уравнений икс равно нулю и икс равно а.
Имеем, систему из двух уравнений икс равно нулю и икс минус а равно нулю или система из двух уравнений икс равно нулю и икс равно а.
 В этой же системе координат построим также прямую а равно анулевое. Теперь по графику легко ответить на вопрос задачи.
В этой же системе координат построим также прямую а равно анулевое. Теперь по графику легко ответить на вопрос задачи. В этой же системе координат построим также прямую а=а0.(а0 – любое число)
В этой же системе координат построим также прямую а=а0.(а0 – любое число)

 .
.