Бросают 3 кубика количество элементарных событий равно: теория-вероятностей / Бросание кубика / Математика

Содержание

Урок теории вероятности по теме «Вероятности событий (при бросании 2 игральных кубиков)». 8-й класс

Педагогические технологии: Технология объяснительно-иллюстрированного обучения, компьютерная технология, личностно-ориентированный подход в обучении, здоровьесберегающие технологии.

Тип урока: урок получения новых знаний.

Продолжительность: 1 урок.

Класс: 8 класс.

Цели урока:

Обучающие:

повторить навыки применения формулы для нахождения вероятности событии и научить применять её в задачах с игральными кубиками;
проводить доказательные рассуждения при решении задач, оценивать логическую правильность рассуждений, распознавать логически некорректные рассуждения.

Развивающие:

развить навыки поиска, обработки и представления информации;
развить умение сравнивать, анализировать, делать выводы;

развить наблюдательность, а также коммуникативные умения.

Воспитательные:

воспитать внимательность, усидчивость;
сформировать понимание значимости математики как способа познания окружающего мира.

Оборудование урока: компьютер, мультимедиа, маркеры, копи-устройство mimio (или интерактивная доска), конверт ( в нем находится задание для практической работы, домашней работы, три карточки: желтого, зеленого, красного цветов), модели игральных кубиков.

План урока

Организационный момент.

— На предыдущем уроке мы познакомились с формулой классической вероятности.

Вероятностью Р наступления случайного события А называется отношение m к n, где n – это число всех возможных исходов эксперимента, а m – это число всех благоприятных исходов

— Формула представляет собой так называемое классическое определение вероятности по Лапласу, пришедшее из области азартных игр, где теория вероятностей применялась для определения перспективы выигрыша. Эта формула применяется для опытов с конечным числом равновозможных исходов.

Вероятность события = Число благоприятных исходов / число всех равновозможных исходов

Таким образом, вероятность – это число от 0 до 1.

Вероятность равна 0, если событие невозможное.

Вероятность равна 1, если событие достоверное.

— Решим задачу устно: На книжной полке стоят 20 книг, из них 3 справочника. Какова вероятность, что взятая с полки книга не окажется справочником?

Решение:

Общее число равновозможных исходов – 20

Число благоприятных исходов – 20 – 3 = 17

Р =17 / 20 = 0,85.

Ответ: 0,85.

2. Получение новых знаний.

А теперь вернемся к теме нашего урока: “Вероятности событий”, подпишем её в своих тетрадях.

Цель урока: научиться решать задачи на нахождение вероятности при бросании кубика или 2-х кубиков.

Наша сегодняшняя тема связана с игральным кубиком или его еще называют игральной костью. Игральная кость известна с древности. Игра в кости — одна из древнейших, первые прообразы игральных костей найдены в Египте, и датируются они XX веком до н. э. Имеется множество разновидностей, от простых (выигрывает выкинувший большее количество очков) до сложных, в которых можно использовать различные тактики игры.

Самые древние кости датируются ХХ веком до н. э., обнаружены в Фивах. Первоначально кости служили орудием для гаданий. По данным археологических раскопок в кости играли повсеместно во всех уголках земного шара. Название произошло от первоначального материала — костей животных.

Древние греки считали, что кости изобрели лидийцы, спасаясь от голода, чтобы хоть чем-то занять свои умы.

Игра в кости получила отражение в древнеегипетской, греко-римской, ведической мифологии. Упоминается в Библии, “Илиаде”, “Одиссее”, “Махабхарате”, собрании ведических гимнов “Ригведа”. В пантеонах богов хотя бы один бог являлся обладателем игральных костей как неотъемлемого атрибута http://ru.wikipedia.org/wiki/%CA%EE%F1%F2%E8_%28%E8%E3%F0%E0%29 — cite_note-2.

После падения Римской Империи игра распространилась по Европе, особенно увлекались ей во времена Средневековья. Поскольку игральные кости использовались не только для игры, но и для гадания, церковь неоднократно пыталась запретить игру, для этой цели придумывались самые изощрённые наказания, но все попытки заканчивались неудачей.

Согласно данным археологии, в кости играли и в языческой Руси. После крещения православная церковь пыталась искоренить игру, но среди простого народа она оставалась популярной, в отличие от Европы, где игрой в кости грешила высшая знать и даже духовенство.

Война, объявленная властями разных стран игре в кости породила множество различных шулерских уловок.

В век Просвещения увлечение игрой в кости постепенно пошло на спад, у людей появились новые увлечения, их больше стали интересовать литература, музыка и живопись. Сейчас игра в кости не столько широко распространена.

Правильные кости обеспечивают одинаковые шансы выпадения грани. Для этого все грани должны быть одинаковыми: гладкими, плоскими, иметь одинаковую площадь, скругления (если они имеются), отверстия должны быть просверлены на одинаковую глубину. Сумма очков на противоположных гранях равна 7.

Математическая игральная кость, которая используется в теории вероятности,- это математический образ правильной кости. Математическая кость не имеет ни размера, ни цвета, ни веса и т.д.

При бросании игральной кости (кубика) может выпасть любая из шести ее граней, т.е. произойти любое из событий— выпадение от 1 до 6 точек (очков).

Но никакие две и более граней одновременно появиться не могут. Такие события называют несовместными.

— Рассмотрим случай, когда бросают 1 кубик. Выполним № 2 в виде таблицы.

событие	Число благоприятных исходов	Общее число исходов	вероятность
А: “ выпало число 4”
В: “ выпало число 5”
С: “ выпало число меньше 3”
Д: “ выпало число 8”
Е: “ выпало нечетное число меньше 3”

— Теперь рассмотрим случай, когда бросают 2 кубика.

Если на первом кубике выпало одно очко, то на втором может выпасть 1, 2, 3, 4, 5, 6.Получим пары (1;1), (1;2), (1;3), (1;4), (1;5), (1;6) и так с каждой гранью. Все случаи можно представить в виде таблицы из 6-ти строк и 6-ти столбцов:

Таблица элементарных событий

1; 1

2; 1

3; 1

4; 1

5; 1

6; 1

1; 2

2; 2

3; 2

4; 2

5; 2

6; 2

1; 3

2; 3

3; 3

4; 3

5; 3

6; 3

1; 4

2; 4

3; 4

4; 4

5; 4

6; 4

1; 5

2; 5

3; 5

4; 5

5; 5

6; 5

1; 6

2; 6

3; 6

4; 6

5; 6

6; 6

— У вас на парте лежит конверт.

— Возьмите из конверта листок с заданиями.

-Сейчас вы выполните практическое задание, воспользовавшись таблицей элементарных событий.

Покажите штриховкой события, благоприятствующие событиям:

Задание 1. “Выпало одинаковое число очков”;

получим

1; 1 2; 1 3; 1 4; 1 5; 1 6; 1
1; 2 2; 2 3; 2 4; 2 5; 2 6; 2
1; 3 2; 3 3; 3 4; 3 5; 3 6; 3
1; 4 2; 4 3; 4 4; 4 5; 4 6; 4
1; 5 2; 5 3; 5 4; 5 5; 5 6; 5
1; 6 2; 6 3; 6 4; 6 5; 6 6; 6
Задание 2. “Сумма очков равна 7”;

получим

1; 1 2; 1 3; 1 4; 1 5; 1 6; 1
1; 2 2; 2 3; 2 4; 2 5; 2 6; 2
1; 3 2; 3 3; 3 4; 3 5; 3 6; 3
1; 4 2; 4 3; 4 4; 4 5; 4 6; 4
1; 5 2; 5 3; 5 4; 5 5; 5 6; 5
1; 6 2; 6 3; 6 4; 6 5; 6 6; 6
Задание 3. “Сумма очков не меньше 7”.
Что значит “не меньше”? ( Ответ — “больше, или равно”)

1; 1 2; 1 3; 1 4; 1 5; 1 6; 1
1; 2 2; 2 3; 2 4; 2 5; 2 6; 2
1; 3 2; 3 3; 3 4; 3 5; 3 6; 3
1; 4 2; 4 3; 4 4; 4 5; 4 6; 4
1; 5 2; 5 3; 5 4; 5 5; 5 6; 5
1; 6 2; 6 3; 6 4; 6 5; 6 6; 6
А теперь найдем вероятности событий, для которых в практической работе заштриховывали благоприятствующие события.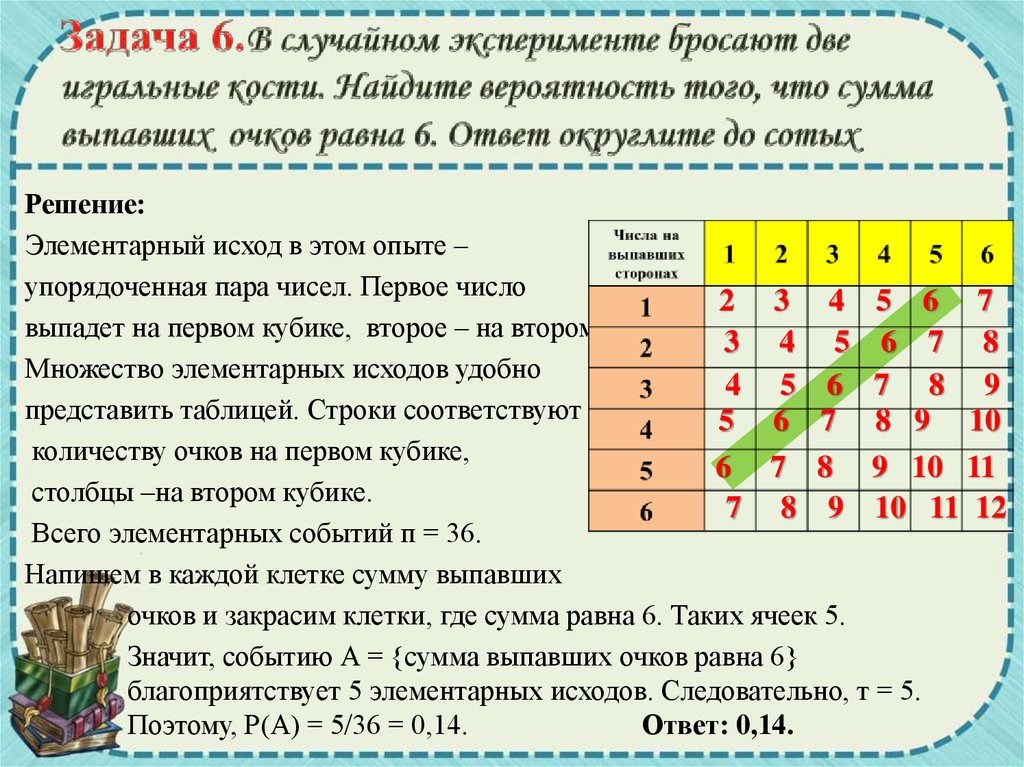
Запишем в тетрадях №3
Задание 1.

Общее число исходов — 36

Число благоприятствующих исходов — 6

Р = 6/36=1/6.

Ответ: 1/6.

Задание 2.

Общее число исходов — 36

Число благоприятствующих исходов — 6

Р = 6/36=1/6.

Ответ: 1/6.

Задание 3.

Общее число исходов- 36

Число благоприятствующих исходов — 21

Р = 21/36=7/12.

Ответ: 7/12.
№4. Саша и Влад играют в кости. Каждый бросает кость два раза. Выигрывает тот, у кого выпавшая сумма очков больше. Если суммы очков равны, игра оканчивается вничью. Первым бросал кости Саша, и у него выпало 5 очков и 3 очка. Теперь бросает кости Влад.
а) В таблице элементарных событий укажите (штриховкой) элементарные события, благоприятствующие событию “Выиграет Влад”.
б) Найдите вероятность события “Влад выиграет”.

3. Физкультминутка.
Если событие достоверное — мы все дружно хлопаем,
Если событие невозможное — мы все вместе топаем,
Если событие случайное — покачаем головой / вправо-влево
“В корзине 3 яблока (2 красных, 1 зеленое).
— Из корзины вытащили 3 красных – (невозможное)
— Из корзины вытащили красное яблоко - (случайное)
— Из корзины вытащили зеленое яблоко – (случайное)
— Из корзины вытащили 2 красных и 1 зеленое – ( достоверное)
Решим следующий номер.
№5.
Правильную игральную кость бросают два раза. Какое событие более вероятно:
А: “Оба раза выпало 5 очков”;
В: “В первый раз выпала 2 очка, во второй 5очков” ;
С: “Один раз выпало 2 очка, один раз 5 очков”?
Решение:
Разберем событие А: общее число исходов-36, число благоприятствующих исходов- 1 (5;5)
Р = 1/36.
Разберем событие В: общее число исходов-36, число благоприятствующих исходов- 1 (2;5)
Р = 1/36.
Разберем событие С: общее число исходов-36, число благоприятствующих исходов- 2 (2;5 и 5;2)
Р = 2/36=1/18.
Ответ: событие С.

4. Постановка домашнего задания.
1. Вырезать развертку, склеить кубики. Принести на следующий урок.
2. Выполнить 25 бросков. Результаты записать в таблицу: (на следующем уроке можно ввести понятие частоты )

События Количество выпадений
“Сумма очков 6”
“Сумма очков не менее 5”
“Сумма очков не более 5”
3. Решите задачу: Бросают две игральные кости. Вычислите вероятность:
а) “Сумма очков равна 6”;
б) “Сумма очков не менее 5”;
в) “На первой кости очков больше, чем на второй”.

5. Подведение итогов.
Учащиеся отвечают на вопросы: Что нового узнали на уроке?
В конце урока./ с помощью карточек трёх цветов : жёлтого, зеленого, красного/
У ребят на партах в конвертах лежат карточки. По просьбе учителя, учащиеся поднимают карточку соответствующего цвета.
— Поднимите зеленую, если вы всё поняли.
— Желтую, если есть небольшие недочеты и есть над чем работать.
— Красную, если не совсем разобрались в теме.
Приложение 1
Приложение 2
ИСТОЧНИКИ:
1. Тюрин Ю.Н., Макаров А.А., Высоцкий И.Р., Ященко И.В. 2008. Теория вероятностей и статистика.
2.Картинки с сайта
Рожица- http://www.livegif.ru/archive/the_best/11_6. html

Школа- http://www.allforchildren.ru/pictures/school/school19-04.gif

Сова- http://www.allforchildren.ru/pictures/school/school10-01.gif

Игральный кубик бросают 1 раз какова вероятность. Вероятность игральной кости
Объясните принцип решения задачи. Игральную кость бросили один раз. Какова вероятность того, что выпало менее 4 очков? и получил лучший ответ
Ответ от Дивергент[гуру]
50 процентов
Принцип крайне прост. Всего исходов 6: 1,2,3,4,5,6
Из них три удовлетворяют условию: 1,2,3, а три не удовлетворяют: 4,5,6. Поэтому вероятность равна 3/6=1/2=0,5=50%
Ответ от I am superman [гуру]
Всего может выпасть шесть вариантов (1,2,3,4,5,6)
И з этих вариантов 1, 2, и 3 — меньше чем четыре
Значит 3 ответа из 6
Чтобы вычислить вероятность делим благоприятный расклад ко всему, т. е. 3 на 6 = 0,5 или 50%
Ответ от Ўрий Довбыш [активный]
50%
подели 100% на количество чисел на кости,
а потом умнож процент полученый, на количесто, которое тебе надо узнать, то есть на 3)
Ответ от Иван Панин [гуру]
я точно не знаю, готовлюсь к ГИА, но учительница сегодня что то рассказывала, только про вероятность машин, так как я понял, отношение показывается дробью, с верху число благоприятное, а с низу по моему вообще общее, ну у нас про машины было так: В фирме такси в данный момент свободно 3 чёрных, 3 жёлтых и 14 зелёных машин. К заказчику выехала одна из машин. Найти вероятность того, что к нему приедет жёлтое такси. Так вот, жёлтых такси 3 и из всего кол-ва машин их 3, получается сверху дроби пишем 3, т. к. это благоприятное число машин, а снизу пишем 20, т. к. всего машин в таксопарке 20, вот и получается вероятность 3 к 20 или 3/20 дробью, ну это я так понял…. Как с костями точно не знаю, но может помог чем…
Ответ от 3 ответа [гуру]
Привет! Вот подборка тем с ответами на Ваш вопрос: Объясните принцип решения задачи. Игральную кость бросили один раз. Какова вероятность того, что выпало менее 4 очков?
Задачи на вероятность игральной кости не менее популярны, чем задачи о подбрасывании монет. Условие такой задачи обычно звучит так: при бросании одной или нескольких игральных костей (2 или 3), какова вероятность того, что сумма очков будет равна 10, или число очков равно 4, или произведение числа очков, или делится на 2 произведение числа очков и так далее.
Применение формулы классической вероятности является основным методом решения задач такого типа.
Одна игральная кость, вероятность.
Достаточно просто обстоит дело с одной игральной костью. определяется по формуле: P=m/n, где m — это число благоприятствующих событию исходов, а n — число всех элементарных равновозможных исходов эксперимента с подбрасыванием кости или кубика.
Задача 1. Один раз брошена игральная кость. Какова вероятность выпадения четного числа очков?
Поскольку игральная кость собой представляет кубик (или его еще называют правильной игральной костью, на все грани кубик выпадет с одинаковой вероятностью, так как он сбалансированный), у кубика 6 граней (число очков от 1 до 6, которые обычно обозначаются точками), это значит, что в задаче общее число исходов: n=6. Событию благоприятствуют только исходы, при которых выпадает грань с четными очками 2,4 и 6, у кубика таких граней: m=3. Теперь можем определить искомую вероятность игральной кости: P=3/6=1/2=0.5.
Задача 2. Брошен один раз игральный кубик. Какова вероятность, что выпадет не менее 5 очков?
Решается такая задача по аналогии с примером, указанным выше. При бросании игрального кубика общее число равновозможных исходов равно: n=6, а удовлетворяют условие задачи (выпало не менее 5 очков, то есть выпало 5 или 6 очков) только 2 исхода, значит m=2. Далее находим нужную вероятность: P=2/6=1/3=0.333.
Две игральные кости, вероятность.
При решении задач с бросанием 2-х игральных костей, очень удобно пользоваться специальной таблицей выпадения очков. На ней по горизонтали откладывается число очков, выпавших на первой кости, а по вертикали — число очков, которое выпало на второй кости. Заготовка имеет такой вид:
Но возникает вопрос, что же будет в пустых ячейках таблицы? Это зависит от задачи, которую потребуется решить. Если в задаче речь идет о сумме очков, тогда туда записывается сумма, а если про разность — значит записывается разность и так далее.
Задача 3. Брошены одновременно 2 игральные кости. Какова вероятность выпадения суммы менее 5 очков?
Для начала необходимо разобраться какое будет общее число исходов эксперимента. Все было очевидно при бросании одной кости 6 граней кубика — 6 исходов эксперимента. Но когда уже две кости, то возможные исходы можно представить как упорядоченные пары чисел вида (x, y), где х показывает сколько на первой кости выпало очков (от 1 до 6), а у — сколько выпало очков на второй кости (от 1 до 6). Всего таких числовых пар будет: n=6*6=36 (в таблице исходов им как раз соответствуют 36 ячеек).
Теперь можно заполнить таблицу, для этого в каждую ячейку заносится число суммы очков, которые выпали на первой и второй кости. Заполненная таблица выглядит так:
Благодаря таблице определим число исходов, которые благоприятствуют событию » выпадет в сумме менее 5 очков». Произведем подсчет числа ячеек, значение суммы в которых будет меньше числа 5 (это 2, 3 и 4). Такие ячейки для удобства закрашиваем, их будет m=6:
Учитывая данные таблицы, вероятность игральной кости равняется: P=6/36=1/6.
Задача 4. Было брошено две игральные кости. Определить вероятность того, что произведение числа очков будет делиться на 3.
Для решения задачи составим таблицу произведений очков, которые выпали на первой и на второй кости. В ней сразу же выделим числа кратные 3:
Записываем общее число исходов эксперимента n=36 (рассуждения такие же как в предыдущей задаче) и число благоприятствующих исходов (число ячеек, которые закрашены в таблице) m=20. Вероятность события равняется: P=20/36=5/9.
Задача 5. Дважды брошена игральная кость. Какова вероятность, что на первой и второй кости разность числа очков будет равна от 2 до 5?
Чтобы определить вероятность игральной кости запишем таблицу разностей очков и выделим в ней те ячейки, значение разности в которых будет между 2 и 5:
Число благоприятствующих исходов (число ячеек, закрашенных в таблице) равно m=10, общее число равновозможных элементарных исходов будет n=36. Определит вероятность события: P=10/36=5/18.
В случае простого события и при бросании 2-х костей, требуется построить таблицу, затем в ней выделить нужные ячейки и их число поделить на 36, это и будет считаться вероятностью.
Цели урока:
Учащиеся должны знать:
определение вероятности случайного события;
уметь решать задачи на нахождение вероятности случайного события;
уметь применять теоретические знания на практике.
Задачи урока:
Образовательные: создать условия для овладения учащимися системы знаний, умений и навыков с понятиями вероятности события.
Воспитательные: формировать у учащихся научное мировоззрение
Развивающие: развивать у учащихся познавательный интерес, творческие способности, волю, память, речь, внимание, воображение, восприятие.
Методы организации учебно-познавательной деятельности:
наглядные,
практические,
по мыслительной деятельности: индуктивный,
по усвоению материала: частично-поисковый, репродуктивный,
по степени самостоятельности: самостоятельная работа,
стимулирующие: поощрения,
виды контроля: проверка самостоятельно решенных задач.
План урока
Устные упражнения
Изучение нового материала
Решение заданий.
Самостоятельная работа.
Подведение итогов урока.
Комментирование домашнего задания.
Оборудование: мультимедийный проектор (презентация), карточки (самостоятельная работа)
Ход урока
I. Организационный момент.

Организация класса в течение всего урока, готовность учащихся к уроку, порядок и дисциплина.
Постановка целей учения перед учащимися, как на весь урок, так и на отдельные его этапы.
Определить значимость изучаемого материала, как в данной теме, так и во все курсе.
II. Повторение
1. Что такое вероятность?
Вероятность – возможность исполнения, осуществимости чего-нибудь.
2. Какое определение дает основатель современной теории вероятностей А.Н. Колмогоров?
Вероятность математическая – это числовая характеристика степени возможности появления какого-либо определенного события в тех или иных определенных, могущих повторяться неограниченное число раз условиях.
3. Какое классическое определение вероятности дают авторы школьных учебников?
Вероятностью Р(А) события А в испытании с равновозможными элементарными исходами называется отношение числа исходов m, благоприятствующих событию А, к числу n всех исходов испытания.
Вывод: в математике вероятность измеряется числом.
Сегодня мы с вами продолжим рассматривать математическую модель “игральная кость”.
Предметом исследования в теории вероятностей являются события, появляющиеся при определенных условиях, которые можно воспроизводить неограниченное количество раз. Каждое осуществление этих условий называют испытанием.

Испытание – бросание игральной кости.

Событие – выпадение шестерки или выпадение четного числа очков.
Выпадение каждой грани при многократном бросании кубика имеет одинаковую вероятность (игральная кость правильная).
III. Устное решение задач.

1. Игральную кость (кубик) бросили один раз. Какова вероятность того, что выпало 4 очка?
Решение. Случайный эксперимент – бросание кубика. Событие – число на выпавшей грани. Граней всего шесть. Перечислим все события: 1, 2, 3, 4, 5, 6. Значит п = 6. Событию А = {выпало 4 очка} благоприятствует одно событие: 4. Поэтому т = 1. События равновозможные, поскольку подразумевается, что кубик честный. Поэтому Р(А) = т/п = 1/6 = 0,17.
2. Игральную кость (кубик) бросили один раз. Какова вероятность того, что выпало не более 4 очков?
п = 6. Событию А = {выпало не более 4 очков} благоприятствует 4 события: 1, 2, 3, 4. Поэтому т = 4. Поэтому Р(А) = т/п = 4/6 = 0,67.
3. Игральную кость (кубик) бросили один раз. Какова вероятность того, что выпало менее 4 очков?
Решение. Случайный эксперимент – бросание кубика. Событие – число на выпавшей грани. Значит п = 6. Событию А = {выпало менее 4 очков} благоприятствует 3 события: 1, 2, 3. Поэтому т = 3. Р(А) = т/п = 3/6 = 0,5.
4. Игральную кость (кубик) бросили один раз. Какова вероятность того, что выпало нечетное число очков?
Решение. Случайный эксперимент – бросание кубика. Событие – число на выпавшей грани. Значит п = 6. Событию А = {выпало нечетное число очков} благоприятствует 3 события: 1,3,5. Поэтому т = 3. Р(А) = т/п = 3/6 = 0,5.
IV. Изучение нового

Сегодня рассмотрим задачи, когда в случайном эксперименте используются две игральные кости или выполняются два, три броска.
1. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что сумма выпавших очков равна 6. Ответ округлите до сотых.
Решение. Исход в этом опыте – упорядоченная пара чисел. Первое число выпадет на первом кубике, второе – на втором. Множество исходов удобно представить таблицей.
Строки соответствуют количеству очков на первом кубике, столбцы – на втором кубике. Всего элементарных событий п = 36.
1 2 3 4 5 6
1 2 3 4 5 6 7
2 3 4 5 6 7 8
3 4 5 6 7 8 9
4 5 6 7 8 9 10
5 6 7 8 9 10 11
6 7 8 9 10 11 12
Напишем в каждой клетке сумму выпавших очков и закрасим клетки, где сумма равна 6.
Таких ячеек 5. Значит, событию А = {сумма выпавших очков равна 6} благоприятствует 5 исходов. Следовательно, т = 5. Поэтому, Р(А) = 5/36 = 0,14.
2. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 3 очка. Результат округлите до сотых.
п = 36.
Событию А = {сумма равна 3} благоприятствуют 2 исходов. Следовательно, т = 2.
Поэтому, Р(А) = 2/36 = 0,06.
3. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет более 10 очков. Результат округлите до сотых.
Решение. Исход в этом опыте – упорядоченная пара чисел. Всего событий п = 36.
Событию А = {в сумме выпадет более 10 очков} благоприятствуют 3 исхода.
Следовательно, т
4. Люба дважды бросает игральный кубик. В сумме у неё выпало 9 очков. Найдите вероятность того, что при одном из бросков выпало 5 очков.
Решение Исход в этом опыте – упорядоченная пара чисел. Первое число выпадет при первом броске, второе – при втором. Множество исходов удобно представить таблицей.
Строки соответствуют результату первого броска, столбцы – результату второго броска.
Всего событий, при которых сумма очков 9 будет п = 4. Событию А = {при одном из бросков выпало 5 очков} благоприятствует 2 исхода. Следовательно, т = 2.
Поэтому, Р(А) = 2/4 = 0,5.
5. Света дважды бросает игральный кубик. В сумме у неё выпало 6 очков. Найдите вероятность того, что при одном из бросков выпало 1 очко.
Первое бросание
Второе бросание
Сумма очков
Равновозможных исходов – 5.
Вероятность события р = 2/5 = 0,4.
6. Оля дважды бросает игральный кубик. В сумме у нее выпало 5 очков. Найдите вероятность того, что при первом броске выпало 3 очка.
Первое бросание
Второе бросание
Сумма очков
+ =
+ =
+ =
+ =
Равновозможных исходов – 4.
Благоприятствующих исходов – 1.
Вероятность события р = 1/4 = 0,25.
7. Наташа и Витя играют в кости. Они бросают игральную кость по одному разу.
Выигрывает тот, кто выбросил больше очков. Если очков выпало поровну, то наступает ничья. В сумме выпало 8 очков. Найдите вероятность того, что Наташа выиграла.
Сумма очков
+ =
+ =
+ =
+ =
+ =
Равновозможных исходов – 5.
Благоприятствующих исходов – 2.
Вероятность события р = 2/5 = 0,4.
8. Таня и Наташа играют в кости. Они бросают игральную кость по одному разу. Выигрывает тот, кто выбросил больше очков. Если очков выпало поровну, то наступает ничья. В сумме выпало 6 очков. Найдите вероятность того, что Таня проиграла.
Таня Наташа Сумма очков
+ =
+ =
+ =
+ =
+ =
Равновозможных исходов – 5.
Благоприятствующих исходов – 2.
Вероятность события р = 2/5 = 0,4.
9. Коля и Лена играют в кости. Они бросают игральную кость по одному разу. Выигрывает тот, кто выбросил больше очков. Если очков выпало поровну, то наступает ничья. Первым бросил Коля, у него выпало 3 очка. Найдите вероятность того, что Лена не выиграет.
У Коли выпало 3 очка.
У Лены равновозможных исходов – 6.
Благоприятствующих проигрышу исходов – 3 (при1 и при 2 и при 3).
Вероятность события р = 3/6 = 0,5.
10. Маша трижды бросает игральный кубик. Какова вероятность того, что все три раза выпадут чётные числа.
У Маши равновозможных исходов – 6 · 6 · 6 = 216.
Благоприятствующих проигрышу исходов – 3 · 3 · 3 = 27.
Вероятность события р = 27/216 = 1/8 = 0,125.
11. В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 16 очков. Результат округлите до сотых.

Решение.
Вторая Третья Сумма очков
+ + =
+ + =
+ + =
+ + =
+ + =
+ + =
Равновозможных исходов – 6 · 6 · 6 = 216.
Благоприятствующих исходов – 6.
Вероятность события р = 6/216 = 1/36 = 0,277… = 0,28. Следовательно, т = 3. Поэтому, Р (А) = 3/36 = 0,08.
V. Самостоятельная работа.

Вариант 1.
Игральную кость (кубик) бросили один раз. Какова вероятность того, что выпало не менее 4 очков? (Ответ:0,5)
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 5 очков. Результат округлите до сотых. (Ответ:0,11)
Аня дважды бросает игральный кубик. В сумме у нее выпало 3 очка. Найдите вероятность того, что при первом броске выпало 1 очко. (Ответ:0,5)
Катя и Ира играют в кости. Они бросают игральную кость по одному разу. Выигрывает тот, кто выбросил больше очков. Если очков выпало поровну, то наступает ничья. В сумме выпало 9 очков. Найдите вероятность того, что Ира проиграла. (Ответ:0,5)
В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 15 очков. Результат округлите до сотых. (Ответ:0,05)

Вариант 2.
Игральную кость (кубик) бросили один раз. Какова вероятность того, что выпало не более 3 очков? (Ответ:0,5)
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 10 очков. Результат округлите до сотых. (Ответ:0,08)
Женя дважды бросает игральный кубик. В сумме у нее выпало 5 очков. Найдите вероятность того, что при первом броске выпало 2 очка. (Ответ:0,25)
Маша и Даша играют в кости. Они бросают игральную кость по одному разу. Выигрывает тот, кто выбросил больше очков. Если очков выпало поровну, то наступает ничья. В сумме выпало 11 очков. Найдите вероятность того, что Маша выиграла. (Ответ:0,5)
В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 17 очков. Результат округлите
VI.
Домашняя работа
В случайном эксперименте бросают три игральные кости. В сумме выпало 12 очков. Найдите вероятность того, что при первом броске выпало 5 очкаов Результат округлите до сотых.
Катя трижды бросает игральный кубик. Какова вероятность того, что все три раза выпадут одинаковые числа?
VII. Итог урока

Что нужно знать для нахождения вероятности случайного события?
Для вычисления классической вероятности нужно знать все возможные исходы события и благоприятные исходы.

Классическое определение вероятности применимо только к событиям с равновозможными исходами, что ограничивает область его применения.

Для чего в школе изучаем теорию вероятности?
Многие явления окружающего нас мира поддаются описанию только с помощью теории вероятностей.
Литература
Алгебра и начала математического анализа.10-11 классы: учеб. для общеобразовательных учреждений: базовый уровень / [Ш.А.Алимов, Ю.М.Колягин, М.В.Ткачева и др.]. – 16-е изд., перераб. – М.: Просвещение, 2010. – 464 с.
Семенов А.Л. ЕГЭ: 3000 задач с ответами по математике. Все задания группы В / – 3-е изд., перераб. и доп. – М.: Издательство “Экзамен”, 2012. – 543с.
Высоцкий И.Р., Ященко И.В. ЕГЭ 2012. Математика. Задача В10. Теория вероятностей. Рабочая тетрадь /Под ред. А.Л.Семенова и И.В.Ященко. – М.: МЦШМО, 2012. – 48 с.
Задача 19 (ОГЭ — 2015, Ященко И.В.)
Оля, Денис, Витя, Артур и Рита бросили жребий — кому начинать игру. Найдите вероятность того, что начинать игру должна будет Рита.
Решение
Всего начинать игру могут 5 человек.
Ответ: 0,2.
Задача 19 (ОГЭ — 2015, Ященко И.В.)
В кармане у Миши было четыре конфеты — «Грильяж», «Маска», «Белочка» и «Красная шапочка», а также ключи от квартиры. Вынимая ключи, Миша случайно выронил одну конфету. Найдите вероятность того, что потеряась конфета «Маска».
Решение
Всего вариантов — 4.
Вероятность того, что Миша выронил конфету «Маска» равна
Ответ: 0,25.
Задача 19 (ОГЭ — 2015, Ященко И.В.)
Игральную кость (кубик) бросили один раз. Какова вероятность того, что выпало число очков, не меньшее, чем 3?
Решение
Всего различных вариантов выпадания очков на кубике — 6.
Число очков, не меньшее, чем 3, может быть: 3,4,5,6 — то есть 4 варианта.
Значит вероятность равна P = 4/6 = 2/3.
Ответ: 2/3.
Задача 19 (ОГЭ — 2015, Ященко И.В.)
Бабушка решила дать внуку Илюше на дорогу какой-нибудь случайно выбранный фрукт. У нее было 3 зеленых яблока, 3 зеленые груши и 2 желтых банана. Найдите вероятность того, что Илюша получит от бабушки фрукт зеленого цвета.
Решение
3+3+2 = 8 — всего фруктов. Из них зеленых — 6 (3 яблока и 3 груши).
Тогда вероятность того, что Илюша получит от бабушки фрукт зеленого цвета, равна
P = 6/8 =3/4 = 0,75.
Ответ: 0,75.
Задача 19 (ОГЭ — 2015, Ященко И.В.)
Игральную кость бросают два раза. Найдите вероятность того, что оба раза выпало число, большее 3.
Решение
6*6 = 36 — всего вариантов выпадения чисел при двух бросках игральной кости.
Нам подходят варианты:
Всего таких вариантов — 9.
Значит вероятность того, что оба раза выпало число, большее 3, равна
P = 9/36 = 1/4 = 0,25.
Ответ: 0,25.
Задача 19 (ОГЭ — 2015, Ященко И.В.)
Игральную кость (кубик) бросают 2 раза. Найдите вероятность того, что один раз выпало число, большее 3, а другой раз — меньшее 3.
Решение
Всего вариантов: 6*6 = 36.
Нам подходят следующие исходы:
Как решить задачу с 3 кубиками?
Вероятность также известна как возможность. Это означает математику случая, которая торгует вероятным событием. Значение обозначается от нуля до единицы. В математике было показано, что Вероятность угадывает вероятность того, что события произойдут. По сути, вероятность — это масштаб, в котором что-то должно произойти.
Вероятность
Чтобы лучше понять вероятность, возьмем пример с бросанием игральной кости, возможные результаты 1, 2, 3, 4, 5 и 6. Вероятность того, что выпадет любой из благоприятных исходов, равна 1/6. Поскольку вероятность возникновения любого из событий одинакова, то и шансы получить любое вероятное число одинаковы, в данном случае это либо 1/6, либо 50/3.
Формула вероятности
Вероятность события = {Количество благоприятных событий} ⁄ {количество всех событий}
P(A) = {Количество вариантов возникновения А} ⁄ {Общее количество событий}
КУБИКИ
Игральные кости – это небольшие кубики с от одной до шести меток или точек на гранях, которые используются в играх для получения случайной цифры. Кости — это маленькие подбрасываемые блоки с отмеченными сторонами, которые могут останавливаться на несколько цифр. Они используются для создания случайных фигур, часто как часть дополнительных настольных игр, а также игр в кости, настольных игр, ролевых игр и азартных игр.
Обычный кубик представляет собой куб, на каждой из шести граней которого видно разное количество цифр от одного до шести. При подбрасывании или броске кубик останавливается, и на его большей стороне появляется случайное число от одного до шести, при этом каждое событие равновероятно. Кости также могут иметь вогнутую или неровную форму, а их грани могут быть отмечены цифрами или символами вместо точек. Загруженные кости разыгрываются, чтобы обслуживать одни результаты, а не другие, для побега или развлечения.
Как решить задачу с тремя кубиками?
Решение:
Возможность броска шестигранных трех кубиков будет 1, 2, 3, 4, 5 и 6 точек на каждом (трех) кубиках.
Три кубика бросаются одновременно, количество достижимых исходов может быть 6 ³ = (6 × 6 × 6) = 216, потому что на каждом кубике есть числа от 1 до 6 на точках.
Теперь рассмотрим возможные суммы при броске трех костей. Наименьшая достижимая сумма возникает, когда все кости наименьшие или по одной на каждую. Это дает сумму трех, когда мы бросаем три кости, то есть (1, 1, 1). Наибольшее число на кубике — шесть, а это означает, что наибольшая возможная сумма, выпадающая, когда на всех трех кубиках выпадают шестерки, равна 18, т. е. (6, 6, 6). При броске n игральных костей минимально достижимая сумма равна n, а наибольшая достижимая сумма равна 6n. Есть только один способ, когда три кости могут составить 3,
3 направления для 4
6 для 5
10 для 6
15 для 7
21 для 8
25 для 9
90 для 27 27 на 11
25 на 12
21 для 13
15 для 14
10 для 15
6 для 16
3 для 17
1 для 18
20 9009 выше, для трех игральных костей возможные суммы включают каждое число из от трех до 18. Рассчитайте вероятность, используя план сложения и признав, что мы рассматриваем способы разделения целого числа на абсолютно три целых числа. Например, чтобы получить сумму трех, есть только один способ, т. е. 3 = 1 + 1 + 1. Поскольку каждая кость индивидуальна по сравнению с другими, такую сумму, как четыре, можно получить тремя различными способами:0003
1 + 1 + 2
1 + 2 + 1
2 + 1 + 1
Аргументы прямого сложения можно использовать для определения количества способов создания других сумм. Разделы для каждой суммы следующие:
3 = 1 + 1 + 1
4 = 1 + 1 + 2
5 = 1 + 1 + 3 = 2 + 2 + 1
6 = 1 + 1 + 4 = 1 + 2 + 3 = 2 + 2 + 2
7 = 1 + 1 + 5 = 2 + 2 + 3 = 3 + 3 + 1 = 1 + 2 + 4
8 = 1 + 1 + 6 = 2 + 3 + 3 = 4 + 3 + 1 = 1 + 2 + 5 = 2 + 2 + 4
9 = 6 + 2 + 1 = 4 + 3 + 2 = 3 + 3 + 3 = 2 + 2 + 5 = 1 + 3 + 5 = 1 + 4 + 4
10 = 6 + 3 + 1 = 6 + 2 + 2 = 5 + 3 + 2 = 4 + 4 + 2 = 4 + 3 + 3 = 1 + 4 + 5
11 = 6 + 4 + 1 = 1 + 5 + 5 = 5 + 4 + 2 = 3 + 3 + 5 = 4 + 3 + 4 = 6 + 3 + 2
12 = 6 + 5 + 1 = 4 + 3 + 5 = 4 + 4 + 4 = 5 + 2 + 5 = 6 + 4 + 2 = 6 + 3 + 3
13 = 6 + 6 + 1 = 5 + 4 + 4 = 3 + 4 + 6 = 6 + 5 + 2 = 5 + 5 + 3
14 = 6 + 6 + 2 = 5 + 5 + 4 = 4 + 4 + 6 = 6 + 5 + 3
15 = 6 + 6 + 3 = 6 + 5 + 4 = 5 + 5 + 5
16 = 6 + 6 + 4 = 5 + 5 + 6
17 = 6 + 6 + 5
18 = 6 + 6 + 6 благоприятные события } ⁄ {количество всех событий}, или 216. Результаты:
Возможность получения суммы 3: 1/216 = 0,0046 × 100 = 0,5%
Возможность получения суммы 4: 3 /216 = 0,0138 × 100 = 1,4%
Возможность получить сумму 5: 6/216 = 0,0277 × 100 = 2,8%
Возможность получения суммы 6: 10/216 = 0,0462 × 100 = 4,6%
Возможность получения суммы 7: 15/216 = 0,069 × 100 = 7,0%
Возможность получения суммы 8: 21/216 = 0,097 × 100 = 9,7%
Возможность получения суммы 9: 25/216 = 0,115 × 100 = 11,6%
Возможность получения суммы 10: 27/216 = 0,125 × 100 = 12,5%
Возможность получить сумму 11: 27/216 = 0,125 × 100 = 12,5%
Возможность получить сумму 12: 25/216 = 0,115 × 100 = 11,6%
Возможность получения суммы 13: 21/216 = 0,097 × 100 = 9,7%
Возможность получения суммы 14: 15/216 = 0,069 × 100 = 7,0%
Возможность получения суммы 15: 10/216 = 0,0462 × 100 = 4,6%
Возможность получения суммы 16: 6/216 = 0,0277 × 100 = 2,8%
Возможность получения суммы 17: 3/216 = 0,013 × 100 = 1,4%
Вероятность получения суммы 18: 1/216 = 0,0046 × 100 = 0,5%
Как видно, крайние значения 3 и 18 наименее вероятны. Наиболее вероятны суммы, находящиеся посередине.
Примеры задач
Вопрос 1: Брошены три кости. Найдите вероятность того, что в сумме выпадет 5.
Решение:
Одновременно бросают три кости, количество достижимых результатов может быть 6 ³ = (6 × 6 × 6) = 216, потому что каждая кость имеет от 1 до 6 чисел на своих точках.
Количество благоприятных событий получения суммы 5 = 6
т.е., (1, 1, 3), (1, 3, 1), (3, 1, 1), (2, 2, 1), (2, 1, 2) и (1, 2, 2)
Таким образом, вероятность наступления всего 5
P(A) = {Количество благоприятных событий} ⁄ {количество всех событий}
= 6/216
= 1/36
Вопрос 2: Три кости бросают вместе. Найти вероятность того, что в сумме выпадет почти 5.
Решение:
Одновременно бросают три кости, количество достижимых исходов может быть 6 ³ = (6 × 6 × 6) = 216 потому что каждая кость имеет от 1 до 6 чисел на своих точках.
Количество событий, происходящих всего не более 5 = 10
т. е. (1, 1, 1), (1, 1, 2), (1, 2, 1), (2, 1, 1), ( 1, 1, 3), (1, 3, 1), (3, 1, 1), (2, 2, 1) и (1, 2, 2).
Таким образом, вероятность наступления в общей сложности не более 5
P(E) = {Количество благоприятных событий} ⁄ {количество всех событий}
= 10/216
= 5/108
3 Вопрос : бросают вместе три игральные кости. Найдите вероятность того, что в сумме выпадет не менее 5,9.0010
Решение:
Одновременно бросаются три кости, количество достижимых результатов может быть 6 ³ = (6 × 6 × 6) = 216, потому что на каждой кости выпадает от 1 до 6 чисел. .
Количество случаев, когда всего меньше 5 = 4
т. е. (1, 1, 1), (1, 1, 2), (1, 2, 1) и (2, 1, 1).
Таким образом, вероятность того, что всего произойдет меньше 5
P(E) = {Количество благоприятных событий } ⁄ {Количество всех событий}
= 4/216
= 1/54
Таким образом, вероятность выпадения не менее 5 = 1 – P (всего меньше 5)
= 1 – 1/54
= ( 54 – 1)/54
= 53/54
Вопрос 4: Брошены три игральные кости. Найдите вероятность того, что в сумме выпадет 6.
Решение:
Одновременно бросают три кости, количество достижимых результатов может быть 6 ³ = (6 × 6 × 6) = 216, потому что каждая кость имеет от 1 до 6 чисел на своих точках.
Количество событий всего 6 = 10
т. е. (1, 1, 4), (1, 4, 1), (4, 1, 1), (1, 2, 3), (1 , 3, 2), (2, 1, 3), (2, 3, 1), (3, 1, 2), (3, 2, 1) и (2, 2, 2).
Таким образом, вероятность наступления всего 6
P(E) = {количество благоприятных событий} ⁄ {количество всех событий}
= 10/216
= 5/108
Вопрос 5: Три кости бросают вместе. Найдите вероятность того, что в сумме выпадет 8.
Решение:
Три кости бросаются одновременно, количество достижимых результатов может быть 6 ³ = (6 × 6 × 6) = 216, потому что на каждой кости на точках выпадает от 1 до 6 чисел.
Количество событий всего 8 = 21
т. е. (2, 2, 4), (4, 2, 2), (2, 4, 2), (1, 5, 2), (2) , 5, 1), (5, 1, 2), (2, 1, 5), (1, 2, 5), (3, 3, 2), (3, 2, 3), (2, 3) , 3) и так далее…
Таким образом, вероятность наступления всего 8
P(E) = {Количество благоприятных событий } ⁄ {Количество всех событий}
= 21/216

Событие и вероятность [MathWiki]
Давайте начнем с простого эксперимента, бросив обычную шестигранную игральную кость на совершенно плоской поверхности.
Исход может быть один, два, три, четыре, пять (как на картинке) или шесть. Если мы бросьте кости, всегда выпадает один из этих шести исходов, т.е. можно найти каждый результат броска костей в списке. И каждый из этих результатов исключает другие, т.е. г., если выпадет пятерка, мы не могли получить в одно и то же время два или шесть или любой другой из перечисленные исходы (у нас всего один кубик, а он показывает пять). Исходы эксперимента/процесса со случайными результатами, обладающими такими свойствами, называются элементарные события . Таким образом, при обычном броске шестигранной кости один, два, три, четыре, пять и шесть являются элементарными событиями.
Обратите внимание, что один и тот же эксперимент/процесс может иметь множество различные наборы элементарных событий в зависимости от что хотел померить. Например, пусть у нас есть две пустыни: пустыня 1 и пустыня 2. И мы не в состоянии выбрать, что съесть, однако, один должен быть выбран. Если бы у нас оказалась одна и та же шестигранная игральная кость, и мы хотим использовать ее для выбора между пустынями мы можем определить элементарные события броска костей просто нечетный (имеется в виду десерт 1) и четный (имеется в виду десерт 2). Это также элементарное событие броска шестигранной кости, так как с каждым броском всегда появляется один из этих двух результатов. И результат броска одновременно могут быть как нечетными, так и четными, т. е. исходы исключают друг друга.
Приведите пример множества исходов броска игральной кости, которые нельзя использовать в качестве элементарных событий. Ответ Результат
$1:=$ «результат кратен $3$» и результат
$2:=$ «результат кратен $2$».
В таком случае при выпадении $1$ или $5$ результат не не принадлежат ни к одному из этих исход, как если бы мы бросали кости, у нас вообще не было результата. И, выбрасывая $6$, мы получаем оба результата одновременно, так как $6$ кратно $2$, а также $3$.
Обозначим через $\Omega$ множество элементарных событий некоторого эксперимента/процесса со случайными исходами. В нашем примере мы фиксируем $\Omega=\{1,2,3,4,5,6\}$.
Что такое $\Omega$ в случае
подбрасывание двусторонней монеты; Ответ $\Omega=\{\text{орел},\text{решка}\}$
выбор карты из стандартного набора; Ответ $\Omega$ — колода карт по $52$
выбор точки из единичного интервала $[0, 1]$. Ответ $\Omega=[0, 1]$
Подмножество $A$ в $\Omega$ называется событием .
Таким образом, событие – это любой факт, который может произойти в результате эксперимента/процесса. Он состоит из элементарных событий. Элементарное событие — это «наименьшее» возможное событие.
Например, $A:=\text{«выбрасываем пятерку»}$ — это событие (тоже элементарное событие), а $B:=\text{«исход кратен 3»}$ — событие, состоящее из двух элементарных событий (т. е. значение равно $3$ или $6$). Событие $B$ не является элементарным событием.
Приведите несколько примеров событий, касающихся:
подбрасывание монеты; Ответ $A:=\text{«мы бросаем решку»}$
выбор карты из стандартного набора; Ответ $A:=\text{«мы выбираем лицевую карту»}$
погода завтра; Ответ $A:=\text{«завтра дождь»}$
безопасность системы. Ответ $A:=\text{«злоумышленник входит в систему без авторизации»}$
Пусть у нас есть алгоритм, в котором $x$ вычисляется броском игральной кости:
$x\leftarrow\{1,2,3,4,5,6\}$
, если $2$ делит $x$, возвращается $0$
если $3$ делится на $x$, вернуть $0$
вернуть $1$.
Какие события дают результат $0$? Ответ Выход $0$ задается событиями $\text{«2 делит}\ x \text{«}$ и $\text{«3 деления}\ x \text{«}$.
Какие события дают результат $1$? Ответ Выход $1$ задается событием $\text{«2 и 3 не делятся}\ x \text{«}$.
Опишите события с точки зрения элементарных событий. Отвечать $\text{«2 деления}\ x \text{«}=\{2, 4, 6\}$, $\text{«3 деления}\ x \text{«}=\{3, 6\} $, $\text{«2 и 3 не делятся}\ x \text{«}=\{1, 5\}$
В начале эксперимента/процесса со случайными результатами мы не знаем, каким будет результат. Однако мы можем описать результат, перечислив все элементарные события (если их конечное множество) и присвоение каждому элементарному событию вероятности.
Вероятность — это числовой показатель между $0$ и $1$ показывает, насколько вероятно событие.
Вероятность $0$ означает, что событие никогда не произойдет, а вероятность $1$ означает, что событие произойдет. Конечно.
Например, вероятность события $A:=\text{«мы выбрасываем семерку»}$ равна $0$ (обозначается: $\text{Pr}[A]=0$) для обычных шестигранных игральных костей . И если $A:=\text{«мы бросаем число, меньшее или равное 6»}$, тогда $\text{Pr}[A]=1$, так как одно из элементарных событий $1$, $2$, $3$, $4$, $5$, $6$ происходит всегда, если кости брошены.
Для любого эксперимента/процесса со случайными результатами
сумма вероятностей всех элементарных событий всегда равна $1$.
Это свойство можно использовать для вычисления вероятности некоторого события. Например, таблица ниже показывает вероятности состояний машин на фабрике, и мы хотим знать, каково недостающая вероятность.
Состояние машин Вероятность
Доступен для использования, используется
Доступен для использования, не используется 0,09
В разобранном виде 0,03
Отмечая, что «доступно для использования, используется», «доступно для использования, но не используется», «разбитые» определяют все элементарные события, отсутствующие вероятности $\text{Pr}[\text{«доступен для использования, используется»}]=1-0,09-0,03=0,88$.
Если вероятность того, что машины будут доступны для использования, равна $0,92$, то какова вероятность того, что машины разваливается? Ответ $\text{Pr}[\text{«машины сломаны»}]=1-0,92=0,08$
Какова вероятность того, что эксплойт не сработает?
Ответ $\text{Pr}[\text{«сбой эксплойта»}]=1-0,1-0,52=0,38$
Теперь давайте найдем вероятности элементарных событий нашего броска костей. Давайте начнем с того, что просто бросим кости и считая, сколько раз мы получаем каждое элементарное событие.
Частное $\frac{\text{количество единиц (как количество событий)}}{\text{количество бросков}}$ описывает вероятность того, что мы получим $1$ при броске костей и оценивает вероятность $\text{Pr}[A]$, где $A:=\text{«мы бросаем единицу»}$. То же верно и для других элементарных событий. Как вы видете из таблицы выше (ВНИМАНИЕ! количество рулонов должно быть достаточно большим), все элементарные события должны быть равновероятными. Учитывая, что вероятности все равны, их $6$, а сумма вероятности элементарных событий всегда $1$, получаем для броска костей
$1$ 9041
$A$ $1$ $2$ $3$ $4$ $5$
$\text{Pr}[A]$ $\frac{1}{6}$ $\frac{1}{6}$ $\frac{1}{6}$ $\frac{1}{6}$ $\frac{1}{6}$ $\frac{1}{6}$
Такая таблица (элементарные события с вероятностями) называется распределение вероятностей эксперимента/процесса (в нашем случае распределение вероятностей броска костей). Он описывает результат эксперимента/процесса со случайными результатами.
Если число элементарных событий конечно и они равновероятны (т.е. с равными вероятностями), то вероятность события $A$ равна
$$\text{Pr[A]}=\frac{\text{количество элементарных событий в}\ A}{\text{количество всех элементарных событий}}$$
Она называется формулой классической вероятности.
Таким образом, действительно, $P[\text{«мы выбрасываем единицу»}]=\frac{1}{6}$. И, например, $P[\text{«результат нечетный»}]=\frac{3}{6}=\frac{1}{2}$, так как событие состоит из $3$ элементарных события: $1$, $3$ и $5$.
Присвойте вероятности следующим событиям:
получение «Королевы» путем случайного взятия карты из полной колоды игральных карт номиналом $52$; Ответ В колоде $4$ ферзя, поэтому $\text{Pr}[\text{«получение ферзя»}]=\frac{4}{52}=\frac{1}{13}$
получение красных конфет путем случайного выбора конфет из пакета конфет, содержащего красные конфеты по 18$, зеленые конфеты по 12$ и желтые конфеты по 10$; Ответ Общее количество конфет в пачке $40$ и $18$ красных, поэтому $\text{Pr}[\text{«получение красных конфет»}]=\frac{18}{40}=\frac{ 9}{20}$
выбор четного числа случайным образом из чисел от $1$ до $11$. Ответ Существует $5$ четных чисел от $1$ до $11$, поэтому $\text{Pr}[\text{«выбор четного числа»}]=\frac{5}{11}$
Чтобы полностью понять допущение «элементарные события равновероятны» в формуле классического вероятности, заменим шестерку на кубике другой пятеркой ($\Omega=\{1,2,3,4,5\}$). Тогда здравый смысл подсказывает, что $5$ должно встречаться в два раза чаще затем другие исходы (на костях две пятерки, а все остальные исходы только один раз). Таким образом, не все элементарные события равновероятны. Если мы по-прежнему пытаемся использовать формулу классической вероятности получаем $\text{Pr}[\text{«мы выбрасываем пятерку»}]=\frac{1}{5}$. Однако правильное распределение вероятностей для такой кости равно
$A$ $1$ $2$ $3$ $4$ $5$
$\text{Pr}[A]$ $\frac{1}{6}$ $\frac{1}{6}$ $\frac{1}{6}$ $\frac{1}{6}$ $\frac{2}{6}$
Результат получается, если заметить, что кости имеют 6 различных сторон, которые равновероятны. Таким образом, событие $\text{«мы выбрасываем пятерку»}$ означает две стороны из шести.
У Боба на полке есть рабочие видеокарты за 5 долларов и нерабочая за 2 доллара. Он не знает, какие из них какие, поэтому он спрашивает 3 друга (чтобы быть уверенным), какова вероятность того, что получить нерабочий, просто взяв один с полки? Одноклассник согласился купить рабочий и Боб хочет приложить к сделке минимум усилий.
Мэри говорит: «Это $\frac{1}{2}$, потому что видеокарта либо работает, либо не работает».
Дэн говорит: «Это $\frac{2}{5}$, потому что есть $5$ рабочих видеокарт и $2$ нерабочих».
Алиса говорит: «Это $\frac{2}{7}$, потому что есть видеокарты за $7$, а $2$ не работают».
Кто из друзей Боба прав? Какие ошибки совершают те, кто не прав?
Ответ Алисе
Какова вероятность случайного выбора буквы «О» из следующих слов:
ШКОЛА Ответ Эксперимент в данном случае имеет неравновероятные исходы — буква «О» встречается в 2 раза чаще остальных букв, поэтому $\text{Pr}[\text{«получаем О»}]= \frac{2}{6}=\frac{1}{3}$.
No related posts.